Classifying the degree of exposure of customers to COVID-19 in the restaurant industry: A novel intuitionistic fuzzy set extension of the TOPSIS-Sort

Abstract

Despite the rigid public safety protocols of the restaurant sector amid the COVID-19 pandemic in an effort to restart economic activities, customers do not feel secure eating at a sit-in restaurant, which is associated with prolonged restrictions on movement. As a mitigating initiative, holistically evaluating customers’ perceived degree of exposure to COVID-19 in restaurants is deemed relevant in the design of mitigation measures. Such an agenda is associated with multiple attributes under decision-making uncertainty within the framework of multiple criteria sorting (MCS). Thus, this work addresses this problem domain by proposing an intuitionistic fuzzy set extension of the previously developed TOPSIS-Sort (i.e., IF TOPSIS-Sort). As a case demonstration, 40 restaurants are evaluated under six attributes that define exposure to COVID-19. With 250 survey participants, the IF TOPSIS-Sort assigns 10, 13, and 17 restaurants to low, moderate, and high exposure classes, respectively. With this classification, crucial insights are offered to the restaurant industry for planning and policy formulation. To determine its effectiveness, a comparative analysis was carried with other distance-based MCS methods. Findings reveal that the proposed method is pessimistic and that other methods tend to underestimate the assignments, which may be counterintuitive, especially in applications related to public health. These sorting differences may be associated with addressing the vagueness and uncertainty in decision-making within the IF TOPSIS-Sort platform. The proposed novel IF TOPSIS-Sort is sufficiently generic for other domain sorting applications and contributes to the MCS literature.

1. Introduction

At the end of 2019, reported cases of pneumonia appeared in China and were later named as novel coronavirus disease (COVID-19) [1]. Since then, the virus has spread worldwide, prompting the World Health Organization to declare a state of a pandemic on 11 March 2020 [2]. The COVID-19 pandemic has a massive impact on overall healthcare systems, with a direct influence on every area of human life, including the socio-economic conditions in almost all countries. It has a remarkable detrimental effect on multiple dimensions, not just the disease itself but also the global economy. The governments in many countries have established border closures, travel restrictions, and quarantines to ’flatten the curve’ [3] and control the spread of the virus. Several governments have implemented partial or total closure on most of its hospitality businesses, including restaurants, while in other areas, it has been allowed to operate for obvious economic reasons. There were reports that, amidst the need for social distancing and limited human traffic, the restaurant industry is one of the worst industries affected by the COVID-19 outbreak [4]. The prospect for the future of restaurants is unwelcoming, with analysts predicting that more than half of restaurants would not survive [5]. A strategic shift to sustain market appeal throughout the crisis caused by the pandemic is of vital significance [6].

As the deficit in the hospitality sector is comparatively high because of the high operational costs, the viability of many hospitality businesses relies heavily on the growing demand for their goods and services [7]. Given the limitations of businesses, there is an immediate need to provide incentives and relief through various compromise initiatives, such as grants, tax cuts, and debt reduction cuts, among others. In addition, as more countries partially open lockdowns, restaurants, and food establishments, there is a need to change sitting arrangements and procedures in such a way as to have a degree of protection and a sense of safety to customers [8]. Such measures include using contactless menu boards, a payment system, regularly scheduled sanitization of tables, health checks of diners, offering special offers, and business promotions to boost and obtain more customers [9]. Despite measures on stimulating more customers, restaurants must still minimize the number of people, especially in the indoor environment. Current findings suggest that the lesser the people, the lower the concentration of airborne virus-carrying particles [10]. The more an individual interacts with others, and the longer that interaction is, the higher the risk of COVID-19 spread. The risk of spread increases depending on the type of food establishment, from lowest to highest risk, from take-out fast-food restaurant to a food establishment that is not spaced at least six feet apart, respectively. Furthermore, personal prevention practices (e.g., handwashing), ventilation system, environmental cleaning, and disinfection are essential in reducing exposure [11].

Despite the rigid safety protocol actions of hotels and restaurants, customers generally do not feel secure eating at a sit-in restaurant, flying to a destination, and staying at a hotel during this pandemic [12]. As lockdown restrictions are lifted, restaurant and food industries with low home-based work capabilities and high face-to-face interactions are likely to experience slower recoveries as consumers might be apprehensive about patronizing them [13]. However, customer sentiment analysis study shows that a substantial portion of restaurant customers (64.71%) and a significant percentage of customers (70.42%) agree that the use of different technologies in the delivery of services would be necessary for the COVID-19 setting to reduce human-to-human interaction (e.g., robotic service systems, electronic payment such as pay or contactless bank cards, digital menu options that can be accessed on smartphones and other mobile devices using QR codes, contactless digital transfers, keyless access, touchless elevators) [12]. The results indicate that incorporating and implementing new technologies into restaurant and food operations is likely to be crucial in the foreseeable future. From a general exposure point of view, these virus-enforced changes affect restaurants in several aspects of the hospitality industry.

While the hospitality industry gears on the infrastructure end of the continuum of challenges brought about by the effort of containing the spread, the customer end approach is not well explored in the literature. One crucial aspect of this domain, particularly in restaurants, is the vague understanding of the customers on the overall condition of the restaurant in terms of customers’ perceived exposure to COVID-19. Such an evaluation that promotes inclusive understanding across many dimensions would mitigate the fear of customers in restaurant visits, as a holistic view of their COVID-19 exposure becomes available to them. On the restaurant side, such an evaluation provides crucial information on designing mitigation strategies to improve customers’ perception of their exposure when dining. Thus, this agenda is expected to help initiate the recovery of the restaurant industry. Collectively, this question becomes relevant: “How do customers evaluate their perceived degree of exposure to COVID-19 in different restaurants?” Although a similar problem domain was espoused by Yamagishi and Ocampo [14] and Ocampo and Yamagishi [15] in the case of tourist sites, the emerging domain literature has not explored such a research question. Thus, this work advances this gap by offering a methodology in classifying a pre-defined number of restaurants according to how customers perceive their degree of exposure to COVID-19. Such an initiative requires a complex evaluation of multiple, even conflicting, attributes that define the perceived degree of exposure. Under multiple attributes, the evaluation becomes holistic and responsive to the needs of the customers and the restaurant value chain. With this, a multiple criteria sorting method (MCS) is proposed in this work. In an MCS problem, alternatives (e.g., restaurants) are assigned to one or more of a finite and completely ordered set of homogeneous decision classes (e.g., perceived degrees of exposure) based on evaluations of multiple attributes [16], [17]. The classes considered here are ordered and pre-defined for the assignment of the alternatives. The semantic definition of the classes depends on the sorting domain under consideration [17].

Based on the four classifications of Roy [18], sorting problems are under a group of methods known as classification problems. These problems involve assigning a set of alternatives to homogeneous classes [19], and various multi-attribute decision-making (MADM) methods were proposed to address these problems. Ishizaka and Nemery [20] have distinguished three types of classification methods: (1) nominal classification methods, (2) sorting methods, and (3) clustering or unsupervised classification methods. The first type involves the assignment of alternatives to pre-defined classes with no preference order. This contrasts with sorting methods, where the action involves assigning alternatives to completely ordered pre-defined classes. The complete preference structure is provided by the decision-makers, arranged from best to worst. Finally, the clustering methods extract the clusters or classes from the dataset (i.e., not pre-defined). In the sorting methods, the classes are defined either by limiting profiles or by one or several reference actions (i.e., central profiles) [21].

Some MCS methods based on MADM include ELECTRE TRI [22], PROMETHEE TRI [23], PROMSORT [24], [25], FlowSort [26], ELECTRE TRI-C [27], THESEUS [28], AHPSort [29], ELECTRE-SORT [20], FlowSort-GDSS [30], Fuzzy FlowSort [31], TOPSIS-Sort [32], AHPSort II [33], GAHPSort [21], FAHPSORT [34], MACBETHSort [35], VIKORSORT [36], and CODAS-SORT [37]. Note that the list is not intended to be comprehensive. This work contributes to the soft computing literature by further extending the efficacy of the TOPSIS-Sort as an MCS method. TOPSIS, proposed by Hwang and Yoon [38], selects the best alternative with the shortest Euclidean distance from the positive-ideal solution and the longest distance from the negative ideal solution. Among several extensions of the TOPSIS method, the integration of the intuitionistic fuzzy set (IFS) theory proposed by Atanassov [39] gains prominence in the current literature. IFS theory is a generalization of the fuzzy set theory proposed by Zadeh [40], which handles vagueness and uncertainty in computing. While the classical fuzzy set theory introduces a membership function, the IFS extends this concept to include a non-membership function. The first formulation of the intuitionistic fuzzy TOPSIS (IF-TOPSIS) approach was presented by Boran et al. [41], applied in a supplier selection problem. Since then, several applications were reported, with some formulations having a certain degree of modifications. These include applications in evaluating renewable energy technologies [42], advanced manufacturing technology [43], smartphone selection [44], alternative vehicle technologies [45], supplier selection of problems [46], [47], investment selection [48], rural logistics center location [49], site selection of wind power plants [50], sustainable supplier selection [51], [52], and credit risk application [53].

As an extension of TOPSIS, TOPSIS-Sort was developed as an MCS approach. Recently, a similar application of the TOPSIS-Sort in evaluating the perceived exposure of tourists to COVID-19 in tourist sites was reported by Yamagishi and Ocampo [14]. However, the main drawback of the formulation of Sabokbar et al. [32], including the extensions developed recently by de Lima Silva and de Almeida Filho [54] and de Lima Silva et al. [55], is that evaluation of the items for sorting does not address vagueness and uncertainty usually present in eliciting judgments. Thus, this work explores the integration of IFS theory within the framework of TOPSIS-Sort. As the current literature has not explored such integration, this work is the first attempt to develop such a computational procedure. To demonstrate the proposed novel approach, a case study of sorting restaurants as to the customers’ perceived degree of exposure to COVID-19 is carried out in this work. This work is the first of its kind in addressing (1) the use of intuitionistic fuzzy (IF) TOPSIS-Sort in the public health domain, and (2) the application of such novel methodology in aiding economic recovery amidst the COVID-19 pandemic. It advances the emerging literature of COVID-19 by assisting the restaurant value chain in further maintaining public health while slowly reopening the industry. Finally, it contributes to the MCS literature by proposing a novel IFS extension of the TOPSIS-Sort.

The remainder of the paper is as follows: Section 2 provides some preliminaries of TOPSIS, IFS, and TOPSIS-Sort. Section 3 presents a background of the case study and demonstrates the proposed IF TOPSIS-Sort approach in sorting restaurants for perceived exposure of customers to COVID-19. Comparisons of the results with the traditional TOPSIS-Sort, as well as other recently proposed distanced-based MCS methods, are described in Section 4. A discussion of the findings is highlighted in Section 5. It ends with a conclusion and discussion of future work in Section 6.

2. Preliminaries

2.1. The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)

When decision-makers are confronted with problems that involve evaluations of a collection of pre-defined alternatives under multiple attributes (or criteria), MADM methods offer a robust set of tools. Within the MADM context, Roy [18] described four problem formulations: (1) choice problems, (2) sorting problems, (3) ranking problems, and (4) description problems. Please refer to Roy [18] for the discussion of these formulations. TOPSIS is a member of a family of MADM methods within the choice problem formulation. Initially introduced by Hwang and Yoon [38], TOPSIS selects the best alternative from a finite collection of homogeneous alternatives evaluated under a finite set of decision attributes (or criteria). The fundamental principle of TOPSIS is that the best alternative should have the shortest distance from the positive-ideal solution and have the longest distance from the negative-ideal solution generated from the domain decision problem. The positive-ideal solution maximizes the maximization-seeking criteria (or benefits criteria) and minimizes the minimization-seeking (or cost criteria). In contrast, the negative-ideal solution maximizes the cost criteria and minimizes the benefit criteria [38]. This method has been applied in various domain applications in the literature. Due to its prominence, multiple reviews on the applications of the original TOPSIS formulation (i.e., excluding its extensions) have been reported by Behzadian et al. [56], Shukla et al. [57], Yadav et al. [58], and Divya et al. [59].

Under a group decision-making environment of $G$ decision-makers, the computational steps of the TOPSIS method are the following:

• 1.Construct a decision matrix $X^k={\left(x_{ij}^k\right)}_{m\times n}$, with $x_{ij}^k$ representing the evaluation score of the $i$th alternative ($i=1,2,\dots ,m$) on the $j$th criterion ($j=1,2,\dots ,n$) elicited by the decision-maker $k=1,2,\dots ,G$.
• 2.Aggregate the decision matrices $X^k$ into $X={\left(x_{ij}\right)}_{m\times n}$ using a pre-defined aggregation function (e.g., weighted mean).
• 3.
  Calculate the normalized decision matrix $R={\left(r_{ij}\right)}_{m\times n}$ using Eq. (1).

  $$r_{ij}=\raisebox{1ex}{$x_{ij}$}\!\left/ \!\raisebox{-1ex}{${\left(\sum _{i=1}^m{x}_{ij}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$}\right.\forall i,j$$ (1)
• 4.
  Obtain the weighted normalized decision matrix $V={\left(v_{ij}\right)}_{m\times n}$ using Eq. (2)

  $$v_{ij}=r_{ij}\times w_j\forall i,j$$ (2)

  where $w_j>0,{\sum }_{j=1}^n{w}_j=1$ represents the priority weight of criterion $j$ via a pre-defined prioritization (i.e., weight-generating) method.
• 5.
  Determine the positive-ideal ($A^{+}$) and negative-ideal ($A^{-}$) solutions, using Eqs. (3), (4), respectively.

  $$A^{+}=\left\{\left(\underset{i}{max}{v}_{ij}|j\in C_b\right),\left(\underset{i}{min}{v}_{ij}|j\in C_c\right)\right\}=\left\{v_j^{+}|j=1,2,\dots ,n\right\}$$ (3)

  $$A^{-}=\left\{\left(\underset{i}{min}{v}_{ij}|j\in C_b\right),\left(\underset{i}{max}{v}_{ij}|j\in C_c\right)\right\}=\left\{v_j^{-}|j=1,2,\dots ,n\right\}$$ (4)

  where $C_b$ is the set of benefit (or maximization-seeking) criteria while $C_c$ represents the set of cost (or minimization-seeking) criteria.
• 6.
  Calculate the separation measures using an $m$-dimensional Euclidean distance. The separation measures of each alternative from the positive-ideal solution (i.e., $S_i^{+}$) and the negative-ideal solution (i.e., $S_i^{-}$), respectively, are as follows:

  $$S_i^{+}={\left(\sum _{j=1}^n{\left(v_{ij}-v_j^{+}\right)}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\forall i$$ (5)

  $$S_i^{-}={\left(\sum _{j=1}^n{\left(v_{ij}-v_j^{-}\right)}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\forall i$$ (6)
• 7.
  Using Eq. (7), obtain the relative closeness coefficient ($R{C}_i$) of the alternative $i$.

  $$R{C}_i=\frac{S_i^{-}}{S_i^{+}+S_i^{-}}\forall i$$ (7)
• 8.Rank the $R{C}_i$ values in decreasing order. The best alternative $i$ has the largest $R{C}_i$ value.

2.2. Intuitionistic fuzzy set (IFS) theory

Introduced by Atanassov [39], the intuitionistic fuzzy set (IFS) theory is a generalization of the classical fuzzy set theory (FST) proposed by Zadeh [40] in handling vagueness and uncertainty in computing information. While the FST only introduces a membership function, the IFS theory is characterized by a membership function, a non-membership function, and a hesitancy degree that respectively express support, opposition, and neutrality in eliciting information [39]. Such characteristics offer a significant advantage over the FST as they can better reflect the vagueness of decision-making, particularly when eliciting judgment. Govindan et al. [60] detailed three main benefits of the IFS theory under a decision-making environment. First, it offers the ability to model unknown information via the degree of hesitation. In the practical application (e.g., COVID-19 pandemic), decision-makers are usually unsure about their preferences, and the IFS theory is more suitable in extracting such preferences (i.e., opinions) than the FST. Secondly, it is characterized by three grades of information that can better capture uncertainty. Finally, the traditional FST only handles the degree of “agreement” but fails to represent the degree of “disagreement”, often depicted in eliciting judgments.

The following provides some fundamental concepts of the IFS relevant in this work.

Definition 1 [40] —

Suppose $X$ is a finite, non-empty set. The set of 2-tuple $A=\left\{x,{\mu }_A\left(x\right):x\in X,{\mu }_A\left(x\right)\in \left[0,1\right]\right\}$ is a fuzzy set where ${\mu }_A\left(x\right)$ is a membership function of $x$ in $A$.

Definition 2 [61] —

A triangular fuzzy number can be defined as a triplet $A=\left(l,m,u\right)$ and the membership function ${\mu }_A\left(x\right)$ is as follows:

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}\hfill 0\hfill & \hfill x<l\hfill \\ \hfill \left(x-l\right)/\left(m-l\right)\hfill & \hfill l\le x\le m\hfill \\ \hfill \begin{array}{c}\hfill \left(u-x\right)/\left(u-m\right)\hfill \\ \hfill 0\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill m\le x\le u\hfill \\ \hfill x>u\hfill \end{array}\hfill \end{array}\right\}.$$ (8)

Definition 3 [39] —

Suppose $X$ is a finite, non-empty set. Then an IFS $A$ in $X$ is defined as

$$A=\left\{〈x,{\mu }_A\left(x\right),v_A\left(x\right)〉:x\in X\right\},$$ (9)

where ${\mu }_A\left(x\right):X\to \left[0,1\right]$ and $v_A\left(x\right):X\to \left[0,1\right]$ such that $0\le {\mu }_A\left(x\right)+v_A\left(x\right)\le 1,x\in X$. ${\mu }_A\left(x\right)$ and $v_A\left(x\right)$ represent the membership function and the non-membership function, respectively, of $x\in X$ to $A$. ${\pi }_A\left(x\right)$ expresses the degree of lack of knowledge of every $x\in X$ to $A$, and $0\le {\pi }_A\left(x\right)\le 1$. ${\mu }_A\left(x\right)$, $v_A\left(x\right)$, and ${\pi }_A\left(x\right)$ follow Eq. (10)

$${\pi }_A\left(x\right)=1-{\mu }_A\left(x\right)-v_A\left(x\right),x\in X.$$ (10)

${\pi }_A\left(x\right)$ is also referred to as the intuitionistic index of $x$ in $A$.

Definition 4 [62] —

For a fixed universe $E$, the IFS $A$ can be interpreted as a mapping $E\to \left[0,1\right]\times \left[0,1\right]$ and it can be defined by a 2-tuple $〈{\mu }_A\left(x\right),v_A\left(x\right)〉$ where for $x\in E$, ${\mu }_A\left(x\right)$ denotes the degree of membership of $x$ and $v_A\left(x\right)$ denotes the degree of non-membership of $x$ to $A$; and ${\mu }_A\left(x\right)$ and $v_A\left(x\right)$ satisfy the condition ${\mu }_A\left(x\right)+v_A\left(x\right)\le 1$. The set $B$ is a standard fuzzy subset when ${\mu }_A\left(x\right)+v_A\left(x\right)=1$. The crispification operation is a mapping of $\left[0,1\right]\times \left[0,1\right]\to \mathbb{R}$. Here, $E=\mathbb{R}$ for IFS.

2.3. Intuitionistic fuzzy TOPSIS

The steps of the IF-TOPSIS formulation proposed by Boran et al. [41] are detailed as follows:

• 1.
  Construct an individual IF decision matrix ${\tilde{X}}^k={\left({\tilde{x}}_{ij}^k\right)}_{m\times n}$ for each decision-maker $k$. It is represented as:

  $${\tilde{X}}^k=\left(\begin{array}{ccc}\hfill \left({\mu }_{11}^k,v_{11}^k,{\pi }_{11}^k\right)\hfill & \hfill \left({\mu }_{12}^k,v_{12}^k,{\pi }_{12}^k\right)\hfill & \hfill \begin{array}{cc}\hfill \cdots \hfill & \hfill \left({\mu }_{1n}^k,v_{1n}^k,{\pi }_{1n}^k\right)\hfill \end{array}\hfill \\ \hfill \left({\mu }_{21}^k,v_{21}^k,{\pi }_{21}^k\right)\hfill & \hfill \left({\mu }_{22}^k,v_{22}^k,{\pi }_{22}^k\right)\hfill & \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{2n}^k,v_{2n}^k,{\pi }_{2n}^k\right)\hfill \end{array}\hfill \\ \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{m1}^k,v_{m1}^k,{\pi }_{m1}^k\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{m2}^k,v_{m2}^k,{\pi }_{m2}^k\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill \ddots \hfill & \hfill ⋮\hfill \end{array}\hfill \\ \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{mn}^k,v_{mn}^k,{\pi }_{mn}^k\right)\hfill \end{array}\hfill \end{array}\hfill \end{array}\right)$$ (11)

  where ${\tilde{x}}_{ij}^k=\left({\mu }_{ij}^k,v_{ij}^k,{\pi }_{ij}^k\right)$, ${\pi }_{ij}^k=1-{\mu }_{ij}^k-v_{ij}^k$, is an IFS representation.
• 2.
  Aggregate the IF decision matrices into $\tilde{X}={\left({\tilde{x}}_{ij}\right)}_{m\times n}={\left(\left({\mu }_{ij},v_{ij},{\pi }_{ij}\right)\right)}_{m\times n}$ with the use of the IFWA operator proposed by Xu [63]. ${\tilde{x}}_{ij}$ is computed using Eq. (12).

  $${\tilde{x}}_{ij}=IFWA\left({\tilde{x}}_{ij}^1,{\tilde{x}}_{ij}^2,\dots ,{\tilde{x}}_{ij}^G\right)=w_1{\tilde{x}}_{ij}^1\oplus w_2{\tilde{x}}_{ij}^2\oplus \cdots \oplus w_G{\tilde{x}}_{ij}^G=\left(1-\prod _{k=1}^G\left(1\right)\right)-\left({\left({\mu }_{ij}^k\right)}^{w_k},\prod _{k=1}^G{\left(v_{ij}^k\right)}^{w_k},\prod _{k=1}^G{\left(1-{\mu }_{ij}^k\right)}^{w_k}-\prod _{k=1}^G{\left(v_{ij}^k\right)}^{w_k}\right)$$ (12)

  where $w_k\in \left[0,1\right]$, ${\sum }_{k=1}^G{w}_k=1$, represents the weight of the decision-maker $k$. For $w_k=\frac{1}{G}$ $\left(k=1,\dots ,G\right)$, the IFWA operator is reduced to an intuitionistic fuzzy averaging (IFA) operator of $G$ dimension, defined as $\text{IFWA}\left({\tilde{x}}_{ij}^1,{\tilde{x}}_{ij}^2,\dots ,{\tilde{x}}_{ij}^G\right)=\frac{1}{G}\left({\tilde{x}}_{ij}^1\oplus {\tilde{x}}_{ij}^2\oplus \cdots \oplus {\tilde{x}}_{ij}^G\right)$.

The aggregate IF decision matrix $\tilde{X}$ is represented in Eq. (13).

$$\tilde{X}=\left(\begin{array}{ccc}\hfill \left({\mu }_{11},v_{11},{\pi }_{11}\right)\hfill & \hfill \left({\mu }_{12},v_{12},{\pi }_{12}\right)\hfill & \hfill \begin{array}{cc}\hfill \cdots \hfill & \hfill \left({\mu }_{1n},v_{1n},{\pi }_{1n}\right)\hfill \end{array}\hfill \\ \hfill \left({\mu }_{21},v_{21},{\pi }_{21}\right)\hfill & \hfill \left({\mu }_{22},v_{22},{\pi }_{22}\right)\hfill & \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{2n},v_{2n},{\pi }_{2n}\right)\hfill \end{array}\hfill \\ \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{m1},v_{m1},{\pi }_{m1}\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{m2},v_{m2},{\pi }_{m2}\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill \ddots \hfill & \hfill ⋮\hfill \end{array}\hfill \\ \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{mn},v_{mn},{\pi }_{mn}\right)\hfill \end{array}\hfill \end{array}\hfill \end{array}\right)$$ (13)

• 3.
  Determine the priority weights of the set of criteria. Assume that the decision-maker $k$ elicits judgment on the importance of criterion $j$ with an IF number, represented by ${\tilde{w}}_j^k=\left({\mu }_j^k,v_j^k,{\pi }_j^k\right)$. The priority weights of the criteria are computed following the IFWA operator of Xu [63]. Eq. (14) represents the required computation:

  $${\tilde{w}}_j=IFWA\left({\tilde{w}}_j^1,{\tilde{w}}_j^2,\dots ,{\tilde{w}}_j^G\right)=w_1{\tilde{w}}_j^1\oplus w_2{\tilde{w}}_j^2\oplus \cdots \oplus w_G{\tilde{w}}_j^G=\left(1-\prod _{k=1}^G\left(1\right)\right)\left({\left(-{\mu }_j^k\right)}^{w_k},\prod _{k=1}^G{\left(v_j^k\right)}^{w_k},\prod _{k=1}^G{\left(1-{\mu }_j^k\right)}^{w_k}-\prod _{k=1}^G{\left(v_j^k\right)}^{w_k}\right)$$ (14)

  Here, ${\tilde{w}}_j=\left({\mu }_j,v_j,{\pi }_j\right)$, $\forall j$.
• 4.
  Establish the weighted IF decision matrix $\widetilde{{\rm Y}}={\left({\tilde{v}}_{ij}\right)}_{m\times n}={\left({\mu }_{{\tilde{v}}_{ij}},v_{{\tilde{v}}_{ij}},{\pi }_{{\tilde{v}}_{ij}}\right)}_{m\times n}$. In this case, ${\tilde{v}}_{ij}={\tilde{x}}_{ij}\otimes {\tilde{w}}_j$ is a product of two IF sets. The following definition of Atanassov [39] governs such operation:

  $${\tilde{x}}_{ij}\otimes {\tilde{w}}_j=\left\{\left(x,{\mu }_{ij}\cdot {\mu }_j,v_{ij}+v_j-v_{ij}\cdot v_j\right)|x\in X\right\}$$ (15)

  and

  $${\pi }_{{\tilde{v}}_{ij}}=1-v_{ij}-v_j-{\mu }_{ij}\cdot {\mu }_j+v_{ij}\cdot v_j$$ (16)

  $\tilde{V}$ is represented in Eq. (17)

  $$\tilde{V}=\left(\begin{array}{ccc}\hfill \left({\mu }_{{\tilde{v}}_{11}},v_{{\tilde{v}}_{11}},{\pi }_{{\tilde{v}}_{11}}\right)\hfill & \hfill \left({\mu }_{{\tilde{v}}_{12}},v_{{\tilde{v}}_{12}},{\pi }_{{\tilde{v}}_{12}}\right)\hfill & \hfill \begin{array}{cc}\hfill \cdots \hfill & \hfill \left({\mu }_{{\tilde{v}}_{1n}},v_{{\tilde{v}}_{1n}},{\pi }_{{\tilde{v}}_{1n}}\right)\hfill \end{array}\hfill \\ \hfill \left({\mu }_{{\tilde{v}}_{21}},v_{{\tilde{v}}_{21}},{\pi }_{{\tilde{v}}_{21}}\right)\hfill & \hfill \left({\mu }_{{\tilde{v}}_{22}},v_{{\tilde{v}}_{22}},{\pi }_{{\tilde{v}}_{22}}\right)\hfill & \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{{\tilde{v}}_{2n}},v_{{\tilde{v}}_{2n}},{\pi }_{{\tilde{v}}_{2n}}\right)\hfill \end{array}\hfill \\ \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{{\tilde{v}}_{m1}},v_{{\tilde{v}}_{m1}},{\pi }_{{\tilde{v}}_{m1}}\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill ⋮\hfill \\ \hfill \left({\mu }_{{\tilde{v}}_{m2}},v_{{\tilde{v}}_{m2}},{\pi }_{{\tilde{v}}_{m2}}\right)\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill \ddots \hfill & \hfill ⋮\hfill \end{array}\hfill \\ \hfill \begin{array}{cc}\hfill \dots \hfill & \hfill \left({\mu }_{mn},v_{mn},{\pi }_{{\tilde{v}}_{mn}}\right)\hfill \end{array}\hfill \end{array}\hfill \end{array}\right)$$ (17)
• 5.
  Determine the IF positive-ideal solution (${\tilde{A}}^{+}$) and the IF negative-ideal solution (${\tilde{A}}^{-}$), using Eqs. (18), (19), respectively.

  $${\tilde{A}}^{+}=\left({\mu }_j^{+},v_j^{+}\right)$$ (18)

  $${\tilde{A}}^{-}=\left({\mu }_j^{-},v_j^{-}\right)$$ (19)

  where

  $${\mu }_j^{+}=\left(\left(\underset{i}{max}{\mu }_{{\tilde{v}}_{ij}}|j\in C_b\right),\left(\underset{i}{min}{\mu }_{{\tilde{v}}_{ij}}|j\in C_c\right)\right)$$ (20)

  $$v_j^{+}=\left(\left(\underset{i}{min}{v}_{{\tilde{v}}_{ij}}|j\in C_b\right),\left(\underset{i}{max}{v}_{{\tilde{v}}_{ij}}|j\in C_c\right)\right)$$ (21)

  $${\mu }_j^{-}=\left(\left(\underset{i}{min}{\mu }_{{\tilde{v}}_{ij}}|j\in C_b\right),\left(\underset{i}{max}{\mu }_{{\tilde{v}}_{ij}}|j\in C_c\right)\right)$$ (22)

  $$v_j^{-}=\left(\left(\underset{i}{max}{v}_{{\tilde{v}}_{ij}}|j\in C_b\right),\left(\underset{i}{min}{v}_{{\tilde{v}}_{ij}}|j\in C_c\right)\right)$$ (23)
• 6.
  Calculate the separation measures $S_{IF}^{+}$ and $S_{IF}^{-}$ using the Euclidean distance defined by Szmidt and Kacprzyk [64]. Eq. (24), (25) presents the required computations:

  $$S_{IF}^{+}=\sqrt{\frac{1}{2n}\sum _{j=1}^n\left({\left({\mu }_{{\tilde{v}}_{ij}}-{\mu }_j^{+}\right)}^2+{\left(v_{{\tilde{v}}_{ij}}-v_j^{+}\right)}^2+{\left({\pi }_{{\tilde{v}}_{ij}}-{\pi }_j^{+}\right)}^2\right)}$$ (24)

  $$S_{IF}^{-}=\sqrt{\frac{1}{2n}\sum _{j=1}^n\left({\left({\mu }_{{\tilde{v}}_{ij}}-{\mu }_j^{-}\right)}^2+{\left(v_{{\tilde{v}}_{ij}}-v_j^{-}\right)}^2+{\left({\pi }_{{\tilde{v}}_{ij}}-{\pi }_j^{-}\right)}^2\right)}$$ (25)

• 7.
  Obtain the relative closeness coefficient ($R{C}_{iIF}$) of the alternative $i$.

  $$R{C}_{iIF}=\frac{S_{IF}^{-}}{S_{IF}^{+}+S_{IF}^{-}}$$ (26)
• 8.Rank the alternatives in decreasing order on the basis of $R{C}_{iIF}^{+}$.

2.4. TOPSIS-sort

The computational steps of the TOPSIS-Sort are discussed in the following. Note that most notations here were lifted from the original formulation of Sabokbar et al. [32]. Assume that a given decision problem consists of $m$ alternatives (e.g., restaurants), $n$ criteria, and $h$ classes $\left\{g_1,g_2,\dots ,g_h\right\}$.

• 1.Assuming that individual decision matrices are aggregated using a pre-defined aggregation method, construct the aggregate decision matrix $X={\left(x_{ij}\right)}_{m\times n}$.
• 2.Define the set of limit profiles of $h$ classes for each criterion, denoted as $P^j=\left\{\left(p_l^{1j},p_u^{1j}\right),\left(p_l^{2j},p_u^{2j}\right),\dots ,\left(p_l^{hj},p_u^{hj}\right)\right\}$, where $\left(p_l^{1j},p_u^{1j}\right)$, $\left(p_l^{2j},p_u^{2j}\right)$, and $\left(p_l^{hj},p_u^{hj}\right)$ are the limit profiles of classes $g_1$, $g_2$, and $g_h$, respectively. The upper limit of class $e=1,2,\dots ,h$ is denoted as $p_u^{ej}$, while the lower limit is denoted as $p_l^{ej}$.
• 3.Add the profiles to the decision matrix, denoted as $\Lambda =\left(X,P\right)={\left({\lambda }_{ij}\right)}_{m\times n}$.
• 4.
  Normalize $\Lambda$ with Eq. (27). The resulting matrix is $\mathrm{E}={\left({\varepsilon }_{ij}\right)}_{m\times n}$.

  $${\varepsilon }_{ij}=\left(\left(\left(\frac{{\lambda }_{ij}}{\underset{\mathit{ij}}{max}{\lambda }_{ij}}\right|j\in C_b\right),\left(1-\left(\frac{{\lambda }_{ij}}{\underset{\mathit{ij}}{max}{\lambda }_{ij}}\right|j\in C_c\right)\right)$$ (27)
• 5.Perform step 3 through step 7 of the traditional TOPSIS method, as discussed in Section 3.1.
• 6.Determine the values of $R{C}_i$ ($\forall i$) of $\mathrm{E}$.
• 7.Obtain the values of $R{C}_j^{p_u^e}$ and $R{C}_j^{p_l^e}$, which denote, respectively, the deviation of the upper limit profile of the class $e$ from the ideal solution and the deviation of the lower limit profile of the class $e$ from the ideal solution.
• 8.
  Compare the $R{C}_i$ values with $R{C}_j^{p_u^e}$ and $R{C}_j^{p_l^e}$ following Eq. (28).

  $$R{C}_j^{p_l^e}<R{C}_i<R{C}_j^{p_u^e}\forall i,e$$ (28)
• 9.The alternatives with $R{C}_i>R{C}_j^{p_l^e}$ and $R{C}_i<R{C}_j^{p_u^e}$ are assigned to class $e$. In this step, all alternatives are assigned to their appropriate classes.

3. Application of the proposed methodology in sorting the degrees of exposure of customers to COVID-19 in restaurants

3.1. Case study

The Philippine consumer sector is projected to be one of the markets severely affected by the government’s countrywide restriction. The National Economic and Development Authority, the socio-economic planning arm of the Philippine government, expects a cumulative loss in gross value added (current prices) of Php 428.7 to Php 1355.6 billion, equivalent to 2.1 to 6.6% of nominal GDP in 2020 [65]. This would indicate a reduction in real GDP growth in the Philippines to −0.6 to 4.3% in 2020 without mitigation strategies. Consequently, timely and sufficient government interventions remain crucial to mitigate the spiral setback of COVID-19. As a response measure, the Philippine government has set out a survival and recovery framework in the proposed legislative bill, which aims to allocate more than Php 160 billion to social development and economic stimulus. The recently approved national budget of Php 4.5 trillion for 2021, 9.9% more than the PHP 4.1 trillion budget for this year which represents 21.8% of the GDP were introduced. Also, the government endorses the Act on Corporate Restructuring and Tax Benefits for Businesses as one of the major economic stimulus programs for post-pandemic recovery. This reform aims to reduce the corporate income tax rate from 30% to 25% to encourage more investment and strengthen the country’s economic ecosystem [66].

Not just in the Philippines but worldwide, the pandemic recession has created ripple effects on the hospitality industry, notably the hotel/restaurant/catering (HORECA) sector, and the commercial restaurant system, resulting in a loss of revenue, consumer traffic, and reputation. These effects are brought about by the prolonged restriction on movement and stigma triggered by the pandemic. To address the stigma, the Philippine government has introduced initiatives to restore confidence and adapt to the “new normal” that would emerge from the country’s response to COVID-19. Such measures aim to promote the collaboration of retail and restaurant owners with delivery service providers to support establishment owners who cannot integrate delivery services into their operations and encourage new players into the delivery services sector [67], [67].

To maintain public health, the Trade and Industry Department [68] introduces the minimum health standards in four recovery domains: physical, information, cognitive, and social, as described by Linkov and Trump [69]. These minimum health standards are implemented in dine-in restaurants and fast food establishments allowed to operate. Such measures include placing information materials at the entrance and other visible locations, compliance with “no-mask, no-access policy”, social distancing guidelines, the capacity of customers who are allowed entry, sanitation programs, and alternate modes of ordering, picking up, and payment gateways. Moreover, establishments are mandated to have the following at the entry premises: a disinfectant foot bath, queueing area, calibrated thermal scanner, alcohol rubbing, and customer health checklist. The established guidelines require installation of enhanced dine-in systems for establishments like visible floor markers, adequate ventilation, the one-meter distance of each table, provision of food menus per table, face-to-face seating with appropriate table dividers, contactless ordering, disinfection of high-risk areas such as order and bar counters after 30 min, defined take away or pick-up area, prohibition of buffet and self-service station, including food, condiments, and utensils, among others. Likewise, the regulations guarantee proper health and safety for restaurant workers by monitoring the temperature before and after work shifts, compliance with appropriate personal hygiene, hand washing at least once an hour or every encounter with guests, mandatory wearing of personal protective equipment, and compulsory declaration of health information and whereabouts for contact tracing documentation.

Despite these measures and guidelines implemented by the government and the industry, the restaurant sector is still facing an array of challenges related to the customers’ stigma and perception of their exposure to COVID-19 when dining in restaurants. A holistic evaluation becomes a crucial initiative to identify restaurants where the perceived exposure of customers to COVID-19 is minimal in order to encourage them to dine in. This could be analogous to the approach proposed by Yamagishi and Ocampo [14] and Ocampo and Yamagishi [15] in evaluating the degree of exposure of tourists to COVID-19 in tourist sites. Moreover, such an evaluation would provide insights on determining areas for improvement on the part of the industry. Such insights are essential to encourage more customers to avail of their goods and services while ensuring that their public health is appropriately observed. Due to the various aspects that must be considered, as well as the uncertainty of information in the evaluation process, a methodology that seeks holistic evaluation under uncertainty becomes a need. This work addresses this case by offering such a rigorous approach.

3.2. The computational steps of the intuitionistic fuzzy TOPSIS-Sort method

The application of the novel intuitionistic fuzzy set extension of the TOPSIS-Sort comprises the following steps:

Step 1: Establish the list of attributes that would define the perceived degree of exposure of customers to COVID-19 in restaurants.

The list of attributes was provided by a consensus of an expert group of six members with rich knowledge on the foodservice industry (i.e., particularly on the HORECA sector), hospitality and tourism management, systems modeling, multi-attribute decision-making, pandemics modeling, public health protocols, and local culture and conditions in the Philippines. Comprehensive discussions were made in a focus group discussion to ensure that the attributes are not whimsical. Table 1 shows the list of attributes along with their corresponding codes and brief description. The group provided the description column in consensus.

Table 1.

Attributes defining the degree of exposure of customers to COVID-19 in restaurants.

Code	Attributes	Description
A1	Proximity	The degree of exposure associated with the distance of the travel route and the length of the travel time from the city center to the restaurant
A2	The available mode of transportation	The degree of exposure associated with the types of transportation facilities (e.g., types of public/private transport, terminals, ports) available to reach the restaurant
A3	Available hygiene facilities and equipment	The degree of exposure associated with the perceived availability of hygiene facilities and equipment (e.g., hand washing station, non-contact alcohol dispenser, thermal scanner, footbath, and others) in the restaurant
A4	Physical environment	The degree of exposure associated with the perceived ventilation, queuing area, customer entry, provision of table dividers, food menus per table, and customer seating
A5	Duration	The degree of exposure associated with the length of stay of the customers in the restaurant
A6	Customer traffic	The degree of exposure associated with the known average volume of customer arrivals in the restaurant

Step 2: Obtain the list of restaurants.

The case under consideration is the Province of Cebu in Central Philippines. Cebu is one of the highly urbanized cities in the Philippines, which is also considered one of the hubs of domestic and international flights. With the onset of the COVID-19 pandemic, the local governments of the Province of Cebu have implemented drastic protocols in line with the measures directed by the national government. These measures were discussed by Ocampo and Yamagishi [70]. As the Philippine government is slowly loosening quarantine restrictions to initiate economic recovery, restaurants, and the hospitality industry are gradually opening to customers with a set of public health measures enforced. To support the agenda of restarting economic activities while maintaining public health, 40 restaurants under different categories were identified for customers to assess their degree of COVID-19 exposure. Table 2 presents this list, along with the corresponding codes of the restaurants for easier recall, and some of their relevant information.

Table 2.

List of restaurants with their relevant information.

Category	Code	Restaurants	Address
Buffet	R1	Vikings Luxury Buffet	SM City Cebu, Cebu City
	R2	Buffet 101	City Time Square, Mandate City
	R3	Cabalen	SM City Cebu, Cebu City
Deli and Meat shop	R4	Tinderbox Wine and Deli Shop	Banilad, Cebu City
	R5	Acacia Steakhouse	Capitol, Cebu City
Family restaurant	R6	Top of Cebu	Busay, Cebu City
	R7	Rico’s Lechon	Mandaue City
	R8	Hukad	SM City Cebu, Cebu City
	R9	Lantaw Floating Restaurant	Cordova, Cebu
	R10	Choobi-choobi	Mabolo, Cebu City
Coffee and tea shops	R11	Starbucks	Cebu City
	R12	Bo’s Coffee	Cebu City
	R13	Macau Imperial Tea	Cebu City
	R14	KM 21	Cantipla, Cebu City
	R15	Crate Cafe	Cebu City
Food parks	R16	Sugbo Mercado	IT Park, Cebu City
	R17	Larsian Barbecue	Fuente Osmena, Cebu City
	R18	Tambayan Food Park	Consolacion, Cebu
	R19	SM Food Court	Cebu City
Cafeteria	R20	Sutukil Seafood Market	Mactan, Lapu-lapu City
	R21	Intoy’s Bakasihan	Cordova, free standing
	R22	Mr. A	Cebu City
	R23	Orange Karenderia	Cebu City, Mandaue city
	R24	Duko-Duko	Catmon, Cebu
Ethnic restaurant	R25	Nonki Japanese	Cebu City
	R26	La Vie Parisienne	Gorordo Ave, Cebu City
	R27	Casa Verde	Ayala Center Cebu, Cebu City
	R28	Lemon Grass	Ayala Center Cebu, Cebu City
	R29	Samguypsalamat Unli-Korean Meat	Cebu City
	R30	Shaka Hawaiian	IT Park, Cebu City
	R31	Maya Mexican	Cebu City
	R32	Giuseppe Pizzeria and Sicilian Roast	Mactan, Lapu-lapu City
Fast-food restaurant	R33	Jollibee	Colonnade Mall, Cebu City
	R34	McDonald’s	Jones Avenue, Cebu City
	R35	Chowking	Near Sto. Nino, Cebu City
	R36	Mang Inasal	Parkmall, Mandaue City
Hotel restaurants	R37	Cafe Bai	Bai Hotel, Mandaue City
	R38	Cafe Marco	Nivel Hills, Cebu City
	R39	Feria	Radisson Blu, Cebu City
	R40	Abaca Boutique Resort and Restaurant	Mactan, Lapu-lapu City

Step 3. Determine the priority IF weights of the attributes.

Google Forms containing a two-part questionnaire was distributed online to 400 respondents who are personal contacts of the research team. These respondents are composed of professionals, academics, undergraduate and graduate students, and acquaintances who have a high frequency of dining out (i.e., through personal knowledge and social media engagement), with sufficient knowledge on the attributes identified in this work as well as on the list of restaurants. With complete instructions, the questionnaire was presented to these respondents, and they were asked if they (1) are willing to perform the evaluations and (2) have sufficient knowledge on both the attributes and identified restaurants. Out of the 400 contacts, 250 responses were gathered (i.e., 62.5% response rate) over 14 days. The first part of the survey involves evaluating the relevance of the attributes on customers’ perceived exposure to COVID-19 using the linguistic evaluation scale shown in Table 3, along with the corresponding IFS.

Table 3.

Linguistic terms for rating the relevance of attributes.

Linguistic terms	IFS
High relevance	$\left(1,0\right)$
Between moderately high and high relevance	$\left(0.75,0.10\right)$
Moderately high relevance	$\left(0.60,0.25\right)$
Between moderate and moderately high relevance	$\left(0.50,0.40\right)$
Moderate relevance	$\left(0.50,0.50\right)$
Between moderately low and moderate relevance	$\left(0.40,0.50\right)$
Moderately low relevance	$\left(0.25,0.60\right)$
Between low and moderately low relevance	$\left(0.10,0.75\right)$
Low relevance	$\left(0,1\right)$

To determine the weights of the attributes, Eq. (14) is used. These weights are shown in Eq. (29)

$${\tilde{W}}_{\left({\tilde{w}}_1,{\tilde{w}}_2,{\tilde{w}}_3,{\tilde{w}}_4,{\tilde{w}}_5,{\tilde{w}}_6\right)}={\left(\begin{array}{c}\hfill \left(0.9424,0.0426,0.0150\right)\hfill \\ \hfill \left(0.9830,0.0132,0.0039\right)\hfill \\ \hfill \begin{array}{c}\hfill \left(0.9971,0.0024,0.0005\right)\hfill \\ \hfill \left(0.9900,0.0074,0.0026\right)\hfill \\ \hfill \begin{array}{c}\hfill \left(0.9726,0.0210,0.0064\right)\hfill \\ \hfill \left(0.9759,0.0177,0.0063\right)\hfill \end{array}\hfill \end{array}\hfill \end{array}\right)}^T$$ (29)

Step 4. Generate the IF decision matrix $\tilde{X}$

The second part of the questionnaire requires the respondents to elicit judgments on the susceptibility of the restaurant on the identified perceived exposure attributes using the linguistic evaluation scale shown in Table 4. These evaluations generate $G$ IF decision matrices, with elements denoted as ${\tilde{x}}_{ij}^k$ representing the judgment of the decision-maker $k$ on the susceptibility of restaurant $i$ on attribute $j$. Using the aggregation method described in Eq. (12), the corresponding aggregate IF evaluation rating ${\tilde{x}}_{ij}$ is obtained. Table 5 presents the IF decision matrix $\tilde{X}$.

Table 4.

Linguistic evaluation scale for rating the restaurants.

Linguistic terms	IFS
Extreme relevance	$\left(1,0\right)$
Very high relevance	$\left(0.85,0.05\right)$
High relevance	$\left(0.70,0.20\right)$
Moderate relevance	$\left(0.40,0.50\right)$
Low relevance	$\left(0.25,0.60\right)$
Very low relevance	$\left(0,1\right)$

Table 5.

The aggregate IF decision matrix $\tilde{X}$.

Restaurants	A1	A2	A3	A4	A5	A6
R1	(0.895,0.069,0.036)	(0.942,0.039,0.018)	(0.961,0.027,0.012)	(0.964,0.024,0.012)	(0.928,0.046,0.026)	(0.961,0.025,0.013)
R2	(0.912,0.059,0.029)	(0.940,0.041,0.020)	(0.949,0.035,0.016)	(0.962,0.025,0.013)	(0.921,0.052,0.027)	(0.952,0.032,0.016)
R3	(0.900,0.066,0.034)	(0.929,0.048,0.023)	(0.952,0.033,0.015)	(0.946,0.035,0.018)	(0.920,0.051,0.029)	(0.954,0.030,0.016)
R4	(0.890,0.074,0.036)	(0.927,0.050,0.023)	(0.938,0.042,0.019)	(0.932,0.044,0.023)	(0.902,0.065,0.034)	(0.937,0.042,0.021)
R5	(0.899,0.070,0.032)	(0.923,0.052,0.024)	(0.952,0.034,0.014)	(0.936,0.041,0.022)	(0.887,0.072,0.040)	(0.941,0.039,0.020)
R6	(0.921,0.056,0.023)	(0.962,0.028,0.010)	(0.956,0.031,0.012)	(0.931,0.048,0.021)	(0.913,0.059,0.028)	(0.928,0.050,0.022)
R7	(0.918,0.054,0.027)	(0.923,0.053,0.024)	(0.965,0.025,0.010)	(0.929,0.046,0.025)	(0.894,0.069,0.037)	(0.923,0.050,0.028)
R8	(0.915,0.056,0.029)	(0.940,0.041,0.019)	(0.952,0.033,0.015)	(0.946,0.035,0.019)	(0.898,0.066,0.036)	(0.947,0.034,0.019)
R9	(0.944,0.040,0.016)	(0.964,0.026,0.010)	(0.964,0.026,0.010)	(0.932,0.046,0.022)	(0.902,0.064,0.034)	(0.944,0.037,0.019)
R10	(0.894,0.071,0.035)	(0.924,0.052,0.024)	(0.970,0.022,0.009)	(0.942,0.038,0.019)	(0.896,0.068,0.036)	(0.935,0.043,0.022)
R11	(0.935,0.045,0.021)	(0.952,0.033,0.015)	(0.975,0.018,0.007)	(0.950,0.033,0.017)	(0.935,0.044,0.021)	(0.972,0.019,0.009)
R12	(0.937,0.043,0.020)	(0.939,0.042,0.019)	(0.971,0.021,0.008)	(0.953,0.031,0.016)	(0.947,0.036,0.016)	(0.955,0.030,0.015)
R13	(0.926,0.050,0.024)	(0.955,0.031,0.014)	(0.969,0.022,0.009)	(0.958,0.027,0.014)	(0.910,0.060,0.031)	(0.966,0.023,0.011)
R14	(0.911,0.063,0.026)	(0.931,0.049,0.020)	(0.945,0.038,0.017)	(0.917,0.058,0.026)	(0.901,0.067,0.032)	(0.921,0.054,0.024)
R15	(0.936,0.044,0.019)	(0.935,0.044,0.021)	(0.974,0.019,0.007)	(0.967,0.022,0.010)	(0.936,0.043,0.021)	(0.967,0.022,0.010)
R16	(0.978,0.015,0.007)	(0.966,0.022,0.011)	(0.988,0.008,0.003)	(0.990,0.007,0.003)	(0.972,0.018,0.010)	(0.990,0.007,0.003)
R17	(0.986,0.010,0.004)	(0.977,0.016,0.007)	(0.994,0.005,0.002)	(0.992,0.006,0.002)	(0.986,0.010,0.004)	(0.989,0.007,0.003)
R18	(0.979,0.014,0.007)	(0.978,0.015,0.006)	(0.990,0.007,0.003)	(0.991,0.006,0.003)	(0.981,0.013,0.006)	(0.988,0.008,0.004)
R19	(0.953,0.031,0.016)	(0.954,0.030,0.016)	(0.983,0.012,0.005)	(0.982,0.012,0.006)	(0.966,0.022,0.011)	(0.983,0.012,0.006)
R20	(0.952,0.032,0.016)	(0.967,0.023,0.010)	(0.982,0.013,0.005)	(0.981,0.013,0.006)	(0.948,0.034,0.017)	(0.962,0.024,0.013)
R21	(0.958,0.030,0.012)	(0.958,0.030,0.012)	(0.975,0.018,0.007)	(0.972,0.019,0.009)	(0.933,0.045,0.022)	(0.966,0.023,0.011)
R22	(0.917,0.055,0.029)	(0.940,0.041,0.019)	(0.968,0.022,0.009)	(0.964,0.025,0.012)	(0.945,0.036,0.018)	(0.965,0.023,0.011)
R23	(0.986,0.010,0.004)	(0.982,0.013,0.005)	(0.997,0.002,0.001)	(0.996,0.003,0.001)	(0.993,0.005,0.002)	(0.995,0.004,0.002)
R24	(0.973,0.019,0.008)	(0.973,0.019,0.008)	(0.992,0.006,0.002)	(0.989,0.008,0.003)	(0.981,0.013,0.006)	(0.988,0.009,0.004)
R25	(0.986,0.010,0.004)	(0.985,0.011,0.004)	(0.996,0.003,0.001)	(0.997,0.002,0.001)	(0.992,0.005,0.002)	(0.995,0.004,0.001)
R26	(0.899,0.068,0.034)	(0.906,0.062,0.032)	(0.951,0.036,0.013)	(0.932,0.047,0.021)	(0.898,0.069,0.034)	(0.910,0.060,0.030)
R27	(0.897,0.069,0.034)	(0.878,0.082,0.040)	(0.947,0.038,0.015)	(0.929,0.048,0.023)	(0.865,0.088,0.047)	(0.923,0.052,0.024)
R28	(0.910,0.061,0.028)	(0.919,0.055,0.025)	(0.958,0.030,0.012)	(0.954,0.031,0.015)	(0.906,0.062,0.032)	(0.939,0.042,0.019)
R29	(0.909,0.063,0.028)	(0.906,0.066,0.028)	(0.954,0.033,0.013)	(0.938,0.043,0.019)	(0.872,0.085,0.042)	(0.906,0.064,0.030)
R30	(0.943,0.039,0.018)	(0.943,0.040,0.017)	(0.970,0.021,0.009)	(0.960,0.026,0.013)	(0.960,0.028,0.013)	(0.967,0.023,0.010)
R31	(0.887,0.076,0.038)	(0.911,0.062,0.027)	(0.949,0.036,0.014)	(0.912,0.060,0.028)	(0.878,0.082,0.040)	(0.902,0.068,0.030)
R32	(0.952,0.032,0.016)	(0.946,0.037,0.017)	(0.964,0.025,0.011)	(0.969,0.021,0.010)	(0.946,0.036,0.018)	(0.974,0.018,0.008)
R33	(0.963,0.025,0.012)	(0.960,0.028,0.012)	(0.967,0.023,0.010)	(0.977,0.015,0.008)	(0.960,0.027,0.013)	(0.976,0.016,0.008)
R34	(0.964,0.024,0.012)	(0.965,0.024,0.011)	(0.978,0.015,0.007)	(0.985,0.010,0.005)	(0.976,0.016,0.008)	(0.984,0.011,0.005)
R35	(0.961,0.027,0.012)	(0.959,0.028,0.013)	(0.974,0.018,0.008)	(0.973,0.018,0.009)	(0.957,0.028,0.015)	(0.971,0.019,0.010)
R36	(0.946,0.036,0.018)	(0.930,0.046,0.023)	(0.951,0.032,0.017)	(0.963,0.024,0.013)	(0.924,0.049,0.027)	(0.952,0.032,0.016)
R37	(0.934,0.046,0.020)	(0.946,0.038,0.016)	(0.954,0.034,0.013)	(0.942,0.040,0.019)	(0.905,0.063,0.032)	(0.932,0.046,0.022)
R38	(0.921,0.055,0.024)	(0.932,0.048,0.020)	(0.953,0.034,0.013)	(0.949,0.036,0.015)	(0.904,0.066,0.030)	(0.923,0.055,0.023)
R39	(0.912,0.062,0.026)	(0.927,0.051,0.022)	(0.960,0.030,0.010)	(0.924,0.054,0.023)	(0.901,0.070,0.029)	(0.899,0.071,0.030)
R40	(0.924,0.054,0.022)	(0.927,0.052,0.021)	(0.948,0.038,0.014)	(0.950,0.036,0.013)	(0.900,0.068,0.032)	(0.903,0.067,0.030)

Step 5. Normalize the IF decision matrix $\tilde{X}$

Sabokbar et al. [32] emphasized that one way to generate the limit profiles of the pre-defined classes is to implement the normalization presented in Step 4 of the TOPSIS-Sort. Thus, the presentation of the augmented matrix $\tilde{\Lambda }$ is postponed at this point. However, since the elements of $\tilde{X}$ are IFS, Eq. (27) could not be used. With this, we modify it by showing

$${\tilde{\varepsilon }}_{ij}=\left(\left(\left(\frac{{\tilde{x}}_{ij}}{\underset{\mathit{ij}}{max}{\tilde{x}}_{ij}}\right|j\in C_b\right),\left(E^{\ast }-\left(\frac{{\tilde{x}}_{ij}}{\underset{\mathit{ij}}{max}{\tilde{x}}_{ij}}\right|j\in C_c\right)\right)$$ (30)

$E^{\ast }$ is defined as a unit IFS where $E^{\ast }=\left(1,0\right)$ [71]. A similar notion of Boran et al. [41] is adopted in this work in defining ${max}_{\mathit{ij}}{\tilde{x}}_{ij}$, ${\tilde{\lambda }}_{ij}=\left({\mu }_{{\tilde{x}}_{ij}},v_{{\tilde{x}}_{ij}},{\pi }_{{\tilde{x}}_{ij}}\right)$, as shown in Eq. (31).

$$\underset{\mathit{ij}}{max}{\tilde{x}}_{ij}=\left(\underset{\mathit{ij}}{max}{\mu }_{{\tilde{x}}_{ij}},\underset{\mathit{ij}}{min}{v}_{{\tilde{x}}_{ij}}\right)$$ (31)

For this case, ${max}_{\mathit{ij}}{\tilde{x}}_{ij}=\left(0.997,0.002\right)$. Now, Eq. (30) involves a division operation of two IFSs. As a resolution, we adopted the proposed operation defined by Chen [72]. Given two IFS ${\tilde{x}}_{ij}=\left({\mu }_{{\tilde{x}}_{ij}},v_{x_{ij}},{\pi }_{{\tilde{x}}_{ij}}\right)$ and ${max}_{\mathit{ij}}{\tilde{x}}_{ij}=({max}_{\mathit{ij}}{\mu }_{{\tilde{x}}_{ij}},{min}_{\mathit{ij}}{v}_{{\tilde{x}}_{ij}},1-{max}_{\mathit{ij}}{\mu }_{{\tilde{x}}_{ij}}-{min}_{\mathit{ij}}{v}_{{\tilde{x}}_{ij}})$, then the operation $\frac{{\tilde{x}}_{ij}}{{max}_{\mathit{ij}}{\tilde{x}}_{ij}}$ is defined as [72]:

$$\frac{{\tilde{x}}_{ij}}{\underset{\mathit{ij}}{max}{\tilde{\lambda }}_{ij}}=\left(\frac{{\mu }_{{\tilde{x}}_{ij}}}{\underset{\mathit{ij}}{max}{\mu }_{{\tilde{x}}_{ij}}},\frac{v_{{\tilde{x}}_{ij}}-\underset{\mathit{ij}}{min}{v}_{{\tilde{x}}_{ij}}}{1-\underset{\mathit{ij}}{min}{v}_{{\tilde{x}}_{ij}}}\right)$$ (32)

with the following conditions:

• (i)${\tilde{x}}_{ij}\le {max}_{\mathit{ij}}{\tilde{x}}_{ij}$, ${max}_{\mathit{ij}}{\mu }_{{\tilde{x}}_{ij}}\ne 0$, ${min}_{\mathit{ij}}{v}_{{\tilde{x}}_{ij}}\ne 1$, and
• (ii)${\mu }_{{\tilde{x}}_{ij}}{min}_{\mathit{ij}}{v}_{{\tilde{x}}_{ij}}-{max}_{\mathit{ij}}{\mu }_{{\tilde{x}}_{ij}}{v}_{{\tilde{x}}_{ij}}\ge {\mu }_{{\tilde{x}}_{ij}}-{max}_{\mathit{ij}}{\mu }_{{\tilde{x}}_{ij}}$.

Condition (i) can be directly verified as a straightforward implication of Eq. (31) and the ${\tilde{\lambda }}_{ij}$ entries of Table 5. Condition (ii) is verified by checking all ${\tilde{x}}_{ij}$ in Table 5.

The $E^{\ast }-\frac{{\tilde{x}}_{ij}}{{max}_{\mathit{ij}}{\tilde{x}}_{ij}}$ term of Eq. (30) requires a “subtraction” of two IFS. In this case, we adopt the result of Riecan and Atanassov [71], which suggests that under Zadeh’s intuitionistic fuzzy subtraction (i.e., defined as an operation ${-}_{Z,1}$), $E^{\ast }{-}_{Z,1}A=\overline{A}$ where $\overline{A}$ is the classical negation of IFS $A$. Define $A=\left\{〈x,{\mu }_A\left(x\right),v_A\left(x\right)〉:x\in X\right\}$ as an IFS. Then,

$$\overline{A}=\left\{〈x,{\mu }_A\left(x\right),v_A\left(x\right)〉:x\in X\right\}=\left\{〈x,v_A\left(x\right),{\mu }_A\left(x\right)〉:x\in X\right\}$$ (33)

As a computational example, let ${\tilde{x}}_{12}=\left(0.895,0.069,0.036\right)$ and ${max}_{\mathit{ij}}{\tilde{x}}_{ij}=\left(0.997,0.002\right)$. Using Eqs. (32), (33), then

$${\tilde{\varepsilon }}_{ij}=\left(\left(1,0\right)-\left(\frac{0.895}{0.997},\frac{0.069-0.002}{1-0.002}\right)\right)=\left(\left(1,0\right)-\left(0.898,0.067\right)\right)=\left(0.067,0.898\right)$$

The normalized IF decision matrix denoted as $\tilde{E}={\left({\tilde{\varepsilon }}_{ij}\right)}_{m\times n}$, is shown in Table 6. For brevity, we augment Table 6 and denote the entire matrix as $\tilde{\Lambda }=\left(\tilde{E},\tilde{P}\right)$ with the introduction of the IF limit profiles. The research team identifies $h$ classes along with their limit profiles. In the case application, three classes were identified: low exposure, moderate exposure, and high exposure. For each attribute, their limit profiles in IFS are $\left(\left(0.070,0.900\right),\left(0.050,0.930\right)\right)$, $(\left(0.050,0.930\right),\left(0.020,0.950\right))$, and $\left(\left(0.020,0.950\right),\left(0.003,0.980\right)\right)$, respectively, as agreed by the research team. For easy representation, let $p1=\left(0.070,\right)\left(0.900\right),p2=\left(0.050,0.930\right),p3=\left(0.020,0.950\right),p4=\left(0.003,0.980\right)$.

Table 6.

The normalized IF decision matrix augmented by limit profiles.

Restaurants	A1	A2	A3	A4	A5	A6
R1	(0.067,0.898,0.035)	(0.037,0.945,0.018)	(0.025,0.964,0.011)	(0.022,0.967,0.011)	(0.044,0.931,0.025)	(0.023,0.964,0.013)
R2	(0.057,0.915,0.028)	(0.039,0.942,0.019)	(0.033,0.952,0.015)	(0.023,0.965,0.012)	(0.050,0.924,0.027)	(0.030,0.955,0.015)
R3	(0.064,0.903,0.033)	(0.046,0.931,0.022)	(0.031,0.955,0.014)	(0.033,0.949,0.018)	(0.049,0.923,0.029)	(0.028,0.956,0.015)
R4	(0.072,0.892,0.035)	(0.048,0.930,0.022)	(0.040,0.941,0.019)	(0.043,0.935,0.023)	(0.063,0.904,0.033)	(0.040,0.940,0.020)
R5	(0.068,0.901,0.031)	(0.051,0.926,0.024)	(0.032,0.954,0.014)	(0.039,0.939,0.022)	(0.071,0.890,0.040)	(0.037,0.943,0.019)
R6	(0.054,0.924,0.022)	(0.026,0.964,0.010)	(0.029,0.959,0.012)	(0.046,0.933,0.020)	(0.057,0.916,0.027)	(0.048,0.930,0.022)
R7	(0.053,0.921,0.027)	(0.051,0.926,0.023)	(0.023,0.968,0.009)	(0.044,0.932,0.024)	(0.067,0.897,0.037)	(0.048,0.925,0.027)
R8	(0.054,0.918,0.028)	(0.039,0.942,0.019)	(0.031,0.955,0.014)	(0.033,0.949,0.018)	(0.064,0.901,0.036)	(0.032,0.949,0.018)
R9	(0.038,0.946,0.016)	(0.024,0.967,0.009)	(0.024,0.966,0.010)	(0.044,0.935,0.022)	(0.062,0.905,0.033)	(0.036,0.946,0.018)
R10	(0.069,0.896,0.035)	(0.051,0.926,0.023)	(0.020,0.972,0.008)	(0.036,0.945,0.019)	(0.066,0.899,0.035)	(0.041,0.938,0.021)
R11	(0.043,0.937,0.020)	(0.031,0.955,0.014)	(0.016,0.978,0.006)	(0.031,0.953,0.016)	(0.042,0.937,0.020)	(0.017,0.974,0.009)
R12	(0.042,0.940,0.019)	(0.040,0.941,0.019)	(0.019,0.974,0.007)	(0.029,0.956,0.015)	(0.035,0.950,0.016)	(0.028,0.957,0.015)
R13	(0.048,0.928,0.024)	(0.029,0.957,0.013)	(0.020,0.972,0.008)	(0.025,0.961,0.014)	(0.058,0.912,0.030)	(0.021,0.969,0.010)
R14	(0.061,0.914,0.025)	(0.047,0.933,0.020)	(0.036,0.947,0.016)	(0.056,0.919,0.025)	(0.065,0.903,0.032)	(0.053,0.924,0.024)
R15	(0.042,0.939,0.019)	(0.042,0.938,0.020)	(0.017,0.977,0.006)	(0.020,0.970,0.010)	(0.041,0.939,0.020)	(0.020,0.970,0.010)
R16	(0.013,0.981,0.006)	(0.020,0.969,0.011)	(0.006,0.991,0.003)	(0.005,0.993,0.002)	(0.016,0.974,0.009)	(0.005,0.992,0.003)
R17	(0.008,0.988,0.003)	(0.014,0.979,0.007)	(0.003,0.996,0.001)	(0.004,0.995,0.002)	(0.008,0.988,0.004)	(0.005,0.992,0.003)
R18	(0.012,0.982,0.006)	(0.013,0.981,0.006)	(0.005,0.993,0.002)	(0.004,0.994,0.002)	(0.011,0.983,0.006)	(0.006,0.990,0.003)
R19	(0.029,0.955,0.016)	(0.029,0.956,0.015)	(0.010,0.985,0.005)	(0.010,0.985,0.005)	(0.020,0.969,0.011)	(0.010,0.985,0.005)
R20	(0.030,0.955,0.016)	(0.021,0.970,0.010)	(0.011,0.984,0.005)	(0.011,0.983,0.006)	(0.032,0.951,0.017)	(0.022,0.965,0.012)
R21	(0.028,0.961,0.012)	(0.028,0.961,0.012)	(0.016,0.978,0.006)	(0.017,0.975,0.008)	(0.043,0.936,0.021)	(0.021,0.969,0.010)
R22	(0.053,0.919,0.028)	(0.039,0.942,0.019)	(0.020,0.971,0.009)	(0.023,0.966,0.011)	(0.034,0.948,0.018)	(0.021,0.968,0.011)
R23	(0.008,0.989,0.003)	(0.011,0.985,0.004)	(0.000,1.000,0.000)	(0.001,0.999,0.000)	(0.003,0.996,0.001)	(0.002,0.997,0.001)
R24	(0.017,0.976,0.007)	(0.017,0.975,0.007)	(0.004,0.995,0.001)	(0.006,0.991,0.003)	(0.011,0.984,0.005)	(0.007,0.991,0.003)
R25	(0.008,0.989,0.003)	(0.009,0.987,0.004)	(0.001,0.999,0.000)	(0.000,1.000,0.000)	(0.003,0.995,0.001)	(0.002,0.997,0.001)
R26	(0.066,0.901,0.033)	(0.060,0.909,0.032)	(0.034,0.954,0.012)	(0.045,0.934,0.020)	(0.067,0.900,0.033)	(0.058,0.912,0.030)
R27	(0.067,0.899,0.033)	(0.080,0.880,0.040)	(0.036,0.950,0.014)	(0.046,0.932,0.022)	(0.086,0.867,0.046)	(0.050,0.926,0.024)
R28	(0.060,0.913,0.028)	(0.054,0.922,0.025)	(0.028,0.961,0.012)	(0.029,0.957,0.014)	(0.060,0.909,0.031)	(0.040,0.941,0.019)
R29	(0.061,0.911,0.027)	(0.064,0.908,0.027)	(0.031,0.957,0.012)	(0.041,0.941,0.019)	(0.084,0.875,0.042)	(0.062,0.909,0.029)
R30	(0.037,0.945,0.017)	(0.038,0.946,0.016)	(0.019,0.973,0.008)	(0.024,0.963,0.013)	(0.026,0.962,0.012)	(0.021,0.970,0.010)
R31	(0.074,0.889,0.037)	(0.060,0.914,0.026)	(0.034,0.952,0.014)	(0.058,0.914,0.028)	(0.080,0.880,0.039)	(0.066,0.905,0.029)
R32	(0.030,0.955,0.015)	(0.036,0.948,0.016)	(0.023,0.967,0.010)	(0.019,0.971,0.009)	(0.034,0.949,0.017)	(0.016,0.976,0.008)
R33	(0.023,0.965,0.011)	(0.026,0.962,0.012)	(0.021,0.970,0.009)	(0.013,0.979,0.007)	(0.025,0.963,0.012)	(0.014,0.979,0.007)
R34	(0.022,0.966,0.011)	(0.022,0.967,0.010)	(0.013,0.981,0.006)	(0.008,0.988,0.004)	(0.014,0.979,0.007)	(0.009,0.987,0.004)
R35	(0.025,0.963,0.012)	(0.026,0.961,0.013)	(0.016,0.977,0.007)	(0.016,0.975,0.009)	(0.026,0.960,0.014)	(0.017,0.974,0.009)
R36	(0.034,0.949,0.017)	(0.045,0.933,0.023)	(0.030,0.954,0.016)	(0.023,0.965,0.012)	(0.047,0.926,0.027)	(0.030,0.955,0.015)
R37	(0.044,0.937,0.020)	(0.036,0.948,0.016)	(0.032,0.956,0.012)	(0.038,0.944,0.018)	(0.062,0.907,0.031)	(0.044,0.934,0.022)
R38	(0.054,0.923,0.023)	(0.046,0.934,0.020)	(0.032,0.955,0.012)	(0.034,0.952,0.014)	(0.064,0.906,0.030)	(0.053,0.925,0.022)
R39	(0.060,0.914,0.026)	(0.049,0.930,0.021)	(0.028,0.962,0.009)	(0.052,0.926,0.022)	(0.068,0.903,0.029)	(0.069,0.901,0.030)
R40	(0.052,0.926,0.022)	(0.050,0.930,0.021)	(0.036,0.950,0.014)	(0.034,0.953,0.013)	(0.066,0.903,0.031)	(0.065,0.905,0.030)
p1	(0.070,0.900,0.030)	(0.070,0.900,0.030)	(0.070,0.900,0.030)	(0.070,0.900,0.030)	(0.070,0.900,0.030)	(0.070,0.900,0.030)
p2	(0.050,0.930,0.020)	(0.050,0.930,0.020)	(0.050,0.930,0.020)	(0.050,0.930,0.020)	(0.050,0.930,0.020)	(0.050,0.930,0.020)
p3	(0.020,0.950,0.030)	(0.020,0.950,0.030)	(0.020,0.950,0.030)	(0.020,0.950,0.030)	(0.020,0.950,0.030)	(0.020,0.950,0.030)
p4	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)

Step 6. Construct the weighted IF decision matrix $\widetilde{{\rm Y}}={\left({\tilde{v}}_{ij}\right)}_{m\times n}={\left({\mu }_{{\tilde{v}}_{ij}},v_{{\tilde{v}}_{ij}},{\pi }_{{\tilde{v}}_{ij}}\right)}_{m\times n}$.

Let $\tilde{\Lambda }={\left({\tilde{\lambda }}_{ij}\right)}_{m\times n}={\left({\mu }_{{\tilde{\lambda }}_{ij}},v_{{\tilde{\lambda }}_{ij}},{\pi }_{{\tilde{\lambda }}_{ij}}\right)}_{m\times n}$. Then the weighted IF decision matrix $\widetilde{{\rm Y}}={\left({\tilde{v}}_{ij}\right)}_{m\times n}={\left({\mu }_{{\tilde{v}}_{ij}},v_{{\tilde{v}}_{ij}},{\pi }_{{\tilde{v}}_{ij}}\right)}_{m\times n}$ where ${\tilde{v}}_{ij}={\tilde{\lambda }}_{ij}\otimes {\tilde{w}}_j$ is obtained using Eqs. (15), (16). For instance, ${\tilde{\lambda }}_{11}=\left(0.067,0.898,0.035\right)$ and ${\tilde{w}}_j=\left(0.9424,0.0426,0.0150\right)$, then ${\tilde{v}}_{ij}=(0.067\mathrm{\ast }0.9424,0.898+0.0426-0.898\mathrm{\ast }0.0426,1-0.898-0.0426-0.067\mathrm{\ast }0.9424+0.898\mathrm{\ast }0.0426)=\left(0.063,0.902,0.035\right)$. Table 7 reports the matrix $\widetilde{{\rm Y}}$.

Table 7.

The weighted IF decision matrix $\widetilde{{\rm Y}}$.

Restaurants	A1	A2	A3	A4	A5	A6
R1	(0.063,0.902,0.035)	(0.037,0.946,0.018)	(0.025,0.964,0.011)	(0.021,0.967,0.011)	(0.043,0.932,0.025)	(0.023,0.964,0.013)
R2	(0.054,0.918,0.028)	(0.038,0.943,0.019)	(0.033,0.952,0.015)	(0.023,0.965,0.012)	(0.048,0.925,0.026)	(0.029,0.956,0.015)
R3	(0.060,0.907,0.033)	(0.046,0.932,0.022)	(0.031,0.955,0.014)	(0.033,0.949,0.018)	(0.048,0.924,0.028)	(0.027,0.957,0.015)
R4	(0.068,0.897,0.035)	(0.047,0.931,0.022)	(0.040,0.941,0.019)	(0.042,0.935,0.023)	(0.061,0.906,0.033)	(0.039,0.941,0.020)
R5	(0.064,0.905,0.031)	(0.050,0.927,0.024)	(0.032,0.954,0.014)	(0.039,0.939,0.022)	(0.069,0.892,0.039)	(0.036,0.944,0.019)
R6	(0.051,0.927,0.022)	(0.025,0.965,0.010)	(0.029,0.959,0.012)	(0.046,0.934,0.020)	(0.056,0.917,0.027)	(0.047,0.931,0.022)
R7	(0.050,0.924,0.026)	(0.050,0.927,0.023)	(0.023,0.968,0.009)	(0.044,0.932,0.024)	(0.065,0.899,0.036)	(0.047,0.927,0.027)
R8	(0.051,0.921,0.028)	(0.038,0.943,0.019)	(0.031,0.955,0.014)	(0.032,0.949,0.018)	(0.062,0.903,0.035)	(0.032,0.950,0.018)
R9	(0.036,0.949,0.015)	(0.024,0.967,0.009)	(0.024,0.966,0.010)	(0.043,0.935,0.022)	(0.060,0.907,0.033)	(0.035,0.947,0.018)
R10	(0.065,0.901,0.034)	(0.050,0.927,0.023)	(0.020,0.972,0.008)	(0.036,0.945,0.019)	(0.064,0.901,0.035)	(0.040,0.939,0.021)
R11	(0.040,0.940,0.020)	(0.031,0.955,0.014)	(0.016,0.978,0.006)	(0.031,0.953,0.016)	(0.041,0.939,0.020)	(0.017,0.975,0.009)
R12	(0.039,0.942,0.019)	(0.039,0.942,0.019)	(0.019,0.974,0.007)	(0.028,0.956,0.015)	(0.034,0.951,0.016)	(0.027,0.958,0.015)
R13	(0.045,0.931,0.023)	(0.029,0.958,0.013)	(0.020,0.972,0.008)	(0.025,0.961,0.014)	(0.056,0.914,0.030)	(0.020,0.969,0.010)
R14	(0.057,0.918,0.025)	(0.046,0.934,0.020)	(0.036,0.947,0.016)	(0.055,0.920,0.025)	(0.063,0.905,0.031)	(0.051,0.925,0.024)
R15	(0.040,0.942,0.019)	(0.041,0.939,0.020)	(0.017,0.977,0.006)	(0.020,0.970,0.009)	(0.040,0.940,0.020)	(0.020,0.971,0.010)
R16	(0.012,0.981,0.006)	(0.020,0.969,0.011)	(0.006,0.991,0.003)	(0.005,0.993,0.002)	(0.016,0.975,0.009)	(0.005,0.992,0.003)
R17	(0.008,0.989,0.003)	(0.014,0.980,0.007)	(0.003,0.996,0.001)	(0.004,0.995,0.002)	(0.008,0.989,0.004)	(0.005,0.992,0.003)
R18	(0.011,0.983,0.006)	(0.013,0.981,0.006)	(0.005,0.993,0.002)	(0.004,0.994,0.002)	(0.011,0.984,0.005)	(0.006,0.990,0.003)
R19	(0.028,0.957,0.015)	(0.028,0.957,0.015)	(0.010,0.985,0.005)	(0.010,0.985,0.005)	(0.020,0.970,0.011)	(0.009,0.986,0.005)
R20	(0.028,0.956,0.015)	(0.020,0.970,0.009)	(0.011,0.984,0.005)	(0.011,0.983,0.006)	(0.031,0.952,0.017)	(0.022,0.966,0.012)
R21	(0.026,0.962,0.012)	(0.027,0.961,0.012)	(0.015,0.978,0.006)	(0.017,0.975,0.008)	(0.042,0.937,0.021)	(0.021,0.969,0.010)
R22	(0.050,0.923,0.028)	(0.039,0.943,0.018)	(0.020,0.971,0.009)	(0.022,0.966,0.011)	(0.034,0.949,0.017)	(0.021,0.969,0.011)
R23	(0.007,0.989,0.003)	(0.011,0.985,0.004)	(0.000,1.000,0.000)	(0.001,0.999,0.000)	(0.003,0.996,0.001)	(0.002,0.997,0.001)
R24	(0.016,0.977,0.007)	(0.017,0.976,0.007)	(0.004,0.995,0.001)	(0.006,0.991,0.003)	(0.011,0.984,0.005)	(0.006,0.991,0.003)
R25	(0.008,0.989,0.003)	(0.009,0.988,0.004)	(0.001,0.999,0.000)	(0.000,1.000,0.000)	(0.003,0.995,0.001)	(0.002,0.997,0.001)
R26	(0.062,0.905,0.033)	(0.059,0.910,0.031)	(0.034,0.954,0.012)	(0.045,0.935,0.020)	(0.065,0.902,0.033)	(0.056,0.914,0.030)
R27	(0.063,0.904,0.033)	(0.079,0.882,0.039)	(0.036,0.950,0.014)	(0.046,0.932,0.022)	(0.084,0.870,0.046)	(0.049,0.927,0.024)
R28	(0.056,0.917,0.027)	(0.053,0.923,0.025)	(0.028,0.961,0.012)	(0.029,0.957,0.014)	(0.059,0.910,0.031)	(0.039,0.942,0.019)
R29	(0.058,0.915,0.027)	(0.063,0.909,0.027)	(0.031,0.957,0.012)	(0.040,0.941,0.019)	(0.081,0.877,0.041)	(0.060,0.910,0.029)
R30	(0.035,0.948,0.017)	(0.037,0.947,0.016)	(0.019,0.973,0.008)	(0.024,0.963,0.013)	(0.025,0.963,0.012)	(0.020,0.970,0.010)
R31	(0.069,0.894,0.037)	(0.059,0.915,0.026)	(0.034,0.952,0.014)	(0.057,0.915,0.028)	(0.078,0.883,0.039)	(0.064,0.906,0.029)
R32	(0.028,0.957,0.015)	(0.035,0.949,0.016)	(0.023,0.967,0.010)	(0.019,0.972,0.009)	(0.033,0.950,0.017)	(0.016,0.977,0.008)
R33	(0.022,0.967,0.011)	(0.025,0.963,0.012)	(0.021,0.970,0.009)	(0.013,0.980,0.007)	(0.024,0.964,0.012)	(0.014,0.979,0.007)
R34	(0.021,0.968,0.011)	(0.022,0.968,0.010)	(0.013,0.981,0.006)	(0.008,0.988,0.004)	(0.014,0.979,0.007)	(0.009,0.987,0.004)
R35	(0.024,0.965,0.012)	(0.026,0.962,0.012)	(0.016,0.977,0.007)	(0.016,0.975,0.008)	(0.025,0.961,0.014)	(0.017,0.974,0.009)
R36	(0.032,0.951,0.017)	(0.044,0.934,0.023)	(0.030,0.954,0.016)	(0.022,0.966,0.012)	(0.046,0.928,0.026)	(0.029,0.956,0.015)
R37	(0.041,0.939,0.020)	(0.035,0.949,0.016)	(0.032,0.956,0.012)	(0.038,0.944,0.018)	(0.060,0.909,0.031)	(0.043,0.936,0.021)
R38	(0.050,0.926,0.023)	(0.045,0.935,0.020)	(0.032,0.955,0.012)	(0.034,0.952,0.014)	(0.063,0.908,0.029)	(0.051,0.926,0.022)
R39	(0.057,0.918,0.026)	(0.049,0.930,0.021)	(0.028,0.963,0.009)	(0.051,0.927,0.022)	(0.066,0.905,0.029)	(0.067,0.903,0.03)
R40	(0.049,0.929,0.022)	(0.049,0.930,0.021)	(0.036,0.950,0.014)	(0.034,0.953,0.013)	(0.064,0.905,0.031)	(0.064,0.907,0.03)
p1	(0.066,0.904,0.030)	(0.069,0.901,0.030)	(0.070,0.900,0.030)	(0.069,0.901,0.030)	(0.068,0.902,0.030)	(0.068,0.902,0.03)
p2	(0.047,0.933,0.020)	(0.049,0.931,0.020)	(0.050,0.930,0.020)	(0.049,0.931,0.020)	(0.049,0.931,0.020)	(0.049,0.931,0.02)
p3	(0.019,0.952,0.029)	(0.020,0.951,0.030)	(0.020,0.950,0.030)	(0.020,0.950,0.030)	(0.019,0.951,0.029)	(0.020,0.951,0.03)
p4	(0.003,0.981,0.016)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.980,0.017)	(0.003,0.98,0.017)

Step 7. Determine the IF positive-ideal solution (${\tilde{A}}^{+}$) and the IF negative-ideal solution (${\tilde{A}}^{-}$). ${\tilde{A}}^{+}{\tilde{A}}^{-}$ is given in Box I

Box I.

$${\tilde{A}}^{+}=\left(\begin{array}{c}\hfill \left(0.069,0.894,0.037\right),\left(0.079,0.882,0.039\right),\left(0.070,0.900,0.030\right),\left(0.069,0.901,0.030\right),\hfill \\ \hfill \left(0.084,0.870,0.046\right),\left(0.068,0.902,0.030\right)\hfill \end{array}\right)$$

$${\tilde{A}}^{-}=\left(\begin{array}{c}\hfill \left(0.003,0.989,0.008\right),\left(0.003,0.988,0.009\right),\left(0.000,1.000,0.000\right),\left(0.000,1.000,0.000\right),\hfill \\ \hfill \left(0.003,0.996,0.001\right),\left(0.002,0.997,0.001\right)\hfill \end{array}\right)$$

Using Eq. (18) to Eq. (23), then

Note that upon applying Eq. (30), the attributes are effectively transformed into maximizing (benefit) attributes. This information must be taken into consideration when using Eq. (18) to Eq. (23).

Step 8. Compute the separation measures $S_{IF}^{+}$ and $S_{IF}^{-}$.

Using Eqs. (24), (25), $S_{IF}^{+}$ and $S_{IF}^{-}$ are obtained. Table 8 presents these measures.

Table 8.

Values of $S_{IF}^{+}$, $S_{IF}^{-}$, and $R{C}_{iIF}$.

Restaurants	$S_{IF}^{+}$	$S_{IF}^{-}$	${RC}_{iIF}$	Restaurants	$S_{IF}^{+}$	$S_{IF}^{-}$	${RC}_{iIF}$
R1	0.05169	0.04710	0.47678	R23	0.09140	0.00334	0.03523
R2	0.04735	0.04765	0.50161	R24	0.08355	0.00968	0.10387
R3	0.04314	0.05262	0.54950	R25	0.09163	0.00305	0.03222
R4	0.03274	0.06327	0.65895	R26	0.02841	0.06784	0.70487
R5	0.03430	0.06276	0.64657	R27	0.02360	0.07780	0.76727
R6	0.04489	0.05281	0.54057	R28	0.04013	0.05530	0.57945
R7	0.03632	0.06038	0.62443	R29	0.02840	0.07129	0.71510
R8	0.04193	0.05361	0.56115	R30	0.06201	0.03140	0.33614
R9	0.05003	0.04838	0.49160	R31	0.02331	0.07681	0.76717
R10	0.03905	0.06024	0.60668	R32	0.06242	0.03056	0.32865
R11	0.05855	0.03638	0.38320	R33	0.07008	0.02266	0.24429
R12	0.05612	0.03731	0.39933	R34	0.07741	0.01574	0.16895
R13	0.05421	0.04295	0.44202	R35	0.06884	0.02366	0.25583
R14	0.03147	0.06366	0.66916	R36	0.05038	0.04283	0.45946
R15	0.05798	0.03644	0.38595	R37	0.04312	0.05172	0.54536
R16	0.08171	0.01192	0.12732	R38	0.03872	0.05621	0.59216
R17	0.08748	0.00591	0.06324	R39	0.03345	0.06559	0.66226
R18	0.08526	0.00764	0.08228	R40	0.03612	0.06093	0.62781
R19	0.07311	0.02092	0.22252	p1	0.01378	0.08334	0.85814
R20	0.06894	0.02533	0.26874	p2	0.03628	0.05747	0.61302
R21	0.06409	0.03015	0.31993	p3	0.05774	0.03873	0.40145
R22	0.05668	0.03883	0.40652	p4	0.08189	0.01481	0.15316

Step 9. Obtain the relative closeness coefficient ($R{C}_{iIF}$).

Using Eq. (26), the $R{C}_{iIF}$ value for each alternative $i$ was obtained. These values are also shown in Table 8.

Step 10. Sort the restaurants according to their appropriate class, following the rule embodied in Eq. (28).

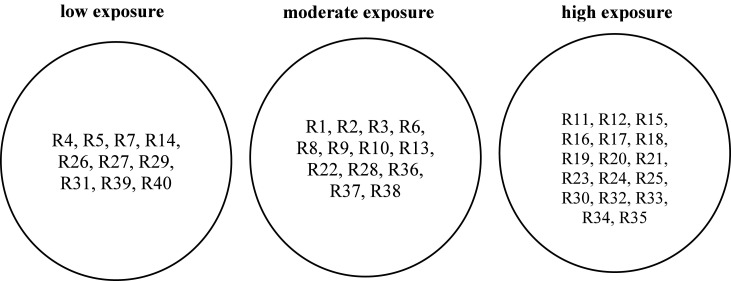
The final sorting of the restaurants according to the perceived exposure of consumers to COVID-19 is shown in Fig. 1.

Fig. 1.

The assignment of restaurants to different classes.

4. Comparative analysis with the proposed method

4.1. Comparison with the TOPSIS-Sort

To compare the efficacy of the results of the proposed IF TOPSIS-Sort with those of the TOPSIS-Sort proposed by Sabokbar et al. [32], also demonstrated by Yamagishi and Ocampo [14], the same case problem of sorting restaurants on the perceived exposure of customers to COVID-19 is considered. Instead of the linguistic evaluation scale presented in Table 3, Table 4, we used a 9-point and 6-point Likert scale, respectively. The aggregate decision matrix is shown in Table 9.

Table 9.

Aggregate decision matrix for the TOPSIS-Sort.

Restaurants	A1	A2	A3	A4	A5	A6
R1	3.740	3.832	3.868	4.016	3.908	4.004
R2	3.696	3.828	3.784	3.996	3.816	3.908
R3	3.740	3.784	3.820	3.948	3.876	3.952
R4	3.632	3.732	3.780	3.840	3.780	3.828
R5	3.620	3.728	3.808	3.872	3.744	3.840
R6	3.556	3.700	3.712	3.616	3.624	3.612
R7	3.776	3.748	3.824	3.868	3.808	3.864
R8	3.784	3.852	3.816	3.932	3.780	3.948
R9	3.688	3.760	3.836	3.760	3.780	3.848
R10	3.720	3.740	3.892	3.916	3.752	3.856
R11	3.768	3.840	3.832	3.912	3.776	4.020
R12	3.744	3.816	3.840	3.956	3.836	3.904
R13	3.780	3.848	3.872	3.956	3.724	3.928
R14	3.508	3.616	3.712	3.632	3.660	3.644
R15	3.732	3.784	3.856	3.936	3.792	3.928
R16	4.076	4.044	4.224	4.328	4.192	4.328
R17	4.092	4.052	4.236	4.328	4.200	4.232
R18	4.068	4.032	4.184	4.256	4.128	4.180
R19	3.904	3.968	4.116	4.228	4.052	4.160
R20	3.892	3.924	4.088	4.132	3.948	4.016
R21	3.820	3.828	3.976	3.964	3.812	3.948
R22	3.836	3.844	3.932	4.000	3.940	4.004
R23	4.152	4.048	4.460	4.452	4.336	4.392
R24	3.940	3.936	4.212	4.212	4.080	4.168
R25	4.112	4.080	4.360	4.496	4.284	4.308
R26	3.740	3.792	3.736	3.804	3.712	3.768
R27	3.696	3.648	3.724	3.788	3.692	3.716
R28	3.708	3.740	3.800	3.924	3.764	3.772
R29	3.676	3.624	3.760	3.788	3.640	3.700
R30	3.848	3.808	3.928	4.012	3.976	4.004
R31	3.688	3.652	3.764	3.736	3.636	3.628
R32	3.908	3.884	3.960	4.036	3.968	4.064
R33	3.960	3.920	3.940	4.140	4.020	4.088
R34	3.980	3.964	4.088	4.224	4.160	4.156
R35	3.956	3.960	4.040	4.112	4.052	4.096
R36	3.856	3.820	3.956	4.040	3.900	3.904
R37	3.776	3.796	3.716	3.780	3.744	3.748
R38	3.656	3.696	3.652	3.700	3.624	3.588
R39	3.652	3.660	3.632	3.640	3.576	3.516
R40	3.664	3.648	3.632	3.664	3.656	3.592

The set of limit profiles for the low, moderate, and high exposure classes is $P=\{\left(0.200,0.150\right),\left(0.150,0.080\right),\left(0.080,\right)\left(0.030\right)\}$, after applying the normalization process in Eq. (7). The weights of the attributes are the following:

$$W_{\left(w_1,w_2,w_3,w_4,w_5,w_6\right)}={\left(\begin{array}{c}\hfill 0.157\hfill \\ \hfill 0.164\hfill \\ \hfill \begin{array}{c}\hfill 0.176\hfill \\ \hfill 0.176\hfill \\ \hfill \begin{array}{c}\hfill 0.161\hfill \\ \hfill 0.166\hfill \end{array}\hfill \end{array}\hfill \end{array}\right)}^T$$ (34)

Following the computational steps of the TOPSIS-Sort detailed in Section 2.4, the assignments of the restaurants are shown in Table 10. It also presents a comparison of the results of both IF TOPSIS-Sort and TOPSIS-Sort.

Table 10.

Comparing the sorting assignment results of IF TOPSIS-Sort and TOPSIS-Sort.

Codes	Restaurants	Classification by IF TOPSIS-Sort	Classification by TOPSIS-Sort
R1	Vikings Luxury Buffet	Moderate	Moderate
R2	Buffet 101	Moderate	Moderate
R3	Cabalen	Moderate	Moderate
R4	Tinderbox Wine and Deli Shop	Low	Low
R5	Acacia Steakhouse	Low	Low
R6	Top of Cebu	Moderate	Low
R7	Rico’s Lechon	Low	Moderate
R8	Hukad	Moderate	Moderate
R9	Lantaw Floating Restaurant	Moderate	Low
R10	Choobi-choobi	Moderate	Moderate
R11	Starbucks	High	Moderate
R12	Bo’s Coffee	High	Moderate
R13	Macau Imperial Tea	Moderate	Moderate
R14	KM 21	Low	Low
R15	Crate Cafe	High	Moderate
R16	Sugbo Mercado	High	High
R17	Larsian Barbecue	High	High
R18	Tambayan Food Park	High	High
R19	SM Food Court	High	Moderate
R20	Sutukil Seafood Market	High	Moderate
R21	Intoy’s Bakasihan	High	Moderate
R22	Mr. A	Moderate	Moderate
R23	Orange Karenderia	High	High
R24	Duko-Duko	High	Moderate
R25	Nonki Japanese	High	High
R26	La Vie Parisienne	Low	Low
R27	Casa Verde	Low	Low
R28	Lemon Grass	Moderate	Low
R29	Samguypsalamat Unli-Korean Meat	Low	Low
R30	Shaka Hawaiian	High	Moderate
R31	Maya Mexican	Low	Low
R32	Giuseppe Pizzeria and Sicilian Roast	High	Moderate
R33	Jollibee	High	Moderate
R34	McDonald’s	High	Moderate
R35	Chowking	High	Moderate
R36	Mang Inasal	Moderate	Moderate
R37	Cafe Bai	Moderate	Low
R38	Cafe Marco	Moderate	Low
R39	Feria	Low	Low
R40	Abaca Boutique Resort and Restaurant	Low	Low

Table 10 shows that the novel IF TOPSIS-Sort assigns 10 restaurants to the low exposure class, 13 restaurants to the moderate exposure class, and 17 restaurants to the high exposure class. On the other hand, using the TOPSIS-Sort, 14 restaurants are assigned to the low exposure class, 21 restaurants to the moderate exposure class, and 5 restaurants to the high exposure class. Aside from the adjustments in the assignments of the IFS scale for each linguistic term in Table 3, Table 4, and the differences in the limit profiles introduced in both methods, these differences of the results may be associated with the vagueness and uncertainty in decision-making following the integration of the IFS in the proposed IF TOPSIS-Sort. Also, the results may suggest that the TOPSIS-Sort underestimates the COVID-19 exposure of customers as more restaurants are assigned to low and moderate exposure classes when the results of the IF TOPSIS-Sort are considered as the reference. These underestimations may be counterintuitive to the stakeholders of the restaurant sector, particularly the customers, as the end-users of these results.

4.2. Comparisons with other MCS methods

In this subsection, we compare the proposed IF TOPSIS-Sort method with other relevant MCS methods. Similar to how MADM methods are categorized (e.g., [73]), currently, the collection of MCS methods present in the domain literature could be grouped into outranking approaches (e.g., ELECTRE TRI, PROMSORT, PROMETHEE TRI, FlowSort, ELECTRE TRI-C, THESEUS, ELECTRE-SORT, FlowSort-GDSS, Fuzzy FlowSort), pairwise comparison methods (e.g., AHPSort, GAHPSort, AHPSort II, FAHPSORT, MACBETHSort), and distance-based methods (e.g., TOPSIS-Sort, VIKORSORT, CODAS-SORT). It is noteworthy that MCS methods based on outranking approaches dominate the current MCS literature. On the basis of these groups, we compare the proposed IF TOPSIS-Sort with those of its kind (i.e., VIKORSORT, CODAS-SORT). Interestingly, these methods were just recently reported, and their applications are quite limited, although [15] recently demonstrated the use of the VIKORSORT in addressing a similar problem in tourist sites. The VIKORSORT was developed by Demir et al. [36] on the basis of the VIKOR [74], [75], [76], while the CODAS-SORT was proposed by Ouhibi and Frikha [37] with CODAS [77] as its base MADM method. Additionally, despite the popularity of outranking MCS methods, the presence of a number of parameters within the PROMETHEE and ELECTRE methods makes them potentially more sensitive to differences in the assignment of alternatives than the IF TOPSIS-Sort. Thus, comparing the IF TOPSIS-Sort with VIKORSORT and CODAS-SORT, both having limited computational parameters, provides reasonable insights into its performance. Following their algorithms detailed by Demir et al. [36] and Ouhibi and Frikha [37] for the VIKORSORT and the CODAS-SORT, respectively, Table 11 presents the assignments.

Table 11.

Assignments of restaurants to classes with IF TOPSIS-Sort, VIKORSORT, and CODAS-SORT.

Class	IF TOPSIS-Sort (Proposed method)	VIKORSORT [36]	CODAS-SORT [37]
Low exposure	$|${R4, R5, R7, R14, R26, R27, R29, R31, R39, R40}$|$$=$ 10	$|${R2, R4, R5, R6, R7, R9, R10, R12, R14, R26, R27, R28, R29, R31, R37, R38, R39, R40}$|$$=$ 18	{$|$R4, R5, R6, R9, R14, R26, R27, R28, R29, R31, R37, R38, R39, R40}$|$$=$ 14
Moderate exposure	$|${R1, R2, R3, R6, R8, R9, R10, R13, R22, R28, R36, R37, R38}$|$$=$ 13	$|${R1, R3, R8, R11, R13, R15, R17, R18, R19, R20, R21, R22, R24, R30, R32, R33, R34, R35, R36}$|$$=$ 19	$|${R1, R2, R3, R7, R8, R10, R11, R12, R13, R15, R19, R20, R21, R22, R30, R32, R33, R34, R35, R36}$|$$=$ 20
High exposure	$|${R11, R12, R15, R16, R17, R18, R19, R20, R21, R23, R24, R25, R30, R32, R33, R34, R35}$|$$=$ 17	$|${R16, R23, R25}$|$$=$ 3	{$|$R16, R17, R18, R23, R24, R25}$|$$=$ 6

Table 11 shows that the VIKORSORT yields the assignment of 18, 19, and 3 restaurants to low, moderate, and high exposure classes, respectively. On the other hand, the CODAS-SORT generates 14 restaurants for low, 20 to moderate, and 6 to high exposure class. Some observations can be outlined. First, all restaurants sorted in the high exposure class by VIKORSORT and CODAS-SORT are identified by the IF TOPSIS-Sort in the same class, although CODAS-SORT includes R17, R18, and R24 which were not assigned by the VIKORSORT in the high exposure class. However, IF TOPSIS-Sort encompasses CODAS-SORT assignments by adding 11 more restaurants in the high exposure class. These restaurants (i.e., R11, R12, R15, R19, R20, R21, R30, R32, R33, R34, R35) are assigned to the moderate exposure class in the CODAS-SORT, and similarly in the VIKORSORT. Secondly, some assignments in the moderate class by IF TOPSIS-Sort (e.g., R6, R9, R28, R37, R38) belong to the low exposure class in the VIKORSORT and CODAS-SORT. Finally, all restaurants in the low exposure class by IF TOPSIS-Sort are all assigned similarly by the VIKORSORT and CODAS-SORT methods. Aside from the differences in the judgment elicitation scales, minor adjustments in the limit profiles, and few parameters in the three methods, these observations may imply that the two methods (i.e., VIKORSORT, CODAS-SORT) underestimate the assignments of restaurants, that is, restaurants assigned in the worse class (e.g., high exposure) in the proposed IF TOPSIS-Sort are assigned to a better class (i.e., moderate exposure) by these two methods. These underestimations may be associated with integrating the IFS theory, which provides a platform for handling vagueness and uncertainty when decision-makers elicit judgments within the TOPSIS-Sort. Considering the application demonstrated in this work, these underestimations are counterintuitive under a pandemic where public health is a crucial agenda alongside the need for an economic restart.

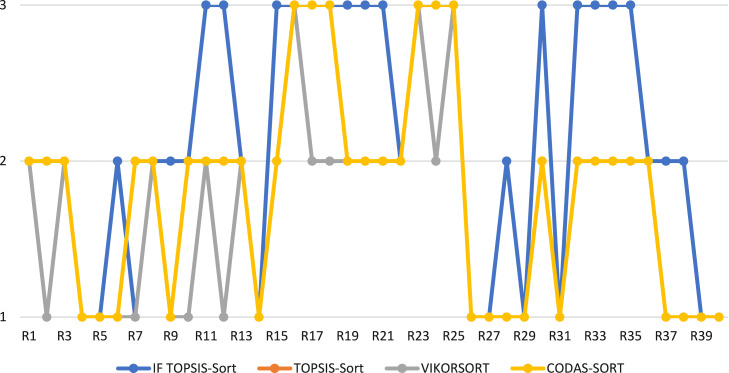
To gain a deeper insight into the differences between the proposed method and the other MCS methods under consideration, a similarity ratio metric introduced by Keshavarz Ghorabaee et al. [78] is adopted. The similarity ratio $S_r$ is defined as

$$S_r=\frac{\sum _{i=1}^m{w}_i\left(x_i,y_i\right)}{m},x_i,y_i\in \left\{\text{low exposure},\text{moderate exposure},\text{high exposure}\right\}$$

where,

$$w_i\left(x_i,y_i\right)=\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)\begin{array}{c}\hfill \mathrm{if}{x}_i=y_i,\hfill \\ \hfill \mathrm{if}{x}_i\ne y_i,\hfill \end{array}$$

$m$ is the number of alternatives (i.e., restaurants), $x_i$ is the class of the $i$th alternative using the first MCS method, and $y_i$ is the class of the $i$th alternative using the second MCS method. Consequently, $S_r=1$ for any two methods implies full consistency of all assignments. Table 12 provides the values of $S_r$.

Table 12.

$S_r$ values for comparing the relevant MCS methods.

	IF TOPSIS-Sort	TOPSIS-Sort	VIKORSORT	CODAS-SORT
IF TOPSIS-Sort	1	0.550	0.475	0.575
TOPSIS-Sort	–	1	0.850	0.975
VIKORSORT	–	–	1	0.825
CODAS-SORT	–	–	–	1

It can be shown that the three MCS methods (i.e., TOPSIS-Sort, VIKORSORT, CODAS-SORT) generally have consistent assignments with $S_r\ge 0.8$ values. It is worth mentioning that this work sets the first attempt to offer an actual case comparative analysis on the performance of these recently proposed distance-based methods. Despite their differences in normalization and aggregation procedures, as well as the type of distance a particular method promotes, sorting a set of alternatives with these MCS methods yields comparable assignments 80% of the time. On the other hand, the proposed IF TOPSIS-Sort, with similar normalization and aggregation process with the TOPSIS-Sort, only yields approximately 50% similar assignments. This insight on the difference in assignments can be reasonably attributed to the vagueness and uncertainty in decision-making, which was not addressed with the TOPSIS-Sort. By letting labels 1, 2, and 3 take the low exposure, moderate, and high exposure classes, Fig. 2 offers a pictorial representation of the differences in assignments between the proposed IF TOPSIS-Sort and the other MCS methods. Aside from R6, the proposed method provides pessimistic assignments of the restaurants by sorting some restaurants to a worse class than the class assignment using other comparable distance-based MCS methods. To verify if the assignments are acceptable and appropriate in the case application, we interviewed the members of the expert group who are all familiar with all the restaurants considered in this study. We asked their views on whether assigning the 11 restaurants (i.e., R11, R12, R15, R19, R20, R21, R30, R32, R33, R34, R35) to the high exposure class instead of the moderate exposure class is more appropriate. The following describes their views. First, restaurants R11, R12, and R15 are coffee shops in an enclosed air-conditioned environment. As argued in the recent literature, this type of environment enables COVID-19 spread (e.g., [10]). They also noticed that the locations of these facilities have high customer traffic, which may compromise social distancing measures. In addition, they argued that customers visiting these restaurants are more likely to stay in groups in not less than two hours on average, as depicted in the local setting. These observations are highly relevant in the three attributes: physical environment (A4), duration (A5), and customer traffic (A6). Secondly, they take similar positions with restaurants R19, R20, R21, R30, and R32. Although they are located in open spaces, experts noted a high volume of traffic and some reservations with the queuing area, customer entry, provision of table dividers, food menus per table, and customer seating. Lastly, R33, R34, and R35 are fast-food restaurants, and experts maintained that these restaurants have issues with hygiene facilities and equipment, physical environment, and customer traffic that could be attributed to an elevated chance for customers of spreading COVID-19. Thus, assigning these restaurants to the high exposure class is acceptable and appropriate.

Fig. 2.

A comparative analysis of assignments between IF TOPSIS-Sort and other MCS methods.

5. Discussion

The proposed IF extension of the TOPSIS-Sort advances the MCS literature as it handles vagueness and uncertainty present in eliciting decisions better than the TOPSIS-Sort. Furthermore, its application, which is demonstrated in this work, contributes to the restaurant industry as it provides customers an approach to evaluate their degree of exposure to COVID-19 in the restaurants under evaluation. This is crucial in initiating the recovery of the sector. In sorting the restaurants according to their exposure classes, it is essential to note that out of 40 restaurants, the customers perceived 10 of them (i.e., R4, R5, R7, R14, R26, R27, R29, R31, R39, R40) in the low exposure class, while 13 (i.e., R1, R2, R3, R6, R8, R9, R10, R13, R22, R28, R36, R37, R38) in the moderate exposure class, and 17 (i.e., R11, R12, R15, R16, R17, R18, R19, R20, R21, R23, R24, R25, R30, R32, R33, R34, R35) in the high exposure class. Some insights could be generated from these results. First, buffet restaurants are all in the moderate exposure class. Second, deli and meat shop restaurants are in low exposure, while family restaurants are in the low to moderate exposure classes. Third, popular coffee shops (e.g., Starbucks and Bo’s Coffee) are perceived in the high exposure class, while small ones are in the low and moderate classes. Fourth, all food parks (i.e., the dining area is usually surrounded by restaurant stores) are assigned in the high exposure class. Fifth, cafeteria restaurants are primarily assigned to the high exposure class, as well as fast-food restaurants. Sixth, ethnic restaurants have no general classifications. Customers might depend on the individual characteristics of these restaurants via the exposure attributes identified in this work. Lastly, hotel restaurants are in the low to moderate exposure classes.

These insights offer a few implications. Customers must take additional precaution measures in those restaurants classified under the high exposure class. If dining in these restaurants is inevitable, social distancing measures and public health standards (e.g., wearing masks, face shields, frequent handwashing, and contact tracing mechanisms) must be strictly observed. Note that those in the high exposure class (e.g., popular coffee shops, food parks, fast food, and cafeteria) are restaurants with high customer arrivals where social distancing protocols are likely to be compromised. The government must take aggressive initiatives so that social distancing measures are enforced in these restaurants. On the other hand, it can also be argued that those in the moderate class, generally buffet restaurants, must also carry out appropriate measures to maintain their status or to identify those areas in the set of attributes where they could still further improve. Deliberate actions of the management of these restaurants, such as aggressive advertising and promotion activities while highlighting their public health protocols in place, would further encourage customers to avail their dine-in service. Lastly, those in the low to moderate classes (i.e., family and hotel restaurants) must leverage this customer’s perception and initiate promotion activities for customers to avail of their products and services. The restaurant industry, as well as the government, may consider them as benchmarks for other restaurants or industries with product and service offerings. While these insights are interesting, stakeholders must adopt them with caution. Note that the selection of the restaurants and the distribution of these among restaurant categories may be a limitation to the relevance of these insights. Some of these insights may be case-specific and idiosyncratic and must be used to complement other findings.

The efficacy of the proposed novel IF TOPSIS-Sort is demonstrated in this work. In comparison with the TOPSIS-Sort, the proposed MCS method overcomes the limitation of the latter in handling vagueness and uncertainty, which are natural consequences in human decision-making. It must be observed in Table 10 that the TOPSIS-Sort “under-classify” some restaurants sorted in a higher exposure class in the IF TOPSIS-Sort. That is, some of those sorted in the moderate exposure class in the IF TOPSIS-Sort were classified as low exposure in the TOPSIS-Sort. Also, some of those in the high exposure class in the IF TOPSIS-Sort were assigned by TOPSIS-Sort to moderate exposure. Consider R33, R34, and R35 in the fast-food category as a case in point. With the IF TOPSIS-Sort, these restaurants are assigned to the high exposure class. This contrasts with the TOPSIS-Sort, where they are classified under moderate exposure. This observation is also consistent when the performance of the proposed IF TOPSIS-Sort is compared to other distance-based MCS methods, such as the VIKORSORT and the CODAS-SORT. It is found out that the sorting process demonstrated by the IF TOPSIS-Sort is pessimistic in such a way that some restaurants assigned by VIKORSORT and CODAS-SORT in better classes are assigned in worse classes by the proposed IF TOPSIS-Sort. In turn, the VIKORSORT and CODAS-SORT underestimate the assignments of some restaurants. This “underestimation” incidence happens 45% (18 out of 40 restaurants) of the time of the TOPSIS-Sort, and around 50% of the VIKORSORT and CODAS-SORT. Validation of the expert group yields support of a “stricter” sorting of the proposed method. This underestimation may be attributed to the vagueness and uncertainty in decision-making within the MCS framework, which were not addressed in VIKORSORT and CODAS-SORT. Such an incidence of underestimation may offer counterintuitive insights to the decision-makers, especially when these insights offer decision aid under a pandemic condition. However, this scenario must be treated with caution since, aside from the uncertainty factor, other aspects such as the IFS scale in use and the differences in the implications of the chosen limit profiles may offer insights into these differences in sorting results. Nevertheless, with the case of assigning restaurants to their appropriate class of perceived degree of exposure of customers to COVID-19, the proposed IF TOPSIS-Sort has been demonstrated as one of the possible MCS methods to be considered.

6. Conclusion and future work

This work offers an IFS extension of the TOPSIS-Sort as an MCS method. Incorporating the IFS in the MCS process provides a more suitable way of dealing with vagueness and uncertainty in decision-making. In the evaluation process, both at the attributes and alternatives level, the ratings are expressed in linguistic terms characterized by IFS values – a generalized expression of uncertainty that overcomes the limitations of the standard fuzzy set. While the efficacy of the proposed novel IF TOPSIS-Sort was demonstrated in a case study of sorting restaurants regarding the customers’ degree of exposure to COVID-19, it is worth noting that the developed method has a generic structure to be used in other MCS application domains. The use of IF TOPSIS-Sort in the case provides the following contributions and insights: (1) the proposed approach could handle MCS problems under uncertainty with computational efficiency (i.e., with an increased number of attributes or alternatives), which offers considerable potential for other domain applications, (2) it successfully sorts restaurants into three classes (i.e., low, moderate, and high exposure), and the efficiency of increasing the number of classes by adding limit profiles also remains a potential, and (3) the proposed method overcomes the limitations of the previously established TOPSIS-Sort in handling uncertainty. The results of the case application provide insights to stakeholders in the restaurant sector in appropriately designing and implementing measures as the industry is slowly recovering amidst the pandemic. Also, when compared to other distance-based MCS methods (i.e., VIKORSORT, CODAS-SORT), the proposed IF TOPSIS-Sort offers a distinct advantage as those distance-based MCS methods tend to underestimate the assignments of restaurants to a better class, rather than to a worse class as appropriately assigned by the proposed method.

Nevertheless, this work is not free from limitations. First, the case findings may be subject to a limited number of restaurants, with unequal distributions of restaurants in each category. Future work could explore other hospitality sectors with a large number of alternatives or items under consideration. Second, the application of the IF TOPSIS-Sort in the same problem domain could be expanded to other geographical locations with different political, social, and cultural frames. Third, future research may explore additional attributes for the MCS process. Fourth, sensitivity analysis of the proposed IF TOPSIS-Sort in terms of varying the IFS scale and the IF limit profiles is an interesting future work. Fifth, the effect of addressing vagueness and uncertainty, as in the IF TOPSIS-Sort, may be thoroughly investigated in future works with strong empirical findings. Finally, the use of other fuzzy TOPSIS-Sort extensions (e.g., hesitant fuzzy sets, type-2 fuzzy sets, neutrosophic sets) could be explored. In addition, the growing interest in the three-way decisions initially proposed by Yao [79] can be extended to an MCS problem. Initial insights on the integration of three-way decisions via IFS [80] and Pythagorean fuzzy sets [81] within the computational framework of TOPSIS were already reported, and future work on their extension to an MCS platform is undeniably interesting.

CRediT authorship contribution statement

Lanndon Ocampo: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing – original draft, Visualization, Supervision, Project administration. Reciel Ann Tanaid: Data curation, Writing – original draft. Ann Myril Tiu: Data curation, Writing – original draft. Egberto Selerio Jr.: Data curation, Software, Formal analysis. Kafferine Yamagishi: Data curation, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.