Abstract
Purpose:
11C-UCB-J PET imaging, targeting synaptic vesicle glycoprotein 2A (SV2A), has been shown to be a useful indicator of synaptic density in Alzheimer’s disease (AD). For SV2A imaging, a decrease in apparent tracer uptake is often due to the combination of gray-matter (GM) atrophy and SV2A decrease in the remaining tissue. Our aim is to reveal the true SV2A change by performing partial volume correction (PVC).
Methods:
We performed two PVC algorithms, Müller-Gärtner (MG) and ‘iterative Yang’ (IY), on 17 AD participants and 11 cognitive normal (CN) participants using the brain-dedicated HRRT scanner. Distribution volume VT, the rate constant K1, binding potential BPND (centrum semiovale as reference region), and tissue volume were compared.
Results:
In most regions, both PVC algorithms reduced the between-group differences. Alternatively, in hippocampus, IY increased the significance of between-group differences while MG reduced it (VT, BPND and K1 group differences: uncorrected: 20%, 27%, 17%; MG: 18%, 22%, 14%; IY: 22%, 28%, 17%). The group difference in hippocampal volume (10%) was substantially smaller than any PET measures. MG increased GM binding values to a greater extent than IY due to differences in algorithm assumptions.
Conclusion:
11C-UCB-J binding is significantly reduced in AD hippocampus, but PVC is important to adjust for significant volume reduction. After correction, PET measures are substantially more sensitive to group differences than volumetric MRI measures. Assumptions of each PVC algorithm are important and should be carefully examined and validated. For 11C-UCB-J, the less stringent assumptions of IY support its use as a PVC algorithm over MG.
1. Introduction
Alzheimer’s disease (AD) is the most common form of dementia and affects 5.5 million people in the United States and this number is projected to reach 13.8 million by 2050 (Alzheimer’s Association 2017). Synaptic loss has been found to correlate with cognitive deficits (Terry et al., 1991) and synaptic damage can be detected at the prodromal stages of AD (Overk and Masliah, 2014). Recently, the tracer 11C-UCB-J (Finnema et al., 2016; Nabulsi et al., 2016) has demonstrated its excellent properties in targeting the synaptic vesicle glycoprotein 2A (SV2A), an essential vesicle membrane protein, and thus can be a biomarker for synaptic density. 11C-UCB-J PET imaging has been shown to be a highly useful indicator of synaptic density in AD (Chen et al., 2018; Mecca et al., 2020).
In PET, to perform accurate quantification of tracer uptake, several physical effects must be corrected, i.e., Compton scatter, random coincidences, photo-electric attenuation, radioactive decay and patient motion. However, even if all the above effects are fully corrected, brain PET quantification is still limited by the partial volume effect (PVE) (Rousset et al., 2007), which is mainly caused by the limited spatial resolution of the PET scanner. A net spill-out for high-uptake regions leads to tracer underestimation while a net spill-in to low-uptake regions causes overestimation. The magnitude of PVE is dependent on the regional contrast (which can be time-dependent) as well as the size of each region, i.e., smaller regions typically suffer greater PVE than larger regions. In general, within a uniform region, PVE affects the boundary portions, i.e., voxels which are less than 2.5 times the full width at half maximum (FWHM) of the system resolution (Soret et al., 2007) away from the edge. Therefore, even for the brain-dedicated high-resolution research tomograph (HRRT) scanner (de Jong et al., 2007), with a spatial resolution of 2.5~3.0 mm in FWHM, all the gray-matter (GM) regions suffer from PVE. For neurodegenerative disorders, e.g., AD, progressive atrophy occurs in many brain regions. Such volume decrease causes brain structures, especially the thin sulci and gyri of the GM, to be more susceptible to PVE. Therefore, a decrease in apparent tracer uptake is often due to the combination of GM atrophy and SV2A density decrease in the remaining tissue. Also, potential therapeutics for AD may increase synaptic density, as suggested in preclinical animal studies (Smith et al., 2018; Toyonaga et al., 2019). To reveal true synaptic density changes using 11C-UCB-J, PVE should be corrected.
Various partial volume correction (PVC) methods have been developed and a detailed survey (Erlandsson et al., 2012) summarized the pros and cons of each method. Most methods can be divided into 2 categories: PVC performed during image reconstruction or post-reconstruction. The latter is more often used given its greater ease in implementation; these methods can be further divided into region-of-interest (ROI)-based and image-based methods. A ROI-based method treats each region as a whole and only tries to recover its mean value. The geometric transfer matrix (GTM) method (Rousset et al., 1998) is a widely used ROI-based method that accounts for spillover effects between multiple ROIs, assuming activity within each region is uniform. The main disadvantage of a ROI-based method is that it only provides a corrected mean value for each ROI but does not provide a PVC image. In contrast, an image-based method performs PVC for each voxel in the target regions. For example, the Müller-Gärtner (MG) method (Muller-Gartner et al., 1992) targets all GM voxels, and the white-matter (WM) and cerebrospinal fluid (CSF) are treated as background regions. MG requires an accurate estimate of the WM regional activity and assumes uniform tracer uptake in WM. In addition, MG does not account for spill-in and spill-out between GM regions. Another image-based method, ‘iterative Yang’ (IY) (Erlandsson et al., 2012), provides a voxel-based PVC image and corrects for PVE among GM regions. In IY, the correction map is updated iteratively and the final correction map is applied to the original PET image to perform voxel-based PVC. Since it includes between-region PVE, IY may provide a more accurate correction than MG.
The over-arching goal of this study is to evaluate the impact of PVC on quantitative SV2A imaging using FreeSurfer-segmented (Fischl, 2012) regions in a sample of 28 participants: 17 AD and 11 cognitively normal (CN). Our more specific aims are to compare the effects of two PVC algorithms, MG (Muller-Gartner et al., 1992) and IY (Erlandsson et al., 2012) in this sample and to compare the performance of the two algorithms in discriminating AD from CN participants.
2. Materials and methods
2.1. Human subjects
A total of 17 AD (further comprised of 6 with dementia and 11 with MCI) and 11 CN participants were included in this study. Participants ranged in age from 58 to 82 (14 M/14F). These participants were a subset of those reported in (Mecca et al., 2020), since the sample was restricted to individuals with arterial input functions. See participant details in (Mecca et al., 2020). All participants received a PET scan with [11C]Pittsburgh Compound B ([11C]PiB) to determine the presence of amyloid-β (Aβ) as previously described (Mecca et al., 2018). MCI and dementia participants without Aβ accumulation and CN participants with Aβ accumulation were excluded. The study protocol was approved by the Yale University Human Investigation Committee and Radiation Safety Committee.
2.2. PET data acquisitions
The participants underwent 11C-UCB-J (Finnema et al., 2016) (550±208 MBq) PET dynamic studies on the HRRT (de Jong et al., 2007). Arterial blood samples were obtained, and metabolite correction was performed as described previously (Finnema et al., 2018). Dynamic image reconstruction was performed using MOLAR (Carson et al., 2003) (2 iterations × 30 subsets) with event-by-event motion correction based on the Polaris Vicra NDI Systems (Jin et al., 2013). A dynamic study of 60 min duration with dynamic frames of 30 s × 6, 1 min × 3, 2 min × 2 and 5 min × 10 were used. Attenuation correction was performed based on a transmission scan acquired prior to the PET scan. Single scatter simulation (Watson et al., 1996) was used for scatter correction.
2.3. MR acquisition and region segmentation
Each participant underwent Magnetic Resonance (MR) imaging with magnetization-prepared rapid gradient-echo sequence on a 3T Siemens-Trio with a circularly polarized head coil. Images were 256 × 256 × 176 slices with 0.98 × 0.98 × 1.0 mm in voxel size. Individual MR images were analyzed by FreeSurfer using the option to create binary segmented images of skull, extra-cerebral CSF, air cavities, and remaining head tissue in addition to the brain. In total, 109 regions of interests (ROIs) were created for each subject (Fischl, 2012; Greve et al., 2016). The entire WM ROI, the ROIs of cerebral white matter, was created by merging cerebellum white matter, ventral diencephalon, pons and brain stem. The ROI label numbers are listed in Supplemental Table 1.
2.4. Image registration
Averaged 0–10 min PET image were aligned to their corresponding MR image via rigid registration using mutual information as the similarity metric. This PET-MR transformation was applied to each motion-corrected PET dynamic frame. We also warped the automated anatomic labeling (AAL) (Tzourio-Mazoyer et al., 2002) atlas into each individual MR image through nonlinear registration using BioImageSuite software (Joshi et al., 2011) to generate centrum semiovale (CS) values for the MG method (see below).
2.5. Partial volume correction
MG (Muller-Gartner et al., 1992) and IY (Erlandsson et al., 2012) PVC approaches were applied to each dynamic frame. For MG, the 109 FreeSurfer-segmented regions were merged to produce whole GM, entire WM and CSF regions (See Supplemental Table 1 for details). For each dynamic frame, the mean value of the CS region was used as the WM value for MG (Rossano et al., 2019). This CS ROI was defined in AAL space and resliced into the individual MR space. For IY, a correction image is created iteratively. Using the PVC image from the previous iteration, regional means are computed, and a piecewise uniform image is built. This image is smoothed with the PSF kernel, and the correction image is calculated as the ratio of the unsmoothed to smoothed images. Spatially invariant 3 mm in FWHM Gaussian PSF kernel is used in this study. Note that MG assumes CSF to have no activity, therefore no spill-out correction from CSF to GM is performed in MG. However, IY does not assume null CSF activity. The mathematical definitions of the two algorithms can be found in the Supplemental Materials. Note that MG was used in our previous 11C-UCB-J studies (Chen et al., 2018; Mecca et al., 2020; Chen et al., 2021 bib4). Therefore, we chose to use MG as the baseline PVC method; IY was chosen since it was reported by Thomas et al. (Thomas et al., 2016) as an excellent PVC method, which has preferable properties, e.g., self-initialization (see Discussion for details).
2.6. Tracer kinetic modeling and image analysis
For each scan, voxel-by-voxel kinetic analysis, using the one-tissue compartment (1TC) model with the metabolite-corrected arterial plasma curves (Finnema et al., 2018) was performed using 0–60 min of data. Two parametric images were generated: the distribution volume VT, the tissue to plasma concentration ratio at equilibrium reflecting specific plus nonspecific binding, and K1, the rate of entry of tracer from blood to tissue. Given its minimal specific binding (Rossano et al., 2019), CS was used as the reference region. Binding potential (BPND) was calculated as BPND = (VT - VT(CS))/VT(CS).
2.7. Statistical analysis
Comparison of FreeSurfer-derived region volumes, K1, VT and BPND values between diagnostic groups was performed using two-tailed unpaired student’s t-test with p<.05 for significance. VT and BPND comparisons were made for uncorrected data and for data corrected by MG and IY. For correlation analysis of% change due to PVC vs. region size, linear regression was applied to estimate the slope and intercept and p value using Prism 8 (GraphPad Software, San Diego, CA).
3. Results
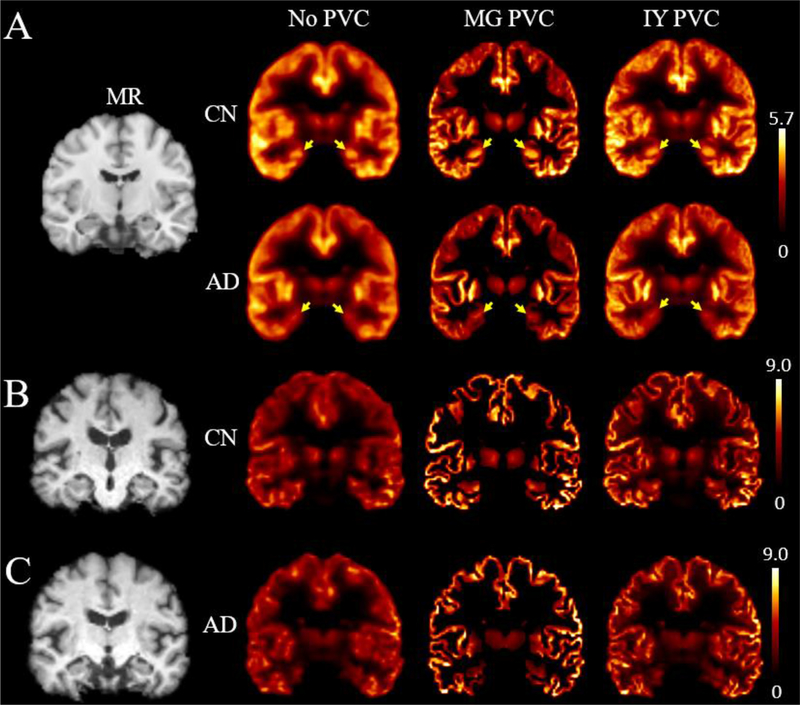
Individual MNI-space (Tzourio-Mazoyer et al., 2002) BPND maps were averaged over CN and AD groups and shown in Fig. 1. Before PVC, binding was visibly lower in AD than CN at the hippocampus (arrows). This difference was maintained after applying both PVC methods. After MG or IY, contrast and resolution restoration in GM was clearly visible. Visually, MG yielded higher binding in most GM regions. The MG image may appear artificially sharper than IY, since only GM voxels are shown in the MG image (MG only corrects GM voxels), whereas the entire brain is shown for IY.
Fig. 1.
(A) Averaged SV2A BPND maps for CN and AD in the automated anatomic labeling (AAL) space. Yellow arrows denote the hippocampus. The template MR is shown for reference. Only gray matter values are shown in the MG PVC image, i.e., CSF and WM voxels were set to zero, whereas the entire brain is shown for IY. (B-C) SV2A BPND map examples for CN and AD. AD: Alzheimer’s disease; CN: cognitive normal; IY: iterative Yang; MG: Müller-Gärtner.
VT and BPND values are shown in Tables 1 and 2, respectively. Before PVC, consistent with earlier findings (Chen et al., 2018; Mecca et al., 2020), tracer uptake (VT) was significantly lower in the hippocampus in AD compared to CN. Specifically, VT in the hippocampus was 20% lower in the AD group (p=.0011); for BPND, this difference was 27% (p=.0014). The uptake rate constant K1, reflective of blood flow, in the hippocampus was also 17% lower in the AD group (Supplemental Table 2; p=.0177). Interestingly, in the entorhinal cortex, MG reduced the VT (BPND) group difference from 19% (23%) to 12% (12%) and reduced the BPND significance from p=.0051 to not significant (NS). In contrast, IY maintained the VT (BPND) group difference at 20% (23%), changed the significance from NS to p=.006 for VT, and maintained the BPND group difference significance (p=.0108). VT and BPND group difference (14% and 16%) in the amygdala lost its significance (p=.0339 and 0.0371) after PVC using both methods. The volumes (Table 3) of the hippocampus, amygdala, and entorhinal cortex were significantly lower in the AD group. Given the differences in both uptake and volume, PVC is needed to decouple volume loss from SV2A loss per unit volume.
Table 1.
VT (mL/cm3) mean (standard deviation), before and after PVC for CN and AD groups.
| Method | no-PVC |
MG |
IY |
||||||
|---|---|---|---|---|---|---|---|---|---|
| ROI | CN | AD | p | CN | AD | p | CN | AD | p |
|
| |||||||||
| Amygdala | 17.79(2.29) | 15.32(3.16) | .0339 | 22.56(3.12) | 20.24(3.61) | 19.95(2.77) | 17.45(3.47) | ||
| Caudate | 16.17(3.40) | 15.24(2.94) | 23.00(4.47) | 21.97(3.97) | 19.46(4.20) | 18.25(3.54) | |||
| Cerebellum Cortex | 14.24(1.61) | 13.92(1.91) | 16.06(1.89) | 15.74(2.19) | 14.93(1.69) | 14.63(2.00) | |||
| Ant. Cingulate | 21.42(2.62) | 19.94(3.30) | 34.82(4.02) | 33.29(6.23) | 28.34(3.44) | 26.14(4.41) | |||
| Post. Cingulate | 19.63(2.49) | 18.26(2.99) | 29.82(3.41) | 29.33(4.53) | 24.37(3.07) | 23.17(3.40) | |||
| Entorhinal | 16.25(2.51) | 13.21(2.56) | 22.97(3.80) | 20.31(3.49) | 18.51(3.12) | 14.89(3.11) | .0058 | ||
| Frontal | 20.04(2.06) | 18.83(3.43) | 33.21(3.10) | 32.16(6.23) | 27.00(2.67) | 25.57(4.47) | |||
| Hippocampus | 13.43(1.58) | 10.70(2.11) | .0011 | 17.26(2.01) | 14.12(2.57) | .0021 | 14.69(1.81) | 11.41(2.41) | .0007 |
| Occipital | 19.37(1.76) | 18.61(2.72) | 31.91(3.19) | 30.51(4.73) | 26.21(2.51) | 24.87(3.68) | |||
| Pallidum | 14.14(1.62) | 13.49(2.19) | 16.51(2.04) | 15.67(2.55) | 13.74(1.77) | 12.95(2.13) | |||
| Parietal | 20.67(1.69) | 18.81(3.53) | 35.03(3.01) | 33.01(6.40) | 28.54(2.32) | 26.02(4.70) | |||
| Precuneus | 21.33(1.70) | 19.73(3.58) | 33.72(3.19) | 32.81(5.87) | 28.27(2.34) | 26.52(4.47) | |||
| Putamen | 22.33(2.27) | 22.22(3.59) | 27.67(2.86) | 27.58(4.52) | 25.65(2.73) | 25.53(4.00) | |||
| Temporal | 20.55(2.37) | 18.54(2.95) | 31.56(3.44) | 29.27(4.79) | 26.69(3.06) | 24.14(3.84) | |||
| Thalamus | 13.33(1.76) | 12.23(1.94) | 15.43(2.04) | 14.21(2.25) | 14.14(1.82) | 12.99(2.02) | |||
| Centrum Semiovale | 4.05(0.48) | 4.00(0.64) | N/A | N/A | 4.06(0.48) | 4.00(0.64) | |||
| Entire White Matter | 12.03(1.33) | 11.68(2.95) | N/A | N/A | 8.75(1.09) | 8.81(1.61) | |||
| GM average | 18.05 | 16.60 | 26.10 | 24.68 | 22.03 | 20.30 | |||
P value denotes the statistical significance between CN and AD. AD: Alzheimer’s disease; CN: cognitive normal; IY: iterative Yang; MG: Müller-Gärtner. Blank p values indicate p>.05.
Table 2.
BPND mean (standard deviation), before and after PVC for CN and AD group.
| Method | no-VC |
MG |
IY | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ROI | CN | AD | p | CN | AD | p | CN | AD | p |
|
| |||||||||
| Amygdala | 3.41(0.47) | 2.86(0.74) | .0371 | 4.59(0.64) | 4.10(0.81) | 3.94(0.59) | 3.41(0.87) | ||
| Caudate | 2.98(0.62) | 2.84(0.65) | 4.67(0.78) | 4.54(0.90) | 3.79(0.79) | 3.61(0.84) | |||
| Cerebellum Cortex | 2.54(0.40) | 2.51(0.40) | 2.99(0.46) | 2.97(0.47) | 2.71(0.44) | 2.70(0.45) | |||
| Ant. Cingulate | 4.31(0.52) | 4.01(0.60) | 7.65(1.02) | 7.35(1.07) | 6.02(0.81) | 5.58(0.92) | |||
| Post. Cingulate | 3.86(0.42) | 3.58(0.51) | 6.40(0.74) | 6.39(0.83) | 5.03(0.49) | 4.84(0.68) | |||
| Entorhinal | 3.02(0.53) | 2.34(0.61) | .0051 | 4.70(0.90) | 4.13(0.81) | 3.58(0.73) | 2.77(0.79) | .0108 | |
| Frontal | 3.98(0.51) | 3.71(0.54) | 7.27(0.98) | 7.04(0.95) | 5.71(0.79) | 5.41(0.76) | |||
| Hippocampus | 2.33(0.31) | 1.70(0.52) | .0014 | 3.28(0.41) | 2.57(0.63) | .0029 | 2.64(0.37) | 1.89(0.63) | .0014 |
| Occipital | 3.83(0.57) | 3.70(0.61) | 6.96(1.08) | 6.70(0.98) | 5.53(0.86) | 5.30(0.94) | |||
| Pallidum | 2.50(0.33) | 2.39(0.34) | 3.09(0.41) | 2.94(0.44) | 2.40(0.37) | 2.25(0.34) | |||
| Parietal | 4.15(0.60) | 3.72(0.67) | 7.73(1.08) | 7.28(1.15) | 6.11(0.88) | 5.54(0.94) | |||
| Precuneus | 4.32(0.62) | 3.95(0.63) | 7.41(1.14) | 7.24(1.02) | 6.04(0.89) | 5.67(0.86) | |||
| Putamen | 4.54(0.52) | 4.58(0.55) | 5.87(0.66) | 5.93(0.76) | 5.36(0.69) | 5.42(0.74) | |||
| Temporal | 4.10(0.53) | 3.68(0.68) | 6.84(0.91) | 6.38(1.06) | 5.63(0.79) | 5.11(0.97) | |||
| Thalamus | 2.29(0.25) | 2.07(0.36) | 2.81(0.28) | 2.57(0.41) | 2.49(0.26) | 2.27(0.38) | |||
| GM Average | 3.48 | 3.18 | 5.48 | 5.21 | 4.47 | 4.12 | |||
p value denotes statistical significance between CN and AD. AD: Alzheimer’s disease; CN: cognitive normal; IY: iterative Yang; MG: Müller-Gärtner. Blank p values indicate p>.05.
Table 3.
Volume (mL) mean (standard deviation) over participants, for CN and AD group derived from FreeSurfer.
| Method | Volume |
||
|---|---|---|---|
| ROI | CN | AD | p |
|
| |||
| Amygdala | 2.78(0.39) | 2.29(0.43) | .005 |
| Caudate | 6.00(1.36) | 6.09(0.75) | |
| Cerebellum Cortex | 100.36(8.21) | 103.39(9.06) | |
| Ant. Cingulate | 6.16(1.10) | 6.41(1.18) | |
| Post. Cingulate | 9.26(1.46) | 8.96(1.61) | |
| Entorhinal | 3.65(0.67) | 2.78(0.58) | .001 |
| Frontal | 126.89(13.75) | 129.92(14.16) | |
| Hippocampus | 7.31(0.68) | 6.54(0.98) | .030 |
| Occipital | 39.74(4.38) | 42.21(6.29) | |
| Pallidum | 3.40(0.44) | 3.59(0.35) | |
| Parietal | 85.62(11.84) | 86.89(10.68) | |
| Precuneus | 16.16(2.17) | 15.76(2.45) | |
| Putamen | 8.03(0.78) | 8.10(0.94) | |
| Temporal | 81.10(7.05) | 76.78(8.76) | |
| Thalamus | 12.82(1.40) | 12.99(0.90) | |
| Average | 33.95 | 34.18 | |
AD: Alzheimer’s disease; CN: cognitive normal. Blank p values indicate p>.05.
After applying PVC, MG increased GM values (Table 1) more than IY in both cohorts in all GM regions. Specifically, with MG, hippocampus VT (Table 1), BPND (Table 2) and K1 (Supplemental Table 2) increased by 29±15%, 41±18% and 26±13%, respectively for CN and 32±24%, 51±37% and 32±26% for AD. With IY, hippocampal increases were much smaller: VT, BPND and K1 increased by 9 ± 13%, 13±16% and 4 ± 13%, respectively for CN and 7 ± 23%, 11±37% and 5 ± 21% for AD. For the CS reference region (for computing BPND), we found no between-group differences in VT (Table 1) in both no-PVC (CN 4.05 vs. AD 4.00, p=.82) and IY PVC (4.06 vs. 4.00, p=.81). This indicates that the small CS region was not affected by PVE.
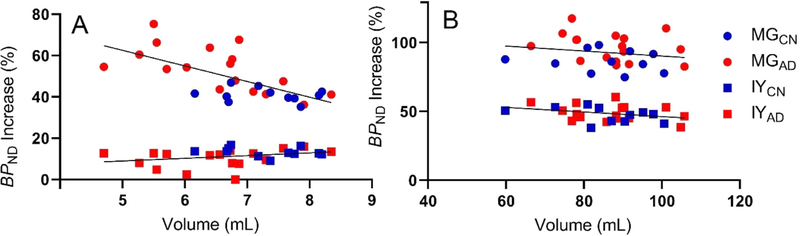
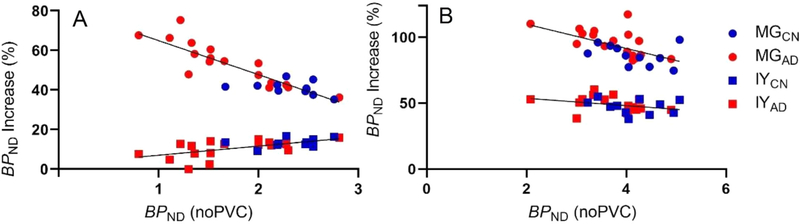
We observed a large difference in the magnitude of PVC change between methods. To examine this difference, Fig. 2A shows the relationship between the percent increase of hippocampal BPND vs. bilateral hippocampal volume. Intuitively, for high-uptake GM regions, a negative correlation between the percent increase of hippocampal BPND vs. hippocampal volume might be expected, i.e., the larger the region, the smaller the correction factor. Indeed, in hippocampus, MG change and region volume were negatively correlated (r2=0.45, p=.0001), but this was not found for IY (r2=0.09, p=.11). In cortical regions, neither PVC method showed obvious trends (parietal cortex shown in Fig. 2B), except for temporal cortex with MG which showed a significant negative correlation with volume (r2=0.23, p=.009). The BPND % increase due to IY was also positively correlated with uncorrected BPND in hippocampus (r2=0.39, p=.0004) (Fig. 3A) while the same correlation was significantly negative for MG (r2=0.76, p<.0001). MG also showed significant negative correlations in frontal, parietal, and temporal cortices (NS in occipital cortex). In contrast, IY showed non-significant trends in all cortical regions. Parietal cortex is shown as an example in Fig. 3B. Similar results for VT are shown in Supplemental Figure 2.
Fig. 2.
Volume vs. BPND percent increase in the hippocampus (A) and parietal cortex (B) for all subjects. CN subjects shown in blue and AD subjects shown in red. In hippocampus, a negative correlation was observed for MG, but not for IY. In parietal cortex, negative correlations were observed for both MG and IY. AD: Alzheimer’s disease; CN: cognitive normal; MG: Müller-Gärtner; IY: iterative Yang.
Fig. 3.
BPND without PVC vs. BPND % increase in hippocampus (A) and parietal cortex (B). In hippocampus, negative correlation was observed for MG, while a mild positive correlation was found for IY. In parietal cortex, the correlations were negative (significant for MG). AD: Alzheimer’s disease; CN: cognitive normal; MG: Müller-Gärtner; IY: iterative Yang.
BPND coefficients of variation (CoV) across subjects were calculated per region per group (Supplemental Table 3). CoVs in the CN group were very similar without PVC or with either PVC method. For the AD group, IY CoVs were slightly higher than uncorrected values, and MG provided lower CoVs than IY, particularly in temporal cortex. For instance, hippocampus CoVs were similar in the CN group (no-PVC vs. MG vs. IY: 13.2% vs. 12.4% vs. 13.9%) but were numerically lower with MG in AD (30.7% vs. 24.7% vs. 33.2%).
In terms of group differences, after applying MG, the magnitude of between-group differences in hippocampus VT, BPND and K1 decreased to 18%, 22% and 14%, respectively, with less statistical significance for all three parameters compared to no-PVC (20%, 27% and 17%); see Tables 1 and 2 and Supplemental Table 2. In contrast, after applying IY, the between-group differences in VT and BPND increased to 22% and 28%, respectively, with increased or equal significance (p=.0007 and 0.0014, respectively) as compared to no-PVC. The magnitude of between-group differences in hippocampal K1 did not change but had increased significance with IY (p=.0113). Consistent with (Chen et al., 2018), lower BPND in entorhinal cortex in AD (Table 2) did not maintain significance with MG (p=.0952), however, the difference was significant (p=.0108) with IY. A similar pattern was present for K1.
4. Discussion
PET measurements suffer from PVE, and PVC algorithms can be useful in appropriate cases. For example, in neurodegenerative conditions such as AD, loss of GM tissue is a confounding factor in interpreting PET signals. To properly use 11C-UCB-J to assess SV2A density in AD, PVC can be useful to separate atrophy from SV2A loss in the remaining tissue. In this study, we applied two PVC algorithms, MG and IY, to cohorts of CN and AD participants. In this study, only datasets with arterial sampling for kinetic modeling were included, and the CS was used as the reference region to calculate BPND. Without PVC, we observed significantly lower BPND in hippocampus of AD compared to CN subjects. As shown in the Table 2, in most regions, we found that both PVC algorithms reduced the percent differences between the AD and CN group means. Interestingly, in hippocampus, IY slightly increased the magnitude of the group difference, while MG reduced it. In other words, IY suggested that PVE may reduce the hippocampal SV2A group differences, but MG suggested the opposite. Also, after applying PVC, MG increased GM binding much more than IY in each cohort. To understand these performance differences, we must consider the different assumptions of the two algorithms.
All PVC algorithms make assumptions about the tracer distribution, imaging physics and reconstruction algorithms. Violations of those assumptions may lead to inaccurate corrections and even erroneous conclusions (Greve et al., 2016). The following assumptions were made in one or both algorithms:
Assumption (1): MG assumes uniformity of the WM region and requires a partial volume corrected WM value as an input. IY does not treat WM differently than GM or CSF regions. As suggested by Rossano et al. (Rossano et al., 2019), a 2-mL CS region is relatively immune to PVE (at least for the HRRT), and that result was replicated using IY (Table 1). Using IY, the mean VT in the entire WM was tabulated by merging several regions (see Table 1). We found that the mean WM VT after IY was approximately twice that of the CS region, which would imply that there is non-uniformity in 11C-UCB-J WM uptake. One contributing factor may be white matter interstitial neurons (WMINs) which are present in the entire gyral WM in humans and animals (Sedmak and Judas, 2019). Gyral WM is therefore likely to contain higher specific 11C-UCB-J uptake than deep WM, i.e., the CS region.
Assumption (2): MG assumes zero uptake in the CSF and thus did not correct for potential spill-in from CSF to GM, while IY treated the CSF on the cortical surface and CSF in the ventricles as separate regions. Based on the IY results, the extra-cerebral and ventricle CSF mean VT values were approximately 200% and 50% higher than the CS value, respectively, which suggests that the assumption of null activity in the CSF may not hold. Note that these values could reflect a lack of full convergence of the reconstruction, as was found previously (Rossano et al., 2019). Due to limited number of OSEM iterations and its non-negativity constraint, even if CSF had zero activity, the apparent tracer uptake would be greater than zero. In addition, since the CSF on the surface of the cortex is anatomically thin and is adjacent to high-uptake regions, any inaccurate PSF modeling in the reconstruction and the PVC process (see assumption 4) may result in erroneous activity estimates.
To evaluate the assumption, a postmortem study was conducted, where a rhesus macaque was euthanized after 18F-SynVesT-1 injection and CSF was collected by lumber puncture. Although much lower than brain activity (~1%, data not shown), lumbar CSF was greater than zero. The kinetics of 11C-UCB-J and 18F-SynVesT-1 are similar, suggesting that 11C-UCB-J CSF activity is also greater than zero. Also, activity in brain ventricles is expected to be higher than lumbar CSF. The impact of CSF activity on PVC was also discussed in a previous 18F-FDG study (Greve et al., 2016).
Assumption (3): the MG algorithm does not correct for spill-in and spill-out in between different GM regions. The wide range of VT values (Table 1) across different GM regions showed that spill-in and spill-out between GM regions could be important to correct, especially for the hippocampus, which had ~20–30% lower values than nearby GM regions, e.g., amygdala and entorhinal cortex. In contrast, IY separately corrected based on 109 brain regions, which did correct for PVE between GM regions.
Assumption (4): both MG and IY algorithms assumed a spatially uniform Gaussian PSF (3 mm in FWHM), whereas studies (Kotasidis et al., 2014; Jian et al., 2015) had shown that the PSF of HRRT is an anisotropic Gaussian kernel, e.g., the PSF FWHM is different in radial and tangential directions, suggesting that spatially variant PSF modeling for the HRRT is desirable. The use of resolution modeling in the OSEM reconstruction with a limited number of iterations added further complexity, since image resolution will vary with the local contrast due to differences in convergence speed (Rossano et al., 2019), so the 3-mm image-space Gaussian PSF was only an approximation for the HRRT. Note that the HRRT has higher resolution than a typical clinical scanner (~5–6 mm). One way to assess the accuracy of the resolution assumptions made in any PVC algorithm would be to perform scans of the same subject on two different scanners.
Understanding the assumptions of each PVC algorithm and the impact of errors in these assumptions on the results is critical for accurate PVC. To further characterize the difference between the two algorithms, e.g., as shown in the Table 1, the VT in hippocampus (parietal) of MG is approximately 17% (23%) higher than IY among CN, we performed simulation studies (see details in the supplemental material). We found that assumption (1) accounts for ~9% (8%) difference, assumption (2) accounts for ~8% (14%) while assumption (3) accounts for less than 1% (1%) in hippocampus (parietal cortex). Based on this analysis, MG is found very sensitive to the input WM value and MG is likely to have overestimated the GM regions by assuming uniformity of WM and thus using an underestimated CS value, i.e., only the central lower CS value was used. In addition, MG is also very sensitive to the CSF uptake assumption and MG is believed to have further overestimated GM regions by ignoring PVE from the CSF (either due to real or apparent uptake). Assuming CSF to be zero can lead to ~8% (14%) over-estimation for hippocampus (parietal) uptake. Inter-GM PVE can be considered minimal (1%), if not negligible. These considerations lead to the conclusion that IY may provide a theoretically more accurate PVC method than MG for 11C-UCB-J. Again, we emphasize that the above analysis was performed for HRRT, which operates at a better resolution than most commercial PET scanners.
In this study, the magnitude of increases in K1 and VT were very similar after PVC for both algorithms (Supplemental Table 2 and Table 1), which is mainly due to the similarity in GM:WM contrast in these two measures. Specifically, regions with high flow (K1) also have high SV2A density (VT), so the clearance constant k2 (=K1/VT) is quite uniform in the brain, so the GM:WM contrast is relatively stable through the entire scan. This is not the case for tracers with more specific binding distributions where image contrast changes during the scan.
Here, the volumes of three regions (hippocampus, entorhinal cortex and amygdala) were significantly smaller in AD compared to CN, as shown in Table 3. Significantly smaller VT values (Table 1), but with larger magnitude of difference than volume, were also observed in these regions without PVC. After applying IY, the group% difference in VT for hippocampus and entorhinal cortex slightly increased from 20.3% to 22.3% and 18.7% to 19.6%, respectively. This result indicates that in the hippocampus and entorhinal cortex, CN subjects suffered slightly greater PVE than the AD subjects, therefore, PVC increased uptake to a greater extent in these two regions for CN than AD. It is also counterintuitive, since conventional wisdom states that regions with smaller volume, e.g., hippocampus in AD, suffer greater PVE. However, PVE depends both on object size and the local contrast, i.e., this conventional wisdom only applies if the volume difference is the primary effect producing PVE. However, here, because the VT in AD hippocampus is quite low, the contrast to the local WM is small, which means that hippocampus suffered little PVE in AD. Because the CN VT values were higher in hippocampus, even with the larger object size, the net PVE was larger than in AD. Therefore, in the hippocampus, after IY PVC, the difference between AD and CN increased. Similar analysis can also be applied to entorhinal cortex. We note that MG showed opposite results, i.e., AD had larger PVE than CN in the hippocampus (Fig. 2A), as compared to the above IY results. Given the unique scenario of hippocampus for 11C-UCB-J and the inaccurate assumptions made by MG, we believe the results yielded by IY would be more accurate. Here, we add the cautionary note that our findings shall only apply to 11C-UCB-J and in general, even with the same PVC algorithm, any findings after PVC should be treated as application-specific.
After PVE correction, for the hippocampus, a larger BPND disease group difference (27% for IY, Table 2) was found than the volume difference (10%, Table 3). This indicates that SV2A PET imaging is more sensitive than volumetric MR in measuring CN and AD group differences in this region.
In addition to MG and IY, there are several additional PVC algorithms. For instance, Rousset et al. proposed the GTM method, which performs PVC at the regional mean level. One disadvantage of the GTM method is that when a very small region is used, due to the nature of matrix inversion, the PVC results can be unstable (Schwarz et al., 2019; Thomas, 2012). Erlandsson et al. (Erlandsson et al., 2012) proposed a multi-target correction (MTC) method, which is an extension of MG. This method is very similar to GTM except that MTC produces a PVC image while GTM only yields corrected means for each ROI. Meltzer et al. (Meltzer et al., 1990) proposed another PVC method, which corrects for PVE at CSF. Another method Erlandsson et al. also proposed another GTM-based method, region-based voxel-wise (RBV) (Erlandsson et al., 2012), which has been shown to be very similar to IY but requires MTC to provide initial values for each ROI. In contrast, IY does not require this initialization and provided stable measures with rapid convergence.
We recently reported widespread synaptic reductions in AD compared to CN participants in a larger cohort using cerebellum as a reference region (Mecca et al., 2020). Here, we only included a subset of those subjects who underwent arterial blood sampling for kinetic modeling, and we used CS as reference region for computation of BPND. Although cerebellum may have unique practical advantages as a reference region in studies of AD, we are also interested in using 11C-UCB-J to assess SV2A/synaptic density in multiple neuropsychiatric disorders, where CS may be of more generally utility. In the present study, no VT difference (averaged over CN and AD) was found in CS between non-PVC and IY PVC (4.02±0.56 vs. 4.02±0.56, p=.13, two tailed paired t-test), indicating no PVE in the CS region. However, in our recent study (Mecca et al., 2020), cerebellum yielded greater effect sizes for between-group differences, presumably due to less variability in the larger cerebellum region than the 2-mL CS region but potentially also to small group differences in displaceable uptake in the CS region (discussed in (Mecca et al., 2020)). However, a larger CS region corrected for PVE by IY may merit further investigation as an alternative to cerebellum in AD studies, if it can provide an accurate and unbiased estimate of non-displaceable binding without introducing additional variability.
FreeSurfer was used in this study to perform brain ROI segmentation, whereas a study by Goubran et al. (Goubran et al., 2020) showed that error may occur in hippocampus segmentation using FreeSurfer. To assure the segmentation quality, for every study, a radiologist (TT) examined the segmentation map by superposing it with the MR image in a slice-by-slice fashion.
Finally, we summarize our study limitations and future directions: 1) As discussed earlier, the GM:WM contrast for 11C-UCB-J is relatively stable through the entire scan, which is unique to 11C-UCB-J and therefore, generalization to other tracers should be studied carefully in the future; 2) The focus of this study is performing PVC analysis for absolute quantification using dynamic 11C-UCB-J, but note that such results can be a simplified 11C-UCB-J protocol, per Naganawa et al. (Naganawa et al., 2021). In the future, we will perform PVC evaluation for SUV-ratios acquired by the short acquisition protocols; 3) The HRRT has better resolution than most commercial scanners. In the future, we will perform head-to-head PVC comparison between HRRT and other commercial PET scanners, e.g., Siemens Biograph mCT; 4) In this study, we assumed the HRRT image PSF to be a single spatial invariant Gaussian function, in part due to its dual-layer crystal design to minimize depth-of-interaction effects. As reported previously, alternative resolution models for the HRRT are spatial variant (Jian et al., 2015) or a sum of two Gaussian functions with different FWHMs (Comtat et al., 2008). In the future, we will examine such effects.
Conclusion
11C-UCB-J binding is significantly lower in the hippocampus of AD patients compared to CN, but due to volume reductions, PVC is needed. The choice of PVC algorithm is important, and the assumptions behind each algorithm should be carefully assessed. The MG algorithm yielded much larger increases in VT and BPND than IY due to different assumptions, specifically WM uniformity and apparent activity in the CSF. Considering these factors as well as the inclusion of inter-GM correction, IY provides a theoretically more accurate PVC method than MG. Using IY, the statistical significance and the magnitude of group differences in hippocampus and entorhinal cortex increased. The magnitude of group differences between AD and CN were substantially larger in PVC-corrected PET measures than volumetric MR measures.
Supplementary Material
Acknowledgment
This work was funded by NIH grants P50AG047270, R01AG052560, R01AG062276, K23AG057794, P30AG066508. This publication was also made possible by CTSA grant UL1 TR000142 from the National Center for Advancing Translational Sciences. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official view of NIH.
Footnotes
Declaration of Competing Interest
The other authors declare that they have no conflict of interest.
Ethics declarations
Ethical approval
The study protocol involving human participants was approved by the Yale Human Investigation Committee, the Yale-New Haven Hospital Radiation Safety Committee, and the Yale University Radiation Safety Committee. Study procedures were performed in accordance with federal guidelines and regulations of the United States for the protection of human research subjects contained in Title 45 Part 46 of the Code of Federal Regulations (45 CFR 46).
Consent to participate
Informed consent was obtained from all individual participants included in the study.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2021.118248.
References
- Alzheimer’s Association, 2017. 2017 Alzheimer’s disease facts and figures. Alzheimers Dement 13, 325–373. [Google Scholar]
- Carson RE, Barker W, Liow J−S, Adler S, Johnson C, 2003. Design of a motion–compensation OSEM list-mode algorithm for resolution-recovery reconstruction of the HRRT. IEEE Nucl. Sci. Symp. Conf. Rec.M16–6. [Google Scholar]
- Chen MK, Mecca AP, Naganawa M, Finnema SJ, Toyonaga T, Lin SF, et al. , 2018. Assessing synaptic density in alzheimer disease with synaptic vesicle glycoprotein 2A positron emission tomographic imaging. JAMA Neurol. doi: 10.1001/jamaneurol.2018.1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M−K, Mecca AP, Naganawa M, Gallezot J−D, Toyonaga T, Mondal J, et al. , 2021. Comparison of [11C]UCB-J and [18F]FDG PET in Alzheimer’s disease: a tracer kinetic modeling study. J. Cereb. Blood Flow Metab. doi:, 0:0271678X211004312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comtat C, Sureau FC, Sibomana M, Hong IK, Sjoholm N, Trebossen R, 2008. Image based resolution modeling for the HRRT OSEM reconstructions software. In: 2008 IEEE Nuclear Science Symposium Conference Record, pp. 4120–4123. [Google Scholar]
- de Jong HW, van Velden FH, Kloet RW, Buijs FL, Boellaard R, Lammertsma AA, 2007. Performance evaluation of the ECAT HRRT: an LSO-LYSO double layer high resolution, high sensitivity scanner. Phys. Med. Biol 52, 1505–1526. doi: 10.1088/0031-9155/52/5/019. [DOI] [PubMed] [Google Scholar]
- Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF, 2012. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys. Med. Biol 57, R119–RR59. [DOI] [PubMed] [Google Scholar]
- Finnema SJ, Nabulsi NB, Eid T, Detyniecki K, Lin S-f, Chen M−K, et al. , 2016. Imaging synaptic density in the living human brain. Sci. Transl. Med 8. doi: 10.1126/scitranslmed.aaf6667, 348ra96–ra96. [DOI] [PubMed] [Google Scholar]
- Finnema SJ, Nabulsi NB, Mercier J, Lin SF, Chen MK, Matuskey D, et al. , 2018. Kinetic evaluation and test-retest reproducibility of [(11)C]UCB-J, a novel radioligand for positron emission tomography imaging of synaptic vesicle glycoprotein 2A in humans. J. Cereb. Blood Flow Metab 38, 2041–2052. doi: 10.1177/0271678X17724947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, 2012. FreeSurfer. Neuroimage 62, 774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goubran M, Ntiri EE, Akhavein H, Holmes M, Nestor S, Ramirez J, et al. , 2020. Hippocampal segmentation for brains with extensive atrophy using three-dimensional convolutional neural networks. Hum. Brain Mapp. 41, 291–308. doi: 10.1002/hbm.24811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve DN, Salat DH, Bowen SL, Izquierdo-Garcia D, Schultz AP, Catana C, et al. , 2016. Different partial volume correction methods lead to different conclusions: an (18)F-FDG-PET study of aging. Neuroimage 132, 334–343. doi: 10.1016/j.neuroimage.2016.02.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jian Y, Yao R, Mulnix T, Jin X, Carson RE, 2015. Applications of the line-of-response probability density function resolution model in PET list mode reconstruction. Phys. Med. Biol 60, 253–278. doi: 10.1088/0031-9155/60/1/253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X, Mulnix T, Gallezot JD, Carson RE, 2013. Evaluation of motion correction methods in human brain PET imaging–a simulation study based on human motion data. Med. Phys 40, 102503. doi: 10.1118/1.4819820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi A, Scheinost D, Okuda H, Belhachemi D, Murphy I, Staib LH, et al. , 2011. Unified framework for development, deployment and robust testing of neuroimaging algorithms. Neuroinformatics 9, 69–84. doi: 10.1007/s12021-010-9092-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotasidis FA, Angelis GI, Anton-Rodriguez J, Markiewicz P, Lionheart WR, Reader AJ, et al. , 2014. Image-Based Spatially Variant and Count Rate Dependent Point Spread Function on the HRRT. IEEE T Nucl. Sci 61, 1192–1202. [Google Scholar]
- Mecca AP, Barcelos NM, Wang S, Bruck A, Nabulsi N, Planeta-Wilson B, et al. , 2018. Cortical beta-amyloid burden, gray matter, and memory in adults at varying APOE epsilon4 risk for Alzheimer’s disease. Neurobiol. Aging 61, 207–214. doi: 10.1016/j.neurobiolaging.2017.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mecca AP, Chen M−K, O’Dell RS, Naganawa M, Toyonaga T, Godek TA, et al. , 2020. In vivo measurement of widespread synaptic loss in Alzheimer’s disease with SV2A PET. Alzheimer’s Dement. doi: 10.1002/alz.12097, n/a.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer CC, Leal JP, Mayberg HS, Wagner HN Jr., Frost JJ, 1990. Correction of PET data for partial volume effects in human cerebral cortex by MR imaging. J. Comput. Assist. Tomogr. 14, 561–570. doi: 10.1097/00004728-199007000-00011. [DOI] [PubMed] [Google Scholar]
- Muller-Gartner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, et al. , 1992. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: mRI-based correction for partial volume effects. J. Cereb. Blood Flow Metab 12, 571–583. doi: 10.1038/jcbfm.1992.81. [DOI] [PubMed] [Google Scholar]
- Nabulsi NB, Mercier J, Holden D, Carre S, Najafzadeh S, Vandergeten MC, et al. , 2016. Synthesis and preclinical evaluation of 11C-UCB-J as a PET tracer for imaging the synaptic vesicle glycoprotein 2A in the brain. J. Nucl. Med 57, 777–784. doi: 10.2967/jnumed.115.168179. [DOI] [PubMed] [Google Scholar]
- Naganawa M, Gallezot J−D, Finnema SJ, Matuskey D, Mecca A, Nabulsi NB, et al. , 2021. Simplified quantification of <sup>11</sup>C-UCB-J PET evaluated in a large human cohort. J. Nucl. Med 62, 418. doi: 10.2967/jnumed.120.243949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overk CR, Masliah E, 2014. Pathogenesis of synaptic degeneration in Alzheimer’s disease and Lewy body disease. Biochem. Pharmacol 88, 508–516. doi: 10.1016/j.bcp.2014.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossano S, Toyonaga T, Finnema SJ, Naganawa M, Lu Y, Nabulsi N, et al. , 2019. Assessment of a white matter reference region for (11)C-UCB-J PET quantification. J. Cereb. Blood Flow Metab doi: 10.1177/0271678X19879230, 271678X19879230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset O, Rahmim A, Alavi A, Zaidi H, 2007. Partial volume correction strategies in PET. PET Clin. 2, 235–249. doi: 10.1016/j.cpet.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Rousset OG, Ma Y, Evans AC, 1998. Correction for partial volume effects in PET: principle and validation. J. Nucl. Med 39, 904–911. [PubMed] [Google Scholar]
- Schwarz CG, Gunter JL, Lowe VJ, Weigand S, Vemuri P, Senjem ML, et al. , 2019. A comparison of partial volume correction techniques for measuring change in serial amyloid PET SUVR. J. Alzheimers Dis. 67, 181–195. doi: 10.3233/JAD-180749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedmak G, Judas M, 2019. The total number of white matter interstitial neurons in the human brain. J. Anat 235, 626–636. doi: 10.1111/joa.13018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LM, Zhu R, Strittmatter SM, 2018. Disease-modifying benefit of Fyn blockade persists after washout in mouse Alzheimer’s model. Neuropharmacology 130, 54–61. doi: 10.1016/j.neuropharm.2017.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soret M, Bacharach SL, Buvat I, 2007. Partial-volume effect in PET tumor imaging. J. Nucl. Med. 48, 932–945. [DOI] [PubMed] [Google Scholar]
- Terry RD, Masliah E, Salmon DP, Butters N, DeTeresa R, Hill R, et al. , 1991. Physical basis of cognitive alterations in Alzheimer’s disease: synapse loss is the major correlate of cognitive impairment. Ann. Neurol 30, 572–580. doi: 10.1002/ana.410300410. [DOI] [PubMed] [Google Scholar]
- Thomas BA, Cuplov V, Bousse A, Mendes A, Thielemans K, Hutton BF, et al. , 2016. PETPVC: a toolbox for performing partial volume correction techniques in positron emission tomography. Phys. Med. Biol 61, 7975–7993. doi: 10.1088/0031-9155/61/22/7975. [DOI] [PubMed] [Google Scholar]
- Thomas BA, 2012. Improved Brain PET Quantification Using Partial Volume Correction Techniques. University College; London, London, UK. [Google Scholar]
- Toyonaga T, Smith LM, Finnema SJ, Gallezot JD, Naganawa M, Bini J, et al. , 2019. In vivo synaptic density imaging with (11)C-UCB-J detects treatment effects of saracatinib in a mouse model of Alzheimer disease. J. Nucl. Med 60, 1780–1786. doi: 10.2967/jnumed.118.223867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, et al. , 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Watson CC, Newport D, Casey ME, 1996. A single scatter simulation technique for scatter correction in 3D pet. Comp. Imag. Vis. 4, 255–268. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.