Unusually thick shear-softening surface of micrometer-size metallic glasses

Summary

The surface of glass is crucial for understanding many fundamental processes in glassy solids. A common notion is that a glass surface is a thin layer with liquid-like atomic dynamics and a thickness of a few tens of nanometers. Here, we measured the shear modulus at the surface of both millimeter-size and micrometer-size metallic glasses (MGs) through high-sensitivity torsion techniques. We found a pronounced shear-modulus softening at the surface of MGs. Compared with the bulk, the maximum decrease in the surface shear modulus (G) for the micro-scale MGs reaches ~27%, which is close to the decrease in the G upon glass transition, yet it still behaves solid-like. Strikingly, the surface thickness estimated from the shear-modulus softening is at least 400 nm, which is approximately one order of magnitude larger than that revealed from the glass dynamics. The unusually thick surface is also confirmed by measurements using X-ray nano-computed tomography, and this may account for the brittle-to-ductile transition of the MGs with size reductions. The unique and unusual properties at the surface of the micrometer-size MGs are physically related to the negative pressure effect during the thermoplastic formation process, which can dramatically reduce the density of the proximate surface region in the supercooled liquid state.

Graphical abstract

Public summary

• •The shear modulus and thickness of metallic glass (MG) surface is determined through torsion testing on micrometer-size wires
• •The surface region of MG wires has a significant shear-modulus softening close to the supercooled liquid, yet still behaves solid-like
• •The thickness of the soft surface of MG wires is at least 400 nm, which is about one order of magnitude larger than those revealed from surface dynamics
• •The unusually thick surface accounts for the brittle-to-ductile transition of the MGs with size reduction

Introduction

The surface of glass has become a fascinating and active research area owing to its fundamental importance and technological interest. With reduced constraint on the surface atoms, the glass surface could exhibit unique properties inaccessible by its bulk counterpart, and is crucial for understanding many fundamental processes and properties of glass solids, including glass transition, relaxation dynamics, and mechanical performance.1, 2, 3 For example, the glass surface displays enhanced atomic dynamics with several orders of magnitude faster than that of the bulk and behaves as “liquid-like,”4, 5, 6 which has a pronounced effect on glass transition and crystallization as the size of the glass is reduced.7, 8, 9, 10 Studies on polymer thin films have revealed that the glass transition temperature can be significantly reduced when the film thickness is below a critical value.^7,8 On the other hand, the surface mobility increases much more slowly with increasing temperature than that in bulk, resulting in anomalous thermal stability⁹ and crystallization behaviors, such as the formation of superlattice at the surface.¹⁰ In the recent work by Ma et al., the fast surface dynamics enabled the cold joining of metallic glass (MG) ribbons under ultrasonic vibrations, which is used to synthesize bulk MGs or metallic glass-glass composites.¹¹ The surface also plays an important role in many mechanical behaviors and properties in glasses, such as lubrication and friction,¹² wear,¹³ corrosion,¹⁴ and irradiation,¹⁵ which are well known to occur at the surface. Proper modifications or treatments¹⁶ at glass surfaces have been shown to effectively improve the plasticity/ductility of MGs due to impeding the propagation of shear bands or cracks by the surface layer.

Despite its fundamental and practical importance, the nature of the surface of glass remains poorly understood. A common notion is that the glass surface is a nanometer-thin layer that behaves in liquid-like fashion. Earlier studies proposed that the liquid-like dynamics only exist in a very thin surface layer with a thickness^17,18 comparable with the size of cooperatively rearranging regions (on the order of 10 Å) at temperatures near the glass transition temperature T_g. Later, direct measurements¹⁹ of thin polymer films showed that the T_g is largely reduced when the size is below several tens of nanometers, indicating that the thickness of the surface layer is much larger than the size of the cooperatively rearranging regions. This has been confirmed by precise probing of the distribution of localized T_g or spatial dynamics from the glass surface to the inner region, which shows that the enhanced surface dynamics could extend dozens of nanometers into the interior of glasses. However, compared with the surface dynamics, the mechanical properties of glass surface have rarely been studied and reported due to the difficulty of experimental characterization. The nanoindentation technique may detect the surface's hardness and modulus, but it is difficult to exclude the effect of the adjacent region near the surface. Nevertheless, friction and wear behaviors of various glasses^12,13 suggest that the mechanical responses of the glass surface may behave in solid-like manner and exist in a region much thicker than that of the liquid-like region, as the glass dynamics reveal.

In this study, using high-sensitivity torsion techniques we found a shear-modulus softening region at the surface of both millimeter-size and micrometer-size metallic glasses. The surface exhibits a softening of the shear modulus as large as ~27% relative to the bulk, which is close to the instantaneous shear modulus upon glass transition. The surface thickness estimated from the shear-modulus softening and X-ray nano-computed tomography (CT) extends at least 400 nm, which is strikingly larger than that revealed from the glass dynamics. The underlying physics of the remarkable surface properties, as well as their correlation with size-induced brittle-ductile transition in MGs, are also discussed.

Results

Shear-modulus softening at the surface of bulk MGs and MGWs

Micrometer metallic glassy wires (MGWs) were made by hot-drawing bulk MG rods in the supercooled liquid region (see materials and methods and Figure S1). Figures 1A and 1B show images of micrometer-size Pd₄₀Ni₁₀Cu₃₀P₂₀ MGWs with different diameters viewed by an optical camera and scanning electron microscope, respectively. It can be seen that the hot-drawn MGWs exhibit a smooth surface and excellent roundness. The amorphous nature of the MGWs was confirmed using the broad halo in X-ray diffraction measurement (Figure S2). The torsion tests for the MGWs were conducted using a high-resolution micro-torsion tester, as shown in Figure 1C. More details of the micro-torsion tester are given in materials and methods. The reliability of the micro-torsion tester was verified using standard micrometer tungsten wires, as shown in Figures S3–S5 and Table S1. Figures 1D–1H show the typical in situ torsion process for the MGW with a diameter of 86 μm, whereby the sample is axially twisted with surface shear strain increasing from 0% to 4%.

Figure 1.

Hot-drawn MGWs and micro-torsion tests

(A and B) Optical (A) and scanning electron microscopy (B) images of the hot-drawn MGWs show good diameter uniformity and surface quality.

(C) The high-resolution micro-torsion tester used in this work.

(D–H) In situ view of an 86-μm-diameter MGW being loaded in torsion (D) with an increased surface shear strain from 0% to 4% (E–H).

If one applies a torque T to a cylindrical sample with a homogeneous shear modulus from the surface to the inner core, the shear stress, τ_s and the shear strain, γ_s, at the surface can be evaluated as follows:²⁰

$${\tau }_{\text{s}}=\frac{16T}{\pi D^3},\begin{array}{ll}\hfill & \hfill \end{array}{\gamma }_{\text{s}}=\frac{D\phi }{2L}\text{,}$$ (Equation 1)

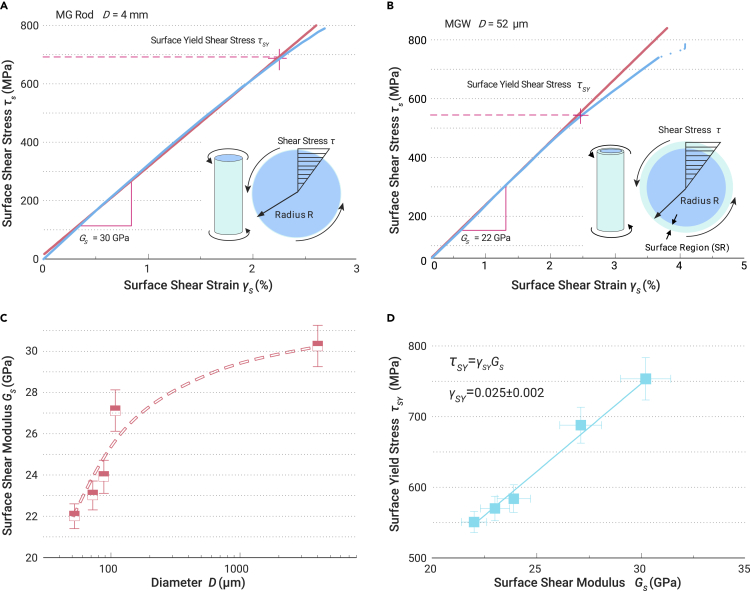
where D and L are the diameter and the gauge length of the cylindrical sample, respectively, and φ (rad) is the measured torsion angle. The surface shear modulus G_s can be obtained from the slope of the linear τ_s-γ_s relation. If the cylindrical sample is composed of a soft surface layer and a hard core with a shear modulus G_s and G_i, respectively, the shear stress τ_s and shear strain γ_s at the surface can also be given by Equation 1 based on the force balance at the surface-inner interface (see materials and methods). The surface shear modulus G_s can be obtained by fitting the slope of the linear τ_s-γ_s relation. Figures 2A and 2B show the typical τ_s-γ_s curves obtained from the tested torque-angle (T − φ) data for a bulk MG rod with a diameter of 4 mm and an MGW with a diameter of 52 μm, respectively. As can be seen, the τ_s-γ_s curve of the bulk MG rod is nearly linearly elastic, with only a small deviation before the final fracture. In contrast, the curve of the MGW shows an obvious deviation from linear elasticity at an intermediate point, indicating an obvious inelasticity or plasticity during the torsion process. For a cylinder sample loaded in torsion, material yielding will first occur at the surface region due to the gradient distribution of the shear stress on the cross-section of the cylinder, as illustrated in the insets of Figures 2A and 2B. Therefore, the intermediate deviation in the τ_s-γ_s curve of the MGW indicates that a soft layer at the surface first yields as the torque reaches a critical value. For the bulk MG rod, however, the thickness of the surface layer is too thin as compared with the diameter (see the inset of Figure 2A), and the influence of surface yielding on the τ_s-γ_s curve is small. This resulted in a nearly linear elastic behavior in the τ_s-γ_s curve before the final fracture.

Figure 2.

Measured shear modulus and yield stress showing obvious softening at the surface of the MGWs

(A and B) Surface shear stress-strain (τ_s-γ_s) curves for the 4-mm-diameter bulk MG rod (A) and the 52-μm-diameter MGW (B). Insets show the gradient distribution of the shear stress τ in the cross-sections of the cylinders under the torsion load.

(C) Surface shear modulus (G_s) of the MGs decreases with decreasing diameters, where the maximum reduction in G_s is ~27%.

(D) The surface yield stress τ_SY of the MGs is linearly correlated with G_s by τ_SY=γ_SYG_s, with a yield surface shear strain γ_SY = 0.025 ± 0.002.

By fitting the linear elastic segment of the τ_s-γ_s curve, the surface shear modulus G_s for the bulk MG rod and the MGW were determined to be 30 ± 1 GPa and 22.0 ± 0.6 GPa, respectively. The surface region of the MGW is much softer than that of the bulk MGW rod, with a maximum reduction of ~27% in the shear modulus. Such a large reduction in the shear modulus implies that the amorphous structure at the surface of the MGW is distinctly different from that of the bulk structure. Strikingly, the reduced shear modulus is very close to the instantaneous shear modulus (G_∞) of supercooled liquids.²¹ The shear-modulus reduction could be further extrapolated into the nanometer-size MGWs. According to the reduction trend, an MGW with a diameter of ~100 nm could have a surface shear modulus of 4.8 GPa, very close to that of the liquid state, which is consistent with the liquid-like surface properties as reported in the previous studies.^5,10,11 It is also notable that compared with the shear modulus (~35 GPa) of the bulk MG with the same composition measured using the ultrasonic method,²¹ the G_s of the 4-mm-diameter MG rod measured here is still lower by ~14%. This result indicates that the shear-softening region still exists at the surface of bulk MGs.

With this method, the surface shear moduli of the MGWs with different diameters were obtained (Figure S6) from all of the τ_s-γ_s curves of the various MGWs. As shown in Figure 2C, the G_s of the MGWs gradually decreases with the reduction in diameter, implying a size dependence of the surface softening. The shear yield stress of the surface region τ_SY was determined for the MGWs with different diameters by taking the point at which the curve deviates significantly from linearity. The τ_SY of the MGs also shows a size dependence similar to that of G_s. Figure 2D gives the plot of the τ_SY versus the G_s for the MGWs with different diameters, which can be well fitted by the relation τ_SY = γ_SYG_s with the fitted value γ_SY =0.025 ± 0.002. The linear relation between τ_SY and G_s implies that the surface region of the different MGWs has a constant critical shear strain at the yielding point. According to the cooperative shearing model (CSM),²² the decreasing shear modulus of a glass will reduce the energy barrier for the plastic shear flow, but will not change the critical strain for the shear process. The constant value of the shear strain γ_SY obtained from the torsion tests here is also close to the average values (γ_SY = 0.027 ± 0.002) obtained from the compression tests of ~30 MG samples with different compositions.²² It is also noteworthy that the thick surface region revealed by the shear-modulus softening has a solid-like nature, since the surface could sustain static torsion load. This is different from the nanometer-thin liquid-like surface layer as revealed by the dynamics of glasses.^4,19 We also performed analysis of the surface chemical compositions of the MGWs through X-ray photoelectron spectroscopy (XPS) and energy-dispersive X-ray spectroscopy (EDX) on the surface of an MGW. As shown in Figure S7, the XPS results show that the measured fraction of oxygen is quite small (~1.41%), and the EDX results also show that no obvious oxidation occurs on the surface of the MGW. It can be inferred that there may be a very small amount of oxides existing either in the form of dispersed metallic oxide particles or in the form of an ultrathin oxidation surface layer, which will not affect the measurement of the surface shear modulus.

After thermal annealing, the shear modulus at the surface region will increase as compared with that of the as-cast state, e.g., from 27 GPa to 32 GPa for the annealed MGWs with a diameter of ~101.5 μm (Figure S8). However, the G of the inner core also increases after annealing and is estimated to be ~37 GPa based on the ultrasonic data of the bulk MGs.²¹ In this sense, thermal annealing will diminish the shear-modulus difference between the surface region and the inner core, yet will not completely eliminate the difference. The annealing-induced increase in the shear modulus of MGs can be generally attributed to the structural relaxation via the annihilation of free volume.²³ However, possibly due to the different constraints for the atoms at the surface and inner region,²⁴ the annealing-induced diffusion of the free volumes did not lead to a uniform distribution of the shear modulus throughout the entire sample.

Thickness of the shear-softening surface

We next estimate the thickness of the surface reflected by the shear-modulus softening. With the increase in torque, the surface region of the MGWs will first yield, while the inner core is still in the elastic regime. Thus, the increase in torque will deviate from the initial linear elastic portion after surface yielding. Assuming a perfect elastic-plastic deformation behavior for the glass surface region, the torque T after the surface yielding is calculated as^20,25

$$T=2\pi \left[{\int }_0^{R-SR}{\tau }_{\text{i}}\left(\rho \right){\rho }^{2}d\rho +{\int }_{R-SR}^R{\tau }_{\text{SY}}{\rho }^{2}d\rho \right]\text{,}$$ (Equation 2)

where R is the radius of the cylinder, SR is the thickness of the soft surface region, τ_i(ρ) is the shear stress of the inner core at the radial position ρ, and τ_SY is the yield stress of the surface region. After the surface yielding, τ_SY remained at a constant value while τ_i(ρ) linearly increased with strain. The τ_i(ρ) can be evaluated using τ_i(ρ)= G_iγ_i(ρ) = G_iρφ_i/L, where G_i and φ_i and the shear modulus and the torsion angle of the inner core, respectively, and L is the gauge length of the sample. In this way, the torque T after the surface yielding is integrated to become

$$T=\left[\frac{\pi G_{\text{i}}}{2L}{\left(R-SR\right)}^4\right]\phi +\frac{2\pi {\tau }_{\text{SY}}}{3}\left[R^3-{\left(R-SR\right)}^3\right]\text{.}$$ (Equation 3)

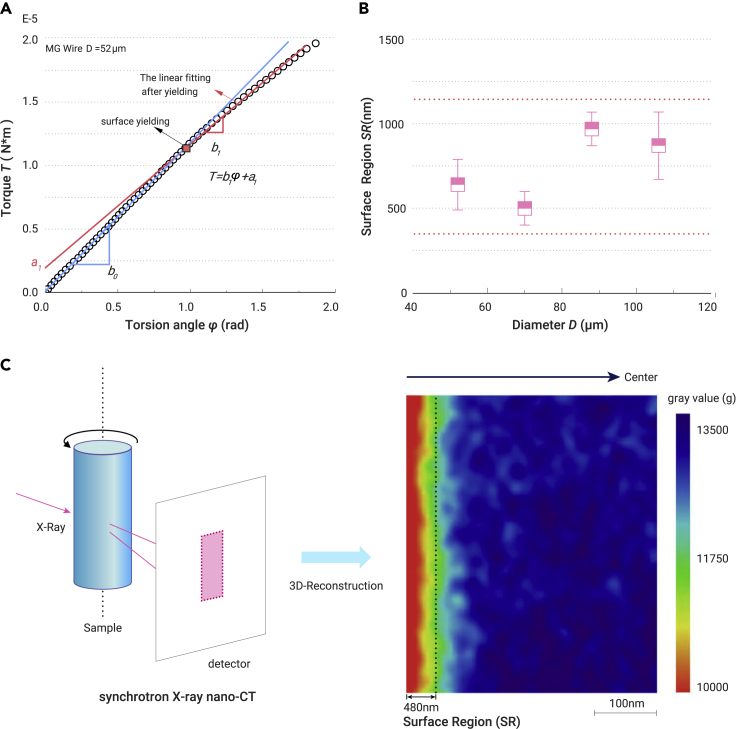
According to Equation 3, one can see that the torque T is linearly related to φ by T= b₁φ + a₁, where the slope b₁ = πG_i(R − SR)⁴/2L and the intercept a₁ = 2πτ_SY[R³ − (R − SR)³]/3, at the initial segment after the surface yielding. As such, the thickness of the surface region SR can be obtained by fitting the Tφ data just after surface yielding. Figure 3A shows the typical experimental T-φ curve for the 52-μm-diameter MGW under torsion load. In the elastic deformation stage, the torque T linearly increases with the torsion angle φ (rad) along a slope of b₀. Until the surface region yields, the curve starts to deviate from linearity and then continues to increase in a quasi-linear manner. By fitting the T-φ curve just after the deviation with Equation 3, we can obtain the thickness of the surface region of MGWs. With this method, we evaluated the SR of the MGWs with different diameters (52 μm, 70 μm, 88 μm, and 108 μm) (Figure 3B). It can be seen that the thickness of the softening surface region is in the range of 400–1,000 nm and seems to have no good scaling relation with the diameter of the samples. Here it is interesting that the measured SR with the mechanical method is almost one order of magnitude larger than that estimated from glass surface dynamics in which the thickness of the surface is around a few tens of nanometers or even smaller.²⁶ Different from the shear-modulus softening, the thickness measured here seems to have no direct correlation with the size of MGs, implying a generalized formation mechanism for the surface region of MGs. After the final torsion fracture, we examined the fracture morphologies of the MGWs where indeed a surface layer with a significant plastic-flow behavior was observed (Figure S9). The thickness of this plastic-flow layer is approximately 500 nm, which is well consistent with the results from the fitting of the Tφ curve.

Figure 3.

Determination of the thickness of the surface region of MGs

(A) After surface yielding, the initial segment of the torque-angle (Tφ) curve for the 52-μm-diameter MGW is linearly fitted by the equation T = b₁φ + a₁.

(B) The determined thicknesses of the surface regions for the MGWs with different diameters is in the range of 400–1,000 nm.

(C) Synchrotron X-ray nano-CT experiment detecting the microstructure of the MGWs. The 2D gray-value image (longitudinal central cross-section near the surface) of an MGW clearly shows a low-density surface region with a thickness of ~500 nm.

The analysis above is primarily based on a clear-cut interface model in which the shear modulus of the surface region is assumed to be constant, whereas in real MGs the shear modulus may continuously increase from the surface to the inner. If one assumes that the surface has a continuously varied elastic modulus, simple theoretical analysis shows that the shear modulus measured from the linear portion of the stress-strain curve is the average shear modulus weighted by ρ² of the surface region (ρ is the distance from the point at the surface region to the center). However, the thickness estimated from the diffusive interface is the same as that obtained from the clear-cut interface model.

Nano-computed tomography of MGWs

The thickness of the surface region is also confirmed by the synchrotron X-ray nano-CT. A two-dimensional (2D) gray-value (g) image near the surface is cut from the longitudinal central cross-section of an MGW's three-dimensional (3D) structure, which is reconstructed by synchrotron X-ray nano-CT, as shown in Figure 3C. The g of the local region, i.e., the longitudinal central cross-section of the constructed 3D structure of the axisymmetric MGW near the surface, has a linear relation with the local absorption coefficient of the tested sample, which is positively proportional to the local density of the studied material. In the inner portion, the inhomogeneous distribution of g suggests fluctuations in local densities or structural heterogeneity of the MGWs. Near the surface region, the g is much smaller than that of the inner portion, indicating a low-density region at the surface. The thickness of the low-density surface region is ~500 nm, which is in good agreement with the evaluated value from the fitting results. It is worth noting that the thickness of the soft surface region obtained here coincides with the critical size for the occurrence of the brittle-to-ductile transition of MGs reported in the literature.^27,28 When the size of MGs is reduced below approximately 400 nm, the deformation mechanism changes from shear band formation to homogeneous deformation, and the plasticity is abruptly enhanced. It is anticipated that the pronounced shear-modulus softening in the surface region may closely correlate with the size-induced brittle-to-ductile transition in MGs.

Discussion

The torsion tests and nano-CT experiments clearly demonstrated that there is an unusual thick shear-softening region at the surface of MGs, and the thickness of the region (>400 nm) is nearly one order of magnitude larger than that obtained from glass dynamics (a few tens of nanometers).²⁶ However, it should be stated that what was measured using the torsion test is the average shear modulus of the surface region, while the surface of real MGs should be a region with a continuously varied elastic modulus or density from the top surface to the inner core. In this case, the top layer on the surface region may have a very low shear modulus and high atomic mobility, similar to that of liquids. Hence, the top layer of the surface region is merely the “liquid-like” glass surface, as extensively studied in the literature. In fact, the thickness of the liquid-like surface was estimated from the direct dynamic measurements directly, such as by electronic correlation microscopy²⁶ or indirectly via the measurements on T_g.^4,8 Beneath the top liquid-like layer there is still a region with significant softening, but it behaves in “solid-like” manner. In this sense, our finding of the thick surface region over 400 nm is not contradictory to the liquid-like surface layer of a few tens of nanometers reported in many previous studies.

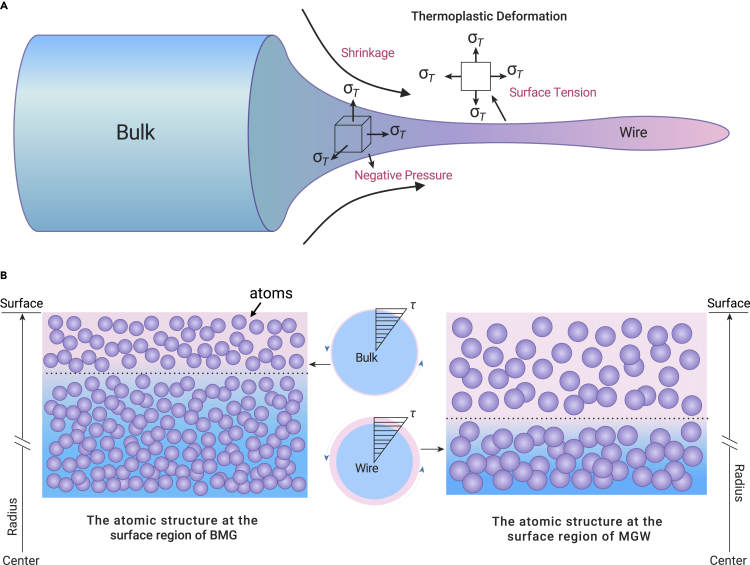
The main finding of the present work is that the shear-modulus softening of glass surface shows a size dependence. This has not been revealed by previous studies, implying that the formation process of the MGWs has an important effect on softening at the surface. The MGWs were formed by drawing the bulk MG rods in the supercooled liquid region, as schematically shown in Figure 4A. During this process, the MG rod in the supercooled liquid state is subjected to tensile drawing stress along the axis direction. In addition, the constraint of the surface tension stress on the rapid shrinkage of the cross-section of the rod will also result in tension stress along the radial and peripheral directions (Figure 4A). Therefore, the drawing sample in the supercooled liquid state is in fact subjected to triaxial tensile stresses along the axial, radial, and peripheral directions, i.e., in the negative pressure state (Figure 4A). According to previous studies, a liquid, such as water, tends to have a reduced density when subjected to negative pressure:24, 25, 26, 27, 28, 29, 30, 31 the larger the negative pressure, the larger the density reduction.²⁹ Due to this effect, the negative pressure should be relatively larger at the surface and gradually decrease toward the inner area and finally form a wire with a lower-density surface with abundant free volumes. In addition, the cooling rate during the drawing process should be very high considering that the drawing process is accomplished in a very short time (typically less than 1 s), while the diameter is reduced by approximately two orders of magnitude (from 1 mm to 52 μm) with a significant increase in the specific surface area. As a result, the abundant free volume can be frozen in the surface region³² (Figure 4B). This ultimately results in a pronounced shear-modulus softening at the surface of the MGWs. As the cooling rate during drawing is closely related to the ultimate diameter of the MGWs, we can attribute the unusual surface properties reported here to the combined effects of cooling rate, size, and negative pressure during the formation process of the MGWs.

Figure 4.

Schematic diagram illustrating the physical origin of surface softening of MGWs

(A) Negative pressure originates from the interaction between the abrupt diameter shrinkage and the surface tension in a bulk MG rod being drawn in the supercooled liquid state.

(B) Schematic diagram of the atomic structure (pink circles represent atoms) of the surface region of bulk MG (BMG) and MGW. Due to the high cooling rate, the atoms of the MGW are loosely packed with abundant free volume, causing pronounced surface softening.

As the second derivative of free energy with respect to the strain, elastic moduli are sensitive to the internal structure of glassy solids, and thus play an important role in understanding their properties.^12,33 Correlations between the elastic moduli and other physical properties, such as glass transition,³⁴ relaxations,³⁵ and deformations,³⁶ have been found in MGs. In principle, the elastic and plastic properties related to the internal structure of MGs can be tuned by rejuvenation,^37,38 and the rejuvenation of MGs to a liquid state can be achieved by continuous injection of external energies through thermal or mechanical methods. However, the change in elastic constants during the rejuvenation reported for bulk MGs is generally small.³⁹ Here, a pronounced shear-modulus softening was observed at the surface region of the MGWs. The maximum decrease in the shear modulus at the surface of the MGWs can reach ~27%, which would not be accessible by the bulk MGs for all events. Such a large reduction in the shear modulus implies that the amorphous structure at the surface of the MGWs is distinctly different from that of the bulk structure. In fact, the shear modulus of the glass surface is almost close to the instantaneous shear modulus (G_∞) of the supercooled liquid, implying that the surface may have an amorphous structure similar to the static structure of the supercooled liquid.

It is noted that the pronounced shear-modulus softening at the surface of the MGWs influences the overall deformation behaviors of the MGWs. In general, G is considered to be the primary parameter that controls the energy barrier of elementary shear events.²² Lowering G_s renders the occurrence of a shear plastic flow that is much easier in the surface region.²² This ultimately affects the overall deformation and fracture of glasses.⁴⁰ We investigated the fracture morphology of the MGWs and the bulk MG rod after torsion fracture, as shown in Figure 5. The bulk MG rod fails at an angle of 47° with respect to the axial direction (Figure 5A). Since the loading mode is pure shear, the fracture along ~45° inclined to the axial direction in the torsion in fact corresponds to the fracture vertical to the loading axis in tension, suggesting a brittle fracture behavior dominated by the Mode I crack, similar to what occurs in ceramics.⁴¹ The fracture angles of the MGWs, in contrast, are much smaller than that of the bulk MG rod and decrease with decreasing diameters, as shown in Figures 5B–5D. The fracture plane for the 52-μm-diameter MGW is nearly flat (Figure 5D), which corresponds to the Mode III crack and is the same as the torsion fracture of ductile alloys.⁴² With a size reduction, the fracture of the MGWs shows increased resistance to the Mode I crack and is gradually dominated by the Mode III crack, finally leading to an in-plane shear fracture. Thus, a transition from brittle to ductile in torsion fracture with decreasing size is identified in the MGs. For rod-shaped samples under torsion load, the fracture often is initiated at the surface region. Hence, the surface quality and properties are crucial to the fracture behaviors. In this study, the different torsion fracture behaviors between the MGWs and the bulk MG rods distinctly indicate the significant effect of pronounced surface softening on the overall deformation behaviors of MGs.

Figure 5.

Effects of surface softening on torsion fracture behavior of MGs

The fracture angle of MGs decreases with decreasing diameters (D = 4 mm [A], 108 μm [B], 88 μm [C], and 52 μm [D]), indicating a surface softening-induced brittle-to-ductile transition in the torsion fracture of MGs with size reduction.

Conclusion

In summary, we performed a series of torsion tests on both micrometer-size MGWs and bulk MG rods, from which a correlation between the shear modulus and the size of MGs was discovered. Shear-modulus softening behavior is found at the surface of the MGWs, with a maximum reduction of ~27%. The shear modulus and yield stress at the surface region of MGs are found to be size dependent, while the yield strain maintains a constant value. The thickness of the surface region of the MGWs with different diameters is determined to be at least 400 nm, which is much larger than that commonly revealed by surface dynamics (dozens of nanometers). The pronounced shear-modulus softening at the surface is related to the preparation conditions of the MGWs, such as cooling rate, size, and negative pressure effects. As most MGs (including bulk MGs) are obtained by the rapid quenching method from the liquid state, our results can be generic to all MGs quenched from liquids or supercooled liquids. In addition, it has been shown recently that MG films prepared by physical vapor deposition also exhibit a surface with pronounced shear-modulus softening.²⁴ Therefore, it seems that the phenomenon of softening of the surface region is universal, regardless of the preparation methods. This may be related to some universal feature of the glass surface. Finally, we note that many processes, such as friction, lubrication, wear, corrosion, and irradiation, are well known to occur on glassy surfaces. A softening surface with a thickness of hundreds of nanometers also has a great influence on the initiation and propagation of shear bands and cracks, thus affecting the plasticity and fracture of MGs. Hence, these findings regarding the properties of the softening surface region are also useful for tuning and designing the properties of glassy materials.

Materials and methods

Materials preparation and characterization

Pd₄₀Cu₃₀Ni₁₀P₂₀ (at atomic percent) MG was chosen for this study due to its excellent glass-forming and thermoplastic abilities. Alloy ingots were prepared by inductively melting appropriate amounts of high-purity elements Pd (purity: 99.99% in mass), Cu (purity: 99.99% in mass), Ni (purity: 99.99% in mass), and P (purity: 99.90% in mass) in a quartz tube under a Ti-gettered argon atmosphere. Glassy rod samples with different diameters (1 mm and 4 mm) were produced using the conventional suction casting method. MGWs with diameters ranging from 52 μm to 108 μm were made by drawing the 1-mm-diameter bulk MG rods in the supercooled liquid state.⁴³ The device and schematic diagram for drawing the MGWs are shown in Figure S1. By varying the drawing force, wires with different diameters and lengths were achieved. The smaller the drawing force, the smaller the diameter. The amorphous nature of all MG samples was verified using the X-ray diffraction method (Figure S2). After the tests, the torsion fracture morphology of both the bulk MG rods and the MGWs were examined using a scanning electron microscope (FEI XL30 S-FEG).

Torsion tests

Bulk MG rods 4 mm in diameter and 40 mm in length were used for the macro-torsion tests in which the samples were axially twisted to fracture at a strain rate of ~2 × 10⁻⁴ s⁻¹ with a commercial Instron E10000 testing system. The torsion tests of the MGWs were performed using a specially designed micro-torsion tester.^44,45 The MGW samples were made with a gauge length of ~1.7 mm and then axially twisted to fracture at a strain rate of ~2 × 10⁻⁴ s⁻¹. The micro-torsion tester was developed on the basis of electromagnetism whereby a coil-magnet component was used for actuating and torque measurement. When the current flowed through the coil, the torque, produced by the ampere force, could be easily measured by recording the current. The relationship between the torque and the current, which was calibrated using a Sartorius BP211D analytical balance, exhibits excellent linearity (Figure S3). Thus, the torque can be obtained by precise measurement of the current.

To obtain an estimation of the reliability of the micro-torsion tester, we measured the surface shear modulus (G_s) of tungsten wires in which all conditions were the same as those in the torsion tests of the MGWs. In contrast to the MGs, the surface shear stress-strain curves of the tungsten wires show a perfectly linear elasticity (Figure S4). The measured G_s is 159.5 GPa (±5%) for the 100-μm-diameter sample and 153.8 GPa (±5%) for the 50-μm-diameter sample. Both of these are very close to the intrinsic value, 156 GPa, of the tungsten given by MatWeb, confirming the reliability of the measured results of the MGs by the micro-torsion tester.

We also examined the shear-fracture strain of the MGWs using a different torsion device, which mainly consists of a commercial stepping motor (Figure S5) and is motivated by the current. During the torsion tests, the samples of the MGWs were also axially twisted at a strain rate of ~2 × 10⁻⁴ s⁻¹. Once the samples fractured, the tests were stopped and the rotation angle was recorded to evaluate the surface shear strain. The obtained fracture shear strain at the surface of the samples is 4.1% for the 88-μm-diameter MGW and 3.8% for the 52-μm-diameter MGW (Table S1), in good agreement with that measured by the micro-torsion tester. As such, the reliability of the micro-torsion tester was examined using a strain measurement. In addition, the micro-torsion technique was also verified using an improved torsion pendulum technique⁴⁶ with torsion tests of copper wires.

Synchrotron X-ray nano-CT detection

The density fluctuations of the MGW were detected using synchrotron X-ray nano-CT in a high-vacuum chamber at room temperature. The nano-CT test was performed using a synchrotron X-ray energy of 8 keV at beamline 4W1A of the Beijing Synchrotron Radiation Facility. The voxel size of the 3D structure reconstructed using the synchrotron X-ray nano-CT was 64.1 nm × 64.1 nm × 64.1 nm. A 32-bit float-type gray value (g) was assigned to each voxel of the reconstructed structure. The g of the local region in the structural image Figure 3C (i.e., the longitudinal central cross-section of the constructed 3D structure of the axisymmetric MGW near the surface) has a linear relation with the local absorption coefficient of the tested sample,⁴⁷ which is positively proportional to the local density of the studied material.⁴⁸ Thus, the local density fluctuations of the MGW near the surface can be reflected by the distribution of g (Figure 3C). The spatial resolution of the detecting tests reaches ~100 nm.

Determining the shear stress and shear strain at the surface

For an MGW composed of a soft surface layer with a thickness SR and a hard core with a radius (R − SR) under a torsion load, the relationship between the applied torque T and the shear stress can be written as follows:^20,25

$$T={\int }_0^{R-SR}{\tau }_{\text{i}}\left(\rho \right)2\pi {\rho }^{2}d\rho +{\int }_{R-SR}^R{\tau }_{\text{s}}\left(\rho \right)2\pi {\rho }^{2}d\rho \text{,}$$ (Equation 4)

where ρ is the radial position, τ_i(ρ) is the shear stress of the inner core, and τ_s(ρ) is the shear stress of the surface region. In the elastic regime, the shear stress can be evaluated by τ(ρ) = Gγ(ρ) = Gρφ/L, where φ is the torsion angle. G is the shear modulus. γ(ρ) is the shear strain. and L is the gauge length of the sample. By rearranging Equation 4, one can find

$$T={\int }_0^{R-SR}{G}_{\text{i}}\frac{\rho {\phi }_{\text{i}}}{L}2\pi {\rho }^{2}d\rho +{\int }_{R-SR}^R{G}_{\text{s}}\frac{\rho {\phi }_{\text{s}}}{L}2\pi {\rho }^{2}d\rho \text{,}$$ (Equation 5)

where G_i and φ_i is the shear modulus and the torsion angle of the inner core, respectively; and G_s and φ_s are the shear modulus and the torsion angle of the surface region, respectively. The torque T can be integrated to become

$$T=\frac{G_{\text{i}}{\phi }_{\text{i}}}{L}\frac{\pi }{2}\left[{(R-SR)}^4\right]+\frac{G_{\text{s}}{\phi }_{\text{s}}}{L}\frac{\pi }{2}\left[R^4-{(R-SR)}^4\right]\text{.}$$ (Equation 6)

The shear stress of the inner core τ_i(ρ) and the surface region τ_s(ρ) are balanced with each other at the interface ρ = (R − SR). Therefore, G_iφ_i(R − SR)/L = G_sφ_s(R − SR)/L. By rearranging Equation 6, one can find

$$T=\frac{\pi R^3}{2}\frac{G_{\text{s}}R{\phi }_{\text{s}}}{L}=\frac{\pi D^3}{16}{G}_{\text{s}}{\gamma }_{\text{s}}=\frac{\pi D^3}{16}{\tau }_{\text{s}}\text{,}$$ (Equation 7)

where D is the diameter of the MGW. The surface shear stress τ_s and surface shear strain γ_s can be written as follows:

$${\tau }_{\text{s}}=\frac{16T}{\pi D^3},{\gamma }_{\text{s}}=\frac{D{\phi }_{\text{s}}}{2L}\text{.}$$ (Equation 8)

Published Online: April 16, 2021