Generic Seebeck effect from spin entropy

Abstract

How magnetism affects the Seebeck effect is an important issue of wide concern in the thermoelectric community but remains elusive. Based on a thermodynamic analysis of spin degrees of freedom on varied d-electron-based ferromagnets and antiferromagnets, we demonstrate that in itinerant or partially itinerant magnetic compounds there exists a generic spin contribution to the Seebeck effect over an extended temperature range from slightly below to well above the magnetic transition temperature. This contribution is interpreted as resulting from transport spin entropy of (partially) delocalized conducting d electrons with strong thermal spin fluctuations, even semiquantitatively in a single-band case, in addition to the conventional diffusion part arising from their kinetic degrees of freedom. As a highly generic effect, the spin-dependent Seebeck effect might pave a feasible way toward efficient “magnetic thermoelectrics.”

Graphical abstract

Public summary

• •Magnetism can offer a significant contribution to thermoelectricity
• •A generic Seebeck effect exists in magnetic conductors as a result of transport spin entropy of delocalized d electrons
• •The magnetocaloric effect and the Seebeck effect are thermodynamically correlated with each other

Introduction

The Seebeck coefficient (α) is a key parameter determining the efficiency of useful thermoelectric devices. It measures temperature-difference-induced electric voltage in a conducting solid, being essentially a non-equilibrium thermal transport phenomenon. Nevertheless, in special circumstances this effect can be well depicted thermodynamically by employing thermodynamic state variables. One such example is the scaling at low-temperature limit, where electron diffusive transport is suppressed, between α and the electronic specific heat C_el—a fundamental thermodynamic property—in a wide range of materials spanning from simple to correlated metals.¹ Reflecting electron transport kinetics, diffusive characteristics such as the energy-dependent charge mobility can generate a large Seebeck effect too,² as was also revealed by charge-scattering engineered thermoelectricity in nanoscaled materials.³

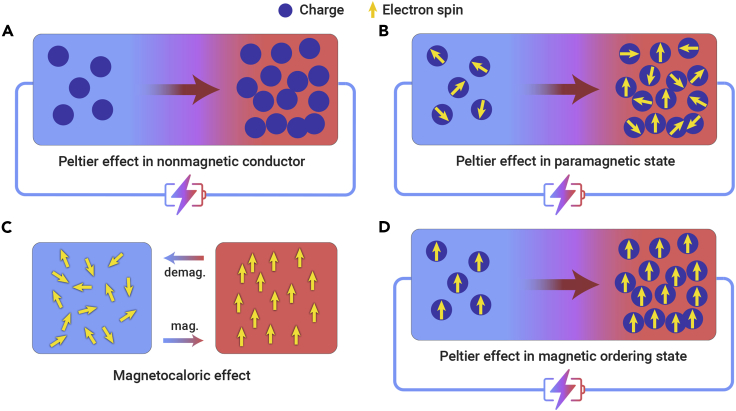
Recent years have witnessed increasing efforts to pursue large values of α in magnetic materials.4, 5, 6 A general understanding gained so far is that a spin-dependent Seebeck effect (SdSE) might be a material-specific property related to magnon drag, spin fluctuation, or spin-dependent scattering of conduction electrons. No generic SdSE has been known. Here, we demonstrate for a large number of d-electron-based magnetic conductors with ferromagnetic (FM), weakly ferromagnetic (WFM), or antiferromagnetic (AFM) transition that a sizable SdSE takes place over a wide temperature range from slightly below to well above the ordering temperature. This additional Seebeck effect, denoted as α_m, traces back to the thermodynamics of spin degrees of freedom, i.e., spin entropy, via thermal spin fluctuations of (partially) delocalized magnetic d electrons, referred to in the comparison of the Peltier effect between nonmagnetic (Figure 1A) and magnetic (Figure 1B) conductors. In the latter case, delocalized d electrons are responsible for both collective magnetism and thermoelectric transport. With spin entropy being the principal origin, the SdSE is expected to respond to magnetic-field scaling to the magnetocaloric effect, a thermodynamic property whereby field-induced spin-entropy change is feasible to make effective solid cooling (Figures 1A–1D). Note that the Peltier effect, i.e., the reverse phenomenon of the Seebeck effect, is demonstrated in Figures 1A, 1B, and 1D because it provides a better comparison with the magnetocaloric effect given their common features in solid-state cooling.

Figure 1.

Illustrative comparison between two relevant solid-cooling effects: the Peltier and magnetocaloric effects

(A) The conventional Peltier effect arising from charge diffusion in a nonmagnetic conductor.

(B) Enhanced Peltier effect of a magnetic conductor in high-entropy paramagnetic state, involving the thermodynamics of both kinetic and spin degrees of freedom. It differs from (A) because of the thermal spin fluctuations that carry significant spin entropy.

(C) A magnetocaloric cycle consisting of magnetization (low entropy) and demagnetization (high entropy) processes of a magnet, where charge carriers are not a necessary ingredient.

(D) When sufficiently strong magnetic field is applied or temperature reduced to well below T_C/T_N, spin polarization occurs and reduces the spin entropy involved in thermoelectric transport, restoring a situation similar to that of (A).

The difference of the demagnetized (B) and magnetized (D) Peltier effect scales to the magnetocaloric effect, as shown in (C). Blue and red colors of the sample denote heat absorption and release, respectively.

Thermodynamic considerations

In a conducting solid exposed to a temperature difference dT, both chemical (μ) and electrical potential (eψ) change thermodynamically at the two ends. In a standard setting of thermoelectric measurements, the dT-induced voltage measures the difference of electrochemical potential,$\overline{\mu }$ = μ + eψ. Approximately, the Seebeck effect in response to dT arises in two parts:^7,8

$$-\alpha =\frac{1}{e}\frac{\text{d}\mu }{\text{d}T}+\frac{\text{d}\psi }{\text{d}T}\text{.}$$ (Equation 1)

Here e is the free electron charge. The first term is purely thermodynamic and is known as the Kelvin formula.⁹ The second includes kinetic information arising from charge relaxation processes. It is sometimes referred to as theoretical or effective Seebeck effect,⁷ as compared with the experimental one detecting both.

From thermodynamic consideration of an electronic system, the chemical potential μ is related to the derivative of the total electronic entropy S with respect to the carrier number N of the system,⁹

$$\text{d}\mu /\text{d}T=-\text{d}S/\text{d}N\text{.}$$ (Equation 2)

Equations 1 and 2 show that α probes entropy S per charge carrier as long as the details of electron kinetics can be ignored or is of minor importance. In magnetic conductors, the relevant spin entropy S_m is of interest and S_m = k_Blng, with k_B being the Boltzmann constant and g the total number of spin configurations. Hence, the well-known Heikes formula,¹⁰ α_m = −(k_B/e)∂lng/∂N, can naturally be obtained. This is applicable to systems of interacting localized electrons and valid at high enough temperatures where all the spin degrees of freedom are active.

Next we consider the spin entropy of an FM compound on a more general basis within the mean-field approximation,¹¹ whereas AFM state can be represented by two antiferromagnetically coupled FM sublattices:

$$S_{\text{m}}\left(T,H\right)=R\left[\ln \frac{\sinh \left(\frac{2J+1}{2J}X\right)}{\sinh \left(\frac{X}{2J}\right)}-X{B}_{\text{J}}\left(X\right)\right]\text{.}$$ (Equation 3)

Here R is the molar gas constant, B_J(X) the Brillouin function with X = g_LJμ_BH_eff/k_BT, J the total angular momentum, μ_B the Bohr magneton, and g_L the Lande factor. The effective field H_eff reads

$$H_{\text{eff}}=H+\frac{3k_{\text{B}}{T}_{\text{C}}{B}_{\text{J}}\left(X\right)}{{\mu }_{\text{B}}{g}_{\text{L}}\left(J+1\right)}\text{,}$$ (Equation 4)

where the first and second terms at the right-hand side represent external and molecular field, respectively. Equations 3 and 4 are frequently employed to estimate the magnetocaloric effect near a magnetic transition.¹¹

Results and discussion

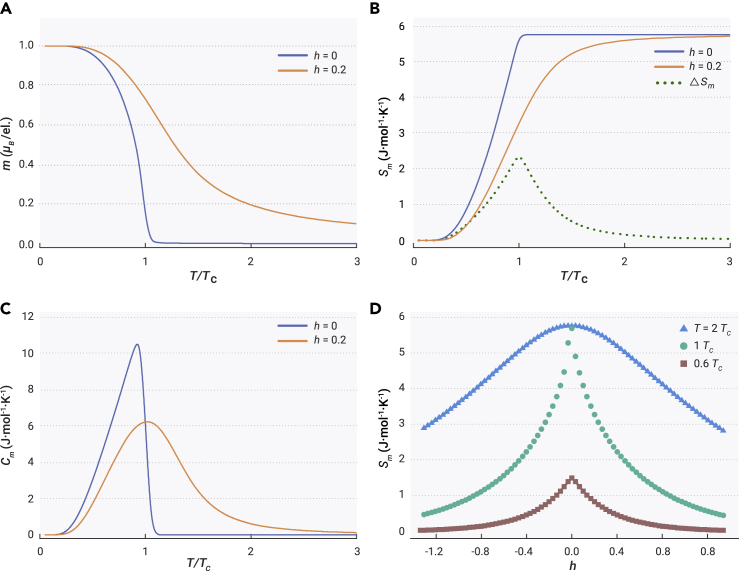
The results of mean-field consideration are summarized in Figures 2A–2D. Figure 2A shows the magnetization per electron m = g_LJμ_BB_J(X) as a function of T for zero and a finite magnetic field h = 0.2. Figure 2B displays their corresponding S_m(T); it saturates to Rln2 = 5.76 J/mol K, the magnetic entropy associated with the ground-state doublet, immediately at T_C for h = 0, whereas the saturation trend is slowed down in finite field. The spin-entropy difference ΔS_m (dashed line) is the magnetocaloric effect and assumes a peak at T_C. Figure 2C shows the magnetic specific heat, which usually is the directly measured quantity for estimating S_m, and Figure 2D the isothermal field suppression of S_m at selected temperatures. As depicted by Equation 2, the steplike profile of S_m(T) (Figure 2B) characteristic of the magnetic ordering indicates a steplike change of α_m(T) at T_C if the magnetic d electrons are itinerant or partially itinerant, and α_m(H) at constant temperature will decrease analogous to S_m(H) (see Figure 2D). The additional contribution α_m to the Seebeck effect marks the difference of the Peltier cooling shown in Figures 1A and 1B.

Figure 2.

Mean-field thermodynamics of an FM spin system with g_L = 2 and J = 1/2

The magnetization m (A), the spin entropy S_m (B), and the magnetic contribution to specific heat C_m (C) are shown as a function of temperature in zero and finite field. (D) displays isothermal change of S_m(h) in selected temperatures. In (B), the magnetocaloric effect ΔS_m (dashed line) estimated as the spin-entropy change between zero and finite field is also shown. h = μ_BH/k_BT_C is the reduced magnetic field by the ordering temperature.

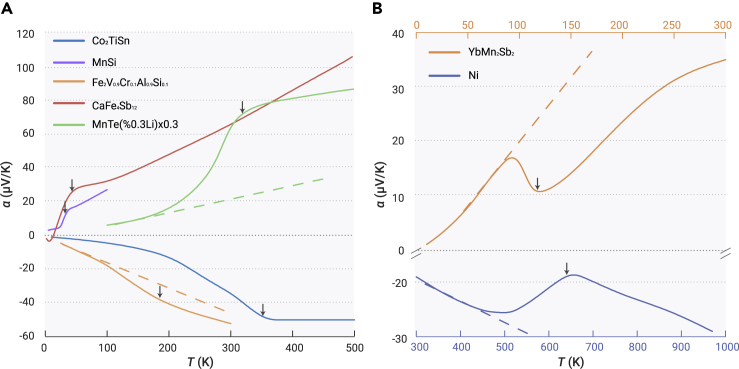
To substantiate the spin-entropy contribution to α(T), in Figure 3 we compile currently available literature data of various d-electron-based magnets, which are either FM, WFM, or AFM (see also Table 1). A generic, steplike increase of α(T) at T ≈ T_C or T_N is observed for all of them. To avoid complex transport properties caused by spin-density-wave gap in the AFM cases, sample choice is made for those with a simple resistivity drop below T_C/T_N, derived from reduced spin scattering. These materials are further classified into two categories: in Figure 3A the steplike α_m(T) has the same sign with the background α₀(T), namely, the conventional diffusion contribution; in Figure 3B, however, their signs are opposite due to the competing polarity of conduction and magnetic d bands.

Figure 3.

Temperature-dependent Seebeck effect of varied d-electron-based FM, WFM, and AFM conductors

For all these magnets, a steplike magnetic contribution α_m(T) emerges on top of a sublinear background α₀(T) (dashed line) that is derived from conventional charge-diffusion effect. The sublinear background is drawn for only a part of the samples for the sake of clarity. Note that α_m(T) and α₀(T) have same signs in the materials shown in (A) and opposite signs in (B) (see text). The vertical arrows mark the positions of T_C or T_N (for WFM compounds, the position of the maximum in magnetic susceptibility).

Table 1.

Characterization of the steplike SdSE in some typical d-electron-based FM, WFM, and AFM materials

Materials	Magnetic ordering	TC/TN	αstep	MO	Refs.
		(K)	(μV/K)	(μB)
Co2TiSn	FM	355	−40	1.97	Balke et al.,12, 13 Barth et al.12, 13
MnSi	FM	29	8	0.45	Lamago et al.,14, 15 Hirokane et al.14, 15
Ni	FM	627	10	~0.6	Tang et al.,16, 17 Abadlia et al.16, 17
CaFe4Sb12	WFM	50a	∼15	0.5	Takabatake et al.,18, 19 Schnelle et al.18, 19
Fe2V0.9Cr0.1Al0.9Si0.1	WFM	160	7	0.4	Tsujii et al.5
MnTe (0.3% Li)	AFM	307	150	4.55	Zheng et al.6
YbMn2Sb2	AFM	120	−15	3.6b	Nikiforov et al.,20, 21 Morozkin et al.20, 21

Among these, Co₂TiSn and CaFe₄Sb₁₂ are representatives of a large group of magnetic Heusler and filled skutterudite compounds, respectively, with similar α(T) profiles, see Balke et al.12, 18 and Takabatake et al.12, 18

^aWhile a clear indication of ferromagnetic ordering is absent, CaFe₄Sb₁₂ shows a shoulder at T ≈ 50 K in magnetic susceptibility due to incipient ferromagnetism.¹⁹

^bIn YbMn₂Sb₂, magnetic moment originates from Mn d bands and divalent Yb ion is nonmagnetic.

Despite the variety of the materials shown in Table 1, one sees a rough scaling between the steplike change in α_m(T), α_step, and the ordered moment M_o, except for YbMn₂Sb₂. This hints at a thermodynamic relationship between the two quantities. In-depth investigations into the SdSE of WFM compounds Fe₂V_1−xCr_xAl_1−ySi_y (Tsujii et al.⁵) and CaFe₄Sb₁₂ (Takabatake et al.¹⁸), whose cooperative magnetism has been known to be due to itinerant 3d bands, have shown that applying a magnetic field can suppress α_m, evidencing the involvement of strong spin fluctuations. The spin-entropy description can readily capture the saturation of α_m(T) above T_C/T_N because S_m(T) saturates, or, equivalently, the spin degrees of freedom are fully restored. Phenomenologically, paramagnetic spin fluctuations of itinerant d electrons contribute to the Seebeck effect by transferring spin entropy in addition to their kinetic one (see Figure 1B). To verify this proposition, field-tuned α_m(H) will be discussed semiquantitatively in terms of the spin entropy S_m(H) (Figure 2D) by focusing on MnSi (Figures 4A and 4B). By contrast, the steplike α_m(T) in Li-doped MnTe has recently been interpreted based on local-moment picture and paramagnon-electron drag.⁶ The difficulties arising in the local-moment explanation will be explained below. Here, we note that the electronic structure of this compound is determined by the combined effect of an exchange splitting of Mn-3d states and a strong hybridization with Te-5p states.²² The strong p-d hybridization can partially delocalize the 3d states and cause their contribution to transport,²³ appealing for a spin-entropy scenario as well.

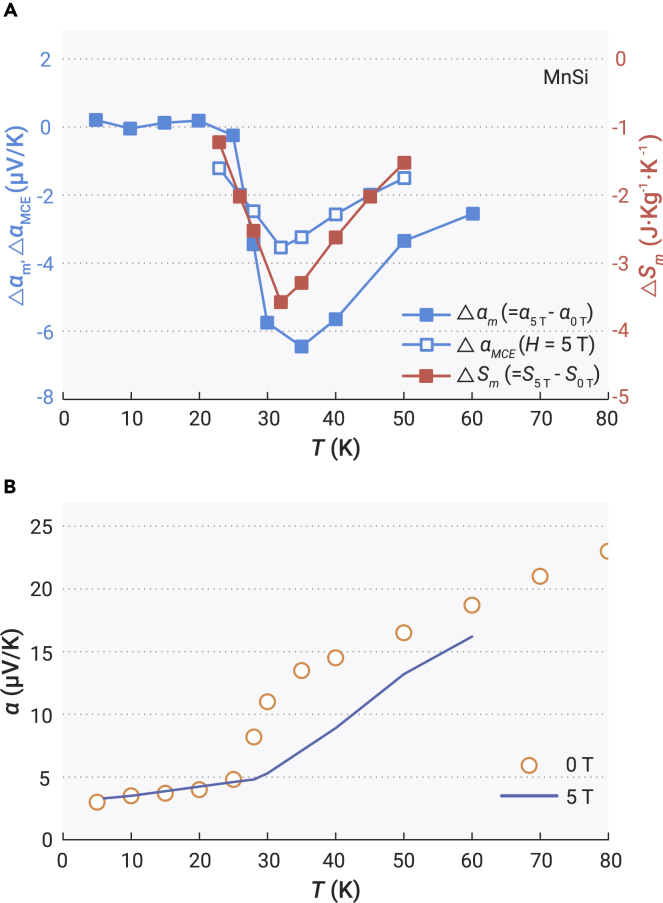
Figure 4.

Thermoelectric vs magnetocaloric effects in MnSi

(A) Comparison between the measured magneto-Seebeck effect Δα_m = α_5T − α_0T (left axis) and the magnetocaloric effect ΔS_m for H = 5 T (right axis) for MnSi.²⁴ By considering 0.89 d-hole/MnSi obtained from Hall measurement,²⁵ the values of ΔS_m can be converted to those of Δα_MCE(T) in unit μV/K (see text), which agree reasonably with those of Δα_m.

(B) The measured values of α(T) for H = 0 T and 5 T,¹⁵ from which Δα_m is obtained.

Nickel and YbMn₂Sb₂ shown in Figure 3B are distinctive because their α_m(T) reveals an opposite sign to the sublinear background α₀(T). For nickel, this feature can be explained by considering its ferromagnetism derived from intersite d-hole hopping (nickel has an almost full d shell),²⁶ which gives rise to a positive spin-entropy contribution on top of the overall negative α₀(T) dominated by the 4s bands at the Fermi level. Aside from the sign problem, the correlation between α(T) and the specific heat C(T) near T_C has long been known for nickel,¹⁶ in line with the spin-entropy scenario. Likewise, in YbMn₂Sb₂, a negative step of α_m(T), appears on a positive α₀(T), due to the competition of magnetic 3d electrons of Mn²⁺ and the Sb-5p valence bands. Here, Yb is nonmagnetic.

While not included in Figure 3, a prominent case where spin entropy has been invoked to interpret the SdSE is NaCo₂O₄ (Terasaki et al.²⁷), a paramagnet with Curie-Weiss behavior. Field-induced reduction of α(H) scaling to H/T, a feature derivable from Equation 3 assuming T_C = 0, has been considered evidence of spin-entropy contribution.²⁸ This argument was rationalized in terms of hopping conduction of local 3d electrons.²⁹ Electronic-structure calculation performed later on found that this compound locates at an itinerant magnetism instability with large electronic density of states derived from 3d orbitals.³⁰ Within the itinerant picture, the α(H) profile of NaCo₂O₄ is also approachable by considering magnetic-field tuning to spin polarization at the Fermi level.³¹ Here, spin entropy is involved in shaping the electronic structure, as concluded from recent angle-resolved photoemission spectroscopy experiments.³² In this sense, NaCo₂O₄ appears to be a special case of considerable d-electron-derived SdSE with a vanishing T_C.

To quantitatively verify the correlation between spin entropy and SdSE, below we scrutinize α(T, H) of MnSi. MnSi is a prototype of itinerant ferromagnet with long-wavelength helical modulation of spin structure. Applying magnetic field reduces the spin entropy near T_C, as quantified by the static magnetocaloric effect ΔS_m (see Figure 2B and Arora et al.²⁴). Consequently, the transport spin entropy detected by α_m is expected to diminish as well (Equation 2 and Figure 1A). Correspondence between the two quantities obtained experimentally is demonstrated in Figure 4A: Δα_m (left axis) reveals a negative peak close to T_C ≈ 29 K; see also Figure 4B for the measured α(T) at H = 0 and 5 T (Hirokane et al.¹⁵), from which Δα_m is obtained as their difference. An apparent scaling between Δα_m and ΔS_m (H = 5 T, right axis, Arora et al.²⁴) can be observed. Hall-effect measurements reveal a simple one-band ordinary Hall resistivity with carrier concentration ∼0.89 d-hole/MnSi, along with an anomalous contribution derived from ferromagnetism.²⁵ On this basis, ΔS_m reported in unit of J/kg K can be readily converted in accordance to the unit of α, μV/K, by normalizing by the carrier density of d holes. The hence obtained spin-entropy-derived Seebeck effect, denoted as Δα_MCE(T) (blue empty squares in Figure 4A), reveals a reasonable agreement with the measured Δα_m(T) (blue solid squares in Figure 4A) within a factor of 2. This yields compelling evidence that the thermodynamics of delocalized d-electron spin degrees of freedom contribute substantially to the SdSE near and above the magnetic ordering temperature.

The SdSE herein identified is generic to magnetic materials that are FM, WFM, AFM, or even paramagnetic near a magnetic instability with at least partially itinerant magnetism. It is a thermodynamic consequence originating from the spin degrees of freedom pertinent to magnetic d electrons. A large number of candidate compounds with significant SdSE can be found in the literature but are left out of our focus because their diffusion part α₀(T) is already complex, plaguing a reliable analysis of α_m(T). These include, for example, Fe₃GeTe₂ (May et al.³³), the mother compounds of iron-based superconductors³⁴ and various manganese oxides.³⁵ Thermoelectricity enhancement recently found in some magnetic ion-doped semiconductors36, 37, 38 may share the same origins, yielding a practical way to further optimize current thermoelectric materials. Likewise, a spin-entropy contribution is also expected in transverse thermoelectricity, i.e., the Nernst effect, as recently discussed for a magnetic semimetal Co₃Sn₂S₂ by Geishendorf et al.³⁹ Unlike MnSi, the transport and static spin entropy may generally deviate from a quantitative scaling because the magnetic d bands may not be the only active bands responsible for transport, or are rather localized as in a magnetic insulator. In the latter case, α_m may reduce to zero despite a large S_m.

As already mentioned, magnon drag offers an alternative explanation of SdSE, resorting to the kinetics of spin waves interacting with conduction electrons. It in general applies to the ordered phase of local spins⁴⁰ but has been recently extended to the paramagnetic regime far above T_C/T_N.⁶ Applying this scenario to d-electron-based magnets is not straightforward due to their correlated nature with competing localized-itinerant duality. Such magnetic character invalidates the assumption of two physically independent but interacting fluids (conduction electrons and magnons) for the magnon-drag effect. Some even apparent difficulties arise when applying magnon drag to paramagnetic state. One is the sign problem as discussed for Ni: here, the magnon-drag effect appears only well below T_C (T < 500 K) and is known to be negative due to the conduction 4s band, namely, in accordance with the polarity of majority carriers.⁴⁰ However, α_m(T) near and above T_C is positive (Figure 3B), hinting at a different origin. Also, the large α_m(T) contribution can be observed up to more than 10 times the T_C/T_N (see, e.g., CaFe₄Sb₁₂ in Figure 3A), where as far as we know coherent spin fluctuations (magnons) have not been confirmed for any materials. Supposing the steplike α_m(T) is due to paramagnon drag, one would also expect a corresponding paramagnon thermal conductivity. This has been confirmed in none of the aforementioned materials. Finally, we stress that while the spin-entropy scenario does not rely on magnons to drag electrons, thermal spin fluctuations, which offer a standard approach to describe itinerant magnetism,⁴¹ are crucial because they are the way by which large spin degrees of freedom are activated.

The physics underlying the α-C_el scaling at 0 K limit in a wide range of correlated compounds¹ can be traced back to spin entropy as well. The hybridization between local and conduction bands bring about spin-fluctuation-dressed quasiparticles that are responsible for both transport and thermodynamics, leading to enhanced values of both α and C_el. This enhancement may, to a certain degree, persist up to even room temperature if the hybridization is strong enough. This is the case for the paramagnetic intermediate-valence compound CePd₃,⁴² where the optimized figure of merit zT amounts to ∼0.3.⁴³ By contrast, in itinerant magnets of FM, WFM, or AFM type as discussed herein, significant spin entropy is drastically accumulated upon approaching the ordering temperature. By choosing magnetic materials with appropriate values of T_C/T_N, the consequent SdSE can offer more design flexibility for thermoelectric application in a particular temperature range.

Conclusion

In conclusion, based on a thermodynamic analysis we have attributed the excess SdSE near and above T_C/T_N in a wide range of d-electron-based magnets to spin entropy of (partially) delocalized d electrons with strong thermal spin fluctuations. The fundamental correlation between the Seebeck effect and spin entropy appears highly instructive for future exploration of useful magnetic thermoelectrics. Furthermore, identification of the physical origin of the SdSE also helps us to understand the nature of collective magnetism in d-electron-based systems, which is often not straightforward because of the localized-itinerant duality and its influence on transport properties.

Materials and methods

The calculations of magnetization, spin entropy, and specific heat shown in Figures 2A–2D are based on the mean-field approximation assuming the Brillouin function description of the spin system. To better verify our proposal on the spin-entropy-derived Seebeck effect, we focus on some representative d-electron-based ferromagnetic, weakly ferromagnetic, and antiferromagnetic conductors whereby a nearly T-linear background, i.e., the conventional diffusion contribution to the Seebeck effect in metal, can be confirmed. These materials show at least partially delocalized features in their collective magnetism and have been experimentally investigated previously regarding the Seebeck effect. All experimental data on the Seebeck effect can be found in literature.

Published Online: March 25, 2021

Lead contact website

http://english.iop.cas.cn/pe/?id=1955