Turnover modulates the need for a cost of resistance in adaptive therapy

Abstract

Adaptive therapy seeks to exploit intra-tumoral competition to avoid, or at least delay, the emergence of therapy resistance in cancer. Motivated by promising results in prostate cancer, there is growing interest in extending this approach to other neoplasms. As such, it is urgent to understand the characteristics of a cancer which determine whether or not it will respond well to adaptive therapy. A plausible candidate for such a selection criterion is the fitness cost of resistance. In this paper, we study a general but simple mathematical model to investigate whether the presence of a cost is necessary for adaptive therapy to extend the time to progression beyond that of a standard-of-care continuous therapy. Tumor cells were divided into sensitive and resistant populations and we model their competition using a system of two ordinary differential equations based on the Lotka-Volterra model. For tumors close to their environmental carrying capacity a cost was not required. However, for tumors growing far from carrying capacity, a cost may be required to see meaningful gains. Notably, it is important to consider cell turnover in the tumor, and we discuss its role in modulating the impact of a resistance cost. To conclude, we present evidence for the predicted cost-turnover interplay in data from 67 prostate cancer patients undergoing intermittent androgen deprivation therapy. Our work helps to clarify under which circumstances adaptive therapy may be beneficial and suggests that turnover may play an unexpectedly important role in the decision making process.

Introduction

The evolution of drug resistance is one of the biggest challenges in cancer therapy. In one of the first papers on chemotherapy, Farber and colleagues [1] already reported not only unprecedented remissions in children suffering from acute leukemia, but also that these remissions were temporary. For many patients this pattern still holds true today, and applies to both chemo- as well as targeted therapies.

Research aiming to combat drug-resistance has traditionally focused on developing drugs which target either the resistance mechanism or kill the cell through a different route. As an alternative to this molecular approach, a number of authors have proposed that resistance could be delayed, if not averted, through changes in drug-scheduling [2, 3, 4, 5, 6]. Current treatment schedules are designed to maximize cell kill by treating at the maximum tolerated dose (MTD) as frequently as toxicity permits. However, if drug-resistant cells are present a priori or develop during therapy, such aggressive treatment releases these cells from the competition for space and resources and facilitates their growth, a process known as “competitive release” [3, 4, 7]. Inspired by approaches used in the management of invasive species and agricultural pests, Gatenby et al [4, 7] proposed “adaptive therapy” which aims not to eradicate the tumor, but to control it. Therapy is applied to reduce tumor burden to a tolerable level but is subsequently modulated or withdrawn to maintain a pool of drug-sensitive cancer cells. Over the past ten years, studies have shown that adaptive therapy can extend time to progression (TTP) in vivo in ovarian [7], and breast cancer [8], and most recently in melanoma [9]. Moreover, the interim analysis of the first human trial of adaptive therapy, applied to the treatment of metastatic, castrate-resistant prostate cancer with androgen deprivation therapy, reported an increase in TTP of at least 10 months and a reduction in cumulative drug usage of 53% [10].

The success of adaptive therapy in prostate cancer has spurred interest in extending the protocol to other cancers such as thyroid cancer and melanoma (clinicaltrials.gov identifiers NCT03630120 and NCT03543969, respectively). As such, it is urgent to understand the characteristics of a cancer that determine whether it will respond well to adaptive therapy, or not. Bacevic et al [11] showed through in vitro experiments and an agent-based computational model that it is important that cells are spatially constrained, as otherwise the competition is too weak to effectively control the growth of resistant cells. Furthermore, through ODE modeling they found that the fitness of the resistant population when the population is rare is a key determinant of the benefit derived from adaptive therapy [11]. These results were corroborated by Gallaher et al [12] who compared two adaptive therapy strategies to MTD using an agent-based model which modeled resistance as a continuous trait. They further found that the rate of spatial mixing through migration, and the rate of acquisition of resistance through mutation, were key factors in determining the benefit from adaptive therapy, and which adaptive therapy strategy was most effective. Using a nonspatial game theory model, West et al [13] showed that the stronger the selection against resistance in the absence of drug, the longer adaptive therapy can be expected to extend TTP. Taking a more general approach, Hansen et al [6, 14] demonstrated that the decision of whether to treat aggressively or not, depends on the dominant mechanism of resistant cell production (clonal expansion vs de novo acquisition), and the initial resistant cell number. By making the simplifying assumption that progression can be predicted purely from the governing equation of the resistant population, they derive an explicit form of the decision boundary for a simple ordinary differential equations (ODE) model [6, 14]. Most recently, Smalley et al [9] showed that adaptive therapy can be beneficial even in the light of phenotypic plasticity, but that in order to achieve optimal results personalization of the treatment schedule is required.

However, a factor which is still poorly understood is the so-called “cost of resistance”. This refers to the idea that while a resistance adaptation confers a fitness advantage under drug exposure, it may come at a fitness cost in a treatment-free environment [4, 15]. Resistance costs have been widely studied in agricultural pests and antibiotic resistance [16] and may be measured in different ways (Figures 1A–C). An example in the cancer literature can be found in Gallaher et al [12] who report that doxorubicin-resistant MCF7Dox breast cancer cells replicate 50% slower compared to their sensitive counterparts, and that in competition experiments the sensitive cells outcompete the resistant cells in the absence of the drug. This is likely because these cells use P-Glycoprotein-related efflux pumps to resist treatment, for which they have to divert energy away from proliferation towards running of the pumps [12, 17]. Similar observations have been made in colorectal, lung and other cancers in response to chemo- [18, 19] as well as targeted therapies [9, 11, 20]. In their original work on adaptive therapy, Gatenby et al [4, 7] used the cost of resistance to motivate adaptive therapy, and most theoretical studies since have made this assumption [11, 12, 13].

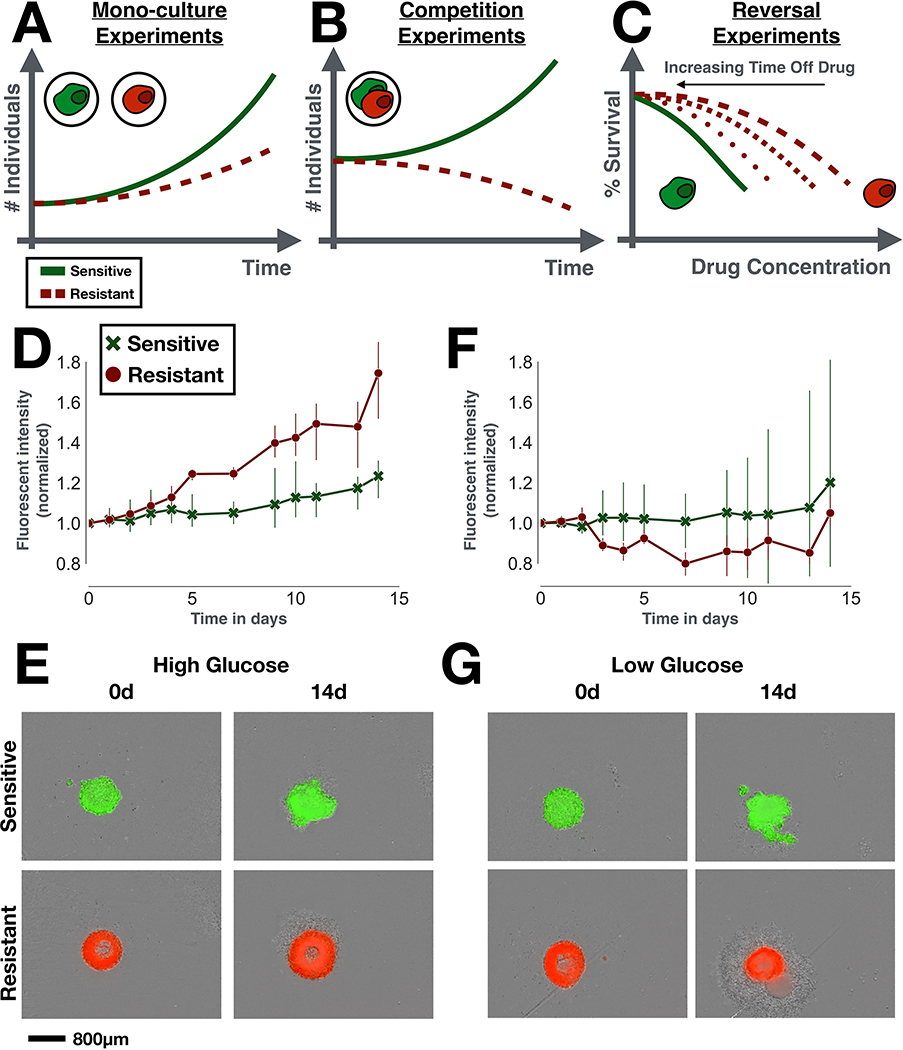
Figure 1:

Resistance costs in theory and in practice. A-C) The three main experimental designs used to test for a cost of resistance (all done in drug-free conditions). A) Mono-culture experiments test for changes in growth rate, size, migration rate etc of the resistant strain in isolation. B) Competition experiments compare the abundance of sensitive and resistant cells in co-culture over time. C) Reversal experiments examine the rate at which drug resistance is lost, if the drug is withdrawn. To do so, the resistant population is cultured in a drug-free environment, and its drug response is tested at regular time intervals. D-G) In vitro spheroid experiments comparing the growth of doxorubicin-sensitive and resistant MCF7 cells in mono-culture. Sensitive and resistant cells were GFP and RFP tagged, respectively. D) In normal medium, resistant cells grow faster than sensitive cells, showing that resistance does not necessarily have to be costly (n = 3 per group; t-test of relative size change from baseline at 14d: t_3,3 = 4.0,p = 0.02). E) Representative images of the initial (0d) and final time points (14d) from D, illustrating how the resistant spheroids expand more than the sensitive spheroids in normal glucose conditions. F) Under glucose starvation this advantage is lost (n = 3 per group; t-test of relative size change from baseline at 14d: t_3,3 = −0.5,p = 0.66). This shows that the environmental context has to be considered when studying fitness costs. G) Representative images of the initial (0d) and final time points (14d) from G, showing how resistant spheroids are more affected when glucose is withdrawn (decrease in size, formation of large corona of debris around the spheroid). E and G show the fluorescent signal overlaid on the bright-field image. For experimental details see Section S1 in the Supplementary Data.

However, not all resistance mechanisms come at a cost, and the magnitude of any cost depends on a cell’s genetic and environmental context [9, 18, 20]. Despite using identical experimental protocols, Jensen et al [18], for example, find that some of their colorectal cancer cell lines exhibit a cost, whilst others did not, and some even showed increased fitness. Similar findings were made by Smalley et al [9] for melanoma. Moreover, when we repeat the experiments by Gallaher et al [12] in 3-D spheroids, we find that drug-resistant MCF7 cells now grow faster than their sensitive counterparts (Figures 1D&E). However, when we reduce the glucose concentration in the culture medium, this advantage is lost (Figures 1F&G; see also Figures S1A&B). Finally, it is not clear that the presence of a cost guarantees a quick return to sensitivity if drug is withdrawn. For example, while Smalley et al [9] found that one melanoma cell line returned to sensitivity within 6 weeks after drug withdrawal, another remained resistant for months, an observation also made elsewhere [11, 18, 21]. Given this wide range of possibilities for how a resistant population might, or might not, differ from their sensitive counterparts, it is important to clarify the relationship between resistance costs and the success of adaptive therapy.

In this paper we use a simple mathematical model to address this question. We divide the tumor into drug-sensitive and drug-resistant cells and model their growth with two ODEs. We compare the TTP under standard-of-care continuous therapy with that of the adaptive therapy algorithm used in the clinical trial by Zhang et al [10], first in the absence, and subsequently in the presence, of a cost. We will show how increased tumor density and small levels of pre-existing resistance maximize the benefit of adaptive relative to continuous therapy as these conditions maximize the effect of competition between sensitive and resistant cell populations. Subsequently, we will demonstrate that turnover is a key factor to consider, not only to understand the impact of a resistance cost, but also to assess the ability to control a tumor with adaptive therapy more generally. To conclude, we present an analysis of intermittent androgen deprivation therapy in prostate cancer, which provides evidence for our modeling results, and illustrates how our insights can help to improve our understanding of resistance management in a specific disease setting.

Materials and methods

Mathematical model

Tumors are heterogeneous populations of cells with differential responses to drug, indicating a degree of pre-existing resistance in most tumors [22, 23, 24]. To model this heterogeneity, we assume two competing cell types: drug-sensitive cells, S(t), and fully resistant cells, R(t), modeled via the following equations:

$$\frac{dS}{dt}=r_S\left(1-\frac{S+R}{K}\right)\left(1-\frac{2d_D}{D_{Max}}D(t)\right)S-d_{T}S,$$ (1)

$$\frac{dR}{dt}=r_R\left(1-\frac{R+S}{K}\right)R-d_{T}R,$$ (2)

$$N(t)=S(t)+R(t),$$ (3)

with initial conditions:

$$N(0)=N_0,S(0)=S_0,\text{and}R(0)=R_0,$$

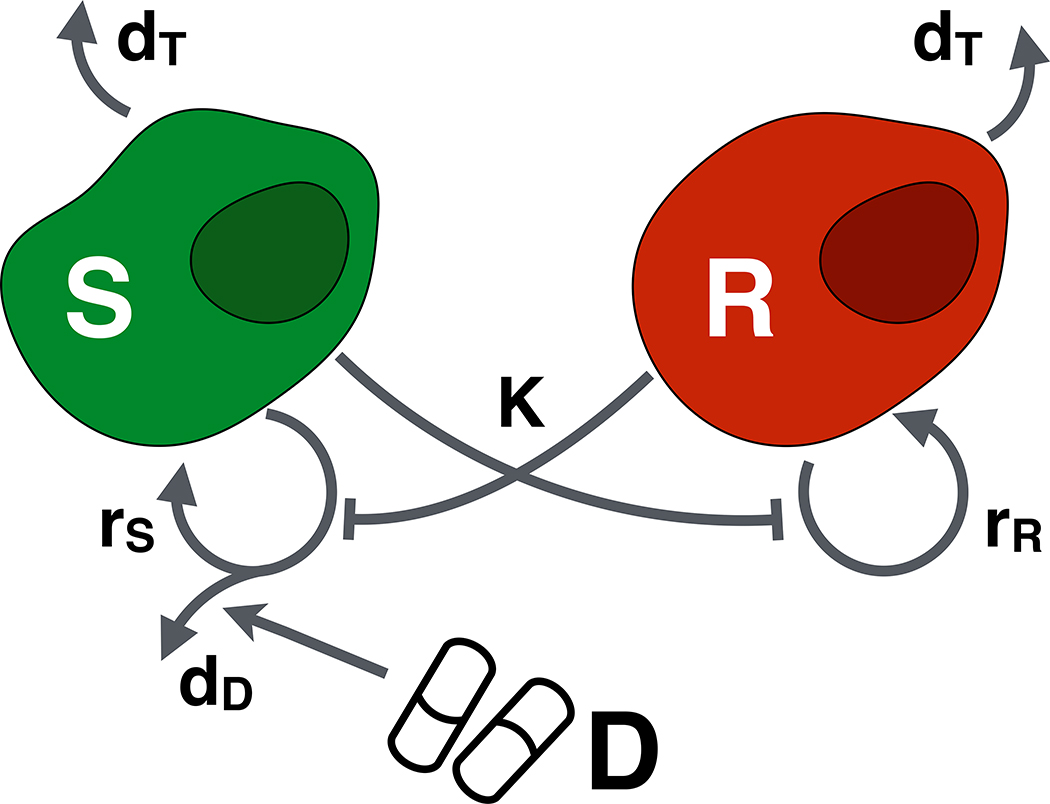
where N₀ = S₀ + R₀. The model is derived based on the following assumptions (Figure 2):

• In isolation each population grows logistically with proliferation rates r_S and r_R, where the fraction of dividing cells decays linearly from 1 to 0 as the population approaches its environmental carrying capacity, K. Furthermore, cells die at a density-independent rate d_T, where for simplicity we assume that this turnover rate is the same for both populations.

• Cells compete for resources and space according to the Lotka-Volterra competition model. This means that the presence of the competitor reduces a population’s growth rate in a fashion that is linearly proportional to the competitor’s population density. For simplicity we will assume that inter- and intra-species competition coefficients are identical, and equal to one.

• Only actively dividing cells are killed by the drug. Many chemotherapies induce DNA damage or inhibit the cell division machinery, which induces apoptosis only in cells that attempt to divide. We will adopt the classical Norton-Simon model [25] which assumes that cell kill increases linearly with the drug dose, D(t), so that at MTD a fraction d_D of dividing cells are killed. The factor of 2 in the drug response accounts for the fact that if a cell dies during mitosis not only the potential daughter but also the mother are lost.

• Progression is driven primarily by pre-existing resistant cells, and resistance acquisition during treatment is negligible. Viossat and Noble [26] have recently shown that inclusion of genetic mutation does not significantly impact the benefits of adaptive therapy in simple models such as ours. Incorporating phenotypic cell plasticity which may occur at a much higher rate (e.g. [27]) will be subject to future research.

• To illustrate our key results, the main text of the paper will assume that the resistance cost manifests itself solely in the growth rate r_R, as this is the way a cost is typically modeled (e.g. [11, 12, 23]). For a discussion of other types of cost see Figures S2A–E and Section S2 of the Supplementary Data.

Figure 2:

The mathematical model. Drug-sensitive (S) and resistant cells (R) proliferate at rates, r_S and r_R, respectively, and die at rate d_T. Proliferating sensitive cells die at a rate d_D when exposed to drug, D. Finally, both populations compete for resources, where K denotes the total (shared) environmental carrying capacity.

We will consider two treatment schedules:

1. Continuous therapy at the MTD, D_Max: D(t) = D_Max∀t.

2. Adaptive therapy which withdraws treatment once a 50% decrease from the initial tumor size is achieved, and reinstates it once the original tumor size (N₀) is reached:

   $$D\left(t\right)=\{\begin{array}{c}{D}_{Max},untilN\left(t\right)<50\%N_0\\ 0,untilN\left(t\right)=N_0\end{array}$$

In order to facilitate numerical simulation of the model, we non-dimensionalize Equations (1)–(3) using r_S as a time scale, and K as a scale for the cell densities (Table 1). For details of the non-dimensionalization, the numerical methods, and a steady state analysis, see Sections S3 and S4, Table S1 and Figures S3A–C of the Supplementary Data, respectively. For completeness we also consider a model in which birth is constant but death is density-dependent, which we find yields similar results (Section S5 and Figures S4A–D of the Supplementary Data). The code associated with our analyses is available at: https://github.com/MathOnco/AT_costOfResistance_LVModel

Table 1:

Mathematical model parameters and their ranges.

Parameter	Description	Value	Reference
	Time in days
$\begin{array}{c}t\\ s(t):=\frac{S(t)}{K}\\ r(t):=\frac{R(t)}{K}\end{array}$	Sensitive cell density (normalized)	0.0 – 1.0
	Resistant cell density (normalized)	0.0 – 1.0
$n(t):=\frac{S(t)+R(t)}{K}$	Total tumor cell density (normalized)	0.0 – 1.0
d(t) = D(t)/DMax	Drug dose (normalized)	0.0 – 1.0
rs	Sensitive cell proliferation rate and model time scale	0.027d−1	Adopted from [10].
${\widehat{r}}_R:=\frac{r_R}{r_S}$	Resistant cell proliferation rate (normalized)	0.5 – 1.0	Lower limit: [12]; Upper limit: assumption of no cost
K	Environmental carrying capacity and scale for cell densities	n/a	Defined implicitly via n0
${\widehat{d}}_T:=\frac{d_T}{r_S}$	Cell turnover rate (normalized)	0.0 – 0.5	Lower limit: assumption of no turnover; Upper limit: see Section S6
d^D := 2dD	Drug-induced cell kill (see text for further explanation)	1.5	Adopted from [28]
D Max	Maximum tolerated dose	n/a	Implicitly defined via d^D.
$n_0:=\frac{N_0}{K}$	Initial tumor cell density (normalized)	0.1 – 0.75	Parameter sweep; values within this range reported by [33]
$f_R:=\frac{R_0}{N_0}$	Initial resistant cell fraction	0.001 – 0.1	Parameter sweep; values within this range reported by [24]

Parameterizing the model

Given the key role which prostate cancer has played in the development of adaptive therapy we parametrize our model according to this disease. As such, we adopt the proliferation rate for sensitive cells given in [10] (r_S = 0.027d⁻¹) as our time scale and the drug kill parameter dˆ_D = 1.5 from [28]. For the other parameters we perform parameter sweeps within their biologically realistic ranges. All parameters, their definitions and their ranges are summarized in Table 1.

Analysis of patient data

In order to test our predictions we fit our model to publicly available, longitudinal response data from prostate cancer patients undergoing intermittent androgen deprivation therapy [29]. The data was downloaded from http://www.nicholasbruchovsky.com/clinicalResearch.html. Patients who developed a metastasis were excluded, so to avoid potentially confounding effects from a change in the number of lesions, yielding data from a total of 67 patients. The model was fitted to each patient by minimizing the root mean squared difference between the normalized PSA measurements, yˆ(t)/yˆ(0), where yˆ(t) is the PSA measurement at time t, and the normalized predicted cell density, n(t)/n₀. The values for r_S and dˆ_D were fixed as in Table 1, and the remaining four parameters (rˆ_R, dˆ_T, n₀, and f_R) were allowed to vary freely between the following bounds: rˆ_R ∈ [0,1], dˆ_T ∈ [0,1], n₀ ∈ [0.1,1], and f_R ∈ [1 × 10⁻⁵,0.25]. Fitting was done using the Levenberg–Marquardt algorithm, and repeated 25 times for each patient starting from different initial parameter combinations, with the best fit according to the Akaike Information Criterion taken forward for analysis. For 15 patients no satisfactory fit could be obtained (r² < 50% or failure to capture later stage cycles) and these were excluded from all further analyses. Classification of patients into relapsing and non-relapsing was taken from the annotation provided in the data, where relapse is defined as a series of three sequential increases of serum PSA > 4.0μg/L despite castrate levels of serum testosterone. An overview of all fits is shown in Figure S5. Fitting was done using the lmfit package in Python [30].

Results

In advanced cancers, curative approaches rarely show durable complete response. Instead, treatment success is often defined by how long therapy can prevent the tumor from progressing beyond a certain size (i.e. TTP). Herein we compare the model-predicted TTP for both adaptive (TTP_AT) and continuous therapy (TTP_CT), respectively, using RECIST criteria (20% increase in tumor size from the pre-treatment baseline). We show that time gained by adaptive therapy depends on the following tumor characteristics: initial tumor density (n₀; see Figure 3), initial levels of pre-existing resistance (f_R; see Figure 3), cost of resistance (r_R < r_S; see Figure 4), and the density-independent cell turnover rate (d_T; see Figure 4). While we focus here on prostate cancer, our theoretical insights apply more broadly. For application of our work to breast cancer, see Figures S6A&B.

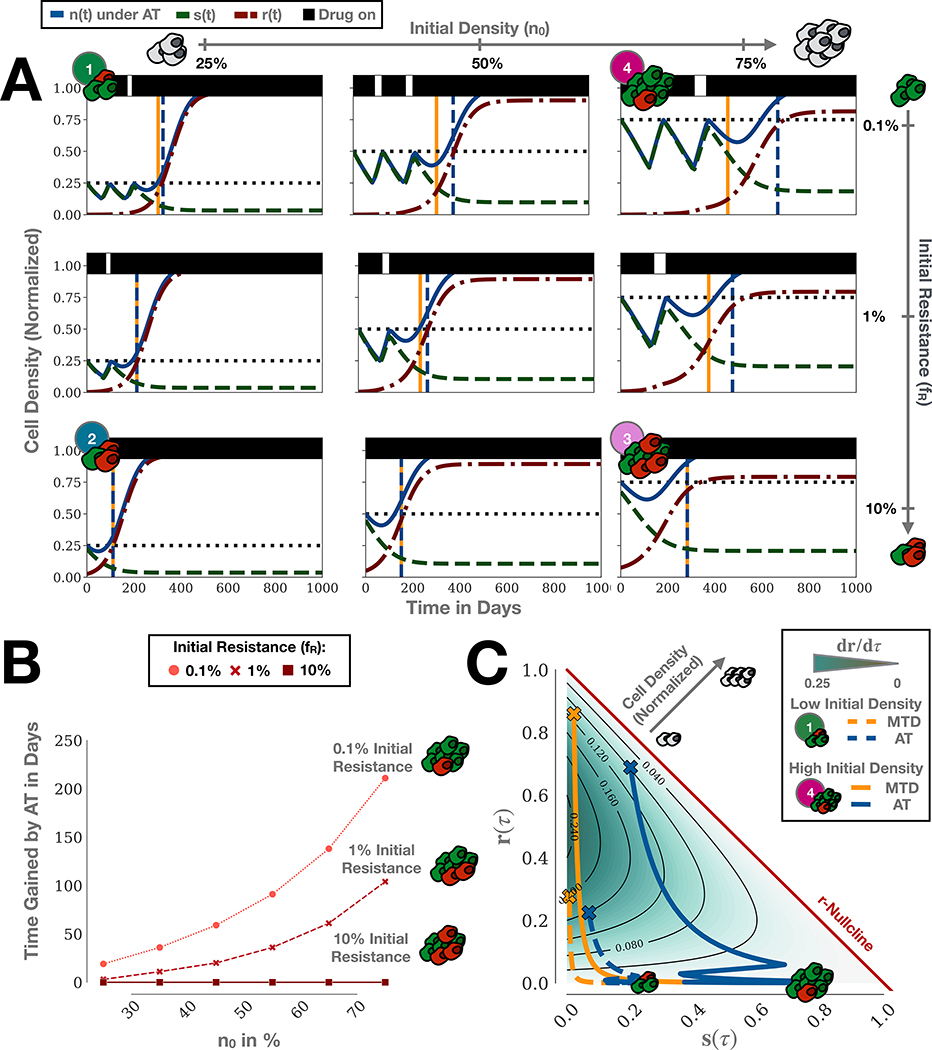
Figure 3:

Adaptive therapy (AT) can extend TTP compared to continuous therapy even in the absence of a cost of resistance. For simplicity, we are assuming no turnover here (dˆ_T = 0). A) Simulations of adaptive therapy for a cohort of tumors with different initial compositions. Vertical dashed lines indicate the time of progression of continuous (yellow) and adaptive therapy (blue), respectively. B) Gain in TTP by adaptive compared to continuous therapy as a function of initial proximity to the carrying capacity and abundance of resistance. C) dr/dτ as a function of s and r, together with treatment trajectories for Tumors 1 ((n₀,f_R) = (25%,0.1%)) & 4 ((n₀,f_R) = (75%,0.1%)) from A. Crosses indicate progression. This shows how adaptive therapy extends TTP by minimizing dr/dτ via competition, and demonstrates that for certain tumors adaptive therapy can extend TTP even if no cost of resistance is present.

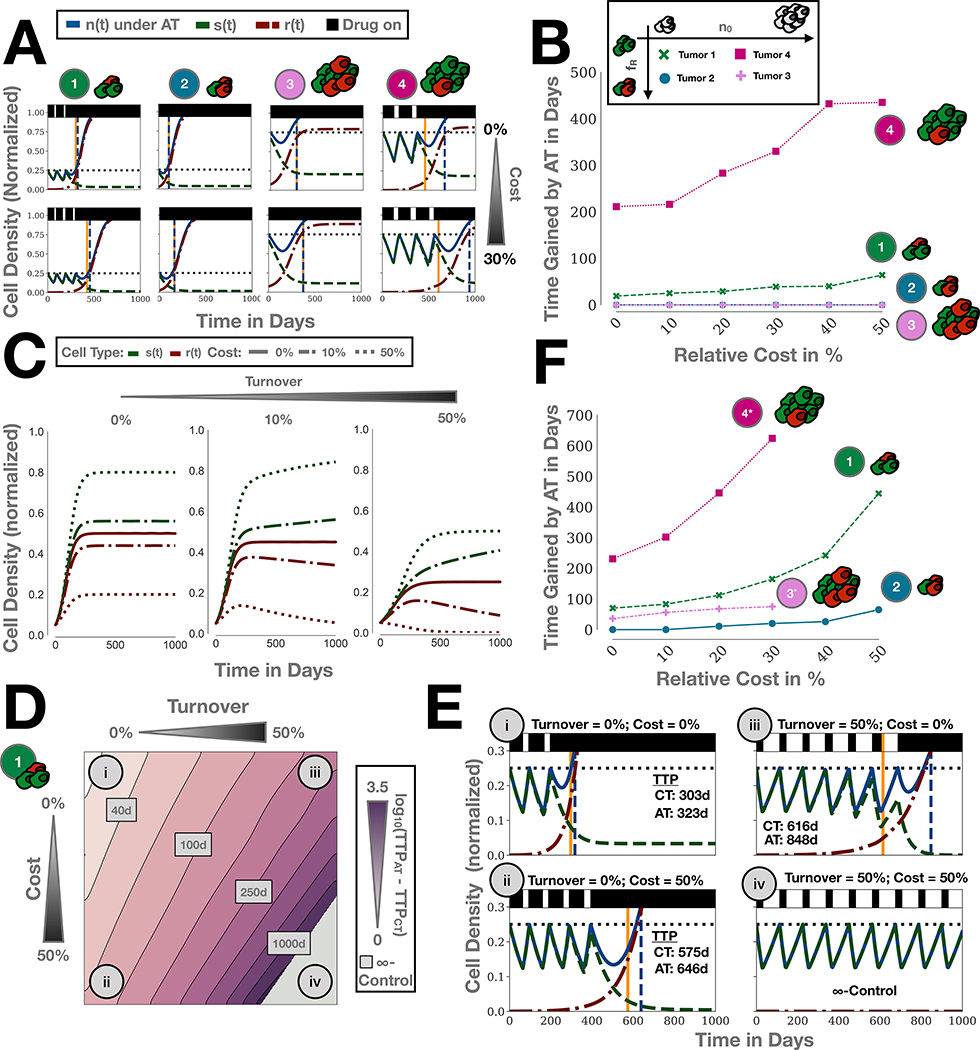
Figure 4:

The impact of a resistance cost on adaptive therapy depends on cellular turnover. A) In the absence of turnover (dˆ_T = 0) a cost enhances adaptive therapy only when resistance is rare and tumors are close to carrying capacity. Simulations of Tumors 1–4 from Figure 3A with and without a 30% cost of resistance (rˆ_R = 70%; Tumors 1 & 4 given in Figure 3; Tumor 2: (n₀,f_R) = (25%,10%); Tumor 3: (n₀,f_R) = (25%,10%)). B) Parameter sweep of the benefit of adaptive therapy (TTP_AT-TTP_CT) for different levels of costs for Tumors 1–4, corroborating the results in A). Note that the curves for Tumor 3 & 4 overlap. C) Simulation of a competition experiment (no drug; n₀ = 10%, f_R = 50%), showing that the impact of a cost on the selection against resistance is modulated by cellular turnover. D) Impact of turnover on adaptive therapy for Tumor 1 for different values of cost. Turnover increases the benefit of adaptive therapy and amplifies the effect of a cost. E) Simulations of the treatment dynamics for four combinations of cost and turnover corresponding to the four case studies highlighted in B. F) Parameter sweep as in B) but with a turnover of 25%. Turnover increases TTP gained by adaptive therapy both in the presence and absence of a resistance cost for a range of different tumor compositions (Tumors 1 and 2 as in Figure 3A; Tumor 3*: (n₀,f_R) = (50%,10%); Tumor 4*: (n₀,f_R) = (50%,0.1%); above a cost of 30% Tumors 3* and 4* become indefinitely controllable and so no TTP can be obtained).

Adaptive therapy extends TTP even without a resistance cost

In the absence of a resistance cost, adaptive therapy still results in significant improvements in TTP over continuous therapy. To illustrate this, in Figure 3A we show representative simulations of adaptive therapy for different values of tumor density (plots, left to right), and pre-existing resistance (top to bottom). Each sub-panel shows sensitive (red lines), resistant (green) and total (blue) populations over time under adaptive therapy dosing. Treatment administration is illustrated by black bars at the top of the graphs. This shows that TTP_AT (vertical blue dashed lines) exceeds TTP_CT (vertical yellow) under a range of conditions, and for the combination of low resistance and high tumor density (top right panel). Figure 3B quantifies time gained (TTP_AT - TTP_CT) for a range of tumor density and resistance values. For our parameter sweep, we find that adaptive therapy can extend TTP by between 3 and 104 days when the initial resistance fraction is f_R = 1%, and by between 19 and 211 days when f_R = 0.1%. Finally, we note that in the worst case scenario (f_R = 10%), adaptive therapy becomes indistinguishable from continuous therapy, so that while there is no benefit, the patient has also not progressed faster than under standard-of-care (bottom row in Figure 3A and Figure 3B).

Adaptive therapy treatment vacations provide a benefit only if intratumoral competition is strong

Moreover, we find that each of the two characteristics of the tumor’s initial composition has a distinct impact on the treatment dynamics. As we increase the initial abundance of resistant cells from 0.1% to 10%, we decrease the number of completed adaptive therapy cycles (Figure 3A). In the most extreme case, at 10% initial resistance, treatment can not decrease the tumor burden sufficiently to trigger any treatment withdrawal in the three tumors. In contrast, increasing the initial tumor density, which biologically corresponds to greater competition for resources, does not alter the adaptive therapy cycle number, but does increase the benefit delivered by each cycle. For example, even though all tumors with 1% initial resistance complete one adaptive therapy cycle, a meaningful benefit in TTP is only achieved in the case when the tumor is 75% saturated (Figure 3A). The reason for this is that the competition exerted by sensitive cells only has significant impact on the growth of the resistant cells if the tumor is close to K. In summary, for adaptive therapy to provide a benefit the tumor burden must undergo a sufficient decline to allow for treatment withdrawal (small f_R), and competition within the tumor must be sufficiently strong to noticeably slow the expansion of the resistant population (proximity to K).

Adaptive therapy extends TTP by minimizing the resistant population growth rate

How can we explain the benefit of adaptive over continuous therapy in the absence of a cost of resistance? We apply the framework by Hansen et al [6] to derive the following explanation. Progression is primarily driven by the expansion of the resistant population, as drug-sensitive cells are easily depleted by additional treatment. Thus, the more a treatment strategy can inhibit the resistant population growth rate, dR/dt, whilst also maintaining control of the tumor size overall, the longer TTP. To illustrate this, we plot dr/dτ (the non-dimensional form of dR/dt) as a function of the tumor composition in Figure 3C. In this representation a tumor lesion is seen as a point in a two-dimensional space, where its x-position represents the current relative density of sensitive cells, s(τ), and its y-position the current density of resistant cells, r(τ). Each point is colored according to the resistant population growth rate. This representation clearly illustrates how high tumor densities (see inset grey arrow) are generally associated with lower resistant growth rates. Re-writing Equation (2) as:

$$\frac{dR}{dt}(S,R,T)=\underset{Growth}{\underbrace{\left(r_R-d_T\right)R}}-\underset{Intra-SpecificCompetition}{\underbrace{\frac{r_{R}R}{K}R}}-\underset{Inter-SpecificCompetition}{\underbrace{\frac{r_{R}S}{K}R}}$$ (5)

shows that this slow-down occurs due to intra- and inter-specific competition. Importantly, while a cost in r_R modulates the strength of growth inhibition through competition, it is not required (as also illustrated in Figure 3C).

During therapy, the composition of a tumor changes, so that treatment corresponds to a trajectory through the S−R space. In Figure 3C we show trajectories of continuous (yellow) and adaptive therapy (blue) for two tumors corresponding to Tumors 1 & 4 in Figure 3A. As can be seen, continuous therapy trajectories tend to traverse regions of high resistant growth (dark green shading). In contrast, these same regions are avoided under adaptive therapy regimens, especially for Tumor 4. Again we can formalize this using Equation (2): If S_CT(t) and S_AT(t) denote the density of sensitive cells after t subsequent days of treatment under continuous and adaptive therapy, respectively, then we have that S_CT(t) ≤ S_AT(t) because continuous therapy does not provide sensitive cells with an opportunity to recover. Assuming that the tumor is still far from progression (R << S) so that the resistant cells primarily compete with sensitive cells, the resistant growth rate is greater for continuous $\left({\frac{dR}{dt}|}_{CT}\right)$ than for adaptive therapy $\left({\frac{dR}{dt}|}_{AT}\right)$: ${\frac{dR}{dt}|}_{CT}\approx (r_R-d_T)R-\frac{r_R{S}_{CT}}{K}R\ge (r_R-d_T)R-\frac{r_R{S}_{AT}}{K}R\approx {\frac{dR}{dt}|}_{AT}.$

This implies that adaptive therapy can provide a benefit even in the absence of a cost of resistance. This benefit increases with increased tumor density as S_AT/K can be maintained large for longer. In addition, this implies that the longest control in this model can be achieved by maintaining the tumor burden as close to its original size as possible, in order to maximize the effects of inter-specific competition. To demonstrate this, we simulate adaptive treatment in which drug is withdrawn after a greater than, and a smaller than, 50% burden reduction (Figures S7A&B). This suggests that, assuming the larger burden is tolerable, the longest TTP can be achieved by the algorithm with the smallest burden reduction.

In the absence of turnover, cost of resistance increases time gained by adaptive therapy only when resistant cells are initially rare

Next, we examine the role of a resistance cost. Figures 4A & B compare low density tumors (Tumor 1 and 2, repeated from Figure 3) with high density tumors (Tumor 3 and 4). As expected, TTP_AT (blue line) increases with a cost of resistance in all four cases (Figure 4A). However, an increase of the benefit of adaptive over continuous therapy is only seen when tumors are close to K and resistant cells are rare, as in Tumors 1 and 4. In contrast, in highly resistant tumors, a cost of resistance increases the TTP in roughly equal terms for continuous and adaptive therapy. This effect is consistent for a wide range of resistance cost values (Figure 4B).

Turnover mediates the impact of a cost of resistance

So far we have assumed that the turnover of tumor cells is negligible. However, tumors are subject to resource starvation and immune predation, resulting in continuous tumor turnover (see Section S6 for further discussion). In Figure 4C we show how such turnover modulates the impact of a resistance cost on the competition between sensitive and resistant cells in the absence of drug. Increasing the cost of resistance (dashed lines) leads to lower levels of resistance in untreated populations. Importantly, while a cost reduces the number of resistant cells, these cells never go extinct in the absence of turnover (Figure 4C). In contrast, if we introduce intrinsic cellular turnover (dˆ_T > 0), resistant cells go extinct over time (Figure 4C). Selection against resistance depends not only on the cost of resistance but also the turnover rate.

How does this insight affect adaptive therapy? In Figure 4D we show TTP_AT as a function of turnover and cost for Tumor 1. If turnover is low, then a large cost of resistance results only in small gains for adaptive therapy, as seen by comparing Cases i and ii in Figures 4D & E. In contrast, if turnover is high, then adaptive therapy provides significant benefits even if the resistance cost is small, or completely absent (Case i vs iii in Figures 4D & E). We also observe in Case iv that once turnover increases beyond a threshold of (1 − 1.2n₀)rˆ_R the tumor becomes indefinitely controllable in the model, so that continuous and adaptive therapy maintain the tumor below the size for progression forever (see Section S7 for further discussion).

Next, we examine how this result generalizes as we change the initial tumor density and resistance fraction. We repeat the cost-gain relationship analysis from Figure 4B with a turnover rate of dˆ_T = 25%. As Tumors 3 & 4 are indefinitely controllable in this parameter regime (see Figures S8A–C), we replace them by tumors with a slightly lower initial density (n₀ = 50%), denoted by Tumors 3* & 4*, respectively. We find that all but the less dense and highly resistant tumor (Tumor 2) benefit from adaptive therapy even in the absence of a resistance cost (Figure 4F). Interestingly, Tumor 3* did not benefit from adaptive therapy in the absence of turnover (Figure 3A; bottom row, center panel), but with turnover, adaptive therapy becomes superior to continuous therapy. Moreover, in all cases a cost of resistance now increases the time gained with adaptive therapy. To test the robustness of our findings to the model assumptions, we re-formulate our model from a density-dependent birth to a density-dependent death model which assumes that cells proliferate at a constant rate and die at a rate proportional to the cell density. This further corroborates our main result that turnover increases the effect of competition between sensitive and resistance cells (Section S5 and Figures S4A–D).

The balance between cost and turnover predicts relapse in patients undergoing intermittent androgen deprivation therapy

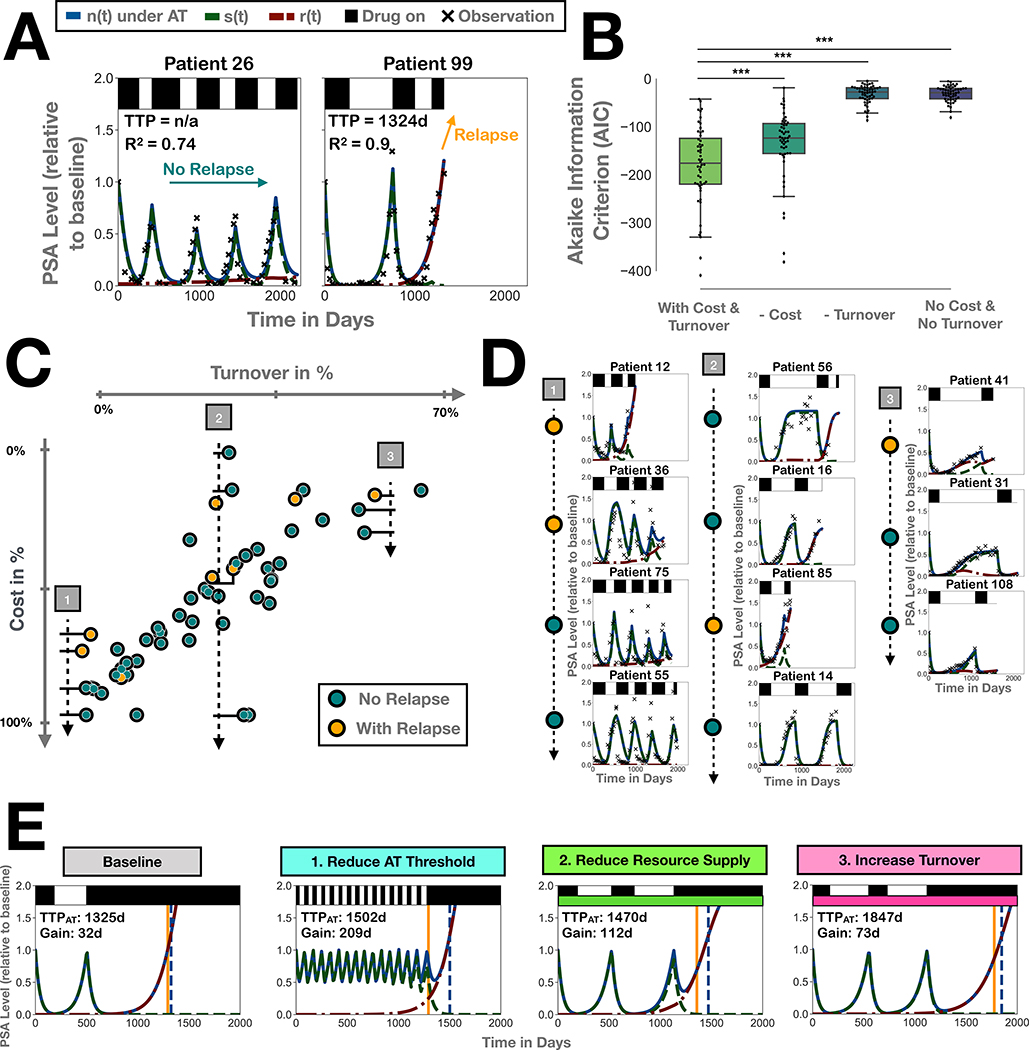
Our theoretical analyses indicate that the success of resistance management depends on an interaction between resistance costs and cellular turnover. To test this hypothesis we fit our model to publicly available, longitudinal tumor burden data from 67 patients undergoing intermittent androgen deprivation treatment for recurrent, locally advanced prostate cancer [29]. After an initial 36 week lead-in period, treatment of these patients was withdrawn whenever prostate specific antigen (PSA) levels were below 4.0 μg/L and was re-instated when PSA levels exceeded 10 μg/L, resulting in treatment cycles similar to adaptive therapy [29]. Using the monthly serum PSA measurement as a marker of tumor burden we fit the values for cost, turnover, n₀, and f_R for each patient, fixing all other parameters as before (Table 1). We find that even though our model was constructed as a conceptual tool, it can recapitulate individual patient dynamics for a majority of patients, and that it can describe patients who continuously respond, as well as those who eventually relapse (Figure 5A; for an overview of all patients see Figure S5).

Figure 5:

The role of cost and turnover in patients undergoing intermittent androgen deprivation therapy (data from Bruchovsky et al [29]). A) Representative fits showing that the model can recapitulate treatment dynamics of both patients who continue to respond to treatment, as well as those who eventually relapse. B) Removing turnover or cost as a variable in the model significantly decreases the goodness-of-fit across the patient cohort, indicating both variables are important in explaining response. Stars denote p-values of less than 1% in paired student t-tests. C) Plot of the estimates for turnover and cost (each point represents one patient) showing a defined spread consistent with our predictions from Figure 4D and the study inclusion criteria. Patients below and above this line would likely not have met the study inclusion criteria due to insufficient response in the lead-in phase or due to lack of relapse after primary therapy. Moreover, patients with relapse tend to fall in the lower half space (note the inverted y-axis), indicating that patients with relapse are defined not by small absolute values of cost, but by values which are small relative to the estimated turnover. D) Examples of patient fits along three transects through the space in C), showing how turnover and cost separate patients with different cycle dynamics, and patients with and without relapse. Note that even though patients 56 and 16 are marked as non-relapsing, it is not known whether they responded in the final therapy cycle. E) 3 Strategies to improve tumor control by increasing competition, illustrated on Patient 99 from A) (Parameters: n₀ = 10%,f_R = 1.25 × 10⁻³%,rˆ_R = 79%,dˆ_T = 44%). Baseline: adaptive therapy with drug withdrawal after a 99% tumor burden reduction, mimicking the Bruchovsky protocol [29]. Strategy 1: adaptive therapy with drug withdrawal at 50%. Strategy 2: secondary drug to reduce K (here by 50%). Strategy 3: secondary drug to increase turnover (here by 20%).

Next we examine what role turnover and cost play in the response dynamics. Analysis of the fitted parameters shows a value of cost and turnover far from 0 in most patients (Figure S9). In fact, setting turnover or cost, or both, to 0 significantly decreases the goodness-of-fit relative to the available degrees-of-freedom, demonstrating the importance of both in understanding treatment dynamics (Figure 5B). Moreover, we find that estimates for turnover and cost show a strong negative correlation with most patients clustering closely along a line in parameter space (Pearson’s correlation coefficient: 0.77; Figure 5C). This trade-off, which is not imposed but emerges from the fitting, supports our hypothesis of the importance of turnover. Firstly, no patient falls into the region in which both turnover and cost, and so response, are small, presumably because such patients would not have achieved PSA level normalization in the lead-in phase required for study inclusion (compare to Figure 4D). Similarly, no patients are seen in the bottom right corner where our model predicts long term tumor control, consistent with the fact that all patients in the study were refractory after initial therapy. Subsequently, we investigate whether differences in turnover or cost are predictive of whether a patient will relapse. While there is no difference in either variable in isolation (Figure S9; p-value in Mann-Whitney U tests > 5%), we observe that patients with a relapse tend to have smaller values of cost than patients with a similar level of turnover in whom no relapse occurs (Figure 5C). Consistent with this observation we find that the difference in the sum of cost and turnover between patients with and without relapse is statistically significant (Mann-Whitney U test; U = 82; p < 1%). To illustrate this we show three sets of examples in Figure 5D. This also shows how different regions in turnover-cost space correspond to different types of patient dynamics, with patients with lower estimates for turnover tending to have shorter drug off periods, than patients with high values of turnover (Transect 1 vs 3). To sum up, this analysis demonstrates that turnover and cost are important in describing patient response to intermittent androgen deprivation treatment, and that it is their combination which has to be considered to understand outcome.

Improving adaptive therapy by amplifying competition

We deduce that there are three ways in which one may amplify intra-tumoral competition and improve tumor control with adaptive therapy (Figure 5E). Firstly, one can lower the threshold for treatment withdrawal, so that treatment is withdrawn earlier and more frequently, assuming the increased tumor burden is acceptable. Secondly, one can target the environmental carrying capacity, for example by administering an anti-angiogenic drug to reduce the supply of nutrients. Finally, one can increase cell death of both sensitive and resistant cells to reduce the growth of resistant cells and the strength of selection against them if a cost is present. This may be done, for example, by adding low dose chemotherapy. In Figure 5E we illustrate each strategy on Patient 99 who relapses during intermittent androgen deprivation treatment. Interestingly, while it is Strategy 1 which optimizes the gain of adaptive relative to continuous therapy, it is Strategy 3 which maximizes absolute TTP. This suggests that depending on the clinical aim, different strategies, or combinations of these, may be optimal.

Discussion

With four clinical trials of adaptive therapy already ongoing (clinicaltrials.gov identifiers: NCT02415621; NCT03511196; NCT03543969; NCT03630120) and more in preparation [31], it is important to develop criteria to identify which patients might benefit from adaptive therapy over standard MTD approaches. Intuitively, it appears that the presence of a fitness cost of resistance might serve as an inclusion criterion. However, a cost does not guarantee resistance control [11, 12]. Moreover, Zhang et al [10] do not report a resistance cost in vitro, yet find that adaptive therapy extends median TTP by over 10 months in patients.

The aim of this paper is to consolidate these findings and develop an understanding of the circumstances under which a resistance cost is required, and under which circumstances it is not. To do so, we developed a simple two-population Lotka-Volterra competition model and treated it according to the adaptive therapy algorithm from Zhang et al [10]. We have shown that the time gained compared to continuous therapy depends on four key factors:

i) the initial fraction of resistant cells (f_R), ii) the proximity of the tumor to environmental carrying capacity (n₀), iii) the resistant cell proliferation rate (r_R), and iv) the rate of cellular turnover (d_T). While the importance of the first two factors has been recognised previously [6, 11, 12], it has been unclear how they interact with the latter two. Firstly, we show that a resistance cost is not necessary for adaptive therapy to extend TTP. If the tumour is close to carrying capacity, and resistance is rare, then adaptive therapy can achieve significant gains even in the absence of a cost. We demonstrate how to use the work by Hansen et al [6] to explain this result mathematically and how it may be visualized for a non-mathematical audience using phase plane techniques. Viossat and Noble [26] have recently applied this approach to a broad class of tumor models, and we recommend their paper for a detailed discussion of how some of our results may be generalized. Finally, it is worth pointing out that resistance costs may also manifest themselves in other ways. For example, in the 3-D spheroids in Figure 1, there is significantly more debris around the resistant spheroids than around their sensitive counterparts (see also Figure S1 and Section S1.4), suggesting a potentially higher turnover in resistant compared to sensitive cells. Our analysis easily extends to costs in the turnover rate and carrying capacity (Section S2).

Given its pivotal role, an important question to ask is: what is a tumor’s carrying capacity? Carrying capacity is defined as the population size at which growth saturates [32]. As such it is a multi-faceted concept which may be defined at different spatial scales, and which may vary over time and space. For example, one can define a systemic carrying capacity for the whole body, or local carrying capacities for individual tumor lesions. Moreover, because of spatial heterogeneity in resource supply, or available space, different lesions, or even different regions within the same tumor, may have different carrying capacities. Importantly, while tumors, especially solid tumors, are likely far away from their fatal, systemic carrying capacity, they may be close to their tissue or sub-tissue level capacity [33].

Furthermore, carrying capacity is a dynamic quantity which changes over time. It is determined by space and resource availability, which will change as the tumor recruits vasculature and stromal support, or gains the ability to invade surrounding tissue. Moreover, it is determined by the ratio of birth to death in the tumor. Working with the popular r − K form of the logistic growth equation this fact is easily overlooked, and results in the misleading perception that r and K are independent. A key contribution of this paper is to highlight that not only environmental constraints, but also the cells’ proliferation and death rates, determine the impact of intra-tumoral competition. The shorter a cell’s life span, the fewer opportunities it will have to divide, and the greater will be the impact of interference through intra- and inter-specific competition. Changes in the proliferation or death rate, due to mutation, immune predation, or treatment, will alter the tumor’s carrying capacity and so the competition between tumor cells. The relationship between r and K has been an area of intense debate in ecology, centered in particular around the so-called r −K selection hypothesis [32]. Realization of their inter-dependence has been an important step in consolidating ecological and evolutionary theory [34, 35, 36], and may similarly help to improve our understanding of tumor evolution, and treatment response.

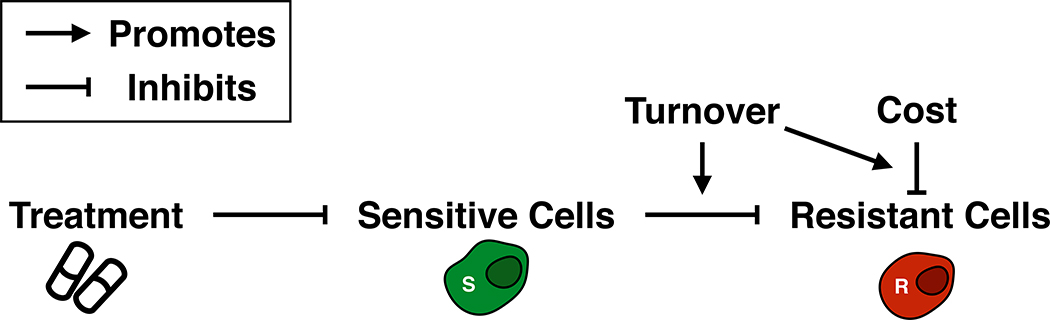
An important implication of this dynamic view of carrying capacity is that tissue turnover plays a role in adaptive therapy (Figure 6). Specifically, our modeling indicates that higher turnover facilitates the control of drug-resistance and that if a resistance cost is present, its benefit depends not on its absolute value, but on its value relative to the turnover rate. We test this hypothesis by fitting our model to response data from prostate cancer patients undergoing intermittent androgen deprivation therapy. This shows that both cost and turnover are required to explain the treatment dynamics, as their removal significantly reduces goodness-of-fit, even when a penalty for the additional degrees-of-freedom is applied. Interestingly, and contrary to our expectations, we do not find a difference in turnover when we test for differences between patients who relapse and those who do not. Possibly, this is because tumors with higher turnover may also harbor more resistance as these tumors will have passed through more generations before detection [37], although we do not detect such a correlation ourselves. However, when we examine both cost and turnover together, we see that patients who relapse tend to be defined by a smaller combination of cost and turnover than patients without a relapse. While these results should be viewed with some caution, as neither cost nor turnover were measured directly, they are consistent with our hypothesis, and show how our insights may help to understand treatment response.

Figure 6:

The interplay between cost of resistance and turnover in adaptive therapy. Sensitive cells slow the growth of resistant cells through competition, but are killed by treatment. A cost of resistance reduces the resistant growth rate. Turnover amplifies the impact of both a cost of resistance and the strength competition.

One reason why it was difficult to test our hypothesis more directly is that relatively little is known about turnover rates in human tumors. Most available data was collected between the 1960s and 1990s based on a method pioneered by Steel [38]. This method compares the potential doubling time expected from the fraction of dividing cells as identified by chemical labelling to the actual observed volumetric doubling time. Interestingly, most of these studies found that tumors grew significantly slower than expected, suggesting that the rate of cell death closely matches that of cell production (see Section S6 and Table S2 for further discussion; [38, 39, 40]). Yet all of these measurements are indirect. In light of our findings we advocate that more focus should be put on quantifying the turnover rates in tumors. Not only may information on turnover rates help to identify suitable candidates for adaptive therapy, it may also be important in interpreting data from experimental model systems. For example, while in vitro no resistance cost may be observed, tumor control may still be possible in vivo or in patients as turnover, via greater nutrient deprivation, and immune suppression will intensify competition, and amplify even small fitness differences.

We make a number of simplifications in our model. Firstly, similar to previous studies [6, 11] we assume that the tumor is not curable. However, as can be seen in Figure 4E, including a resistance cost and greater turnover also result in fewer cells at the nadir during continuous therapy. This implies that the tumors in which adaptive therapy will be most effective are those in which continuous therapy just misses being curative, an observation also made elsewhere [3, 12]. Thus, the very long gains predicted under adaptive therapy have to be viewed with some skepticism, since in a proportion of these patients continuous therapy would have potentially cured the tumor. That being said, adaptive therapy is intended for advanced settings in which the available treatment is rarely curative, which suggests that such cases will be rare [4, 41]. Moreover, it seems plausible that if one finds that adaptive therapy controls the tumor very well, one could then decide to switch to a curative approach. In fact, adaptive therapy has been shown to have stabilizing effects on tumor vasculature [8], which suggests that a curative approach may be even more effective after an initial period of adaptive therapy.

Secondly, we make the simplifying assumption that resistance is pre-existing and that progression is driven solely by clonal expansion of this subpopulation. However, there is mounting evidence that acquisition of resistance is a multi-step process in which genotype- and environment-mediated cell plasticity (e.g. via growth factors [27] or ECM stiffness [42]) play a key role. While previous research, for example, in melanoma [9] has shown that adaptive therapy can still succeed despite this plasticity, it does pose additional challenges for resistance management [6, 14, 26]. Growth-factor driven interactions can result in spatial, non-linear evolutionary games between sub-populations, whose dynamics may change with environmental conditions [20]. Future research should examine adaptive therapy in the context of this plasticity in more detail.

A further important caveat of our study is that we do not account for the potential health risks associated with the increased tumor burden under adaptive therapy. As a result, our model predicts that the longest TTP can be achieved by keeping the tumor as close to its initial size as possible. This is true for most studies in this area ([7, 9, 11, 13, 28]). However, a higher tumor level increases the potential for de novo resistance acquisition and metastasis, and under certain circumstances these costs may outweigh the benefits of adaptive therapy [6, 26, 43]. Investigating the risks of adaptive therapy is an important direction of future research.

In order to facilitate analysis, we neglect the impact of space in this manuscript. However, previous work [11, 12] has demonstrated that the tumor’s spatial architecture is an important factor in adaptive therapy. If resistant cells can be “trapped” by surrounding sensitive cells, the tumor may be controlled for a long time [11, 12], as resistant cells are close to their local carrying capacity. This may negate the need for a resistant cost for small values of initial burden, and would define carrying capacity in a local fashion. At the same time, by creating gaps in the layer of surrounding cells, turnover may facilitate escape of trapped resistant cells, so that the benefit derived from high turnover may be smaller than expected from the ODE model. In addition, it would allow us to examine the impact of microenvironmental factors such as the stiffness of the extra-cellular matrix, acidity of the micro-environment, or presence of stromal support, which are known to affect drug resistance [42]. We have already started to test how our current predictions translate to a spatial model, and have made a pre-print of our results available on bioRxiv [44].

To conclude, we want to highlight interesting parallels to the pest and antibiotic resistance management literature, which have investigated resistance costs since the mid-20^th century (see [45] for an early review of resistance costs in insecticides). Firstly, also in these fields it is a controversial issue [16, 46, 47, 48]. For example, Bergelson et al [46] find that out of 88 studies examining the cost question in plants, 44 show a cost, 40 find no difference and 4 even observe a benefit to resistance. This is because the fitness effect of a resistance adaptation depends on the resistance mechanism, the genetic, and the environmental context [15, 16, 46]. Thus, in developing adaptive therapy we should not assume the presence of costs nor that they are uniform throughout space and time. Importantly, resistance management can be successful despite this uncertainty. For example, the resistance management scheme for the insecticide producing Bacillus thuringensis (Bt) crop has been successful despite inconclusive evidence regarding the presence of resistance costs [47, 48]. The reason for this success lies in integration of multiple treatment modalities [49, 50]. As such, we advocate multi-drug approaches in which one, or several drugs, are given adaptively. Initial theoretical work on multi-drug adaptive therapy has already been carried out [28, 51, 52], and we have illustrated here how by targeting the resource availability or turnover in a tumor with secondary drugs one can greatly enhance tumor control. We also note that while abiraterone was given adaptively in the initial prostate cancer adaptive therapy trial (NCT02415621), patients were concurrently receiving a continuous dose of Lupron which suppresses systemic testosterone production and reduces the cancer’s supply of growth factors. A follow-up study now gives both Abiraterone and Lupron in an adaptive fashion (NCT03511196). Going forward it will be important to extend this work to develop multi-modal strategies which exploit a cost of resistance, yet are robust if this cost disappears due to environmental or genetic compensation. With better understanding of tumor growth, resistance costs, and turnover rates, adaptive therapy can be more carefully tailored to patients who stand to benefit from it the most.

Statement of Significance:

Tumor cell turnover modulates the speed of selection against drug-resistance by amplifying the effects of competition and resistance costs; as such, turnover is an important factor in resistance management via adaptive therapy.