Using integrated modeling to support the global eradication of vaccine-preventable diseases

Abstract

The long-term management of global disease eradication initiatives involves numerous inherently dynamic processes, health and economic trade-offs, significant uncertainty and variability, rare events with big consequences, complex and inter-related decisions, and a requirement for cooperation among a large number of stakeholders. Over the course of more than 16 years of collaborative modeling efforts to support the Global Polio Eradication Initiative, we developed increasingly complex integrated system dynamics models that combined numerous analytical approaches, including differential equation-based modeling, risk and decision analysis, discrete-event and individual-based simulation, probabilistic uncertainty and sensitivity analysis, health economics, and optimization. We discuss the central role of systems thinking and system dynamics in the overall effort and the value of integrating different modeling approaches to appropriately address the trade-offs involved in some of the policy questions. We discuss practical challenges of integrating different analytical tools and we provide our perspective on the future of integrated modeling.

Introduction

The long-term management of global disease eradication involves numerous inherently dynamic processes, health and economic trade-offs, significant uncertainty and variability, rare events with big consequences, complex and inter-related decisions, and a requirement for cooperation among many stakeholders. As we launched a collaborative modeling effort to support the Global Polio Eradication Initiative (GPEI) in 2001, we recognized that to adequately characterize the complexity, we needed to develop integrated models. Over the course of the collaboration, we combined numerous analytical approaches, including systems thinking, deterministic and stochastic differential equation-based (DEB) modeling, discrete-event and individual-based simulation, risk and decision analysis, and probabilistic uncertainty and sensitivity analysis to explore and optimize appropriate health economic metrics of policy interest. This paper provides a brief background on polio eradication and an overview of the main modeling tools that we used in the context of this extensive collaboration. We motivate our choice to integrate multiple modeling tools within system dynamics models based on the policy questions we addressed and the limitations of the individual tools. We then provide an example of how we integrated a discrete-event simulation within a global model for long-term poliovirus risk management. Finally, we discuss key lessons learned related to the use of integrated models and specifically discuss the role of system dynamics modeling and systems thinking as a key foundation for the development and application of integrated models.

Polio eradication

Infection with one of the three wild poliovirus serotypes leads to paralytic poliomyelitis disease (polio) in a small fraction of previously uninfected and unvaccinated individuals (i.e., 1/200, 1/2000, and 1/1000 for serotypes 1, 2, and 3, respectively) (Nathanson and Kew 2010). Polio patients who experience paralysis of the lungs require artificial respiration and some do not survive the disease, while the surviving patients and those with paralysis of the limbs typically suffer some level of residual paralysis for the rest of their lives. Until the late 1950s, polio terrified people, with a peak of 21,000 reported polio cases in the United States in 1952. After the first successful large-scale polio vaccine trials in 1954 in the United States (Francis et al. 1955), most developed countries began using poliovirus vaccines on a massive scale. This led to significant reductions in polio incidence and eventually eliminated transmission of indigenous wild polioviruses in developed countries. However, developing countries continued to experience an estimated hundreds of thousands of polio cases per year. On the heels of the success of smallpox eradication (Fenner et al. 1988) and progress towards polio elimination from the Americas (Hinman et al. 1987), in 1988 the World Health Assembly resolved to eradicate poliomyelitis by the year 2000 (World Health Assembly 1988), which led to the launch of the GPEI. Despite rapid success in most countries and ending polio cases caused by naturally occurring serotype 2 wild polioviruses globally by 1999, the world missed the deadline and continues to work towards the primary goal of interrupting all remaining wild poliovirus transmission. The world certified 4 of the 6 World Health Organization Regions as free of all wild poliovirus transmission, certified the global eradication of serotype 2 wild polioviruses in 2015 (Global Polio Eradication Initiative 2015)), and did not report any evidence of serotype 3 wild poliovirus transmission since 2012 (Kew et al. 2014). As of late 2017, three polio-endemic countries (i.e., Afghanistan, Nigeria, and Pakistan) continue to sustain indigenous serotype 1 wild poliovirus transmission (World Health Organization 2017).

Poliovirus spread may occur either as a result of oral ingestion by susceptible individuals of fecal matter excreted as the virus replicates in the intestines of infected individuals (i.e., fecal-oral transmission) or via oral inhalation by susceptible individuals of aerosol droplets excreted as the virus replicates in the cavities behind the nose and mouth of infected individuals (i.e., oropharyngeal transmission) (Melnick 1997). The evidence suggests that fecal-oral transmission dominates in settings of poor sanitation and hygiene while oropharyngeal transmission probably represents the primary mode of spread in developed countries (Chin et al. 1961; Duintjer Tebbens et al. 2013a). Both natural infections with polioviruses and vaccination result in the production of antibodies that limit the ability of polioviruses to replicate in the host. The resulting active immunity most likely completely prevents the development of polio disease in the event of any future infections. While active immunity does not fully prevent reinfections, it limits the amount of virus excreted after a reinfection. Population immunity to poliovirus transmission refers to the collective ability of all individuals in a population to participate in transmission, regardless of their individual protection from polio disease. Endemic wild poliovirus transmission in the absence of vaccination naturally leads population immunity to transmission to hover around an equilibrium level, while interrupting transmission requires use of vaccines to raise immunity far enough above this level such that the wild virus does not find enough susceptible individuals to sustain transmission (Thompson et al. 2013b).

Although global eradication may seem like a straightforward goal, numerous complexities pose important challenges for the polio endgame. First, eradication represents an unforgiving goal that remains elusive as long as any community in any country does not achieve sufficiently high population immunity to interrupt and prevent transmission (Thompson and Duintjer Tebbens 2017b). Unfortunately, maintaining high enough population immunity to transmission after wild poliovirus elimination proved challenging in areas with poor health systems and conditions conducive to intense fecal-oral transmission. Since the GPEI succeeded in bringing the number of endemic countries to 4 in 2006, numerous outbreaks involving 39 previously polio-free countries proved that all countries need to maintain high population immunity to poliovirus transmission until all countries interrupt wild poliovirus transmission (Thompson et al. 2013a; Mach et al. 2014). Consequently, all countries remain stakeholders in the GPEI, creating strong incentives to cooperate (Thompson and Duintjer Tebbens 2008a) in the context of important global variability in wealth and development, population densities, and other factors that affect poliovirus transmission, preferences, and cultural attitudes. Second, given that unlike for smallpox most poliovirus infections remain asymptomatic, outbreaks involve many times more infected people than clinical cases, which means that reactive vaccination efforts often fail to prevent further transmission and that even with high-quality clinical surveillance, some possibility exists of undetected transmission. Third, poliovirus behavior remains highly complex and continues to involve numerous uncertainties despite extensive polio research for over a century.

The two very different poliovirus vaccines that exist contribute significantly to the complexity of poliovirus immunity and risk management. The live, attenuated oral poliovirus vaccine (OPV) contains weakened viruses that mimic a natural infection (Sutter et al. 2013). An OPV infection thus stimulates the same kind of intestinal and oropharyngeal immunity as a wild poliovirus infection, which prevents paralysis in the event of a later poliovirus exposure and substantially reduces the probability, duration, and infectiousness of subsequent infections. Given that OPV causes a live poliovirus infection, the vaccine virus can spread to immunize contacts, which provides an additional benefit. Unfortunately, however, the attenuated strains in OPV only involve a few key attenuating mutations that make the virus less transmissible and virulent than wild polioviruses (Minor 2016). The longer the virus replicates, the greater the chance that it will lose the attenuating mutations and acquire the ability to cause paralysis and more readily transmit. In a population with low immunity levels, the OPV virus can find enough susceptible hosts to continue to replicate and evolve to become a circulating vaccine-derived poliovirus (cVDPV) that can cause outbreaks similar to wild poliovirus outbreaks (Duintjer Tebbens et al. 2013d; Burns et al. 2014). Outbreaks of cVDPVs to date occurred in countries that interrupted wild poliovirus transmission but did not subsequently sustain high enough OPV coverage, including possible still ongoing serotype 2 cVDPV transmission in Nigeria that started 12 years ago (Etsano et al. 2016). In addition, continued replication can occur in certain individuals with primary immunodeficiencies (PIDs) to cause immunodeficiency-associated vaccine-derived polioviruses (iVDPVs)(Duintjer Tebbens et al. 2015b; Macklin et al. 2017). Like cVDPVs, iVDPVs behave similarly to wild polioviruses in laboratory experiments and could thus lead to future reintroduction of outbreak-causing polioviruses, although to date no known iVDPV outbreaks occurred and uncertainty exists about the potential transmissibility of iVDPVs.

The second type of poliovirus vaccine is the injectable, inactivated poliovirus vaccine (IPV), which contains a killed poliovirus that cannot spread or revert to a form that causes paralysis (Vidor and Plotkin 2013). IPV stimulates systemic immunity that induces antibodies in the blood and prevents any subsequent poliovirus infections from invading the central nervous system to cause paralysis. However, IPV does not provide much intestinal immunity, which means that subsequent live poliovirus exposure can result in an intestinal infection similar to infection in fully susceptible individuals, which can spread via fecal-oral transmission. IPV appears to stimulate sufficient immunity to significantly reduce oropharyngeal poliovirus infections and oropharyngeal transmission. The experience with IPV in high-income settings suggests that the oropharyngeal immunity provided by IPV suffices to prevent widespread transmission (Stickle 1964; Lapinleimu 1984; Oostvogel et al. 1994). However, IPV experience in developing countries in the absence of OPV use remains very limited, and an episode of widespread wild poliovirus transmission without any detected polio cases in an Israeli population with sub-optimal hygiene but very high IPV-only coverage demonstrated that polioviruses can transmit (probably driven by fecal-oral transmission) in an IPV-only vaccinated population (Anis et al. 2013; Kalkowska et al. 2015a). IPV remains much more expensive to use than OPV, and unlike OPV drops, requires medically-trained personnel for the needle injection.

Due to the risks of OPV, the GPEI recognized the need to globally coordinate cessation of OPV use after wild poliovirus eradication to prevent all polio, which the World Health Assembly endorsed in 2008 (World Health Assembly 2008). Given the certification of serotype 2 wild poliovirus eradication (Global Polio Eradication Initiative 2015), in late April-early May 2016 the GPEI started the process of globally-coordinated OPV cessation by switching all trivalent OPV, which contains all three serotypes, to bivalent OPV, which contains only serotypes 1 and 3. This unprecedented rapid roll-out of a new vaccine in 155 countries using OPV at that time effectively withdrew all serotype 2 OPV (Hampton et al. 2016). Serotype 2 monovalent OPV now remains available only from a stockpile for outbreak response. The GPEI recommended as a prerequisite to the trivalent to bivalent OPV switch that all countries should introduce at least one dose of IPV (which contains all 3 serotypes) into their immunization schedules. This would provide some serotype 2 immunity and protection from paralysis to children born after the trivalent to bivalent OPV switch, depending on the fraction of children who receive the IPV dose and develop an immune response. The world thus entered a new era in which for the first time newborn children do not get exposed to any serotype 2 wild or OPV-related polioviruses. Given the limited effect of IPV on population immunity to fecal-oral poliovirus transmission, this means that global population immunity to serotype 2 transmission will decline to unprecedented low levels (Duintjer Tebbens and Thompson 2014). The GPEI hopes to stop serotype 1 wild poliovirus transmission in 2018, and if successful in managing the risks after serotype 2 OPV cessation, hopes to stop all OPV use approximately 3–4 years after the last wild poliovirus case.

Overview of modeling tools

Table 1 provides an overview of the main modeling tools we used during our collaborative effort to support the GPEI, their key strengths, and their limitations if used in isolation. The last column includes selected polio-related policy questions that we addressed by using these tools by themselves. Many of these models then served as components for our integrated models. For brevity, we assume familiarity of the readers with each of the tools and we do not attempt to provide an exhaustive list of all the potential modeling tools relevant to system dynamics practice or beyond. Rather, we focus on the key strengths and limitations based primarily on our polio modeling experience.

Table 1:

Overview of modeling tools to potentially combine in an integrated system dynamics model

Modeling tool	Strengths	Limitations if used by itself	Polio-related policy questions addressed by use of the given tool by itself
Systems thinking	* Identify and communicate dynamic complexity * Maintain system perspective	* Qualitative	* What does the global polio surveillance system look like, what are the key delays and outputs (Kalkowska et al. 2015b)?
Deterministic DEB modeling	* Account for aggregate-level feedbacks, accumulation, and delays * Ability to focus on and systematically identify critical dynamic complexity * Highly extendable with complimentary approaches	* Steady-state errors * Stocks never reach 0 * Potentially unrealistic distributions implied by delay processes or aging chains * Only captures average- behavior (i.e., ignores randomness in transitions, uncertainty about averages for stocks, and variability around these averages)	* What can we learn for the future from dynamic modeling of past polio experiences (Duintjer Tebbens et al. 2005; Duintjer Tebbens et al. 2013c)? * What are the trade-offs between speed and coverage of outbreak response immunization (Thompson et al. 2006a)? * What are key polio under-vaccinated subpopulations in the United States, what are the trends, and what are the implications for the national polio vaccine stockpile (Thompson et al. 2012)? * What are the impacts of various immunization options on poliovirus transmission and population immunity to poliovirus transmission in various settings of interest (Thompson et al. 2012; Kalkowska et al. 2014b; Kalkowska et al. 2014a; Duintjer Tebbens et al. 2015c; Kalkowska et al. 2015a; Thompson and Duintjer Tebbens 2015a; Thompson et al. 2015b; Duintjer Tebbens and Thompson 2017b; Thompson and Duintjer Tebbens 2017b)? * How does expanding the target age groups of immunization campaigns affect polio incidence and population immunity to transmission (Duintjer Tebbens et al. 2014)? * What are the best strategies to manage various risks associated with the implementation of OPV cessation (Duintjer Tebbens and Thompson 2014; Thompson and Duintjer Tebbens 2014a; Duintjer Tebbens et al. 2016b; Duintjer Tebbens et al. 2016a; Duintjer Tebbens et al. 2016c)?
Stochastic DEB modeling	* Account for feedbacks, accumulation, delays, and stochastic variability in transitions between stocks	* Computationally more intensive and less tractable than deterministic DEB models * Still subject to steady-state errors and unrealistic distributions implied by delay processes	* How do different decision rules perform to prioritize resources for multiple eradicable diseases (Duintjer Tebbens and Thompson 2009)? * What is the probability of undetected poliovirus circulation as a function of time since the last detection (Kalkowska et al. 2012; Kalkowska et al. 2015b)?
DES modeling	* Accounts for feedback, accumulation, delays, and stochastic variability in transitions between stocks based on individual-level variability	* Computationally more intensive and less tractable than DEB models * Less easy to identify feedback structure	* What is the expected prevalence of iVDPV excretors after OPV cessation and how does this depend on iVDPV surveillance and polio antiviral drug properties (Duintjer Tebbens et al. 2015b)?
Agent-based modeling	* Accounts for feedbacks, accumulation, delays, stochastic variability in transitions between stocks, and individual-level variability, interactions, and decisions	* Computationally highly intensive * Systems perspective sometimes not explicit * Depends on adequate detailed-level data * Not easily amenable to uncertainty and sensitivity analysis	* How do assumptions about contact networks affect modeled poliovirus outbreaks (Rahmandad et al. 2011)? * How might a wild poliovirus introduced into an under-vaccinated North American Amish community propagate geographically (Kisjes et al. 2014)?
Decision analysis	* Structures complex decision space * Deals with conditional probabilities and/or choices	* Traditionally does not account for dynamic complexity	* What are the key poliovirus risk management options for countries and the world (Sangrujee et al. 2003; Thompson and Duintjer Tebbens 2012; Thompson et al. 2013a)? * What are possible frameworks to assess the value of information obtained through poliovirus surveillance (de Gourville et al. 2006) ?
Economic modeling	* Characterizes economic inputs * Supports evaluation of trade-offs in the context of limited resources * Facilitates evaluation of behavioral responses to economic incentives * Facilitates optimization of resources and economic outcomes	* Ignores population-level or other dynamics * Ignores uncertainty and variability	* What are the costs of post-eradication policies (Duintjer Tebbens et al. 2006b)? * What are the costs of the Global Polio Laboratory Network (de Gourville et al. 2006)? * What are the true costs of different IPV formulations and delivery options (Thompson and Duintjer Tebbens 2014b)? * What are the national incentives to stop OPV and what does this mean for global coordination (Thompson and Duintjer Tebbens 2008a)?
Probabilistic risk analysis, including expert judgment	* Quantifies impact of random events with rigorous methods based on probability and statistics * Accounts for dependence between random variables * Quantifies uncertainty and variability using available data and/or expert judgment * Identifies knowledge gaps and research priorities	* Requires significant effort * Depends on quality of available evidence/data and/or expert knowledge	* What are the risks of poliovirus reintroductions in the post-eradication era (Duintjer Tebbens et al. 2006a)? * What is the evidence-base to assess poliovirus immunity, transmission, and evolution, and what are the key limitations of the existing studies (Duintjer Tebbens et al. 2013a; Duintjer Tebbens et al. 2013d)? * What are the consensus and uncertainty related to estimates to characterize poliovirus immunity and transmission and what future studies may fill key knowledge gaps (Duintjer Tebbens et al. 2013b)?
(Probabilistic) uncertainty and sensitivity analysis	* Helps understand and communicate impact of uncertainty * Accounts for non-linearity and interaction and/or dependence between uncertain inputs (depending on method) * Helps prioritize research to fill knowledge gaps	Always used in combination with other modeling tools	* What are the key uncertainties affecting the net benefits of long-term poliovirus risk management options (used in combination with integrated models) (Duintjer Tebbens et al. 2008a; Duintjer Tebbens and Thompson 2016b)? * What are the key uncertainties affecting the net benefits of policies to manage long-term iVDPV risks (used in combination with DES and integrated models) (Duintjer Tebbens and Thompson 2017a)?

In Table 1, systems thinking refers to the general approach of considering the system behavior by explicitly but qualitatively mapping its components and the dynamic relationships between them, including feedback loops and delays (e.g., using causal loop and stock-and-flow diagrams) (Sterman 2000). Systems thinking represents a powerful tool to identify and think through dynamic complexity, to effectively communicate this complexity among diverse stakeholders, and to preserve a system perspective in the face of complex problems because of the conceptual clarity provided by mapping the system. However, if not combined with any actual simulations, systems thinking remains qualitative and thus does not provide quantitative projections, which necessitates the use of one or more other modeling tools, including those listed in Table 1. We used systems thinking by itself to map out the global polio surveillance system, which helped to identify key delays and clarify the types of information obtained by different types of surveillance (Kalkowska et al. 2015b).

Deterministic DEB modeling relies on compartments and fractional transition rates to represent the stocks and flows, respectively, which govern system behavior. Deterministic DEB modeling probably represents the most widely applied and time-tested system dynamics modeling tool (Sterman 2000) and consequently the methodology is well-developed with numerous software packages available to facilitate rapid implementation, execution, and analysis. Deterministic DEB models typically focus on aggregate level behavior based on the average characteristics of the objects that make up a stock (e.g., people, molecules, production units). For many systems, the behavior indeed depends primarily on the system structure and interactions between the aggregate components (Sterman 2000). By focusing on aggregate behavior, deterministic DEB models excel at highlighting critical dynamic complexity and demonstrating how these dynamics quantitatively affect outcomes. Moreover, one can add detail or complexity to deterministic DEB models by disaggregating stocks and deterministic DEB models can flexibly extend or integrate with complimentary tools, which most system dynamics software packages already support. Well-documented limitations of DEB models relate to the approximations inherent in characterizing aggregate-level behavior, which can lead to steady state errors and unrealistic distributions implicit in delay processes or aging chains that ignore the arrival time in stocks (Sterman 2000; Eberlein et al. 2012). Furthermore, fractional rate-based processes that drain stocks cannot make these stocks go to absolute 0, while in reality complete depletion of some stocks can occur (e.g., populations can reach 0 prevalence of an infection and inventories can become completely empty). While methodologies exist within the deterministic DEB modeling framework to circumvent these limitations (Eberlein et al. 2012; Duintjer Tebbens and Thompson 2015b), by their nature deterministic DEB models used by themselves only produce a single realization of the system behavior based on the average characteristics of its components. This ignores both randomness in the number of transitions between stocks due to stochastic variability in the populations represented by a stock around their population averages (i.e., variability within stocks) and uncertainty about these averages. We used deterministic DEB models of poliovirus transmission (Duintjer Tebbens et al. 2005; Duintjer Tebbens et al. 2013c) to derive many important policy insights, including the critical importance of responding rapidly to outbreaks, even at the expense of initially lower coverage (World Health Organization 2005b; Thompson et al. 2006a), the counter-intuitive need to intensify OPV use prior to its cessation as opposed to a gradual phase-out (Duintjer Tebbens and Thompson 2014; Kalkowska et al. 2014b; Kalkowska et al. 2014a; Thompson and Duintjer Tebbens 2014a), the need to synchronize OPV cessation and verify the complete withdrawal of OPV (Duintjer Tebbens et al. 2016b; Duintjer Tebbens et al. 2016a; Duintjer Tebbens et al. 2016c), and numerous insights related to different OPV and IPV vaccination strategies to achieve and maintain eradication in specific settings (Thompson et al. 2012; Duintjer Tebbens et al. 2014; Kalkowska et al. 2014b; Kalkowska et al. 2014a; Duintjer Tebbens et al. 2015c; Kalkowska et al. 2015a; Thompson and Duintjer Tebbens 2015a; Thompson et al. 2015b; Duintjer Tebbens and Thompson 2017b; Thompson and Duintjer Tebbens 2017b).

Stochastic DEB models maintain the exact same structure and level of aggregation as deterministic DEB models. However, by using non-negative integer values for stocks and randomly drawing transitions between stocks, stochastic DEB models address the limitations from deterministic DEB models related to stocks never reaching absolute zero and stochastic variability in the transitions between stocks, respectively. Different methods to do so may either randomly determine the exact time intervals between transitions that occur in the system (e.g., the Gillespie method) (Gillespie 1976) or use a fixed time step to randomly determine the number of transitions that occur in the system during this time step (e.g., using Poisson draws) (Bartlett 1956). The cost of making the models more realistic in this way comes from a substantial increase in computational intensity and tractability. For example, the Gillespie method becomes exceedingly slow for systems with large numbers of units contained in stocks, large numbers of stocks and flows, and short time constants, while Poisson-based methods require care with the choice of time step and in some cases the order of transitions. Both methods require repeated stochastic iterations to capture the distribution of possible system behaviors. Stochastic DEB models maintain the same limitations as deterministic DEB models related to steady-state errors, distributions implied by delay or aging processes that ignore the arrival time in a stock, and uncertainty and variability around the averages. We used stochastic DEB models to address policy questions related to the potential for undetected poliovirus circulation after the apparent last detection of transmission because these required consideration of the randomness in times between infections (i.e., transitions from susceptible to infected), the resulting symptoms (i.e., paralytic or not), and the behavior at stock levels near 0 (Kalkowska et al. 2012; Kalkowska et al. 2015b). These models resulted in insights related to the time required to reach a high confidence that transmission stopped and how this depends on setting-specific factors like population immunity to transmission and seasonal fluctuations in poliovirus transmissibility (Kalkowska et al. 2012; Kalkowska et al. 2015b), which helped to inform policies about when to certify global wild poliovirus eradication and stop OPV use.

Discrete-event simulation (DES) models address two additional limitations of DEB models by explicitly tracking each object in a stock. This makes it possible to 1) assign properties to the individual objects to stochastically or deterministically characterize variability around the average properties, and 2) track the arrival time of individual objects in a certain state, which allows more realistic distributions of when transitions to another state occur. Similar to stochastic DEB models using the Gillespie method, DES models assume that the transitions can occur at any point in time (i.e., discrete events) with no changes in the state of the system between events. Tracking each object and the need to perform multiple iterations increases the computational costs and decreases the tractability of DES models compared to deterministic or stochastic DEB models, although the use of Poisson draws in a DES model can maintain the two advantages of DES modeling with a much faster fixed time step approximation. Furthermore, DES models traditionally do not focus on dynamic complexity, making it more difficult to identify and explain the feedback structure. We used a DES model to describe the prevalence of the rare event of excretion of iVDPVs as a function of time after OPV cessation (Duintjer Tebbens et al. 2015b). Dating back the start of OPV use in the 1960s, only approximately 100 identified individuals whose immune systems failed to clear poliovirus infections excreted for more than 6 months (Macklin et al. 2017). While the absence of a system to identify these individuals certainly implies a much larger true cumulative incidence, the current and future instantaneous prevalence of iVDPV excretors remains too small to model in an aggregate way. Moreover, the stochastic variability in the duration of excretion, with observations ranging from 6 months to over 30 years (Dunn et al. 2015), critically affects the long-term risks to the broader population. However, the causes of spontaneous recovery from infection, if it occurs before a patient dies, remain unknown. The survival of PID patients depends on their characteristics and treatment status, which may fluctuate over time. The acquisition of long-term infections by PID patients depends on whether they get exposed to OPV and whether the OPV infection persists for long enough to evolve to an iVDPV, which occurs only in a small fraction of PID patients for unknown reasons. All of these complexities make modeling of iVDPV prevalence well-suited for a DES framework. The DES model we developed tracked all patients with PIDs to generate key events in their lifetime related to polio risks and provides stochastic realizations of the number of iVDPV excretors over time (Duintjer Tebbens et al. 2015b). Doing so provided insights about the potential effect of antivirals drugs on iVDPV prevalence and estimated that the vast majority of iVDPV excretors remain undetected because they do not present with paralytic symptoms, which highlighted the need for PID surveillance.

Agent-based modeling provides one further level of disaggregation by modeling all individual objects that comprise stocks in a DEB model as agents with their own characteristics and actions (Rahmandad and Sterman 2008). Agents may interact with each other through a network structure from which system level feedback behavior emerges. Agent-based methods represent the most flexible methods among those in Table 1 in that they can build in variability at any desired level of detail while still fully accounting for dynamic complexity. However, this comes at a significant computational cost, especially for systems involving large numbers of agents. Furthermore, because the dynamic complexity remains embedded in the rules that govern the behavior of individual agents, the system perspective remains implicit, which complicates identification of dominant feedbacks or other important dynamic complexity. Like all stochastic methods, the results will differ for each run of the model. With the large number of stochastic processes typically involved in agent-based models, applying the models may take many iterations to determine with statistical confidence whether any specific observation represents a statistical fluke or a true effect. For example, it may take thousands of model runs to determine whether a small change in a policy leads to a significant benefit. Due to their complexity, agent-based models require abundant high-quality data to support their many assumptions, but these often do not exist, particularly in the context of health interventions for developing countries. This means that agent-based models often need to rely on assumptions not based on direct data, but unfortunately systemically testing the impact of this uncertainty remains challenging due to the computational complexity of the models and their stochastic nature. We used agent-based models of poliovirus transmission to explore how the choice of network structure affects the behavior (Rahmandad et al. 2011), which highlighted the challenges with choosing an appropriate structure in the absence of data to support such a choice. Nevertheless, in the context of modeling the spatial spread of a potential wild poliovirus introduction into the under-vaccinated North American Amish population, we invested in learning as much as possible about the activity and connection structure among these communities to support an agent-based approach (Kisjes et al. 2014). This work suggested that the occurrence of large outbreaks coincided with the occurrence of relatively rare events that bring together distant Amish communities (e.g., weddings) and provided some bounds on the expected extent of any outbreaks to support contingency planning.

Decision analysis provides formal concepts and methodologies to support making choices under uncertainty (Raiffa 1997). The methods include graphical tools (e.g., decision trees, influence diagrams) to structure problems involving probabilities and choices and numerical tools to work through the probabilities and options. These tools prove particularly useful when dealing with conditional probabilities and sequential and/or conditional choices (e.g., what is the best option given that event A happened after we made choice B?). The related field of decision theory provides a theoretical foundation about what constitute rational decisions under uncertainty, including the notion that a rational decision maker choses the option with the highest expected subjective utility (Savage 1954). Value-of-information analysis builds on this theory to provide a helpful decision analytical tool to determine how the costs of acquiring more information trade off against the ability to make decisions with better expected outcomes using the added information (Yokota and Thompson 2004). Decision analytical tools traditionally view systems and choices through a purely probabilistic lens and as such do not account for dynamic complexity when used by themselves. We used decision trees to structure the numerous inter-related pre- and post-eradication policy choices from a national and global perspective (Sangrujee et al. 2003; Thompson and Duintjer Tebbens 2012; Thompson et al. 2013a), which provided necessary clarity about the options and also helped us to communicate some of the variability among key stakeholders (i.e., the decision trees faced by some countries differed from those of other countries, which helped us explain why global policies needed to consider different conditions, values, and preferences held by different decision makers). Similarly, we developed a value-of-information framework to help quantify the information provided by investments in global polio surveillance (de Gourville et al. 2006).

Economic modeling in a broad sense includes many integrated approaches to characterize economic systems, although in Table 1 we interpret this as a catch-all category for methods that support the evaluation of trade-offs in the context of limited resources, including the evaluation of how economic incentives impact the behaviors and choices of individual actors (e.g., game theory) and optimization of resources. Specifically, health economic modeling characterizes the costs of different health interventions and compares these to their expected health benefits with the aim of supporting the allocation of scarce resources to the different interventions. Much of the health economic modeling methodology focuses on appropriately measuring the costs and benefits (or effectiveness) of interventions in a way that allows comparison across different opportunities for investment. Cost-effectiveness analyses provide one of the most popular health economic modeling tools to compare interventions by looking at the incremental costs of an intervention divided by the health gain provided by the intervention (i.e., the incremental cost-effectiveness ratio) (Gold et al. 1996). Benefit-cost analyses support metrics that facilitate comparison of cost and benefits, including returns on investment and incremental net benefits, and also represent popular public policy economic modeling tools (Asian Development Bank 2013). Performing health economic analyses requires capturing all relevant costs from a consistent perspective (e.g. payer vs. societal), expressing health gains on a comparable scale (e.g., quality-adjusted life years), appropriately discounting future outcomes, and to some extent performing uncertainty and sensitivity analyses. However, traditional methods typically view cost-effectiveness by computing effectiveness or benefits without consideration of feedbacks or other dynamics (i.e., looking at streams of costs over time assuming the intervention changes the state but not the dynamics of the system). Specifically, cost-effectiveness analyses often compare the effects of a treatment on a cohort of patients based on how individuals in the cohort who receive the intervention respond to the treatment, without considering potential externalities or systemic changes resulting from applying an intervention. We conducted some health economics studies to better inform the costs of polio policies (de Gourville et al. 2006; Duintjer Tebbens et al. 2006b; Thompson and Duintjer Tebbens 2014b), although we used only integrated models to look at cost-effectiveness and to characterize net benefits of interventions. We used game theory to make the case for cooperation to establish a global OPV stockpile and to demonstrate that global coordination represents the only acceptable option for OPV cessation based on explicit consideration of OPV cessation or continuation incentives (Thompson and Duintjer Tebbens 2008a). We also used linear programming and iterative searching to optimize vaccine stockpile sizes under certain conditions and objectives (Duintjer Tebbens et al. 2010; Duintjer Tebbens and Thompson 2017d).

The field of probabilistic risk analysis includes various tools to identify, characterize, and combine risks within a system (Bedford and Cooke 2001) and supports the use of expert judgment to characterize uncertainties and develop inputs for risk analysis models (Cooke 1991). Grounded in probability theory, the strengths of these tools include their ability to rigorously account for the impact of rare events, distributions with long tails, and the dependence between random variables or processes. Methods such as fault trees and event trees can help identify failure modes within complex systems involving many components. However, traditionally, probabilistic risk analysis methods do not explicitly account for dynamic complexity. Expert judgment tools can help to quantify uncertainty in the absence of good data. These methods range from informal Delphi-type methods focused on consensus building to structured and mathematically rigorous methods to elicit and combine subjective probability distributions (Cooke 1991). While even highly trained experts remain notoriously bad at providing probabilistic assessments due to cognitive biases (Kahneman et al. 1982), structured expert judgment methods rely on calibration techniques to minimize these biases and objectively weigh experts based on their performance. Less formal methods may help collectively identify knowledge gaps to motivate further research by the experts and can help modelers better understand the evidence and system complexity. In addition, expert assessments may factor in knowledge derived from unpublished studies that remain inaccessible to the modelers. Conducting expert elicitations adds significant effort to a modeling project and remains inherently limited by the knowledge of the experts, which ultimately depends on empirical observations and the state of the subject research field. We used semi-structured methods to collectively review the evidence base related to poliovirus transmission, evolution, and immunity (Duintjer Tebbens et al. 2013a; Duintjer Tebbens et al. 2013d) and to elicit numerical assessments about related model inputs (Duintjer Tebbens et al. 2013b). These processes substantially improved our understanding of poliovirus behavior, improved the rigor of our model inputs, provided bounds for model calibration and for uncertainty and sensitivity analysis, summarized the literature and state of knowledge for the broader scientific community, and helped motivate studies to address uncertainty about waning of poliovirus immunity and mixed use of IPV and OPV.

All quantitative methods rely on assumptions and model inputs, which always involve some degree of uncertainty. Non-probabilistic sensitivity analysis methods aim to identify the most influential model inputs by varying model inputs individually (univariate methods) or simultaneously (multivariate methods) over their uncertainty ranges and recording which changes most affect the output (Duintjer Tebbens et al. 2008b). Common limitations of simple univariate methods that only evaluate the model at both ends of the uncertainty range of a model input include that they do not account for curvature (i.e., the effect of a model input on the model output per unit of change in the model input varies across the uncertainty range of the model input due to non-linearities in the model) and interactions (i.e., the effect of a model input depends on the values of other model inputs). Design-of-experiments methods can address these limitations in a non-probabilistic way by running the model at discrete points of the multi-dimensional uncertainty space and making inferences about the effect of individual inputs or combinations of inputs. Despite existing approaches to limit the number of points needed to evaluate model input sensitivity, design-of-experiment methods require many model runs for a large number of uncertain model inputs. Probabilistic sensitivity analysis methods use random sampling to appropriately cover the uncertainty space and specify statistical measures that quantify the importance of uncertain inputs. The measures can account for both curvature and interactions in the model and methods exist to also account for any dependencies between model inputs, although this remains mathematically the most challenging. One advantage of using probabilistic sensitivity analysis is that the random sample allows a construction of a full uncertainty distribution of the model output, which may facilitate communication of the uncertainty in the model. Understanding the uncertainty in the model is important to interpret the results and grapple with trade-offs between benefits and risks. Understanding the relative importance of model inputs can help prioritize research to fill knowledge gaps and motivate value-of-information analyses. Performing uncertainty and sensitivity analyses requires extra human and computational effort and thus the appropriate choice of methods depends on whether the added effort results in sufficient policy-relevant information. In addition to uncertainty about model input values, uncertainty can also arise from structural model assumptions. Methods to address this type of uncertainty in a probabilistic way would require assigning probabilities to different structural assumptions. We used various uncertainty and sensitivity analysis methods for our polio modeling, with the most extensive efforts documented in separate manuscripts in the context of integrated health economic models that directly informed policy decisions (see next section on integrated models) (Duintjer Tebbens et al. 2008a; Duintjer Tebbens and Thompson 2016b).

All quantitative methods above require some statistical and data analytical methods and use available data. In the context of abundant high-quality data of dynamically stable or static systems, statistical methods can result in good predictions and/or automated discovery of patterns in the data and ever increasing computational power supports numerous applications of big data and machine learning (Murphy 2012). The ability to automate these data-based methods makes them particularly suitable in the context of a continuous stream of new data to inform predictions. Statistical methods can also help to quantify the uncertainty in model inputs to inform uncertainty and sensitivity analysis. However, data-based methods depend on sufficient high quality data, which often represents a challenge, particularly in global health. Furthermore, such methods cannot account for unobservable processes that may affect behaviors (e.g., asymptomatic virus transmission, which does not result in clinical cases). Most importantly, they do not account for dynamic complexity, making them poorly suited for predictions in the context of systems whose behavior changes non-linearly due to feedback structures. In addition, they require data to support inferences, such that the analyses inherently reflect retrospective events (observations) and/or designed tests of interventions (e.g., clinical or field trials).

Integrated system dynamic models to support polio eradication

Table 2 provides an overview of integrated models we developed in the context of our collaboration with the GPEI in response to questions that we felt required an integrated approach. The last column shows the software platforms we used to implement the models. Our polio modeling efforts began in 2001 with a retrospective health and economic analysis of the benefits of polio vaccination in the United States (Thompson and Duintjer Tebbens 2006). Methodological questions about how cost-effectiveness ratios and net benefits of investments change over time and how the choice of disease modeling approach affects the results provided the initial motivation for this work. This work also filled a gap in the literature about the cumulative historic and future benefits of US investments in polio vaccination and by extension the benefits of polio vaccination in developed countries and the economic benefits of vaccines in general. Although cost-effectiveness methodology at the time framed analyses from a static perspective (Gold et al. 1996), the field of dynamic transmission modeling compellingly demonstrated the positive externalities associated with vaccination by not only protecting vaccine recipients but also unvaccinated individuals who benefit from improved population immunity (Anderson and May 1991; Fine 1993). Some of these studies also integrated economic aspects within their models to analyze disease control efforts (Rowley and Anderson 1994; Williams et al. 1996a; Geoffard and Philipson 1997; Paltiel et al. 2005), and some studies used dynamic models in their cost-effectiveness analyses (Guyatt et al. 1993; Williams et al. 1996b; Brisson and Edmunds 2002). However, the prevailing health economic guidance did not recognize the importance of dynamically modeling infectious disease transmission (Gold et al. 1996). Motivated by methodological questions, we built on the dynamic transmission modeling literature and a conceptual integrated dynamic cost-effectiveness analysis of a hypothetical vaccine (Edmunds et al. 1999) to develop our first integrated model for polio (Thompson and Duintjer Tebbens 2006). This model combined our deterministic DEB poliovirus transmission model (Duintjer Tebbens et al. 2005) with cost data and health economic methods to demonstrate how cost-effectiveness ratios may change over time and depend on model choice (Thompson and Duintjer Tebbens 2006). Specifically, we found that a hypothetical decision maker in 1955 weighing the use of polio vaccines for the next 50 years using a static model would underestimate the benefits of vaccination by 30% compared to the same evaluation based on the observed polio incidence or the expected incidence using the dynamic transmission model. This work provided the first study to directly and retrospectively compare the difference between a static and a dynamic cost-effectiveness analysis for an actual vaccine (Thompson and Duintjer Tebbens 2006). A decade later, most current health economic analyses for infectious diseases incorporate dynamic transmission models, and various international guidelines for the economic evaluation of infectious diseases now recommend the use of dynamic models (World Health Organization 2008; Pitman et al. 2012). Integrating dynamic transmission modeling into the economic analysis further allowed us to quantify the benefits of polio vaccination from a population perspective rather than a cohort perspective while still adhering to accepted standards for the economic evaluation of health interventions (Gold et al. 1996). The resulting estimate of over $180 billion (year 2002 dollars) of retrospective and expected future net benefits of the polio vaccination program in the United States highlighted the importance of valuing the prevention of the unobserved undesirable outcomes (i.e., characterizing the counterfactual) when evaluating policy choices.

Table 2:

Integrated models related to polio eradication.

Integrated model description	Motivating questions	Analytical methods integrated	Publications that use or describe the integrated model	Software platform(s) used
Health economic model of US polio vaccination	* What are the historic and future health benefits of polio vaccination in the US? * How did cost-effectiveness ratios change over the course of the efforts? * How much does the choice of linear vs. dynamic model to estimate disease cases affect the results?	* Deterministic DEB modeling * Health economic modeling	(Thompson and Duintjer Tebbens 2006)	Mathematica
Health economic model of global post-eradication policies	* What is the best combination of policies after certification of global wild poliovirus eradication? * What are the expected benefits of polio eradication vs. control? * What are the historic and future health benefits of global polio eradication efforts? * What uncertainties most affect our ability to make decisions?	* Systems thinking * Deterministic DEB modeling * Decision analysis * Health economic modeling * Probabilistic and statistical risk analysis * Probabilistic uncertainty and sensitivity analysis	(Thompson and Duintjer Tebbens 2007; Duintjer Tebbens et al. 2008a; Thompson and Duintjer Tebbens 2008b; Thompson et al. 2008; Duintjer Tebbens et al. 2011; Thompson et al. 2015a)	Mathematica (model), Vensim (diagrams and interactive model application)
Stockpile optimization framework	* What are the different ways to frame an emergency outbreak response vaccine stockpile optimization problem (after cessation of regular use of the vaccine)? * What is the optimal stockpile composition over time given a known demand for outbreak response vaccine?	* Systems thinking * Deterministic DEB modeling * Linear programming	(Duintjer Tebbens et al. 2010)	Mathematica (model), Vensim (diagrams)
Global model for long-term poliovirus risk management	* What is the best global polio immunization policy for 2013–2052? * What are the costs and benefits of different risk management policies (e.g., use of antiviral drugs, outbreak response strategies, synchronization of OPV cessation, intensification of OPV use prior to cessation, development of new poliovirus vaccines)? * What are the vaccine needs for different endgame strategies? * What is the optimal stockpile composition over time given an uncertain demand for outbreak response vaccine? * What are the most important sources of risk? * What are key outstanding uncertainties?	* Systems thinking * Deterministic DEB modeling (informed by semi-structured expert judgment and systematic review) * Decision analysis * Health economic modeling * Discrete-event simulation * Probabilistic risk analysis * Probabilistic uncertainty and sensitivity analysis * Optimization (iterative)	(Duintjer Tebbens et al. 2015a; Duintjer Tebbens and Thompson 2015a; Thompson and Duintjer Tebbens 2015b; Duintjer Tebbens et al. 2016b; Duintjer Tebbens et al. 2016d; Duintjer Tebbens and Thompson 2016a; Duintjer Tebbens and Thompson 2016b; Duintjer Tebbens and Thompson 2017a; Duintjer Tebbens and Thompson 2017d; Thompson and Duintjer Tebbens 2017a)	Java (model), Amazon Web Services (execution of Java model)
Health economic analysis of travel vaccination requirements	* What are the costs and benefits of imposing temporary recommendations for vaccination on countries with wild poliovirus transmission?	* Systems thinking * Health economic modeling * Discrete-event simulation * Probabilistic uncertainty and sensitivity analysis	(Duintjer Tebbens and Thompson 2017c)	Java

As we reached out to GPEI experts at the US Centers for Disease Control and Prevention in 2001 to develop the tools to address transmissions dynamics (i.e., the deterministic DEB model) within a health economic framework, questions naturally emerged about using the tools prospectively to inform global polio eradication decisions. The initial remit of the ensuing collaboration involved the health economic evaluation of 5 possible future vaccine strategies using IPV and OPV that global policy makers considered relevant at that time for the future post-eradication era. However, initial exploration of this relatively narrow policy question led to the realization that the policy space involved much more complexity and that we needed to modify and expand the tools we developed for the US retrospective study to tackle the global, prospective questions. Discussions with our collaborators made clear that post-eradication policy involved not only decisions about vaccine choice but also about coordination of these choices, vaccine delivery, surveillance, vaccine stockpiling and outbreak response strategies, containment of polioviruses in laboratories, and management of iVDPV risks. Moreover, these decisions depended on each other and carried different implications for different countries, which compromised attempts to develop consensus about a single policy and helped to facilitate discussions about appropriate policies for different broad categories of stakeholders. Facing limitations in the extent with which we could convey this complexity in the existing dynamic transmission and health economic framework, we developed decision trees to structure the complexity of the post-eradication choices and highlight the differences between countries (Sangrujee et al. 2003). In addition to bringing structure to the enormous complexity involved in post-eradication policies, the decision trees also helped us simplify the analysis by eliminating dominated or unlikely combinations of decisions.

As we reviewed the literature on OPV-related risks (Duintjer Tebbens et al. 2006a), we recognized that the outcomes of different post-eradication policies depend heavily on the occurrence of rare events with potentially devastating consequences. In particular, policies involving OPV cessation would dramatically alter global population immunity in the long term, resulting in the potential for explosive outbreaks if any poliovirus reintroductions would occur long after OPV cessation. Given that deterministic DEB models do not generate rare, random events, we recognized that our model needed to exogenously introduce rare, stochastic poliovirus introductions in the deterministic DEB model. The deterministic DEB transmission model accounted for the dynamic changes of population immunity to poliovirus transmission as a function of vaccination choices and allowed us to estimate the consequences of any poliovirus reintroductions after eradication, while the probabilistic model generated random poliovirus introductions based on statistical analysis of the data, extrapolation into the future, and extensive discussions with subject matter experts (Duintjer Tebbens et al. 2006a). The resulting ability to visually communicate the results for different “possible futures” (i.e., realizations of post-eradication poliovirus reintroductions) (Thompson et al. 2015a) proved particularly helpful for policy makers to grapple with trade-offs between costs and cases and between a low risk of a very bad outcome and a high risk of a less bad outcome. Specifically, our model suggested that in most stochastic iterations stopping OPV use globally resulted in very low numbers of polio cases in the post-eradication era, but with low probability (rare iterations) it resulted in very large outbreaks, while continued OPV use would almost certainly lead to continued frequent but smaller cVDPV outbreaks (Thompson et al. 2008). The prospect of a world in which a vaccine continued to cause outbreaks in the absence of the naturally occurring virus provided a strong motivation to stop OPV use. Furthermore, in expectation, continued OPV use would result in higher numbers of cases in addition to continued significant costs, which helped support the global consensus that OPV use should stop after wild poliovirus eradication (World Health Organization 2005a; World Health Assembly 2008).

Integrating the stochastic risks highlighted the impact of different stochastic realizations of stochastic events for post-eradication decisions, even if the rates of these events were known with full certainty (i.e., stochastic variability). In reality, uncertainty exists about the rates themselves as well, particularly in light of the inherent problems of extrapolating pre-eradication event rates to an unprecedented post-eradication world with a dramatically different population immunity profile. While we attempted to account for this change to the best of our ability, uncertainty about the rates remains, along with uncertainty about the true costs and the behavior of polioviruses and immunity. Building on our review of methods for uncertainty and sensitivity analyses specifically applied to integrated health economic analyses (Duintjer Tebbens et al. 2008b), we expended significant efforts to comprehensively and probabilistically analyze the sensitivity of the model results to its uncertain inputs and to report the overall uncertainty in its main outcomes. This resulted in a separate manuscript (with a lengthy technical appendix) just about the uncertainty and sensitivity analyses (Duintjer Tebbens et al. 2008a). This exercise helped interested policy makers understand the impact of assumptions and the extent of uncertainty in the model. Perhaps more importantly, it helped identify key knowledge gaps for which additional research could reduce critical uncertainty and improve outcomes. Specifically, showing the impact of the uncertainty about the future costs and effectiveness of IPV use in developing countries (Thompson et al. 2008) helped motivate significant investments by some of the GPEI partners into research and development of more affordable IPV vaccines and administration technologies, and clinical trials about the impact of IPV on transmission.

We recognized many themes from systems thinking in our work and benefitted enormously from the ability to structure our polio eradication models within the systems thinking framework. One of the most impactful benefits of systems thinking came from an ability to pinpoint an inherent challenge with disease eradication: as the number of cases dwindles, it becomes more difficult to motivate financial support to finish the job. This challenge became apparent as delays in eradication and high costs led prominent voices to suggest the world should give up on polio eradication and switch to a goal of merely controlling the disease (Arita et al. 2006). In response, we demonstrated that a myopic focus on the perceived costs per remaining case, which increases with approaching eradication, would lead to a wavering commitment to finish eradication. This myopic view would result in a resurgence in cases and economically suboptimal oscillations typical for a balancing feedback loop with a delay. As detailed elsewhere (Thompson and Duintjer Tebbens 2008b), presenting this fundamental behavior strengthened the intuitive case to avoid a wavering commitment and instead remain committed to eradication. Complemented with a rigorous economic analysis of control vs. eradication in low-income countries using our integrated models (Thompson and Duintjer Tebbens 2007), we helped turn the threat of a wavering commitment into a re-affirmed global commitment to global polio eradication, with strong declarations by the World Health Organization and a substantial expansion of the GPEI partnership (Thompson et al. 2015a). Another integrated health economic model allowed us to adequately capture positive externalities such as the administration of Vitamin A supplements during polio immunization activities and the broader impact of disease prevention on productivity and well-being (Duintjer Tebbens et al. 2011), which supported GPEI efforts to raise significant financial resources.

The probability and consequences of poliovirus introductions after eradication and OPV cessation motivated the establishment of an OPV stockpile to rapidly respond to post-eradication outbreaks (Fine et al. 2001; Thompson and Duintjer Tebbens 2008a). This led to questions about the optimal stockpile size, which in turn led to questions about the appropriate objective function. To aid vaccine stockpile planning after OPV cessation, we used systems thinking to provide a stock-and-flow structure of the vaccine supply chain and we integrated this with a high-level dynamic model of global outbreak propagation (Duintjer Tebbens et al. 2010). Combination of the vaccine supply chain model with the transmission model exposed a critical reinforcing feedback loop in stockpile management: a failure to meet the demand for vaccine to respond to an outbreak in a timely fashion will create more demand for vaccine as the outbreak expands geographically, which in turn makes it more difficult to meet the increased vaccine demand in a timely fashion. The strength of this feedback loop increases with time after cessation of vaccination because outbreaks grow more rapidly with lower population immunity to transmission. Perhaps even more troubling, the mere threat of a stock-out could hold back efforts to respond with sufficient vaccine, which creates a risk of needing much more vaccine later. We formulated possible framings of stockpile optimization problems and demonstrated a linear programming approach to solve for the optimal bulk and finished vaccine stocks over time (Duintjer Tebbens et al. 2010). Subsequent work highlighted the fundamental difference in stockpile management for vaccines that remain in production due to the ability to use vaccine before it expires (i.e., rotating stockpile) (Thompson and Duintjer Tebbens 2016). This work fits within a growing field that integrates epidemiological modeling with logistics (Gani et al. 2005; Lee et al. 2006; Arinaminpathy and McLean 2008; Siddiqui and Edmunds 2008; Institure of Medicine 2012; Spiliotopoulou et al. 2013; Auping et al. 2016).

As the knowledge about the virus and the available tools and strategies evolved and gained complexity, the policy questions also increased in complexity. For example, the introduction of serotype-specific OPV created new policy options to sequentially stop different OPV serotypes after global eradication of the corresponding wild poliovirus serotypes. Similarly, efforts to make IPV available to all countries created innovative strategies involving OPV-IPV co-administration and development of antiviral drugs to treat iVDPV excretors created a new risk management option that did not exist when our collaboration started. Reliance on serotype-specific OPV also significantly increased the ability of populations to sustain poliovirus transmission of the omitted serotype(s), which increased cVDPV risks. While our original post-eradication model assumed a “run-up” of sustained OPV-only use of all three types in all low- and middle-income countries followed by coordinated cessation of all OPV, the “run-up” had become much more complicated and the new GPEI strategy dictated cessation of serotype 2 OPV in 2016 (regardless of wild poliovirus eradication of the other two serotypes) with a prerequisite of at least one IPV dose in all countries (World Health Organization 2013). The emerging questions motivated us to substantially revise our deterministic DEB transmission model and make it the basis for an updated integrated global model for long-term poliovirus risk management. We expanded the deterministic DEB transmission model to include serotype-dependence, additional immunity states (e.g., for mixed OPV-IPV immunity), explicit differentiation between fecal-oral and oropharyngeal transmission, and the evolution process from OPV to VDPV (Duintjer Tebbens et al. 2013c). This revised deterministic DEB model reflected an extensive effort to collaboratively synthesize the available evidence with subject matter experts (Duintjer Tebbens et al. 2013a; Duintjer Tebbens et al. 2013d), complement the data using semi-structured expert judgment (Duintjer Tebbens et al. 2013b), and calibrate the model to ensure consistent behavior with observations across a diverse set of epidemiological situations while remaining internally consistent (Duintjer Tebbens et al. 2013c). Methodologically, we succeeded in circumventing the limitations of deterministic DEB models related to unrealistic distributions and fractional stocks through the use of a multi-stage processes combined with thresholds to approximate the OPV evolution process. This allowed the model to generate cVDPV outbreaks endogenously instead of introducing them exogenously based on imperfect extrapolations from limited data. Specifically, we modeled OPV evolution over a larger number of reversion stages (stocks) and introduced a die-out threshold to set the force of infection coming from any reversion stage to zero when the prevalence becomes very small. The approach worked to both model cVDPV outbreaks in places that experienced them in the past and to ensure the absence of cVDPV outbreaks in places where none emerged (Duintjer Tebbens et al. 2013c).

Although the revised deterministic DEB model endogenously accounted for cVDPV risks, we still needed to develop and integrate our DES model of iVDPV prevalence (Duintjer Tebbens et al. 2015b) within the updated global model for long-term risk management to track iVDPV risks in detail. The updated global model thus included the deterministic DEB model, the DES model, and other components (Duintjer Tebbens et al. 2015a). Figure 1 provides an overview of the major components of the global model. The global model divides the world into 710 spatially homogenous subpopulations of approximately 10 million people to characterize the global variability in conditions and enable a simplified characterization of mixing between subpopulations (grouped into epidemiological blocks of 10 and larger geographical regions of variable size). The global model runs the deterministic DEB model for poliovirus transmission and OPV evolution for all of the 710 subpopulations and for each serotype to track serotype-specific population immunity to transmission over time and as a function of policy choices about OPV cessation and IPV use. Inside the deterministic DEB model, we further play out any outbreaks triggered by any random poliovirus reintroductions, including their detection through surveillance and the outbreak response, which remains limited by the amount of OPV available from a stockpile (Duintjer Tebbens et al. 2016d; Duintjer Tebbens and Thompson 2017d). Thus, the random poliovirus risks and the DEB model realizations for all policy choices ultimately lead to costs and cases, which we convert to economic outcomes (e.g., incremental cost-effectiveness ratios and incremental net benefits) using health economic modeling.

Figure 1:

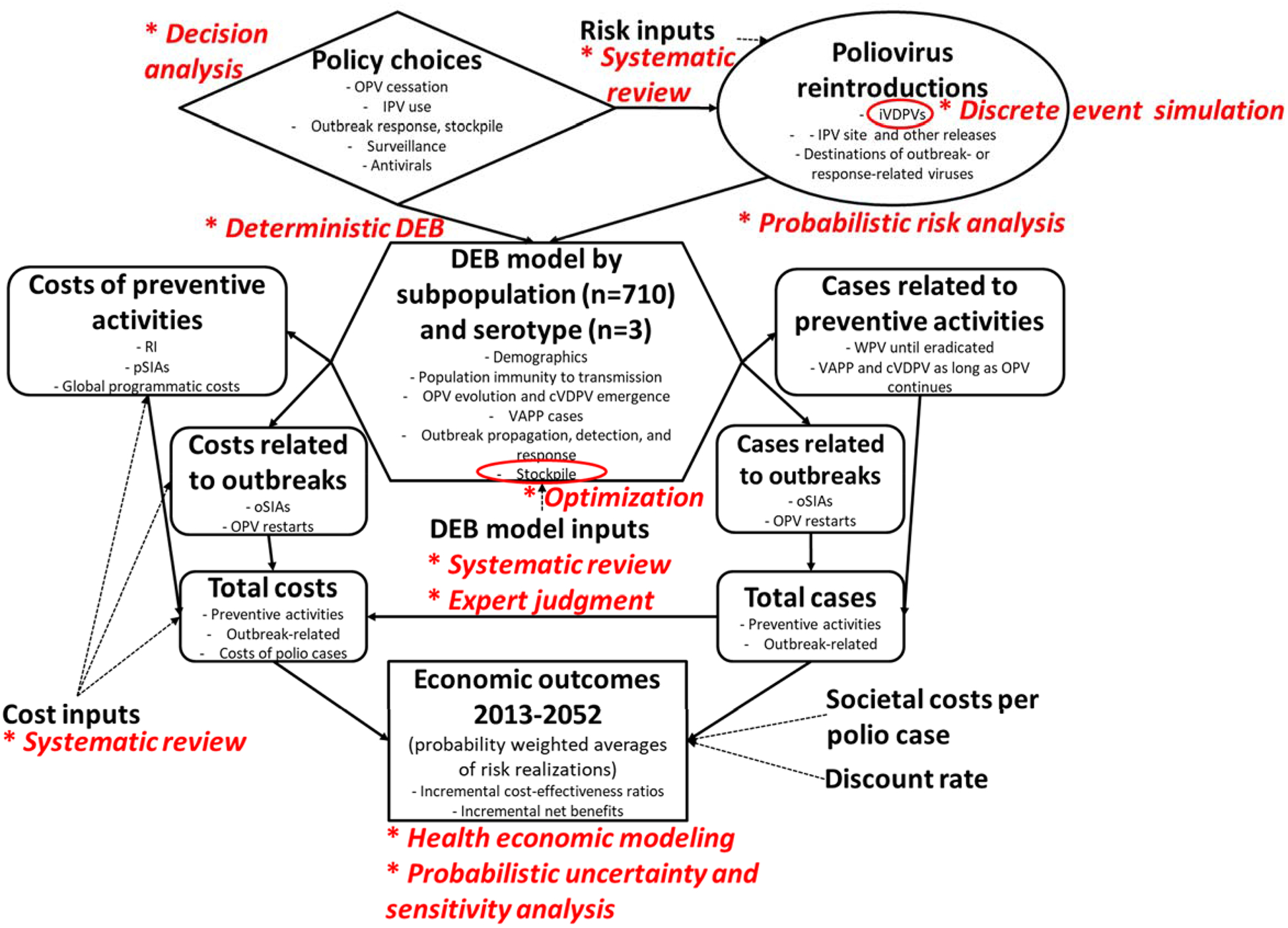
Diagram of main global model structure with analytical tools for each component indicated in red italics and following an asterisk.

Abbreviations: cVDPV, circulating vaccine-derived poliovirus; DEB, differential equation-based; IPV, inactivated poliovirus vaccine; iVDPV, immunodeficiency-associated vaccine-derived poliovirus; OPV, oral poliovirus vaccine; oSIA, outbreak response supplemental immunization activity; pSIA, preventive supplemental immunization activity; RI, routine immunization; VAPP, vaccine-associated paralytic poliomyelitis; WPV, wild poliovirus

The updated global model identified OPV cessation with a limited time of IPV use in all countries as the best post-eradication vaccination strategy that promises billions of dollars in incremental net benefits going forward, but also emphasized the critical importance of managing the risks (Duintjer Tebbens et al. 2015a). Using the global model, we performed a number of analyses related to specific risk management strategies to estimate their value and explore uncertainties. For example, we highlighted the important role that IPV costs continue play with respect to the overall economic benefits of the polio endgame (Duintjer Tebbens and Thompson 2016b), explored outbreak response strategies (Duintjer Tebbens et al. 2016d), estimated significant potential economic benefits associated with the development of a new poliovirus vaccine with the benefits but without the risks of OPV (Duintjer Tebbens and Thompson 2016a), demonstrated the importance of screening for non-paralytic iVDPV excretors to achieve the benefits of antiviral drugs that may stop iVDPV infections in PID patients (Duintjer Tebbens et al. 2016c), and highlighted the impact of specific time delays in the vaccine supply chain on the optimal stockpile size, which turned out greater than planned (Duintjer Tebbens and Thompson 2017d).

Finally, Table 1 shows an example of a small yet integrated model we developed to assess the costs and benefits of traveler vaccination aimed at reducing the risk of wild poliovirus importation outbreaks in previously polio-free countries (Duintjer Tebbens and Thompson 2017c). We developed a simple DES model to randomly generate outbreaks from historic outbreak and incidence data. The model accounted for the possibility of outbreak propagation into multiple countries and we used a causal loop diagram to highlight this critical diffusion feedback. We built on our earlier work to integrate the DES model into a health economic modeling framework, quantify the uncertainty, and identify key uncertain inputs. Thus, within a short period of time, we developed, executed and analyzed this simple integrated model, strengthened the economic case for the recommended travel vaccinations, and influenced the criteria for imposing them.

Example: Integrating discrete-event simulation within the global model

To illustrate how and why we integrated multiple analytical tools, we provide a specific example based on our characterization of iVDPV risks in the global model. Figure 2 gives a high-level causal loop diagram of the main factors affecting iVDPV risks. The link to the variable Global OPV use policies indicates an interaction of the iVDPV behavior with the rest of the global model. Given that poliovirus transmissibility correlates with risk factors for PID survival, we tied PID survival in a population to the transmissibility of polioviruses in that population, which dynamic infection transmission models typically characterize as the basic reproduction number (R0, defined as the average number of secondary infections generated by a single infection in an otherwise entirely susceptible population) (Diekmann et al. 1990; Anderson and May 1991). A small fraction of PID patients experience iVDPV infections (e.g., following receipt of OPV), which makes OPV use an important risk factor for iVDPVs and leads to the reinforcing feedback loop in Figure 1. However, OPV use also maintains high population immunity to poliovirus transmission, which as long as it continues will prevent iVDPV excretors from triggering outbreaks, as shown by the balancing feedback loop. After regular OPV use stops, the dynamics dramatically change and the ultimate control of outbreaks caused by iVDPVs depends on the strength of the reinforcing and balancing feedback loops. Until the global cessation of serotype 2 OPV in 2016, only countries that can sustain high enough population immunity with IPV alone stopped OPV use. Consequently, no iVDPV outbreaks occurred to date, with confirmation and availability biases potentially leading to underestimation of the risk (i.e., concluding that the chances that iVDPVs lead to outbreaks must be low because we have observed iVDPV excretors but no iVDPV outbreaks). The survival of PIDs in high-R0 settings, the rate of spontaneous recovery from iVDPV infections, and the potential ability of polio antiviral drugs to clear iVDPV infections all remain uncertain, and consequently so do the risks from iVDPVs.

Figure 2:

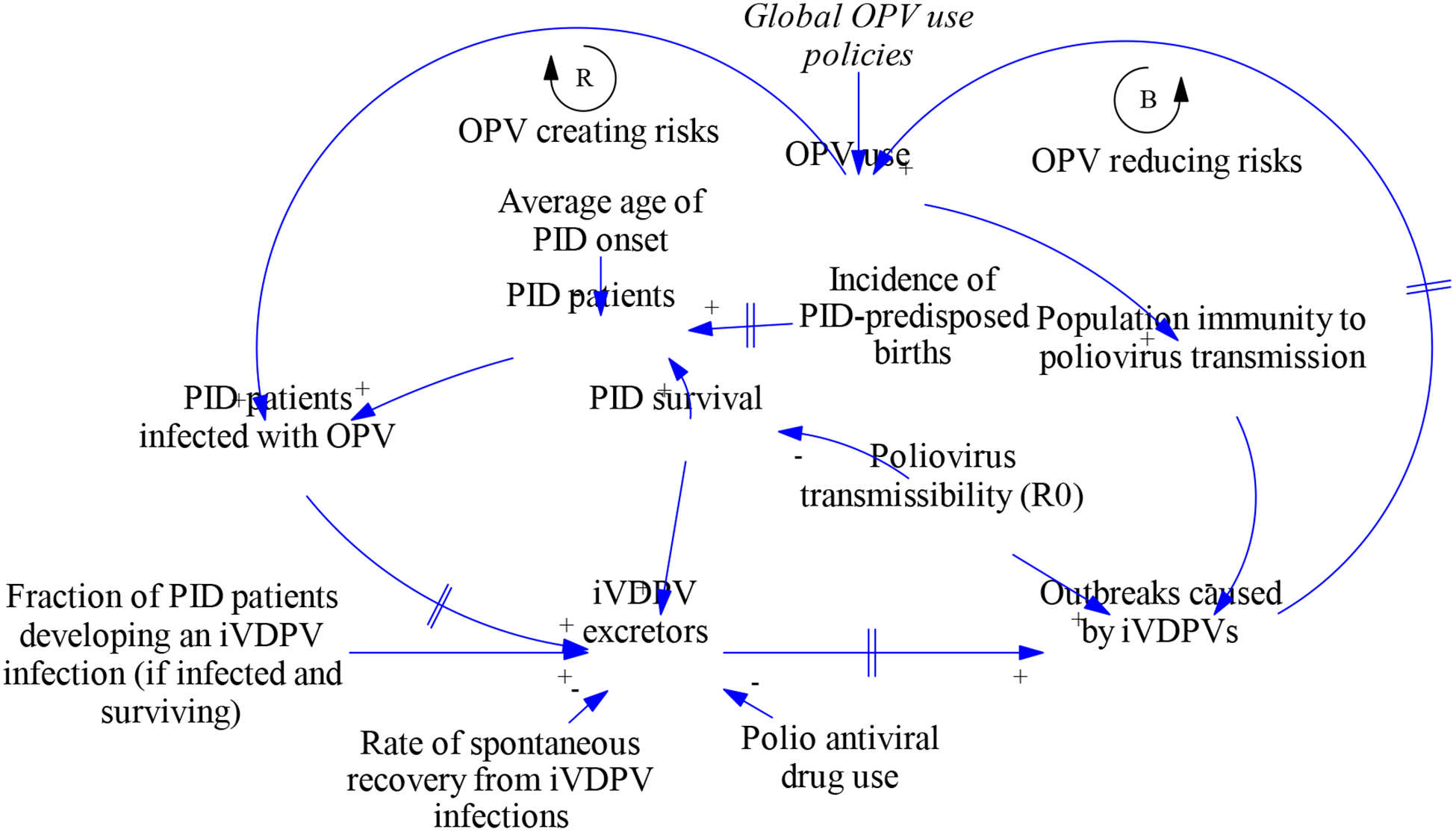
Causal loop diagram related to iVDPV behavior

Abbreviations: iVDPV, immunodeficiency-associated vaccine-derived poliovirus; OPV, oral poliovirus vaccine; PID, primary immunodeficiency

The DES model tracks all events relevant to polio risks during the lifetime of all global PID patients, including PID onset, receipt of intravenous immunoglobulin (which increases survival but does not prevent poliovirus infection), OPV infections, paralysis (if any, since most patients remain non-paralytic), recovery from OPV infections, and death. To adequately represent the available survival data for PID patients in the DES model, we used a continuous cohorting approach (Eberlein et al. 2012; Duintjer Tebbens and Thompson 2015b). The DES model produces stochastic realizations of the number of active iVDPV excretors as a function of time. Figure 3 shows 4 realizations of the DES model, with the results shown by World Bank income level and in total. The model assumed global cessation of serotype 2 OPV in 2016 and cessation of the remaining OPV serotypes in 2019, with most high-income countries already stopping OPV use of all serotypes around the year 2000. The realizations show substantial stochastic variability in the tail of excretion after OPV cessation in each income level. Including uncertainty in the model inputs results in even more stochastic variability, with similar mean times until the last excretor stops but a greater chance of very long excretion by at least one individual (i.e., a more skewed distribution) (Duintjer Tebbens and Thompson 2017a).

Figure 3:

Four realizations of the discrete-event simulation model, showing the monthly number of active long-term iVDPV excretors

Figure 4:

Integration of DES model within the global model

Abbreviations and notation: DES, discrete event simulation; IPV, inactivated poliovirus vaccine; iVDPV, immunodeficiency-associated vaccine-derived poliovirus; OPV, oral poliovirus vaccine; PID, primary immunodeficiency; PITT, population immunity to transmission; R0, basic reproduction number; s, subpopulation; t, time

Figure 4 shows how we integrated the DES model within the global model. The diagram indicates deterministic relationships as functions, f, of the arguments indicated, and random processes as probability functions, p, with key dependencies indicates in the corresponding parentheses. Integration occurs at several levels. First, the global model assumptions about vaccine use, demographics, income levels, and poliovirus R0 values in each subpopulation feed into the DES model. The DES model then generates random realizations of the prevalence of all PID patients over time and the prevalence of iVDPV excretors (as shown in Figure 3). For each active iVDPV excretor, the global model randomly generates contacts with the general population of the subpopulation in which the iVDPV excretor resides. Given that the DEB model requires a minimum die-out threshold of prevalence before population-level virus transmission can begin, we need to determine for each iVDPV excretor contact with the general population whether the contact leads to population-level transmission (i.e., an effective introduction). We determine this randomly using a probability that increases with decreasing population immunity to transmission at the time of the contact. If an effective iVDPV introduction occurs, then this may or may not lead to an outbreak, again depending on population immunity to transmission at the time of the introduction (i.e., an effective iVDPV introduction may only lead to very limited transmission, as probably occurred in Minnesota in 2005 (Alexander et al. 2009)). If an outbreak occurs, then the global model deterministically simulates the resulting spread, detection of the outbreak, and outbreak response. The global model further triggers exportations to other subpopulations deterministically based on the number of accumulated infections and then randomly determines the destination of the virus exportation based on the global mixing structure. If the outbreak response involves OPV, then this may lead to new iVDPV infections (and also exportations of OPV viruses). The global model uses the assumptions about the probability of PID patients acquiring iVDPV infections given OPV use and the random realization of the prevalence of PID patients from the DES model to randomly determine the occurrence of secondary effective introductions due to newly created iVDPV excretors (or outbreak virus or OPV exportations). These may trigger new outbreaks at a later time or in a different subpopulation.

Figure 5 shows an example of iVDPV risk results with 5 realizations of the iVDPV risks for serotype 2, including potential outbreak response with OPV and the creation of new iVDPV excretors. All runs restrict the use of OPV for outbreak response to 5 years after OPV cessation based on the risk and likely reluctance of using OPV longer after cessation. In run 1, an iVDPV excretor continues to excrete for a very long time, but as this occurs in a high-income country it does not lead to any major outbreaks. Run 2 shows that the use of OPV to respond to an earlier iVDPV outbreak creates a new iVDPV excretor, but no new effective iVDPV introductions. Run 3 does not involve any serotype 2 iVDPV outbreaks or new excretors. Runs 2 and 4 both involve some OPV use for outbreak response that creates new iVDPV excretors, with the OPV use for outbreak response in run 4 triggering a new outbreak that ultimately gets controlled. Run 5 shows an unrepresentative and deliberately selected rare realization of the global model in which a new iVDPV excetor causes a new outbreak more than 5 years after OPV cessation, which ultimately leads to a need to globally restart OPV use because IPV-alone cannot control the outbreak. Such OPV restarts (i.e., because of new iVDPV excretors of any serotype) occurred in only 0.7% of 1,000 global model iterations, although this model made some optimistic assumptions about risk management activities that the GPEI did not adopt (Duintjer Tebbens and Thompson 2017a).

Figure 5:

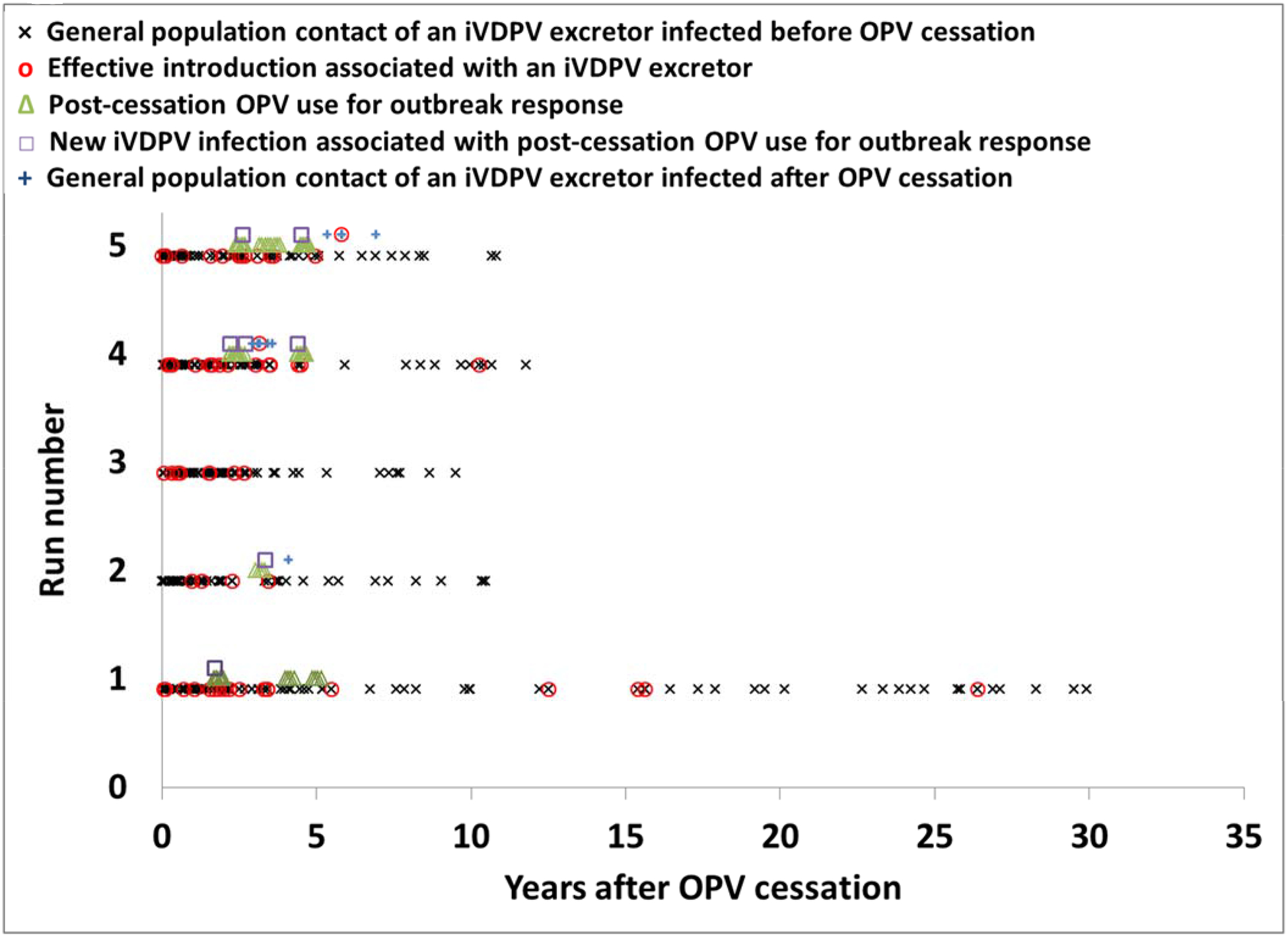
Integrated global model results for 5 realizations for serotype 2 showing contacts of iVDPV excretors with a general population (generated by the DES model), resulting effective infections and potential OPV outbreak response (generated by the global model), and potential new iVDPV infections caused by post-cessation OPV use (generated by the global model using PID patients generated by the DES model). Runs 1–4 represent a quasi-random selection (i.e., the first 4 global model realizations), run 5 represents a selected, non-representative and rare realization in which an outbreak caused by a new iVDPV excretor ultimately triggered an OPV restart.

Abbreviations and notation: DES, discrete event simulation; iVDPV, immunodeficiency-associated vaccine-derived poliovirus; OPV, oral poliovirus vaccine; PID, primary immunodeficiency

Lessons learned

From a practical standpoint, implementing the integration of different analytical tools requires additional efforts to learn the tools and to make them interact appropriately. For example, integrating the DES model with DEB components of the global model required several adjustments. First, we opted for the slowly converging Euler integration method to accommodate the use of non-continuous inputs from outside of the DEB model, including virus introductions and immunization campaigns on specific days. Second, to ensure fair comparison between policy choices, one realization of PID patients must use the same random numbers to generate effective infections for all policy scenarios. Thus, we created files containing sufficient random numbers for each PID patient to simulate an iVDPV infection in the event that, in the integrated global model, the patient would later acquire an infection from post-cessation OPV use. While more cumbersome, the use of files to pass information between components instead of internal data structures facilitates post hoc analysis of results and allows reuse of the same simulations to later perform additional policy analyses while maintaining stochastic comparability to the original analysis. We opted to write our most recent integrated models in a basic programming language (i.e., JAVA) to maintain full control and flexibility of all aspects, although higher level software increasingly facilitates the seamless integration of a wide range of analytical tools. Third, the global model takes significant computer resources, and consequently we use cloud computing to perform large numbers of global model runs. Running a single iteration of the full global model from 2016–2053 required 24–48 hours on a conventional modern processor (e.g., 2.6 Gigahertz Intel Core i7). Using the cloud allowed us to run numerous iterations in parallel to reach 1,000 iterations of the global model for each of several major policy options. The computational cost did not primarily result from the integration of the various components, but from the need to address global policy questions while reasonably characterizing global mixing and global variability using 710 subpopulations. The use of 710 subpopulations and 3 serotypes implies that the global model must run 2130 versions of the DEB model simultaneously, which each include numerous stocks for multiple age groups, immunity states, OPV reversion stages, waning stages, infection stages, and transmission routes (Duintjer Tebbens et al. 2013c). As documented above, not all policy questions involve all of the interrelatedness and complexity from the global model, while other questions required a finer resolution than 10 million people. Thus, we recognize the importance of remaining flexible with respect to the choice of appropriate level of integration and granularity to answer any given policy question. We also developed ways to re-use existing runs for different purposes to extract insights from minimal additional runs. For example, we adapted the 1,000 base case iterations post hoc to address new questions related to vaccine needs (Duintjer Tebbens and Thompson 2015a), synchronization of OPV cessation (Duintjer Tebbens et al. 2016b), and stockpile management (Duintjer Tebbens and Thompson 2017d). Similarly, we noticed that the majority of iterations controlled all outbreaks and gave qualitatively similar results, while only a small subset drove the overall economic results because the uncontrolled outbreaks in those iterations forced a need to restart OPV. Recognizing this dichotomy, for subsequent analyses of alternative risk management policies, we ran only a small subset of the qualitatively similar iterations and all the OPV restart iterations to provide reasonably robust insights at a much lower computational cost (Duintjer Tebbens and Thompson 2016a; Duintjer Tebbens and Thompson 2017a).

Prior publications offer further details about the process of using integrated models to influence decisions (Thompson et al. 2006b; Thompson and Duintjer Tebbens 2008b; Thompson et al. 2015a). We specifically highlight that the communication of results from complex, integrated models remains a challenge that warrants continued attention. Crossing boundaries between disciplines implies more work to effectively communicate with different stakeholders. The limited time available to present model findings at policy fora often implies a need to focus presentations on insights rather than methods, but this can leave methodological questions unanswered. In our experience, successfully influencing decisions includes at least four main ingredients. First, subject matter expertise remains critical to develop empirically grounded methods. Second, to encourage scientific rigor and increase credibility, we recognize the value of peer review and we document all methods and assumptions in technical appendices so that subject matter experts can carefully review the inputs and modelers can replicate the models. In this context, publication across disciplinary boundaries remains a challenging but necessary process that takes time and perseverance. Third, continuous communication with policy makers remains critical to ensure that models anticipate the right questions, create awareness of the models and insights, and maintain relationships with the stakeholders. Determining the right questions represent a mutual process, with the input from policy makers dealing with financial, political, and operational pressures and the input from decision-oriented modelers that maintain a systems overview providing complimentary perspectives. Fourth, spending sufficient time on the presentation of insights to non-modeling audiences pays off. Without it, the value of all the efforts to develop models diminishes.

Developing and analyzing a complex model takes a long time. Whether such investments and long lead times remain justified depends on the specific models and questions. For example, the long lead times make integrated models less good at rapidly addressing emerging questions in entirely new areas. The inability to rapidly update a complex integrated model as policies or events unfold represents a limitation. However, in our experience, making the up-front investments to develop an integrated model gave us the flexibility to subsequently address emerging policy questions in a holistic manner and to deal with all the complexities that matter. For example, our integrated models allowed us to consider the overall system-wide impact (in terms of expected net health economic benefits) of evolving technologies for risk management rather than merely addressing the isolated impacts (e.g., only on costs or only on cases in one hypothetical situation without consideration of the probability that this situation occurs or feedback within the system) (Duintjer Tebbens and Thompson 2016a; Duintjer Tebbens and Thompson 2017a). As noted in the travel vaccination example, not all integrated models need structural complexity and high computational resources. In that example, we focused on the intuitively most important system features (i.e., international outbreak propagation) and ignored lower level complexities. However, integration of different tools remained necessary to address the policy question.

Discussion

This paper demonstrates the feasibility and value of integrating multiple analytical tools in the context of highly complex and high-stakes global health decisions. The article highlights that both integrated models and modeling tools used by themselves can provide helpful insights and that the nature of the policy questions motivates the level of integration. Integration provides a complimentary approach to address the limitations of individual methods while maintaining their strengths. For example, while the reality of rare events with high consequences for long-term poliovirus risk management motivated the reliance on probabilistic approaches, this does not imply a need to abandon deterministic DEB approaches. Quite to the contrary, the use of DEB modeling specifically and system dynamics more generally remains central throughout our efforts and yielded some of the most impactful analyses. The use of other system dynamics modeling approaches such as DES modeling, agent-based modeling, and probabilistic methods to propagate uncertainty provided complimentary insights and proved necessary to address a global problem like disease eradication at all relevant levels.

Systems thinking provided a central framework to understand the system behavior and recognize problems. Not surprisingly given the dynamic complexity involved in global polio eradication, over the years we observed many of the central themes of systems thinking (Sterman 2000). For example, infectious disease transmission involves the classical diffusion feedback, but this remains challenging to grasp for decision makers who face strong pressures to minimize resources and show short-term returns on investment. Reducing vaccination in polio-free countries (i.e., cutting corners) to focus on endemic areas resulted in multiple waves of outbreaks that rapidly spread from country to country (i.e., because outbreaks breed outbreaks) and ultimately ended up diverting resources from polio eradication efforts in endemic areas to manage outbreaks. Focusing on the serotype of highest urgency in India by switching to a serotype 1 monovalent vaccine resulted in the unintended consequence of major outbreaks of the other serotypes and subsequent fire-fighting behavior as priorities shifted (Duintjer Tebbens and Thompson 2009). The need to intensify OPV use prior to cessation represents an example of worse before better. Further, misunderstanding of the nature of accumulation of susceptible children after OPV cessation, which some may misperceive as an instantaneous change in population immunity, resulted in a reluctance to use OPV for outbreak response after OPV cessation in areas that failed to sufficiently intensify OPV use prior to OPV cessation. However, delaying OPV use for outbreak response only creates more future demand for OPV as outbreaks spread and the susceptible population grows, which strains the OPV stockpile. Stockpile management itself involves a long time delay between the production of bulk and finished vaccine, which complicates optimization of the stockpile and vaccine supply in general (Duintjer Tebbens et al. 2016c; Duintjer Tebbens and Thompson 2017d).

As computational power, analytical methods, and software continue to improve, we anticipate an increasing role for integrated models to address big questions involving complex systems. While increasing emphasis on big data focuses on better explaining detailed processes, we anticipate this detail-oriented development will also increase the demand for systems thinking to structure complex problems and maintain a holistic overview of the full system. Increasingly sophisticated data-analytical and statistical methods can inform historical patterns and predict short-term trends, but understanding the full short and long term implications of complex decisions requires an integrated system perspective.

Biographies

Radboud J. Duintjer Tebbens received his applied mathematics degrees and served on the faculty at Delft University of Technology. He is the Vice President of Kid Risk, Inc., where he develops integrated models to inform complex and high-stakes global health policies.

Kimberly M. Thompson received degrees and served on the faculty at Harvard University and the Massachusetts Institute of Technology. She is the President and Founder of Kid Risk, Inc., which aims to empower kids, parents, policy makers, and others to make better decisions when managing children’s risks (www.kidrisk.org).