Abstract
Arteries adapt to their mechanical environment by undergoing remodeling of the structural scaffold via the action of matrix metalloproteinases (MMPs). Cell culture studies have shown that stretching vascular smooth muscle cells (VSMCs) positively correlates to the production of MMP-2 and -9. In tissue level studies, the expression and activation of MMP-2 and -9 are generally higher in the outer media. However, homogeneous mechanical models of arteries predict lower stress and strain in the outer media, which appears inconsistent with experimental findings. The effects of heterogeneity may be important to our understanding of VSMC function, since arteries exhibit structural heterogeneity across the wall. We hypothesized that local stresses, computed using a heterogeneous mechanical model of arteries, positively correlate to the levels of MMP-2 and -9 in situ. We developed a model of the arterial wall accounting for nonlinearity, residual strain, anisotropy, and structural heterogeneity. The distributions of elastin and collagen fibers in situ, measured in the media of porcine carotid arteries, showed significant non-uniformities. Anisotropy was represented by the direction of collagen fibers measured by the helical angle of VSMC nuclei. The points at which the collagen fibers became load bearing were computed assuming a uniform fiber strain and orientation under physiological loading conditions; an assumption motivated by morphological measurements. The distributions of circumferential stresses, computed using both heterogeneous and homogeneous models, were correlated to the distributions of expression and activation of MMP-2 and -9 in porcine common carotid arteries incubated in an ex vivo perfusion organ culture system under physiological conditions for 48 hours. While strains computed using incompressibility were identical in both models, the heterogeneous model, unlike the homogeneous model, predicted higher circumferential stresses in the outer layer correlated to the expressions and activations of MMP-2 and -9. This implies that localized remodeling occurs in the areas of high stress and agrees with results from cell culture studies. The results support the role of mechanical stress in vascular remodeling and the importance of structural heterogeneity in understanding mechanobiological responses.
Keywords: modeling, blood vessels, vascular smooth muscle cells, matrix metalloproteinase, vascular remodeling
Introduction
The mechanosensitive functions of VSMCs are responsible for vascular remodeling. Hence, knowledge of the mechanical environment of VSMCs is essential in understanding the adaptive and maladaptive changes in the structure and function of arteries. The effect of mechanical environment on cell functions has been studied at both the tissue and cell levels. Tissue level studies provide information regarding the distribution of biological responses of cells in their natural environment. Cell culture studies allow better control of mechanical stimuli applied to cells in an artificial environment. Since mechanical stress cannot be measured, mechanical models are needed to help interpret results from tissue level studies using relationships established in cell culture studies.
Most widely used mechanical models of arteries are either phenomenological or structural models. Pseudoelastic models, originally proposed by Fung [1], consider arterial tissue to be hyperelastic and use strain energy functions (SEFs) to describe the mechanical properties of arteries [2, 3]. Phenomenological models (e.g., [4]) can provide insight into mechanical properties of arteries but cannot identify the cause of observable changes in them. Because changes in mechanical properties caused by aging or progression of vascular diseases can include changes in the amount, spatial distribution or properties of the basic structural constituents, efforts in mechanical modeling of arteries have focused on structure-based approaches. Three types of structural models have been proposed: multi-layer models, composite models, and constrained mixture models. Multi-layer models account for differences in the material properties of the medial and adventitial layers by using either different SEFs [5] or material constants [6, 7] for each layer. Composite models account for the distinctive material properties of structural components. In these models, the SEF of arterial tissue is expressed as the sum of the SEFs of structural components [8, 9]. In addition to the features of composite models, constrained mixture models include the fractions of elastin and collagen fibers. They also include the gradual recruitment to load bearing of initially wavy collagen fibers using a function for collagen recruitment [10, 11]. Thus, these models accounted for the different reference lengths for strains in the structural components.
Most of the published mechanical models of arteries assumed homogeneous mechanical properties across the media. Assuming homogeneity, a single function for collagen recruitment and area fractions of structural components measured at the tissue level were used in mechanical models. Excluding the effects of residual strains in the unloaded state, these models predict a non-uniform distribution of circumferential stresses with the maximum at the intimal surface [12-14]. Including the effects of residual strains significantly reduces the circumferential stress gradient [15-18]. However, the distribution of circumferential stresses is generally still not uniform with higher circumferential stress at the inner surface, since residual strain is often not sufficient to yield uniform stress distributions [19].
Arteries exhibit heterogeneity in their structure and material properties across the wall thickness. Vito et al. [20] measured the distribution of strains in cross sections of canine thoracic aorta and showed an increased stiffness near the outer wall. Also, residual stresses depend on tissue components at the microscopic level [21, 22]. The mechanical heterogeneity of the arterial wall is presumably due to the structural heterogeneity. The distributions of elastin and collagen fibers, the major components of the extracellular matrix (ECM), are known to be non-uniform through the arterial wall. In many types of arteries, the area fraction of collagen fibers increases while that of elastin decreases from the intima to the adventitia [23, 24]. In addition, the diameter of collagen fibrils progressively increases from the intima to the adventitia [25]. Using a simple phenomenological model for vascular growth, Taber and Humphrey [26] suggested heterogeneous material properties of bovine carotid arteries with stiffer outer layers. They also suggested that growth in arteries correlates better with stress than with strain. Thus, the structural heterogeneity of arteries is expected to influence the distributions of VSMC responses in situ.
The expression and activation of MMP-2 and MMP-9, also known as gelatinase A and B, are known to be mechanosensitive. MMP-2 and -9 are able to degrade similar substrates [27], including elastin and gelatin, and involved in VSMC migration and the formation of intimal hyperplasia [28]. MMP-9, but not MMP-2, is involved with VSMC-mediated assembly of fibrillar collagen [28] and gel contraction [29]. Results from cell culture studies showed that the production of MMP-2 and -9 by VSMCs increased in response to static [30] or cyclic stretching [31]. Ex vivo, tissue level studies showed that the expression and activation of MMP-2 and -9 were higher in the outer media of arteries [32] and veins [33]. Similar distributions of MMP-2 and -9 were also observed in porcine coronary arteries in vivo [34]. Combining these results suggests that VSMCs in the outer media are expected to experience higher mechanical stress and/or strain. However, interpreting these results in terms of the stress and strain distributions across the arterial wall is problematic using a homogeneous mechanical model, which generally predicts higher stress and strain at the inner surface.
Since strain in the arterial wall is constrained by the tubular geometry of arteries and incompressibility, we hypothesized that local stresses influence VSMC function and positively correlate to the levels of expression and activation of MMP-2 and -9 in situ. We developed a heterogeneous model of arteries and correlated circumferential stress to the expression and activation of MMP-2 and -9 in porcine carotid arteries conditioned to physiologic loading in an ex vivo organ culture system.
Materials and Methods
Organ Culture Experiment
Fresh porcine common carotid arteries were harvested from six to seven-month-old pigs at a local abattoir. Immediately after excision, arteries were washed with ice-cold PBS (Dulbecco’s phosphate buffered saline, Sigma, St. Louis, MO) supplemented with 1% antibiotic-antimycotic solution (Sigma) in the lumen and were transported to the laboratory in PBS at 4°C. After testing the arteries for leaks, segments of 50 to 70 mm were prepared from locations between 10 mm and 100 mm upstream of the carotid bifurcation.
The arteries were cultured 48 hours in the ex vivo perfusion organ culture system described previously [35] and modified to include bi-axial control of the mechanical environment [36]. Briefly, the arteries were mounted in physiological orientation between two cannulae in the organ culture chamber for perfusion in their in vivo flow direction. Then, the flow loop was filled with preheated (37°C) perfusion medium. The chamber was filled with bath medium and sealed to maintain sterility. Both the perfusion and bath medium were composed of Dulbecco’s modified Eagle’s medium (DMEM, Sigma) supplemented with sodium bicarbonate (3.7 g/L, Sigma), L-glutamine (2 mmol/L, Sigma), antibiotic-antimycotic solution (10 ml/L, Sigma), and calf serum (10% by volume, HyClone, Logan, UT). Dextran (6.3% by weight, average molecular weight 170,000; Sigma) was added to the perfusion media to acquire a fluid viscosity of blood (4×10−3 Pa·s). The viscosity was measured with a Cannon-Fenske viscometer (Cannon Instrument Co., State College, PA). The system was placed in an incubator in a 5% CO2 + 95% air mixture maintained at 37°C.
To mimic the physiological loading condition, arteries were stretched to in vivo length (axial stretch ratio, λ = 1.5) and perfused with a pulsatile flow at a transmural pressure of 100 ± 20 mmHg. Initially, the arteries were unstretched and subjected to a minimal flow to prevent possible damage to the tissue by abrupt changes in the mechanical environment. The stretch ratio of the arteries, the flow rate of the perfusion medium and mean luminal pressure were gradually increased to in vivo levels over three hours. The flow rate was controlled to maintain a mean shear stress (τ) of 1.5 Pa based on the Poiseulle relationship,
| (1) |
where D is the lumen diameter of the vessel, μ is the viscosity of the medium, and Q is the flow rate [37]. The conditions corresponding to the physiological mechanical environment, once achieved, were maintained for 48 hours. Since arteries were subjected to short-term responses, vasomotor response of arteries was not measured in this study. Vascular contractile responses were previously validated in 7-day culture experiments using the same system [35, 36].
At the end of the organ culture, the contractile response of VSMCs was disabled by adding 10−4 mol/L of sodium nitroprusside (Sigma) into the flow loop 30 minutes before the flow was stopped. This served to prevent a reflex response during tissue processing. After removal, each artery was divided into three segments. Two short segments (~5 mm) were embedded in Tissue-Tek® optimum cutting temperature (OCT) compound (Sakura Finetek, Torrance, CA) and frozen in liquid nitrogen for immunohistochemistry and in situ zymography. The remaining segment was reattached to cannulae and fixed in 10% formalin at pressure and in vivo length to preserve the microstructure at the mean incubating pressure (100 mmHg).
Histological Measures
The histology of arterial tissue provides information on how VSMCs respond to mechanical stimuli as well as the structure of arteries. Using microscopic images of cross sections and assuming axisymmetric microstructure and biological responses, the intramural distributions of structural components and of MMP-2 and -9 expression and activation were quantified semi-automatically using MATLAB®. First, the intima and the outer boundary of the external elastic lamina (EEL) were traced manually. The microscopic images of arterial cross sections were then mapped to an idealized circular ring prior to quantification. Average inner and outer diameters of the arteries at physiologic loading (100 mmHg, λ = 1.5) and no load (0 mmHg, λ = 1.0) from pressure-diameter relations (n = 9) [38] were used as the dimensions of idealized circular rings representing the physiologic and no load configurations, respectively. The cross section of a segment fixed at 100 mmHg and in vivo stretch was mapped to a circular ring representing the physiologic configuration. The cross section of a segment fixed at no load was mapped to a circular ring representing the no load configuration, which was then transformed to the physiologic configuration assuming incompressibility. The circular ring was divided into 51 layers of constant thickness (~ 11 μm) representing approximately half of the width of a VSMC [39].
Elastin
Elastin was visualized using its autofluorescence [40]. Elastin exhibits more intense autofluorescence than other ECM proteins when visualized at fluorophore excitation/emission maxima of 480/535 nm [41]. Images were taken directly from 7 μm paraffin sections using an FITC filter cube and a ×10 objective lens on a Nikon fluorescent microscope. The spatial resolution of the image was 0.46 μm/pixel (~ 1 million pixels per layer).
The area fraction of elastin in each layer was assumed, using the rationale provided by Baraga et al. [42], to be linearly proportional to the mean intensity of elastin autofluorescence, measured by 8-bit gray level, in that layer. The average intensity of pixels in the ith layer (Iei, i = 1, 2,… 51), where 1st layer is the inner-most layer and 51st layer is the outer-most layer, was measured automatically.
Collagen fibers
Collagen fibers are birefringent and were visualized using polarized microscopy and staining to enhance the birefringence. Picrosirius red staining is known to be specific to collagen [43] and increases birefringence in a concentration and staining time-dependent manner [44]. After the elastin images were taken, the sections were deparaffinized and stained for 75 minutes with 0.1% Sirius red F3B (Direct Red 80, Sigma-Aldrich) in saturated picric acid (Sigma) solution. Then the sections were washed in 0.5% acetic acid in dH2O for 5 minutes. After the sections were dehydrated in ascending grade alcohols followed by xylene, a drop of Permount® (Fisher Scientific, Pittsburgh, PA) was applied to the tissue section prior to placing the cover glass. The images were taken with a ×10 objective lens and two linear polarizers. A partial image of collagen fibers was taken with the slide located between two polarizers with their polarization directions crossed. A second image was taken with the crossed polarizers rotated 45° with respect to the setting used for the first image. The two images were superimposed to generate a complete image of collagen fibers.
The area fraction of collagen fibers in each layer was assumed to be linearly proportional to the mean intensity of collagen birefringence, measured by 8-bit gray level, in that layer. The level of collagen birefringence depends on various factors including the thickness [44-46], the orientation [47, 48], the maturity [48, 49], and the type of collagen fibers [50]. These factors affect the collagen birefringence but the net result is that more intense birefringence represents higher mechanical strength and stiffness. However, it is a difficult task to formulate an explicit mathematical relationship between collagen birefringence and the area fraction of collagen fibers due to the lack of a comprehensive understanding of its relationship to some of these factors. As a first approximation, the average pixel intensity in the ith layer (Ici, i = 1, 2,… 51) was assumed to be proportional to the area fraction of collagen fibers in the ith layer.
Immunohistochemistry
Immunostaining for MMP-2 or MMP-9 was performed on 7 μm frozen sections to quantify the distributions of the expressions of MMP-2 and -9. Sections were thawed for 10–30 minutes immediately before use at room temperature. The sections were first fixed in acetone for 5 minutes. After preincubation with 0.3% hydrogen peroxide in methanol to block endogenous peroxidase activity, tissue sections were blocked with 10% normal horse serum (Vector Laboratories, Burlingame, CA) in PBS (Sigma) for 20 minutes at room temperature. Specimens were then incubated for 60 minutes at room temperature in a humid chamber with primary antibodies for MMP-2 or MMP-9 (EMD Biosciences, San Diego, CA) diluted to 5 mg/L in PBS. After being washed in PBS, sections were incubated for 30 minutes in a humid chamber with biotinylated secondary antibodies in PBS plus 2% horse serum, followed by incubation for 1 hour with VECTASTATIN® Elite® ABC Kit reagent (Vector Laboratories). Gray-Black stain was developed using DAB substrate kit (Vector Laboratories). Because the slides were used for the quantification of gelatinase expression, nuclei were not counterstained.
Images of immunostained sections were taken using a conventional brightfield microscope. To quantify the area fraction of expression of MMP-2 or -9, a threshold mask was defined by sampling pixel intensities in the visually identified positive stains [51]. The threshold was applied to each image and the area fraction of MMP-2 or -9 positive pixels in each layer was computed.
In situ zymography
The activation of MMP-2 and -9 was detected using in situ zymography as described previously [52]. Briefly, fluorescent substrate (gelatin from pig skin conjugated to Oregon Green® 488 dye, Molecular Probes, Eugene, OR) in PBS (1 g/L) was mixed (1:1 by volume) with 1% low gelling temperature agarose (Sigma-Aldrich) melted in reaction buffer (50 mmol/L Tris-HCl, pH 7.4, containing 10 mmol/L CaCl2, and 0.05% Brij 35) at 50°C. The substrate solution (10 μl) was spread on pre-warmed glass slides and allowed to gel at room temperature. Frozen sections (7 μm) of specimens were mounted on top of the substrate film and incubated in a humid and dark chamber at 37°C up to 4 days.
Images of in situ zymography were taken using a fluorescent microscope with a FITC filter cube. The distribution of substrate lysis, shown as dark areas, represents the activities of MMP-2 and -9. A threshold for each image was determined independently to detect localized gelatinolytic activities. Then, each image was converted to a binary image using the threshold. The area fraction of gelatinolytic activity in each layer was computed and recorded.
Mechanical Model
A heterogeneous model of an artery was developed accounting for elastin and collagen fibers which together are responsible for the mechanical response of arteries [53, 54]. For comparison purpose, a homogeneous model of an artery was also formulated. In both models, an artery was considered as a thick-walled circular tube, which is a constrained mixture of two nonlinear elastic incompressible materials, elastin and collagen fibers. The zero stress configuration of arterial tissue was taken as the opened-up configuration after a radial cut of an unloaded ring.
For the heterogeneous model, we introduced two novel approaches to account for the structural heterogeneity of the arterial media. First, we included the non-uniform distributions of elastin and collagen fibers across the arterial wall. Second, the reference configuration for the strain of collagen fibers, a ‘recruiting point’, was assumed to vary across the arterial wall.
Using the notation given in Fig. 1, the deformation from the zero stress (Fig. 1a) to the loaded configuration (Fig. 1b) is described by the relations,
| (2) |
where μ, χ, and λ are deformation parameters, Φ is the opening angle, and l and L are lengths of an arterial segment at the zero stress state and at the loaded state, respectively. An arbitrary point (R, Θ, Z) in the zero stress configuration is mapped to a point (r, θ, z) in the loaded configuration. Following the theory of finite deformations, stretch ratios in the radial, circumferential, and axial directions are, respectively,
| (3) |
Figure 1.
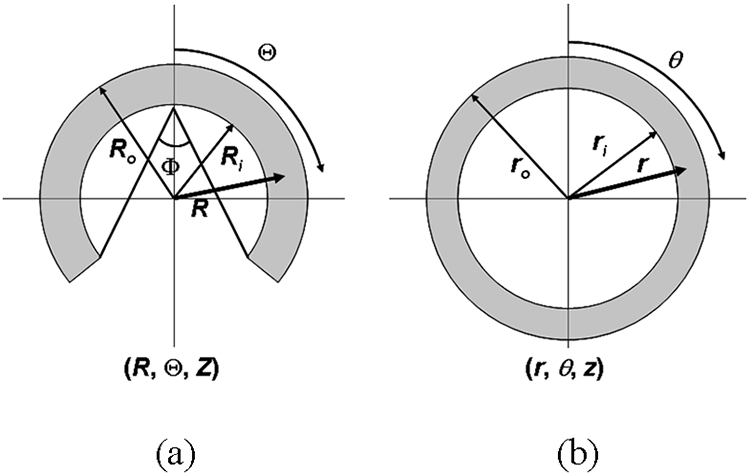
(a) The configuration of an artery at the zero stress state and (b) the loaded state. An arbitrary point (R, Θ, Z) in the zero stress configuration is mapped to a point (r, θ, z) in the loaded configuration.
The material was assumed to be incompressible (λrλθλz = 1), hence
| (4) |
Integrating Eq. (4) yields
| (5) |
Elastin provides structural support at all strains. Thus, the principal components of Green strain experienced by elastin are
| (6) |
Based on the histological observations, the structure of collagen fibers was modeled as left- and right-handed helices aligned at an angle of helical deviation (θh) with respect to the circumferential direction (Fig. 2a). The stretch ratio of arterial tissue in the direction of fibers (λh) is
| (7) |
where θh0 is a helical deviation at the zero stress configuration (Fig. 2b). Initially undulated collagen fibers become straightened once a strain along a helix reaches a recruiting point (Fig. 2b), which was assumed to vary through the thickness in the heterogeneous model. Once straightened, collagen fibers become load-bearing and the stretch ratio (λc) and Green strain of collagen fibers (Ec) are
| (8) |
| (9) |
Figure 2.
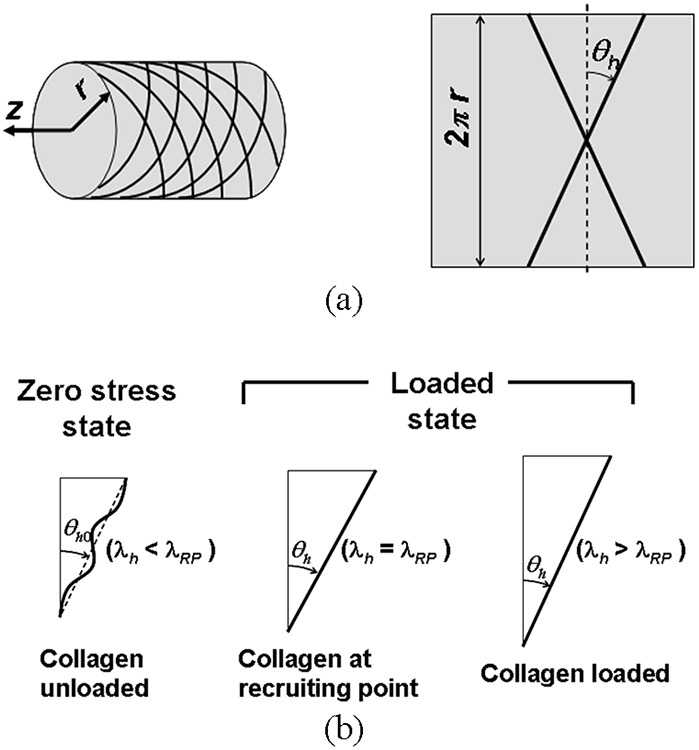
(a) Schematic of collagen fiber arrangements in the model. Collagen fibers were modeled as helices at an angle of ±θh. (b) The configurations of a collagen fiber at the zero stress state, recruiting point, and loaded state, where λh is the stretch ratio of arterial tissue in the direction of fibers and λRP is the stretch ratio along the helix at a recruiting point.
Since collagen fibers are not straightened at zero stress, we enforced λRP > 1 through the arterial wall.
Assuming variation of the recruiting point across the wall thickness, an additional assumption was introduced. It is hypothesized that the collagen fibers experience identical strain and orientation at physiological pressure (100 mmHg) and axial stretch (λ = 1.5); an assumption motivated by histological and structural considerations. It is expected that strains in VSMCs are closely associated with strains in collagen fibers. Therefore, the introduced assumption implies that VSMCs are at uniform strain under physiological loading, which is in agreement with the experimental observations [55]. This assumption was also validated by morphological measurements of VSMC nuclei. The helical deviation and length of VSMC nuclei were observed to be uniform through the arterial wall under physiologic loading [56]. VSMC nuclei are co-aligned with collagen fibers in the arterial media [57, 58].
Elastin was assumed to be a neo-Hookean material [9], for which the SEF is
| (10) |
ce is a material constant and I1 is the first invariant of the Green strain tensor.
Undulated collagen fibers are not load-bearing and hence are assumed to store no strain energy. Once straightened, collagen fibers gradually stiffen the arterial wall and were modeled by an exponential SEF:
| (11) |
where cc1 and cc2 are material constants. Note that if cc2 is much smaller than 1,
| (12) |
and Wc becomes a quadratic function of Green strain with coefficient cc1.
Considering the arterial tissue as a constrained mixture, the SEF of the intact arterial tissue is the sum of the SEFs of elastin and collagen fibers weighted by area fractions of each component:
| (13) |
where fe and fc are the area fractions of elastin and collagen fibers, respectively. With the axisymmetric assumption, the area fractions of elastin and collagen fibers vary only in the radial direction.
Implementation of Mechanical Model
The average pixel intensities of elastin and collagen fibers in each concentric layer were assumed to be proportional to the area fractions of elastin and collagen fibers. The proportionality is maintained at local and tissue levels, hence
| (14) |
where subscript k is e for elastin or c for collagen fibers, fki is the area fraction of each component in the ith layer, Fk is the area fraction of each component in the arterial wall, is the average pixel intensity of each component in the arterial wall. Now, the area fraction of each component in the ith layer is given as
| (15) |
is the normalized average pixel intensity of each component in the ith layer, and the area-weighted average of yields one. Thus, the area fraction of each component in the ith layer is decoupled into the tissue-level area fraction and normalized distribution of each component.
The tissue-level area fractions are constants and coupled with material constants in the constitutive equation. Hence, we defined area fraction weighted material constants:
| (16) |
where and are the area fraction-weighted material constants for elastin and collagen fibers, respectively.
Using the area fraction-weighted material constants, the modified SEFs of elastin and collagen fibers are
| (17) |
| (18) |
Hence, the SEF of the intact arterial tissue becomes
| (19) |
where and are the normalized average pixel intensities of elastin and collagen fibers, respectively, and vary only in the radial direction.
The average of previously reported pressure-diameter relations (n = 9) measured using healthy porcine carotid arteries stretched to in vivo length (λ = 1.5) at ten pressure points [38] was used to determine strain distributions assuming incompressibility. The average opening angle of 41.87° (n = 13) using fresh arteries and average helical deviation of 8.43° measured from VSMC nuclei (n = 1010) in two arteries fixed at 100 mmHg and in vivo stretch were also used to determine strains of each component [56].
Taking the pressure at the outer surface measured as a gauge pressure to be zero, force equilibrium at each of ten pressure-diameter points gives
| (20) |
where PE is the luminal pressure measured experimentally, and e is the error associated with regression analysis defined as the difference between PE and computed pressure using the model (PT).
Equation (20) forms a mathematical model for multivariate nonlinear regression with ten data points. Using both numerical and analytical methods, four unknown parameters, three material constants and uniform stretch ratio of collagen fibers at 100 mmHg and λ = 1.5, were determined by minimizing the error function (Ω) defined as
| (21) |
where m indicates each experimental data point.
For comparison purpose, a homogeneous model was also formulated and analyzed. In the homogeneous model, the distributions of elastin and collagen fibers were assumed to be uniform across the arterial wall:
| (22) |
Since a recruiting point is constant in the homogeneous model, four unknown parameters are three material constants and the constant stretch ratio in the direction of the collagen fibers at a recruiting point (λRP). These parameters were also determined by minimizing Eq. (21).
Statistical Analysis
The hypothesis that local stresses positively correlate to the levels of MMP-2 and -9 expression and activation was tested by calculating the Spearman rank correlation coefficients (rs) between the computed circumferential stress using the heterogeneous or homogeneous model and MMP-2 positive stained area fraction, MMP-9 positive stained area fraction, or substrate (gelatin) lysis area fraction for each specimen. Groups of correlation coefficients (n = 5 for each) were tested for zero mean using the single-sample Student’s t-test. Because the correlation coefficients are not normally distributed, they were transformed with the Fisher transformation and considered as samples from normal distribution with unknown mean and variance. A p-value of 0.05 was considered as statistically significant in all cases.
Results
The Distribution of ECM Components
Images of elastin showed the internal elastic lamina (IEL) with strong autofluorescence along with thin elastin lamellae between VSMC layers (Fig. 3a). The EEL was thick and composed of rather discontinuous elastin fragments. Elastin was not observed in the adventitia. Although elastin lamellae were discretely distributed through the media, they were continuously branching and merging through the circumference of arterial cross section. The average pixel intensity of elastin autofluorescence in each layer was mostly uniform in the media and high in the IEL and the EEL (Fig. 3b).
Figure 3.
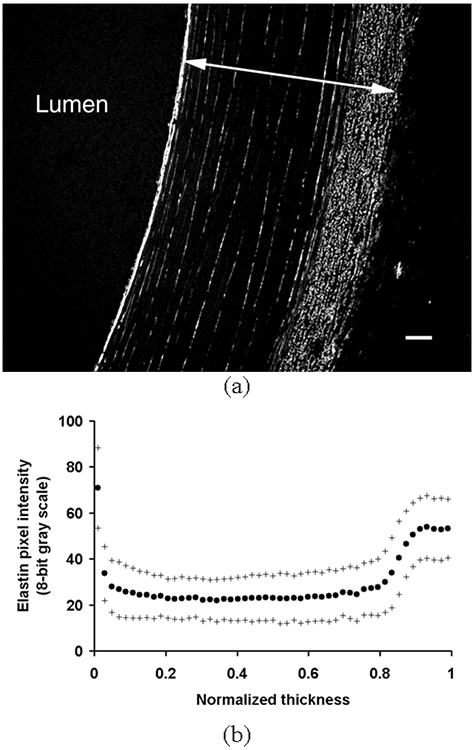
(a) A representative image of elastin structure taken from arteries fixed at 100 mmHg and in vivo stretch (λ = 1.5). An arrow indicates one normalized thickness. Bar = 50 μm. (b) The average area intensity of pixels due to elastin autofluorescence in each layer was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5).
The birefringence of collagen fibers was strongest in the adventitia mainly due to its high content of structural collagen type I fibers, which were mostly observed as thick and long fiber bundles (Fig. 4a). Although the birefringence of collagen fibers was high in the EEL, they were discontinuous and fragmented unlike in the adventitia. The average pixel intensity of collagen birefringence in each layer was greatest near the EEL with a small peak in the IEL (Fig. 4b). The collagen birefringence was relatively uniform in the inner media and gradually increased toward the EEL.
Figure 4.
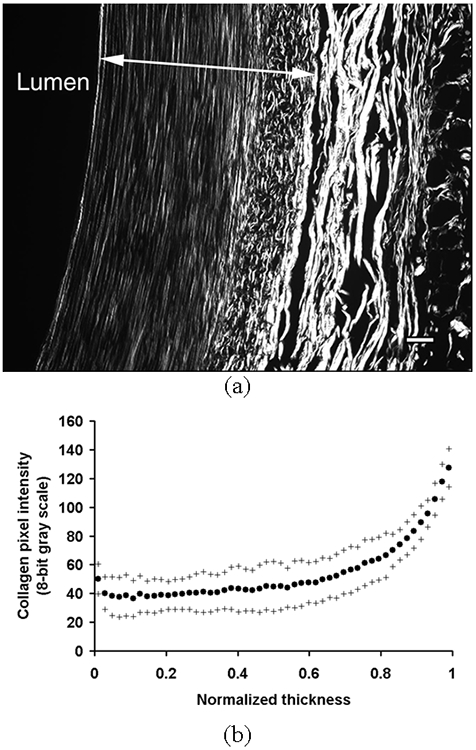
(a) A representative image of collagen structure taken from arteries fixed at 100 mmHg and in vivo stretch (λ = 1.5). An arrow indicates one normalized thickness. Bar = 50 μm. (b) The average area intensity of pixels due to collagen birefringence in each layer was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5).
The Distribution of Circumferential Stress
The highest circumferential stress computed using the heterogeneous model was at the outer boundary (Fig. 5a). The gradient of circumferential stress was the highest near the intima. The circumferential stress decreased sharply at the boundary between the IEL and the media, and gradually increased toward the outer layer. The circumferential stress was low and generally uniform in the inner media.
Figure 5.
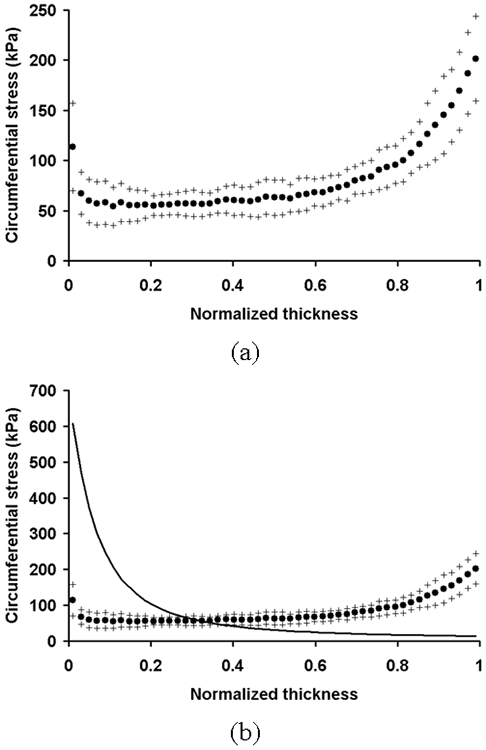
(a) The distribution of circumferential stress computed using the heterogeneous model. The circumferential stress in each layer computed using the heterogeneous model was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5). (b) The distribution of circumferential stress computed using the homogeneous model (solid line). It is plotted with the circumferential stress distribution in the heterogeneous model.
The circumferential stress computed using the homogeneous model was the highest at the intimal layer and gradually decreased toward the outer layer (Fig. 5b). The intramural distribution of circumferential stress computed using the heterogeneous model showed the opposite trend and was more uniform compared to the one computed using the homogeneous model.
The Distributions of Expression and Activation of MMP-2 and -9
The expressions of MMP-2 and -9 were mostly localized near the IEL, the outer media, and the EEL (Fig. 6 and 7, respectively). The activities of MMP-2 and -9 were mostly localized in the outer media and the EEL (Fig. 8). The expression and activation of MMP-2 and -9 significantly increased toward the outer layer (p < 0.01).
Figure 6.
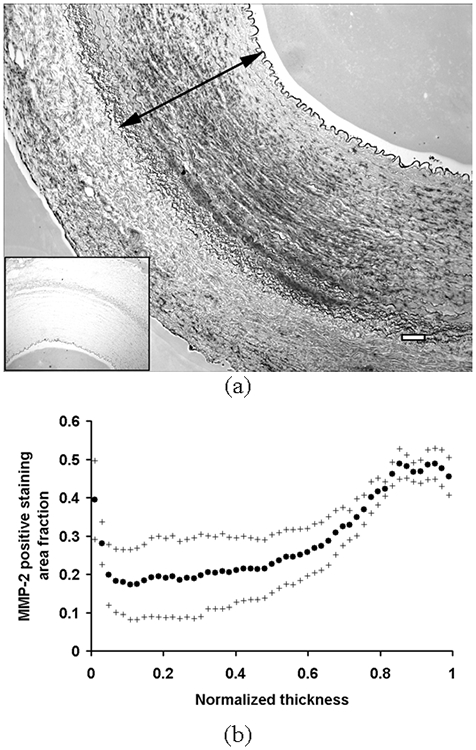
(a) A representative image of the immunostaining for MMP-2. Areas positively stained for MMP-2 appear to be dark gray-black. Negative control is shown together in a small window. An arrow indicates one normalized thickness. Bar = 100 μm. (b) The average area fraction of pixels positively stained for MMP-2 in each layer was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5).
Figure 7.
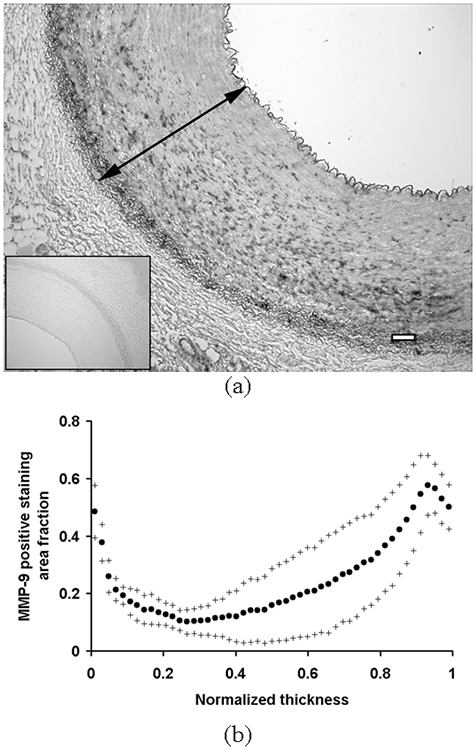
(a) A representative image of the immunostaining for MMP-9. Areas positively stained for MMP-9 appear to be dark gray-black. Negative control is shown together in a small window. An arrow indicates one normalized thickness. Bar = 100 μm. (b) The average area fraction of pixels positively stained for MMP-9 in each layer was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5).
Figure 8.
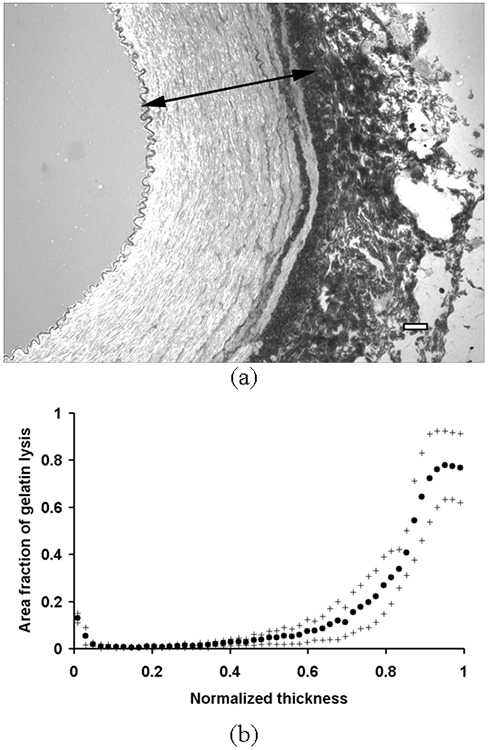
(a) A representative image of in situ zymography. Dark regions indicate localized gelatinolytic activities. An arrow indicates one normalized thickness. Bar = 100 μm. (b) The average area fraction of gelatinolytic activities in each layer was plotted against the normalized thickness as mean (•) ± S.D. (+) (n = 5).
Correlation between Circumferential Stress and MMP-2 and -9
Table 1 shows the Spearman rank correlation coefficients between the computed circumferential stress and the expression and activation of MMP-2 and -9 for individual specimens. The circumferential stress computed using the heterogeneous model positively correlated to the expression of MMP-2 (mean rs = 0.72; p = 0.01; n = 5), the expression of MMP-9 (mean rs = 0.70; p < 0.01; n = 5), and the activation of MMP-2 and -9 (mean rs = 0.80; p < 0.01; n = 5). However, the circumferential stress computed using the homogeneous model negatively correlated to the expression of MMP-2 (mean rs = −0.79; p < 0.01; n = 5), the expression of MMP-9 (mean rs = −0.56; p = 0.01; n = 5), and the activation of MMP-2 and -9 (mean rs = −0.86; p < 0.01; n = 5). Circumferential strain computed using incompressibility with respect to the zero stress configuration yielded same negative correlation as the circumferential stress in the homogeneous model.
Table 1.
Spearman rank correlation coefficients (rs) between the circumferential stress (σθ) and the expression and activation of MMP-2 and -9.
| σθ vs. MMP-2 expression | σθ vs. MMP-9 expression | σθ vs. gelatinolytic activity | ||||
|---|---|---|---|---|---|---|
| heterogeneous | homogeneous | heterogeneous | homogeneous | heterogeneous | homogeneous | |
| #1 | 0.7054 | −0.8586 | 0.8613 | −0.4767 | 0.6709 | −0.9001 |
| #2 | 0.9233 | −0.8757 | 0.8172 | −0.6173 | 0.9360 | −0.8828 |
| #3 | 0.4017 | −0.6219 | 0.7442 | −0.8170 | 0.7788 | −0.8734 |
| #4 | 0.9383 | −0.8907 | 0.3231* | −0.2179† | 0.9543 | −0.9119 |
| #5 | 0.6506 | −0.7079 | 0.7300 | −0.6545 | 0.6434 | −0.7070 |
All correlations were statistically significant (p < 0.01
p < 0.05) except one case (
p = 0.06).
Circumferential stresses computed using both the heterogeneous and the homogeneous models significantly correlated to the expression and activation of MMP-2 and -9. However, the heterogeneous model predicted that higher circumferential stress in the ECM scaffold correlates to higher expression and activation of MMP-2 and -9, while the homogeneous model predicted the opposite relationship, which is inconsistent with the positive correlation between MMP-2 and -9 and mechanical stretch established in cell culture studies.
Discussion
We recorded significant variations in the amounts of elastic fibers through the thickness in porcine common carotid arteries. The area fraction of elastin was highest at the IEL and was generally uniform through most of the media with a moderate increase in the EEL. The area fraction of collagen fibers gradually increased toward the outer boundary of the media. The observed distributions of area fractions of elastin and collagen fibers were quantitatively in agreement with the results from previous studies [23-25]. The observed distributions of ECM components suggest that the outer layer of the media may provide more mechanical strength than the inner layer. The IEL showed a small peak in the area fraction of collagen fibers suggesting its role in providing mechanical strength at the inner boundary of the media. The higher content of matrix proteins at both sides of the media suggests the importance of passive mechanical support in these regions.
The heterogeneity of ECM components likely contributes to localized cell activities in response to the mechanical stimuli. The distributions of elastin and collagen fibers may influence the variation in coupling between matrix proteins and cells through the arterial wall and affect the mechanical environment sensed by VSMCs. Many studies support specific roles of individual ECM proteins in transmitting mechanical signals to anchored cells. Wilson et al. [59] suggested that specific matrix-cell interactions may be involved in mechanotransduction, which may differ from those involved in adhesion. Koyama et al. [60] showed that the structure of cytoskeleton and the formation of focal adhesions depend on the type of ECM proteins to which cells are anchored to. Many studies suggest that ECM-cytoskeleton interactions are involved in mechanotransduction, which appears to be mediated by transmembrane ECM receptors such as integrin [59, 61].
In this study, the distributions of elastin and collagen fibers through the arterial wall were measured using their optical properties. Such optical measures are influenced by many factors such as conditions for staining and imaging. The opacity of the embedding medium and photo bleaching of the sections can cause variations in the overall intensity of elastin images. Conditions for staining to enhance collagen birefringence can cause variations in the overall intensity of collagen images. Thus, the optical measurements are semi-quantitative. Assuming that the average intensity of pixels is linearly proportional to the concentration of matrix protein in the area of interest, means that the normalized distributions of elastin and collagen fibers are maintained regardless of their estimated concentrations.
The expression and activation of MMP-2 and -9 were generally higher in the outer media. The current results qualitatively agree with previous observations, which reported higher expression and activation of MMP-2 and -9 in the outer media of arteries ex vivo [32] or in vivo [34]. Previous cell culture studies showed that mechanical stretch positively correlates to the production of MMP-2 and -9 by VSMCs [30, 31]. Thus, the localization of MMP-2 and -9 could be associated with the mechanical role of the outer media in response to the alteration in blood pressure. Arteries used in this study were collected from six to seven-month-old pigs, suggesting that we detected the expression and activation of MMP-2 and -9 in physiologic conditions.
MMP-2 and -9 are also expressed and activated by other types of cells, especially macrophages and fibroblasts in the media and adventitia. Once released, MMP-9 can diffuse into the interstitial space due to its low tissue retention [33], which may affect the distribution of the expression and activation of MMP-9 shown in this study. However, the EEL forms a barrier, which is expected to block free diffusion of such molecules between the media and the adventitia. Since the distributions of MMP-2 and -9 were quantified in the range between the IEL and the EEL, the contributions of fibroblasts in the adventitia and the diffusion of MMP-9 on our results were considered minimal. Also, the effects of inflammatory cells on the expression and activation of MMP-2 and MMP-9 were considered small, since they were harvested from young healthy pigs and no additional recruitment of inflammatory cells is expected in an ex vivo organ culture system. Major limitations of ex vivo organ culture experiments are the lack of interactions between arteries and surrounding tissue, including blood, and thus the inability to induce inflammatory responses seen in in vivo experiments [62].
We developed a heterogeneous model of the arterial wall taking into account the natural fiber distributions. This model is a novel extension of the constrained-mixture models and represents the heterogeneous structure of the arterial media. Introduction of microstructural information into mechanical modeling is needed to improve the utility of such models for the study of cellular behaviors. As a first step, we investigated potential effects of the heterogeneity of ECM components on the transmural distributions of stresses and its implications for the physiological response of VSMCs.
The transmural distributions of circumferential stresses were computed using the heterogeneous and homogeneous models. The stress computed using the heterogeneous model generally increased toward the outer layer and was high in the IEL and the EEL. This was significantly different from the homogeneous model where the stress peaked at the intima and decreased toward the outer layer. The result of the heterogeneous model suggests that both boundaries of the media, especially the outer media, may provide more mechanical support against pressure loading. The distribution of stress computed using the heterogeneous model was closer to a uniform distribution when compared to the stress distribution computed using the homogeneous model. Such a distribution is mainly due to the distribution of collagen fibers and the assumption introduced about collagen recruiting. This implies that the residual stress is not sufficient to make a uniform stress distribution.
Limitations of the model stem from the assumptions used. For instance, the reference configurations of collagen fibers were computed assuming a uniform strain distribution under physiologic conditions. Although it is a reasonable hypothesis based on the histological observations of VSMC morphology, the information on the reference configurations of collagen fibers is not readily available for verification. Also, more experimental data are needed to better represent material properties of structural components.
Using the heterogeneous model, circumferential stress positively correlates to the levels of MMP-2 and -9 expression and activation by VSMCs in situ. However, the hypothesis of this study is not acceptable using the homogeneous model. Circumferential strain computed assuming incompressibility with respect to the zero stress configuration also negatively correlated to the levels of MMP-2 and -9. This suggests that the reference state for strains of VSMCs is different from the zero stress configuration, since uniform distribution of VSMC lengths is expected under physiologic loading [55]. Thus, strains at the tissue level may not be the strain sensed by VSMCs. Assuming that the cells are uniformly coupled to substrates in cell culture experiments, it is reasonable to expect that mechanical stress as well as strain positively correlates to the production of MMP-2 and -9 by VSMCs. Therefore, the association and correlation of circumferential stress in the heterogeneous model with the expression and activation of MMP-2 and -9 is in agreement with results from cell culture studies. We interpret this agreement as support for the validity of the heterogeneous model and the likely importance of mechanical stress in arterial modeling.
The remodeling activities of VSMCs may correlate better with stresses rather than strains. It is well accepted that the arterial wall remodels by thickening in response to increased wall stress in order to decrease it back to normal levels [63, 64]. This implies that areas of high stress may be sites of localized remodeling. Fridez et al. [65] observed that, in response to induced hypertension, the outermost layers of rat carotid arteries thicken more as compared to the inner layers. This suggests that stress in the outermost layer may be higher than that in the inner layer, which is consistent with the stress distribution computed using the heterogeneous model. Xu et al. [66] showed that induced hypertension also initiates rapid gene expression for collagen type I predominantly in the outer media and adventitia of rabbit aortas. Increased collagen support, as the authors note, suggests that these zones of the aortic wall may provide an increase in tensile support. The heterogeneous model shows the importance of mechanical stress in understanding these results. In contrast to these results, Matsumoto and Hayashi [64] observed a higher thickening of the innermost layer in the adaptation of rat aortas to Goldblatt hypertension at 8 weeks. The difference between results may due to experimental methods, the type of arteries, and/or the host animal of arteries.
We conclude that the type of tissue and the heterogeneity of the tissue microstructure, whether in the arterial wall or tissue engineered construct, should be considered explicitly when using mechanical models to better understand, predict and potentially control cellular functions in situ.
Acknowledgements
This work was supported by funding from the Georgia Tech/Emory Center (GTEC) for the Engineering of Living Tissues, an Engineering Research Centers (ERC) program of the National Science Foundation under award number EEC-9731643 and the NHLBI R01 64689 from the National Institute of Health. Porcine carotid arteries were generously donated by Holifield Farms of Conyers, GA.
References
- [1].Fung YC, 1965, Foundations of Solid Mechanics, Prentice-Hall, Englewood Cliffs, NJ. [Google Scholar]
- [2].Humphrey JD, 1995, "Mechanics of the Arterial Wall: Review and Directions," Crit. Rev. Biomed. Eng, 23(1-2), pp. 1–162. [PubMed] [Google Scholar]
- [3].Vito RP and Dixon SA, 2003, "Blood Vessel Constitutive Models - 1995-2002," Annu. Rev. Biomed. Eng, 5, pp. 413–439. [DOI] [PubMed] [Google Scholar]
- [4].Brossollet LJ and Vito RP, 1996, "A New Approach to Mechanical Testing and Modeling of Biological Tissues, with Application to Blood Vessels," J. Biomech. Eng, 118, pp. 433–439. [DOI] [PubMed] [Google Scholar]
- [5].von Maltzahn WW, Besdo D, and Wiemer W, 1981, "Elastic Properties of Arteries: a Nonlinear Two-Layer Cylindrical Model," J. Biomech, 14(6), pp. 389–397. [DOI] [PubMed] [Google Scholar]
- [6].von Maltzahn WW, Warriyar RG, and Keitzer WF, 1984, "Experimental Measurements of Elastic Properties of Media and Adventitia of Bovine Carotid Arteries," J. Biomech, 17(11), pp. 839–847. [DOI] [PubMed] [Google Scholar]
- [7].Rachev A, 1997, "Theoretical Study of the Effect of Stress-Dependent Remodeling on Arterial Geometry under Hypertensive Conditions," J. Biomech, 30(8), pp. 819–827. [DOI] [PubMed] [Google Scholar]
- [8].Holzapfel GA and Weizsäcker HW, 1998, "Biomechanical Behavior of the Arterial Wall and Its Numerical Characterization," Comput. Biol. Med, 28, pp. 377–392. [DOI] [PubMed] [Google Scholar]
- [9].Holzapfel GA, Gasser TC, and Stadler M, 2002, "A Structural Model for the Viscoelastic Behavior of Arterial Walls: Continuum Formulation and Finite Element Analysis," Eur. J. Mech. A/Solids, 21, pp. 441–463. [Google Scholar]
- [10].Wuyts FL, Vanhuyse VJ, Langewouters GJ, Decraemer WF, Raman ER, and Buyle S, 1995, "Elastic Properties of Human Aortas in Relation to Age and Atherosclerosis: a Structural Model," Phys. Med. Biol, 40(10), pp. 1577–1597. [DOI] [PubMed] [Google Scholar]
- [11].Zulliger MA, Fridez P, Hayashi K, and Stergiopulos N, 2004, "A Strain Energy Function for Arteries Accounting for Wall Composition and Structure," J. Biomech, 37, pp. 989–1000. [DOI] [PubMed] [Google Scholar]
- [12].Vito RP and Hickey J, 1980, "The Mechanical Properties of Soft Tissues-II: the Elastic Response of Arterial Segments," J. Biomech, 13, pp. 951–957. [DOI] [PubMed] [Google Scholar]
- [13].Chuong CJ and Fung YC, 1983, "Three-Dimensional Stress Distribution in Arteries," J. Biomech. Eng, 105, pp. 268–274. [DOI] [PubMed] [Google Scholar]
- [14].Vorp DA, Rajagopal KR, Smolinski PJ, and Borovetz HS, 1995, "Identification of Elastic Properties of Homogeneous, Orthotropic Vascular Segments in Distension," J. Biomech, 28(5), pp. 501–512. [DOI] [PubMed] [Google Scholar]
- [15].Chuong CJ and Fung YC, 1986, "On Residual Stresses in Arteries," J. Biomech. Eng, 108, pp. 189–192. [DOI] [PubMed] [Google Scholar]
- [16].Matsumoto T and Hayashi K, 1996, "Stress and Strain Distribution in Hypertensive and Normotensive Rat Aorta Considering Residual Strain," J. Biomech. Eng, 118(1), pp. 62–73. [DOI] [PubMed] [Google Scholar]
- [17].Rachev A, Stergiopulos N, and Meister J-J, 1996, "Theoretical Study of Dynamics of Arterial Wall Remodeling in Response to Changes in Blood Pressure," J. Biomech, 29(5), pp. 635–642. [DOI] [PubMed] [Google Scholar]
- [18].Chaudhry HR, Bukiet B, Davis A, Ritter AB, and Findley T, 1997, "Residual Stresses in Oscillating Thoracic Arteries Reduce Circumferential Stresses and Stress Gradients," J. Biomech, 30(1), pp. 57–62. [DOI] [PubMed] [Google Scholar]
- [19].Peterson SJ and Okamoto RJ, 2000, "Effect of Residual Stress and Heterogeneity on Circumferential Stress in the Arterial Wall," J. Biomech. Eng, 122(4), pp. 454–456. [DOI] [PubMed] [Google Scholar]
- [20].Vito RP, Whang MC, Glagov S, and Aoki T, 1991, "The Distribution of Strains and Stresses in the Arterial Cross Section," Proc. of the 1991 ASME Winter Annual Meeting, Atlanta, GA. [Google Scholar]
- [21].Greenwald SE, Moore JE, Rachev A, Kane TPC, and Meister J-J, 1997, "Experimental Investigation of the Distribution of Residual Strains in the Artery Wall," J. Biomech. Eng, 119, pp. 438–444. [DOI] [PubMed] [Google Scholar]
- [22].Matsumoto T, Goto T, and Sato M, 2002, "Residual Stress and Strain in the Lamellar Unit of the Aorta: Experiment and Analysis," Proc. of the 4th World Congress Biomechanics, Calgary, Canada. [DOI] [PubMed] [Google Scholar]
- [23].Feldman SA and Glagov S, 1971, "Transmedial Collagen and Elastin Gradients in Human Aortas: Reversal with Age," Atherosclerosis, 13, pp. 385–394. [DOI] [PubMed] [Google Scholar]
- [24].Hasan N and Greenwald SE, 1995, "Variation in the Concentration of Scleroproteins across the Arterial Wall," J. Pathol, 176(Suppl), pp. 26A. [Google Scholar]
- [25].Merrilees MJ, Tiang KM, and Scott L, 1987, "Changes in Collagen Fibril Diameters across Artery Walls Including a Correlation with Glycosaminoglycan Content," Connect. Tissue Res, 16, pp. 237–257. [DOI] [PubMed] [Google Scholar]
- [26].Taber LA and Humphrey JD, 2001, "Stress-Modulated Growth, Residual Stress, and Vascular Heterogeneity," J. Biomech. Eng, 123(6), pp. 528–535. [DOI] [PubMed] [Google Scholar]
- [27].Dollery CM, McEwan JR, and Henney AM, 1995, "Matrix Metalloproteinases and Cardiovascular Disease," Circ. Res, 77(5), pp. 863–868. [DOI] [PubMed] [Google Scholar]
- [28].Johnson C and Galis ZS, 2004, "Matrix Metalloproteinase-2 and -9 Differentially Regulate Smooth Muscle Cell Migration and Cell-Mediated Collagen Organization," Arterioscler. Thromb. Vasc. Biol, 24, pp. 54–60. [DOI] [PubMed] [Google Scholar]
- [29].Defawe OD, Kenagy RD, Choi C, Wan SYC, Deroanne C, Nusgens B, Sakalihasan N, Colige A, and Clowes AW, 2005, "MMP-9 Regulates both Positively and Negatively Collagen Gel Contraction: a Nonproteolytic Function of MMP-9," Cardiovasc. Res, 66, pp. 402–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Asanuma K, Magid R, Johnson C, Nerem RM, and Galis ZS, 2003, "Uniaxial Strain Upregulates Matrix-Degrading Enzymes Produced by Human Vascular Smooth Muscle Cells," Am. J. Physiol. Heart Circ. Physiol, 284, pp. H1778–H1784. [DOI] [PubMed] [Google Scholar]
- [31].O'Callaghan CJ and Williams B, 2000, "Mechanical Strain-Induced Extracellular Matrix Production by Human Vascular Smooth Muscle Cells: Role of TGF-β1," Hypertension, 36(3), pp. 319–324. [DOI] [PubMed] [Google Scholar]
- [32].Chesler NC, Ku DN, and Galis ZS, 1999, "Transmural Pressure Induces Matrix-Degrading Activity in Porcine Arteries Ex Vivo," Am. J. Physiol, 277(5 pt 2), pp. H2002–9. [DOI] [PubMed] [Google Scholar]
- [33].Mavromatis K, Fukai T, Tate M, Chesler N, Ku DN, and Galis ZS, 2000, "Early Effects of Arterial Hemodynamic Conditions on Human Saphenous Veins Perfused Ex Vivo," Arterioscler. Thromb. Vasc. Biol, 20, pp. 1889–1895. [DOI] [PubMed] [Google Scholar]
- [34].Wilson SH, Herrmann J, Lerman LO, Holmes DR, Napoli C, Ritman EL, and Lerman A, 2002, "Simvastatin Preserves the Structure of Coronary Adventitial Vasa Vasorum in Experimental Hypercholesterolemia Independent of Lipid Lowering," Circulation, 105(5), pp. 415–418. [DOI] [PubMed] [Google Scholar]
- [35].Han H-C and Ku DN, 2001, "Contractile Responses in Arteries Subjected to Hypertensive Pressure in Seven-Day Organ Culture," Ann. Biomed. Eng, 29, pp. 467–475. [DOI] [PubMed] [Google Scholar]
- [36].Davis NP, Han HC, Wayman B, and Vito RP, 2005, "Sustained Axial Loading Lengthens Arteries in Organ Culture," Ann. Biomed. Eng, 33(7), pp. 867–877. [DOI] [PubMed] [Google Scholar]
- [37].Ku DN, 1997, "Blood Flow in Arteries," Annu. Rev. Fluid Mech, 29, pp. 399–434. [Google Scholar]
- [38].Davis NP, 2002, "Axial Stretch as a Means of Lengthening Arteries: an Investigation in Organ Culture," Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA [Google Scholar]
- [39].Todd ME, Laye CG, and Osborne DN, 1983, "The Dimensional Characteristics of Smooth Muscle in Rat Blood Vessels: a Computer-Assisted Analysis," Circ. Res, 53, pp. 319–331. [DOI] [PubMed] [Google Scholar]
- [40].Blomfield J and Farrar JF, 1967, "Fluorescence Spectra of Arterial Elastin," Biochem. Biophys. Res. Commun, 28(3), pp. 346–351. [DOI] [PubMed] [Google Scholar]
- [41].Fitzmaurice M, Bordagaray JO, Engelmann GL, Richards-Kortum R, Kolubayev T, Feld MS, Ratliff NB, and Kramer JR, 1989, "Argon Ion Laser-Excited Autofluorescence in Normal and Atherosclerotic Aorta and Coronary Arteries: Morphologic Studies," Am. Heart J, 118(5 pt 1), pp. 1028–1038. [DOI] [PubMed] [Google Scholar]
- [42].Baraga JJ, Rava RP, Taroni P, Kittrell C, Fitzmaurice M, and Feld MS, 1990, "Laser Induced Fluorescence Spectroscopy of Normal and Atherosclerotic Human Aorta Using 306-310 nm Excitation," Lasers Surg. Med, 10(3), pp. 245–261. [DOI] [PubMed] [Google Scholar]
- [43].Junqueira LCU, Bignolas G, and Brentani RR, 1979, "Picrosirius Staining Plus Polarization Microscopy, a Specific Method for Collagen Detection in Tissue Sections," Histochem. J, 11, pp. 447–455. [DOI] [PubMed] [Google Scholar]
- [44].Canham PB, Finlay HM, Kiernan JA, and Ferguson GG, 1999, "Layered Structure of Saccular Aneurysms Assessed by Collagen Birefringence," Neurol. Res, 21(7), pp. 618–626. [DOI] [PubMed] [Google Scholar]
- [45].Junqueira LCU, Montes GS, and Krisztan RM, 1979, "The Collagen of the Vertebrate Peripheral Nervous System," Cell Tissue Res., 202, pp. 453–460. [DOI] [PubMed] [Google Scholar]
- [46].Junqueira LCU, Montes GS, and Sanchez EM, 1982, "The Influence of Tissue Section Thickness on the Study of Collagen by the Picrosirius-Polarization Method," Histochemistry, 74(1), pp. 153–156. [DOI] [PubMed] [Google Scholar]
- [47].Ehlers EG, 1987, Optical Mineralogy: Theory and Technique, Blackwell Scientific Publications, Palo Alto, CA, pp. 29. [Google Scholar]
- [48].Whittaker P, Kloner RA, Boughner DR, and Pickering JG, 1994, "Quantitative Assessment of Myocardial Collagen with Picrosirius Red Staining and Circularly Polarized Light," Basic Res. Cardiol, 89(5), pp. 397–410. [DOI] [PubMed] [Google Scholar]
- [49].Szendroi M, Vajta G, Kovacs L, Schaff Z, and Lapis K, 1984, "Polarization Colours of Collagen Fibres: a Sign of Collagen Production Activity in Fibrotic Processes," Acta Morphol. Hung, 32(1), pp. 47–55. [PubMed] [Google Scholar]
- [50].Wolman M and Kasten FH, 1986, "Polarized Light Microscopy in the Study of the Molecular Structure of Collagen and Reticulin," Histochemistry, 85(1), pp. 41–49. [DOI] [PubMed] [Google Scholar]
- [51].Lee RT, Schoen FJ, Loree HM, Lark MW, and Libby P, 1996, "Circumferential Stress and Matrix Metalloproteinase 1 in Human Coronary Atherosclerosis: Implications for Plaque Rupture," Arterioscler. Thromb. Vasc. Biol, 16(8), pp. 1070–1073. [DOI] [PubMed] [Google Scholar]
- [52].Galis ZS, Sukhova GK, and Libby P, 1995, "Microscopic Localization of Active Proteases by In Situ Zymography: Detection of Matrix Metalloproteinase Activity in Vascular Tissue," FASEB J., 9(10), pp. 974–980. [DOI] [PubMed] [Google Scholar]
- [53].Torrance HB and Shwatz S, 1961, "The Elastic Behaviour of the Arterial Wall," J. R. Coll. Surg. Edinb 7, pp. 55. [PubMed] [Google Scholar]
- [54].Conklin BS, Richter ER, Kreutziger KL, Zhong D-S, and Chen C, 2002, "Development and Evaluation of a Novel Decellularized Vascular Xenograft," Med. Eng. Phys, 24, pp. 173–183. [DOI] [PubMed] [Google Scholar]
- [55].Fung YC, 1984, Biodynamics: Circulation, Springer-Verlag, New York, NY, pp. 64–65. [Google Scholar]
- [56].Kim Y, 2007, "Correlation between MMP-2 and -9 Levels and Local Stresses in Arteries Using a Heterogeneous Mechanical Model," Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA [Google Scholar]
- [57].Canham PB, Finlay HM, Whittaker P, and Starkey J, 1986, "The Tunica Muscularis of Human Brain Arteries: Three-Dimensional Measurements of Alignment of the Smooth Muscle Mechanical Axis, by Polarized Light and the Universal Stage," Neurol. Res, 8(2), pp. 66–74. [DOI] [PubMed] [Google Scholar]
- [58].Finlay HM, Dixon JG, and Canham PB, 1991, "Fabric Organization of the Subendothelium of the Human Brain Artery by Polarized-Light Microscopy," Arterioscler. Thromb. Vasc. Biol, 11, pp. 681–690. [DOI] [PubMed] [Google Scholar]
- [59].Wilson E, Sudhir K, and Ives HE, 1995, "Mechanical Strain of Rat Vascular Smooth Muscle Cells is Sensed by Specific Extracellular Matrix/Integrin Interactions," J. Clin. Invest, 96(5), pp. 2364–2372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Koyama H, Raines EW, Bornfeldt KE, Roberts JM, and Ross R, 1996, "Fibrillar Collagen Inhibits Arterial Smooth Muscle Proliferation through Regulation of Cdk2 Inhibitors," Cell, 87, pp. 1069–1078. [DOI] [PubMed] [Google Scholar]
- [61].Carey DJ, 1991, "Control of Growth and Differentiation of Vascular Cells by Extracellular Matrix Proteins," Annu. Rev. Physiol, 53, pp. 161–177. [DOI] [PubMed] [Google Scholar]
- [62].Capers Q, Alexander RW, Lou P, De Leon H, Wilcox JN, Ishizaka N, Howard AB, and Taylor WR, 1997, "Monocyte Chemoattractant Protein-1 Expression in Aortic Tissues of Hypertensive Rats," Hypertension, 30(6), pp. 1397–1402. [DOI] [PubMed] [Google Scholar]
- [63].Liu SQ and Fung YC, 1989, "Relationship between Hypertension, Hypertrophy, and Opening Angle of Zero-Stress State of Arteries Following Aortic Constriction," J. Biomech. Eng, 111, pp. 325–335. [DOI] [PubMed] [Google Scholar]
- [64].Matsumoto T and Hayashi K, 1994, "Mechanical and Dimensional Adaptation of Rat Aorta to Hypertension," J. Biomech. Eng, 116, pp. 278–283. [DOI] [PubMed] [Google Scholar]
- [65].Fridez P, Zulliger M, Bobard F, Montorzi G, Miyazaki H, Hayashi K, and Stergiopulos N, 2003, "Geometrical, Functional, and Histomorphometric Adaptation of Rat Carotid Artery in Induced Hypertension," J. Biomech, 36, pp. 671–680. [DOI] [PubMed] [Google Scholar]
- [66].Xu C, Zarins CK, Bassiouny HS, Briggs WH, Reardon C, and Glagov S, 2000, "Differential Transmural Distribution of Gene Expression for Collagen Types I and III Proximal to Aortic Coarctation in the Rabbit," J. Vasc. Res, 37(3), pp. 170–182. [DOI] [PubMed] [Google Scholar]


