Dynamic cardiac PET motion correction using 3D normalized gradient fields in patients and phantom simulations

Abstract

This work expands on the implementation of 3D normalized gradient fields to correct for whole-body motion and cardiac creep in [N-13]-ammonia patient studies and evaluates its accuracy using a dynamic phantom simulation model.

Methods.

A full rigid-body algorithm was developed using 3D normalized gradient fields including a multi-resolution step and sampling off the voxel grid to reduce interpolation artifacts. Optimization was performed using a weighted similarity metric that accounts for opposing gradients between images of blood pool and perfused tissue without the need for segmentation. 43 retrospective dynamic [N-13]-ammonia PET/CT rest/adenosine-stress patient studies were motion corrected and the mean motion parameters plotted at each frame time point. Motion correction accuracy was assessed using a comprehensive dynamic XCAT simulation incorporating published physiologic parameters of the heart’s trajectory following adenosine infusion as well as corrupted attenuation correction commonly observed in clinical studies. Accuracy of the algorithm was assessed objectively by comparing the errors between isosurfaces and centers of mass of the motion corrected XCAT simulations.

Results.

In the patient studies, the overall mean cranial-to-caudal translation was 7 mm at stress over the duration of the adenosine infusion. Non-invasive clinical measures of relative flow reserve and myocardial flow reserve were highly correlated with their invasive analogues. Motion correction accuracy assessed with the XCAT simulations showed an error of <1 mm in late perfusion frames that broadened gradually to < 3mm in earlier frames containing blood pool.

Conclusion.

This work demonstrates that patients undergoing [N-13]-ammonia dynamic PET/CT exhibit a large cranial-to-caudal translation related to cardiac creep primarily at stress and to a lesser extent at rest, which can be accurately corrected by optimizing their 3D normalized gradient fields. Our approach provides a solution to the challenging condition where the image intensity and its gradients are opposed without the need for segmentation and remains robust in the presence of PET-CT mismatch.

Introduction

Absolute myocardial blood flow (MBF) provides critical information on heart function that cannot be discerned from relative perfusion processing such as with balanced triple vessel disease^1,2 or diffuse microvascular dysfunction^3,4. The data collection protocol for estimating MBF presents several technical challenges including consistency of the arterial input function^5–7, trade-offs in kinetic models with scan duration^8,9, choice of temporal sampling^10–12, motion between positron emission tomography (PET) and computed tomography (CT) acquisitions¹³, and motion within the thoracic cavity^14,15. The long acquisition durations (4–10min) increase the likelihood of patient motion at rest and following pharmacological stress, where approximately one-quarter of PET/CT acquisitions exhibit PET-CT mismatch^13,16 and greater than half exhibit heart motion within the thorax^14,17. Gross patient motion such as PET-CT mismatch in myocardial perfusion imaging (MPI) can produce regions of under-corrected activity concentration that may be interpreted as perfusion defects^13,18. Motion within the thorax commonly follows administration of pharmacologic vasodilators, such as adenosine or regardenoson, where the heart translates up to 10mm within the thoracic cavity¹⁵ irrespective of gross patient motion¹⁴. In single photon emission computed tomography (SPECT) exercise stress, this motion event has been described as cardiac creep¹⁹ and the related phenomenon in pharmacological-stress PET has been described as deep breathing²⁰, non-returning motion¹⁴ or cardiac creep¹⁷. We refer to cardiac motion within the thoracic cavity as cardiac creep throughout this work. It is argued that cardiac creep has a greater effect on MBF accuracy than PET-CT scan mismatch^21,22. In brief, as the physiological stressor takes effect, the overall lung volume increases as breathing becomes labored causing the heart to move in the caudal direction with some rotation in the thoracic cavity relative to its resting position. At the termination of pharmacologic stress, the lung volume decreases and the heart gradually returns to a resting position but not necessary the same position prior to pharmacologic stress. This motion phenomenon has a substantial impact on estimates of MBF and should be addressed^23–25 but automatic tools and validated techniques are lacking in the clinic²⁶.

Motion correction techniques in nuclear medicine are mature and have undergone extensive optimization but these have largely been focused on brain which is rigid in nature²⁷. Cardiac creep in the thoracic cavity is decidedly more complex however structures outside the right and left ventricle have relatively low uptake with lower diagnostic value. It has been shown that rigid-body registration (e.g. 6-degrees of freedom (dof): 3-translational + 3-rotational) is sufficient for submillimeter registration accuracy of the heart’s coronary vessels during free breathing, ignoring peripheral structures²⁸. Many groups have been successful correcting for heart motion between the perfused left ventricle and CT²⁹ using 3- and 6-dof rigid body approaches though fewer have addressed motion along the entire time-series starting from radiopharmaceutical administration where blood pool signal rises to a maximum and decreases as the myocardial tissue is perfused^20,30,31.

Motion correction between early images comprised of blood signal and late images of perfused myocardium is a challenging problem as these signals are inverted from one another and occupy different anatomical spaces. Secondly, the motion trajectory of the heart during breathing undergoes translations (predominantly cranial-to-caudal) but also rotational events^28,32 that have been addressed with manual correction¹⁴ and automated algorithms^15,31. The large changes in signal intensity and its varying spatial distribution complicates the application of similarity metrics based on intensity patterns. Mutual information is a common choice in these scenarios but as we later demonstrate can be a poor indicator of similarity. Lee et al. proposed a translation-only registration algorithm based on 3D normalized gradient fields, which adds additional spatial information where gradient edges between images of blood pool and perfused myocardium occupy the same space though opposed in direction³⁰. In this work we have expanded the implementation of 3D normalized gradient fields to include a fully rigid-body (6-dof) approach using a weighted cost function that accounts for opposing gradients. In addition, we provide a fully dynamic simulation of cardiac creep using the XCAT phantom as “ground truth” to evaluate the algorithm’s accuracy and compare these findings to results in patients. We compare invasive coronary angiography measures of coronary flow reserve (CFR) and fractional flow reserve (FFR) to their non-invasive analogue measures of myocardial flow reserve (MFR) and relative flow reserve (RFR), respectively. We hypothesize that motion correction will improve the correlation between invasive and image-based measures of coronary flow compared to uncorrected data.

Materials and Methods

Patient Studies

43 patients were enrolled from the Seoul National University Hospital (n=38), Chonnam National University Hospital (n=4) and Samsung Medical Center (n=1) who had a positive [N-13]-ammonia PET scan. Patient datasets were collected between February 2013 and May 2014 as part of our prospective DEMYSTIFY (dynamic PET/CTA-fused imagery) clinical study³³. Including [N-13]-ammonia dynamic PET, all patients received coronary computed tomography angiography (CTA) and invasive coronary angiography (ICA). The study was approved by the institutional review board of the Seoul National University Hospital, Chonnam National University Hospital, Samsung Medical Center, and Emory University. All patients underwent coronary angiography, no more than 90 days prior to their PET study, performed using clinical procedures previously described by our team^34,35. Briefly, coronary flow reserve (CFR) and fractional flow reserve (FFR) were computed from thermodilution and aortic pressure measurements collected at rest and during hyperemic flow using a continuous intravenous infusion of 140 μg/kg/min adenosine, respectively. CFR was calculated by dividing the resting by the sustained hyperemic thermodilution transit time and FFR was determined by dividing the measure distal arterial pressure by the proximal aortic pressure during hyperemia. Finally, index of microcirculatory resistance (IMR) was estimated in all integrated vessels as the product of the distal arterial pressure and mean transit time during hyperemia. All patients had an IMR < 25, considered the cutoff for microvascular disease³⁶.

PET Myocardial Perfusion Protocol and Processing

One day prior to the PET study, patients were instructed to abstain from caffeinated or xanthine-containing foods and beta-blockers. On the day of the PET study, subjects were placed supine and a computed tomography (CT) scan was collected for localization and estimation of attenuation. All subjects underwent a 10 minute dynamic PET collected on a Biograph 40 PET/CT (Siemens Medical Solutions, Erlangen, Germany) immediately following a 370 MBq bolus of [N-13]-ammonia. Approximately, 1 hour later, an additional 10 minute dynamic stress study was collected by first intravenously administering adenosine (140 μg/kg/min) for 3 minutes prior to the administration of [N-13]-ammonia. Adenosine infusion was terminated at 6 minutes total duration. PET list mode data were divided into 21 frames (12 × 10 sec, 6 × 30 sec, 2 × 60 sec, 1 × 180 sec) and reconstructed with a 3-dimensional ordered-subset expectation maximization algorithm (4 iterations, 8 subsets) including all data corrections to a 168 × 168 × 111 matrix with 1.85 × 1.85 x. 3mm voxels. A post-reconstruction filter of 5 mm full-width-at-half-maximum was applied to all frames.

Simulations of pharmacological stress

The extended cardiac-torso (XCAT) digital phantom was employed to simulate an adenosine-stress dynamic time-series with cardiac creep. XCAT uses nonuniform rational B-splines to define the 4D anatomical organ position based on the 3D visible human CT dataset and gated magnetic resonance (MR) images at an arbitrary voxel size³⁷. The default heart base was adjusted to be 1 cm thick at diastole and 1.5 cm thick at systole including the papillary muscle as is consistent with normal values³⁸. The maximum diaphragm motion (max_diaphragm_motion) was adjusted to 5mm displacement as measured from coronary angiograms during free breathing^28,32. Cardiac creep was simulated by dynamically adjusting the cranial-to-caudal heart position (Z_tr) and its anterior-posterior rotation (d_XZ_rotation). Prior work has shown an average maximum cranial-to-caudal translational displacement of the heart following adenosine of 9.9 +/− 5.3 mm¹⁵, therefore we have chosen to simulate a range from 0 mm to 10 mm with a rotation along the anterior-posterior axis ranging from 2 to 6-degrees adjusted linearly over the translational range. Physiological data from adenosine administrations in healthy male subjects shows that the diaphragm’s excursion reaches a maximum at 30–40 sec post adenosine infusion³⁹, therefore all simulations begin with the heart in the maximum cranial-to-caudal position. At completion of the adenosine infusion 3 minutes post [N-13]-ammonia administration, the heart returns to its resting position on a trajectory modeled by a gamma variate over a duration of two minutes starting at the peak cranial-to-caudal position and ending at the XCAT default position. Over the time-course of the simulated motion, the right and left diaphragm scale parameters (rdiaph_liv_scale and ldiaph_scale) were linearly adjusted to correctly position the lung field relative to the heart and liver dome.

Simulation of regional radioactivity concentrations of the myocardium and blood pool were supplied by generating a time-activity curve using a representative patient derived arterial input function and the two tissue compartment model described by Hutchins et al.⁸ with the input parameters K₁ = 1.4 mL/min/g-tissue, k₂ = 0.23/min, k₃ = 0.13/min, total blood volume (TBV) = 0.2 and no metabolite correction. Peripheral organ activities were estimated manually by drawing regions of interest (ROI) on clinical patients and normalizing those ROIs to normally perfused myocardial tissue. Over the simulated time-series, lung, liver and pericardium activity were set to 1/7^th of the myocardial tissue activity and all other peripheral organs (e.g. skin, muscle, esophagus, gall bladder, larynx, stomach, bone, bone marrow, and spleen) were set between 1/15^th and 1/20^th of the myocardial tissue activity. A second simulation was performed with the heart at the rest position (e.g. XCAT default position) with no creep throughout the dynamic series for use as the “ground truth” in determining the registration algorithm accuracy. In both the rest and stress simulations, a binary mask of the left and right ventricle was created for each frame that were used later to assist with computing registration accuracy as described below. Heart and respiratory motion were turned on and adjusted to rates published in patients undergoing pharmacologic stress with adenosine^40–42. Attenuation maps based on 511 keV photon energy were generated for each frame to model attenuation in the reconstruction process prior to adding Poisson noise.

Activity and attenuation mu-map pairs were generated using the same frame sampling as the patient data. Activity maps were convolved with a N-13 range kernel to simulate resolution degradation effects and fore-projected in 2D. Decay correction was removed, attenuation was applied using the corresponding paired mu-map, and Poisson noise added that was consistent with our patient datasets. The fore-projected data were corrected for attenuation using a single attenuation map generated from the last frame in the time-series. Clinically, this is equivalent to acquiring a CT while the patient’s heart is at rest and using that data to correct for attenuation in all frames of the time-series. In the presence of cardiac creep, early frames with cranial-to-caudal motion will have a mismatch in the heart’s position between the simulated emission data and attenuation map resulting in corrupted attenuation correction. This is consistent with our clinical protocol, where the CT is acquired prior to adenosine and [N-13]-ammonia infusion. Simulated data were then reconstructed using an ordered subset expectation maximization of 5 iterations and 8 subsets, corrected for decay, and post-image smoothed with a 5mm Gaussian kernel. The final matrix size was 168 × 168 × 70 pixels with a voxel size of 2.23 × 2.23 × 3.13 mm.

Motion Correction

Dynamic [N-13]-ammonia PET images were corrected for motion using a pairwise technique where each frame of the time-series (moving image) was aligned to a standard reference frame (fixed image) comprised of the last frame in the dynamic series. The algorithm uses the basic scheme described in⁴³ modified for 3-D gradient fields as shown in figure 1, including a multi-resolution step, sampler, interpolator, cost function and optimizer. Gradient fields preserve the spatial information and normalization removes the large changes in vector scale as activity concentrations change over time. The automatic image registration (AIR) coordinate system described by Woods et al.⁴⁴ was used for sample transformation with linear interpolation between the moving and fixed images. To minimize interpolation artifacts, sample points were selected randomly off-grid over the heart on a summation image of the fixed and moving images⁴⁵. Figure 2 demonstrates the local minima artifact that results from on-grid sampling and its suppression when samples are shifted off-grid as demonstrated by other groups^46–48. When comparing the normalized mutual information similarity on the native images to the normalize cosine similarity of 3D normalized gradient fields, the function minimum is more sharply defined with a comparatively larger metric change per step. Optimization was performed with the Powell multi-dimensional directional set method⁴⁹ using the center of mass as the initial condition for the first resolution step and up-sampled optimized parameters on subsequent resolution steps.

Figure 1.

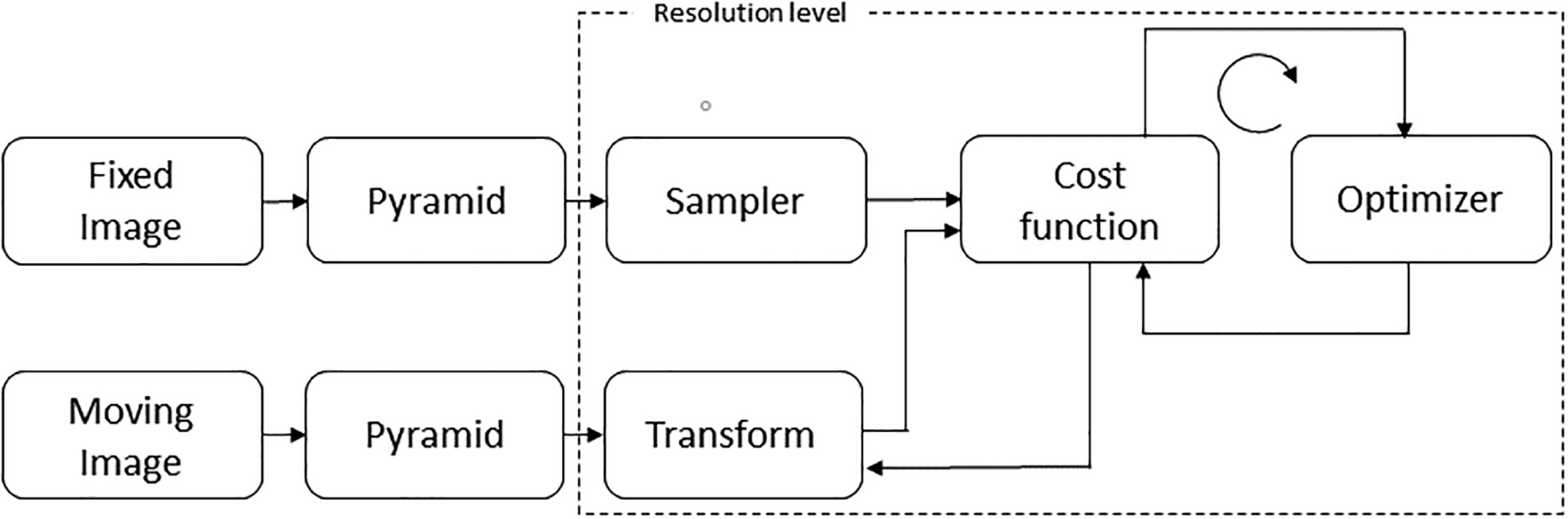
Motion correction scheme adapted from Klein et al.⁴³ showing the processing steps of the algorithm approach. The fixed and moving image inputs are normalized 3D gradient field volumes. The hashed line represents the hierarchical pyramid resolution stage.

Figure 2.

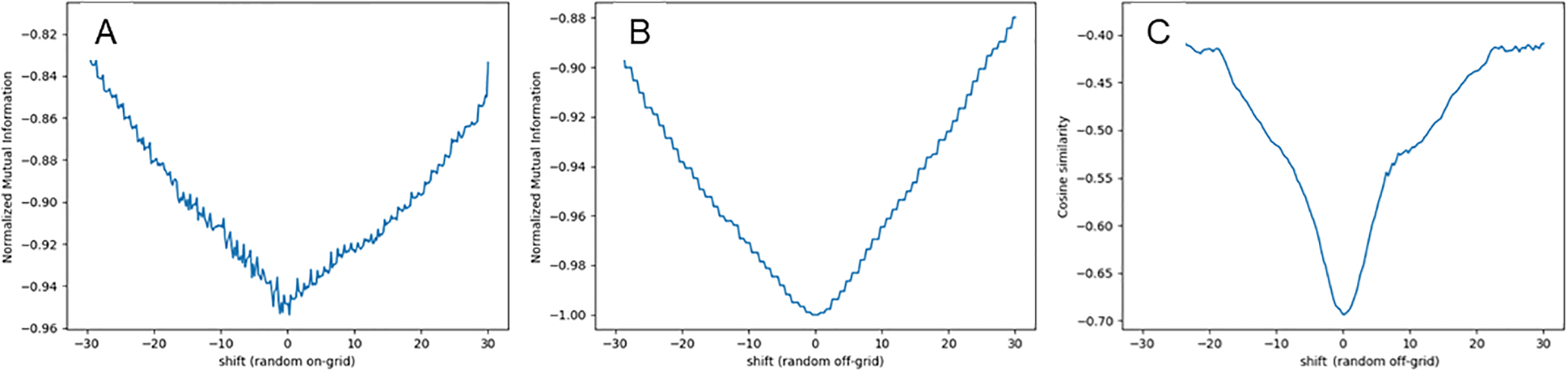
Computed similarity metric values from a 1D x-axis shift (in pixels) of a blood pool image with a perfused tissue image (A) normalized mutual information from a random sample of points on-grid, (B) normalized mutual information from a random sample of points off-grid, and (C) cosine similarity of the 3-D gradient field images from a random sample of points off-grid.

To accommodate moving and fixed image pairs where opposing gradients represent the same boundary, such as comparing a blood pool image to the reference frame, the cost function was weighted by the angle, $a_{v^f,v^m}\left(p\right)$, between the moving and fixed volumes at each point⁵⁰. Briefly, weights favored small angles and those close to Pi as described by Pluim,

$$a_{v^f,v^m}\left(p\right)=\text{arccos}(\frac{\nabla v^f\left(p\right)\cdot \nabla v^m\left(p\right)}{\left|\nabla v^f\left(p\right)\right|\cdot \left|\nabla v^m\left(p\right)\right|})$$ (eqn. 1)

$$w\left(p\right)=\frac{cos\left(2\times a_{v^f,v^m}\left(p\right)\right)+1}{2}$$ (eqn. 2)

Where ∇v^m(p) and ∇v^f(p) denote the gradient of the moving (m) or fixed (f) image at voxel p and |∇v^f(p)| is the magnitude. To further emphasize strong gradients in the moving and fixed images, the weights were multiplied by the minimum of the normalized gradient magnitudes yielding a normalized gradient similarity metric as described by Pluim,

$$G\left(F,M\right)={\sum }_{\left(v^f,v^m\right)\in \left(F,M\right)}w\left(p\right)\times min\left(\left|\nabla v^f\left(p\right)\right|\cdot \left|\nabla v^m\left(p\right)\right|\right)$$ (eqn. 3)

where F and M are the values of the 3D gradient fields in the fixed and moving images, respectively. In both the XCAT and patient datasets, a binary mask was created encompassing the heart which established the boundaries of the sample points for the motion correction algorithm. The peak concentration was found within the masked region and frames with less than 10% of the peak value were determined to contain insufficient counts and ignored by the algorithm.

Geometrical Evaluation

At the completion of the motion correction, masks created as part of the stress simulations were transformed using the final optimized motion correction parameters at full resolution. Accuracy of the motion correction algorithm was assessed objectively by comparing the isosurfaces of the rest mask with the motion corrected stress mask using marching cubes as described in our past work on MR/PET registration^51,52. The purpose of using the masks in place of the simulated data is because the stress images have corrupted attenuation correction based on a resting attenuation scan and this would bias the true left and right ventricle surface isocontours compared to the rest data. Registration errors were determined by computing the Euclidean distances between the motion corrected stress mask and rest mask on a per frame basis at each surface voxel. In addition, we computed the residual differences in the center of mass (COM) and rotational angles (relative to the COM) of the heart after motion correction at each frame with respect to the rest dataset. This analysis was repeated again using 3-dof (translations only) for comparison to the full 6-dof approach.

Patient Data Evaluation

The translational motion trajectories from the final optimized parameters in all patients were summed and displayed as the mean and standard error for rest and stress at each frame. We modeled the rate of change of the cranial-to-caudal motion as function of time starting from the end of adenosine infusion to the end of the scan and compared this to the estimate used in our XCAT simulations. Mean translational and rotational parameters from the patient data for the first 180 sec of imaging while adenosine was on-board were tabulated with their standard deviations. Finally, we qualitatively compared the image quality, specifically the presence of attenuation correction errors, from a representative patient study to a XCAT simulation with similar cardiac creep.

Myocardial blood flow (MBF) was computed before and after motion correction in the patient datasets using the methods described by Hutchins et al. 1990⁸ that includes first-pass extraction fraction correction⁵³. Briefly, images were reoriented along the short axis and regions of interest were defined on a summed image, consisting of the last half of the acquisition duration, using a region spanning 3mm on either side of the center line of the myocardium from apex to base. The ROI for the arterial input function was defined by placing a 10mm spherical ROI at the left ventricle base on the frame with the maximum arterial phase concentration. Time-activity curves were extracted from all three major vascular territories (left main artery (LAD), left circumflex (LCX), right coronary artery (RCA)) by applying the ROI mask to all frames. Estimated parameters (K₁ [mL/min-g] = Flow [mL/min-g] × Extraction, k₂ [1/min] and k₃ [1/min], total blood volume) were iteratively determined using a Powell optimizer to minimize the residual summed squares weighted by frame duration. Metabolite correction of the arterial input function was not performed. For each vessel territory that had a CFR determined by ICA, the non-invasive correlate measure, myocardial flow reserve (MFR), was computed by dividing the MBF at stress by the MBF at rest. Similarly, for each vessel territory that had a FFR determined by ICA the non-invasive correlate, relative flow reserve (RFR), was computed by dividing the MBF at stress in that vessel by the MBF at stress in a reference region. The RFR reference region is the maximum hyperemic MBF from the three vessel territories as described previously^35,54.

Statistical Analysis

All continuous variables are presented with descriptive statistics. Correlations were performed with Pearson’s r and 95% confidence intervals were computed using a z-score transformation. When comparing correlations between the uncorrected and motion corrected data, confidence intervals that did not overlap were considered statistically different. Measures from more than one territory in an individual patient were treated as independent measures in the analysis.

Results

Figure 3 shows a representative patient case and XCAT simulation at select frame times (e.g mid-point times) reformatted in the short-axis for a maximum of 10 mm cardiac creep. Early in the administration, the left ventricle cavity starts caudal relative to the reference frame position and slowly moves in the caudal-to-cranial direction after termination of the adenosine infusion at 180 sec. Just over a minute following termination of the adenosine (e.g. at frame mid-point 255 sec), the heart has largely returned to the reference frame position. In both the patient and XCAT simulation data, artificial areas of hyperintensity, highlighted by the arrows in Figure 3, are most notable in early frames where PET-CT mismatch is greatest due to the occurrence of cardiac creep and use of the resting CT for attenuation correction. In particular, errors in image intensity are most notable along high contrast boundaries including the lung-liver interface and lateral left ventricle wall-lung interface. Later in the time-series, starting at approximately 255 sec, the heart position recovers from the cardiac creep event and the PET-CT mismatch improves resulting in normalization of the hyperintense artifacts.

Figure 3.

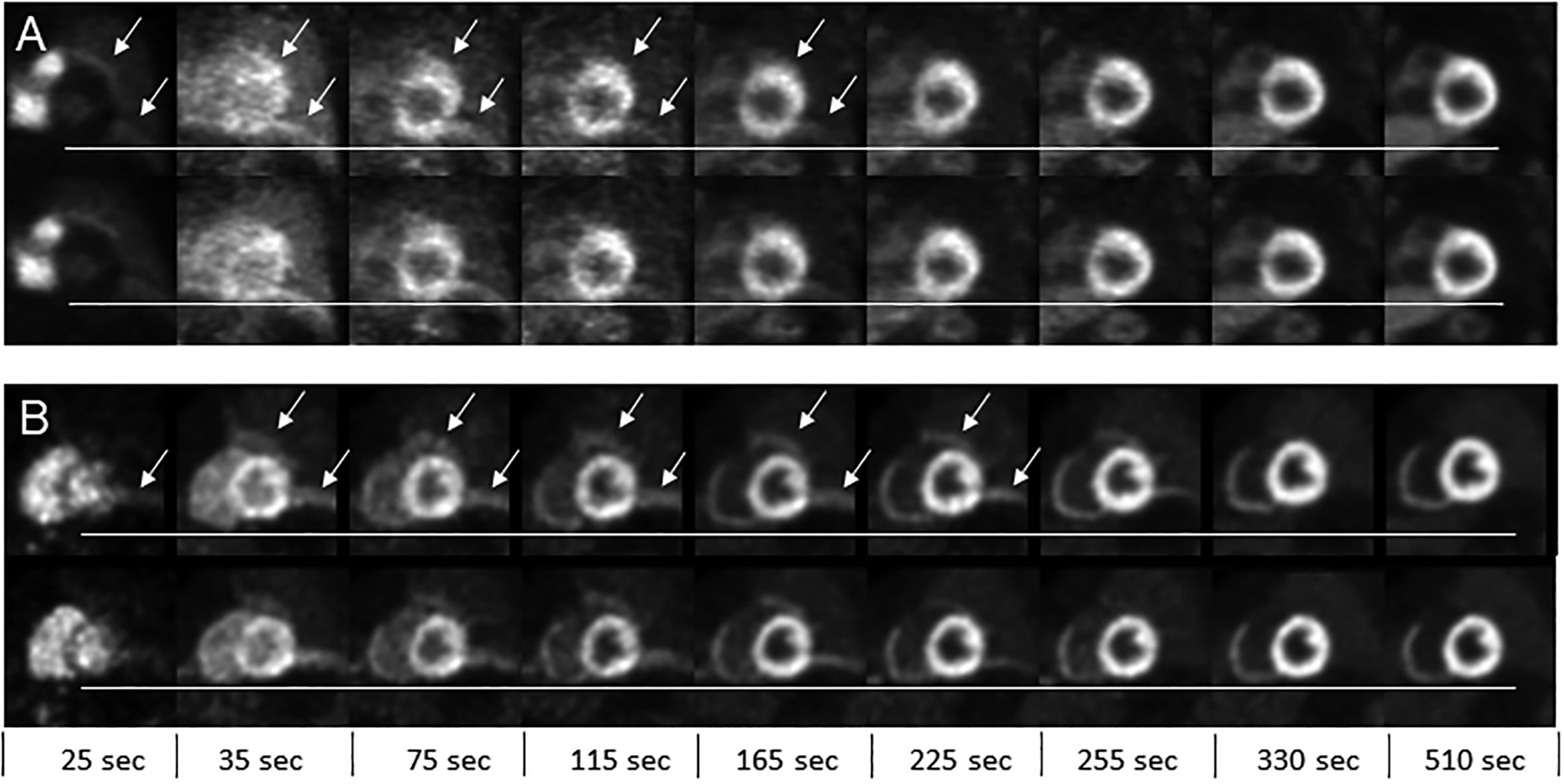
Reformatted short axis slices at select frame times (e.g. mid-point times) shown for (A) a patient study and (B) 10 mm cardiac creep simulation. The top row in each panel are the uncorrected images and bottom row are motion corrected images. The horizontal line served as a visual reference to assess the change in heart position over the selected frames. The arrows show areas of artificially high activity concentration due to mismatch between the PET and CT during attenuation correction. These errors are present on both the uncorrected and motion corrected image but indicated in the top row only for each panel.

Overall, there is more resolution degradation in the representative patient study compared to the XCAT phantom shown in Figure 3 likely due to differences in intra-scan motion and lower count statistics. In addition, the noise texture is higher compared to the XCAT simulations in earlier frames up to 4 min post injection. These differences are likely attributed to intra-scan motion and non-uniformities within peripheral areas of normal uptake (e.g. physiological noise) that were not included in the XCAT simulation. Furthermore, the representative patient in Figure 3 has higher relative uptake in their liver and stomach relative to their myocardium in comparison to the XCAT simulations, which adds to the difference in noise texture. Overall, there was considerable variability in liver and bowel uptake within the patient scans whereas the XCAT peripheral tissues had the same time-varying concentration for all simulations.

Geometrical Evaluation

To objectively compare the accuracy of our results with “ground truth”, we compared isosurfaces between the rest and motion corrected stress masks of the XCAT simulation data. The simulated rest data contain no motion and are in the same position as the reference image (fixed image) used to motion correct the stress simulations. Euclidean distances between the extracted isosurfaces are reported as density histograms with centered 0.5 mm bins for six simulations of cardiac creep in figure 4. Agreement was found to be excellent (< 1mm) in late frames greater than 135 sec with a gradual broadening of the density histogram (< 3mm) between 75 and 135sec, and excellent agreement again between 15 and 25 sec (< 2mm). Agreement at 35 sec post [N-13]-ammonia administration was poorest, but less than 4 mm for all conditions, and represents the time point where blood and tissue contrast are of similar magnitude. We hypothesize that fewer and smaller gradient edges were available to sample at the 35 sec time point to compute the similarity metric thus contributing to this increased error when compared to other frames. Activity concentration within the first frame (e.g. 5 sec) was below the 10% threshold for inclusion in the algorithm and are shown in figure 4 for completeness. Residuals of the COM distances and rotational angles (about the COM) for all registered frames and creep simulations were grouped and density histograms created with centered 0.5 mm and 0.5 degree bins, respectively. Figure 5 shows that > 90% of the COM and rotation residuals are within a 2mm and 2-degrees range, respectively. A small bias was observed of approximately −0.5 mm in the Anterior/Posterior residuals and approximately −1.0 degree for rotations along the Anterior/Posterior axis. We hypothesize that these observed biases are clinically insignificant for the clinical and simulated resolutions used in this work. Finally, when comparing results from 3-dof to 6-dof, we observed a broadening in the density distributions at all frames, most noticeably in early frames where the simulated rotations were largest (see Figure S-1, Supplementary Data). Similarly, the COM measures for 3-dof were also broader when compared to 6-dof (see Figure S-2, Supplementary Data). These findings were expected given that a known rotation was introduced in the XCAT model but, importantly, this demonstrates that the algorithm is capable of optimizing rotational misregistration. Secondly, these findings showed that excluding rotational degrees of freedom from dynamic cardiac datasets where rotations are observed may result in suboptimal motion correction.

Figure 4.

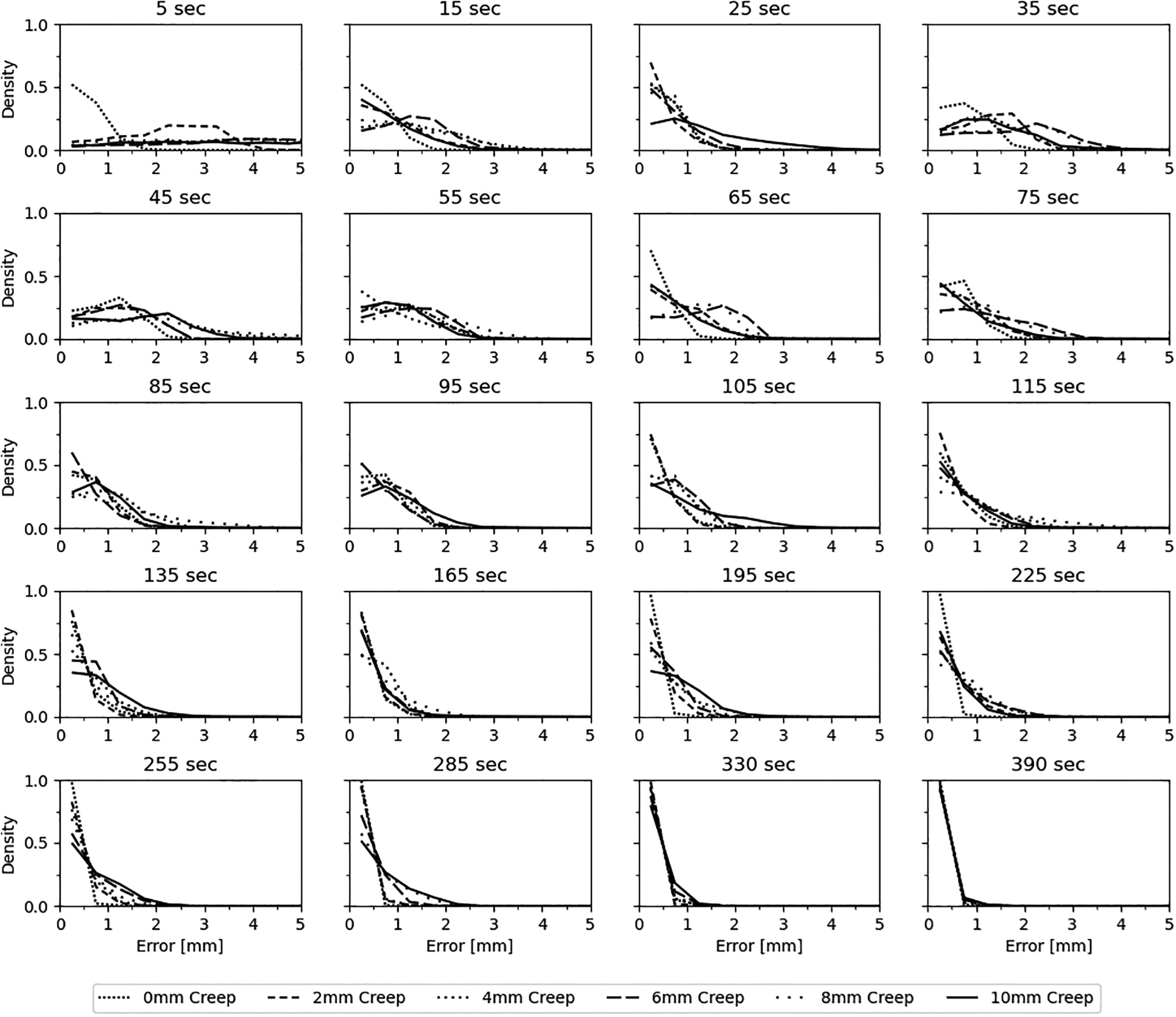
Density plots of the Euclidean distance between the rest “ground truth” and motion corrected stress masks of the XCAT simulations. Bins are 0.5 mm and centered on the x-axis. Times displayed are frame mid-point times post [N-13]-ammonia administration.

Figure 5.

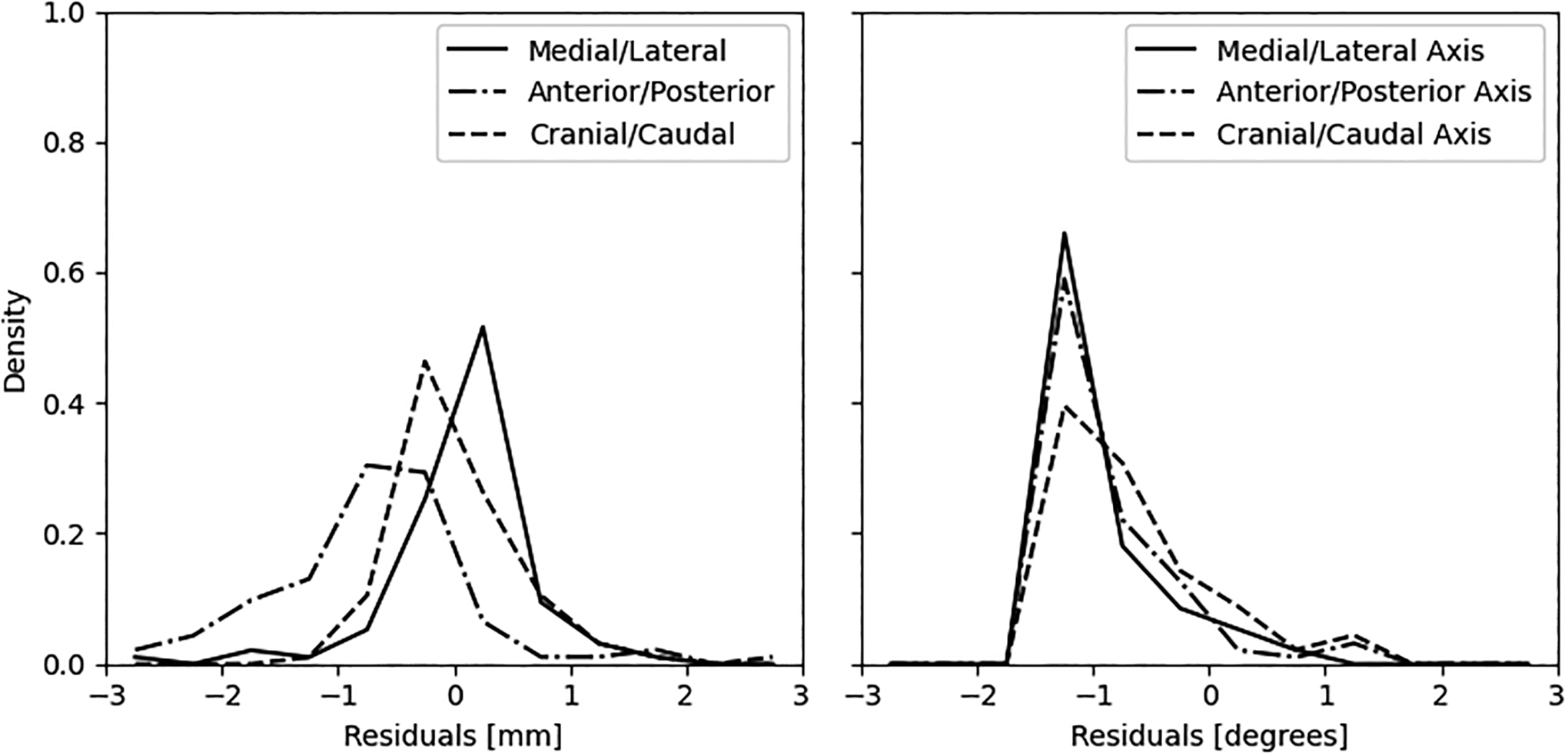
Density plots of the (A) residual center of mass distances and (B) residual rotations about the center of mass, between the rest “ground truth” and motion corrected stress masks of the XCAT simulations. Bins are 0.5 mm and 0.5 degrees centered on the x-axis, respectively.

Patient Studies

Figure 6 shows the mean and standard error of the translational distances computed per frame for all patients. The first frame in all patient datasets did not meet the minimum count threshold to be included in the algorithm, therefore these points were not plotted in figure 6. As we expected from literature findings with adenosine pharmacologic stress, the dynamic PET acquisition starts with the heart caudal relative to its resting position. At approximately 165 to 195 sec post injection, the heart begins its return to its resting position which is consistent with the end of the adenosine infusion at 180sec. We examined the associations between mean Tz per frame across all subjects and each of the rotation parameters and found a significant correlation of −0.81 (p < 0.0001) for Tz vs. Rx at stress and 0.80 (p < 0.0001) for Tz vs. Rz at stress. The return of the heart from the time of its maximum cranial-to-caudal extent (45 sec post-injection at rest, 195 sec post-injection at stress) to its final position at 510 sec post-injection was approximate 1.1 %/sec at rest and 1.8%/sec at stress. When examining the first 180sec of [N-13]-ammonia imaging at stress, the overall mean displacement was −7.0 ± 7.1 mm in the cranial-to-caudal direction. Of the 43 patients, a total of 37 vessels had measures of CFR and 89 vessels has measures of FFR. Figure 7 shown the correlation of CFR vs MFR and FFR vs RFR for the uncorrected and motion corrected datasets. Although the correlations improved with motion correction, these changes were not statistically different since the confidence intervals overlapped.

Figure 6.

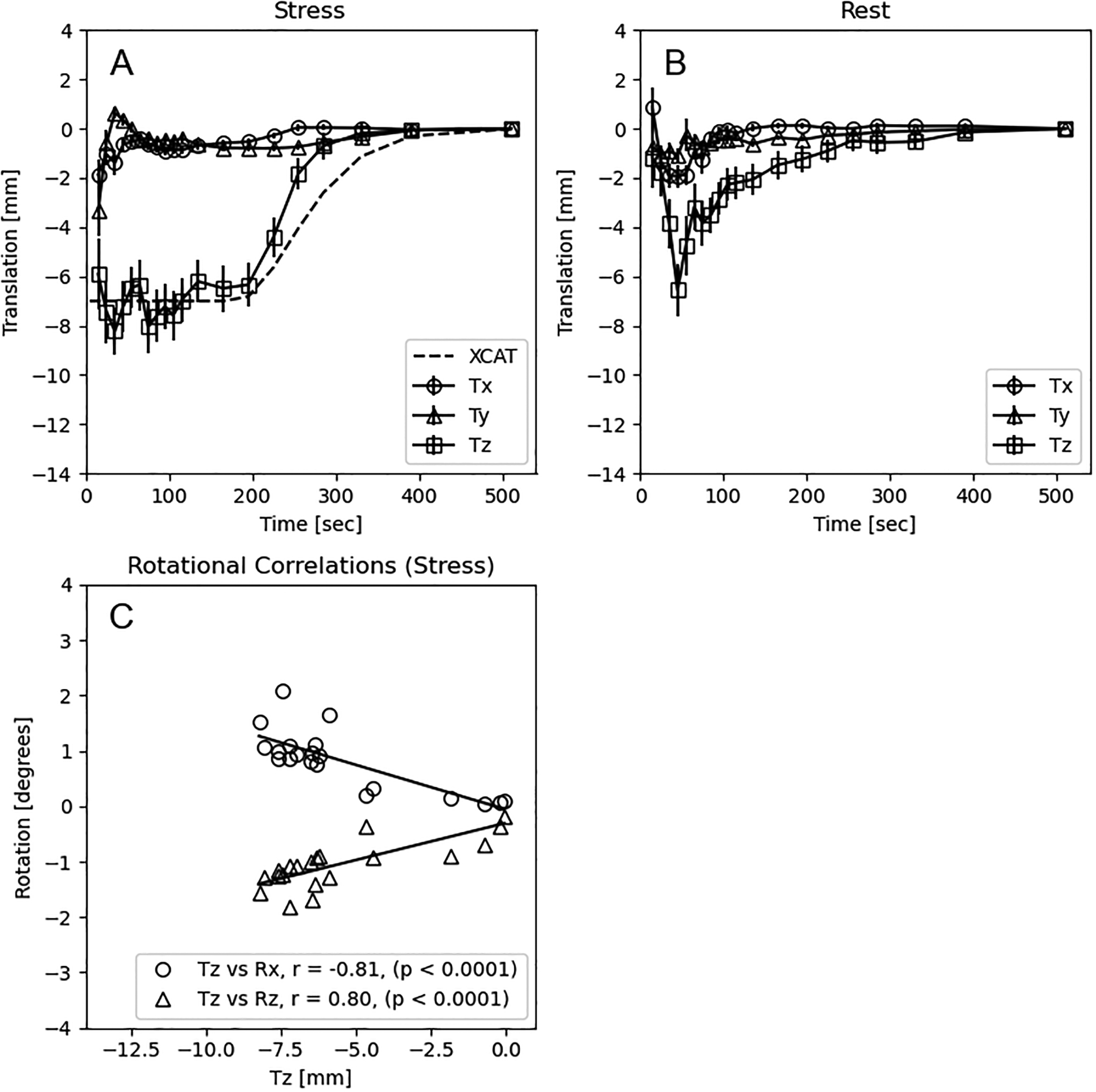
Mean (± standard error) translations in the x (Tx: (+)anterior/posterior), y (Ty: (+)medial/lateral), and z (Tz: (+)cranial/caudal) directions as computed from the transaxial images in 43 patients at (A) stress and (B) rest. (C) Rotational correlations between mean Tz, Rx (anterior/(+)posterior), and Rz((+)cranial/caudal) for each dynamic frame. P-values are uncorrected for multiple comparisons. The dashed line in (A) is the modeled motion for an 8mm cardiac creep in the XCAT simulation.

Figure 7.

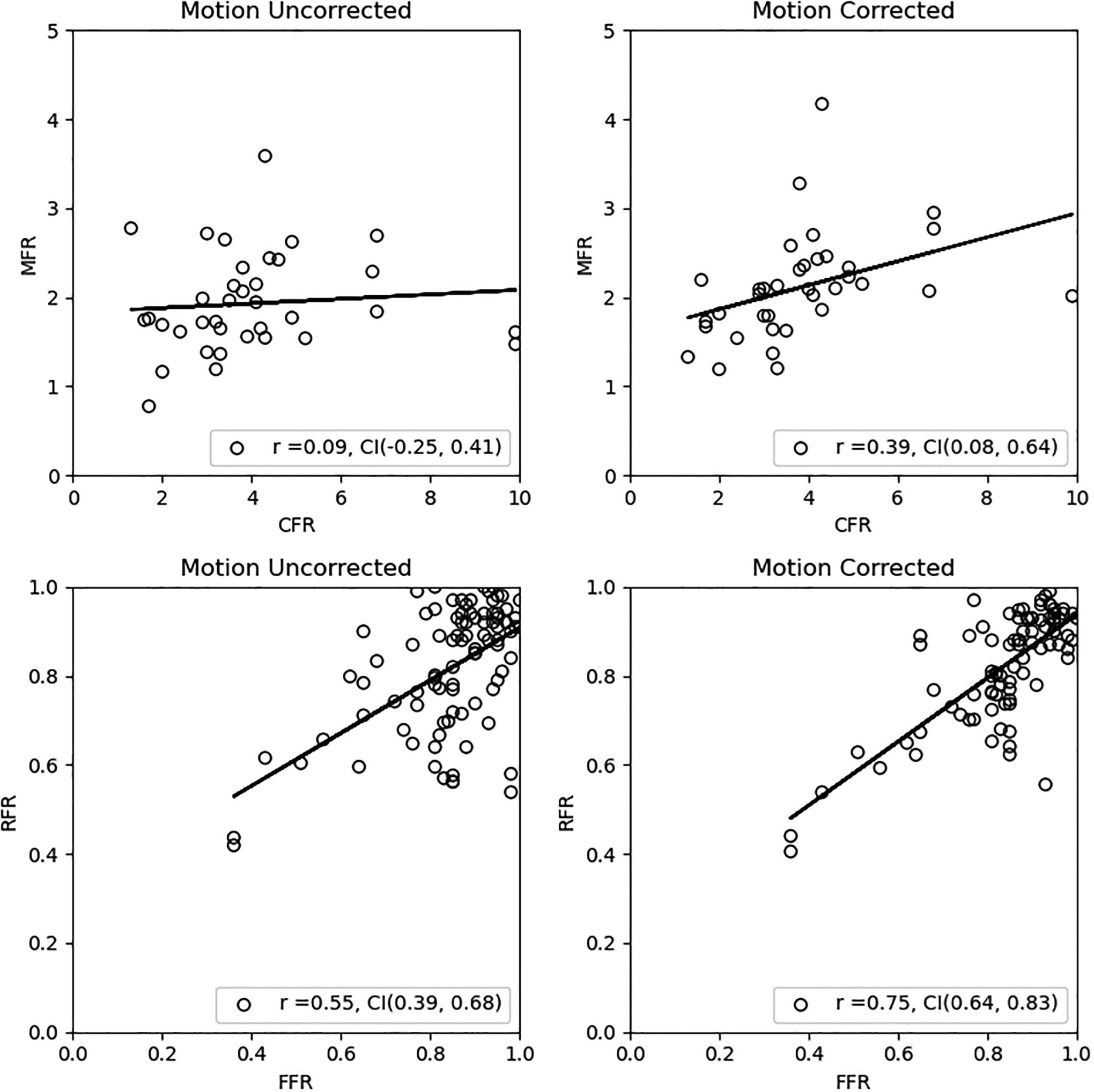
Correlations and 95% confidence intervals of CFR vs MFR and FFR vs RFR before and after motion correction. Confidence intervals are 95% based on transformed t-statistics of the Pearson correlation.

Discussion

We report on the development of a gradient-based motion correction algorithm for dynamic cardiac PET that employs 6 degrees-of-freedom and a weighted cost function to account for opposing gradients between the blood pool and perfused tissue phases. We employed a dynamic phantom model of cardiac creep utilizing XCAT that provides a realistic “ground truth” for evaluation of the algorithm’s accuracy. The XCAT simulation parameters were based on literature reports describing the respiratory and cardiac trajectories following administration of the adenosine pharmacologic. With regard to attenuation correction, a common practice is to acquire CT data prior to pharmacologic administration or following completion of the PET acquisition. In the former situation, the heart is in the rest position and in the latter the effects of adenosine have largely subsided and the heart returns to a rest position which may be different than that prior to the pharmacologic administration^14,17. To simulate this clinical observation in XCAT, the CT used for attenuation correction was obtained from the last frame and applied to all previous frames in the dynamic time-series. This simulates the corrupted attenuation correction in the early uptake frames that is commonly observed in clinical protocols at stress and demonstrated in figure 3. Lastly, we introduced a modest rotation of the heart along the anterior-posterior axis to replicate rotation events we have observed clinically and described by other groups^14,15,20 but have not been well characterized in the nuclear medicine literature.

Following the end of adenosine infusion in our patient studies, the heart returned to its resting position along the cranial-to-caudal trajectory quicker than modeled in our simulations and observed by other groups^14,15. In addition, we show for the first time a strong correlation between the cranial-to-caudal motion and rotations along the anterior\posterior axis and cranial\caudal axis at stress, although this effect was small. Interestingly, cranial-to-caudal motion was observed during rest, which was an unexpected finding but consistent with findings from other groups^15,30.

Prior work examining dynamic cardiac PET motion correction has employed similarity metrics based on correlation of image intensity and modification of the similarity metric to address flipping of the correlation sign when comparing blood pool to perfused tissue images. Turkington et al.²⁰ included five individualized segmented templates that varied based on the activity distribution in the time-series to ensure the correlation metric remained positive during optimization. Their work was evaluated on a smaller number of subjects and did not address rotational degrees of freedom but noted that their inclusion would be desired. Woo et al.³¹ included both a local similarity bounded to the left ventricle and global similarity that included the entire field-of-view while utilizing a full rigid-body (6-degrees of freedom) model. The local similarity was weighted to positive correlations and, when approaching zero, the global similarity metric dominated. Both Turkington et al. and Woo et al. lacked a ground truth for evaluating algorithm accuracy but reported the largest motion correction events occurring in the first few frames of the dynamic time-series of their patient populations, which is consistent with our findings.

Motion correction based on gradient fields was introduced initially for the brain⁵⁰ and later adapted for dynamic cardiac studies³⁰. An advantage of using gradient fields is that edges between different time points in the dynamic time-series are concordant and opposing gradient directions can be addressed by weighting or computing the magnitude. Lee et al. employed weights to address opposing gradients by iteratively segmenting the right and left ventricle cavities from myocardial tissue where the sign of their similarity metric was changed based on the frame position in the time-series. Their work addressed translations only and used manual registration by expert readers to establish ground truth finding that the greatest motion events occurred in the initial uptake period, which is consistent with the results in this work. Important advancements of our approach compared to that reported by Lee et al., are the addition of rotational degrees of freedom and weighting of the 3-D gradient field angles in the similarity metric that alleviates the need to segment the heart into ventricular and tissue regions. In addition, we have incorporated a multi-resolution step and off-grid sampling, which are well-documented features that improve registration robustness^43,45,55,56.

The use of XCAT as a ground truth in dynamic PET has been reported previously in the context of assessing gross body motion between the PET and CT acquisitions²². Our comprehensive simulation includes PET-CT mismatch observed in clinical protocols and physical factors from imaging to specifically address cardiac drift, which is the most common motion event observed in dynamic cardiac imaging and affects up to half of all studies^14,17. The ability to incorporate realistic physiological measures with XCAT provides an objective alternative to truth established by expert observers, which can be subject to operator bias^22,57. In this work, poorer performance of the algorithm was observed in the earlier frames when the blood pool and myocardial tissue had similar intensity and we hypothesize that may be due to fewer gradient surfaces available for computation of the similarity metric. In these cases, it may be informative to add additional similarity measures to improve the reliability at these points in the time-series, such as mutual information⁵⁰.

The literature is mixed on the overall mean translational extent of cardiac creep following pharmacological stress but the severity of motion does appear to depend on choice of pharmacologic stress agent¹⁴. Vleeming et al., showed that the maximum cranial-to-caudal displacement was significantly greater with adenosine at 9.9 mm compared to regadenoson at 7.1 mm¹⁵ while other groups reported more modest motion events of less than 2 mm in a patient population using adenosine³¹ and less than 5mm in a patient population using regadenoson³⁰. Our patient findings show a mean cranial-to-caudal translation of 7 mm which is larger than some reports^20,30,31 but in good agreement with others^14,15,17. This discrepancy could be explained by the recent observation that cardiac creep events are more frequent than, and distinct from, gross patient motion. Past work addressing motion based on a similarity metric computed over the entire field-of-view would have likely underestimated cardiac creep events. The importance of addressing motion is well-accepted as these events can alter estimates of absolute myocardial blood flow as well as introduce additional variance^14,22–25.

FFR, and to lesser extent CFR, are important clinical measures in guiding revascularization, and our group is developing tools to measure imaging analogues, such as RFR, to localize flow abnormalities along the vessel^33,58. Overall, we show lower correlations between CFR vs. MFR compared to FFR vs. RFR, which is consistent with published reports³⁵. Although not statistically significant, we show a trend of improved correlation between these invasive and non-invasive measures after motion correction.

With the advent of deep learning techniques, there are opportunities to develop motion correction algorithms that transform images within the context of convolutional neuro networks (CNN)^59,60, more recently applied to dynamic cardiac PET⁶¹. In the latter work, the approach is supervised thus relying on expert readers to determine the 3-dof transform per time point that serves as the learning target, which has recently been shown to have higher variability than using unsupervised automated algorithms^22,57. It may be optimal in these cases to use a traditional unsupervised motion correction algorithm to determine the input to target transform for training the CNN, then run the trained model on optimized computing hardware (e.g. GPUs) to take advantage of the increased speeds relative to traditional approaches.

Limitations exist with our approach, specifically all phantom simulations used a normal heart condition with the same input contrast, frame sampling and degrading physical factors. Secondly, it is difficult to simulate the natural physiological noise present in PET such as local variations in activity distributions within cardiac and peripheral organ compartments. Local variations in activity can be large with [N-13]-ammonia such as high uptake in lung and liver, which may contribute erroneous gradient information if not carefully masked during the sample selection. Image based registration approaches poorly address some motion events that can be severe, such as intra-frame motion occurring over long frame durations, and these may be better solved by data-driven estimates of motion trajectories that can be incorporated into the reconstruction process^62,63. Because there is no ground for in vivo MBF measurements, we examined the correlation of CFR and FFR with their non-invasive correlates to evaluate improvements in accuracy between uncorrected and motion corrected cardiac dynamic PET. Higher correlation does not strictly imply improved agreement, as the Pearson contains a bias component compared to true measures of agreements such as the concordance correlation coefficient⁶⁴. Although the blood flow protocols for PET and ICA were designed to reproduce the physiological state between modalities by delivering the same adenosine dose intravenously, some variability is expected due to differences in physiological states since the measurements were not done simultaneously. Finally, the study was likely underpowered to detect significant differences between our invasive and non-invasive measures in the patient population.

Conclusions

This work presents a robust rigid-body motion correction approach based on the application of 3D normalized gradient fields for dynamic cardiac PET. We have demonstrated excellent accuracy and robustness of the algorithm using a comprehensive XCAT simulation that incorporates known physiological motions of the heart within the thoracic cavity during adenosine pharmacologic stress. Our approach does not require segmentation or weighting of tissue regions in the cost function and performs well in the presence of attenuation artifacts commonly present from PET-CT mismatch.