A Tract-Specific Framework for White Matter Morphometry Combining Macroscopic and Microscopic Tract Features

Abstract

Diffusion tensor imaging plays a key role in our understanding of white matter (WM) both in normal populations and in populations with brain disorders. Existing techniques focus primarily on using diffusivity-based quantities derived from diffusion tensor as surrogate measures of microstructural tissue properties of WM. In this paper, we describe a novel tract-specific framework that enables the examination of WM morphometry at both the macroscopic and microscopic scales. The framework leverages the skeleton-based modeling of sheet-like WM fasciculi using the continuous medial representation, which gives a natural definition of thickness and supports its comparison across subjects. The thickness measure provides a macroscopic characterization of WM fasciculi that complements existing analysis of microstructural features. The utility of the framework is demonstrated in quantifying WM atrophy in Amyotrophic Lateral Sclerosis, a severe neurodegenerative disease of motor neurons. We show that, compared to using microscopic features alone, combining the macroscopic and microscopic features gives a more holistic characterization of the disease.

1. Introduction

Diffusion tensor imaging (DTI) has become an indispensable tool for studying white matter (WM) both in normal populations and in populations with brain disorders because of its unparalleled ability to depict in vivo the intricate architecture of WM [1]. Many techniques have been developed recently for localizing WM differences across populations using DTI. The tract-based spatial statistics (TBSS) developed by Smith et al. [2] signficantly advanced the traditional whole-brain voxel-based WM analysis by harnessing the power of statistics on the skeleton structure of WM. However, the whole-brain approach of the TBSS fundamentally limits its anatomical specificity. Recognizing the importance of tract-specific analysis, many groups have recently developed innovative techniques for analyzing individual WM tracts with either tubular geometry [3,4,5] or sheet-like appearance [6].

This recent explosion of advances in tract-specific analysis is in large part made possible by our success in robustly segmenting individual WM tracts using diffusion data. The availability of tract segmentations presents a new opportunity for assessing macroscopic properties of a tract in addition to the standard quantification of microscopic features derived from diffusion data, such as, fractional anisotropy (FA). In this paper, we propose a tract-specific framework that, to the best of our knowledge, enables for the first time the joint analysis of tract morphometry in both macroscopic and microscopic scales. In particular, we leverage the skeleton-based modeling of sheet-like tracts proposed by Yushekvich et al. [6] to derive tract thickness maps. We show how the thickness information can be combined with microstructural features, such as FA, to enhance our understanding changes in WM morphometry. The potential of the proposed framework was illustrated in an application to quantify WM atrophy in Amyotrophic Lateral Sclerosis (ALS), a severe neurodegenerative disease.

The rest of the paper is organized as follows: Sec. 2 describes the proposed framework in detail and discusses its application in ALS. Sec. 3 reports the results from the ALS study that demonstrates the strength of combining information from different scales. Future works are discussed in Sec. 4.

2. Methods

The proposed framework has three components: (1) WM parcellation that segments the tracts of interest in all the study subjects; (2) skeleton surface-based tract modeling and matching that establishes spatial correspondence of the tracts across the study cohort and enables thickness measurement on the tracts; (3) statistical analysis that combines both thickness and standard diffusion measurement. The following discusses each component in detail.

2.1. White Matter Parcellation

We adopt the atlas-based segmentation strategy that has been successfully applied in the literature [7, 6, 3]. It involves WM parcellation in a population-averaged DTI template using fiber tractography. The parcellation in the template is then mapped to individual subjects via spatial correspondence between the template and the subjects established with image registration. If appropriate, an existing template, such as the ICBM-DTI-81 template [8], can be used. Here we choose the more general approach of deriving a population-specific template from the subject data, which simultaneously establishes spatial correspondence between the template and the subjects as part of the construction.

Construction of the Population-Averaged DTI Template.

We choose the template construction method described in [9]. The method has been tailored for DT-MR data by employing a high-dimensional tensor-based image registration algorithm shown to improve upon scalar-based alternatives. Briefly, the initial average image is computed as a log-Euclidean mean [10] of the input DT-MR images. The average is then iteratively refined by repeating the following procedure: register the subject images to the current average, then compute a refined average for the next iteration as the mean of the normalized images. This procedure is repeated until the average image converges.

Tract Parcellation in the Template.

We follow the approach described in [6] and parcellate the template into individual WM tracts using an established fiber tracking protocol [11]. The validity of such an approach, WM segmentation by tracking in a DTI template like ours, has recently been demonstrated by Lawes et al. [7] in a comparison to classic postmortem dissection. Our framework focuses on the tracts that have a major portion that is sheet-like. As identified in [6], six major tracts fit into this category: corpus callosum (CC), corticospinal tracts (CST), inferior fronto-occipital tracts (IFO), inferior longitudinal tracts (ILF), superior longitudinal tracts (SLF), and uncinates (UNC). White matter tracts that are more appropriately represented by tubular models have been extensively studied in the literature [3, 4, 5] and are not considered here. After fiber tractography, binary 3D segmentations of individual tracts are generated by labeling voxels in the template through which at least one fiber passes.

Tract Parcellation in the Subjects.

The tracts of interest in each subject are parcellated by mapping the binary segmentations delineated in the template to the subject space using the spatial correspondence between the template and the subject determined above. In practice, this involves, for each subject, first inverting the transformation that aligns the subject to the template and then using the resulting inverse transformation to warp the template space segmenation into the subject space. The transformations derived from [9] have well-defined inverse since they are constrained to be diffeomorphic with strictly positive Jacobian determinant everywhere in the image domain.

2.2. Skeleton Surface-Based Tract Modeling and Matching

Skeleton surfaces have been shown to be a natural way of modeling sheet-like WM tracts using either direct skeletonization [2] or deformable modeling with the continous medial representation (cm-rep) [6]. In our framework, we choose to adopt the cm-rep approach because its ability to enforce a consistent skeleton topology – a 2D surface patch in our case – across subjects, which the direct skeletonization approach can not. The consistency in skeleton topology is essential for establishing spatial correspondence across subjects.

The cm-reps are models that describe the skeleton and the boundary of a geometrical object as parametric digital surfaces with predefined topology. The models describe the geometrical relationship between the skeleton and the boundary by defining a synthetic skeleton consisting of a parametric medial surface represented as a dense triangular surface mesh and a radial field defined over the surface. The radial field specifies, for each vertex on the mesh, the radius of a sphere centered at the vertex. The boundary of the object represented by the cm-rep is uniquely determined and can be computed from the synthetic skeleton via inverse skeletonization [12].

In our framework, we use the standard deformable fitting algorithm described in [12] to fit the cm-reps to the tract segmentations in the individual subjects and leverage two key feature of the cm-reps. First, the model enables a natural definition of thickness. The sphere associated with a point on the skeleton is tangent to the boundary surface at a pair of points (which may coincide at edges of the skeleton). The thickness at the point can then be estimated as the diameter of the sphere, which is two times the radial field [12]. Second, it establishes spatial correspondence across the subjects via the shape-based coordinate system that parametrizes the entire interior of the model. Because the line segments connecting a point on the skeleton to the points of tangency of the associated sphere, known as the “spokes”, are orthogonal to the boundary and no two spokes intersect inside the model, it allows the definition of a coordinate system for interior of the object based entirely on the shape of the object, where two of the coordinate values parametrize the skeleton surface and the third gives the position of a point on the spokes.

2.3. Statistical Analysis of Thickness and Diffusion Features

The deformable modeling of subject-space tract segmentations using the cm-rep approach produces a parametric skeleton surface with an associated thickness map for each tract of each subject. Using the dimensionality reduction approach described in [2,6], diffusion features of interest can be similarly projected onto the same skeleton surface of each subject. We adopt the strategy originally proposed in [2] to minimize the adverse effect of errors in image alignment. Specifically, for each point on the surface, we search along its two spokes, find the location with the highest FA, then assign its diffusion features to the point.

These maps of thickness and diffusion properties computed for each subject in the same shape-based coordinate frame enable a combined analysis of both macroscopic and microscopic features. In our framework, we apply univariate statistical mapping on thickness and diffusion features separately to gain complementary tract information at different scales. A nonparametric statistical mapping of group differences is implemented as described in [6]. Briefly, we compute a two-sample t-test at each point on the skeleton surface of a tract and correct for multiple comparison with the standard permutation-based non-parametric cluster analysis introduced by Nichols et al. [13].

In addition, we utilize a novel multivariate analysis [14] to directly exploit the relationship between thickness and diffusion properties. Specifically, for each subject, we build a joint probability density function (pdf) of thickness and diffusion properties which captures the interdependencies of thickness and diffusion features as provided solely by the data. The pdf of a subject is estimated by determining the fraction of points on its skeleton surface with a particular value of thickness and diffusion properties (See Fig. 2 for an example). We use this pdf as the multivariate high-dimensional descriptor of the associated WM tract to summarize its macroscopic and microscopic properties jointly. Statistical testing for group differeces with these high-dimensional descriptors is then done via the same nonparametric test as the univariate statistical mappings above, except here the test is done in the functional domain of the pdf rather than the spatial domain of the skeleton surface.

Fig. 2.

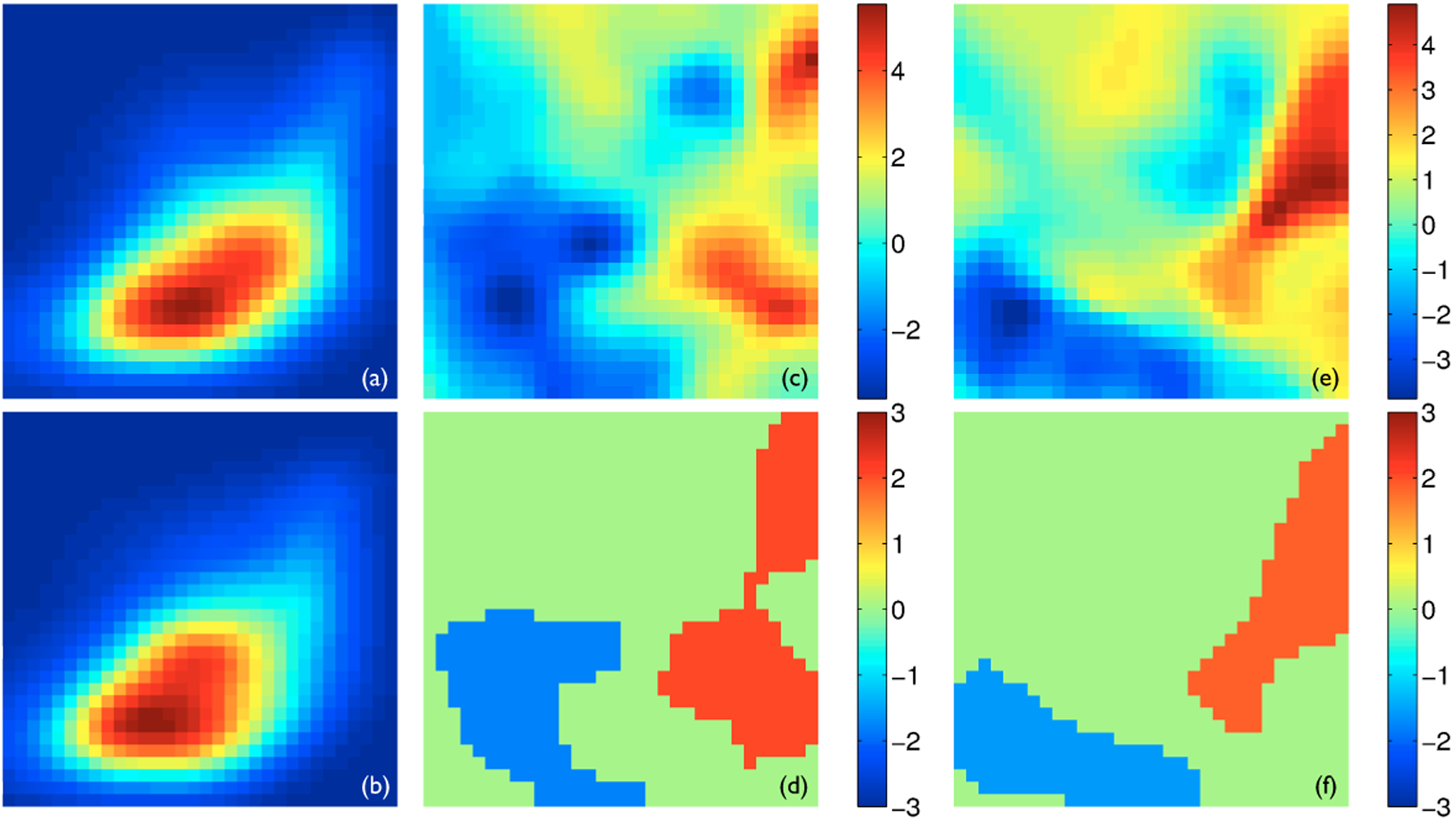
The joint analysis of thickness and FA. In all panels, FA is plotted along the horizontal axis and varies from 0.1 to 0.7, while thickness is plotted along the vertical axis and varies from 0 to 8 mm. Both values are plotted in linear scale. Panels (a) and (b) show the joint pdfs of the left CST averaged for all the healthy controls and all the ALS patients, respectively, with the hot color corresponding to higher density. Panels (c) and (e) show the t-statistics maps of comparing the joint pdfs of the healthy controls to those of the ALS patients for the left and right CSTs, respectively. Panels (d) and (f) show the significant clusters with z-scores determined via permutation-based non-parametric testing for the left and right CSTs, respectively. The red clusters corresponds to larger density in the healthy controls and the blue clusters higher density in the ALS patients.

2.4. Application: WM Atrophy in ALS

We demonstrate the proposed analysis in an application to identify WM changes in ALS. The present study consisted of 8 ALS patients and 8 healthy controls. Diffusion tensor imaging was performed on a 3T Siemens scanner with a 12-direction diffusion sequence (b = 1000 s/mm²). For each subject, 40 axial slices with in-plane resolution of 1.72×1.72 mm and thickness of 3.0 mm were acquired. Because of the existing hypothesis that ALS strongly affects the motor pathway, only the left and right CSTs were included in the analysis. Two univariate statistical mappings on thickness and FA were first performed, followed by the multivariate analysis using the joint pdfs of thickness and FA. The clusters with FWE-corrected p-value < 0.05 were deemed significant in all analyses.

3. Results

The results of the two univariate statistical mappings are shown in Fig. 1. Two significant clusters of reduced thickness in ALS compared to healthy controls were found with one on each CST. The cluster on the left CST corresponds to the internal capsule and the one on the right CST maps to Broadmann area (BA) 6, the premotor cortex and supplementary motor cortex. One significant cluster of reduced FA in ALS was found on the left CST, which maps to BA 1, 2 & 3, the primary somatosensory cortex, BA 4, the primary motor cortex. Evidently, the macroscopic changes highlighted by the thickness analysis provides a more complete picture of WM atrophy caused by ALS than the microscopic changes identified by the FA analysis alone.

Fig. 1.

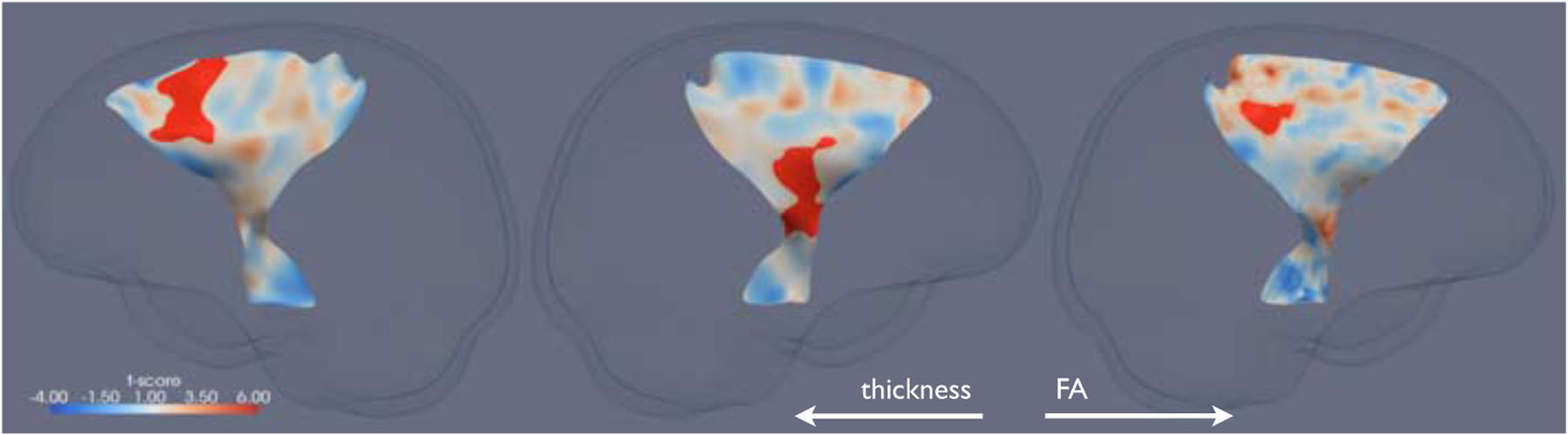
The significant clusters of reduced thickness and FA in ALS compared to healthy controls (in red) overlaid on the corresponding t-statistics maps on the skeleton surfaces of the CSTs. From left to right: the thickness cluster and t-statistics map for the right CST, the thickness cluster and t-statistics map for the left CST, the FA cluster and t-statistics map for the left CST. Note that image left corresponds to physical right.

The results of the multivariate analysis using the joint pdfs of thickness and FA are shown in Fig. 2. The appearance of the joint pdfs is illustrated in Panels (a) and (b) using the joint pdfs of the left CSTs averaged for the healthy controls and the ALS patients, respectively. The two visibly different pdfs indicate that the healthy controls have more regions of large FA and thickness while the ALS have more areas of low FA and thickness. A similar pattern is observed for the right CST (not shown). These observations are supported by subsequent non-parametric statistical testing. Panels (c) and (e) show the t-statistics maps of comparing the joint pdfs of the healthy controls to those of the ALS patients. The significant clusters, determined by permutation-based multiple comparison correction, were shown in Panel (d) for the left CST and (f) for the right CST. The red clusters represent the areas of higher density in the healthy controls – high FA, while the blue clusters pinpoint the regions of higher density in the ALS patients – low FA and low thickness.

The significant clusters from the joint analysis can be better understood by mapping them back into the spatial domain, i.e., onto the skeleton surfaces of the CSTs of the individual subjects. Specifically, for each of the four clusters and for each subject group, we determined a cluster-membership probability map of the corresponding CST skeleton surface. Each of these maps were computed by finding, at each point on the corresponding skeleton surface, the probability of the location with their FA and thickness values falling within the corresponding cluster for the corresponding subject group. For instance, for some point V on the left CST, if 4 out of 8 healthy controls have their FA and thickness values at V fall within the red cluster on the left CST, then the probability map of the healthy controls for the red cluster on the left CST will have a value of 0.5 at V.

The four probability maps corresponding to the two clusters on the left CST are shown in Fig. 3. One striking observation is that, for both the healthy controls and the ALS patients, the red cluster is mapped to almost identical anatomical areas, including, from interior to superior, the cerebral peduncle, the internal capsule, and the primary motor and somatosensory areas (BA 1–4). For these areas, the cluster-membership probability is significantly less in ALS compared to the healthy controls. Because the red cluster corresponds to high FA, this finding indicates that some of the high FA normally found in these areas in the healthy controls are compromised and replaced by lower FA in ALS. Similarly, the blue cluster is mapped to near identical anatomical areas, including the premotor area (BA 6) and the peripheral of the structures. For these areas, the cluster-membership probability is significantly higher in ALS compared to the healthy controls. Since the blue cluster corresponds to low FA and thickness, this finding suggests that some of the normal FA and thickness found in these areas in the healthy controls are compromised and replaced by lower FA and thickness. Similar observations can be made with the probability maps on the right CST (not shown). Compared to the results of the univariate results, these results appear to give a more complete depiction of the extent of WM atrophy in this severe neurodegenerative disease.

Fig. 3.

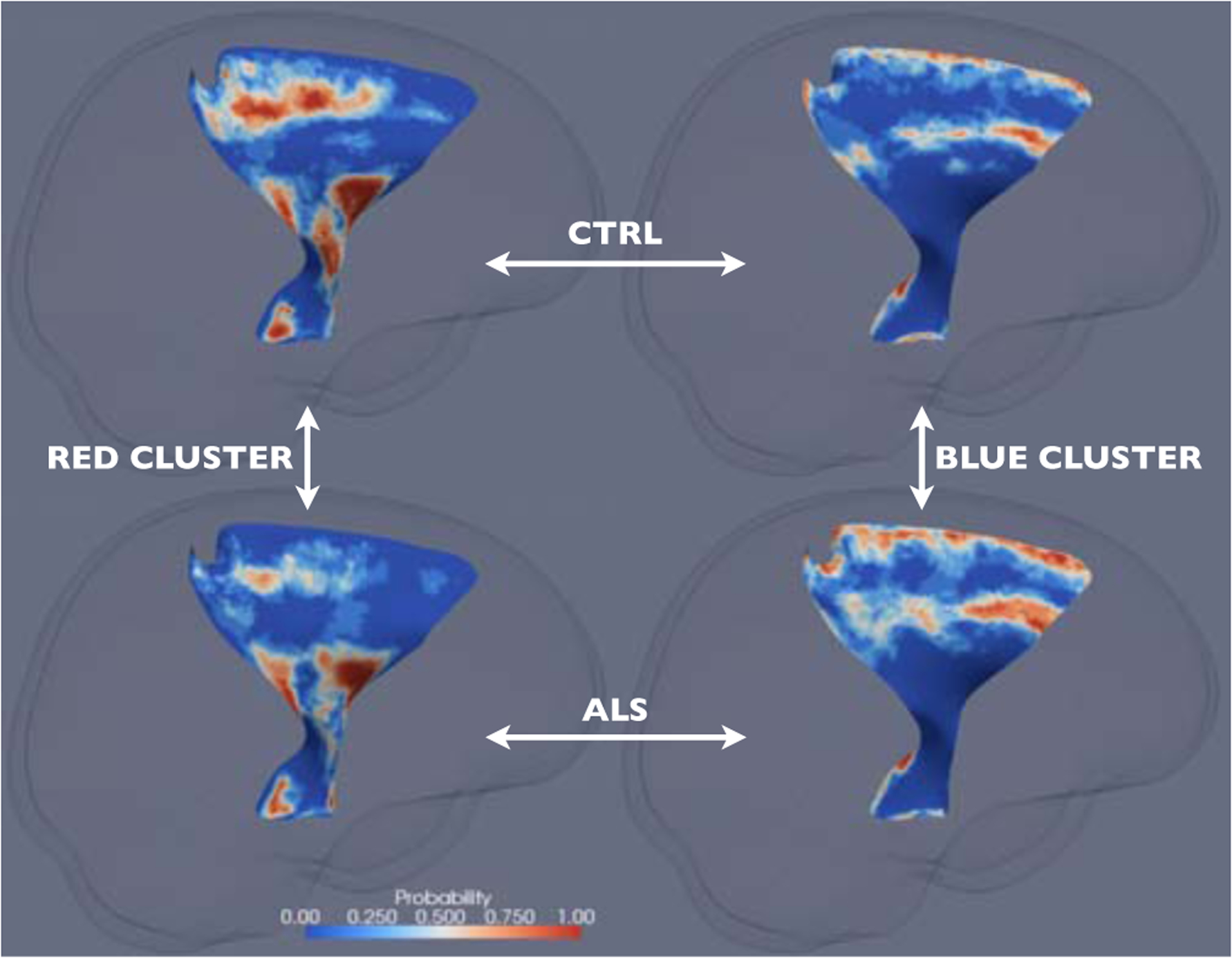
The cluster-membership probability maps on the left CST for the red cluster and the healthy controls (top left), the red cluster and the ALS patients (bottom left), the blue cluster and the healthy controls (top right), and the blue cluster and the ALS patients (bottom right). See Sec. 3 for details.

4. Discussion

In this paper, we described a new tract-specific framework that supports the evaluation of WM morphometry at both the macroscopic and microscopic scales. The potential of the framework was illustrated with an application to assess WM atrophy in ALS. In the future, we plan to explore extending the novel multivariate analysis framework for tubular WM tracts proposed recently by Goodlett et al. [3] to sheet-like tracts. This should enhance our ability to capture additional patterns of morphological differences in the spatial domain.