The omnigenic model and polygenic prediction of complex traits

Summary

The omnigenic model was proposed as a framework to understand the highly polygenic architecture of complex traits revealed by genome-wide association studies (GWASs). I argue that this model also explains recent observations about cross-population genetic effects, specifically the low transferability of polygenic scores and the lack of clear evidence for polygenic selection. In particular, the omnigenic model explains why the effects of most GWAS variants vary between populations. This interpretation has several consequences for the evolutionary interpretation and practical use of GWAS summary statistics and polygenic scores. First, some polygenic scores may be applicable only in populations of the same ancestry and environment as the discovery population. Second, most GWAS associations will have differing effects between populations and are unlikely to be robust clinical targets. Finally, it may not always be possible to detect polygenic selection from population genetic data. These considerations make it difficult to interpret the clinical and evolutionary meanings of polygenic scores without an explicit model of genetic architecture.

The omnigenic model was proposed as a framework to understand the highly polygenic architecture of complex traits revealed by genome-wide association studies (GWASs). I argue that this model also explains recent observations about cross-population genetic effects, specifically the low transferability of polygenic scores and the lack of clear evidence for polygenic selection. In particular, the omnigenic model explains why the effects of most GWAS variants vary between populations. This interpretation has several consequences for the evolutionary interpretation and practical use of GWAS summary statistics and polygenic scores. First, some polygenic scores may be applicable only in populations of the same ancestry and environment as the discovery population. Second, most GWAS associations will have differing effects between populations and are unlikely to be robust clinical targets. Finally, it may not always be possible to detect polygenic selection from population genetic data. These considerations make it difficult to interpret the clinical and evolutionary meanings of polygenic scores without an explicit model of genetic architecture.

Introduction

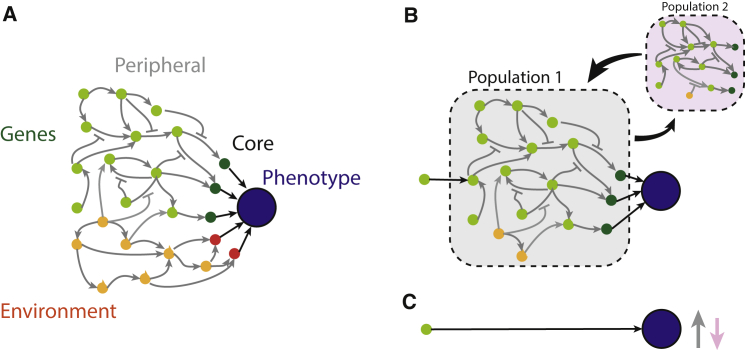
One of the clearest findings of genome-wide association studies is that, for many phenotypes, associated genetic variation is spread over many variants distributed widely across the genome.¹ One surprising aspect is that for many traits, heritability is not largely confined to genes or pathways directly associated with the trait.^2,3 Indeed, the idea that variants across almost the entire genome could have direct additive effects on any particular phenotype seems biologically implausible. The omnigenic model^2,4 reconciles this by partitioning genes not by pathway, but by their proximity in terms of causality to the phenotype. “Core” genes are those for which the gene product has a direct effect on the phenotype. There are typically few such genes and therefore genetic variants that affect function or regulation of those genes (“core variants”) explain a small proportion of the heritability. Conversely, “peripheral” genes affect the phenotype indirectly, through a network of interactions with other peripheral and core genes (Figure 1A). Because there are many more such genes, most of the heritability of any particular trait is explained by variants that affect peripheral—rather than core—genes (“peripheral variants”). Though not part of the model as originally proposed, this idea could naturally be extended to environmental effects—“core” and “peripheral” environmental effects are those with direct and indirect effects on phenotype. Gene-by-environment interactions would then provide another layer of complexity.

Figure 1.

The omnigenic model

(A) Schematic of the omnigenic model (after Liu et al.⁴). Genetic factors in green and environmental factors in orange, with arrows showing interactions. Peripheral factors are lightly shaded whereas core factors with direct effects on phenotype are darkly shaded.

(B) A gene’s-eye perspective. A single peripheral gene’s effect on the phenotype is filtered through part of the network (gray box).

(C) The GWAS perspective. The effect of a causal variant as measured by an association study in a single population (gray arrow in C) is the expected value of its effect, with respect to the distribution of genetic (i.e., allele frequencies) and environmental factors in the population. In a different population (pink box in B), the weights and possibly structure of the network change, leading to a different expected effect size (pink arrow in C).

The model is not a literal dichotomization—undoubtedly many core genes also have peripheral effects, and some genes are more peripheral than others. Nonetheless, it provides a useful conceptual framework in which to think about how to interpret genetic associations. From a peripheral gene’s perspective (Figure 1B), its effect on the phenotype is filtered through the peripheral network. Imagine that the nodes represent gene expression levels, and the edges are weighted by the multiplicative effect of one gene’s expression on another. Then the effect of a causal peripheral variant on the phenotype is given by the sum, over all possible paths to the phenotype, of the product of node values and edge weights. In practice, the network may contain features other than gene expression, for example chromatin- or replication-related features. From the GWAS perspective (Figure 1C), all this complexity is ignored, and only the net effect of the variant is measured. Since expression levels (i.e., node values) vary between individuals, the effect of actually perturbing a peripheral variant may be different between individuals. However, for two individuals from the same population, the node values are drawn from the same distribution (by definition, a population has little or no genetic or environmental substructure) and therefore, the expected effect of the variant is the same in every individual. This is why association studies work (if the direction of effect of every variant were random in each individual, there would be no associations).

Polygenic scores across populations

Things become more complicated when comparing genetic effects across populations. It seems likely that the effects of core variants should be largely consistent. If increasing expression of a core gene increases the phenotype in one population then it should also do so in another. Assuming that the effects of (for example) cis-regulatory variants are conserved, core variants should then have similar effects in different populations. Conversely, because the effects of peripheral variants are integrated over interactions with environmental and genetic factors which vary across populations, their phenotypic effects will differ across populations. From the gene’s perspective in Figure 1B, a different population means a different network (in terms of weights and potentially topology). Because gene expression levels vary across populations, the node values of individuals from different populations are drawn from different distributions, and therefore the expected effect of any peripheral variant is different—akin to background effects in classical genetic terminology. There is little or no epistatic variance within populations,⁵ which is consistent with this type of pervasive interaction leading to additive genetic variance.^6,7

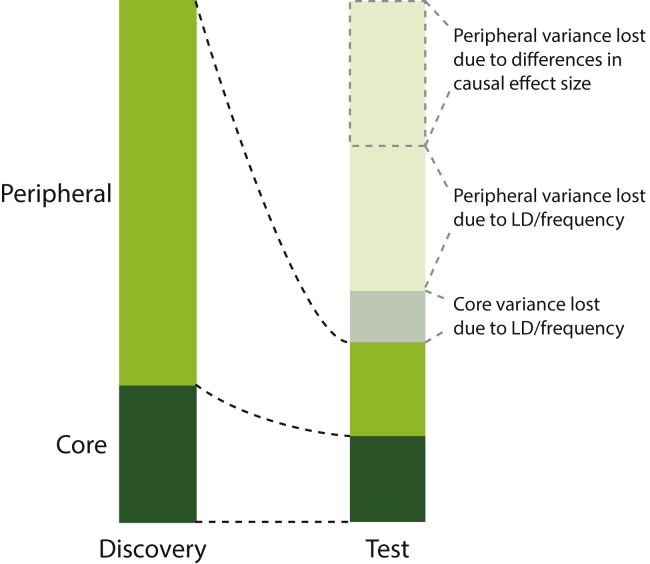
The omnigenic model therefore naturally explains why many GWAS loci replicate across populations but show evidence of heterogeneity in effect size. For example, over a range of traits, 94% of genomic-wide significant variants identified in Biobank Japan GWAS have the same direction of effect in a European population, but the correlation of effect size is only 0.11 (though 0.87 for variants that are genome-wide significant in both populations).⁸ Similarly, of 8,979 genome-wide significant variant-phenotype associations from the GWAS catalog, 1,444 nominally replicate in the multi-ethnic PAGE consortium but with effect sizes on average 14% lower in the Hispanic/Latino population and 46% lower in the African American population.⁹ While this can be partially explained by differences in linkage structure, the predictive power of polygenic risk scores (PRSs) decreases by more than would be expected given differences in allele frequency and linkage disequilibrium structure¹⁰ and direct estimates of cross-population genetic correlations are less than 1,^8,11, 12, 13 suggesting substantial differences in causal effect size and even direction. It is hard to imagine how this could be the case for a core variant. Similarly, a peripheral gene that regulated many core genes in a consistent way (a “master regulator”) might have consistent effects. On the other hand, most peripheral variants, despite having consistent effects on their peripheral genes, would have different phenotypic effects after filtering through a different gene/environment network. Since such variants make up most of the heritability (Figure 2), the majority of associated variants would have different effect sizes across populations.

Figure 2.

Conceptual schematic of the loss of variance explained in a population different to the discovery population

Some of the lost variance could potentially be recovered through statistical approaches, but some (dashed outline) could not, and would provide an upper bound on the transferability of the polygenic score.

Empirical estimates of genetic correlations support this model although with differences among traits. A recent comparison of 52 traits between UK Biobank and Biobank Japan found that point estimates of genetic effect correlations (r_g; which includes differences in allele frequency) ranged from 0.39 to 1.1.⁸ Representative complex traits include type II diabetes (r_g = 0.95), height (r_g = 0.82), and BMI (r_g = 0.76). Another study estimated genetic correlations of causal effect sizes between European and Asian populations for a different set of 21 traits from UK Biobank and GERA to range from effectively 0 to 1 with a mean of 0.55.¹¹ Under the omnigenic model, such differences among traits would be expected due to differences in the structure and complexity of the peripheral gene network, the nature and extent of environmental interactions, and the genetic architecture of the trait. For example, in some cases a substantial proportion of heritability may be explained by rare variants.^14,15 Rare variants have different properties than common variants, for example in terms of their effect size distribution,¹⁶ population specificity,¹⁷ and environmental stratification.^18,19 Differences in the proportion of heritability explained by rare variants would therefore contribute to differences in transferability among traits, although it is not clear in which direction. Similarly, differences in environment will make a potentially large but difficult-to-estimate contribution if there are substantial environmental interactions. Evidence that there are, for some traits, substantial environmental interactions comes from the observation that even within a population, the predictive power of polygenic scores can differ substantially across environmental strata.²⁰

One consequence of this interpretation would be that there may be limited opportunity to improve the cross-population transferability of polygenic scores through statistical approaches. Because most of the heritability would be contained in variants with unpredictably different effect sizes in different populations, there would be no way to apply polygenic scores developed in one population to another without losing some amount of accuracy, even if the causal variants were known. Improvements in transferability due to fine-mapping causal variants or incorporating local ancestry would be limited because these approaches would not capture the interactions driving the difference in effect size. Some improvement is possible. For example, state-of-the-art fine mapping has been shown to improve prediction R² of European-derived PRS in East Asian ancestry populations from about 55% to 61% of the European accuracy.²¹ This is a significant increase which may be possible to improve further but the omnigenic model suggests that, even if we knew all the causal variants precisely, there would be some upper bound on the possible improvement. Incorporating global ancestry would provide additional improvement²² if the interactions are genetic but not if they are environmental. Ultimately, to achieve parity in predictive accuracy, there may be no way around carrying out GWASs in populations of the same ancestry as those in which one wants to predict. For traits where environmental interactions make a substantial contribution to the effect of peripheral genes, then even that would not be sufficient and it would be necessary to carry out the GWAS in the test population itself, or at least in one that shares both ancestry and environment.

Polygenic selection

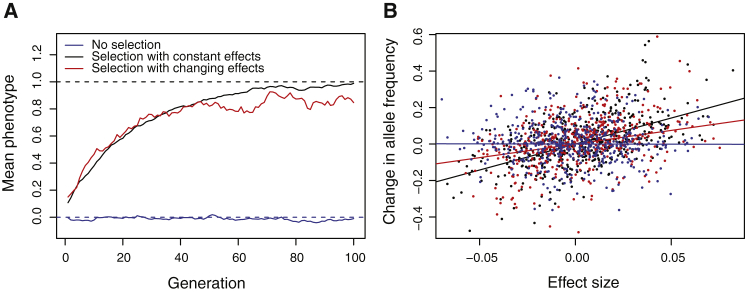
If effect sizes differ across populations then they must also differ across time. This fundamentally affects the way in which selection operates on complex traits, and explains why, despite our intuition that polygenic selection should be very common, it has been very difficult to detect. It is often assumed that the response to selection on highly polygenic traits is driven by small but correlated shifts in the frequencies of associated variants.²³ This can be detected by looking for shifts in allele frequency that are systematically correlated with the allelic effect sizes.^24,25 However, if the phenotypic effects of most variants vary over time, then the correlation between frequency shifts and effect size would be reduced (Figure 3). Depending on the rate of change of effect size, we might see little or no correlation between the estimated effect sizes in any particular population and the direction or magnitude of long-term shifts in frequency. Polygenic selection would still occur, but there would be no detectable genomic signature. Core variants would behave as expected but since they explain a small proportion of heritability, the response to selection would be dominated by peripheral variants.

Figure 3.

Simulation of polygenic selection

When effect sizes change over time, polygenic adaption still occurs but the relationship between effect size and allele frequency change is attenuated.

(A) Population mean phenotype as a function of time in a Wright-Fisher population of 1,000 sexually reproducing haploid individuals with 1,000 unlinked alleles, each with phenotypic effect drawn from a N(0, 0.025) distribution. Before generation 0 (not shown), the optimal fitness is 0 (dashed blue line) After generation 0, the optimal fitness in the no selection case (blue) remains the same, while in the selection cases (black and red), it is 1. In both cases the fitness function is a standard Gaussian distribution function around the optimum. In the case of changing effects (red), the effect of each allele changes every generation by an amount drawn from a N(0, 0.0025) distribution.

(B) Change in frequency against effect size in generation 100 for alleles that are still polymorphic. Each point represents a single allele and solid lines show the regression of change in frequency against effect size for the three different scenarios. In the case of selection with changing effects (red line), the correlation between effect size and frequency change is lower compared to the case of constant effect size (black line), even though selection is equally effective. Since the correlation between effect size and frequency is the signal that drives most tests for polygenic selection, this explains why such tests may not detect selection under this model.

This may explain why, despite the plausibility of directional polygenic selection as a mode of adaptation, genomic evidence for it has remained so elusive. The strongest signals of selection²⁵ have been shown to be mostly artifactual, driven by residual population stratification in the original GWAS.^26,27 While some studies still find evidence for directional selection^28,29—albeit weaker than previously believed—they may also be affected by other artifacts that are less well characterized.^30,31 This lack of evidence can be explained if directional polygenic selection can occur without a clear genomic signature in the form of a correlation between allele frequency changes and phenotypic effect. On the other hand, as others have recently observed, changing environment and stabilizing selection can generate such a signal, even if there is no directional selection.³² Taken together, these points suggest that it is not possible to reconstruct polygenic selection on complex traits based on genomic evidence alone. More productive strategies might involve joint analysis of genomic, environmental, and phenotypic data.

Rethinking environmental effects

Such an analysis might also involve rethinking the way in which we model environmental effects. A natural extension of the omnigenic model is to view the effect of environment on phenotype in the same way. In such an “omni-environmental” model, “core” environmental factors would have direct effects on the phenotype. Examples might be the effect of UV radiation on skin pigmentation, or the effect of starvation on BMI. Meanwhile, many “peripheral” environmental variables would have a nonzero effect on the phenotype, although their effects would be unpredictable and moderated by interactions with many other environmental factors. For example, rainfall might affect body size by changing diet, but the precise effect would depend on which crops were grown, the values of other environmental factors, and so on. Just as with genetic effects, the effect sizes of core environmental effects would be consistent across populations, while peripheral environmental effects would vary unpredictably. Interactions between peripheral genes and peripheral environmental factors would also contribute to this variation. The relative magnitudes of core and environmental effects probably differ enormously between phenotypes, just as for core and environmental genetic effects

Discussion

If the interpretation of the omnigenic model presented here is correct, it places limitations on the usefulness of polygenic scores. Some traits might inherently have relatively high transferability. Others might be substantially improved through statistical approaches. But for some traits, polygenic scores might be largely specific to a particular ancestry, possibly even to a particular environmental setting. Existing data provide few clues as to how to guess where different traits fall on this scale. For example, type 2 diabetes, which we might expect to have a substantial component of environmental interactions, exhibits very high genetic corrections at least in some (though not all) studies.^8,11 On the other hand, many molecular biomarkers, which we might expect to have simpler architecture than multifactorial disease phenotypes, exhibit low transferability and evidence of substantial heritability at peripheral genes.^3,8 For such traits, highly predictive polygenic scores for a particular population would require large GWASs in a population that is similar, both in terms of ancestry and environment. Because sample sizes in the hundreds of thousands or millions are required to train highly predictive scores, it might be impossible to develop accurate polygenic scores for groups that are smaller or inhabit unusual environments. On the other hand, even in these cases, the scores retain some predictive power, and their performance can easily be empirically tested so, with awareness of these limitations, they could still be useful to some extent. This interpretation would also imply a limit to the usefulness of polygenic scores for studying the evolution of complex traits. If the phenotypic effects of variants vary over time, then allele frequency and effect size distributions that have been interpreted in terms of directional, stabilizing, or background selection may need to be reinterpreted. In particular, it may be hard to draw conclusions about polygenic evolution without an explicit model of this process.

This interpretation of the omnigenic model also leads to a number of testable predictions. As explained above, it predicts that fine-mapping and including local ancestry will not, in general, substantially improve the transferability of polygenic scores. Effect sizes will depend on global ancestry and environment, not local ancestry at causal variants. It predicts that the estimated effects of causal variants will differ between populations, with the magnitude of the effect proportional to genetic distance and environmental divergence between the populations. Finally, it predicts that effect sizes at core genes (for example, identified through functional experiments) will be more similar across populations than the effect sizes at peripheral genes. This actually suggests a way to identify core genes, by looking for variants with the most consistent effects across populations—or across environmental strata within population—rather than the largest or most significant effects. This represents a potentially powerful way to prioritize GWAS hits for follow-up since core genes would make the most (perhaps only) promising drug targets. The ability to do this is one major advantage of diverse GWAS cohorts and biobanks with data on environmental covariates. Currently, the limiting factor in the quantitative analysis of this model (for example, estimating the correlation in effect sizes at causal variants) is the lack of accessible, non-European ancestry GWAS datasets, something that could be resolved in the next few years.

We have learned an enormous amount about the genetic architecture of complex traits through GWASs but interpreting this knowledge in the context of biological processes has been difficult. With unprecedented sample sizes and an increasing focus on cross-population studies, now may be a good time to rethink the way we interpret these data and to develop models of complex trait architecture, like the omnigenic model, that are both consistent with data and biologically plausible.

Methods

For the simulations shown in Figure 2, we simulated a population of size N = 1,000 haploid individuals, each carrying M = 1,000 unlinked loci with nonzero effects on phenotype y. The effect of variant j on the phenotype in generation t is denoted ${\beta }_j^t$ and is initially drawn from a N(0,0.025) distribution. The phenotype of individual i in generation t is given by $y_i^t=\sum _{j=1}^M{\beta }_j^t{X}_{ij}^t$ where $X_{ij}^t$ is the genotype of individual i at variant j in generation t. Each individual in generation t+1 chooses its two parents at random from the individuals in generation t, choosing individual i with probability proportional to $\phi \left(y_i^t-\mu \right)$ where $\mu$ is the optimal fitness, and then chooses one of the two parental alleles randomly at each locus. In all cases, we burn-in the simulation with $\mu =0$ for 100 generations before running the simulation for an additional 100 generations as shown in Figure 2. In the “no selection” case, the variant effects and fitness optimum remain constant for all t. In the “selection with constant effects case,” the variant effects remain constant, but the fitness optimum $\mu =1$ after the burn-in iterations. In the “selection with changing effects” case, $\mu =1$ and at each generation we set $b_j^{t+1}={\beta }_j^t+z_j^t$, and then set ${\beta }_j^{t+1}=b_j^{t+1}\left(\frac{s.d.\left({\beta }_j^{t+1}\right)}{s.d.\left(b_j^{t+1}\right)}\right)$ where $z_j^t\sim N\left(\mathrm{0,0.0025}\right)$ and SD indicates the standard deviation over variants j. This perturbs the effect sizes while keeping the overall distribution of effect sizes constant. In Figure 2 we plot the phenotypic mean $\frac{1}{N}\sum _{i=1}^N{y}_i^t$ against t in the left panel, and the change in allele frequency of each variant ${\Delta }_j=\frac{1}{N}\sum _{i=1}^N\left(X_{ij}^{100}-X_{ij}^1\right)$ against its effect size ${\beta }_j^{100}$ in the right panel.