Perm-waved human hair: a thermorheologically complex shape memory composite

Abstract

A “permanent” bent shape can be imposed on a straight human hair by a two-stage reduction/oxidation (perm-waving) process. The process relies on the molecular level on sulfhydryl/disulfide interchange as bond exchange reaction (BER). We expected a well-documented transition temperature around 60°C to be the trigger for the shape memory (SM) process of perm-waved hair. We confirm the existence of the SM process as such and investigate its time and temperature dependence. The results show a two-stage SM behavior, implying two distinct variations of the BER. The model to fit the data contains two fractional, normalized, elastic bending rigidities, which are strictly compensatory. They show Arrhenius-type temperature dependence and a common activation energy (E_A) of ∼−12 kJ/mol. The characteristic relaxation time for the first SM process shows little, if any, temperature dependence (E_A = −4 ± 2.7 kJ/mol). This is in contrast to the second process (E_A = −58 ± 5.5 kJ/mol) but in line with the expected properties of the suggested BERs. None of the parameters shows any sign of the expected trigger transition (∼60°C). We hypothesize that this specific transition occurs only for large tensile deformations, when specific SS bonds in the intermediate filaments of hair are activated. There is thus no specific “trigger” transition for the SM behavior of bent, perm-waved hair.

Significance

The term “permanent waving” describes the impartation of a stable bending deformation onto straight hair. Practical observations seem to suggest a lack of permanence. We investigate the time-dependent shape changes of permed hairs in water over a range of temperatures. We analyze the data on the basis of two viscoelastic shape memory processes, assuming two types of dynamic bond exchanges for the disulfide bonds in the hair proteins. We expected a transition around 60°C to trigger shape memory. To our profound surprise, no such transition could be found. This makes perm-waved hair an “atypical” shape memory material. The results give interesting and novel insights into the complex structure/property relationships for hair as a biological composite material.

Introduction

Hair grooming practices frequently make use of hair shape changes, which may either be transient or perceived as permanent (1,2).

In the first case, water and/or heat are applied to impart a nonpermanent shape change to hair (straight → curly; curly → straight) by what is traditionally referred to as “cohesive” set (3). On a molecular basis, the process is dependent on the breaking and reformation of hydrogen bonds in the fiber/matrix structure of hair as a biological composite (2,4). The recovery of the original form for cohesively set hair is a classic shape memory (SM) process. The process is controlled by the viscoelastic properties of hair (5, 6, 7, 8) and is triggered by its glass transition, which is highly dependent on water content (9,10).

The term “permanent waving” describes the impartation of a stable bending deformation onto hair by a two-stage reduction/oxidation process. The corresponding treatment is the permanent straightening of naturally wavy hair. The imposition of this type of hair deformation is achieved by breaking/reducing disulfide (SS) bonds in the fiber under alkaline aqueous conditions while it is deformed. The bonds are reformed through an oxidative treatment step while the hair remains in the deformed state (2,11). The underlying bond exchange reaction (BER)—that is, the process of the relocation of the covalent bonds in equilibrium with the new form of hair—is referred to as sulfhydryl/disulfide (SH/SS) interchange (12). For this specific BER, a transition around 60°C in water at neutral pH has been extensively reported (13, 14, 15, 16, 17, 18, 19). We thus expected this transition to trigger hair shape recovery after permanent waving.

Apart from academic interest in the various SM mechanisms of hair, the motivation for this study also came from practical observations. These suggest a lack of true permanence of the hair style, perceived as a considerable loss of curliness over time.

Once we had confirmed the existence of the SM process as such, it was our objective to develop a model-based systematization of the viscoelastic processes underlying the shape memory (recovery) of perm-waved hair in water. Our approach incorporates the principles of hair structure (2,20,21) and concepts for shape memory polymers (22,23). A special focus is on various aspects of polymer viscoelasticity (24) and on the behavior of thermorheologically complex materials (25, 26, 27). Our considerations benefitted from research on hydrothermally activated, dynamic covalent networks of “smart” bonds (28,29) in shape memory polymers.

Materials and methods

Sample preparation

Hair loops were treated on a cylindrical roller and then cut to measure the remaining bending deformation. This is a convenient measure of the efficiency of a permanent or nonpermanent waving treatment with a close proximity to the practical situation (8,30, 31, 32).

All experiments were performed on a commercial sample of untreated, mixed, Caucasian, medium brown hair, obtained in the form of flat tresses (∼1 g/cm; Fa.Kerling, Backnang, Germany).

To determine bending recovery, a hair of ∼20 cm in length was taken at random from a tress. It was wound around a 12-mm cylinder made from polyvinylchloride (PVC) under a constant load of 200 mg and fixed at both ends with drops of nail polish. Care was taken to wind the hairs such that their axis was normal to the cylinder axis. Because of the ratio of hair versus cylinder diameter (max 100 μm vs. 12 mm), shear strains in the fiber are well below the limits of linear viscoelasticity (<1%) (10,32). The cylinder was then immersed in water for 30 min (20°C) to allow complete stress relaxation. Permanent set was achieved by then suspending the cylinder in a beaker and applying the following treatment sequence (30,31):

• Reduction: 1 M thioglycolic acid, pH 9, 20 min, 20°C

• 1)Rinse: continuous exchange of demineralized water, 20 min, 20°C

• Reoxidation: 2.3% H₂O₂, pH 7, 20 min

• 2)Rinse: continuous exchange of demineralized water, 20 min, 20°C

After the final rinsing step, the cylinder was removed from the beaker. The hair loops were cut without delay to yield partially opened hair rings. These were collected, dried under ambient conditions, and combined into a “hair pool” of ultimately ∼200 specimens. The pool of specimens was stored under ambient room conditions (∼55% relative humidity (rh), 22°C) for further use. It was assumed that under these conditions, when hair is well below its glass transition (10), no further change to the chemical fiber state would occur—at least not in the time window of their use (33,34). Fiber rings were used within a time window of 1 week to 1 month so that experiments were done at times well removed from the treatment stage.

Measurements of bending recovery

We determined the time-dependent opening (recovery) of groups of hair loops (30,31) in water for temperatures between 35 and 95°C. This temperature range includes the expected transition around 60°C. The shape memory process was expected to be fast enough to be observable on an experimentally viable timescale (35).

For the experiments, five hair rings were taken at random from the fiber pool and dropped into a petri glass dish with demineralized water at room temperature and left to equilibrate for 30 min. This time was considered as sufficient to relax any “nonpermanent” viscoelastic processes related to the hydrogen bonds in hair (cohesive set) (8,35). After this period, the loops were removed from the dish and directly dropped into a double-walled, thermostated glass dish with a flat bottom containing water at temperatures between 35 and 95°C.

The diameters of the partially opened loops were determined by taking calibrated images at 17 predetermined and convenient times for up to 480 min. The readings were spaced roughly equally on the log-timescale. The first image was taken after ∼15 s, which was considered as adequate for temperature equilibration for the hair fibers. Because 15 s is short compared with the next reading at 120 s, the initial recovery readings were defined as effectively taken at t = 0. The lowest temperature (35°C) was chosen to be well above the usual fluctuations of room temperature in a laboratory so that a stable temperature could be maintained by heating alone.

Tests with sets of five hair rings were conducted in duplicate. For each experiment, data at a given time point were combined as means. This was an experimental necessity because, as a result of intermittent image taking, individual fiber loops in a set could not be reliably traced over the experimental time range. However, this turned out to be only a minor problem because differences between recovery values for duplicate tests were consistently <0.02 for all time points.

Time-dependent recovery R_ec(t) of a group of hairs is given by (30, 31, 32)

$$R_{ec}\left(t\right)=\mathit{1}-D/d\left(t\right),$$ (1)

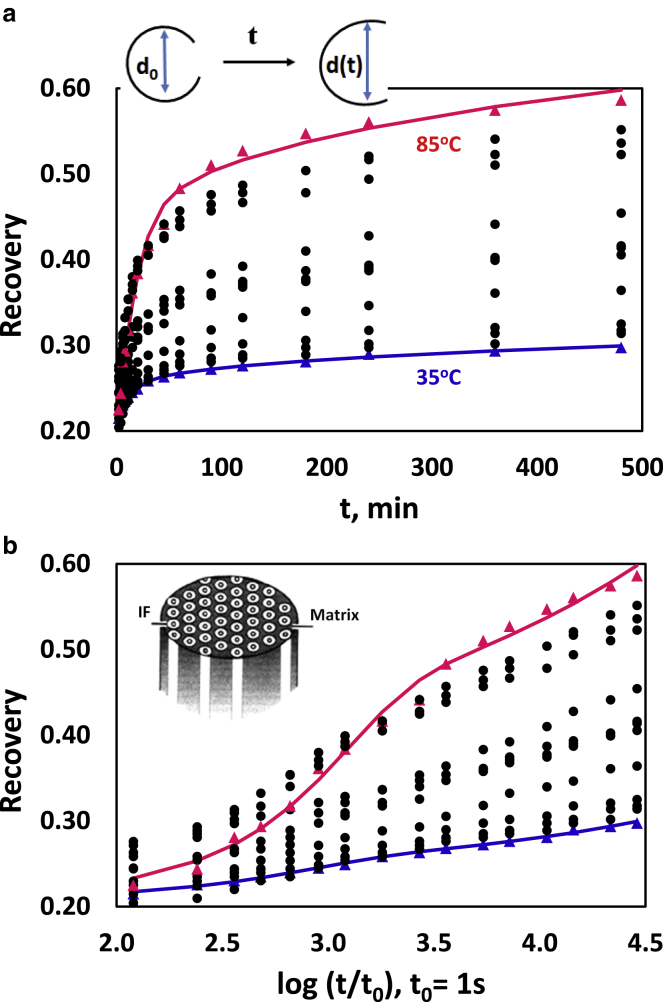
where D is the diameter of the cylinder on which the fibers were treated. d(t) is the time-dependent mean diameter of the circles defined by the shapes of the partially opened fiber rings (see inset in Fig. 1 a). d(0) is the initial reading of the experiment at around 15 s. When R_ec > 0.5, the ring length covers less than half of the circumference of the circle it defines. In this case, the distance between the ring ends is taken as the length of an arc of the circle from which diameter readings were calculated. Fig. 1, a and b summarizes the results.

Figure 1.

(a) Recovery values (means, N = 5) at the temperatures in the experimental range versus time (min). Lines through the lowest (35°C) and the highest (85°C) set of data are the fits according to Eq. 9, using curve specific parameter values. Data sets are presented in 5°C steps for the experimental temperature range. It just so happened that the data for 85°C rather than 95°C provided the highest final recovery values. The inset gives a description of the measurement of the hair loops. (b) Data and fits as for (a) but for the log (t, s) scale to highlight the specific structure of the curves are shown. The inset gives a simple graphical representation of the IF/matrix composite structure in the cortex of hair (adapted from (3,4)). To see this figure in color, go online.

Development of a model equation for the description of shape memory/recovery

We base our approach on the well-documented morphological structure of hair as a biological, high-performance, fiber/matrix composite (4,17,18,20). Intermediate filaments (IFs) in the core (cortex) of hair are aligned with the fiber axis and embedded in a matrix of IF-associated, amorphous proteins. This is the conventional, mechanical two-phase model for keratins, as shown in the inset of Fig. 1 b (2,3,8,21).

Central to our approach is the assumption of a general analogy between shape memory from nonpermanent cohesive and from permanent bending deformation (36,37). During permanent waving, a hair is bent. The bending moment of the initially straight hair is relaxed under alkaline condition through reduction of ∼20–40% of the cross-links (12,38). These links are formed by the double-amino-acid cystine between and within protein chains. The highly reactive S⁻ groups, resulting from the reduction, react with stressed disulfide bonds through SH/SS interchange (14,15). Through this BER, SS bonds are broken and reformed in equilibrium with the bent configuration of the hair, thus stabilizing the perm-wave. Hair is thus an example for a biological composite with a clear link between dynamic bonds in its protein structure and a macroscopic response. The description above is summarized in the chemical equation below:

$$⧗-S_1^{-}+⧗-S_2\sim S_3-⧗\to ⧗-S_1-S_2-⧗+⧗-S_3^{-}$$ (1)

The first part on the left-hand side of the chemical equation represents the free S₁⁻ group formed from an SH-group under the alkaline conditions of reduction with thioglycolic acid (see experimental above). The S₁⁻ group is attached via a methylene group to a protein chain (⧗–) and reacts with an unreduced, stressed disulfide bond (-S₂∼S₃-). On the right-hand side, an unstressed bond has formed (-S₁-S₂-), and the free S₃⁻ group is released. This group will then react with another stressed disulfide bond in what is essentially an autocatalytic process. The new bent configuration of the hair is stabilized through the reoxidation of ∼70–80% of the SH groups to form new cross-links (2,30,38). Upon releasing the hair from its constraints on the roller after reduction/reoxidation, it spontaneously opens to a new stable, bent state, which puts the newly formed SS bonds under stress.

As a basis for the analysis of the recovery data, we suggest a fundamental analogy between the shape memory processes related to cohesive as well as permanent set. Against this background, the time-dependent recovery from permanent set, R_ec(t), is assumed to be controlled by the general principles of linear viscoelasticity (5). The core principle is the interaction of the bending rigidities of the straight and the bent hair state according to Denby’s equation, as an approximation of the Boltzmann Superposition Principle (6,8,24,30,32). We formulate Denby’s (6) equation as (8,30,31)

$$R_{ec}\left(t\right)=B\left(t\right)/B\left(t-w\right).$$ (2)

B(t) is the time-dependent bending rigidity of the initially straight hair, starting at t = 0. B(t) is relaxed through the reduction process to a constant value B_re. The subscript relates to the reduction process. B_re remains unchanged under further processing—that is, during rinsing and reoxidation (30,31). It is thus the elastic stiffness, which remains unaffected by the chemical processes and is assumed to be equal for both the deformation and the recovery process. B(t-w) is the time-dependent bending rigidity of the hair in its bent configuration after processing, when it is released at time w. At the time of release of a hair loop from the roller—that is, at (t-w) = 0—the fiber shows the initial bending stiffness of the reoxidized hair B_ro (30). Setting w = 0, this yields for the time dependence of the overall recovery process:

$$R_{ec}\left(t\right)=B_{re}/B\left(t\right).$$ (3)

Equation 3 implies the assumption of eventual total recovery $\left({\lim }_{t\to \infty }{R}_{ec}\left(t,T\right)=1\right)$. This is in line with the general behavior of shape memory polymers (39) and more specifically with observations for wool (40). As a consequence of $R_{ec}\left(t\right)\to \mathit{1},B\left(t\right)$ will approach B_re as limiting elastic value.

On the basis of previous investigations (7,8,10), we formulate for B(t)

$$B\left(t\right)=B_{re}+\mathit{\Delta }B\Psi \left(t\right).$$ (4)

In the context of the two-phase model for keratins, B_re is associated with the partly α-helical, elastic IFs in hair (30,31). ΔB is the limiting, elastic bending rigidity of the matrix, and Ψ(t) is its relaxation function.

Introducing Eq. 4 into Eq. 3 to fit the data showed that a single relaxation process (41,42) is in fact insufficient to describe the sigmoid shape of the curves in Fig. 1 b. To approach this problem, we found it plausible (35,43, 44, 45) to expand Eq. 4 to contain two relaxation processes as

$$B\left(t\right)=B_{re}+\mathit{\Delta }{B}_1{\Psi }_1\left(t\right)+\mathit{\Delta }{B}_2{\Psi }_2\left(t\right).$$ (5)

ΔB₁ and ΔB₂ are the fractional bending rigidities, and Ψ₁(t) andΨ₂(t) are the relaxation functions for the first and the second recovery process, accordingly.

Building on the suggested analogy between cohesive and permanent set, the relaxation functions are both a priori but, plausibly (8,32), expected to conform to the well-known and widely used Kohlrausch-Williams-Watt (KWW) function (46, 47, 48, 49, 50) as

$$\Psi \left(t\right)=exp{\left(-t/\tau \right)}^m,$$ (6)

where τ is the characteristic relaxation time, and m is the related shape factor. These parameters control the position and the width of the relaxation function—namely, on the log-timescale (see Fig. 1 b). Combining Eqs. 5 and 6, we introduce τ₁ and τ₂ as the characteristic relaxation times for the two processes, and m₁ and m₂ are their individual shape factors.

Before combining the equations further, we introduce further normalizations as

$$\mathit{\Delta }{B}_{n\mathit{1}}=\mathit{\Delta }{B}_{\mathit{1}}/B_{re}$$ (7)

and

$$\mathit{\Delta }{B}_{n\mathit{2}}=\mathit{\Delta }{B}_{\mathit{2}}/B_{re}.$$ (8)

ΔB_n1 and ΔB_n2 are the normalized fractional bending rigidities for each of the recovery processes. In what follows, these will be referred to as “bending intensities.”

Similar as tensile moduli (35,51), bending rigidities (Eq. 5) will be temperature dependent. This temperature dependence is expected (52) to be less for B_re as a property of the partly α-helical IFs compared with ΔB₁ and ΔB₂ as properties of the largely (53) amorphous matrix. Also, temperature dependence is assumed for the characteristic relaxation times. In contrast, m factors are both assumed as temperature independent. This is in line with time/temperature superposition principles for polymers (24,26) and analogous to the time/humidity superposition characteristics of keratins (7,8).

This finally yields the time- and temperature-dependent recovery function R_ec(t,T) as basis to fit the data in Fig. 1:

$$R_{ec}\left(t,T\right)=\frac{1}{1+\Delta B_{n1}\left(T\right)exp\left[-{\left(\frac{t}{{\tau }_1\left(T\right)}\right)}^{m_1}\right]+\Delta B_{n2}\left(T\right)exp\left[-{\left(\frac{t}{{\tau }_2\left(T\right)}\right)}^{m_2}\right]}.$$ (9)

Equation 9 describes the shape memory of a very special case of a thermorheologically complex material (25,27).

Control of data overfitting

Equation 9 contains an overall of six parameters, which ideally would be determined from the experimental data through a nonlinear fit procedure. For this investigation Excel solver (Excel 2016; Microsoft, Redmond, WA) as well as Statistica (V13; Tibco Software Inc., Palo Alto, CA 2017) were applied.

Because of the rather “simple” shape of the curves in Fig. 1, a and b, it was to be expected that substantial problems with overfitting would occur. This problem would be especially pronounced at low temperatures, for which contributions from the second, longer-term process were small. Working with the data, the problem of overfitting showed itself by large variations of parameter values, which were consistently associated with very high values for the coefficient of determination (r² > 0.99). Also, there were obvious compensation effects between ΔB_n1, ΔB_n2 and m₁, m₂ values.

For our final approach to data analysis on the basis of Eq. 9, we decided to introduce specific values for m₁ and m₂. These were based on considerations of the specifics of the underlying SM processes, as discussed below. By this, we succeeded to avoid compensation effects during curve fitting and improve precisions for both the relaxation times and the bending intensities.

There is a wealth of considerations in the literature on the nature of the KWW function and on specific values of the shape parameter (48, 49, 50). In the current context, we found an article by Pagnotta et al. (54) especially helpful. They applied the KWW function for dielectric data of the lysozyme/water system and modeled its glass transition as a percolation process. As limiting values for the shape of the KWW function, they report m = 1 at high and an extrapolated value of m = 0.35 at low temperatures (54). For a completely different system, namely spin-glasses, Phillips (55) gives essentially the same temperature-dependent, limiting values of m = 1 on the one hand and m → 1/3 (T → T_g) on the other. In spin-glasses, relaxation or, rather, magnetic reorganization occurs through short-range exchange interactions. Such a process could be considered as an analog to SH/SS interchange. We find this correspondence interesting, remarkable, and helpful.

Equation 6 is a simple, exponential, viscoelastic Debye process for m = 1. It may also be viewed as a cumulative Weibull distribution function (56). Here, m = 1 would signify that the failure rate, e.g., of bonds, is constant over time. Equation 6 with m = 1 also describes a classical chemical first-order process, which proceeds at a rate that depends linearly on only one reactant concentration. A KWW process with m = 1 extends over ∼2–3 decades on the log-timescale (t/τ = 0.01, Ψ = 0.99; t/τ = 10, Ψ < 0.001). Fig. 2 shows such curves for ΔB_n1(t) for the limiting temperatures of the experimental range.

Figure 2.

The relaxation curves for the normalized bending intensities for the two viscoelastic contributions to matrix shape memory (ΔB_n1, ΔB_n2) against log (time) (see Eq. 9). The curves for ΔB_n1 are the two lower curves, and those for ΔB_n2 are the two upper curves. The curves are based on fits of Eq. 9 to experimental data for 35 and 95°C using specific parameter values from Figs. 4 and 5. Inflection points of the curves are given by log(τ_i), for which the values are given on the graph. To see this figure in color, go online.

Tobolsky (52) described a first-order process for the stress relaxation in rubber at high temperatures. He associated the process with the cleavage of chemical bonds either along chains or at cross-links. The stress at any given point in time during the experiment is proportional to the number of cross-links still unbroken. In this context, he introduced the term “chemical” relaxation.

The hypothesis of the stress-induced cleavage of polysulfide cross-links during rubber relaxation may be linked to the situation in reduced and reoxidized hair (57). After reoxidation and repeated rinsing, only ∼70–80% of S⁻ groups, formed through reduction, will have reformed into SS bonds (38). Under the more or less neutral pH after rising free SH groups will remain in the hair. These are less reactive compared with the S⁻ group for SH/SS interchange (57).

For ΔB_n1(t), we propose the following molecular mechanism. Fig. 3 a shows the situation after spontaneous, initial recovery, where the free S₃H group is left adjacent to two stressed SS bonds. The following SH/SS interchanges are driven by the fact that stressed SS bonds have a lower activation energy than unstressed bonds. If we assume that the free S₃H group moves “downward” by pure chance, this will finally leave the S₆H group, isolated from the remaining, stressed S₁S₂ bond (see Fig. 3 c). As long as sufficient numbers of SH groups in the neighborhood of stressed SS bonds are present, the process may be expected to show a constant failure rate. This process may also be seen as an autocatalytic process (58) in the matrix proteins of hair. Whatever the model consideration for the process, the cumulative Weibull distribution/KWW function with m = 1 would be a plausible analytical description. This suggestion is supported by the observation that relaxation of hair during reduction follows consistently the m = 1 kinetic pathway (11,59).

Figure 3.

Graphical representation of the state of the SS bonds in the matrix during the shape memory processes after perm-waving (adapted from (3,11,20)). Two protein chains are considered, which are displaced (sheared) against each other (as indicated by the arrows) because of the interacting bending moments, according to Eq. 3. For graphical reasons, shearing enables a more straightforward presentation of the mechanisms compared with bending. (a) After shearing upon release of the bent and perm-waved hair, the two protein chains in the matrix are linked through stressed disulfide bonds. S₃H represents a free sulfhydryl group, remaining in the fiber after processing. (b) Rather than with the adjacent S₁S₂ bond, the group, by pure chance, is assumed to enter alternatively into an equivalent bond exchange reaction (BER) with the stressed S₄S₅ bond. This leads to the unstressed S₃S₅ bond and the free S₄H group. (c) This new group will then interact with the stressed S₆S₇ bond to form the unstressed S₄S₇ bond and the free S₆H group. This group is now well removed from the remaining, stressed S₁S₂ bond. To see this figure in color, go online.

Once the ΔB_n1(t) process has taken place, remaining free SH groups and strained SS bonds are far apart (see Fig. 3 c). They will only meet each other through extended chain movements in the wider structure of the matrix. These may be associated with a chain percolation/diffusion process or various other models for molecular movement, consistent with the KWW function (48,50,60).

Pagnotta et al. (54) and Philipps (55), for very diverse systems, found limiting lower values for m in Eq. 6, which are consistent with the “universal” value of m ≈ 1/3 (49). This yields a relaxation function over ∼6–7 decades of time. The value has been observed for or is consistent with the relaxation and creep curves for a wide variety of materials (49,61,62), including, metals, glasses, polymers, rubbers, bone (45), and keratins (7,8).

Investigations on the recovery of human hair from cohesive set (8) have given an experimental value of m = 0.28 ± 0.02. In view of the suggested analogy between the shape memory processes related to cohesive and permanent set, respectively, we have pragmatically chosen m₂ = 0.3 to fit the ΔB_n2(t) process in Eq. 9. This appears reasonable when considering the range and the anticipated precision of the experimental and theoretical m values (61). Fig. 2 gives KWW/m = 0.3 curves for ΔB_n2(t,T) for the limiting temperatures of the experimental range.

Results

Fig. 1a shows recovery versus time for selected temperatures to cover the experimental range. For all temperatures, an initial recovery of ∼20% is followed by a rapid further increase for which the extent increases with temperature. Beyond times of ∼100 min, the curves appear to follow a slow, somewhat linear process in which slopes again increase with temperature. This is analogous to the characteristic behavior of polymers under creep conditions (24). The maximal recovery, which was observed over the experimental time range and at the highest temperatures (85–95°C), was ∼55–60%.

To get a better view of the fine structure of the recovery process, Fig. 1 b realizes a plot of recovery against log (time) for the data sets. On the log(t) scale, the recovery curves exhibit a nonsymmetrical, sigmoid shape. The shape is rather faint at lower temperatures (<60°C), where it shows itself as an apparent linear increase, but becomes increasingly obvious at higher temperatures (∼80–90°C).

The start values of the curves in Fig. 1 b—that is, the initial recoveries—are on the basis of Eq. 2, given as

$$R_{ec}\left(\mathit{0}\right)=B_{re}/B\left(\mathit{0}\right).$$ (10)

The analysis of the experimental R_ec(0) values shows that there is no significant dependence on temperature and a mean (±SE) of 0.225 ± 0.0041 is observed. This implies equal temperature dependencies for the parameters in Eq. 10 so that effects of the expected transition at around 60°C would be compensated.

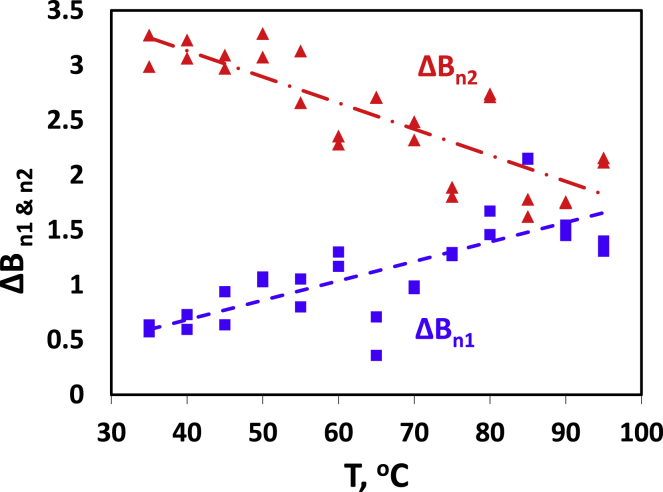
Fig. 4 summarizes the data for ΔB_n1 and ΔB_n2 versus temperature. ΔB_n1 increases and ΔB_n2 decreases essentially linearly in a strictly compensatory manner, as implicit in Eq. 9. For lower temperatures (35°C+), the intensity of the first process is low and the second process clearly dominates recovery, accordingly, with a ratio of ∼6:1. At the high end of the experimental range (80°C+), intensities become essentially equal for the two processes. There is no indication of the suggested transition for the BER at around 60°C, related to SH/SS interchange (14,16,19).

Figure 4.

Normalized intensities of partial bending intensities, ΔB_n1 and ΔB_n2 versus temperature, as indicated (see Eqs. 7 and 8). Regression lines through the data are given to highlight linearity. To see this figure in color, go online.

To investigate temperature dependence, ΔB_n1 and ΔB_n2 data are transformed, assuming Arrhenius-type behavior:

$$\mathit{\Delta }{B}_n\left(T\right)=Cexp\left(-E_A/RT\right).$$ (11)

Plots of ln(ΔB_n) versus 1/T show for both ΔB_n1 and ΔB_n2 good straight-line fits with process-specific intercepts of C and slopes of (−E_A/R). E_A is the activation energy for the bending intensity, and R is the gas constant. The parameter values are given in Table 1. Because of the perceived graphical redundancy with respect to Fig. 4, no graph is given for the Arrhenius relationships.

Table 1.

Arrhenius-equation fits (seeEq. 11) for the parameters ofEq. 9

Parameter	C ± SE	(−EA/R) ± SE	EA ± SE, kJ/mol	r2
ΔBn1	5.5 ± 1.08	−1.8 ± 0.36	15 ± 3.0	0.512
ΔBn2	−2.4 ± 0.47	1.1 ± 0.16	−9 ± 1.3	0.664
ln τ1	5.1 ± 0.97	0.5 ± 0.33	−4 ± 2.7	0.285
ln τ2	−8.8 ± 1.97	7.1 ± 0.67	−59 ± 5.5	0.824

The data underlying the fits are graphically summarized in Figs. 4 and 5. The slopes of the straight lines and thus the activation energies (E_A) are highly significant on the 95% level (p < 0.001, N = 26) for all cases except for ln τ₁ (p = 0.16; set in italics). C, y axis intercept; (−E_A/R), slope; E_A, activation energy; SE, standard error; r², coefficient of determination.

ΔB_n1 increases and ΔB_n2 decreases with temperature, so that calculated activation energies, derived from the Arrhenius-plots, are positive (15 kJ/mol) and negative (−9 kJ/mol), respectively (see Table 1).

Fig. 5 summarizes the data for the characteristic relaxation times of the two processes in an Arrhenius plot as ln τ_i versus 1/T. The slope of the straight line fit for ln τ₁ is not significant on the 95% confidence level (p = 0.16), and the data conform to a mean (±SE, N = 26) of ln τ₁ = 6.48 ± 0.055. In the given experimental context, ln τ₁ is thus found to be effectively independent of temperature. This yields a characteristic relaxation time for the first, fast process of ∼11 min (652 s). The activation energy, which is formally calculated for ln τ₁, is very low and lacks precision with –4 ± 2.7 kJ/mol (see Table 1). The value is significantly different from zero only on the 84% confidence level.

Figure 5.

Data for the characteristic relaxation times (s) τ₁ (•) and τ₂ () in an Arrhenius plot as ln(τ_i) versus 1/T (N = 26). Straight lines are fitted through the data. The coefficients for the linear fit equations are given in Table 1. The position of the anticipated, but conspicuously absent, transition around 60°C is marked. To see this figure in color, go online.

The temperature dependence of the characteristic relaxation time for the second, slow process (τ₂) is quite pronounced, in contrast. It decreases significantly with temperature and essentially linearly in the Arrhenius plot. Within the experimental temperature limits, τ₂ varies between ∼13 days (35°C) and ∼9 h (95°C). The fit in Fig. 5 yields an activation energy of −58 ± 5.5 kJ/mol (see Table 1).

Discussion

General considerations

The recovery curves, which we observed in the range of 35–95°C in water, indicate a two-stage process of shape memory (see Fig. 1 b). It is interesting to note that the temperature above which the second process seems to become more apparent coincides with the expected transition temperature (∼60°C). Such a combination of a fast and slow process can be seen in the relaxation curves of wool in water (1–90°C) (35). Namely, the second process is suppressed at low pH (35), supporting the notion that the relaxation mechanism is related to SH/SS interchange. The assumption of two relaxation processes is also broadly supported by the investigation by Wall et al. (43) on multiple relaxation processes in hair.

The presumed analogy between cohesive and permanent set leads to the application of the Denby equation. The analysis of the recovery curves is based on two independent and consecutive viscoelastic processes for which the relaxation functions are assumed to be of the KWW type (8,32,48). To enable a stable fit of the data through Eq. 9 and against the background of general considerations (54,55), we introduce specific shapes for the viscoelastic functions. We base these on the hypothesis of two different BER mechanisms of SH/SS interchange of stressed disulfide bonds. On this basis, we could successfully fit the overall shape memory/recovery curves and determine the temperature dependencies of the bending intensities ΔB_n1 and ΔB_n2 and of the characteristic relaxation times τ₁ and τ₂.

Bending intensities

Over the experimental temperature range (35–95°C), ΔB_n1 increases 2.8 times, whereas ΔB_n2 in parallel decreases to 0.56, assuming a linear fit and taking 35°C as point of reference (see Fig. 4). The relative changes are much larger than would be expected from the drop of modulus over the temperature range for wool and hair (∼20% (15,35,51)).

The tensile modulus of wool and hair in water is mainly a property of the partly α-helical IFs with a relatively small contribution by the amorphous protein matrix (3,21,63). The temperature dependencies of ΔB_n1 and ΔB_n2 imply in view of Eqs. 7 and 8 substantial temperature dependencies of the fractional bending rigidities of ΔB₁ as well as of ΔB₂, which are considered as properties of the amorphous matrix. Such significant changes of both bending intensities with temperature appear reasonable because water has a strong plasticizing effect on the matrix (7,10).

Given the strictly compensatory relationship between ΔB_n1 and ΔB_n2, their activation energies have opposite signs. However, the difference between the absolute values for their E_A values appears rather puzzling at first sight. Our explanation for this problem follows the following line of thought. The elastic tensile modulus of hair is essentially a property of the IFs. In water, it decreases with temperature (51), consistent with an activation energy of E_A = −3.7 ± 0.46 ≈ −4 kJ/mol. This is in good agreement with earlier results for wool (−3.9 kJ/mol (35)). We assume this value to be a reasonable estimate for the activation energy of B_re [E_A(B_re)], as a property of the IFs. From Eqs. 7 and 8 and with the values in Table 1, it can be shown that

$$E_A\left(\mathit{\Delta }{B}_1\right)=E_A\left(\mathit{\Delta }{B}_{n\mathit{1}}\right)+E_A\left(B_{re}\right)=\mathit{15}-\mathit{4}=\mathit{11}\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l}$$ (12)

and

$$E_A\left(\mathit{\Delta }{B}_2\right)=E_A\left(\mathit{\Delta }{B}_{n\mathit{2}}\right)+E_A\left(B_{re}\right)=-9-\mathit{4}=-13\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l}.$$ (13)

In view of the underlying assumptions, the absolute values for the outcomes of Eqs. 12 and 13 are considered as being essentially equal at |E_A| ≈ 12 kJ/mol. As a condition inherent to Eq. 9, the partial bending rigidities thus show the same activation energies, though with opposite signs. They thus change in a consistent and truly compensatory manner. Because the opposite signs for the activation energies are imposed by the compensatory nature of Eq. 9 and because bending rigidities will decrease with temperature, we assign an estimate for the “true” activation energy of −12 kJ/mol to both ΔB₁ and ΔB₂.

The fractional bending rigidities ΔB₁ and ΔB₂ are associated with the amorphous matrix component. Accordingly, the result that their activation energy of ≈−12 kJ/mol is ∼3 times higher than the estimate for E_A(B_re) (≈ −4 kJ/mol), as a property of the partially crystalline IFs, appears reasonable. Because of the axially oriented filament/matrix structure of the hair fiber core (cortex), torsional properties are largely a property of the matrix (3). Feughelman and Mitchell (64) investigated the torsional modulus of wool fibers in water at temperatures between 7 and 44°C. Their data conform to E_A = −16 ± 2.2 kJ/mol. This value is in satisfactory agreement with the value of −12 kJ/mol, as given above. This supports the underlying assumption of ΔB_1&2 as being matrix properties.

We were surprised that the results for ΔB_n1&n2(T) in Fig. 4 show no indication of the expected transition around 60°C (17, 18, 19). Initially, we assigned this absence to possible thermal compensation effects in Eqs. 7 and 8. However, the differences between the activation energies for B_re and ΔB_{1 &2} do not support this view but rather suggest the factual absence of the transition.

Characteristic relaxation times

The characteristic relaxation time for the first SM process (τ₁) is found to only show a very small and statistically nonsignificant dependence on temperature [E_A(τ₁) = −4 ± 2.7 kJ/mol]. It is interesting to note, however, that Haly and Snaith (41) found a similarly low value (E_A = −0.65 kcal/mol = −2.7 kJ/mol) for the second stage of the recovery of wool fibers from tensile cohesive set. They consider this low value as being consistent with a bond exchange mechanism, for which the required energy is small. This corresponds to the mechanism that we propose for the first process of shape recovery, as discussed above. It also fits into the framework of the suggested formal analogy of shape memory/recovery processes for cohesive and permanent set. Though the accurate determination of the variation of τ₁ with temperature is thus somewhat beyond the resolution of our method, E_A(τ₁) = −4 kJ/mol appears to be a reasonable estimate in the context of the literature (41).

In contrast, the activation energy for τ₂ is much higher [E_A(τ₂) = −58 kJ/mol] and in reasonable agreement with E_A = −47 kJ/mol as determined by Wall et al. (43) for the second, long-term relaxation in hair. The value is somewhat lower but of the same order as the value determined by Weigmann et al. (15) for relaxation through SH/SS interchange (−96 kJ/mol). Furthermore, it is important to note that neither of the τ₁ nor the τ₂ values shows any indication of the expected transition in the region of 60–70°C, in line with the observations for ΔB_n1&n2.

Conclusions

Our investigation of the SM behavior of perm-waved hair has revealed two underlying viscoelastic recovery processes. Central for our approach to the analysis of the data is the assumption of a fundamental analogy between shape memory from cohesive set on the one hand and from permanent set on the other. Cohesive set and the related shape recovery are based on the breaking and reformation of hydrogen bonds—namely, under the action of water and temperature (3,21). For this case, the humidity-dependent glass transition of hair is a well-defined and classical “trigger” (8,10). In the case of permanent set, the SS bonds dynamically form and reform through SH/SS interchange. For this BER, we had reasons (13, 14, 15, 16, 17, 18) to expect the trigger temperature to be around 60°C in water at neutral pH (16). However, our results show no sign of this transition.

We note that this transition has generally been observed under conditions of high tensile strains in wool and hair (13, 14, 15, 16, 17, 18,65). Such strains are well outside the range relevant for perm-wave formation (30,31). The conspicuous absence of the transition in our results indicates that there is a significant difference between SH/SS-driven recovery from low bending strains compared with high tensile strains. This is in line with the differences of the viscoelastic performance of keratin fibers at low strains in the linear viscoelastic and at high strains in the nonlinear region, respectively (17,66).

The main difference between low (<2%) and higher strains is the degree of α→β transition in the helical segments of the IFs (63). The IFs contain in fact only very few SS bonds—namely, in the 2B segments (63). These segments only unfold at high strains in what is called the postyield region of hair (ε > ≈ 30%) and under special conditions (at higher temperatures in water or under reductive condition) (63). With the absence of the transition at low strains, we hypothesize that the 60°C transition in water is a BER specific to the SS bonds in the 2B segments of the IFs at high strains.

In summary, we hypothesize that the shape memory performance of perm-waved hair is dependent on the smooth temperature dependence of the exchange reactions of covalent bonds in the matrix of the hair composite, considered as autocatalytic, rather than on a well-defined trigger transition. This leads us to classify this behavior as “atypical.”

For the practical context, our investigation explains why a perm-wave may occasionally show unsatisfactory shape formation and stability. This will happen, namely, if hair is not extensively rinsed between processing steps, in line with good hair styling practice (67). We attribute this instability to a higher survival rate of SH or even more reactive S⁻ groups if the internal pH is not sufficiently readjusted toward neutral. The enhanced concentration of SH groups will facilitate the first, fast SM process.

For well-processed hair, the stability of the wave will depend on the second, long-term recovery process. If we assume 45°C as a reasonable upper limit for water temperature for washing hair (12), the mean relaxation time for this process is ∼7–8 days. For all practical purposes, the wave will thus be perceived as permanent. Certain lifestyle habits (e.g., frequent sauna visits: 100°C, τ₂ ≈ 7 h) may, nevertheless, enhance the consumer perception of hair shape instability.

Against this background, we conclude that the need for reprocessing of permed hair after ∼6–8 weeks is mainly due to hair regrowths. The additional perceived loss of shape toward the hair tips is, in our view, not associated with a genuine lack of stability of hair shape or the action of special trigger stimuli (23). We rather attribute it to changes/damage imparted to the morphological structures of the hair through natural weathering processes (a combination of UV exposure, humidity, and heat (68)) or further common grooming practices (bleaching, dyeing (69)).

Finally, we are well aware that our decision to neglect certain factors may impose limitations on to the current analysis. First, the assumption of a homogeneous reductive/oxidative treatment is of only limited validity (70,71), namely, in view of the differences of the accessibility of the disulfide bonds (72). Second, the treatment will impart changes/damage to the IFs as well as the matrix in hair (73,74). These may, however, be largely compensated due to the structure of Eq. 9. Third, we did not consider a special role for the outer layer of hair, the cuticle (2). It is well known that the chemical, physical, and mechanical properties of the cuticle deviate markedly from those of the cortex (2,70,75). Though we maintain that the consistency of our results justifies the underlying simplifications and restrictions, we nevertheless believe that the refinement of the approach may provide substantial academic as well as practically relevant challenges and opportunities for further investigations.

Author contributions

Conceptualization, F.J.W. and G.W.; Data Organization, C.J. and T.J.D.; Formal Analysis, F.J.W. and T.J.D.; Investigation, G.W. and C.J.; Methodology, F.J.W., G.W., C.J., and T.J.D.; Project Administration, F.J.W. and C.J.; Resources, C.J. and T.J.D.; Supervision, F.J.W. and G.W.; Visualization, F.J.W.; Writing – Original Draft Preparation, F.J.W., G.W., C.J., and T.J.D.; Writing – Review and Editing, F.J.W. and G.W.

Editor: Mark Alber.