Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2021 Jul 13;120(17):3544–3549. doi: 10.1016/j.bpj.2021.07.009

ColBuilder: A server to build collagen fibril models

Agnieszka Obarska-Kosinska 1,2, Benedikt Rennekamp 1,3,4, Aysecan Ünal 1,3, Frauke Gräter 1,3,4,∗
PMCID: PMC8456305  PMID: 34265261

Abstract

Type I collagen is the main structural component of many tissues in the human body. It provides excellent mechanical properties to connective tissue and acts as a protein interaction hub. There is thus a wide interest in understanding the properties and diverse functions of type I collagen at the molecular level. A precondition is an atomistic collagen I structure as it occurs in native tissue. To this end, we built full-atom models of cross-linked collagen fibrils by integrating the low-resolution structure of collagen fibril available from x-ray fiber diffraction with high-resolution structures of short collagen-like peptides from x-ray crystallography and mass spectrometry data. We created a Web resource of collagen models for 20 different species with a large variety of cross-link types and localization within the fibril to facilitate structure-based analyses and simulations of type I collagen in health and disease. To easily enable simulations, we provide parameters of the modeled cross-links for an Amber force field. The repository of collagen models is available at https://colbuilder.h-its.org.

Significance

Collagen I is the most abundant protein in our body. Modeling and simulations of collagen as it occurs in connective tissue can enhance our understanding of collagen function in health and disease. However, a straightforward path toward an atomistic model of collagen I, including its various and chemically unique cross-links across tissues, is lacking. Our Web resource, ColBuilder, available at https://colbuilder.h-its.org, shall fill this gap. It makes collagen I models available across species and tissues by allowing different choices of cross-link types and positions for further computational analyses and simulations.

Introduction

Collagen is a major high-performance material of the human body. It confers to the connective tissue extraordinary viscoelasticity and resilience. Type I collagen forms triple helices composed of two collagen α-1(I) chains and one collagen α-2(I) chain, which are ∼1000 aa long and rich in glycines, prolines, and hydroxyprolines. Triple helices are aligned in bundles, in which the individual triple helices (∼300 nm long) are staggered relative to one another, resulting in a 67-nm-wide pattern of gap and overlap regions (1,2).

The helices are enzymatically connected by covalent cross-links between specific lysine side chains (Fig. 1). Initially, divalent cross-links between two side chains are formed, which can further react to form trivalent cross-links, connecting three side chains (3). Cross-link types and abundance critically decide on the mechanical response of collagen (4,5) and have recently been shown to change under mechanical load (6).

Figure 1.

Figure 1

Open in a new tab

Types of enzymatic collagen cross-links. Divalent cross-links are formed between two side chains, one of the telopeptide region and the other one of the triple helical regions of the neighboring collagen molecule. Trivalent cross-links are formed between two residues of the telopeptide region of one collagen molecule and one of the triple helical regions of the neighboring collagen molecule. To see this figure in color, go online.

Mechanical properties of type I collagen are well characterized experimentally (7), and there is wide interest in understanding these and other functions on the molecular level. Structural analyses, molecular modeling of protein-protein interactions or disease mutants, or molecular simulations to study dynamical and mechanical properties (8, 9, 10, 11) require an atomistic model of a collagen fibril as a starting point. The best resolution structure of type I collagen that includes the three-dimensional packing and cross-linking of triple helices has been a milestone in our understanding of collagen structure, mechanics, and function. However, this structure has only been solved at 5.4 Å.

On the other hand, a large additional body of data on collagen I structure from x-ray crystallography of short triple helices and on collagen I cross-linking from mass spectrometry are available that can further refine our view on collagen I as it occurs in native fibers.

We here used an integrative modeling approach to build fully atomistic models of collagen fibrils using available structural and biochemical data. The models are based on the 5.4-Å structure of Orgel et al. (2) and are in accordance with currently available additional data not used for the modeling, such as heavy-atom labeling (12) and neutron diffraction (13). Our online repository includes a large set of type I collagen structures of different sequences and cross-linking scenarios representing different species, tissue types, and ages. The available atomistic structures can aid the structural interpretation of experimental biochemical, mechanical, or functional data. They are a basis for further modeling and molecular simulations such as molecular dynamics (MD), as we also provide Amber force field parameters. It thus fills a gap in the collagen I field, as long as high-resolution data from native fibrils remain to be lacking.

Materials and methods

Collagen modeling

Generally, our modeling approach is to fit available higher-resolution biochemical data into lower-resolution structural data (see Fig. S1). We started with modeling Rattus norvegicus collagen, for which the sequence of collagen α-1(I) chain (residues 152–1207 of the sequence of P02454 UniProt accession number) and the sequence of collagen α-2(I) chain (residues 86–1125 of the sequence of P02466 UniProt accession number) were used.

The overall shape of collagen molecules and their relative packing within the collagen fibril were based on the low-resolution fibril structure from R. norvegicus (PDB: 3HR2) obtained with x-ray fiber diffraction (2). As stated, local interactions within the triple helices were modeled based on distance restraints derived from high-resolution collagen structures. These restraints were generated based on a collagen model built using THeBuScr (14), which allows building idealized models of single, straight collagen triple helix based on statistical parameters derived from high-resolution collagen-like peptides structures. The atomic model of the collagen triple helix was constructed using Modeller (15) by taking the PDB: 3HR2 structure as a template and replacing the template interatomic distance restraints with the high-resolution distance restraints. The N-telopeptide region was modeled using PDB: 3HR2 as a template. Two N-terminal residues missing in the original fibril structure were added at the N-terminus of the collagen α-2(I) chain. The model of the collagen fibril bundle was reconstructed by applying the symmetry information derived from the PDB: 3HR2 structure to the triple helix model.

C-telopeptide remodeling

Both telopeptides are predicted as intrinsically disordered. The electron density in this region from x-ray fiber diffraction does not allow definition of the preferred conformation, or rather a conformational ensemble, of these peptides within the fibril (Fig. S5). The C-telopeptide in the context of the neighboring triple helix was remodeled to allow the insertion of the missing 12 C-terminal residues of the collagen α-2(I) chain and two residues of both collagen α-1(I) chains such that the formation of divalent and trivalent cross-links was feasible. To this end, we used ISOLDE (16) for imposing distance restraints that enabled both divalent and trivalent cross-link reconstruction.

It is important to note that our models show the telopeptides in an extended conformation, which was necessary to accommodate the full collagen I sequence and the cross-links. As such, they differ from the hairpin conformation of the C-telopeptides suggested previously (2).

Homology modeling of type I collagen from other species

The models of the type I collagen fibril from other species were built using homology modeling based on the rat collagen I model. This was possible for 19 more species, for which sequence information was available and which did not require insertions or deletions of more than two residues when aligned to rat collagen sequences. The proline residues reported as being hydroxylated in biochemical studies or predicted as hydroxylated based on similarity as stated in UniProt (17) were modified to hydroxyprolines using Modeler. The resulting steric clashes between side chains were resolved using Phenix (18).

Parametrization of cross-links

The cross-links were parametrized for the Amber99 force fields. First, structures of cross-link molecules were built and capped with acetyl (ACE) and N-methyl (NME) residues using Maestro (19). Second, the geometry was optimized and the electrostatic potential was calculated using B3LYP/6-31G∗ method (20,21) in Gaussian (22). Third, the partial atomic charges were derived using the electrostatic potential using the restrained electrostatic potential fitting procedure (23) as implemented in Antechamber (24). During the fitting, the atoms of NME and ACE residues were constrained to have the same charges as in Amber99 force fields (25). Next, the resulting force field parameters were converted to Gromacs format using Acpype (26). To add as few new parameters as possible, we selected only the parameters that were missing in Amber99SB∗-ildnp force field (27,28), and we added them to the force field. All newly introduced parameters, such as cross-link topologies, special bonds, partial charges, and bonded parameters, are shown in Supporting material.

Modeling of cross-links within collagen fibril

Cross-links were added to the collagen fibril models by first changing the cross-linked lysine residues to modified residues harboring the chemical groups composing the cross-links using Modeller (15) and then connecting them by so-called special bonds in Gromacs (29). The resulting structure was optimized in Gromacs as follows: for each cross-link, a fragment of six neighboring helices around the cross-link, spanning around 20 residues along the fibril, was selected. The fragment was solvated in a TIP3P water model (30) with Na+ and Cl− ions at a concentration of 150 mM and minimized using the steepest-descent method with a step size of 1 pm and tolerance of 1000 kJ/mol/nm. The fragments of the minimized cross-links were then combined with the rest of the collagen model.

Web resource

Models for all combinations were precalculated and made available through an interactive Web form, which allows selecting the species (20 different choices), cross-link types (eight different choices), and cross-link composition (individual choices among cross-link types at different collagen sites within the same model). On the one hand, users can download PDB files containing models of a complete, 300-nm, single triple helix, which include the symmetry record allowing for the generation of the collagen fibril bundles of any size. On the other hand, we also provide models of predefined bundles of collagen fibril fragments, comprising 41 triple helices, spanning one central overlap and one gap region (the latter in two parts), as shown in Fig. 3. These models of fibril bundles are ready to use in MD simulations, e.g., using Gromacs. To this end, a tar archive with a complete modified Amber99SB∗-ildnp force field can be downloaded. Additionally, this archive contains a directory with only the additional cross-link parameters, which in turn can then be integrated into any Amber99 force field as well. In particular, it also contains parametrized residues for all cross-link types available in ColBuilder as described above. The Web repository, https://colbuilder.h-its.org, was built using JavaScript and LiteMol (31).

Figure 3.

Figure 3

Open in a new tab

Example model of a type I collagen fibril available through the ColBuilder Web resource. The model corresponds to a representative unit of a human collagen fibril with eight pyridinoline (PYD) N-terminal cross-links and eight hydroxylysino-keto-norleucine (HLKNL) C-terminal cross-links. It comprises 41 triple helices spanning one central overlap and one gap region (in two parts, left and right). Triple helices are colored according to the staggering distance; cross-links are shown in blue or colored by atom type. To see this figure in color, go online.

MD simulations

To validate our models, we performed MD simulations using Gromacs 2018.6 and 2020.3 (27) with time steps of 2 fs. A Verlet cutoff scheme was used with a cutoff distance of 1 nm, and long-range electrostatic interactions were accounted using the particle mesh Ewald method (32). LINear Constraint Solver (LINCS) procedure was used to constrain H-bonds (33).

Besides our reference model species, R. norvegicus, we selected two more species (Pongo abelii and Loxodonta africana) and, for each species, used two fibril models with either divalent or trivalent cross-links, leading to six models that were used for detailed testing. We expect these choices to be representative of the whole set of models that we created.

As stated in the Web resource section, the fibril fragments span in total one gap and one overlap region. Solvating the models with TIP3P water (30) in a periodic box and neutralizing the charges with counterions, we reach a total system size in the order of 2.5 million atoms. The system was relaxed with an energy minimization using steepest descent. Afterward, 10 ns of NVT followed by 10 ns of NPT equilibration were used to adjust the temperature and the pressure of the system, respectively. The temperature was stabilized at 300 K by the v-rescale thermostat (34) with a time constant of 0.1 ps. The pressure was maintained at 1 bar by a Parinello-Rahman barostat (35) with isotropic coupling with a time constant of 0.2 ps. During the 100-ns production run, rotational restraints were applied on each terminus to prevent the unwinding of the triple helices via the enforced rotation protocol (36). We performed two production runs for each model (three species with divalent or trivalent cross-links), resulting in 12 different simulations with a total simulation time of 1200 ns.

Results and discussion

Model of collagen I: from R. norvegicus to other species

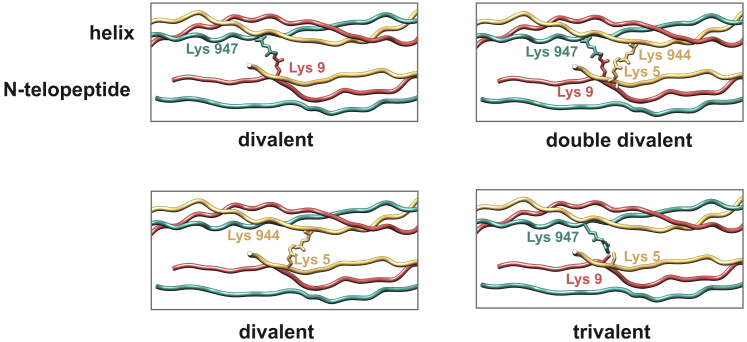
We first constructed a full-atom model of collagen from a representative species, R. norvegicus, which was later used as a template to build models from other species. This specific model,with divalent hydroxylysino-keto-norleucine (HLKNL) cross-links, has been published previously (37), and we shortly summarize the procedure here (see Materials and methods for details). In the original fibril structure (3HR2), 16 residues were missing in the C-telopeptide region: 12 C-terminal residues (YDFGFEGGFYRA) of the collagen α-2(I) chain, two C-terminal residues (RA) of each of the collagen α-1(I) chains. The lysine residues at the C-telopeptide region acting as precursors for the divalent cross-links were positioned in the initial fibril model such that divalent cross-links can be constructed between them. For the trivalent cross-links, however, one residue was positioned too far to be connected with other cross-linked residues without imposing a severe conformational change of the backbone (Fig. S2). Thus, we remodeled the structure of the C-telopeptides in the context of the neighboring triple helix to allow the insertion of the missing fragments such that the formation of divalent and trivalent cross-links was feasible. We also added two missing residues at the N-terminus of the collagen α-2(I) chain. The lysine residues at the N-telopeptide, which act as precursors for the divalent cross-links, were positioned in the initial fibril model such that both divalent and trivalent cross-links between them could be formed. The model of the collagen fibril bundle was reconstructed by applying the symmetry information derived from the 3HR2 structure to the triple helix model. Finally, we reconstructed divalent and trivalent cross-links (Fig. 1) in the collagen fibril model (Fig. 2). Because pairs of cross-linked lysine residues are not unambiguously defined by the available mass spectrometry data (3), we built the models for all possible pairs of lysine residues that were properly positioned for the cross-link formation (Fig. 2; Figs. S3 and S4).

Figure 2.

Figure 2

Open in a new tab

Positioning of cross-links. Examples are shown for cross-links between the N-telopeptide (bottom) and an adjacent triple helix (top). Chains and the cross-linked residues of these chains are color-coded (green, red: α1, yellow: α2). For a complete list of possible cross-link positions, see Figs. S3 and S4. To see this figure in color, go online.

We then used the model of rat collagen to model the type I collagen from 19 other species. For all models, we built the corresponding full fibril models and reconstructed all possible cross-links.

We provide all models for download through an interactive Web resource (see Materials and methods for details). In total, type I collagen fibril models from 20 species with different combinations of cross-link types observed in collagen can be retrieved from the website (Fig. 3).

MD simulations and comparison to structural data

To validate our models, we performed MD simulations of three representative collagen species both with divalent and trivalent cross-links as described in the Materials and methods. We expect this representation to be representative of the whole set of models and show the combined analysis of the data for all of them here.

The modeled conformation of the telopeptide regions results in a 32.8-nm overlap region (Fig. 4 a). Given a 67.6-nm-long characteristic banding pattern (D-period), the overlap region spans 0.485D in our model. However, this can be considered an upper limit because the high disorder will further shrink this estimate as a result of the high mobility of the telopeptide region. For this reason, we measured the respective distances and the resulting overlap-to-d ratio in our MD simulations. As shown in Fig. 4 c, the overlap distance decreases, especially at the beginning of the simulations, leading on average to a ratio of ∼0.465. Hence, the modeled telopeptide conformation falls within the range of previous experimental estimates of this ratio (between 0.40 and 0.48D) (1,13,38,39).

Figure 4.

Figure 4

Open in a new tab

Comparison to experimental data. (a) Overlap/gap ratio as given by the length of overlap region (measured as shown in the upper figure) and overall D-period length is at most, taking full telopeptide region into account, 0.485/0.515. (b) Distribution of Tyr (blue) and His (red) along fiber model as observed in our model and 3HR2 with different telopeptide conformation is shown and compared with regions, in which iodination (marking Tyr and His) is above the noise (boxed areas, Orgel et al. (12)). (c) Gap and overlap lengths for the complete set of our 12 simulations: starting from a configuration as shown in (a), the overlap distances and, hence, the average ratio decreases to ~0.465/0.535 (bold line: average, transparent lines: individual replica) (d) All-to-all distances between the center of masses of the triple helix (a cross-sectional slice of the overlap region thereof) at 0, 50, and 100 ns simulation time. The counts in the histograms are summed up across all our models, whereas an exemplary slice for one individual replica (R. norvegicus, HLKNL cross-link) is shown on the right. The dashed lines in the histogram indicate the average distance to nearest, next, and over-next nearest neighbors. To see this figure in color, go online.

Furthermore, the heavy-atom labeling data also agree with the extended telopeptide conformation put forward here (Fig. 4 b).

Third, we investigated the stability of the packing of the collagen molecules. Fig. 4 d shows the all-to-all distances between the center of masses of the triple helices. This was done by looking into a slice of the fibril in the overlap region (in the middle of the system), for which exemplary densities are shown to the right of the histogram. Importantly, the average distances to nearest and next-nearest neighbors stay constant, as indicated by the dashed lines. This shows that, despite some expected fluctuations of the finite-size fibril model, the interhelical distances stay in line with the x-ray data used for modeling.

Lastly, we point out that one model (R. norvegicus with divalent HLKNL cross-links) has been previously employed in MD simulations (37,40), underlining potential use cases of the repository: in both studies, mechanical properties of collagen were investigated in different aspects by applying pulling MD simulations.

Taken together, the atomistic collagen models dynamically explore a conformational space that is close to the x-ray fiber diffraction data and also in line with other experimental observations (gap/overlap ratio and heavy-atom labeling). However, given the lack of high-resolution data for collagen I and the high disorder of the telopeptide regions, we note that our atomistic models in this region represent only one of the possible conformations that allow for accommodating divalent as well as trivalent cross-links, and the structure of this region should be interpreted with caution.

Conclusions

The key advantage of the repository is that it provides complete and refined models accompanied by force field parameters that can be used for atomistic MD simulations, including pulling simulations (37,40).

We expect the repository to facilitate the structural investigation of a wide range of collagen aspects, such as molecular interactions with other proteins, localization of other cross-links, disease mutants, or others. In the future, we will update—and invite the community to contribute to—the repository with new models and force fields. Those could include improved models if new experimental structures of the fibril will become available, new force field parameters for other collagen cross-links such as advanced glycation end products (29), as well as other atomistic and coarse-grained force fields that incorporate these cross-links and prove suitable for collagen’s unique secondary and tertiary structure.

Acknowledgments

We thank Dr. Grzegorz Chojnowski for advice on structure refinement.

The authors acknowledge support by the Klaus Tschira Foundation, the Excellence Cluster CellNetworks, the Center for Modelling and Simulation in the Biosciences (BIOMS) of Heidelberg University, the Volkswagen Foundation through an Experiment! grant, the Gauss Centre for Supercomputing (GCS) e.V. (www.gauss-centre.eu) for providing computing time on the GCS Supercomputer SuperMUC-NG at Leibniz Supercomputing Centre (www.lrz.de) and the German Research Foundation (DFG) through grant INST 35/1134-1 FUGG. This research was conducted within the Max Planck School Matter to Life supported by the German Federal Ministry of Education and Research (BMBF) in collaboration with the Max Planck Society.

Editor: Jianhan Chen.

Footnotes

Agnieszka Obarska-Kosinska's present address is Max PIanck Institute for Biophysics, Frankfurt am Main, Germany.

Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.07.009.

Supporting material

Document S1. Figs. S1–S5 and Table S1
mmc1.pdf (2.3MB, pdf)
Document S2. Article plus supporting material
mmc2.pdf (3.5MB, pdf)

References

  • 1.Hodge A.J., Petruska J.A. In: Aspects of Protein Structure. Ramachandran G.N., editor. Academic Press; 1963. Recent studies with the electron microscope on ordered aggregates of the tropocollagen molecule; pp. 289–300. [Google Scholar]
  • 2.Orgel J.P., Irving T.C., Wess T.J. Microfibrillar structure of type I collagen in situ. Proc. Natl. Acad. Sci. USA. 2006;103:9001–9005. doi: 10.1073/pnas.0502718103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Eyre D.R., Weis M.A., Wu J.J. Advances in collagen cross-link analysis. Methods. 2008;45:65–74. doi: 10.1016/j.ymeth.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Depalle B., Qin Z., Buehler M.J. Influence of cross-link structure, density and mechanical properties in the mesoscale deformation mechanisms of collagen fibrils. J. Mech. Behav. Biomed. Mater. 2015;52:1–13. doi: 10.1016/j.jmbbm.2014.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Gautieri A., Passini F.S., Snedeker J.G. Advanced glycation end-products: mechanics of aged collagen from molecule to tissue. Matrix Biol. 2017;59:95–108. doi: 10.1016/j.matbio.2016.09.001. [DOI] [PubMed] [Google Scholar]
  • 6.Stammers M., Niewczas I.S., Clark J. Mechanical stretching changes crosslinking and glycation levels in the collagen of mouse tail tendon. J. Biol. Chem. 2020;295:10572–10580. doi: 10.1074/jbc.RA119.012067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Fratzl P. Springer; New York: 2008. Collagen - Structure and Mechanics. [Google Scholar]
  • 8.Masic A., Bertinetti L., Fratzl P. Osmotic pressure induced tensile forces in tendon collagen. Nat. Commun. 2015;6:5942. doi: 10.1038/ncomms6942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Misof K., Rapp G., Fratzl P. A new molecular model for collagen elasticity based on synchrotron X-ray scattering evidence. Biophys. J. 1997;72:1376–1381. doi: 10.1016/S0006-3495(97)78783-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Puxkandl R., Zizak I., Fratzl P. Viscoelastic properties of collagen: synchrotron radiation investigations and structural model. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002;357:191–197. doi: 10.1098/rstb.2001.1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kwansa A.L., De Vita R., Freeman J.W. Tensile mechanical properties of collagen type I and its enzymatic crosslinks. Biophys. Chem. 2016;214–215:1–10. doi: 10.1016/j.bpc.2016.04.001. [DOI] [PubMed] [Google Scholar]
  • 12.Orgel J.P., Wess T.J., Miller A. The in situ conformation and axial location of the intermolecular cross-linked non-helical telopeptides of type I collagen. Structure. 2000;8:137–142. doi: 10.1016/s0969-2126(00)00089-7. [DOI] [PubMed] [Google Scholar]
  • 13.Hulmes D.J.S., Miller A., Berthet-Colominas C. Interpretation of the low-angle meridional neutron diffraction patterns from collagen fibres in terms of the amino acid sequence. Int. J. Biol. Macromol. 1980;2:338–346. [Google Scholar]
  • 14.Rainey J.K., Goh M.C. An interactive triple-helical collagen builder. Bioinformatics. 2004;20:2458–2459. doi: 10.1093/bioinformatics/bth247. [DOI] [PubMed] [Google Scholar]
  • 15.Šali A., Blundell T.L. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
  • 16.Croll T.I. ISOLDE: a physically realistic environment for model building into low-resolution electron-density maps. Acta Crystallogr. D Struct. Biol. 2018;74:519–530. doi: 10.1107/S2059798318002425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.UniProt Consortium UniProt: a worldwide hub of protein knowledge. Nucleic Acids Res. 2019;47:D506–D515. doi: 10.1093/nar/gky1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Liebschner D., Afonine P.V., Adams P.D. Macromolecular structure determination using X-rays, neutrons and electrons: recent developments in Phenix. Acta Crystallogr. D Struct. Biol. 2019;75:861–877. doi: 10.1107/S2059798319011471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Schrödinger LLC . Schrödinger LLC; New York: 2016. Schrödinger release 2016–2: Maestro, version 10.6. [Google Scholar]
  • 20.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
  • 21.Becke A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
  • 22.Frisch M.J., Trucks G.W., Fox D.J. Gaussian Inc.; Wallingford, CT: 2016. Gaussian 09, revision A.02; p. 27. [Google Scholar]
  • 23.Bayly C.I., Cieplak P., Kollman P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 1993;97:10269–10280. [Google Scholar]
  • 24.Wang J., Wang W., Case D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006;25:247–260. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
  • 25.Bayly C.I., Merz K.M., Spellmeyer D.C. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
  • 26.Sousa da Silva A.W., Vranken W.F. ACPYPE - Antechamber python parser interface. BMC Res. Notes. 2012;5:367. doi: 10.1186/1756-0500-5-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Best R.B., Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Abraham M.J., Murtola T., Lindahl E. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1:19–25. [Google Scholar]
  • 30.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
  • 31.Sehnal D., Deshpande M., Koča J. LiteMol suite: interactive web-based visualization of large-scale macromolecular structure data. Nat. Methods. 2017;14:1121–1122. doi: 10.1038/nmeth.4499. [DOI] [PubMed] [Google Scholar]
  • 32.Darden T., York D., Pedersen L. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
  • 33.Hess B. P-LINCS: a parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 2008;4:116–122. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
  • 34.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  • 35.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
  • 36.Kutzner C., Czub J., Grubmüller H. Keep it flexible: driving macromolecular rotary motions in atomistic simulations with GROMACS. J. Chem. Theory Comput. 2011;7:1381–1393. doi: 10.1021/ct100666v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Zapp C., Obarska-Kosinska A., Gräter F. Mechanoradicals in tensed tendon collagen as a source of oxidative stress. Nat. Commun. 2020;11:2315. doi: 10.1038/s41467-020-15567-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Bradshaw J.P., Miller A., Wess T.J. Phasing the meridional diffraction pattern of type I collagen using isomorphous derivatives. J. Mol. Biol. 1989;205:685–694. doi: 10.1016/0022-2836(89)90314-8. [DOI] [PubMed] [Google Scholar]
  • 39.Thomlin S.G., Worthington C.R. Low-angle X-ray diffraction patterns of collagen. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1956;235:189–201. [Google Scholar]
  • 40.Rennekamp B., Kutzki F., Gräter F. Hybrid kinetic Monte Carlo/molecular dynamics simulations of bond scissions in proteins. J. Chem. Theory Comput. 2020;16:553–563. doi: 10.1021/acs.jctc.9b00786. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figs. S1–S5 and Table S1
mmc1.pdf (2.3MB, pdf)
Document S2. Article plus supporting material
mmc2.pdf (3.5MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES