Sleep Apnea and Poor COVID-19 Outcomes: Beware of Causal Intermediates and Colliders

To the Editor:

We read with interest the report by Cade and colleagues on the association between obstructive sleep apnea (OSA) and adverse outcomes such as hospitalization and death among adults with coronavirus disease (COVID-19) (1). We commend the authors for asking this important research question and their thorough analysis. However, for each of the three outcomes that they investigated, the effect of OSA as measured by the odds ratio was progressively attenuated as additional variables were adjusted for. It is possible that a portion of this attenuation may be due to overadjustment bias (2).

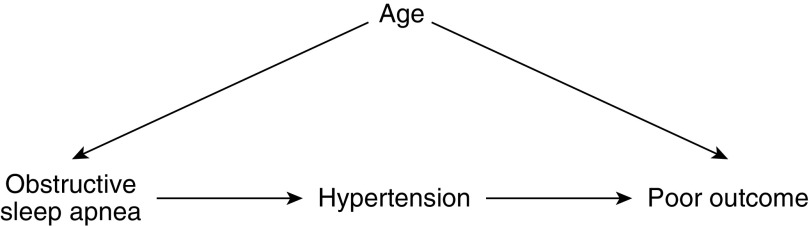
Overadjustment bias occurs when a data analyst controls for an intermediate variable on the causal path from the exposure variable (e.g., OSA) to the outcome (e.g., hospitalization due to COVID-19) (2). Causal diagrams may be used to identify causal intermediates and hence avoid overadjustment bias (2, 3). Figure 1 is a causal diagram known as a directed acyclic graph (DAG). In this simplified DAG from a hypothetical study, OSA is the exposure and the endpoint is poor outcome (PO), which represents the composite endpoint of inpatient admission, receipt of mechanical ventilation, or death. OSA may lead to hypertension, which in turn is a risk factor for a PO. Hypertension is a causal intermediate on the path between OSA and PO. According to this DAG, hypertension should not be adjusted for using stratification or other techniques such as multiple regression modeling. Controlling for (adjusting for) an intermediate will prevent the estimation of the total causal effect of OSA on PO (3).

Figure 1.

Directed acyclic graph for the effect of obstructive sleep apnea on poor outcome among patients with coronavirus disease (COVID-19). Age is a confounder of the association, whereas hypertension is a causal intermediate.

In Figure 1, the data analyst believes the patient’s age is a confounder of the association between OSA and PO. A confounder is a variable that is related to both the exposure and the outcome yet is not an effect of the exposure (4). When inspecting a DAG, a variable can be identified as a confounder of the association between the exposure and the outcome if it is a common cause of the exposure variable and the outcome (3). Confounders should be adjusted for.

An additional benefit of DAGs is the ability to identify colliders. A collider is a variable where two arrowheads meet (3). In other words, a collider is a variable that is in the middle of an inverted fork in a DAG (5). In Figure 2 (again, representing an association that may be studied in a hypothetical study), hypertension is a collider on the path from OSA to PO. Variable U in Figure 2 is an unmeasured variable, such as a medication or illness, that affects the risk of both hypertension and PO. If the data analyst controls for hypertension but does not control for U in this situation, then collider stratification bias will occur (3, 6). Controlling for a collider can result in a bias that is strong enough to move the observed association in a direction that is opposite of the true effect (3). Interestingly, in the analysis by Cade and colleagues, the odds ratio for the outcome of inpatient admission moved from 1.55 in the unadjusted model to 0.91 in model 4 (1). Without additional information, we cannot offer a reason why the odds ratio shifted to the other side of the null value of 1 in Cade’s study.

Figure 2.

Directed acyclic graph for the effect of obstructive sleep apnea on poor outcome among patients with coronavirus disease (COVID-19). Hypertension is a collider on the path from obstructive sleep apnea to poor outcome. U is an unmeasured variable such as a medication or illness.

DAGs are useful tools for identifying the minimally sufficient set of variables to control for to reduce confounding bias (3). Investigators may disagree over which DAG is correct for any given possible association. The DAGs presented here are overly simplistic. A freely available tool for creating DAGs is DAGitty (available at www.dagitty.net).