Summary
Deep‐water access is arguably the most effective, but under‐studied, mechanism that plants employ to survive during drought. Vulnerability to embolism and hydraulic safety margins can predict mortality risk at given levels of dehydration, but deep‐water access may delay plant dehydration. Here, we tested the role of deep‐water access in enabling survival within a diverse tropical forest community in Panama using a novel data‐model approach.
We inversely estimated the effective rooting depth (ERD, as the average depth of water extraction), for 29 canopy species by linking diameter growth dynamics (1990–2015) to vapor pressure deficit, water potentials in the whole‐soil column, and leaf hydraulic vulnerability curves. We validated ERD estimates against existing isotopic data of potential water‐access depths.
Across species, deeper ERD was associated with higher maximum stem hydraulic conductivity, greater vulnerability to xylem embolism, narrower safety margins, and lower mortality rates during extreme droughts over 35 years (1981–2015) among evergreen species. Species exposure to water stress declined with deeper ERD indicating that trees compensate for water stress‐related mortality risk through deep‐water access.
The role of deep‐water access in mitigating mortality of hydraulically‐vulnerable trees has important implications for our predictive understanding of forest dynamics under current and future climates.
Keywords: deep‐water access, drought tolerance, drought‐induced mortality, hydraulic vulnerability and safety margins, hydrological droughts, rooting depths, safety‐efficiency trade‐off, tropical forest
Introduction
Drought‐induced mortality in tropical forests may have significant global implications. Tropical forests play a disproportionately large role in the global carbon and energy cycles (Bonan, 2008), and support half of global biodiversity (Wright, 2005), but face a threat from intensifying droughts (Malhi et al., 2009; Doughty et al., 2015; Xu et al., 2019). Tropical forests are considered an especially drought‐vulnerable biome given the combination of climate risk and vegetation sensitivity (Meir et al., 2015). Still, mortality events in the tropics are rarely as large as those in temperate and boreal zones (McDowell et al., 2018a), leading to questions regarding the role of large trait‐diversity and hydraulic strategies in mitigating mortality events. Furthermore, mortality rates are increasing in some tropical regions (Brienen et al., 2015; Hubau et al., 2020) and widespread drought‐induced tree mortality has occurred across the tropics for specific functional groups (Phillips et al., 2010; Hilker et al., 2014; Bennett et al., 2015; Chitra‐Tarak et al., 2018). State‐of‐the‐art dynamic global vegetation models (DGVMs) struggle to capture these drought‐induced vegetation dynamics in the tropics (Galbraith et al., 2010; Powell et al., 2013, 2018), because underlying mechanisms of drought tolerance are not fully understood nor quantified.
Plants rely on a variety of structural and functional mechanisms to avoid or tolerate a drought, from deep‐water access, increased root production, hydraulic redistribution, embolism resistance, adjustment of leaf area (deciduousness) to change in leaf angle, reductions in stomatal conductance, upregulation of aquaporins, osmotic regulation and stem water storage capacitance (McDowell et al., 2008). Deep‐water access is arguably the most effective, yet under‐studied mechanism. As plant‐available water varies with depth, trees within the same forest with different rooting depths, depending on species and size (Meinzer et al., 1999; Chitra‐Tarak et al., 2018; Brum et al., 2019), differ in their experience during a drought, and thus in their growth and mortality responses (Chitra‐Tarak et al., 2018). A key bottleneck in community‐wide testing of this mechanism has been a lack of data in both trees’ rooting or water‐sourcing depths, and plant‐available soil water at those depths. A recent meta‐analysis documented maximum rooting depths for 318 tree species, that is, < 0.5% of > 60 000 tree species in the World (Beech et al., 2017; Fan et al., 2017). Furthermore, only a small fraction of those are tropical, even though > 90% of the World’s tree diversity resides in the tropics (Slik et al., 2015). The use of stable isotopes of water as a tracer provides an indirect measure of water sourcing depths by matching the isotopic value in xylem water to those in soil pore water at different depths. However, such data are rare (Evaristo et al., 2016). DNA barcoding of roots (Jones et al., 2011) may be used to estimate species‐specific rooting depths or profiles, but DNA barcode libraries for tropical forests are still under development, and the method may be cost‐prohibitive for the extent of sampling required. In general, community‐scale data collection for rooting or water‐sourcing depths is a formidable challenge in species‐rich tropical forests.
Characterizing the essential constraints to model species‐rich communities (Wright et al., 2010; Christoffersen et al., 2016; Maréchaux & Chave, 2017; Bartlett et al., 2019; Koven et al., 2020; Lu et al., 2020) entails identifying the topography of plant trait trade‐offs in different environments, and how these relate to demographic rates (growth, recruitment and mortality). Significant efforts have been invested into identifying and linking universal drought indices, aboveground traits and demographic rates. Such efforts have found correlations between vulnerability to embolism and hydraulic safety margins and mortality (Anderegg et al., 2016), although numerous counter examples also exist (Hoffmann et al., 2011; Paddock III et al., 2013; Nardini et al., 2015; Venturas et al., 2016; Johnson et al., 2018). Deep roots may mitigate hydraulic vulnerability (Brum et al., 2019) and mortality risk, in particular during hydrological (rather than meteorological) droughts. Nonetheless, the interaction between rooting depths, aboveground hydraulic traits, hydrological droughts quantified over the whole soil‐column and mortality outcomes are hardly studied.
In this paper, we estimate plant‐available water in the whole‐soil column in a tropical forest, and inversely estimate rooting depths of co‐occurring tree species from their growth responses, with a series of model calibrations and validation. We evaluate how rooting depth is linked to aboveground hydraulic traits and mortality rates through seven census intervals over a 35‐year period that experienced El Niño droughts of a variety of intensity, frequency and duration (Condit, 2017; Detto et al., 2018). Our hypotheses are that (1) deep‐rooted trees have hydraulic traits associated with rapid water transport but cavitation‐vulnerable xylem resulting from greater and more reliable water availability at depth (see Tables 1 and 2); and that, (2) deep‐rooted species have lower mortality rates during droughts resulting from a lower exposure to water stress compared to shallow‐rooted species. To our knowledge this is the first study to test for a mechanistic link between plant‐available water in the whole‐soil column, tree above‐ and belowground hydraulic traits, and multidecadal mortality outcomes for a species‐rich tropical forest.
Table 1.
The symbol, definition and units of key traits used in the simulations and analyses.
| Symbol | Definition | Units | |
|---|---|---|---|
|
|
Soil water potential at depth | MPa | |
| leaf, stem | Water potential of leaf, or stem, respectively | MPa | |
|
|
Bulk leaf turgor loss point, the leaf where turgor potential = 0 | MPa | |
| crit or 20,leaf | leaf at 20% loss of leaf conductance | MPa | |
|
|
stem at 88% loss of stem conductivity | MPa | |
|
|
Seasonal minimum leaf water potential, the most negative leaf measured at midday in the dry season | MPa | |
| min ‐ 88,stem | Aboveground hydraulic safety margin | MPa | |
| K leaf | Leaf‐area specific hydraulic conductance of leaf | mmol m−2 s−1 MPa−1 | |
| K max,leaf | Maximum leaf area‐specific hydraulic conductance of leaf | mmol m−2 s−1 MPa−1 | |
| K max,stem | Maximum stem area‐specific hydraulic conductivity of stem | kg m−1 s−1 MPa−1 | |
| FLC leaf | Ratio between current and maximum leaf‐area specific hydraulic conductance of leaf | ‐ | |
| WSG | Wood specific gravity | g cm−3 | |
| LMA | Leaf mass per unit area | g m−2 | |
| 2Hxylem | 2H of tree xylem sap | ‰ |
Table 2.
Hypotheses for association between effective rooting depth (ERD) and aboveground hydraulic traits.
| Variable | Deeper ERD | Shallower ERD | |
|---|---|---|---|
| K max,stem | Higher | Lower | |
|
|
Less negative | More negative | |
|
|
Less negative | More negative | |
| min– 88,stem | Narrower | Wider |
Materials and Methods
This work combines hydrology, physiology and demography of a tropical forest at Barro Colorado Island, Panama, to inform the inverse model for rooting depths; validates the model, and tests hypotheses pertaining to relationship of rooting depths with aboveground hydraulic traits, drought exposure and mortality (Fig. 1). We defined species‐specific effective rooting depths (ERD) as the depth at which the growth factor determined by soil water potential and leaf hydraulic traits best explained species’ growth dynamics over 25 years. Developing a novel, empirical inverse model, we estimated ERDs for large trees of 29 species. The ERD model incorporated the impact of atmospheric and hydrological drought on growth, and was constrained with species‐specific leaf vulnerability curves. For the latter, we used existing data for eight species and developed trait‐based proxies for the rest (based on data for a total of 21 species). We obtained the daily dynamics of soil water potential in the whole‐soil column (≤ 13 m) over the 25 years by locally parameterizing a 1D hydrological water balance of the forest within a land surface model for an average vegetation type. The water balance was calibrated on available measurements, in particular continuous soil moisture data in three surface layers (over the first meter of soil), stream discharge and evapotranspiration.
Fig. 1.
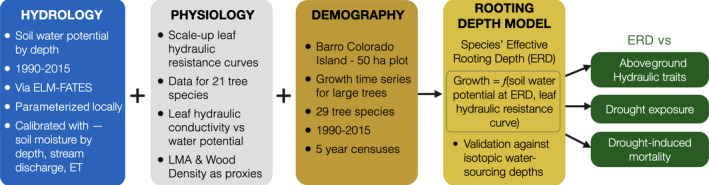
A schematic diagram outlining the methods workflow, which combines hydrology, physiology and demography of the tropical forest at Barro Colorado Island to inform the inverse model for rooting depths; validates it, and tests hypotheses pertaining to relationship of rooting depths with aboveground hydraulic traits, drought exposure, and drought‐induced mortality. ELM‐FATES, Energy Exascale Earth System Land Model coupled with the Functionally Assembled Terrestrial Ecosystem Simulator; ET, evapotranspiration; LMA, leaf mass per unit area.
We validated our ERD estimates against existing stable hydrogen isotope ratios ( 2Hxylem) for a subset of six tree species as independent observations. We evaluated whether ERD was associated with aboveground hydraulic traits, sourcing the latter from a set of rare datasets for six to seven species that overlapped with our assessment of ERD. We tested the relationship of ERD with xylem vulnerability to embolism, branch hydraulic safety margins, leaf turgor loss point and maximum stem‐specific hydraulic conductivity. We analyzed whether ERD is correlated with mortality dynamics of large trees for evergreen and deciduous species over 35 years marked by several El Niño events. Finally, to test whether ERD explained risk of drought‐induced mortality, we analysed species‐level exposure to water stress.
Study site description
We conducted this study at Barro Colorado Island (BCI), Panama. The entire island is forested and classified as a tropical moist forest in the Holdridge Life Zone system. Long‐term hydrological monitoring at BCI began in 1972, whereas demographical monitoring began with the 50 ha ForestGEO plot establishment in 1981–82 (Condit, 1998; Hubbell et al., 1999; Anderson‐Teixeira et al., 2014). Rainfall at BCI is seasonal with a mean annual total of 2627 mm ( 516 SD; 1985–2019) and a pronounced dry season from mid‐December through April with < 100 mm of rainfall per month (Paton, 2019a, 2020). In the 50 ha (1000 m × 500 m) old growth forest plot, all stems 1 cm diameter at breast height (dbh) were mapped, tagged with a unique number, identified to species and measured every five years through 1985–2015 for growth, mortality as well as recruitment of new stems into the 1‐cm dbh size class (Condit, 2017). This inventory represents 321 woody species, 28% of which are at least partly dry‐season deciduous (Condit et al., 2000). The plot elevation is 120–160 m above sea level, and thus the elevation range is only 40 m (Harms et al., 2001). Soils are homogeneous with red light clays accounting for 72% of the plot (Baillie et al., 2007). The topsoil field texture is silty clay loam that gradually fines to silty clay in the subsoil. Soil is mostly free draining, but restricted subsoil permeability gives rise to temporary wet season ponding. Detailed descriptions of the climate, geology, flora and fauna of BCI can be found elsewhere (Croat, 1978; Leigh et al., 1982; Gentry, 1990).
Model for ERD
ERD model description
Roots could impact tree growth through two factors: (1) water uptake; and (2) nutrient uptake. Because our study was situated in an old‐growth tropical forest, we assumed that nutrients are mainly concentrated in the shallow soil layers derived from litter decomposition, and that rooting depths do not substantially affect nutrient uptake. Because our study site has a dry season, we expected that rooting depth is a key factor affecting tree growth. We defined species‐specific effective rooting depth (ERD) as the depth at which a soil moisture growth limitation factor, , determined by the soil water potential and hydraulic traits best explained species’ diameter growth dynamics. is used to approximate the amount of stomatal closure due to water stress in the soil. In this study, we used the fractional loss of hydraulic conductivity of the leaf ( leaf) to estimate . leaf is calculated as a fraction of maximum leaf conductivity ,
| (Eqn 1) |
where leaf, current leaf hydraulic conductance; , maximum leaf hydraulic conductance (see Table 1 for trait symbols and their definitions). The dynamics of leaf are estimated from the species‐specific relationship between leaf vs leaf, referred to as the leaf hydraulic vulnerability curve (Sack & Scoffoni, 2012). The vulnerability to loss of hydraulic conductivity arises not only from embolism, but also from extra‐xylem processes (Scoffoni & Sack, 2017). Because pre‐dawn leaf generally approaches soil, this allowed us to substitute leaf with soil in leaf hydraulic vulnerability curves for each species – defined below in Eqn 4 using species‐specific parameters and – to predict maximum diurnal for each day ,
| (Eqn 2) |
was obtained as the maximum value of using Eqn 2. leaf is strongly related to photosynthetic capacity (Brodribb et al., 2002). Because we were interested in relating leaf to 5‐year average diameter growth observations, we ignored diurnal dynamics of leaf.
Many other intrinsic and extrinsic factors limit plant growth, including soil moisture, vapor pressure deficit (VPD), radiation, leaf area seasonality (Brodribb et al., 2002; Lawrence et al., 2019). VPD affects growth nonlinearly, with growth increasing with VPD up to a VPD threshold, then decreasing as leaf pores (stomata) close, reducing water uptake (Yang et al., 2019; Grossiord et al., 2020). To account for the nonlinear impact of VPD on growth, we used predicted gross primary productivity (GPP; hereafter, ) from a locally derived polynomial relationship between GPP and VPD (Supporting Information Dataset S1; Fig. S1). Apart from stomatal control, leaf deciduousness may further limit water uptake and growth.
We therefore tested alternate structures of empirical growth models (Methods S1, Eqns S1–S6, including Eqn S3 or Eqn 3), or inverse models of ERD, in which we regressed species‐specific growth against multiplicative or additive effects of one or more growth factors calculated daily and averaged over 5‐yearly censuses: , and the leaf area index (LAI). Incorporation of radiation did not improve model‐fitting, possibly due to the coincidence of higher temperature, higher radiation and lower humidity during the dry season at BCI.
The best empirical growth model, or inverse ERD model, structure that we found (see model validation and selection below) to describe daily average tree growth for species in the census interval is described as follows, in which , and thus , is driven by soil water dynamics at :
| (Eqn 3) |
where |, conditionals; nt , total number of days in census interval ; * indicates that the variable has been standardized to range between 0 and 1 (within species for leaf); and , model coefficients; , model error term. See Methods S1 for all of the alternate model structures tested (Eqns S1–S6).
We evaluated different model structures and for each we estimated species ERD as the depth at which soil water dynamics () best explained observed dynamics of growth (see below) via modeled growth . Our growth model, or inverse ERD model, does not explicitly use rooting profiles, but identifies soil water dynamics at a single depth as the central tendency that influences the observed growth dynamics the most. We modeled multiple hydrological realizations of soil water‐potential dynamics (see below). Incorporating this uncertainty, we defined species ERD as the median ( SE) of best‐fit depths across all hydrological realizations for soil water dynamics () (Eqn S7). See Methods S2 for statistics for identifying best‐fit ERD.
Growth data
For diameter growth estimates, to minimize the effect of light variation among trees, we selected only large trees ( 30 cm diameter at breast height (dbh)) in the 50‐ha plot and also species whose maximum height was 30 m (hereafter, canopy species) and thus are likely to be fully exposed to the sun. Calculating individual tree growth rates across six 5‐yearly censuses (1990–2015; Condit et al., 2019; Condit, 2019), removing outliers, obtaining residuals from a dbh model of growth to account for the size effect on growth (Methods S3), we estimated species growth time series (cm yr−1) as the median of standardized dbh model residuals, for only those species ( = 29) with complete records for at least three trees (median 10, maximum 111 trees per species).
Leaf hydraulic vulnerability curves
We obtained leaf hydraulic vulnerability curves ( vs leaf) for adult trees of 21 common species at BCI from J. Zailaa et al. (unpublished; see Dataset S2 for brief description of methods) described as:
| (Eqn 4) |
where and , fitted species‐specific parameters; , error term. These 21 species included eight of the 29 species selected for ERD estimation. For the remaining 22 species, we obtained vulnerability curves using trait‐based proxies. We identified scaling relationships between fitted parameters and in Eqn 4 and two traits; namely, WSG, the wood specific gravity, and LMA, the leaf mass per unit area (Wright et al., 2010; see Dataset S3). We fitted polynomial equations described as,
| (Eqn 5) |
| (Eqn 6) |
( and , error terms).
As these fits explained a large proportion of variation in parameters and (see results), we sequentially used Eqns 5 and 6 to predict parameters and , respectively, for the 22 ERD species without direct data and estimated leaf hydraulic vulnerability curves using Eqn 4. We thus obtained parameters and for all of the 29 ERD species for use in Eqn 2. We also estimated species 20,leaf using their vulnerability curves.
Leaf area index (LAI)
In some of the alternative models for effective rooting depth, we explored the effect of seasonality in LAI on growth. We assumed species‐specific mean seasonal curves for LAI (standardized between 0 and 1; unitless), informed by a combination of long‐term records for leaf‐fall (Wright & Cornejo, 1990) and leaf lifetime (Osnas et al., 2018) (see Dataset S4; Methods S4; Fig S2).
Using ELM‐FATES to model soil matric potentials,
ELM‐FATES model description
We calibrated water availability by depth over the forest’s rooting zone, we used the Energy Exascale Earth System Land Model (ELM; Caldwell et al., 2019), coupled with the Functionally Assembled Terrestrial Ecosystem Simulator (FATES; Koven et al., 2020) (hereafter, ELM‐FATES). ELM is a land model that, among many features, simulates the physics and conservative dynamics of water, energy and carbon fluxes. In particular, soil hydrological fluxes are resolved vertically among discrete soil layers (1D) in a similar way to the CLM4.5 (Oleson et al., 2013). FATES is a community‐based, open‐source model used for studying climate–vegetation interactions. FATES is a vegetation demography model, with a size‐structured group of plants (cohorts) and successional trajectory‐based patches based on the ecosystem demography (Moorcroft et al., 2001) approach. FATES couples to ELM by a common interface of water and carbon fluxes. Detailed descriptions for ELM and FATES can be found elsewhere (Fisher et al., 2010, 2015; Bisht et al., 2018; Koven et al., 2020).
We ran ELM with FATES vegetation, in which the ELM model simulates interception, throughfall, canopy drip, infiltration, evaporation, surface runoff, subsurface drainage, redistribution within the soil column, and groundwater discharge and recharge so as to simulate changes in canopy water, surface water, soil water by depth and water in an unconfined aquifer (omitting processes relevant to snow, wetlands or lakes). (See Methods S5 for a water balance equation (Eqn S10) and a note on how soil water dynamics is simulated in ELM‐FATES.) The soil profile is discretized into ≤ 15 exponentially distributed soil layers with layer node depth . Here, ; = (0.01, 0.03, 0.06, 0.12, 0.21, 0.37, 0.62, 1, 1.7, 2.9, 4.7, 7.8, 13) m.
ELM‐FATES model parameterization
In order to parameterize catchment hydrology in ELM‐FATES, we identified 11 parameters relevant for the water balance, determined their ranges based on literature for the study site, else for the tropics (Table S1), and ran 5000 simulations using Latin Hypercube Sampling (LHS; Stein, 1987) from this global parameter space. Notably, we leveraged local data for soil hydraulic conductivity by depth (Godsey et al., 2004; Fig. S3), and instead of the ELM default soil texture‐based pedo‐transfer functions, we estimated parameters of soil retention curves using existing data for gravimetric water content vs soil (Kupers et al., 2019; Eqn S11). (See Methods S6.)
We ran ELM‐FATES for the 5000‐member 11‐parameter ensemble with hourly climate drivers measured at the BCI meteorological station over 1985–2018 (Faybishenko & Paton, 2021) initialized with the observed stand structure from the 50‐ha plot (Condit et al., 2019) in a single site mode. As our key interest here was on deriving soil water availability, we ran ELM‐FATES in a lower‐complexity configuration: static stand structure (see Methods S5), and with a single plant functional type (PFT) of evergreen trees. The latter was chosen as only 9.7% of BCI crown area is dry‐season deciduous (Condit et al., 2000) and addition of a dry‐deciduous PFT did not significantly alter results (not shown).
ELM‐FATES model calibration
We calibrated ELM‐FATES over 2012–2018 against three key fluxes and states in the water balance equation, namely: (1) evapotranspiration ET from the flux tower by the 50‐ha plot (2012–2017; Dataset S2; Table S2); (2) local stream discharge (2012–2018; Dataset S5; Paton, 2019b); and (3) soil volumetric water content (VWC) from two sources: (i) a long‐term (2012–2018) record of VWC averaged across three vertical time domain reflectometry (TDR) probes over the depth 0–15 cm from three locations near the flux tower (Dataset S6; Fig. S4), and (ii) plot‐wide snap‐shot measurements of VWC during the dry season of 2015 and 2016 at depths of 0.15, 0.4 and 1 m (1299 samples covering all soil types and habitats; Kupers et al., 2019). (See Methods S7.)
For ELM‐FATES calibration we calculated an objective function (Eqn S12) for each of the 5000‐member ensembles by equally weighting standardized root mean square error (RMSE) between observations and simulations across all fluxes and states mentioned above, and then identified 100 parameter ensemble members that minimized the objective function, ensuring that soil moisture dynamics‐by‐depth was captured correctly (Methods S7). (See Table S1 for the ranges of best‐fit values for different parameters.)
Soil water potential dynamics and hydrological droughts
We ran ELM‐FATES with the best‐fit 100 ensemble members from 1985–2018, with the first five years used for model spin‐up. Extreme hydrological droughts were identified by depth as days for which was more negative than the 5th percentile of for a given day of the year.
ELM‐FATES model evaluation
We evaluated ELM‐FATES by calculating RMSE between simulated and observed long‐term daily VWC for the depths of 0.1, 0.4 and 1 m (2016–2018), based on a dataset we had left out during calibration. We obtained these observations from three horizontal TDR probes at the depths of 0.1, 0.4 and 1 m at a location near the vertical probes (Dataset S6).
ERD model structure selection
We used 2Hxylem as an independent observation to validate the ERD models. As root water‐uptake is generally a nonfractionating process, tree 2Hxylem reflects the signature of source water. Given a vertical gradient of 2H in soil and groundwater, 2Hxylem provides an index of rooting depth (Dawson & Ehleringer, 1991). We leveraged 2Hxylem from BCI (Meinzer et al., 2001) for the dry season of March 1997 as this period showed largest seasonal divergence in 2Hxylem among species and vertically in soil and groundwater 2H at natural abundance level (Fig. S5).
For comparison with modeled ERD, we removed six species from the Meinzer et al. (1999) dataset to account for the uncertainty in their water‐sourcing depths. 2Hxylem from leafless trees may not be linked with water sourced at the time of measurement and thus may not be comparable to species that had leaves. Leaflessness status of sampled trees is not recorded in Meinzer et al. (2001). We therefore removed five species that are typically leafless in March–April (Joseph S. J. Wright, personal observation), that is, the months of 2Hxylem sampling. 2H to soil depth relationship was particularly uncertain for 2H > −40‰, so from the remaining dataset, we removed one species, Guapira standleyana, with 2Hxylem of −28.9‰ 3.7SE (see Fig. S5). For each model of ERD (Eqns 3, S1–S6), modeled species ERD was regressed against species 2Hxylem for a maximum of six species.
Relationships between ERD and aboveground hydraulic traits
We evaluated whether ERD was associated with aboveground hydraulic traits sourcing the latter from existing datasets (Wolfe et al., 2019, 2021) for seven species that overlapped with our assessment of ERD. We regressed species ERD against maximum stem hydraulic conductivity (n = 7), leaf turgor loss point tlp (n = 7), vulnerability to embolism from cavitation 88,stem measured in terms of pressure at which 88% of is lost (n = 7), and hydraulic safety margins min – 88,stem (n = 6). (See Datasets S7–S9 and Table S3 for data collection and estimation of these variables.)
Mortality analyses and species‐specific drought exposure
In order to test whether ERD plays a role in mitigating mortality risk, we calculated mortality rates for large trees (here, 10 cm dbh) in the 50‐ha plot for species with ERD estimates (all canopy species with maximum height 30 m) as well as average abundance of ≥ 20 trees in the plot ( = 28) (Condit et al., 2019). For each of the seven census intervals in the 35‐yr record (1981, 1985, 1990, 1995, 2000, 2005, 2010, 2015), mortality rate, (% yr−1) for species for two successive censuses, and , was calculated as , where and are the total number of large trees of species present in the 50‐ha plot in and dead in , respectively, and is the duration based on mean dates of and .
Dry season deciduous species may escape drought exposure via leaf deciduousness, so we analyzed deciduous and evergreen species separately. Tree species on BCI are scored by expert botanists as one among four leaf habits – evergreen, brevideciduous, facultative deciduous and obligate deciduous (Meakem et al., 2018; Dataset S4). We pooled all deciduous leaf habits together (hereafter, ‘deciduous’ for brevity) and regressed species ERD against species for each census interval for deciduous ( = 16) and evergreen species ( = 12) separately.
As an indicator of exposure to water stress, we use a species‐specific critical hydraulic threshold, crit, here defined as 20,leaf. The duration of exposure to water stress, and thus the potential for realized hydraulic risk, was defined for each species as the proportion of days in each census interval of the simulation period (1990–2015) during which soil water potentials in the soil layer matching species ERD, , were more negative than species crit.
All statistical analyses were conducted in the R statistical environment (v.4.0.3; R Core Team, 2020).
Results
Soil water dynamics by depth and hydrological droughts
The 100 ELM‐FATES ensemble members with the best fits to observed soil moisture dynamics captured soil moisture seasonality at multiple depths (Fig. 2a,b), including the out‐of‐sample observations. These simulations also captured the dynamics in stream discharge (Fig. 2c) and in evapotranspiration (Fig. 2d), slightly underestimating peak discharge in wet years and slightly overestimating peak ET. The reduction in parameter range (Table S1) in the best‐fit ensembles compared to the tested global ranges showed that the model calibration was primarily sensitive to the Ball‐Berry stomatal slope parameter (fates_leaf_BB_slope), the ELM root distribution parameter that regulates the depth of the rooting profile (fates_rootb_par), soil hydraulic conductivity (HKSAT) profile especially at depth, and the adjustment factor (HKSAT_ADJ) that modifies soil hydraulic conductivity to account for macroporosity and direct flow paths (Figs S6, S7). The distribution of maximum depth of soil water dynamics, and thus ecosystem root zone depth, across the 100 hydrological realizations encompassed 95% CI of 2.9–13 m (median 4.7 m).
Fig. 2.
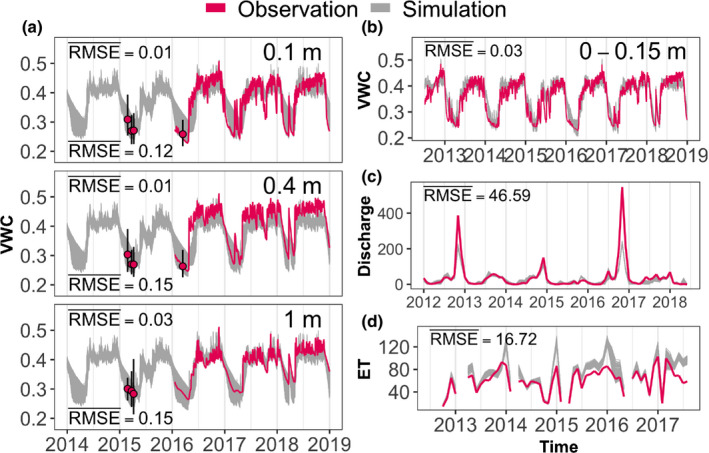
Energy Exascale Earth System Land Model coupled with the Functionally Assembled Terrestrial Ecosystem Simulator (ELM‐FATES) calibration and evaluation. Observations (red lines and points) vs simulations (gray lines) from 100 best‐fit ensemble‐member runs of ELM‐FATES are shown for daily volumetric water content (VWC) by depth for horizontal time domain reflectometry (TDR) probes at three depths (0.1, 0.4 and 1 m; a) and for an average of three vertical TDR probes (0–0.15 m; b); monthly stream discharge (Discharge, c) and monthly evapotranspiration from the flux tower (ET, d). Red points in panel a show average, manual plot‐wide observations of VWC with 95% CI (error bars). All observations (red lines and points) were in‐sample, except for VWC data from the horizontal probes (red lines in a) which were out‐of‐sample. Values in inset are average RMSE across the 100 best‐fit simulations. For (a), values at the top are for manual, plot‐wide VWC and those at the bottom are for VWC from TDR probes. VWC is in units of cm3 cm−3, whereas ET and Discharge are in mm per month.
Analysis of soil water potential dynamics by depth z from 0.01 to 13 m obtained from the best‐fit simulations (Fig. S8) revealed that every 5‐yr census interval had at least one extreme hydrological drought year, but each interval varied in terms of number of extreme years, drought intensity, drought seasonality and duration (Fig. 3). Hydrological droughts in census interval 1990–1995 were marked by a prolonged dry season, whereas those during 2000–2005 and 2005–2010 distinctly occurred in the wet season, effectively extending the dry season into the wet season (Fig. 3). Across the simulation period 1990–2015, simulated remained above −0.5 MPa from depths of 1.7–13 m (Fig. S8).
Fig. 3.
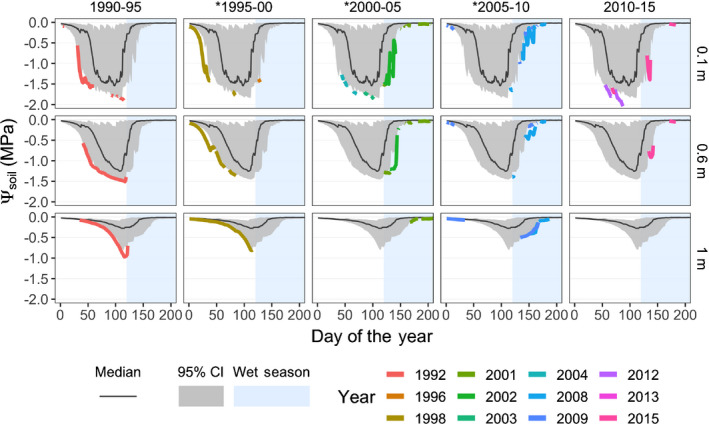
Occurrence of extreme hydrological droughts by census intervals (horizontal panels) at three representative depths: 0.1, 0.6 and 1 m (vertical panels). Mean (black lines) and lower half of 95% distribution (grey areas) of soil water potential for a given day of year (DOY) and depth are shown (same across all census intervals). by DOY for a year (colored line) is only shown if at least one DOY was more negative than the 5th percentile of for that DOY. Note the distinctive features of extreme droughts that occurred during the three periods indicated by asterisks: all three periods featured extreme hydrological droughts that either prolonged over the dry season (1995–2000), or occurred in the wet season, effectively extending the dry season (2000–2005, 2005–2010).
Predictors of leaf hydraulic vulnerability curves
Parameters of leaf vulnerability curves were predictable from WSG and LMA (Fig. 4). WSG and LMA explained a large proportion of variance in parameter (Eqn 5; Adj. 2 = 0.69, P < 0.001). WSG and parameter explained a large proportion of variance in parameter (Eqn 6; Adj. R 2 = 0.74, P < 0.001; see also Fig. S9). This predictive power allowed us to estimate leaf vulnerability curves used in the ERD models for 22 ERD species that lacked direct observations (among 29 ERD species) (Table S4; Fig. S10).
Fig. 4.
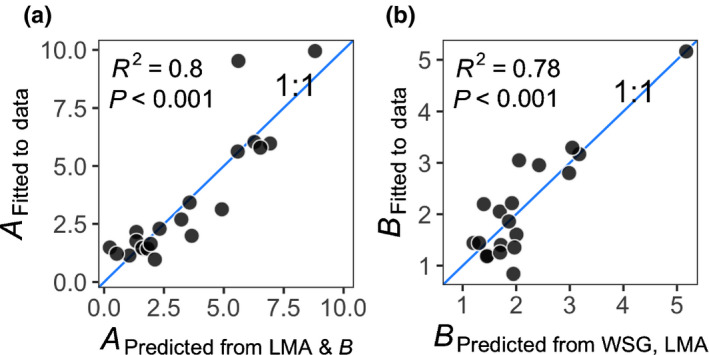
Parameters (panel a) and (panel b) for the leaf vulnerability curves that were fitted to observed data on vs leaf for 21 species (Eqn 4) vs those that were predicted from a set of models based on trait‐proxies (Eqns 5, 6). Goodness‐of‐fit ( 2) and significance levels are given in inset.
Effective rooting depths
The best ERD model (Eqn 3; Notes S1) explained a large fraction of the variance in 2Hxylem ( 2 = 0.9, P = 0.004, = 6; Fig. 5; see also Fig. S11). This model included an effect of VPD and not LAI (Eqn 3).
Fig. 5.
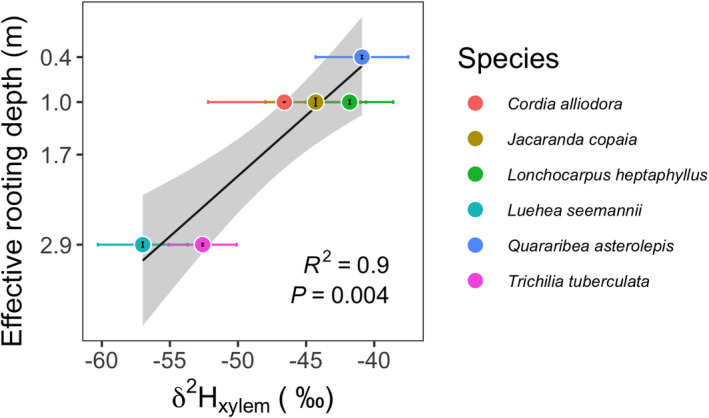
Modeled effective rooting depth (ERD; mean 1SE (m)) vs dry‐season stable isotopic concentration 2Hxylem (mean 1SE; ‰) for six canopy species from Barro Colorado Island. 2Hxylem data are from Meinzer et al. (1999).
Modeled ERD for the 29 large ( 30 cm DBH) trees of canopy species varied from 0.4 m to 7.8 m (Fig. 6). Evergreen and deciduous species had similar ranges of ERDs, but a greater proportion of deeper ERD species tended to be evergreen rather than deciduous – a group composed of a variety of categories of deciduousness (Fig. 6). Notably, two species, Luehea seemannii and Trichilia tuberculata, that Meinzer et al. (1999) found to have 2Hxylem values between soil water and groundwater, suggesting that these species sourced most of the water from depths > 1 m and likely to have sourced some portion of groundwater, also were identified by our model with ERD > 1 m (2.9 m for both species; Fig. 5).
Fig. 6.
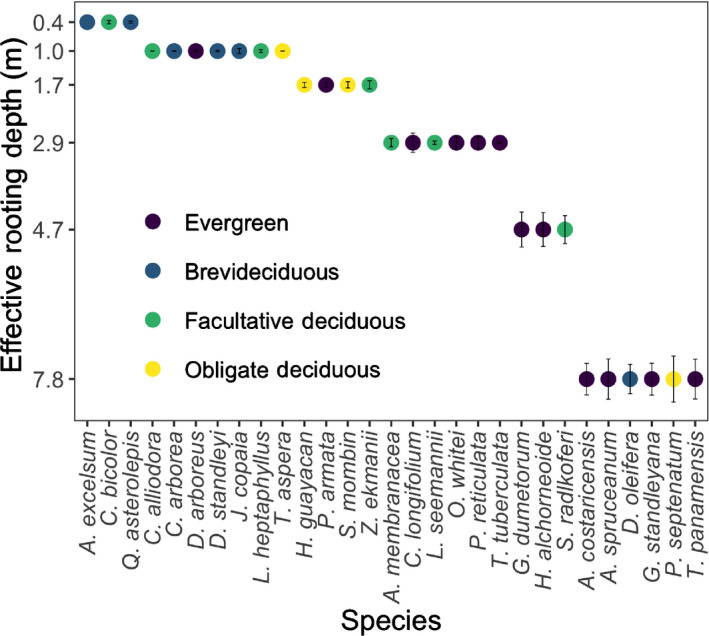
Modeled effective rooting depth (ERD; mean 1SE (m)) for 29 large, canopy species of Barro Colorado Island. A species ERD is defined as the median, across 100 hydrological realizations, of soil layer depth at which soil water dynamics () best explained observed dynamics of species growth for each realization. As soil layers in the hydrological model are discretely resolved into exponentially increasing depths, so is the ERD axis. Species are color coded by leaf habit. See Table S4 for species' complete scientific names.
Relationships between ERD and aboveground hydraulic traits
Species with deeper ERD showed greater (Spearman’s = 0.87, P = 0.01; Fig. 7a), less negative leaf tlp ( = 0.75, P = 0.05; Fig. 7b), less negative 88,stem and thus greater vulnerability to xylem embolism from cavitation ( = 0.8, P = 0.03; Fig. 7c), and narrower aboveground hydraulic safety margins ( min – 88,stem, = −0.87, P = 0.02; Fig. 7d). (See Fig. S12 for the full correlation matrix.)
Fig. 7.
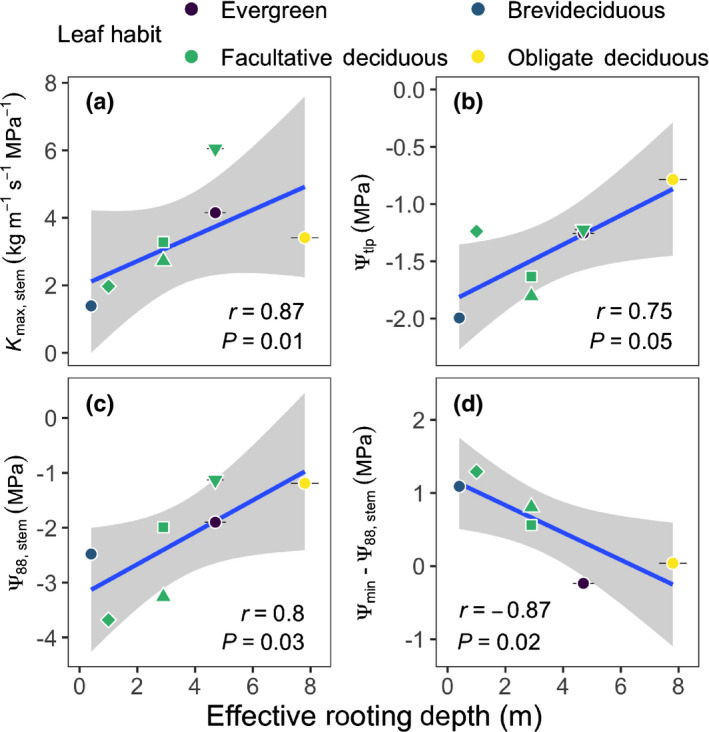
Modeled effective rooting depth (ERD) vs hydraulic properties for seven canopy species found on Barro Colorado Island (Panama); namely, maximum stem area‐specific hydraulic conductivity of stem (; a), bulk leaf turgor loss point, the leaf where turgor potential = 0 ( tlp; b), stem at 88% loss of stem conductivity ( 88,stem; c), and aboveground hydraulic safety margin ( min– 88,stem; d). Spearman’s and significance levels are given in panel insets. Linear model fits (blue lines) with confidence bands (gray area) are shown for significant fits at = 0.05. Species are color‐coded by leaf habit. Multiple species in Facultative deciduous leaf‐habit are distinguished by shapes.
Effective rooting depths, mortality and hydrological droughts
Among the seven census‐intervals over 1982–2015 for which we analyzed relationship of ERD with mortality rates, six intervals were associated with occurrence of one or more El Niño events (Condit, 2017; Detto et al., 2018). Of the six intervals with El Niño events, ERD explained 30–40% variation in mortality rates among evergreen species during five intervals (1982–1985, 1985–1990, 1995–2000, 2000–2005 and 2005–2010) such that species mortality rates decreased with deeper ERD (P‐values < 0.05 for four intervals and 0.06 for one interval; Fig. 8). For deciduous species, ERD explained 11–16% variation in mortality in four intervals with El Niño events, but P‐values were not significant (Fig. S13).
Fig. 8.
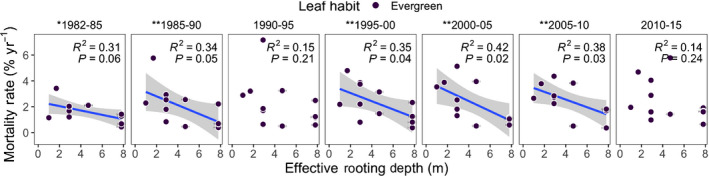
Mortality rate (mean 1SE (% yr−1)) vs modeled effective rooting depth (ERD; mean 1SE (m)) for 12 evergreen, canopy species found on Barro Colorado Island over seven census intervals (1981–2015). 2 and significance levels for linear model fits are given in panel insets. Model fits (blue lines) with confidence bands (gray area) are only shown for periods with significant fits. Census interval significance: , = 0.05; = 0.1.
Our analysis of hydrological droughts ranged from 1990 to 2015 and revealed distinctive extreme, prolonged hydrological droughts for the census‐intervals 1995–2000, 2000–2005 and 2005–2010, for which ERD explained significant mortality (Fig. 3). ERD also explained significant mortality in earlier droughts (1982–1985 and 1985–1990; Condit, 2017), not covered by our estimates.
On average, species exposure to water stress (% days < crit) exponentially declined with ERD (Figs 9, S14), indicating that species with shallower ERD spent greater time under significant hydrological drought, and thus likely experienced greater hydraulic risk (Notes S2). Exposure to water stress increased over the three periods for which ERD explained significant mortality (Figs 9, S11), although it also was high in 1990–1995 for the shallowest ERD (Fig. 9), but without elevated mortality rates (Fig. 8).
Fig. 9.

Modeled effective rooting depth (ERD; horizontal‐axis) vs time spent beyond critical hydraulic threshold (vertical axis) by census interval (colored bars) for 12 evergreen species included in the mortality analyses (Fig. 8). Each bar represents the average time species of the same ERD spent beyond species‐specific critical hydraulic thresholds in a given interval, that is, the proportion of days for which was more negative than species crit, defined as 20,leaf, and where is the soil depth matching species ERD. SEM shown over each bar when available. Note the squared y‐axis scale.
Discussion
We introduce a novel approach for estimating effective rooting depths (ERD) using 25 years of tree growth, species‐specific leaf vulnerability curves, modeled soil water potential profiles, and observed vapor pressure deficit (VPD) (Eqn 3; Figs 1, 6). Our predictions of ERD were consistent with estimates using 2Hxylem (Fig. 5). Our analyses suggest that co‐occurring large canopy tree species with deeper ERD were associated with higher aboveground hydraulic efficiency, but lower safety (Fig. 7). Nevertheless, evergreen but not deciduous species with deeper ERD showed significantly lower mortality rates than shallower ERD species (Figs 8, S11). This ERD–mortality relationship was significant in five of six census intervals that had experienced one or more El‐Niño events, over seven census intervals studied in total (1982–2015). Quantifying extreme droughts in the whole soil column over 1990–2015 revealed that ERD explained significant levels of mortality in periods when extreme soil droughts prolonged the dry season water stress (Fig. 3). Species exposure to water stress exponentially declined with deeper ERD (Fig. 9). Because extreme, sustained water stress increases risk of mortality via hydraulic failure and/or carbon starvation, deeper ERD may mitigate drought‐induced mortality by limiting exposure to water stress (Rowland et al., 2015; McDowell et al., 2018b). We thus demonstrate, for the first time, a link between species trade‐offs in above‐ and belowground hydraulic traits, drought exposure through extreme hydrological droughts quantified over the whole soil column, and large ( 10 cm diameter at breast height) tree mortality across several El‐Niño events over 35 years.
Drought strategies designed to mitigate realized hydraulic risks
If investments in stress‐tolerance traits come at a cost, such insurance may not pay off if the risk of stress is not realized. Our findings suggest, on the one hand, that species with investment in deep roots can afford the hydraulically efficient, but risky, suite of traits (Fig. 7), because access to a reliable deep‐water resource ensures that for them hydraulic risk is not realized (Fig. 9). On the other, shallow‐rooted species pay the cost of hydraulic safety in terms of efficiency, adapted for an environment in which hydraulic risk is significant, as extreme droughts cause exponentially greater water stress in shallow soil layers (Figs 9, S6).
Extreme, prolonged El‐Niño droughts (Fig. 3) in our study may have crossed even the greater tolerance limits of shallow‐rooted species leading to their greater mortality compared to deep‐rooted species (Fig. 8). Hydraulic risk for shallow‐rooted species may have been exacerbated in our 35‐yr study period in which extreme water‐deficit years were more frequent than those in the last century (Condit, 2017). The greater survival of deep‐rooted species that we observed may not continue into the future if droughts intensify.
We found significant ERD–mortality relationships during extreme water stress for evergreen but not deciduous species (Figs 8, S11); consistent with the expectation that deciduous species also can avoid water stress via leaf drop. This also is consistent with the observation that species distributions along local (BCI) and regional (Panama) moisture gradients are correlated with leaf turgor loss point ( tlp) for evergreen but not deciduous species (Kunert et al., 2021). Studies that simultaneously assess coordination between leaf phenology, rooting depth and hydraulic traits are almost absent for the tropics and warrant future consideration (Oliveira et al., 2021). Our analyses for ERD–hydraulic trait relationships were limited to only seven species, but covered all species of different leaf phenologies (Fig. 7), so here we assume that the trend in the ERD–hydraulic trait relationships holds true across all species of different leaf phenologies. We also found that the range of ERDs overlapped across leaf phenology, but evergreen species tend to have deeper ERDs (Fig. 6), consistent with observations by Meinzer et al. (1999) and elsewhere (Fan et al., 2017; Smith‐Martin et al., 2020; Oliveira et al., 2021). Whether deciduous species also have more efficient and vulnerable hydraulics at BCI as is observed elsewhere remains to be studied (Markesteijn et al., 2010, 2011; Gleason et al., 2016; Xu et al., 2016). Leaf phenologies at BCI are numerous and complicated and warrant further research.
Drought exposure integral to assessing drought‐induced mortality
Our study brings attention to the need for assessing drought sensitivity in terms of species drought exposure and realized hydraulic risk by accounting for hydrological drought and tree rooting depths. We found that species accessing deeper water had greater xylem vulnerability to embolism and narrower branch hydraulic safety margins (Fig. 7). These traits are commonly identified as proxies for mortality risk (Anderegg et al., 2016), but in fact were associated with species with less drought exposure that had lower mortality. Hydraulic risk was balanced by investment in deep roots (Figs 3, 8).
Our results are consistent with recent studies that analyzed rooting or water‐sourcing depths vs hydraulic traits and mortality rates during extreme droughts (Nardini et al., 2015; Venturas et al., 2016; Johnson et al., 2018; see also Brum et al., 2017, 2019; Rowland et al., 2015). Globally, large trees tend to exhibit greater growth reductions, lower post‐drought resilience and greater increases in mortality relative to their understory counterparts (Phillips et al., 2010; Bennett et al., 2015). Our finding that deep‐water access buffers drought‐induced mortality in large trees is relevant for understanding drought resistance, resilience and recovery (Bennett et al., 2015; McGregor et al., 2021). Future studies should test the ERD–mortality relationship on a greater number of species.
Our result of lower mortality in deep‐rooted trees contrasts with the inverse model finding of Chitra‐Tarak et al. (2018) (hereafter, CT2018) in which deeper ERD species in a South‐Asian seasonally dry tropical forest had higher mortality in a rare, prolonged drought. The hydrological model in CT2018 revealed that the multi‐year drought exhausted the deep soil and even bedrock water availability (also see, Goulden & Bales 2019; Ivanov et al., 2012). By contrast, our hydrological modeling at BCI found that soil for depths deeper than 2.9 m did not cross critical hydraulic threshold ( crit) of the most sensitive tree species (−0.17 MPa) for all of the dry seasons and droughts during 1990–2015 (Notes S1). Mean annual rainfall of 1095 mm in CT2018 compared to 2627 mm at BCI, and precipitation to potential evapotranspiration ratio of nearly one in CT2018 compared to nearly two in BCI, are major factors in the different mortality responses. At BCI, deep soil layers were recharged annually (Fig. S6), whereas in CT2018 they were not. The contrast between the two studies highlights the combined role of seasonal precipitation input and site‐specific hydrology in modulating the mortality risk for deep‐rooted species.
Modeling effective rooting depths at the tree community level
By estimating ERD for large trees of 29 canopy tree species (Fig. 6), we make an important advance in modeling effective rooting depths at the community level in species‐rich tropical forests. Our best ERD model is a key improvement over the model of CT2018 as we employ a physiologically meaningful representation, fewer parameters and corroboration with tree and soil data for 2H.
Our ERD model predicts daily maximum diurnal leaf hydraulic vulnerability ( leaf) assuming that it is equivalent to soil. Our model ignores other factors that buffer soil drying such as stem water storage capacitance (Wolfe, 2017), and may thus have overestimated ERD, especially in those species for which capacitance is important as a drought‐avoidance strategy, for example, the deciduous species (Borchert & Pockman, 2005). Future studies should investigate the role of capacitance on estimating ERD.
Although ERD models have the potential to estimate ERDs for entire tree communities, during their development phase, ERD models may need to be validated against data for a subset of representative species of the community, as this study did. ERD models should be tested across varied climates and forest types, covering contrasting plant strategies and possibly seasonality in ERDs. Direct observations of rooting depths and stable water isotope‐based water‐sourcing depths will be important datasets for such validation; although the interpretation of isotopic data is still under research (Adams et al., 2020; Bowers et al., 2020; Deurwaerder et al., 2020).
Future directions
The relationships that we identify between above‐ and belowground traits, vertical profile of soil water status and mortality rates are important for representing diversity in dynamic global vegetation models (DGVMs), which intrinsically rely on the parameterization of contrasting life history strategies (Scheiter et al., 2013) and the simulation of competition between those strategies. In the context of trait filtering models, if we used the hydraulic trait information without knowledge of their relationship to rooting depth, models would likely kill the ‘risky’ strategy trees in droughts, which would, in fact, be the opposite result from that observed in this study. A key outcome of this study is thus the relationships between hydraulic traits and ERD that could be plugged into a DGVM of BCI. To assimilate ERDs, DGVMs could vary rooting parameters such that the centroid of the species water‐uptake profiles match ERDs. We found that leaf mass per unit area (LMA) and wood specific gravity (WSG) were strong predictors of leaf hydraulic vulnerability curves (Fig. 4). Albeit future studies should undertake sensitivity analyses for uncertainties involved, our finding offers the promise of a greater ability to parameterize the ‘hard’ hydraulic traits with the abundant ‘soft’ trait data, thus allowing for a better representation of forest hydrodynamics. The relationships between ERD and aboveground hydraulic traits that we find, thus provide important insights on how to model rooting depths and their coordination or trade‐offs with other traits, in order to better represent the functional diversity of tropical forests and their trajectories into the future.
Our inverse ERD model was parameterized on 5‐year growth data, with five data points over a 25‐yr period, which decoupled climate events and demographic outcomes. Future studies could better constrain the ERD model with higher frequency growth data such as those from dendrometer bands. At high temporal resolution, however, the role of reversible dehydration in tree diameter change increases (Chitra‐Tarak et al., 2015; Chitra‐Tarak, 2016; Mencuccini et al., 2017), but that may provide an avenue to include stem water storage and dynamic rooting depths in ERD models. Three of our exploratory ERD models included leaf area index (LAI) seasonality, but we did not select them as they worsened the fit with growth data for many species (Fig. S9). Our interpretation of this result is that VPD and leaf hydraulic vulnerability curves may be adequate to explain inter‐census differences in growth (via stomatal control), but also acknowledge that our estimates of seasonality of LAI is a tentative estimate that combines leaf‐fall data and the timing of leaf‐gain backtracked from leaf lifetime, and omits inter‐annual variation. Species‐level leaf‐fall data from litter‐traps that we used includes large within‐species variability in leaf‐fall timing, and so may not have captured tree‐level seasonality in deciduousness (Methods S4). Future studies may improve models of LAI seasonality and make use of data from new technologies such as drone based monitoring of LAI in species‐rich tropical forests (Park et al., 2019).
Although our ERD model empirically predicts growth via estimating leaf from soil of a specific depth, mechanistic models that account for plant hydrodynamics and other processes influencing growth are likely to predict growth more accurately, and thus ERD and hydraulic risk (Sperry et al., 1998; Christoffersen et al., 2016; Duursma et al., 2018; Yang et al., 2019). Although data needs for parameterizing such models could be greater (e.g. hydraulic vulnerability curves and capacitance for roots, stems and leaves), adding a degree of parameter uncertainty in community‐wide application, such models hold greater promise in improving our understanding of plant physiology (see, e.g., Johnson et al., 2018).
As in CT2018, with water availability resolved for a 1D column, we interpret our ERD estimates as revealing relative differences among species’ effective rooting depths rather than absolute depths. To estimate absolute depths and topographic variation in ERD within or across species, future studies may use soil moisture dynamics from a distributed hydrological model (e.g. Schwantes et al., 2018). We note that data availability on soil water retention curves ( soil vs volumetric water content (VWC)), hydraulic conductivity (K soil) by depth, soil moisture by depth, stream discharge and evapotranspiration were important for effective calibration of our 1D hydrological model. We recommend widespread and coordinated collection of these variables as well as water‐table levels in forest‐inventory sites to allow for estimation of tree water environments.
Conclusions
Establishing relationships between environment, traits and demographic outcomes of plants is imperative for developing a predictive plant ecology. Tree rooting depths and actual water environments through hydrological rather than meteorological droughts nonetheless are rarely studied. To the best of our knowledge, this is the first study to test for a mechanistic link between plant‐available water in the whole‐soil column, tree above‐ and belowground hydraulic architecture and long‐term mortality outcomes for a species‐rich forest. We report here that deep‐water access plays a role in mitigating mortality of otherwise vulnerable stem hydraulics. This has important implications for our predictive understanding of tropical forest dynamics under current and future climate. Our community‐scale framework for modeling effective rooting depths and leaf vulnerability curves indicates the possibilities in expanding the use of these critical, rare observations in species‐rich forests towards community‐scale generalizations.
Author contributions
Conceptualization: RC‐T. Data curation: BF, SRP for climate drivers. SRP for stream discharge. MD for GPP, ET, TDR, bulk density. SJK for manual GWC and GWC vs . NK, JZ, KJA‐T, LS for leaf hydraulics, BTW for stem hydraulics. RP and SA for the BCI 50ha plot censuses. SJW for maximum tree height, WSG, LMA, deciduousness, leaf fall and leaf lifetime. Formal analysis: RC‐T, CX. MD for upgrading GPP‐VPD relationship and LAI seasonality. Funding acquisition: SMM, JC, CX, NGM, LMK. Investigation: RC‐T, CX (SMM and LR for an exploratory version). Methodology: RC‐T, CX (SMM and LR for an exploratory version). Project administration: RC‐T, Resources: SMM, BF, SRP, MD, SJK, NK, JZ, KJA, LS, BTW, SJW. Software: RC‐T; RAF, RGK, CDK, CX, RC‐T for ELM‐FATES. Supervision: CX, SMM, BDN, Validation: RC‐T. Visualization: RC‐T, Writing – original draft: RC‐T. Writing – review & editing: RC‐T, CX, KAT, MD, RAF, RGK, CDK, LMK, NK, SJK, NGM, BDN, SRP, LR, LS, JMW, BTW, CW, SJW, JZ, SMM. See https://casrai.org/credit/ for the taxonomy of credits.
Supporting information
Dataset S1 Microclimatic and flux tower data.
Dataset S2 Leaf hydraulic conductivity and vulnerability to cavitation.
Dataset S3 Wood specific gravity (WSG) and leaf mass area (LMA).
Dataset S4 Leaf deciduousness categories.
Dataset S5 Stream discharge from the Conrad catchment.
Dataset S6 Volumetric water content.
Dataset S7 Stem maximum hydraulic conductivity and vulnerability to cavitation.
Dataset S8 Leaf turgor loss point.
Dataset S9 Aboveground hydraulic safety margins.
Fig. S1 Observed relationship between GPP and VPD at Barro Colorado Island.
Fig. S2 Seasonal variation in estimated standardized LAI for 29 species at Barro Colorado Island.
Fig. S3 Ensembles of soil hydraulic conductivity variation by depth for Conrad Trail Stream Catchment, Barro Colorado Island (data from Godsey et al., 2004).
Fig. S4 Volumetric water content vs. TDR data for a vertical TDR probe used for TDR probe calibration.
Fig. S5 δ2H of soil water by depth measured at Barro Colorado Island (data from Meinzer et al., 1999).
Fig. S6 Parameter sensitivity of ELM‐FATES soil water content and evapo‐transpiration.
Fig. S7 Parameter sensitivity of ELM‐FATES stream discharge.
Fig. S8 ELM‐FATES predicted soil water potential dynamics by depth over 1990–2018.
Fig. S9 Leaf hydraulic vulnerability curves fitted to observed K leaf vs Ψleaf data for 21 tree species from Barro Colorado Island.
Fig. S10 Percent loss of leaf hydraulic conductivity curves for ERD species, including curves fitted to K leaf vs Ψleaf as well as those based on scaling relationships with LMA and WSG.
Fig. S11 Effective rooting depths (ERD) vs δ2Hxylem for each of the ERD model structures tested.
Fig. S12 Correlation matrix between ERD and hydraulic traits.
Fig. S13 Mortality rates for deciduous species across census intervals from 1985–2015 vs ERD.
Fig. S14 Modeled effective rooting depths of deciduous species vs time spent beyond critical hydraulic threshold.
Methods S1 Alternative structures for effective rooting depth model.
Methods S2 Statistics for identifying best‐fit ERD.
Methods S3 Processing of forest census data for growth estimates.
Methods S4 Leaf area index calculations.
Methods S5 Details of the ELM‐FATES model.
Methods S6 Details for ELM‐FATES model parameterization.
Methods S7 ELM‐FATES calibration.
Notes S1 ERD model structure selection.
Notes S2 Additional results for exposure to water stress.
Table S1 ELM‐FATES parameters used to generate ensembles, with description, prescribed global ranges, rationale for the choice of ranges and references, as well as ranges for best‐fit ensembles.
Table S2 QA/QC procedure applied to eddy covariance fluxes.
Table S3 Aboveground hydraulic traits data from Wolfe et al. (2019) and Wolfe et al. (2021) used for comparison with ERD.
Table S4 Leaf vulnerability curve parameters A & B, K max, leaf and Ψ20,leaf by source (data or model) for the 29 species with ERD estimates.
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Acknowledgements
This research was supported as part of the Next Generation Ecosystem Experiments‐Tropics, funded by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research. Funding also was provided to RC‐T and SMM through an NSF grant (1137366). LR was deputed to Indo‐French Cell for Water Sciences on an IRD Fellowship. An NSF grant to Smithsonian Institution’s ForestGEO (Dimensions 1046113) partially supported this work via RC‐T and SMM. BTW was supported by the National Institute of Food and Agriculture, US Department of Agriculture, McIntire Stennis project under LAB94493. LS was supported by the National Science Foundation award 2017949. RAF was supported by the National Center for Atmospheric Research, which is funded by the National Science Foundation. MD was supported by the Carbon Mitigation Initiative at Princeton University. The BCI forest dynamics research project, founded by Stephen P. Hubbell and Robin B. Foster and sustained for many years by Richard Condit, is now managed by Rolando Pérez (RP), Suzanne Lao and Stuart Davies under the ForestGEO program of the Smithsonian Tropical Research in Panama. Numerous organizations have provided funding, principally the US National Science Foundation, and hundreds of field workers have contributed. Comments from editor Jarmila Pitterman and three anonymous reviewers helped improve and clarify this manuscript.
Data availability
ELM‐FATES source code, simulation outputs for best‐fit parameter ensemble members and all of the R scripts to reproduce the manuscript are available (Chitra‐Tarak et al., 2020). Data sources for all other datasets used are provided throughout the manuscript.
References
- Adams RE, Hyodo A, SantaMaria T, Wright CL, Boutton TW, West JB. 2020. Bound and mobile soil water isotope ratios are affected by soil texture and mineralogy, whereas extraction method influences their measurement. Hydrological Processes 34: 991–1003. [Google Scholar]
- Anderegg WRL, Klein T, Bartlett M, Sack L, Pellegrini AFA, Choat B, Jansen S. 2016. Meta‐analysis reveals that hydraulic traits explain cross‐species patterns of drought‐induced tree mortality across the globe. Proceedings of the National Academy of Sciences, USA 113: 5024–5029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson‐Teixeira KJ, Davies SJ, Bennett AC, Gonzalez‐Akre EB, Muller‐Landau HC, Wright SJ, Abu Salim K, Almeyda Zambrano AM, Alonso A, Baltzer JLetal. 2014. CTFS‐ForestGEO: a worldwide network monitoring forests in an era of global change. Global Change Biology 21: 528–549. [DOI] [PubMed] [Google Scholar]
- Baillie I, Elsenbeer H, Barthold F, Grimm R, Stallard R. 2007. Semi‐detailed soil survey of Barro Colorado Island, Panama. A report . Smithsonian Tropical Research Institute. [WWW document] URL https://striresearch.si.edu/bci‐soil‐map/.
- Bartlett MK, Detto M, Pacala SW. 2019. Predicting shifts in the functional composition of tropical forests under increased drought and CO2 from trade‐offs among plant hydraulic traits. Ecology Letters 22: 67–77. [DOI] [PubMed] [Google Scholar]
- Beech E, Rivers M, Oldfield S, Smith PP. 2017. GlobalTreeSearch: the first complete global database of tree species and country distributions. Journal of Sustainable Forestry 36: 454–489. [Google Scholar]
- Bennett AC, McDowell NG, Allen CD, Anderson‐Teixeira KJ. 2015. Larger trees suffer most during drought in forests worldwide. Nature Plants 1: 15139–15145. [DOI] [PubMed] [Google Scholar]
- Bisht G, Riley WJ, Hammond GE, Lorenzetti DM. 2018. Development and evaluation of a variably saturated flow model in the global E3SM Land Model (ELM) version 1.0. Geoscientific Model Development 11: 4085–4102. [Google Scholar]
- Bonan GB. 2008. Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320: 1444–1449. [DOI] [PubMed] [Google Scholar]
- Borchert R, Pockman WT. 2005. Water storage capacitance and xylem tension in isolated branches of temperate and tropical trees. Tree Physiology 25: 457–466. [DOI] [PubMed] [Google Scholar]
- Bowers WH, Mercer JJ, Pleasants MS, Williams DG. 2020. A combination of soil water extraction methods quantifies the isotopic mixing of waters held at separate tensions in soil. Hydrology and Earth System Sciences 24: 4045–4060. [Google Scholar]
- Brienen RJW, Phillips OL, Feldpausch TR, Gloor E, Baker TR, Lloyd J, Lopez‐Gonzalez G, Monteagudo‐Mendoza A, Malhi Y, Lewis SLetal. 2015. Long‐term decline of the Amazon carbon sink. Nature 519: 344–348. [DOI] [PubMed] [Google Scholar]
- Brodribb TJ, Holbrook NM, Gutiérrez MV. 2002. Hydraulic and photosynthetic co‐ordination in seasonally dry tropical forest trees. Plant, Cell & Environment 25: 1435–1444. [Google Scholar]
- Brum M, Teodoro GS, Abrahão A, Oliveira RS. 2017. Coordination of rooting depth and leaf hydraulic traits defines drought‐related strategies in the campos rupestres, a tropical montane biodiversity hotspot. Plant and Soil 420: 467–480. [Google Scholar]
- Brum M, Vadeboncoeur MA, Ivanov V, Asbjornsen H, Saleska S, Alves LF, Penha D, Dias JD, Aragão LEOC, Barros Fetal. 2019. Hydrological niche segregation defines forest structure and drought tolerance strategies in a seasonal Amazon forest. Journal of Ecology 107: 318–333. [Google Scholar]
- Caldwell PM, Mametjanov A, Tang Qi, Van Roekel LP, Golaz J‐C, Lin W, Bader DC, Keen ND, Feng Y, Jacob Retal. 2019. The DOE E3SM coupled model version 1: description and results at high resolution. Journal of Advances in Modeling Earth Systems 11: 4095–4146. [Google Scholar]
- Chitra‐Tarak R. 2016. Eco‐hydrology of a seasonally dry tropical forest: tree growth, below‐ground water dynamics and drought‐vulnerability. PhD Thesis. Indian Institute of Science, Bangalore, India.
- Chitra‐Tarak R, Ruiz L, Dattaraja HS, Kumar MSM, Riotte J, Suresh HS, McMahon SM, Sukumar R. 2018. The roots of the drought: hydrology and water uptake strategies mediate forest‐wide demographic response to precipitation. Journal of Ecology 106: 1495–1507. [Google Scholar]
- Chitra‐Tarak R, Ruiz L, Pulla S, Dattaraja HS, Suresh HS, Sukumar R. 2015. And yet it shrinks: A novel method for correcting bias in forest tree growth estimates caused by water‐induced fluctuations. Forest Ecology and Management 336: 129–136. [Google Scholar]
- Chitra‐Tarak R, Xu C, Aguilar S, Anderson‐Teixeira K, Chambers J, Detto M, Faybishenko B, Fisher R, Knox R, Koven Cetal. 2020. Soil water potentials (1990–2018) from a calibrated ELM‐FATES, and rooting depth analyses scripts, PA‐BCI, Panama. 2.0. NGEE Tropics Data Collection. doi: 10.15486/ngt/1696806. [DOI]
- Christoffersen BO, Gloor M, Fauset S, Fyllas NM, Galbraith DR, Baker TR, Rowland L, Fisher RA, Binks OJ, Sevanto SAetal. 2016. Linking hydraulic traits to tropical forest function in a size‐structured and trait‐driven model (TFS vol 1‐Hydro). Geoscientific Model Development Discussions 1–60. [Google Scholar]
- Condit R. 1998. Tropical forest census plots: methods and results from Barro Colorado Island, Panama and a comparison with other plots. Berlin, Germany: Springer Science & Business Media. [Google Scholar]
- Condit R. 2019. BCI 50‐ha Plot Taxonomy , v6, DataONE, Dataset. doi: 10.15146/R3FH61. [DOI]
- Condit R, Pérez R, Aguilar S, Lao S, Foster R, Hubbell S. 2019. Complete data from the Barro Colorado 50‐ha plot: 423617 trees, 35 years, v3. DataONE, Dataset. doi: 10.15146/5xcp-0d46. [DOI]
- Condit R, Pérez R, Lao S, Aguilar S, Hubbell SP. 2017. Demographic trends and climate over 35 years in the Barro Colorado 50 ha plot. Forest Ecosystems 4: 1–13. [Google Scholar]
- Condit R, Watts K, Bohlman SA, Pérez R, Foster RB, Hubbell SP. 2000. Quantifying the deciduousness of tropical forest canopies under varying climates. Journal of Vegetation Science 11: 649–658. [Google Scholar]
- Croat TB. 1978. Flora of Barro Colorado Island. Stanford, CA, USA: Stanford University Press. [Google Scholar]
- Dawson TE, Ehleringer JR. 1991. Streamside trees that do not use stream water. Nature 350: 335–337. [Google Scholar]
- Detto M, Wright SJ, Calderón O, Muller‐Landau HC. 2018. Resource acquisition and reproductive strategies of tropical forest in response to the El Niño–Southern Oscillation. Nature Communications 9: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deurwaerder HPTD, Visser MD, Detto M, Boeckx P, Meunier F, Zhao L, Wang L, Verbeeck H. 2020. Diurnal variation in the isotope composition of plant xylem water biases the depth of root‐water uptake estimates. Biogeosciences Discussions 2020: 1–48. [Google Scholar]
- Doughty CE, Metcalfe Db, Girardin C, Amézquita FF, Cabrera DG, Huasco WH, Silva‐Espejo Je, Araujo‐Murakami A, da Costa Mc, Rocha Wetal. 2015. Drought impact on forest carbon dynamics and fluxes in Amazonia. Nature 519: 78–82. [DOI] [PubMed] [Google Scholar]
- Duursma RA, Blackman CJ, Lopéz R, Martin‐StPaul NK, Cochard H, Medlyn BE. 2018. On the minimum leaf conductance: its role in models of plant water use, and ecological and environmental controls. New Phytologist 221: 693–705. [DOI] [PubMed] [Google Scholar]
- Evaristo J, McDonnell JJ, Scholl MA, Bruijnzeel LA, Chun KP. 2016. Insights into plant water uptake from xylem‐water isotope measurements in two tropical catchments with contrasting moisture conditions. Hydrological Processes 30: 3210–3227. [Google Scholar]
- Fan Y, Miguez‐Macho G, Jobbágy EG, Jackson RB, Otero‐Casal C. 2017. Hydrologic regulation of plant rooting depth. Proceedings of the National Academy of Sciences, USA 114: 10572–10577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faybishenko B, Paton S. 2021. PA‐BCI Meteorological dataset 1985–2018 . 1.0. NGEE Tropics Data Collection. doi: 10.15486/ngt/1771850. [DOI]
- Fisher R, McDowell N, Purves D, Moorcroft P, Sitch S, Cox P, Huntingford C, Meir P, Woodward FI. 2010. Assessing uncertainties in a second‐generation dynamic vegetation model caused by ecological scale limitations. New Phytologist 187: 666–681. [DOI] [PubMed] [Google Scholar]
- Fisher RA, Muszala S, Verteinstein M, Lawrence P, Xu C, McDowell NG, Knox RG, Koven C, Holm J, Rogers BMetal. 2015. Taking off the training wheels: the properties of a dynamic vegetation model without climate envelopes, CLM4.5(ED). Geoscientific Model Development 8: 3593–3619. [Google Scholar]
- Galbraith D, Levy PE, Sitch S, Huntingford C, Cox P, Williams M, Meir P. 2010. Multiple mechanisms of Amazonian forest biomass losses in three dynamic global vegetation models under climate change. New Phytologist 187: 647–665. [DOI] [PubMed] [Google Scholar]
- Gentry AH. 1990. Four neotropical rainforests. New Haven, CT, USA: Yale University Press. [Google Scholar]
- Gleason SM, Westoby M, Jansen S, Choat B, Hacke UG, Pratt RB, Bhaskar R, Brodribb TJ, Bucci SJ, Cao K‐Fetal. 2016. Weak tradeoff between xylem safety and xylem‐specific hydraulic efficiency across the world’s woody plant species. New Phytologist 209: 123–136. [DOI] [PubMed] [Google Scholar]
- Godsey S, Elsenbeer H, Stallard R. 2004. Overland flow generation in two lithologically distinct rainforest catchments. Journal of Hydrology 295: 276–290. [Google Scholar]
- Goulden ML, Bales RC. 2019. California forest die‐off linked to multi‐year deep soil drying in 2012–2015 drought. Nature Geoscience 12: 632–637. [Google Scholar]
- Grossiord C, Buckley TN, Cernusak LA, Novick KA, Poulter B, Siegwolf RTW, Sperry JS, McDowell NG. 2020. Plant responses to rising vapor pressure deficit. New Phytologist 226: 1550–1566. [DOI] [PubMed] [Google Scholar]
- Harms KE, Condit R, Hubbell SP, Foster RB. 2001. Habitat associations of trees and shrubs in a 50‐ha neotropical forest plot. Journal of Ecology 89: 947–959. [Google Scholar]
- Hilker T, Lyapustin AI, Tucker CJ, Hall FG, Myneni RB, Wang Y, Bi J, de Moura YM, Sellers PJ. 2014. Vegetation dynamics and rainfall sensitivity of the Amazon. Proceedings of the National Academy of Sciences, USA 111: 16041–16046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann WA, Marchin RM, Abit P, Lau OL. 2011. Hydraulic failure and tree dieback are associated with high wood density in a temperate forest under extreme drought. Global Change Biology 17: 2731–2742. [Google Scholar]
- Hubau W, Lewis SL, Phillips OL, Affum‐Baffoe K, Beeckman H, Cuní‐Sanchez A, Daniels AK, Ewango CEN, Fauset S, Mukinzi JMetal. 2020. Asynchronous carbon sink saturation in African and Amazonian tropical forests. Nature 579: 80–87. [DOI] [PubMed] [Google Scholar]
- Hubbell SP, Foster RB, O’Brien ST, Harms KE, Condit R, Wechsler B, Wright SJ, de Lao SL. 1999. Light‐gap disturbances, recruitment limitation, and tree diversity in a Neotropical forest. Science 283: 554–557. [DOI] [PubMed] [Google Scholar]
- Ivanov VY, Hutyra LR, Wofsy SC, Munger JW, Saleska SR, de Oliveira RC, de Camargo PB. 2012. Root niche separation can explain avoidance of seasonal drought stress and vulnerability of overstory trees to extended drought in a mature Amazonian forest. Water Resources Research 48: 351–421. [Google Scholar]
- Johnson DM, Domec J‐C, Berry ZC, Schwantes AM, McCulloh KA, Woodruff DR, Polley HW, Wortemann R, Swenson JJ, Mackay DSetal. 2018. Co‐occurring woody species have diverse hydraulic strategies and mortality rates during an extreme drought. Plant, Cell & Environment 41: 576–588. [DOI] [PubMed] [Google Scholar]
- Jones FA, Erickson DL, Bernal MA, Bermingham E, Kress WJ, Herre EA, Muller‐Landau HC, Turner BL. 2011. The roots of diversity: below ground species richness and rooting distributions in a tropical forest revealed by DNA barcodes and inverse modeling. PLoS ONE 6: e24506–e24510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koven CD, Knox RG, Fisher RA, Chambers JQ, Christoffersen BO, Davies SJ, Detto M, Dietze MC, Faybishenko B, Holm Jetal. 2020. Benchmarking and parameter sensitivity of physiological and vegetation dynamics using the Functionally Assembled Terrestrial Ecosystem Simulator (FATES) at Barro Colorado Island, Panama. Biogeosciences 17: 3017–3044. [Google Scholar]
- Kunert N, Zailaa J, Herrmann V, Muller‐Landau HC, Wright SJ, Pérez R, McMahon SM, Condit RC, Hubbell SP, Sack Letal. 2021. Leaf turgor loss point shapes local and regional distributions of evergreen but not deciduous tropical trees. New Phytologist 230: 485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupers SJ, Wirth C, Engelbrecht BMJ, Rüger N. 2019. Dry season soil water potential maps of a 50 hectare tropical forest plot on Barro Colorado Island, Panama. Scientific Data 6: 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence DM, Fisher RA, Koven CD, Oleson KW, Swenson SC, Bonan G, Collier N, Ghimire B, Kampenhout L, Kennedy Detal. 2019. The community land model version 5: description of new features, benchmarking, and impact of forcing uncertainty. Journal of Advances in Modeling Earth Systems 11: 4245–4287. [Google Scholar]
- Leigh EGJ, Rand AS, Windsor DM. 1982. The ecology of a tropical forest: seasonal rhythms and long‐term changes. Washington, DC, USA: Smithsonian Institution Press. [Google Scholar]
- Lu Y, Duursma RA, Farrior CE, Medlyn BE, Feng X. 2020. Optimal stomatal drought response shaped by competition for water and hydraulic risk can explain plant trait covariation. New Phytologist 225: 1206–1217. [DOI] [PubMed] [Google Scholar]
- Malhi Y, Aragão LEOC, Galbraith D, Huntingford C, Fisher R, Zelazowski P, Sitch S, McSweeney C, Meir P. 2009. Exploring the likelihood and mechanism of a climate‐change‐induced dieback of the Amazon rainforest. Proceedings of the National Academy of Sciences, USA 106: 20610–20615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maréchaux I, Chave J. 2017. An individual‐based forest model to jointly simulate carbon and tree diversity in Amazonia: description and applications. Ecological Monographs 87: 632–664. [Google Scholar]
- Markesteijn L, Poorter L, Bongers F, Paz H, Sack L. 2011. Hydraulics and life history of tropical dry forest tree species: coordination of species’ drought and shade tolerance. New Phytologist 191: 480–495. [DOI] [PubMed] [Google Scholar]
- Markesteijn L, Poorter L, Paz H, Sack L, Bongers F. 2010. Ecological differentiation in xylem cavitation resistance is associated with stem and leaf structural traits. Plant, Cell & Environment 34: 137–148. [DOI] [PubMed] [Google Scholar]
- McDowell N, Allen CD, Anderson‐Teixeira K, Brando P, Brienen R, Chambers J, Christoffersen B, Davies S, Doughty C, Duque Aetal. 2018a. Drivers and mechanisms of tree mortality in moist tropical forests. New Phytologist 219: 851–869. [DOI] [PubMed] [Google Scholar]
- McDowell N, Allen CD, Anderson‐Teixeira K, Brando P, Brienen R, Chambers J, Christoffersen B, Davies S, Doughty C, Duque Aetal. 2018b. Drivers and mechanisms of tree mortality in moist tropical forests. New Phytologist 219: 851–869. [DOI] [PubMed] [Google Scholar]
- McDowell N, Pockman WT, Allen CD, Breshears DD, Cobb N, Kolb T, Plaut J, Sperry J, West A, Williams DGetal. 2008. Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytologist 178: 719–739. [DOI] [PubMed] [Google Scholar]
- McGregor IR, Helcoski R, Kunert N, Tepley AJ, Gonzalez‐Akre EB, Herrmann V, Zailaa J, Stovall AEL, Bourg NA, McShea WJetal. 2021. Tree height and leaf drought tolerance traits shape growth responses across droughts in a temperate broadleaf forest. New Phytologist 231: 601–616 [DOI] [PubMed] [Google Scholar]
- Meakem V, Tepley AJ, Gonzalez‐Akre EB, Herrmann V, Muller‐Landau HC, Wright SJ, Hubbell SP, Condit R, Anderson‐Teixeira KJ. 2018. Role of tree size in moist tropical forest carbon cycling and water deficit responses. New Phytologist 219: 947–958. [DOI] [PubMed] [Google Scholar]
- Meinzer FC, Andrade JL, Goldstein G, Holbrook NM, Cavelier J, Wright SJ. 1999. Partitioning of soil water among canopy trees in a seasonally dry tropical forest. Oecologia 121: 293–301. [DOI] [PubMed] [Google Scholar]
- Meinzer FC, Clearwater MJ, Goldstein G. 2001. Water transport in trees: current perspectives, new insights and some controversies. Environmental and Experimental Botany 45: 239–262. [DOI] [PubMed] [Google Scholar]
- Meir P, Mencuccini M, Dewar RC. 2015. Drought‐related tree mortality: addressing the gaps in understanding and prediction. New Phytologist 207: 28–33. [DOI] [PubMed] [Google Scholar]
- Mencuccini M, Salmon Y, Mitchell P, Hölttä T, Choat B, Meir P, O'Grady A, Tissue D, Zweifel R, Sevanto Setal. 2017. An empirical method that separates irreversible stem radial growth from bark water content changes in trees: theory and case studies. Plant, Cell & Environment 40: 290–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moorcroft PR, Hurtt GC, Pacala SW. 2001. A method for scaling vegetation dynamics: the ecosystem demography model (ED). Ecological Monographs 71: 557. [Google Scholar]
- Nardini A, Casolo V, Borgo AD, Savi T, Stenni B, Bertoncin P, Zini L, McDowell NG. 2015. Rooting depth, water relations and non‐structural carbohydrate dynamics in three woody angiosperms differentially affected by an extreme summer drought. Plant, Cell & Environment 39: 618–627. [DOI] [PubMed] [Google Scholar]
- Oleson K, Bonan GB, Drewniak B, Huang M, Koven CD, Levis S, Lawrence DM, Li F, Riley WJ, Subin ZMetal. 2013. Technical description of version 4.5 of the Community Land Model (CLM) (no. NCAR/TN‐503+STR). doi: 10.5065/D6RR1W7M. [DOI]
- Oliveira RS, Eller CB, Barros FdV, Hirota M, Brum M, Bittencourt P. 2021. Linking plant hydraulics and the fast‐slow continuum to understand resilience to drought in tropical ecosystems. New Phytologist 230: 904–923. [DOI] [PubMed] [Google Scholar]
- Osnas JLD, Katabuchi M, Kitajima K, Wright SJ, Reich PB, Bael SAV, Kraft NJB, Samaniego MJ, Pacala SW, Lichstein JW. 2018. Divergent drivers of leaf trait variation within species, among species, and among functional groups. Proceedings of the National Academy of Sciences, USA 115: 201803989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paddock W III, Davis S, Pratt B, Jacobsen A, Tobin M, López‐Portillo J, Ewers F. 2013. Factors determining mortality of adult chaparral shrubs in an extreme drought year in California. Aliso 31: 49–57. [Google Scholar]
- Park JY, Muller‐Landau HC, Lichstein JW, Rifai SW, Dandois JP, Bohlman SA. 2019. Quantifying leaf phenology of individual trees and species in a tropical forest using unmanned aerial vehicle (UAV) images. Remote Sensing 11: 1534. [Google Scholar]
- Paton S. 2019a. Monthly Summary_BCI, horizontal. The Smithsonian Institution. Dataset. doi: 10.25573/data.10059455.v13. [DOI]
- Paton S. 2019b. Barro Colorado Island, Conrad Catchment_Runoff. Dataset. The Smithsonian Institution. doi: 10.25573/data.10042478.v2. [DOI]
- Paton S. 2020. Yearly Reports_Barro Colorado Island. The Smithsonian Institution. Dataset. doi: 10.25573/data.11799111.v1. [DOI]
- Phillips OL, van der Heijden G, Lewis SL, López‐González G, Aragão LEOC, Lloyd J, Malhi Y, Monteagudo A, Almeida S, Dávila EAetal. 2010. Drought‐mortality relationships for tropical forests. New Phytologist 187: 631–646. [DOI] [PubMed] [Google Scholar]
- Powell TL, Galbraith DR, Christoffersen BO, Harper A, Imbuzeiro HMA, Rowland L, Almeida S, Brando PM, Costa ACL, Costa MHetal. 2013. Confronting model predictions of carbon fluxes with measurements of Amazon forests subjected to experimental drought. New Phytologist 200: 350–365. [DOI] [PubMed] [Google Scholar]
- Powell TL, Koven CD, Johnson DJ, Faybishenko B, Fisher RA, Knox R, McDowell NG, Condit R, Hubbell SP, Wright SJetal. 2018. Variation in hydroclimate sustains tropical forest biomass and promotes functional diversity. New Phytologist 219: 932–946. [DOI] [PubMed] [Google Scholar]
- R Core Team . 2020. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Rowland L, Lobo‐do‐Vale RL, Christoffersen BO, Melém EA, Kruijt B, Vasconcelos SS, Domingues T, Binks OJ, Oliveira AAR, Metcalfe Detal. 2015. After more than a decade of soil moisture deficit, tropical rainforest trees maintain photosynthetic capacity, despite increased leaf respiration. Global Change Biology 21: 4662–4672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack L, Scoffoni C. 2012. Measurement of leaf hydraulic conductance and stomatal conductance and their responses to irradiance and dehydration using the evaporative flux method (EFM). Journal of Visualized Experiments. doi: 10.3791/4179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheiter S, Langan L, Higgins SI. 2013. Next‐generation dynamic global vegetation models: learning from community ecology. New Phytologist 198: 957–969. [DOI] [PubMed] [Google Scholar]
- Schwantes AM, Parolari AJ, Swenson JJ, Johnson DM, Domec J, Jackson RB, Pelak N, Porporato A. 2018. Accounting for landscape heterogeneity improves spatial predictions of tree vulnerability to drought. New Phytologist 220: 132–146. [DOI] [PubMed] [Google Scholar]
- Scoffoni C, Sack L. 2017. The causes and consequences of leaf hydraulic decline with dehydration. Journal of Experimental Botany 68: 4479–4496. [DOI] [PubMed] [Google Scholar]
- Slik JWF, Arroyo‐Rodríguez V, Aiba S‐I, Alvarez‐Loayza P, Alves LF, Ashton P, Balvanera P, Bastian ML, Bellingham PJ, van den Berg Eetal. 2015. An estimate of the number of tropical tree species. Proceedings of the National Academy of Sciences, USA 112: 7472–7477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith‐Martin CM, Xu X, Medvigy D, Schnitzer SA, Powers JS. 2020. Allometric scaling laws linking biomass and rooting depth vary across ontogeny and functional groups in tropical dry forest lianas and trees. New Phytologist 226: 714–726. [DOI] [PubMed] [Google Scholar]
- Sperry JS, Adler FR, Campbell GS, Comstock JP. 1998. Limitation of plant water use by rhizosphere and xylem conductance: results from a model. Plant, Cell & Environment 21: 347–359. [Google Scholar]
- Stein M. 1987. Large sample properties of simulations using Latin hypercube sampling. Technometrics 29: 143. [Google Scholar]
- Venturas MD, MacKinnon ED, Dario HL, Jacobsen AL, Pratt RB, Davis SD. 2016. Chaparral shrub hydraulic traits, size, and life history types relate to species mortality during California’s historic drought of 2014. PLoS ONE 11: e0159145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe BT, Cozzarelli Y, Jaén N. 2021. Stem hydraulic conductivity and vulnerability to cavitation for 26 tree species in Panama. 1.0. NGEE Tropics Data Collection. doi: 10.15486/ngt/1770723. [DOI]
- Wolfe BT, Goldstein G. 2017. Retention of stored water enables tropical tree saplings to survive extreme drought conditions. Tree Physiology 37: 469–480. [DOI] [PubMed] [Google Scholar]
- Wolfe BT, Wu J, Ely K, Serbin S, Rogers A, Dickman T, Collins A, Detto M, Grossiord C, McDowell Netal. 2019. Leaf water potential, Feb2016‐May2016, PA‐SLZ, PA‐PNM, PA‐BCI: Panama. 1.0. NGEE Tropics Data Collection. doi: 10.15486/ngt/1507766. [DOI]
- Wright SJ. 2005. Tropical forests in a changing environment. Trends in Ecology & Evolution 20: 553–560. [DOI] [PubMed] [Google Scholar]
- Wright SJ, Cornejo FH. 1990. Seasonal drought and leaf fall in a tropical forest. Ecology 71: 1165–1175. [Google Scholar]
- Wright SJ, Kitajima K, Kraft NJB, Reich PB, Wright IJ, Bunker DE, Condit R, Dalling JW, Davies SJ, Díaz Setal. 2010. Functional traits and the growth–mortality trade‐off in tropical trees. Ecology 91: 3664–3674. [DOI] [PubMed] [Google Scholar]
- Xu C, McDowell NG, Fisher RA, Wei L, Sevanto S, Christoffersen BO, Weng E, Middleton RS. 2019. Increasing impacts of extreme droughts on vegetation productivity under climate change. Nature Climate Change 9: 948–953. [Google Scholar]
- Xu X, Medvigy D, Powers JS, Becknell JM, Guan K. 2016. Diversity in plant hydraulic traits explains seasonal and inter‐annual variations of vegetation dynamics in seasonally dry tropical forests. New Phytologist 212: 80–95. [DOI] [PubMed] [Google Scholar]
- Yang J, Duursma Ra, De Kauwe Mg, Kumarathunge D, Jiang M, Mahmud K, Gimeno Te, Crous Ky, Ellsworth Ds, Peters Jetal. 2019. Incorporating non‐stomatal limitation improves the performance of leaf and canopy models at high vapour pressure deficit. Tree Physiology 39: 1961–1974. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Dataset S1 Microclimatic and flux tower data.
Dataset S2 Leaf hydraulic conductivity and vulnerability to cavitation.
Dataset S3 Wood specific gravity (WSG) and leaf mass area (LMA).
Dataset S4 Leaf deciduousness categories.
Dataset S5 Stream discharge from the Conrad catchment.
Dataset S6 Volumetric water content.
Dataset S7 Stem maximum hydraulic conductivity and vulnerability to cavitation.
Dataset S8 Leaf turgor loss point.
Dataset S9 Aboveground hydraulic safety margins.
Fig. S1 Observed relationship between GPP and VPD at Barro Colorado Island.
Fig. S2 Seasonal variation in estimated standardized LAI for 29 species at Barro Colorado Island.
Fig. S3 Ensembles of soil hydraulic conductivity variation by depth for Conrad Trail Stream Catchment, Barro Colorado Island (data from Godsey et al., 2004).
Fig. S4 Volumetric water content vs. TDR data for a vertical TDR probe used for TDR probe calibration.
Fig. S5 δ2H of soil water by depth measured at Barro Colorado Island (data from Meinzer et al., 1999).
Fig. S6 Parameter sensitivity of ELM‐FATES soil water content and evapo‐transpiration.
Fig. S7 Parameter sensitivity of ELM‐FATES stream discharge.
Fig. S8 ELM‐FATES predicted soil water potential dynamics by depth over 1990–2018.
Fig. S9 Leaf hydraulic vulnerability curves fitted to observed K leaf vs Ψleaf data for 21 tree species from Barro Colorado Island.
Fig. S10 Percent loss of leaf hydraulic conductivity curves for ERD species, including curves fitted to K leaf vs Ψleaf as well as those based on scaling relationships with LMA and WSG.
Fig. S11 Effective rooting depths (ERD) vs δ2Hxylem for each of the ERD model structures tested.
Fig. S12 Correlation matrix between ERD and hydraulic traits.
Fig. S13 Mortality rates for deciduous species across census intervals from 1985–2015 vs ERD.
Fig. S14 Modeled effective rooting depths of deciduous species vs time spent beyond critical hydraulic threshold.
Methods S1 Alternative structures for effective rooting depth model.
Methods S2 Statistics for identifying best‐fit ERD.
Methods S3 Processing of forest census data for growth estimates.
Methods S4 Leaf area index calculations.
Methods S5 Details of the ELM‐FATES model.
Methods S6 Details for ELM‐FATES model parameterization.
Methods S7 ELM‐FATES calibration.
Notes S1 ERD model structure selection.
Notes S2 Additional results for exposure to water stress.
Table S1 ELM‐FATES parameters used to generate ensembles, with description, prescribed global ranges, rationale for the choice of ranges and references, as well as ranges for best‐fit ensembles.
Table S2 QA/QC procedure applied to eddy covariance fluxes.
Table S3 Aboveground hydraulic traits data from Wolfe et al. (2019) and Wolfe et al. (2021) used for comparison with ERD.
Table S4 Leaf vulnerability curve parameters A & B, K max, leaf and Ψ20,leaf by source (data or model) for the 29 species with ERD estimates.
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Data Availability Statement
ELM‐FATES source code, simulation outputs for best‐fit parameter ensemble members and all of the R scripts to reproduce the manuscript are available (Chitra‐Tarak et al., 2020). Data sources for all other datasets used are provided throughout the manuscript.


