Fluorescence‐Detected Pump–Probe Spectroscopy

Abstract

We introduce a new approach to transient spectroscopy, fluorescence‐detected pump–probe (F‐PP) spectroscopy, that overcomes several limitations of traditional PP. F‐PP suppresses excited‐state absorption, provides background‐free detection, removes artifacts resulting from pump–pulse scattering, from non‐resonant solvent response, or from coherent pulse overlap, and allows unique extraction of excited‐state dynamics under certain conditions. Despite incoherent detection, time resolution of F‐PP is given by the duration of the laser pulses, independent of the fluorescence lifetime. We describe the working principle of F‐PP and provide its theoretical description. Then we illustrate specific features of F‐PP by direct comparison with PP, theoretically and experimentally. For this purpose, we investigate, with both techniques, a molecular squaraine heterodimer, core–shell CdSe/ZnS quantum dots, and fluorescent protein mCherry. F‐PP is broadly applicable to chemical systems in various environments and in different spectral regimes.

Ultrafast pump–probe spectroscopy detected by fluorescence is introduced. Combining sensitive fluorescence detection with ultrafast pulse‐limited time resolution, this approach provides a complementary technique to standard transient absorption.

Introduction

Time‐resolved spectroscopy has revolutionized mechanistic investigations of chemical dynamics, with a Nobel Prize awarded to Ahmed Zewail for his developments in the field of “femtochemistry”.^[1] Since this pioneering work, ever shorter laser pulses provide the shutter for initiating and probing ever faster photo‐physical as well as photo‐chemical processes, from nanoseconds down to the attosecond regime.^[2] An exemplary ultrafast technique is pump–probe (PP) spectroscopy.^[3] There, one pulse called pump is used to excite the sample into an electronically and/or vibrationally excited state, which is then probed by observing the change in transmission of a second pulse after a well‐defined time delay. PP (“transient absorption”) spectroscopy is a very robust technique, capable of following the photo‐induced dynamics across timescales. Applications in physical chemistry include electronic dynamics of energy and charge transfer,^[4] dynamics in photo‐catalysis,^[5] solvation dynamics,^[6] structure of the excited states,^[7] multi‐particle effects,^[8] photo‐product formation such as ring opening,^[9] photo‐reactivity,^[10] coherent motion of nuclear wave‐packets,^[11] or photo‐isomerization.^[12]

Despite its tremendous utility, PP spectroscopy has its limitations. Because signal changes are detected against the bright background of the probe pulse, accurate detection is difficult in samples producing weak signals, such as highly dilute solutions. This has also been a major limitation of transient absorption microscopy.^[13] PP spectroscopy is also problematic in highly scattering samples, as the scattered light is difficult to suppress, especially when the pump and probe spectra overlap.^[14] In some samples, the excited‐state absorption overlaps heavily with the ground‐state‐transition signals, making the contributions difficult to disentangle. Finally, for ultrafast dynamics, off‐resonant signals such as solvent response or cross‐phase modulation overlay the system dynamics, together comprising the so‐called coherent artifact.^[15]

All the mentioned problems can be overcome by changing the detection from a coherent to an incoherent signal, such as fluorescence (FL). Fluorescence can be easily separated from the excitation beams, spatially and/or spectrally, leading to signal detection on a dark background. FL arises only after resonant excitation, so the signal does not include off‐resonant contributions. As we demonstrate, in cases when the excited‐state absorption does not change the FL yield, no excited‐state absorption is present in the signal. Finally, FL detection in microscopy has been developed to perfection and is widely used across disciplines.

There exist several established time‐resolved FL techniques, detecting the spontaneous emission.^[16] These feature streak‐camera measurement or time‐correlated single‐photon counting in the picosecond to nanosecond regime, and up‐conversion or transient grating reaching sub‐picosecond resolution.[¹⁷, ¹⁸] However, due to the gating of the typically relatively slow emission, the time resolution of these techniques is limited by the rate of photon emission. To measure the spectral correlation of excitation and emission on an ultrafast timescale, FL detection has been developed for two‐dimensional electronic spectroscopy (2DES).[¹⁹, ²⁰, ²¹, ²², ²³, ²⁴] The fluorescence‐detected 2DES (F‐2DES) is currently gaining popularity due to the advantages of FL detection as listed above. However, F‐2DES is significantly more complex than PP spectroscopy. It requires two pairs of pulses with scanned interferometric delays, all with stable, modulated phases.

The complexity brings with itself not only the need for advanced instrumentation (required to scan the delays between all pulses and to modulate the phases), but a longer measurement time as well. Finally, interpretation of 2D data can be more involved because, e.g., direct identification of species based on their known linear spectra is not straightforward. An approach developed recently by the Moran group, positioned conceptually between 2DES and PP spectroscopy, measures nonlinear FL induced by two pulses of varying wavelength.^[25] There is thus a trade‐off between the spectral and time resolution.

Despite the advances in F‐2DES, the apparently more straightforward variant of FL‐detected pump–probe (F‐PP) spectroscopy has not been widely pursued. This is somewhat paradoxical, as the early work by Zewail and co‐workers has been of this concept.^[26] Later works with FL detection became motivated by FL microscopy. Using two asynchronous lasers, FL nanosecond lifetime imaging was demonstrated by Dong et al.^[27] More recent works aimed at the femtosecond regime in single molecules. In the non‐perturbative regime near saturation, a two‐pulse scan was used to determine dynamic reorganization^[28] and energy relaxation.^[29] A technique related to our work was realized by Liebel et al., measuring a transient stimulated emission spectrum.^[30] The general downside of the latter approaches is their non‐intuitive, indirect interpretation.

Herein, we introduce F‐PP spectroscopy and demonstrate its features by directly comparing it to conventional PP spectroscopy, performed under identical conditions, both theoretically and experimentally. F‐PP benefits from the sensitive time‐integrated FL detection, while maintaining the time resolution given by the laser pulses. It can track the photo‐induced dynamics across timescales, from femtoseconds to nanoseconds, utilizing the selectivity with respect to the emissive species. At the same time, all established PP interpretation tools such as lifetime maps^[31] or global and target spectral analysis^[32] with identification of known spectral species can be applied to the data. Thus, F‐PP spectroscopy is excellently suited for the study of chemical systems such as fluorescent dyes that were also a research topic of Prof. Hünig.^[33]

Results and Discussion

Principle of F‐PP

In Figure 1, we schematically compare standard PP (left) and F‐PP spectroscopy (right). In a PP setup (Figure 1 A), the probe transmission is detected with and without a prior pump pulse, the relative difference in intensity constituting the PP signal. As a nonlinear spectroscopy technique, PP probes the response of the system perturbed by the pump and probe pulses. This response can be described by the evolution of its density matrix in Liouville space^[34]—its pathway is commonly depicted by double‐sided Feynman diagrams.^[35] For a PP measurement, the action of the pulses in time is shown in Figure 1 C and the response pathway diagrams in Figure 1 E. Initially, the system is assumed to be in its ground state |0⟩. The pump pulse (blue) interacts twice, leaving the system in a population state (of a ground state |0⟩ or an excited state |1⟩), i.e., on the diagonal of the density matrix. The system then evolves for the waiting time T until it interacts with the probe pulse (orange). This produces an optical coherence that leads to a coherent polarization response. Depending on the state evolving during the delay T, there are three types of processes that can be probed: the ground‐state bleach (GSB), stimulated emission (SE), and excited‐state absorption (ESA, photo‐induced absorption). GSB and SE lead to the increase of the detected probe intensity, ESA to its decrease. We follow the transient absorption sign convention for which GSB and SE are counted as negative (i.e., less light absorbed by the sample) and ESA as positive.

Figure 1.

Principles of traditional (left) and fluorescence‐detected (right) pump‐probe spectroscopy. Top row: A) PP and B) F‐PP experimental schemes. Throughout the Figure, pump pulses are depicted in blue, probe pulses in orange, and signals in red. Middle row: Illustration of the action of the pulses in time on the manifolds of states for C) PP and D) F‐PP. Horizontal lines indicate electron‐vibrational states, arrows indicate excitation dynamics. Bottom row: Double‐sided Feynman diagrams for E) PP and F) F‐PP techniques. Time flows upwards, incoming arrows indicate interaction with the respective pulses, outgoing arrows indicate signal emission, and numbers indicate manifolds in the elements of the system density matrix.

In F‐PP spectroscopy (Figure 1 B) as introduced in the present work, the sample excitation after interaction with the pump and probe pulses is monitored by the excited‐state fluorescence. To obtain spectral resolution, we use an interferometrically stable probe pulse pair with varying delay t. This approach is known from Fourier‐transform linear absorption.[³⁶, ³⁷] As in conventional PP spectroscopy, the difference in the emission with and without the preceding pump pulse is of interest. The action of the pump and probe pulses is drawn in Figure 1 D and the response contributions in Figure 1 F. As in PP, the pump pulse (blue) produces a population of the system states, which evolves in waiting time T. Then the probe pulse pair arrives (orange), which probes the oscillatory optical coherence evolution in the time t between the probe pulses. The last interaction with the probe brings the system back to a population state. After the four pulse interactions, the signal is emitted during the system evolution, in case of FL by spontaneous emission. This leads to an additional weighting of the pathways in the total signal by the FL quantum yield of the final states.[²⁰, ²³] The general structure of the Liouville pathways in F‐PP is the same as in PP, with the exception of the presence of an additional ESA‐type pathway (denoted ESA2 in Figure 1 F) in F‐PP. The ESA2 pathway results from the additional interaction with the last pulse field, ends in a doubly excited state, and the FL yield of such a state has deep consequences for the features present in an F‐PP spectrum as we describe below.

We provide a mathematical description of PP and F‐PP in Section S1 of the Supporting Information (SI). The F‐PP signal can be understood as transient FL excitation spectroscopy and reflects the change of the excitation spectrum of the sample, resulting from the preceding interaction with the pump. Depending on the system state after the delay T, the probe can be absorbed (GSB‐type signal), cause stimulated emission (SE), or cause transition into a higher excited state (ESA‐type). When the molecule is in its excited state after the pump (i.e., the molecule is bleached), the probe absorption is decreased. Stimulated emission also decreases excited‐state population and thus the FL. GSB and SE therefore have a negative sign, same as in traditional PP. ESA can lead to increased FL and thus a positive signal, but in typical molecules the higher states rapidly relax non‐radiatively (“Kasha's rule”), and ESA is thus not observed in F‐PP. While in PP the signal can be separated from the pump by its spatial propagation (in the direction of the probe beam), in F‐PP the produced signal results from incoherent spontaneous emission without phase matching. However, the signal can be isolated by selecting the oscillatory component arising from scanning the delay between the two probe pulses. Optionally, for very short waiting time delays comparable to optical coherence dephasing time (tens of femtoseconds), additional cycling of the probe phases φ _1,2 can be used.[³⁸, ³⁹] While F‐PP can be realized in all‐collinear geometry (Figure 1 B), a slightly non‐collinear geometry, standard in PP, works as well, and has been used in this work to facilitate direct comparison between the techniques (Section S2 of SI).

F‐PP and PP of Molecular Heterodimers

Let us compare the PP and F‐PP methods on the example of a molecular heterodimer. We choose a dimer (dSQAB‐3) of squaraine A (SQA) and squaraine B (SQB) molecules, connected by a phenyl spacer[³⁹, ⁴⁰] (Figure 2 A). Squaraine dyes are highly photo‐stable, have large FL quantum yield (here 0.74),^[40] their transition energies are easily chemically tunable, and the electronic coupling can be tuned by the length of the intermolecular spacer.[³⁹, ⁴⁰] The excited states of our dimer can be well described by a Frenkel‐exciton model as two weakly coupled three‐level systems (Figure 2 B). The dynamic processes include excited‐state radiative and non‐radiative decay in ≈3 ns, and an energy transfer between the two squaraines as well as exciton–exciton annihilation, both taking ≈30 fs.[³⁹, ⁴¹] The spectra of the pump and probe beams both cover the dimer absorption (Figure 2 C), and the pulse duration is ≈12 fs for both. The sample preparation and measurement conditions are detailed in Section S3 of the SI.

Figure 2.

Molecular heterodimer. A) Structure of dimer of squaraine A (blue) and squaraine B (red) molecules, weakly coupled due to the relatively long phenyl spacer (green). B) Energy scheme of a molecular dimer made up of three‐level monomer subsystems. Labels indicate ground state |g⟩, one‐exciton states |e⟩, higher excited states |f⟩, and two‐exciton state |ee⟩. States are grouped into manifolds denoted on the right, which are used in Figure 1 C–F. Arrows indicate processes of energy transfer (ET), internal conversion (IC), and energy relaxation (relax). C) Absorption (light solid green), emission (dark dashed green) and laser pulse spectra. The pump and probe beams are interchanged between F‐PP and PP, with the yellow color indicating the probe spectrum for PP and the pump spectrum for F‐PP (PP:Pr/F‐PP:Pu), and vice versa for orange (PP:Pu/F‐PP:Pr).

We accompany the measurement by a simulation (Section S4 of the SI), where we closely follow the experiment, solving a master equation for the density matrix with explicit interaction with light. There, we assume identical pump and probe pulses with 10 fs duration, centered at 1.8 eV. For our calculation we choose a generic molecular heterodimer, and we focus on illustrating the general features of F‐PP compared to PP, not necessarily with the goal of perfect reproduction of our specific experimental data. To ease the identification of the features in the spectra, we choose an energy gap of 0.2 eV and set energy transfer and exciton–exciton annihilation times both to 50 fs and the excited‐state lifetime to 1 ns. The data are shown in Figure 3, comparing calculated PP (Figure 3 A) and F‐PP spectra (Figure 3 B) with experimental PP (Figure 3 C) and F‐PP (Figure 3 D) spectra. We will describe the experimental and theoretical spectra together. There are two excitonic states, |e_A,B⟩ (Figure 2 B), in our dimer almost completely localized at the respective squaraine molecules. Correspondingly, we observe two peaks in the transient spectrum at the respective energies (≈1.72 eV and ≈1.87 eV). The excited‐state absorption features transitions into higher excited states |f_A,B⟩ of the squaraine molecules, as well as into the bi‐exciton state |e_Ae_B⟩. The ESA into the |f_A,B⟩ states is very broad and weak, and in the experiment lies partly outside our probe spectrum.^[39] It is thus difficult to discern in the spectra (the very small positive peak around 1.6 eV and the distortion in the upper‐energy peak around 1.9 eV). The ESA into the bi‐exciton state |e_Ae_B⟩ is, however, present, at the corresponding state energy differences (≈1.72 eV and ≈1.87 eV). With an opposite sign to the GSB and SE, it partially cancels out with the ground‐state transition signals, as we detail further on. In F‐PP there is no ESA‐type signal because of fast internal conversion from the higher excited states and due to an efficient exciton–exciton annihilation of the bi‐exciton state.^[41] The ESA and ESA2 pathways (Figure 1 F) cancel because they have the same FL quantum yield but opposite signs. This cancellation reflects the fact that excitation into a higher state (manifold |2⟩ in Figure 2 B) does not lead to increased emission. As we further describe in the quantum dot sample below, where the ESA is much more prominent, its absence can allow identification of ground‐state transitions which are otherwise hidden in the spectral overlap.

Figure 3.

Theoretical (top) and experimental (bottom) comparison of PP (left) and F‐PP (right) transient spectral data of the dimer of Figure 2. In each panel, the color‐coded image provides transient maps of the spectral shape (vertical) as a function of waiting time T (horizontal). Projections depict spectral slices (right side panels) and time slices (top panels) at marked temporal and energetic positions, respectively. For the experimental data (bottom), the projections include the results of a joint global fit with the same color as the raw data but thicker lines and added partial transparency (for F‐PP only T>0 data were fitted).

The squaraine molecules have a small and fast Stokes shift (≈25 meV within 50 fs),^[40] so there is only a small red shift visible caused by SE (in Figure 3 C,D, just after T=0, at ≈1.7 eV). In the simulated dimers we did not include any Stokes shift. We focus in detail on the dynamic Stokes shift in the sample of mCherry below. We measured both PP and F‐PP at a magic angle orientation between the pump and the probe pulse polarizations to avoid anisotropy in the pump–probe signal.[³, ¹⁴] In the linear excitation regime (Figure S3 in the SI), the dynamics is not influenced by exciton–exciton annihilation.^[8] There are thus only two dominating dynamic processes in the data: energy relaxation and excited‐state decay. At initial times, both states |e_A,B⟩ are excited by the broadband pump. The energy transfer from the upper state |e_A⟩ to the lower state |e_B⟩ taking ≈30 fs (50 fs in the simulation) is visible in a decay of the upper peak (≈1.87 eV) and rise of the lower peak (≈1.72 eV). A joint global fit of the two experimental data sets (with Glotaran^[42]) results in 32 fs for energy relaxation. The decay‐associated spectra (DAS) are described in Section S5 in the SI. The DAS feature a decay at higher energy and rise at lower energy, a clear signature of energy relaxation. At long times, the excited state is in quasi‐stationary equilibrium and both peaks decay. In squaraines, this decay is bi‐exponential, with timescales of ≈420 fs and ≈2.94 ns.^[40]

While both PP and F‐PP contain information on the energy transfer and excited‐state decay, the relative amplitude change during T of the two peaks differs for the two techniques. This difference arises from the response structure (Figures 1 E,F). Initially, both excitonic states |e_A,B⟩ are excited, and thus both peaks are present. In PP, the energy transfer starting from the higher‐energy state leads to a complete decay of the corresponding peak. In a collective basis (Figure 2 B), this is expressed by an ESA pathway cancelling the GSB pathway. This meaning of the ESA pathway has been recently discussed in detail, including the relevant diagrams, in context of 2DES as “re‐excitation” pathway.^[43] In F‐PP, one finds the same energy transfer component to the signal, arising from SE. However, as a consequence of the absence of ESA, the GSB of the upper transition remains, and the corresponding peak does not decay completely. This difference can be understood considering the nature of the detected signal. In PP, the higher‐energy state returns to the ground state, so that the transmission change disappears. In contrast, in F‐PP any excitation present in the excited state decreases the signal, either directly by the transition bleach, or indirectly by exciton–exciton annihilation. As a result, the SE decay is observed on the GSB background in F‐PP. This smaller spectral modulation by energy transfer makes the kinetics less pronounced than in standard PP, which can be seen as a disadvantage of F‐PP. On the other hand, even in the case of rapid energy relaxation (as in our squaraine dimer), the higher‐energy transitions are clearly discernible.

In F‐PP the transient spectrum results from a multiplication with the spectrum of the probe pulse (Figure 2 C), while in PP the probe‐spectrum shape cancels out. This leads to a difference in peak amplitudes between F‐PP and PP, and a spectral shift of the transient peaks. We discussed these effects in more detail in preceding work on F‐2DES.^[39] Unlike in PP, the probe spectrum cannot be easily removed in F‐PP—taking the difference signal relative to the un‐pumped signal would result in division of the spectra by the sample excitation spectrum, and not only by the probe spectrum.

Around time zero, we observe a large modulation in the PP transients, the “coherent artifact” (CA). It originates from coherent interaction of the pump and probe beams in nonlinear processes such as cross‐phase modulation and stimulated Raman scattering.[¹⁵, ⁴⁴] The CA is sensitive to the phase of the pulses and leads to a strong oscillatory modulation of the PP signal in both spectrum and time. Although the CA structure can in principle be reproduced, it does not reflect the desired perturbative system response, and its presence complicates the observation of early‐time dynamics. As the contributing processes are off‐resonant, they do not lead to an excitation of the sample. The CA is thus practically absent in F‐PP, which can be a great advantage, as seen in the global analysis described above. There is a small spike in F‐PP in the region of pulse overlap. This spike arises from “wrongly” time‐ordered response pathways, possibly together with pump–probe interference. Similar to F‐2DES, the F‐PP spectra at T=0, although free from CA, should thus be interpreted with caution, as we also discuss at the end of Section S4 of the SI.

Finally, a large difference between PP and F‐PP is found for the signal before time zero. In PP, there is no signal at negative times. In contrast, in F‐PP the signal corresponds to the decrease of the FL (caused by the probe excitation) with subsequent pumping. Due to the action of the pump arriving after the probe pulse, the probe‐induced FL can be reduced by SE and exciton–exciton annihilation. The spectrum at negative times therefore corresponds to the FL excitation spectrum. This is also visible from the response pathways. The PP response (Figure 1 E) for T<0 decays with the optical coherence dephasing. In contrast, F‐PP diagrams in Figure 1 F (and also in Figure S5 in Section S6 in the SI) for T<0 survive and decay with the excited‐state lifetime only. The amplitude of the GSB and SE diagrams for T<0 remains the same, but they both probe the GSB‐type response. Directly comparing the F‐PP spectra for T<0 and T>0 therefore allows the subtraction of the GSB component. This is a unique feature of F‐PP, with a great potential in isolating the excited‐state dynamics. We show the full negative and positive T scan in Figure S5 in the SI, including the contributing response pathways. We further utilize the possibility of SE isolation for the mCherry protein below.

Compared to PP, F‐PP needs the additional scanning of the probe pulse pair delay to achieve spectral resolution. This leads to a larger number of acquired data points. On the other hand, its higher sensitivity results in the need of less laser shots per data point. A comparison of the measurement time for the two techniques depends on the intensity of the pump–probe signal in PP and of fluorescence in F‐PP. In our setting, the actual acquisition times for PP and F‐PP were very similar.

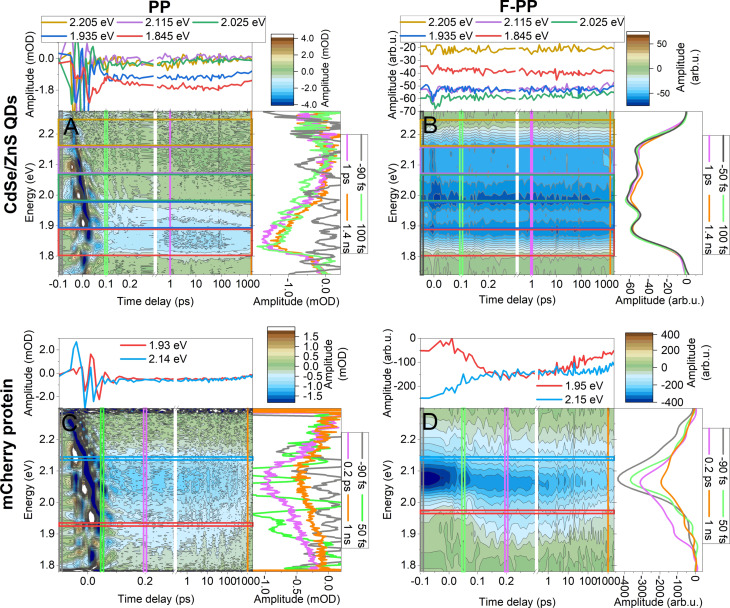
F‐PP and PP of CdSe/ZnS Quantum Dots

To further demonstrate the applicability of F‐PP beyond molecular complexes and to highlight some specific features, we measured two other very different samples: quantum dots and fluorescent protein. The data are shown in Figure 4. First, we measured colloidal core–shell CdSe/ZnS quantum dots (QDs), 6 nm in diameter. Linear spectra and more details can be found in Section S3 of the SI. As before, we measured both PP (Figure 4 A) and F‐PP (Figure 4 B) under the same conditions. In these QDs there are several spectrally overlapping excitonic states.[⁴⁵, ⁴⁶, ⁴⁷] In PP, the higher‐energy exciton transitions are, however, completely overlapped by the ESA into multi‐excitonic states.^[48] As these recombine with a timescale on the order of 100 ps,[⁴⁹, ⁵⁰] their FL yield is the same as that of the one‐exciton states. As a result, similar to the situation in the squaraine dimers, ESA is not present in F‐PP of these QDs. We can thus directly observe the transitions from the ground state to the higher excitonic states. Apart from the exciton line shapes, the F‐PP spectrum in Figure 4 B is modulated by the probe spectrum (Figure S2 in the SI). We note that it is not always the case that ESA pathways do not contribute. An example is the azulene molecule, which fluoresces directly from its S2 state.^[51] In the F‐PP measurement of azulene (not shown), one therefore finds exclusively the ESA2 pathway contributing.

Figure 4.

PP (left) and F‐PP (right) spectra of (top) colloidal CdSe/ZnS core–shell quantum dots in toluene (A,B) and (bottom) mCherry protein (C,D). The color images indicate the transient maps of the spectral shape (vertical) as a function of waiting time T (horizontal). Projections depict spectral slices (right side panels) and time slices (top panels) averaged over indicated temporal and energetic regions, respectively.

In the dynamics of the QD spectra, we observe downward energy relaxation within the one‐exciton manifold (≈400 fs) as well as subsequent excited‐state decay (several ns). The energy transfer can be seen on the lowest‐energy peak trace (≈1.845 eV, red in Figure 4 A,B), whose absolute magnitude slightly increases with T. These dynamics are relatively slow compared to the pulse duration, and thus a selective narrowband excitation of a particular excitonic state would make the dynamics much more pronounced, both in PP and F‐PP. Yet another alternative would be a (F‐)2DES measurement.[⁴⁷, ⁵²]

Finally, there are coherent oscillations discernible in the waiting‐time dynamics. In Figure S7 in Section S7 of the SI we compare the spectrum of the QD early waiting‐time oscillations in the spectral regions marked in Figures 4 A,B. Between 70 and 150 fs, both PP and F‐PP display oscillations at the frequency of the low‐energy optical phonons. F‐PP, being free of the coherent artifact, allows analysis of earlier waiting times than PP. Starting from T=30 fs, we find additional, relatively short‐lived higher‐energy oscillations at energies ranging from 180 meV to 350 meV. Oscillations of such energies correspond to the inter‐excitonic spacing, and lifetimes on the order of 80 fs have been observed in CdSe QDs and were attributed to inter‐excitonic coherences.[⁵², ⁵³] While this explanation is consistent with our results, a more detailed study, possibly utilizing inherently phase‐stable single‐beam‐geometry F‐PP, would provide grounds for unambiguous assignment.

F‐PP and PP of Fluorescent Protein mCherry

Last, we measured the fluorescent protein mCherry, which consists of a CH6 chromophore (Met‐Tyr‐Gly) in a protein beta‐barrel.^[54] This bright protein (FL quantum yield 0.22) has been genetically engineered from red fluorescent protein mRFP1,^[55] for increased extinction coefficient and improved stability against photo‐damage. Direct observation of the dynamic Stokes shift is, however, challenging, as it occurs on an ultrafast timescale. Linear absorption, FL, and laser spectra are shown in Figure S2 in Section S2 of the SI. In Figure 4 C and 4 D we show the PP and F‐PP data, respectively, of mCherry in pH 7.5 phosphate buffer.

In PP there is a large coherent artifact around T=0, obscuring the ultrafast dynamics. In contrast, in F‐PP the dynamic Stokes shift can be clearly seen in the rise of the red‐shifted SE (around 1.95 eV). Fitting the rise of SE with an exponential yields a reorganization time of ≈55 fs, which is fast for the relatively large Stokes shift of 80 meV (see Ref. [55] and Figure S2 in the SI). Excitation of any higher excited states does not increase FL intensity of mCherry, so the ESA and ESA2 pathways cancel. Hence, at positive times, only GSB and SE contribute. An interesting option, which we detail in Section S6 in the SI, is the subtraction of the GSB using the spectra acquired at negative waiting times. Briefly, taking the spectrum acquired at T=−2 ps provides a GSB spectrum, which can be subtracted from the positive‐delay F‐PP. As a result, shown in Figure S6 in the SI, one obtains the dynamics and lineshape of the pure SE. As the Stokes shift in fluorescent proteins is sensitive to their environment,^[56] such a measurement, performed for example in a microscope, could be used as an advanced local probe. While the SE isolation clearly works in the relatively simple case of a single chromophore, acting practically as an electronic two‐level system, the extraction of ultrafast dynamics attributed exclusively to the excited state is a much more general problem.

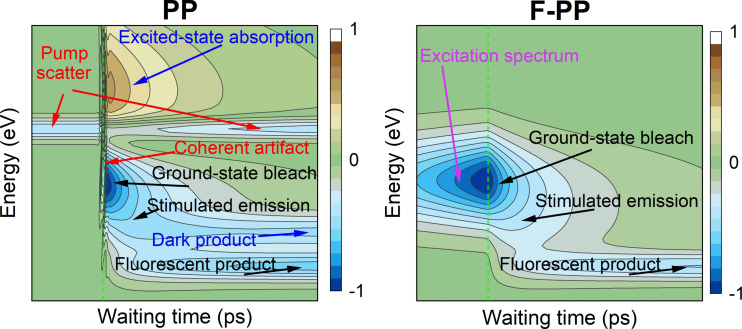
Conclusion

We have demonstrated the working principle of a fluorescence‐detected variant of pump–probe spectroscopy (F‐PP). We have described its principle theoretically, and directly compared its key characteristics to standard pump–probe (PP) spectroscopy, under the same experimental conditions. While enjoying the sensitivity of FL detection, F‐PP retains the time resolution limited only by the pulse duration. Moreover, it is in some aspects complementary to PP, having particular advantages that we discussed. In Figure 5 we summarize the key features present in PP and F‐PP transient spectra. Fundamental differences are that in F‐PP, an off‐resonant response is absent and excited‐state absorption (ESA) is suppressed. Furthermore, the ground‐state excitation spectrum can be extracted at negative times. We have tested F‐PP on three different types of samples: a molecular heterodimer, core–shell quantum dots, and a fluorescent protein. The results illustrate the ability of F‐PP to observe the same processes as PP, including energy transfer, dynamic excited‐state reorganization, coherent oscillatory dynamics, and excited‐state decay. Established techniques for PP data analysis such as global analysis can be applied to F‐PP as well, as we demonstrated for the energy relaxation in squaraine dimers. In addition, there are several trade‐offs between F‐PP and PP. As we have shown, e.g., on the quantum dots, the absence of ESA in F‐PP makes visible excitonic states that are usually hidden in PP. However, at the same time, this makes the energy relaxation dynamics less pronounced, and the information about transitions into higher excited states is absent from F‐PP.

Figure 5.

General features present in the transient spectra of standard pump–probe (PP, left) and its fluorescence‐detected variant (F‐PP, right). The colored maps indicate transient spectra (vertical axis) evolving in the waiting time (horizontal axis). Time zero is indicated by a green dashed line. Features present in both techniques are labeled in black. Features labeled in red are present in PP only and do not reflect the system dynamics. Features labeled in blue are typically present in PP only, while the feature in pink is exclusive for F‐PP. Data were calculated assuming exponential kinetics convoluted with a Gaussian instrument response function (pulse cross‐correlation), Gaussian line shapes of all features, and a cosine‐modulated coherent artefact.

Apart from fundamental differences, F‐PP has practical advantages, related to the sensitive or selective fluorescent detection. A possible application of F‐PP are photo‐induced chemical processes in fluorescent proteins.^[57] Using mCherry protein as an example, we demonstrated the possibility to use negative time delays for the subtraction of the ground‐state bleach contribution from the total signal, leaving the pure excited‐state (stimulated emission) response. The range of applicability of this subtraction deserves a deeper future study, as the assignment of the dynamics to the excited state bears functional significance. F‐PP can be realized in a single‐beam geometry, which makes it easily applicable in a microscope, or in measurements requiring perfect phase stability, such as those of coherent beating. While a disadvantage of F‐PP is the need for the scanning of the interferometric probe pulse delay, an advantage is the sensitive detection by the single‐pixel detector against dark background.

In some sense, F‐PP is complementary to recently developed all‐collinear coherent methods,[³⁸, ⁵⁸] as it aims for fast acquisition and intuitive interpretation, rather than for multidimensional spectra. Compared to fluorescence‐detected 2DES, the experimental implementation of F‐PP is relatively straightforward, without the need for phase modulation or phase cycling, and requiring interferometric stability for the probe pulse pair only. F‐2DES in turn in principle provides more information than F‐PP, due to the additional spectral resolution. On the other hand, the simplicity of F‐PP, both in instrumentation and in interpretation, together with fast acquisition, make it useful and potentially even preferred in a number of applications. These include, for example, following excitation dynamics across timescales, measurement of fragile samples with a limited number of photocycles, or application in a microscope. We are therefore hopeful that F‐PP will become a widespread spectroscopy tool in chemistry and other disciplines.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

P. Malý, T. Brixner, Angew. Chem. Int. Ed. 2021, 60, 18867.