Abstract
Although the P3b component of the event-related brain potential is one of the most widely-studied components, its underlying generators are not currently well understood. Recent theories have suggested that the P3b is triggered by phasic activation of the locus-coeruleus norepinephrine (LC-NE) system, an important control center implicated in facilitating optimal task-relevant behavior. Previous research has reported strong correlations between pupil dilation and LC activity, suggesting that pupil diameter is a useful indicator for ongoing LC-NE activity. Given the strong relationship between LC activity and pupil dilation, if the P3b is driven by phasic LC activity, there should be a robust trial-to-trial relationship with the phasic pupillary dilation response (PDR). However, previous work examining relationships between concurrently recorded pupillary and P3b responses has not supported this. One possibility is that the relationship between the measures might be carried primarily by either inter-individual (i.e., between-participant) or intra-individual (i.e., within-participant) contributions to coupling, and prior work has not systematically delineated these relationships. Doing so in the current study, we do not find evidence for either inter-individual or intra-individual relationships between the PDR and P3b responses. However, baseline pupil dilation did predict the P3b. Interestingly, both the PDR and P3b independently predicted inter-individual and intra-individual variability in decision response time. Implications for the LC-P3b hypothesis are discussed.
Introduction
The P300 (P3b) is a positive-going ERP component. Its amplitude is primarily affected by the temporal frequency of a stimulus, such that stimuli that occur less frequently over time yield higher amplitude (more positive) responses compared to those that have occurred more frequently (see Polich, 2007; Verleger, 2020). P3b amplitude is also known to be affected by attention and motivation (see Polich, 2007). The P3b is commonly elicited via the oddball task, in which the participant is required to differentiate between frequent “standard” stimuli and infrequent “deviant” stimuli (e.g., Donchin et al., 1978). The exact function of the P3b remains under considerable debate, but many theories suggest that the activity underlying this response plays a vital role in facilitating response selection in decision tasks (e.g., O’Connell, Dockree & Kelly, 2012; Philiastides, Heekeren & Sajda, 2014; Twomey et al., 2015; see Verleger et al., 2020 for a comprehensive review). The P3b’s importance to response selection makes it a useful component for understanding the neural computations that underlie effective task performance.
Although much has been learned about both the eliciting conditions and functional significance of the P3b, its neurophysiological origins remain elusive. Early studies investigating the neural generators of the P3b did not lead to any conclusive or likely single generator (for review see Nieuwenhuis et al., 2005; although see Bledowski et al., 2004 & Verleger et al., 1994 for background on areas that make important contributions to the P3b). Instead, the evidence seems to suggest multiple cortical and subcortical regions that contribute to the scalp-recorded P3b response (e.g., Kirino et al., 2000; McCarthy et al., 1997; Pineda et al., 1989; Soltani & Knight, 2000; Smith et al., 1990). Thus, the P3b might better be described as reflecting the activity of a large-scale neuromodulatory system, and one promising candidate is the locus-coeruleus norepinephrine (LC-NE) system (Nieuwenhuis, Aston-Jones & Cohen, 2005; Neiwehnhuis, 2011; Pineda, Foote & Neville, 1989).
The locus-coeruleus, located in the pons, is the brain’s source of norepinephrine (NE; Berridge & Waterhouse, 2003). Adaptive Gain Theory (Aston-Jones & Cohen, 2005) suggests that this system plays an essential role in receiving environmental and contextual information about task goals and utility from the pre-frontal cortex, and then using this information to regulate arousal state and optimize behavioral performance. Research in primates has identified two modes of LC-NE activity: tonic and phasic firing. Tonic activity is roughly linearly related to general arousal level and quadratically related to behavioral performance, such that intermediate tonic activity levels predict the highest task performance (for reviews, see Nieuwenhuis et al., 2005; Aston-Jones & Cohen, 2005). Phasic activity is reflected by transient bursts of high-frequency (~20 Hz) activity superimposed on the tonic signals and is thought to relate to the processing of task-relevant stimuli. It occurs primarily during intermediate levels of tonic arousal after stimulus presentation and is tightly locked to response characteristics (for a review, see Nieuwenhuis, Aston-Jones & Cohen, 2005). Because of its close relationship to task-related events, it is specifically this phasic response that researchers suggest may be reflected by the P3b response (Pineda, Foote & Neville, 1989; Nieuwenhuis et al., 2005).
In detailed reviews, Nieuwenhuis (2011) and Nieuwenhuis and colleagues (2005) outline evidence to support a theoretical framework arguing that the P3b reflects phasic LC-NE activity. Similarly to the P3b, the LC-NE phasic response is also elicited by an oddball paradigm (e.g., Aston-Jones, Rajkowski & Kubiak, 1997; Aston-Jones et al., 1994; Rajkowski, Kubiak & Aston-Jones, 1994; Swick, Pineda, Schacher & Foote, 1994) and is sensitive to attention and motivation (e.g., Berridge & Waterhouse, 2003; Kok, 1990; Kok, 2001; Mückschel et al., 2017; Polich and Kok, 1995; Pribram and McGuinness, 1975; Unsworth et al., 2017). Furthermore, lesions to the LC, direct manipulation of noradrenergic agents, and genetic influences on adrenergic pathways are all known to influence the amplitude of the P3b (Glover et al., 1988; Liu et al., 2009; Pineda et al., 1989; Swick, Pineda & Foote, 1994). Recently, optogenetic stimulation of the LC-NE neurons in rats produced a P3b-like response (Vazey, Moorman & Aston-Jones, 2019). Although there is compelling empirical support for the idea that the P3b may reflect phasic LC-NE activity, it has not been easy to directly confirm this hypothesis in humans. The LC-NE system is a difficult-to-reach imaging target (e.g., Astafiev et al., 2010; Elman et al., 2017; Murphy et al., 2014; though see recent developments in Chen et al., 2014; Dahl et al., 2019; Mather et al., 2020; Priovoulos et al., 2018), and activity in this structure can not be localized via surface M/EEG recordings. To assess whether or not phasic LC-NE activity generates the P3b, consideration of other biomarkers of LC-NE activity can be useful. One such candidate measure is the pupillary response to task-related stimuli.
There is strong evidence to suggest that the pupillary response directly maps onto tonic and phasic activity of the LC-NE system (de Gee et al., 2017; Murphy et al., 2014), such that the pupillary response has been used as a proxy for LC-NE activity in various studies (e.g., Gilzenrat et al., 2010; Nassar et al., 2012; Smallwood et al., 2011; 2012; however, see Joshi & Gold, 2020 for a description of other potential contributors to pupil size). Consistent with this LC-P3b theory, the PDR response is elicited under remarkably similar circumstances as the P3b response (Nieuwenhuis et al., 2011) and the LC phasic response. The oddball task, which is known to elicit a robust P3b response, also elicits a larger PDR to deviant stimuli compared to standards (e.g., Friedman et al., 1973; Gilzenrat et al., 2010; Hong, Walz, & Sajda, 2014; Korn & Bach, 2016; Liao et al., 2016; Marois et al., 2018; Quirins et al., 2018; Steiner & Barry, 2011; Wetzel et al., 2016). Similarly, the antecedent conditions that generate the PDR response are remarkably similar to the antecedent conditions that generate the P3b (e.g., Friedman et al., 1973; Kamp & Donchin, 2015; Murphy et al., 2011). Therefore, taking the PDR as an indirect proxy measurement for LC-NE activity, if the LC-P3b theory is correct, there should be a strong relationship between the P3b and the PDR. However, few studies have examined the two responses simultaneously.
To our knowledge, only two studies have examined the relationship between the P3b and pupil dilation in human subjects (Murphy et al., 2011; Kamp & Donchin, 2015), and both have failed to find evidence in support of a strong relationship between the P3b and PDR. However, it is worth noting a few potential limitations of the design and analyses of these prior studies that could obscure the relationship between P3b amplitude and phasic pupil dilation. First, Kamp & Donchin (2015) used a non-canonical cateogrization task consisting of words and images, which is potentially problematic as conditions vary semantically and can elicit N400 responses at around the same time as the P3b response (e.g., Kutas & Iragui, 1998), potentially confounding the results. Moreover, the canonical two-stimulus oddball task elicits the strongest P3b and PDR responses in humans (e.g., Donchin et al., 1978; Friedman et al., 1973; Gilzenrat et al., 2010; Hong, Walz, & Sajda, 2014; Korn & Bach, 2016; Marois et al., 2018; Polich. 2007; Pritchard, 1981; Steiner & Barry, 2011; Wetzel et al., 2016) as well as robust LC-activity in animal studies (e.g., Aston-Jones et al., 1991, 1994; Rajkowski et al., 1994, 2004; Swick et al., 1994). To date, there has not yet been an investigation on the relationship between pupillary and ERP responses using a canonical, 2-stimulus visual oddball task. Moreover, although both previous studies used single-trial analytical techniques, neither chose an approach that also examines the contribution of individual differnces (i.e., between-subject relationships). Within-subject, intra-individual effects and between-subject inter-individual effect represent independent sources of variability that both contribute to the variability in any given outcome measure (e.g. Boy & Sumner, 2014). Therefore, direct inclusion of both ananlytical techniques in addition to the univariate outcomes would be a useful extension of the literature. Moreover, our approach involved adopting linear mixed-effects models, which allows us to properly model between subject and within subject sources of variation via random effects (i.e., as opposed to Kamp & Donchin (2015), who fit a single linear regression model to the disaggregated data). Additionally, we modeled all single-trial predictors as continuous variables, rather than binning predictors, as this form of aggregation can result in issues such as reduced power to detect effects and increased false positives (e.g. MacCallum et al., 2002; Royston, Altman & Sauerbrei, 2006). Therefore, we conducted a standard, two-stimulus visual oddball task to simultaneously examine pupillary and ERP indices of task-related decision making. Importantly, we separately examined both inter-individual (i.e., between-subjects) and intra-individual (i.e., within-subjects) relationships between the P3b, PDR, and response behavior (decision response time).
Method
Participants
We recruited 36 participants (19 male, 17 female; mean age = 20 years, SE = 0.27) from the subject pool in the Department of Psychology at the University of Illinois. Participants had normal or corrected-to-normal vision and no neurological disorders. All participants were right-handed native English speakers. Note that the handedness and native English speaker inclusion criteria were used because the same participants subsequently completed a language experiment that was unrelated to the current study. We dropped 13 participants due to either error within the eye-tracking system preventing data collection (two participants) or excessive artifact rejections due to blinking (greater than 50% of trials, 11 participants), for a final sample of 23 participants.
Stimuli and Procedure
Participants sat at a distance of 80 cm from a 21-inch CRT computer monitor in a quiet testing room with an ambient luminance of 65 lux. A chinrest was used to minimize head movements. Before the task, they were instructed to maintain their fixation on a fixation cross in the center of the screen and to reduce blinking as much as possible within each block. Stimuli were presented visually via SR-Research EyeLink experimental control software (SR-Research, Kanata, ON). Participants completed a standard two-stimulus oddball task (e.g., Luck et al., 2009). Stimuli were black letters and digits presented on a dark grey background to minimize the pupillary light reflex. Digits were randomly drawn from 1–9 (0 excluded because could be confused with O). Letters were randomly presented between A-K, excluding letters that may be perceptually ambiguous (e.g. B, I). Each stimulus subtended 1.07 degrees of visual angle at the viewing distance. Each stimulus was presented for 200 ms, followed by an inter-stimulus interval of 1500 ms to allow for the slower latency of the pupil response. A total of ten practice trials and 640 stimuli were presented. Experimental stimuli were divided into four blocks of 160 trials. In each half of the session, participants received one block in which digits appeared on 80% of the trials (and thus were standards), and letters appeared on 20% of the trials (and thus were deviants). In the other half of the blocks, the mapping was reversed, such that the letters appeared 80% of the time, and digits appeared on 20% of trials, with order counterbalanced across participants. Participants were asked to classify each stimulus as a standard or deviant by responding on a response pad with the right or left index finger. Response hand was counterbalanced across standard and deviant conditions across blocks, such that every combination of response hand and relative probability for each stimulus was tested for each participant in a separate block. This also helped us control for LC-NE activity elicited by voluntary movement (e.g., Yebra et al., 2019), as the participant was always responding to every stimulus, counterbalanced across the response hand.
EEG and Pupil Recording
We recorded EEG from 26 evenly spaced (for montage, see Figure 1) silver-silver chloride electrodes embedded in an EasyCap (EasyCap, Herrsching, Germany). Electrodes were referenced online to the left mastoid. Additionally, we placed one electrode on the left infraorbital ridge to monitor for vertical eye movements and blinks, and another two electrodes on the outer canthus of each eye to monitor for horizontal eye movements. We kept electrode impedances below five kΩ. The continuous EEG was amplified with a BrainAmp DC (Brain-Vision, LLC, Morrisville, NC) amplifier (high-pass filtered: 0.02 Hz, low-pass filtered: 250 Hz) at a sampling rate of 1000 Hz.
Figure 1.
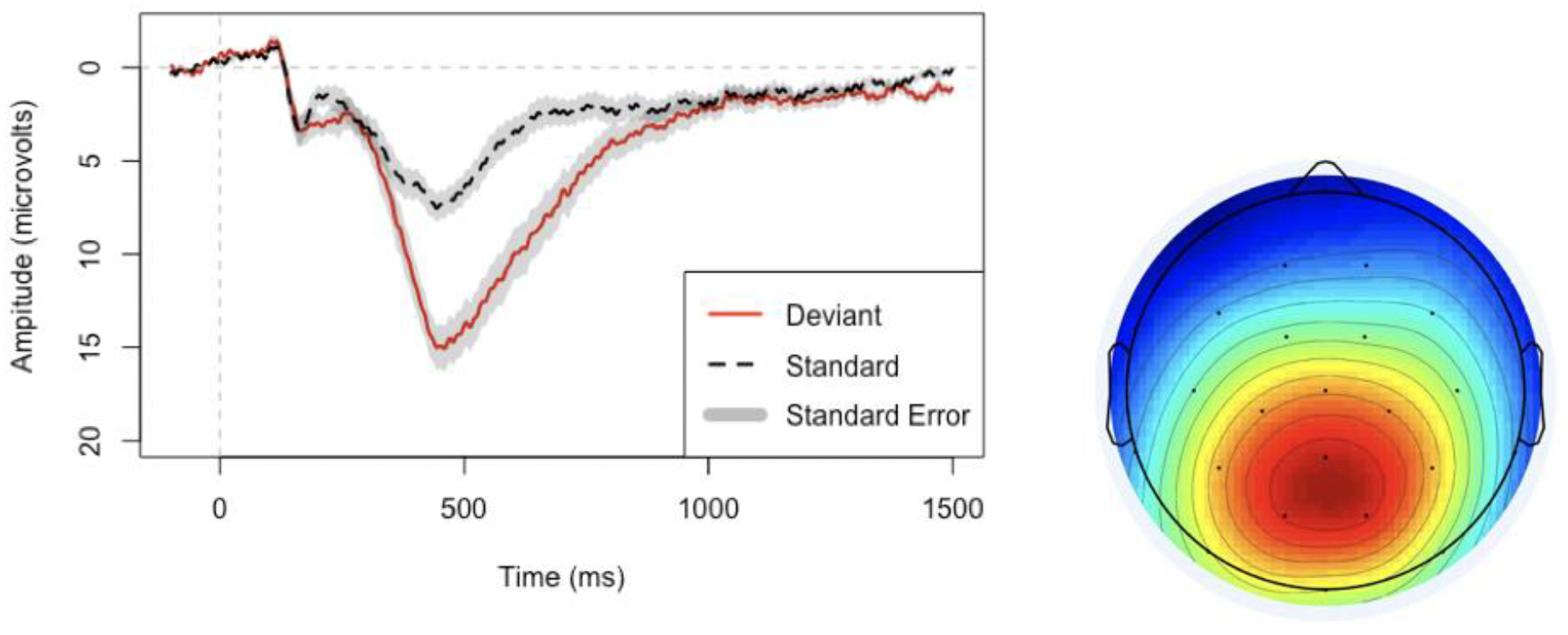
Left: Grand average P3b response to standard (dashed) and deviant (solid) stimuli at electrode MiPa (Midline parietal, the equivalent of Pz in 10–20 system). Negative is plotted up. Gray shades represent standard error of the mean (using inter-individual averages). Baseline is pre-stimulus, −100 ms to 0 ms. Right: Grand average scalp map of the difference wave (deviant - standard) of the P3b response from 298–598 ms.
We recorded pupil data using an Eye-Link 1000 desktop-mounted eye tracker at a sampling rate of 1000 Hz. Each participant was calibrated and validated upon set up to ensure that no issues arose (ie. glasses impeding the eye-tracker) that would prevent quality data collection. We found that we were able to perform valid eye-tracking on all subjects. Viewing was binocular, but only pupil dilation from the right eye was recorded. A fixation correction was presented between each trial to check that the system was still correctly calibrated. In cases where a minor drift occurred, the system auto-corrected before the beginning of the trial. In rare cases where calibration was lost, the experiment was paused, and the eye-tracking system was completely recalibrated before moving forward.
EEG Processing
All EEG analyses were done using the EEGLAB and ERPLAB toolboxes (Lopez-Calderon & Luck, 2014) in MATLAB (The MathWorks, 2019). Data were first downsampled to 250 Hz, and bandpass filtered (0.1 to 30 Hz, roll-off slope: 12 dB/octave). An offline bipolar vertical ocular channel was created for artifact rejection by subtracting the left lower eye electrode from a prefrontal electrode directly above the left eye. Likewise, an offline bipolar horizontal ocular channel was created by subtracting the right horizontal eye channel from the left horizontal eye channel. Data were epoched from −100 ms to 1500 ms relative to stimulus presentation. These epochs were sorted into separate bins for the deviant and standard stimuli for analyses. We performed further artifact rejection offline before averaging, by setting individual thresholds for blinks and eye movements through condition-blind visual inspection. These thresholds were applied to all trials within individual subjects equally. Data were re-referenced offline to the average mastoids. Artifact-free ERPs were averaged by stimulus type (deviant and standard) after subtracting the 100 ms pre-stimulus baseline.
To measure the P3b, we calculated mean amplitude at an apriori midline parietal channel (corresponding approximately to position Pz in the International 10–20 system), where the P3b is typically maximal. An a priori measurement window size of 300 ms was used based on prior work (e.g., Luck et al., 2009). Because the P3b can show a considerable change in latency across task context, we used a collapsed localizer technique across both stimulus types on the grand-averaged ERP to select the temporal region of interest (tROI) (Luck & Gaspelin, 2017). Note that because this approach collapses across the effect of interest (the standard versus deviant trials), this data-driven tROI selection does not bias subsequent analyses (Kriegeskorte et al., 2009). Using this approach, we identified a peak latency of 448 ms and selected a window of 298 to 598 ms. We extracted the mean amplitude of the deviant and standard waveforms from both the subject-averaged ERPs (for the univariate and individual difference analyses) and the individual trials for the intra-individual analyses (see below). Single trial-mean amplitudes were measured at the same channel and in the same time window on the individual trials after single-trial baseline correction (see Payne & Federmeier, 2015, 2017 for more detail).
Pupil-Data Processing
All pupil data were processed using the R language for statistical computing (R Core Team 2019). The pupil data were first epoched from 0–1400 ms using the EyeLink DataViewer software. The epoched pupil data were then imported into R and processed in five steps. The first step was to remove any dilation speed outliers. For this, we followed a similar procedure to that outlined in Kret and Sjak-Shie (2019). Removing dilation speed outliers is vital because some eye-trackers will temporarily identify something as part of the pupil when it is not (i.e., eyelash, etc.). The second step was to identify and remove eye blinks. Eye blinks were identified as gaps in the data of at least 80 ms. Once the eye blinks were identified, 50 ms of data were removed on either side of the blink. If more than 50% of the data on a trial were missing after these first two steps, the trial would be rejected from further processing and analysis. The third step was to use linear interpolation to fill in gaps in the data. The fourth step was to filter the data using a low-pass 12 dB/octave Butterworth filter with a half-amplitude cut-off of 10 Hz. The fifth and final step was to baseline correct the data using a baseline period of 0–50 ms. Using a short, post-stimulus baseline with pupillometry data is justified, given the relatively slow changes of task-evoked pupillary dilation responses. Additionally, given the sustained nature of the PDR, we reduce the likelihood of baselining into an effect of interest from the previous trial by avoiding using a pre-stimulus baseline (though, to be cautious, we do control for pre-stimlus pupil size as well, see data analytical plan below).
To select the appropriate time window for calculating the mean PDR amplitude, we used a mass univariate statistical technique often used in ERP research (Fields & Kuperberg, 2020; Groppe, Urbach & Kutas, 2011). Using the baseline-corrected data and ignoring experimental conditions, we ran a one-sample t-test at each time point, looking for time windows in which the data were significantly different from zero. The t-tests were corrected using the false discovery rate correction (Benjamini and Hochberg, 1995). Using this methodology, a time window of 560 ms to 1400 ms was identified. This time window was used to calculate the mean pupil diameter amplitude for each subject (by condition) and for each individual trial. Trials marked for rejection in either the ERP pre-processing or pupil pre-processing pipeline were rejected in both modalities—therefore, we only included trials with useable data for both the P3b response and PDR. For all statistical analyses, we also excluded error trials, in order to avoid potentially confounding the P3b with the Pe response—a response locked component that occurs after error responses and has similar morphological characteristics to the P3b (Falkenstein et al., 2000; Overbeek et al., 2005).
The average number of trials included in ERP and pupil responses for each subject after excluding error trials and rejecting artifacts was 357.48 (SE = 17.00, range = 198 – 477) for standard trials and 87.26 (SE = 5.35, range = 42–119) for deviant trials.
Data Analysis Plan
Our analytical plan included three stages of analysis. We first analyze and report the univariate responses to confirm the presence of an oddball effect in the P3b, PDR, and response times. Next, we report the inter-individual (between-subjects) relationships between the subject-average P3b, PDR, and RT. Finally, and importantly, we report the intra-individual analyses at the single-trial level to best understand the trial-to-trial dynamics of the P3b and PDR as it relates to behavior. In order to isolate the within-subjects variance, we subject mean-centered our predictors in the intra-individual analyses, allowing us to interpret trial-to-trial change directly in relation to each individual’s own average (Enders & Tofighi, 2007), allowing us to avoid the “uninterpretable blend” (Raudenbush and Byrk 2002, p. 139) of within- and between-subject contributions to the estimated fixed effect in the single trial analyses.
We ran all statistical models in R’s (version 1.1.442) lme4 package (version 1.1–17) using the lmer function. Likelihood ratio tests, calculated using the ‘mixed’ function from the ‘afex’ package (version 0.22–1), were used to test the significance of all fixed effects. To analyze the univariate data, we ran separate linear mixed-effects models for the RT data, PDR data, and P3b data as the response variables. Each model used a fixed effect of condition type (standard vs. deviant) and a random intercept for each subject.
Inter-individual Analyses.
To understand the between-subjects relationships between response time, the PDR, and the P3b response, we ran linear mixed effect models on the subject-average PDR, RT, and P3b responses for the deviant and standard conditions. Subject was treated as a random intercept. We ran two models to explore the relationship between PDR amplitude and P3b amplitude, and each measure’s relationship to behavior. Importantly, we focused on the interaction between each measure and stimulus type—deviant vs. standard. We also included baseline pupil diameter as a covariate for both models, as previous work has documented relationships between baseline pupil size and the PDR (Murphy et al., 2011). For Model 1, we fit a linear mixed-effects model with PDR mean amplitude as the response variable, and with condition type (standard vs. deviant), P3b mean amplitude and their interaction as fixed effects. For Model 2, we fit a linear mixed-effects model with response time as the response variable and with condition type, P3b mean amplitude, the interaction between P3b amplitude and condition type, PDR mean amplitude, and the interaction between PDR amplitude and condition type.
Intra-individual Analyses:
To analyze the intra-individual (within-subject) relationships between PDR, P3b amplitude, and response time, we fit two linear mixed-effects models (which we call Model 3 and Model 4) that followed similar outlines as those described in the above section. Random intercepts by subject were fit for all models1. Model 3 used single-trial PDR mean amplitudes as the response variable, with condition type (standard vs. deviant), single-trial P3b amplitude, and their interaction as fixed effects. For both Model 3 and Model 4, we also included baseline pupil diameter as a control variable. All independent variables were subject-mean standardized to isolate intra-individual variability (Enders & Tofighi, 2007). For Model 4, we used single-trial response times as the response variable with condition type, single-trial PDR mean amplitude, the interaction between PDR amplitude and condition type, single-trial P3b mean amplitude, and the interaction between P3b amplitude and condition type. To facilitate the interpretation of significant interactions, we used the emtrends() function from the emmeans package in R (v1.4.3.01, Lenth, Singmann, & Love, 2018) to calculate simple slopes and their corresponding 95% confidence intervals.
Predictions
Before discussing hypotheses, we note here that, in all following statistical analyses, when we refer to the P3b, we specifically mean the EEG amplitude in microvolts during the P3b spatial-temporal window on a given trial. This is to say, while many studies examining individual differences in P3b effects choose the oddball effect (deviant- standard), we include condition (standard vs. deviant) as an independent variable in predicting P3b amplitude. This strategy was necessary for us to conduct single-trial analyses in the first place, as there is no difference “oddball effect” at the single-trial level, and we aimed for consistency when examining the between-subjects effect as well. Moreover, we note that P3b activity still occurs in standard trials at a lower amplitude (see Polich, 2012).
If the P3b and PDR are driven by the same underlying neural substrate, the LC-NE system, then we would predict that, for both inter-individual and intra-individual analyses, single-trial P3b amplitude would strongly and positively predict PDR amplitude, reflecting strong trial-to-trial relationships between these two signals. As for the relationship of each variable to response time, the literature has been less clear. Previous studies (ie. Kamp & Donchin, 2015; Murphy et al., 2011) that have examined the simultaneous effects of the PDR and P3b responses on response time have yielded mixed results. While Kamp and Donchin (2015) found independent positive effects of P3b and PDR latency on response time in both standard and deviant trials, they observed no relationships with amplitude. Moreover, Murphy et al. (2011) did not see reliable relationships between PDR and RT, but did observe a negative relationship between P3b amplitude and RT. Therefore, we predict that PDR and P3b responses will be related to response time at both the inter and intra-individual level, but we do not have strong directional predictions.
Results
Univariate Results
Participants, on average, responded more accurately to the standard trials compared to the deviant trials (t (22) = 5.36, p <.01, See Table 1), as expected. After removing error trials, we found a robust oddball effect (i.e., the difference between standard and deviant stimuli) for P3b amplitude, PDR amplitude, and response time (See Table 2; Figures 1–3), such that the EEG and pupil responses were larger and response time was slower for deviant stimuli. All descriptive statistics for the PDR, P3b, RT, and accuracy can be found in Table 1. Fixed-effect coefficients for each univariate oddball effect are presented in Table 2.
Table 1.
Descriptive statistics for P3b, PDR, and RT.
| Mean Pupil | SE Pupil | Mean P3b | SE P3b | Mean RT | SE RT | Mean accuracy | SE accuracy | |
|---|---|---|---|---|---|---|---|---|
| All trials-Standard | 36.98 | 1.35 | 5.85 | 0.10 | 470.34 | 1.52 | 0.95 | <.01 |
| All trials-Deviant | 89.00 | 2.76 | 11.17 | 0.20 | 507.66 | 2.52 | 0.85 | <.01 |
| Subject average-Standard | 37.16 | 5.70 | 5.72 | 0.61 | 469.19 | 16.87 | 0.95 | <0.01 |
| Subject average-Deviant | 90.97 | 10.67 | 11.05 | 0.88 | 505.43 | 14.86 | 0.84 | 0.02 |
Table 2.
Univariate data. Condition differences on each outcome variable.
| Beta estimates (unstandardized) | SE | χ2 | df | p | |
|---|---|---|---|---|---|
| P3b amplitude | 5.65 | 0.22 | 618.38 | 1 | <001*** |
| Pupil diameter | 42.74 | 3.06 | 192.72 | 1 | <001*** |
| Reaction Time | 52.62 | 2.87 | 331.32 | 1 | <001*** |
Figure 3.
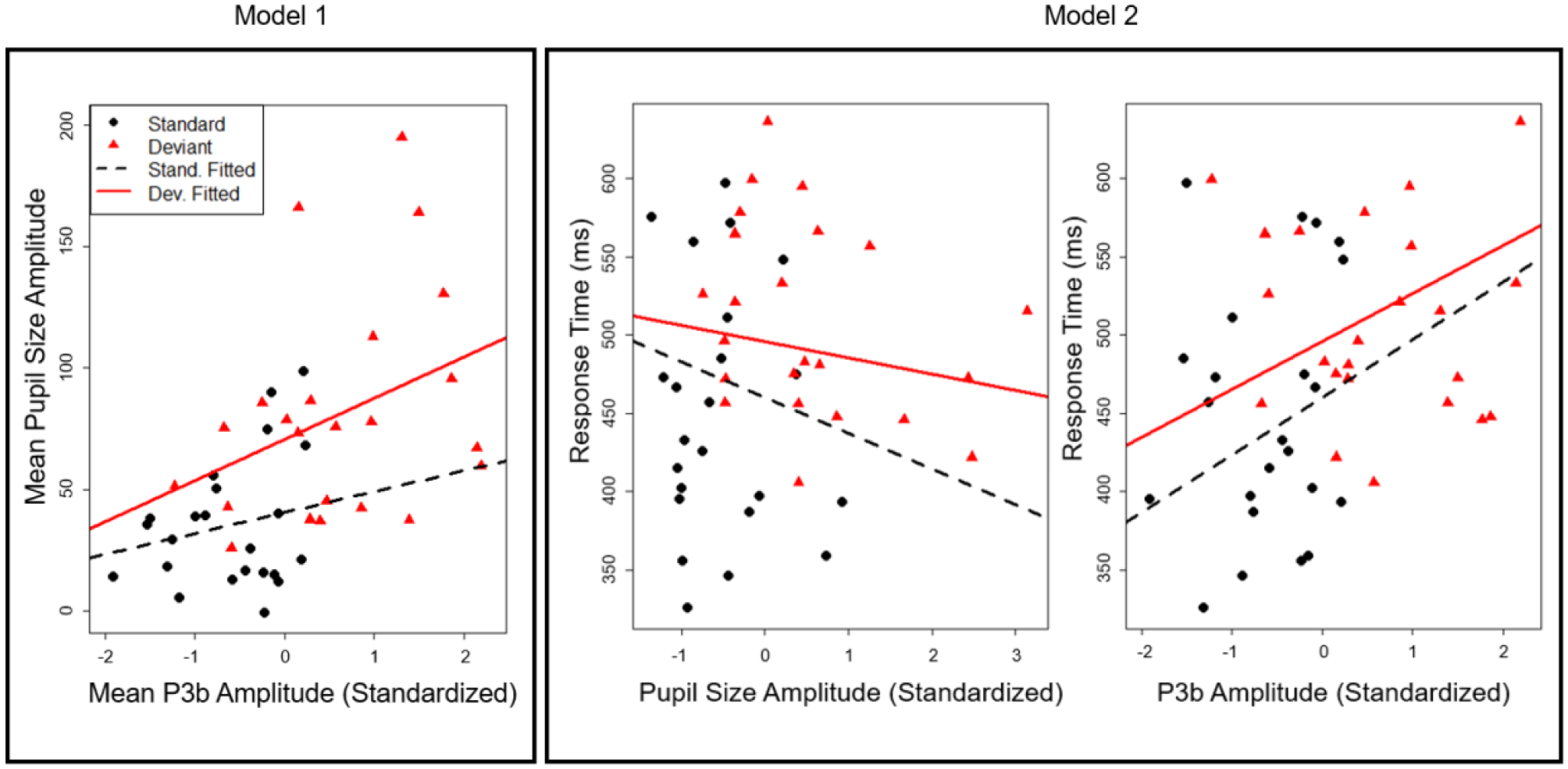
Model predicted best fit lines for P3b amplitude on pupil size (Model 1) and P3b amplitude and pupil diameter on response time (Model 2) at the inter-individual level.
Inter-individual Analyses
Descriptive statistics for all inter-individual and intra-individual analyses can be found in Table 1, and coefficients can be found in Table 3. Before removing error trials, we examined whether an individual’s average P3b or PDR amplitude influenced their average accuracy. After controlling for trial type, we did not find a significant effect of P3b or PDR amplitude on accuracy. All the following results have excluded error trials from analyses. For Model 1, we confirmed what was found in the univariate analysis of PDR—that PDR mean amplitude was predicted by stimulus type, such that deviant stimuli elicited a larger PDR response. However, PDR did not have a significant relationship with P3b amplitude, and the interaction between P3b amplitude and condition type did not predict PDR amplitude (see Figure 4, Model 1). Thus we did not observe strong relationships between the P3b and PDR as a function of individual differences.
Table 3.
Standardized coefficients for all four models.
| Model 1: Inter-individual effects on Pupil Diameter | Beta estimates (standardized) | SE | χ2 | df | p |
|---|---|---|---|---|---|
| Intercept | 40.57 | 9.27 | - | - | - |
| P3b amplitude | 8.68 | 9.61 | 0.81 | 1 | 0.37 |
| Condition | 30.18 | 9.99 | 8.20 | 1 | <.01* |
| P3b amplitude x Condition | 8.26 | 8.27 | 0.96 | 1 | 0.33 |
| Model 2: Inter-individual effects on Reaction Time | |||||
| Intercept | 460.34 | 16.57 | - | - | - |
| P3b amplitude | 36.75 | 11.22 | 8.38 | 1 | <.01* |
| Pupil | −22.89 | 12.89 | 3.01 | 1 | 0.08 |
| Condition | 35.47 | 12.03 | 7.95 | 1 | <.01* |
| Pupil x Condition | 12.51 | 8.41 | 2.11 | 1 | 0.15 |
| P3b amplitude x Condition | −6.14 | 7.90 | 0.59 | 1 | .44 |
| Model 3: Intra-individual effects on Pupil Diameter | |||||
| Intercept | 36.12 | 6.07 | - | - | - |
| P3b amplitude | −0.92 | 1.38 | 0.99 | 1 | .51 |
| Condition | 41.26 | 3.27 | 172.86 | 1 | <.0001*** |
| Baseline Pupil | −26.82 | 1.37 | 377.68 | 1 | <.0001*** |
| P3b amplitude x Condition | 1.85 | 3.07 | 0.55 | 1 | .55 |
| Baseline Pupil x Condition | −1.56 | 3.11 | 0.04 | 1 | .62 |
| Model 4: Intra-individual effects on Reaction Time | |||||
| Intercept | 470.72 | 15.71 | - | - | - |
| P3b amplitude | 3.33 | 1.31 | 6.43 | 1 | 0.01 |
| Pupil | 9.61 | 1.34 | 51.62 | 1 | <.0001*** |
| Condition | 57.69 | 3.20 | 320.57 | 1 | <.0001*** |
| Baseline pupil | 7.84 | 1.34 | 34.34 | 1 | <.0001*** |
| Pupil x Condition | −11.35 | 2.99 | 14.37 | 1 | <.001** |
| P3b amplitude x Condition | −15.97 | 2.93 | 29.72 | 1 | <.0001*** |
| Baseline pupil x Condition | −9.42 | 3.05 | 9.56 | 1 | <.01** |
Figure 4.
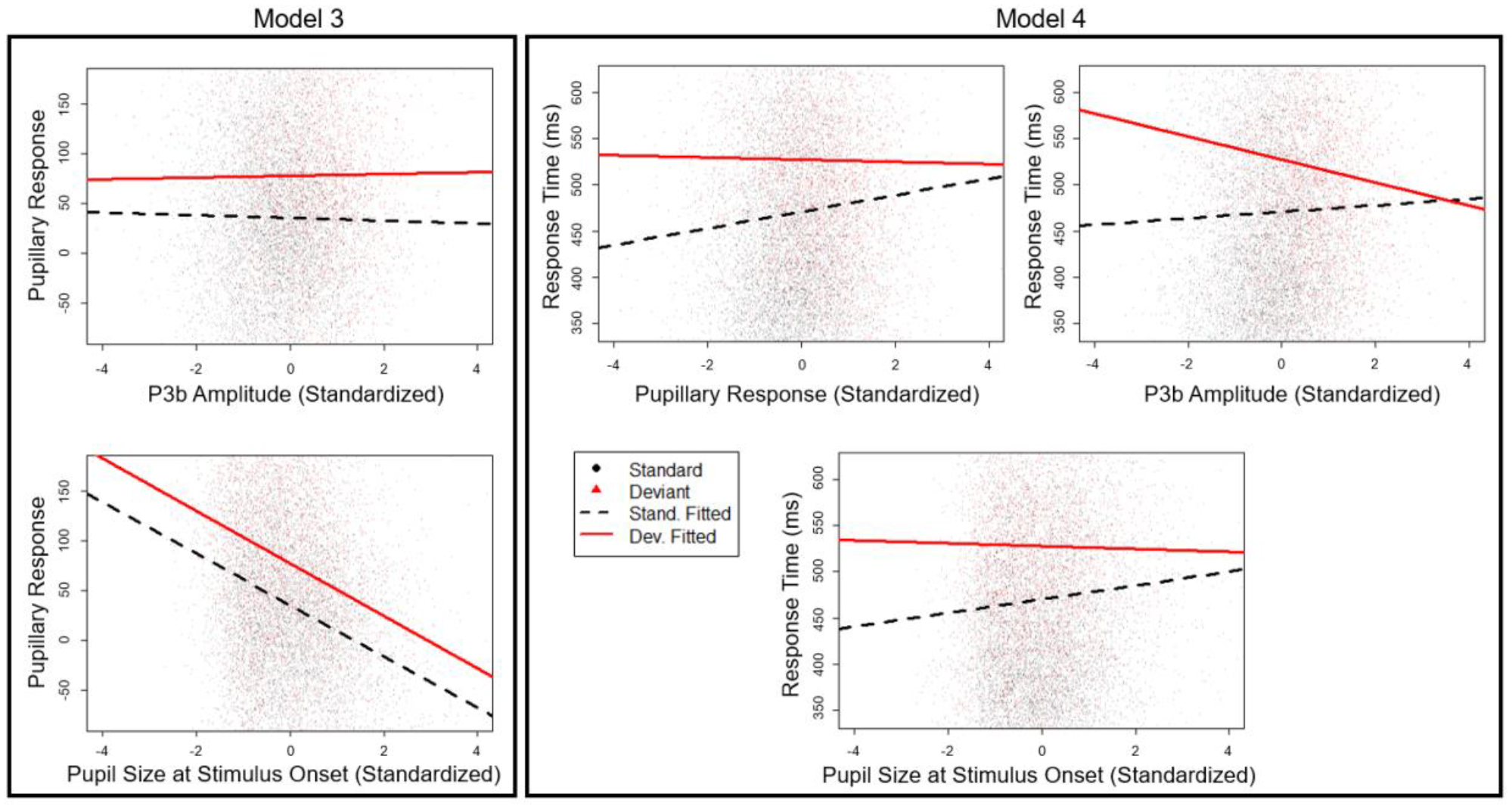
Model predicted best fit lines for P3b amplitude and baseline pupil size on the PDR (Model 3) and P3b amplitude, PDR diameter, and baseline pupil diameter on response time (Model 4) at the intra-individual level.
Our Model 2 analysis found that average response time was significantly slower for deviant stimuli than standard stimuli. There was a marginal but not statistically significant effect of PDR on RT such that larger average PDR amplitudes were associated with faster RTs (i.e., a numerical pattern opposite to our predictions). The interaction with stimulus type was not significant. We found that larger average P3b amplitude was associated with slower average response times overall (See Figure 4, Model 2). This effect was not qualified by an interaction with condition.
Intra-Individual Analyses
For all intra-individual analyses, baseline pupil size was included as a covariate into the models. For Model 3, we did find a main effect of baseline pupil size on the PDR, such that larger baseline pupil size predicted a smaller PDR. There was no interaction with stimulus type. After controlling for this covariate, we found that the results from Model 3 mirrored the results found in both the univariate and interindividual analyses: PDR amplitude was predicted by stimulus type, such that PDR amplitude was larger for deviant stimuli. We found no evidence of intra-individual relationships between PDR amplitude and P3b amplitude, nor was this effect qualified by an interaction with stimulus type.
Model 4 also revealed a main effect of baseline pupil size on reaction time, such that a larger baseline pupil size was associated with slower RTs. This was qualified by an interaction with stimulus type. To interpret this interaction, we calculated the simple slopes for the PDR effect for both deviant and standard and their corresponding confidence intervals. For standards, a larger baseline pupil size predicted a significantly slower RT (simple slope estimate = 7.84; 95% CI = [5.22, 10.46]), but for deviants, baseline pupil size did not predict reaction time.
With baseline pupil size controlled for in the model, we also found that within-person fluctuations in PDR amplitude significantly predicted trial-to-trial variability in RT. This effect was further qualified by an interaction with stimulus type. For standards, trials in which the PDR response was larger than the average for that subject had slower response times (simple slope estimate = 9.61; 95% CI = [6.99, 12.20]). For deviant stimuli, however, we found no relationship between PDR and RT. Furthermore, we found a main effect of P3b single-trial amplitude on RT, such that a larger P3b amplitude predicted a slower RT, consistent with the pattern seen in the individual differences. This was qualified by a significant interaction with stimulus type. For standard stimuli, a larger single-trial P3b amplitude predicted slower reaction time on that trial (simple slope estimate = 3.33; 95% CI = [0.76, 5.90]). However, for deviant stimuli, trials that elicited a larger P3b amplitude than average were associated with a faster response time for that trial (simple slope estimate = −12.65; 95% CI = [−17.77, −7.53]).
Finally, in an exploratory analysis using the same linear mixed-effects structure as the Models 3 and 4, we examined whether or not baseline pupil diameter would significantly predict P3b response. We found a significant interaction between baseline pupil and trial type on P3b response (χ2 (1) = 24.69, p < 0.001). For standard stimuli, trials that began with a larger than average baseline pupil size elicited a larger P3b response (simple slope estimate = 0.70; CI = [0.50, 0.90]. For deviant stimuli, trials that began with a larger than average baseline pupil size elicited a smaller P3b amplitude (simple slope estimate = −0.45; CI = [−0.86, −0.04]).
Discussion
The goal of the current study was to examine behavioral, electrophysiological, and pupillary responses to deviance an oddball paradigm. In particular, our goal was to examine the relationships among each of these responses at the inter-individual and intra-individual level to test whether the phasic task-evoked PDR and the P3b are intercorrelated. Infrequent stimuli elicited a robust P3b, a substantial phasic pupil dilation response (PDR), and a slower RT, demonstrating a uniform “oddball” effect across all modalities. Consistent with prior work (Murphy et al., 2011), we found that baseline pupil diameter predicted the PDR and the P3b. However, we found no evidence of inter-individual or intra-individual relationships between the PDR and P3b. Thus, assuming that the PDR is a proxy for phasic LC-NE activity (e.g., Gilzenrat et al., 2010), these findings suggest complications for the LC-P3b hypothesis. Nevertheless, we did find evidence that PDR and P3b amplitudes each independently predicted behavior.
Kamp & Donchin (2015) found no relationship between the PDR and P3b amplitude. Moreover, neither PDR nor P3b amplitude predicted response time in their study (note, however, that latency measures did predict RT). Murphy et al. (2011) similarly did not find that the PDR and P3b were related. However, they found that larger P3b responses predicted faster RTs to deviant stimli. We found that larger P3bs, relative to the subject’s average, facilitated RTs to deviant stimuli at the single-trial level. We did not observe this relationship between the PDR and RTs for the deviant trials. We found, however, that for standards, both a larger P3b or PDR predicted slower RTs. Collectively, these finding suggests that these two physiological responses may reflect distinct but complementary functional stages that contribute to task-related decision making.
Three separate studies have now examined relationships between the PDR and P3b in an auditory oddball task, a word categorization task, and a visual oddball task. Despite substantial task and analytical differences across studies, none has found evidence for tight coupling between these two phasic responses. Nevertheless, two of the three studies have found that either the amplitude or latency of PDR and the P3b responses each independently predicted RT. Our current study extends this literature by clearly delineating variance in behavior driven by individual differences from variance driven by trial-to-trial within-person fluctuations. These results collectively suggest that, although the P3b response may not be directly coupled to PDR, both the P3b and the PDR have a hand in contributing to subsequent decision behavior. As Kamp & Donchin (2015) suggest, one explanation is that the activity of the (LC-NE mediated) PDR and the P3b each independently reflect separate points of the decision-making process. If this is the case, future work will benefit from utilizing a concurrent EEG and pupillometry design as in the current study, combined with manipulations of various aspects of task demands, to better characterize the functional significance of these largely independent physiological responses to deviance. Interestingly, there does seem to be some preliminary evidence that pre-stimulus pupil size is related to the P3b response (Murphy et al., 2011), and we similarly found that pre-stimulus pupil diameter predicted P3b amplitude. This may represent a fruitful area for future research regarding the LC-NE system’s relationship to the P3b response.
Finally, it is essential to note that other brain regions are involved in the pupillary response beyond the LC-NE system, such as the pretectal olivary nucleus and the superior colliculus (Joshi & Gold, 2020). Hence, although there is compelling evidence that LC activity modulates pupillary responses, and that LC activity and pupil diameter correlate in the oddball task in particular (Joshi & Gold, 2020; Murphy et al., 2014), the reverse inference that pupillary responses directly reflect LC activity alone is challenging to make confidently, and we acknowledge that pupillary responses may reflect contributions from other brain regions.
Simpson’s paradox
Our findings also demonstrated the importance of decomposing between-subject and within-subject covariation. In fact, we observed a complete reversal in the direction of the relationship between the P3b amplitude and RT when comparing effects at the between-subjects and within-subjects level. At the inter-individual level, individuals with larger P3b amplitudes showed slower responses to both standard and deviant stimuli. However, at the intra-individual level, on trials where the P3b was larger than average for that subject, response times were faster for deviant stimuli. Although one may expect and assume similar relationships at the between-subject and within-subjects level, these two levels of analysis reflect different sources of variance and can show completely opposing relationships, a phenomenon known more broadly as Simpson’s paradox (Kievit et al., 2013; Simpson, 1951).
Why do we observe this inversion at the between-subjects and within-subjects level? We speculate here that inter- and intraindividual variability in the P3b may reflect different processes. Given the P3b’s potential role as a neural index of evidence accumulation (e.g., Twomey et al., 2015), individual differences in P3b amplitude observed in the current study may reflect, in part, individual differences in decision criteria. There are reliable differences in the amount of information an individual requires before making a decision (e.g., Bogacz et al., 2006; Ratcliff 1978), known as decision criteria. Decision criteria can vary within individuals as a function of task demands (e.g Frazier & Yu, 2008; Karşılar et al., 2014), but also can represent stable individual differences (e.g., Bianco et al., 2020) in response caution. Under this hypothesis, an individual who requires less evidence to make a decision only needs the P3b to build to a relatively low amplitude before they prepare to respond, whereas those who have higher stable response thresholds require more evidence, yielding a larger P3b before making their decision. Supporting this claim, studies that emphasize the importance of accuracy in various ways, requiring the participant to increase their response caution, do observe larger P3b’s (e.g., Sutton et al., 1978; Yeung & Sanfey, 2004). At this inter-individual level, it is also worth noting that we observed no interaction between standard and deviant stimuli, suggesting that this reflects a more general individual difference in decision criterion that is invariant to stimulus type. Note that speed-accuracy tradeoff studies, which can be considered as manipulations of criterion setting (Bogacz et al., 2006; Wickelgren, 1977), also find that the effects of decision caution apply to both standard and deviant stimuli. One might suspect that cautious individuals would theoretically be more accurate in their responses. However, we did not find evidence that average P3b amplitude predicted accuracy after controlling for trial type. This may simply be because our participants performed the task at very high levels of accuracy (on average 93%) with minimal variance (range = 86% – 98%), making it harder to predict variance in this outcome variable.
In contrast, the within-subject P3b and RT relationship was not only in the opposite direction, but it also did not apply equally to standard and deviant stimuli. Instead, it appeared that on deviant trials specifically, a larger P3b to the stimulus facilitated RT. Rather than a general individual difference in response threshold, these data likely reflect the trial-to-trial dynamics of brain activity implementing stimulus-driven behavior. If we accept that there is a given evidence threshold to respond, then on larger-than-average individual P3b trials, this threshold—whatever it may be for a given individual—is reached more quickly, facilitating RTs to the deviants. We do not observe this relationship in the standard trials. Instead, we find that a larger P3b response predicts longer RTs. We speculate that larger P3b amplitudes to standards may represent trials in which participants nearly miscategorized stimuli as deviant before eventually making the correct response (i.e., these trials began accumulating evidence towards the wrong decision boundary before recovering). This is consistent with an evidence accumulation framework, which would suggest that, in general, one would be “biased” to respond to the standard, and therefore require less evidence to respond (e.g., Ratcliff, 1985; Ratcliff & McKoon, 2008), as evidenced by the quicker RTs to standards across the board. However, on trials in which the participant had a larger P3b, they may have required more evidence to make their decision, resulting in a longer RT.
Conclusion
Three studies using different tasks have now failed to find evidence of strong relationships between the phasic PDR and the P3b response. Assuming the PDR is a valid marker of phasic LC activity, our results are consistent with prior work in suggesting challenges to a strong interpretation of the LC-P3b hypothesis. Nevertheless, both physiological responses independently predicted response behavior, suggesting they may reflect distinct processes that contribute to optimal task-relevant performance. Critically, our results also highlighted the importance of decomposing inter-individual and intra-individual covariation. We observed a complete reversal in the relationship between P3b amplitude and RT at the inter-individual and intra-individual level, which we argue reflects distinct markers of decision making (i.e, individual differences in response caution versus trial-to-trial variability in evidence accumulation). More broadly, we caution researchers to carefully consider both inter- and intra-individual sources of variation in multi-modal studies.
Figure 2.
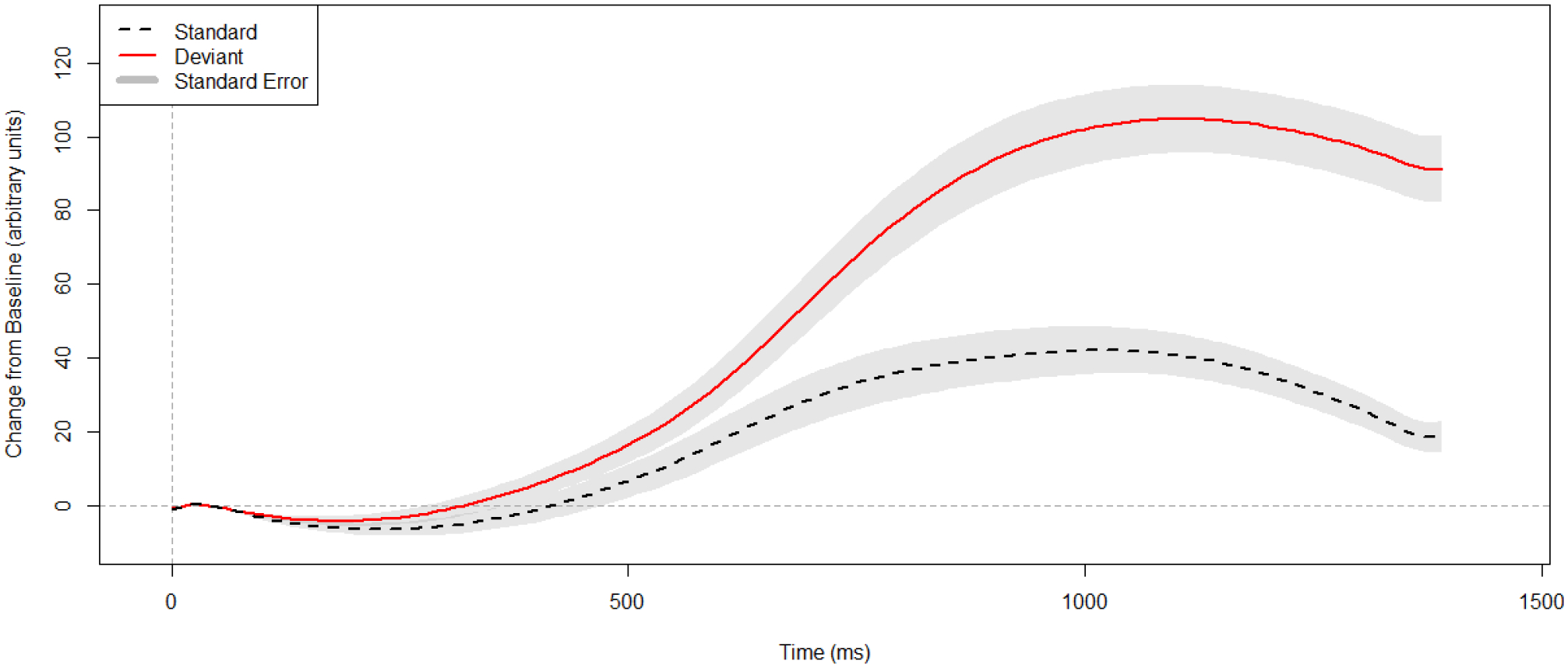
Grand average PDR response to standard (black) and deviant (red) stimuli. Standard error of the mean (using inter-individual averages) is shaded in gray. Positive is plotted up. Baseline is at stimulus, 0–50 ms.
Footnotes
We did follow the advice for random slopes given by Barr and colleagues (2013) to “keep it maximal” and found that adding random slope effects did not significantly alter the outcomes of any of the models. Therefore, to be parsimonious and remain consistent in analyses across all models, we used a random intercept model for each rather than having different random slope structures for each model (see Bates et al., 2015).
References
- Astafiev SV, Snyder AZ, Shulman GL, & Corbetta M (2010). Comment on “Modafinil shifts human locus coeruleus to low-tonic, high-phasic activity during functional MRI” and “Homeostatic sleep pressure and responses to sustained attention in the suprachiasmatic area”. Science, 328(5976), 309–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aston-Jones G, Shipley MT, Chouvet G, Ennis M, Van Bockstaele E, Pieribone V, & Charlety P (1991). Afferent regulation of locus coeruleus neurons: anatomy, physiology and pharmacology. Progress in Brain Research, 88, 47–75. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, Rajkowski J, Kubiak P, & Alexinsky T (1994). Locus coeruleus neurons in monkey are selectively activated by attended cues in a vigilance task. Journal of Neuroscience, 14(7), 4467–4480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aston‐Jones G, & Cohen JD (2005). Adaptive gain and the role of the locus coeruleus–norepinephrine system in optimal performance. Journal of Comparative Neurology, 493(1), 99–110. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, Rajkowski J, & Kubiak P (1997). Conditioned responses of monkey locus coeruleus neurons anticipate acquisition of discriminative behavior in a vigilance task. Neuroscience, 80(3), 697–715. [DOI] [PubMed] [Google Scholar]
- Barr DJ, Levy R, Scheepers C, & Tily HJ (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language, 68(3), 255–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, Kliegl R, Vasishth S, & Baayen H (2015). Parsimonious Mixed Models. arXiv preprint: arXiv:1506.04967.
- Berridge CW, & Waterhouse BD (2003). The locus coeruleus–noradrenergic system: modulation of behavioral state and state-dependent cognitive processes. Brain Research Reviews, 42(1), 33–84. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, & Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological), 57(1), 289–300. [Google Scholar]
- Bianco V, Berchicci M, Quinzi F, Perri RL, Spinelli D, & Di Russo F (2020). Females are more proactive, males are more reactive: neural basis of the gender-related speed/accuracy tradeoff in visuo-motor tasks. Brain Structure and Function, 225(1), 187201. [DOI] [PubMed] [Google Scholar]
- Bledowski C, Prvulovic D, Hoechstetter K, Scherg M, Wibral M, Goebel R, & Linden DE (2004). Localizing P300 generators in visual target and distractor processing: a combined event-related potential and functional magnetic resonance imaging study. Journal of Neuroscience, 24(42), 9353–9360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, & Cohen JD (2006). The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychological Review, 113(4), 700. [DOI] [PubMed] [Google Scholar]
- Boy F, & Sumner P (2014). Visibility predicts priming within but not between people: a cautionary tale for studies of cognitive individual differences. Journal of Experimental Psychology: General, 143(3), 1–31. [DOI] [PubMed] [Google Scholar]
- Chen X, Huddleston DE, Langley J, Ahn S, Barnum CJ, Factor SA, & Hu X (2014). Simultaneous imaging of locus coeruleus and substantia nigra with a quantitative neuromelanin MRI approach. Magnetic Resonance Imaging, 32(10), 1301–1306. [DOI] [PubMed] [Google Scholar]
- Dahl MJ, Mather M, Düzel S, Bodammer NC, Lindenberger U, Kühn S, & Werkle-Bergner M (2019). Rostral locus coeruleus integrity is associated with better memory performance in older adults. Nature Human Behaviour, 3(11), 1203–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Gee JW, Colizoli O, Kloosterman NA, Knapen T, Nieuwenhuis S, & Donner TH (2017). Dynamic modulation of decision biases by brainstem arousal systems. Elife, 6, 1–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin E, Ritter W, & McCallum WC (1978). Cognitive psychophysiology: The endogenous components of the ERP. In Callaway E, Tueting P, & Koslow SH (eds.): Event-Related Brain Potentials in Man (pp. 349–411). New York: Academic Press. [Google Scholar]
- Elman JA, Panizzon MS, Hagler DJ Jr, Eyler LT, Granholm EL, Fennema-Notestine C, … & Kremen WS (2017). Task-evoked pupil dilation and BOLD variance as indicators of locus coeruleus dysfunction. Cortex, 97, 60–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enders CK, & Tofighi D (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychological Methods, 12(2), 121. [DOI] [PubMed] [Google Scholar]
- Falkenstein M, Hoormann J, Christ S, & Hohnsbein J (2000). ERP components on reaction errors and their functional significance: a tutorial. Biological Psychology, 51(2–3), 87–107. [DOI] [PubMed] [Google Scholar]
- Fields EC, & Kuperberg GR (2020). Having your cake and eating it too: Flexibility and power with mass univariate statistics for ERP data. Psychophysiology, 57(2), 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazier P, & Yu AJ (2008). Sequential hypothesis testing under stochastic deadlines. In Advances in Neural Information Processing Systems, 20, 465–472. [Google Scholar]
- Friedman D, Hakerem G, Sutton S, & Fleiss JL (1973). Effect of stimulus uncertainty on the pupillary dilation response and the vertex evoked potential. Electroencephalography and Clinical Neurophysiology, 34(5), 475–484. [DOI] [PubMed] [Google Scholar]
- Gilzenrat MS, Nieuwenhuis S, Jepma M, & Cohen JD (2010). Pupil diameter tracks changes in control state predicted by the adaptive gain theory of locus coeruleus function. Cognitive, Affective, & Behavioral Neuroscience, 10(2), 252–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover A, Ghilardi MF, Bodis-Wollner I, & Onofrj M (1988). Alterations in event-related potentials (ERPs) of MPTP-treated monkeys. Electroencephalography and Clinical Neurophysiology, 71, 461–468. [DOI] [PubMed] [Google Scholar]
- Groppe DM, Urbach TP, & Kutas M (2011). Mass univariate analysis of event‐related brain potentials/fields I: A critical tutorial review. Psychophysiology, 48(12), 1711–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong L, Walz JM, & Sajda P (2014). Your eyes give you away: pre-stimulus changes in pupil diameter correlate with post-stimulus task-related EEG dynamics. PLoS One, 9(3), e91321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S, & Gold JI (2020). Pupil size as a window on neural substrates of cognition. Trends in Cognitive Sciences, 24(6), 466–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamp SM, & Donchin E (2015). ERP and pupil responses to deviance in an oddball paradigm. Psychophysiology, 52(4), 460–471. [DOI] [PubMed] [Google Scholar]
- Karşılar H, Simen P, Papadakis S, & Balcı F (2014). Speed accuracy trade-off under response deadlines. Frontiers in neuroscience, 8(248), 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kievit R, Frankenhuis WE, Waldorp L, & Borsboom D (2013). Simpson’s paradox in psychological science: A practical guide. Frontiers in Psychology, 4(513), 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirino E, Belger A, Goldman-Rakic P, & McCarthy G (2000). Prefrontal activation evoked by infrequent target and novel stimuli in a visual target detection task: an event-related functional magnetic resonance imaging study. Journal of Neuroscience, 20(17), 6612–6618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kok A (1990). Internal and external control: a two-factor model of amplitude change of event-related potentials. Acta Psychologica, 74(2–3), 213–236. [PubMed] [Google Scholar]
- Kok A (2001). On the utility of P3 amplitude as a measure of processing capacity. Psychophysiology, 38(3), 557–577. [DOI] [PubMed] [Google Scholar]
- Korn CW, & Bach DR (2016). A solid frame for the window on cognition: Modeling event-related pupil responses. Journal of Vision, 16(3), 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kret ME, & Sjak-Shie EE (2019). Preprocessing pupil size data: Guidelines and code. Behavior research methods, 51(3), 1336–1342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Simmons WK, Bellgowan PS, & Baker CI (2009). Circular analysis in systems neuroscience: the dangers of double dipping. Nature neuroscience, 12(5), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutas M, & Iragui V (1998). The N400 in a semantic categorization task across 6 decades. Electroencephalography and Clinical Neurophysiology/Evoked Potentials Section, 108(5), 456–471. [DOI] [PubMed] [Google Scholar]
- Lenth R, Singmann H, & Love J (2018). Emmeans: Estimated marginal means, aka least-squares means. R package version, 1(1) [Google Scholar]
- Liao HI, Yoneya M, Kidani S, Kashino M, & Furukawa S (2016). Human pupillary dilation response to deviant auditory stimuli: Effects of stimulus properties and voluntary attention. Frontiers in Neuroscience, 10(43), 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Kiehl KA, Pearlson G, Perrone-Bizzozero NI, Eichele T, & Calhoun VD (2009). Genetic determinants of target and novelty-related event-related potentials in the auditory oddball response. NeuroImage, 46, 809–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Calderon J, & Luck SJ (2014). ERPLAB: an open-source toolbox for the analysis of event-related potentials. Frontiers in human neuroscience, 8, 213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck SJ, & Gaspelin N (2017). How to get statistically significant effects in any ERP experiment (and why you shouldn’t). Psychophysiology, 54(1), 146–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck SJ, Kappenman ES, Fuller RL, Robinson B, Summerfelt A, & Gold JM (2009). Impaired response selection in schizophrenia: Evidence from the P3 wave and the lateralized readiness potential. Psychophysiology, 46(4), 776–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCallum RC, Zhang S, Preacher KJ, & Rucker DD (2002). On the practice of dichotomization of quantitative variables. Psychological Methods, 7, 19–40. [DOI] [PubMed] [Google Scholar]
- Marois A, Labonte’ K, Parent M, & Vachon F (2018). Eyes have ears: Indexing the orienting response to sound using pupillometry. International Journal of Psychophysiology, 123, 152–162. [DOI] [PubMed] [Google Scholar]
- Mather M, Huang R, Clewett D, Nielsen SE, Velasco R, Tu K, … & Kennedy BL (2020). Isometric exercise facilitates attention to salient events in women via the noradrenergic system. NeuroImage, 210, 116560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The MathWorks. (2014). MATLAB, signal processing, and statistics toolboxes. Natick, MA: Author. [Google Scholar]
- McCarthy G, Luby M, Gore J, & Goldman-Rakic P (1997). Infrequent events transiently activate human prefrontal and parietal cortex as measured by functional MRI. Journal of Neurophysiology, 77(3), 1630–1634. [DOI] [PubMed] [Google Scholar]
- Mückschel M, Chmielewski W, Ziemssen T, & Beste C (2017). The norepinephrine system shows information-content specific properties during cognitive control–Evidence from EEG and pupillary responses. NeuroImage, 149, 44–52. [DOI] [PubMed] [Google Scholar]
- Murphy PR, Robertson IH, Balsters JH, & O’Connell RG (2011). Pupillometry and P3 index the locus coeruleus–noradrenergic arousal function in humans. Psychophysiology, 48(11), 1532–1543. [DOI] [PubMed] [Google Scholar]
- Murphy PR, O’Connell RG, O’Sullivan M, Robertson IH, & Balsters JH (2014). Pupil diameter covaries with BOLD activity in human locus coeruleus. Human Brain Mapping, 35(8), 4140–4154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Rumsey KM, Wilson RC, Parikh K, Heasly B, & Gold JI (2012). Rational regulation of learning dynamics by pupil-linked arousal systems. Nature Neuroscience, 15(7), 1040–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuis S, Aston-Jones G, & Cohen JD (2005). Decision making, the P3, and the locus coeruleus--norepinephrine system. Psychological Bulletin, 131(4), 510. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis S (2011). Learning, the P3, and the locus coeruleus-norepinephrine system. In: Mars R, Sallet J, Rushworth M, and Yeung N (Eds.) Neural Basis of Motivational and Cognitive Control. Oxford University Press, p. 209–222. [Google Scholar]
- O’Connell RG, Dockree PM, & Kelly SP (2012). A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nature Neuroscience, 15(12), 1729. [DOI] [PubMed] [Google Scholar]
- Overbeek TJ, Nieuwenhuis S, & Ridderinkhof KR (2005). Dissociable components of error processing: On the functional significance of the Pe vis-à-vis the ERN/Ne. Psychophysiology, 19(4), 319–329. [Google Scholar]
- Payne BR, Lee CL, & Federmeier KD (2015). Revisiting the incremental effects of context on word processing: Evidence from single-word event-related brain potentials. Psychophysiology, 52(11), 1456–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne BR, & Federmeier KD (2017). Pace yourself: Intraindividual variability in context use revealed by self-paced event-related brain potentials. Journal of Cognitive Neuroscience, 29(5), 837–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philiastides MG, Heekeren HR, & Sajda P (2014). Human scalp potentials reflect a mixture of decision-related signals during perceptual choices. Journal of Neuroscience, 34(50), 16877–16889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pineda JA, Foote SL, & Neville HJ (1989). Effects of locus coeruleus lesions on auditory, long-latency, event-related potentials in monkey. Journal of Neuroscience, 9, 81–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polich J, & Kok A (1995). Cognitive and biological determinants of P300: an integrative review. Biological Psychology, 41(2), 103–146. [DOI] [PubMed] [Google Scholar]
- Polich J (2007). Updating P300: an integrative theory of P3a and P3b. Clinical Neurophysiology, 118(10), 2128–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polich J (2012). Neuropsychology of P300. In Luck SJ & Kappenman E (Eds.), Oxford handbook of event-related potential components. New York: Oxford University Press. [Google Scholar]
- Pribram KH, & McGuinness D (1975). Arousal, activation, and effort in the control of attention. Psychological Review, 82(2), 116–149 [DOI] [PubMed] [Google Scholar]
- Priovoulos N, Jacobs HI, Ivanov D, Uludağ K, Verhey FR, & Poser BA (2018). High-resolution in vivo imaging of human locus coeruleus by magnetization transfer MRI at 3T and 7T. NeuroImage, 168, 427–436. [DOI] [PubMed] [Google Scholar]
- Pritchard WS (1981). Psychophysiology of P300. Psychological Bulletin, 89(3), 506–540. [PubMed] [Google Scholar]
- Quirins M, Marois C, Valente M, Seassau M, Weiss N, El Karoui I, … & Naccache L (2018). Conscious processing of auditory regularities induces a pupil dilation. Scientific Reports, 8(1), 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL: https://www.R-project.org/. [Google Scholar]
- Raudenbush SW, & Bryk AS (2002). Hierarchical linear models: Applications and data analysis methods (Vol. 1). Sage Publishing. [Google Scholar]
- Rajkowski J, Kubiak P, & Aston-Jones G (1994). Locus coeruleus activity in monkey: phasic and tonic changes are associated with altered vigilance. Brain Research Bulletin, 35(5–6), 607–616. [DOI] [PubMed] [Google Scholar]
- Rajkowski J, Majczynski H, Clayton E, & Aston-Jones G (2004). Activation of monkey locus coeruleus neurons varies with difficulty and performance in a target detection task. Journal of Neurophysiology, 92(1), 361–371. [DOI] [PubMed] [Google Scholar]
- Ratcliff R (1978). A theory of memory retrieval. Psychological Review, 85(2), 59–108 [Google Scholar]
- Ratcliff R (1985). Theoretical interpretations of the speed and accuracy of positive and negative responses. Psychological Review, 92(2), 212–225. [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural Computation, 20(4), 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Royston P, Altman DG, & Sauerbrei W (2006). Dichotomizing continuous predictors in multiple regression: a bad idea. Statistics in Medicine, 25(1), 127–141. [DOI] [PubMed] [Google Scholar]
- Simpson EH (1951). The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society: Series B, 13, 238–241. [Google Scholar]
- Smallwood J, Brown KS, Tipper C, Giesbrecht B, Franklin MS, Mrazek MD, … & Schooler JW (2011). Pupillometric evidence for the decoupling of attention from perceptual input during offline thought. PloS One, 6(3), 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smallwood J, Brown KS, Baird B, Mrazek MD, Franklin MS, & Schooler JW (2012). Insulation for daydreams: a role for tonic norepinephrine in the facilitation of internally guided thought. PloS One, 7(4), 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith ME, Halgren E, Sokolik ME, Baudina P, Musolino E, Liegeois-Chauvel C, and Chauvel P (1990), The intra-cranial topography of the P3 event-related potential elicited during auditory oddball, Electroencephalography and Clinical Neurophysiology, 76, 235–248. [DOI] [PubMed] [Google Scholar]
- Soltani M, & Knight RT (2000). Neural origins of the P300. Critical Reviews in Neurobiology, 14, 199–224. [PubMed] [Google Scholar]
- Steiner GZ, & Barry RJ (2011). Pupillary responses and event-related potentials as indices of the orienting reflex. Psychophysiology, 48, 1648–1655. [DOI] [PubMed] [Google Scholar]
- Sutton S, Tueting P, Hammer M, & Hakerem G (1978). Evoked potentials and feedback. In Otto DA (Ed.), Multidisciplinary Perspectives in Event-related Potential Research (pp. 184–188). Washington, DC: US Government Printing Office. [Google Scholar]
- Swick D, Pineda JA, Schacher S, & Foote SL (1994). Locus coeruleus neuronal activity in awake monkeys: relationship to auditory P300-like potentials and spontaneous EEG. Experimental Brain Research, 101(1), 86–92. [DOI] [PubMed] [Google Scholar]
- Twomey DM, Murphy PR, Kelly SP, & O’Connell RG (2015). The classic P300 encodes a build‐to‐threshold decision variable. European Journal of Neuroscience, 42(1), 1636–1643. [DOI] [PubMed] [Google Scholar]
- Unsworth N, & Robison MK (2017). A locus coeruleus-norepinephrine account of individual differences in working memory capacity and attention control. Psychonomic Bulletin & Review, 24(4), 1282–1311. [DOI] [PubMed] [Google Scholar]
- Vazey EM, Moorman DE, & Aston-Jones G (2018). Phasic locus coeruleus activity regulates cortical encoding of salience information. Proceedings of the National Academy of Sciences, 115, E9439–E9448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verleger R, Heide W, Butt C, & Kömpf D (1994). Reduction of P3b in patients with temporo-parietal lesions. Cognitive Brain Research, 2(2), 103–116. [DOI] [PubMed] [Google Scholar]
- Verleger R (2020). Effects of relevance and response frequency on P3b amplitudes: Review of findings and comparison of hypotheses about the process reflected by P3b. Psychophysiology, 57, e13542. [DOI] [PubMed] [Google Scholar]
- Wetzel N, Buttelmann D, Schieler A, & Widmann A (2016). Infant and adult pupil dilation in response to unexpected sounds. Developmental Psychobiology, 58(3), 382–392. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA (1977). Speed-accuracy tradeoff and information processing dynamics. Acta Psychologica, 41(1), 67–85. [Google Scholar]
- Yebra M, Galarza-Vallejo A, Soto-Leon V, Gonzalez-Rosa JJ, de Berker AO, Bestmann S, … & Strange BA (2019). Action boosts episodic memory encoding in humans via engagement of a noradrenergic system. Nature Communications, 10(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung N, & Sanfey AG (2004). Independent coding of reward magnitude and valence in the human brain. Journal of Neuroscience, 24, 6258–6264. [DOI] [PMC free article] [PubMed] [Google Scholar]


