What Does the Brønsted Slope Measure in the Phosphoryl Transfer Transition State?

Abstract

The structural and energetic features of phosphate and phosphonate hydrolysis in Protein Phosphatase-1 (PP1) and water are studied using quantum mechanical (QM) cluster models. The calculations are able to reproduce observed kinetic isotope effects and capture several key trends in the experimental Brønsted plots: the ${\beta }_{lg}$ values are rather different for phosphate and phosphonate ester hydrolysis in solution but are similar in PP1. Detailed analyses of structure, charge distribution and bond order of computed transition states support the general conclusion from experimental study that phosphoryl transfer transition states are different for the two classes of substrates in solution but similar in PP1. On the other hand, the microscopic models also highlight notable differences between the phosphate and phosphonate transition states, which are manifested in not only structure but also kinetic isotope effects. Overall, we find that while ${\beta }_{lg}/{\beta }_{EQ,lg}$ generally correlates with the partial charge on leaving group oxygen and the fractional bond order of the breaking P-${\text{O}}_{lg}$ bond, the precise mapping between ${\beta }_{lg}/{\beta }_{EQ,lg}$ and P-${\text{O}}_{lg}$ bond order in the transition state is difficult due largely to the cross talk between breaking and forming P-O bonds. Therefore, further supporting previous analyses of limitations of free energy relations, our results suggest that while free energy relation is a valuable tool for probing the nature of transition state, a quantitative mapping of ${\beta }_{lg}$ and ${\beta }_{lg}/{\beta }_{EQ,lg}$ values to structure or charge in the transition state should be conducted with great care.

Graphical Abstract

1. Introduction

Free energy relation has been extensively used to determine the nature of transition state for solution reactions.^1,2 Using phosphoryl transfer reactions as an example (Scheme 1), by measuring how the reaction rate constant varies with respect to either the nucleophile (nuc) or the leaving group (lg), insights can be obtained regarding the degree of bond formation or bond cleavage in the transition state.³ In principle, the degree of bond formation/cleavage should be evaluated by comparing the change of reaction rate constant log(k) to the change of equilibrium constant log(K_EQ); in practice, however, the value of log(K_EQ) is not always available experimentally and therefore pK_a of the nucleophile/leaving group is often used as a proxy, leading to the Brønsted slopes, ${\beta }_{nuc}=\frac{\partial \mathit{log}(k)}{\partial p{K}_a(nuc)}$ and ${\beta }_{lg}=\frac{\partial \mathit{log}(k)}{\partial p{K}_a(lg)}$. Qualitatively, a large absolute ${\beta }_{lg}$ value is empirically correlated with a significant degree of bond cleavage in the transition state; this is because bond cleavage leads to a significant degree of charge build up in the leaving group, thus the energetics of the transition state (thefore the rate constant) are expected to be sensitive to the substituents on the leaving group. By contrast, for a tight transition state with little bond cleavage, there is little charge build up on the leaving group, thus the rate constant is expected to be insensitive to the substituents on the leaving group, leading to a small absolute ${\beta }_{lg}$ value. Similar discussion can be made for the β_nuc value. When the equilibrium constant can be measured, the degree of bond formation and cleavage can be more quantitatively estimated as β_nuc/β_EQ,nuc and ${\beta }_{lg}/{\beta }_{EQ,lg}$, in which ${\beta }_{EQ,nuc/lg}=\frac{\partial log\left(K_{EQ}\right)}{\partial p{K}_a(nuc/lg)}$. Higher order derivatives (e.g., $p_{xy}=\frac{{\partial }^{2}log(k)}{\partial p{K}_a(nuc)\partial p{K}_a(lg)}$) can be used to measure the correlation between the nucleophile and leaving group effects.

Scheme 1:

Phosphate monoester hydrolysis through a concerted pathway: bond formation to the nucleophile and bond cleavage to the leaving group occur simultaneously but not necessarily synchronously.

For enzyme reactions, free energy relations have also been used to study the nature of the transition state. Such measurement is not as straightforward as the solution counterpart, as the analysis requires the enzyme of interest to react with multiple substrates. Nevertheless, it is increasingly recognized that many enzymes feature promiscuous catalytic activities^4–9 and therefore can be used to measure reliable free energy relations with a broad scope of substrates. Good examples include alkaline phosphatase (AP)^10,11 and Protein Phosphatase-1 (PP1),^12,13 which can bind to a rather broad set of phosphate and sulfate substrates. Free energy relation analysis for these systems is particularly interesting since there is a rich experimental literature on the corresponding solution reactions,³ making it possible to investigate whether these enzymes modify the nature of transition state relative to the uncatalyzed reactions in solution.

Specifically for PP1, recent studies^12,13 by the Hengge lab found that while the ${\beta }_{lg}$ values for phosphate and phosphonate esters hydrolysis in solution are rather different (−0.69 for aryl phosphate esters and −1.23 for aryl phosphonate esters, see Scheme 2), the values are very similar (~−0.30) for these substrates in PP1. The results were interpreted to indicate that PP1 preferentially stabilizes a single type of transition state for phosphate and phosphonate substrates; the lower magnitude of ${\beta }_{lg}$ in PP1 than in solution was interpreted to indicate less charge on the leaving group oxygen, due to interaction with His125 through general acid catalysis.¹³ This is particularly interesting as measurements in AP, which features a rather similar bi-metallic active site, was shown to exhibit different ${\beta }_{lg}$ values for monoester phosphates and diester phosphates, similar to the situation in aqueous solution.^10,11

Scheme 2:

Aryl Phosphate and aryl methylphosphonate substrates studied in this work.

As part of our efforts to better understand the difference between PP1 and AP,¹⁴ we are motivated to revisit the interpretation of free energy relations. As pointed out in both experimental^1–3 and computational^15–18 literature, the free energy relations should be interpreted with care, especially in the absence of β_EQ values. For example, the transition state structure might vary either along or orthogonal to the reaction coordinate, although the magnitude of variation is case-dependent; for phosphate monoesters in solution, experimental data³ suggested a limited range of variation, with the extend of bonding to the nucleophile and leaving group in the transition state spanning the range of 0–0.3; the range is ~0.4–0.6 for phosphate triesters, depending on the value of β_EQ used. In our recent QM/MM simulations of AP,¹⁹ we also observed substantial variations in the transition state structure with respect to the leaving group for both phosphate monoester and diester substrates. This is likely because the enzyme active site is anisotropic and therefore different modes of stabilizations can dominate with different leaving groups, leading to distinct transition state structures; for example, while a good leaving group (nitro-phenol) is adequately stabilized by active site water, a poor leaving group (ethanol) is better stabilized by the zinc ion, leading to different degrees of bond cleavage in the transition state.

Warshel and co-workers have conducted detailed computational analyses for phosphoryl transfer reactions in solution and enzymes,^{15–18,20–22} and considerable efforts were focused on the quantitative analyses of entropic contributions to the free energy of activation.^18,23 Their results suggested that free energy relations, isotope effects or entropies data may not provide decisive evidence in distinguishing the nature of transition state between different phosphate esters. For example, their study of hydrolysis of a series of phosphate and pyrophosphate monoesters^18,21 suggested that the mechanism may change from associative to dissociative, depending on the pK_a of the leaving group, without significantly affecting the free energy relation; this is due in part to the flat nature of the free energy surface that separates the different mechanistic pathways. Nevertheless, considering the broad application of free energy relations in experimental studies, it is worthwhile further dissecting the information content of such analysis with additional phosphoryl transfer enzymes and substrate types.

In this work, we focus on phosphate and phosphonate esters in water and PP1 using QM cluster models.^24,25 While QM/MM simulations have become increasingly more quantitative^26–28 and have been used to study phosphoryl transfer reactions by us and others,^{18,21,29–32} they remain computationally challenging for an enzyme such as PP1, which features two Mn²⁺ ions. Moreover, the calculation of Brønsted values requires a precise (which differs from being accurate) determination of the activation free energy, which would require extensive sampling^18,33 using a QM/MM model. While the cluster models have limitations in terms of absolute accuracy, they are well-suited to study trends among a series of closely related substrates. Our aim here is to contrast trends in ${\beta }_{lg}$ and ${\beta }_{lg}/{\beta }_{EQ,lg}$ for the two types of substrates (phosphate and phosphonate esters) in PP1 vs. in water. With the transition states and ${\beta }_{lg}$ values precisely determined in the cluster models for the different substrates, we will be able to establish what transition state characteristics are best reflected by the ${\beta }_{lg}$ and ${\beta }_{lg}/{\beta }_{EQ,lg}$ values. Indeed, since the electronic structure of the transition state is not straightforward to decompose into group contributions, the empirical correlation based on formal charges and bond-order considerations^1–3 might be overly simplistic. The validity of the QM cluster models adopted here is supported by the observation that they are able to capture key trends in experimental free energy relation data and kinetic isotope effects, as we show below.

In the following, we first summarize the computational methods and models used in this work; we then present results for the phosphoryl transfer transition states for the phosphate and phosphonate esters in water and PP1; we then analyze the correlation between different transition state properties and the estimated ${\beta }_{lg}$ and ${\beta }_{lg}/{\beta }_{EQ,lg}$ values. Finally, we summarize a few key conclusions.

2. Computational Models and Methods

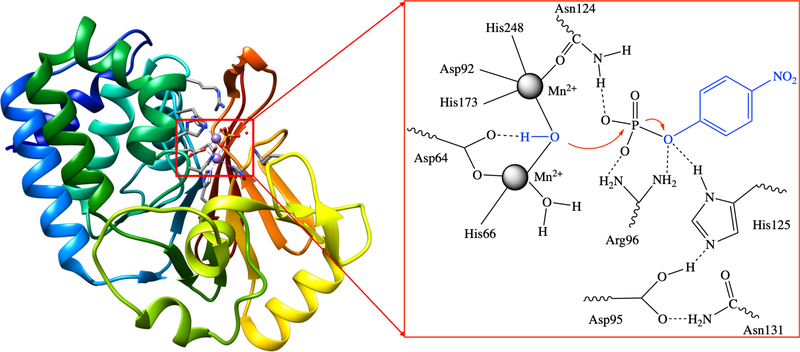
The QM cluster model for PP1 is built based on the PDB structure 4MOV,³⁴ which is for the enzyme expressed in E. coli. The cluster model (see Fig. 1) includes the following groups in the active site: the two Mn²⁺ ions, the bridging hydroxide ion, Asp64, His66, Asp92, Asp95, Arg96, Asn124, His125, Asn131, His173, Arg221, His248 and Tyr272; the total charge for the system including the substrate is +1 for aryl phosphate and +2 for aryl methylphosphonate. The total number of atoms is in the range of 153 to 159 depending on the substrate, which includes (see Scheme 2) seven arylphosphates and seven aryl methylphosphonate with the leaving group pK_a ranging from 7 to 11: para-nitrophenyl (pNPP and pNPMP), parachlorophenyl (pCLPP and pCLPMP), meta-chlorophenyl (mCLPP and mCLPMP), metacyanophenyl (mCNPP and mCNPMP), para-cyanophenyl (pCNPP and pCNPMP), paramethylphenyl (pMPP and pMPMP) and phenyl (PP and PMP). During the calculations, most of the amino acid side chains are truncated at their β-carbons, which are converted to methyl groups. The β-carbon atoms are fixed to their crystallographic positions to mimic the enzyme environment and to prevent unrealistic distortion of the cluster during geometry optimization. For Arg96 and Arg221 in PP1, to limit the size of the QM region but ensure sufficient flexibility, the frozen atom is selected to be the δ-carbon.

Figure 1:

The overall structure of Protein Phosphatase-1 (PP1) and its active site: the nucleophile is a hydroxide bound to two Mn²⁺ ions, and the substrate shown is para-nitrophenyl phosphate.

All geometry optimizations are performed with the conductor-like polarizable continuum solvation model (CPCM)^35,36 with a dielectric constant of 4.0 to approximately account for the missing protein environment, as often done in QM cluster studies.²⁵ Since the active site of PP1 is solvent accessible, one might be concerned that the choice of ϵ = 4.0 is not optimal. For example, His125 was proposed to be a general acid based on structural data,^12,37,38 suggesting that it is doubly protonated. With ϵ = 4.0, His125 prefers to be singly protonated while the nearby Asp95 picks up the additional proton (see Fig. 1); with a higher dielectric constant, the ionized form of the pair of amino acids is better stabilized (see Fig. S1). Nonetheless, test calculations indicate that the dielectric constant has limited effects on the energetics and transition state structure, as shown in Table S1 in the Supporting Information; attempts to search for an alternative transition state that involves general acid catalysis by His125 led to the same transition state, and proton transfer from His125 to the leaving group was found favorable only after the phosphoryl transfer is complete, suggesting that general acid catalysis is not a favorable pathway at least with the current QM cluster model. Thus a value of 4.0 is used for the PP1 cluster models throughout this work. For additional test calculations with higher dielectric constants, see Ref. 14.

For the phosphate and phosphonate hydrolysis in water, the same set of substrates listed in Scheme 2 are used; both water and hydroxide are tested as the nucleophile. While the bulk water is treated with CPCM using a dielectric constant of 78.35, a number of explicit water molecules are included (for examples, see Fig. 2 and Fig. 3) to better describe the solvation of highly charged species. In those calculations, care is exercised to maintain a similar hydrogen-bonding patterns for the series of substrates, so that meaningful free energy relations can be derived from the calculations; the rather linear free energy relations observed below support the validity of the computational model. Further discussion on the importance of including explicit water for the reactions of interest is summarized in Supporting Information.

Figure 2:

Examples for the key structures of phosphate (left column) and phosphonate (right column) hydrolysis in water with hydroxide as the nucleophile. RS, TS and PS represent reactant state, transition state and product state, respectively. Bond lengths for P-O_nuc and P-${\text{O}}_{lg}$ (in Å) optimized from B3LYP-D3/CPCM calculations are shown.

Figure 3:

Same as Fig. 2, but with neutral water as the nucleophile. A solvent-assisted mechanism is followed here as recent computational studies suggested that it is the favorable reaction pathway in solution;^39,40 note that the nucleophilic water in the product state of phosphonate hydrolysis spontaneously deprotonates, leading to the formation of a hydronium ion nearby.

All quantum mechanical calculations are performed using the Gaussian 16 program.⁴¹ Geometry optimizations are performed using the Becke, three-parameter, Lee-Yang-Parr exchange-correlation functional (B3LYP^42–44) with the addition of Grimme’s third version of semi-empirical dispersion correction (D3^45,46). The Def2TZVP basis set^47,48 is used for the Mn²⁺ ions and the 6–31G(d,p) basis set^49–51 is used for the other atoms (C, O, P, S, N, Cl and H) for geometry optimization and vibrational analysis; note that the masses of the frozen atoms are set to large values, which effectively decouple these atoms from the vibrations of other atoms, making the vibrational frequency analysis fully consistent with the geometry optimization protocol, thus no spurious imaginary frequencies are obtained. Since the substrates are highly similar among a given series, vibrational entropy is not expected to make any major contribution to the trends in the computed activation free energies and rate constants. Optimized coordinates for all species involved in the reaction are included in the Supporting Information, and additional discussions on computational benchmarks (e.g., functionals in DFT models for PP1) are summarized in Ref. 14.

3. Results and Discussion

3.1. Brønsted Plots for Phosphate and Phosphonate Ester Hydrolysis in Water

Experimental measurements observed rather different Brønsted slopes for the hydrolysis of phosphate and phosphonate ester hydrolysis in water;¹² the value is −1.23 for aryl phosphate and −0.69 for aryl phosphonate. Considering the solution conditions of the measurements, these values are for water and hydroxide as the nucleophile, respectively. Therefore, it is of interest to use computational studies to investigate whether the measured ${\beta }_{lg}$ values reflect the intrinsic difference between phosphate and phosphonate esters, or the difference is due largely to the different nucleophiles.

As shown in Fig. 4, the computed Brønsted slopes are steeper for phosphate esters than phosphonate esters, regardless of the identity of the nucleophile. This trend is qualitatively consistent with the experimentally measured values, suggesting that there is indeed intrinsic difference between phosphate and phosphonate ester hydrolysis transition states (vide infra). Comparing the computed rate constants for different nucleophiles, the values for phosphate esters are consistently higher when hydroxide is the nucleophile, as expected, although the differences are modest and of 1–2 orders of magnitude; by contrast, the rate for phosphonate hydrolysis is significantly higher with hydroxide as the nucleophile, thus for comparison to experiment, the hydroxide result should be used for phosphonate esters.

Figure 4:

Approximate Brønsted plots for the hydrolysis of (a) arylphosphate (PP) and (b) arylphosphonate (PMP) esters listed in Scheme 2 in water. The rate constants (k) are estimated using transition state theory by $\frac{k_{B}T}{h}exp\left[-\mathrm{\Delta }{G}^{{}^{‡}}/k_{B}T\right]$, and the pK_as are experimental values for the leaving groups; thermal contributions to ΔG^‡ are calculated using the harmonic-oscillator-rigid-rotor approximations.

At a quantitative level, the computed rate constants (water as nucleophile for phosphates, hydroxide as nucleophile for phosphonates) are substantially higher in magnitude compared to the experimental measurements.¹² However, we note that the reactant state in the current calculations has already the nucleophile hydrogen bonded with the substrate (see, for example, Fig. 2 and Fig. 3); as a result, the entropic cost of bringing them together has not been included and the hydrolysis is considered as a unimolecular reaction. Since we expect that this entropic cost is similar for a series of closely related substrates that differ only in the leaving group, the current calculations are adequate for estimating the Brønsted slope. Indeed, the computations have captured the same trends as experiment for the ${\beta }_{lg}$ values of the two classes of substrates, although more quantitative computations require extensive QM/MM free energy simulations, which are left for future work; moreover, as discussed below, the calculated ${\beta }_{lg}/{\beta }_{EQ,lg}$ values agree well with experimental data. It is worth noting that while pure implicit solvent model calculations lead to considerably different structures and energetics, the computed Brønsted slopes are comparable to the microsolvation model results due to systematic error cancellation (see Supporting Information). The work of Warshel and co-workers¹⁸ on phosphate diester hydrolysis in water also indicated that implicit solvent calculations were able to capture experimental trends in free energy relation. On the other hand, recent studies by Kamerlin and co-workers³⁹ highlighted the importance of including explicit solvents to better describe the structure of monoester hydrolysis transition state, as we also find here (see Supporting Information).

3.2. Brønsted Plots for Phosphate and Phosphonate Ester Hydrolysis in PP1

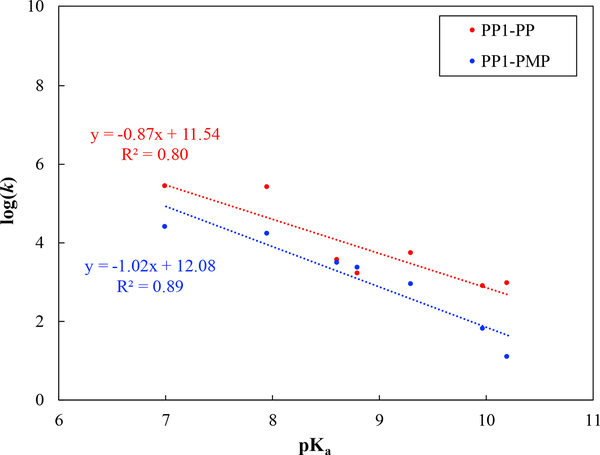
In PP1, the measured ${\beta }_{lg}$ values for phosphate and phosphonate substrates were found to be similar (~−0.30) in experiments.^12,13 With the current QM cluster model, this is also qualitatively captured, as shown in Fig. 5. At a quantitative level, however, the computed ${\beta }_{lg}$ values are larger in magnitude, −0.87 for phosphates and −1.02 for phosphonates. Our computational model only estimates k_cat while the experimental value is based on k_cat/K_m, thus a quantitative agreement between computation and experiment is not expected; moreover, it is possible that the QM cluster model overestimates the ${\beta }_{EQ,lg}$ values, as the computed ${\beta }_{lg}/{\beta }_{EQ,lg}$ values in PP1 fall in the reasonable range (vide infra). The main point of interest concerns the trends in ${\beta }_{lg}$ (and ${\beta }_{lg}/{\beta }_{EQ,lg}$) for the two classes of substrates in solution vs. in the enzyme PP1, and the current model has indeed captured key trends observed in experiments: i.e., ${\beta }_{lg}$ values are distinct for phosphate and phosphonate hydrolysis in water but similar in PP1. Therefore, it is meaningful to use the computational model to analyze to what degree these trends in ${\beta }_{lg}$ reflect structural and electronic properties of phosphoryl transfer transition states for these substrates in different environments. Specifically, we ask whether the trends in ${\beta }_{lg}$ values indeed suggest that the transition states are distinct for phosphate and phosphonate hydrolysis in solution, but are similar in PP1, as concluded in previous studies.^12,13

Figure 5:

Same as Fig. 4, but for the arylphosphate (PP) and arylphosphonate (PMP) substrates hydrolysis in PP1.

3.3. Structure and Bonding of Phosphoryl Transfer Transition States

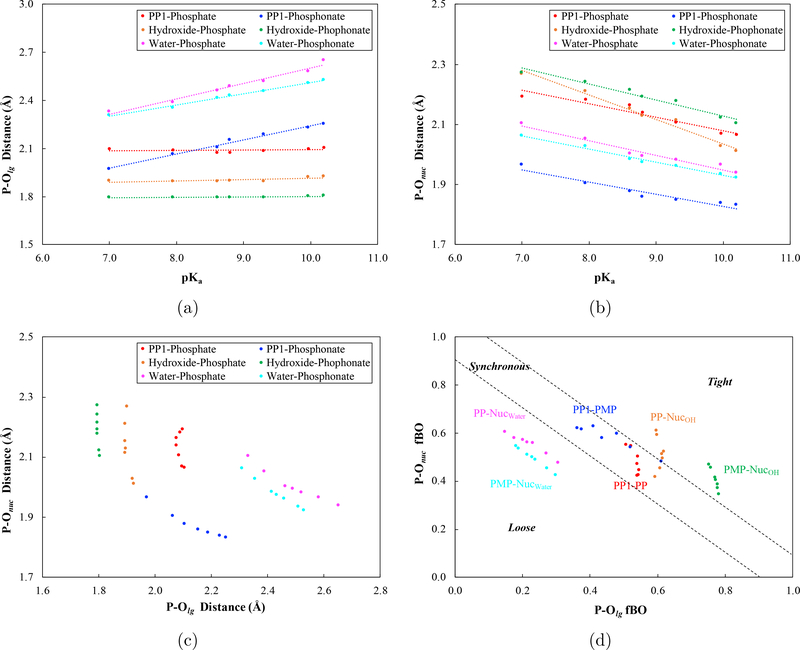
In this section, we compare key structural features of the phosphoryl transfer transition states for the two classes of substrates in different environments; these include the lengths of the breaking (P-${\text{O}}_{lg}$) and forming (P-O_nuc) bonds as well as their sum, which is commonly referred to as the “tightness coordinate”.¹⁹ In addition, we report the fractional bond orders (fBOs) for the breaking and forming bonds in the transition state, as was done in our previous work.^19,52 These results are summarized in Table 1; they are also plotted in Fig. 6 for visual comparisons, and selected transition state structures are shown in Fig. 7. Additional energetic and bond-order data are summarized in the Supporting Information.

Table 1:

Comparison of computed transition state properties for phosphate and phosphonate substrates in PP1^a and water^b,c: distances (d, in Å) and fractional bond orders (fBO^d) of P-O_lg and P-O_nuc.

		Phosphate-NucH2Ob						Phosphonate-NucH2Ob
		P-Onuc		P-Olg		Tightnessf		P-Onuc		P-Olg		Tightnessf
	PKae	d	fBOg	d	fBO	d	fBO	d	fBO	d	fBO	d	fBO
pNPP/pNPMP	7.0	2.10	0.48	2.33	0.31	4.43	0.91	2.06	0.43	2.31	0.30	4.37	0.73
pCNPP/pCNPMP	8.0	2.05	0.52	2.39	0.27	4.44	0.94	2.03	0.45	2.36	0.27	4.38	0.73
mCNPP/mCNPMP	8.6	2.00	0.56	2.46	0.23	4.47	0.97	1.98	0.49	2.41	0.24	4.40	0.73
mCLPP/mCLPMP	8.8	1.99	0.56	2.49	0.21	4.48	0.97	1.97	0.50	2.43	0.23	4.41	0.73
pCLPP/pCLPMP	9.3	1.98	0.57	2.52	0.20	4.50	0.98	1.96	0.51	2.46	0.21	4.42	0.72
PP/PMP	10.0	1.97	0.58	2.58	0.18	4.55	0.98	1.93	0.54	2.51	0.19	4.44	0.73
pMPP/pMPMP	10.2	1.94	0.61	2.65	0.15	4.59	0.99	1.92	0.55	2.53	0.18	4.45	0.73
		Phosphate-NucOH−c						Phosphonate-NucOH−c
		P-Onuc		P-Olg		Tightnessf		P-Onuc		P-Olg		Tightnessf
	pKae	d	fBO	d	fBO	d	fBO	d	fBO	d	fBO	d	fBO
pNPP/pNPMP	7.0	2.27	0.42	1.90	0.59	4.17	1.01	2.27	0.35	1.80	0.78	4.07	1.13
pCNPP/pCNPMP	8.0	2.21	0.45	1.89	0.61	4.10	1.06	2.24	0.37	1.80	0.78	4.04	1.15
mCNPP/mCNPMP	8.6	2.15	0.50	1.89	0.62	4.05	1.11	2.22	0.39	1.80	0.78	4.02	1.17
mCLPP/mCLPMP	8.8	2.13	0.51	1.90	0.61	4.03	1.12	2.19	0.40	1.80	0.77	3.99	1.18
pCLPP/pCLPMP	9.3	2.11	0.52	1.90	0.62	4.01	1.14	2.18	0.41	1.80	0.77	3.98	1.19
PP/PMP	10.0	2.03	0.59	1.92	0.60	3.95	1.19	2.12	0.45	1.80	0.76	3.92	1.21
pMPP/pMPMP	10.2	2.01	0.61	1.93	0.60	3.94	1.21	2.10	0.47	1.80	0.75	3.90	1.22
		PP1-Phosphate						PP1-Phosphonate
		P-Onuc		P-Olg		Tightnessf		P-Onuc		P-Olg		Tightnessf
	PKae	d	fBO	d	fBO	d	fBO	d	fBO	d	fBO	d	fBO
pNPP/pNPMP	7.0	2.19	0.42	2.10	0.54	4.29	0.96	1.97	0.48	1.97	0.61	3.94	1.09
pCNPP/pCNPMP	8.0	2.18	0.43	2.09	0.54	4.27	0.97	1.90	0.54	2.06	0.52	3.97	1.06
mCNPP/mCNPMP	8.6	2.16	0.45	2.08	0.54	4.24	0.99	1.88	0.63	2.11	0.41	3.98	1.04
mCLPP/mCLPMP	8.8	2.14	0.47	2.08	0.54	4.22	1.01	1.86	0.58	2.15	0.44	4.01	1.02
pCLPP/pCLPMP	9.3	2.11	0.50	2.08	0.54	4.19	1.04	1.85	0.60	2.19	0.48	4.04	1.08
PP/PMP	10.0	2.07	0.55	2.10	0.52	4.17	1.07	1.84	0.61	2.23	0.38	4.07	0.99
pMPP/pMPMP	10.2	2.06	0.55	2.11	0.51	4.17	1.06	1.83	0.62	2.25	0.36	4.08	0.98

^a.Native PP1 active site model with Mn²⁺ ion.

^b.The nucleophile is water. Nineteen explicit water molecules surrounding the substrate are included. The bulk water is treated with CPCM.

^c.The nucleophile is hydroxide ion. Eleven and nineteen explicit water molecules surrounding the substrate are included for phosphate and phosphonate, respectively. The bulk water is treated with CPCM.

^d.The fractional bond order (fBO) is given as a fraction of the Wiberg bond order in the transition state relative to the values for P-O_lg and P-O_nuc in the reactant state or the product state, respectively.

^e.Experimental pK_a values of leaving groups.

^f.Tightness is characterized either by the sum of P-O_nuc and P-O_lg distances, or the sum of P-O_nuc and P-O_lg fractional bond orders.

^g.For the case of phosphate hydrolysis in water with water as the nucleophile, the “product state” studied here corresponds to the intermediate state in the solvent assisted mechanism^39,40 and thus has a weak P – O_nuc bond; accordingly, the fBO results shown here are calculated using P-O_nuc Wiberg bond order in the product state when hydroxide is the nucleophile as the reference value.

Figure 6:

Comparison of (a-c) P-O distances and (d) fractional bond orders (fBOs) for optimized transition states structures in PP1 and water using QM cluster models: for the substrates, PP denotes phenyl phosphate, and PMP denotes phenyl phosphonate. For the case of phosphate hydrolysis in water with water as the nucleophile, the “product state” studied here corresponds to the intermediate state in the solvent assisted mechanism^39,40 and thus has a weak P −O_nuc bond; the fBO results labeled as “PP-Nuc_water” are calculated using P-O_nuc Wiberg bond order in the product state when hydroxide is the nucleophile as the reference value. In (a-b), optimized P-${\text{O}}_{lg}$ and P-O_nuc distances in the transition state are plotted against the experimental pK_a values of the leaving group; in (c), the optimized P-${\text{O}}_{lg}$ and P-O_nuc distances in the transition state are plotted against each other, and in (d), the fBOs values for P-${\text{O}}_{lg}$ and P-O_nuc in the transition state are plotted against each other for the different substrates in water and in PP1.

Figure 7:

Examples of optimized transition state structures with cluster models for PP1 with (a) phosphate and (b) phosphonate ester substrates. The cases shown correspond to leaving groups with the lowest and highest pK_a values studied here. The results highlight that phosphate and phosphonate transition state structures respond differently to the nature of the leaving group.

For the uncatalyzed hydrolysis with water as the nucleophile, both P-${\text{O}}_{lg}$ and P-O_nuc vary significantly for phosphate and phosphonate with different leaving groups. For phosphate esters, for example, the bond length for P-O_nuc varies from 1.94 to 2.10 Å, as P-${\text{O}}_{lg}$ varies from 2.65 to 2.33 Å; due to compensation between the two, their sum, i.e., the tightness coordinate, falls in a narrower range between 4.43 and 4.59 Å. By comparison, for phosphonate esters, P-O_nuc spans a similar range from 1.92 to 2.06 Å, while P-${\text{O}}_{lg}$ has a narrower range of 2.53 to 2.31 Å, and the tightness coordinate has an even narrower distribution between 4.37 to 4.45 Å.

The situation is rather different when hydroxide is the nucleophile in water. In this case, curiously, the P-${\text{O}}_{lg}$ distance does not vary much at all for both phosphate and phosphonate as the pK_a of the leaving group changes (see Table 1, and Fig. 6a; similar trend is observed with the implicit solvent); the values for phosphate are consistently larger than those for phosphonates by ~0.1 Å, which corresponds to ~0.15–0.19 difference in fBO values. By contrast, the P-O_nuc varies substantially, for both classes of substrates (Fig. 6b); it ranges from 2.01 to 2.27 Å for phosphates and from 2.10 to 2.27 Å for phosphonates. Compared to transition states with water as the nucleophile, those with hydroxide as the nucleophile are earlier in nature, as reflected by the generally longer P-O_nuc distances and shorter P-${\text{O}}_{lg}$ distances; this trend is consistent with the notion that hydroxide is a stronger nucleophile.

For the phosphoryl transfer in the PP1 cluster model, for which a Mn²⁺-bound hydroxide is the nucleophile, the transition state exhibits different trends for the two classes of substrates (see Fig. 7 for examples). For phosphate esters, the structural features of the transition state resemble those in solution with hydroxide as the nucleophile: the P-${\text{O}}_{lg}$ distance varies little with different leaving groups, while P-O_nuc changes by more than 0.1 Å; compared to the solution case, the transition state in PP1 features a longer P-${\text{O}}_{lg}$ by 0.2 Å, and the tightness coordinate clearly indicates a looser transition state. For phosphonate esters, by contrast, both P-${\text{O}}_{lg}$ and P-O_nuc change significantly as the leaving group varies: P-${\text{O}}_{lg}$ varies from 1.97 to 2.25 Å, and P-O_nuc varies between 1.83 and 1.97 Å. The compensation between them leads to the tightness coordinate being tighter than the solution case for some substrates but looser for others.

To better compare transition state structures and bond orders, we project the transition state onto two dimensions spanned by either the lengths or fBO values of the breaking and forming P-O bonds. As shown in Fig. 6c, the transition states in solution generally do not differ significantly for phosphate and phosphonate esters for a given nucleophile; the largest difference is in the P-${\text{O}}_{lg}$ distance (~0.2 Å) when hydroxide is the nucleophile. However, the transition states for phosphate with water as the nucleophile and for phosphonate with hydroxide as the nucleophile indeed feature very different structures (Fig. 6c) and bond orders (Fig. 6d); this observation is consistent with the significantly different ${\beta }_{lg}$ values observed in both experiment and current calculations for these two conditions. Therefore, significantly different ${\beta }_{lg}$ values indeed reflect distinct transition state structures and bond orders.

Fig. 6c also highlights that transition states for phosphate and phosphonates in PP1 exhibit rather different patterns in the breaking and forming P-O bond lengths. Nevertheless, in terms of fractional bond orders, the transition states in PP1 fall in the range of synchronous region for both substrates (Fig. 6d) since all fBO values for the breaking and forming P-O bonds are in the range of 0.4–0.6. Recall that both experiment and current computations observe similar ${\beta }_{lg}$ values for the two classes of substrates in PP1, thus whether similar ${\beta }_{lg}$ values reflect similar transition states depends on the resolution in the property of interest.

3.4. Degree of P-${\text{O}}_{lg}$ bond cleavage and ${\beta }_{lg}/{\beta }_{EQ,lg}$

It has been proposed^1–3 that the degree of P-${\text{O}}_{lg}$ bond cleavage can be estimated by ${\beta }_{lg}/{\beta }_{EQ,lg}$, in which ${\beta }_{EQ,lg}=\frac{\partial log\left(K_{EQ}\right)}{\partial p{K}_a(lg)}$. The equilibrium constants, K_EQ, however, is not always available from experiment. In this work, we compute K_EQ for the elementary reaction step studied here, and the ratio between ${\beta }_{lg}$ and ${\beta }_{EQ,lg}$ is summarized in Table 2. For the plot of K_EQ against the experimental leaving group pK_a values, see Supporting Information.

Table 2:

Computed β_lg, β_EQ,lg and their ratios in comparison to the experimental data.

	Calculation			Experimental12
System	βlg	βEQ,lg	ratio	βlg	βEQ,lg	ratio
Phosphate-NucH2O	−2.09	−1.72	1.21 (0.85a)	−1.23	−1.35	0.91
Phosphonate-NucH2O	−1.46	−2.15	0.68	–	–	–
Phosphate-NucOH−	−1.86	−2.45	0.76	–	–	–
Phosphonate-NucOH−	−0.89	−2.69	0.33	−0.69	−1.74	0.40
PP1-phosphate	−0.87	−1.68	0.52	−0.32	–	–
PP1-phosphonate	−1.02	−2.51	0.41	−0.30	–	–

^a.The value is obtained by using β_EQ,lg for phosphate hydrolysis with hydroxide as the nucleophile, since the “product state” studied here for phosphate hydrolysis with water as the nucleophile corresponds to the intermediate state in the solvent assisted mechanism.^39,40

For the uncatalyzed reaction in water, with hydroxide ion as the nucleophile, the ${\beta }_{lg}/{\beta }_{EQ,lg}$ values are ~0.8 for phosphate and ~0.3 for phosphonate esters. These values suggest a late and early transition state for phosphate and phosphonate, respectively; the value for phosphonate agrees fairly well with the experimental data of 0.4. These trends are qualitatively consistent with the computed fBO values shown in Table 1, which suggest that phosphonate esters feature a somewhat earlier transition state than phosphate when hydroxide is the nucleophile. At a quantitative level, however, a value ~0.8 for ${\beta }_{lg}/{\beta }_{EQ,lg}$ is not quite congruent with a fBO value of ~0.6 for P-${\text{O}}_{lg}$ (the expected range for a linear mapping is ~0.2).

For the uncatalyzed phosphonate hydrolysis with water as the nucleophile, the computed ${\beta }_{lg}/{\beta }_{EQ,lg}$ value is substantially higher, ~0.7, which indicates a much later transition state. This is consistent with the much lower fBO values (0.18–0.30) computed for P-${\text{O}}_{lg}$. For the phosphate esters, curiously, the computed ${\beta }_{lg}/{\beta }_{EQ,lg}$ values are larger than unity. This might be due to the fact that the “product state” studied here is an intermediate state in the solvent assisted mechanism,^39,40 thus the reverse barrier is small and very sensitive to the hydrogen-bonding network surrounding the substrate, for which the microsolvation model used here does not address adequately. If the ${\beta }_{EQ,lg}$ value from phosphate hydrolysis with hydroxide ion as the nucleophile is applied to estimate ${\beta }_{lg}/{\beta }_{EQ,lg}$, a value of 0.85 is obtained, which is in agreement with the experimental value of 0.91, suggesting that phosphate hydrolysis with water as the nucleophile involves a late transition state; this description is consistent with the low fBO values (0.15–0.31) computed for P-${\text{O}}_{lg}$ in the transition state.

For PP1, the ${\beta }_{lg}/{\beta }_{EQ,lg}$ values fall in the range of 0.4–0.5 for both phosphate and phosphonate substrates, with small variations depending on whether ΔE^‡ or ΔG^‡ is used in the calculations. These values are consistent with the fBO values of 0.4–0.6 for P-${\text{O}}_{lg}$ for both substrates (Table 1). The precise degree of P-${\text{O}}_{lg}$ cleavage in PP1 was not straightforward to determine based on experimental data in Ref.,¹³ due to the lack of measured ${\beta }_{EQ,lg}$ values in PP1. The combination of ${\beta }_{lg}$ and kinetic isotope effect measurements suggested a transition state “with extensive P-O bond fission, in which general acid catalysis is involved, but in which proton transfer lags somewhat behind P-O bond fission”.¹³ As stated above, the general acid mechanism is not observed to be favorable with the current QM cluster model; whether the situation is different with QM/MM simulations is an important topic for future study.

3.5. Charges of O_nuc and $O_{lg}$

To elucidate the nature of transition state, we also analyze the charges on the key atoms involved in the reaction, i.e. O_nuc and ${\text{O}}_{lg}$ atoms. The natural charges obtained from NBO population analysis⁵³ are used and summarized in Table 3. Charge data for other key atoms are summarized in the Supporting Information.

Table 3:

Comparison of natural charges of O_nuc and O_lg in the phosphoryl transfer transition state for phosphate and phosphonate in water and PP1.

	pKa	Phosphate-NucH2O		Phosphonate-NucH2O		Phosphate-NucOH−		Phosphonate-NucOH−		PP1-Phosphate		PP1-Phosphonate
Substrate	LG pKa	Onuc	Olg	Onuc	Olg	Onuc	Olg	Onuc	Olg	Onuc	Olg	Onuc	Olg
pNPP/pNPMP	7.0	−1.00	−0.76	−1.03	−0.79	−1.09	−0.76	−1.10	−0.82	−1.01	−0.82	−1.01	−0.83
pCNPP/pCNPMP	8.0	−0.99	−0.78	−1.03	−0.81	−1.09	−0.77	−1.09	−0.83	−1.01	−0.83	−1.01	−0.83
mCNPP/mCNPMP	8.6	−0.99	−0.79	−1.04	−0.82	−1.09	−0.79	−1.09	−0.84	−1.01	−0.83	−1.00	−0.84
mCLPP/mCLPMP	8.8	−0.99	−0.80	−1.04	−0.82	−1.08	−0.79	−1.09	−0.84	−1.01	−0.83	−1.00	−0.84
pCLPP/pCLPMP	9.3	−1.00	−0.80	−1.04	−0.82	−1.08	−0.79	−1.09	−0.84	−1.01	−0.84	−1.00	−0.84
PP/PMP	10.0	−1.00	−0.81	−1.04	−0.83	−1.08	−0.80	−1.09	−0.84	−1.00	−0.84	−1.00	−0.84
pMPP/pMPMP	10.2	−1.00	−0.81	−1.04	−0.83	−1.08	−0.80	−1.09	−0.84	−1.00	−0.84	−1.00	−0.84

As shown in Table 3, the natural charges are in general fairly insensitive to the nature of the leaving group within a given substrate series; the largest difference observed is 0.05 e. Therefore, natural charges can be considered as a coarse-grained intrinsic property that reflects the electronic structure of the transition state. For phosphate and phosphonate esters in PP1, both O_nuc and ${\text{O}}_{lg}$ charges are highly similar for the two classes of substrates, which is congruent with the similar ${\beta }_{lg}$ (and ${\beta }_{lg}/{\beta }_{EQ,lg}$) values computed here and measured experimentally. For solution reactions, phosphate hydrolysis with water as the nucleophile and phosphonate hydrolysis with hydroxide as the nucleophile indeed feature rather different O_nuc and ${\text{O}}_{lg}$ values; the former differs by ~0.1 e while the latter by ~0.03–0.06 e. Such larger differences are correlated with the distinct ${\beta }_{lg}$ values computed here and measured experimentally. Therefore, the overall trends in O_nuc and ${\text{O}}_{lg}$ natural charges appear to be consistent with trends in ${\beta }_{lg}$ values, as also commented on in previous studies.¹⁸ Compared to the experimental study,¹³ which observed lower ${\beta }_{lg}$ values in PP1 than in solution and thus concluded a lower charge on the leaving group, our calculations find similar charges (~−0.84) on ${\text{O}}_{lg}$ for transition states in PP1 and in solution. This might be related to the observation that the general acid catalysis pathway is not found favorable in the current QM cluster model.

It is also worth examining the charge transfer during phosphoryl transfer reaction. Since the changes of ${\text{O}}_{lg}$ charges during the reaction is relatively small in magnitude, the $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ values may exhibit somewhat larger changes with different leaving groups. Nevertheless, the overall trends in $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ values are qualitatively consistent with those for ${\beta }_{lg}/{\beta }_{EQ,lg}$ (see Table 4). For example, for PP1, the average $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ values are 0.60 and 0.64 for phosphate and phosphonate, respectively, indicating that the transition state is more or less synchronous, in agreement with the fBO values shown in Table 1 and Fig. 6d. This is also in congruent with the ${\beta }_{lg}/{\beta }_{EQ,lg}$ values for phosphate and phosphonate substrates in PP1 (0.52 and 0.41, respectively). For uncatalyzed reactions in solution, phosphate hydrolysis with water as the nucleophile and phosphonate hydrolysis with hydroxide as the nucleophile feature different ${\text{O}}_{lg}$ charge values, as shown in Table 3. The charge ratio values are also different, which is in agreement with the distinct ${\beta }_{lg}/{\beta }_{EQ,lg}$ values. For the phosphate esters with water as nucleophile, the average $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ value is larger than unity, a trend also observed for ${\beta }_{lg}/{\beta }_{EQ,lg}$, which might reflect that the “product state” studied here is not the final hydrolysis product. For phophonate with hydroxide as nucleophile, the ratio is close to zero, suggesting that phosphonate adopts an early transition state in solution, qualitatively in agreement with a small ${\beta }_{lg}/{\beta }_{EQ,lg}$ value (0.33). By comparison, for phosphonate with water as the nucleophile, $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ values are substantially larger, suggesting a much later transition state, in agreement with fBO and ${\beta }_{lg}/{\beta }_{EQ,lg}$ values. The only exception is the case of phosphate hydrolysis with hydroxide as the nucleophile, which leads to $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ values substantially than unity for many cases.

Table 4:

Changes in the natural charge of O_lg in the phosphoryl transfer transition state and product state relative to the reactant state for phosphate and phosphonate hydrolysis in water and PP1.

	pKa	Phosphate-NucH2O			Phosphonate-NucH2O
Substrate	LG pKa	Δq(Olg)TS	Δq(Olg)PS	Ratio	Δq(Olg)TS	Δq(Olg)PS	Ratio
pNPP/pNPMP	7.0	0.07	0.10	0.74	0.04	0.07	0.58
pCNPP/pCNPMP	8.0	0.06	0.07	0.82	0.03	0.05	0.64
mCNPP/mCNPMP	8.6	0.05	0.05	0.91	0.02	0.03	0.68
mCLPP/mCLPMP	8.8	0.05	0.05	0.89	0.02	0.03	0.72
pCLPP/pCLPMP	9.3	0.04	0.03	1.54	0.02	0.03	0.74
PP/PMP	10.0	0.04	0.03	1.59	0.02	0.02	0.82
pMPP/pMPMP	10.2	0.04	0.02	1.69	0.02	0.02	0.84
	pKa	Phosphate-NucOH−			Phosphonate-NucOH−
Substrate	LG pKa	Δq(Olg)TS	Δq(Olg)PS	Ratio	Δq(Olg)TS	Δq(Olg)PS	Ratio
pNPP/pNPMP	7.0	0.08	0.07	1.12	0.01	0.11	0.06
pCNPP/pCNPMP	8.0	0.07	0.05	1.46	0.01	0.07	0.05
mCNPP/mCNPMP	8.6	0.05	0.02	3.00	0.00	0.05	0.02
mCLPP/mCLPMP	8.8	0.05	0.02	2.90	0.00	0.04	0.03
pCLPP/pCLPMP	9.3	0.05	0.02	3.02	0.00	0.04	0.00
PP/PMP	10.0	0.05	0.01	3.75	0.00	0.03	0.00
pMPP/pMPMP	10.2	0.05	0.01	6.80	0.00	0.02	0.00
	pKa	PP1-Phosphate			PP1-Phosphonate
Substrate	LG pKa	Δq(Olg)TS	Δq(Olg)PS	Ratio	Δq(Olg)TS	Δq(Olg)PS	Ratio
pNPP/pNPMP	7.0	0.03	0.08	0.38	0.01	0.05	0.23
pCNPP/pCNPMP	8.0	0.02	0.05	0.48	0.02	0.04	0.37
mCNPP/mCNPMP	8.6	0.03	0.04	0.75	0.01	0.04	0.29
mCLPP/mCLPMP	8.8	0.03	0.03	0.78	0.01	0.03	0.45
pCLPP/pCLPMP	9.3	0.02	0.03	0.75	0.01	0.01	0.86
PP/PMP	10.0	0.02	0.05	0.46	0.01	0.01	0.89
pMPP/pMPMP	10.2	0.02	0.04	0.58	0.01	0.01	1.39

3.6. Kinetic Isotope effect

To better distinguish the microscopic features of the transition states for these substrates, more sensitive probes such as kinetic isotope effects (KIE) are likely required.^52,54 Within the current cluster model, we have calculated the ¹⁸O KIE values for ${\text{O}}_{lg}$ and O_nuc using the harmonic-frequency-rigid-rotor approximation; the data are shown in Table 5, and additional KIE data for non-bridging oxygen atoms are summarized in the Supporting Information. The calculated ${\text{O}}_{lg}$ KIE is in good agreement with experimental data for both pNPP and pNPMP in PP1 and water, suggesting that the current cluster models are able to capture the key structural features of the transition state.

Table 5:

¹⁸O kinetic isotope effect of O_lg and O_nuc for phosphate and phosphonate hydrolysis in water and PP1.

	pKa	Phosphate-NucH2O			Phosphonate-NucOH−
Substrate	LG pKa	Onuc	Olg	Olg Exp.12	Onuc	Olg	Olg Exp.12
pNPP/pNPMP	7.0	0.993	1.020	1.0189	1.027	1.007	1.0098
pCNPP/pCNPMP	8.0	0.990	1.023	–	1.027	1.007	–
mCNPP/mCNPMP	8.6	0.985	1.027	–	1.028	1.007	–
mCLPP/mCLPMP	8.8	0.985	1.025	–	1.026	1.005	–
pCLPP/pCLPMP	9.3	0.985	1.029	–	1.025	1.006	–
PP/PMP	10.0	0.984	1.034	–	1.021	1.006	–
pMPP/pMPMP	10.2	0.983	1.034	–	1.019	1.007	–
	pKa	PP1-Phosphate			PP1-Phosphonate
Substrate	LG pKa	Onuc	Olg	Olg Exp.12	Onuc	Olg	Olg Exp.12
pNPP/pNPMP	7.0	1.007	1.017	1.0170	0.996	1.017	1.0129
pCNPP/pCNPMP	8.0	1.007	1.015	–	0.991	1.027	–
mCNPP/mCNPMP	8.6	1.009	1.015	–	0.989	1.029	–
mCLPP/mCLPMP	8.8	1.008	1.016	–	0.988	1.033	–
pCLPP/pCLPMP	9.3	1.005	1.017	–	0.986	1.033	–
PP/PMP	10.0	1.002	1.017	–	0.986	1.035	–
pMPP/pMPMP	10.2	1.001	1.017	–	0.986	1.037	–

As discussed in previous sections, for uncatalyzed reactions in solution with different nucleophiles, there are large differences in the ${\beta }_{lg}$ values. The KIE values are indeed different for phosphate (with water as nucleophile) and phosphonate (with hydroxide as nucleophile) in water, confirming that the transition state structures are rather different. In PP1, the transition states for phosphate and phosphonate esters exhibit considerable differences, although qualitatively they both feature synchronous transition states with the breaking and forming P-O bond orders being close to 0.5 (Table 1). This is consistent with the observation that pNPP and pNPMP have similar ${\text{O}}_{lg}$ KIE values (Table 5). However, the KIE values for phosphate and phosphonate substrates exhibit different trends: there is no significant change for ${\text{O}}_{lg}$ KIE for phosphates, while the value changes considerably for phosphonates. Moreover, the O_nuc KIE values for phosphates in PP1 are larger than unity, while inverse O_nuc KIE values are observed for phosphonates. These differences in O_nuc and ${\text{O}}_{lg}$ KIE values between phosphates and phophonates further confirm that the two classes of substrates do exhibit distinct features in the transition state as summarized in Table 1, despite their grossly similar synchronous nature. We encourage experimental test of our prediction.

4. Concluding Remarks: What does the Brønsted Slope Measure in the Phosphoryl Transfer Transition State?

Free energy relation is a powerful tool for analyzing transition states for solution and enzyme reactions. Nevertheless, as recognized by previous experimental and computational analysis,^2,3,22 care has to be exercised when interpreting the free energy relation measurements. For example, the extensive analysis by Warshel and co-workers of phosphoryl transfer reactions in solution and enzymes^{15–18,20–22} suggested that the Brønsted slope, isotope effect and activation entropies may not have unique mechanistic interpretations for phosphoryl transfer reactions. For example, effective charges are similar in associative and dissociative mechanisms for phosphate monoesters.²¹ To gain further insights, molecular simulations of additional enzymes and substrate types are of great value for identifying microscopic properties that are highly correlated with the experimental observables, as well as those that exhibit much broader variations.

In this investigation, we have studied the structural and energetic features of phosphate and phosphonate hydrolysis in PP1 and water using QM cluster models. While the computational methodology is not quantitative due to limited sampling and inclusion of a relatively small number of enzyme residues, comparing the results for a series of closely related substrates have provided insights into the interpretation of Brønsted plots for phosphoryl transfer reactions in different environments.

The QM cluster models captured several key trends in the experimental Brønsted plots: the ${\beta }_{lg}$ values are rather different for phosphate and phosphonate ester hydrolysis in solution but are similar in the enzyme PP1;⁵⁵ these results were interpreted as to indicate that the transition states are different for the two classes of substrates in solution but become identical in the enzyme active site. Our microscopic models have provided more nuanced interpretations. Among the structural and bonding properties analyzed herein, we observe that the natural charges on the leaving group and nucleophile oxygen atoms correlate well with the trends in ${\beta }_{lg}$ values; i.e., similar (distinct) ${\beta }_{lg}$ values correlate with similar (distinct) ${\text{O}}_{lg}$ natural charges. The degree of charge accumulation on ${\text{O}}_{lg}$, i.e., the ratio $\mathrm{\Delta }q{\left(O_{lg}\right)}_{TS}/\mathrm{\Delta }q{\left(O_{lg}\right)}_{PS}$ also generally correlates with ${\beta }_{lg}/{\beta }_{EQ,lg}$, which in turn correlates fairly well with the location of the transition state with respect to the product state; e.g., a low ${\beta }_{lg}/{\beta }_{EQ,lg}$ value indicates an early transition state. On the other hand, a quantitative mapping between ${\beta }_{lg}/{\beta }_{EQ,lg}$ and the fractional bond order for the breaking P-${\text{O}}_{lg}$ bond remains difficult; for example, for phosphate hydrolysis in water with hydroxide as the nucleophile, the computed ${\beta }_{lg}/{\beta }_{EQ,lg}$ is ~0.8, while the computed fraction bond order for P-${\text{O}}_{lg}$ in the transition state is ~0.60. We note that the ${\beta }_{lg}/{\beta }_{EQ,lg}$ and fBO values are computed based on the same set of cluster models, thus the lack of quantitative correlation between them is not a result of approximations inherent to the cluster model.

One possible explanation for the lack of quantitative mapping between ${\beta }_{lg}/{\beta }_{EQ,lg}$ and fBO of the breaking bond is that there is a considerable level of compensation between the breaking and forming P-O bonds. Indeed, even though only the leaving group is varied within each substrate series, we often observe that the P-O_nuc distance and bond order respond significantly to the change of leaving group. In fact, in several cases analyzed here (e.g., phosphate ester hydrolysis in PP1 and in water with hydroxide as the nucleophile), the P-${\text{O}}_{lg}$ bond length and bond order hardly vary with respect to the leaving group, while the P-O_nuc values change much more significantly. Due to this crosstalk between the forming and breaking P-O bonds, the ${\beta }_{lg}$ or ${\beta }_{lg}/{\beta }_{EQ,lg}$ values can’t be used to quantitatively interpret the degree of bond cleavage in the transition state. On the other hand, the Brønsted slope appears to be appropriate when discussing the qualitative nature of the transition state, such as synchronous vs. tight (see Fig. 6d).

Our analysis of transition states for uncatalyzed reactions in solution with different nucleophiles also highlights that the intrinsic difference between phosphate and phosphonate hydrolysis is limited. Thus the large difference between the measured ${\beta }_{lg}$ values reflect, to a significant degree, the different nucleophiles (water vs. hydroxide) for the two reactions under different experimental conditions. When this factor is taken into consideration, the similar ${\beta }_{lg}$ values observed for the two classes of substrates in PP1 are less surprising; in fact, the more unexpected observation from our cluster analysis is that the transition states for phosphate and phosphonate esters exhibit considerable differences in how the breaking and forming P-O bonds respond to the change of leaving group, although qualitatively they both feature synchronous transition states with the breaking and forming P-O bond orders being close to 0.5. This is further illustrated with KIE calculations, which point to different trends in both O_nuc and ${\text{O}}_{lg}$ KIEs for phosphate and phosphonate series. We eagerly await the experimental test of our predictions with KIE measurements beyond those reported so far.^52,54

Finally, we note that while the cluster models employed here are likely appropriate for capturing relative trends, they are not sufficient for quantitative comparison with experiments for absolute quantities. For example, the absolute ${\beta }_{lg}$ values are overestimated by the cluster model for both solution and PP1 reactions; for PP1, this might be related to the observation that the general acid pathway is not found favorable with the current QM cluster model. For more quantitative results, adequate sampling is required yet this remains challenging for the current systems since a reliable computation of ${\beta }_{lg}$ values requires both accuracy and precision in the computational methodology. Further developments of QM/MM methods that integrate different levels of theories,^56–58 including machine learning models,^59,60 are promising for ultimately meeting the challenge.