Ranking non-pharmaceutical interventions against Covid-19 global pandemic using global sensitivity analysis—Effect on number of deaths

Abstract

In this study, we use Global Sensitivity Analysis (GSA) to rank four non-pharmaceutical interventions (NPIs) in a deterministic compartmental model that might control Covid-19 related deaths in the United States. The NPIs are social distancing, isolation of infected individuals, identifying asymptomatically infected individuals through testing, and the use of face masks. The model uses a fear-based behavioral model that leads unmasked susceptible individuals to wear masks. The model parameters are estimated from the reported deaths for the United States of America from March 1, 2020 to November 26, 2020. Two GSA tools, the Sobol’ sesntivity indices and Partial Rank Correlation Coefficient are used to obtain the rankings of the input parameters at different stages of the disease propagation. We found that social distancing and outward mask efficiency alone decreases the output uncertainty by 25–45%. Sobol’ second order indices show that the combined effect of social distancing with increased mask usage and identifying and isolating asymptomatically infected individuals decreases uncertainty an additional 10%.

1. Introduction

The world is now facing a pandemic of a novel coronavirus (SARS-Cov-2), which started in Wuhan city of China in December 2019 [1]. As of November 27, 2020, the Covid-19 pandemic had spread across 218 countries and territories worldwide [2], had 60.5 million reported cases and a death toll of 1,426,101 [3]. So far, 12.8 million cases have been reported in the United States with 263,454 Covid-19 related deaths. Furthermore, it has caused significant disruptions in socio-economic foundations [4].

The novel coronavirus spreads through interactions with an infected individual via the respiratory system. Primarily, when an infected individual sneezes, coughs, or talks, the virus can be expelled into the air through droplets or aerosols [5], [6], [7] which can be inhaled by others. It is found that airborne transmission can occur from these aerosols for up to three hours [5]. Furthermore, the virus can survive on surfaces for 2–3 days and can infect when mouths, eyes, or noses are touched with contaminated hands [8], [9].

Due to the socio-economical impact of the Covid-19, it is crucial to create policies that effectively control and mitigate disease transmission. These approaches can be categorized into two, based on their mode of transmission 1) direct infection through droplets or aerosols, and 2) contact with facial orifices from the fomite inoculum deposited on surfaces. Control measures to limit direct infection through droplets include physical distancing, isolation of the exposed through contact tracing, lockdown, preventing large gatherings, shielding high-risk populations, quarantine, use of face masks, and as a pharmaceutical intervention, vaccination. Frequent hand washing and surface disinfecting can be identified as control measures against the second transmission mechanism. It should be noted that all these non-pharmaceutical interventions (NPIs) create an additional strain on the general public. Thus, it is crucial to know the effectiveness of these interventions to make effective decisions with minimum pressure on the population.

Mathematical epidemiological models have been extensively used to predict and understand the dynamics of the Covid-19 transmission [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]. Among various epidemiological models, Kermack-Mckendrick [21], [22] type models are the most popular. In these models, the total population is divided into non-overlapping compartments according to their disease status. The Simplest model, the SIR model, divides the population into three compartments: Susceptible (S), Infected or Infectious (I), and Recovered (R). Disease transmission occurs when an infected individual interacts with the susceptible population.

More advanced versions of the SIR model captures different scenarios in epidemiology. As an example, when there is an incubation period (time required for a susceptible individual to get infected after been exposed to an infected person), an exposed compartment (E) can be added between susceptible and infected compartments (i.e., SEIR model). Similarly, different configurations (e.g., SEIRD (includes death), SEIARD (includes deaths and asymptomatically infected) can be designed to model different scenarios and interventions.

Among the many Covid-19 prediction models [10], [11], [12], [13], [20], [23], [24], [25], [26], some [12], [14], [15], [17], [18], [27], [28], [29] have focused on controlling and mitigating the spreading of the coronavirus. Non-pharmaceutical interventions include the lockdown [12], [14], [15], mask usage [16], [17], [18], physical distancing [14], contact tracing [18], quarantine [10], [14], [15], school closures [15], personal hygiene [16] and isolation of high-risk individuals [15].

The effectiveness of the interventions themselves has been studied by implementing different levels of control [12], [17], [19], and through optimum control theory [19]. Davies et al. [15] used a stochastic age-structured compartmental model to study the importance of 1) school closure, 2) physical distancing, 3) self-isolation of symptomatically infected individuals, and 4) shielding high-risk individuals. Even though all these interventions are found to be effective in reducing the ICU demand, none of them alone could maintain the ICU demand below the capacity. Only the combinations of these interventions effectively kept the ICU demand below capacity.

In this study, we propose global sensitivity analysis (GSA) to rank the effectiveness of NPIs against Covid-19. Sensitivity analysis is a study of how output uncertainty is apportioned to the input parameter uncertainties [30], [31]. It is distinct from the uncertainty analysis that focuses on the model output uncertainties. Sensitivity analysis can be conducted for factor prioritization, parameter fixing, and variance cutting [31], [32], [33], [34]. In factor prioritization, input parameters are ranked according to their influence on the output uncertainty. Factor prioritization allows one to identify the most influential parameter that needs special attention to achieve the highest reduction in output uncertainty. Parameter fixing, on the other hand, recognizes the least significant parameters to the output uncertainty which allows one to simplify the model by fixing those parameters anywhere in their possible value range since their input uncertainty does not contribute significantly to the output variance. In variance cutting, input parameter variances of the influential parameters are identified and are reduced to obtain a threshold output uncertainty [34]. The main application of the variance cutting setting is to assess the risk [33], [34].

Sensitivity analysis methods can be categorized as local and global. In local sensitivity analysis, the input parameters are perturbed one at a time, fixing the others at their nominal values. On the other hand, the global sensitivity methods vary the input parameters simultaneously in their respective parameter space and can capture parameter interactions. Global sensitivity methods can be used for both linear and nonlinear models. Most sensitivity analysis literature uses local sensitivity because it is simple and computationally efficient [30], [33], [34], [35], [36], [37]. According to [30], most of the outcomes and suggestions of such studies are erroneous and misleading.

In this study, we use GSA tools (Partial Rank Correlation Coefficient (PRCC) [38] and Sobol’ sensitivity indices [33], [39], [40]) to rank the input parameters to understand which NPI is the most dominant in controlling the dynamics of Covid-19 progression in the United States. We use the cumulative number of deaths as the quantity of interest (QoI). We develop a deterministic compartmental model and the model parameters are estimated by comparing the model results to the number of reported fatalities in the United States. The time evolution of the sensitivity indices (both Sobol’ and PRCC) is used to understand how model parameters affect the number of deaths at different stages of the disease propagation.

2. Mathematical model

The proposed epidemiological model is a deterministic, compartmental model that divides the total population into 12 compartments (defined in Tabel 1 ) according to their disease status (Fig. 1 ). The model assumes that the birth rate and the non-covid related death rates are equal. Therefore, the constant total population, $N$ can be written as

$$N=S_U+S_M+E_U+E_M+I_U+I_M+A_U+A_M+I_H+I_{ICU}+R+D$$ (1)

Table 1.

Description of the model compartments.

Compartment	Description
$S_U$	Unmasked susceptible
$S_M$	Masked susceptible
$E_U$	Unmasked exposed
$E_M$	Masked exposed
$I_U$	Unmasked symptomatically infected
$I_M$	Masked symptomatically infected
$A_U$	Unmasked asymptomatically infected
$A_M$	Masked asymptomatically infected
$I_H$	Hospitalized
$I_{ICU}$	Admitted to Intensive Care Units
$R$	Recovered
$D$	Death

Fig. 1.

Schematic of the Compartmental Model.

Furthermore, we assume the model parameters are independent of the population demography.

The model is an extension of the basic SEIR model that uses four compartments, Susceptible, Exposed, Infected/Infectious, and Recovered. As shown in Fig. 1, the susceptible population is divided into two compartments as $S_U$ and $S_M$ (subscripts $U$ and $M$ represent unmasked and masked populations, respectively). Similarly, exposed and infected populations are also divided into masked and unmasked categories. The infected population can be further categorized as symptomatically infected ($I_U,I_M$) and asymptomatically infected ($A_U,A_M$). A portion of the infected individuals who show severe symptoms are hospitalized ($I_H$) for medical treatments. The critical hospitalized individuals are then moved to intensive care units ($I_{ICU}$). The infected individuals ($I_U,I_M,A_U,A_M,I_H,I_{ICU}$) can then be transferred into either the recovered (R) or the death (D) compartments. The yellow and red color connections in Fig. 1 represent the recovery and mortality paths, respectively.

The transition from a susceptible to exposed compartment depends on the transmission rate, $\beta \left(t\right)$, the product of transmission probability and the contact rate. In standard SIR or SEIR compartment models, the transition rate from the susceptible to exposed compartment has the form $\beta SI/N$, where $\mathrm{S}/\mathrm{N}$ represents the portion of susceptible individuals. Therefore, $\beta S/N$ is the rate of disease propagation by one infected individual. In the current compartmental model, five infected compartments ($I_U,I_M,A_U,A_M$ and $I_H$) contribute to disease transmission. We assume that the individuals in $I_{ICU}$ and $D$ compartments are entirely isolated from the susceptible individuals and do not contribute to the disease transmission. Hospitalized and asymptomatically infected individuals have relatively lower infectiousness compared to the symptomatically infected [17], [18]. Therefore, the relative infectiousness terms, ${\eta }_A$ and ${\eta }_H$ are used to obtain the contribution of the asymptomatically infected ($A_{U/M}$) and the hospitalized ($I_H$) individuals to the disease transmission, respectively. To differentiate between unmasked and masked infectiousness, our model uses inward (${ϵ}_i$) and outward (${ϵ}_o$) mask efficiencies, which measure the mask’s efficiency to prevent the virus from transferring in or out of the masks [17], [18]. Then the transition rate from $S_U\to E_U$ can be written as

$$S_U\to E_U=\frac{\beta \left(t\right)(I_U+{\eta }_A{A}_U+(1-{ϵ}_o)(I_M+{\eta }_A{A}_M+{\eta }_H{I}_H))}{N-(D+I_{ICU})}{S}_U$$ (2)

Due to the outward mask efficiency, the effective viral shedding of the masked individuals are decreased by a factor of ($1-{ϵ}_o$). The transition rate for $S_M\to E_M$ has an analogous form, but due to the inward efficiency of the mask, only a factor of $1-{ϵ}_i$ contributes to disease transmission. Therefore, the transition rate from $S_M\to E_M$ can be written as

$$\begin{array}{cc}\hfill S_M\to E_M=& \frac{(1-{ϵ}_i)\beta \left(t\right)S_U}{N-(D+I_{ICU})}(I_U+{\eta }_A{A}_U)\hfill \\ & +\frac{(1-{ϵ}_i)\beta \left(t\right)S_U}{N-(D+I_{ICU})}(1-{ϵ}_o)(I_M+{\eta }_A{A}_M+{\eta }_H{I}_H).\hfill \end{array}$$ (3)

The challenging portion of the model is to include behavioral changes [5], [41] to understand how many individuals wear masks or follow social distancing protocols. Most private and public establishments in the United States have a mask policy to reduce disease transmission [42]. However, it is not uncommon to see individuals who do not follow the Center for Disease Control guidelines (high-quality face mask with two or more layers that cover the mouth and nose without any large openings). We assume that the people who fear getting infected would change their behavior with or without legal requirements and so a fear-based mechanism is implemented to transfer individuals from unmasked to masked and masked to unmasked susceptible compartments. The rates ${\kappa }_1$ and ${\kappa }_2$ represent the forward and reverse transition. When the death toll increases, the fear grows with a time delay resulting in a shift in $S_U\to S_M$. The reverse process occurs when there are more recovered and unmasked susceptible populations present in public. The exposed compartment population is directed to either asymptomatically infected or symptomatically infected categories. Here, we assume that the transition rate ($\sigma$) and the fraction of the infected population being asymptomatic ($f$) is independent of whether a person wears a mask or not. Individuals in the $I_U$ compartment might change their behavior when they get tested positive for the coronavirus. To facilitate that, we create a link between $I_U$ and $I_M$. The model considers four mortality rates and recovery rates corresponding to the symptomatically infected, asymptomatically infected, hospitalized and admitted to ICU population groups. A detailed description of all the model parameters are presented in Table 2 .

Table 2.

Description of model parameters.

Parameter	Description
$N$	Total population
$\beta \left(t\right)$	Transmission rate - contact rate $\times$ transmission probability
${\eta }_A$	Infectiousness of asymptomatically infected individuals
	relative to symptomatically infected individuals
${\eta }_H$	Infectiousness of hospitalized individuals relative to
	symptomatically infected individuals
${ϵ}_i$	Inward mask efficiency
${ϵ}_o$	Outward mask efficiency
${\beta }_f$	Rate of fear-induced behavior change
${\lambda }_3$	Exponential delay factor for fear-induced behavior change
${\mu }_f$	The rate at which aware masked susceptible individuals
	move to unmasked susceptible individuals
$\sigma$	The rate at which exposed individuals move to symptomatic
	or asymptomatic infected compartments
	(reciprocal of the incubation period)
$f$	The probability of an infected individual being asymptomatic
$\theta \left(t\right)$	The rate at which individuals in the $I_U$ compartment
	move to the $I_M$ compartment
$\varphi$	The rate at which symptomatically infected individuals move
	to the hospitalized compartment
$\nu$	The rate at which critical hospitalized individuals
	are admitted to the intensive care unit
${\gamma }_I$	The recovery rate of symptomatically infected individuals
${\gamma }_A$	The recovery rate of asymptomatically infected individuals
${\gamma }_H$	The recovery rate of hospitalized individuals
${\gamma }_{ICU}$	The recovery rate of individuals in the ICU compartment
${\delta }_I$	The mortality rate of symptomatically infected individuals
${\delta }_A$	The mortality rate of asymptomatically infected individuals
${\delta }_H$	The mortality rate of hospitalized individuals
${\delta }_{ICU}$	The mortality rate of individuals in the ICU compartment

This model is represented by 12 nonlinear ordinary differential equations Eqs. (4)–(15) and the unknown parameters and rates need to be estimated by matching with the actual data. It should be noted that we assume time-dependent transmission coefficient (i.e., $\beta \left(t\right)$) and transition rate from $I_U\to I_M$ (i.e., $\theta \left(t\right)$) in Eqs. (4)–(15) to obtain the multiple waves we observe in Covid-19 deaths in the United States [2], [3].

$$\begin{array}{cc}\hfill \frac{d{S}_U}{dt}=& -\stackrel{{\zeta }_1}{\overbrace{\frac{\beta \left(t\right)(I_U+{\eta }_A{A}_U+(1-{ϵ}_o)(I_M+{\eta }_A{A}_M+{\eta }_H{I}_H))}{N-(D+I_{ICU})}{S}_U}}\hfill \\ & -\stackrel{{\kappa }_1}{\overbrace{\frac{{\beta }_f(1-e^{-{\lambda }_{3}Dt})D}{N-(D+I_{ICU})}{S}_U}}+\stackrel{{\kappa }_2}{\overbrace{\frac{{\mu }_f(S_U+R)}{N-(D+I_{ICU})}{S}_M}}\hfill \end{array}$$ (4)

$$\begin{array}{cc}\hfill \frac{d{S}_M}{dt}=-& \stackrel{{\zeta }_2}{\overbrace{(1-{ϵ}_i)\frac{\beta \left(t\right)(I_U+{\eta }_A{A}_U+(1-{ϵ}_o)(I_M+{\eta }_A{A}_M+{\eta }_H{I}_H))}{N-(D+I_{ICU})}{S}_M}}\hfill \\ & +\stackrel{{\kappa }_1}{\overbrace{\frac{{\beta }_f(1-e^{-{\lambda }_{3}Dt})D}{N-(D+I_{ICU})}{S}_U}}-\stackrel{{\kappa }_2}{\overbrace{\frac{{\mu }_f(S_U+R)}{N-(D+I_{ICU})}{S}_M}}\hfill \end{array}$$ (5)

$$\frac{d{E}_U}{dt}={\zeta }_1-\sigma E_U$$ (6)

$$\frac{d{E}_M}{dt}={\zeta }_2-\sigma E_M$$ (7)

$$\frac{d{I}_U}{dt}=(1-f)\sigma E_U-\theta \left(t\right)I_U-\varphi I_U-{\gamma }_I{I}_U-{\delta }_I{I}_U$$ (8)

$$\frac{d{I}_M}{dt}=(1-f)\sigma E_M+\theta \left(t\right)I_U-\varphi I_M-{\gamma }_I{I}_M-{\delta }_I{I}_M$$ (9)

$$\frac{d{A}_U}{dt}=f\sigma E_U-{\gamma }_A{A}_U-{\delta }_A{A}_U$$ (10)

$$\frac{d{A}_M}{dt}=f\sigma E_M-{\gamma }_A{A}_M-{\delta }_A{A}_M$$ (11)

$$\frac{d{I}_H}{dt}=\varphi I_U+\varphi I_M-{\gamma }_H{I}_H-\nu I_H-{\delta }_H{I}_H$$ (12)

$$\frac{d{I}_{ICU}}{dt}=\nu I_H-{\gamma }_{ICU}{I}_{ICU}-{\delta }_{ICU}{I}_{ICU}$$ (13)

$$\frac{dR}{dt}={\gamma }_A(A_U+A_M)+{\gamma }_I(I_U+I_M)+{\gamma }_H{I}_H+{\gamma }_{ICU}{I}_{ICU}$$ (14)

$$\frac{dD}{dt}={\delta }_A(A_U+A_M)+{\delta }_I(I_U+I_M)+{\delta }_H{I}_H+{\delta }_{ICU}{I}_{ICU}$$ (15)

2.1. Basic reproduction number (${\mathcal{R}}_0$)

The basic reproduction number denoted by ${\mathcal{R}}_0$ is defined as the number of secondary infections resulting from a single infected individual in a completely susceptible community during its infectious period. We use the next generation matrix based approach [43], [44] to obtain a closed-form expression for the reproduction number (see Eq. (A.6)). Here we consider a special case, where we neglect the time dependence of parameters $\beta \left(t\right)$ and $\theta \left(t\right)$ and assume a constant value for the reproduction number calculations (see Table 2 for parameter definitions). For more information on the method and steps involved in the calculation process, refer to Appendix A.

3. Parameter estimation

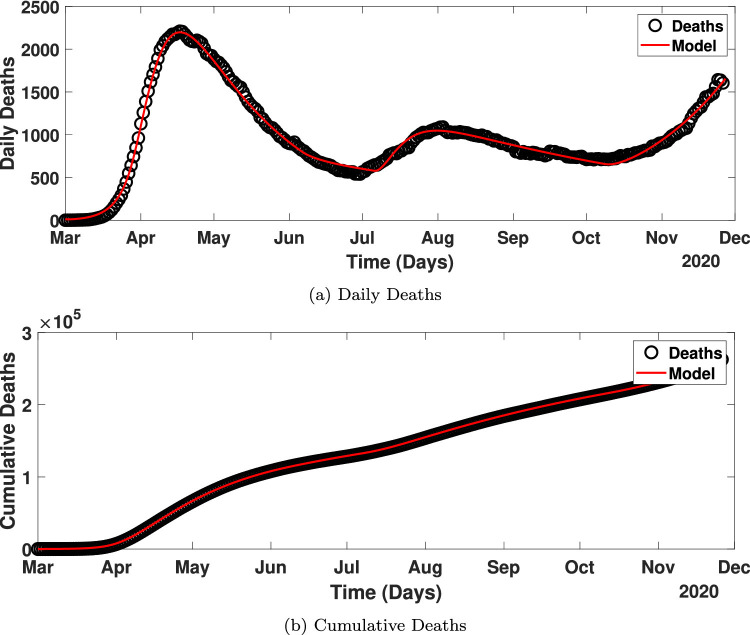
The model parameters in Table 2 are estimated to match the time series fatality data reported in the United States by the Center for Systems Science and Engineering at Johns Hopkins University [45] from March 1, 2020, to November 26, 2020. Fig. 2 shows the number of mortalities related to Covid-19 in the US. The daily reported deaths show fluctuations in the number of deaths, which could be partly due to the different reporting standards across states. To remedy that, a 7-day moving average data are used for parameter estimation (Fig. 2, black circles).

Fig. 2.

The number of Covid-19 deaths reported in the US from March 1, 2020 - November 26, 2020.

The other challenge is the presence of multiple waves of the disease. This could be partly due to the state-wise differences in actions against Covid-19 in terms of the level of enforcement and the timeline [42]. A time-dependent transmission rate had to be used to capture these multiple waves of the disease propagation as shown in Fig. 2. The time-dependent transmission rate $\beta \left(t\right)$ can be written as

$$\begin{array}{c}\hfill \beta \left(t\right)=\{\begin{array}{cc}{\beta }_1+{\beta }_2\hfill & t\le {\tau }_1\hfill \\ {\beta }_1+{\beta }_2{e}^{-{\lambda }_1(t-{\tau }_1)}\hfill & {\tau }_1<t\le {\tau }_2\hfill \\ {\beta }_1+{\beta }_2{e}^{-{\lambda }_1({\tau }_2-{\tau }_1)}+{\beta }_3(1-e^{-{\lambda }_2(t-{\tau }_2)})\hfill & {\tau }_2<t\le {\tau }_3\hfill \\ {\beta }_1+{\beta }_2{e}^{-{\lambda }_1({\tau }_2-{\tau }_1)}+{\beta }_3(1-e^{-{\lambda }_2({\tau }_3-{\tau }_2)})\hfill \\ +{\beta }_4{e}^{-{\lambda }_1(t-{\tau }_3)}\hfill & {\tau }_3<t\le {\tau }_4\hfill \\ {\beta }_5^{\prime }\left(t\right)\hfill & {\tau }_4<t\hfill \end{array}\end{array}$$ (16)

where

$$\begin{array}{cc}\hfill {\beta }_5^{\prime }=& {\beta }_1+{\beta }_2{e}^{-{\lambda }_1({\tau }_2-{\tau }_1)}+{\beta }_3(1-e^{-{\lambda }_2({\tau }_3-{\tau }_2)})\hfill \\ & +{\beta }_4{e}^{-{\lambda }_1(t-{\tau }_3)}+{\beta }_5(1-e^{-{\lambda }_2(t-{\tau }_4)}),\hfill \end{array}$$ (17)

and ${\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4,{\beta }_5,{\lambda }_1,{\lambda }_2,{\tau }_1,{\tau }_2,{\tau }_3$ and ${\tau }_4$ are constants that need to be inferred. Furthermore, the time-dependent $\theta \left(t\right)$ value is defined as

$$\theta \left(t\right)=\{\begin{array}{cc}{\theta }_1\hfill & t<{\tau }_2\hfill \\ {\theta }_2\hfill & {\tau }_2\le t\hfill \end{array}$$ (18)

Relative infectiousness is taken as 0.5 for both asymptomatically infected and hospitalized individuals [17], [18]. It is reported that around 25% of the infected population are asymptomatic [46], hence the value of $f$ is fixed at 0.25. The value of inward and outward mask efficiencies is assumed as 0.5. More information on mask efficiencies can be obtained in [17], [18], [29].

Parameter estimation was done using lsqnonlin [58], a nonlinear least-squares algorithm implemented in MATLAB. Table 3 provides the model parameter estimates and initial conditions used in the current study. It should be noted that the inferred values of parameters ${\beta }_{1\to 5},{\lambda }_{1\to 2},{\theta }_{1\to 2},$ and ${\tau }_{1\to 4}$ are also provided in Table 3. We plot the transient behavior of the transmission coefficient in Appendix B (Fig. B1).

Table 3.

Parameter estimates.

Parameter	Value	Source	Parameter	Value	Source
Model Parameters
${\eta }_A$	0.5	[18], [47]	${\eta }_H$	0.5	[18], [47]
${ϵ}_i$	0.5	[17], [18]	${ϵ}_o$	0.5	[17], [18]
${\beta }_f$	4.8	[48]	${\mu }_f$	0.54	[49], [50]
$f$	0.25	[17], [18], [51]	$\nu$	0.083	[18]
$\sigma$	1/5.1	[17], [18], [52], [53]	$\varphi$	1/5	[18]
${\gamma }_I$	1/10	[18], [54], [55]	${\gamma }_A$	0.13978	[18], [54], [55]
${\gamma }_H$	1/8	[18], [55]	${\gamma }_{ICU}$	1/10	[55]
${\delta }_I$	0.015	[18]	${\delta }_A$	0.0075	[18]
${\delta }_H$	0.015	[18]	${\delta }_{ICU}$	0.0225	[18]
${\beta }_1$	0.225	fitted	${\beta }_2$	0.659	fitted
${\beta }_3$	0.097	fitted	${\beta }_4$	0.5671	fitted
${\beta }_5$	0.10658	fitted	${\lambda }_1$	0.179	fitted
${\lambda }_2$	13.53	fitted	${\lambda }_3$	0.0388	fitted
${\tau }_1$	27.5	fitted	${\tau }_2$	97.98	fitted
${\tau }_3$	127.6	fitted	${\tau }_4$	222.1	fitted
${\theta }_1$	0.1098	fitted	${\theta }_2$	0.847	fitted
Initial Conditions
$N$	$328.2\times {10}^6$	[56]	$S_M(t=0)$	3,276,578	fitted
$E_U(t=0)$	0	assumed	$E_M(t=0)$	0	assumed
$I_U(t=0)$	169	fitted	$I_M(t=0)$	0	assumed
$A_U(t=0)$	440	fitted	$A_M(t=0)$	877	fitted
$I_H(t=0)$	0	[57]	$I_{ICU}(t=0)$	0	[57]
$R(t=0)$	2014	fitted	$D(t=0)$	1	[45]

Fig. B1.

Time variation of transmission coefficient $\beta \left(t\right)$ from March 1, 2020 to November 26, 2020. See Eqs. (16) and (17) for the definition of dependent transmission coefficient and Table 3 for inferred model parameters..

Fig. 3 shows how well the model predictions and inferred input parameter values match with the deaths reported in the US.

Fig. 3.

Comparison of the deaths reported in the US and the model prediction Eqs. (4) - (15) with the inferred parameters in Table 3. (a - daily deaths, b - cumulative deaths).

4. Global sensitivity analysis

As mentioned in the Section 1, we use two GSA methods to find the parameter rankings. This section introduces the Partial Rank Correlation Coefficient (PRCC) and Sobol’ sensitivity indices.

4.1. Partial rank correlation coefficient

PRCC or the Partial Rank Correlation Coefficient is a statistical measure also known as Spearman’s correlation coefficient [38], [59]. It quantifies the nonlinear correlation between input parameters and model output. Unlike the Pearson correlation coefficient [35], [38], PRCC allows users to identify nonlinear correlations to the model output [38]. However, the perturbations of each individual input parameter within their parameter space should result in a monotonically varying behavior in the output. This condition must be satisfied to use PRCC sensitivity indices [38], [59].

The calculation of the PRCC indices is as follows. We consider a model with $p$ number of model parameters. Then, the model output, $y$ can be a written as a function of all the model parameters $x_i$, where $i=1,2,\cdots ,p$ (i.e., $y=f(x_1,x_2,\cdots ,x_p))$. As mentioned earlier, PRCC indices require the model output to vary monotonically when each individual input parameters are perturbed. This can be tested by sampling each parameter within its parameter space, while keeping rest of the model parameters at their nominal/inferred values [38]. The model evaluations corresponding to these perturbations should result in a monotonic behavior.

If the monotonicity condition is satisfied, one can proceed to the PRCC calculations. First, samples for each model parameter should be obtained using their joint probability distribution. It would result in a sample matrix of size, $N\times p$, where $N$ is the sample size. It is recommended to use Latin Hypercube [60] type quasi-random sampling techniques to achieve fast convergence [38]. Then, the a vector of output values (size of $1\times N$) needs to be generated by conducting function evaluations corresponding to each iteration. Then, the PRCC indices (${\rho }_{x_i,y}$) for the parameter $x_i$ can be calculated as [38], [59]

$${\rho }_{x_i,y}=\frac{Cov(x{R}_i,yR)}{\sqrt{Var\left(x{R}_i\right)\times Var\left(yR\right)}}=\frac{{\sum }_{j=1}^N(x{R}_{i,j}-\overline{x{R}_i})(y{R}_j-\overline{yR})}{\sqrt{{\sum }_{j=1}^N{(x{R}_{i,j}-\overline{x{R}_i})}^2}\sqrt{{\sum }_{j=1}^N{(y{R}_j-\overline{yR})}^2}}$$ (19)

where $xR$ and $yR$ represent the rank transformed input matrix and output vector. $Cov$ and $Var$ represent the covariance and variance of the arguments, respectively. The overbars in the quantities represent the sample means. The PRCC indices ranges from -1 to 1. The positive values indicate a positive correlation and negative values indicate negative correlations. The magnitude indicates the importance of each parameter. For more information on the implementation and applications, see [37], [38], [59], [61], [62], [63].

4.2. Sobol’ sensitivity indices

The Sobol’ sensitivity approach is a variance-based sensitivity analysis method. However, the computations are more complex and computationally expensive than the PRCC calculations. Sobol’ sensitivity indices are not limited to linear models or monotonic input-output relationships. The concept behind the Sobol’ approach is to decompose the model output variance apportioned to the input parameter uncertainties [32], [33], [39], [64]. It can be achieved through analysis of variance (ANOVA).

Sobol’ [39] proposed the following total output variance decomposition when the input parameters are independent

$$Var\left(y\right)=\sum _i{V}_i+\sum _i\sum _{j>i}{V}_{ij}+\dots +V_{123\dots p}$$ (20)

where

$$\begin{array}{cc}\hfill V_i& =Va{r}_{x_i}\left(E_{x_i}\left(y\right|x_i)\right),\hfill \\ \hfill V_{ij}& =Va{r}_{x_i,x_j}\left(E_{i,j}\left(y\right|x_i,x_j)\right)-V_i-V_j,\hfill \\ \hfill V_{ijk}& =Va{r}_{x_i,x_j,x_k}\left(E_{x_{ijk}}\left(y\right|x_i,x_j,x_k)\right)-V_{ij}-V_{ik}-V_{jk}-V_i-V_j-V_k,\hfill \\ & etc.\hfill \end{array}$$

The quantity $E\left(y\right|x_i)$ represents the conditional expected value of $y$ given $x_i$, and $Va{r}_{x_i}\left(E_{x_i}\left(y\right|x_i)\right)$ is the first order effect of the parameter $x_i$ on the output uncertainty (i.e., the output variance when the parameter $x_i$ is fixed). Then the Sobol’ first order sensitivity index (Eq. (21)) can be obtained by normalizing the first order effect by the total variance, so that $0\le S_i\le 1$.

$$S_i=\frac{Va{r}_{x_i}\left(E_{x_i}\left(y\right|x_i)\right)}{Var\left(y\right)}$$ (21)

By dividing Eq. (20) by the total output variance, we can obtain

$$\sum _i{S}_i+\sum _i\sum _{j>i}{S}_{ij}+\dots +S_{123\dots p}=1$$ (22)

The term $S_{ij}$, indicates the second-order Sobol’ indices or the effect of second-order parameter interactions on the output uncertainty (i.e., the output variance, when both $x_i$ and $x_j$ are fixed). Similarly, higher order indices (i.e., $S_{ijk},S_{ijkl},\cdots ,S_{123\cdots p}$) provide higher order parameter interactions. The summation of first order and all the higher order indices for parameter $x_i$ calculates the total order index, $S_i^T$. It provides the maximum possible variance reduction that can be obtained by fixing any combination of parameters that includes parameter $x_i$.

The total order Sobol’ index ($S_i^T$) can be calculated as [65], [66]

$$S_i^T=\frac{E_{x_i}\left(Va{r}_{x_i}\left(y\right|x_i)\right)}{Var\left(y\right)}=1-\frac{Va{r}_{x_i}\left(E_{x_i}\left(y\right|x_i)\right)}{Var\left(y\right)}.$$ (23)

Since $S_i^T$ is the sum of the first order and all the higher order indices for parameter $x_i$,

$$\begin{array}{c}\hfill \sum _i{S}_i\le 1,\\ \hfill S_i\le S_i^T.\end{array}$$ (24)

For an additive model, where the parameter interactions/higher order effects are negligible, ${\sum }_i{S}_i=1$ and $S_i=S_i^T$. References [33], [35], [40], [64], [66], [67] provide detailed information on different numerical implementations of these sensitivity indices. We have implemented an in-house code on MATLAB and the algorithm is described in [35], [36]. The current approach utilizes $2(p+1)N$ model calculations to obtain first order, second order and total order Sobol’ indices. The sample size, N is estimated using a trial and error method to ensure convergence of the sensitivity indices, $S_i,S_{ij}$ and $S_i^T$.

4.3. Problem formulation

The proposed mathematical model Eqs. (4) - (15) has 32 model parameters. Furthermore, parameters such as transmission rate, $\beta \left(t\right)$, and the rate at which unmasked symptomatically infected individuals change their behavior to wear masks, $\theta \left(t\right)$ are time-dependent. Handling time-varying parameters in sensitivity analysis is complicated. As an example, let’s consider the transmission rate, $\beta \left(t\right)$. As shown in Eq. (16), it is a function of ${\beta }_{1\to 5},{\tau }_{1\to 4}$ and ${\lambda }_{1\to 2}$. If all these 11 parameters are included for the sensitivity analysis, the perturbations of each parameter would vary both magnitude and shape of $\beta \left(t\right)$. Thus, it could provide nonphysical model behavior. As a solution, two dummy variables ($C_{\beta },C_{\theta }$) are introduced and utilized for the sensitivity analysis as scaling factors for $\beta \left(t\right)$ and $\theta \left(t\right)$, respectively. The nominal value of $C_{\theta }$ and $C_{\beta }$ are fixed at one that keep the transmission rate remains unchanged. It is assumed that the values of ${\beta }_{1\to 5},{\tau }_{1\to 4},{\lambda }_{1\to 2}$ and ${\theta }_{1\to 2}$ are fixed at their inferred values and only the scaling factors $C_{\beta }$ and $C_{\theta }$ are perturbed in the sensitivity analysis. This allows us to reduce the dimensionality of the sensitivity analysis by fixing ${\beta }_{1-5}$, ${\tau }_{1-4},{\lambda }_{1-2}$ and ${\theta }_{1-2}$ from 32 to 21.

In the sensitivity analysis, the scaling parameters, $C_{\theta }$ and $C_{\beta }$ are assumed to vary according to a uniform distribution with and upper and lower bounds of 10% (i.e., $U(0.9,1.1)$). The other parameters used for the sensitivity analysis are ${ϵ}_i,{ϵ}_o,{\beta }_f,{\mu }_f,f,{\eta }_A,{\eta }_H,\nu ,\sigma ,\varphi ,{\gamma }_I,{\gamma }_A,{\gamma }_H,{\gamma }_{ICU},{\delta }_I,{\delta }_A,{\delta }_H$, and ${\delta }_{ICU}$. They are also sampled assuming a uniform distribution; however, they are perturbed ±25% of their nominal values (i.e., $U(0.75X_{Nom},1.25X_{Nom})$). All the initial conditions are kept at their nominal values.

5. Results and discussion

Here we examine the transient behavior of PRCC and Sobol’ sensitivity indices to understand the influence of model parameters on the number of cumulative deaths (i.e., the Quantity of Interest, QoI) at different stages of the disease progression in the US from March 1, 2020, to April 14, 2021.

5.1. Sensitivity analysis - Partial rank correlation coefficient

Here, we conduct sensitivity analysis using the PRCC approach described in the Section 4.1. A sample size of 100,000 is used for the PRCC calculations to ensure the convergence of the sensitivity indices. The validity of the PRCC approach in the context of this research problem is examined by obtaining how the model predictions (i.e., number of cumulative deaths) vary when each input parameter is perturbed within their parameter space, one at a time (Fig. 4 ). Fig. 4 shows four output variations corresponding to four time instances, June 8, 2020 (cyan), September 16, 2020 (blue), December 25, 2020 (red), and April 14, 2021 (black). It should be noted that the y-axis of Fig. 4 is the number of cumulative deaths. It can be seen that all four time instances satisfy the monotonicity requirement of all the model parameters. At early stages (June 8, 2020, and September 16, 2020), all the input parameters have a linear correlation with the number of deaths; however, with time, the nonlinear correlation can be observed. This also shows the importance of conducting global sensitivity analysis instead of local sensitivity as local sensitivity analysis cannot accurately capture nonlinear correlations.

Fig. 4.

Monotonicity requirement for each of the model parameters varied - Quantity of interest - number of cumulative deaths (cyan - June 8, 2020, blue - September 16, 2020, red - December 25, 2020 and black - April 14, 2020). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

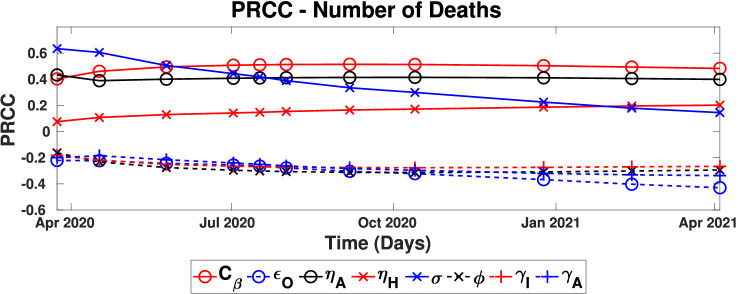
Fig. 5 shows the time evolution of the PRCC coefficients of the influential parameters (i.e., $\max \left|\mathit{PRCC}\right(t\left)\right|\ge 0.15$). Among the influential parameters, $\sigma ,{\eta }_A,{\eta }_H$ and $C_{\beta }$ show a positive correlation on the number of deaths, while ${ϵ}_o,\varphi ,{\gamma }_I$, and ${\gamma }_H$ show a negative correlation.

Fig. 5.

Time evolution of the Partial Rank Correlation Coefficient indices. Only the influential parameters are shown, i.e., $max\left|PRCC\right(t\left)\right|\ge 0.15$. (solid lines - positive correlations, dashed lines - negative correlations).

The positive correlation of $\sigma$ with the number of deaths means that increasing the value of $\sigma$ (or shortening the incubation period) increases the number of deaths. At the early stages, $\sigma$ is the most influential parameter. However, with time its importance decreases. The incubation period governs the rate at which individuals move from the exposed compartment to the infected compartments. In the beginning, the number of infected individuals is low; therefore the rate of transitioning from infected to death or other subsequent compartments is primarily governed by the rate of individuals entering the infected compartment. However, with time more and more individuals accumulate in the infected compartments, and the importance of $\sigma$ decreases.

The measure of social distancing, $C_{\beta }$, has a strong positive influence throughout the disease propagation. When $C_{\beta }$ increases, the rate at which susceptible individuals transfer to the exposed compartment increases that lead to increased mortality. Thus implementing social distancing measures leads $C_{\beta }$ to decrease, results in a decrement in the number of deaths. The other positively correlated parameters are ${\eta }_A$ and ${\eta }_H$, the relative infectiousness of asymptomatically infected and hospitalized individuals, respectively implying that identifying asymptomatically infected individuals and properly isolating them from the society is another effective intervention. The PRCC value of ${\eta }_A$ consistently stays at the same value, but the PRCC value of ${\eta }_H$ increases with time, which could be due to the increased hospitalizations with time.

Among the negatively correlated parameters, outward mask efficiency, ${ϵ}_o$ is the most influential. Increasing the outward mask efficiency would result in a reduction in the transmission rate as high-efficiency masks could prevent most of the aerosol and droplets expelling from an infected individual. The recovery rates of asymptomatically and symptomatically infected individuals also negatively affect the fatalities. Faster recovery rates affect the number of system in two different ways, 1). higher recovery rates remove infected individuals from symptomatically and asymptomatically infected compartments at a higher rate, reducing the amount of infected individuals in the society that contribute to the disease prevalence, 2). number of deaths are proportionate to the number of infections (e.g. death rate of $I_U$ compartment is ${\delta }_I{I}_U$ and since higher recovery rates reduces the number of individuals in $I_U$ compartment, the death rate is also decreases).

5.2. Sobol’ sensitivity indices

We now present Sobol’ sensitivity indices to examine the transient behavior of the input parameters on the model output. Fig. 6 shows the time evolution of Sobol’ first order (Fig. 6(a)) and total order (Fig. 6(b)) indices for the influential parameters. The convergence of the results was obtained with a sample size of 1 million. Therefore, it required 44 million function evaluations, i.e., $2\times (21+1)\times {10}^6$. However, the first and total order indices converged at a faster rate than the second order indices (i.e, first order and total order indices converged with 250,000 samples).

Fig. 6.

Time evolution of the Sobol’ sensitivity indices (a - Sobol’ first order indices, b - Sobol’ total order indices).

From the first glance, it can be seen that Sobol’ first order indices are comparable with the PRCC results. Similar to the PRCC indices, Sobol’ indices also show that $\sigma$ is the most influential parameter in the beginning and with time, its influence decreases. The first order indices show that in April 2020 around 35% of the output uncertainty comes from the input uncertainty of $\sigma$ and it reduces to 5% in October 2020. The transmission coefficient, $C_{\beta }$ also shows a consistent influence of around 20% of the output uncertainty, but it has a slight reduction around October 2020. Similar to the PRCC results, outward mask efficiency shows an increasing trend with time.

Even though both PRCC and Sobol’ first order indices provide similar results, PRCC data cannot provide information on how individual parameters interact with each other. The effect of parameter interactions or higher order effects can be recognized by comparing first order and total order Sobol’ indices. A significant level of interactions can be seen in $C_{\beta },{\eta }_A,\varphi$ and ${\gamma }_I$. The total indices of most parameters show similar trend behavior to the first order indices. As an example, both first and total order indices for the parameter $\sigma$ have a higher value in the beginning and decrease with time. The only difference is the magnitude indicating that parameter interactions do not vary with time. However, parameters $C_{\beta }$ and ${\eta }_A$ show a clear variation in the first and total order sensitivity indices. As an example, the total order indices of the parameter $C_{\beta }$ show a peak around September 2020 while first order indices show a slight drop during that period. The same occurred for ${\eta }_A$ as well. These variations indicate that there is a transient behavior in the higher order effects.

To further understand these transient higher order effects, we calculated second order sensitivity indices. Since $C_{\beta }$ shows the highest level of parameter interactions, the time evolution of the second order Sobol’ indices for parameter $C_{\beta }$ are depicted in Fig. 7 . The parameter $C_{\beta }$ mainly interacts with ${ϵ}_o$ and their strongest influence occurs around December 2020 and results in around 6% output uncertainty (i.e., simultaneous implementation of mask usage and social distancing would result in an additional control over number of deaths). The interaction between $C_{\beta }$ and $\sigma$ has its peak at the beginning, which is around 4.5% of the output uncertainty. A similar interaction can be found in between the parameters ${\eta }_A$ and $\varphi$ which has a similar peak around September 2020.

Fig. 7.

Time evolution of second order Sobol’ indices for parameter $C_{\beta }$.

6. Conclusions

We developed a mathematical model to analyze the effect of the Covid-19 pandemic in the United States and used Sobol’ and PRCC global sensitivity analysis tools to identify the influential non-pharmaceutical interventions. The NPIs included in the mathematical model are social distancing, isolation of infected individuals, identifying asymptomatically infected individuals through testing, and the use of face masks. We used a fear-based model to simulate how individuals change their behavior to wear masks and follow social distancing guidelines.

We inferred model parameters using the number of fatalities reported in the US from March 1, 2020, to November 26, 2020. In the sensitivity analysis, we perturbed all the model parameters $\pm 25\%$ of their inferred values (i.e., assuming uniform distribution), except for parameters $C_{\theta }$ and $C_{\beta }$, which are perturbed $\pm 10\%$. We summarize our findings under two categories, 1. model simplification and prediction uncertainty reduction, 2. ranking of non-pharmaceutical interventions to control and mitigate the Covid-19 pandemic. We used the number of cumulative deaths as the quantity of interest in the sensitivity analysis.

6.1. Model simplification and prediction uncertainty reduction

According to the PRCC sensitivity indices, only the parameters $C_{\beta },{ϵ}_O,$ ${\eta }_A,{\eta }_H,\sigma ,$ $\varphi ,{\gamma }_I$, and ${\gamma }_A$ are found to be influential (i.e., $\left|PRCC\right(t\left)\right|\ge 1.5$). Since the rest of the parameters have little to no influence on the QoI, we can simplify our modeling efforts by fixing these non-influential parameters at their nominal values. According to the first-order indices, these non-influential parameters contribute less than 5% of output uncertainty throughout the time period.

Prediction uncertainty is another issue that model builders and policymakers often face. Here, we suggest an accurate estimation of the aforementioned influential parameters to reduce the prediction uncertainty. As an example, in the beginning, both PRCC and Sobol’ sensitivity indices show that parameter $\sigma$ (i.e., the reciprocal of the incubation period) is the most influential parameter that contributes 35% of the prediction uncertainty. Thus, an accurate estimation of the parameter $\sigma$ would benefit the prediction uncertainty at least in the first few months. Similarly, the prediction of transmission coefficient and relative infectiousness can reduce the output uncertainty significantly (around 30–35%).

6.2. Ranking of non-pharmaceutical interventions against Covid-19

As mentioned earlier, parameter $\sigma$ has the most contribution to the output uncertainty initially and decreases with time. The influence of parameter $C_{\beta }$ increased with time, indicating that social distancing measures have increasing control over the number of Covid-19 related fatalities. Additionally, the parameters ${\eta }_A$ and ${\eta }_H$ (relative infectiousness of asymptomatically infected and hospitalized, respectively) also positively influenced the model output uncertainty, showing the importance of frequent testing to identify asymptomatically infected individuals and of effective isolation from the susceptible population.

Outward mask efficiency and the rate at which unmasked symptomatically infected individuals make behavioral changes to wear masks are factors that decreased the number of deaths. It should be noted that the inward mask efficiency, ${ϵ}_I$ is one of the non-influential parameters even though the outward mask efficiency plays a significant role. To recall, the outward mask efficiency measures the efficiency of the mask preventing the disease transmission from an infected individual, and the inward mask efficiency measures the efficiency of the mask containing the transmission of the disease to a susceptible individual. This means that the influence of an infected individual wearing a high-quality mask is much more beneficial than the influence of a susceptible individual wear a high-quality mask. Therefore, when the demand for high-quality masks is high, priority can be given to the infected individuals, given a sufficient amount of testing being done to identify asymptomatically individuals.

The Sobol’ sensitivity indices showed a similar parameter ranking as PRCC. However, a comparison between the first order and total order sensitivity indices indicated that some parameters have non-zero higher-order effects due to parameter interactions. By estimating the second-order sensitivity indices, we found that simultaneous implementation of non-pharmaceutical interventions is more suitable to control the number of deaths. For example, implementing social distancing and mask usage decreased the output uncertainty up to 6% (i.e., in addition to their individual effects).

Finally, we found that the number of deaths can be decreased by increasing social distancing efforts, effective mask usage, and identifying and isolating asymptomatically infected individuals.

Data availability

Replication code is available from GitHub, https://github.com/khanthanan/Covid-19

CRediT authorship contribution statement

Kalpana Hanthanan Arachchilage: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing – original draft, Writing – review & editing. Mohammed Yousuff Hussaini: Conceptualization, Writing – review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Calculation of Basic Reproduction Number

Here we provide the calculation procedure of the basic reproduction number, ${\mathcal{R}}_0$, for a special case of the mathematical model Eqs. (4)–(15) where the time-dependent parameters, $\beta \left(t\right)$ and $\theta \left(t\right)$, are assumed to be constant (i.e., $\beta \left(t\right)={\beta }_0$, $\theta \left(t\right)={\theta }_0$). We use the next generation matrix approach [43], [44] to calculate the basic reproduction number. The system has a disease-free equilibrium state (DFE) and it is $DFE(S_U=N,S_M=0,E_U=0,E_M=0,I_U=0,I_M=0,A_U=0,A_M=0,I_H=0,I_{ICU}=0,R=0,D=0)$. The system has seven disease compartments and they are $E_U,E_M,I_U,I_M,A_U,A_M,I_H$. As explained in Section 2, we assume the diseased and ICU compartments are completely isolated. Therefore, $D$ and $I_{ICU}$ compartments are not considered as disease compartments.

Then, we decompose the disease compartment model equations Eqs. (6)–(13) such that ${\displaystyle \frac{d\mathcal{M}}{dt}}=\mathcal{F}-\mathcal{V}$, where $\mathcal{M}=[E_U,E_M,I_U,I_M,A_U,A_M,I_H]$.

$$\begin{array}{c}\hfill \mathcal{F}={\left[\begin{array}{ccccccc}{\zeta }_1& {\zeta }_2& 0& 0& 0& 0& 0\end{array}\right]}^T\end{array}$$ (A1)

See Eqs. (4) and (5) for the definitions of ${\zeta }_1$ and ${\zeta }_2$ terms.

$$\begin{array}{c}\hfill \mathcal{V}=\left[\begin{array}{c}\sigma E_U\\ \sigma E_M\\ -(1-f)\sigma E_U+({\theta }_0+\varphi +{\gamma }_I+{\delta }_I)I_U\\ -(1-f)\sigma E_M+(\varphi -{\theta }_0+{\gamma }_I+{\delta }_I)I_M\\ -f\sigma E_U+{\gamma }_A{A}_U+{\delta }_A{A}_U\\ -f\sigma E_M+{\gamma }_A{A}_M+{\delta }_A{A}_M\\ -\varphi (I_U+I_M)+({\gamma }_H+\nu +{\delta }_H)I_H\end{array}\right]\end{array}$$ (A2)

Matrices ${F|}_{DFE}$ and ${V|}_{DFE}$ are calculated as

$$\begin{array}{c}\hfill F_{i,j}{{|}_{DFE}=\frac{\partial {\mathcal{F}}_i}{\partial {\mathcal{M}}_j}|}_{DFE}\\ \hfill V_{i,j}{{|}_{DFE}=\frac{\partial {\mathcal{V}}_i}{\partial {\mathcal{M}}_j}|}_{DFE}\end{array}$$ (A3)

$${F|}_{DFE}=\left[\begin{array}{ccccccc}0& 0& {\beta }_0& {\beta }_0(1-{ϵ}_O)& {\beta }_0{\eta }_A& {\beta }_0{\eta }_A(1-{ϵ}_O)& {\beta }_0{\eta }_H(1-{ϵ}_O)\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$ (A4)

$${V|}_{DFE}=\left[\begin{array}{ccccccc}\sigma & 0& 0& 0& 0& 0& 0\\ 0& \sigma & 0& 0& 0& 0& 0\\ -(1-f)\sigma & 0& k_1& 0& 0& 0& 0\\ 0& -(1-f)\sigma & -{\theta }_0& k_2& 0& 0& 0\\ -f\sigma & 0& 0& 0& {\delta }_A+{\gamma }_A& 0& 0\\ 0& -f\sigma & 0& 0& 0& {\delta }_A+{\gamma }_A& 0\\ 0& 0& -\varphi & -\varphi & 0& 0& k_3\end{array}\right]$$ (A5)

where $k_1={\delta }_I+{\gamma }_I+\varphi +\delta$, $k_2={\delta }_I+{\gamma }_I+\varphi$ and $k_3={\delta }_H+{\gamma }_H+\nu$.

Then the basic reproduction number is given by the dominant eigen value of the new generation matrix ($F{V}^{-1}$) and can be written as

$$\begin{array}{cc}\hfill {\mathcal{R}}_0=& \frac{{\beta }_0{\eta }_f}{{\delta }_A+{\gamma }_A}+\frac{{\beta }_0{\theta }_0(1-{ϵ}_O)(1-f)}{{\delta }_I+{\gamma }_I+\varphi +{\theta }_0}+\frac{{\beta }_0{\theta }_0(1-{ϵ}_O)(1-f)}{({\delta }_I+{\gamma }_I+\varphi )({\delta }_I+{\gamma }_I+\varphi +{\theta }_0)}\hfill \\ \hfill & +\frac{{\beta }_0{\eta }_H\varphi (1-{ϵ}_O)(1-f)}{({\delta }_H+{\gamma }_H+\nu )({\delta }_I+{\gamma }_I+\varphi )}\hfill \end{array}$$ (A6)

At $t=0$, when the value of ${\beta }_0=\beta (t=0)=0.8840$ and ${\theta }_0=\theta (t=0)=0.1098$, the numerical value of ${\mathcal{R}}_0$ becomes 3.0549.