Abstract
Perovskite photovoltaics advance rapidly, but questions remain regarding point defects: while experiments have detected the presence of electrically active defects no experimentally confirmed microscopic identifications have been reported. Here we identify lead monovacancy (VPb) defects in MAPbI3 (MA = CH3NH3+) using positron annihilation lifetime spectroscopy with the aid of density functional theory. Experiments on thin film and single crystal samples all exhibited dominant positron trapping to lead vacancy defects, and a minimum defect density of ~3 × 1015 cm−3 was determined. There was also evidence of trapping at the vacancy complex in a minority of samples, but no trapping to MA-ion vacancies was observed. Our experimental results support the predictions of other first-principles studies that deep level, hole trapping, , point defects are one of the most stable defects in MAPbI3. This direct detection and identification of a deep level native defect in a halide perovskite, at technologically relevant concentrations, will enable further investigation of defect driven mechanisms.
Subject terms: Photovoltaics, Semiconductors
Point defects compromise the electronic performance of hybrid perovskites, yet no experimental identifications have been reported. Here, the authors, for the first time, identify lead monovacancy defect in MAPbI3 using positron annihilation lifetime spectroscopy with the aid of density functional theory.
Introduction
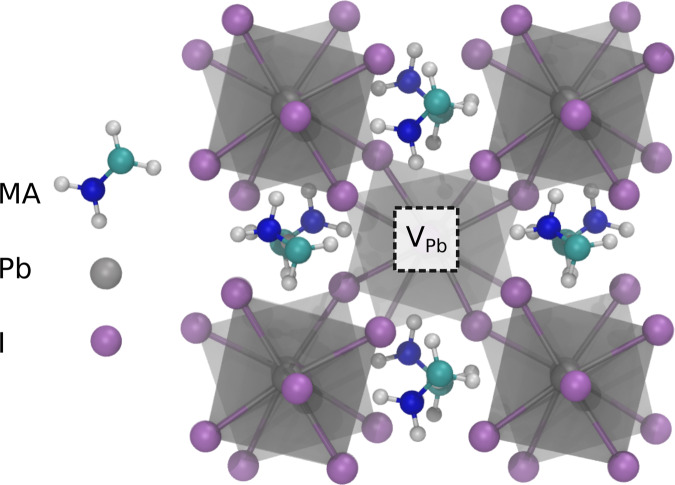
The unprecedentedly rapid development of metal halide perovskite materials has been driven by their favorable optoelectronic properties enabling a new photovoltaic (PV) solar cell technology1, and creating potential for other optoelectronic device applications2,3. Metal halide perovskites have a crystal structure (Fig. 1) with the general formula ABX3, where the B-site metal cation is octahedrally coordinated by X-site halogen anions. In the subgroup of halide perovskites termed hybrid perovskites the more open corner A-sites are occupied by an organic molecule cation. Methylammonium (MA) lead iodide, MAPbI3, is the prototypical metal halide hybrid perovskite. Understanding the origin of the high PV conversion and light emission efficiency remains a central aim of halide-perovskite research2,4. Recently there has been recognition of the importance of defect-assisted carrier recombination via centers which can act to limit the conversion efficiency of solar photovoltaic devices. Ultimately it is necessary to identify and confirm the point defect types present in order to design manufacturing processes for optimum performance. However, since experimental identification of point defects requires the use of spectroscopic methods that provide direct local structural information, or laborious studies to correlate for example electrical measurements across a sequence of chemically controlled sample sets, the vast majority of our present understanding comes from computational research effort4–9. Experimental studies, the subject of this work, are therefore urgently required. Nevertheless, first-principles calculations are providing detailed insight on the possible point defects and their role in fundamental mechanisms responsible for the intriguing materials physics of halide perovskites5,9–13.
Fig. 1. MAPbI3 crystal structure.
Illustrating B-site polyhedra (gray), and showing a Pb vacancy.
Currently our detailed understanding of the point defect physics and chemistry of hybrid perovskites therefore results exclusively from first-principles calculations. Using hybrid functionals and accounting for Spin-Orbit Coupling (SOC)10,11,14 these methods then yield accurate values for the energies of the band edges and the band gap energy which is in the range 1.58–1.60 eV, in good agreement with the experimental value. When combined with appropriate schemes to correct for localized charge within the supercell these approaches enable defect formation energies (DFE) and charge transition levels to be calculated10,13. Studies of the primary native defects in MAPbI3, the three monovacancy, VMA, VPb, VI, the interstitial defects, MAi, Pbi, Ii, and the two relevant antisite defects, IMA, PbI, have been performed5,10,11,13. Point defects with charge transition levels deeper into the band gap are of particular relevance for defect-assisted mechanisms2,4,6–9, such as nonradiative recombination4,11,13. While IMA is reported to have a (0/2–) charge transition level deep in the band gap13, the antisite defects were found to have high DFE values so are expected to have negligible concentrations11. The cation interstitial, Pbi and MAi, yield shallow donor charge transition levels close to the conduction band minimum (CBM)11. By contrast, the iodine interstitial was found to be a deep defect and to have one of the lowest DFE values, and so be one of most stable defects11,13. It exhibits a (+/–) transition level 0.95 eV above the valence band maximum (VBM), the neutral charge state is energetically less favorable than either or . The trapping of two carriers occurs rapidly, but sequentially via the two associated charge transition levels, (0/–) and (+/0) at 0.78 eV above the VBM and 0.58 eV below the CBM, respectively13. The center can enable nonradiative carrier recombination and to quantify the recombination rate both the electron and hole capture rates are required. Recent first-principles calculations conclude that the iodine interstitial is the primary nonradiative recombination center in hybrid perovskites13.
The anion vacancy, VI, is reported to have a shallow donor charge transition level close to the CBM and hence to be normally stable in the positive charge state5,10,11, . The A-site cation (MA) vacancy forms shallow acceptor charge transition level close to the VBM so is normally negatively charged, , but the relatively high DFE imply concentrations are low10. It has recently been shown that the MA vacancy is expected to be noticeably more stable on MAI terminated surfaces5. The B-site cation vacancy, the lead vacancy, VPb, is a deep acceptor defect with a (0/2–) charge transition level 0.5 eV above the VBM5,10,11,13. Again, trapping of carriers is expected to proceed sequentially via the shallow (–/2–) level, 0.13 eV above the VBM, and a deep (0/–) level, ~0.8 eV above the VBM. Nonradiative recombination is controlled by the slowest carrier capture process, which should be electron capture by the (–/2–) level, and some first-principles conclude that VPb might make a limited contribution. The double negative charge state, , is calculated to have small DFE values under all growth conditions and so is one of the most stable defects in MAPbI39–11. It has been proposed that for low Fermi energies will decompose following the reaction10, + = = + + . Recent calculations for PbI2 terminated surfaces predict Ii, VPb and VI are more stable, and that the VPb (0/2–) level, and associated (0/–) and (–/2–) transitions, move deeper into the band gap due to the increased stability of implying an increased contribution to nonradiative recombination5.
Deep-level transient spectroscopy (DLTS)15–17, and thermally stimulated current18, measurements clearly show the presence of deep-level defects in MAPbI3. Defect concentrations have been inferred from DLTS15, and space-charge limited current measurements (SCLC)19, and have been reported to be on the order of 1017 cm−3 or lower7, but caution in the interpretation of SCLC measurements is required20. Furthermore, while DLTS is capable of identifying charge transition energy levels of defects in the gap, it does not of itself give any indication of the chemical identity of point defects in the lattice. Although in principle it should be possible to correlate the experimental energies with those from density functional theory (DFT) calculations, in practice this is challenging. Deep defect energy levels have been reported from a DLTS study of thin film MAPbI3 at CBM – 0.62(1) eV and at CBM – 0.75(1) eV15, and at VBM + 0.84(1) eV from an optical DLTS study of crystal MAPbI316. Both studies referred the experimental defect charge transition energies to the values calculated by Yin et al.21 using the projector augmented wave (PAW) with general gradient approximation (GGA) DFT method and including SOC. The thin film results were attributed to IPb antisite and the IMA antisite on this basis15, while the trap level observed from the crystal study was associated with IPb16. However, the point defect charge transition energy level positions within the gap calculated using PAW-GGA-SOC21 differ markedly from those obtained in more recent calculations using hybrid functionals and including SOC10,11,13. For example, the lead vacancy was predicted to give a single shallow acceptor (–/2–) level in the gap as opposed a deep (0/2–) acceptor level as determined by the hybrid functionals with SOC calculations. While the resulting defect geometries, in particular for defects in their formal charge states, e.g., or , are typically similar for the two calculation schemes, the use of hybrid functionals with the inclusion of SOC and appropriate schemes to correct for localized charge are of critical importance for the determination of charge transition energy level position. The stark differences in the energy level values highlight current uncertainties regarding point defect identification. Furthermore, it has been shown that the set of trap energies detected by DLTS and attributed to the perovskite layer can depend on the partner hole transporting material in the device configuration22. The presence of grain boundary potentials and traps can also complicate the interpretation of DLTS experiments23.
Positron annihilation spectroscopy methods yield information that depends on the local structure of the defect localizing the positron and can provide identification of neutral or negatively charged vacancy–related defects in materials24–26. Positron annihilation lifetime spectroscopy (PALS) enables the experimental detection of multiple positron states. Observation of both perfect lattice annihilation states and longer lifetime defect positron states enables the trapping to vacancy-related defects to be unambiguously established. Comparison of the experimentally determined lifetimes with the DFT calculated values for the perfect material state and of states localized at specific vacancy–related defects26,27 allows the identification of specific point defect types. Moreover, positron lifetime measurements performed using a high intensity positron beam enable depth–profiling of vacancy–related defects from the near-surface down to depths of a few microns28,29.
Here we report the detection and identification of lead vacancy related defects in thin film, and in the near surface region of single crystal MAPbI3 using variable positron implantation energy PALS measurements performed with the high intensity positron beamline (NEPOMUC) at the Heinz Maier–Leibnitz Zentrum (MLZ) research reactor in Garching28,29. Calculations of positron lifetimes using both atomic superposition and projector augmented-wave (PAW) DFT methods for perfect lattice MAPbI3 and relevant vacancy defects are performed. Positrons localize at missing atom defects with open volume, however, for this to occur the local charge of the defect is required to be neutral or negative with respect to the lattice; the trapping rate to positively charged vacancy-related defects is negligible25,26. The lifetime of positrons localized at vacancy defects is a measure of the local electron density, and is a characteristic of the specific vacancy defect type. Similarly, the positron lifetime resulting from annihilation of positrons delocalized in Bloch states in the perfect material, the bulk lifetime, is characteristic for a given material. The vacancy defect positron lifetimes are greater than the bulk lifetime. The primary vacancy defects in MAPbI3 are the anion iodine vacancy, VI, and the two cation vacancies (the larger A-site MA-ion, CH3NH3+, vacancy, VMA, and the B-site, octahedrally coordinated, Pb vacancy, VPb) as shown in Fig. 1. Positrons are expected to trap at either cation vacancy, i.e., the Pb vacancy with local charge of –2 or the MA ion vacancy with a local charge of –1, but will not trap at positively charged anion vacancies.
Results
Density functional theory calculations of the characteristic positron lifetime values
The positron annihilation lifetime values were calculated for annihilation from perfect lattices states, and for states localized at the two negatively charged cation vacancies. They were performed using the atomic superposition method, implemented in the program MIKA-Doppler30,31, and with the PAW method using ABINIT27,32. ABINIT calculations were also performed were the neighbor atoms to the vacancy relaxed according to the forces due to the electron and positron densities (further details of the calculations are given in the theoretical calculations sections of Methods and Supplementary Note 1). The resulting calculated positron state lifetime values for MAPbI3 are given in Table 1. There is approximate agreement between the two calculation methods. The low electron density in MAPbI3 resulted in a long perfect lattice (bulk) positron lifetime in the approximate range 340–350 ps. The positron lifetime for the perovskite B-site, Pb, vacancy was found to be ~369 ps. The resulting positron density localized at a Pb vacancy is shown in Fig. 2. The lifetime value for the more open A-site, MA ion, vacancy was in the approximate range 400–440 ps. Calculations were also performed for the possible A-site vacancy, VMA, iodine interstitial complex and for the possible B-site centered divacancy, . Both yielded lifetime values greater than, and separated from, the Pb vacancy lifetime but were shorter than the VMA value (Table 1). A similar trend in positron lifetime values for the two cation vacancies has been observed in ABO3 perovskite oxide materials with a bulk lifetime in the 150–160 ps range, the VB lifetime typically 180–200 ps, and the VA lifetime in the 280–300 ps range. Both cation vacancy defects have been experimentally observed24,33.
Table 1.
Calculated positron state lifetimes (ps) for perfect lattice and cation vacancy defects in MAPbI3.
| Positron state | MIKA | ABINIT | ABINIT-relaxed |
|---|---|---|---|
| Perfect lattice | 353 | 342 | |
| 369 | 360 | 369 | |
| 377 | |||
| 401 | 414 | 442 | |
| 403 |
Atomic superposition calculations were performed with MIKA-Doppler, PAW-DFT calculations with ABINIT. ABINIT calculations were also performed relaxing the structure in the presence of the positron.
Fig. 2. Calculated positron density at the Pb vacancy in MAPbI3.
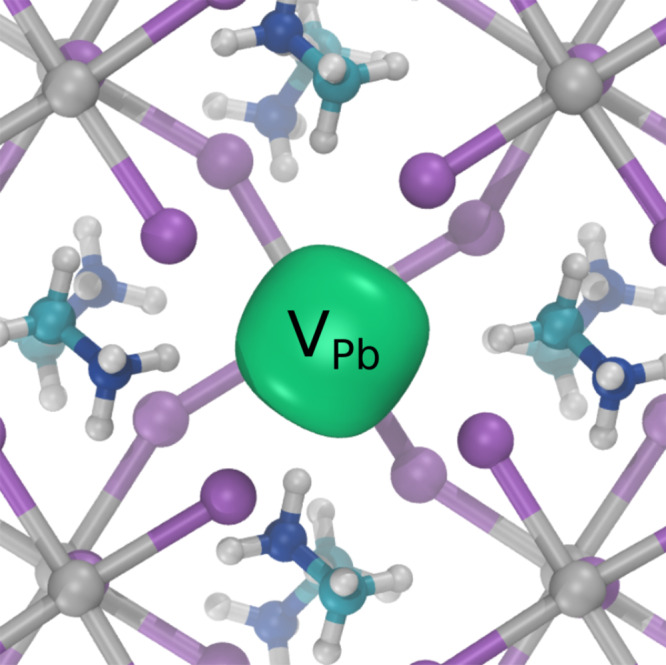
Positron density isosurface shown in green localized at a defect obtained using ABINIT relaxing the structure in the presence of the position.
Variable energy positron annihilation lifetime spectroscopy measurements
These were performed on MAPbI3 thin films from both Oxford (200 nm) and Liverpool (300 nm), and a single crystal grown by inverse temperature crystallization. Figure 3a shows positron lifetime spectra from a thin film and from the near surface of the single crystal while Fig. 3b shows positron implantation profiles for the implantation energies. Positron lifetime spectra were deconvolved to identify the contributing positron state components, see Fig. 4 and Table 2 (complete results are given in Supplementary Note 2). A dominant positron lifetime component with intensity greater than or equal to 92% and an average lifetime value of 370(3) ps was obtained from the spectra measured from all five of the MAPbI3 samples studied.
Fig. 3. Experimental positron lifetime spectra and positron implantation profiles.
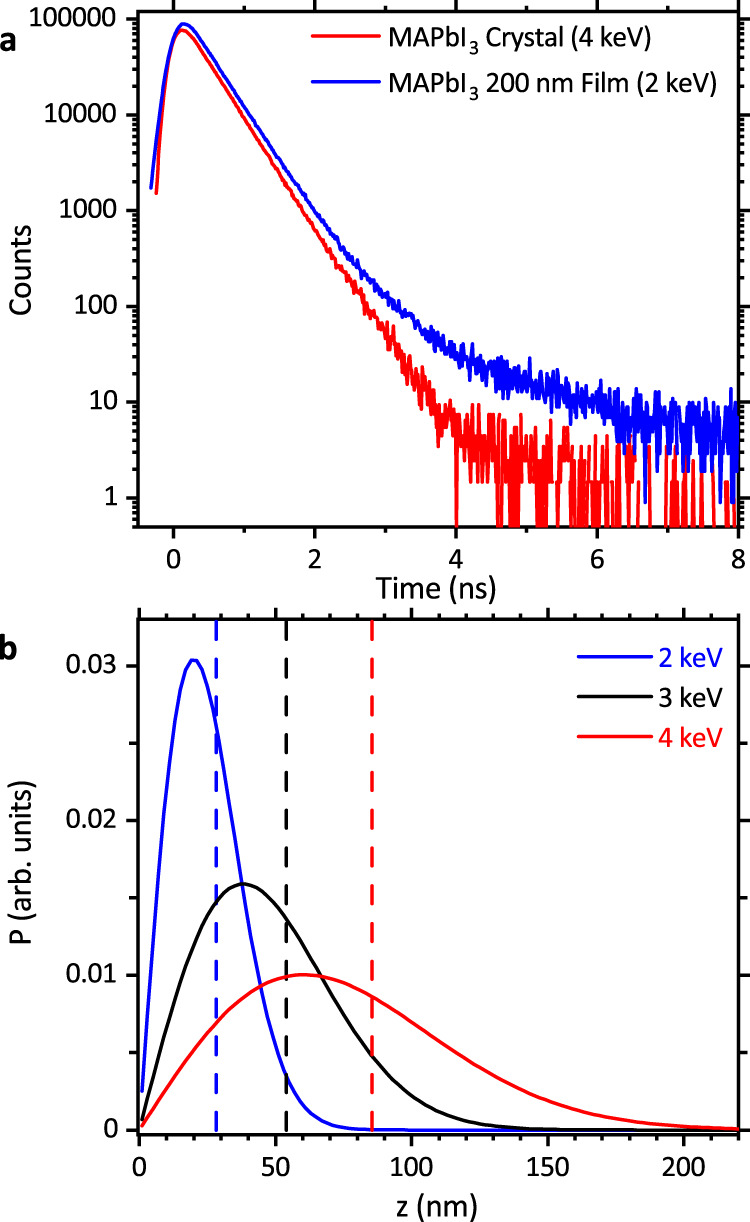
a Lifetime spectra for a 200 nm MAPbI3 film (Oxford), (blue) measured with 2 keV positron implantation energy and for a MAPbI3 crystal (red) at 4 keV. b Markovian positron implantation depth profiles, the mean depths are shown with dashed lines.
Fig. 4. Experimental positron lifetime spectra with deconvolution fit components.

a MAPbI3 crystal with 4 keV implantation energy, both also showing the fitted positron lifetime components. b The 300 nm MAPbI3 film (Liverpool, Anneal A) measured with 2.5 keV positron implantation energy.
Table 2.
Experimental positron lifetime component results for MAPbI3 thin film and single crystal samples.
| Sample | Source | E (keV) | τ1 (ps) | I1 (%) | τ2 (ps) | I2 (%) | τ3 (ns) | I3 (%) | κ2 (s−1) |
|---|---|---|---|---|---|---|---|---|---|
| Film | Oxford | 2 | 119(45) | 2.2(8) | 371(5) | 94(1) | 0.7(1) | 3.5(1.6) | 5.6(2.2) x 109 |
| Crystal | Dundee | 4 | 42(10) | 4.6(5) | 368(4) | 94(3) | 0.6(3) | 1.5(2.5) | 2.0(5) x 1010 |
| Film (Standard) | Liverpool | 2.5 | 109(19) | 2.7(3) | 375(1) | 97.3(2) | 2.3(4) | 0.05(1) | 6.3(1.1) x 109 |
| Film (Anneal A) | Liverpool | 2.5 | 49(27) | 2(1) | 367(1) | 98(1) | 1.4(1) | 0.29(4) | 7.5(1.2) x 109 |
| Film (Anneal B) | Liverpool | 2.5 | 110(24) | 2.3(3) | 370(1) | 97.4(3) | 1.7(1) | 0.27(3) | 1.7(9) x 1010 |
Deconvolved component lifetime values, τ, intensities, I, calculated defect position trapping rates, κ2, and the positron implantation energies, E.
The first component lifetime value (Table 2, Supplementary Note 2) was significantly smaller than the DFT calculated perfect lattice (bulk) lifetime value (Table 1). This reduced bulk lifetime component has low intensity, nevertheless, the experimental lifetime component values can be used to calculate a standard trapping model bulk lifetime value of 342(16) ps (see Supplementary Note 3) which is in agreement with the DFT results (Table 1). The observation of a dominant positron lifetime component (370(3) ps) with a value greater than the experimental standard trapping model calculated bulk lifetime provides direct evidence for trapping to vacancy-related point defects with neutral or negative local charge in all the MAPbI3 samples studied.
Comparing the dominant component experimental lifetime of 370(3) ps with the DFT calculated lifetimes for the two cation vacancies, and , there is very good agreement with Pb vacancy value of ~369 ps (Table 1). By contrast, the calculated positron lifetime value characteristic of the more open twelve coordinated CH3NH3+ site (A-site) is greater than 400 ps. A more detailed consideration of the dominant lifetime component values shows that for four of the five MAPbI3 samples studied the lifetime was in the range 369(2) ps while for the other sample this was 375(1) ps (Supplementary Note 2). The DFT calculated lifetime for the divacancy defect is 377 ps (Table 1) suggesting the possibility of trapping to both and defects. A very low intensity experimental component with a lifetime in the approximate range 600–800 ps was also detected from one of the thin film samples, and from the near surface region of the single crystal (Table 2, Supplementary Tables 1 and 2), is due to the annihilation of positronium (see Supplementary Note 4) and cannot be attributed to a specific defect type.
The observation of lead vacancy defects, and the absence of trapping to MA vacancies, in the studied MAPbI3 samples is consistent with first-principles study predications that , in contrast to , exhibits low DFE values under all growth conditions and so is one of the most stable defects. First principles calculations have provided evidence that lead vacancies are deep level defects capable of trapping holes9–11.
Estimation of lead vacancy concentration
The detection of a weak reduced bulk lifetime component in all the measured spectra enables the rate of positron trapping to vacancy defects, , to be estimated (see Table 2 and Supplementary Note 2). The vacancy defect concentration is related to the trapping rate, , where is the defect specific trapping coefficient. The values for , for negatively charged vacancy defects in various semiconductors, have been reported to be in the range25 ~1 × 1015–3 × 1016 s−1. In consequence, lead vacancy defect densities greater than ~3 × 1015 cm3 are required to yield the experimental defect lifetime component intensities observed from all the MAPbI3 samples measured. Using the more typical value of for negatively charged vacancies of ~2 × 1015 s−1 an average value of defect densities obtained for the samples studies is estimated to be 9(6) × 1016 cm3 (see Supplementary Note 3).
Discussion
Our work demonstrates the experimental detection and identification of native vacancy point defects in thin film and single crystal metal halide perovskite materials. Positron annihilation lifetime spectroscopy, with the aid of two-component DFT calculations, enables the identification of cation vacancy and vacancy cluster defects in MAPbI3. In all the thin film and crystal samples studied a dominant, ≥92% intensity, positron trap with a positron state lifetime of 370(3) ps (Table 2, and Supplementary Note 2) consistent with the DFT calculated value of 369 ps (Table 1) for VPb was observed. The possible trapping to divacancy defects was observed for one of the thin film samples. The lead vacancy related defect density was found to be greater than ~3 × 1015 cm−3 in all samples. Using a more typical value for the positron trapping coefficient for a negatively charged vacancy defect yields an average defect density of 9(6) × 1016 cm3 for the samples studied. No positron trapping to MA vacancy defects was detected. Our results support the predications of first-principles calculations that deep level, hole trapping, point defects are one the most stable defects in MAPbI3 and that MA vacancies are expected to have negligible concentrations. The results are also in agreement with recent low-dose scanning transmission microscopy studies of a metal halide perovskite that provide evidence for the presence of vacancy defects in Pb-I sublattice34. Depth-profiling positron lifetime spectroscopy is demonstrated to be a point defect characterization method that can be applied to metal halide perovskites, enabling the detection and identification of neutral or negatively charged vacancy-related defects.
Methods
Sample preparation
The University of Oxford MAPbI3 films were formed from 40 wt% precursor solution of MAI:PbI2 dissolved in dimethlformamide (DMF). The MAI was made in house35. The precursor solution was coated on a clean FTO coated glass sheets by a consecutive two-step spin-coating process at 1200 rpm and 2000 rpm for 25 s and 12 s, respectively. The films were annealed at 150 °C for 15 min. Two films were top coated with 50 nm PMMA in chlorobenzene. All processing was performed in a nitrogen-filled dry glovebox. All materials were purchased from Sigma-Aldrich or Alfa Aesar and used as received.
The University of Liverpool MAPbI3 films were synthesised using a one-step solution by a DSMO adduct with antisolvent method. A 1:1:1 MAI:PbI2:DMSO in DMF solution was spin-coated, with chlorobenzene added during the spin process removing the DMF and allowing rapid conversion to MAPbI2 on thermal annealing. This produced a standard film, for the anneal A and B films a small additional volume of DMSO, 40 mL and 80 mL, respectively, was present during the anneal. The films were made and packaged entirely in a glovebox, then vacuum sealed. All chemicals were supplied by Sigma-Aldrich with the exception of MAI, which was purchased from Solaronix SAs. All materials were used as received, without further purification processes.
The MAPbI3 crystals measured were grown by the inverse temperature crystallization procedure36. 1 M solutions of PbI2 (99%, Sigma-Aldrich) and MAI (Dyesol Ltd) were prepared in γ-butyrolacetone (>99% Sigma-Aldrich), the solutions were filtered using PTFE filter with 0.2 μm pore size. The filtered solution mixture was placed in a flat-bottomed glass vial and placed in a silicone oil bath maintained at 110 °C. All procedures where carrier out in ambient conditions and 20–30% relative humidity. Crystal structure was confirmed by x-ray diffraction using a Siemens D5000 diffractometer. The crystals exhibited rhombo-hexagonal dodecahedra morphology and had a smooth major facet size of ~8 × 9 mm2.
Positron annihilation
Variable energy positron annihilation lifetime spectroscopy was performed using the PLEPS instrument on the NEPOMUC high intensity beam line at the Heinz Maier–Leibnitz Zentrum (MLZ) research reactor in Garching28,29. Spectra contained 4 × 106 counts. The spectra were fitted using the software package PALSfit Version 3.195 (Technical University of Denmark, Riso Campus)37. The timing instrument resolution function was determined using a SiC standard sample, was described by three Gaussian functions, the resulting full width half maximum values varied from 277 ps to 312 ps for the measurements described. Samples were transferred from an inert gas environment container to the sample chamber and a vacuum established within several minutes. Measurements were also performed on CH3NH3PbI3 thin films with a thin PMMA environment protecting coating and the results were found to be consistent with those obtained from non-coated films (see Supplementary Note 5).
Theory calculations
Positron lifetime calculations were performed using atomic superposition method with the MIKA-Doppler code31. In the calculations we applied the electron-positron enhancement factor30,38 resulting from the parametrization of the data of Arponen and Pajanne39. Supercells of CH3NH3PbI3 comprising 1152 atoms were used for the computationally efficient atomic superposition calculations40. The projector augmented-wave (PAW) method calculations were carried out using the ABINIT code27,32 with the electron-positron correlation functional parametrized by Boronski and Nieminen41. The electronic and positronic densities were updated self-consistently in a double loop. During each subloop, one of the two densities was kept constant while the other was being converged. To account for the imperfect screening of the positron by the electrons in MAPbI3, we applied the gradient correction proposed by Barbiellini et al.30. The generalized gradient approximation (GGA) as parametrized by Perdew, Burke, and Ernzerhof (PBE) was used to describe the electron exchange-correlation interactions42. The positron lifetime calculations were based on a 192-atom supercell with an initial apolar arrangement of the organic cations. The energy cut-off was set to 16 Ha. We used lattice parameters corresponding to the tetragonal phase of CH3NH3PbI3 (a = b = 1.772 nm, c = 1.266 nm)43, and a 1 × 1 × 2 Monkhorst-Pack k-point mesh. The defects were relaxed using forces due to both electron and positron densities until convergence below 1 ps was reached. Additional tests were performed to assess the effect of spin orbit coupling and the use of hybrid functionals on the calculated positron lifetimes (see theoretical calculations section of the Supplementary Note 1). It was found that including SOC reduced the calculated positron lifetime but that using hybrid functionals increased this value and hence the combination resulted in a lifetime in agreement with the GGA without SOC value. Hence the supplementary calculations confirmed the validity of the approach used.
Supplementary information
Acknowledgements
D.J.K. gratefully acknowledges the financial support provided by FRM-II to perform the high-intensity positron beam measurements at Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. J.W. acknowledges funding from the “Area of Advance—Materials Science” at Chalmers University of Technology and the Swedish Research Council (2019–03993). The computations were partly performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and PDC. L.J.P. and K.D. would like to acknowledge support from EPSRC grants EP/N014057/1 m and EP/M024768/1. H.J.S. acknowledges support from EPSRC grant EP/L024667/1. W.E. gratefully acknowledges BMBF-grants 05K13WN1-POSIANALYSE, 05K16WN1-POSITEC and 05K19WN1-POSILIFE of the German Federal Office of Research and Education.
Author contributions
D.J.K. with S.K.P. and L.J.P. designed the study. S.K.P., H.J.S., L.J.P., K.D., and D.J.K. supplied samples. D.J.K., M.D. and W.E. performed the positron annihilation experiments. J.W. performed PAW-DFT calculations and D.J.K. the atomic superposition calculations. D.J.K., with help from J.W. and K.D., wrote the main draft. All authors commented on the manuscript.
Data availability
The positron lifetime data that support the findings of this study and source data for display items has been deposited in figshare with the identifier doi:10.6084/m9.figshare.15031926.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review informationNature Communications thanks Stephan W. H. Eijt and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-25937-1.
References
- 1.Nayak PK, Mahesh S, Snaith HJ, Cahen D. Photovoltaic solar cell technologies: analysing the state of the art. Nat. Rev. Mater. 2019;4:269–285. doi: 10.1038/s41578-019-0097-0. [DOI] [Google Scholar]
- 2.Stranks SD, Hoye RLZ, Di DW, Friend RH, Deschler F. The physics of light emission in halide perovskite devices. Adv. Mater. 2019;31:1803336. doi: 10.1002/adma.201803336. [DOI] [PubMed] [Google Scholar]
- 3.Xu JL, et al. Halide perovskites for nonlinear optics. Adv. Mater. 2020;32:1806736. doi: 10.1002/adma.201806736. [DOI] [PubMed] [Google Scholar]
- 4.Zhang X, Shen JX, Van de Walle CG. First-principles simulation of carrier recombination mechanisms in halide perovskites. Adv. Energy Mater. 2020;10:1902830. doi: 10.1002/aenm.201902830. [DOI] [Google Scholar]
- 5.Ambrosio F, Meggiolaro D, Mosconi E, De Angelis F. Charge localization and trapping at surfaces in lead-iodide perovskites: the role of polarons and defects. J. Mater. Chem. A. 2020;8:6882–6892. doi: 10.1039/D0TA00798F. [DOI] [Google Scholar]
- 6.Han TH, et al. Interface and defect engineering for metal halide perovskite optoelectronic devices. Adv. Mater. 2019;31:1803515. doi: 10.1002/adma.201803515. [DOI] [PubMed] [Google Scholar]
- 7.Jin HD, et al. It’s a trap! On the nature of localised states and charge trapping in lead halide perovskites. Mater. Horiz. 2020;7:397–410. doi: 10.1039/C9MH00500E. [DOI] [Google Scholar]
- 8.Luo DY, Su R, Zhang W, Gong QH, Zhu R. Minimizing non-radiative recombination losses in perovskite solar cells. Nat. Rev. Mater. 2020;5:44–60. doi: 10.1038/s41578-019-0151-y. [DOI] [Google Scholar]
- 9.Motti SG, et al. Defect activity in metal-halide perovskites. Adv. Mater. 2019;31:1901183. doi: 10.1002/adma.201901183. [DOI] [PubMed] [Google Scholar]
- 10.Meggiolaro D, De Angelis F. First-principles modeling of defects in lead halide perovskites: best practices and open issues. ACS Energy Lett. 2018;3:2206–2222. doi: 10.1021/acsenergylett.8b01212. [DOI] [Google Scholar]
- 11.Meggiolaro D, et al. Iodine chemistry determines the defect tolerance of lead-halide perovskites. Energy Environ. Sci. 2018;11:702–713. doi: 10.1039/C8EE00124C. [DOI] [Google Scholar]
- 12.Wiktor J, Ambrosio F, Pasquarello A. Mechanism suppressing charge recombination at iodine defects in CH3NH3PbI3 by polaron formation. J. Mater. Chem. A. 2018;6:16863–16867. doi: 10.1039/C8TA06466K. [DOI] [Google Scholar]
- 13.Zhang X, Turiansky ME, Shen JX, Van de Walle CG. Lodine interstitials as a cause of nonradiative recombination in hybrid perovskites. Phys. Rev. B. 2020;101:140101. doi: 10.1103/PhysRevB.101.140101. [DOI] [Google Scholar]
- 14.Du MH. Density functional calculations of native defects in CH3NH3Pbl3: effects of spin-orbit coupling and self-interaction error. J. Phys. Chem. Lett. 2015;6:1461–1466. doi: 10.1021/acs.jpclett.5b00199. [DOI] [PubMed] [Google Scholar]
- 15.Heo S, et al. Deep level trapped defect analysis in CH3NH3PbI3 perovskite solar cells by deep level transient spectroscopy. Energy Environ. Sci. 2017;10:1128–1133. doi: 10.1039/C7EE00303J. [DOI] [Google Scholar]
- 16.Vu TKO, et al. Defect states of organic lead halide single crystals grown by inverse-temperature crystallization. Appl. Phys. Lett. 2019;115:153302. doi: 10.1063/1.5100952. [DOI] [Google Scholar]
- 17.Yang WS, et al. Iodide management in formamidinium-lead-halide-based perovskite layers for efficient solar cells. Science. 2017;356:1376–1379. doi: 10.1126/science.aan2301. [DOI] [PubMed] [Google Scholar]
- 18.Baumann A, et al. Identification of Trap States in Perovskite Solar Cells. J. Phys. Chem. Lett. 2015;6:2350–2354. doi: 10.1021/acs.jpclett.5b00953. [DOI] [PubMed] [Google Scholar]
- 19.Yang D, et al. Surface optimization to eliminate hysteresis for record efficiency planar perovskite solar cells. Energy Environ. Sci. 2016;9:3071–3078. doi: 10.1039/C6EE02139E. [DOI] [Google Scholar]
- 20.Duijnstee EA, et al. Toward understanding space-charge limited current measurements on metal halide perovskites. ACS Energy Lett. 2020;5:376–384. doi: 10.1021/acsenergylett.9b02720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yin WJ, Shi TT, Yan YF. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014;26:4653–4658. doi: 10.1002/adma.201306281. [DOI] [PubMed] [Google Scholar]
- 22.Hsieh HC, et al. Analysis of defects and traps in N-I-P layered-structure of perovskite solar cells by charge-based deep level transient, spectroscopy (Q-DLTS) J. Phys. Chem. C. 2018;122:17601–17611. doi: 10.1021/acs.jpcc.8b01949. [DOI] [Google Scholar]
- 23.Lourenco MA, Ng WL, Homewood KP, Durose K. A deep semiconductor defect with continuously variable activation energy and capture cross section. Appl. Phys. Lett. 1999;75:277–279. doi: 10.1063/1.124347. [DOI] [Google Scholar]
- 24.Keeble DJ, et al. Identification of A- and B-site cation vacancy defects in perovskite oxide thin films. Phys. Rev. Lett. 2010;105:226102. doi: 10.1103/PhysRevLett.105.226102. [DOI] [PubMed] [Google Scholar]
- 25.Krause-Rehberg, R. & Leipner, H. S. Positron annihilation in semiconductors. (Springer-Verlag, Berlin Heidelberg, 1999).
- 26.Tuomisto F, Makkonen I. Defect identification in semiconductors with positron annihilation: experiment and theory. Rev. Mod. Phys. 2013;85:1583–1631. doi: 10.1103/RevModPhys.85.1583. [DOI] [Google Scholar]
- 27.Wiktor J, Jomard G, Torrent M. Two-component density functional theory within the projector augmented-wave approach: accurate and self-consistent computations of positron lifetimes and momentum distributions. Phys. Rev. B. 2015;92:125113. doi: 10.1103/PhysRevB.92.125113. [DOI] [Google Scholar]
- 28.Hugenschmidt C, Piochacz C, Reiner M, Schreckenbach K. The NEPOMUC upgrade and advanced positron beam experiments. N. J. Phys. 2012;14:055027. doi: 10.1088/1367-2630/14/5/055027. [DOI] [Google Scholar]
- 29.Sperr P, et al. Status of the pulsed low energy positron beam system (PLEPS) at the Munich research reactor FRM-II. Appl Surf. Sci. 2008;255:35–38. doi: 10.1016/j.apsusc.2008.05.307. [DOI] [Google Scholar]
- 30.Barbiellini B, et al. Calculation of positron states and annihilation in solids: a density-gradient-correction scheme. Phys. Rev. B. 1996;53:16201–16213. doi: 10.1103/PhysRevB.53.16201. [DOI] [PubMed] [Google Scholar]
- 31.Torsti T, et al. Three real-space discretization techniques in electronic structure calculations. Phys. Status Solidi B. 2006;243:1016–1053. doi: 10.1002/pssb.200541348. [DOI] [Google Scholar]
- 32.Gonze X, et al. Recent developments in the ABINIT software package. Comput Phys. Commun. 2016;205:106–131. doi: 10.1016/j.cpc.2016.04.003. [DOI] [Google Scholar]
- 33.Keeble DJ, et al. Cation vacancies in ferroelectric PbTiO3 and Pb(Zr,Ti)O3: a positron annihilation lifetime spectroscopy study. Phys. Rev. B. 2007;76:144109–144105. doi: 10.1103/PhysRevB.76.144109. [DOI] [Google Scholar]
- 34.Rothmann MU, et al. Atomic-scale microstructure of metal halide perovskite. Science. 2020;370:eabb5940. doi: 10.1126/science.abb5940. [DOI] [PubMed] [Google Scholar]
- 35.Lee MM, Teuscher J, Miyasaka T, Murakami TN, Snaith HJ. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science. 2012;338:643–647. doi: 10.1126/science.1228604. [DOI] [PubMed] [Google Scholar]
- 36.Saidaminov MI, et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 2015;6:7586. doi: 10.1038/ncomms8586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Olsen JV, Kirkegaard P, Pedersen NJ, Eldrup M. PALSfit: a new program for the evaluation of positron lifetime spectra. Phys. Status Solidi C. 2007;4:4004–4006. doi: 10.1002/pssc.200675868. [DOI] [Google Scholar]
- 38.Barbiellini B, Puska MJ, Torsti T, Nieminen RM. Gradient correction for positron states in solids. Phys. Rev. B. 1995;51:7341–7344. doi: 10.1103/PhysRevB.51.7341. [DOI] [PubMed] [Google Scholar]
- 39.Arponen J, Pajanne E. Angular correlation in positron annihilation. J. Phys. F. 1979;9:2359–2376. doi: 10.1088/0305-4608/9/12/009. [DOI] [Google Scholar]
- 40.Arakcheeva A, Chernyshov D, Spina M, Forro L, Horvath E. CH3NH3Pbl3: precise structural consequences of water absorption at ambient conditions. Acta Crystallogr B. 2016;72:716–722. doi: 10.1107/S2052520616010428. [DOI] [PubMed] [Google Scholar]
- 41.Boronski E, Nieminen RM. Electron-positron density-functional theory. Phys. Rev. B. 1986;34:3820–3831. doi: 10.1103/PhysRevB.34.3820. [DOI] [PubMed] [Google Scholar]
- 42.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 43.Kawamura Y, Mashiyama H, Hasebe K. Structural study on cubic-tetragonal transition of CH3NH3PbI3. J. Phys. Soc. Jpn. 2002;71:1694–1697. doi: 10.1143/JPSJ.71.1694. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The positron lifetime data that support the findings of this study and source data for display items has been deposited in figshare with the identifier doi:10.6084/m9.figshare.15031926.