Hippocampal neurons construct a map of an abstract value space

SUMMARY

The hippocampus is thought to encode a ‘‘cognitive map,’’ a structural organization of knowledge about relationships in the world. Place cells, spatially selective hippocampal neurons that have been extensively studied in rodents, are one component of this map, describing the relative position of environmental features. However, whether this map extends to abstract, cognitive information remains unknown. Using the relative reward value of cues to define continuous ‘‘paths’’ through an abstract value space, we show that single neurons in primate hippocampus encode this space through value place fields, much like a rodent’s place neurons encode paths through physical space. Value place fields remapped when cues changed but also became increasingly correlated across contexts, allowing maps to become generalized. Our findings help explain the critical contribution of the hippocampus to value-based decision-making, providing a mechanism by which knowledge of relationships in the world can be incorporated into reward predictions for guiding decisions.

Graphical Abstract

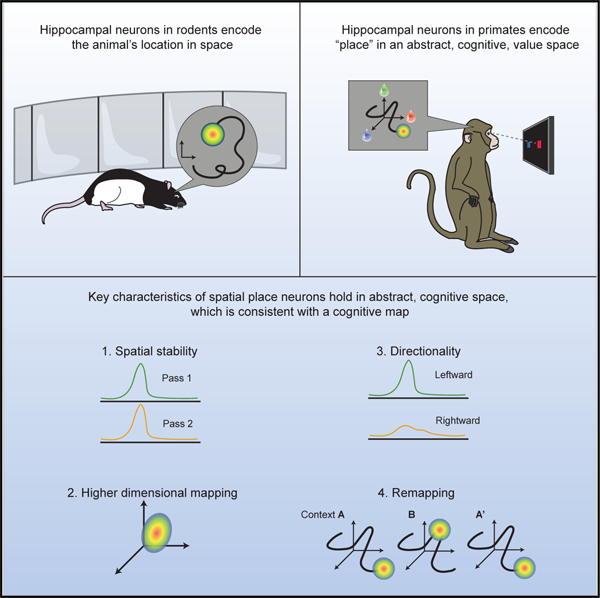
In brief

Single neurons in the primate hippocampus encode ‘‘paths’’ through a purely abstract value space similar to how place cells in rodents encode paths through physical space. Such cognitive maps provide a mechanism by which knowledge of relationships can guide decisions.

INTRODUCTION

Two of the most seminal findings regarding the hippocampus are that hippocampal damage in humans produces a dense amnesia for episodic memory (Eichenbaum, 2013; Scoville and Milner, 1957), and hippocampal neurons in rodents encode a spatial map of the animal’s environment (Moser et al., 2008; O’Keefe and Dostrovsky, 1971). One way to unify these disparate cross-species findings was the proposal that the hippocampus is responsible for encoding a ‘‘cognitive map’’ (Behrens et al., 2018; Buffalo, 2015; Howard et al., 2014; O’Keefe and Nadel, 1978), a network of associations that specifies how various features of the environment relate to one another. Such a map could be used to specify how the various disparate elements of a memory form a discrete episode, or how spatial landmarks form a map of the environment, thereby providing a theoretical framework in which to explain findings in both humans and rodents.

Despite the long-standing claim that hippocampal neurons encode cognitive maps (O’Keefe and Nadel, 1978), the evidence for this assertion is rather weak, relying mainly on the presence of neuronal responses that discriminate non-spatial sensory information (Howard et al., 2014; Ramus and Eichenbaum, 2000; Wood et al., 1999) rather than the representation of a map per se. Although a recent study examined the parametric coding of non-spatial information (Aronov et al., 2017), the experimental manipulation was still a sensory stimulus (auditory tone) rather than a cognitive parameter. Recent work in humans, however, has demonstrated hippocampal fMRI signals that are consistent with the encoding of a cognitive map. For example, Theves et al. (2019) taught humans to categorize abstract stimuli that could be defined in a two-dimensional feature space. Subsequently, the hippocampal response to the stimuli reflected the relative two-dimensional distances between the objects. In other words, the hippocampus appeared to encode distances in a multidimensional, abstract space the same way that it encodes spatial distances in navigational space.

Although sophisticated paradigms have been developed to explore the cognitive map in humans (Constantinescu et al., 2016; Park et al., 2020; Schapiro et al., 2013; Schuck et al., 2016), neural measures in humans lack the spatiotemporal resolution to determine the precise cellular mechanisms that underlie the representation of the cognitive map. In addition, the behavioral paradigms used in humans are typically too complex to easily translate to the animal model. We recently developed a paradigm that required animals to track changing reward values associated with sensory stimuli and showed that performance of the task was dependent on the anterior hippocampus (Knudsen and Wallis, 2020), which is the part of the hippocampus that strongly projects to prefrontal areas responsible for processing reward information (Barbas and Blatt, 1995). Reward is potentially a useful variable by which to probe the existence of the cognitive map because it is an abstract, relational, cognitive parameter that is nevertheless highly salient to animals. We recorded single neuron activity in the anterior hippocampus of two monkeys while they performed this task and found that hippocampal neurons encoded precise relationships between reward-predicting stimuli, deemed ‘‘value place fields,’’ in the space defined by possible reward values. This supports the idea that the hippocampus does not just encode space, but rather uses a multidimensional code to encode a variety of behaviorally relevant relational information.

RESULTS

Two macaques (subjects V and T) performed a task that required them to learn and choose between pairwise combinations of three novel pictures, each associated with the probability of earning a juice reward (Figure 1A; STAR Methods) as described previously (Knudsen and Wallis, 2020). Reward contingencies slowly changed throughout the session, requiring subjects to monitor and adapt their choice behavior. The evolving relationship of the pictures’ values relative to one another could be visualized as a trajectory in an abstract three-dimensional value space, with each axis defining the value of one of the pictures (Figure 1B). Subjects chose the best available picture most of the time (V: 70% ± 2%, 8 sessions; T: 72% ± 2%, 9 sessions) consistent with a simple model-free reinforcement learning (RL) mechanism (mean ± SEM, R² model versus behavior; V: 0.48 ± 0.1; T: 0.62 ± 0.06).

Figure 1. Task and preliminary evidence of value place neurons.

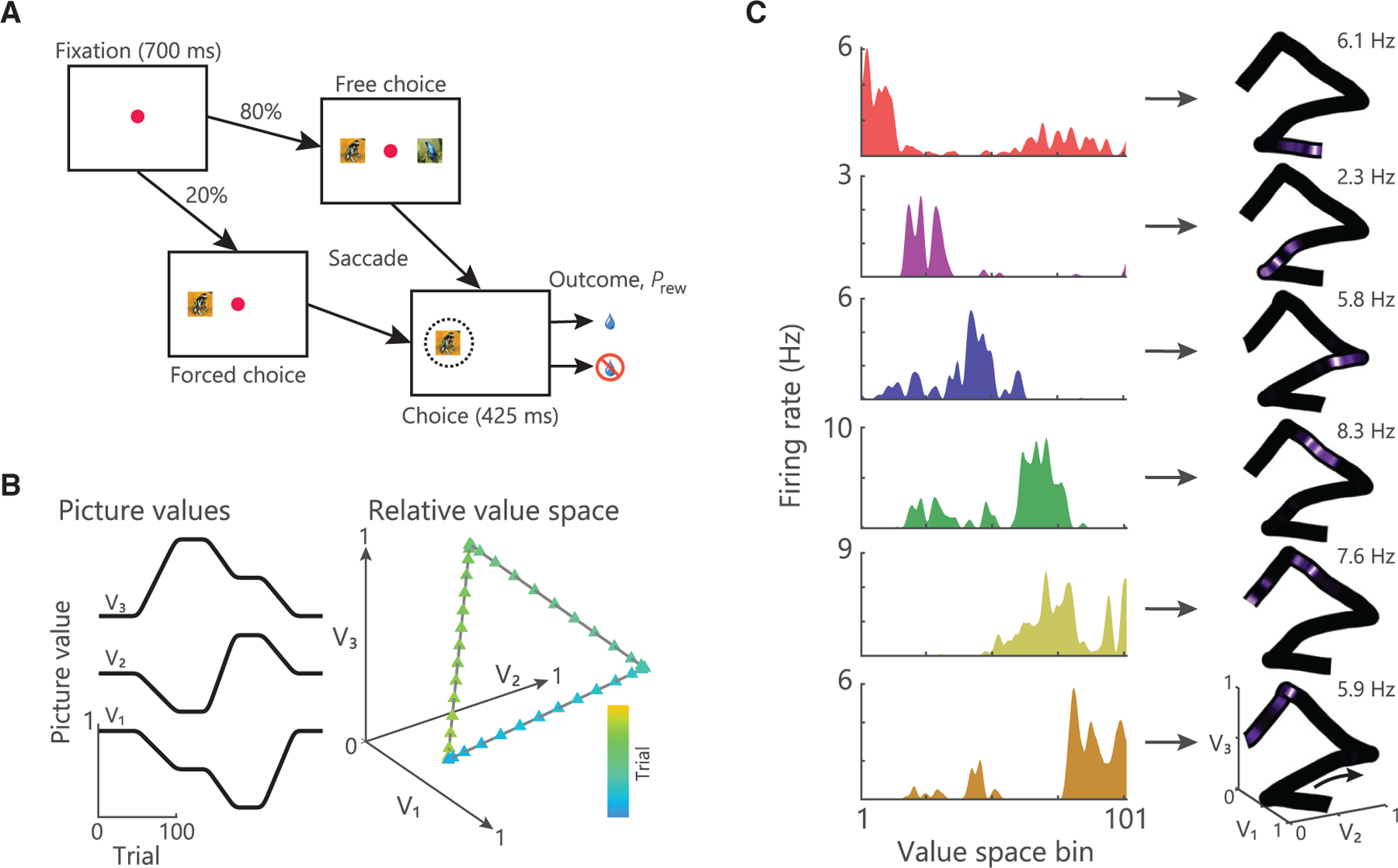
(A) Timeline of a single trial. Subjects centrally fixated for 700 ms and were then presented with either a forced or free choice. Subjects selected pictures via saccades, which resulted in the probabilistic delivery of reward (P_rew).

(B) Example of how the three picture values might change across a session (left) and the resultant trajectory through value space (right).

(C) Left: spike density histograms illustrating place encoding in value space for six hippocampal neurons. Right: firing rates overlaid onto the trajectory through value space mapped from 0 Hz to the peak firing rate as noted in the top right of each panel. These neurons are from a previous dataset (Knudsen and Wallis, 2020), which used the same task design, but arbitrary trajectories through value space. Different neurons were active in distinct regions of value space.

See also Figure S1.

We examined the activity of single neurons recorded from the anterior portion of the primate hippocampus (CA3 and CA1) (Figure S1) during the performance of this task. Many neurons fired bursts of action potentials sporadically over the course of the session. We examined whether this sparse activity encoded task relevant information. We focused on the fixation epoch of the task because our previous results showed that hippocampal activity during the fixation epoch is critical to task performance (Knudsen and Wallis, 2020), and the interpretation of this activity is more straightforward because it is not contaminated by which pictures were presented or the animal’s choice. Many neurons appeared to fire at specific places within value space, which we putatively characterized as value place fields (Figure 1C). Although the remainder of our analyses focuses on the fixation epoch, we observed similar value place fields during the choice epoch, and their location was highly correlated across the two epochs (Figure S2).

Hippocampal neurons encode value place fields

To better understand the behavior of these neurons and their relationship to value space, we designed different trajectories to test several predictions. We first examined whether value place fields were replicable by recording from 396 hippocampal neurons (Figure S1; V: 156 neurons, T: 240) as subjects made repeated traversals of a circular path through value space (Figure 2A). Many neurons appeared to fire at a specific location along the circular path that was consistent across repeated traversals (Figure 2B). To quantify this, we first identified neurons that had significant value space encoding (see STAR Methods). For each of these neurons (V: 107/156 or 69%; T: 100/240 or 42%), we then correlated value space encoding from the first to the second traversal (Figure 2C). Approximately 40% of the value selective neurons fired in a consistent region of value space across both traversals (V: 44/107 or 41%; T: 44/100 or 44%; Pearson’s ρ assessed at p < 0.01). This degree of consistency far exceeded chance levels for shuffled data (Figure 2C; V: 1.5%; T: 1.3%). We performed additional analyses to ensure that this consistency in value space was not an artifact of the temporal periodicity of the two trajectories. Because of differences in the length of drift periods, space and time were only marginally correlated (mean ± SEM Pearson’s correlation between time and space; V: ρ = 0.6 ± 0.01; T: 0.6 ± 0.04). Correlations based solely on time revealed far less consistency between the two trajectories (Figure 2D; V: 5% significant at p < 0.01; T: 2%). In addition, we fit general linear models to examine whether space or time predicted hippocampal firing rates. Very few hippocampal neurons coded time (V: 1/156 or 0.6%; T: 3/240 or 1%). Conversely, significantly more neurons coded space (V: 29/156 or 19%, χ² = 29, p < 0.00001; T: 97/240 or 40%, χ² = 111, p < 0.00001). We also analyzed the spatial distribution of fields from one pass to the next (Figure 2E). There were equivalent numbers of value place fields on both passes (V: 68 versus 74 fields; T: 76 versus 78 fields), approximately uniformly distributed along the length of the trajectory through value space. There was no difference in the mean amount of value space information (bits/spike) encoded by the neurons on pass 1 versus pass 2 (2-sample t test; V: 0.14 ± 0.02 versus 0.15 ± 0.01, t₁₄₆ = ‒0.18, p = 0.86; T: 0.16 ± 0.02 versus 0.12 ± 0.01; t₁₅₂ = 1.1, p = 0.27).

Figure 2. Value place neurons fire consistently during circular traversal.

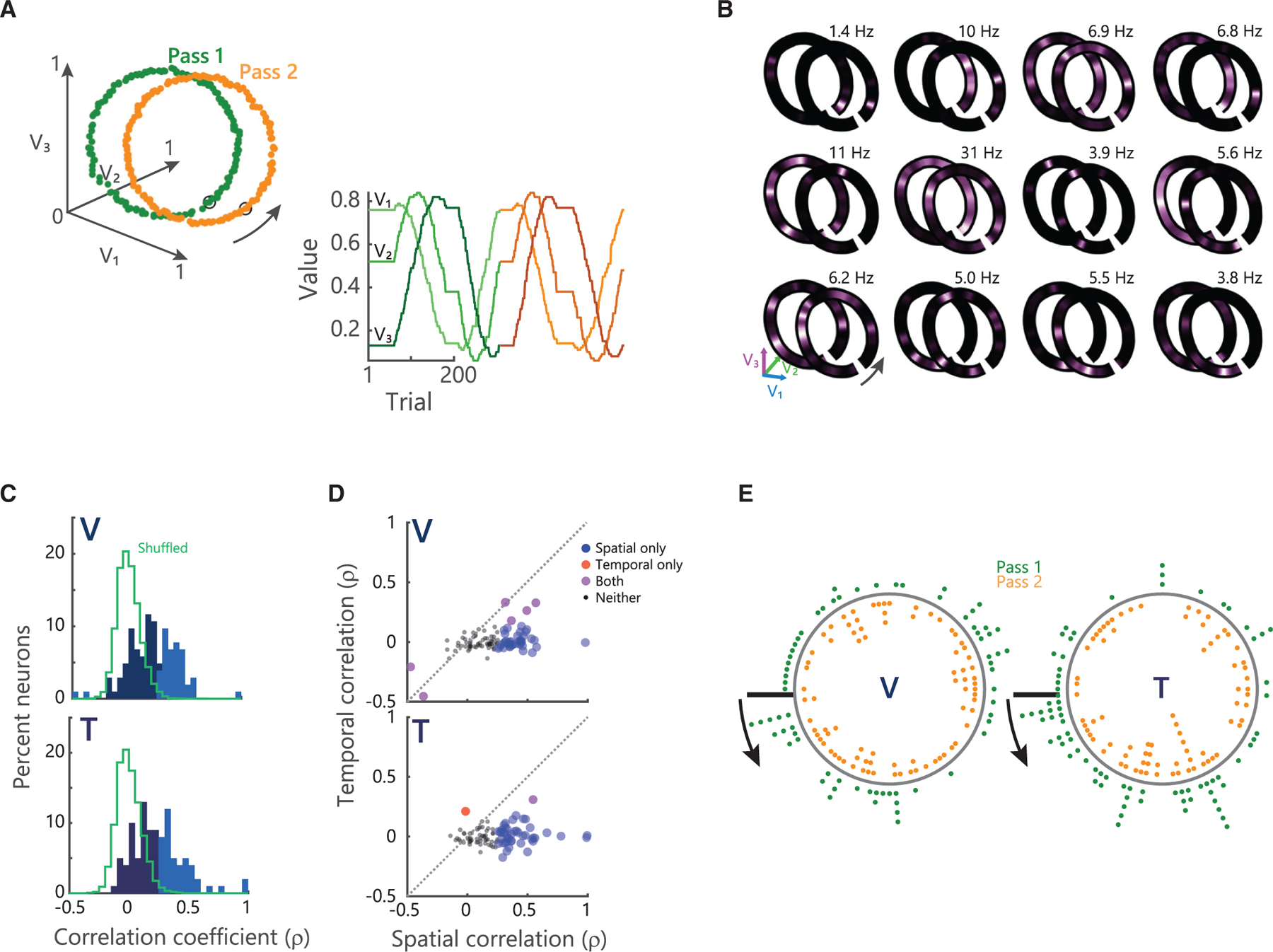
(A) Example circular trajectory. Left: picture values plotted in value space. Data points indicate individual trials. Green corresponds to pass 1 and orange to pass 2. Orange trajectory is offset along the V1 axis for illustrative purposes only. Arrow denotes direction of traversal. Right: picture values plotted in one dimension across the session. Change from green shades to orange shades denotes transition from pass 1 to pass 2. Picture values V1…V3 colored from light to dark shading of given color.

(B) Examples of hippocampal firing rates mapped on to circular trajectories. Peak firing rates across both traversals are noted in the top right of each panel.

(C) Distribution of the spatial correlation of firing rates on the first and second traversal for all identified value place neurons. Lighter shades denote correlations significant at p < 0.01. Green traces show the distribution of correlations for shuffled data.

(D) Scatterplot of spatial and temporal correlations between pass 1 and pass 2. The majority of neurons show significant spatial correlations, but are not significantly temporally correlated.

(E) Distribution of all value place fields on pass 1 (green dots) and 2 (orange dots). Arrows start at value bin 1 (black line) and point in the direction of traversal.

See also Figures S1, S2, S3, and S4.

These results suggest that hippocampal neurons are encoding specific locations within value space, and their value place fields cover the entire value space. However, we also examined whether hippocampal firing might be better explained by other relationships between value parameters (Wallis and Rich, 2011), such as those observed in other brain regions like orbitofrontal cortex (Abe and Lee, 2011; Kennerley et al., 2011; Padoa-Schioppa, 2013; Rich and Wallis, 2014). A priori, it was unlikely that these factors could account for value place fields, because such tuning would result in clustering of value place fields, rather than the relatively even distribution that we observed. Nevertheless, we explicitly tested for this tuning using a regression model (Figure S3; STAR Methods). Many neurons did indeed encode these parameters (assessed by β values at p < 0.01; value sum, value range, value difficulty; V: 32%, 24%, and 15% of 156 neurons, respectively; T: 36%, 26%, and 24% of 240). However, most neurons encoding value place fields did not encode these parameters (V: 73%, 80%, and 86% of 107 neurons encoded value place fields but did not encode value sum, value range, or value difference respectively; T 76%, 85%, and 83% of 100 fields). We also simulated orbitofrontal neuronal response properties, using data that we collected on a previous version of this task (Knudsen and Wallis, 2020) that used less structured trajectories, such as those shown in Figure 1C. We used the best fitting regression model from that study to generate how the neurons would respond on the circular trajectories used in the current study. These simulations did not produce value place fields (Figure S4).

Value place fields on the circular path were constrained to two dimensions. To test the dimensionality of the value place fields, we designed a helical path of similar diameter to the circular path that gradually traversed a third dimension (Figure 3A). Both subjects completed between 2 and 4 loops of the helix per session, although subject V tended to complete 4 loops more often than subject T (V: 3.2 ± 0.4; T: 2.8 ± 0.3). We assessed value place activity in 578 hippocampal neurons (V: 355, T: 223). Approximately 60% had a place field in at least one loop (224/355 or 63%, in V; 136/223 or 61% in T), with consistent numbers of fields on each loop (χ², V: loops 1–4, 140/355, 160/355, 115/282, and 42/90, χ² = 2.8, p = 0.4; T: loops 1–3, 69/223, 75/223, 78/204, χ² = 1.4, p = 0.5). Many value place fields spanned multiple loops of the helix (Figure 3B), although the tuning typically became progressively weaker with increased distance from the center of the field (Figure 3C).

Figure 3. Value place neurons map the extent of three-dimensional value space.

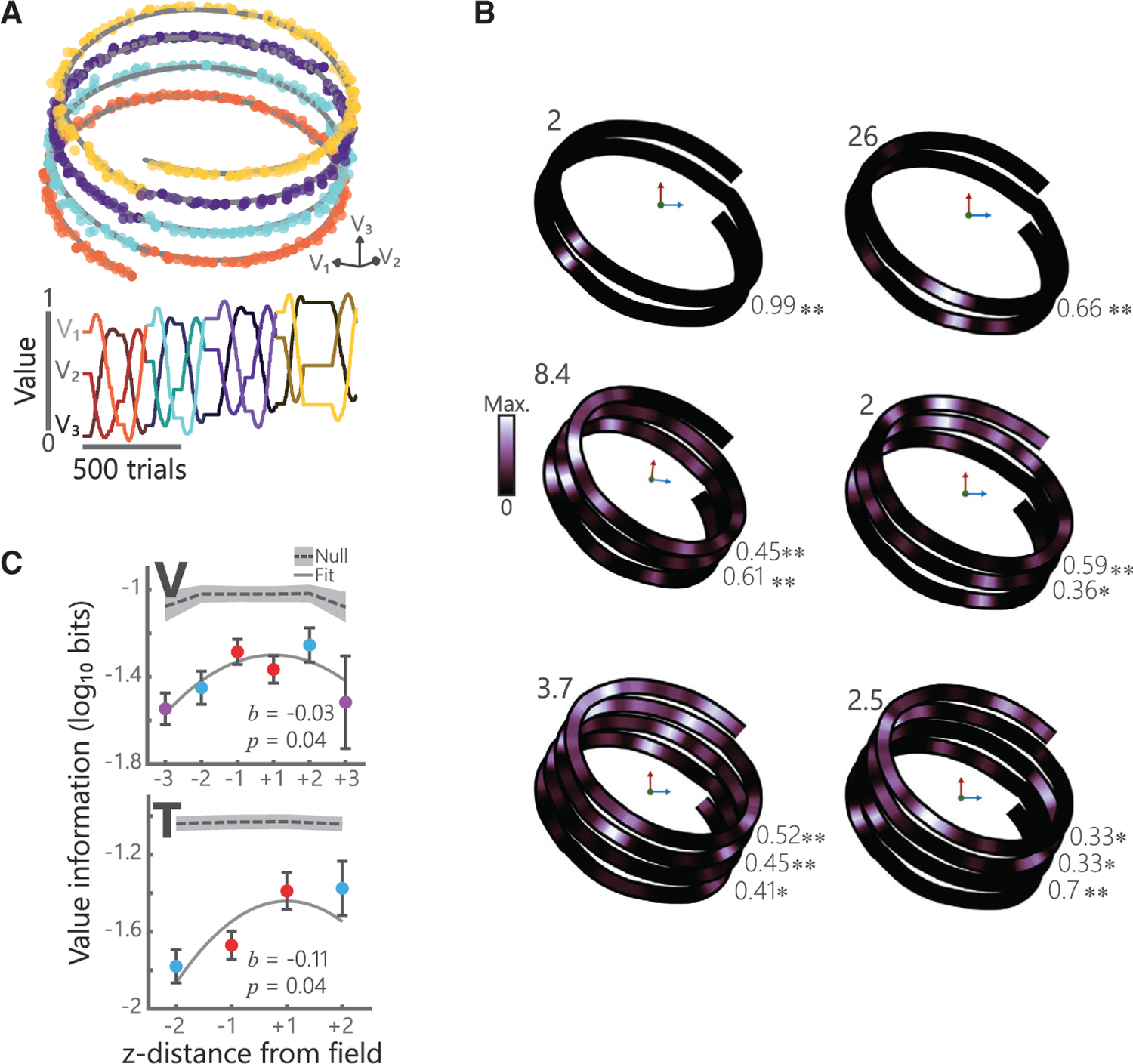
(A) Example helical trajectory from a session where subject V performed 4 loops of the helix. Convention follows Figure 2A.

(B) Single neuron examples showing value place fields in three dimensions for sessions where subjects completed two (left), three (middle), or four (right) loops of the helix. Numbers in the upper left of each plot denote the maximum firing rate of that neuron. Numbers in the bottom right of each plot denote spatial correlations between adjacent loops for each neuron (*p < 0.01, **p < 1 3 10^‒6).

(C) Spatial information of value place fields in three dimensions. For each neuron, 0 was defined as the location with the maximum spatial information and the information content for prior and subsequent loops is illustrated (mean ± SEM). A quadratic fit of log-transformed spatial information, I, by z-distance (lnI = b₀ + b₁[z-distance]²) was significant in both subjects. Gray shading indicates null distributions derived from applying the same procedure to shuffled data (250 shuffles, 95% confidence interval shown).

See also Figures S1, S2, S3, and S4.

Value place cells are directionally sensitive

When a rodent alternates runs down a linear track, hippocampal place cells often form directional fields, such that place activity in one direction of travel is largely uncorrelated from the other (Gothard et al., 1996). We tested whether value place fields had similar directional properties by designing a double lemniscate trajectory through value space (Figure 4A). Subjects made passes through the center of the space from four distal points. This resulted in two passes traversing the central point from the same direction and two passes traversing the central point in opposite directions. Subjects performed the task well, choosing the highest value picture most of the time (mean ± SEM optimal choices, V: 68% ± 1%; T: 63% ± 1%)

Figure 4. Hippocampal neurons encode value place in a directional manner.

(A) Schematic of the double lemniscate task. Convention follows Figure 2A. Gray box indicates the overlap regions.

(B) Five examples of hippocampal neurons encoding position in value space along the double lemniscate trajectory. Top: firing rate for the whole trajectory. The peak firing rate is shown in the upper right. Middle: firing rate on the congruent, rightward passes through the central point. Firing rates are normalized within each pass. Correlation values between the two passes are shown (*p < 0.01, **p < 0.001). Bottom: firing rate on the opposing (up versus down) passes. Opposing trajectories have been rotated to be in alignment for visualization.

(C) Distribution of spatial correlations for congruent (left) and opposing (right) passes through value space for all recorded value place neurons. Colored regions denote significant correlations at p < 0.01; gray lines show shuffled null distributions. The proportion of neurons with significant correlations was greater than chance in all cases (two-sample t tests comparing the absolute values of real and shuffled data), but there were significantly more correlated neurons for congruent versus opposing passes. The bimodality of the actual data and the shuffled data arises from the analysis procedure that we used to account for slight misalignments between trajectories (see STAR Methods).

(D) Examples of value place fields that were positively skewed (top row; S > 0), unskewed (middle row; S ≈ 0), and negatively skewed (bottom row; S < 0). Vertical dashed lines correspond to the field’s CoM. The value F denotes the percent of the value space trajectory that the field spanned. Overall, fields typically spanned ~2% of the trajectory (V: 1.8% ± 2%; T: 1.6% ± 1.8%).

(E) Mean (±SEM) skewness values for different portions of the lemniscate for all value place fields. Significance deviations from zero were determined by one-sample t tests (*p < 0.05, **p < 0.001). The second traversal of the correlated trajectory resulted in a significant negative skew.

See also Figures S1, S2, S3, S4, and S5.

We analyzed 717 hippocampal neurons (V: 365, T: 352) for place activity (see STAR Methods). Consistent with the other trajectories, approximately half of the recorded neurons had a place field on at least one section of the trajectory (Figure 4B) (V: 169/365 or 46%; T: 209/352 or 59%). We correlated place activity along the overlapping portions of the lemniscate, which comprised ~25% of the total trajectory (indicated by the box in Figure 4A). When subjects passed through the center of space in the same direction, 36% of place neurons were significantly positively correlated (Figure 4C) (V: 40/138 or 29%; T: 63/152 or 41%). However, when subjects passed through space in opposite directions, there were significantly fewer positively correlated neurons (V: 12/137 or 9%, T: 11/149 or 7%; V: χ² = 14; T: χ² = 47, both p < 0.001). Additionally, some neurons had significant negative correlations. These neurons were active on opposite ends of the trajectory (Figure 4B, bottom middle example). These neurons were not particularly prevalent. There were approximately three times as many neurons with positive correlations (V: 52, T: 74) compared to those with negative correlations (V: 18, T: 20). It is conceivable that these neurons may have encoded additional structure, such as discriminating the outer or inner portions of the trajectory, but additional experiments with other trajectories would be needed to confirm this.

Traditional spatial place fields are shaped by experience. They are initially Gaussian, but with experience they begin to gradually ramp up in activity as the animal approaches the center of the field, resulting in a negatively skewed place field (Mehta et al., 2000). To examine whether this was the case in our data, for each value place field, we computed a skewness index by comparing firing rates on either side of the field’s center of mass (Figure 4D; STAR Methods). Across the population of value place cells, fields were negatively skewed only on the portion of the trajectory that subjects had previously experienced, that is the second pass along the correlated portion of the trajectory (Figure 4E). This was consistent with behavioral results which showed that subjects used their prior experience along the trajectory. Subjects’ performance significantly improved on the second pass along the correlated portion of the trajectory relative to the first pass (Figure S5). We also saw a skewing of value place fields on the second traversal of the circular trajectory relative to the first (Figure S5), again consistent with skewing reflecting an effect of experience.

Taken together, these results show that hippocampal value place cells conserve two important directional properties observed in rodents running on linear tracks. First, neurons are directionally selective. Value place fields are uncorrelated when the subject traverses the same location in abstract value space in different directions but are correlated when the traversal occurs in the same direction. Second, neurons shape their value place fields with experience, as the animal learns to predict the direction of the trajectory.

Response of value place fields to novel pictures

A common feature of hippocampal place fields is that they are not static, but rather can flexibly remap in response to perturbations of the environment. For example, hippocampal neurons can completely shift their preferred firing location in response to changes in one or more features associated with space, or when the location of reward within an environment changes (Anderson and Jeffery, 2003; Fyhn et al., 2007). These changes reverse when the original context is restored. We tested if these place cell properties occurred in abstract value space by introducing a contextual shift in an A-B-Aʹ block structure using the circular path (Figure 5A). The two A blocks (A and Aʹ) shared a common set of pictures, and the B block used a novel set of pictures while the underlying trajectory through value space was preserved. We hypothesized that the introduction of novel pictures in the B block would require a relearning of stimulus-outcome associations, and hence, would result in a remapping of value place fields.

Figure 5. Changing stimuli while preserving the trajectory induces value place neuron remapping.

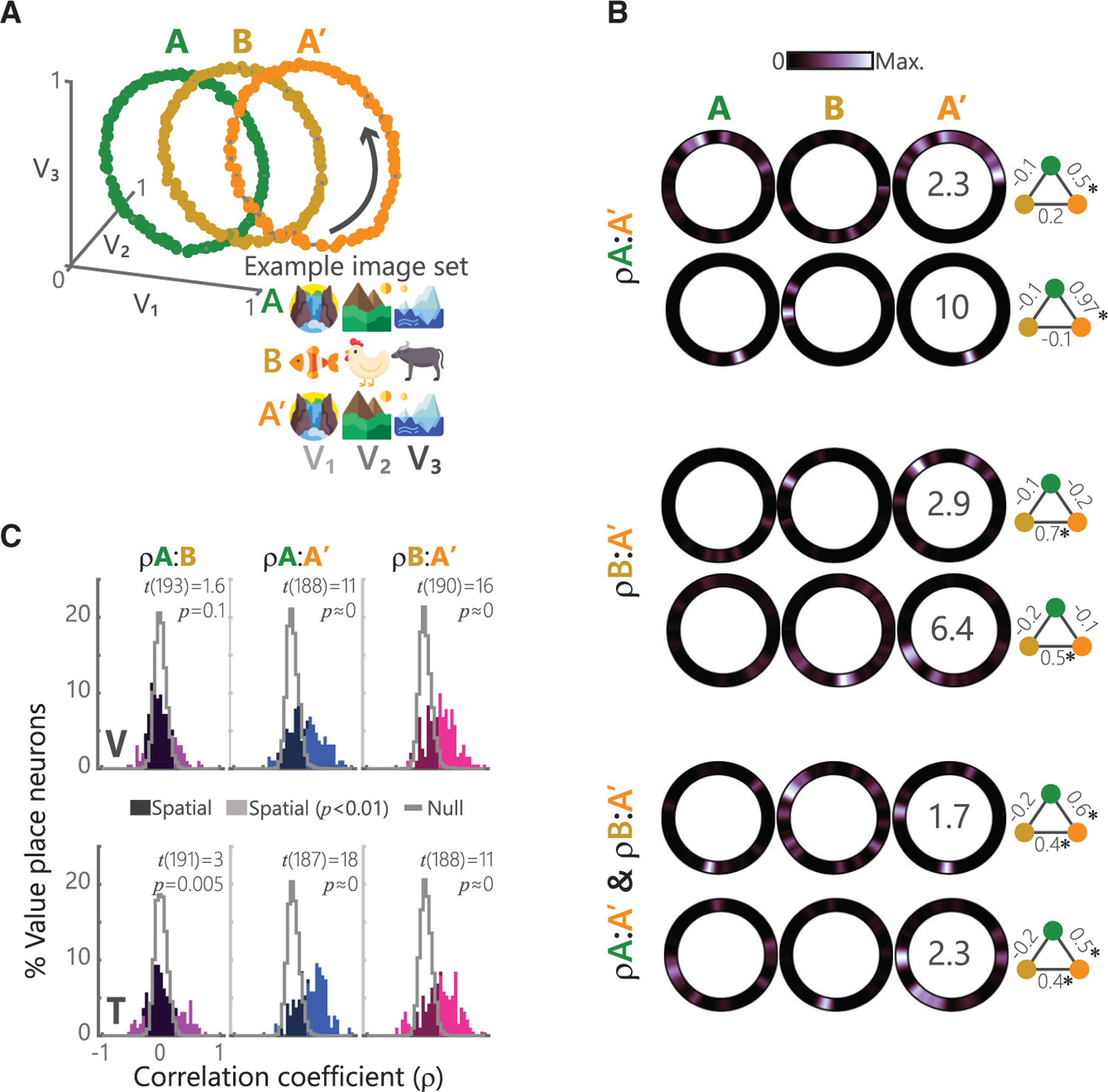
(A) Schematic of the ABAʹ task. Left: convention follows Figure 2A. Right: example picture sets for each block. Picture values V1…V3 follow the trajectories shown in Figure 2A.

(B) Single neuron examples showing three distinct patterns of how value place fields change across blocks. Top: two neurons that were significantly spatially correlated on only the A and Aʹ blocks (ρA:Aʹ). Middle: two neurons spatially correlated on only the B and Aʹ blocks (ρB:Aʹ). Bottom: two neurons that were correlated on both A:Aʹ and B:Aʹ blocks (ρA:Aʹ & ρB:Aʹ). Numbers superimposed on Aʹ block activity denote the peak firing rate of the neuron across all three blocks. The schematic to the right of each neuron displays the pairwise correlations (*p < 0.001) between blocks A (green), B (yellow), and Aʹ (orange).

(C) Distribution of spatial correlation of firing rates for all recorded value place neurons for all pairwise combinations of blocks. Convention follows Figure 2C. Test statistics and p values from a one-sample t test shown.

See also Figures S1, S2, S3, and S4.

We analyzed value place coding in 616 hippocampal neurons (V: 272, T: 344) as described above, quantifying value space fields independently for each block. Many neurons significantly encoded a value place field during at least one block (V: 201/272 neurons or 74%; T: 194/344, 56%). There tended to be an increased number of identified value place fields as subjects traversed from one block to the next (Cochran’s Q test for number of place neurons per block; V: A, 109/272, B, 133/272, Aʹ, 148/272, Q = 17, p = 0.0002; T: A, 110/344, B, 101/344, Aʹ, 130/344, Q = 8.8, p = 0.01) suggesting a recruitment of place neurons.

Many neurons had value place fields in at least two blocks (V: 153/201 or 76%, T: 162/194 or 84%) allowing us to assess how the location of the value field changed. For most neurons, the location of the value place field changed from the A block to the B block (V: 109/153 or 71%, T: 101/162 or 62%). We did not find any consistent pattern in this remapping. However, when the task returned to the A block (Aʹ), three distinct patterns emerged. Some neurons switched back to the original field from block A (Figure 5B, top, V: 29/153 or 19%, T: 35/162 or 22%). Others retained the field from block B (Figure 5B, middle, V: 42/153 or 27%; T: 27/162 or 17%). Still others retained both fields (Figure 5B, bottom, 38/153 or 25%; T: 39/162 or 24%). The net effect of these changes is that across the population there was little correlation in the location of value place fields between block A and block B, but a strong positive correlation between blocks A and Aʹ and blocks B and Aʹ (Figure 5C).

In summary, value place fields were not static: novel pictures induced a remapping that was retained even when the original pictures were restored. These changes could reflect the process by which subjects generalize across picture sets to exploit acquired knowledge of the underlying trajectories.

DISCUSSION

A fundamental goal of neuroscience is to understand how the brain constructs internal representations of the world to flexibly guide behavior. In the Euclidean world, hippocampal place cells form one component of such a representation. However, whether the problem at hand is navigating to the coffee shop or navigating your social network when you arrive, cognitive maps, spatial, sensory, and conceptual alike, appear to share a common computational substrate for the systematic organization of structural information (Behrens et al., 2018). Here, we present findings that single neurons in the primate hippocampus construct a map for an abstract cognitive variable through place-like representations. Specifically, the map identifies the relative value of three choice options. Value place neurons exhibited four canonical properties of their Euclidean counterparts: consistency across experiences, multidimensional tuning, directional selectivity, and remapping in novel contexts.

Hippocampal contributions to reward-based learning

Previous studies have demonstrated that the hippocampus encodes reward information in the context of spatial navigation. For example, Sun et al. (2020) recently found that when rats received reward on every fourth lap around a track, a subpopulation of place neurons were primarily active on one of four laps only, providing an organizational code to track individual episodes in the pursuit of reward. Other hippocampal signals have also been found to correlate with reward. Spatial information decoded from individual theta cycles predicted a rat’s distance to a reward (Wikenheiser and Redish, 2015), whereas hippocampal replays decoded from sharp-wave ripples were biased toward rewarded locations (Pfeiffer and Foster, 2013). Causal manipulations have also implicated a role for the hippocampus in reward processing. Humans and monkeys with hippocampal damage have difficulty making reward-based decisions (Bakkour et al., 2019; Murray et al., 1998), whereas microstimulation of the anterior hippocampus at the theta frequency disrupts reward-based learning (Knudsen and Wallis, 2020). Our results suggest the specific neural code that might underlie these deficits. Value, like space, is an inherently relational construct (Louie et al., 2011; Rangel and Clithero, 2012): we determine the value of a reward relative to other potential outcomes. For example, the exact same reward can be experienced as either positive or negative, depending on whether an alternative choice would have led to a larger or smaller reward (Camille et al., 2004). Hippocampal activity appears optimized for representing a relational code (Eichenbaum et al., 1999; Whittington et al., 2020) and so it appears that it is used for representing a map of the relative value of options to one another, just as it can also be used for representing a map of the relative location of objects to one another. Indeed, results from neuroimaging in humans have suggested that the hippocampus may be broadly implicated in representing abstract relationships in cognitive space (Park et al., 2020; Theves et al., 2019).

Computational accounts have described two distinct mechanisms by which reward outcomes can be learned (Dolan and Dayan, 2013). Model-free reinforcement learning (RL) is associated with habits and skills and relies on trial-and-error, storing or caching the values of past actions, and inflexibly repeating those actions that led to higher values. Model-based RL is associated with goal-directed actions and generates predictions via a computationally expensive process that depends on a model of the task at hand but is also able to flexibly respond to environmental changes. There is substantial overlap between the concept of a task model and a cognitive map (Schapiro et al., 2013; Wikenheiser and Schoenbaum, 2016). Orbitofrontal cortex has been particularly implicated in the representation of task models (Schuck and Niv, 2019; Wikenheiser and Schoenbaum, 2016; Wilson et al., 2014; Zhou et al., 2019). However, it seems unlikely that orbitofrontal cortex would solely be responsible for constructing the cognitive map because it typically encodes little information about sensorimotor contingencies (Abe and Lee, 2011; Padoa-Schioppa and Assad, 2006; Wallis and Miller, 2003). This contrasts with the hippocampus where neurons encode sensorimotor contingencies in addition to spatial and temporal contexts, precisely the kind of information that is essential for building task models (Howard et al., 2014; McKenzie et al., 2014). Thus, it is possible that the orbitofrontal cortex and hippocampus work in conjunction to construct models useful for solving tasks (Niv, 2019). Indeed, we have previously shown that when subjects are performing the same task used in this paper, there is an increase in synchrony in the theta oscillation between orbitofrontal cortex and hippocampus (Knudsen and Wallis, 2020), consistent with a transfer of information between the two structures (Brincat and Miller, 2015). The current results suggest the nature of this transferred information: a concise neural code that represents the value of the potential outcomes relative to one another.

We also found that value place neurons are sensitive to the direction of travel through the location in value space. This is consistent with findings in the spatial domain (Gothard et al., 1996; McNaughton et al., 1983) and subsequent findings in non-spatial domains, for example when mice traverse olfactory gradients (Radvansky and Dombeck, 2018). Thus, it is likely that starting from distinct initial states and observing how these states evolve is enough to encourage directional firing. Directionality also influenced the geometry of the value fields themselves. Opposite direction traversals did not affect field shape, but when a portion of the path was experienced for a second time, fields were negatively skewed. This phenomenon is well documented: as rats make repeated traversals along a linear track, not only do directional place fields emerge with experience (Navratilova et al., 2012), but the fields themselves gradually become negatively skewed (Mehta et al., 2000), reflecting inference about upcoming states. Future research could examine other factors that might influence the geometry of value place fields. For example, it is possible that manipulations of the value space, such as compressing the variance in one dimension (Conen and Padoa-Schioppa, 2019) may affect how fields are shaped, just as the geometry of a spatial environment determines the shape of two dimensional fields (O’Keefe and Burgess, 1996).

Although we have drawn parallels between value place fields and spatial place fields, it is likely that the two maps are instantiated by different parts of the hippocampus. In rodents, the dorsoventral axis demonstrates clear functional differences: dorsal neurons have smaller place field sizes and fewer non-spatial representations than ventral neurons (Jung et al., 1994; Royer et al., 2010), whereas neurons in the intermediate hippocampus fall roughly in between the two poles (Kjelstrup et al., 2008). In contrast, ventral hippocampus is crucial for flexible learning (Avigan et al., 2020), representing task structure (Wikenheiser et al., 2017), and social behavior (Okuyama et al., 2016), high-level behaviors that would benefit from cognitive maps. The dorsoventral axis in the rodent corresponds to the posterior-anterior axis in primates, where there has been a dramatic increase in the size and complexity of the anterior portion of the hippocampus (Inausti, 1993), consistent with the sophistication of the primate behavioral repertoire, and the increase in the size and complexity of the frontal cortex, with which the anterior hippocampus connects (Barbas and Blatt, 1995). Thus, we would predict that value place fields may be preferentially located in the anterior hippocampus relative to the posterior hippocampus, whereas the reverse would be true for spatial place fields.

Generalization of experience

Introduction of novel stimuli while preserving the path through value space induced remapping of value place fields. Similar observations have been made for hippocampal place neurons with respect to physical space (Bostock et al., 1991). For example, remapping of place fields occurred when the color or smell of an arena changed (Anderson and Jeffery, 2003). When the original context was restored, the original place fields returned (Fyhn et al., 2007). A theoretical explanation of what induces remapping has recently been provided by Gershman et al. (2015) and Sanders et al. (2020). They argue that remapping reflects an animal’s attempts to infer whether they are in a different ‘‘state’’ of the world. The lack of overlap in sensory cues between blocks A and B in our task likely favored the inference that there were two different states and so produced remapping. Baram et al. (2021) have also suggested that stimulus changes might be critical to understanding hippocampal remapping. In their account, the entorhinal cortex is responsible for encoding task relationships, while the hippocampus enables generalization by allowing the same task structure to be applied to different sensory stimuli.

Intriguingly, we found that value place field correlations remained high when transitioning from the second context back to the original. Baraduc and colleagues recently observed a similar phenomenon with spatial place fields (Baraduc et al., 2019). Monkeys were trained to forage in two different virtual reality environments, one novel and one familiar. Each environment shared a common underlying spatial structure despite differences in salient landmarks. As the animals learned the novel environment, hippocampal place fields became increasingly correlated with the familiar environment. The authors concluded that this was the underlying neural representation of generalization, whereby a task ‘‘schema’’ is acquired. Consistent with this interpretation, subjects required far less practice in the novel context to achieve good performance, relative to the initial acquisition of the familiar environment. A conceptually similar approach was tested in human participants that learned two image sets corresponding to two different underlying task structures that specified the relationship between the images (Mark et al., 2020). When participants were given a novel image set in a second session, those who had learned the underlying hidden task structure were quickly able to infer relationships between images that were otherwise unknown, suggesting the formation of a schema.

A related possibility is that the correlations observed in Aʹ might reflect the formation of still higher-order schema, for example, perhaps reflecting the co-occurrence of A and B in the same experimental session, or that could flexibly switch between A and B. This would allow the formation of schemas at different levels in a hierarchy of abstraction, which could aid performance on a task, say, that alternated between blocks ABAʹ and CDCʹ on different days. Although speculative, such ideas could be tested in rodents, where chronic recordings across days are more feasible.

Future directions

The results presented here demonstrate the first direct neurophysiological basis of a hippocampal map in a purely cognitive space, providing a crucial link between studies of relational memory and spatial navigation. We also showed that the value space map shares many of the features of the hippocampal map of Euclidean space. This raises the question whether other hippocampal mechanisms, such as replay (Foster, 2017; Foster and Wilson, 2006), theta cycling (Kay et al., 2020), and phase precession (Mehta et al., 2002) are also evident in hippocampal value encoding. Evidence of replay-like activity has been identified in the human brain during the performance of nonspatial tasks (Liu et al., 2019; Schuck and Niv, 2019), but it is not known whether this effect is driven by populations of hippocampal neurons. Furthermore, it is unknown whether value place cells interact in the larger hippocampal-entorhinal system. Activity consistent with grid cells has been demonstrated in the entorhinal cortex in a variety of domains, including olfactory information in the rodent (Bao et al., 2019), spatial information in the monkey (Killian et al., 2012), and conceptual information in humans (Constantinescu et al., 2016). Future work should examine the extent to which cognitive and spatial codes rely on shared underlying neural codes (Whittington et al., 2020).

Limitations of the study

Our data show that when subjects traversed a predefined trajectory through an abstract value space, hippocampal neurons displayed many canonical features of spatial place neuron activity. There are number of limitations to our results. First, unlike physical space, which rodents actively explore, the traversal through value space was passive in our task. Future work will need to consider the activity of hippocampal value place neurons when subjects are actively navigating abstract spaces. Second, results in rodents have shown qualitatively different types of remapping dependent on the extent of contextual changes (Leutgeb et al., 2005). We will likewise need to see how different manipulations of contextual changes affect remapping in the value space. Finally, rodent studies have described clear functional differences along the hippocampal axis. It will be important to examine whether value place fields show analogous functional organization.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Eric Knudsen (eric.knudsen@berkeley.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• The datasets supporting the current work are available on reasonable request from the corresponding author

• The code used to analyze data are available on request from the corresponding author

• Requests for any additional information should be directed to the corresponding author

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Two male rhesus macaques (subjects V and T, respectively) aged 7 and 9 years, and weighing 10 and 13 kg at the time of recording, were used in the current study. Subjects sat head-fixed in a primate chair (Crist Instrument, Hagerstown, MD) and interacted with the task via eye movements digitized with an infrared eye-tracking system (SR Research, Ottawa, Ontario, CN). Subjects each had a large unilateral recording chamber centered over the frontal lobe with access to the temporal lobe. All procedures were carried out as specified in the National Research Council guidelines and approved by the Animal Care and Use Committee and the University of California, Berkeley.

METHOD DETAILS

Task Design

Subjects performed a task in which they were required to choose between pairs of pictures (Knudsen and Wallis, 2020). Each picture had a value to the animal that was defined by the probability that its selection would be rewarded with juice. A single trial started with the presentation of a small, red fixation cue in the center of the screen. Subjects were required to fixate this cue for 700 ms (‘Fixation’ epoch). Following fixation, either one (forced choice, 20% of trials) or two (free choice, 80% of trials) pictures were presented at 8° of visual angle to the left or right of the fixation cue. Picture locations were randomized and counterbalanced, and forced choice trials were randomly interspersed with free choice trials. Subjects were free to visually inspect each available option and ultimately indicated their choice by maintaining fixation on the chosen picture for 425 ms. Following choice, a delay of 500 ms preceded the delivery of the outcome (reward/no reward). Trials were separated by a 2000 ms intertrial interval. Stimulus presentation and behavioral conditions were controlled using the MonkeyLogic toolbox (Hwang et al., 2019).

The relative values of each of three pictures changed over the course of a session. Furthermore, these changes were designed to map a trajectory through a three-axis ‘value space’ defined by the relationships between the values of the three pictures. For example, the point (0.8, 0.4, 0.3) would correspond to the first picture (V₁) having a value of 0.8 (i.e., rewarded 80% of the time it was selected), V₂ a value of 0.4, and V₃ a value of 0.3. We designed three trajectories to test various hypotheses: a circle, a helix, and a looping track defined by two orthogonal lemniscates. The different trajectory configurations were randomly interleaved across recording.

To maintain the motivation of the subjects we interspersed stable periods along the trajectories where reward contingencies did not change. These stable points were placed at intervals of π for the circular and helical paths, and at the extremities of the lemniscate configuration. Drift periods consisted of the periods between stable points when the reward contingencies changed. We varied the rate of change to ensure that each drift traversed between 25 to 40 unique points along the trajectory. An additional constraint was that movement along the trajectory at each step required all three stimuli to have occurred. Thus, the smallest number of trials within each value bin would be two, but was often larger. Finally, each session had a small (~5% of all trials) number of unforced errors where the subjects either did not engage fixation or broke fixation early, resulting in a repeating of the trial. The net result was that drift periods varied from 50 – 158 trials (mean 118 ± 3) for subject V and 50 – 99 (mean 70 ± 2) for subject T. This variability allowed us to unconfound time and position within value space.

Neurophysiological recordings

Subjects were fitted with head positioners and imaged in a 3T scanner (Figure S1A). The resulting images were then used to generate 3D reconstructions of each subject’s skull and target recording locations within the brain. We implanted customized radiolucent recording chambers over the left hemisphere in both subjects. In each recording session, we lowered up to 4 multisite linear probes into the hippocampus (Figure S1B). Electrode trajectories and the appropriate microdrives were defined in software and 3D printed (Form 2, Formlabs, Cambridge, MA) using custom designs (Knudsen et al., 2019). We recorded 2307 hippocampal neurons (V: 1148, T: 1159) over the course of 27 sessions (V: 16 sessions, T: 11 sessions) using a combination of 16- and 32-channel probes with 100 mm contact spacing (Plexon). Our recordings targeted CA1 and CA3 of the anterior portion of the hippocampus. We confirmed our location in the hippocampus via the presence of sharp wave ripples (Figure S1C), prominent theta-band (8–12 Hz) activity (Figure S1D), and complex-spiking (bursting) patterns of neuronal activity (Figure S1E). Neuronal signals were digitized using a Plexon OmniPlex system with continuous spike-filtered signals (200 Hz – 6 kHz) acquired at 40 kHz and local field-filtered signals (0.1 – 250 Hz) sampled at 1 kHz. We transformed single neuron activity into a binary time series at 1 ms resolution, where 1 indicated the presence of a spike and 0 the absence.

QUANTIFICATION AND STATISTICAL ANALYSES

Behavioral modeling and analysis

To determine how a map of value space might affect choice behavior, we used a standard temporal difference RL model (Sutton and Barto, 1998) that learns picture values Q_n by integrating a prediction error arising from the outcomes of choices:

$$Q_{t,n}\leftarrow Q_{t-1,n}+\alpha \left(R_t-Q_{t-1,n}\right)$$

where Q_n is the value of the n^th picture on trial t, R is the outcome of choosing the n^th picture on trial t-1, and α is the learning rate, which dictates how much weighting prediction errors have on value updates. Choices are then made by using the standard softmax-activation function:

$$P_{t,j}=\frac{e^{\beta Q_{t-1,i}}}{e^{\beta Q_{t-1,i}}+e^{\beta Q_{t-1,j}}}$$

where P_t,i is the probability of choosing the picture i over picture j on trial t, and β is the inverse temperature parameter that determines the slope of the choice function, and hence the noisiness of choices. Throughout the paper we use the term V to indicate the objective value of the picture (the actual probability of reward) and Q to indicate the subjective value of the pictures (the animal’s estimate of the value of the picture) derived from the RL model. Optimal fits for both subjects in the TD model were α ~0.1 and β ~4, consistent with our previous work (Knudsen and Wallis, 2020).

Measuring value place fields

Because drift periods were variable in length, our first step was to bin trials to ensure uniformity in our analyses across neurons. We downsampled trajectories to a predetermined number of points; the circular trajectory, individual loops of the helix and passes of the lemniscate path were all tiled to a length of 101 value space bins. Individual trials were then assigned to the appropriate value space bin. Mean neuronal rates during the behavioral epoch of interest were calculated for each bin by dividing the total number of spikes in that bin by the number of trials the subject spent within that bin. For all analyses, these mean rates were used. For visualization, activity was kernel-smoothed with Gaussian kernels (kernel s.d. of 1.2) across bins. Most of our analyses focused on the fixation epoch, defined as the 500 ms from the onset of fixation following the presentation of the fixation cue. We also analyzed the choice epoch, which was defined as 100 to 600 ms following the onset of the pictures (Figure S3).

To identify value space encoding, we used information theoretic measures, analogous to those that have typically been used to define spatial place neurons in rats (Skaggs et al., 1993). Thus, the information content of the value space neuron, I, in bits per second, is calculated as:

$$I=\sum _x\lambda \left(x\right){log}_2\frac{\lambda \left(x\right)}{\lambda }p\left(x\right)$$

where x is the value bin, λ is the neuron’s mean firing rate, λ(x) is the mean firing rate in value bin x, and p(x) is the probability of being in bin x over all trials. We then normalized by λ to express I in units of bits per spike, a measure of how much value information is conveyed at any location in value space by the neuron. For each neuron, we also calculated a null distribution, by shuffling firing rates 1000 times to preserve overall firing rates but remove correlations with task events. Neurons were considered to have significant value place encoding when three criteria were met: a peak binned firing rate above 1 Hz, I greater than two standard deviations (95%) above the null distribution, and I > 0.2.

We measured the directionality of value place fields in two ways. First, for each field, we determined its center of mass, CoM, along the trajectory as:

$$CoM=\frac{{\sum }_{i}F{R}_i{x}_i}{{\sum }_{i}F{R}_i}$$

where FR denotes the firing rate, x is the position, and i defines the extent of the field. We determined the skewness of the field, S, by generating an index of the mean firing rates to either side of the CoM:

$$S=\frac{F{R}_{COM,left}-F{R}_{COM,right}}{F{R}_{COM,left}+F{R}_{COM,right}}$$

Calculation of spatial and temporal correlations

To determine the stability of value place fields from one pass through a trajectory to the next, we performed a correlation analysis. For each value place neuron, we correlated the binned firing rates from each pass, using analogous analyses to those that have been used in the rodent literature to study the stability of spatial place fields (Fyhn et al., 2007; Kinsky et al., 2020; Schwindel et al., 2016). For the circular and helical trajectories, we circularly shifted the trajectories relative to one another by ± 9 value bins and calculated Pearson’s ρ for each shifted pair of passes. We then selected the maximum correlation as the true value. Note that this method can result in strong negative correlations as well as strong positive correlations, due to the circular nature of the data. For example, a neuron might be active in bins 1–5 on the first pass, and 95–100 on the second pass, since these bins are adjacent to one another in value space. To calculate the null distribution of shuffled data, as in Figure 2C, we shuffled trial-by-trial firing rates and then re-mapped these shuffled rates onto the trajectory through value space, before repeating the correlation analysis. For each neuron and pass, this was repeated 1000 times. We employed a similar shifting procedure for the lemniscate space. However, rather than circularly shifting, we first performed a cross correlation bounded at ± 9 value bin lags and computed the Pearson correlation on the lag that produced the largest absolution correlation. This results in fewer correlations at 0 since the procedure is biased toward detecting some correlation. However, the bias is accounted for by our shuffling procedure.

We performed a control analysis to ensure that value space activity was not confounded by a temporal periodicity equivalent to the approximate time taken to complete one pass through the value space. We were able to unconfound this from position within the value space due to variability in length of drift periods. To test for temporal periodicity, we correlated the serial order of trial firing rates for each trajectory, truncating whichever pass was longer. In addition, because space and time were not collinear (mean ± s.e.m. variance inflation factor; V: 1.6 ± 0.02; T: 1.6 ± 0.1), we fit hippocampal firing rates with space and time as independent circular predictors in a generalized linear model:

$$FR={\beta }_0+{\beta }_{1}sin\left(V\right)+{\beta }_{2}cos\left(V\right)+{\beta }_{3}sin\left(t\right)+{\beta }_{4}cos\left(t\right)$$

where V is the spatial position and t is the time elapsed from the start of the session.

Testing tuning of hippocampal neurons to other value parameters

We tested hippocampal firing rates for evidence of encoding other relationships related to value, such as those that have been observed in orbitofrontal cortex (Kennerley et al., 2011; Padoa-Schioppa, 2013). Specifically, we defined three additional value-related parameters that could plausibly be encoded: value sum, Q_sum, which is the sum of the value of the three pictures (Q₁ + Q₂ + Q₃), value range, Q_rng, which is the range of picture values (Q_max - Q_min), and value difficulty, Q_diff, which is the discriminability of the two most valuable pictures (Q_max - Q_mid). These regressors were linearly related to mean firing rates during the fixation epoch, FR_fix, as:

$$F{R}_{fix}=b_0+b_1{Q}_{sum}+b_2{Q}_{rng}+b_3{Q}_{diff}$$

The variance inflation factor for this model was in acceptable bounds for all sessions (< 2.5). Significance was assessed at p < 0.01.

Statistical Testing

All statistical tests are described in the main text or the corresponding figure legends. Error bars indicate standard error of the mean (s.e.m.) unless otherwise specified. All comparisons were two-sided.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: organisms/strains
Non-human primate (macaca mulatta)	UC Davis	N/A
Software and algorithms
MATLAB software used for all quantitative analysis	N/A	https://www.mathworks.com
Offline Sorter used for spike sorting	Plexon	https://plexon.com/
Omniplex	Plexon	https://plexon.com
Monkey Logic Toolbox for MATLAB	NIMH	https://monkeylogic.nimh.nih.gov/
3D Slicer	BNH	https://www.slicer.org
Eyelink 1000 frontend	Eyelink	https://www.sr-research.com/eyelink-1000-plus/
CubeHelix colormap algorithm	Dave Green	http://www.mrao.cam.ac.uk/⁓dag/CUBEHELIX
Other
Plexon V-probes for neurophysiology	Plexon	https://plexon.com

Highlights.

• Hippocampal neurons encode position within an abstract value space

• Value place neurons fire in a consistent part of space and map multiple dimensions

• Direction of travel in value space produces an asymmetrical value space field

• Value place neurons remap in response to changes in experimental context