Frequency Selectivity of Persistent Cortical Oscillatory Responses to Auditory Rhythmic Stimulation

Abstract

Cortical oscillations have been proposed to play a functional role in speech and music perception, attentional selection, and working memory, via the mechanism of neural entrainment. One of the properties of neural entrainment that is often taken for granted is that its modulatory effect on ongoing oscillations outlasts rhythmic stimulation. We tested the existence of this phenomenon by studying cortical neural oscillations during and after presentation of melodic stimuli in a passive perception paradigm. Melodies were composed of ∼60 and ∼80 Hz tones embedded in a 2.5 Hz stream. Using intracranial and surface recordings in male and female humans, we reveal persistent oscillatory activity in the high-γ band in response to the tones throughout the cortex, well beyond auditory regions. By contrast, in response to the 2.5 Hz stream, no persistent activity in any frequency band was observed. We further show that our data are well captured by a model of damped harmonic oscillator and can be classified into three classes of neural dynamics, with distinct damping properties and eigenfrequencies. This model provides a mechanistic and quantitative explanation of the frequency selectivity of auditory neural entrainment in the human cortex.

SIGNIFICANCE STATEMENT It has been proposed that the functional role of cortical oscillations is subtended by a mechanism of entrainment, the synchronization in phase or amplitude of neural oscillations to a periodic stimulation. One of the properties of neural entrainment that is often taken for granted is that its modulatory effect on ongoing oscillations outlasts rhythmic stimulation. Using intracranial and surface recordings of humans passively listening to rhythmic auditory stimuli, we reveal consistent oscillatory responses throughout the cortex, with persistent activity of high-γ oscillations. On the contrary, neural oscillations do not outlast low-frequency acoustic dynamics. We interpret our results as reflecting harmonic oscillator properties, a model ubiquitous in physics but rarely used in neuroscience.

Introduction

Cognitive neuroscience aims to determine the nature of the basic computations underlying cognition and how they are implemented (Marr, 2010; Jonas and Kording, 2017; Krakauer et al., 2017). Neural oscillations are an emergent property of a population of interacting neurons that can be described by few phenomenological parameters, such as phase, amplitude, and frequency (Sejnowski, 1976; Izhikevich, 2006; Deco et al., 2008). According to recent theories, neural oscillatory activity plays a crucial role in the implementation of elemental computations (Buzsáki, 2010; Bastos et al., 2012; Womelsdorf et al., 2014). Indeed, oscillations have the powerful property of implementing algorithms, such as hierarchical parsing (Giraud and Poeppel, 2012), chunking (VanRullen and Koch, 2003), and clocking (Kösem et al., 2014), while being easy to describe mechanistically. From a cognitive neuroscience angle, they constitute an important interface between algorithmic and implementational levels of analyses (Giraud and Arnal, 2018).

Rhythmic stimulation, either sensory or electrical, can be used to modulate neural oscillatory activity, to reveal or optimize brain functions (Thut et al., 2012; Romei et al., 2016). Such modulation is believed to be realized through neural entrainment, defined here as the synchronization in phase or amplitude of neural oscillatory activity to a periodic stimulation (Lakatos et al., 2019; Obleser and Kayser, 2019). At the algorithmic level, entrainment phenomena have been proposed to account for segmentation of speech (Zoefel and VanRullen, 2016; Meyer et al., 2017; Riecke et al., 2018; Wilsch et al., 2018; Zoefel, 2018; Zoefel et al., 2018a), attentional selection during visual or auditory perception (Lakatos et al., 2008; Schroeder and Lakatos, 2009; Mathewson et al., 2012; de Graaf et al., 2013; Spaak et al., 2014; Keitel et al., 2019), perception of the musical beat (Large and Jones, 1999; Fujioka et al., 2012; Lenc et al., 2018), and auditory working memory performance (Albouy et al., 2017). At the implementational level, however, entrainment can occur only if the stimulation is applied at a frequency close to an eigenfrequency of the targeted cell assembly (Izhikevich, 2001; Izhikevich et al., 2003). Thus, depending on whether it is applied at or away from a network's eigenfrequency and whether neural oscillations are self-sustained or not, a rhythmic stimulation will induce oscillatory entrainment, oscillatory resonance, or a superposition of transient event-related potentials. This distinction is at the heart of a vibrant debate concerning the nature of neurophysiological responses, such as steady-state (Nozaradan et al., 2011; Keitel et al., 2019), frequency-following (FFR, response to the fundamental frequency or fine structure of the sound) (Musacchia et al., 2007; Coffey et al., 2016a,b), or envelope-following (EFR, response to the amplitude modulations of the sound) responses (Capilla et al., 2011; Haegens and Zion Golumbic, 2018; Zoefel et al., 2018b; Doelling et al., 2019; Helfrich et al., 2019).

One of the properties of entrainment that is often taken for granted is that its modulatory effect on ongoing oscillations outlasts rhythmic stimulation (Lakatos et al., 2013). In dynamical systems approaches, it corresponds to the fundamental property of underdamping (damping ratio ζ < 1), that is, the ability for a system to maintain a long-lasting oscillation, echo, or reverberation, whose amplitude exponentially decreases toward baseline after the stimulation ends (Pikovsky et al., 2002; Hanslmayr et al., 2019; Helfrich et al., 2019). Strikingly, this property has never been systematically investigated despite being considered as a possible mechanism underlying temporal predictions in multiple cognitive theories, in particular at low (<10 Hz) frequencies: dynamic attending theory (Large and Jones, 1999), multisensory integration (Kösem and van Wassenhove, 2012; Grabot et al., 2017), timing (Kösem et al., 2014), or interpersonal interaction (Hove and Risen, 2009). In the auditory domain especially, where the temporal structure of sound streams is highly informational, either for speech comprehension (Shannon et al., 1995; Zatorre and Belin, 2001; Giraud and Poeppel, 2012) or musical-beat perception (Large and Jones, 1999; Nozaradan et al., 2011; Fujioka et al., 2012; Haegens and Zion Golumbic, 2018), underdamping is believed to be the property that allows the brain to anticipate the sounds. While neural entrainment has been conceptualized as a mechanism of attentional sensory selection (Large and Jones, 1999; Lakatos et al., 2008, 2019; Schroeder and Lakatos, 2009; Obleser and Kayser, 2019), it has also been argued to be automatic, and to occur in passive listening contexts (Fujioka et al., 2012; Henry and Obleser, 2012; Ding and Simon, 2014; Cirelli et al., 2016; Molinaro et al., 2016). Currently, there is no clear evidence (by observation of underdamping of frequency specificity) in favor or against the fact that entrainment can be observed in a passive listening context.

To investigate the damping properties of cortical oscillations during auditory rhythmic stimulation, we recorded whole-brain cortical neurophysiological activity with either stereotactic EEG (sEEG) on epileptic patients implanted for clinical evaluation or magnetoencephalography (MEG) on healthy participants. While sEEG provides the best spatiotemporal resolution and signal-to-noise ratio of human cortical recordings (Parvizi and Kastner, 2018), optimizing our chances to detect long-lasting oscillations, it does not provide a full cortical coverage, which is afforded by the complementary MEG recordings (Baillet, 2017). Participants passively and repetitively listened to a 6 s auditory stream composed of high-frequency tones (∼80 or ∼60 Hz) presented at a rate of 2.5 Hz. Periods of silence separated both successive tones and streams, to allow investigating the damping properties of neural oscillatory responses. We explored the occurrence of cortical neural oscillations during and after presentation of melodic stimuli at both tones (high, ∼80/60 Hz) and stream (low, 2.5 Hz) frequencies.

Based on the auditory literature, we hypothesized that neural underdamping would be selective to low-frequency stimulation and would mainly occur in auditory, but also motor cortical regions (Fujioka et al., 2012; Morillon and Baillet, 2017). Hence, while each tone would evoke a high-γ (∼60/80 Hz) neural response that would end at stimulus offset, the underlying rhythm would entrain δ (2.5 Hz) neural oscillations, characterized with underdamping (i.e., long-lasting activity). In addition to these phase-locked responses, we expected to observe an induced response in the β range (15-30 Hz), whose amplitude would be entrained at the stream rate through a mechanism of phase-amplitude coupling (Fujioka et al., 2012; Cirelli et al., 2014; Chang et al., 2016). We then fitted a damped harmonic oscillator model (Freeman, 1961, 1972), the standard model in physics to study oscillatory phenomena, to the data. We made the hypothesis that this model will allow capturing key aspects of the data, that is, reducing the complexity of the neural response to three interpretable parameters (eigenfrequency, time delay, and damping ratio). We made the hypothesis that this simplification would allow differentiating neural populations based on their dynamics and revealing whether the damping property is region- and frequency-specific.

We thus investigated many possible forms of phase and amplitude synchronization, at both low and high frequencies and in a wide range of cortical regions, in response to our composite auditory rhythmic stimulation. Hence, we investigated the following: (1) whether underdamping occurs at all after passive auditory rhythmic stimulation; (2) if so, whether it depends on the frequency of stimulation; and (3) whether it is region- and/or frequency-specific.

Materials and Methods

Experimental design

Stimulus

The auditory stimulus was a bass riff designed to embed both high- (∼60/80 Hz) and low- (2.5 Hz) frequency acoustic modulations, thereby allowing to study properties of both high- and low-frequency neural oscillations. For a total duration of 6.24 s, it was composed of 16 tones, each lasting 170 ms, presented at a regular pace of 2.56 Hz (i.e., with an interonset interval of 390 ms). The first eight tones had a fundamental frequency of 83 Hz lasting 14 cycles. The last eight tones had a fundamental frequency of 62 Hz lasting 11 cycles. The two series of eight tones were identical repetition of two complex sounds recorded from an acoustic bass guitar. The acoustic envelope was extracted by computing the absolute value of the Hilbert transform of the signal filtered between 50 and 90 Hz, which captures the fundamental frequencies of both sounds. The interstimulus interval was randomly chosen between 2.92, 3.12, and 3.32 s. MEG participants listened to 300 stimuli and sEEG patients 100 stimuli.

Stimulus presentation

The stimuli were presented binaurally to participants at an adjusted comfortable level (∼70 dB) using loudspeakers for sEEG patients and Etymotic insert earphones with foam tips (Etymotic Research) for MEG participants. Presentation was controlled with E-prime 1.1 (Psychology Software Tools). sEEG patients were passively listening. MEG participants were passively listening and simultaneously watching a silent movie. The whole experiment lasted ∼45 min for MEG participants and ∼15 min for sEEG patients.

Common analyses between MEG and sEEG datasets

Software

All analyses were done using MNE-Python (Gramfort et al., 2014), FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) and custom scripts written in Python.

Statistical analysis

Analyses of sEEG data were done following a fixed effect strategy, that is, considering all patients' electrodes collectively in an average brain. Individual differences of brain morphology and connectivity were therefore neglected. This strategy was chosen as each patient had a unique electrode implantation map, thus rendering group statistics inappropriate. For MEG data, the strategy was to reduce the normalized signal estimated at the source-level (vertex) to a statistics across participants before subsequent analyses, typically a t computed from a one-sample t test against 0 across participants. Most of the analyses were thereafter consistent between sEEG and MEG data, as having a single average brain with multiple electrodes is similar to having a single average brain with multiple vertices. The only difference was that the sEEG metrics corresponded to z values, and the MEG metrics to t values. The fixed-effect strategy we used for the sEEG data has a low generalization power alone. However, replicating the effects in the MEG-independent dataset and using a random-effect strategy for the MEG data greatly strengthen our confidence in the generalization of the results.

Align-bin-and-count (ABC) pipeline: estimation of the duration of a cyclic activity

We developed a method to estimate the number of cycles of oscillatory activity present in a neural signal, relative to the number of cycles present in the stimulus. The same procedure has been used extensively throughout the paper, for high- and low-frequency envelope of the evoked response and intertrial phase coherence (ITPC). This method has two objectives: find, if any, all responsive sources (sEEG channels or MEG vertices) and estimate the number of activity cycles they exhibit at a specific oscillatory frequency. Persistent activity was defined as >1 oscillatory cycle after stimulus offset. It can be decomposed in six steps (Fig. 1). The advantage of ABC over more conventional approaches, such as testing ITPC compared with a surrogate distribution, is that it accounts for three potential sources of artifact: (1) the overall power of each source, which can vary greatly (Step 1); (2) the lag between stimulus and neural response onsets (Steps 2 and 3); and (3) the spurious oscillatory activity (smearing) generated by the filtering process (Step 5). Moreover, it is adapted to any kind of signal (evoked response, ITPC, or spectral power) and computationally efficient. The six steps are as follows:

1. z score the activity of each source across time relative to its prestimulus baseline.

2. Find across all sources the lowest threshold such that none shows onset activity before stimulus onset (data-driven threshold estimation). The threshold is the same for all considered sources, and corresponds to the peak of activity observed during the baseline across all sources.

3. Align each source activity such that time 0 corresponds to the moment where its activity crosses the defined threshold.

4. Discretize the continuous activity in time bins, whose duration depends on the acoustic modulation of interest, for example, 1/83 Hz = 12 ms for the 83 Hz tones; 1/2.5 Hz = 390 ms for the 2.5 Hz stimulus presentation rate.

5. Find across all sources the lowest threshold such that none shows an active bin onset before their onset. We need to define another threshold for the bins because binning implies averaging, rendering the value defined in Step 3 irrelevant. Once again, the threshold is the same for all considered sources. This step solves the problem of the smearing induced by the filter: because the filter is symmetric and noncausal, it produces the same artifact before the onset and after the offset. Thresholding to remove spurious activity before the onset also removes spurious activity after the offset.

6. Count the number of consecutive cycles above the threshold defined in Step 5.

Figure 1.

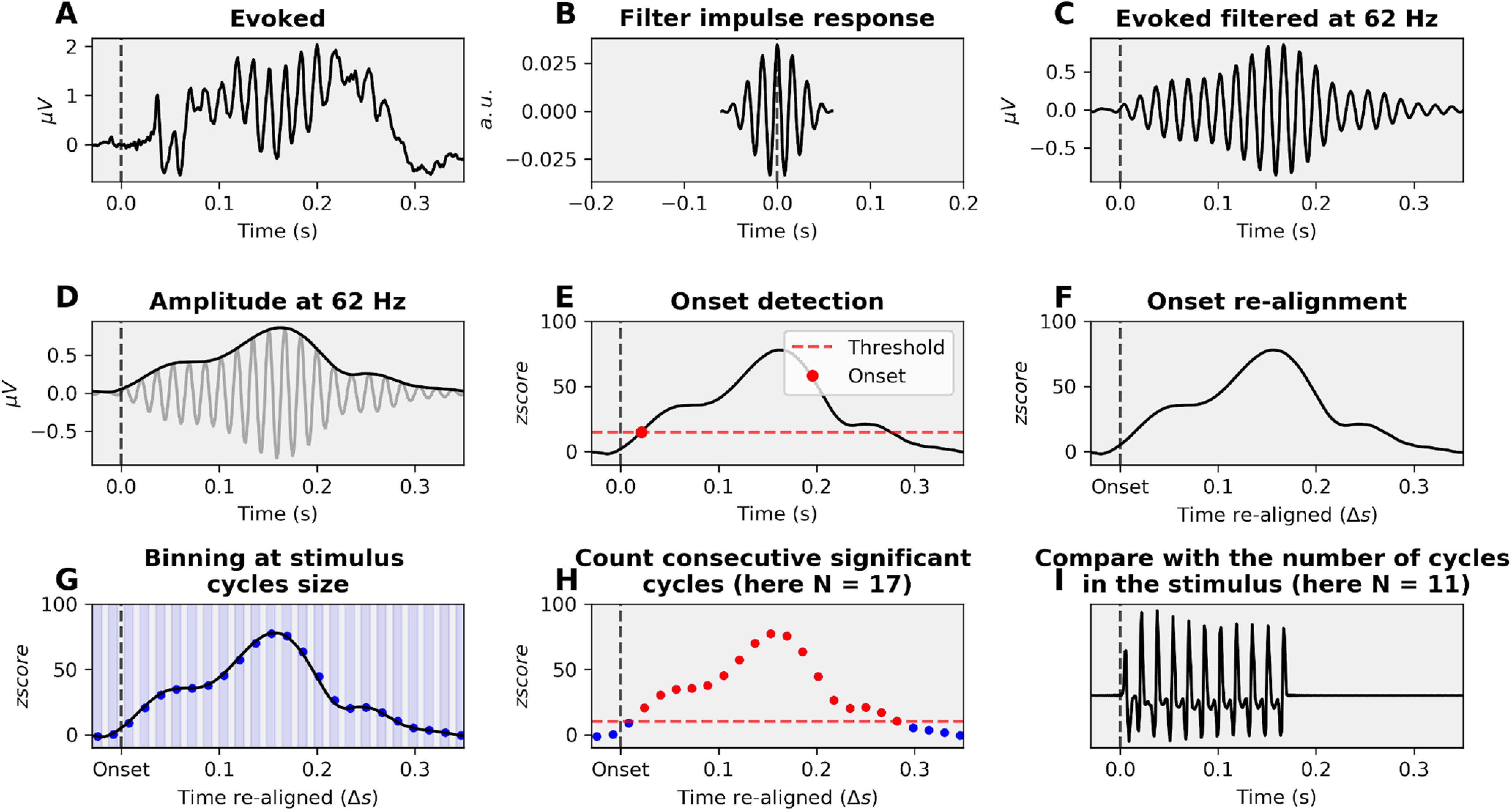
The ABC methodology. A, Signal of interest, here an evoked response. B, Impulse response of the one-pass, zero-phase, noncausal bandpass FIR filter with a hamming window. C, Filtered signal at the frequency of interest, here 62 Hz. D, Extraction of the envelope of the signal, as the absolute value of the Hilbert transform. E, Onset detection. The threshold is chosen such that no channel/vertice shows activity before stimulus onset. F, Signal realignment. G, Binning of activity at the relevant window size (here 1/62 = 16 ms). H, Consecutive significant cycles count. Another threshold is chosen such that no bin of any channel/vertice is significant before onset. I, Comparison between the stimulus number of cycles and the signal number of cycles. Here, the evoked activity shows 6 cycles of activity more than the stimulus.

During Steps 3 and 6, some sources never met the required criterion and are therefore removed from the analyses. These steps thereby induce a selection of the responsive sources. To validate this procedure, we applied it to the acoustic signal itself and confirmed that it correctly identifies the number of cycles actually present in the stimulus (e.g., 11 cycles were estimated for the 62 Hz tones). As the wavelet length decreases with the frequency of interest and as the ABC method uses a binning strategy, all the results are scale free. Therefore, the period duration does not matter for the analysis, as we are counting numbers of cycles and not durations. In this context, there is no specificity of the analysis at 2.6 Hz compared with the analyses at 62 and 83 Hz.

Anatomical MRI acquisition and segmentation

The T1-weighted anatomic MRI (aMRI) was recorded using a 3T Siemens Trio MRI scanner. Cortical reconstruction and volumetric segmentation of participants' T1-weighted aMRI were performed with FreeSurfer (http://surfer.nmr.mgh.harvard.edu/). This includes the following: motion correction, average of multiple volumetric T1-weighted images, removal of nonbrain tissue, automated Talairach transformation, intensity normalization, tessellation of the gray matter white matter boundary, automated topology correction, and surface deformation following intensity gradients. Once cortical models were complete, deformable procedures could be performed, including surface inflation and registration to a spherical atlas. These procedures were used to morph current source estimates of each individual for MEG and channel location for sEEG onto the FreeSurfer average brain for group analysis.

sEEG

Participants

Sixteen patients (5 females, mean age 26.9 years, range 9-46 years; see Table 1) with pharmaco-resistant epilepsy took part in the study. They were implanted with depth electrodes for clinical purposes at the Hôpital de La Timone (Marseille, France). Neuropsychological assessments conducted before sEEG recordings indicated that all participants had intact language functions and met the criteria for normal hearing. None of them had their epileptogenic zone, including the auditory areas as identified by experienced epileptologists. Patients provided informed consent before the experimental session, and the study was approved by the Institutional Review Board of the French Institute of Health (IRB00003888).

Table 1.

sEEG patient's data

Participant	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Total channels	189	224	189	249	206	150	189	224	189	214	184	160	209	192	180	191
Analyzed channels	185	218	183	219	198	139	188	102	188	186	176	158	127	41	152	188
% of analyzed epochs	93	95	97	83	92	68	99	69	92	85	82	86	58	68	53	92
Right PAC + SAC	2	2	1	0	1	1	1	1	0	2	0	0	0	0	2	0
Left PAC + SAC	0	2	0	2	0	0	0	0	2	2	1	1	0	2	0	0

Data acquisition

Depth electrodes (0.8 mm, Alcis) containing 10-15 contacts were used to perform the functional stereotactic exploration. Contacts were 2 mm long and spaced from each other by 1.5 mm. The locations of the electrode implantations were determined solely on clinical grounds. During the recording session, participants lay comfortably in a chair in a sound-attenuated room. sEEG signals were recorded at a sampling rate of 1000 Hz using a 256 channel BrainAmp amplifier system (Brain Products) and bandpass filtered between 0.3 and 500 Hz. A scalp electrode placed in Fz was used as the recording reference.

Anatomical localization of electrodes

Anatomical localization of electrodes was performed using a local software developed at the Hôpital de La Timone (Medina Villalon et al., 2018). First, an automatic procedure coregistered electrode location on the scanner and the patient's MRI. Second, the morphing matrix computed by Freesurfer used to project one individual's brain onto the average brain was applied directly on these locations.

Preprocessing

In order to remove power line artifacts, we first applied a notch filter at 50 Hz and harmonics up to 300 Hz. The signal was then rereference using a bipolar montage; that is, activity of each channel was subtracted from its following neighbor on the electrode. The continuous signal was then epoched from −1 to 9 s relative to the onset of each stimulus. Such long epochs allow to study both the response during the stimulus, from 0 to 6.24 s, and the silence directly following stimulus offset, from 6.24 up to 9 s. No baseline correction was applied, as effects potentially present in the silence can leak to the baseline of the next trial and therefore be removed by any process of baseline correction. For each source, epochs with ±500 µV peak-to-peak amplitude artifacts were rejected. Sources with > 70% rejected epochs were entirely removed, as they most likely contained epileptic discharges. Finally, sources showing low voltage epileptic activity were removed based on visual inspection. Overall, 2648 of 3139 sources were kept, with on average 82 of 100 epochs (Table 1).

Time-frequency decomposition

Trial-by-trial time-frequency decomposition was conducted in a range of 100 frequencies, logarithmically ranging from 2 to 150 Hz. Morlet wavelet transform was applied to the data using the MNE-python function time_frequency.tfr_morlet, with parameter n_cycles = 6. From the resulting complex representation, both ITPC and power were extracted as follows:

$$IT{C}_j^{t,f}=\left|\frac{1}{N}{\displaystyle \sum _{n=0}^N{e}^{i.\arg \left(z_{j,n}^{t,f}\right)}}\right|$$

$$Powe{r}_j^{t,f}=\frac{1}{N}{\displaystyle \sum _{n=0}^N{\left|\left(z_{j,n}^{t,f}\right)\right|}^2}$$

where $z_{j,n}^{t,f}$ designates the complex time-frequency representation of source j at trial n over N, frequency f and time t. Similarly, ${ITPC}_j^{t,f}$designates the ITPC of source j at frequency f and time t, and ${Power}_j^{t,f}$its power.

Frequency following response analysis

In order to study the FFR, we re-epoched the signal from −0.05 to 0.35 s relative to the onset of each tone. We computed the evoked activity as the mean across epochs. In order to study only the high-frequency component of the evoked response, we filtered it between 82 and 84 Hz for the 83 Hz tones and between 61 and 63 Hz for the 62 Hz tones, using a one-pass, zero-phase, noncausal bandpass FIR filter with a hamming window (for the impulse response of the filter, see Fig. 1B). We then extracted the envelope as the absolute value of the Hilbert transform, and applied our ABC pipeline (see Common analyses) to select the responsive sources and estimate the duration of their activity relative to the number of cycles present in the stimuli (14 for the 83 Hz tones and 11 for the 62 Hz tones). The automatically selected thresholds for the onsets (Step 3) were 5.0 z score for the 83 Hz tones and 4.9 for the 62 Hz tones. The automatically selected thresholds for the bin activity (Step 5) were 5.1 for the 83 Hz tones and 4.8 for the 62 Hz.

EFR analysis

We apply the same line of reasoning to investigate the EFR at 2.5 Hz. We computed the evoked activity as the mean across all epochs. We filtered this activity between 1.6 and 3.6 Hz and extracted the envelope. We then apply ABC on this envelope signal (see Common analyses). The selected thresholds were 5.4 for the onsets (Step 3) and 4.3 for the bins (Step 5).

Definition of canonical frequency bands based on auditory cortex activity

Localization of the auditory cortex was based on functional criteria, including latencies and shape of the auditory evoked potentials to pure tones, tested on an independent session. Primary auditory cortex (PAC) was defined by the presence of a P20/N30 complex, and secondary auditory cortex (SAC) by the presence of a P40/N50 complex (Liégeois-Chauvel et al., 1991, 1994). Responses of PAC and SAC were averaged, as no main differences were found in any of our analyses. Definition of canonical frequency bands was then based on the profile of the spectrum of ITPC and power (averaged across time during the stimulus duration, from 0 to 6.24 s). It resulted in an empirical definition of δ (2-3.5 Hz), θ (4-7 Hz), α (8-11 Hz), and γ bands (50-110 Hz). Although not prominent in either the sEEG dataset or in the MEG dataset, we added a β band (12-22 Hz) based on existing literature. Indeed, previous works have shown coupling of the beta band power with the phase of the stimulus envelope at similar paces (Fujioka et al., 2012; Morillon and Baillet, 2017).

ITPC fluctuations at 2.5 Hz

ITPC was first averaged across frequencies inside each frequency band (δ, θ, α, β, and γ). For each band, we then applied the ABC pipeline (see Common analyses) to estimate responsive sources as well as the duration of significant oscillatory activity. Thresholds for onsets (Step 3) were 3.4 (δ), 4.2 (θ), 5.4 (α), 6.3 (β), and 8.2 (γ). Thresholds for the bins (Step 5) were 3.2, 3.7, 3.8, 3.4, and 3.6, respectively.

Temporal response function (TRF) analysis

To analyze power signals, we relied on a recently developed powerful methodology that estimates TRFs by relying on encoding/decoding models of electrophysiological activity (Crosse et al., 2016). TRFs rely on the assumption that the activity can be expressed as a linear convolution between the input stimulus and a filter. The filter is typically unknown and therefore estimated by a least-square ridge regression. We reasoned as follows: if the power is modulated by the envelope of the auditory stimulus, then these fluctuations are informative about the stimulus dynamics. We should therefore be able to train a TRF to decode the envelope based on the power information. If the power continues to exhibit these fluctuations in the silence directly following the offset of the stimulus, we should still be able to decode the envelope oscillations during this post-stimulus period. Furthermore, and contrary to the ABC method, the TRF would reveal effects that are suppressed by baseline correction, as it does not involve baseline correction. We trained a TRF on all available power information, namely, power in all epochs, sources, frequencies, and time points, to decode the envelope of the auditory stimulus. We trained the model on the second part of the auditory stimulus, from 3.12 to 5.85 s after stimulus onset (which corresponds to the presentation of the six 62 Hz tones), and evaluated it on the first part of the stimulus from 0.39 to 2.73 s (which corresponds to the presentation of the six 83 Hz tones), and on the silence directly following, from 6.24 to 8.58 s. The time windows were chosen to have the same length, and to avoid the strong evoked activity present for the first tone and the changing tone. Performance was defined as the coefficient of determination (R²) between the predicted envelope and the actual envelope. The ridge parameter (α = 1000) was chosen to maximize the performance of the TRF on the signal during the first part of the stimulus. In order to reduce dimensionality and improve computational speed, we fitted a principal components analysis (PCA) before the TRF training. To avoid confounds because of this PCA procedure, we fitted it on the power in the second part of the stimulus and applied it without any further adjustments on the power in the first part and in the silence. We kept 60 components, explaining 99% of the total variance.

Damped harmonic oscillator model

We fitted the sEEG data to a damped harmonic oscillator model. The model is described by the following linear differential equation:

$$\frac{{\mathit{dx}}^2}{\mathit{dt}}=\mathit{F}(\mathit{t}-\Delta \mathit{t})-\zeta {\omega }_0\frac{\mathit{dx}}{\mathit{dt}}-{\omega }_0^{2}x$$

We used a grid search approach to find optimal parameters. For each set of parameters, we simulated 100 epochs of the harmonic oscillator time course with random initial conditions, with F being our auditory stimulus. Although analytically solved for any function F, we used a numerical solution (Euler's method with a time step of 1/40,000 s) because our stimulus has no simple functional form. In order to compare model time courses and sEEG data, we apply the same processing steps: bandpass filter, resampling at 1000 Hz, Morlet wavelet transform, extraction of power, and ITPC. Goodness of fit was then measured as the coefficient of determination (R²) of the linear regression between the model ITPC (or power) and the sEEG data ITPC (or power). The grid search explored a wide range of values: ζ logarithmically spaced values between 0.01 and 100 in 25 steps, 2πω₀ logarithmically spaced values between 0.1 and 100 Hz in 25 steps, Δt linearly spaced values between 0 and 400 ms in 20 steps. This procedure was used to fit all sEEG channels and output a parameters matrix of size n_channels × 3. This matrix was used to cluster the electrodes using the k-means algorithm. The optimal number of clusters (k = 3) was selected using the silhouette index, a standard measure that compares the mean intracluster distance and the mean nearest-cluster distance for each sample. Contrary to the ABC method, this modeling approach would reveal effects that are suppressed by baseline correction, as it does not involve baseline correction.

MEG

Participants

We collected data from 15 participants (8 females, median age 27 years, age range 23-40 years) after providing informed consent. All had normal hearing, reported no neurologic deficits, and received 40 euros for their time. The experiment was approved by the National Ethics Committee on research on human subjects.

Data acquisition

MEG data were recorded with a whole-head 4D-neuroimaging system with 248 magnetometers. Participants were lying in horizontal position under the MEG dewar, facing a screen displaying a silent movie. MEG recordings were sampled at 678 Hz and bandpass filtered between 0.3 and 500 Hz. Four head position coils (HPI) measured the head position of participants before each block. Before the session, 2 min of empty room recordings was acquired for the computation of the noise covariance matrix.

Preprocessing

In order to remove power line artifacts, we first applied a notch filter at 50 Hz and harmonics up to 300 Hz. We further low-pass filtered the signal below 150 Hz and resampled it at 500 Hz. An independent components analysis was performed on the bandpass signal between 1 and 30 Hz, and components exhibiting topographical and time courses signatures of eye blinks or cardiac artifacts were removed from the data. The continuous signal was then epoched from −1 to 9 s relative to the onset of each stimulus. No baseline correction was applied. Epochs with ±5 pT peak-to-peak amplitude artifacts were rejected (on average 4.6%).

MRI-MEG coregistration and source reconstruction

The coregistration of MEG data with the individual's structural MRI was conducted by realigning the digitized fiducial points with MRI slices. Using MRILAB (Neuromag-Elekta), fiducials were aligned manually on the MRI slice. Individual forward solutions for all source reconstructions located on the cortical sheet were next computed using a 3 layer boundary element model (Hamalainen and Sarvas, 1989; Mosher et al., 1999) constrained by the individual aMRI. Cortical surfaces were extracted with FreeSurfer and decimated to ∼10,240 sources per hemisphere with 4.9 mm spacing. The forward solution, noise, and source covariance matrices were used to calculate the depth-weighted (default parameter γ = 0.8) and noise-normalized dynamic statistical parametric mapping (Dale et al., 2000) inverse operator. This unitless inverse operator was applied using a loose orientation constraint on individuals' brain data by setting the transverse component of the source covariance matrix to 0.2 (default value). The reconstructed current orientations were pooled by taking the norm, resulting in manipulating only positive values. The reconstructed dynamic statistical parametric mapping estimates time series and time-frequency plane were morphed onto the FreeSurfer average brain for group analysis and common referencing.

Time-frequency decomposition

Trial × trial time-frequency decomposition was performed using the same procedure and same parameters as for the sEEG.

Frequency following response analysis

As for sEEG, we epoched data, computed the evoked response, filtered it at the stimulus fundamental frequency, extracted the envelope, and applied a z score normalization. We applied a t test against 0 across participants at each time point and each source. We then applied the ABC pipeline (see Common analyses) to select the responsive sources and estimate the duration of their activity. Thresholds for MEG were manually fixed, and corresponded to p < 0.01 (t statistic ∼2.7, df = 14).

Low-frequency amplitude analysis

As for sEEG, we computed the evoked response, filtered it at the stimulus fundamental frequency, extracted the envelope, and applied a z score normalization. Then, we applied a t test against 0 across participants at each time point and each source. We then followed the ABC pipeline (see Common analyses) with a p < 0.01 threshold.

Anatomical localization of the auditory cortex

We relied on an anatomic criterion to localize the auditory cortex. We used the Destrieux atlas (Destrieux et al., 2010), labeled temporal transverse, comprising primary and secondary auditory cortices (left hemisphere “S_temporal_transverse-lh”: 564 vertices, right hemisphere “S_temporal_transverse-rh” 413 vertices). We first applied a singular value decomposition to the time courses of each source within the label and used the scaled and sign-flipped first right-singular vector as the label time course. The scaling was performed such that the power of the label time course was the same as the average per-vertex time course power within the label.

ITPC fluctuations at 2.5 Hz

Similarly to sEEG, ITPC was first averaged across frequencies inside each frequency band, for each participant, source, frequency band, and time point. We z scored the signal across time compared with its baseline. We then applied a t test against 0 across participants. We used the ABC pipeline (see Common analyses) as previously, with a p < 0.01 threshold.

TRF analysis

The TRF model was fitted on sensor space in MEG to reduce computational load. Furthermore, sensors contain the same amount of information as sources, thus estimating TRF on sensors or on sources is theoretically equivalent. We therefore trained the model on all available power information, namely, power in all participants, sensors, epochs, frequencies, and time points, to decode the envelope of the auditory stimulus. The ridge parameter (α = 1.0 × 10⁸) was chosen to maximize the performance of the TRF on the signal during the first part of the stimulus (as for sEEG). In order to reduce dimensionality and improve computational speed, we fitted a PCA before the TRF training. We kept 101 components, explaining 99% of the total variance.

Results

High-frequency acoustic modulations (∼60/80 Hz) induce long-lasting neural FFRs

We first investigated the FFR (i.e., the neural evoked response at the fundamental frequency of the tones). The main goal of this analysis was to identify sEEG/MEG sources for which an FFR was observed and then to estimate whether this activity outlasted the duration of the stimulus. For this purpose, we developed a method that we refer to as ABC (see Materials and Methods; Fig. 1), in which we treat each oscillatory cycle as a bin of activity and estimate how many consecutive active bins are present in the neural signal. This method accounts for differences in power between sources, lag between stimulus and neural response and spurious oscillations arising from filtering smearing (see Materials and Methods). This allows us to accurately estimate the duration of each significant neural response and infer whether it outlasts stimulus duration or not. In order to study the FFR, we applied ABC to the envelope of narrow-band filtered signals (83 or 62 Hz). Importantly, we confirmed the validity of this method by applying the filter and ABC to the sound stimuli themselves, which yielded an accurate estimate of their number of cycles. Long-lasting activity duration could therefore not arise from spurious filtering smearing (de Cheveigné and Nelken, 2019).

Analyses of sEEG recordings first reveal that FFRs are present in a wide cortical network, extending well beyond auditory cortex (13% of all recorded sites for 83 Hz, 21% for 62 Hz; Fig. 2J,K, white and colored dots). This network comprises auditory regions (Heschl gyrus and planum temporale bilaterally, extending to superior and middle temporal gyri) and also comprises premotor and motor regions (bilateral precentral gyrus and right premotor cortex) as well as associative regions involved in higher-level auditory processing (bilateral inferior parietal lobule and left inferior frontal gyrus). The FFR persists beyond stimulus duration in a substantial proportion of the responding sEEG sources (118 of 424 corresponding to 28% at 83 Hz and 232 of 669 corresponding to 35% at 62 Hz). The number of cycles of oscillatory activity can exceed that of the stimulus by up to 11 cycles at 83 Hz and 8 cycles at 62 Hz (∼180% of stimulus duration; Fig. 2H,I). The anatomic location of sEEG sources whose activity outlasts stimulus duration is also comprised within the entire dual-stream auditory cortical processing pathway (Rauschecker and Scott, 2009) (Fig. 2J,K): in the anteroventral stream, from auditory to inferior frontal cortex (auditory cortex, medial part of the superior temporal gyrus, middle temporal gyrus, and left pars triangularis of the inferior frontal gyrus) and in the postero-dorsal stream, from auditory to motor cortex (posterior part of the superior temporal gyrus, inferior parietal lobule, precentral gyrus, and right premotor cortex).

Figure 2.

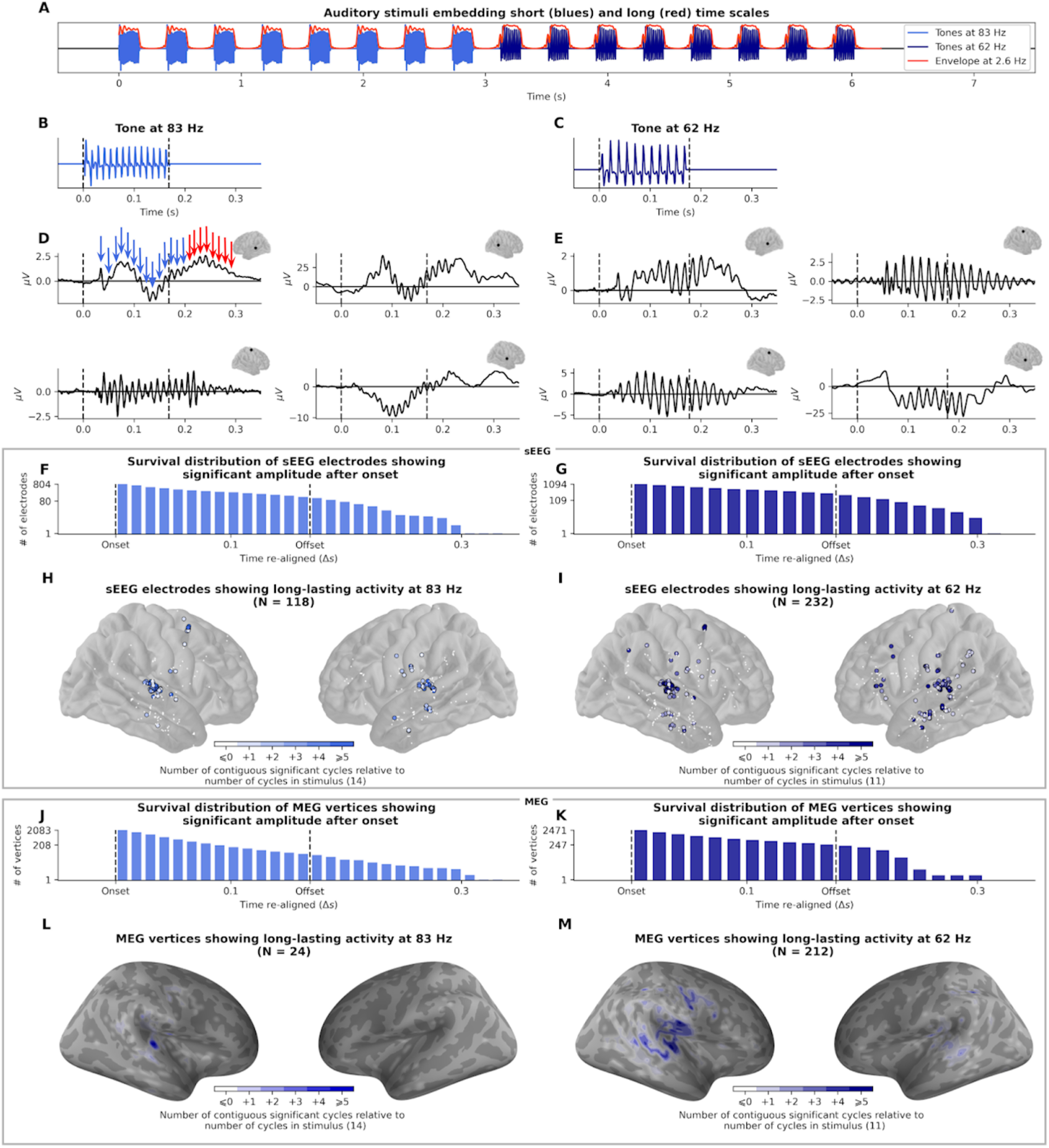
Estimation of FFR duration (83 and 62 Hz). A, Auditory stimulus of 8 tones with high-frequency carriers at 83 Hz followed by 8 tones at 62 Hz presented at a 2.5 Hz rate (envelope). B, C, Waveform of the 83 and 62 Hz tones, made up of 14 and 11 oscillatory cycles, respectively. D, E, Evoked unfiltered response of 8 example sEEG channels, from different participants and different brain regions (Heschl's gyrus, motor cortex, and superior temporal sulcus). After a small delay, the neural response contains more cycles than the stimuli (highlighted in red arrows, 14 + 8 = 22 cycles in this example). F, G, Survival distribution of sEEG channels with consecutive significant activity after onset; 118 and 232 channels outlast the 0.170 s duration of the 83 and 62 Hz stimuli, respectively. H, I, Localization of sEEG channels showing an FFR during the stimulus. Channels with activity outlasting stimulus duration are circled. Color intensity indicates the number of cycles outlasting stimulus duration. J, K, Survival distribution of MEG vertices activity showing consecutive significant activity after onset. L, M, Localization of MEG vertices showing an FFR. Color intensity indicates the number of cycles outlasting stimulus duration.

We ran supplementary analyses to further control for the presence of artifacts that could arise from spurious filtering smearing. First, persistent FFR can be seen clearly in unfiltered evoked responses (examples are presented in Fig. 2D,E). Second, instead of applying the relevant filter (centered around the frequency of stimulation), we applied an irrelevant filter (centered around the frequency of the other stimulus; e.g., 83 Hz filter to the 62 Hz stimulus response). Our rationale was that, if the result is spurious, the frequency of the narrow-band filter will not impact the result. Using “irrelevant” filters, the proportion of electrodes that show a persistent activity dramatically drops to 5% after the 83 Hz auditory stimulus and to 3% after the 62 Hz auditory stimulus. This demonstrates that artifacts that could arise from spurious filtering smearing did not contaminate the analyses.

MEG data substantiate the sEEG results, revealing FFR in superior and inferior temporal gyri, precentral gyrus, and supramarginal gyrus. Again, the FFR persists beyond stimulus duration (24 of 395 corresponding to 6% at 83 Hz and 212 of 858 corresponding to 25% at 62 Hz). The number of cycles of oscillatory activity can exceed that of the stimulus by up to 12 cycles at 83 Hz and 8 cycles at 62 Hz (∼180% of stimulus duration; Fig. 2L,M). Similarly, the localization of the MEG sources whose activity outlasts stimulus duration comprises regions of the auditory network (superior temporal gyrus, inferior parietal lobule, and right precentral gyrus).

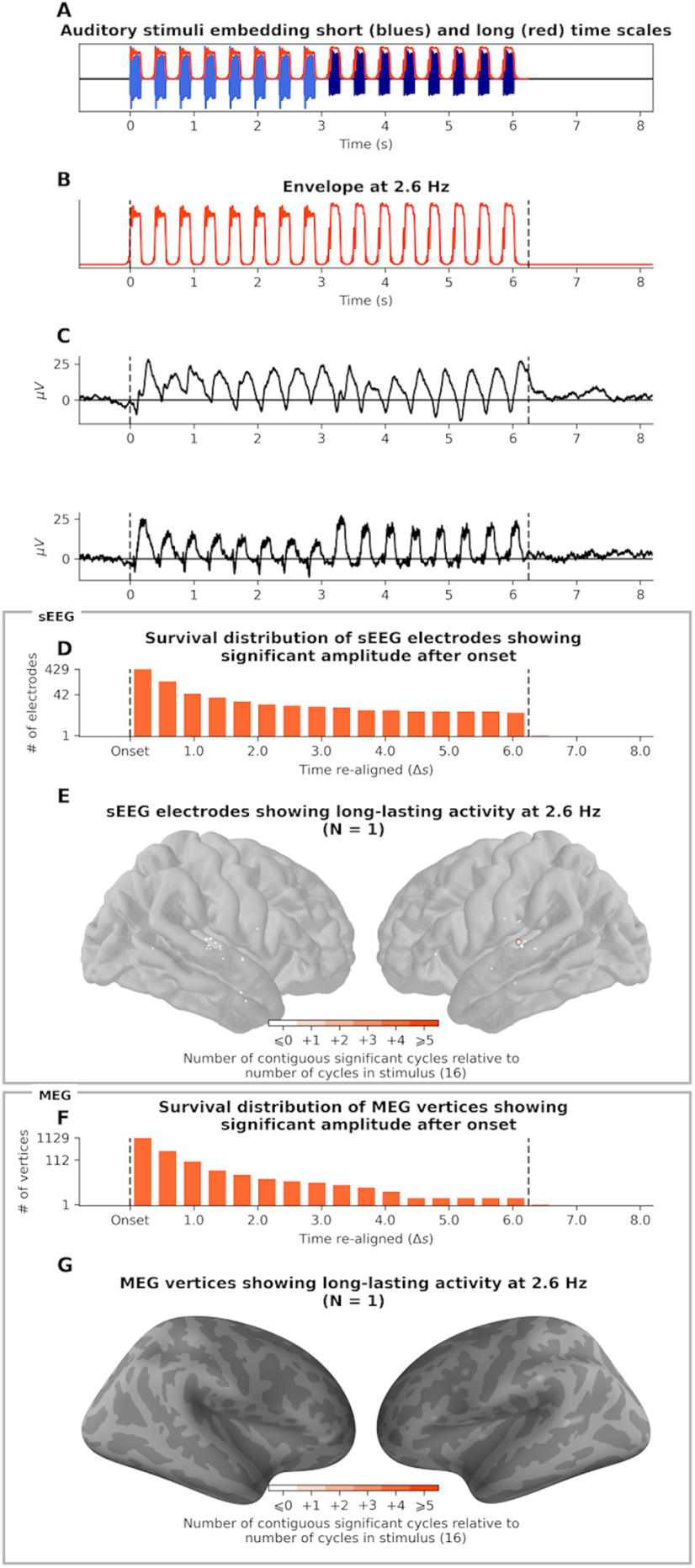
Low-frequency acoustic modulations (2.5 Hz) do not induce long-lasting neural EFRs

We used the same approach to investigate the neural response to the low-frequency amplitude modulations of the auditory stream, known as EFR. Each tone of sequence was separated by a fixed interonset interval of 390 ms, resulting in a 2.5 Hz amplitude-modulated temporal envelope (Fig. 3B). We applied ABC to the envelope of the 2.5 Hz narrow-band filtered signals (Fig. 3C).

Figure 3.

Estimation of EFR duration (2.5 Hz). A, Auditory stimulus. B, Waveform of the envelope fluctuation at 2.5 Hz. C, Evoked unfiltered response of two example sEEG channels, from different participants, both in Heschl's gyrus. D, Survival distribution of sEEG channels with consecutive significant activity after onset. Channels whose activity lasts >16 cycles outlast the duration of the stimulus (N = 1 channel). E, Localization of sEEG channels having an EFR. The channel with long-lasting activity is circled. Color intensity indicates the number of cycles of post-stimulus activity (1). F, Survival distribution of MEG vertices activity showing consecutive significant activity after onset. G, Localization of MEG vertices that have an EFR. Color intensity indicates the number of cycles of post-stimulus activity (no vertex shows persistent activity except one with one cycle).

sEEG recordings analyses reveal that, similarly to FFR, a wide cortical network presents an EFR (Fig. 3E). It comprises auditory regions (bilateral Heschl gyrus, planum temporale, and middle temporal gyrus), motor regions (bilateral precentral gyrus), and associative regions (left inferior frontal gyrus). However, unlike FFR, no long-lasting EFRs were observed. Only one (/40 responsive) sEEG source has a response that outlasts stimulus offset, and only by a single cycle (Fig. 3E). Similarly, MEG results did not reveal outlasting EFR (Fig. 3G), except for one source (/32) exceeding by a single cycle the stimulus duration. Thus, low-frequency acoustic modulations do not induce outlasting EFRs.

The two previous analyses investigated the N-to-N relationship between the stimulus frequency and the brain oscillatory activity: a frequency-specific neural oscillation (62, 83, or 2.5 Hz) in response to a frequency-specific oscillating stimulus. However, nesting (e.g., cross-frequency phase-phase or phase-amplitude coupling) phenomena exist and play an important role in shaping brain dynamics (Buzsáki, 2006; Canolty et al., 2006; Jensen and Colgin, 2007; Canolty and Knight, 2010). We therefore broadened our analysis to all neural activity phase-locked to the stimulus. These N-to-M components were revealed by a time-frequency decomposition, using the ITPC, a measure that quantifies the amount of phase consistency across trials for each frequency and time bin. A high ITPC is indicative of strong phase-locking to the stimulus for a particular frequency and a particular time point.

In order to investigate whether low-frequency (2.5 Hz) acoustic stimulation induces any long-lasting ITPC, we thus decomposed the neural activity into five frequency bands of interest, defined based on the response of the auditory cortex. We estimated both the power time-frequency plane, quantifying the trial-averaged response amplitude of each frequency in time (induced activity), and the ITPC plane (phase-locked activity). We then computed the mean and variance across time of both power and ITPC of each frequency during the presentation of the stimulus (for sEEG, see Fig. 4; for MEG, see Fig. 5). This resulted in five spectral distributions, revealing clear and recurring spectral peaks and troughs (Fig. 4C,E) at which neural activity was modulated during stimulus presentation, in the δ (2-3.5 Hz), θ (4-7 Hz), α (8-11 Hz), β (12-22 Hz), and γ bands (50-110 Hz). In particular, we chose to investigate the β band (12-22 Hz), as existing literature reports the implication of beta activity in the encoding of the temporal structure of acoustic stimuli (Fujioka et al., 2012; Cirelli et al., 2014; Chang et al., 2016).

Figure 4.

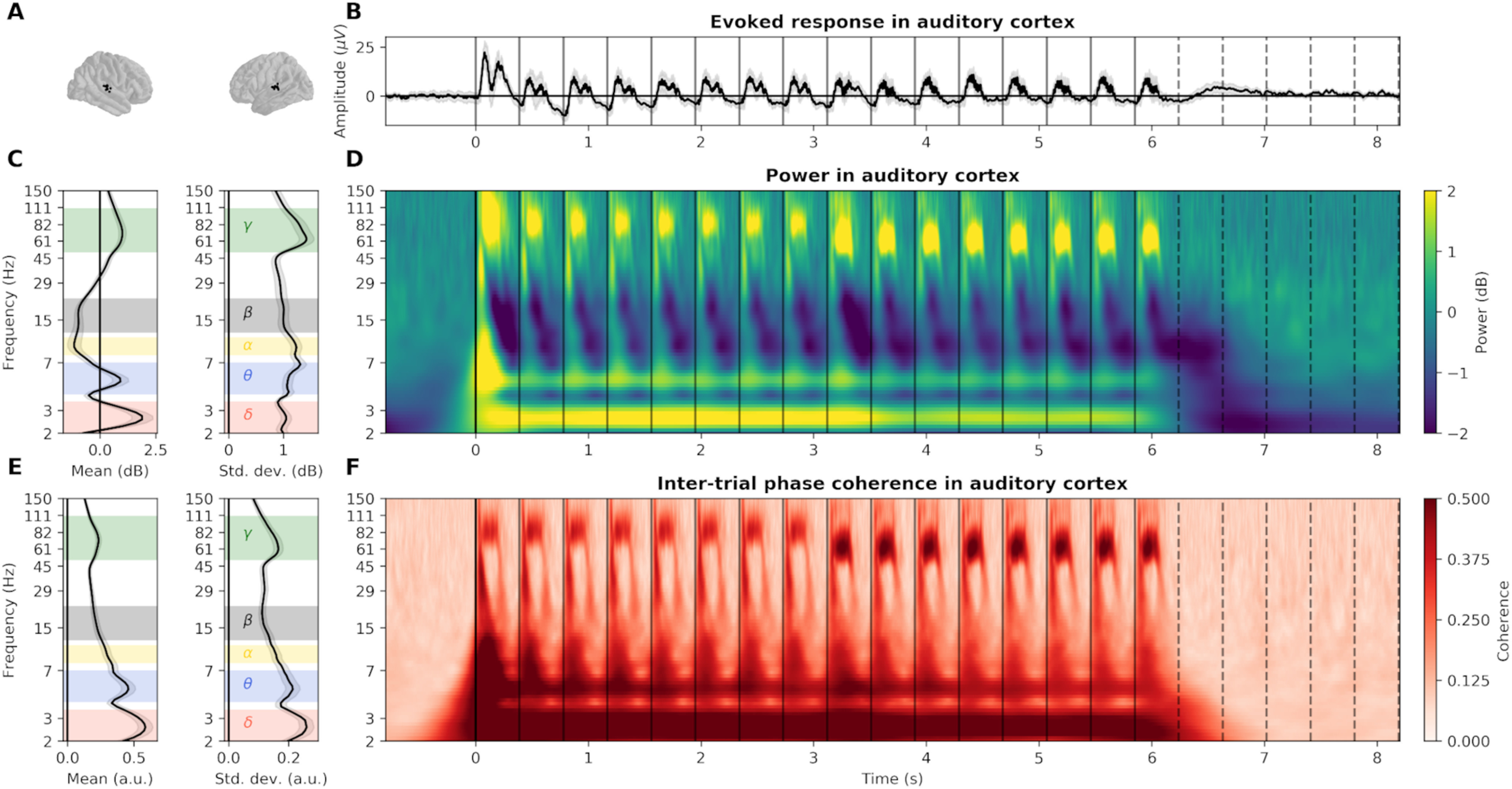
Detailed EFR in auditory cortex recorded with sEEG. A, Localization of the sEEG channels located in bilateral auditory cortices. B, Evoked response, averaged across channels. Gray shaded area represents the SEM across sources. Vertical plain and dotted lines, respectively, indicate the onset of each tone and their theoretical continuation in the silence. C, Left, Average and (right) SD of power over time during stimulus presentation (0-6.2 s). Selected frequency bands are indicated by colored shaded areas (δ: 2-3.5 Hz; θ: 4-7 Hz; α: 8-11 Hz; β: 12-22 Hz; γ: 50-110 Hz). D, Power, averaged across channels, in dB relative to baseline. E, Left, Average and (right) SD of ITPC over time during the presentation of the stimulus. F, ITPC, averaged across channels. Note the presence of the FFR first at 80 Hz and then at 60 Hz both in power and ITPC, reflecting the change of tone fundamental frequency at ∼3 s.

Figure 5.

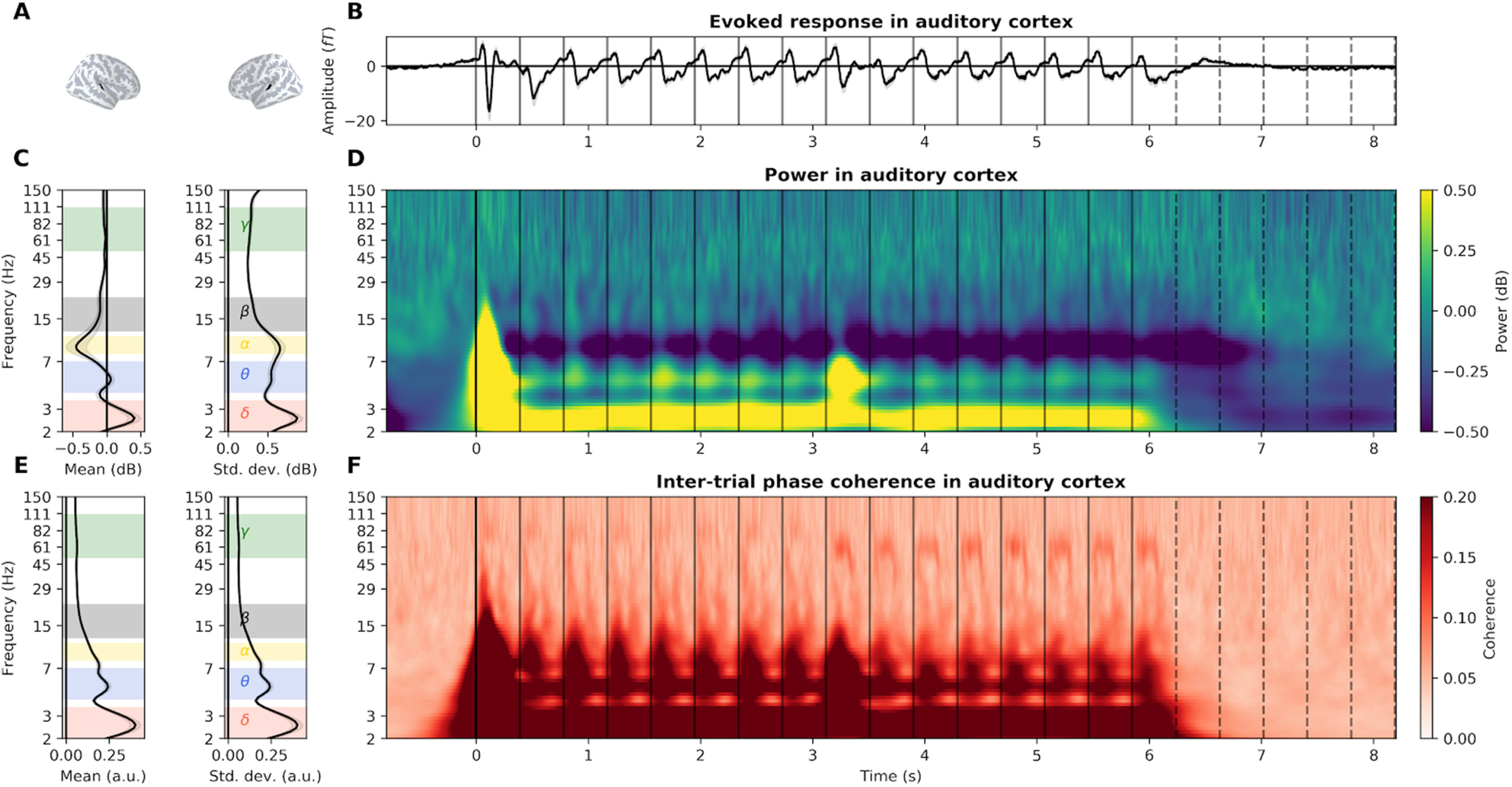
Detailed EFR in the auditory cortex recorded with MEG. A, Localization of the MEG vertices located in bilateral auditory cortices. B, Evoked response. Gray shaded area represents the SEM across participants. Vertical plain and dotted lines, respectively, indicate the onset of each tone and their theoretical continuation in the silence. C, Left, Average and (right) SD of power over time during stimulus presentation (0-6.2 s). Selected frequency bands are indicated by colored shaded areas (δ: 2-3.5 Hz; θ: 4-7 Hz; α: 8-11 Hz; β: 12-22 Hz; γ: 50-110 Hz). D, Power, averaged across participants, in dB relative to baseline. E, Left, Average and (right) SD of ITPC over time during the presentation of the stimulus. F, ITPC, averaged across participants.

We then applied the ABC procedure on all sEEG/MEG sources and all frequency bands ITPC to identify active sources and estimate their activity duration. sEEG and MEG recordings consistently reveal the spatial extent of the neural response for each defined frequency band. Stimulation induces a large-scale evoked response, encompassing auditory, motor, and associative regions in the δ and γ bands. On the contrary, α, β, and γ responses are more focal, in the bilateral superior temporal gyrus, and, for α and γ responses, also in the precentral gyrus. Critically, none of these evoked responses outlasts significantly the stimulus duration. In the δ band only, a tiny proportion of channels (1% in sEEG, 6 of 531, <0.1% in MEG, 4 of 5124) outlasts the stimulus by one cycle.

The neural response can be split into phase-locked activity, revealed by ITPC, and induced activity, revealed by power averaging across trials (Tallon-Baudry and Bertrand, 1999). If the low-frequency auditory modulation does not probe a long-lasting phase-locked response, effects could still be present in the induced activity. For completeness, we therefore tested this hypothesis. We used machine learning to train a model (TRF) (Crosse et al., 2016) to decode the stimulus with a linear combination of induced power in all sources and all frequencies delayed in time. We reasoned as follows: if power is modulated by the envelope of the auditory stimulus, then these fluctuations are informative about the stimulus. We should therefore be able to train a TRF model to decode the envelope based on power data. If power continues to exhibit these fluctuations during the silent period directly following the offset of the stimulus, we should still be able to decode the envelope oscillations (see Materials and Methods). In sEEG (Fig. 6A,B), the model performs remarkably well, predicting the stimulus envelope in the trained set with a coefficient of determination R² of 0.97 (z = 22, p < 0.001 compared with surrogate distribution), and with an R² of 0.71 in the testing set (z = 16, p < 0.001). When applied on the power directly following stimulus offset, the TRF performances drop to chance, with an R² of −0.03 (z = −0.09, p = 0.57). Similar results were found in MEG (Fig. 6C,D), where the model predicts the stimulus envelope in the trained set with a coefficient of determination R² of 0.97 (z = 18, p < 0.001 compared with surrogate distribution), and with an R² of 0.40 in the testing set (z = 7.4, p < 0.001). When applied on the power directly following the stimulus offset, performance drops to chance, with an R² of 0.03 (z = 0.43, p = 0.19). Thus, even when combining activity from all frequencies and sources, we are unable to detect information linked to the 2.5 Hz envelope modulation.

Figure 6.

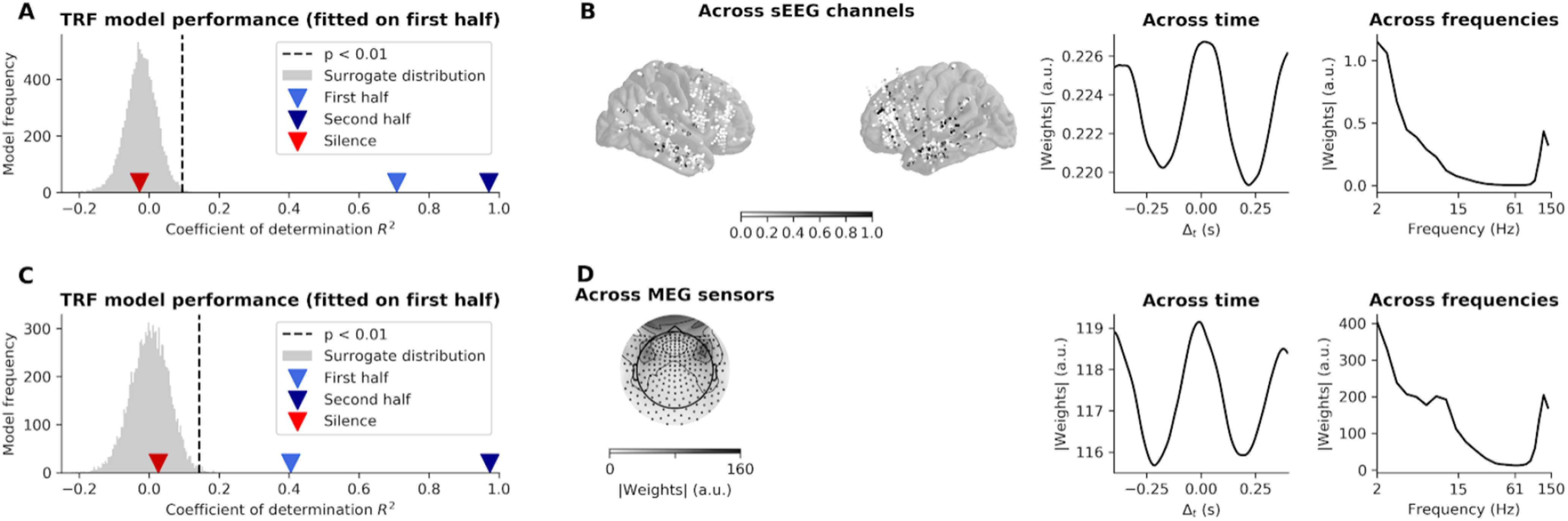
Decoding of the stimulus envelope in sEEG and MEG power data. A, Performance of the decoding model (TRF), trained on the power signal (2-150 Hz) of sEEG data recorded during presentation of the second half of the stimulus (62 Hz tones) and generalized to the first half of the stimulus (83 Hz) tones and the post-stimulus silence. Performance is assessed by the coefficient of determination R² obtained between the envelope reconstructed from the neural data and the actual stimulus envelope. Gray distribution indicates performance of TRF model on surrogate data. B, Marginal distributions of TRF weights (in absolute value) of sEEG data. Values are averaged in the sEEG channels (left), time (middle), and frequencies (right). C, Performance of the decoding model trained on MEG data. D, Marginal distributions TRF weights (in absolute value) of MEG data.

A model of damped harmonic oscillator captures the dissociation between high- and low-frequency responses

Oscillatory phenomena are common in nature. The damped harmonic oscillator, used to describe very different systems (e.g., spring/mass systems, pendulums, torques, and electrical circuits), is the standard model in physics. Despite being simple, powerful, and well suited to the description of neural mass dynamics (Freeman, 1961, 1972), this model has received little attention in the cognitive neuroscience community. By analogy to a spring/mass system (Fig. 7A), it is described by the canonical differential equation for linear oscillation as follows:

$$\frac{d{x}^2}{dt}=F\left(t-\Delta t\right)-\zeta {\omega }_0\frac{dx}{dy}-{\omega }_0^{2}x$$

$$\lambda =\frac{1}{\zeta {\omega }_0}$$

where x is the amplitude of the neural activity, ζ is the damping ratio, F is the stimulus amplitude, Δt is a time delay to account for transmission delays in the peripheral auditory system, and 2πω₀ is the eigenfrequency of the system. The damping ratio ζ is a key latent variable, as it constrains the activity of the system after the end of the stimulation. Overdamped systems (ζ > 1) show no oscillation after the end of the stimulation, whereas underdamped systems (ζ < 1) show oscillatory behavior with an amplitude decaying at an exponential decay of time constant λ. For example, a system with ζ = 0.1 and eigenfrequency 2πω₀ = 1 Hz will take λln2 ≈ 7 s to return to half of its activity (i.e., ∼ 7 cycles after the end of the stimulation). This goes beyond the debate on “self-sustained oscillators versus superposition of transient event-related potentials” insofar, as damping is a general property encompassing both interpretations. From a functional point of view, underdamping is the property that matters. The damped harmonic oscillator is thus a good model to clarify and quantify this question.

Figure 7.

The auditory cortex as a damped harmonic oscillator. A, By analogy to a spring/mass system, the model is composed of the trajectory of a center of mass (neural amplitude; black), a spring (a force pushing the system toward a fixed point, or baseline; blue), a damper (dissipation of energy, phase dispersion, negative feedback; green), and a driving force (the auditory stimulus amplitude; red). B, Fit quality (R²) of the harmonic oscillator to the auditory cortex ITPC as a function of model parameters. Models with ζ < 1 are underdamped; models with ζ > 1 are overdamped. The best fitting model, highlighted in red ($\zeta$= 13, $2\pi {\omega }_0$= 2.1 Hz, $\Delta t$ = 40 ms), explains 78% of the ITPC variance. C, Evoked activity of the best fitting model. D, Power of the best fitting model. E, ITPC of the best fitting model.

The three free parameters of this model (ζ, 2πω₀, and Δt) were fitted on the average power and ITPC time-frequency responses of the auditory cortex (see Materials and Methods). The model performs remarkably well, explaining 38% of the power variance and 78% of the ITPC variance. We next focused on ITPC data. Although linear and simple, the model captures key aspects of the auditory cortex response (Fig. 7D,E): clear frequency following responses at 83 and 62 Hz, stronger responses to 62 than 83 Hz tones, onset and offset responses to each tone in all frequencies, strong phase coherence at 2.5 Hz, and harmonics at 5 and 10 Hz. The best fitting model has parameters ζ = 13, 2πω₀ = 2.1 Hz and Δt = 40 ms (Fig. 7B). Its damping ratio ζ ≫ 1 indicates strong overdamping (i.e., absence of oscillatory dynamics after the end of the stimulation), thus reproducing our previous results.

In order to differentiate neural populations with different dynamics, we fitted the harmonic oscillator model to each sEEG channel (Fig. 8). After thresholding unexplained data (R² < 5%, 257 channels survived), a clustering algorithm (k-means, optimal silhouette index at k = 3; see Materials and Methods) yielded three clusters. Each cluster consists of a set of parameters and an associated topography. The first two clusters have a relatively low eigenfrequency 2πω₀ (0.73 Hz [first decile: 0.43, ninth decile: 2.1] and 2.1 Hz [1.3, 7.5]). Importantly and confirming our previous analyses, these two classes have a high damping ratio ζ (1.6 [1.0, 13] and 4.6 [0.6, 100]). Again replicating the model-free analyses for ITPC in the δ and θ band, the low-frequency clusters comprise bilateral auditory regions, but also associative regions situated along the two auditory pathways (superior and medial temporal gyrus, precentral gyrus, and bilateral inferior frontal gyrus). Conversely, the third cluster has radically different dynamics: a relatively high eigenfrequency 2πω₀ (60 Hz [27, 100]) and low damping ratio (0.08 [0.03, 0.6]). These parameters indicate an exponential decay of the amplitude of the oscillation after the end of the stimulation of time constant (λ = 0.9 s [0.12, 2.2]). The sEEG channels constituting this cluster are located in auditory cortices, precentral gyrus, medial temporal gyrus, and right inferior frontal gyrus. Overall, these three clusters confirm the dissociation between high- and low-frequency damping properties: the low-frequency clusters (0.7 and 2 Hz) show overdamping, whereas the high-frequency cluster (60 Hz) shows strong underdamping.

Figure 8.

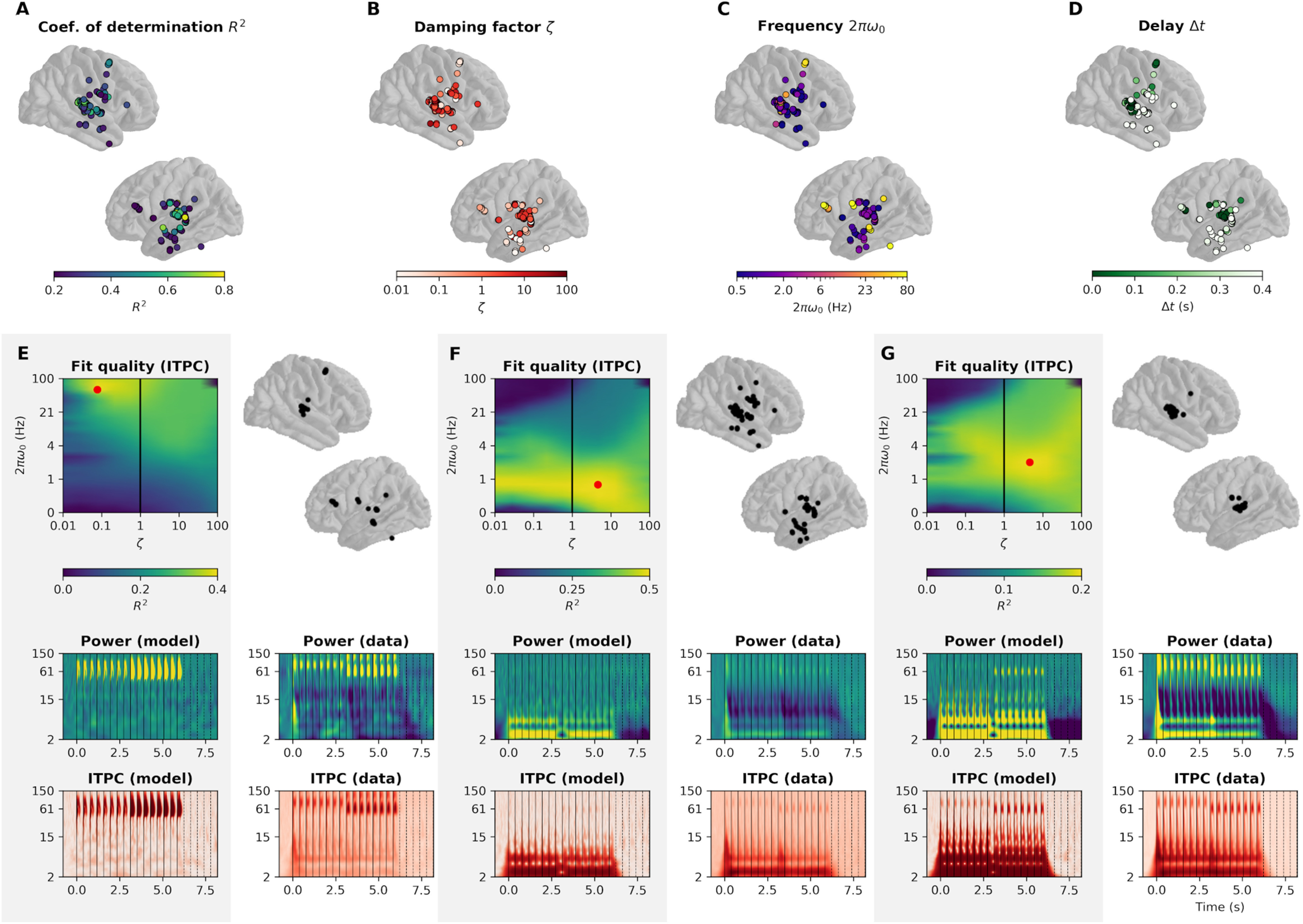
Clustering of electrodes based on best fitting parameters. A, Coefficient of determination of the linear regression between ITPC of the best fitting model and ITPC of the data. B, Damping ratio ζ of the best fitting model. C, Eigenfrequency 2πω₀ of the best fitting model. D, Time delay Δt of the best fitting model. E, Cluster 1. Left, Average fit quality (R²) as a function of model parameters. The best fitting model is highlighted in red. Right, Topography of the sEEG channels included in the cluster. Bottom left, Power and ITPC of the best fitting model for this cluster. Bottom right, Average power and ITPC of the sEEG channels included in the cluster. F, Cluster 2. G, Cluster 3. Only channels with R² > 5% are shown.

Discussion

During passive listening of a rhythmic stream of tones, the human brain exhibits two types of neural responses: (1) a high-γ oscillatory response, phase-locked to the fundamental frequency of the tones, that persists up to 10 cycles after stimulus offset; and (2) a complex set of responses encompassing all frequencies, evoked or induced by tones onset, offset, and the low-frequency acoustic rhythm, that does not persist long after stimulus offset (≤1 oscillatory cycle). These two responses are well captured by three classes of damped harmonic oscillators: two with a low eigenfrequency (0.7 and 2 Hz) and a high damping ratio (ζ > 1), and one with a high eigenfrequency (60 Hz) and a low damping ratio (ζ < 1).

Absence of persistent low-frequency neural oscillations during passive auditory perception

Current theories of speech (Giraud and Poeppel, 2012) and musical-beat (Large and Jones, 1999) perception capitalize on dynamical system theories to describe the interplay between neural and acoustic dynamics. Before estimating the capacity of neural oscillations to entrain to sensory stimulations, a clear understanding of the nature of the neural oscillations at play during auditory processing is mandatory. Previous findings have emphasized that rhythmic auditory stimuli principally drive activity at the rate of stimulation, typically in the δ-θ (<8 Hz) range, (Luo and Poeppel, 2007; Ghitza, 2013; Doelling et al., 2014) and also induce beta band (∼20 Hz) power modulations (Fujioka et al., 2012; Cirelli et al., 2014; Chang et al., 2016). Using precise stereotactic recordings, we show that rhythmic stimulation induces a complex response at the level of the auditory cortex composed of the following: (1) evoked activity at the low (∼2.5 and ∼5 Hz harmonic) and high (∼60/80 Hz) rates of acoustic stimulation, combined with transient bursts at tones onset and offset, visible across all frequencies; and (2) induced deactivation in the α and β ranges (7-30 Hz; Figs. 4 and 5). Of note, these results, obtained with high-quality sEEG recordings (Parvizi and Kastner, 2018) and straightforward time-frequency analyses are not subjected to spurious oscillatory artifacts, typically observed after complex signal processing, such as epochs oversampling or phase-amplitude coupling (Lozano-Soldevilla et al., 2016).

Next, we investigated whether any of the neural responses recorded throughout the cortex present the underdamping property considered as one of the most compelling arguments for entrainment (Lakatos et al., 2013). Radically, we found that, across frequencies and cortical regions, none of the responses evoked or induced by low-frequency (2.5 Hz) auditory stimulation outlasts the stimulus duration. Model-based analyses confirmed that an overdamped oscillator was the best fitting model (i.e., an oscillator with no oscillatory behavior after the end of the stimulus), thereby confirming the conclusions of the model-free analyses.

Different models of neural entrainment describe it either as resulting from the passive mechanistic coupling of neural oscillators with a rhythmic stimulation (Large and Jones, 1999; Obleser and Kayser, 2019) or as an attentional mechanism of sensory selection that involves network-level interactions between higher-order (motor or attentional) regions and sensory cortices (Lakatos et al., 2008, 2019; Schroeder and Lakatos, 2009; Haegens and Zion Golumbic, 2018; Rimmele et al., 2018). Our results are thus incompatible with the idea that the auditory cortex can be modeled as an isolated underdamped harmonic low-frequency (δ) oscillator (Large and Jones, 1999; Doelling et al., 2019). They are also inconsistent with the idea that beta band-induced activity entrains at the beat rate during passive listening (Fujioka et al., 2012). However, recent studies have shown low-frequency entrainment in auditory or visual regions in task-specific contexts, in particular, in tasks that involve selective attention to one of two presented rhythmic streams (Lakatos et al., 2013; Spaak et al., 2014), attention to the moment of occurrence of a target (Mathewson et al., 2012), or attention to the rhythm of a speech stream (Kösem et al., 2018; van Bree et al., 2021). Behavioral studies have also revealed improvements in auditory detection when targets are presented in phase with a rhythmic stimulus, even after several cycles of silence (Large and Jones, 1999; Hickok et al., 2015). Here, we reveal that such a mechanism does not occur during passive perception. To explain the divergence between our results and previous papers that have reported entrainment, we can hypothesize that low-frequency neural entrainment is an active, task-dependent phenomenon. Mechanistic explanations are still lacking, although our results are in line with recent proposals linking entrainment and attention, in which low-order input regions depend on top-down weighting to exhibit neural entrainment to input streams (Barczak et al., 2018; Rimmele et al., 2018; Lakatos et al., 2019). In such integrative models, top-down systems modulate sensory processing in a proactive and temporally flexible manner to enact entrainment phenomena. Thus, entrainment could reflect selective attention: rhythmic input streams are differentially prioritized, and only the attended stream, being weighted by top-down modulation, entrains oscillations.

A first limitation of this interpretation is that a weak oscillatory response at low frequency could be masked by a strong omission response elicited at the end of the stimulus. However, we do not see any omission response, probably because we repeated the same auditory stream throughout the experiment, which was hence fully predictable. A second limitation is that we have used simple stimuli, with a small informational content. In studies using more complex stimuli, such as speech, the richer temporal structure and the fact that some events carry information about future events (predictive events) could trigger automatically the underdamping of low-frequency oscillations. However, other studies have reported underdamping of low-frequency oscillations using simple stimuli, such as pure tones (Lakatos et al., 2013; Spaak et al., 2014), making the choice of simple stimuli less critical. A third limitation is that low frequencies were carried by the envelope of the stimulus, whereas high frequencies were carried by the fundamental frequency of the stimuli. This confounding factor cannot be excluded. However, it is known that amplitude-modulated sounds at ∼60/80 Hz produce the same phase-locked evoked responses in the high-γ range (Liégeois-Chauvel et al., 2004) as the one we observe. Furthermore, amplitude-modulated sounds give rise to a perception of pitch similar to complex tones (Walker et al., 2011). Thus, it is most probable that the frequency range is the key parameter to explain the damping differences we observe between low and high neural oscillations. These results are actually compatible with dynamical system approaches, which model neural population behaviors and provide important insights on the nature of neural oscillations. For example, fundamental differences between high- and low-frequency oscillations have been described. High-frequency oscillations are used in the context of small neural ensembles, such as populations of coupled excitatory and inhibitory neurons (pyramidal interneuronal γ or PING networks), whereas low-frequency oscillations usually involve coupled nodes in a network, global ensembles, and long-range connections (Buzsáki and Draguhn, 2004). Underdamping at such low frequencies is highly unexpected during passive stimulation, whereas it is expected for higher-frequency regimens (>40 Hz).

Presence of persistent high-frequency neural oscillations throughout the cortex

High-frequency phase-locked neural responses to auditory stimulation have been mostly studied at the level of the brainstem (Skoe and Kraus, 2010; Krizman and Kraus, 2019). Recordings of the auditory brainstem responses have been developed to assess the integrity of subcortical auditory relays via transient responses to very short sounds (clicks). The use of complex sounds of greater duration has allowed the analysis of a sustained response named FFR mimicking the fundamental frequency (and higher harmonics) of the auditory stimulus. Traditionally assessed using a three-electrodes scalp EEG montage, the sources of the auditory brainstem response, as their name suggests, were considered to be of subcortical origin, notably in the inferior colliculi and medial geniculate bodies (Russo et al., 2004; Kraus and Nicol, 2005; Chandrasekaran and Kraus, 2010; Skoe and Kraus, 2010; Tichko and Skoe, 2017; Bidelman, 2018; White-Schwoch et al., 2019). However, the sources of the FFR have recently been subject to intense debate. Three recent papers, using MEG/EEG (Coffey et al., 2016a, 2021) and fMRI (Coffey et al., 2016b), have convincingly demonstrated that cortical sources, especially Heschl's gyrus, also contribute to the scalp-recorded FFR in passive listening contexts. In this vein, our results confirm the presence of a high-γ oscillatory response phase-locked to the fundamental frequency of the tones in the auditory cortex. Surprisingly, we also demonstrate that the FFR is actually present in widespread cortical regions, well beyond what was previously observed. Our MEG results are confirmed by the highly spatially precise and localized sEEG data. The presence of the FFR in such regions could be mediated by the white matter tracts that connect the auditory cortex and different parts of the PFC along separate anterior and posterior projection streams (Rauschecker and Scott, 2009). The fact that an FFR is also present in high-level, integrative cortical regions, such as the motor cortex, supramarginal gyrus, medial temporal lobe, or the inferior frontal gyrus, sheds a new light on previous findings showing FFR differences across several types of populations (musical experts, language experts, language impaired populations). For instance, a larger FFR to the fundamental frequency of a sound may well be because of a greater involvement of integrative cortical regions, and may not necessarily imply modifications of subcortical activity via a corticofugal pathway (Wong et al., 2007; Kraus and Chandrasekaran, 2010). Nonetheless, subcortical specificity may be critical with high-frequency features, such as harmonics or speech formants (Krizman and Kraus, 2019).

The FFR at 62 Hz appears to be more widespread on the cortex and more persistent than the FFR at 83 Hz. The model suggests that this is because the 62 Hz stimulation is closer to the eigenfrequency of the oscillators (60 Hz on average). However, this could also be because of the presence of a 1/f noise, impacting 83 Hz responses >62 Hz responses.

Crucially, we reveal that the FFR presents an underdamping of up to 10 cycles (i.e., an oscillatory phase-locked response that persists after stimulus offset). This reflects a passive mechanistic coupling of neural oscillations with a rhythmic stimulation, and is usually modeled with small neural ensembles, such as populations of coupled excitatory and inhibitory neurons (PING networks). Thus, the FFR is not only a one-to-one representation of the stimulus, a succession of evoked potentials, but acts as a linear oscillatory filter. The functional role of this property is unknown, but it has been suggested that “it could serve as a fine-scale temporal predictor for frequency information, enhancing stability and reducing susceptibility to degradation that could be useful in real-life noisy environments” (Coffey et al., 2021).

The damped harmonic oscillator as a model of neural oscillatory activity

The damped harmonic oscillator is standard in physics to study oscillatory phenomena (e.g., spring/mass systems, pendulums, torques, and electrical circuits). It is defined by a linear second-order differential equation, derived from Newton's second law. Previous works have shown that this model is well suited to study neural mass dynamics (Freeman, 1972), that is, spatial averaging of thousands of neurons, in particular in modeling the evoked response (Freeman, 1961). Although simple and powerful, this model has received little attention in cognitive neuroscience. This lack of interest could arise from the fact that the harmonic oscillator is a phenomenological model, as its parameters capture properties of the neural ensemble and do not refer to physical quantities of the individual neurons, such as excitability or conductance (Hodgkin and Huxley, 1952; Wilson and Cowan, 1973). However, disposing of these biological constraints allows to model with very few parameters the emergent dynamics of the local population, the neural mass (i.e., the sEEG signal that we record). In our data, the apparent complexity of the neural response (multiple frequencies, onset and offset responses, harmonics) is indeed reducible to the interaction between the stimulus and a damped harmonic oscillator with three free parameters (ζ, 2πω₀, and Δt). Furthermore, three clusters of parameters are enough to describe the diversity of cortical responses to a rhythmic auditory stimulation: two overdamped low-frequency (0.7 and 2 Hz) and one underdamped high-frequency (60 Hz) oscillators. These three clusters show a topology that is consistent with known cerebral networks, namely, bilateral auditory cortices, ventral and dorsal auditory pathways (Rauschecker and Scott, 2009). Given the very limited range of frequencies presented (2.5, 62, and 83 Hz), the interpretation of the 2πω₀ eigenfrequency parameter is limited. The recovered values most probably reflect a mixture of the “true” eigenfrequencies of the recorded neural populations and the stimulus frequencies. The reported values should thus be taken as coarse indexes of “low” versus “high” eigenfrequencies. Refining these values would require presenting a wider range of frequencies.

Concerning the interpretation of the damping parameter, the dichotomy “underdamping versus overdamping” is usually confounded with the dichotomy “self-sustained oscillator versus superposition of transient event-related potentials.” Indeed, evoked responses are also modeled with oscillators (Jansen and Rit, 1995), and can either stop right after the end of the stimulation (overdamping), because of strong energy dissipation/phase dispersion, or continue to oscillate for a while (underdamping). While damping is thus the property that matters from a functional point of view, it can refer to different physiological realities. In particular, two hypotheses yet remain to be clarified: (1) If the neural response is linear, the damping reflects energy dispersion. (2) If the response is nonlinear, the damping could also reflect phase dispersion of multiple sustained oscillators. The progressive desynchronization of their phase would induce on average a similar exponential damping.

Finally, it should be noted that the harmonic oscillator is one special case of the broader set of linear filters, widely used in engineering of brain-computer interface. An important objective of this field of research is to define the encoding/decoding function that bridges the stimulus and the brain's response. Popular models (Crosse et al., 2016; de Cheveigné et al., 2018; Anumanchipalli et al., 2019) are filters, usually approximated by linear regression with regularization because of the large number of fitted parameters. The harmonic oscillator greatly simplifies the regularization problem, as it constrains the space of solution to only three free parameters, without losing explanatory power. Furthermore, analytical solutions are known for any given driving force, which again simplifies the problem by providing solutions with a very low computational cost. Overall, this model is a promising candidate for brain-computer interface engineering, by offering a simple, straightforward encoding/decoding function.