Abstract
Despite abundant measurements of bacterial growth rate, cell size, and protein content, we lack a rigorous understanding of what sets the scale of these quantities and when protein abundances should (or should not) depend on growth rate. Here, we estimate the basic requirements and physical constraints on steady-state growth by considering key processes in cellular physiology across a collection of Escherichia coli proteomic data covering ≈4,000 proteins and 36 growth rates. Our analysis suggests that cells are predominantly tuned for the task of cell doubling across a continuum of growth rates; specific processes do not limit growth rate or dictate cell size. We present a model of proteomic regulation as a function of nutrient supply that reconciles observed interdependences between protein synthesis, cell size, and growth rate and propose that a theoretical inability to parallelize ribosomal synthesis places a firm limit on the achievable growth rate. A record of this paper’s transparent peer review process is included in the supplemental information.
In brief
Identifying factors that determine growth rate has long been central to the study of bacterial physiology. Belliveau and Chure et al. present order-of-magnitude estimates of the proteomic requirements for various biological processes in Escherichia coli across growth rates and compare them to experimental measurements. This reveals translation to be key in defining the growth rate, while other processes are precisely tuned with little excess. The influence of physiological parameters on growth rate is explored using a simple mathematical model.
Graphical Abstract
INTRODUCTION
The observed range of bacterial growth rates is enormously diverse. In natural environments, some microbial organisms may double only once per year (Mikucki et al., 2009) while in comfortable laboratory conditions, growth can be rapid with several divisions per hour (Schaechter et al., 1958). This six-order-of-magnitude difference in timescales of growth encompasses different microbial species and lifestyles, yet even for a single species such as Escherichia coli, the growth rate can be modulated over a large range by tuning the type and amount of nutrients in the growth medium (Liu et al., 2005). This remarkable plasticity in growth rate illustrates the intimate relationship between environmental conditions and the rates at which cells convert nutrients into new cellular material—a relationship that has remained a major topic of inquiry in bacterial physiology for over a century (Jun et al., 2018).
A key discovery in bacterial physiology of the past 70 years was the identification of bacterial “growth laws” (Schaechter et al., 1958); empirical relationships that relate the bacterial growth rate to the protein and RNA composition of the intracellular milieu in a number of different species. Over the past decade, a flurry of work (Molenaar et al., 2009; Scott et al., 2010; Klumpp and Hwa, 2014; Basan et al., 2015; Dai et al., 2016; Erickson et al., 2017) has examined these growth laws at a quantitative level, developing a series of phenomenological models from which the growth laws naturally emerge. In parallel, a “molecular revolution” in biology has yielded an increasingly refined molecular census of the cell, particularly for bacteria such as the microbial workhorse E. coli (Schmidt et al., 2016; Davidi et al., 2016). In light of the now expansive trove of quantitative biological data, it is important to revisit several of the evergreen questions about bacterial growth and physiology that were originally raised by microbiologists in the middle of the 20th century. Further, it is timely to consider whether different measurements of the proteomic content are concordant. Specifically, what biological processes are the primary determinants for how quickly bacterial cells can grow and reproduce. Why do cells modulate the absolute numbers and relative ratios of their molecular constituents in response to changes in growth rate or nutrient availability? These questions remain under intense inquiry and have implicated processes ranging from ribosomal biogenesis and transcription to cell wall and lipid synthesis as key determinants of growth rate and cell size (Bremer and Dennis, 2008; Scott et al., 2010; Si et al., 2017; Vadia et al., 2017; Harris and Theriot, 2018; Büke et al., 2020; Zhang et al., 2020).
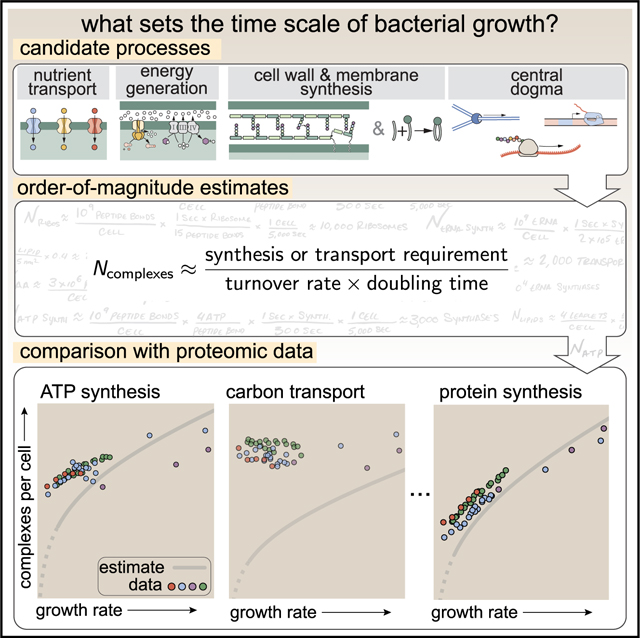
In this work, we consider these two questions in E. coli by considering both the biosynthetic capacity of key cellular processes—meaning, the minimal number of enzymes needed to synthesize one cell’s worth of a particular biomolecule given the observed doubling time—as well as the physical constraints given the now well-characterized change in cell size as a function of growth rate (Taheri-Araghi et al., 2015; Si et al., 2017; Basan et al., 2015). As a result of an array of high-quality proteome-wide measurements under diverse growth conditions, we have generated a census that allows us to explore how the number of key molecular players change as a function of growth rate. Here, we have assembled a singular dataset of protein copy numbers using measurements collected over the past decade via mass spectrometry (Schmidt et al., 2016; Peebo et al., 2015; Valgepea et al., 2013) or ribosomal profiling (Li et al., 2014) of the composition of the E. coli proteome across a gamut of growth rates. Due to notable changes in both cell size and cellular composition as a function of growth rate (Bremer and Dennis, 2008; Taheri-Araghi et al., 2015), as well as differences in normalization and standardization schemes used in each experimental work, substantial care was taken to ensure consistency on a per cellular basis (Figure 1A; see the supplemental information for a detailed analysis and further discussion). To our knowledge, this compiled and curated dataset represents the most comprehensive view to date of the E. coli proteome, covering ≈4,000 proteins and 36 unique growth rates, with the observed abundance of any given protein being directly comparable between datasets and across growth rates. This allows us to interrogate the E.-coli-specific physiology underlying the observed abundances while minimizing the effects of experimental noise as ≈75% of the proteins are observed in at least two separate datasets.
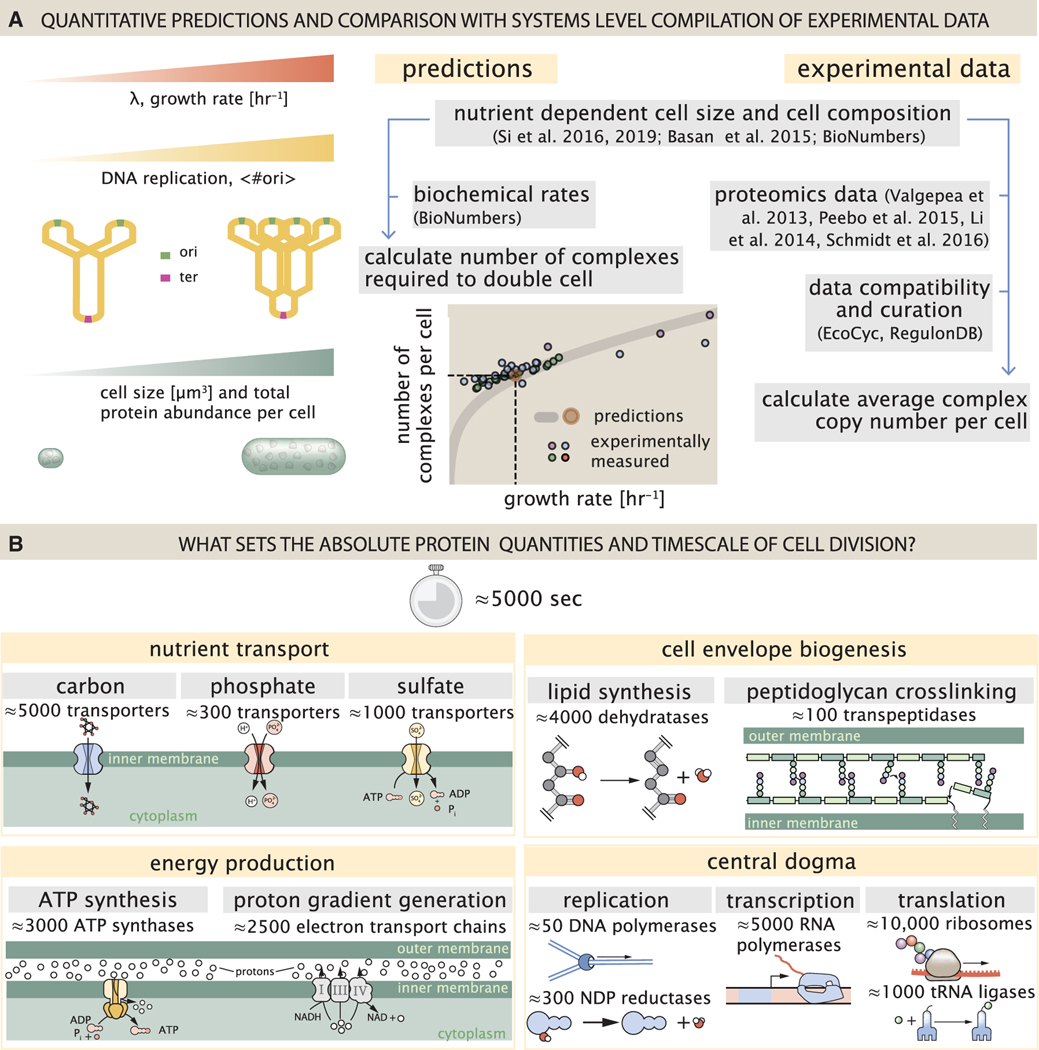
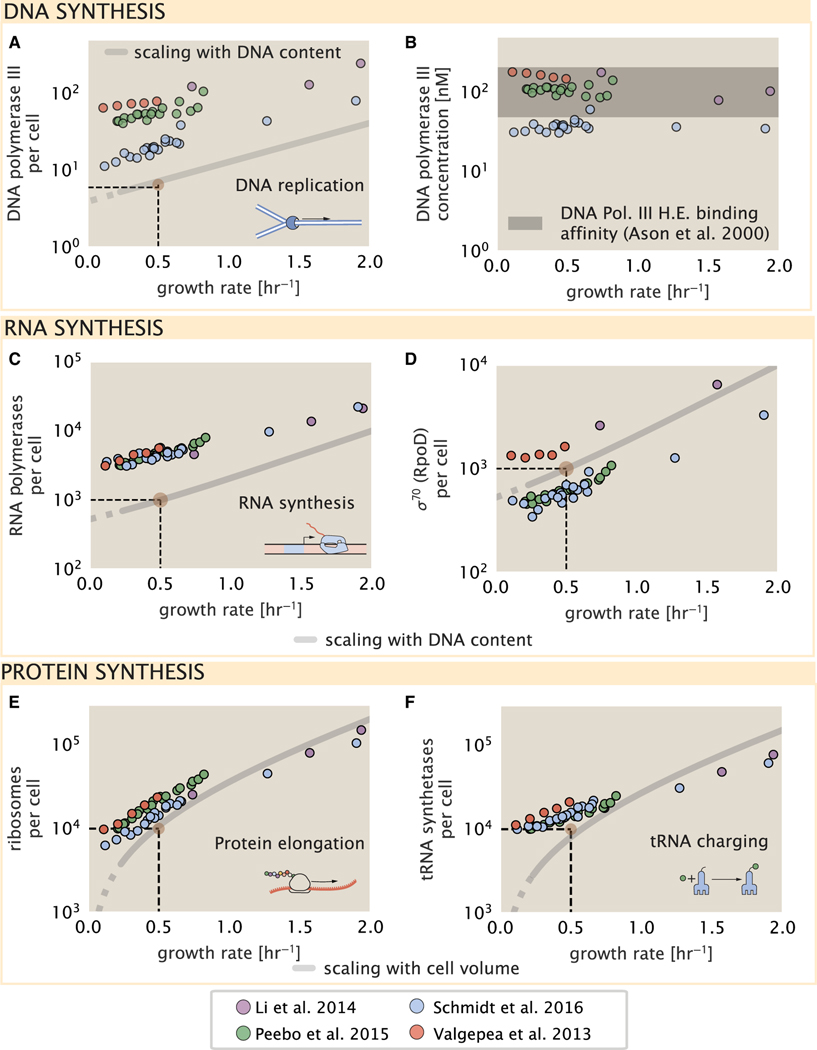
Figure 1. Quantitative predictions of required protein abundances across key transport and synthesis processes necessary for cell division.
(A) The growth rate dependent changes in bacterial size and composition provide a basis to both predict the protein abundances necessary to double a cell, and compile and compare proteomic measurements on a per cell basis across the recent datasets from Schmidt et al. (2016); Li et al. (2014); Peebo et al. (2015), and Valgepea et al. (2013). Predictions rely on the wealth of molecular turnover rate measurements and additional data tabulated on the BioNumbers Database (bionumbers.hms.harvard.edu, Milo et al. [2010]).
(B) We consider an array of processes necessary for a cell to double its molecular components, broadly grouped into four classes. These categories are nutrient transport across the cell membrane, cell envelope biogenesis, energy production (namely, ATP synthesis), and processes associated with the central dogma. Numbers shown are the approximate number of complexes of each type observed at a growth rate of 0.5 h −1, or a cell doubling time of ≈5,000 s.
By compiling molecular turnover rate measurements for many of the fundamental processes associated with bacterial growth, we make quantitative order-of-magnitude estimates across key cellular processes in nutrient transport, cell envelope biogenesis, energy generation, and the central dogma (Table S1; schematized in Figure 1B) to determine whether our current understanding of the kinetics of these processes are sufficient to explain the magnitude of the observed protein copy numbers across conditions. We consider each set of processes in turn and explore which process(es) may impose a limit as to how quickly cells can replicate. The census, combined with these estimates, provide a window into the question of whether the rates of central processes such as energy generation or DNA synthesis vary systematically as a function of cell growth rate by altering protein copy number, and in particular, whether any of these processes pose a molecular bottleneck or rate-limiting step. Though of course others have systematically examined the growth rate dependence for specific processes, our intent here was rather to provide a synthesis across a broad range of processes required in cellular growth.
For the majority of the processes considered, we find that the protein copy numbers are apparently tuned for the task of cell doubling across a continuum of growth rates. This suggests that most processes must be operating near their maximal biosynthetic capacity, particularly under moderate to fast growth rates, with cellular protein abundances increasing at faster growth rates to support the more rapid cell doublings. This observation contrasts with the perspective that there exists any single process that is the arbiter of growth rate. Rather, it is through the coordinated increase in protein abundance across these disparate processes that E. coli is able to increase its growth rate as nutrient conditions improve. This hypothesis is bolstered by the observation that, when we consider the change in cell size and the diminishing surface area to volume ratio at faster growth rates, there still appears to be sufficient space in the cell membrane for the key proteins required for energy production and nutrient uptake.
Given an observed importance of parallelization, where the synthesis of additional proteins provides increased biosynthetic capacity of each cellular process, our analysis also provides insight into the well-characterized dependence of growth rate on ribosomal mass fraction. Here, a theoretical inability to parallelize ribosomal protein synthesis places a firm upper bound on the achievable growth rate that is observed at moderate to fast growth rates, where ribosomes appear maximally utilized and where the proteomic requirements for other cellular processes still appear to be maintained. Importantly, the strict dependence between the maximal growth rate and ribosomal mass fraction coincides with the regime where the growth laws appear most valid (Amir, 2017; Scott et al., 2010). This enables us to suggest that the long-observed correlation between growth rate and cell size (Schaechter et al., 1958; Si et al., 2017) can be simply attributed to a required increase in absolute number of ribosomes per cell under conditions supporting extremely rapid growth. To better understand how the observed alterations in absolute protein abundances influence growth rate across different nutrient conditions, we consider a minimal model of cellular growth rate control to quantitatively explore the influence of proteomic composition and cell size on growth rate. Our conclusions from these analyses provide important insight into how E. coli regulates growth across both nutrient-poor and nutrient-rich regimes and identifies fundamental constraints in bacterial growth more broadly.
The “order-of-magnitude estimation protocol”
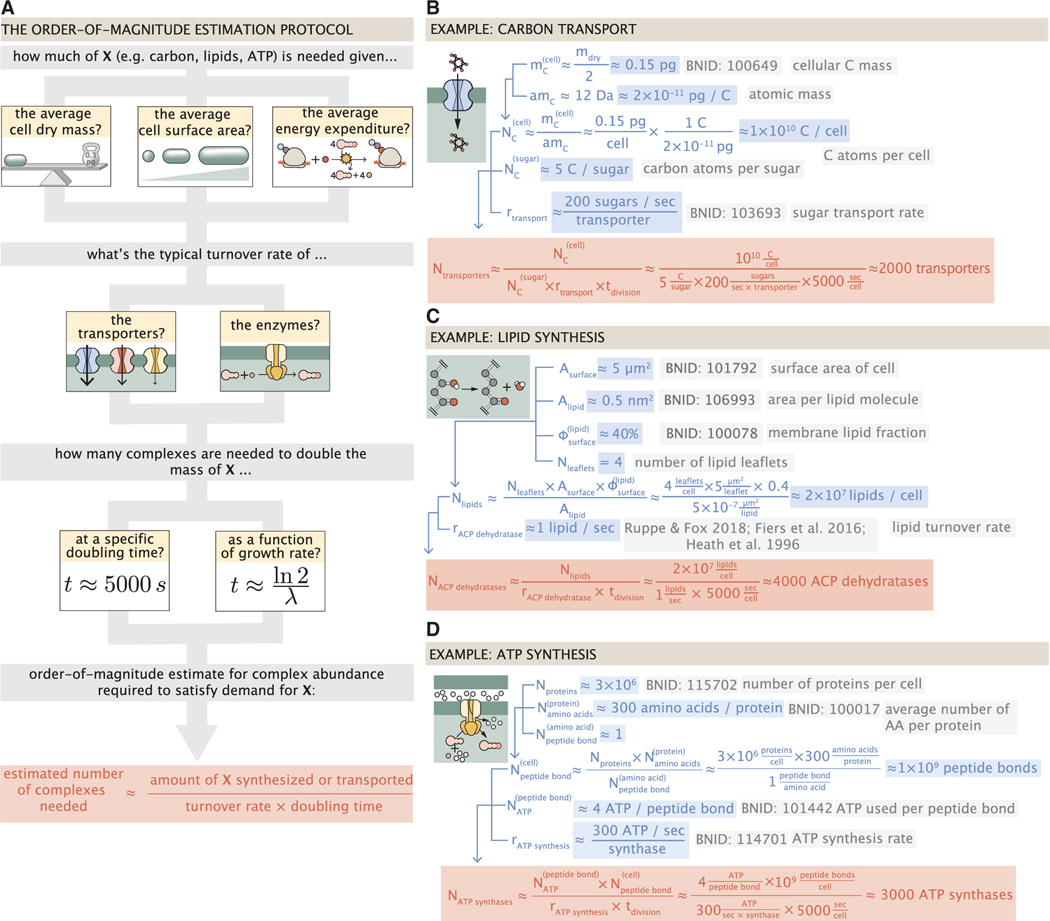
This work relies heavily on “back-of-the-envelope” estimates to understand the growth-rate-dependent abundances of molecular complexes. This moniker arises from the limitation that any estimate should be able to fit on the back of a postage envelope, meaning that we frequently make reasonable assumptions to arrive at approximate answers rather than performing a detailed calculation with the objective of high precision and many significant digits (Mahajan, 2010). All of the estimates performed in this work follow the same basic “protocol,” as is outlined in Figure 2A. For any given cellular process, we begin our estimate by first determining “how much” of a given molecule must be transported or synthesized to enable a doubling of cell biomass. For example, these molecules may be carbon atoms (in the form of transported sugars), the lipids making up the cell membrane, or the ATP that is consumed in doubling of the proteome.
Figure 2. The order-of-magnitude estimate protocol and examples for fundamental cellular processes.
(A) Nearly all order-of-magnitude estimates undertaken in this work follow the same basic estimate scheme. For a given process, we first consider how much of a given material X (e.g., carbon atoms, lipid molecules, or ATP) the cell must transport or synthesize. This is dependent on the elemental composition of the cellular dry mass, the cellular surface area, or the cellular energy expenditure. With a value for the amount to be synthesized, we consider how quickly the process can occur given the literature values of the in vivo or in vitro kinetics of the key complexes involved in the process. The number of complexes needed to meet the synthetic or transport demand is dependent on the doubling time of the cell, which can be taken to be a specific value or evaluated over a continuum of growth rates. Together, these three quantities can be combined to estimate the number of complexes needed to meet the demand in a given time, highlighted in red, with order-of-magnitude or better precision. Example estimates are given for (B) the number of carbon transporters, (C) the number of lipid synthesis enzymes, and (D) the number of ATP synthases. Similar diagrams of other estimates can be found in Table S1.
With numbers in hand for the amount of the material to be synthesized/transported we turn our focus to the central players of these works, the molecular complexes. The vast literature of in vivo and in vitro biochemistry has left us replete with quantitative properties of kinetic rates. We use this primary literature— and, when possible, their entries on the BioNumbers database (Milo et al., 2010) denoted with their accession numbers as BNIDs) —as a means to approximate the typical flux of material through a single enzyme, transporter, or biochemical pathway. To assemble these quantities into a singular estimate for the number of molecular complexes needed for a given process, we require a sense of the amount of time in which the synthesis/transport must take place. In this work, we consider two temporal regimes. First, we present a “point estimate” of the number of complexes needed to facilitate a doubling time of around 5,000 s, or a growth rate λ of ≈0.5 h−1. We choose this archetypal growth rate as it is the clearest narrative way to present our estimates and is the growth regime that the proteomic data heavily sample. This point estimate is always presented as a translucent brown point in the plots that follow.
Additionally, we also explore these estimates across a continuum of growth rates. The continuum estimates, displayed as a gray curve on the various plots, relax some of the assertions made while formulating the point estimate and incorporate empirical findings from the literature of how cell masses, volumes, and surface areas scale with the cellular growth rate (Si et al., 2017, 2019; Basan et al., 2015; Ojkic et al., 2019). As we rely on empirical descriptions of how volume, mass, and surface area scale with the growth rate, the point and continuum estimates may not always exactly agree. Finally, as growth rates become very slow (), protein degradation and cellular homeostasis may become an important factor (Feist et al., 2007; Stouthamer, 1973), one that we have chosen to ignore for the purposes of this work. Thus, we have indicated this region in the plots that follow as a dashed line to indicate that estimates in this regime may be too simplistic.
Figure 2A shows a schematic representation of this “estimation protocol.” In Figure 2B, we present a series of three examples, each considering a different scaling dependence as shown in the top panel of A. In estimating the number of carbon transporters (Figure 2B), we consider how many carbon atoms must be transported to double the biomass and use the elemental composition of the cell dry mass as a means to do so. In Figure 2C, we consider the cell surface area to estimate how many lipid molecules must be synthesized and, as described later, the number of ACP dehydratases needed for their synthesis. Finally, Figure 2D shows an estimate for the number of ATP molecules that must be consumed, given that peptide bond formation is the primary energy expenditure of growth. Similar diagrams for all estimate categories outlined in Figure 1B are provided in Table S1.
Nutrient transport
Here, we begin by considering the critical transport processes diagrammed in Figure 1B. We consider how cells scavenge building blocks (namely carbon, sulfur, and phosphorus) from the environment and the kinetics of nutrient transporters. We then calculate an estimated number of transporters required to support a given growth rate, and we compare these calculations with proteomic data.
In order to build new cellular mass, the molecular and elemental building blocks must be scavenged from the environment in different forms. Carbon, for example, is acquired via the transport of carbohydrates and sugar alcohols with some carbon sources receiving preferential treatment in their consumption (Monod, 1947). Phosphorus, sulfur, and nitrogen, on the other hand, are harvested primarily in the forms of inorganic salts, namely phosphate, sulfate, and ammonium/ammonia (Jun et al., 2018; Assentoft et al., 2016; Stasi et al., 2019; Antonenko et al., 1997; Rosenberg et al., 1977; Willsky et al., 1973). All of these compounds have different membrane permeabilities (Phillips, 2018), and most require some energetic investment either via ATP hydrolysis or through the proton electrochemical gradient to bring the material across the hydrophobic cell membrane.
The elemental composition of E. coli has received much quantitative attention over the past half century (Neidhardt et al., 1991; Taymaz-Nikerel et al., 2010; Heldal et al., 1985; Bauer and Ziv, 1976), providing us with a starting point for estimating how many atoms of each element must be scavenged from the environment: ≈50% carbon (BioNumbers, ID [BNID]: 100649; obtained from the BioNumbers database, Milo et al. [2010], ≈15% nitrogen [BNID: 106666], ≈3% phosphorus [BNID: 100653], and 1% sulfur [BNID: 100655]) with the remainder being attributable to oxygen, hydrogen, and various transition metals. Here, we estimate the abundance and growth rate dependence of a variety of transporters responsible for carbon uptake, and provide more extensive investigation of the other critical elements in the supplemental information “Estimates across fundamental biological processes.” Using ≈0.3 pg as the typical E. coli dry mass at a growth rate of ≈0.5 h−1 (BNID: 103904), coupled with the approximation that z50% of this mass is carbon, we estimate that ≈1×1010 carbon atoms must be brought into the cell in order to double all of the carbon-containing molecules.
Typical laboratory growth conditions provide carbon as a single class of sugar (such as glucose, galactose, or xylose) often transported cross the cell membrane by a transporter complex specific to that particular sugar. One such mechanism of transport is via the phosphotransferase system (PTS), which is a highly modular system capable of transporting a diverse range of sugars with high specificity (Escalante et al., 2012). The glucose-specific component of this system transports ≈200 glucose molecules (≈1,200 carbon atoms) per second per transporter (BNID: 114686). Making the assumption that this is a typical sugar transport rate for the PTS system, coupled with the need to transport ≈1 × 1010 carbon atoms, we then expect on the order of ≈2,000 transporters must be expressed per cell in order to bring in enough carbon atoms. We find, however, that the experimental measurements exceed this by several fold (Figure 3A), implying that the cell is capable of transporting more carbon atoms than strictly needed for biosynthesis. This holds true even at the fastest growth rates, with cells exhibiting no apparent growth rate dependence.
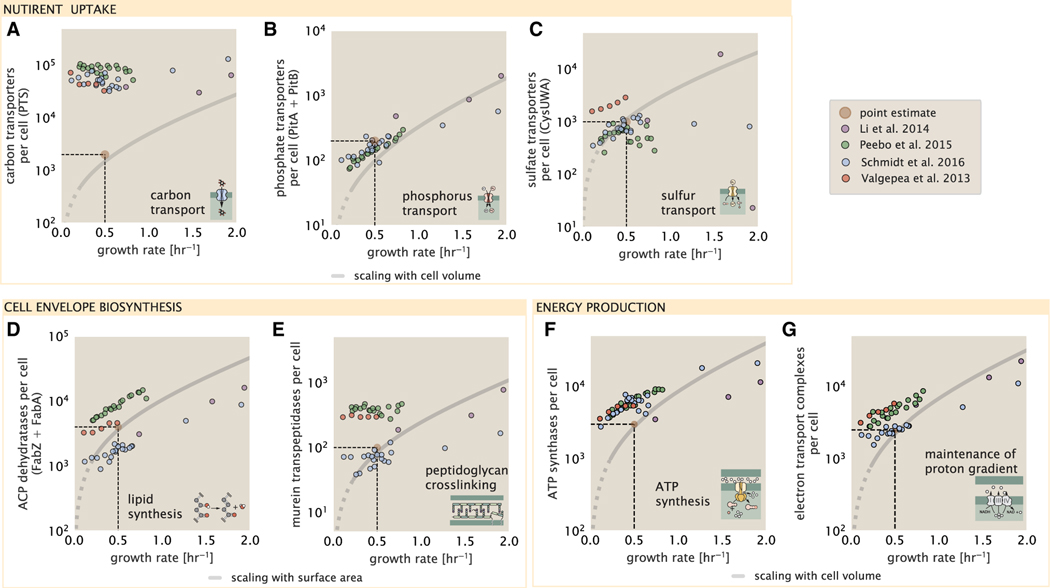
Figure 3. Key processes required for nutrient uptake, cell wall biogenesis and energy synthesis during growth.
Dashed black lines indicate order of magnitude estimate needed at a growth rate of ≈0.5 per h (light-brown point), while the gray line accounts for the growth rate dependence changes in cell size and doubling time. Dashed region of gray line represents growth rates with a doubling time ≥ 3 h where protein maintenance costs may be important but are not considered.
(A) Estimate for the minimum number of generic carbohydrate transport systems. Colored points correspond to the mean number of complexes involved in carbohydrate import (complexes annotated with the gene ontology terms GO:0009401 and GO:0098704) for different growth conditions across different published datasets.
(B) Number of PitA phosphate transport systems needed to maintain a 3% phosphorus dry mass.
(C) Number of CysUWA complexes necessary to maintain a 1% sulfur E. coli dry mass and the experimentally observed complex copy numbers using the transporter stoichiometry [CysA]2[CysU][CysW][Sbp/CysP].
(D) Number of ACP dehydratases necessary to form functional phospholipids, which is assumed to be a rate-limiting step on lipid synthesis, and the experimentally observed complex copy numbers using the stoichiometries [FabA]2 and [FabZ]2.
(E) Number of peptidoglycan transpeptidases needed to complete maturation of the peptidoglycan and experimental measurements of the transpeptidase complexes, following the stoichiometries [MrcA]2, [MrcB]2, [MrdA]1, and [MrdB]1.
(F) Number of F1-F0 ATP synthase complexes needed to accommodate peptide bond formation and other NTP dependent processes and experimental measurements following the stoichiometry [AtpE]10[AtpF]2[AtpB][AtpC][AtpH] [AtpA]3[AtpG][AtpD]3.
(G) Number of electron transport chain complexes needed to maintain a membrane potential of −200 mV. Points in plot correspond to the average number of complexes identified as being involved in aerobic respiration by the GO identifier GO:0019646. These complexes include cytochromes bd1 ([CydA][CydB][CydX] [CydH]), bdII ([AppC][AppB]), bo3,([CyoD][CyoA][CyoB][CyoC]) and NADH:quinone oxioreductase I ([NuoA][NuoH][NuoJ][NuoK][NuoL][NuoM][NuoN][NuoB] [NuoC] [NuoE][NuoF][NuoG][NuoI]) and II ([Ndh]).
This constancy in the expression appears to be specific to glucose transporters, which are known to be the preferential carbon source (Monod, 1947; Liu et al., 2005; Aidelberg et al., 2014), and stands in contrast with other species of transporters for glycerol, xylose, or fructose, which we find match the required transporter abundances according to the achieved doubling time (adjusting for the specific carbon source in terms of number of carbon atoms per molecule and the rate of transport for the particular transporter species) (Figure S1). This also contrasts with our observations for uptake of phosphorus and sulfur, which turn out to align well with our expectations across different growth conditions (Figures 3B and 3C and discussed further in the supplemental information “estimates across fundamental biological processes”). In summary, we researched and integrated quantitative information about cellular composition, nutrient transport, and transporter kinetics to estimate the minimum nutrient transporter copy numbers required across a spectrum of growth rates, and a comparison of these calculations to proteomic data suggests E. coli devotes excess proteomic resources toward glucose uptake but otherwise tunes transporter copy numbers to better match the nutrient requirements given their doubling time.
Lastly, we consider nutrient transport in the context of a different question: what sets an upper limit on very fast growth? If acquisition of nutrients was acting as a bottleneck on cellular growth, the growth rate could be theoretically increased simply by expressing more transporters, but is this feasible at a physiological level? A way to approach this question is to compute the amount of space in the bacterial membrane that could be occupied by nutrient transporters. Considering a rule-of-thumb for the surface area of E. coli of about 5 μm2 (BNID: 101792), we expect an areal density for 2,000 transporters to be approximately a few hundred transporters per μm2. For a typical transporter occupying about 50 nm2, this amounts to about only ≈1% of the total inner membrane surface area (Szenk et al., 2017). In contrast, bacterial cell membranes typically have densities of ≈1 × 105 proteins/mm2 (Phillips, 2018), with roughly 60% of the surface area occupied by protein (BNID: 100078), implying that the cell could easily accommodate more transporters. There are, however, additional constraints on the space that can be devoted to nutrient uptake due to occupancy by proteins involved in processes such as cell wall synthesis and energy production, and we will consider this further in the coming sections.
Cell envelope biogenesis
In this section, we consider the synthesis of lipids as well as the complexes involved in assembling the peptidoglycan scaffold that makes up the cell envelope. We discuss rate-limiting steps in fatty acid and peptidoglycan synthesis, calculate the copy number of fatty-acid synthases and peptidoglycan transpeptidases required to support a given growth rate, and compare these predictions to data. In contrast to nutrient transporters, which support the synthesis of biomolecules throughout the cell and therefore need to scale with the cell size, here, we must consider the synthesis of components that will need to scale with the surface area of the cell.
E. coli is a rod-shaped bacterium with a remarkably robust length-to-width aspect ratio of ≈4:1 (Harris and Theriot, 2018; Ojkic et al., 2019). The membranes of E. coli are composed of a variety of different lipids, each of which are unique in their structures and biosynthetic pathways (Sohlenkamp and Geiger, 2016). Recently, a combination of stochastic kinetic modeling (Ruppe and Fox, 2018) and in vitro kinetic measurements (Ranganathan et al., 2012; Yu et al., 2011) has revealed remarkably slow steps in the fatty-acid synthesis pathways, which may serve as the rate-limiting reactions for making new membrane fatty acids (that become components of a variety of membrane lipids) in E. coli. One such step is the removal of hydroxyl groups from the fatty-acid chain by ACP dehydratase that leads to the formation of carbon-carbon double bonds. This reaction, catalyzed by proteins FabZ and FabA (Yu et al., 2011), has been estimated to have kinetic turnover rates of ≈1 dehydration per second per enzyme (Ruppe and Fox, 2018). Thus, given this rate and the need to synthesize ≈2 × 107 lipids over 5,000 s, one can estimate that a typical cell requires ≈4,000 ACP dehydratases. This is in reasonable agreement with the experimentally observed copy numbers of FabZ and FabA (Figure 3D), though here, we also find notable discordance between measurements from different studies that may reflect systematic biases in how these measurements were performed.
The exquisite control of bacteria over their cell shape is due primarily to a stiff, several nanometer thick meshwork of polymerized disaccharides that makes up the cell wall termed the peptidoglycan. The formation of the peptidoglycan is an intricate process involving many macromolecular players (Shi et al., 2018; Morgenstein et al., 2015), whose coordinated action synthesizes the individual subunits and integrates them into the peptidoglycan network that maintains cell shape and integrity even in the face of large-scale chemical and osmotic perturbations (Harris and Theriot, 2018; Shi et al., 2018). Due to the extensive degree of chemical crosslinks between glycan strands, the entire peptidoglycan is a single molecule comprising ≈3% of the cellular dry mass (BNID: 1019360), making it the most massive molecule in E. coli. The polymerized unit of the peptidoglycan is a N-acetylglucosamine and N-acetylmuramic acid disaccharide, of which the former is functionalized with a short pentapeptide. With a mass of ≈1,000 Da, this unit, which we refer to as a murein subunit, is polymerized to form long strands in the periplasm which are then attached to each other via their peptide linkers. Together, these quantities provide an estimate of ≈5 × 106 murein subunits per cell.
There are various steps which one could consider a priori to be a limiting process in the synthesis of peptidoglycan, including the biosynthesis steps that occur in the cytoplasm, the transglycosylation reaction, which adds new subunits to the glycan strands, and the formation of the peptide crosslinks between strands (Shi et al., 2018; Morgenstein et al., 2015; Lovering et al., 2012; Barreteau et al., 2008). Despite the extensive mechanistic characterization of these components, quantitative characterization of the individual reaction rates along their entire kinetic pathway remain scarce and make identification of any particularly slow steps difficult. However, recent measurements for the crosslinking machinery (transpeptidases, Catherwood et al., 2020) of the peptidodglycan, which provides lateral structural integrity to the peptidoglycan shell, have found the turnover of transpeptidases to be rather slow (≈2 crosslinking reactions per second). As the primary mechanism of subunit integration occurs by a complex with both transglycosylation and transpeptidation activities (Shi et al., 2018), we therefore consider the transpeptidation reaction as a reasonable candidate for a rate-limiting step in growth as it is vital for cell size and shape homeostasis. We estimate that on the order of ≈100 transpeptidases per cell are needed for complete maturation of the peptidoglycan, given a division time of ≈5,000 s; a value that is comparable with experimental observations (Figure 3E). Expanding this estimate to account for the changing mass of the peptidoglycan as a function of growth rate (gray line in Figure 3E) predicts an order-of-magnitude increase in the abundance of the transpeptidases when the growth rate is increased by a factor of four. Here, however, the measured complex abundances across the different proteomic datasets show systematic disagreements and obfuscates any significant dependence on growth rate.
Lastly, we consider whether cell envelope biogenesis may set a cap on fast growth. While the processes explored above represent a small portion of the proteins devoted to cell envelope biogenesis, we find it unlikely that envelope biogenesis limits cellular growth in general. The relative amount of mass required for lipid and peptidoglycan components will decrease at faster growth rates due to a decrease in the cell’s surface area to volume ratio. Furthermore, despite the slow catalytic rate of fatty-acid synthesis and transpeptidation, there appears to be sufficient protein abundance to support growth. For FabZ and FabA in lipid synthesis, experimental data and recent computational modeling has shown that the rate of fatty-acid synthesis can be drastically increased by increasing the concentration of FabZ (Yu et al., 2011; Ruppe and Fox, 2018). With a proteome size of ≈ 3 × 106 proteins, a hypothetical 10-fold increase in expression from 4,000 to 40,000 ACP dehydratases would result in a paltry ≈1% increase in the size of the proteome.
Energy production
Cells consume and generate energy predominantly in the form of nucleoside triphosphates (NTPs). The high-energy phosophodiester bonds of (primarily) ATP power a variety of cellular processes that drive biological systems away from hermodynamic equilibrium. We therefore turn to the synthesis of ATP as another process that may limit growth, which will also require us to consider the maintenance of the electrochemical proton gradient that powers it. In this section, we calculate the energy required to build a daughter cell, the number of ATP synthases needed to supply this energy budget, and the number of electron transport complexes necessary to power the ATP synthases. We then compare these predictions with proteomic data.
Hydrolysis of the terminal phosphodiester bond of ATP into ADP (or alternatively GTP into GDP) and an inorganic phosphate provides the thermodynamic driving force in a wide array of biochemical reactions. One such reaction is the formation of peptide bonds during translation, which requires ≈2 ATPs for the charging of an amino acid to the tRNA and ≈2 GTPs for the formation of each peptide bond. Assuming the ATP costs associated with error correction and post-translational modifications of proteins are negligible, we can make the approximation that each peptide bond has a net cost of ≈4 ATP (BNID: 101442). Formation of GTP from ATP is achieved via the action of nucleoside diphosphate kinase, which catalyzes this reaction without an energy investment (Lascu and Gonin, 2000). We therefore consider all NTP requirements of the cell to be functionally equivalent to being exclusively ATP. In total, the energetic costs of peptide bond formation consumes ≈80% of the cells ATP budget (BNID: 107782, 106158, 101637, 111918; Lynch and Marinov [2015]; Stouthamer [1973]) and is primarily produced by the F1-F0 ATP synthase—a membrane-bound rotary motor which under ideal conditions can yield ≈300 ATP per second (BNID: 114701; Weber and Senior [2003]).
To estimate the total number of ATP equivalents consumed during a cell cycle, we make the approximation that there are ≈ 3 × 106 proteins per cell with an average protein length of ≈300 peptide bonds (BNID: 115702, 108986, 104877). With ≈4 ATP equivalents per peptide bond, we find that the typical E. coli cell consumes ≈ 5 × 109 ATP per cell cycle on protein synthesis alone. Assuming that each ATP synthases operates at its maximal speed, ≈3,000 ATP synthases are needed to keep up with the energy demands of the cell. This estimate is comparable with the experimental observations, shown in Figure 3F. Since this estimate assumes all ATP is synthesized via ATP synthase and neglects synthesis via fermentative metabolism, this may explain why at the fastest growth rates (≈ 2 h−1), our continuum estimate predicts more synthase than is experimentally observed (data points below the gray line in Figure 3F at fast growth rates). Here, E. coli enters a type of overflow metabolism where non-respiratory routes for ATP synthesis become more pronounced and provide the remaining ATP demand (Molenaar et al., 2009; Zhuang et al., 2011; Szenk et al., 2017).
In order to produce ATP, the F1-F0 ATP synthase itself must consume energy. Rather than burning through its own product (and violating thermodynamics), this intricate macromolecular machine has evolved to exploit the electrochemical potential established across the inner membrane through cellular respiration. This electrochemical gradient is manifest by the pumping of protons into the intermembrane space via the electron transport chains as they reduce NADH. In E. coli, this potential difference is ≈−200 mV (BNID: 102120). However, each rotation of an ATP synthase shuttles ≈4 protons into the cytosol (BNID: 103390). With a few thousand ATP synthases producing ATP at their maximal rate, the potential difference would be rapidly abolished in a few milliseconds if it were not being actively maintained. A recent work (Szenk et al., 2017) examined the respiratory capacity of the E. coli electron transport complexes using structural and biochemical data, revealing that each electron transport chain rapidly pumps protons into the intermembrane space at a rate of ≈1,500 protons per second (BIND: 114704, 114687). Using our estimate of the number of ATP synthases required per cell, coupled with these recent measurements, we estimate that ≈3000 electron transport complexes would be necessary to facilitate the ≈5 × 106 protons per second diet of the cellular ATP synthases. This estimate is in agreement with the number of complexes identified in the proteomic datasets (Figure 3F). Altogether, the agreement between our two estimates and the proteomic data supports the hypotheses embedded in our calculations: each ATP synthase is accompanied by ≈1 functional electron transport chain, with both complexes operating near their maximum rate across a range of growth conditions.
Limits on biosynthesis within a crowded cell
Our estimates thus far have focused on the biochemistry at the periphery of the cell, with the processes of nutrient transport, cell envelope biogenesis, and energy generation all requiring space to perform their biological functions. The cell’s surface area, however, does not scale as rapidly as cell size (Harris and Theriot, 2018), and there will be diminishing space available at the periphery to support the proteomic requirements at faster growth rates. It is therefore necessary to consider the consequences of a changing cell size and surface area to volume ratio in our effort to identify limitations on growth. Here, we use our analysis of ATP production to better understand this constraint.
In our estimate of ATP production above we found that a cell demands about 5 × 109. ATP per cell cycle or ≈1 × 106ATP/s. With a cell volume of roughly 1 fL (BNID: 100004), this corresponds to about 2 × 1010 ATP per fL of cell volume, in line with previous estimates (Stouthamer, 1973) and within 3–4 fold of more extensive calculations (Feist et al., 2007; Szenk et al., 2017). In Figure 4A, we plot this ATP demand as a function of the surface area to volume ratio in green, where we have considered a range of cell shapes from spherical to rod-shaped with an aspect ratio (length/width) equal to 4. In order to consider the maximum ATP that could be produced, we consider the amount of ATP that can be generated by a membrane filled with ATP synthase and electron transport complexes and a maximal production rate of about 3 ATP / (nm2•s) (Szenk et al., 2017). This is shown in blue in Figure 4A, which shows that at least for the growth rates observed (right column in plot), the energy demand is roughly an order of magnitude less. Interestingly, Szenk et al. (2017) found that ATP production by respiration is less efficient than by fermentation on a per membrane area basis, due to the additional proteins of the electron transport chain. This suggests that, even under anaerobic growth, cells will have sufficient membrane space for ATP production.
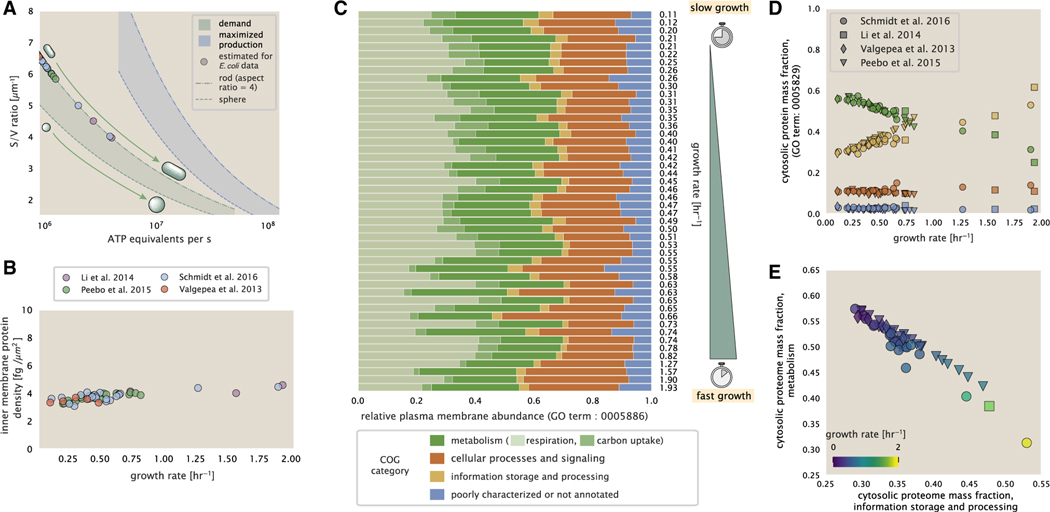
Figure 4. Influence of cell size and surface area to volume ratio on ATP production and inner membrane composition.
(A) Scaling of ATP demand and maximum ATP production through respiration as a function of surface area to volume ratio. Cell volumes of 0.5 fL to 50 fL were considered, with the dashed ( - -) line corresponding to a sphere and the dash-dot line (−.) reflecting a rod-shaped bacterium like E. coli with a typical aspect ratio (length/width) of 4 (Shi et al., 2018). The ATP demand is calculated as 106 ATP/(μm3 s), while the maximum ATP production rate is taken to be 3 ATP / (nm2•s) (Szenk et al., 2017), with calculations of E. coli volume and surface area detailed in supplemental information section “estimation of cell size and surface area.” In this calculation, 50% of the bacterial inner membrane is assumed to be protein, with the remainder lipid.
(B) Total protein mass per μm2 calculated for proteins with inner membrane annotation (GO term: 0005886).
(C) Relative protein abundances are grouped by their COG annotations (“metabolic,” “cellular processes and signaling,” “information storage and processing,” and “poorly characterized or not annotated”) for the data from Schmidt et al. (2016). Metabolic proteins are further separated into respiration (F1-F0 ATP synthase, NADH dehydrogenase I, succinate:quinone oxidoreductase, cytochrome bo3 ubiquinol oxidase, cytochrome bd-I ubiquinol oxidase) and carbohydrate transport (GO term: GO:0008643). Note that the elongation factor EF-Tu can also associate with the inner membrane but was excluded in this analysis due to its high relative abundance (roughly identical to the summed protein shown in B).
(D) Relative cytosolic protein abundances (GO term: 0005886), grouped by their COG annotations, are plotted as a function of growth rate.
(E) The relative cytosolic protein abundances (GO term: 0005886) associated with the “information storage and processing” and “metabolic” COG categories are plotted against each other and highlight the larger mass fraction devoted to “information storage and processing” at faster growth rates.
Importantly, this analysis highlights that there will indeed be a maximum attainable cell size due to the limited capacity to provide resources as the cell increases in size. The maximum energy production shown in Figure 4A, however, does represent a somewhat unachievable limit since the inner membrane also includes other proteins like those we have considered for nutrient transport and cell wall biogenesis. To better understand the overall proteomic makeup of the inner membrane, we therefore used gene ontology (GO) annotations (Ashburner et al., 2000; The Gene Ontology Consortium, 2019) to identify all proteins embedded or peripheral to the inner membrane (GO term: 0005886). Those associated but not membrane-bound include proteins such as MreB and FtsZ that must nonetheless be considered as a vital component occupying space on the membrane. Surprisingly, we find that the total protein mass per μm2 is nearly constant across growth rates (Figure 4B), even though the volumetric demand for resources grows with cell size and growth rate. Interestingly, when we consider the distribution of proteins grouped by their clusters of orthologous groups (COG) (Tatusov et al., 2000), the relative abundance of each category is nearly constant across growth rates (Figure 4C). This suggests that no one process (energy production, nutrient uptake, etc.) is dominating even at fast growth rates and is in line with our supposition that each of the processes we have considered so far are not fundamentally limiting the maximum growth rate.
In contrast, when we apply such an analysis to cytosolic proteins (GO term: 0005829), we observe a clear change in the proteomic composition (Figures 4D and 4E). Particularly, with increasing growth rates there is a substantial increase in the relative protein mass associated with “information storage and processing.” This category includes proteins such as DNA polymerase, RNA polymerase, and ribosomes that are associated with the processes of the central dogma, whose increase is predominantly at the expense of “metabolic” proteins as shown in Figure 4E. The notable anticorrelation provides a more extensive characterization of a trend that is consistent with previous reports (Scott et al., 2010; Hui et al., 2015; Zhu and Dai, 2019). In the next section, we therefore turn our attention to the processes of the central dogma.
Processes of the central dogma
Up to this point, we have considered a variety of transport and biosynthetic processes that are critical to acquiring and generating new cell mass and primarily seated at the cell membrane. We now turn our focus to some of the most important processes, which must be undertaken irrespective of the growth conditions—those of the central dogma. Specifically, we explore the abundance requirements of DNA polymerase, RNA polymerase, and ribosomes, with the latter two expected to have important consequences on the rate of accumulation in mRNA and protein abundances over the course of a cell cycle (Lin and Amir, 2018).
To successfully divide and produce viable progeny, the DNA must be faithfully replicated and segregated into each nascent cell. In rapidly growing cultures, bacteria like E. coli can initiate as many as 10–12 replication forks at a given time (Bremer and Dennis, 2008; Si et al., 2017), suggesting only ≈10 DNA polymerases are needed. However, as shown in Figure 5A, DNA polymerase III is nearly an order of magnitude more abundant while still maintaining a predicted growth rate dependence. This discrepancy can be understood by considering its binding constant to DNA. In vitro characterization has quantified the KD of DNA polymerase III holoenzyme to single-stranded and double-stranded DNA to be 50 and 200 nM, respectively (Ason et al., 2000) Figure 5B (discussed further, along with the synthesis of dNTP building blocks in supplemental information “additional process of the central dogma”).
Figure 5. Processes of the central dogma.
(A) The minimum number of DNA polymerase holoenzyme complexes needed to facilitate replication of the genome. Points correspond to the total number of DNA polymerase III holoenzyme complexes ([DnaE]3[DnaQ]3[HolE]3[DnaX]5[HolB] [HolA][DnaN]4[HolC]4[HolD]4) per cell.
(B) The effective concentration of DNA polymerase III holoenzyme (see supplemental information section “estimation of cell size and surface area” for calculation of cell size). Shaded region corresponds to the range of KD values measured by Ason et al. (2000), from 50 to 200 nM.
(C) The number of RNA polymerase core enzymes, with measurements corresponding to the average number given a subunit stoichiometry of [RpoA]2[R-poC][RpoB].
(D) The abundance of σ70 as a function of growth rate along with the same prediction from (C).
(E) Number of ribosomes required to synthesize 109 peptide bonds with an elongation rate of 15 peptide bonds per second.
(F) Number of tRNA synthetases that will supply the required amino acid demand. The sum of all tRNA synthetases copy numbers are plotted ([ArgS], [CysS], [GlnS], [GltX], [IleS], [LeuS], [ValS], [AlaS]2, [AsnS]2, [AspS]2, [TyrS]2, [TrpS]2, [ThrS]2, [SerS]2, [ProS]2, [PheS]2[PheT]2, [MetG]2, [lysS]2, [HisS]2, [GlyS]2[GlyQ]2). Dashed black lines indicate order of magnitude estimate needed at a growth rate of ≈0.5 per h (light-brown point), while the gray line accounts for the growth rate dependence changes in cell size and doubling time. Dashed region of gray line represents growth rates with a doubling time ≥ 3 h where protein maintenance costs may be important but are not considered.
We now turn our attention to the transcription of DNA to form RNA. Here, we focus on the synthesis of rRNA, which make up the majority of RNA in the cell, and discuss the synthesis of mRNA and tRNA further in the supplemental information “additional process of the central dogma.” rRNA serves as the catalytic and structural component of the ribosome, comprising approximately 2/3 of the total ribosomal mass, and is decorated with ≈50 ribosomal proteins. Each ribosome contains three rRNA molecules of lengths 120, 1,542, and 2,904 nucleotides (BNID: 108093), meaning each ribosome contains ≈4,500 nucleotides overall. In vivo measurements of the kinetics of rRNA transcription have revealed that RNA polymerases are loaded onto the promoter of an rRNA gene at a rate of ≈1 per s (BNID: 111997, 102362). If RNA polymerases are constantly loaded at this rate, then we can assume that ≈1 functional rRNA unit is synthesized per second per rRNA operon. At a growth rate of ≈0.5 h−1, the average cell has ≈1 copy of its chromosome and therefore approximately ≈7 copies of the rRNA operons, producing ≈7 rRNA units per second. With a 5,000-second division time, this means the cell is able to generate around 3 × 104 functional rRNA units, comparable within an order of magnitude to the number of ribosomes per cell.
How many RNA polymerases are then needed to constantly transcribe the required rRNA? If one polymerase is loaded once every second on average (BNID: 111997), and the transcription rate is ≈40 nucleotides per second (BNID: 101094), then the typical spacing between polymerases will be ≈40 nucleotides. With a total length of ≈4,500 nucleotides per operon and 7 operons per cell, the number of RNA polymerases transcribing rRNA at any given time is then ≈1,000 per cell. We also find that cells require on the order of another ≈400 RNAP for the synthesis of mRNA and tRNA, predicting a total of ≈1,500 RNAP to satisfy its transcriptional demands. As is revealed in Figure 5C, this estimate is about an order of magnitude below the observed number of RNA polymerase complexes per cell (≈5,000–7,000). Consistent with this discrepancy, roughly 80% of RNAP is reported to be transcriptionally inactive and a large majority of this fraction is non-specifically bound to DNA and in search for promoters from which to start transcription (Klumpp and Hwa, 2008; Patrick et al., 2015). In Figure 5D, we find that the predicted RNA polymerase copy number indeed is more comparable with the abundance of σ−70 (RpoD), the primary workhorse sigma factor for transcription in E. coli. We can conclude that the observed RNA polymerase abundances are generally sufficient for what appears needed for growth.
We conclude our dialog between back-of-the-envelope estimates and comparison with the proteomic data by examining the final process in the central dogma—translation. We begin with an estimate of the number of ribosomes needed to double the cellular proteome. While the rate at which ribosomes translate is well known to depend on the growth rate (Dai et al. [2018], a phenomenon we consider later in this work) we begin by making the approximation that translation occurs at a modest rate of ≈15 amino acids per s per ribosome (BNID: 100233). Using this approximation and our previous estimate of 109 peptide bonds per cell at a growth rate of 0.5 h−1, we can easily arrive at an estimate of ≈104 ribosomes needed per cell to replicate the entire protein mass, which proves comparable with the experimental observations (Figure 5E). While the ribosome is responsible for the formation of peptide bonds, we do not diminish the importance of charging tRNAs with their appropriate amino acid, a process with occurs with remarkable fidelity. In Figure 5F, we show our estimate for the required number of tRNA synthetases, which shows similar accord with the experimental data and is discussed further in the supplemental information “estimates across fundamental biological processes.”
Having completed our circuit through key processes of cellular growth outlined in Figure 1B, we can now take stock of our understanding of the observed growth rate dependence and abundances of various protein complexes. We note that, broadly speaking, these simple estimates have been reasonably successful in quantitatively describing the observations in the proteomic data. Importantly, this agreement suggests that the proteome of E. coli is predominantly tuned in composition and absolute abundance to match the growth rate requirements without any one process representing a singular bottleneck or rate-limiting step in division.
In our effort to identify key limitations on growth, there are two notable observations worthy of additional emphasis here. The first is a recurring theme throughout the estimates investigated here, which is that any inherent biochemical rate limitation can be overcome by expressing more proteins. We can view this as a parallelization of each biosynthesis task, which helps explain why bacteria tend to increase their protein content and cell size as growth rate increases (Ojkic et al., 2019). The second, and ultimately the most significant in defining the cellular growth rate, is that the synthesis of ribosomal proteins presents a special case where parallelization is not possible and thereby imposes a limit on the fastest possible growth rate. Each ribosome has ≈7,500 amino acids across all of its protein components which must be strung together as peptide bonds through the action of another ribosome. Once again using a modest elongation rate of ≈15 amino acids per s, we arrive at an estimate of ≈500 s or ≈7 min to replicate a single ribosome. This limit, as remarked upon by others (Dill et al., 2011; Reuveni et al., 2017; Kostinski and Reuveni, 2020), serves as a hard theoretical boundary for how quickly a bacterium like E. coli can replicate.
Maximum growth rate is determined by the rate of ribosomal synthesis
In the closing sections of this work, we return to the motivating questions posed in the introduction—what biological processes are the primary determinants for how quickly bacterial cells can grow and reproduce, and why do cells modulate the absolute numbers and relative ratios of their molecular constituents in response to changes in growth rate or nutrient availability? In the next two sections we begin by considering the consequences of the 7-minute limit set by ribosomal synthesis in the context of the available proteomic data and measured growth rates. In the final section, we consider how total protein abundance, ribosomal content, and chromosomal replication are intertwined in their control over the cellular growth rate. To do so, we take a more careful view, increasing the sophistication of our analysis by exchanging our order-of-magnitude estimates for a minimal mathematical model of growth rate control. This is defined by parameters with tangible connections to the biological processes underlying cellular growth and protein synthesis. We will draw on the analysis thus far but also draw on other theoretical and experimental work in order to develop a more complete synthesis around these questions.
The 7-min speed limit assumes all proteins in the cell are ribosomal. In order to connect this to the experimental data (and physiological reality more broadly), first, we need to relax this assumption and determine a translation-limited growth rate. Here, we will assume that the cell is composed of Npep peptide bonds and R ribosomes, whose precise values will depend on the growth rate λ. The protein subunits of each ribosomal protein sum to a total of ≈7,500 amino acids as noted earlier, which we denote by LR. With an average mass of an amino acid of mAA≈ 110 Da (BNID: 104877), the total ribosomal mass fraction is given by
| (Equation 1) |
For exponentially growing cells (Godin et al., 2010), the rate of cellular growth λ will be related to the rate of protein synthesis via
| (Equation 2) |
where rt is the translation rate. Here, we have introduced a multiplicative factor fa, which represents the fraction of the ribosomes that are actively translating. This term allows us to account for immature or non-functional ribosomes or active sequestration of ribosomes through the action of the secondary messenger alarmone (p)ppGpp in poorer nutrient conditions (Hauryliuk et al., 2015).
Combining Equations 1 and 2 results in an expression for a translation-limited growth rate, which is given by
| (Equation 3) |
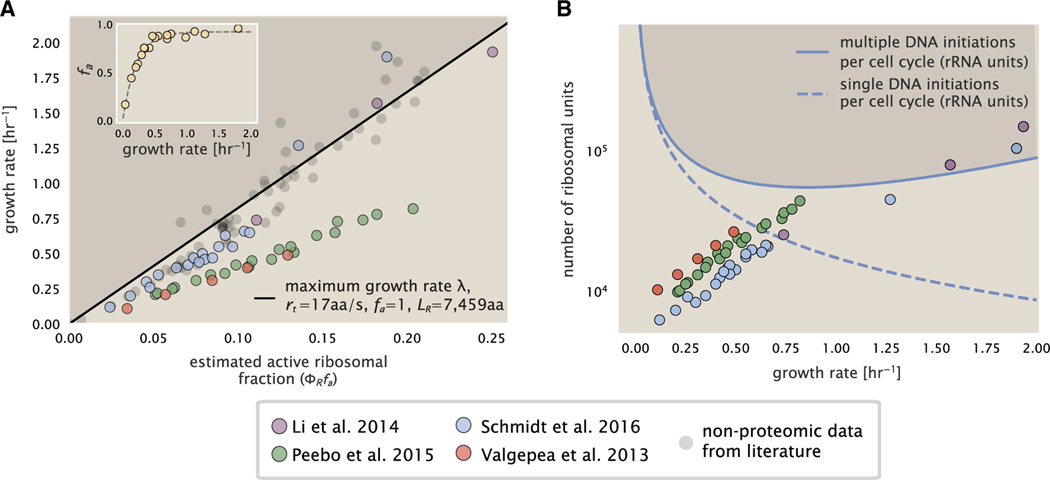
This result, derived in a similar manner by others (Dennis et al., 2004; Klumpp et al., 2013), reflects mass-balance under steady-state growth and has long provided a rationalization of the apparent linear increase in E. coli’s ribosomal content as a function of growth rate (Maalœ, 1979; Dennis et al., 2004; Scott et al., 2010; Dai et al., 2016). Figure 6A shows this growth rate plotted as a function of the ribosomal mass fraction (black line). In the regime where all ribosomes are active (fa = 1) and the entire proteome is composed of ribosomal proteins = 1), indeed, this line intercepts the maximum theoretical growth rate of rt/LR, and a ≈7-min doubling time for E. coli.
Figure 6. Limitations on ribosomal protein synthesis and growth rate.
(A) Translation-limited growth rate as a function of the actively translating ribosomal fraction. The actively translating ribosomal fraction is calculated using the estimated values of fa from Dai et al. (2016) (shown in inset; see supplemental information “calculation of active ribosomal fraction” for additional detail). Shaded region defines boundary due to constraint set on growth rate by Equation 3. The solid line is calculated for an elongation rate of 17 peptide bonds per s. Gray data points show additional measurements based on measurements of cellular RNA to protein ratio, with the cellular RNA to protein ratio divided by 2.1 (Dai et al., 2016) and come from Forchhammer and Lindahl (1971); Bremer and Dennis (2008); Scott et al. (2010); Dai et al. (2016); Si et al. (2017).
(B) Maximum number of rRNA units that can be synthesized as a function of growth rate. Solid curve corresponding to the rRNA copy number is calculated by multiplying the number of rRNA operons by the estimated number of at each growth rate. The quantity was calculated using Equation 4 and the measurements from Si et al. (2017). The dashed line shows the maximal number of functional rRNA units produced from a single chromosomal initiation per cell cycle. Shaded region defines boundary due to maximal rRNA synthesis.
Connecting Equation 3 to the proteomic data, however, requires knowledge of fa at each growth rate as proteomic measurements only provide a measure of . While commonly considered constant with growth rate (Young and Bremer, 1976; Klumpp et al., 2013; Bosdriesz et al., 2015; Kostinski and Reuveni, 2020), Dai et al. (2016) recently inferred fa as a function of the growth rate (Figure 6A, inset), revealing that while fa is close to 1 at growth rates above 0.75 h−1, it drops dramatically at slower growth rates. Using these data, we inferred the approximate active fraction (see supplemental information section “calculation of active ribosomal fraction”) at each growth rate and used this to compute (Figure 6A, colored points). Importantly, these data skirt the translation-limited growth rate determined using Equation 3, where we have taken rt to be the maximal elongation rate of 17 amino acids per s measured by Dai et al. (2016). There is a notable discrepancy between the data collected in Schmidt et al. (2016), Li et al. (2014) and that collected from Valgepea et al. (2013), and Peebo et al. (2015). When compared with other measurements (non-proteomic based) of the active ribosome mass fraction based on measurements of total RNA to total protein mass ratios (Figure 6A, gray points), the data from Valgepea et al. (2013) and Peebo et al. (2015) are notably different, suggesting there may be a systematic bias in these two sets of measurements.
The absolute ribosome copy number is limited by rRNA synthesis under rapid growth
Even under idealized experimental conditions, however, E. coli rarely exhibits growth rates above 2 h−1 (Bremer and Dennis, 2008), which is still well below the synthesis rate of a single ribosome, and below the maximum growth rates reported for several other bacteria (Roller et al., 2016). While we have considered potential limits imposed by translation of ribosomal “proteins,” we must also consider potential limiting regimes specific to the synthesis of rRNA. Due to multiple initiations of chromosomal replication per cell doubling, the effective number of rRNA operons increases with growth rate and will do so in proportion to the average number of chromosomal origins per cell, . This later parameter is set by how often replication must be initiated in order to keep up with the cell doubling time τ, whose time may be shorter than the cell cycle time (referring to the time from replication initiation to cell division) (Dennis et al., 2004; Ho and Amir, 2015). This is quantified by
| (Equation 4) |
where the doubling time τ is related to the growth rate by τ = log(2)/λ. As the rRNA operons are predominantly located close to the origin of replication (BNID: 100352), we make the simplifying assumption that that the number of rRNA operons will be directly proportional to . We used the experimental measurements of τcyc and τ (Figure S10) to calculate with Equation 4 as a function of growth rate. For growth rates above about 0.5 h−1, tcyc is approximately constant at about 70 min, implying an exponential increase in and the rRNA operon copy number for growth rates above 0.5 h−1.
Returning to our rule-of-thumb that one functional rRNA unit is produced per second per transcribing operon, we can estimate the maximum number of ribosomes that could be made as a function of growth rate (Figure 6B, blue curve). This provides a useful reference alongside the proteomic measurements, particularly in the regime of fast growth. For growth rates above about 1 h−1 in particular, we find that cells will need to transcribe rRNA near their maximal rate. The convergence between the maximum rRNA production and measured ribosome copy number shows that rRNA synthesis begins to present a physical bottleneck at the fastest growth rates in E. coli due to the still-limited copies of rRNA genes. While the rapid pace of rRNA synthesis is well documented (Neidhardt et al., 1991; Bremer and Dennis, 2008), this analysis helps highlight the difficulty in increasing absolute ribosome abundance further, given the apparent scaling in measured ribosome copy numbers and still-limited number of rRNA gene copies on the chromosome.
Simultaneous tuning of total protein mass and ribosome copy number increase growth rate under nutrient-limited growth
While the preceding two sections highlight a dominant role for ribosomes in setting the achievable growth rate, our analysis thus far has also shown how the proteomic content and cell size will need to change in response to variable growth conditions and growth rate. Here, we now return to the second question posed in the introduction—why do cells modulate the absolute numbers and relative ratios of their molecular constituents in response to changes in growth rate or nutrient availability? In this final section, we consider how the nutrient-dependent changes in total protein content per cell and proteomic composition influence the achievable growth rate.
The variable demand on resources as a function of growth condition places an optimization challenge for the cell—how are the translational demands of the entire proteome met without investing resources in the production of excess ribosomes? This question, more frequently presented as a question of optimal resource allocation, has been the target of an extensive dialog between experiment and theory over the past decade. In now seminal works, Scott et al. (2010, 2014) present an elegant treatment of resource allocation through partitioning of the proteome into sectors—one of which being ribosome-associated proteins whose relative size ultimately defines the total cellular growth rate. In more recent years, this view has been more thoroughly dissected experimentally (Klumpp et al., 2013; Basan et al., 2015; Dai et al., 2016, 2018; Erickson et al., 2017). However, the quantitative description of these observations is often couched in terms of phenomenological constants and effective parameters with the key observable features of expression often computed in relative, rather than absolute, abundances. Furthermore, these approaches often exclude or integrate away effects of cell size and chromosome content, which we have found through our estimates to have important connections to the observed cellular growth rate and proteomic content.
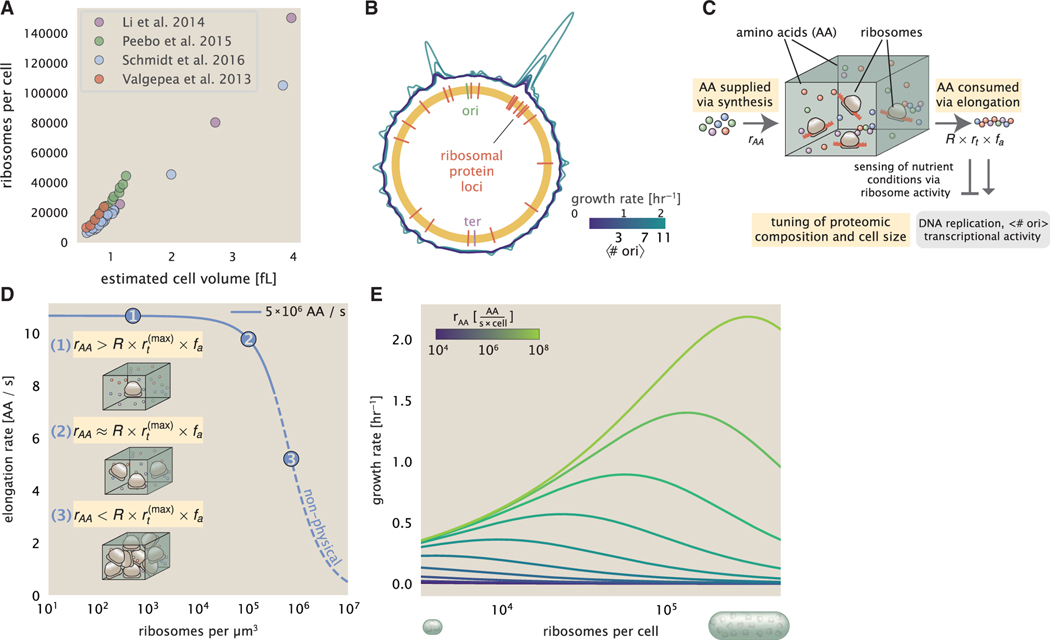
The specific mechanisms of growth rate control under nutrient limitation that lead to the observed scaling in cell size in E. coli and other bacteria, however, has remained unclear and continues to be intensely investigated (Si et al., 2017; Harris and Theriot, 2018; Ojkic et al., 2019). From our estimates, we see that the smaller, more economical cell sizes (i.e., smaller proteomic mass) observed in poorer nutrient conditions is consistent with a view that cells are also minimizing total protein abundance to better match their specific growth rate requirements. Under translation-limited growth conditions (λ ≈ 0.7 h−1), cells can then only increase their growth rate by increasing ribosome content. The simple addition of more ribosomes is likely constrained by macromolecular crowding (Delarue et al., 2018; Soler-Bistué et al., 2020), and we find that the cellular ribosome concentration increases 3–4-fold across growth conditions, compared with a roughly 20-fold change in absolute ribosome abundance (Figure 7A). Importantly, the major deviations in protein abundance with growth rate can be solely attributed to the required bias in ribosomal protein synthesis. To see this, we have calculated the position-dependent protein expression across the chromosome by a running Gaussian average of protein copy number (20 kbp SD averaging window) based on each gene’s transcriptional start site (Figure 7B). Since E. coli cells add a constant volume per origin of replication (Si et al., 2017), we have median-subtracted the measured protein copy numbers and colored each growth condition from the proteomic data according to .
Figure 7. Coordination of cell size and proteomic composition via ribosome activity.
(A) Plot of the ribosome copy number estimated from the proteomic data against the estimated cell size (see supplemental information “estimation of cell size and surface area” for details on the calculation of cell size).
(B) A running Gaussian average (20 kbp SD) of protein copy number is calculated for each growth condition considered by ( Schmidt et al., 2016) based on each gene’s transcriptional start site. Since total protein abundance increases with growth rate, protein copy numbers are median subtracted to allow comparison between growth conditions. are estimated using data from Si et al. (2017) (see supplemental information “estimation of for additional details).
(C) We consider a unit volume of cellular material composed of amino acids (colored spheres) provided at a supply rate rAA. These amino acids are polymerized by a pool of ribosomes (brown blobs) at a rate rt × R × fa, where rt is the elongation rate, R is the ribosome copy number in the unit volume, and fa is the fraction of those ribosomes actively translating. In addition to determining total protein synthesis rate, the nutrient status is gauged by any accumulation of de-acylated tRNAs and synthesis of the secondary messenger (p)ppGpp, which ultimately determine , cell size, and proteomic composition.
(D) The observed elongation rate is plotted as a function of the number of ribosomes. The three points correspond to three regimes of ribosome copy numbers and are shown schematically on the left-hand side. The region of the curve shown as dashed lines represents a non-physical copy number but is shown for illustrative purposes. This curve was generated using an amino acid supply rate of 5 × 106 AA / s, a maximal elongation rate of 17.1 AA / s, fa = 1, and a unit cell volume of 1 fL. See supplemental information “derivation of minimal model for nutrient-mediated growth rate control” for additional model details.
(E) The cellular growth rate is plotted as a function of total cellular ribosome copy number for different cellular amino acid supply rates, with blue and green curves corresponding to low and high supply rates, respectively. As the ribosome copy number is increased, so too is the cell size and total protein abundance Npep.
To more quantitatively consider the dependencies between cell size, ribosome abundance, and growth rate, we lastly consider a minimal model of growth rate control. For bacteria like E. coli, cell size will vary approximately in proportion to the total protein mass Kubitschek et al., 1984; Basan et al. (2015), and we will again consider a cell containing a total number of peptide bonds Npep and R ribosomes. Following from Equation 2, the rate of total protein synthesis and cellular growth rate λ will depend on the ribosomal elongation rate rt that each ribosome proceeds at. The elongation rate rt will ultimately depend on how quickly ribosomes can match codons with an amino-acyl tRNA, along with the subsequent steps of peptide bond formation and translocation (Figure 7C). This ultimately depends on the cellular concentration of amino acids, which we treat as a single effective species, [AA]eff. Here, we follow a similar strategy to that employed by others (Klumpp and Hwa, 2014; Dai et al., 2016) and apply a coarse-grained description of translation that allows for a reversible binding of the amino-acyl tRNAs followed by an irreversible addition of the amino acid into the peptide chain (further described in the supplemental information section “derivation of minimal model for nutrient-mediated growth rate control”). More extensive analyses of amino acid supply and consumption have been considered elsewhere (Elf and Ehrenberg (2005); Bosdriesz et al. (2015); Hu et al., 2020).
Having found that cells do not appear limited in their ability to synthesize and charge tRNA, we determine the rate of peptide elongation rt and achievable growth rate as simply depending on the supply of amino acids (and, therefore, also amino-acyl tRNAs), through a parameter rAA in units of AA per second, and the rate of amino acid consumption by protein synthesis (rt × R × fa). The parameter rAA will depend on the specific nutrient conditions, as well as the fraction of the proteome devoted to the supply of amino-acyl tRNAs, and we will consider its value a reflection of the nutrient quality. In Figure 7D, we illustrate how the elongation rate will depend on the ribosomal copy number for constant rAA, and further described in the supplemental information section “derivation of minimal model for nutrient-mediated growth rate control.”
To relate elongation rate to growth rate, we constrain the set of parameters based on our available proteomic measurements; namely, we restrict the values of R, Npep, and cell size V to those associated with the amalgamated proteomic data (described in the supplemental information section “estimation of total protein content per cell”). We then consider how changes in the nutrient conditions, through the parameter rAA, influence the maximum growth rate as determined by Equation 3. Under this scenario, R and V become interdependent parameters, while in supplemental information section “Relaxing the interdependence of R and V” and Figure S12, we discuss the resulting growth rate when R and V are treated as independent parameters and may be more relevant to physiological perturbations such as protein overexpression (Basan et al., 2015). Figure 7E shows how the growth rate depends on the rate of amino acid supply rAA as a function of the cellular ribosome copy number and the cell volume. A feature immediately apparent from the plot is the presence of a maximal growth rate that increases with increasing rAA. Importantly, there is a particular combination of values for R, Npep, and cell size V where growth rate λ is maximized. This shows that increasing the ribosomal concentration beyond the cell’s metabolic capacity will have the adverse consequence of depleting the supply of amino acids and lead to a concomitant decrease in the elongation rate rt (Figure 7D) and growth rate. This helps us understand that while it is important for cells to increase their ribosomal content and total protein content (and hence, also cell size) in order to increase growth rate, cells will better maximize their achievable growth rate by tuning these parameters according to nutrient conditions, since this is ultimately what allows cells to reach the peak for each curve shown in Figure 7E.
Also of note is the growth rate trends observed at low values of rAA (purple and blue lines in Figure 7E), representative of growth in nutrient-poor media. This regime is of particular interest due to deviations from expectations of ribosomal and cell size scaling that follow from the bacterial growth law (Dai et al., 2016; Amir, 2017; Zheng et al., 2020). Here, there no longer exists a peak in the maximum growth rate, at least within the range of physiologically relevant ribosome copy numbers considered. This is the regime, associated with slower growth rates, where cells limit their pool of actively translating ribosomes by decreasing fa (Figure 6A, inset). By reducing the fraction of actively translating ribosomes, cells instead appear to be prioritizing their pool of available amino acids [AA]eff in order to increase their translation elongation rate. Consistent with this hypothesis and our model, while inhibition of translation with chloramphenicol further reduces the fraction of actively translating ribosomes fa, it results in an increase in the elongation rate that has been observed experimentally (Dai et al., 2016) (Figure S13 and further discussion in relation to other models of translation elongation in supplemental information section “derivation of minimal model for nutrient-mediated growth rate control”). We can then view this slower growth regime (λ 0.7 h−1) as one that no longer prioritizes translation, with cells more limited by their amino acid supply (Forchhammer and Lindahl, 1971; Pedersen, 1984; Elf and Ehrenberg, 2005). Indeed, since ribosomes are not fully engaged in translation, cells are no longer maximizing growth rate according to their potential translation-limited rate. There are likely physiological benefits to this for a bacterium in an uncertain nutrient environment, with an excess pool of ribosomes potentially enabling more rapid recovery upon improvements in nutrient conditions (Bosdriesz et al., 2015; Bergkessel et al., 2016).
DISCUSSION
Continued experimental and technological improvements have led to a treasure trove of quantitative biological data (Hui et al., 2015; Schmidt et al., 2016; Si et al., 2017; Gallagher et al., 2020; Peebo et al., 2015; Valgepea et al., 2013), and an ever advancing molecular view and mechanistic understanding of the constituents that support bacterial growth (Taheri-Araghi et al., 2015; Morgenstein et al., 2015; Si et al., 2019; Karr et al., 2012; Kostinski and Reuveni, 2020; Macklin et al., 2020). In this work, we have compiled and curated what we believe to be the state-of-the-art knowledge on proteomic copy number across a broad range of growth conditions in E. coli. Beyond compilation, we have taken a detailed approach in ensuring that the absolute protein abundances reported are directly comparable across growth rates and datasets, allowing us to make assertions about the physiology of E. coli rather than chalking up discrepancies from our simple estimates to experimental noise and systematic errors. For example, while there was notable disagreement in the measurements from different studies in some cases (e.g., cell envelope biosynthesis in Figure 3E, or DNA synthesis in Figure 5A), our predictions were consistent with the trends observed in the data on the whole. We have made this data accessible through a GitHub repository, and an interactive figure that allows exploration of specific protein and protein complex copy numbers.
Through a series of order-of-magnitude estimates that traverse key steps in the bacterial cell cycle, this proteomic data have been a resource to guide our understanding of two key questions: what biological processes limit the absolute speed limit of bacterial growth, and how do cells alter their molecular constituents as a function of changes in growth rate or nutrient availability? While not exhaustive, our series of estimates provide insight on the scales of macromolecular complex abundance across four classes of cellular processes—the transport of nutrients, the production of energy, the synthesis of the membrane and cell wall, and the numerous steps of the central dogma.
In general, the copy numbers of the complexes involved in these processes were in reasonable agreement with our order-of-magnitude estimates. Since many of these estimates represent soft lower-bound quantities, this suggests that cells do not express proteins grossly in excess of what is needed for a particular growth rate. Rather, cells maintain protein abundances that while nearly rate limiting, they are nevertheless sufficient for the require biosynthetic capacity given available nutrient conditions and the observed doubling time. Several exceptions, however, also highlight the dichotomy between a proteome that appears to “optimize” expression according to growth rate and one that must be able to quickly adapt to environments of different nutritional quality. Take, for example, the expression of carbon transporters. Shown in Figure 3A, we find that cells always express a similar number of carbohydrate transporters irrespective of growth condition. Normalizing transporter abundance to total cellular mass, this would result in a decrease in mass fraction associated with carbon uptake for increasing growth rates and improved nutrient conditions, consistent with previous work (You et al., 2013; Hui et al., 2015). At the same time, it is interesting to note that many of the alternative carbon transporters are still expressed in low but non-zero numbers (≈10–100 copies per cell) across growth conditions. This may relate to the regulatory configuration for many of these operons, which require the presence of a metabolite signal in order for alternative carbon utilization operons to be induced (Monod, 1949; Laxhuber et al., 2020). Furthermore, upon induction, these transporters are expressed and present in abundances in close agreement with a simple estimate (Figure S1).
Of the processes illustrated in Figure 1B, we arrive at a perspective where the different processes of bacterial growth all must be carefully coordinated to support rapid growth, but where ribosomal abundance sets a firm upper limit on the achievable growth rate. This is in some sense unsurprising given the long-held observation that E. coli and many other organisms vary their ribosomal abundance as a function of growth conditions and growth rate (Scott et al., 2010; Metzl-Raz et al., 2017). However, through our dialog with the proteomic data, two additional key points emerge. The first relates to our question of what process sets the absolute speed limit of bacterial growth. While a cell can parallelize many of its processes simply by increasing the abundance of specific proteins or firing multiple rounds of DNA replication, this is not so for synthesis of ribosomes as has been noted by others (Dill et al., 2011; Reuveni et al., 2017; Kostinski and Reuveni, 2020). The translation time for each ribosome (≈7 min) places an inherent limit on the growth rate that can only be surpassed if the cell were to increase their polypeptide elongation rate, or if they could reduce the total protein and rRNA mass of the ribosome. The second point relates to the long-observed correlations between growth rate and cell size (Schaechter et al., 1958; Si et al., 2017), and between growth rate and ribosomal mass fraction. While both trends have sparked tremendous curiosity and driven substantial amounts of research in their own regards, these relationships are themselves intertwined. In particular, E. coli’s protein content is reasonably well-tuned according to their growth rate, there is a predominant need for cells to increase their absolute number of ribosomes under conditions of rapid growth that require cells to also grow in size.
On the question of how bacteria actually achieve the simultaneously tuning of their ribosomal abundance, total proteomic content, and the extent of replication, much work points to the role of secondary messengers like (p)ppGpp (Cashel and Gallant, 1969; Nomura et al., 1984). While most commonly associated with a dynamic global response to changes in nutrient conditions through the stringent response, (p)ppGpp increasingly appears to play a role in both the control of the active ribosomal fraction and cell size homeostasis under steady-state nutrient-limited growth (Dai et al., 2016; Zhu and Dai, 2019; Büke et al., 2020; Vadia et al., 2017; Parker et al., 2020). In E. coli, an accumulation of de-acylated tRNAs at the ribosome’s A-site leads to a strong increase in (p)ppGpp synthesis activity by the enzyme RelA (Hauryliuk et al., 2015), providing a direct way to sense and adjust ribosomal content according to the level of charged tRNAs, as was shown in the work of Bosdriesz et al. (2015). (p)ppGpp and co-regulator DksA also strongly repress rRNA synthesis and ribosomal protein gene expression (Paul et al., 2004; Jin et al., 2012), and there is more recent evidence that (p)ppGpp acts to inhibit the initiation of DNA replication and DNA supercoiling near the origin of replication (Kraemer et al., 2019; Fernández-Coll et al., 2020). E. coli cells are well documented to add a constant volume per origin of replication that is robust to a remarkable array of cellular perturbations (Si et al., 2017) and many bacteria have been found to positively vary nucleoid size with cell size (Campos et al., 2018; Gray et al., 2019). It will be interesting to further consider how control by (p)ppGpp aids in tuning and cell size to better match available nutrients conditions.
While the generation of new ribosomes plays a dominant role in growth rate control, there exist other physical limits to the function of cellular processes. One of the key motivations for considering energy production was the physical constraints on total volume and surface area as cells vary their size (Harris and Theriot, 2018; Ojkic et al., 2019). As E. coli get larger at faster growth rates, an additional constraint begins to arise in energy production and nutrient uptake due to the relative decrease in total surface area, where ATP is predominantly produced (Szenk et al., 2017). Specifically, the cell interior requires an amount of energy that scales cubically with cell size, but the available surface area only grows quadratically (Figure 4A). While this threshold does not appear to be met for E. coli cells growing at 2 h−1 or less, it highlights an additional constraint on growth given the apparent need to increase cell size in order to grow faster. This limit is relevant even to eukaryotic organisms, whose mitochondria exhibit convoluted membrane structures that nevertheless remain bacteria-sized organelles (Guo et al., 2018). In the context of bacterial growth and energy production more generally, we have mainly limited our analysis to the aerobic growth conditions associated with the proteomic data, and further consideration will be needed for anaerobic growth.
This work is by no means meant to be a complete dissection of bacterial growth rate control, and there are many aspects of the bacterial proteome and growth that we neglected to consider. For example, other recent work (Liebermeister et al., 2014; Hui et al., 2015; Schmidt et al., 2016) has explored how the proteome is structured. In the work of Hui et al. (2015), the authors coarse-grained the proteome into six discrete categories being related to either translation, catabolism, anabolism, and others related to signaling and core metabolism. The relative mass fraction of the proteome occupied by each sector could be modulated by external application of drugs or simply by changing the nutritional content of the medium. While we have explored how the quantities of individual complexes are related to cell growth, we acknowledge that higher-order interactions between groups of complexes or metabolic networks at a systems level may reveal additional insights into how these growth rate dependences are achieved. This is exemplified by recent work highlighting a role for “P-sector” divisor proteins in setting cell size (Si et al., 2019; Panlilio et al., 2020; Serbanescu et al., 2020), where quantitative treatment of the allocation of cellular resources toward ribosomal and division protein synthesis can help account for morphological changes under nutrient shifts or translational perturbations. Furthermore, while we anticipate the conclusions summarized here are applicable to a wide collection of bacteria with similar lifestyles as E. coli, other bacteria and archaea may have evolved other strategies that were not considered. Further experiments with the level of rigor now possible in E. coli will need to be performed in a variety of microbial organisms to learn more about how regulation of proteomic composition and growth rate control has evolved over the past 3.5 billion years.
STAR★METHODS
Detailed methods are provided in the online version of this paper and include the following:
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Rob Phillips (phillips@pboc.caltech.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
All data, code, and figure generation scripts are publicly available as a GitHub repository (https://github.com/rpgroup-pboc/growth_limits) and is accessible via [https://doi.org/10.5281/zenodo.4091457]. We invite the community to fork this repository and open constructive issues with comments regarding the analysis, annotation, or findings of the work.
The published article includes two data sets generated during this study. Data S1 combines all data of annotated complexes and protein-level abundances, while Data S2 contains abundances of each individual complex.
Original proteomic data sets used in this work are provided in the key resources table.
Any additional information required to reproduce this work is available from the Lead contact.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
|
| ||
| E. coli proteomic data | Valgepea et al., 2013Mol. BioSyst.9 pp. 2344–2358. DOI: 10.1039/c3mb70119k | http://www.rsc.org/suppdata/mb/c3/c3mb70119k/c3mb70119k.xlsx |
| E. coli proteomic data | Li et al., 2014Cell157 pp. 624–635. DOI: 10.1016/j.cell.2014.02.033 | https://ars.els-cdn.com/content/image/1-s2.0-S0092867414002323-mmc1.xlsx |
| E. coli proteomic data | Peebo et al., 2015. Mol. Biosyst.11 pp. 1184–1193. DOI: 10.1039/c4mb00721b | http://www.rsc.org/suppdata/mb/c4/c4mb00721b/c4mb00721b1.xlsx |
| E. coli proteomic data | Schmidt et al., 2016Nat. Biotech.34 pp. 108 – 110. DOI: 10.1038/nbt.3418 | https://static-content.springer.com/esm/art%3A10.1038%2Fnbt.3418/MediaObjects/41587_2016_BFnbt3418_MOESM18_ESM.xlsx |
|
| ||
| Software and algorithms | ||
|
| ||
| Python version 3.8.8 distributed via Anaconda | Python Software Foundation; Anaconda Org | http://www.anaconda.org |
| Matplotlib Python Plotting Library version 3.3.4 | Matplotlib Organization | https://matplotlib.org/ |
| Pandas Python DataFrame Library version 1.2.4 | Pydata Organization | https://pandas.pydata.org/ |
| Adobe Illustrator 2020 | Adobe Incorporated | https://www.adobe.com/products/illustrator |
| Pathway Tools | SRI International | https://bioinformatics.ai.sri.com/ptools/ |
METHOD DETAILS
All data used in this work was collected from primary published literature (see key resources table), though great care was taken to standardize the measurements such that they are directly comparable, despite being taken in slightly different conditions using different methodologies and by different research groups.
The protein abundance data were cleaned and standardized as described in the supplemental information and collated into a singular long-form tidy.csv file. Annotation of molecular complexes was performed using Python scripts and the PathwayTools utilities available via BioCyc (Karp et al., 2019). The combined data of annotated complexes and protein-level abundances is provided as Data S1. The abundances of each individual complex (rather than abundances of individual proteins) is available as Data S2.
Analysis code and figure generation
All code used in the data cleaning, standardization, and figure generation is made publicly available as a GitHub repository available via https://github.com/rpgroup-pboc/growth_limits and the [https://doi.org/10.5281/zenodo.4091457]. Code used in the processing, data cleaning, and annotation is located in the code/processing subdirectory. All code used for figure generation is located in the code/figures subdirectory.
Interactive figures
Associated with this work are two interactive figures that allow for deeper exploration of the data and the the minimal mathematical model. These figures are hosted at the paper website https://rpgroup.caltech.edu/growth_limits and their code is available on the associated GitHub repository.
Supplementary Material
Highlights.
Key biological processes are considered as potential growth-rate-limiting steps
A near-comprehensive dataset of the E. coli proteome across growth rates is presented
Order-of-magnitude estimates suggest little inefficiency across key processes
Translation emerges as a rate-governing process and we explore constraints on growth rate
ACKNOWLEDGMENTS
We thank Matthias Heinemann, Alexander Schmidt, and Gene-Wei Li for additional input regarding their data. We also thank all members of the Phillips, Theriot, Kondev, Garcia labs, as well as Ron Milo and Terry Hwa for useful discussions. We thank Suzannah M. Beeler, Jonas Cremer, Avi Flamholz, Soichi Hirokawa, and Manuel Razo-Mejia for reading and providing comments on drafts of this manuscript. R.P. is supported by La Fondation Pierre-Gilles de Gennes, the Rosen Center at Caltech, and the NIH 1R35 GM118043 (MIRA). J.A.T. is supported by the Howard Hughes Medical Institute, and NIH grant R37-AI036929. N.M.B is a HHMI fellow of the Jane Coffin Childs Memorial Fund. H.G.G. is supported by the Burroughs Wellcome Fund Career Award at the Scientific Interface, the Sloan Research Foundation, the Human Frontiers Science Program, the Searle Scholars Program, the Shurl & Kay Curci Foundation, the Hellman Foundation, the NIH Director’s New Innovator Award (DP2 OD024541-01), and an NSF CAREER award (1652236). D.S.F. is supported by an NSF award (PHY-1607606) and the NIH (NIH R01-AI13699201).
J.A.T. is chief scientific advisor at the Allen Institute for Cell Science (Seattle, WA, 98109).
Footnotes
DECLARATION OF INTERESTS
The authors otherwise declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cels.2021.06.002.
SUPPORTING CITATIONS
The following references appear in the supplemental information: Abelson et al., 1974, Baba et al., 2006, Belliveau et al., 2018, Booth et al., 1979, Datsenko and Wanner, 2000, Dong et al., 1996, Fijalkowska et al., 2012, Gama-Castro et al., 2016, Ge et al., 2003, Harris et al., 2001, Helmstetter and Cooper, 1968, Ireland et al., 2020, Jensen et al., 2001, Jun et al., 2018, Keseler et al., 2017, Khademi et al., 2004, Lex et al., 2014, Lu et al., 2003, Pedersen et al., 1978, Ramos and Kaback, 1977, Rudd et al., 2016, Sánchez-Romero et al., 2011, Sekowska et al., 2000, Sirko et al., 1995, Soufi et al., 2015, Svenningsen et al., 2017, Taniguchi et al., 2010, van Heeswijk et al., 2013, Virtanen et al., 2020, Volkmer and Heinemann, 2011, Zhang et al., 2014a, Zhang et al., 2014b.
REFERENCES
- Abelson HT, Johnson LF, Penman S, and Green H. (1974). Changes in RNA in relation to growth of the fibroblast: II. The lifetime of mRNA, rRNA, and tRNA in resting and growing cells. Cell 1, 161–165. 10.1016/0092-8674(74)90107-X. [DOI] [PubMed] [Google Scholar]
- Aidelberg G, Towbin BD, Rothschild D, Dekel E, Bren A, and Alon U. (2014). Hierarchy of non-glucose sugars in Escherichia coli. BMC Syst. Biol 8, 133. 10.1186/s12918-014-0133-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amir A. (2017). Is cell size a spandrel? eLife 6, 18261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antonenko YN, Pohl P, and Denisov GA (1997). Permeation of ammonia across bilayer lipid membranes studied by ammonium ion selective microelectrodes. Biophys. J 72, 2187–2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. (2000). Gene ontology: tool for the unification of biology. Nat. Genet 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ason B, Bertram JG, Hingorani MM, Beechem JM, O’Donnell M, Goodman MF, and Bloom LB (2000). A model for Escherichia coli DNA polymerase III holoenzyme assembly at primer/template ends. DNA triggers A change in binding specificity of the γ complex clamp loader. J. Biol. Chem 275, 3006–3015. 10.1074/jbc.275.4.3006. [DOI] [PubMed] [Google Scholar]
- Assentoft M, Kaptan S, Schneider HP, Deitmer JW, de Groot BL, and MacAulay N. (2016). Aquaporin 4 as a NH3 channel. J. Biol. Chem 291, 19184–19195. 10.1074/jbc.M116.740217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baba T, Ara T, Hasegawa M, Takai Y, Okumura Y, Baba M, Datsenko KA, Tomita M, Wanner BL, and Mori H. (2006). Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol. Syst. Biol 2, 2006.0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barreteau H, Kovač A, Boniface A, Sova M, Gobec S, and Blanot D. (2008). Cytoplasmic steps of peptidoglycan biosynthesis. FEMS Microbiol. Rev 32, 168–207. 10.1111/j.1574-6976.2008.00104.x. [DOI] [PubMed] [Google Scholar]
- Basan M, Zhu M, Dai X, Warren M, Sévin D, Wang YP, and Hwa T. (2015). Inflating bacterial cells by increased protein synthesis. Mol. Syst. Biol 11, 836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer S, and Ziv E. (1976). Dense growth of aerobic bacteria in a bench-scale fermentor. Biotechnol. Bioeng 18, 81–94. 10.1002/bit.260180107. [DOI] [PubMed] [Google Scholar]
- Belliveau NM, Barnes SL, Ireland WT, Jones DL, Sweredoski MJ, Moradian A, Hess S, Kinney JB, and Phillips R. (2018). Systematic approach for dissecting the molecular mechanisms of transcriptional regulation in bacteria. Proc. Natl. Acad. Sci. USA 115, E4796–E4805. 10.1073/pnas.1722055115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergkessel M, Basta DW, and Newman DK (2016). The physiology of growth arrest: uniting molecular and environmental microbiology. Nat. Rev. Microbiol 14, 549–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth IR, Mitchell WJ, and Hamilton WA (1979). Quantitative analysis of proton-linked transport systems. The lactose permease of Escherichia coli. Biochem. J 182, 687–696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosdriesz E, Molenaar D, Teusink B, and Bruggeman FJ (2015). How fast-growing bacteria robustly tune their ribosome concentration to approximate growth-rate maximization. FEBS Journal 282, 2029–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremer H, and Dennis PP (2008). Modulation of chemical composition and other parameters of the cell at different exponential growth rates. EcoSal Plus 3, 1–48. [DOI] [PubMed] [Google Scholar]
- Büke F, Grilli J, Lagomarsino MC, Bokinsky G, and Tans S. (2020). ppGpp is a bacterial cell size regulator. bioRxiv. 10.1101/2020.06.16.154187. [DOI] [PubMed] [Google Scholar]
- Campos M, Govers SK, Irnov I, Dobihal GS, Cornet F, and Jacobs-Wagner CJ (2018). Genomewide phenotypic analysis of growth, cell morphogenesis, and cell cycle events in Escherichia coli. Mol. Syst. Biol 14, e7573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cashel M, and Gallant J. (1969). Two compounds implicated in the function of the RC gene of Escherichia coli. Nature 221, 838–841. [DOI] [PubMed] [Google Scholar]
- Catherwood AC, Lloyd AJ, Tod JA, Chauhan S, Slade SE, Walkowiak GP, Galley NF, Punekar AS, Smart K, Rea D, et al. (2020). Substrate and stereochemical control of peptidoglycan cross-linking by transpeptidation by Escherichia coli PBP1B. J. Am. Chem. Soc 142, 5034–5048. 10.1021/jacs.9b08822. [DOI] [PubMed] [Google Scholar]
- Dai X, Zhu M, Warren M, Balakrishnan R, Okano H, Williamson JR, Fredrick K, and Hwa T. (2018). Slowdown of translational elongation in Escherichia coli under hyperosmotic stress. mBio 9, 281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai X, Zhu M, Warren M, Balakrishnan R, Patsalo V, Okano H, Williamson JR, Fredrick K, Wang YP, and Hwa T. (2016). Reduction of translating ribosomes enables Escherichia coli to maintain elongation rates during slow growth. Nat. Microbiol 2, 16231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datsenko KA, and Wanner BL (2000). One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proc. Natl. Acad. Sci. USA 97, 6640–6645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidi D, Noor E, Liebermeister W, Bar-Even A, Flamholz A, Tummler K, Barenholz U, Goldenfeld M, Shlomi T, and Milo R. (2016). Global characterization of in vivo enzyme catalytic rates and their correspondence to in vitro kcat measurements. Proc. Natl. Acad. Sci. USA 113, 3401–3406. 10.1073/pnas.1514240113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delarue M, Brittingham GP, Pfeffer S, Surovtsev IV, Pinglay S, Kennedy KJ, Schaffer M, Gutierrez JI, Sang D, Poterewicz G, et al. (2018). mTORC1 controls phase separation and the biophysical properties of the cytoplasm by tuning crowding. Cell 174, 338–349.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis PP, Ehrenberg M, and Bremer H. (2004). Control of rRNA synthesis in Escherichia coli: a systems biology approach. Microbiol. Mol. Biol. Rev 68, 639–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill KA, Ghosh K, and Schmit JD (2011). Physical limits of cells and proteomes. Proc. Natl. Acad. Sci. USA 108, 17876–17882. 10.1073/pnas.1114477108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong H, Nilsson L, and Kurland CG (1996). Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J. Mol. Biol 260, 649–663. [DOI] [PubMed] [Google Scholar]
- Elf J, and Ehrenberg M. (2005). Near-critical behavior of aminoacyl-tRNA pools in E. coli at rate-limiting supply of amino acids. Biophys. J 88, 132–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erickson DW, Schink SJ, Patsalo V, Williamson JR, Gerland U, and Hwa T. (2017). A global resource allocation strategy governs growth transition kinetics of Escherichia coli. Nature 551, 119–123. 10.1038/nature24299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escalante A, Salinas Cervantes A, Gosset G, and Bolívar F. (2012). Current knowledge of the Escherichia coli phosphoenolpyruvate–carbohydrate phosphotransferase system: peculiarities of regulation and impact on growth and product formation. Appl. Microbiol. Biotechnol 94, 1483–1494. 10.1007/s00253-012-4101-5. [DOI] [PubMed] [Google Scholar]
- Feist AM, Henry CS, Reed JL, Krummenacker M, Joyce AR, Karp PD, Broadbelt LJ, Hatzimanikatis V, and Palsson BØ (2007). A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol 3, 121. 10.1038/msb4100155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Coll L, Maciag-Dorszynska M, Tailor K, Vadia S, Levin PA, Szalewska-Palasz A, and Cashel M. (2020). The absence of (p)ppGpp renders initiation of Escherichia coli chromosomal DNA synthesis independent of growth rates. mBio 11, 45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fijalkowska IJ, Schaaper RM, and Jonczyk P. (2012). DNA replication fidelity in Escherichia coli: A multi-DNA polymerase affair. FEMS Microbiol. Rev 36, 1105–1121. 10.1111/j.1574-6976.2012.00338.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forchhammer J, and Lindahl L. (1971). Growth rate of polypeptide chains as a function of the cell growth rate in a mutant of Escherichia coli 15. J. Mol. Biol 55, 563–568. [DOI] [PubMed] [Google Scholar]
- Gallagher LA, Bailey J, and Manoil C. (2020). Ranking essential bacterial processes by speed of mutant death. Proc. Natl. Acad. Sci. USA 117, 18010–18017. 10.1073/pnas.2001507117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gama-Castro S, Salgado H, Santos-Zavaleta A, Ledezma-Tejeida D, Muñiz-Rascado L, García-Sotelo JS, Alquicira-Hernández K, Martínez-Flores I, Pannier L, Castro-Mondragón JA, et al. (2016). RegulonDB version 9.0: high-level integration of gene regulation, coexpression, motif clustering and beyond. Nucleic Acids Res 44, D133–D143. 10.1093/nar/gkv1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge J, Yu G, Ator MA, and Stubbe J. (2003). Pre-steady-state and steady-state kinetic analysis of E. coli Class I ribonucleotide reductase. Biochemistry 42, 10071–10083. 10.1021/bi034374r. [DOI] [PubMed] [Google Scholar]
- Godin M, Delgado FF, Son S, Grover WH, Bryan AK, Tzur A, Jorgensen P, Payer K, Grossman AD, Kirschner MW, and Manalis SR (2010). Using buoyant mass to measure the growth of single cells. Nat. Methods 7, 387–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray WT, Govers SK, Xiang Y, Parry BR, Campos M, Kim S, and Jacobs-Wagner C. (2019). Nucleoid size scaling and intracellular organization of translation across bacteria. Cell 177, 1632–1648.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y, Li D, Zhang S, Yang Y, Liu JJ, Wang X, Liu C, Milkie DE, Moore RP, Tulu US, et al. (2018). Visualizing intracellular organelle and cytoskeletal interactions at nanoscale resolution on millisecond timescales. Cell 175, 1430–1442.e17. [DOI] [PubMed] [Google Scholar]
- Harris LK, and Theriot JA (2018). Surface area to volume ratio: a natural variable for bacterial morphogenesis. Trends Microbiol 26, 815–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris RM, Webb DC, Howitt SM, and Cox GB (2001). Characterization of PitA and PitB from Escherichia coli. J. Bacteriol 183, 5008–5014. 10.1128/JB.183.17.5008-5014.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauryliuk V, Atkinson GC, Murakami KS, Tenson T, and Gerdes K. (2015). Recent functional insights into the role of (p)ppGpp in bacterial physiology. Nat. Rev. Microbiol 13, 298–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heldal M, Norland S, and Tumyr O. (1985). X-ray microanalytic method for measurement of dry matter and elemental content of individual bacteria. Appl. Environ. Microbiol 50, 1251–1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmstetter CE, and Cooper S. (1968). DNA synthesis during the division cycle of rapidly growing Escherichia coli B/r. J. Mol. Biol 31, 507–518. [DOI] [PubMed] [Google Scholar]
- Ho PY, and Amir A. (2015). Simultaneous regulation of cell size and chromosome replication in bacteria. Front. Microbiol 6, 662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu XP, Dourado H, Schubert P, and Lercher MJ (2020). The protein translation machinery is expressed for maximal efficiency in Escherichia coli. Nat. Commun 11, 5260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui S, Silverman JM, Chen SS, Erickson DW, Basan M, Wang J, Hwa T, and Williamson JR (2015). Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol 11, 784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ireland WT, Beeler SM, Flores-Bautista E, McCarty NS, Röschinger T, Belliveau NM, Sweredoski MJ, Moradian A, Kinney JB, and Phillips R. (2020). Deciphering the regulatory genome of Escherichia coli, one hundred promoters at a time. eLife 9, e55308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen RB, Wang SC, and Shapiro L. (2001). A moving DNA replication factory in Caulobacter crescentus. EMBO J 20, 4952–4963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin DJ, Cagliero C, and Zhou YN (2012). Growth rate regulation in Escherichia coli. FEMS Microbiol. Rev 36, 269–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jun S, Si F, Pugatch R, and Scott M. (2018). Fundamental principles in bacterial physiology-history, recent progress, and the future with focus on cell size control: a review. Rep. Prog. Phys 81, 056601. 10.1088/1361-6633/aaa628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karp PD, Billington R, Caspi R, Fulcher CA, Latendresse M, Kothari A, Keseler IM, Krummenacker M, Midford PE, Ong Q, et al. (2019). The BioCyc collection of microbial genomes and metabolic pathways. Brief. Bioinform 20, 1085–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karr JR, Sanghvi JC, Macklin DN, Gutschow MV, Jacobs JM, Bolival B, Assad-Garcia N, Glass JI, and Covert MW (2012). A whole-cell computational model predicts phenotype from genotype. Cell 150, 389–401. 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keseler IM, Mackie A, Santos-Zavaleta A, Billington R, Bonavides-Martínez C, Caspi R, Fulcher C, Gama-Castro S, Kothari A, Krummenacker M, et al. (2017). The EcoCyc database: reflecting new knowledge about Escherichia coli K-12. Nucleic Acids Res 45, D543–D550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khademi S, O’Connell J, Remis J, Robles-Colmenares Y, Miercke LJW, and Stroud RM (2004). Mechanism of ammonia transport by Amt/MEP/Rh: structure of AmtB at 1.35 Å. Science 305, 1587–1594. 10.1126/science.1101952. [DOI] [PubMed] [Google Scholar]
- Klumpp S, and Hwa T. (2008). Growth-rate-dependent partitioning of RNA polymerases in bacteria. Proc. Natl. Acad. Sci. USA 105, 20245–20250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klumpp S, and Hwa T. (2014). Bacterial growth: global effects on gene expression, growth feedback and proteome partition. Curr. Opin. Biotechnol 28, 96–102. 10.1016/j.copbio.2014.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klumpp S, Scott M, Pedersen S, and Hwa T. (2013). Molecular crowding limits translation and cell growth. Proc. Natl. Acad. Sci. USA 110, 16754–16759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kostinski S, and Reuveni S. (2020). Ribosome composition maximizes cellular growth rates in E. coli. Phys. Rev. Lett 125, 028103. 10.1103/PhysRevLett.125.028103. [DOI] [PubMed] [Google Scholar]
- Kraemer JA, Sanderlin AG, and Laub MT (2019). The stringent response inhibits DNA replication initiation in E. coli by modulating supercoiling of oriC. mBio 10, 822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubitschek HE, Baldwin WW, Schroeter SJ, and Graetzer R. (1984). Independence of buoyant cell density and growth rate in Escherichia coli. J. Bacteriol 158, 296–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lascu I, and Gonin P. (2000). The catalytic mechanism of nucleoside diphosphate kinases. J. Bioenerg. Biomembr 32, 237–246. 10.1023/A:1005532912212. [DOI] [PubMed] [Google Scholar]
- Laxhuber KS, Morrison MJ, Chure G, Belliveau NM, Strandkvist C, Naughton KL, and Phillips R. (2020). Theoretical investigation of a genetic switch for metabolic adaptation. PLoS One 15, e0226453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lex A, Gehlenborg N, Strobelt H, Vuillemot R, and Pfister H. (2014). UpSet: visualization of intersecting sets. IEEE Trans. Vis. Comput. Graph 20, 1983–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li GW, Burkhardt D, Gross C, and Weissman JS (2014). Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell 157, 624–635. 10.1016/j.cell.2014.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liebermeister W, Noor E, Flamholz A, Davidi D, Bernhardt J, and Milo R. (2014). Visual account of protein investment in cellular functions. Proc. Natl. Acad. Sci. USA 111, 8488–8493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin J, and Amir A. (2018). Homeostasis of protein and mRNA concentrations in growing cells. Nat. Commun 9, 4496. 10.1038/s41467-018-06714-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu M, Durfee T, Cabrera JE, Zhao K, Jin DJ, and Blattner FR (2005). Global transcriptional programs reveal a carbon source foraging strategy by Escherichia coli. J. Biol. Chem 280, 15921–15927. 10.1074/jbc.M414050200. [DOI] [PubMed] [Google Scholar]
- Lovering AL, Safadi SS, and Strynadka NC (2012). Structural perspective of peptidoglycan biosynthesis and assembly. Annu. Rev. Biochem 81, 451–478. 10.1146/annurev-biochem-061809-112742. [DOI] [PubMed] [Google Scholar]
- Lu D, Grayson P, and Schulten K. (2003). Glycerol conductance and physical asymmetry of the Escherichia coli glycerol facilitator GlpF. Biophys. J 85, 2977–2987. 10.1016/S0006-3495(03)74718-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, and Marinov GK (2015). The bioenergetic costs of a gene. Proc. Natl. Acad. Sci. USA 112, 15690–15695. 10.1073/pnas.1514974112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maalœ O. (1979). Regulation of the protein-synthesizing machinery. ribosomes, trna, factors, and so on. In Biological Regulation and Development, vol 1, Goldberger R, ed. (Springer; ), pp. 487–542. [Google Scholar]
- Macklin DN, Ahn-Horst TA, Choi H, Ruggero NA, Carrera J, Mason JC, Sun G, Agmon E, DeFelice MM, Maayan I, et al. (2020). Simultaneous cross-evaluation of heterogeneous E. coli datasets via mechanistic simulation. Science 369, eaav3751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahajan S. (2010). Street-Fighting Mathematics. The Art of Educated Guessing and Opportunistic Problem Solving (MIT Press; ). [Google Scholar]
- Metzl-Raz E, Kafri M, Yaakov G, Soifer I, Gurvich Y, and Barkai N. (2017). Principles of cellular resource allocation revealed by condition-dependent proteome profiling. eLife 6, e03528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikucki JA, Pearson A, Johnston DT, Turchyn AV, Farquhar J, Schrag DP, Anbar AD, Priscu JC, and Lee PA (2009). A contemporary microbially maintained subglacial ferrous “ocean”. Science 324, 397–400. [DOI] [PubMed] [Google Scholar]
- Milo R, Jorgensen P, Moran U, Weber G, and Springer M. (2010). BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res 38, D750–D753. 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molenaar D, van Berlo R, de Ridder D, and Teusink B. (2009). Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol 5, 323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monod J. (1947). The phenomenon of enzymatic adaptation and its bearings on problems of genetics and cellular differentiation. Selected Papers in Molecular Biology by Jacques Monod 1947, 223–289. [Google Scholar]
- Monod J. (1949). The growth of bacterial cultures. Annu. Rev. Microbiol 3, 371–394. [Google Scholar]
- Morgenstein RM, Bratton BP, Nguyen JP, Ouzounov N, Shaevitz JW, and Gitai Z. (2015). RodZ links MreB to cell wall synthesis to mediate MreB rotation and robust morphogenesis. Proc. Natl. Acad. Sci. USA 112, 12510–12515. 10.1073/pnas.1509610112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neidhardt FC, Ingraham J, and Schaechter M. (1991). Physiology of the Bacterial Cell - A Molecular Approach, vol 1 (Elsevier). [Google Scholar]
- Nomura M, Gourse R, and Baughman G. (1984). Regulation of the synthesis of ribosomes and ribosomal components. Annu. Rev. Biochem 53, 75–117. [DOI] [PubMed] [Google Scholar]
- Ojkic N, Serbanescu D, and Banerjee S. (2019). Surface-to-volume scaling and aspect ratio preservation in rod-shaped bacteria. eLife 8, 642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panlilio M, Grilli J, Tallarico G, Iuliani I, Sclavi B, Cicuta P, and Lagomarsino MC (2020). Threshold accumulation of a constitutive protein explains E. coli cell division behavior in nutrient upshifts. bioRxiv 10.1101/2020.08.03.233908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker DJ, Lalanne JB, Kimura S, Johnson GE, Waldor MK, and Li GW (2020). Growth-optimized aminoacyl-tRNA synthetase levels prevent maximal tRNA charging. Cell Syst. 11, 121–130.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patrick M, Dennis PP, Ehrenberg M, and Bremer H. (2015). Free RNA polymerase in Escherichia coli. Biochimie 119, 80–91. 10.1016/j.biochi.2015.10.015. [DOI] [PubMed] [Google Scholar]
- Paul BJ, Barker MM, Ross W, Schneider DA, Webb C, Foster JW, and Gourse RL (2004). DksA: a critical component of the transcription initiation machinery that potentiates the regulation of rRNA promoters by ppGpp and the initiating NTP. Cell 118, 311–322. [DOI] [PubMed] [Google Scholar]
- Pedersen S. (1984). Escherichia coli ribosomes translate in vivo with variable rate. EMBO J. 3, 2895–2898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen S, Bloch PL, Reeh S, and Neidhardt FC (1978). Patterns of protein synthesis in E. coli: a catalog of the amount of 140 individual proteins at different growth rates. Cell 14, 179–190. [DOI] [PubMed] [Google Scholar]
- Peebo K, Valgepea K, Maser A, Nahku R, Adamberg K, and Vilu R. (2015). Proteome reallocation in Escherichia coli with increasing specific growth rate. Mol. Biosyst 11, 1184–1193. 10.1039/C4MB00721B. [DOI] [PubMed] [Google Scholar]
- Phillips R. (2018). Membranes by the numbers. In Physics Biological Membranes (Springer; ), pp. 73–105. [Google Scholar]
- Ramos S, and Kaback HR (1977). The relationship between the electrochemical proton gradient and active transport in Escherichia coli membrane vesicles. Biochemistry 16, 854–859. 10.1021/bi00624a007. [DOI] [PubMed] [Google Scholar]
- Ranganathan S, Tee TW, Chowdhury A, Zomorrodi AR, Yoon JM, Fu Y, Shanks JV, and Maranas CD (2012). An integrated computational and experimental study for overproducing fatty acids in Escherichia coli. Metab. Eng 14, 687–704. 10.1016/j.ymben.2012.08.008. [DOI] [PubMed] [Google Scholar]
- Reuveni S, Ehrenberg M, and Paulsson J. (2017). Ribosomes are optimized for autocatalytic production. Nature 547, 293–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roller BRK, Stoddard SF, and Schmidt TM (2016). Exploiting rRNA operon copy number to investigate bacterial reproductive strategies. Nat. Microbiol 1, 16160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg H, Gerdes RG, and Chegwidden K. (1977). Two systems for the uptake of phosphate in Escherichia coli. J. Bacteriol 131, 505–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudd SG, Valerie NCK, and Helleday T. (2016). Pathways controlling dNTP pools to maintain genome stability. DNA Repair 44, 193–204. 10.1016/j.dnarep.2016.05.032. [DOI] [PubMed] [Google Scholar]
- Ruppe A, and Fox JM (2018). Analysis of interdependent kinetic controls of fatty acid synthases. ACS Catal. 8, 11722–11734. 10.1021/acscatal.8b03171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Romero MA, Molina F, and Jiménez-Sánchez A. (2011). Organization of ribonucleoside diphosphate reductase during multifork chromosome replication in Escherichia coli. Microbiology (Reading) 157, 2220–2225. 10.1099/mic.0.049478-0. [DOI] [PubMed] [Google Scholar]
- Schaechter M, MaalØe O, and Kjeldgaard NO (1958). Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. Microbiology 19, 592–606. [DOI] [PubMed] [Google Scholar]
- Schmidt A, Kochanowski K, Vedelaar S, Ahrné E, Volkmer B, Callipo L, Knoops K, Bauer M, Aebersold R, and Heinemann M. (2016). The quantitative and condition-dependent Escherichia coli proteome. Nat. Biotechnol 34, 104–110. 10.1038/nbt.3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott M, Gunderson CW, Mateescu EM, Zhang Z, and Hwa T. (2010). Interdependence of cell growth and gene expression: origins and consequences. Science 330, 1099–1102. [DOI] [PubMed] [Google Scholar]
- Scott M, Klumpp S, Mateescu EM, and Hwa T. (2014). Emergence of robust growth laws from optimal regulation of ribosome synthesis. Mol. Syst. Biol 10, 747. 10.15252/msb.20145379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekowska A, Kung HF, and Danchin A. (2000). Sulfur metabolism in Escherichia coli and related bacteria: facts and fiction. J. Mol. Microbiol. Biotechnol 2, 145–177. [PubMed] [Google Scholar]
- Serbanescu D, Ojkic N, and Banerjee S. (2020). Nutrient-dependent tradeoffs between ribosomes and division protein synthesis control bacterial cell size and growth. Cell Rep. 32, 108183. [DOI] [PubMed] [Google Scholar]
- Shi H, Bratton BP, Gitai Z, and Huang KC (2018). How to build a bacterial cell: MreB as the foreman of E. coli construction. Cell 172, 1294–1305. 10.1016/j.cell.2018.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Si F, Le Treut G, Sauls JT, Vadia S, Levin PA, and Jun S. (2019). Mechanistic origin of cell-size control and homeostasis in bacteria. Curr. Biol 29, 1760–1770.e7. 10.1016/j.cub.2019.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Si F, Li D, Cox SE, Sauls JT, Azizi O, Sou C, Schwartz AB, Erickstad MJ, Jun Y, Li X, and Jun S. (2017). Invariance of initiation mass and predictability of cell size in Escherichia coli. Curr. Biol 27, 1278–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirko A, Zatyka M, Sadowy E, and Hulanicka D. (1995). Sulfate and thiosulfate transport in Escherichia coli K-12: evidence for a functional overlapping of sulfate-and thiosulfate-binding proteins. J. Bacteriol 177, 4134–4136. 10.1128/jb.177.14.4134-4136.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohlenkamp C, and Geiger O. (2016). Bacterial membrane lipids: diversity in structures and pathways. FEMS Microbiol. Rev 40, 133–159. 10.1093/femsre/fuv008. [DOI] [PubMed] [Google Scholar]
- Soler-Bistué A, Aguilar-Pierlé S, Garcia-Garcerá M, Val ME, Sismeiro O, Varet H, Sieira R, Krin E, Skovgaard O, Comerci DJ, et al. (2020). Macromolecular crowding links ribosomal protein gene dosage to growth rate in Vibrio cholerae. BMC Biol. 18, 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soufi B, Krug K, Harst A, and Macek B. (2015). Characterization of the E. coli proteome and its modifications during growth and ethanol stress. Front. Microbiol 6, 198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stasi R, Neves HI, and Spira B. (2019). Phosphate uptake by the phosphonate transport system PhnCDE. BMC Microbiol. 19, 79. 10.1186/s12866-019-1445-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stouthamer AH (1973). A theoretical study on the amount of ATP required for synthesis of microbial cell material. Antonie Leeuwenhoek 39, 545–565. 10.1007/BF02578899. [DOI] [PubMed] [Google Scholar]
- Svenningsen SL, Kongstad M, Stenum T.S.n., Muñoz-Gómez AJ, and Sørensen MA (2017). Transfer RNA is highly unstable during early amino acid starvation in Escherichia coli. Nucleic Acids Res 45, 793–804. 10.1093/nar/gkw1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szenk M, Dill KA, and de Graff AMR (2017). Why do fast-growing bacteria enter overflow metabolism? Testing the membrane real estate hypothesis. Cell Syst. 5, 95–104. 10.1016/j.cels.2017.06.005. [DOI] [PubMed] [Google Scholar]
- Taheri-Araghi S, Bradde S, Sauls JT, Hill NS, Levin PA, Paulsson J, Vergassola M, and Jun S. (2015). Cell-size control and homeostasis in bacteria. Curr. Biol 25, 385–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taniguchi Y, Choi PJ, Li GW, Chen H, Babu M, Hearn J, Emili A, and Xie XS (2010). Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 329, 533–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatusov RL, Galperin MY, Natale DA, and Koonin EV (2000). The COG database: a tool for genome-scale analysis of protein functions and evolution. Nucleic Acids Res. 28, 33–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taymaz-Nikerel H, Borujeni AE, Verheijen PJT, Heijnen JJ, and van Gulik WM (2010). Genome-derived minimal metabolic models for Escherichia coli MG1655 with estimated in vivo respiratory ATP stoichiometry. Biotechnol. Bioeng 107, 369–381. 10.1002/bit.22802. [DOI] [PubMed] [Google Scholar]
- The Gene Ontology Consortium (2019). The Gene Ontology resource: 20 years and still GOing strong. Nucleic Acids Res. 47, D330–D338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vadia S, Tse JL, Lucena R, Yang Z, Kellogg DR, Wang JD, and Levin PA (2017). Fatty acid availability sets cell envelope capacity and dictates microbial cell size. Curr. Biol 27, 1757–1767.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valgepea K, Adamberg K, Seiman A, and Vilu R. (2013). Escherichia coliachieves faster growth by increasing catalytic and translation rates of proteins. Mol. Biosyst 9, 2344–2358. 10.1039/c3mb70119k. [DOI] [PubMed] [Google Scholar]
- van Heeswijk WC, Westerhoff HV, and Boogerd FC (2013). Nitrogen assimilation in Escherichia coli: putting molecular data into a systems perspective. Microbiol. Mol. Biol. Rev 77, 628–695. 10.1128/MMBR.00025-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright JEW, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in python. Nat. Methods 17, 261–272. 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkmer B, and Heinemann M. (2011). Condition-dependent cell volume and concentration of Escherichia coli to facilitate data conversion for systems biology modeling. PLoS One 6, e23126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber J, and Senior AE (2003). ATP synthesis driven by proton transport in F1F0-ATP synthase. FEBS Lett. 545, 61–70. 10.1016/S0014-5793(03)00394-6. [DOI] [PubMed] [Google Scholar]
- Willsky GR, Bennett RL, and Malamy MH (1973). Inorganic phosphate transport in Escherichia coli: involvement of two genes which play a role in alkaline phosphatase regulation. J. Bacteriol 113, 529–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You C, Okano H, Hui S, Zhang Z, Kim M, Gunderson CW, Wang YP, Lenz P, Yan D, and Hwa T. (2013). Coordination of bacterial proteome with metabolism by cyclic AMP signalling. Nature 500, 301–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young R, and Bremer H. (1976). Polypeptide-chain-elongation rate in Escherichia coli B/r as a function of growth rate. Biochem. J 160, 185–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X, Liu T, Zhu F, and Khosla C. (2011). In vitro reconstitution and steady-state analysis of the fatty acid synthase from Escherichia coli. Proc. Natl. Acad. Sci. USA 108, 18643–18648. 10.1073/pnas.1110852108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Jiang W, Nan J, Almqvist J, and Huang Y. (2014a). The Escherichia coli CysZ is a pH dependent sulfate transporter that can be inhibited by sulfite. Biochim. Biophys. Acta 1838, 1809–1816. 10.1016/j.bbamem.2014.03.003. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Aboulwafa M, and Saier MH (2014b). Regulation of crp gene expression by the catabolite repressor/activator, cra, in Escherichia coli. J. Mol. Microbiol. Biotechnol 24, 135–141. 10.1159/000362722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Brambilla E, Li R, Shi H, Lagomarsino MC, Sclavi B, and Bulman Z. (2020). A decrease in transcription capacity limits growth rate upon translation inhibition. mSystems 5, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H, Bai Y, Jiang M, Tokuyasu TA, Huang X, Zhong F, Wu Y, Fu X, Kleckner N, Hwa T, and Liu C. (2020). General quantitative relations linking cell growth and the cell cycle in Escherichia coli. Nat. Microbiol 5, 995–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu M, and Dai X. (2019). Growth suppression by altered (p)ppGpp levels results from non-optimal resource allocation in Escherichia coli. Nucleic Acids Res 47, 4684–4693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuang K, Vemuri GN, and Mahadevan R. (2011). Economics of membrane occupancy and respiro-fermentation. Mol. Syst. Biol 7, 500. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data, code, and figure generation scripts are publicly available as a GitHub repository (https://github.com/rpgroup-pboc/growth_limits) and is accessible via [https://doi.org/10.5281/zenodo.4091457]. We invite the community to fork this repository and open constructive issues with comments regarding the analysis, annotation, or findings of the work.
The published article includes two data sets generated during this study. Data S1 combines all data of annotated complexes and protein-level abundances, while Data S2 contains abundances of each individual complex.
Original proteomic data sets used in this work are provided in the key resources table.
Any additional information required to reproduce this work is available from the Lead contact.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
|
| ||
| E. coli proteomic data | Valgepea et al., 2013Mol. BioSyst.9 pp. 2344–2358. DOI: 10.1039/c3mb70119k | http://www.rsc.org/suppdata/mb/c3/c3mb70119k/c3mb70119k.xlsx |
| E. coli proteomic data | Li et al., 2014Cell157 pp. 624–635. DOI: 10.1016/j.cell.2014.02.033 | https://ars.els-cdn.com/content/image/1-s2.0-S0092867414002323-mmc1.xlsx |
| E. coli proteomic data | Peebo et al., 2015. Mol. Biosyst.11 pp. 1184–1193. DOI: 10.1039/c4mb00721b | http://www.rsc.org/suppdata/mb/c4/c4mb00721b/c4mb00721b1.xlsx |
| E. coli proteomic data | Schmidt et al., 2016Nat. Biotech.34 pp. 108 – 110. DOI: 10.1038/nbt.3418 | https://static-content.springer.com/esm/art%3A10.1038%2Fnbt.3418/MediaObjects/41587_2016_BFnbt3418_MOESM18_ESM.xlsx |
|
| ||
| Software and algorithms | ||
|
| ||
| Python version 3.8.8 distributed via Anaconda | Python Software Foundation; Anaconda Org | http://www.anaconda.org |
| Matplotlib Python Plotting Library version 3.3.4 | Matplotlib Organization | https://matplotlib.org/ |
| Pandas Python DataFrame Library version 1.2.4 | Pydata Organization | https://pandas.pydata.org/ |
| Adobe Illustrator 2020 | Adobe Incorporated | https://www.adobe.com/products/illustrator |
| Pathway Tools | SRI International | https://bioinformatics.ai.sri.com/ptools/ |