Abstract
This paper develops a threshold-augmented dynamic multi-country model (TGVAR) to quantify the macroeconomic effects of the Covid-19 pandemic. We show that there exist threshold effects in the relationship between output growth and excess global volatility at individual country levels in a significant majority of advanced economies and several emerging markets. We then estimate a more general multi-country model augmented with these threshold effects as well as long term interest rates, oil prices, exchange rates and equity returns to perform counterfactual analyses. We distinguish common global factors from trade-related spillovers, and identify the Covid-19 shock using GDP growth projection revisions of the IMF in 2020Q1. We account for sample uncertainty by bootstrapping the multi-country model estimated over four decades of quarterly observations. Our results show that, without policy support, the Covid-19 pandemic would cause a significant and long-lasting fall in world output, with outcomes that are quite heterogenous across countries and regions. While the impact on China and other emerging Asian economies are estimated to be less severe, the United Kingdom, and several other advanced economies may experience deeper and longer-lasting effects. Non-Asian emerging markets stand out for their vulnerability. We show that no country is immune to the economic fallout of the pandemic because of global interconnections as evidenced by the case of Sweden. We also find that long-term interest rates could temporarily fall below their pre-Covid-19 lows in core advanced economies, but this does not seem to be the case in emerging markets.
Keywords: Threshold-augmented Global VAR (TGVAR), International business cycle, Covid-19, Global volatility, Threshold effects
1. Introduction
There is no doubt that the rapid spread of Covid-19 across the world and policy measures to contain it (including physical distancing, lockdowns, and business closures) have led to large negative economic shocks, not experienced before. The adverse economic effects of the pandemic at individual country levels have also become accentuated by trade and financial linkages that have been on the rise since the Second World War. Unlike a typical macroeconomic disturbance, the Covid-19 shock and its economic fallout have brought about simultaneous disruptions to demand and supply in a totally new economic environment, where consumers and firms have faced with additional uncertainties about the disease itself (its spread, new variants, possible cure and vaccination effectiveness).
On the supply side, infections have reduced labor supply and productivity; and lockdowns, business closures and social distancing have caused supply disruptions. On the demand side, layoffs and the loss of income (from morbidity, quarantines, and unemployment) and worse economic prospects have affected households’ consumption and firms’ investment. The extreme uncertainty about the path, duration, magnitude, and impact of the Covid-19 pandemic has resulted in financial market volatility. Countries or regions that rely heavily on oil revenues, tourism, and exports of goods and services have been particularly vulnerable. Moreover, domestic disruptions have spilled over to other countries through trade, financial, and global value chain linkages. The severity of the Covid-19 shock and the heterogeneity of its outcome across different sectors of the economy and population groups also present new methodological challenges, and shed doubts on the validity of standard log-linearized approximation routinely used in the empirical macroeconomic modelling.
Key challenges with the empirical economic analysis of Covid-19 include the following: how to identify the shock, how to account for its non-linear effects, and how to quantify its effects while accounting for spillovers, common global factors, network effects and uncertainty. This paper contributes to the literature by addressing these issues in a coherent multi-country framework. We offer an identification strategy for the Covid-19 shock considering that a synthetic control method cannot be applied in the context of a global pandemic. Specifically, we use the GDP growth revisions of the International Monetary Fund (IMF) in April and June 2020 compared to their end-2019 projections to identify the Covid-19 shock. We show that there exist threshold effects in the relationship between global financial market volatility and output growth at individual country levels in a significant majority of advanced economies and in the case of several emerging market countries. We develop a threshold-augmented dynamic multi-country model (TGVAR) to estimate the global as well as country-specific macroeconomic effects of the identified Covid-19 shock. We distinguish common global factors from trade network effects and account for sample uncertainty based on the constellation of disturbances that the global economy had experienced in the past four decades as well as their spillovers and interactions. Finally, we show how the model can be used for counterfactual analysis. This approach is very different from scenario analyses or forecasts that are unconditional statements and need not be model based.
We use Generalized Impulse Response Functions (GIRFs) to study the counterfactual impact of the identified Covid-19 shock on the global economy as well as on the 33 individual countries in our sample. In linear models, GIRFs possess the following key features: (i) proportionality (namely, potential outcomes are linear in the size of the shock); (ii) state independence (that is, the effects of the shocks do not vary in recessions or expansions); and (iii) model invariance (namely, the underling model is invariant to the shock under consideration). However, none of these features apply to non-linear dynamic models, which as argued a priori and established empirically, are more likely to be relevant for the analysis of large shocks, such as Covid-19. By using a threshold-augmented dynamic multi-country model, we are able to allow for (i) non-proportional impacts of large and small shocks; (ii) state-dependency; and (iii) more persistent outcomes. See Koop et al. (1996).
Standard GVAR modelling is designed to explicitly account for economic and financial interdependencies across markets and countries, and was originally proposed by Pesaran et al. (2004) and further developed by Dees et al. (2007). It features elements of time series, panel data, and factor analysis, and is particularly useful in studying the international macroeconomic effects of various shocks. The standard GVAR model comprises 33 country/region-specific sub-models. These individual models are solved in a global setting where core macroeconomic variables of each economy are related to corresponding foreign variables (constructed exclusively to match the international trade pattern of the country under consideration) as well as global variables. This framework is able to account for various transmission channels, including trade relationships, as well as financial and commodity price linkages. This is important at the current juncture, as many countries face a multi-layered shock comprising a health emergency, domestic economic disruptions, plummeting external demand, tighter financial conditions, and a collapse in commodity prices.
The GVAR model has been used in a range of studies, such as stress testing of banks by the European Central Bank regulators, the analysis of China’s growing importance for the global economy (Cesa-Bianchi et al., 2012 and Cashin et al., 2016, Cashin et al., 2017b), the international macroeconomic transmission of weather shocks Cashin et al. (2017a), the impact of commodity price shocks—see Mohaddes and Pesaran, 2016, Mohaddes and Pesaran, 2017 for the global macroeconomic consequences of country-specific oil-supply shocks and Cashin et al. (2014) and Mohaddes and Raissi (2019) for the differential effects of demand- and supply-driven commodity price shocks—, and other real and financial shocks—see, for instance, Cesa-Bianchi et al. (2020) and the GVAR handbook edited by Mauro and Pesaran (2013) for empirical applications from 27 contributors—, as well as in forecasting—see Pesaran et al. (2009) and Bussière et al. (2012) for the earliest GVAR forecasting applications to the global economy. For an extensive survey of the latest theoretical developments in GVAR modelling and the numerous empirical analyses, see Chudik and Pesaran (2016) and Chapter 33 of Pesaran (2015).
Our counterfactual results show that the pandemic could reduce the world real GDP by 3 percent below its model-generated path without the shock by the end of 2021. While China and other emerging Asian economies are estimated to be less severely affected, the United Kingdom, and several other advanced economies may experience deeper and longer-lasting effects. Among non-Asian emerging market economies, however, the economic impact of Covid-19 varies substantially, depending on domestic factors (economic structures, health preparedness, and the scale of lockdowns) as well as external disturbances (plunging trade, collapsing tourism, volatility in capital flows, and fluctuations in commodity prices). There is a significant degree of uncertainty around all these counterfactual outcomes which we try to quantify (while abstracting from the large-scale fiscal support that followed later in 2020). Importantly, our findings underscore the role of spillovers which we quantify for the case of Sweden considering its different approach toward the pandemic (i.e., a less stringent strategy). We show that no country is immune to the economic fallout of the pandemic because of interconnections. We also estimate that the Covid-19 pandemic would lower long-term interest rates temporarily by about 100 basis points below their historical lows in core advanced economies. In contrast, the impact on long-term interest rates in emerging markets has a wide range, including significant upside risks.
Our paper also relates to a rapidly growing literature that investigates the macroeconomic effects of Covid-19. McKibbin and Fernando (2020) explore the global macroeconomic effects of different scenarios of how Covid-19 might evolve sing a hybrid DSGE/CGE model. They underscore the importance of spillover effects and show that even a contained outbreak could significantly impact the global economy in the short run. Bonadio et al. (2020) study the impact of Covid-19 on output growth in 64 countries and investigate the contribution of global supply chains to these adverse effects. Ludvigson et al. (2020) quantify the macroeconomic impact of Covid-19 in the United States using a VAR framework and a gauge of the magnitude of the Covid-19 shock in relation to past costly disasters. Baqaee and Farhi (2020) consider possible non-linearities in response to the Covid-19 shock in a multi-sectoral model. They develop a disaggregated structural model with input–output linkages, as well as downward nominal wage rigidities and a zero lower bound constraint on nominal policy rate to study the effects of supply and demand shocks associated with Covid-19. They demonstrate how these shocks are amplified or mitigated by nonlinearities, and quantify their effects using disaggregated data from the United States. Another paper which highlights the importance of nonlinearity is Céspedes et al. (2020). They build a threshold macroeconomic model of a pandemic and show how such a shock can have large magnification effects. Finally, Milani (2020) uses a GVAR model to underscore the importance of countries’ interconnections in the evolution of Covid-19 and its unemployment effects.
The rest of the paper is organized as follows. Section 2 highlights the importance of threshold effects in the growth–global volatility relationship. Section 3 develops the threshold-augmented dynamic multi-country (TGVAR) model. Section 4 quantifies the macroeconomic effects of Covid-19 under uncertainty using TGVAR. Finally, Section 5 offers some concluding remarks. Additional results are provided in three appendices.
2. Threshold effects: global volatility and growth
Threshold effects have been used in the literature primarily in the context of autoregressions pioneered by Tong (1990). These models are known as threshold autoregressions (TAR) and allow the parameters of the autoregressive model to switch between two or more values. Extension of TAR models to multi-variate systems has been considered by Tsay (1998). Hansen (2011) provides a recent review of TAR models, and discusses their empirical applications in economics in areas such as growth dynamics, stock return volatility and forecasting.
Given the global nature of Covid-19, and to capture its non-linear economic effects, we focus on a global measure of realized volatility, and consider its possible impact on country-specific output growth. To measure global volatility, we use the following
| (1) |
where is the PPP-GDP weight of country i, we index countries as , and is the country-specific realized volatility of equity returns during quarter t, computed from daily observations:
| (2) |
where is the equity return during day in quarter t in country , and is the number of trading days in quarter t. The country-specific realized volatility measures, , have been used in the literature to investigate the effects of uncertainty on growth. Here we focus on a global volatility measure, as opposed to country-specific ones, to better capture the effects of global uncertainty, which is more akin to Covid-19.
One could use other measures of global volatility as well. For example, instead of averaging country-specific realized volatilities, we could first take the average of equity returns across countries and then compute the realized volatility of global equity. Let be the global daily equity return defined by
using PPP-GDP weights as before. Then realized volatility of global equity returns is given by
| (3) |
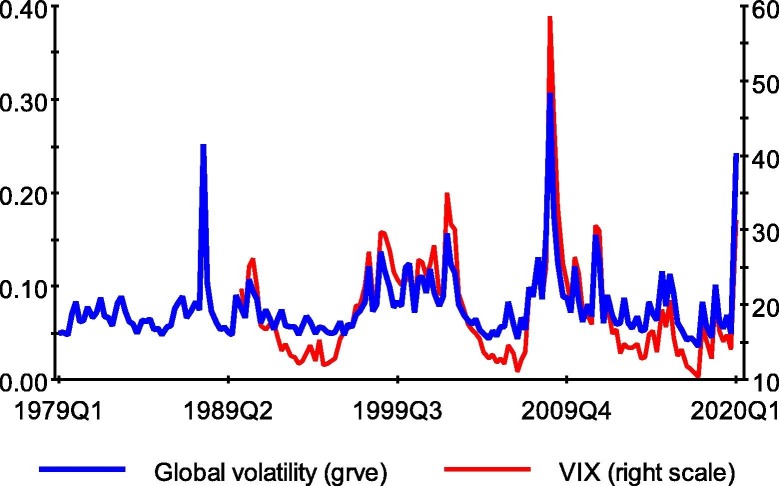
A widely-used alternative measure of global volatility in the literature is the option-implied volatility, or VIX. While the VIX captures the stock market’s expectation of volatility based on S&P 500 index options and is only available from 1990, our preferred measure of global volatility, , is based on realized equity returns for a large number of countries and is available for the last four decades. Note that the correlation of and VIX is 89.8%, therefore, seems to follow the VIX index well but not too closely (see Fig. 1 ), thus capturing, to some degree, some of the volatilities that originate from emerging economies. Appendix B systematically compares these three measures of global volatility and shows that is superior to other measures in terms of fit.1 Therefore, in what follows, we report the results based on the measure of global volatility.
Fig. 1.
Covid-19 and Past Episodes of Heightened Stock Market Volatility, 1979Q1–2020Q1. Notes: The global realized volatility of equity returns, , is aggregated using PPP-GDP weights. The correlation between the two variables is 0.90.
We begin our econometric analysis with the following simple multi-country threshold-augmented dynamic output growth model:
| (4) |
where , is the first difference of the logarithm of real GDP for country i during quarter t, and is the global volatility threshold variable, is an indicator variable that takes the value of unity if event occurs and zero otherwise, is the global realized volatility defined by (1), and is a threshold parameter, assumed to be the same across countries under consideration. is the idiosyncratic error assumed to be serially uncorrelated with a zero mean.
The above specification only allows for intercept shifts in output growth equations, thus treating the threshold variable, , as another common factor, with the threshold parameter estimated by pooling across countries. Modelling other forms of threshold effects, including country-specific thresholds, will unduly complicate the modelling exercise and is beyond the scope of the present paper. We model the threshold effects with respect to lagged values of the realized volatility variable, and rely on standard common factor analysis to capture possible simultaneity between output growths and volatility. See Section 3.
The results of estimating Eq. (4) for advanced and emerging economies are summarized in Table 1 . In addition to reporting the estimates of and , we also report the estimate of the proportion of times that the threshold is exceeded, denoted by p. The threshold parameter, , is estimated by grid search and is allowed to take different values for advanced and emerging economies. The estimate of for advanced economies at is slightly larger than the value of estimated for emerging economies. Given these estimates, the global volatility threshold variable is statistically significant in 15 out of the 19 (80%) advanced economies in our sample. But the results are much weaker for emerging economies, with only 4 statistically significant effects out of the 14 emerging economies in our sample. Nevertheless, all statistically significant threshold affects were negative, suggesting that excessive global volatility is generally associated with lower output growth subsequently. There are a numbers of channels through which excessive global financial market volatility can adversely affect economic growth. They include higher precautionary savings by households, lower or delayed investment by firms due to increased uncertainty and weaker demand prospects, and a higher cost of raising capital owing to higher funding costs in a volatile environment. See, for example, Cesa-Bianchi et al. (2020) and the references therein. In normal conditions where global volatility is low (below the threshold ), financial markets are able to price the volatility risk, and therefore weaken the relationship between output growth and the volatility factor. But during periods of heightened volatility, that occur very rarely, it is difficult to price the volatility risk properly and it is thus more likely for excess volatility to show up as statistically significant in output growth equations.
Table 1.
Estimates of Threshold Coefficient , Threshold Parameter , and AR(1) Coefficients in Threshold-augmented AR Specifications, 1979Q2–2019Q4.
| (a) Advanced economies: = 3.09% and, = 0.156 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t-ratio | t-ratio | |||||||||||
| Australia | −0.0059† | −1.88 | 0.26‡ | 3.48 | 7.8% | 0.0069 | ||||||
| Austria | −0.0208‡ | −5.10 | −0.17† | −2.28 | 13.5% | 0.0087 | ||||||
| Belgium | −0.0079‡ | −2.54 | 0.22‡ | 2.86 | 9.6% | 0.0066 | ||||||
| Canada | −0.0071‡ | −2.50 | 0.48‡ | 7.10 | 28.1% | 0.0061 | ||||||
| Finland | −0.0203‡ | −3.37 | 0.02 | 0.23 | 6.1% | 0.0129 | ||||||
| France | −0.0064‡ | −2.99 | 0.31‡ | 4.01 | 17.5% | 0.0045 | ||||||
| Germany | −0.0174‡ | −4.35 | −0.03 | −0.37 | 10.0% | 0.0084 | ||||||
| Italy | −0.0076‡ | −2.51 | 0.31‡ | 4.16 | 16.8% | 0.0063 | ||||||
| Japan | −0.0083† | −1.86 | 0.21† | 2.55 | 6.8% | 0.0095 | ||||||
| Korea | −0.0030 | −0.40 | 0.02 | 0.22 | −1.1% | 0.0163 | ||||||
| Netherlands | −0.0128‡ | −3.99 | 0.17† | 2.23 | 13.6% | 0.0069 | ||||||
| Norway | −0.0133‡ | −2.44 | −0.29‡ | −4.00 | 10.4% | 0.0120 | ||||||
| New Zealand | −0.0029 | −0.74 | 0.20‡ | 2.60 | 3.4% | 0.0086 | ||||||
| Singapore | −0.0107∗ | −1.32 | 0.23‡ | 2.98 | 6.5% | 0.0174 | ||||||
| Spain | −0.0035† | −2.14 | 0.76‡ | 14.99 | 62.4% | 0.0034 | ||||||
| Sweden | −0.0247‡ | −4.64 | −0.35‡ | −4.62 | 16.3% | 0.0112 | ||||||
| Switzerland | −0.0095‡ | −2.74 | 0.17† | 2.18 | 8.3% | 0.0073 | ||||||
| United Kingdom | −0.0047∗ | −1.51 | 0.30‡ | 4.07 | 12.4% | 0.0066 | ||||||
| United States | −0.0096‡ | −3.29 | 0.33‡ | 4.55 | 19.9% | 0.0062 | ||||||
| MG (equally weighted) | −0.0103‡ | −6.60 | 0.17‡ | 2.76 | ||||||||
| MG (PPP-GDP weighted) | −0.0092‡ | −6.27 | 0.26‡ | 4.47 | ||||||||
| (b) Emerging economies: = 4.94% and = 0.129 | ||||||||||||
| t-ratio | t-ratio | |||||||||||
| Argentina | −0.0061 | −0.93 | 0.53‡ | 7.78 | 27.2% | 0.0180 | ||||||
| Brazil | −0.0082∗ | −1.36 | 0.22‡ | 2.93 | 5.5% | 0.0166 | ||||||
| Chile | −0.0065 | −0.95 | 0.26‡ | 3.25 | 6.0% | 0.0187 | ||||||
| China | 0.0035 | 0.88 | 0.32‡ | 4.17 | 9.0% | 0.0110 | ||||||
| India | −0.0071 | −1.12 | −0.24‡ | −3.04 | 4.5% | 0.0171 | ||||||
| Indonesia | −0.0093∗ | −1.32 | 0.01 | 0.12 | −0.1% | 0.0195 | ||||||
| Malaysia | −0.0074∗ | −1.44 | 0.31‡ | 4.03 | 11.7% | 0.0137 | ||||||
| Mexico | −0.0156‡ | −3.09 | 0.14∗ | 1.85 | 7.9% | 0.0137 | ||||||
| Peru | −0.0189† | −2.01 | 0.37‡ | 5.04 | 14.5% | 0.0258 | ||||||
| Philippines | 0.0034 | 0.64 | 0.16† | 2.03 | 1.3% | 0.0143 | ||||||
| South Africa | −0.0018 | −0.71 | 0.54‡ | 8.09 | 29.1% | 0.0068 | ||||||
| Saudi Arabia | 0.0075 | 1.32 | 0.61‡ | 9.94 | 38.2% | 0.0157 | ||||||
| Thailand | −0.0263‡ | −3.60 | 0.01 | 0.13 | 6.6% | 0.0199 | ||||||
| Turkey | −0.0294‡ | −3.27 | −0.02 | −0.27 | 5.2% | 0.0247 | ||||||
| MG (equally weighted) | −0.0087‡ | −2.99 | 0.23‡ | 3.53 | ||||||||
| MG (PPP-GDP weighted) | −0.0038 | −1.02 | 0.18 | 1.58 | ||||||||
Notes: Our threshold-augmented dynamic output growth model is given by , where is the first difference of the logarithm of real GDP in country i during quarter t and . is an indicator variable that takes the value of unity if event occurs and zero otherwise. is a measure of global volatility defined by (1), and is the threshold parameter. The estimation sample is 1979Q2 to 2019Q4. Statistical significance is denoted by and ‡, at 10%, 5% and 1% levels, respectively.
Overall, while we manage to detect threshold effects in the output growth–global volatility relationship in many advanced economies (80 percent of cases), similar results for emerging markets are less pervasive (with threshold effects being statistically significant in 30 percent of cases) for the following reason. Compared to advanced countries, exposure to global equity markets is lower in emerging market economies (that is, they have less developed capital markets and rely more on the banking sector for credit intermediation). Nonetheless, in these countries output growth could well be non-linearly affected by localized events (e.g., natural disasters; banking, currency and sovereign crises) or external shocks (e.g., commodity price volatility and capital flow reversals), and be exacerbated by country-specific characteristics (internal and external imbalances). However, these types of threshold effects will not be captured by our econometric specification that focuses on the global realized volatility of equity returns that is more reflective of developments in advanced economies. 2
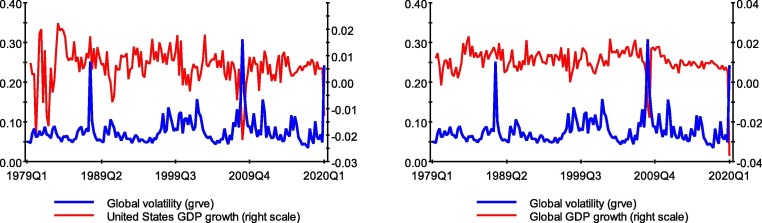
The above findings underscore the importance of allowing for threshold effects in studying the macroeconomic consequences of Covid-19—which, considering its unprecedented nature, generated a sharp tightening in global financial conditions (Fig. 1). Specifically, global equity markets sold off sharply through mid-March 2020 as the pandemic spread across the world. From end-2019 to trough, the S&P 500 index in the United States fell 30 percent. Stock prices in other major economies experienced declines of similar magnitude and flight to safety resulted in sharp capital outflows from emerging market economies. Notwithstanding the improvement in global risk sentiment since March amid large-scale liquidity injections by major central banks and a gradual relaxation of lockdowns in many countries, output recovery is expected to be gradual with GDP growth in many economies expected to be negatively affected by the previous bout of financial market volatility (Fig. 2 ).
Fig. 2.
Global Volatility and GDP Growth, 1979Q2–2020Q1. Notes: Global realized volatility of equity returns, , and global GDP growth are both aggregated using PPP-GDP weights.
3. A threshold augmented GVAR (TGVAR) model with global latent factors
In what follows, we study the implications of Covid-19 for the global economy. In doing so we build on the GVAR literature and develop a threshold-augmented dynamic multi-country framework, which we refer to as Threshold-augmented GVAR, or TGVAR for short. The proposed modelling framework takes into account both the temporal and cross-sectional dimensions of the data; real and financial drivers of economic activity; interlinkages and spillovers that exist between different regions/countries; and the global common factors, as well as network effects (e.g., through trade linkages). This is crucial as the impact of shocks (and importantly that of Covid-19) cannot be reduced to a single country but rather involves multiple regions/countries, and this impact may be amplified or dampened depending on the degree of openness of the countries (both trade and financial) and their economic structures. Informed by the results in Section 2, we also allow for threshold effects in the output growth equation arising from global financial market volatility. Moreover, in contrast to the standard GVAR models that rely on trade-weighted averages to capture both local and global effects, we treat these effects separately. Before describing our model specification, we provide a short exposition of the methodology and data.
3.1. Data and variables
We consider a world economy composed of interconnected countries. Our focus is to model output growth and its responses to common shocks, either directly or indirectly through equity and bond markets. Specifically, for each economy i, we include the logarithm of real GDP (), nominal long-term interest rate (), the logarithm of real equity prices (), and the logarithm of the real exchange rate (the nominal exchange rate deflated by the consumer price index), . Data on these variables are obtained from the updated GVAR data set which includes 33 countries and covers the period 1979Q2 to 2019Q4. For a detailed description of data sources and related transformations see Mohaddes and Raissi (2020).
To avoid highly persistent variables we work with first-differences and denote the endogenous country-specific variables by
| (5) |
The U.S. economy is denoted by , with the remaining economies indexed by , in no particular order. For estimation we suppose that is available over the period , although the bond and equity variables, and , are not available for some of the countries in our dataset. Therefore, the dimension of , which we denote by , differs across countries. Let , and collect all country-specific variables in a single vector .
Given the focus of our analysis, we augment the standard GVAR model with observed and unobserved external common factors. We consider changes in log oil prices, , and global volatility, , as common observed factors and include them in the vector
| (6) |
In addition, we use the weighted cross-sectional averages of the following four variables to capture unobserved common factors:
| (7) |
where is the PPP-GDP weight of country i, and similarly , and . One could also apply the principal component analysis (PCA) to , but that would involve estimating the number of common factors and deciding whether the PCA is applied to different components of separately or to all of its four components together. The weighted cross section averages, , and , are likely to be closely correlated with the first principal component of ,and , for , respectively.
To link the global aggregates to the country-specific variables, we introduce a weights matrix, , and define it such that
| (8) |
In addition to global aggregates, we also allow for transmission of shocks through the trade channel and consider country-specific trade-weighted averages
| (9) |
where are the trade weights, , and .For empirical application, the trade weights are computed as three-year averages:3
| (10) |
where is the bilateral trade of country i with country j during a given year t and is calculated as the average of exports and imports of country i with j, and (the total trade of country i) for and 2016, in the case of all countries. A similar procedure is followed for the construction of , and . As it is well known in the GVAR literature, the country-specific aggregates relate to through the following links
where is the matrix of trade weights for country i.
The main difference between the two sets of aggregates, and , for , is the weights used in their construction. These two variables are likely to be highly correlated contemporaneously. The reason for considering both aggregates (cross-section averages) is to distinguish the effects of global factors from local (trade related) effects, captured by country-specific trade linkages. Also to avoid multi-collinearity and related identification problems, we include only lagged country-specific cross-section averages, , and rely on global cross-section averages, , to capture contemporaneous effects of global factors.
3.2. Global and individual country specifications
We specify the following equations for and
| (11) |
and
| (12) |
| (13) |
where , and is the vector of reduced form global shocks, with
We consider the following country-specific threshold-augmented models:
| (14) |
for , where the threshold indicator, , is defined by
| (15) |
The country-specific models in (14) are intended to capture the individual country VAR dynamics as well as common factors, , and local effects, . We have also confined the threshold variable, , to affect the intercepts only, but we do allow for these effects to vary across countries. These are pragmatic choices that we had to make to keep the model sufficiently parsimonious so that to obtain reasonably reliable estimates of the unknown parameters. We expect the threshold event, namely periods where , to be quite rare and therefore to be most important in terms of its direct effect on output growth, which is best characterized by a shift in the intercept term. The possible effects of such rare events on growth persistent is likely to be of second order importance. Moreover, we limited the heterogeneity in by estimating only two threshold values, one pooled value for advanced economies and one for emerging markets.
We allow the country-specific error vectors, , to be cross-sectionally weakly correlated. Adding non-granular (local) cross-section averages, of the dependent variables, , also known as spatial lags, to the right side of (14) is common in the spatial literature, where the contemporaneous correlation (after controlling for lags and common factors) is fully parametrized by introducing spatial lags, which, if specified correctly, would then identify geographical origins of the shocks. We do not attempt to fully parametrize the cross sectional correlation of . For this reason, we only include lagged values of in the country-specific models.
Another important reason for why we do not include as a regressor is the fact that, for a number of countries, some trading partners have a large weight in country-specific trade-weighted averages . For example, U.S. is the dominant trading partner of Canada, with its trade weight exceeding 70 percent of the total. In such cases, we would expect that contemporaneous values of to be correlated with , even if . Including non-granular contemporaneous cross-section averages of the dependent variable in (14), would consequently result in inconsistent least squares estimation, owing to correlation between and the non-granular cross-sectional averages (spatial lags) even when n is large, and a full maximum likelihood or GMM type estimation will be required.
Eqs. (11), (12) are specifications for global variables and global aggregates. Eq. (14), for , relates to country specific models. Eq. (15) links the threshold indicator with the vector of global variables. Moreover, we have two additional linking equations. Eq. (8) links global aggregates with , and
| (16) |
links the vector of country-specific trade-weighted averages to the full vector of endogenous variables, , and is the matrix of pre-determined weights.
3.3. The TGVAR representation
Substituting (13) for in (14), we obtain
| (17) |
where , and . Note that the substitution of the global model (13) for in the country-specific models (14) avoids the possibility of the rank-deficiency problem discussed in Section 4.1 of Chudik et al. (2016). In addition, it allows for an error structure that explicitly features common and idiosyncratic shocks. Our approach differs from the earlier GVAR models in the literature that only rely on the conditional country-specific equations in (14) and the marginal equation for the observed common variables in (11). In contrast, (17) utilizes the Eq. (12) for as well. This approach is also adopted by Cesa-Bianchi et al. (2020) and Chudik et al. (2020).
Stacking (17) for , we obtain
| (18) |
where ,
is an vector of threshold indicators, and
Substituting identity (16) for in (18 ), we have
Partitioning
and substituting (8) for , we obtain
| (19) |
Substituting identity (8) for in equations for in (11), we have
| (20) |
Stacking (19), (20), we obtain the following TGVAR representation for the full set of observables, the vector ,
| (21) |
where
| (22) |
Also
| (23) |
where ,
| (24) |
is a vector of reduced form shocks, composed of global () and idiosyncratic shocks ().
Given our focus on the output effects of the Covid-19 shock, and to keep the analyses empirically manageable, we consider the effects of the threshold variable on the output growth variables only, and accordingly set . Without loss of generality, we identify advanced economies by and the emerging market countries by . Moreover, currently available time series observations do not allow for the estimation of country-specific threshold effects which capture rare events. Thus, we can only estimate two threshold parameters, distinguishing between advanced and emerging economies:
| (25) |
Thresholds and are estimated by a grid-search method outlined in Appendix A. We excluded the threshold indicator from a few countries, where .
Finally, given the dominant role played by U.S. in the global financial markets, we exclude , and from the U.S. model by restricting the corresponding rows of the coefficient matrices and to zero vectors.
3.4. Identification of the Covid-19 shock
Identifying the economic effects of Covid-19 is not a straightforward task as our historical sample is not informative about such a shock. Also considering the truly global nature of the pandemic, it is not possible to compare economic outcomes from countries affected by Covid-19 with a control group that has not been buffeted by the Covid-19 shock. At best, we could compare economic outcomes across countries that followed different strategies to mitigate the spread of the pandemic. This approach is also limited as most countries have followed very similar approaches (for example, lockdowns) with just a few exceptions (such as Sweden which we consider below), and they differ mainly in terms of the timing of the implemented social distancing policies (for example, Germany and the United Kingdom). Here we adopt a historical country-specific approach and identify the Covid-19 shock by comparing the IMF’s GDP projections for Q1 to Q4 of 2020 formed at the end of 2019—before the spread of the pandemic and when no one (including the IMF) could have predicted the global economic disruption that was brought about by the pandemic—to the same projections prepared in April 2020. We attribute the IMF’s GDP projection revisions in 2020Q1 to the Covid-19 shock. In effect, we assume that the short-term IMF projections at the end of 2019 were free from systemic bias and can be used as potential outcomes in the absence of the Covid-19 shock. We believe this is a reasonable identifying assumption, in view of the unprecedented nature of the Covid-19 pandemic. Accordingly, we assume that up to 2019Q4 (), is given by (23), but for Q1 to Q4 of 2020, it is given by
| (26) |
where corresponds to the Covid-19 shock in the period . We assume for , but it is nonzero for . To identify we will use the size of IMF’s projection revisions at the end 2020Q1.
Let be the April 2020 IMF World Economic Outlook (WEO) GDP growth projections for country i in quarters of 2020, and be the associated January 2020 IMF WEO projections. We compute the April-January projection revisions as
and . Assuming that developments surrounding Covid-19 were the only dominant developments behind the projection revisions, we use , for to infer . Note that growth outturns in 2020 were subsequently affected by the massive scale-up of policy actions by governments (for example, global fiscal support was increased from $3.3 trillion in April 2020 to $16 trillion in April 2021). To the extent possible, we try to abstract from these factors in our counterfactual analysis to identify the Covid-19 shock from policy responses to mitigate its effects. For this reason and as expected, the actual growth outturns in 2020 (reported in Table 2 ) were somewhat different from the April 2020 growth projections of the IMF that served as our baseline.4
Table 2.
IMF Growth Projections versus Outturns (2020Q4 over 2019Q4 in percent) and the Size of Fiscal Support in 2020 (in percent of GDP).
| IMF Proj. April 2020 | Actual | Fiscal Support | IMF Proj. April 2020 | Actual | Fiscal Support | |||
|---|---|---|---|---|---|---|---|---|
| Australia | −7.2 | −1.1 | 16.1 | Argentina | −7.2 | −4.4 | 3.9 | |
| Austria | −6.6 | −5.7 | 11.7 | Brazil | −5.8 | −1.2 | 8.8 | |
| Belgium | −5.2 | −5.4 | 8.0 | Chile | 0.2 | −0.1 | 8.2 | |
| Canada | −5.4 | −3.2 | 14.6 | China | 4.9 | 6.2 | 4.8 | |
| Finland | −3.6 | −1.1 | 2.5 | India | 7.4 | 0.4 | 3.3 | |
| France | −5.0 | −4.5 | 7.6 | Indonesia | 2.8 | −2.1 | 4.5 | |
| Germany | −5.2 | −2.8 | 11.0 | Malaysia | 1.7 | −3.5 | 4.5 | |
| Italy | −7.2 | −6.2 | 8.5 | Mexico | −7.4 | −4.4 | 0.7 | |
| Japan | −3.2 | −1.4 | 15.9 | Peru | −3.8 | −1.7 | 7.3 | |
| Korea | −1.3 | −1.4 | 4.5 | Philippines | −0.2 | −7.9 | 2.7 | |
| Netherlands | −6.6 | −2.9 | 4.5 | Saudi Arabia | −0.5 | −4.0 | 2.2 | |
| New Zealand | −7.0 | 1.1 | 19.3 | South Africa | −7.2 | −4.2 | 5.9 | |
| Norway | −8.5 | −0.7 | 4.2 | Thailand | −3.4 | −4.6 | 8.2 | |
| Singapore | −3.1 | −2.4 | 16.0 | Turkey | −8.4 | 5.8 | 1.9 | |
| Spain | −7.0 | −9.1 | 7.6 | |||||
| Sweden | −4.8 | −2.1 | 4.2 | |||||
| Switzerland | −7.4 | −1.7 | 7.3 | |||||
| United Kingdom | −5.3 | −9.5 | 16.2 | |||||
| United States | −5.4 | −2.4 | 25.5 |
Sources: Fiscal Monitor Database of Country Fiscal Measures in Response to COVID-19; Haver Analytics. Notes: Fiscal Support includes discretionary spending and revenue measures in response to Covid-19 and its economic fallout since January 2020.
3.4.1. Using IMF projections to infer
Let us define as the matrix that selects all output growth variables from the vector , namely
We set individual elements of that correspond to GDP to be given by the corresponding , and use the historical correlations of the reduced form errors to estimate the remaining elements. This yields
| (27) |
where , in which is the estimate of and . The innovations, for are computed recursively as
| (28) |
In (27), (28), we infer the sequence of shocks , using revisions in the IMF projections for the paths of GDP and the corresponding predictions of our global model. Specifically, we define the Covid-19 effects by the difference
| (29) |
where is a counterfactual realization of the global economy after the Covid-19 shock hit the economy, namely , and is the conditional expectation of global economy without the Covid-19 shock, conditioning on the information . The distribution of can be computed by stochastically simulating and as described in Sections A.3, A.4 of Appendix A. The distribution of captures both the estimation uncertainty (as is common in impulse-responses analysis) and the uncertainty related to realization of future idiosyncratic shocks (in contrast to impulse-response analysis).
4. The effects of Covid-19 on economic activity and long-term interest rates
Our model includes 33 economies, which together cover more than of world GDP, see Table 3 . For presentation of our results, we create a euro area block comprising 8 of the 11 countries that initially joined the Euro in 1999: Austria, Belgium, Finland, France, Germany, Italy, Netherlands, and Spain. The time series data for the euro area are constructed as cross-sectionally weighted averages of the domestic variables, using Purchasing Power Parity GDP weights, averaged over the 2014 to 2016 period. In addition to the euro area we also consider a further seven regions, see Table 3.
Table 3.
Countries and Regions in the TGVAR Model.
| Advanced Economies | Euro Area | Emerging Economies | Emerging Asia | |||
|---|---|---|---|---|---|---|
| Australia | Austria | (excl. China) | (excl. China ) | |||
| Austria | Belgium | Argentina | India | |||
| Belgium | Finland | Brazil | Indonesia | |||
| Canada | France | Chile | Malaysia | |||
| Finland | Germany | India | Philippines | |||
| France | Italy | Indonesia | Thailand | |||
| Germany | Netherlands | Malaysia | ||||
| Japan | Spain | Mexico | Latin America | |||
| Korea | Peru | Argentina | ||||
| Netherlands | Advanced Asia Pacific | Philippines | Brazil | |||
| Norway | Australia | South Africa | Chile | |||
| New Zealand | Japan | Saudi Arabia | Mexico | |||
| Singapore | Korea | Thailand | Peru | |||
| Spain | New Zealand | Turkey | ||||
| Sweden | Singapore | Other Emerging | ||||
| Switzerland | Economies | |||||
| United Kingdom | Other Advanced | China | Turkey | |||
| United States | Economies | South Africa | ||||
| Canada | Saudi Arabia | |||||
| Norway | ||||||
| Sweden | ||||||
| Switzerland | ||||||
| United Kingdom |
4.1. Real GDP effects are large and persistent
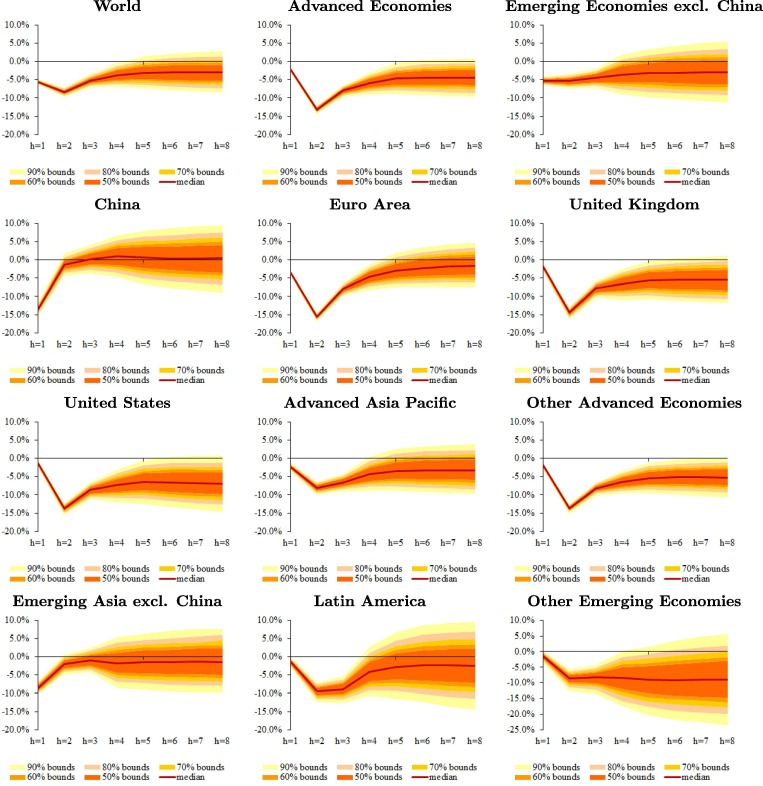
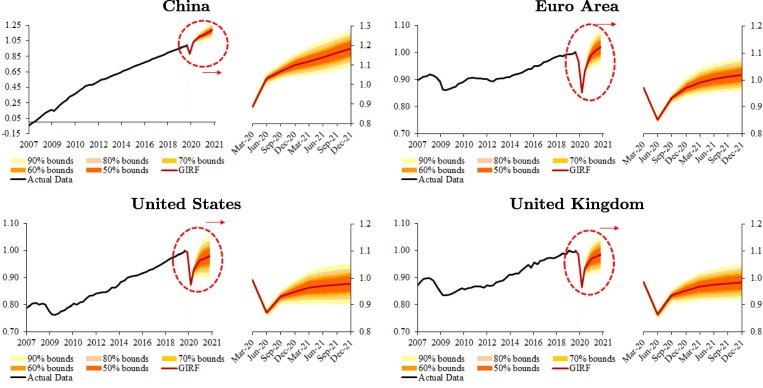
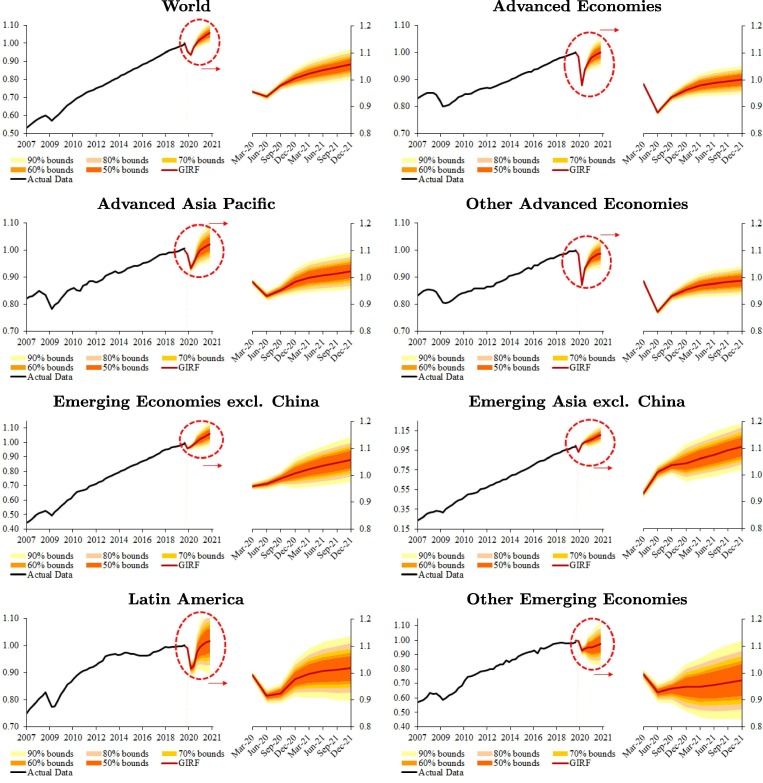
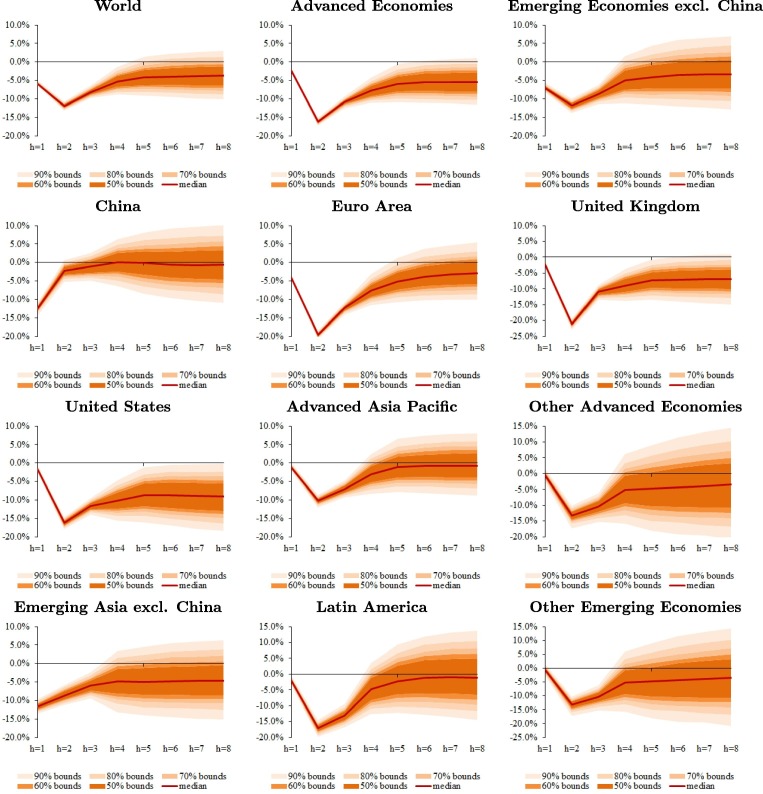
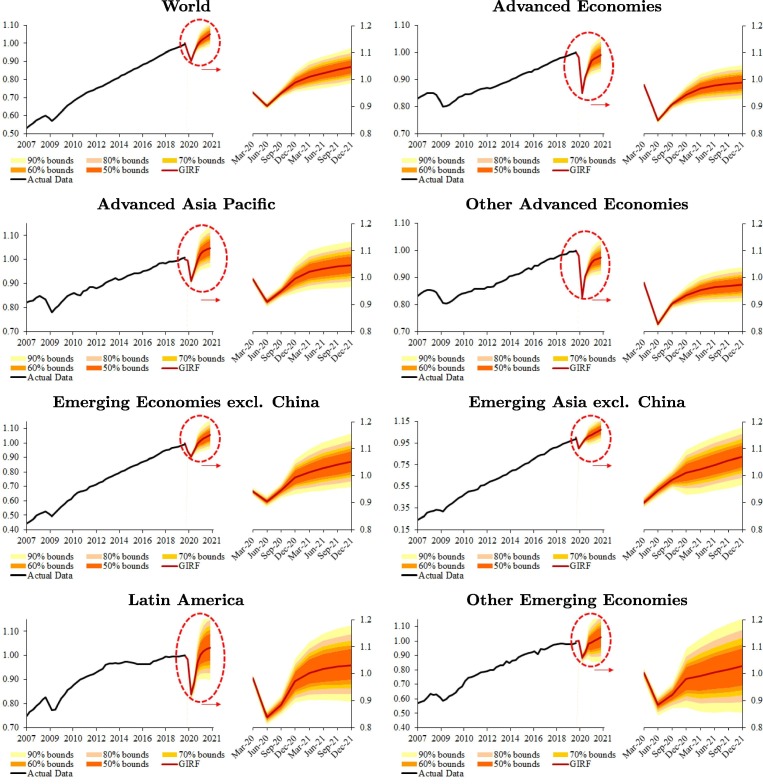
Fig. 3 reports the results of our counterfactual exercise for real GDP between 2020Q1 and 2021Q4.5 The solid lines are the generalized impulse responses of real GDP following the Covid-19 shock, while the bounds represent the range of likely outcomes given the constellation of shocks experienced over the past four decades. Note that the median impulse responses for 2020Q1–Q4 match the April 2020 growth projections of the IMF by design. Uncertainty around these projections are pervasive because of the severity and duration of the Covid-19 pandemic, global spillovers, financial market volatility, the efficacy of policy actions to protect firms and households, and the success of pharmaceutical interventions to contain the spread of the virus. Overall, the Covid-19 pandemic would leave the 2021 GDP about 3 percentage points lower than the model-generated forecast of global GDP in the absence of Covid-19. The adverse impact on Advanced Economies is particularly large—ranging from 2 percentage points below pre-crisis path of GDP by the end of 2021 in the euro area to 6.5 percentage points in the United States. 6
Fig. 3.
The Impact of Covid-19 on Real GDP (percent deviation from baseline). Notes: The impact is in percent and the horizon is quarterly. This figure plots quantiles of defined by (29).
Among emerging markets, however, the economic impact of Covid-19 varies substantially. In addition to domestic shocks (health crisis and lockdowns), these countries faced a range of external shocks in early 2020 as well (plunging trade, collapsing tourism, capital outflows, falling commodity prices), albeit to varying degrees, and have different economic structures (those relying heavily on certain sectors are naturally more vulnerable to the adverse macroeconomic effects of the pandemic). China appears to be an exception largely because most of the country had reopened by early April and its lower size of inward spillovers. Emerging Asia excluding China is expected to be less affected by Covid-19 than Latin America. This is partly due to higher commodity dependence of the latter and tighter financing conditions initially, as well as being less successful is containing the pandemic.
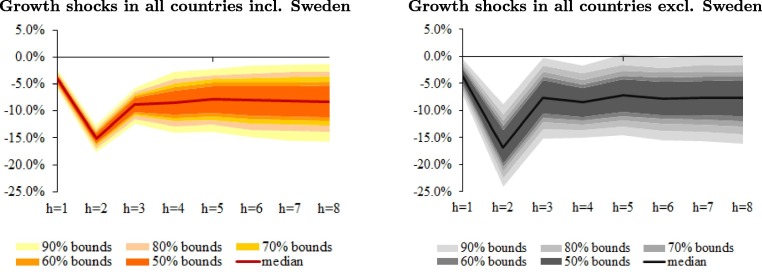
Fig. 4 reports the results of our counterfactual exercise for real GDP of Sweden under two scenarios: (i) growth shock in all 33 countries in our sample arising from the Covid-19 pandemic and (ii) growth shock in all countries except for Sweden. Comparing the two sets of results highlights the importance of spillovers through disruptions in global supply chains, travel, and tourism. The results in Fig. 4 illustrate that no country can shield itself from the adverse economic effects of Covid-19 by following less stringent lockdowns.
Fig. 4.
Spillovers to Sweden (percent deviation from baseline). Notes: The impact is in percent and the horizon (h) is quarterly.
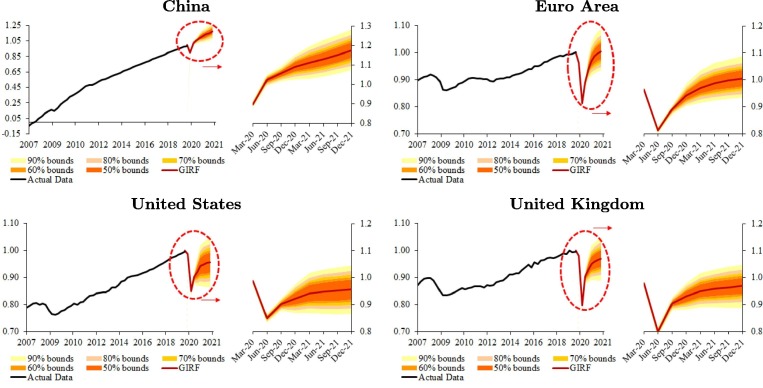
Fig. 5, Fig. 6 report the results of our counterfactual exercise for the evolution of real GDP following the Covid-19 shock relative to the 2019Q4 output levels rather than the model-generated forecasts of real GDP in the absence of Covid-19. In other words, we assess how long it will take for different countries/regions to return to their 2019Q4 real GDP levels following the Covid-19 shock. Informed by the April 2020 vintage of the IMF growth projections and our counterfactuals, global activity is estimated to trough in the second quarter of 2020, recovering thereafter. The estimated recovery in global activity is mainly driven by Asian economies (most notably China) while the United States and the United Kingdom are less likely to recuperate income losses by the end of 2021 (that is, their GDP is projected to end 2021 below 2019Q4 levels by about 2 and 1.5 percent with high probability, respectively). Consistent with the results in Fig. 3, China’s real GDP is expected to recover rapidly the lost ground, while non-Asian emerging economies are likely to take longer to achieve a full recovery. In all cases, there is a significant amount of uncertainly around the counterfactual GDP paths. See also Table 4 for likely growth outcomes. Note that these growth outcomes will be significantly worse if one were to use the updated projection revisions of the IMF in June 2020 to gauge the size of the shock rather than the April vintage (see Appendix C for details). This is because in June, the IMF updated its GDP projections based on more information about the pathway of the pandemic and the intensity and efficacy of containment efforts. The IMF, therefore, downgraded its projections of growth in the first half of 2020 and portrayed a more gradual recovery thereafter than previously projected.
Fig. 5.
Dynamics of Real GDP Following the Covid-19 Shock (in logs; 2019Q4 = 1).
Fig. 6.
Dynamics of Regions’ Real GDP Following the Covid-19 Shock (in logs; 2019Q4 = 1).
Table 4.
Growth Outcomes Following the Covid-19 Shock (percent change).
| Q4 over Q4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2019 | 2020 |
2021 |
|||||||
| Median | pctl | Median | pctl | pctl | Median | pctl | |||
| Advanced Economies | 1.4 | −6.8 | −3.7 | −0.9 | 1.7 | 3.9 | 6.3 | ||
| United States | 2.4 | −9.7 | −5.1 | −0.8 | −0.1 | 3.2 | 6.4 | ||
| Euro Area | 0.8 | −6.4 | −3.0 | 0.6 | 2.5 | 5.0 | 7.6 | ||
| France | 1.0 | −4.9 | −1.4 | 2.3 | 1.2 | 3.5 | 5.8 | ||
| Germany | 0.4 | −8.6 | −3.4 | 2.3 | 1.0 | 3.6 | 5.8 | ||
| Italy | 0.1 | −9.7 | −5.3 | −1.0 | 0.8 | 3.9 | 7.1 | ||
| Japan | −0.5 | −8.6 | −3.2 | 2.9 | 0.0 | 3.4 | 6.4 | ||
| United Kingdom | 1.3 | −9.1 | −4.7 | −0.7 | 1.3 | 3.3 | 5.7 | ||
| Canada | 1.5 | −8.5 | −4.1 | 0.5 | −0.4 | 4.3 | 8.6 | ||
| Emerging Markets (excl. China) | 3.0 | −4.7 | 0.8 | 6.4 | 2.3 | 4.9 | 7.4 | ||
| Emerging Asia (excl. China) | 4.6 | −2.5 | 4.3 | 11.5 | 4.6 | 5.9 | 7.2 | ||
| Latin America | 0.5 | −8.8 | −2.3 | 4.6 | −1.6 | 4.1 | 8.7 | ||
| China | 6.1 | 4.3 | 10.0 | 15.7 | 4.8 | 7.9 | 10.3 | ||
4.2. Long-term interest rates face downward pressures
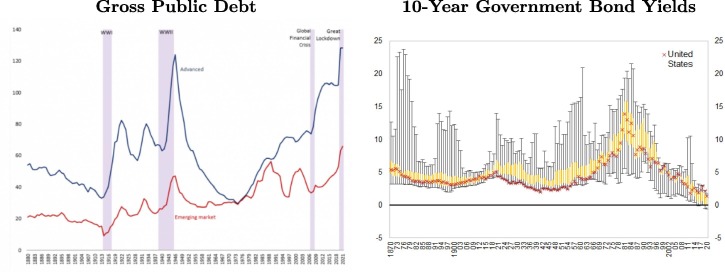
Global public debt is expected to reach its highest recorded level (about 100 percent of global GDP and higher than the post-World War II peaks) partly driven by the massive fiscal response to the Covid-19 pandemic (9.2 percent of 2020 GDP in additional spending and foregone revenue globally as of April 2021). At the same time, the 10-year government bond yields are at their historical lows and negative in several advanced economies (Fig. 7 ). To the extent that borrowing costs stay at low levels, they make it easier to service public debt. Fig. 8 reports the results of our counterfactual exercise for long-term interest rates between 2020Q1 and 2021Q4. For advanced economies (especially those that are perceived to be safe havens), long-term interest rates are estimated to temporarily fall even below their pre-Covid levels as the crisis raises precautionary savings and dampens investment demand. However, the same cannot be said about emerging market economies where borrowing rates can increase rapidly as shown by the upper range of our counterfactual exercise in Fig. 8. Among safe havens, Japan appears to be an exception possibly driven by Bank of Japan’s policy of yield-curve control.
Fig. 7.
Public Debt and Market Interest Rates (in percent of GDP and percent respectively). Sources: Gaspar and Gopinath, 2020, Jordà et al., 2019, and IMF staff calculations. Note: The sample for the interest rates includes Australia, Belgium, Canada, Denmark, Finland, France, Germany, Italy, Japan, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland, the United Kingdom, and US. The figure shows the interquartile range (yellow bars) and the 10th and 90th percentiles (whiskers). Red markers signify the United States. Data for 2020 are through the end of March.
Fig. 8.
The Impact of Covid-19 on Long-term Interest Rates (percentage points deviation from baseline). Notes: The impact is in percentage points and the horizon (h) is quarterly.
These predictions are largely borne out by actual data. For example, in the first half of 2020, 10-year government bond yields in the United States, the United Kingdom, and Germany fell by 111, 44, and 10 basis points, respectively, and that of Japan increased by 10 basis points—all within our counterfactual ranges displayed in Fig. 8. Among emerging markets, South Africa experienced a 137 basis points increase in its 10-year government bond yields during the first half of 2020—again within our prediction ranges.
5. Concluding remarks
The Covid-19 pandemic has been a shock like no other, initiating simultaneous demand and supply disruptions. In addition, it led to a sharp tightening in global financial market conditions during the first quarter of 2020. Using quarterly data over the past four decades, we first showed that global financial market volatility (beyond certain thresholds) can adversely affect economic growth in a significant majority (80 percent) of advanced countries and for several emerging market economies. We then developed a threshold-augmented dynamic multi-country model, or TGVAR for short, to study the global macroeconomic effects of Covid-19. We identified the country-specific Covid-19 shocks by comparing IMF’s GDP projections for Q1 to Q4 of 2020 formed at the end of 2019 (before the spread of the pandemic) to the same projections prepared in April 2020. Finally, using the TGVAR model we quantified the range of likely macroeconomic outcomes following the Covid-19 shock.
Our results showed that the Covid-19 pandemic could lead to long-lasting declines in world real GDP with varied effects across regions/countries. The impact of Covid-19 on the UK, and several other advanced economies could be particularly severe, while China and other emerging Asian economies are estimated to fare better. We also estimated that the Covid-19 pandemic can temporarily lower long-term interest rates below their pre-Covid-19 lows in core advanced economies, but the reverse outcome is predicted for emerging markets, with implications for debt servicing costs. Our findings highlighted the importance of policy interventions to restore the normal functioning of financial markets, as well as adopting other measures (fiscal and liquidity) that can limit bankruptcies of viable firms and support incomes of households. These measures would likely limit the amount of scarring.
Note that the pandemic resurfaces in waves—that is, with every easing of social distancing restrictions, the infection rates rise again, requiring the re-imposition of local restrictions, as we saw in Europe and the US in late 2020 and India lately—dampening economic activity and confidence. Appendix C shows how more up-to-date information about the pathway of the pandemic (considering its rarity) can affect our predictions.
Footnotes
We are grateful to Ron Smith, Serena Ng and participants at the ASSA 2021 Virtual Annual Meeting, CAMA global webinar series, EcoMod2021 International Conference on Economic Modeling and Data Science, NBER Summer Institute 2021 Forecasting & Empirical Methods Conference, and CEBRA 2021 Annual Meeting for helpful comments. We would also like to thank the Editor in charge of our paper (Mark M. Spiegel) and two anonymous referees for helpful comments and suggestions. The views expressed here are those of the authors and do not necessarily represent those of the Federal Reserve Bank of Dallas, the Federal Reserve System, the International Monetary Fund or IMF policy.
See in particular Fig. B.1 in the Appendix, which compares the average Mean Square Errors (MSE) of the threshold-augmented dynamic output growth models for the two alternative measures of volatility, and .
As a robustness check, we are able to detect the presence of threshold effects in a larger number of economies if we start the sample from 1990Q1. See Appendix B for the estimation results and other details.
As an additional robustness check, we also re-estimated the model using weights based on data on a longer period from 1990–2016 and obtained very similar results. These results are not reported here but available upon request.
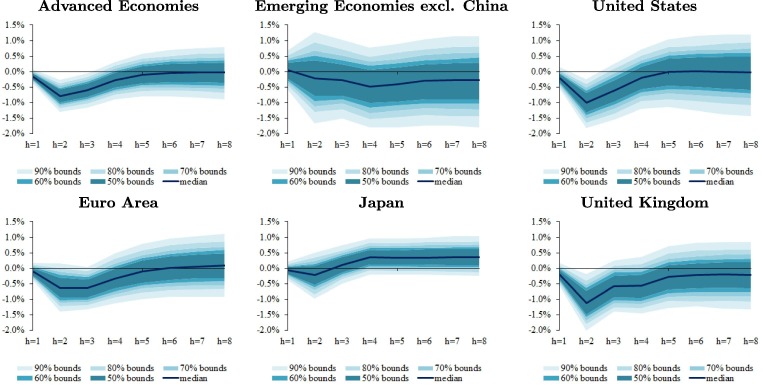
Chudik et al. (2021) show that government spending and revenue actions have prevented a more severe global economic contraction—including through spillovers. They estimate that, at the global level, such actions have mitigated the fall in global growth in 2020 by more than 2 percentage points.
The codes for the TGVAR model are available here: https://dx.doi.org/10.17632/5kp6h6ttx3.
As we explained above, the 2020 growth outturn in the United States was subsequently affected by the country’s massive fiscal support (amounting to 25.5 percent of GDP since January 2020).
The choice of implies that at least two time periods have nonzero threshold values, using the full sample 1979Q2 to 2019Q4 as well as the 1990Q1–2019Q4 subsample. We use in the simple multi-country threshold augmented dynamic model specifications, given by ( 4). In the full-scale TGVAR specifications (14), where many more country-specific coefficients are estimated, we set .
Abstracting from threshold effects, econometric justification for these regressions is provided by Chudik and Pesaran (2011).
Historical VIX data can be downloaded from here: https://www.cboe.com/tradable_products/vix/vix_historical_data/. This data is subject to a change in methodology that occured in September 22, 2003.
Appendix A. Estimation and simulation of TGVAR
This appendix provides technical details on the estimation and simulation of the threshold-augmented GVAR (TGVAR) model. Section A.1 describes how we estimate the model, while Section A.2 explains the bootstrapping procedure we use to capture the uncertainty of the parameter estimates. Sections A.3, A.4 outline how we simulate and , respectively.
A.1. Estimation of TGVAR models
Let and .7 We set , and our grid set for is given by
| (A.1) |
where is quantile of , and is the global volatility measure for quarter t, defined by (1).
The in ,
| (A.2) |
is estimated by least squares. For a given , we set for all i belonging either to advanced and emerging economies, and estimate8
| (A.3) |
by least squares. Estimates of (A.2), (A.3) are used to obtain the GVAR representation for :
| (A.4) |
as described in the main text, where , and is vector of ones. Let denote the estimated residuals in (A.4 ). We compute
| (A.5) |
and
| (A.6) |
where is the index set of advanced economies, and is the index set of emerging economies.
Given the estimates and , we set if economy i belongs to the group of advanced economies and if economy i belongs to the group of emerging economies. Then (A.3) is re-estimated using or (depending on the country grouping). We have excluded the threshold variable from countries where . The corresponding GVAR model is then estimated and solved based on (A.2), (A.3). In particular, using hats to denote the corresponding estimates, we have
A.2. Bootstrapping the TGVAR model
This section describes how we generate bootstrap replications of and , denoted as , and , for the replication.
-
1.
We generate , and , for , as a random shuffle of and , respectively.
-
2.We set and , and for , we compute
(A.7)
recalling that if economy i belongs to the group of advanced economies, and if economy i belongs to the group of emerging economies.(A.8) -
3.
We check for all i (advanced and emerging). If not, repeat steps 1–3 until this condition is satisfied.
- 4.
is given by and .
A.3. Simulation of
Bootstrap replications for (conditional prediction of the model in the absence of Covid-19 shock) are generated recursively for . Let .
-
1.
We generate , and , for , as a random shuffle of and , respectively.
-
2.For we compute
(A.10)
where are the bootstrap replication r of computed as described in Section A.2.(A.11) -
3.For , we compute
(A.12) (A.13) -
4.
Steps are repeated for . Mean of is estimated as , and quantiles of are estimated as quantiles of .
A.4. Simulation of
For , we first compute
| (A.14) |
where is the vector of shock sizes, and
| (A.15) |
For , we compute
| (A.16) |
| (A.17) |
| (A.18) |
where and are the bootstrap replications of and described in Section A.2.
Bootstrap replications for are generated recursively for .
-
1.
We generate , and , for , as a random shuffle of and , respectively.
- 2.
-
3.For , we compute
(A.21) (A.22) -
4.
Steps are repeated for . Quantiles of are estimated as quantiles of .
Appendix B. Threshold effects
This appendix provides additional results on the choice of the global volatility measure (Section B.1) and and on the robustness of the threshold effects to the choice of the sample period (Section B.2).
B.1. Alternative measures of global volatility
In addition to our preferred measure of global volatility, or —given by (1)—, we consider the realized volatility of the global equity returns, or —given by (3)--, and the VIX index, (http://www.cboe.com/vix). The VIX index is available on the CBOE website from 1990.9 To differentiate among these measures, we compute the average of squared residuals (MSE) of the threshold-augmented dynamic output growth models . We plot the minimized MSE for different values of the threshold parameter (). We consider indicator-specific grids of thresholds defined by the set ; namely, the indicator-specific grid of thresholds is given by quantiles of the given indicator, .
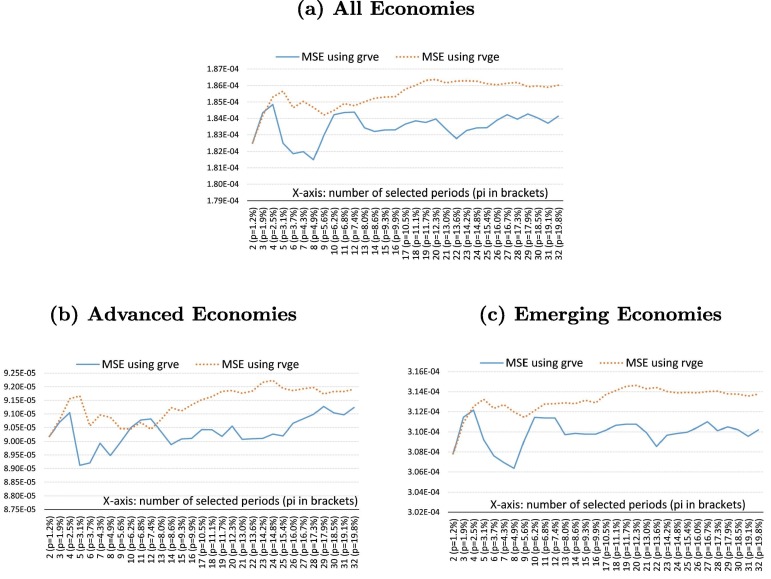
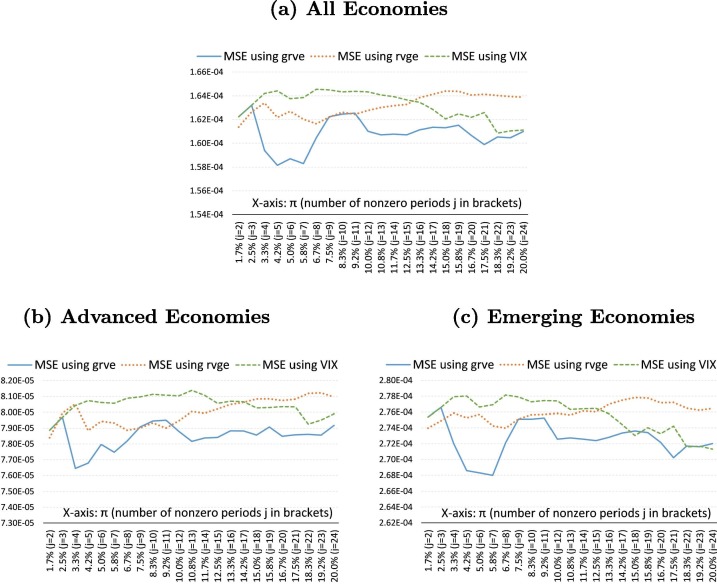
Fig. B.1 plots the MSEs for different values of (j) using the full sample 1979Q2–2019Q4 for and . To facilitate comparisons with the VIX index, Fig. B.2 shows the MSEs for the subsample 1990Q1–2019Q4, using all three global volatility measures. Each of these figures shows the MSEs for the full set of economies, as well as the subsamples of advanced countries and emerging markets. The results clearly show that the measure performs best in terms of MSEs in all cases considered, and is preferred over the other two measures. Note that the underlying regression models contain the same number of estimated parameters and as a result the MSE outcomes across the three measures are comparable. Therefore, we conclude that data speaks in favor of , which happened to be our choice based on our a priori arguments spelled out in the paper.
Fig. B.1.
MSE Objective Functions Using the 1979Q2–2019Q4 Subsample. Notes: This chart shows average MSE of the threshold-augmented dynamic output growth models estimated for the grid of threshold values (x-axis) for two choices of volatility measures: (solid blue line), and (dotted orange line).
Fig. B.2.
MSE Objective Functions Using the 1990Q1–2019Q4 Subsample. Notes: This chart shows average MSE of the threshold-augmented dynamic output growth models estimated for the grid of threshold values (x-axis) for three choices of volatility measures: (solid blue line), (dotted orange line) and (dashed green line).
B.2. Robustness of threshold effects to the choice of sample period (1990Q1–2019Q4 subsample)
We also investigate the robustness of our threshold effects to the choice of time period. To this end we consider the sub-sample 1990Q1–2019Q4 which excludes the 1987 stock market crash whose macroeconomic impact was rather short lived, avoids breaks in error variances due to the so called “Great Moderation”, and better captures the trade and financial market globalization of emerging economies that gathered pace post 1990. The results, in Table B.1 , show that in 16 advanced economies and 5 emerging markets (out of 19 and 14 countries in each income group, respectively), global volatility () (i.e., beyond the threshold ) is associated with lower output growth subsequently. While the estimate of remains unchanged, we are able to detect the presence of threshold effects in a larger number of economies.
Table B.1.
Estimates of Threshold Coefficient , Threshold Parameter , and AR(1) Coefficients in Threshold-augmented AR Specifications, 1990Q1–2019Q4.
| (a) Advanced economies: = 3.33% and = 0.156 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t-ratio | t-ratio | |||||||||||
| Australia | −0.0064† | −2.18 | 0.08 | 0.92 | 3.3% | 0.0058 | ||||||
| Austria | −0.0222‡ | −4.93 | −0.21† | −2.39 | 16.1% | 0.0081 | ||||||
| Belgium | −0.0128‡ | −3.72 | 0.05 | 0.58 | 12.2% | 0.0063 | ||||||
| Canada | −0.0101‡ | −3.88 | 0.48 | 6.37 | 38.9% | 0.0049 | ||||||
| Finland | −0.0225‡ | −3.28 | 0.12 | 1.26 | 11.8% | 0.0125 | ||||||
| France | −0.0086‡ | −3.49 | 0.29 | 3.22 | 25.6% | 0.0042 | ||||||
| Germany | −0.0195‡ | −4.69 | 0.00 | 0.04 | 18.1% | 0.0073 | ||||||
| Italy | −0.0129‡ | −3.65 | 0.15 | 1.54 | 17.9% | 0.0061 | ||||||
| Japan | −0.0133‡ | −2.56 | 0.13 | 1.35 | 9.1% | 0.0092 | ||||||
| Korea | −0.0110∗ | −1.56 | 0.23† | 2.50 | 7.3% | 0.0134 | ||||||
| Netherlands | −0.0136‡ | −5.01 | 0.34 | 4.37 | 37.0% | 0.0049 | ||||||
| Norway | −0.0131† | −2.23 | −0.29 | −3.24 | 8.8% | 0.0114 | ||||||
| New Zealand | −0.0003 | −0.08 | 0.33 | 3.69 | 9.2% | 0.0069 | ||||||
| Singapore | −0.0121 | −1.23 | 0.19† | 2.06 | 5.0% | 0.0182 | ||||||
| Spain | −0.0048‡ | −2.38 | 0.70 | 11.13 | 59.7% | 0.0036 | ||||||
| Sweden | −0.0246‡ | −4.29 | −0.14 | −1.51 | 12.3% | 0.0102 | ||||||
| Switzerland | −0.0134‡ | −3.49 | 0.08 | 0.89 | 11.3% | 0.0071 | ||||||
| United Kingdom | −0.0084‡ | −2.49 | 0.28 | 2.99 | 18.2% | 0.0059 | ||||||
| United States | −0.0118‡ | −4.19 | 0.24 | 2.65 | 26.9% | 0.0049 | ||||||
| MG (equally weighted) | −0.0127‡ | −9.02 | 0.16‡ | 3.01 | ||||||||
| MG (PPP-GDP weighted) | −0.0121‡ | −14.75 | 0.21‡ | 6.66 | ||||||||
| (b) Emerging economies: = 5.83% and = 0.129 | ||||||||||||
| t-ratio | t-ratio | |||||||||||
| Argentina | −0.0089 | −1.25 | 0.43‡ | 5.27 | 19.3% | 0.0183 | ||||||
| Brazil | −0.0091∗ | −1.41 | 0.04 | 0.38 | 0.2% | 0.0165 | ||||||
| Chile | −0.0104† | −1.83 | 0.11 | 1.13 | 3.2% | 0.0142 | ||||||
| China | 0.0033 | 0.73 | 0.18∗ | 1.94 | 1.7% | 0.0117 | ||||||
| India | −0.0056 | −0.90 | −0.22† | −2.39 | 3.2% | 0.0156 | ||||||
| Indonesia | −0.0060 | −1.01 | 0.32‡ | 3.61 | 9.5% | 0.0153 | ||||||
| Malaysia | −0.0112† | −1.87 | 0.22† | 2.38 | 9.0% | 0.0145 | ||||||
| Mexico | −0.0158‡ | −3.01 | 0.16∗ | 1.80 | 10.9% | 0.0129 | ||||||
| Peru | −0.0121∗ | −1.35 | 0.21† | 2.35 | 4.3% | 0.0231 | ||||||
| Philippines | −0.0042 | −1.16 | 0.20† | 2.22 | 4.7% | 0.0091 | ||||||
| South Africa | −0.0027∗ | −1.28 | 0.60‡ | 8.08 | 37.7% | 0.0053 | ||||||
| Saudi Arabia | −0.0027 | −0.69 | 0.63‡ | 9.15 | 40.9% | 0.0101 | ||||||
| Thailand | −0.0325‡ | −3.74 | −0.07 | −0.83 | 9.3% | 0.0220 | ||||||
| Turkey | −0.0275‡ | −2.60 | −0.08 | −0.84 | 4.1% | 0.0268 | ||||||
| MG (equally weighted) | −0.0104‡ | −4.04 | 0.19‡ | 2.99 | ||||||||
| MG (PPP-GDP weighted) | −0.0042 | −1.15 | 0.12 | 1.63 | ||||||||
Notes: Our threshold-augmented dynamic output growth model is given by , where is the first difference of the logarithm of real GDP in country i during quarter t and . is an indicator variable that takes the value of unity if event occurs and zero otherwise. is a measure of global volatility defined by (1), and is the threshold parameter. The estimation sample is 1990Q1 to 2019Q4. Statistical significance is denoted by and ‡, at 10%, 5% and 1% levels, respectively.
Appendix C. Counterfactual analysis using June-January IMF projection revisions
The IMF revised its growth projections down for most countries in June as the extent of the Covid-19 shock and its economic fallout became clearer. In this appendix, we use these updated projections to gauge the size of the GDP shock arising from the Covid-19 pandemic. Let be the June 2020 IMF World Economic Outlook (WEO) GDP growth projections for country i in quarters of 2020, and be the associated January 2020 IMF WEO projections. We compute the June-January projection revisions as
and . Assuming that developments surrounding Covid-19 were the only dominant developments behind the projection revisions, we use , for to infer and repeat the counterfactual analysis in Section 3. The results are reported in Fig. C.1, Fig. C.2, Fig. C.3, Table C.1 . While the new estimates are qualitatively similar to those reported in the main text, they indicate worse growth outcomes and longer recoveries quantitatively.
Table C.1.
Growth Outcomes Following the Covid-19 Shock Using June-January IMF Projection Revisions (percent change).
| Q4 over Q4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2019 | 2020 |
2021 |
|||||||
| Median | pctl | Median | pctl | pctl | Median | pctl | |||
| Advanced Economies | 1.4 | −8.9 | −5.6 | −2.1 | 2.0 | 4.9 | 7.7 | ||
| United States | 2.4 | −13.2 | −7.9 | −2.5 | −0.4 | 3.9 | 7.2 | ||
| Euro Area | 0.8 | −9.8 | −5.9 | −1.4 | 3.5 | 6.8 | 10.4 | ||
| France | 1.0 | −10.6 | −6.3 | −1.5 | 2.2 | 5.0 | 8.2 | ||
| Germany | 0.4 | −11.7 | −5.1 | 2.0 | 2.4 | 4.9 | 7.4 | ||
| Italy | 0.1 | −12.7 | −7.8 | −2.3 | 2.0 | 5.8 | 10.1 | ||
| Japan | −0.5 | −10.8 | −4.0 | 3.0 | 1.3 | 5.0 | 9.0 | ||
| United Kingdom | 1.3 | −11.9 | −7.0 | −1.9 | 0.8 | 4.3 | 6.9 | ||
| Canada | 1.5 | −12.3 | −7.1 | −1.7 | −1.6 | 4.9 | 10.9 | ||
| Emerging Markets (excl. China) | 3.0 | −6.8 | −0.5 | 6.0 | 2.8 | 5.9 | 9.1 | ||
| Emerging Asia (excl. China) | 4.6 | −7.1 | 1.2 | 9.5 | 4.0 | 5.9 | 7.7 | ||
| Latin America | 0.5 | −10.7 | −2.8 | 5.5 | 0.4 | 6.2 | 11.7 | ||
| China | 6.1 | 2.7 | 9.2 | 15.3 | 4.5 | 7.7 | 11.3 | ||
Fig. C.1.
The Impact of Covid-19 on Real GDP Using June-January IMF Projection Revisions (percent deviation from baseline). Notes: The impact is in percent and the horizon is quarterly. This figure plots quantiles of defined by (29).
Fig. C.2.
Dynamics of Real GDP Following the Covid-19 Shock Using June-January IMF Forecast Revisions (in logs; 2019Q4 = 1).
Fig. C.3.
Dynamics of Regions’ Real GDP Following the Covid-19 Shock Using June-January IMF Projection Revisions (in logs; 2019Q4 = 1).
Research data
Data available in data repository at https://data.mendeley.com/datasets/5kp6h6ttx3.
References
- Baqaee, D.R., Farhi, E., 2020. Nonlinear Production Networks with an Application to the Covid-19 Crisis. CEPR Discussion Paper No. DP14742.
- Bonadio, B., Huo, Z., Levchenko, A.A., Pandalai-Nayar, N., 2020. Global Supply Chains in the Pandemic. NBER Working Paper No. 27224. [DOI] [PMC free article] [PubMed]
- Bussière, M., Chudik, A., Sestieri, G., 2012. Modelling Global Trade Flows: Results from a GVAR Model. Globalization and Monetary Policy Institute Working Paper 119, Federal Reserve Bank of Dallas.
- Cashin P., Mohaddes K., Raissi M. In: Understanding and Avoiding the Oil Curse in Resource-Rich Arab Economies. Elbadawi I.A., Selim H., editors. Cambridge University Press; Cambridge: 2016. The Global Impact of the Systemic Economies and MENA Business Cycles; pp. 16–43. [Google Scholar]
- Cashin P., Mohaddes K., Raissi M. Fair Weather or Foul? The Macroeconomic Effects of El Niño. J. Int. Econ. 2017;106:37–54. [Google Scholar]
- Cashin P., Mohaddes K., Raissi M. China’s Slowdown and Global Financial Market Volatility: Is World Growth Losing Out? Emerging Markets Rev. 2017;31:164–175. [Google Scholar]
- Cashin P., Mohaddes K., Raissi M., Raissi M. The Differential Effects of Oil Demand and Supply Shocks on the Global Economy. Energy Econ. 2014;44:113–134. [Google Scholar]
- Cesa-Bianchi A., Pesaran M.H., Rebucci A. Uncertainty and Economic Activity: A Multicountry Perspective. Rev. Financ. Stud. 2020;33(8):3393–3445. [Google Scholar]
- Cesa-Bianchi A., Pesaran M.H., Rebucci A., Xu T. China’s Emergence in the World Economy and Business Cycles in Latin America. Economia, J. LACEA. 2012;12:1–75. [Google Scholar]
- Chudik A., Grossman V., Pesaran M.H. A Multi-country Approach to Forecasting Output Growth Using PMIs. J. Economet. 2016;192(2):349–365. [Google Scholar]
- Chudik, A., Mohaddes, K., Raissi, M., 2021. Covid-19 Fiscal Support and its Effectiveness. Economics Letters 205, 109939/1–5. [DOI] [PMC free article] [PubMed]
- Chudik A., Pesaran M.H. Infinite Dimensional VARs and Factor Models. J. Economet. 2011;163:4–22. [Google Scholar]
- Chudik A., Pesaran M.H. Theory and Practice of GVAR Modeling. J. Econ. Surv. 2016;30(1):165–197. [Google Scholar]
- Chudik, A., Pesaran, M.H., Mohaddes, K., 2020. Identifying Global and National Output and Fiscal Policy Shocks Using a GVAR. Adv. Economet. 41, 143–189. Essays in Honor of Cheng Hsiao.
- Céspedes, L.F., Chang, R., Velasco, A., 2020. The Macroeconomics of a Pandemic: A Minimalist Model. NBER Working Paper No. 27228.
- Dees S., di Mauro F., Pesaran M.H., Smith L.V. Exploring the International Linkages of the Euro Area: A Global VAR Analysis. J. Appl. Economet. 2007;22:1–38. [Google Scholar]
- di Mauro, F., Pesaran, M.H. (Eds.). 2013. The GVAR Handbook: Structure and Applications of a Macro Model of the Global Economy for Policy Analysis. Oxford University Press. ISBN-10: 0199670080.
- Gaspar V., Gopinath G. Fiscal Policies for a Transformed World. IMFBlog. 2020 [Google Scholar]
- Hansen B. Threshold Autoregressions in Economics. Stat. Interface. 2011;4:123–127. [Google Scholar]
- Jordà, s., K. Knoll, D. Kuvshinov, M. Schularick, and A.M. Taylor (2019, 04). The Rate of Return on Everything, 1870–2015. The Quarterly Journal of Economics 134(3), 1225–1298.
- Koop G., Pesaran M., Potter S.M. Impulse Response Analysis in Nonlinear Multivariate Models. J. Economet. 1996;74(1):119–147. [Google Scholar]
- Ludvigson, S.C., Ma, S., Ng, S., 2020. COVID-19 and the Macroeconomic Effects of Costly Disasters. NBER Working Paper No. 26987.
- McKibbin, W.J., Fernando, R., 2020. The Global Macroeconomic Impacts of COVID-19: Seven Scenarios. CAMA Working Paper 19/2020.
- Milani F. COVID-19 Outbreak, Social Response, and Early Economic Effects: A Global VAR Analysis of Cross-Country Interdependencies. J. Populat. Econ. 2020 doi: 10.1007/s00148-020-00792-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohaddes K., Pesaran M.H. Country-Specific Oil Supply Shocks and the Global Economy: A Counterfactual Analysis. Energy Econ. 2016;59:382–399. [Google Scholar]
- Mohaddes K., Pesaran M.H. Oil Prices and the Global Economy: Is it Different this Time Around? Energy Econ. 2017;65:315–325. [Google Scholar]
- Mohaddes K., Raissi M. The U.S. Oil Supply Revolution and the Global Economy. Empirical Econ. 2019;57:1515–1546. [Google Scholar]
- Mohaddes, K., Raissi, M., 2020. Compilation, Revision and Updating of the Global VAR (GVAR) Database, 1979Q2-2019Q4. University of Cambridge: Judge Business School (mimeo).
- Pesaran M.H. Oxford University Press; Oxford: 2015. Time Series and Panel Data Econometrics. ISBN-10: 0198736916. [Google Scholar]
- Pesaran M.H., Schuermann T., Smith L.V. Forecasting Economic and Financial Variables with Global VARs. Int. J. Forecast. 2009;25(4):642–675. [Google Scholar]
- Pesaran M.H., Schuermann T., Weiner S. Modelling Regional Interdependencies using a Global Error-Correcting Macroeconometric Model. J. Bus. Econ. Stat. 2004;22:129–162. [Google Scholar]
- Tong H. Oxford University Press; Oxford: 1990. Non-linear Time Series: a Dynamical System Approach. Oxford Statistical Science Series. ISBN-10: 0198523009. [Google Scholar]
- Tsay R.S. Testing and Modeling Multivariate Threshold Models. J. Am. Stat. Assoc. 1998;93(443):1188–1202. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data available in data repository at https://data.mendeley.com/datasets/5kp6h6ttx3.