Accurate assembly of minority viral haplotypes from next-generation sequencing through efficient noise reduction

Abstract

Rapidly evolving RNA viruses continuously produce minority haplotypes that can become dominant if they are drug-resistant or can better evade the immune system. Therefore, early detection and identification of minority viral haplotypes may help to promptly adjust the patient’s treatment plan preventing potential disease complications. Minority haplotypes can be identified using next-generation sequencing, but sequencing noise hinders accurate identification. The elimination of sequencing noise is a non-trivial task that still remains open. Here we propose CliqueSNV based on extracting pairs of statistically linked mutations from noisy reads. This effectively reduces sequencing noise and enables identifying minority haplotypes with the frequency below the sequencing error rate. We comparatively assess the performance of CliqueSNV using an in vitro mixture of nine haplotypes that were derived from the mutation profile of an existing HIV patient. We show that CliqueSNV can accurately assemble viral haplotypes with frequencies as low as 0.1% and maintains consistent performance across short and long bases sequencing platforms.

INTRODUCTION

Rapidly evolving RNA viruses, such as human immunodeficiency virus (HIV), hepatitis C virus (HCV), influenza A virus (IAV), SARS and SARS-CoV-2 form populations of closely related genomic variants inside infected hosts (1–10). The intra-host viral populations include minority viral variants that are frequently responsible for drug resistance, immune escape and disease transmission (11–24). Therefore, accurately predicting minority viral populations from extremely large and noisy viral genomic data is important for biomedical research, epidemiology and clinical applications. Although this problem has recently attracted significant interest from the biomedical research community (25–27), numerous obstacles still delay next-generation sequencing (NGS) integration into the viral studies. The last decade witnessed numerous attempts to employ NGS and bioinformatics methods for reconstructing intra-host viral populations. These methods are not accurate enough for clinical and epidemiological applications since they cannot reliably identify haplotypes accounting for a substantial portion of the population. Existing methods are ill-equipped to assemble closely related haplotypes and have elevated false-positive rates. Additionally, there is only one in vitro viral sequencing benchmark for validation of haplotyping tools (27), and to convincingly demonstrate that such tools are ready for clinical and epidemiological applications, new comprehensive sequencing benchmarks are urgently required (28).

NGS technologies now provide versatile opportunities to study viral populations. In particular, the popular Illumina MiSeq/HiSeq platforms produce 25–320 million reads, which allow multiple coverage of highly variable viral genomic regions. This high coverage is essential for capturing rare variants. Ability of NGS technologies to efficiently identify minority variants have recently gained U.S. Food & Drug Administration (FDA) approval. However, haplotyping of heterogeneous viral populations (i.e. assembly of full-length genomic variants and estimation of their frequencies) is extremely complicated due to the vast number of sequencing reads, the need to assemble an unknown number of closely related viral sequences and to identify and preserve low-frequency variants. Single-molecule sequencing technologies, such as PacBio, provide an alternative to short-read sequencing by allowing full-length viral variants to be sequenced in a single pass. However, the high level of sequence noise due to background or platform-specific sequencing errors produced by all currently available platforms makes inference of low-frequency genetically close variants especially challenging, since it is required to distinguish between real and artificial genetic heterogeneity produced by sequencing errors.

Recently, a number of computational tools for inference of viral quasispecies populations from NGS reads have been proposed (28), including Savage (26), PredictHaplo (29), aBayesQR (30), QuasiRecomb (31), HaploClique (32), VGA (33), VirA (34,35), SHORAH (36), ViSpA (37), QURE (38) and others (39–43). Even though these algorithms proved useful in many applications, accurate and scalable viral haplotyping remains a challenge. In particular, inference of low-frequency viral variants is still problematic, while many computational tools designed for the previous generation of sequencing platforms have severe scalability problems when applied to datasets produced by state-of-the-art technologies.

Previously, several tools, such as V-phaser (44), V-phaser2 (45) and CoVaMa (46) exploited linkage of mutations for single nucleotide variant (SNV) calling rather than haplotype assembly, but they do not accommodate sequencing errors when deciding whether two variants are linked. These tools are also unable to detect the frequency of mutations above sequencing error rates (47). The 2SNV algorithm (48) accommodates errors in links and was the first such tool to be able to correctly detect haplotypes with a frequency below the sequencing error rate.

We propose a novel method that can accurately identify minority haplotypes from NGS reads consisting of three steps. First, we extract pairs of statistically linked mutations. Second, we find maximal sets of pairwise linked mutations (cliques) where each clique corresponds to a set of mutations in a minority haplotype. Finally, we assign each read to the closest clique, and for each clique, we form a haplotype as a consensus of reads assigned to it.

All haplotyping tools require solid and convincing validation benchmarks (49,50). The true viral variants and their distribution are only known for simulated data (51), but sequencing errors, variation of coverage depth, polymerase chain reaction bias and systematic noise are difficult to simulate [see e.g. (52)]. Therefore experimental sequencing benchmarks that provide an adequate evaluation of haplotyping tools are necessary.

By now, there are only two experimental sequencing benchmarks—(i) Illumina sequencing reads consisting of a mixture of five HIV-1 strains (HIV5exp, see Table 1) (27) and (ii) PacBio sequencing reads from a sample consisting of ten IAV viral variants (IAV10exp, see Table 1) (48). In the HIV5exp, five different HIV-1 strains each having 20% frequency were prepared to mimic an intra-host viral population. Unfortunately, this benchmark is not realistic enough since the observed intra-host viral populations consist of variants that are much closer to each other than different strains and contain both frequent and rare variants (53). The IAV10exp benchmark significantly better mimics the intra-host viral population since its variants are very similar to each other and the variant frequencies are realistically non-uniform. Thus, similar to the IAV10exp benchmark, it would be beneficial to develop Illumina benchmarks which adequately imitate intra-host viral populations containing closely related minority variants.

Table 1.

Four experimental and two simulated sequencing datasets of human immunodeficiency virus type 1 (HIV-1) and IAV

Name	Type	Virus	#haplotypes	Haplotype frequencies	Hamming distance
HIV9exp	experimental	HIV-1	9	0.2-50%	0.22-2.1%
HIV2exp	experimental	HIV-1	2	50-50%	1.2%
HIV5exp	experimental	HIV-1	5	20-20%	2-3.5%
IAV10exp	experimental	IAV	10	0.1-50%	0.1-1.1%
HIV7sim	simulated	HIV-1	7	14.3-14.3%	0.6-3%
IAV10sim	simulated	IAV	10	0.1-50%	0.1-1.1%

The datasets contain MiSeq and PacBio reads from intra-host viral populations consisting of two to ten variants each with frequencies in the range of 0.1–50%, and Hamming distances between variants in the range of 0.1–3.5%.

To validate our method’s performance, we have introduced two novel in vitro sequencing HIV-1 benchmarks, which consist of Illumina MiSeq experiments on haplotype mixtures based on the mutation profile from an existing patient.

Finally, there is an essential gap in existing quality measures of intra-host viral population assembly. Up-to-date, instead of populations (i.e. haplotypes with their frequencies), only sets of reconstructed and the ground truth haplotypes are compared (29). Here we propose to measure differences between haplotype populations using Matching Error and the Earth mover’s distance (EMD) which account for both the distances between haplotypes and their frequencies.

MATERIALS AND METHODS

CliqueSNV algorithm idea

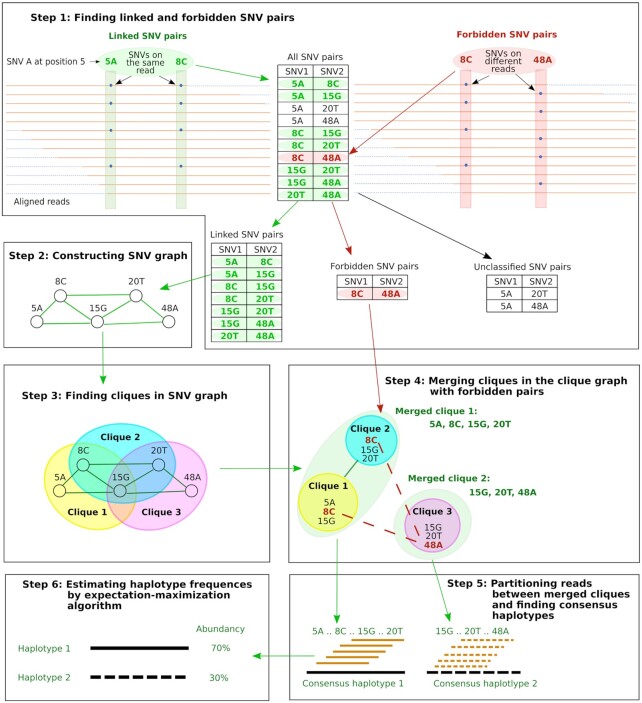
A schematic diagram of the CliqueSNV algorithm is shown in Figure 1. The algorithm takes aligned reads as input and infers haplotype sequences with their frequencies as output. The method consists of six steps:

Figure 1.

Schematic representation of the CliqueSNV algorithm. Here, SNV is a single nucleotide variation.

1. Step 1 uses aligned reads to build the consensus sequence and identifies all SNVs. Then all pairs of SNVs are divided into three groups: linked, forbidden and unclassified. Each SNV is represented as a pair (p, n) of its position p and nucleotide value n in the aligned reads. If there are enough reads that have two SNVs (p, n) and (p′, n′) simultaneously, then we estimate probability that there are no haplotypes simultaneously containing both SNVs (see CliqueSNV algorithm details). If this probability is low, then the algorithm classifies these two SNVs as linked. Otherwise, we estimate probability that there is a sufficiently frequent haplotype simultaneously containing both SNVs (see CliqueSNV algorithm details). If this probability is low, then the algorithm classifies these two SNVs as a forbidden pair. If the both estimated probabilities are not small, then the pair of SNVs remains unclassified.

2. In Step 2, we build a graph G = (V, E) with a set of nodes V representing SNVs, and a set of edges E connecting linked SNV pairs.

3. Ideally, SNVs of each true minority haplotype form a clique in G. A maximal clique C⊆V is a set of nodes such that (u, ) ∈ E for any u, 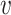∈ C and for any x∉C there is u ∈ C such that (x, u)∉E. Step 3 finds all maximal cliques in G.

4. For real sequencing data, the linkage between some SNV pairs may be undetected due to sequencing noise, uneven coverage, or the shortness of the NGS reads. As a result, a single clique corresponding to a haplotype will be split into several overlapping cliques. Step 4 merges such overlapping cliques. In order to avoid merging distinct haplotypes, two cliques are not merged if they contain a forbidden SNV pair.

5. Step 5 assigns each read to a merged clique with which it shares the largest number of SNVs. Then CliqueSNV builds a consensus haplotype from all reads assigned to a single merged clique.

6. Finally, haplotype frequencies are estimated via an expectation-maximization (EM) algorithm in Step 6.

Similarly to Predicthaplo, CliqueSNV splits the global problem into a sequel of several reconstruction tasks of increasing genome length. We start with a local reconstruction with the read-fragment long region of maximum coverage. Then the SNV graph G is enriched with links between SNVs from the same reconstructed haplotype in the processed region. We progressively increase the region currently analysed by the read-fragment length until it covers the entire haplotypes’ length.

Intra-host viral population sequencing benchmarks

We tested the ability of CliqueSNV to assemble haplotype sequences and estimate their frequencies from PacBio and MiSeq reads using four real (experimental) and two simulated datasets from HIV and IAV samples (Table 1). Each dataset contains between two to ten haplotypes with frequencies of 0.1 to 50%. The Hamming distances between pairs of variants for each dataset are shown in Supplementary Figure S1.

Experimental datasets

1. HIV-1 subtype B plasmid mixtures and MiSeq reads (HIV2exp and HIV9exp). We designed nine in silico plasmid constructs comprising a 950-bp region of the HIV-1 subtype B polymerase (pol) gene that were then synthesized and cloned into pUCIDT-Amp (Integrated DNA Technologies, Skokie, IL, USA). Each clone was confirmed by Sanger sequencing. This 950-bp region at the beginning of pol contains known protease and reverse transcriptase genes that are monitored for drug-resistant mutations and is monitored with sequence analysis for patient care. Each of these plasmids contains a specific set of point mutations chosen using mutation profiles of patient p7 from a real clinical study (53) to create nine unique synthetic HIV-1 pol haplotypes. Different proportions of these plasmids were mixed and then sequenced using an Illumina MiSeq protocol to obtain 2×300-bp reads (see Supplementary Methods). HIV2exp and HIV9exp are mixtures of two and nine variants, respectively.

2. HIV-1 subtype B mixture and MiSeq reads (HIV5exp and HIV5full). This dataset consists of Illumina MiSeq 2×250-bp reads with an average read coverage of ∼20 000× obtained from a mixture of five HIV-1 isolates: 89.6, HXB2, JRCSF, NL43 and YU2 available at (27). Isolates have pairwise Hamming distances in the range from 2 to 3.5% (27 to 46-bp differences). The original HIV-1 sequence length was 9.3 kb and the benchmark consisting of all reads forms the HIV5full benchmark. The biologically relevant beginning of pol with a length of 1.3 kb forms the HIV5exp benchmark.

3. Influenza A mixture and PacBio reads (IAV10exp). This benchmark contains ten IAV virus clones that were mixed at a frequency of 0.1–50%. The Hamming distances between clones ranged from 0.1 to 1.1% (2–22–bp differences) (48). The 2 kb-amplicon was sequenced using the PacBio platform yielding a total of 33 558 reads with an average length of 1973 nucleotides.

Simulated datasets

1. HIV-1 subtype B mixture and MiSeq reads (HIV7sim). This benchmark contains simulated Illumina MiSeq reads with a 10k-coverage of 1-kb pol sequences. The reads were simulated from seven equally distributed HIV-1 variants chosen from the NCBI database: AY835778, AY835770, AY835771, AY835777, AY835763, AY835762, and AY835757. The Hamming distances between clones are in the range from 0.6-3.0% (6 to 30-bp differences). We used SimSeq (54) for generating reads.

2. Influenza A mixture and MiSeq reads (IAV10sim). This benchmark contains simulated IAV Illumina MiSeq reads with the same IAV haplotypes and their frequencies as for the IAV10exp benchmark. The sequencing of a 2kb-amplicon with 40k coverage with paired Illumina MiSeq reads was simulated by SimSeq (54) with the default sequencing error profile in SimSeq.

3. 10-strain HCV mixture C (HCV10sim). This is a mixture of 10 strains of HCV, Subtype 1a, with a total sequencing depth of 20000× (i.e. 400000 reads) (55). The haplotypes were obtained from true HCV genomes in the NCBI nucleotide database and have a pairwise divergence varying from 6% to 9%. Paired-end reads were simulated at relative frequencies between 5% and 13% per haplotype, i.e. a sequencing depth varies from 1000× to 4600× per haplotype.

4. 3- and 15-strain ZIKV mixture (ZIKV3sim and ZIKV15sim). ZIKV3sim consists of three master strains extracted from the NCBI nucleotide database. ZIKV15sim consists of the same three master strains and four mutants for each master strain (55). The pairwise divergence varies between 1% and 12% and the reads were simulated at relative frequencies varying from 2% to 13.3%. The total sequencing depth for this dataset is again 20000×.

Validation metrics for viral population inference

Precision and recall

Inference quality is typically measured by precision and recall.

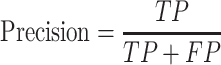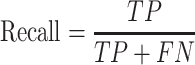where TP is the number of true predicted haplotypes, FP is the number of false predicted haplotypes and FN is the number of undiscovered haplotypes.

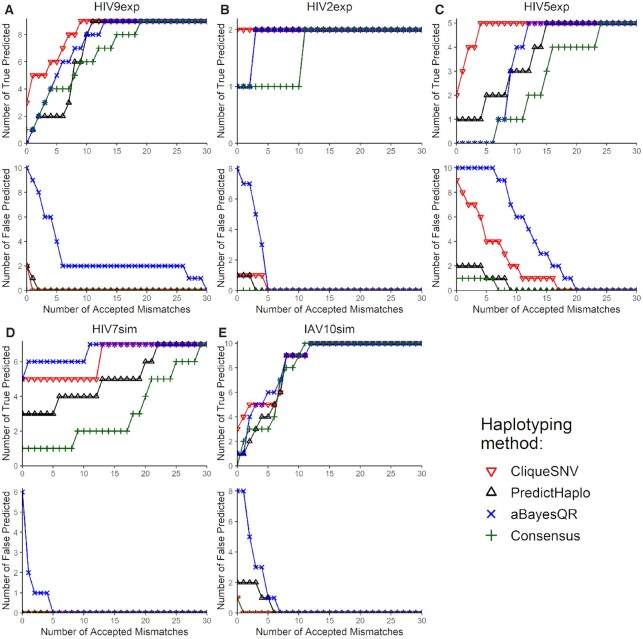
It is also important to count precision and recall when a certain number of mismatches are allowed. Following (29) we introduced an acceptance threshold, which is the number of mismatches permitted for a predicted haplotype to count as a TP. We report the numbers TP and FP for acceptance allowing from 0 to 30 mismatches (see Figure 2).

Figure 2.

The number of true and false predicted haplotypes depending on the number of accepted mismatches for five benchmarks: (A) HIV9exp; (B) HIV2exp; (C) HIV5exp; (D) HIV7sim; (E) IAV10sim. Two haplotypes are regarded identical if the Hamming distance between them is at most the number of accepted mismatches.

Matching errors between populations

However, precision and recall do not take into account (i) distances between true and inferred viral variants as well as (ii) the frequencies of the true and inferred viral variants. Instead, we chose to use analogues of precision and recall defined for populations as follows.

Let T = {(t, f_t)}, be the true haplotype population, where f_t is the frequency of the true haplotype t, ∑_{t ∈ T}f_t = 1. Similarly, let P = {(p, f_p)}, be the reconstructed haplotype population, where f_p is the frequency of the reconstructed haplotype p, ∑_{p ∈ P}f_p = 1. Let d_pt be the distance between haplotypes p and t. Thus, instead of precision, we used the matching errorE_{T → P} which measures how well each reconstructed haplotype p ∈ P weighted by its frequency is matched by the closest true haplotype.

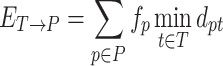Indeed, precision increases while E_{T → P} decreases and reaches 100% when E_{T → P} = 0. Similarly, instead of recall, we propose to use the matching errorE_{T ← P} which measures how well each true haplotype t ∈ T weighted by its frequency is matched by the closest reconstructed haplotype (56).

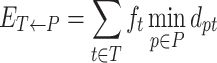Note that recall increases while E_{T ← P} decreases and reaches 100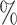 when E_{T ← P} = 0.

Earth mover’s distance (EMD) between populations

The matching errors described above match haplotypes of true and reconstructed populations but do not match their frequencies. In order to simultaneously match haplotype sequences and their frequencies, we allowed for a fractional matching when portions of a single haplotype p of population P are matched to portions of possibly several haplotypes of T and vice versa. Thus, we separated f_p into f_pt’s each denoting portion of p matched to t such that f_p = ∑_{t ∈ T}f_pt, f_pt ≥ 0. Symmetrically, f_t’s are also separated into f_pt’s, i.e, ∑_{p ∈ P}f_pt = f_t. Finally, we chose f_pt’s minimizing the total error of matching T to P which is also known as Wasserstein metric or the EMD between T and P (57,58).

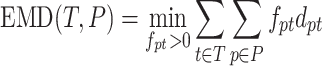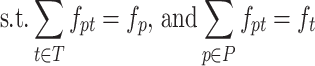EMD is efficiently computed as an instance of the transportation problem using network flows.

EMDs can vary a lot over different benchmarks since they may have different complexities, which depends on the number of true variants, the frequency distribution, the similarity between haplotypes, sequencing depth, sequencing error rate, and many other parameters. Hence, we measured the complexity of a benchmark as the EMD between the true population and a population consisting of a single consensus haplotype (59).

CliqueSNV algorithm details

Data input for CliqueSNV consists of PacBio or Illumina reads from an intra-host viral population aligned to a reference genome. A deletion is treated as a special nucleotide, i.e. it is just one of five possible alleles. Insertions are identified after alignment and should be used to extend the reference. Output is the set of inferred viral variant RNA sequences with their frequencies. The formal high-level pseudocode of the CliqueSNV algorithm is described in the supplementary materials. Below we describe in detail the six major steps of CliqueSNV that are schematically presented in Figure 1.

Step 1: Finding linked and forbidden SNV pairs. At a given genomic position I, the most frequent nucleotide is referred to as a major variant and is denoted 1. Let us fix one of the less frequent nucleotide (referred to as a minor variant) and denote it 2. A pair of variants at two distinct genomic positions I and J is referred to as a 2-haplotype. Let O₂₂ be the observed count of the 2-haplotype (22) in the reads covering positions I and J. In this step, CliqueSNV tries to decide whether the observed O₂₂ reads are sequencing errors or they are produced by an existing haplotype containing the 2-haplotype (22).

The pairs of minor variants (referred to as SNV pairs) are classified into three categories: linked, forbidden, and unclassified. An SNV pair is linked if it is extremely unlikely that there is no sufficiently frequent haplotype containing both minor variants is very low. On the other side, an SNV pair is forbidden if it is extremely unlikely that the corresponding minor variants belong to the same haplotype of sufficient frequency. All other SNV pairs are referred to as unclassified.

Below we estimate the probability of observing at least x ≥ O₂₂ reads given that the true frequency T₂₂ of the 2-haplotype (22) is at most t (by default t = 0.001). This probability should be low enough so that false positive linked pairs would be virtually impossible, i.e. we require that the expected number of false positive linked pairs be <0.05. Therefore, this probability should be less than 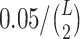, where L is the haplotype length.

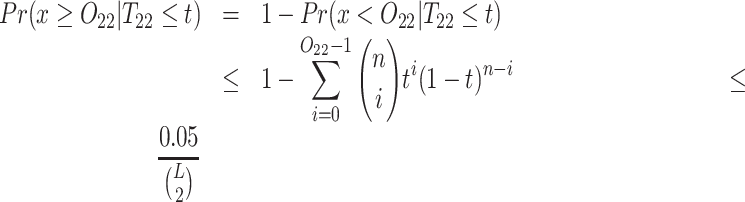(1)

Pairs of SNVs passing this linkage test (1) are classified as a linked SNV pairs.

For every other pair of SNVs, we check whether they can be classified as a forbidden SNV pair, i.e. whether the probability of observing at most x ≤ O₂₂ reads is low enough (<0.05) given that the 2-haplotype (22) has frequency T₂₂ ≥ t (by default t = 0.001). Similarly, we require that the expected number of false positive forbidden pairs be <0.05.

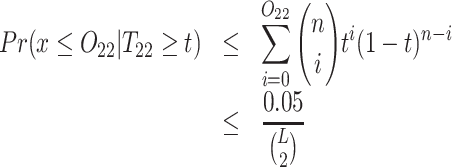(2)

Pairs of SNVs passing this linkage test (2) are classified as a forbidden SNV pairs.

Step 2: Constructing the SNV graph. The SNV graph G = (V, E) consists of vertices corresponding to minor variants and edges corresponding to linked pairs of minor variants from different positions. If the intra-host population consists of very similar haplotypes, then the number of true SNVs corresponding to non-isolated vertices in the graph G is very small which makes the number of edges very small as well. Indeed, the PacBio dataset for IAV encompassing 2500 positions is split into 10 000 vertices, while the SNV graph contains only 700 edges, and, similarly, the simulated Illumina read dataset for the same haplotypes contains only 368 edges.

Note that the isolated minor variants correspond to genotyping errors unless they have a significant frequency. This fact allows us to estimate the number of errors per read, assuming that all isolated SNVs are errors. As expected, the distribution of the PacBio reads has a heavy tail (see Supplementary Figure S4), which implies that most reads are (almost) error free, while a small number of heavy-tail reads accumulate most of the errors. The heavy-tail reads are difficult to correct, and they are uniformly distributed across haplotypes. Therefore, their removal drastically reduces number of errors but does not affect frequency of rare haplotypes. Our analysis allows the identification of such reads, which can then be filtered out. By default, we filter out 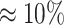of PacBio reads, but we do not filter out any Illumina reads. The SNV graph is then constructed for the reduced set of reads. Such filtering allows the reduction of systematic errors and refines the SNV graph significantly.

Step 3: Finding cliques in the SNV graph G. Although the MAX CLIQUE is a well-known NP-complete problem and there may be an exponential number of maximal cliques in G, a standard Bron–Kerbosch algorithm requires little computational time since G is very sparse (60).

Step 4: Merging cliques in the clique graph C_G. The clique graph C_G = (C, F, L) consists of vertices corresponding to cliques in the SNV graph G and two sets of edges F and L. A forbidding edge (p, q) ∈ F connects two cliques p and q with at least one forbidden pair of minor variants from p and q respectively. A linking edge (p, q) ∈ L connects two cliques p and q, (p, q)∉F, with at least one linked pair of minor variants from p and q, respectively. Any true haplotype corresponds to a maximal (L∖F)-connected subgraph H of C_G which is connected with edges from L and does not contain any edge from F [see Figure 1 (4)].

Unfortunately, even deciding whether there is a L-path between p and q avoiding forbidding edges is known to be NP-hard (61). We find all subgraphs H as follows (see Supplementary Figure S5): (i) connect all pairs of vertices except connected with forbidding edges, (ii) find all maximal super-cliques in the resulted graph 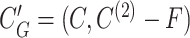using (60), (iii) split each super-clique into L-connected components and (iv) output maximal L-connected components.

Step 5: Partitioning reads between merged cliques and finding consensus haplotypes. Let S be the set of all positions containing at least one minor variant in V. Let q_S be an major clique corresponding to a haplotype with all major variants in S. The distance between a read r and a clique q equals the number of variants in q that are different from the corresponding nucleotides in r. Each read r is assigned to the closest clique q (which can possibly be q_S). In case of a tie, the read r contributes only 1/n frequency to consensus, where n is the number of closest cliques. Usually, the number of closest cliques is 1, although in a case of of IAV, when most cliques share the same position, a significant portion of reads is assigned to multiple cliques (see Supplementary materials S6–8).

Finally, for each clique q, CliqueSNV finds the consensus (q) of all reads assigned to q. Then 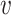(q) is extended from S to a full-length haplotype by setting all non-S positions to major SNVs.

Step 6: Estimating haplotype frequencies by using the EM algorithm. CliqueSNV estimates the frequencies of the assembled intra-host haplotypes via an EM algorithm similar to the one used in IsoEM (62). Let K be the number of assembled viral variants, and let α be the probability of sequencing error. EM algorithm works as follows:

1. Initialize frequencies of viral variants ,

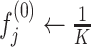   Compute the probability of l_i-long read r_i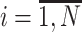, being emitted by viral variant ,

   ,

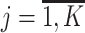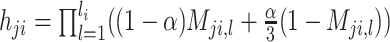   where M_{ji, l} - indicator if i-th read coincides with j-th viral variant in the position l

2. (Expectation) Update the amount of read r_i emitted by the jth viral variant

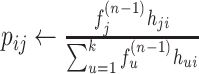
3. (Maximization) Update the frequency of the jth viral variant

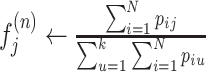
4. if 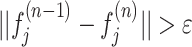, then n ← n + 1 and go to step 2

5. Output estimated frequencies

RESULTS

Performance of haplotyping methods

We compared CliqueSNV to the 2SNV, PredictHaplo and aBayesQR haplotyping methods. Since CliqueSNV, PredictHaplo and aBayesQR use Illumina reads, we compared them using the HIV9exp, HIV2exp, HIV5exp, HIV7sim and IAV10sim datasets. Since CliqueSNV, 2SNV and PredictHaplo can also use PacBio reads, we compared them using the IAV10exp dataset. We also used consensus sequences in the comparisons (59) because of its simplicity and to evaluate sequences most similar to those generated by the Sanger sequencing method (63). Finally, we validated scalability of CliqueSNV, PredictHaplo and aBayesQR with respect to the length of the genomic region using benchmarks from Table 2.

Table 2.

Full-length viral genome datasets

Name	Type	Virus	#haplotypes	Haplotype frequencies	Hamming distance	Region length
HCV10sim	simulated	HCV	10	5–13%	6–9%	8992
ZIKV3sim	simulated	ZIKV	3	16–60%	3–10%	9929
ZIKV15sim	simulated	ZIKV	15	2–13%	1–12%	9929
HIV5full	experimental	HIV-1	5	20–20%	1–6%	9275

Three simulated sequencing datasets HCV10sim, ZIKV3sim, ZIKV15sim and one experimental sequencing dataset HIV5full.

The precision and recall of haplotype discovery for each method is provided in Table 3. CliqueSNV had the best precision and recall for five of the six datasets. For the HIV5exp dataset, PredictHaplo was more conservative and predicted less false positive variants (better precision) than CliqueSNV.

Table 3.

Prediction statistics of haplotype reconstruction methods using experimental and simulated (a) MiSeq and (b) PacBio datasets

(a)
	CliqueSNV		aBayesQR		PredictHaplo
Benchmark	Precision	Recall	Precision	Recall	Precision	Recall
HIV9exp	0.60	0.33	0.00	0.00	0.00	0.00
HIV2exp	0.66	1.00	0.11	0.50	0.50	0.50
HIV5exp	0.18	0.40	0.00	0.00	0.33	0.20
HIV7sim	1.00	0.71	1.00	0.42	0.45	0.71
IAV10sim	0.75	0.30	0.11	0.10	0.33	0.10
(b)
	CliqueSNV		2SNV		PredictHaplo
Benchmark	Precision	Recall	Precision	Recall	Precision	Recall
IAV10exp	1.00	1.00	0.82	0.90	0.70	0.70

The precision and recall was evaluated stringently such that if a predicted haplotype has at least one mismatch to its closest answer, then that haplotype is scored as a false positive.

Following study (29), we also showed how precision and recall grew with the reduction of restriction on mismatches (Figure 2). The number of true predicted haplotypes for CliqueSNV was always greater than that of the other methods on real experimental sequencing benchmarks indicating that CliqueSNV more accurately identified the true haplotypes. The number of falsely predicted haplotypes for CliqueSNV was always lower than those for aBayesQR, but similar to those predicted by PredictHaplo on four out of five datasets indicating that both CliqueSNV and PredictHaplo had the best precision with MiSeq datasets.

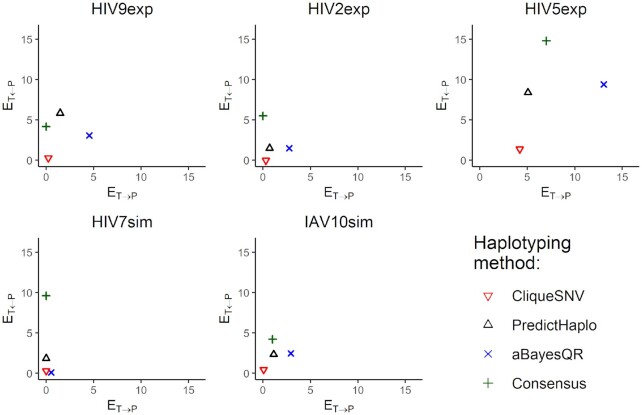
Matching distance analysis showed that matching distances E_{T ← P} and E_{T → P} are better for CliqueSNV than for both PredictHaplo and aBayesQR on four out of five MiSeq datasets (Figure 3). For HIV7sim, E_{T ← P} for aBayesQR was slightly better than for CliqueSNV. Using HIV9exp, HIV2exp, HIV7sim and IAV10sim datasets, the E_{T ← P} and E_{T → P} for CliqueSNV were very close to zero indicating that the predictions were almost perfect. Since E_{T ← P} and E_{T → P} correlate with precision and recall, matching distance analysis indicates that CliqueSNV had a better precision, and significantly outperformed both PredictHaplo and aBayesQR. Since aBayesQR had a higher E_{T → P} on MiSeq datasets, it is more likely to make more false predictions. Notably, on the HIV7sim dataset, aBayesQR outperformed both CliqueSNV and PredictHaplo by E_{T ← P}.

Figure 3.

Matching distances E_{T ← P} and E_{T → P} between the true haplotype population T and the reconstructed haplotype population P for five benchmarks.

The EMD between the predicted and true haplotype populations for all five MiSeq datasets are shown in Figure 4. The exact EMD values are provided in Table 4. CliqueSNV provided the lowest (the best) EMD across all tools on four out of five MiSeq benchmarks. For the simulated and PacBio datasets, CliqueSNV had almost a zero EMD indicating a low error in predictions. PredictHaplo had a lower EMD than aBayesQR on four out of five MiSeq datasets. aBayesQR has almost a zero EMD with the HIV7sim dataset and outperformed CliqueSNV, while using the HIV5exp dataset, aBayesQR performed poorer than other methods.

Figure 4.

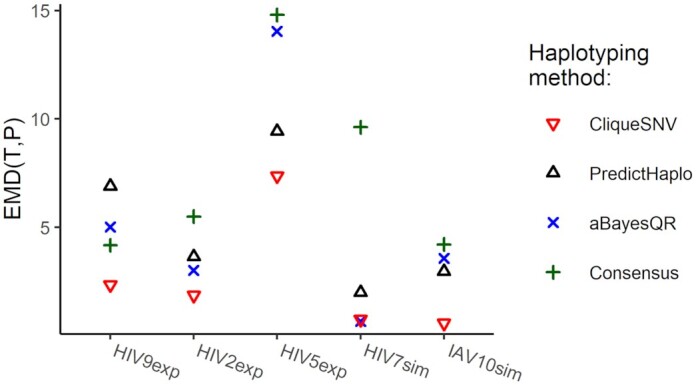
EMD between true and reconstructed haplotype populations for five benchmarks.

Table 4.

EMD from predicted haplotypes to the true haplotype population and haplotyping method improvement

(a)
	Consensus	CliqueSNV		aBayesQR		PredictHaplo
Benchmark	EMD	EMD	Impr.	EMD	Impr.	EMD	Impr.
HIV9exp	4.18	2.35	1.78	5.02	0.83	6.90	0.61
HIV2exp	5.50	1.87	2.94	3.02	1.82	3.65	1.51
HIV5exp	14.80	7.37	2.01	14.05	1.05	9.43	1.57
HIV7sim	9.63	0.76	12.72	0.67	14.4	2.00	4.80
IAV10sim	4.22	0.59	7.2	3.57	1.18	2.97	1.42
(b)
	Consensus	CliqueSNV		2SNV		PredictHaplo
Benchmark	EMD	EMD	Impr.	EMD	Impr.	EMD	Impr.
IAV10exp	4.22	0.22	19.18	0.23	18.35	0.38	11.12

Four haplotyping methods(aBayesQR, CliqueSNV, Consensus, PredictHaplo) are benchmarked using five MiSeq (A) and one PacBio datasets (B). The column Impr. (improvement) shows how much better is prediction of haplotyping method over inferred consensus, and it is calculated as , 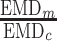where EMDc is an EMD for consensus, and EMDm is an EMD for method.

Next, CliqueSNV, 2SNV and PredictHaplo were compared using the IAV10exp benchmark dataset (see Supplementary Table S1). CliqueSNV correctly recovered all ten true variants, including the haplotype with frequencies significantly below the sequencing error rate. 2SNV recovered nine true variants but found one false positive. PredictHaplo recovered only seven true variants and falsely predicted three variants. To further explore the precision of these three methods with the IAV10exp data, we simulated low-coverage datasets by randomly subsampling n = 16K, 8K, 4K reads from the original data. For each dataset, CliqueSNV found at least one true variant more than both 2SNV and PredictHaplo.

Finally, Table 5 reports the performance of three methods on full-length genomes. We normalize EMD over the genomic length so that the resulted EMD are in the same range and can be compared for different genomic regions. On average, CliqueSNV for all lower bounds on frequency (2, 5 and 10%) outperforms PredictHaplo, but for two out of four full-length benchmarks PredictHaplo is more accurate than CliqueSNV.

Table 5.

EMD from predicted haplotypes to the true haplotype population for 1K-, 2K-, 5K-long and full-length genomic regions for HIV, HCV and ZIKV benchmarks

			CliqueSNV
Benchmark	Length	Consensus	2%	5%	10%	PredictHaplo	aBayesQR
HCV10sim	1K	1.109	0.080	0.037	0.143	1.479	did not finish
	2K	3.397	0.714	0.854	1.923	0.981	did not finish
	5K	3.719	3.729	3.729	1.431	0.450	did not finish
	full-length	3.335	3.335	3.335	1.217	0.140	did not finish
ZIKV3sim	1K	2.408	0.015	0.015	0.015	0.100	0.086
	2K	2.388	0.020	0.020	0.020	0.092	did not finish
	5K	2.182	0.010	0.010	0.010	0.031	did not finish
	full-length	2.168	0.007	0.007	0.007	0.016	did not finish
ZIKV15sim	1K	3.368	1.123	1.335	1.840	3.640	1.345
	2K	3.571	1.469	1.339	3.128	7.037	1.807
	5K	3.506	1.379	1.778	1.698	6.701	did not finish
	full-length	3.803	1.254	1.643	2.801	6.014	did not finish
HIV5full	1K	1.480	0.696	0.350	0.590	0.943	1.405
	2K	3.460	2.081	2.100	2.626	2.825	3.100
	5K	2.384	2.219	1.500	1.997	2.267	did not finish
	full-length	3.189	2.968	2.557	2.273	1.811	did not finish
Average over all benchmarks		2.957	1.401	1.371	1.438	2.203	1.548*

The EMD is normalized by the genomic region length, i.e. we report the EMD per 100 genomic positions. Comparison is performed for Clique-SNV with three different frequency thresholds: 2, 5 (default) and 10%, aBayesQR and PredictHaplo . The aBayesQR did not finish in majority of samples. The best EMD for each benchmark is in bold font.

Runtime comparison

To compare the computational run time of each method, we used the same PC (Intel(R) Xeon(R) CPU X5550 2.67GHz ×2 8 cores per CPU, DIMM DDR3 1333 MHz RAM 4Gb ×12) with the CentOS 6.4 operating system. The runtime of CliqueSNV is sublinear with respect to the number of reads while the runtime of PredictHaplo and 2SNV exhibit super-linear growth. For the 33k IAV10sim reads the CliqueSNV analysis took 21 s, while PredictHaplo and 2SNV took around 30 min. The runtime of CliqueSNV is quadratic with respect to the number of SNVs rather than by the length of the sequencing region (Supplementary Figure S2).

We also generated five HIV-1 variants within 1% Hamming distance from each other, which is the estimated genetic distance between related HIV variants from the same person (64). Then we simulated 1M Illumina reads for sequence regions of length 566, 1132, 2263 and 9181 nucleotides for which CliqueSNV required 37, 144, 227 and 614 seconds, respectively, for analyzing these datasets (Supplementary Figure S3). For the HIV2exp benchmark, aBayesQR, PredictHaplo and CliqueSNV required over 10 h, 24 min and only 79 s, respectively. Finally, for four full-length benchmarks, the CliqueSNV is 2–10× faster than PredictHaplo depending on lower bound on the haplotype frequency, while ABayesQR is more than 100× slower and manged to handle only short genomic regions (see Supplementary Table S2).

DISCUSSION

Assembly of haplotype populations from noisy NGS data is one of the most challenging problems of computational genomics. High-throughput sequencing technologies, such as Illumina MiSeq and HiSeq, provide deep sequence coverage that allows discovery of rare, clinically relevant haplotypes. However, the short reads generated by the Illumina technology require assembly that is complicated by sequencing errors, an unknown number of haplotypes in a sample, and the genetic similarity of haplotypes within a sample. Furthermore, the frequency of sequencing errors in Illumina reads is comparable to the frequencies of true minor mutations (41). The recent development of single-molecule sequencing platforms such as PacBio produce reads that are sufficiently long to span entire genes or small viral genomes. Nonetheless, the error rate of single-molecule sequencing is exceptionally high reaching 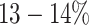(65), which hampers PacBio sequencing to detect and assemble rare viral variants.

We developed CliqueSNV, a new reference-based assembly method for reconstruction of rare genetically related viral variants such as those observed during infection with rapidly evolving RNA viruses like HIV, HCV and IAV. We demonstrated that CliqueSNV infers accurate haplotyping in the presence of high sequencing error rates and is also suitable for both single-molecule and short-read sequencing. In contrast to other haplotyping methods, CliqueSNV infers viral haplotypes by detection of clusters of statistically linked SNVs rather than through assembly of overlapping reads used with methods such as Savage (26).

Applied to the novel in vitro sequencing HIV-1 benchmark, CliqueSNV correctly reconstructed 87% of the intra-host haplotype population. At the same time, other state-of-the-art tools were not able to recover even a single haplotype without errors. Additionally, we have used the only previously known and commonly used in vitro benchmark (27) and simulated datasets to evaluate the accuracy of existing haplotyping methods. In contrast to the existing methods, CliqueSNV was able to detect minority haplotypes at a low 0.1% frequency and distinguish minority haplotypes differently in only two base pairs. We have also validated CliqueSNV on Illumina reads from full-length genomes where it is faster and more accurate than PredictHaplo on average.

We also believe that CliqueSNV can be applied to Nonopore sequencing data. We ran CliqueSNV on 4k-long spike gene region for 9 samples of SARS-CoV-2 with 300–900 bp read length. In each sample, CliqueSNV managed to reconstruct two to six haplotypes which is within the number of haplotypes identified for the same region from Illumina reads for similar SARS-CoV-2 samples.

Although very accurate and fast, CliqueSNV has some limitations. Unlike Savage (26), CliqueSNV is not a de novo assembly tool and requires a reference viral genome. This obstacle could easily be addressed by using Vicuna (59) or other analogous tools to first assemble a consensus sequence from the NGS reads, which can then be used as a reference. Another limitation is for variants that differ only by isolated SNVs separated by long conserved genomic regions longer than the read length which may not be accurately inferred by CliqueSNV. While such situations usually do not occur for viruses, where mutations are typically densely concentrated in different genomic regions, we plan to address this limitation in the next version of CliqueSNV.

The ability to accurately infer the structure of intra-host viral populations makes CliqueSNV applicable for studying viral evolution, transmission and examining the genomic compositions of RNA viruses. In addition, we envision that the application of our method could be extended to other highly heterogeneous genomic populations, such as metagenomes, immune repertoires and cancer cell genes.

DATA AVAILABILITY

The datasets HIV2exp and HIV9exp have been deposited in the Sequence Read Archive under accession number SRR12042289 and SRR12042290, respectively.

The links to the datasets and the consensus sequences of the individual strains are available at https://github.com/Sergey-Knyazev/CliqueSNV-validation/ blob/master/relevant_haplotypes/HIV9exp.fasta

Software

CliqueSNV is available at https://github.com/vtsyvina/CliqueSNV

Validation scripts

Validation notebook is available through docker container that contains all instructions, related dependencies and input datasets at https://hub.docker.com/r/amelnyk3/clique_snv_validation/.

Notes

Disclaimer: The findings and conclusions in this paper are those of the authors and do not necessarily represent the official position of the CDC.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NIH [1R01EB025022-01, in part to A.Z., P.S.]; NSF [CCF-1619110 , in part to A.Z., CCF-2047828 to P.S., DBI-2041984, in part to S.M.]; Ministry of Science and Higher Education of the Russian Federation Grant [075-15-2020-926 to Y.P.]; Molecular Basis of Disease at Georgia State University (in part) (to S.K., V.T., A.M.). Funding for open access charge: NSF [DBI-2041984].

Conflict of interest statement. None declared.