Abstract
Introduction
Inductively coupled plasma mass spectrometry (ICP-MS) experiments generate complex multi-dimensional data sets that require specialist data analysis tools.
Objective
Here we describe tools to facilitate analysis of the ionome composed of high-throughput elemental profiling data.
Methods
IonFlow is a Galaxy tool written in R for ionomics data analysis and is freely accessible at https://github.com/wanchanglin/ionflow. It is designed as a pipeline that can process raw data to enable exploration and interpretation using multivariate statistical techniques and network-based algorithms, including principal components analysis, hierarchical clustering, relevance network extraction and analysis, and gene set enrichment analysis.
Results and Conclusion
The pipeline is described and tested on two benchmark data sets of the haploid S. Cerevisiae ionome and of the human HeLa cell ionome.
Supplementary Information
The online version contains supplementary material available at 10.1007/s11306-021-01841-z.
Keywords: Ionomics, Network biology, Galaxy platform
Introduction
The multi-omics era has seen an increase in the acquisition of multivariate and megavariate datasets to describe the functional genetic patterns that arise from multiple levels of complexity of the cell, including the genome, the epigenome, the transcriptome, the metabolome, the proteome, the lipidome and the ionome (Fondi & Liò, 2015; Haas et al., 2017; Pinu et al., 2019).
In particular the ionome, defined as the elemental composition of an organism, is studied through the quantitative and simultaneous measurement of intracellular elements and changes in their composition in response to environmental and genetic perturbations (Salt et al., 2008). Inductively coupled plasma mass spectrometry (ICP-MS) is a technology used in systems biology and clinical research to profile the concentration of elements within samples and cells of living organisms (Amais et al., 2020; Barkla et al., 2016; Baxter, 2010; Konz et al., 2017; Meyer et al., 2018). This technology has been coupled with screening experiments using genetic modifications to study genome-wide genetic associations that are revealed by phenotypical cellular responses at the level of element abundances, in diverse model organisms, including yeast (Danku et al., 2009; Eide et al., 2005; Yu et al., 2012), and plants (Baxter et al., 2008; Chao et al., 2011; Salt et al., 2008).
Ionome data sets are generally analysed using multivariate statistical techniques such as principal components analysis (PCA) and clustering, as well as methods for network inference and analysis. These approaches have shown to be effective in revealing patterns of correlation between intracellular abundances of different elements and between elemental profiles of different samples (Eide et al., 2005; Iacovacci et al., 2020; Yu et al., 2012). However, at present, no bioinformatics pipeline exists that allows the performance of this type of analysis in a standardised fashion. For this reason, we developed IonFlow, an R-based Galaxy tool designed for the analysis of ionome data sets from ICP-MS experiments. The software is freely available on Galaxy (https://usegalaxy.org/, Jalili et al., 2020) and is designed to have a simple user-friendly interface.
Materials and methods
Workflow
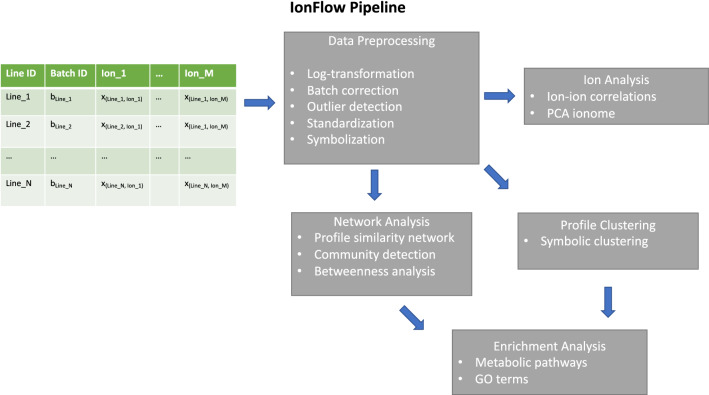
In Fig. 1 we schematically outline the IonFlow pipeline. The format of the raw data is a csv table describing a set of N measurements (rows) of the concentration of M distinct elements (columns). Because usually the elements are profiled via mass-spectrometry in the form of ions, we also refer to them as ‘ions’ here (but note these ions may be complex adducts). The column Line describes the variable associated with the N measurements, which can be a gene ID associated to a single-gene mutant of a model organism under study.
Fig. 1.
The functional architecture of the IonFlow pipeline
Multiple samples of the same line can be present (repeated line ids in the rows) and one column in the table (Batch_ID in figure) typically provides the batch identification number, a label that groups the measurements according to the experimental design, describing for example the samples that were measured in the same batch or that were measured in the same plate, and is used to correct the data for batch effects (Mertens, 2017).
Data pre-processing
The PreProcessing function processes the raw data according to a series of sequential operations.
Log-transformation raw data are automatically log-transformed, a common practice in the analysis of mass spectrometry data, which improves analysis of features (ions concentrations) by transforming the data to a distribution that is closer to a Gaussian distribution (Mertens, 2017).
-
Batch correction three arguments of the function give the user a customised way to normalise the data for batch effects; these are method_norm, for setting the batch correction method, control_use which indicates how to use the control lines for batch correction, and control_lines, a string specifying the cell lines to be used as control. If the parameter method_norm is equal to “none”, no correction is performed; if “median” is assigned as a value, then all the measurements of each ion m in batch b are scaled by the median value of the corresponding ion in that batch; if “median + std” is assigned to the parameter the concentrations are further scaled by the standard deviation (std) of the ion concentrations within the batch.
When the parameter control_use is set to “all” then all lines in the batch are used to compute the batch median and std; when control_use is set to “control” the batch median and std are computed using a subset of lines specified in the character vector control_lines passed to the function. Finally, if control_use is set to “control.out”, all lines except the control lines are used to compute the values of batch median and std.
-
Outlier detection after all measurements are normalised to their batches, outlier values are detected and removed according to three alternative methods that can be specified by the input parameter method_outliers. thres_outl is a threshold variable that is passed to the function to define outlier measurements. When method_outliers is set to “log.FC.distance” outliers are detected as the values in concentrations that are thres_outl times above or below the zero median reference value. When the method is “mad”, concentration values that deviate at least ± thres_outl median absolute deviations are considered outliers. When the method is “IQR” the upper and lower limits for outlier concentrations correspond respectively to (Q1—thres_outl x IQR) and (Q3 + thres_outl x IQR), where Q1 and Q3 are the first and third quartile values and IQR is the interquartile range.
After outlier concentration values are detected, all samples containing at least one outlier value in their ion profile are removed from the data set. The user can also set the parameter method_outliers to “none” in order to skip the outlier analysis.
-
Profile Standardisation the normalised and filtered concentration values are then standardised. Two options are available through the input parameter stand_method. If it is equal to “std” the concentration values of each ion m are scaled by the standard deviation of all values, if equal to “mad” then the values are scaled by the median absolute deviation, which is a robust estimator of the std when the overall number of measurements is not very large. The user can also pass to the function a vector stdev of length M containing user-defined scaling values and set stand_method to “custom” for a custom standardisation.
After standardisation the z-score profiles are aggregated at the line level by computing for each line the median value of the m-th element from the z-score profiles associated to the samples of that line.
Profile Symbolisation a value thres_symb, corresponding to a threshold in unit of standard deviation, is passed to the function and cell line symbolic profiles are extracted from their corresponding z-score profiles. The m-th element of the symbolic profile will be equal to + -1 if the corresponding element in the z-score profile is, respectively, above thres_symb or below -thres_symb, or otherwise it will equal 0.
The PreProcessing function provides the user with the following outputs:
stats.raw.data a table containing the statistic of the unprocessed elemental concentrations measured.
stats.batches a table containing the statistic of the batch corrected elemental concentrations across batches.
stats.outliers a table containing the statistic of measurements detected as outlier.
stats.std a table containing the scaling values used to standardise the elements.
data.long a table containing the raw data of elemental concentrations.
data.line.logFC a table containing batch corrected profiles (line aggregated).
data.line.zscores a table containing z-score profiles (line aggregated).
data.line.symb a table containing symbolic profiles (line aggregated).
plot.overview a plot overviewing all values of elemental concentrations after batch correction and outlier detection.
plot.hist a plot containing histograms describing the distribution of z-scores for each element.
plot.change.stat a histogram plot describing the statistic of number of changed elements per cell line.
plot.change.dir a histogram plot describing the statistic of increase and decrease of elemental abundances across cell lines.
plot.medians a line plot of batch median values of element log-transformed concentrations.
plot.CV a line plot of absolute coefficients of variation of the element log-transformed concentrations across batches.
Analysis of ions
The IonAnalysis function is designed to perform an exploratory analysis of the elemental variability and of the correlations between the different measured ions using multivariate statistical methods including PCA and relevance networks inference (Butte & Kohane, 1999; Butte et al., 2000; Liang et al., 1998; Werhli et al., 2006). The function takes as input a data frame of z-score profiles of the type data.line.zscores returned by the PreProcessing function, a parameter thres_ion_corr representing a correlation threshold (default value set to 0.15), and a parameter method_ion_corr that specifies a measure to compute correlation coefficients compatible with the cor function (default method “pearson”) from the R package stats (Team, 2019). The function outputs the following results to the user:
data.pca.loads a table containing the loadings of each element along the first two Principal Components.
plot.pca an overview plot of the PCA analysis of the z-score profiles.
plot.corr a correlation plot showing the pattern of element-element correlations extracted from the z-score profiles.
plot.net a plot showing the relevance network between the elements given the input correlation threshold: nodes represent elements and the width of the link between two elements is proportional to their correlation coefficient.
plot.heat a heatmap showing the clustering of rows and columns of the input z-score profile matrix using the R hclust(stats) method “ward.D” and the Euclidean distance, which has been shown to be a powerful nonlinear combination (Szekely & Rizzo, 2005).
Clustering and network analysis of profiles
The IonAnalysis function focuses on the relations between the ions/features of the pre-processed data (columns of the data frame of z-score profiles). The ProfileClustering and the GeneticNetwork functions deal with the analysis of the z-score profiles to study the relations between the cell lines/observations of the data set.
The ProfileClustering function is designed to cluster lines based on the similarity of their symbolic profiles according to their Hamming distance. It takes as input a data frame of the type data.line.symb returned by the PreProcessing function, and uses three additional parameters: min_clust_size, an integer which corresponds to the minimal size in terms of number of lines that defines a cluster to be of interest (default equal to 10); h_tree, an integer which corresponds to the Hamming distance that defines the clusters (the default algorithm uses h_tree = 0 and groups together lines with identical symbolic profiles, meaning that their Hamming distance is zero); and filtering_zero_string, a logical parameter that removes from the input dataset the lines with all zeros in their symbolic profile, that can be interpreted as a cluster with no-phenotype of a phenotype consistent with the control lines.
ProfileClustering gives as output:
clusters.vector a table containing the cluster id of each line.
tab.clusters a table reporting the cluster size of each cluster (number of genes).
tab.clusters.subset a table reporting the cluster size of each cluster (number of genes) only for clusters of a selected size (size greater than min_clust_size).
The GeneticNetwork function is designed (i) to extract a relevance network between the lines based on their profile similarity and (ii) to perform a graph analysis which includes community detection (Bianconi et al., 2014; Fortunato, 2010) and betweenness analysis (Latora et al., 2017), and (iii), to provide the means for network visualisation. The function is based on the methodology described in (Iacovacci et al., 2020). It takes as input a data frame of the type data.line.zscores and the following additional parameters: method_corr specifies a similarity/correlation measure to extract the relevance network; supported options include “pearson”, “spearman”, “kendall” from the cor(stats) R function, “cosine” from the cosine(lsa) R function (Wild, 2007), and “mahal_cosine” (Mahalanobis cosine) and “hybrid_mahal_cosine” (hybrid Mahalanobis cosine) (Iacovacci et al., 2020; Patil & Deore, 2014). The parameter thres_corr corresponds to the correlation threshold that define relevant similarities (the default value is set to 0.7). The parameter network_modules, can be set to “louvain”, in which case network modules are defined using the Louvain algorithm for community detection (Blondel et al., 2008), or “input”, in which case the network modules are passed as input to a cluster_vector object of the type clusters.vector returned by ProfileClustering and in addition cluster name labels can be passed as an object cluster_label_vector. The parameter n_labels is an integer proportional to how many nodes will be labelled in one of the output plots and is set to 3 as the default. R network packages used in the function include igraph (Csardi, 2013) and network (Butts, 2008).
GeneNetwork produces as output:
network an edge list describing the network between the lines.
network.modules a table containing network modules id’s of nodes.
stats.impact_betweenness a table reporting the values of network betweenness and the impact of each line in the network. The impact is defined as the L2 norm of the z-score profile and it is an indicator of the overall deviation in elemental abundance.
plot.network produces a plot showing the relevance network between the lines given the input correlation threshold.
plot.impact_betweenness produces a scatter plot of network betweenness versus impact for each line.
Enrichment analysis
In the case of dataset analysis where lines can be associated with genes (for example single gene knock-outs mutants) the user can perform a gene set enrichment analysis for KEGG metabolic pathways or GO Ontology terms by taking as gene sets the clusters obtained from the ProfileClustering or the network modules from the GeneNetwork function. The function is available for three different organisms, namely yeast, mouse and human.
The functions KeggEnricher and GOEnricher take as input a vector cluster_vector of the type clusters.vector or network.modules; a parameter pval specifying the p-value for the enrichment significance threshold; a character vector gene_uni specifying the gene universe list to be used (the default is NULL, in which case lines in cluster_vector also represent the gene universe); and a parameter annot_pkg which specifies the database to be used (for yeast S.Cerevisiae genes it has to be set to “org.Sc.sgd.db”, for mouse to “org.Mm.eg.db”, and for human to “org.Hs.eg.db”).
Additionally, the function GOEnricher takes as input a parameter ont to indicate which types of ontology should be used: “BP” for biological processes, “MF” for molecular functions, and “CC” for cellular components.
The genes in cluster_vector and gene_uni must be listed as ORF or ENTREZ IDS for yeast or ENTREZ IDS for human and mouse.
KeggEnricher and GOEnricher give as the output:
enrichment.summary a table summarising the results from the enrichment analysis.
enrichment.full.results a table containing cluster-specific details of the enrichment analysis.
Results and discussion
Case study 1: the genetic network of the S. Cerevisiae ionome
To illustrate the IonFlow pipeline we have used the iHUB Yeast Ionome data set (Yu et al., 2012), a large collection of population-average intracellular concentrations of 14 different elements (Ca, Cd, Co, Cu, Fe, K, Mg, Mn, Mo, Na, Ni, P, S, and Zn) quantified using ICP-MS in a collection of 4945 S. cerevisiae haploid mutant cell lines, where in each cell line a single non-essential ORF (open reading frame) was deleted. ICP-MS data were normalised by optical density (OD). Experimental details of the dataset are described in (Danku et al., 2009). Most of the cell lines (4207) were measured in 4 replicates, 684 lines in 8 replicates, 48 lines in 12 replicates, and 2 lines in 16 replicates giving a total of 26,976 samples screened in 305 different plates. Also, 4 control lines were present on the plates, generally in replicates of 4, namely BY4741, YDL227C, YLR396C, YPR065W.
ICP-MS raw data and OD corrected data can be downloaded from the iHUB (https://www.ionomicshub.org/yeast/beta/DataSearch.action). A table with the OD corrected data used in this study is available at https://github.com/wanchanglin/ionflow.
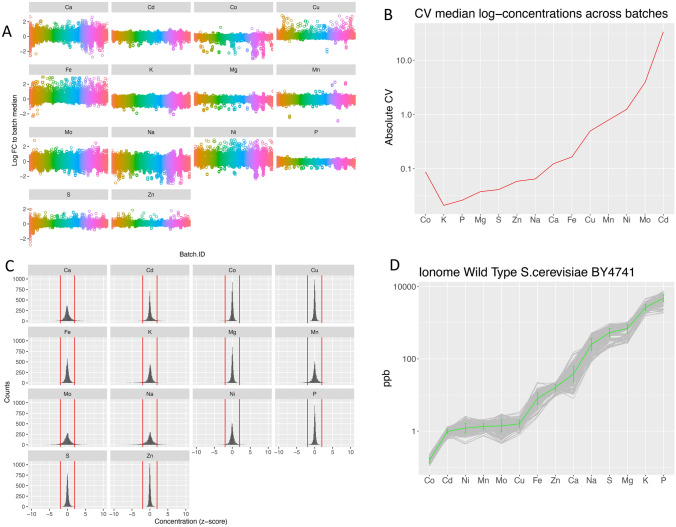
In Fig. 2 we show some diagnostic output plots from the PreProcessing function after the raw data are processed. A plate-based normalisation of ion concentrations was enforced using the median value of all available lines in each plate. Outliers were defined as concentrations values deviating more than 3 times from the median after normalisation and all lines containing outlier values in their profiles were removed. Figure 2A shows the log-transformed normalised values across the plates (batches) after outlier detection and removal, and Fig. 2B shows the absolute coefficient of variation of the ions across plates (batches). The normalised profiles were standardised using the standard deviation of the ions measured across all samples and Fig. 2C shows the z-score distributions of the ions in the lines after standardisation together with the threshold set for the symbolisation (± 2 standard deviations).
Fig. 2.
IonFlow diagnostic analysis of the yeast S. Cerevisiae ionome data set from the PreProcessing function. A The log-transformed normalised element concentrations are visualised across batches after outlier detection and removal. Different colours indicate different measurement plates (batches). B Absolute coefficient of variation of the elements across batches. C The distributions of the element z-score concentration values across the yeast mutants after standardisation together with the threshold (red vertical lines) set for the symbolisation. D The S. Cerevisiae BY4741 wild type ionome is shown, estimated by computing the mean value (green line) of the within-batch median concentrations (grey lines) (Color figure online)
We also repeated the PreProcessing using only the samples of the control line BY4741, a wild type yeast strain, and from the output table we converted back the in-plate median log-transformed concentration to the original part per billion (ppb) scale. In Fig. 2D the S.Cerevisiae BY4741 wild type ionome is shown, that was estimated from the mean value (green line) of the within-plate median measured concentrations (grey lines). The plot reveals that the elements with higher across-median CV (Fig. 2B) are, in general, the ones that are present in lower absolute concentration, as expected from an experimental perspective.
It is of interest to compare Fig. 2D with a previously reported diploid S.Cerevisia ionome quantification (Cyert & Philpott, 2013; Eide et al., 2005) to gain insights into the genetic background and the external cellular environment and how they play a role in the internal elemental balance of the cell. Despite the level of potentially toxic elements such as cadmium and sodium being artificially increased in the yeast growth media for the data set under study (Danku et al., 2009) most of the elements agree in order of magnitude with the level reported in (Cyert & Philpott, 2013).
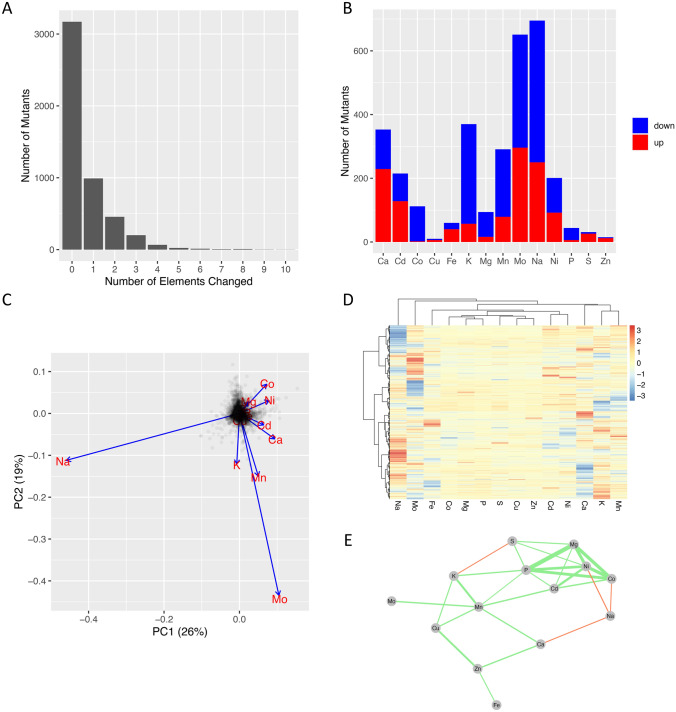
We then proceeded to the analysis of the processed z-score profiles and symbolic profiles from the PreProcessing function. In Fig. 3A, B the data.line.symb table is used to produce a histogram plots that describe the statistics of changes in the yeast ionome for the selected symbolic threshold. Figure 3A reveals that most lines (3171, ~ 75%) do not show any change at the level of their symbolic profile, and that, for most of the remaining lines that show a phenotype, the probability of having a profile with k altered ions decreases exponentially with k. Figure 3B illustrates the changes by element, together with the change direction, and it is interesting to note that copper, zinc, iron and sulphur, that have an essential role in the cell in shaping protein structure/function and acting as enzyme cofactors (Cyert & Philpott, 2013), are the elements that are less likely to be altered and that also show a preferential increase in the directionality of the change, suggesting that robust mechanisms must exist in S.cerevisiae to control the homeostasis of these elements and that their decrease is likely to produce unviable mutants.
Fig. 3.
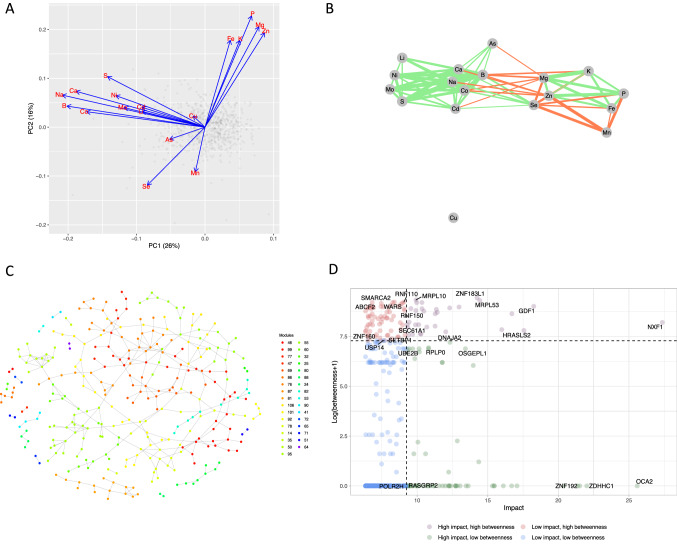
Elemental analysis of the yeast S. Cerevisiae ionome data set. A The statistic of the number of altered elements per yeast knockout mutant; 75% of mutants do not show any change at the level of their symbolic profile given a ± 2 z-scores threshold, and the probability of having a profile with k altered elements decreases exponentially with k. B The statistic of changes by element, together with the change of direction (increase or decrease in concentration with respect to the mean). C mutant elemental profiles are visualised in the plane of PC1 vs PC2; the projected eigenvector length (blue vectors) is proportional to the variance of the elements and the angle between the projected eigenvectors is proportional to the correlation of abundances across the mutants between the corresponding elements. D Hierarchical clustering of the z-score profiles. E Relevance network (relevance threshold 0.15) describing the element-element correlations: green/red links indicate positive/negative correlations respectively, and the width of the link is proportional to the absolute correlation value (Pearson’s correlation) (Color figure online)
This elemental analysis was extended via the IonAnalysis function (in Fig. 3C–E the output plots are shown). The PCA plot (Fig. 3C) shows, as expected, that the projected eigenvector length (blue vectors) is proportional to the variance of that element in the data (Fig. 3B) and that the smaller the angle between the projected eigenvectors, the more the ions are likely to be clustered together when hierarchical clustering analysis is performed using their z-score profile across the lines (Fig. 3D). Figure 3E depicts the relevance network extracted from the element-element correlations using the default threshold and Pearson’s correlation coefficient (green links indicate positive correlations, while red links indicate negative correlations). Mg and P, that show a preferential change in direction towards a decrease in intracellular concentration, are the most correlated elements and are significantly clustered with Ni and Co, and Cd, which is consistent with results reported in (Eide et al., 2005). It is interesting to note that the observed correlation is likely to reflect ATP consumption in activation of gene-deletion compensatory mechanisms, given that most of the Mg2+ intracellular ions are bound to ATP and ribosomes (Milo & Phillips, 2015). Na and K, that are mostly found within the cell as monovalent ions Na+ and K+, are weakly correlated to other elements, and the fact that sodium appears to be mostly anticorrelated with other elements might reflect the difficulty in its quantification due to various contamination sources (Milo & Phillips, 2015).
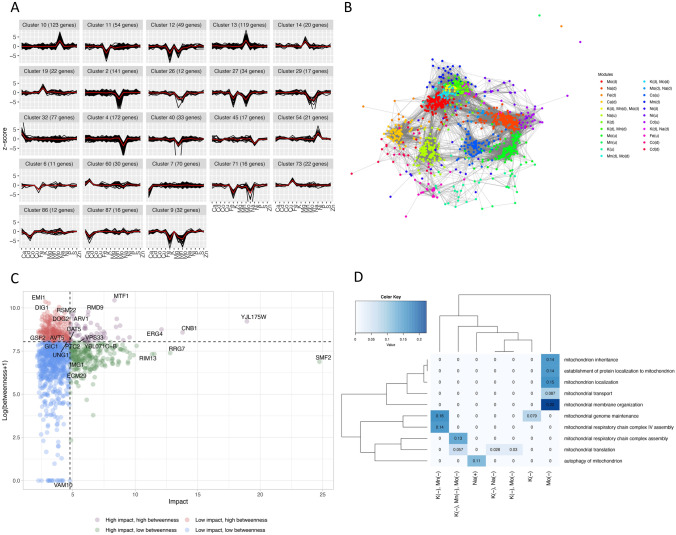
The symbolic profiles were then clustered using the ProfileClustering function with default parameter choice and the resulting cluster vector was given as input as the modules vector to the GeneticNetwork function together with the z-score elemental profiles in order to perform a network analysis of the profile correlations between the mutant lines. For this analysis the cosine similarity was used as the correlation measure and a relevance correlation threshold of 0.7 was chosen.
Figure 4A shows the z-score profiles of the lines clustered according to ProfileClustering for all clusters with a minimum size of 10 lines corresponding to the most common ionome phenotypes (average within-cluster profiles are shown in red). Figure 4B shows a visualisation of the genetic network inferred from elemental profile correlations between the knock-out mutants found in the most common phenotypes. Nodes represent genes, edges represent a genetic association (deletion produces a similar phenotype), and the network modules correspond to the clusters in Fig. 4A, with labels describing the cluster features in terms of altered elemental levels (‘u’ indicates up, ‘d’ indicates down). Figure 4C reports the plot of impact versus betweenness for all nodes in the network. The impact is defined as the L2 norm of the z-score profile and it is a measure of the overall alteration of a profile, while the betweenness quantifies the role of a node in bridging between modules. Nodes are categorised and coloured according to high/low impact and high/low betweenness. These in turn are determined by including in the high group the 25% highest values of each descriptor. The 3 nodes with highest impact and the 3 nodes with highest betweenness are also labelled within each category. SMF2, a very important manganese transporter, has the highest impact, with a z-score for Mn of approximately − 25 (25 standard deviations below the median value). MTF1, a mitochondrial gene from cluster 10, which shows reductions of K and of Na levels, is the gene with highest betweenness.
Fig. 4.
Mutant elemental profile analysis of the yeast S. Cerevisiae ionome data set. A The z-score profiles (grey lines) of the mutants revealing the most common phenotypes are shown together with the average within-cluster profile (red lines); the clustering, based on the similarity between the mutant’s symbolic profiles, was performed using the ProfileClustering function. B The genetic relevance network inferred from elemental profile correlations between the knockout mutants found in the most common phenotypes is shown (cosine similarity, relevance threshold 0.7); the nodes represent genes, and the edges represent a genetic association (correlated elemental profile in response to deletion); the network modules correspond to the phenotype clusters in A, with labels describing the cluster features in terms of altered elemental levels (‘u’ indicates up level, ‘d’ indicates down level). C Impact versus network betweenness analysis of the network nodes; the impact is defined as the L2 norm of the z-score profile. D Gene clusters enrichment analysis performed with the GOEnricher function; the heatmap shows the percentage of universe genes annotated for all enriched mitochondrial terms in function of the cluster phenotypic characteristics (Color figure online)
Finally, the GOEnricher function was used to perform a biological process enrichment analysis of the common clusters. Results revealed that several of these clusters were enriched by mitochondrial related processes suggesting that mitochondrial dysfunction is associated with disruption of ion homeostasis.
The heatmap in Fig. 4D shows the percentage of genes annotated for given mitochondrial terms that are found inside each cluster enriched for that term. These results imply that the genome partition obtained from the ionome data is biologically informative and that mitochondrial enriched clusters are in general associated with reduction of specific elements; namely potassium, sodium, manganese and molybdenum.
Case study 2: the HeLa ionome
To provide a second illustrative example we processed another ionome data set that describes concentrations of trace elements in human HeLa cells obtained through a genome-wide high-throughput siRNA/ionomics screen (Malinouski et al., 2014). Data were not pre-processed, instead the z-score profiles provided by the authors of the study were used as additional benchmark data for the elemental analysis and for the genetic network analysis. The z-score data contains normalised and standardised concentration measurements for 18 elements (As, B, Ca, Cd, Co, Cu, Fe, K, Li, Mg, Mn, Mo, Na, Ni, P, S, Se, and Zn) profiled for 775 mutant lines of HeLa cells, each having a single different gene silenced.
In Fig. 5A, B results from the ion analysis are shown. The profiles projected onto the first two principal components, along with the ion loadings are shown in Fig. 5A while the relevant ion-ion correlation network is displayed in Fig. 5B. While some relations between the ions such as correlated levels of Mg and P can still be identified in this ionome, the overall interpretation is difficult, probably due to the cancerous nature and rapid proliferation of the HeLa cells (Pavlova & Thompson, 2016). The genetic network analysis is illustrated in Fig. 5C, D. All profiles with an impact below the median impact value were filtered out (387 lines). The genetic network (Fig. 5C) between the selected lines was extracted using a relevance threshold of 0.6 and the Mahalanobis cosine as a correlation measure, which is more effective when profiles are characterised by an extended, dense pattern of element-element correlations (Fig. 5B) such as in this case. Nodes are coloured according to network modules assessed by the Louvain community detection algorithm. Isolated nodes are not visualised in the plot. Table 1 reports the results of the enrichment analysis for KEGG metabolic pathways obtained with the KEGGEnricher function for the network modules.
Fig. 5.
IonFlow analysis of the human ionome data set from HeLa cells. A PCA of the elemental profiles of the knockdown mutants. B The relevance element-element correlation network is shown (Pearson’s correlation, relevance threshold 0.15). C The genetic relevance network between selected high-impact elemental profiles of knockdown mutants is depicted (Mahalanobis cosine similarity, relevance threshold 0.6); nodes are coloured according to network modules found via network community detection. D Impact-betweenness analysis of the knockdown mutants
Table 1.
results of the KEGG pathway enrichment analysis on the network modules of the genetic network extracted from the HeLa cell ionome
| Cluster | KEGGID | P value | Count | Size | Term |
|---|---|---|---|---|---|
| 69 | 3013 | 0.06249663 | 3 | 20 | RNA transport |
| 81 | 52 | 0.0016808 | 3 | 6 | Galactose metabolism |
| 81 | 4910 | 0.00735846 | 4 | 18 | Insulin signaling pathway |
| 81 | 4114 | 0.01940962 | 3 | 13 | Oocyte meiosis |
| 106 | 4114 | 0.01387635 | 3 | 13 | Oocyte meiosis |
| 101 | 10 | 0.00088208 | 4 | 12 | Glycolysis/gluconeogenesis |
| 101 | 4270 | 0.0084409 | 3 | 11 | Vascular smooth muscle contraction |
| 78 | 3050 | 0.0674506 | 4 | 21 | Proteasome |
| 95 | 4666 | 0.0464702 | 3 | 14 | Fc gamma R-mediated phagocytosis |
| 95 | 4810 | 0.07688909 | 3 | 17 | Regulation of actin cytoskeleton |
| 55 | 5016 | 0.02274157 | 4 | 20 | Huntington's disease |
| 55 | 4141 | 0.04970889 | 3 | 15 | Protein processing in endoplasmic reticulum |
| 55 | 240 | 0.07943879 | 3 | 18 | Pyrimidine metabolism |
| 60 | 4270 | 0.02379386 | 3 | 11 | Vascular smooth muscle contraction |
In Fig. 5D the impact-betweenness analysis of the knockdown mutants is plotted. Among the high impact and high betweenness genes is NFX1, that plays a role in the export of mRNA of the HSP70 family (whose members are known to become strongly upregulated by heavy metals such as arsenic, cadmium and copper) and MRPL53, a component of the mitochondrial large ribosomal subunit.
Conclusion
We presented IonFlow, a tool that makes the analysis of ionomics data accessible to Galaxy users and that allows them to quickly explore, visualise, and interpret their data via multivariate approaches used in the field of ionomics including PCA, correlation analysis, network inference and enrichment analysis. IonFlow also incorporates recently developed methods for ionome data sets, such as ion-profile-specific similarity measures (Iacovacci et al., 2020) that optionally, can be used by the user. Each function of IonFlow was described in detail and the pipeline was tested on two large benchmark ionome datasets, the ionome of haploid S.Cervisieae and the ionome of HeLa human cells, to illustrate its applicability and its outputs within two concrete case studies.
We showed that IonFlow is very versatile and it can be used to process raw data as well as directly process normalised and standardised data for advanced analysis such as genetic network extraction and study of element-element correlations. For these reasons IonFlow is of interest for researchers dealing with ionomics experiments beyond those performed with ICP–MS technology and its applicability potentially extends to the analysis of metabolomics data.
Supplementary Information
Below is the link to the electronic supplementary material.
Acknowledgements
J.L.G., and R.C.G. acknowledge funding from the Wellcome Trust funded project MetaboFlow, grant reference number 202952/D/16/Z.
Author contributions
Methodology: JI, WL, JLG, and RCG; software development: JI and WL; formal analysis: JI and WL; writing: JI, WL, JG, and RCG; funding acquisition: JLG and RCG; supervision: JLG, RCG All authors have read and agreed to the published version of the manuscript.
Declarations
Conflict of interest
The authors declare no conflict of interests.
Data availability
Data and R codes are freely accessible at https://github.com/wanchanglin/ionflow.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J. Iacovacci and W. Lin have contributed equally to this work.
Contributor Information
J. Iacovacci, Email: j.iacovacci@imperial.ac.uk
R. C. Glen, Email: r.glen@imperial.ac.uk
References
- Amais, R. S., Donati, G. L., & Arruda, M. A. Z. (2020) ICP-MS and trace element analysis as tools for better understanding medical conditions. TrAC Trends in Analytical Chemistry, 116094.
- Barkla BJ, Vera-Estrella R, Raymond C. Single-cell-type quantitative proteomic and ionomic analysis of epidermal bladder cells from the halophyte model plant Mesembryanthemum crystallinum to identify salt-responsive proteins. BMC Plant Biology. 2016;16:1–16. doi: 10.1186/s12870-016-0797-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baxter I. Ionomics: The functional genomics of elements. Briefings in Functional Genomics. 2010;9:149–156. doi: 10.1093/bfgp/elp055. [DOI] [PubMed] [Google Scholar]
- Baxter IR, Vitek O, Lahner B, Muthukumar B, Borghi M, Morrissey J, Guerinot ML, Salt DE. The leaf ionome as a multivariable system to detect a plant's physiological status. Proceedings of the National Academy of Sciences. 2008;105:12081–12086. doi: 10.1073/pnas.0804175105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianconi G, Darst RK, Iacovacci J, Fortunato S. Triadic closure as a basic generating mechanism of communities in complex networks. Physical Review E. 2014;90:042806. doi: 10.1103/PhysRevE.90.042806. [DOI] [PubMed] [Google Scholar]
- Blondel VD, Guillaume J-L, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment. 2008;2008:P10008. doi: 10.1088/1742-5468/2008/10/P10008. [DOI] [Google Scholar]
- Butte, A. J., & Kohane, I. S. (1999) Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements, Biocomputing 2000, (pp. 418–429). World Scientific. [DOI] [PubMed]
- Butte AJ, Tamayo P, Slonim D, Golub TR, Kohane IS. Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proceedings of the National Academy of Sciences. 2000;97:12182–12186. doi: 10.1073/pnas.220392197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butts CT. network: A package for managing relational data in R. Journal of Statistical Software. 2008;24:1–36. doi: 10.18637/jss.v024.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao D-Y, Gable K, Chen M, Baxter I, Dietrich CR, Cahoon EB, Guerinot ML, Lahner B, Lü S, Markham JE. Sphingolipids in the root play an important role in regulating the leaf ionome in Arabidopsis thaliana. The Plant Cell. 2011;23:1061–1081. doi: 10.1105/tpc.110.079095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csardi, M. G. (2013). Package ‘igraph’. Last accessed 3, 2013.
- Cyert MS, Philpott CC. Regulation of cation balance in Saccharomyces cerevisiae. Genetics. 2013;193:677–713. doi: 10.1534/genetics.112.147207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danku JM, Gumaelius L, Baxter I, Salt DE. A high-throughput method for Saccharomyces cerevisiae (yeast) ionomics. Journal of Analytical Atomic Spectrometry. 2009;24:103–107. doi: 10.1039/B803529F. [DOI] [Google Scholar]
- Eide DJ, Clark S, Nair TM, Gehl M, Gribskov M, Guerinot ML, Harper JF. Characterization of the yeast ionome: A genome-wide analysis of nutrient mineral and trace element homeostasis in Saccharomyces cerevisiae. Genome Biology. 2005;6:1–13. doi: 10.1186/gb-2005-6-9-r77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fondi M, Liò P. Multi-omics and metabolic modelling pipelines: Challenges and tools for systems microbiology. Microbiological Research. 2015;171:52–64. doi: 10.1016/j.micres.2015.01.003. [DOI] [PubMed] [Google Scholar]
- Fortunato S. Community detection in graphs. Physics Reports. 2010;486:75–174. doi: 10.1016/j.physrep.2009.11.002. [DOI] [Google Scholar]
- Haas R, Zelezniak A, Iacovacci J, Kamrad S, Townsend S, Ralser M. Designing and interpreting ‘multi-omic’experiments that may change our understanding of biology. Current Opinion in Systems Biology. 2017;6:37–45. doi: 10.1016/j.coisb.2017.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacovacci J, Peluso A, Ebbels T, Ralser M, Glen RC. Extraction and integration of genetic networks from short-profile omic data sets. Metabolites. 2020;10:435. doi: 10.3390/metabo10110435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalili V, Afgan E, Gu Q, Clements D, Blankenberg D, Goecks J, Taylor J, Nekrutenko A. The Galaxy platform for accessible, reproducible, and collaborative biomedical analyses: 2020 update. Nucleic Acids Research. 2020;48:W395–W402. doi: 10.1093/nar/gkaa434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konz T, Migliavacca E, Dayon L, Bowman G, Oikonomidi A, Popp J, Rezzi S. ICP-MS/MS-based ionomics: A validated methodology to investigate the biological variability of the human ionome. Journal of Proteome Research. 2017;16:2080–2090. doi: 10.1021/acs.jproteome.7b00055. [DOI] [PubMed] [Google Scholar]
- Latora V, Nicosia V, Russo G. Complex networks: Principles, methods and applications. Cambridge University Press; 2017. [Google Scholar]
- Liang, S., Fuhrman, S., & Somogyi, R. (1998). Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pacific symposium on biocomputing (pp. 18–29). [PubMed]
- Malinouski M, Hasan NM, Zhang Y, Seravalli J, Lin J, Avanesov A, Lutsenko S, Gladyshev VN. Genome-wide RNAi ionomics screen reveals new genes and regulation of human trace element metabolism. Nature Communications. 2014;5:1–11. doi: 10.1038/ncomms4301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mertens, B. J. (2017). Transformation, normalization, and batch effect in the analysis of mass spectrometry data for omics studies. Statistical Analysis of Proteomics, Metabolomics, and Lipidomics Data Using Mass Spectrometry, 1–21.
- Meyer S, Markova M, Pohl G, Marschall TA, Pivovarova O, Pfeiffer AF, Schwerdtle T. Development, validation and application of an ICP-MS/MS method to quantify minerals and (ultra-) trace elements in human serum. Journal of Trace Elements in Medicine and Biology. 2018;49:157–163. doi: 10.1016/j.jtemb.2018.05.012. [DOI] [PubMed] [Google Scholar]
- Milo R, Phillips R. Cell biology by the numbers. Garland Science; 2015. [Google Scholar]
- Patil SA, Deore PJ. Principle Component Analysis (PCA) and Linear Discriminant Analysis (LDA) based Face Recognition. International Journal of Computers and Applications. 2014;975:8887. [Google Scholar]
- Pavlova NN, Thompson CB. The emerging hallmarks of cancer metabolism. Cell Metabolism. 2016;23:27–47. doi: 10.1016/j.cmet.2015.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinu FR, Beale DJ, Paten AM, Kouremenos K, Swarup S, Schirra HJ, Wishart D. Systems biology and multi-omics integration: Viewpoints from the metabolomics research community. Metabolites. 2019;9:76. doi: 10.3390/metabo9040076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salt DE, Baxter I, Lahner B. Ionomics and the study of the plant ionome. Annual Review of Plant Biology. 2008;59:709–733. doi: 10.1146/annurev.arplant.59.032607.092942. [DOI] [PubMed] [Google Scholar]
- Szekely GJ, Rizzo ML. Hierarchical clustering via joint between-within distances: Extending Ward's minimum variance method. Journal of Classification. 2005;22:151–184. doi: 10.1007/s00357-005-0012-9. [DOI] [Google Scholar]
- Team, R. C. (2019) R: A language and environment for statistical computing (version 3.5. 1) [Computer software]. R Foundation for Statistical Computing.
- Werhli AV, Grzegorczyk M, Husmeier D. Comparative evaluation of reverse engineering gene regulatory networks with relevance networks, graphical Gaussian models and Bayesian networks. Bioinformatics. 2006;22:2523–2531. doi: 10.1093/bioinformatics/btl391. [DOI] [PubMed] [Google Scholar]
- Wild, F. (2007). An LSA package for R. Proceedings of the 1st International Conference on Latent Semantic Analysis in Technology Enhanced Learning (LSA-TEL'07), (pp. 11–12).
- Yu D, Danku JM, Baxter I, Kim S, Vatamaniuk OK, Vitek O, Ouzzani M, Salt DE. High-resolution genome-wide scan of genes, gene-networks and cellular systems impacting the yeast ionome. BMC Genomics. 2012;13:1–25. doi: 10.1186/1471-2164-13-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and R codes are freely accessible at https://github.com/wanchanglin/ionflow.