Why Was There More Household Stock Market Participation During the COVID-19 Pandemic?

Abstract

Although the nation was experiencing an economic downturn due to the COVID-19 pandemic outbreak, we nonetheless observed an increase in household equity share value relative to both domestic market capitalization and retail investors’ trading volume. In this paper, we aim to interpret the reasons underlying this seemingly unexpected phenomenon. We investigate portfolio choices with stocks, bonds, and life annuities under an inverse S-shaped probability distortion function. The results indicate that people invest more heavily in risky assets and buy more annuities when reducing their savings in risk-free accounts, which is indeed consistent with the reality.

1. Introduction

Because the worldwide outbreak of the novel coronavirus disease 2019 (COVID-19) in 2020, financial markets have generally experienced unprecedented changes. For example, the United States (US) stock market declined dramatically in March, triggering four circuit breakers (Mazur et al., 2021, Xu, 2021, Albulescu, 2021, Baker et al., 2020, Zhang et al., 2020). Crude oil recorded negative prices for the first time in history on April 20, 2020, and post-April represents one of the oil market’s most volatile periods (Akhtaruzzaman et al., 2021a, Corbet et al., 2020, Devpura and Narayan, 2020, Mensi et al., 2020, Salisu et al., 2020, Sharif et al., 2020). Gold prices have experienced a smaller decline since the outbreak of COVID-19, which was followed by an upside trend starting in February 2020. Moreover, the literature shows that gold is a safe haven asset for both the stock and oil markets (Akhtaruzzaman et al., 2020, Mensi et al., 2020, Salisu et al., 2021). In addition, empirical studies have also indicated that both financial and non-financial firms have experienced significant increases in conditional correlations between stock returns (Akhtaruzzaman et al., 2021b, Gharib et al., 2021, Okorie and Lin, 2021, So et al., 2021).

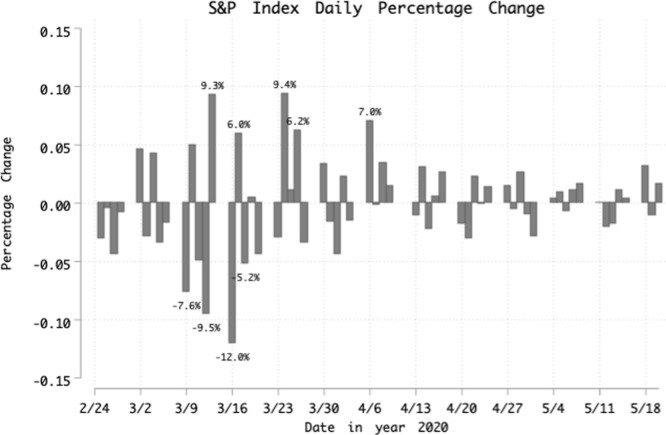
In this paper, our concern is the dramatic drop experienced in stock prices in the US equity market, which triggered four circuit breakers in March 2020. Conversely, the market subsequently surged significantly due to the government’s economic support programs, commercial COVID-19 treatment hopes, and for other reasons (as shown in Fig. 1). As a consequence, we find that the ratio of the household equity share value relative to US domestic market capitalization increases, according to quarterly financial accounts report from the Federal Reserve Board and statistics from the World Federation of Exchanges. We call this ratio the “percentage of household equity ownership”.1 Specifically, the percentage of household equity ownership rose from 66.92% in the second quarter of 2019 to 68.33% in the second quarter of 2020 as a response to the COVID-19 pandemic. Ortmann et al. (2020) documented a significant increase in retail investors’ trading activities such that the average weekly trading intensity increased by 13.9% as the number of COVID-19 cases doubled. This phenomenon has happened several times during economic downturns, shown in Table 1.2 Between the second quarter (Q2) of 2008 and 2020 Q2, every time there is an economic downturn, the household equity ownership percentage rises without exclusion. For example, it occurs four times over the 2008–2020 period—2010 Q2–2011 Q2, 2014 Q2–2015 Q2, 2015 Q2–2016 Q2, and 2019 Q2–2020 Q2—as shown in Table 1. These phenomena are puzzling because the classical literature on portfolio choice (Merton, 1971, Milevsky and Young, 2007) concludes that an increase in volatility should lead to less risky investment by households.

Fig. 1.

The daily percent change in the S&P 500 index, February 24, 2020–May 20, 2020. Note: We observe that the probability of both large losses and large gains increases significantly.

Table 1.

Percentage of household equity ownership, 2008 Q2–2020 Q2.

Year	(1) Household equity	(2) US Domestic	Percentage of household
	Value (trillions)	Market capitalization (trillions)	Equity ownership ((1)/(2))
2008 Q2	11.63	13.90	83.72%
2009 Q2	8.55	18.93	45.17%
2010 Q2	10.03	22.17	45.24%
2011 Q2	13.01	19.59	66.40%
2012 Q2	12.82	23.19	55.28%
2013 Q2	15.54	24.90	62.39%
2014 Q2	19.13	30.40	62.92%
2015 Q2	20.10	30.20	66.57%
2016 Q2	20.15	29.10	69.23%
2017 Q2	22.95	33.30	68.92%
2018 Q2	25.31	38.26	66.15%
2019 Q2	26.88	40.17	66.92%
2020 Q2	26.78	39.20	68.33%

Note: The quarterly household equity value data are from the Federal Reserve Board, and the quarterly US domestic market capitalization data are from the World Federation of Exchanges, which is the sum of New York Stock Exchange and Nasdaq market data for the United States. We observe that every time there is an economic downturn, the household equity ownership percentage rises definitely.

Empirically, the aforementioned phenomena are related to the literature on individuals’ risk attitudes and investment behaviors under financial market shock conditions (Gollier, 2001, Zhou, 2020, Guiso et al., 2018, Weber et al., 2013, Hoffmann et al., 2013). It is interesting to note that Hudomiet et al. (2011) and Necker and Ziegelmeyer (2016) found that households increased their risk/return expectations after the financial crisis, which follows the same pattern observed during the recent COVID-19 pandemic.

Some new studies have been published regarding retail investors’ investment behaviors during the recent COVID-19 crisis that measure investors’ market expectations and risk attitudes (Gormsen and Koijen, 2020, Landier and Thesmar, 2020, Hanspal et al., 2020). Hanspal et al. (2020) reported that US households expected a faster recovery of the post-COVID-19 stock market compared to previous crashes, and believed that the economic downturn represented a favorable opportunity for stock market entry.

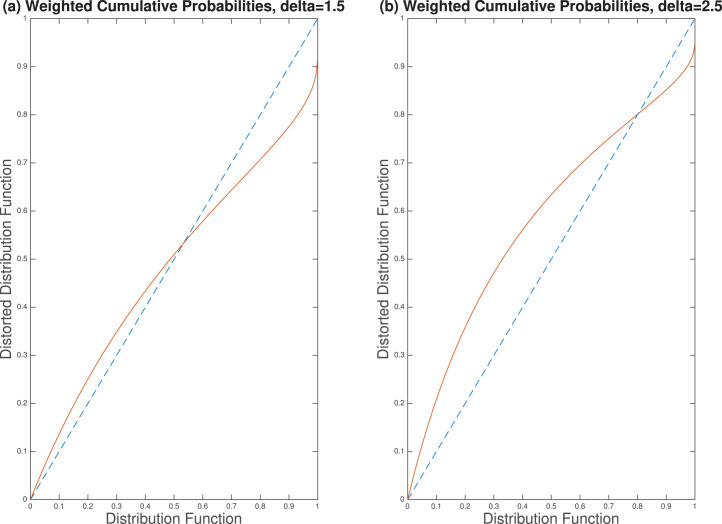
Therefore, we must unravel individuals’ seemingly inconsistent investment behaviors under financial market shock conditions. Most of the existing literature explores this issue from an empirical perspective; few theoretical studies have been done to the best of our knowledge. To fill this gap, we aim to explain this phenomenon by using a theoretical household portfolio model. In this study, we build a dynamic portfolio choice model with stocks, bonds, and annuities under financial market shock conditions and solve for the optimal annuitization, investment, and consumption strategies to maximize lifetime utility. The key is that, to capture the significantly negative and positive rates of return that occur in a short time, we characterize the asymmetric, two-sided skewness with an inverse, S-shaped probability distortion function rather than other models in the previous literature (Merton, 1976, Heston, 1993, Eraker et al., 2003, Kou et al., 2017, Bates, 1996), which is shown in Fig. 2.

Fig. 2.

Proposed probability distortion functions. Note: We observe that this probability distortion function assigns additional probabilities at the two extremes.

2. Model

2.1. Technical preliminaries

Due to the inverse S-shaped representation of the two-sided and skewed stock price distribution, the optimal asset allocation model is no longer a concave maximization problem. To tackle this issue, we propose a probability distortion function to capture this two-sided skewness under a stochastic process framework, which enables us to obtain the optimal solutions to the maximization problem.

Specifically, we first define our newly proposed probability weighting function for a good fit to the two-sided skewness.

$$F^{\star }\left(x_t\right)=1-\frac{1}{1-\delta \cdot lnS\left(x_t\right)}$$ (2.1)

with the distortion parameter $\delta >0$, $x_t$ being the stock price at time $t$, $S\left(x_t\right)$ being the survival function of the original stock price distribution such that $S\left(x_t\right)=Prob(X_t>x_t)$, and $F^{\star }\left(x_t\right)$ being the distorted cumulative distribution function such that $F^{\star }\left(x_t\right)=Prob(X_t^{\star }\le x_t)$. Our proposed probability distortion function with various distortion parameters is shown in Fig. 3.

Fig. 3.

Proposed probability distortion function with distortion parameters ($\delta =1.5$ and $\delta =2.5$, respectively). Note: We observe that a probability weighting function with $\delta =2.5$ assigns more probabilities at the low extreme than that with $\delta =1.5$, implying that people are more fearful of large losses than hopeful for large gains.

Then, using techniques proposed by Young and Zariphopoulou (2000) and Hertzler (2003), we derive the stochastic diffusion equation for a two-sided, skewed stock price process as follows:

$$d{X}_t^{\star }=[\gamma \frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta }{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}+\frac{2}{b}{X_t^{\star }}^{\gamma }{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}(-1+\frac{2\delta }{1+\delta {\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }})]dt+{\left(2\frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta +1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}\right)}^{\frac{1}{2}}d{B}_t$$ (2.2)

with shape parameter $\beta$, scale parameters $\sigma$, $\gamma$, and $b$, in which $\gamma$ and $b$ determine the shape of the process volatility, $B_t$ is the standard Brownian motion process. The stock prices $X_t$ are set to local values around the current price.

The detailed mathematical derivation is shown in Appendix A.

2.2. The financial market and policyholders

On the financial market, an individual can deposit money in a bank account at a risk-free interest rate $r$. Alternatively, they can invest in a risky asset that we approximate locally by a stochastic process whose local stable solution is Formula (2.2).

We consider an individual with a future lifetime following a random variable ${\tau }_d$. We assume that ${\tau }_d$ follows an exponential distribution with the parameter $\lambda$. $\lambda$ is the force of mortality. Then, the price of a life annuity that pays $1 per year continuously until the individual dies is given by the following equation:

$$\overline{a}={\int }_0^{\infty }{e}^{-rs}{e}^{-\lambda s}ds=\frac{1}{r+\lambda }$$ (2.3)

Here, we consider a commutable life annuity, which a policyholder can purchase or surrender any amount at any point in time. The surrender charge is proportional to the price of the life annuity. That is, the surrender value $1 of the annuity income is $\$(1-p)\overline{a}$ with $0⩽p⩽1$, of which $p$ is the proportional surrender charge.

In our model, there are two separate accounts—wealth accounts and annuity accounts. Wealth accounts consist of bonds and risky stock investments, whereas annuity accounts include only life annuities. Following Yaari (1965), we consider a retiree without a bequest motive that is risk averse and characterized by a constant relative risk aversion utility function, which is consistent with other portfolio selection studies. That is,

$$u\left(c\right)=\frac{c^{1-\alpha }}{1-\alpha }$$

In $\alpha >0$ and $\alpha \ne 1$, in which $\alpha$ is the risk aversion parameter.

2.3. Wealth dynamics and value function

In this study, we assume that the retiree consumes at a rate of $c_t$ at time $t$. ${\pi }_t$ represents the amount of money invested in the stock market at time $t$. $A_t$ is the amount of life annuity income at time $t$. The initial endowments at time $s$ in the wealth and annuity accounts are $W$ and $A$, respectively.

We first derive the investment and consumption strategies by assuming that the amount in the annuity account remains the same at time $s$. Therefore, there are four types of changes in the wealth account: this includes the interest from bonds, the returns from stock, and the proceeds from annuities minus consumption.

With the assumption that the stock price follows a process with a two-sided distribution as a local stable solution, the wealth dynamics is as follows:

$$d{W}_t=\{r(W_t-{\pi }_t)+\frac{{\pi }_t}{X_t^{\star }}[\gamma \frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta }{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}+\frac{2}{b}{X_t^{\star }}^{\gamma }{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}(-1+\frac{2\delta }{1+\delta {\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }})]-c_t+A_t\}dt+\frac{{\pi }_t}{X_t^{\star }}{\left(2\frac{{\sigma }^{\beta }}{\beta }{X_t^{\star }}^{\gamma -\beta +1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}\right)}^{\frac{1}{2}}d{B}_t$$ (2.4)

with the initial endowments $A_s=A⩾0$ and $W_s=W⩾0$.

The control processes are the corresponding investment strategy ${\left\{{\pi }_t\right\}}_{t⩾s}$ and consumption strategy ${\left\{c_t\right\}}_{t⩾s}$.

In this model, the individual seeks to maximize his or her lifetime utility $U$ with the endowments $A_s=A,W_s=W$. The value function is as follows:

$$U(A_s,W_s)=\underset{{\pi }_t,c_t}{sup}\mathbb{E}\left[{\int }_s^{{\tau }_d}{e}^{-rt}u\left(c_t\right)dt\right|A_s=A,W_s=W]=\underset{{\pi }_t,c_t}{sup}\mathbb{E}\left[{\int }_s^{\infty }{e}^{-(r+\lambda )t}u\left(c_t\right)dt\right|A_s=A,W_s=W]$$ (2.5)

According to stochastic control theory, we derive the corresponding Hamilton–Jacobi–Bellman (HJB) equation (Yong and Zhou, 1999) as shown below. Here, we omit a similar verification theorem as Theorem 2.1 in Wang and Young (2012).

$$(r+\lambda )U=(r{W}_t+A_t)U_w+\underset{{\pi }_t}{max}\{[-r{\pi }_t+{\pi }_t[\gamma \frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}+\frac{2}{b}{X_t^{\star }}^{\gamma -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}(-1+\frac{2\delta }{1+\delta {\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }})]]U_w+{\pi }_t^2\left[\frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}\right]U_{ww}\}+\underset{c_t}{max}(\frac{c_t^{1-\alpha }}{1-\alpha }-c_t{U}_w)$$ (2.6)

where $U_w$ is the first derivative of lifetime utility $U$ concerning wealth $W_t$, and $U_{ww}$ is the second derivative of lifetime utility $U$ for wealth $W_t$.

Maximizing the portion of the HJB equation involving investment and consumption strategies, the investment and consumption strategies can be explicitly obtained as follows:

$${\pi }_t=-\frac{[\gamma \frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}+\frac{2}{b}{X_t^{\star }}^{\gamma -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}(-1+\frac{2\delta }{1+\delta {\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }})-r]U_w}{2\frac{{\sigma }^{\beta }}{b\beta }{X_t^{\star }}^{\gamma -\beta -1}{e}^{{\left(\frac{X_t^{\star }}{\sigma }\right)}^{\beta }}{U}_{ww}}$$ (2.7)

$$c_t=U_w^{-\frac{1}{\alpha }}$$ (2.8)

In this study, because the partial differential equation is not explicitly solvable, we use a numerical method. The key idea underlying this algorithm is the discretization of the wealth–annuity space. The detailed numerical algorithm is demonstrated in Appendix B.

3. Results and discussion

3.1. Annuitization strategy

In this subsection, we display an individual’s annuitization strategy under financial market shock and compare it with that on a regular stock market.

We use an annuity–wealth equilibrium line to represent one’s annuitization strategy, as shown in Fig. 4. That is, when an individual’s endowment is located on the right of the equilibrium line, they will continue to buy more annuities until reaching the equilibrium line. When his or her endowment is located on the left, they will not buy more annuities or surrender his or her existing annuities. This is consistent with the semi-explicit results in Wang and Young (2012).

Fig. 4.

The annuitization strategy on a regular stock market ($r=0.04$, $\lambda =0.04$, $\alpha =2.00$, $p=0.25$). Note: People with endowments on the right-hand side of the annuity–wealth equilibrium line will continue to buy annuities until they reach the equilibrium line. People with endowments on the left-hand side of the equilibrium line will neither buy more annuities nor surrender their existing annuities.

Fig. 5 compares the annuitization strategy under financial market shock and a regular stock market. We find that in the financial market shock scenario, people will have more annuities and less wealth. More specifically, those retirees with an amount of wealth that exceeds a certain threshold would decide to keep only a certain amount in the wealth account and the rest in the annuity account. Therefore, after the occurrence of a financial market shock, those who are endowed with a relatively small amount of wealth are motivated to go from doing nothing to buying more annuities.

Fig. 5.

The comparison of the annuity–wealth equilibrium line under financial market shock and on a regular stock market ($r=0.04$, $\lambda =0.04$, $\alpha =2.00$, $p=0.25$, $\delta =1.50$). Note: This shows that people with a probability distortion function on the perceived stock price distribution will have more annuities and less wealth. In other words, the probability distortion function drives people to buy more annuities until they reach the equilibrium state.

We find this result to be mostly consistent with the reality during the COVID-19 pandemic. According to LIMRA Secure Retirement Institute data, total annuity sales in the US dropped 14% below those of 2019 to 159.2 billion during the first 9 months of 2020, whereas registered index-linked annuity (RILAs) sales increased 26% from those of 2019 in the first 9 months of 2020, which was extraordinarily attractive during the economic downturn. We believe the reason for its strong performance during the COVID-19 pandemic is that the RILA is an annuity that offers investment growth opportunity when limiting downside risk.

There is theoretical support in the existing literature concluding that this asymmetric, two-sided probability distortion function, which skews the loss side more than the gain side, mainly works to increase an individual’s risk aversion (Hong et al., 1987, Jaspersen et al., 2019). This conclusion largely supports our results that annuity purchases increased, especially during the recent COVID-19 pandemic, as the downward US stock market price was still the primary trend.

3.2. Investment strategy

Maximizing the portion of HJB equation that is dependent upon the investment strategy, we explicitly obtain the investment strategy as follows:

$${\pi }_t=-\frac{[\frac{1}{b}\gamma \frac{{\sigma }^{\beta }}{\beta }{X}_t^{\gamma -\beta -1}{e}^{{\left(\frac{X_t}{\sigma }\right)}^{\beta }}+\frac{2}{b}{X}_t^{\gamma -1}{e}^{{\left(\frac{X_t}{\sigma }\right)}^{\beta }}(-1+\frac{2\delta }{1+\delta {\left(\frac{X_t}{\sigma }\right)}^{\beta }})-r]U_w}{2X_t^{\gamma -\beta -1}\frac{{\sigma }^{\beta }}{b\beta }{e}^{{\left(\frac{X_t}{\sigma }\right)}^{\beta }}{U}_{ww}}$$ (3.1)

Fig. 6 compares the investment strategy under financial market shock and that on a regular stock market. The investment strategy under financial market shock is indicated by the pink circle; the one on a regular stock market is displayed by the blue point. Fig. 6 indicates that people tend to invest more under financial market shock than on a regular stock market.

Fig. 6.

The comparison of the investment strategy under financial market shock and the investment strategy on a regular stock market ($r=0.04$, $\lambda =0.04$, $\alpha =2.00$, $p=0.25$, $\delta =1.50$). Note: This figure indicates that people under financial market shock tend to invest more in the stock market than people on the regular market.

We believe there are two reasons. First, this financial market shock was triggered by an exogenous shock, unlike other financial market shocks. Therefore, aside from an economic downturn, there is also occasionally positive news such as government support programs, economic relief policy instruments, and commercial COVID-19 treatment hopes, which precipitate positive economic growth expectations (Seven and Yılmaz, 2021, Zhang et al., 2020, Zaremba et al., 2020). With COVID-19, we have already witnessed crucial changes including improved access to technology and computer literacy, acceptance of remote work, an upgrade of skills, increased education of the workforce, to name a few, all of which indicate positive prospects. In fact, another great health shock in history—the 1918 influenza outbreak—led to the international society a higher level of welfare in the long run, which may have encouraged people to have positive economic growth expectations. Although this influenza caused tremendous loss of life and depressed overall economic activity, it also provided great opportunities to improve various social aspects such as medical technology, the public healthcare system, public health facilities, government emergency power, the social security system, and health-related industries (Garrett, 2007, Barry, 2005). Therefore, as the existing literature has determined, when people hold positive expectations about economic growth, it drives them to seek potential high rates of return.

Second, because on a stock market under financial market shock people buy more annuities, which are designed to protect them from the reduction in consumption, they are more motivated to invest in riskier assets for more future consumption. There is a rich literature demonstrating that an increase in income-related risk makes households less willing to bear a rate-of-return risk, thus reducing their demand for risky securities, and vice versa (Duffie and Zariphopoulou, 1993, Bertaut and Haliassos, 1997, Kimball, 1990).

4. Conclusions

Inspired by the increase in household equity share value relative to domestic market capitalization and retail investors’ trading volume during the recent COVID-19 pandemic, we aim to provide an interpretation of this seemingly unexpected phenomenon that cannot be simply explained by a volatility increase as in the classical literature. In this study, we characterize stock prices’ asymmetric, two-sided skewness during financial market shock conditions as an inverse, S-shaped probability distortion function, build a stochastic portfolio choice model with stocks, bonds, and annuities, and then solve for the optimal investment and annuitization strategies. We find that under financial market shock, individuals tend to buy more annuities and hold riskier assets, which is mostly consistent with reality. We believe this is because of the good fit of the inverse S shaped probability distortion function in capturing the stock price distribution under financial market shock. For one thing, it mainly works to increase individuals’ risk aversion; for another, its positive skewness captures investors’ optimistic economic expectations. Therefore, individuals buy more annuities to guarantee a certain and steady cash flow, whereas they invest in riskier assets to pursue a higher return that is driven by positive expectations about economic growth.

Funding

Wenyuan Zheng gratefully acknowledge financial support from the Ministry of Education of Humanities and Social Science Project Fund of China [Grant 18YJC630263]. Bingqing Li gratefully acknowledges financial support from the National Natural Science Foundation of China [Grant 71671094]. Zhiyong Huang gratefully acknowledges financial support from the National Natural Science Foundation of China [Grant 71804151]. The funder had no role in study design, data collection, and analysis, decision to publish, or preparation of the manuscript.

CRediT authorship contribution statement

Wenyuan Zheng: Conceptualization, Methodology, Formal analysis, Writing Original Draft, Writing - Review & Editing. Bingqing Li: Conceptualization, Methodology, Formal analysis, Writing Original Draft, Writing - Review & Editing, Supervision. Zhiyong Huang: Writing - Review & Editing. Lu Chen: Conceptualization, Methodology, Formal analysis, Writing Original Draft, Writing - Review & Editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.