Abstract
The magnetization M of an Fe(Se, Te) single crystal has been measured as a function of temperature T and dc magnetic field H. The sample properties have been analyzed in the case of a magnetic field parallel to its largest face H||ab. From the M(T) measurement, the Tc of the sample and a magnetic background have been revealed. The superconducting hysteresis loops M(H) were between 2.5 K and 15 K showing a tilt due to the presence of a magnetic signal measured at T > Tc. From the M(H) curves, the critical current density Jc(H) has been extracted at different temperatures showing the presence of a second magnetization peak phenomenon. By extracting and fitting the Jc(T) curves at different fields, a pinning regime crossover has been identified and shown to be responsible for the origin of the second magnetization peak phenomenon. Then, the different kinds of pinning centers of the sample were investigated by means of Dew-Hughes analysis, showing that the pinning mechanism in the sample can be described in the framework of the collective pinning theory. Finally, the values of the pinning force density have been calculated at different temperatures and compared with the literature in order to understand if the sample is promising for high-current and high-power applications.
Keywords: iron-based superconductors, dc magnetic properties, second magnetization peak phenomenon, pinning force, magnetism and superconductivity
1. Introduction
In 2008, the discovery of the iron-based superconductors (IBSs) [1] was received with great interest by the scientific community primarily because it was largely believed that magnetism and superconductivity could not coexist. After the first studies on these new compounds, it was clear that they seemed to overcome the HTS weak points. In fact, the IBSs showed low anisotropy values [2,3,4,5,6,7] and a preferable superconductor–normal–superconductor (SNS) behavior of the grain boundary junctions [8,9,10]. Despite their low Tc values, it has been demonstrated that the IBSs can be suitable for magnet and wire production and/or high-power applications and high-current transport thanks to their high values of critical current density Jc, irreversibility field and upper critical field [11,12,13,14,15,16] as well as their good inter-grain connectivity [8,13,17,18]. Among the various IBS families, the 11 family has attracted a lot of interest due to its very simple crystalline structure and to the possibility of easily doping it with several elements of the periodic table [19,20,21,22,23] in order to improve the superconducting properties of the compounds. Among the compounds of the 11 family, Fe(Se, Te) is one of the most studied compounds in recent years due to its relatively high Tc (for single crystals between 12 K and 14.5 K), its chemical stability and also because it does not present poisonous elements in its stoichiometry. Moreover, the high values of critical current density and upper critical field makes this compound appealing in view of power applications [11,24,25,26]. Among the features of Fe(Se, Te), there is a rich variety of vortex phenomena together with the presence of particular pinning structures (such as columnar defects, twin boundaries, etc.) which can generate the interesting second magnetization peak phenomenon. It is characterized by an anomalous increasing trend of Jc with increasing magnetic fields [27,28,29,30,31,32,33] which attracts even more interest to the samples presenting this phenomenon due to their capability to sustain high currents at high magnetic fields. In this work, we present an analysis of the pinning properties of a single crystal having twin boundaries in the case of a magnetic field applied along its largest face (H||ab). Based on our previous studies, the second magnetization peak phenomenon manifests when the field is applied perpendicular to its largest face (H||c) [34], and we explore further the vortex behavior of the material in the H||ab field configuration in terms of this phenomenon and its associated pinning features. First, we obtained the Tc of the sample by means of an M(T) measurement. Then, we extracted the critical current densities as a function of field from the superconducting hysteresis loops at different temperatures. After that, by fitting the established functional dependencies of Jc(T) at different magnetic fields within the frames of the Kim model and the Dew-Hughes pinning force scaling approach, the different kinds of pinning centers of the Fe(Se, Te) single crystal have been analyzed. In addition, we have identified surface (planar) type pinning centers in certain field and temperature ranges. Finally, starting from the Jc(H) curves, the pinning force density values at different temperatures were calculated and compared with values reported in the literature, confirming the suitability of this material for high-power applications.
2. Materials and Methods
An FeSe0.5Te0.5 twinned single crystal sample with dimensions 3 × 3 × 0.2 mm3 (a × b × c) fabricated by means of the Bridgman technique was analyzed. The fabrication details are reported elsewhere [34]. By means of SEM-EDX analysis, a slightly deviated final stoichiometry Fe0.96Te0.59Se0.45 was found and it is typical for the crystal growth and synthesis in FeSeTe [35,36,37,38] and in the basic compound FeSe [39,40,41]. The sample was characterized using dc magnetic measurements in “parallel field configuration”, i.e., with the magnetic field applied parallel to its largest face (H||ab). The magnetization as a function of the temperature M(T) and of the magnetic field M(H) was measured by means of a Quantum Design PPMS-9T equipped with a VSM option. The residual trapped field inside the PPMS dc magnet was reduced below 1 × 10−4 T before each measurement following the procedure reported elsewhere [42,43]. The M(T) measurement was performed in zero field cooling (ZFC)-field cooling (FC) conditions. In particular, the sample was cooled down to 2.5 K in a zero magnetic field, then a field of 0.01 T was switched on and the data were acquired for increasing temperatures up to 300 K. After that, the sample was cooled down while acquiring FC magnetization. In terms of the M(H) measurements, the sample was cooled down to the measurement temperature in the absence of field and thermally stabilized for about 30 min. Then, the magnetic field was ramped with a sweep rate equal to 0.01 T/s to reach +9 T, then back to −9 T, and finally to +9 T again to acquire the complete hysteresis loop.
The pinning force Fp values, expressed in N/m3, were calculated at different temperatures using the formula where B is the applied magnetic field H expressed in T.
3. Results and Discussion
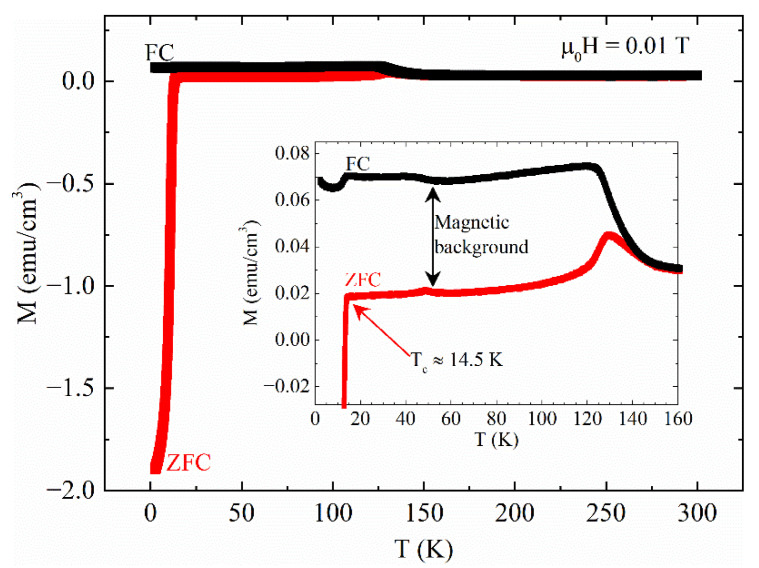
The superconducting critical temperature Tc of the sample was obtained by performing a M(T) measurement in zero field cooling (ZFC)-field cooling (FC) conditions with an applied field of 0.01 T. The result is shown in Figure 1. The Tc was determined as the value of the temperature corresponding to the onset of the ZFC branch. As indicated by a red arrow in the inset of Figure 1, where an enlargement of the curve in the region of the superconducting transition is reported, this value is approximately 14.5 K, in agreement with the literature [38,44,45,46,47]. It is worth underlining the presence of a non-zero signal above Tc in the ZFC magnetization together with a magnetic irreversibility between the ZFC and FC curves (indicated by a double arrow in the inset of Figure 1) usually associated with a magnetic background. This could be due to magnetic impurities present in the sample as already reported for Fe(Se, Te) [35,36,37,38]. It is worth underlining that the magnetic background width in the H||ab configuration (this article) is about 15 times larger than the H||c configuration reported in Ref. [34] on the same sample. This could be ascribed to the fact that the material is magnetically anisotropic and that the magnetic signal is more activated when the field is parallel to the ab face.
Figure 1.
Magnetization as a function of temperature M(T) measured in ZFC-FC conditions with an applied magnetic field H = 0.01 T. Inset: a magnification of the temperature region between 0 K and 160 K shows the presence of a magnetic background. The red arrow indicates the Tc of the sample.
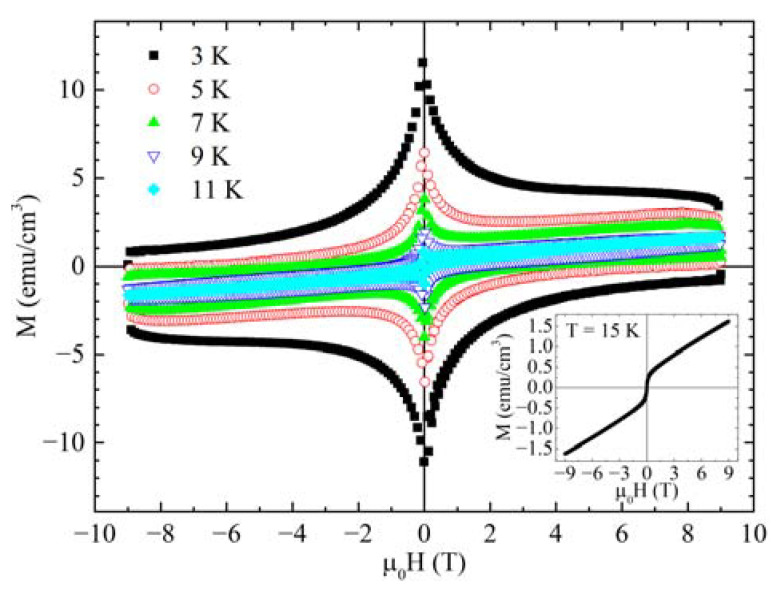
To investigate the superconducting and pinning properties of the sample, the M(H) measurements were performed at different temperatures in the range between 2.5 K and 15 K. In the main panel of Figure 2, the superconducting hysteresis loops are reported. It is important to underline that the curves are slightly tilted due to the presence of the magnetic background. To explore the contribution of the magnetic background to the overall signal, the M(H) curve just above Tc, i.e., T = 15 K, was measured and is shown in the inset of Figure 2. Comparing this curve with the superconducting ones, it can be noted that the M(H) signal at T = 15 K is not negligible, especially at high magnetic fields and high temperatures. Nevertheless, the width of M(H) in the superconducting state is much larger than the hysteresis of the magnetic curve at T = 15 K. However, before calculating the critical current density Jc, the magnetic contribution was subtracted from the superconducting hysteresis loops, by using an analogous procedure to the one reported in Ref. [48], in order to be completely sure that it does not influence the calculation of Jc.
Figure 2.
Superconducting hysteresis loops at different temperatures. Inset: magnetic hysteresis loop at T = 15 K.
At this point, the critical current density as a function of the magnetic field Jc(H) was extracted at different temperatures by using the Bean critical state model [49,50]:
| (1) |
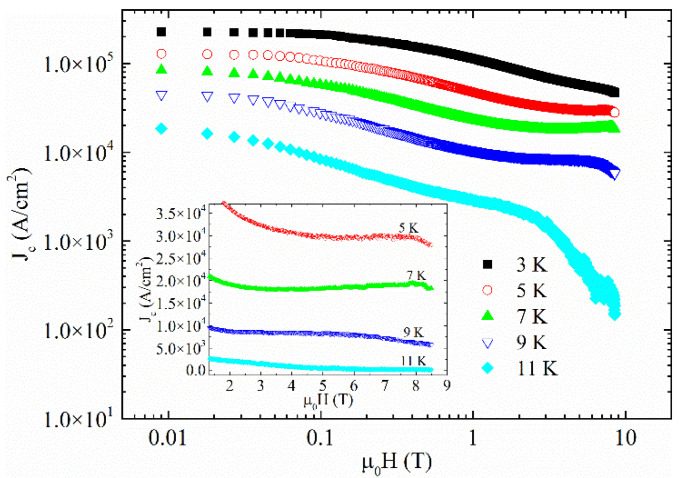
where ΔM = Mdn − Mup is the difference between the magnetization measured for decreasing (Mdn) and increasing (Mup) applied fields, respectively. b (cm) and c (cm) are the length and width of the cross section of the crystal perpendicular to the applied field. The obtained Jc(H) curves are reported in Figure 3. Observing the curves in the main panel and in the inset of Figure 3, it can be noted that a second magnetization peak phenomenon appears for T ≤ 7 K which is not visible at first sight when looking at the M(H) curves. In general, the Jc(H) curves have a field decrease that prevents determining the irreversibility field Hirr (evaluated as Jc ≈ 100 A/cm2) even for the highest temperature shown in Figure 3 (11 K) and at 9 T.
Figure 3.
Critical current densities as a function of field at different temperatures. Inset: a magnification of the curves near the region of the second magnetization peak phenomenon is shown.
In order to deeply study the Jc(H) anomalous behavior reported in Figure 3, the Jc curves as a function of temperature Jc(T) at different fields were extracted from the Jc(H). In particular, by fitting the Jc(T) behavior with several pinning models reported in the literature [51,52,53,54,55,56,57], it is possible to determine the pinning regime acting in the sample. Among the pinning models, the three equations that best fit our experimental data across the field range are the following ones:
| (2) |
| (3) |
| (4) |
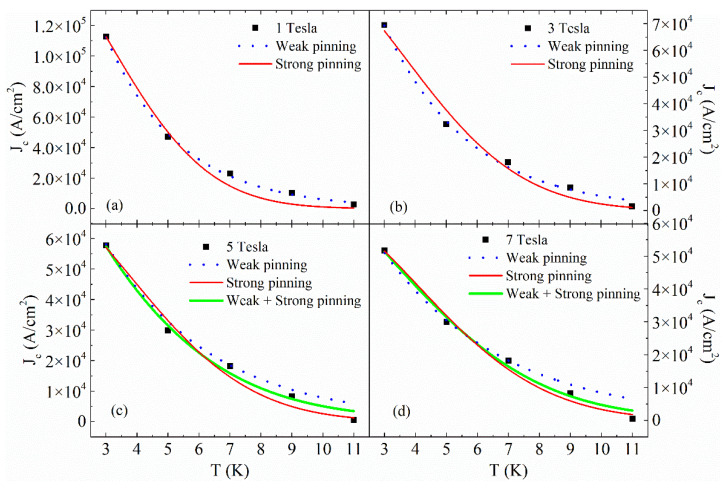
where is the value of Jc at T = 0 K, and T0 is the characteristic pinning energy of weak (typically point-like) pinning defects [58,59,60]; characterizes the contribution to the Jc at T = 0 K and T* is the vortex pinning energy of strong pinning centers [59,61,62,63]. The absolute zero critical current approximation is an important fitting parameter since its physical meaning arbitrarily marks the elimination of the thermal fluctuation effects due to the flux creep. Specifically, the fitting procedure has shown a weak pinning behavior for 0 T < H ≤ 4 T due to point-like defects and a weak + strong pinning behavior for 5 T ≤ H < 9 T due to the gradual activation of the twin boundaries present in this sample. In Figure 4, examples of the performed fit at different magnetic fields are reported while in Table 1 the fit parameters values are reported. In a very recent work on the same sample but in the H||c configuration [33], it has been demonstrated that the weak to strong pinning crossover in a sample presenting the second magnetization peak phenomenon triggers its onset. Here, it is worth underlining that the complete crossover to a strong pinning regime is not reached, indicating a delay in the complete vortex crossover into the strong defects. It is important to note that we are assuming the same triggering mechanism in the H||ab configuration since the results reported in Ref. [33] are independent of anisotropy.
Figure 4.
Temperature dependence of Jc at H = 1 T (a) and H = 3 T (b) fitted with weak pinning equation (blue dotted line) and strong pinning equation (red solid line); temperature dependence of Jc at H = 5 T (c) and H = 7 T (d) fitted with the weak pinning equation (blue dotted line), the strong pinning equation (red solid line) and the combination of weak and strong pinning equations (solid green line).
Table 1.
Parameters values of the fit procedure performed in Figure 4.
| Fit Parameter | ||||
|---|---|---|---|---|
| (A/cm2) | 390,640 | 205,490 | 137,140 | 110,070 |
| T0 (K) | 2.41 | 2.76 | 3.5 | 3.9 |
| (A/cm2) | 177,780 | 93,400 | 77,455 | 67,570 |
| T* (K) | 7.70 | 9.09 | 9.40 | 10.00 |
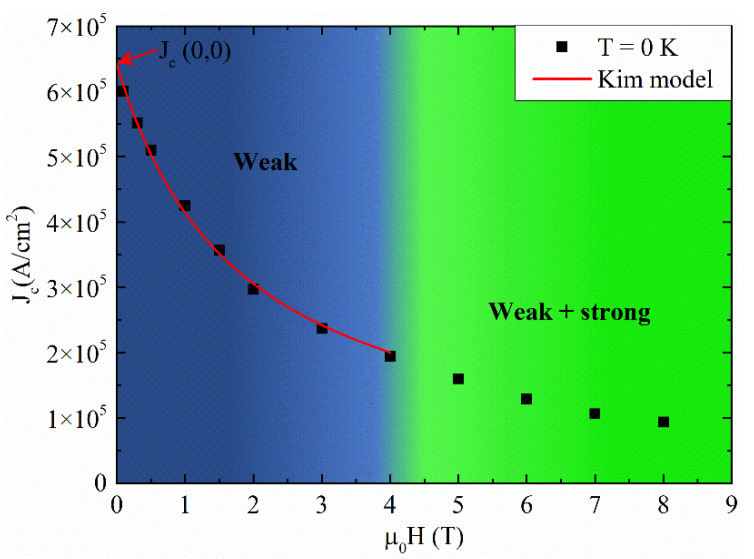
From the fitting procedure, we can determine the Jc(H) at zero temperature dividing its behavior in a weak and a weak + strong pinning region as reported in Figure 5. Moreover, the weak pinning region, highlighted in blue in Figure 5, can be fitted with the dependence expressed by the Kim model well [64,65,66] which is plausible for describing the field behavior of a superconductor in the presence of an homogenous distribution of point-like defects. From the fit reported in Figure 5 (red solid line), the zero field and temperature critical current density Jc(0,0) can be extracted: Jc(0,0) ≈ 6.42 × 105 A/cm2.
Figure 5.
Magnetic field dependence of Jc at T = 0 K. The red solid line is the fit of the Jc(H) at T = 0 K with the Kim model.
In order to obtain more information about the type of defects present in the sample, the Dew-Hughes model [67] can be used. In particular, the normalized pinning force density Fp is calculated and plotted as a function of the reduced magnetic field (h = H/Hirr):
| (5) |
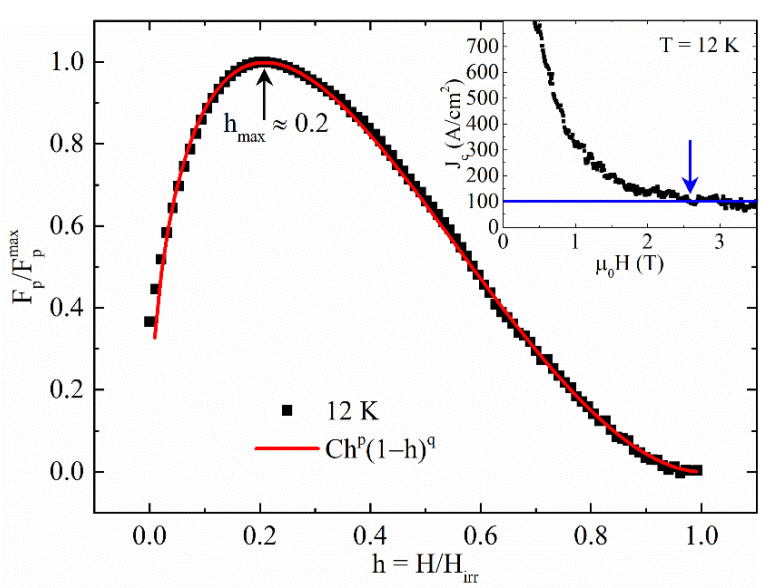
where C, p and q are fitting parameters that allow individuation of the pinning type of the material. Equation (5) takes into account a maximum in the Fp vs. h behavior. In particular, for δl pinning, the Fp/Fpmax maximum occurs at hmax = 0.33 with C = 27.8, p = 1 and q = 2 in the case of point pins, at hmax = 0.20 with C = 3.5, p = 0.5 and q = 2 in the case of surface pins, while no maximum occurs with C = 1, p = 0 and q = 2 in the case of volume pinning. For δTc pinning, the maximum is expected for higher h than δl pinning (see Ref. [67]). Therefore, to use Equation (5), it is necessary to know the irreversibility field but, as mentioned before, this is not possible for the Jc(H) curves up to 11 K. For this reason, the Jc(H) values at T = 12 K have been calculated (see inset of Figure 6). For T = 12 K, Jc is approximately equal to 100 A/cm2 at Hirr = 2.6 T (see the blue arrow in the inset of Figure 6) and so it is possible to apply the Dew-Hughes method. The result is reported in the main panel of Figure 6 where Fp/Fpmax vs. h behavior is shown.
Figure 6.
Normalized pinning force density ( as a function of the reduced magnetic field H/Hirr at T = 12 K fitted with Equation (5) (red solid line). Inset: determination of Hirr at T = 12 K (Hirr = 2.6 T).
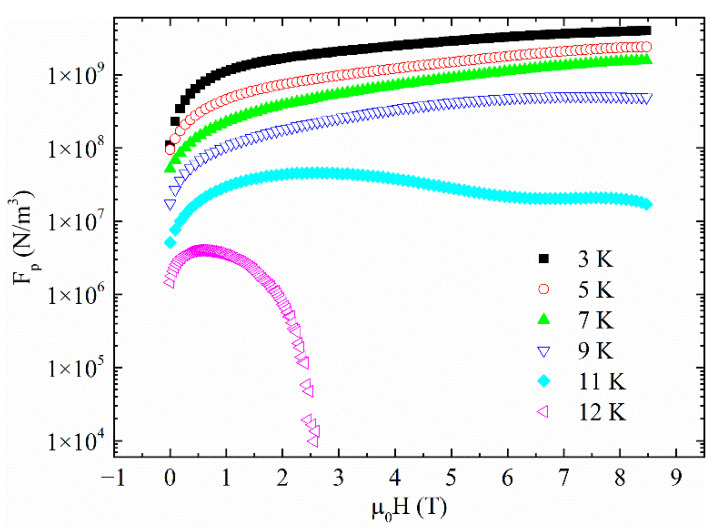
The fit of Equation (5) with the experimental data gives hmax ≈ 0.2 with C = 3.33, p = 0.49 and q = 1.86, thus indicating that the surface pins dominate the pinning mechanism inside our samples at T = 12 K. Finally, since the sample has shown a second magnetization peak phenomenon, it is interesting to study the field dependence of the pinning force at different temperatures and to calculate the pinning force values, comparing them with the literature. The results are reported in Figure 7. It can be noted that the Fp values decrease with increasing temperature following the Jc behavior. On the other hand, it is worth underlining that for T < 9 K, the pinning force curves have a monotonic increasing trend with increasing magnetic field. This feature could be exploited since these temperatures are typically considered for power applications of superconductivity. Moreover, comparing the Fp values with those reported in the literature [16,38,68,69], it can be noted that they are similar to the values reported for other Fe(Se, Te) single crystals (107 ÷ 109 N/m3) but they are much higher if compared with bulk and polycrystalline Fe(Se, Te) samples (105 ÷ 107 N/m3). It is worth underlining that our Fp values have been compared with the H||c field configuration reported in the literature. This is not a problem since it is well known that Fe(Se, Te) is a weakly anisotropic material [6,70,71]. It is also an interesting observation that IBS systems tend to show stronger pinning abilities in samples with high crystalline morphology, such as thin films [11,72,73,74], due to the effective naturally formed disorder. This will have a positive effect on the power stability and performance of various nano/micro-superconducting devices which similarly are affected by the vortex motion. These high pinning force values together with the presence of the second magnetization peak phenomenon indicate that the material can be promising for high-current and high-power applications.
Figure 7.
Pinning force density as a function of field at different temperatures.
4. Conclusions
We have studied an Fe(Se, Te) twinned single crystal fabricated by the Bridgman technique by analyzing the dc magnetic measurements as a function of temperature and magnetic field. In particular, the magnetic field was applied in a parallel field configuration H||ab. By using M(T) measurements, we have obtained Tc = 14.5 K and noted the presence of a magnetic background, probably due to magnetic impurities present in the sample. A magnetic background was also observed in the superconducting hysteresis loops M(H) performed at different temperatures which showed a tilt in their behaviors. After subtracting the magnetic signal, the critical current density Jc at different temperatures was extracted from the M(H) curves, showing the presence of a second magnetization peak phenomenon which allowed the sample to sustain high Jc values even at high magnetic fields. Extracting the Jc(T) curves from the Jc(H) ones, we analyzed them in terms of weak and strong pinning regimes acting in the sample. Based on the Kim model analysis, it was found that in the parallel field geometry, the Fe(Se, Te) crystal (as for H||c in our previous studies) similarly undergoes a pinning crossover from a weak pinning regime, ascribed to planar point-like defects, to a weak + strong pinning regime due to the gradual activation of the twin boundaries. However, in this case the SMP features are much broader and the consequent non-monotonous peak change of Jc is observed only in certain temperature (closer to Tc) and high field ranges. After that, using Dew-Hughes analysis, we identified that the dominating pinning mechanism from surface (planar) defects affects the vortex system at 12 K. Finally, we calculated the pinning force density Fp values, noting that they have an interesting monotonous increasing trend as a function of magnetic field at temperatures exploitable in practical situations. The Fp values of the sample were compared with the ones reported in the literature, noting that they are much higher with respect to the polycrystalline and bulk sample values, confirming the suitability of the sample in its use for high-power applications.
Acknowledgments
The authors acknowledge the project ‘HiBiSCUS’—Grant No. 201785KWLE, supported by MIUR-PRIN. Moreover, this work has been carried out within the framework of the inter-academic Italian–Bulgarian research project 2019–2021 (Department of Physics ‘E R Caianiello’—CNR-SPIN unit, University of Salerno and the Institute of Solid State Physics ‘Georgi Nadjakov’, Bulgarian Academy of Sciences).
Author Contributions
Conceptualization, A.G., K.B. and E.N.; methodology, A.G. and K.B.; validation, A.G., K.B. and M.P.; formal analysis, A.G. and A.L.; investigation, A.G., K.B., V.T., A.L. and G.G.; resources, G.G.; data curation, A.G., K.B., V.T. and E.N.; writing—original draft preparation, A.G. and K.B.; writing—review and editing, V.T., E.N., A.L., G.G. and M.P.; visualization, E.N., G.G. and M.P.; supervision, G.G. and M.P.; project administration, G.G. and M.P.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project ‘HiBiSCUS’—Grant No. 201785KWLE, supported by MIUR-PRIN.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data sets that support the findings in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kamihara Y., Watanabe T., Hirano M., Hosono H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008;130:3296–3297. doi: 10.1021/ja800073m. [DOI] [PubMed] [Google Scholar]
- 2.Yuan H.Q., Singleton J., Balakirev F.F., Baily S.A., Chen G.F., Luo J.L., Wang N.L. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature. 2009;457:565–568. doi: 10.1038/nature07676. [DOI] [PubMed] [Google Scholar]
- 3.Yamamoto A., Jaroszynski J., Tarantini C., Balicas L., Jiang J., Gurevich A., Larbalestier D.C., Jin R., Sefat A.S., McGuire M.A., et al. Small anisotropy, weak thermal fluctuations, and high field superconductivity in Co-doped iron pnictide Ba(Fe1−xCox)2As2. Appl. Phys. Lett. 2009;94:062511. doi: 10.1063/1.3081455. [DOI] [Google Scholar]
- 4.Tarantini C., Gurevich A., Jaroszynski J., Balakirev F., Bellingeri E., Pallecchi I., Ferdeghini C., Shen B., Wen H.H., Larbalestier D.C. Significant enhancement of upper critical fields by doping and strain in iron-based superconductors. Phys. Rev. B Condens. Matter Mater. Phys. 2011;84:184522. doi: 10.1103/PhysRevB.84.184522. [DOI] [Google Scholar]
- 5.Galluzzi A., Buchkov K.M., Nazarova E., Tomov V., Grimaldi G., Leo A., Pace S., Polichetti M. Pinning energy and anisotropy properties of a Fe(Se, Te) iron based superconductor. Nanotechnology. 2019;30:254001. doi: 10.1088/1361-6528/ab0c23. [DOI] [PubMed] [Google Scholar]
- 6.Grimaldi G., Leo A., Martucciello N., Braccini V., Bellingeri E., Ferdeghini C., Galluzzi A., Polichetti M., Nigro A., Villegier J.-C., et al. Weak or Strong Anisotropy in Fe(Se, Te) Superconducting Thin Films Made of Layered Iron-Based Material? IEEE Trans. Appl. Supercond. 2019;29:2895744. doi: 10.1109/TASC.2019.2895744. [DOI] [Google Scholar]
- 7.Leo A., Braccini V., Bellingeri E., Ferdeghini C., Galluzzi A., Polichetti M., Nigro A., Pace S., Grimaldi G. Anisotropy effects on the quenching current of Fe(Se, Te) Thin Films. IEEE Trans. Appl. Supercond. 2018;28:8234633. doi: 10.1109/TASC.2017.2786460. [DOI] [Google Scholar]
- 8.Katase T., Ishimaru Y., Tsukamoto A., Hiramatsu H., Kamiya T., Tanabe K., Hosono H. Advantageous grain boundaries in iron pnictide superconductors. Nat. Commun. 2011;2:409. doi: 10.1038/ncomms1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Galluzzi A., Polichetti M., Buchkov K., Nazarova E., Mancusi D., Pace S. Evaluation of the intragrain critical current density in a multidomain FeSe crystal by means of dc magnetic measurements. Supercond. Sci. Technol. 2015;28:115005. doi: 10.1088/0953-2048/28/11/115005. [DOI] [Google Scholar]
- 10.De Gennes P.G. Boundary effects in superconductors. Rev. Mod. Phys. 1964;36:225–237. doi: 10.1103/RevModPhys.36.225. [DOI] [Google Scholar]
- 11.Lei H., Wang K., Hu R., Ryu H., Abeykoon M., Bozin E.S., Petrovic C. Iron chalcogenide superconductors at high magnetic fields. Sci. Technol. Adv. Mater. 2012;13:054305. doi: 10.1088/1468-6996/13/5/054305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Galluzzi A., Buchkov K., Tomov V., Nazarova E., Kovacheva D., Leo A., Grimaldi G., Pace S., Polichetti M. Mixed state properties of iron based Fe(Se, Te) superconductor fabricated by Bridgman and by self-flux methods. J. Appl. Phys. 2018;123:233904. doi: 10.1063/1.5032202. [DOI] [Google Scholar]
- 13.Hosono H., Yamamoto A., Hiramatsu H., Ma Y. Recent advances in iron-based superconductors toward applications. Mater. Today. 2018;21:278–302. doi: 10.1016/j.mattod.2017.09.006. [DOI] [Google Scholar]
- 14.Galluzzi A., Buchkov K., Nazarova E., Tomov V., Grimaldi G., Leo A., Pace S., Polichetti M. Transport properties and high upper critical field of a Fe(Se, Te) iron based superconductor. Eur. Phys. J. Spec. Top. 2019;228:725–731. doi: 10.1140/epjst/e2019-800169-5. [DOI] [Google Scholar]
- 15.Si W., Han S.J., Shi X., Ehrlich S.N., Jaroszynski J., Goyal A., Li Q. High current superconductivity in FeSe0.5Te0.5 coated conductors at 30 tesla. Nat. Commun. 2013;4:1347. doi: 10.1038/ncomms2337. [DOI] [PubMed] [Google Scholar]
- 16.Zignani C.F., De Marzi G., Corato V., Mancini A., Vannozzi A., Rufoloni A., Leo A., Guarino A., Galluzzi A., Nigro A., et al. Improvements of high-field pinning properties of polycrystalline Fe(Se, Te) material by heat treatments. J. Mater. Sci. 2019;54:5092–5100. doi: 10.1007/s10853-018-03218-5. [DOI] [Google Scholar]
- 17.Ma Y. Progress in wire fabrication of iron-based superconductors. Supercond. Sci. Technol. 2012;25:113001. doi: 10.1088/0953-2048/25/11/113001. [DOI] [Google Scholar]
- 18.Nazarova E., Balchev N., Nenkov K., Buchkov K., Kovacheva D., Zahariev A., Fuchs G. Transport and pinning properties of Ag-doped FeSe0.94. Supercond. Sci. Technol. 2015;28:025013. doi: 10.1088/0953-2048/28/2/025013. [DOI] [Google Scholar]
- 19.Chen N., Ma Z., Liu Y., Li X., Cai Q., Li H., Yu L. Influence of Sn doping on the phase formation and superconductivity of FeSe0.93. J. Alloys Compd. 2014;588:418–421. doi: 10.1016/j.jallcom.2013.11.121. [DOI] [Google Scholar]
- 20.Lan F., Ma Z.Q., Liu Y.C., Chen N., Cai Q., Li H., Barua S., Patel D., Hossain M.S.A., Kim J.H., et al. The formation of nano-layered grains and their enhanced superconducting transition temperature in Mg-doped FeSe0.9 bulks. Sci. Rep. 2014;4:6481. doi: 10.1038/srep06481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nazarova E., Balchev N., Nenkov K., Buchkov K., Kovacheva D., Zahariev A., Fuchs G. Improvement of the superconducting properties of polycrystalline FeSe by silver addition. Supercond. Sci. Technol. 2015;28:125013. doi: 10.1088/0953-2048/28/12/125013. [DOI] [Google Scholar]
- 22.Sudesh, Rani S., Varma G.D. Effect of Sb and Si doping on the superconducting properties of FeSe0.9. Phys. C Supercond. Appl. 2013;485:137–144. doi: 10.1016/j.physc.2012.12.001. [DOI] [Google Scholar]
- 23.Liu C.-J., Bhaskar A., Huang H.-J., Lin F.-H. Transport properties of Bi-doped FeSe superconductor up to 700 K. Appl. Phys. Lett. 2014;104:252602. doi: 10.1063/1.4885718. [DOI] [Google Scholar]
- 24.Mizuguchi Y., Takano Y. Review of Fe chalcogenides as the simplest Fe-based superconductor. J. Phys. Soc. Japan. 2010;79:102001. doi: 10.1143/JPSJ.79.102001. [DOI] [Google Scholar]
- 25.Mizuguchi Y., Deguchi K., Tsuda S., Yamaguchi T., Takeya H., Kumakura H., Takano Y. Fabrication of the Iron-Based Superconducting Wire Using Fe(Se, Te) Appl. Phys. Express. 2009;2:083004. doi: 10.1143/APEX.2.083004. [DOI] [Google Scholar]
- 26.Palombo M., Malagoli A., Pani M., Bernini C., Manfrinetti P., Palenzona A., Putti M. Exploring the feasibility of Fe(Se, Te) conductors by ex-situ powder-in-tube method. J. Appl. Phys. 2015;117:213903. doi: 10.1063/1.4921902. [DOI] [Google Scholar]
- 27.Miu D., Noji T., Adachi T., Koike Y., Miu L. On the nature of the second magnetization peak in FeSe1−xTex single crystals. Supercond. Sci. Technol. 2012;25:115009. doi: 10.1088/0953-2048/25/11/115009. [DOI] [Google Scholar]
- 28.Tamegai T., Sun Y., Yamada T., Pyon S. Critical Current Density and Vortex Dynamics in Fe(Te,Se) Annealed in Various Atmosphere. IEEE Trans. Appl. Supercond. 2016;26:1–5. doi: 10.1109/TASC.2016.2542000. [DOI] [Google Scholar]
- 29.Galluzzi A., Buchkov K., Tomov V., Nazarova E., Leo A., Grimaldi G., Nigro A., Pace S., Polichetti M. Second Magnetization Peak Effect in a Fe(Se, Te) iron based superconductor; Proceedings of the Journal of Physics: Conference Series; Salerno, Italy. 10–13 July 2018; Bristol, UK: IOP Publishing; 2019. p. 012012. [DOI] [Google Scholar]
- 30.Bonura M., Giannini E., Viennois R., Senatore C. Temperature and time scaling of the peak-effect vortex configuration in FeTe0.7Se0.3. Phys. Rev. B. 2012;85:134532. doi: 10.1103/PhysRevB.85.134532. [DOI] [Google Scholar]
- 31.Hossaini S.J., Ghorbani S.R., Arabi H., Wang X.L., Lin C.T. Temperature and field dependence of the flux pinning mechanisms in Fe1.06Te0.6Se0.4 single crystal. Solid State Commun. 2016;246:29–32. doi: 10.1016/j.ssc.2016.07.030. [DOI] [Google Scholar]
- 32.Das P., Thakur A.D., Yadav A.K., Tomy C.V., Lees M.R., Balakrishnan G., Ramakrishnan S., Grover A.K. Magnetization hysteresis and time decay measurements in FeSe0.50Te0.50: Evidence for fluctuation in mean free path induced pinning. Phys. Rev. B Condens. Matter Mater. Phys. 2011;84:214526. doi: 10.1103/PhysRevB.84.214526. [DOI] [Google Scholar]
- 33.Polichetti M., Galluzzi A., Buchkov K., Tomov V., Nazarova E., Leo A., Grimaldi G., Pace S. A precursor mechanism triggering the second magnetization peak phenomenon in superconducting materials. Sci. Rep. 2021;11:7247. doi: 10.1038/s41598-021-86728-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Galluzzi A., Buchkov K., Tomov V., Nazarova E., Leo A., Grimaldi G., Nigro A., Pace S., Polichetti M. Evidence of pinning crossover and the role of twin boundaries in the peak effect in FeSeTe iron based superconductor. Supercond. Sci. Technol. 2018;31:015014. doi: 10.1088/1361-6668/aa9802. [DOI] [Google Scholar]
- 35.Tsurkan V., Deisenhofer J., Günther A., Kant C., Klemm M., von Nidda H.-A., Schrettle F., Loidl A. Physical properties of FeSe0.5Te0.5 single crystals grown under different conditions. Eur. Phys. J. B. 2011;79:289–299. doi: 10.1140/epjb/e2010-10473-5. [DOI] [Google Scholar]
- 36.Wittlin A., Aleshkevych P., Przybylińska H., Gawryluk D.J., Dłuzewski P., Berkowski M., Puźniak R., Gutowska M.U., Wiśniewski A. Microstructural magnetic phases in superconducting FeTe0.65Se0.35. Supercond. Sci. Technol. 2012;25:065019. doi: 10.1088/0953-2048/25/6/065019. [DOI] [Google Scholar]
- 37.Sivakov A.G., Bondarenko S.I., Prokhvatilov A.I., Timofeev V.P., Pokhila A.S., Koverya V.P., Dudar I.S., Link S.I., Legchenkova I.V., Bludov A.N., et al. Microstructural and transport properties of superconducting FeTe0.65Se0.35 crystals. Supercond. Sci. Technol. 2017;30:015018. doi: 10.1088/0953-2048/30/1/015018. [DOI] [Google Scholar]
- 38.Zignani C.F., De Marzi G., Grimaldi G., Leo A., Guarino A., Vannozzi A., della Corte A., Pace S. Fabrication and Physical Properties of Polycrystalline Iron-Chalcogenides Superconductors. IEEE Trans. Appl. Supercond. 2017;27:1–5. doi: 10.1109/TASC.2016.2646063. [DOI] [Google Scholar]
- 39.McQueen T.M., Huang Q., Ksenofontov V., Felser C., Xu Q., Zandbergen H., Hor Y.S., Allred J., Williams A.J., Qu D., et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B. 2009;79:014522. doi: 10.1103/PhysRevB.79.014522. [DOI] [Google Scholar]
- 40.Onar K., Yakinci M.E. Solid state synthesis and characterization of bulk β-FeSe superconductors. J. Alloys Compd. 2015;620:210–216. doi: 10.1016/j.jallcom.2014.09.045. [DOI] [Google Scholar]
- 41.Zignani C.F., Corato V., Leo A., De Marzi G., Mancini A., Takano Y., Yamashita A., Polichetti M., Galluzzi A., Rufoloni A., et al. Fabrication and Characterization of Sintered Iron-Chalcogenide Superconductors. IEEE Trans. Appl. Supercond. 2016;26:1–5. doi: 10.1109/TASC.2016.2539978. [DOI] [Google Scholar]
- 42.Galluzzi A., Mancusi D., Cirillo C., Attanasio C., Pace S., Polichetti M. Determination of the Transition Temperature of a Weak Ferromagnetic Thin Film by Means of an Evolution of the Method Based on the Arrott Plots. J. Supercond. Nov. Magn. 2018;31:1127–1132. doi: 10.1007/s10948-017-4281-4. [DOI] [Google Scholar]
- 43.Galluzzi A., Nigro A., Fittipaldi R., Guarino A., Pace S., Polichetti M. DC magnetic characterization and pinning analysis on Nd1.85Ce0.15CuO4 cuprate superconductor. J. Magn. Magn. Mater. 2019;475:125–129. doi: 10.1016/j.jmmm.2018.11.119. [DOI] [Google Scholar]
- 44.Mizuguchi Y., Tomioka F., Tsuda S., Yamaguchi T., Takano Y. Substitution Effects on FeSe Superconductor. J. Phys. Soc. Japan. 2009;78:074712. doi: 10.1143/JPSJ.78.074712. [DOI] [Google Scholar]
- 45.Sales B.C., Sefat A.S., McGuire M.A., Jin R.Y., Mandrus D., Mozharivskyj Y. Bulk superconductivity at 14 K in single crystals of Fe1+yTexSe1−x. Phys. Rev. B Condens. Matter Mater. Phys. 2009;79:094521. doi: 10.1103/PhysRevB.79.094521. [DOI] [Google Scholar]
- 46.Putti M., Pallecchi I., Bellingeri E., Cimberle M.R., Tropeano M., Ferdeghini C., Palenzona A., Tarantini C., Yamamoto A., Jiang J., et al. New Fe-based superconductors: Properties relevant for applications. Supercond. Sci. Technol. 2010;23:034003. doi: 10.1088/0953-2048/23/3/034003. [DOI] [Google Scholar]
- 47.Yeh K.-W., Huang T.-W., Huang Y., Chen T.-K., Hsu F.-C., Wu P.M., Lee Y.-C., Chu Y.-Y., Chen C.-L., Luo J.-Y., et al. Tellurium substitution effect on superconductivity of the α-phase iron selenide. EPL (Europhys. Lett.) 2008;84:37002. doi: 10.1209/0295-5075/84/37002. [DOI] [Google Scholar]
- 48.Galluzzi A., Polichetti M., Buchkov K., Nazarova E., Mancusi D., Pace S. Critical current and flux dynamics in Ag-doped FeSe superconductor. Supercond. Sci. Technol. 2017;30:025013. doi: 10.1088/1361-6668/30/2/025013. [DOI] [Google Scholar]
- 49.Bean C.P. Magnetization of hard superconductors. Phys. Rev. Lett. 1962;8:250–253. doi: 10.1103/PhysRevLett.8.250. [DOI] [Google Scholar]
- 50.Bean C.P. Magnetization of High-Field Superconductors. Rev. Mod. Phys. 1964;36:31–39. doi: 10.1103/RevModPhys.36.31. [DOI] [Google Scholar]
- 51.Griessen R., Hai-Hu W., Van Dalen A.J.J., Dam B., Rector J., Schnack H.G., Libbrecht S., Osquiguil E., Bruynseraede Y. Evidence for mean free path fluctuation induced pinning in YBa2Cu3O7 and YBa2Cu4O8 films. Phys. Rev. Lett. 1994;72:1910–1913. doi: 10.1103/PhysRevLett.72.1910. [DOI] [PubMed] [Google Scholar]
- 52.Savvides N. Flux creep and transport critical current density in high-Tc superconductors. Phys. C Supercond. 1990;165:371–376. doi: 10.1016/0921-4534(90)90369-P. [DOI] [Google Scholar]
- 53.Murakami M., Fujimoto H., Gotoh S., Yamaguchi K., Koshizuka N., Tanaka S. Flux pinning due to nonsuperconducting particles in melt processed YBaCuO superconductors. Phys. C Supercond. 1991;185–189:321–326. doi: 10.1016/0921-4534(91)91993-E. [DOI] [Google Scholar]
- 54.Yeshurun Y., Malozemoff A.P. Giant flux creep and irreversibility in an Y-Ba-Cu-O crystal: An alternative to the superconducting-glass model. Phys. Rev. Lett. 1988;60:2202–2205. doi: 10.1103/PhysRevLett.60.2202. [DOI] [PubMed] [Google Scholar]
- 55.Jackson D.J.C., Das M.P. Melting of the flux line lattice. Supercond. Sci. Technol. 1996;9:713–727. doi: 10.1088/0953-2048/9/9/001. [DOI] [Google Scholar]
- 56.Yom S.S., Hahn T.S., Kim Y.H., Chu H., Choi S.S. Exponential temperature dependence of the critical transport current in Y-Ba-Cu-O thin films. Appl. Phys. Lett. 1989;54:2370. doi: 10.1063/1.101531. [DOI] [Google Scholar]
- 57.Hsiang T.Y., Finnemore D.K. Superconducting critical currents for thick, clean superconductor—Normal-metal—Superconductor junctions. Phys. Rev. B. 1980;22:154–163. doi: 10.1103/PhysRevB.22.154. [DOI] [Google Scholar]
- 58.Blatter G., Feigel’Man M.V., Geshkenbein V.B., Larkin A.I., Vinokur V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994;66:1125–1388. doi: 10.1103/RevModPhys.66.1125. [DOI] [Google Scholar]
- 59.Polat A., Sinclair J.W., Zuev Y.L., Thompson J.R., Christen D.K., Cook S.W., Kumar D., Chen Y., Selvamanickam V. Thickness dependence of magnetic relaxation and E-J characteristics in superconducting (Gd-Y)-Ba-Cu-O films with strong vortex pinning. Phys. Rev. B Condens. Matter Mater. Phys. 2011;84:024519. doi: 10.1103/PhysRevB.84.024519. [DOI] [Google Scholar]
- 60.Christen D.K., Thompson R. Current problems at high Tc. Nature. 1993;364:98–99. doi: 10.1038/364098a0. [DOI] [Google Scholar]
- 61.Plain J., Puig T., Sandiumenge F., Obradors X., Rabier J. Microstructural influence on critical currents and irreversibility line in melt-textured YBa2Cu3O7-x reannealed at high oxygen pressure. Phys. Rev. B. 2002;65:104526. doi: 10.1103/PhysRevB.65.104526. [DOI] [Google Scholar]
- 62.Nelson D.R., Vinokur V.M. Boson localization and correlated pinning of superconducting vortex arrays. Phys. Rev. B. 1993;48:13060–13097. doi: 10.1103/PhysRevB.48.13060. [DOI] [PubMed] [Google Scholar]
- 63.Hwa T., Le Doussal P., Nelson D.R., Vinokur V.M. Flux pinning and forced vortex entanglement by splayed columnar defects. Phys. Rev. Lett. 1993;71:3545–3548. doi: 10.1103/PhysRevLett.71.3545. [DOI] [PubMed] [Google Scholar]
- 64.Kim Y.B., Hempstead C.F., Strnad A.R. Critical Persistent Currents in Hard Superconductors. Phys. Rev. Lett. 1962;9:306–309. doi: 10.1103/PhysRevLett.9.306. [DOI] [Google Scholar]
- 65.Kim Y.B., Hempstead C.F., Strnad A.R. Magnetization and Critical Supercurrents. Phys. Rev. 1963;129:528–535. doi: 10.1103/PhysRev.129.528. [DOI] [Google Scholar]
- 66.Poole C.P. Superconductivity. Academic Press; Cambridge, MA, USA: 2007. [Google Scholar]
- 67.Dew-Hughes D. Flux pinning mechanisms in type II superconductors. Philos. Mag. 1974;30:293–305. doi: 10.1080/14786439808206556. [DOI] [Google Scholar]
- 68.Yadav C.S., Paulose P.L. The flux pinning force and vortex phase diagram of single crystal FeTe0.60Se0.40. Solid State Commun. 2011;151:216–218. doi: 10.1016/j.ssc.2010.11.030. [DOI] [Google Scholar]
- 69.Onar K., Özçelik B., Güler N.K., Okazaki H., Takeya H., Takano Y., Yakinci M.E. Enhanced physical properties of single crystal Fe0.99Te0.63Se0.37 prepared by self-flux synthesis method. J. Alloys Compd. 2016;683:164–170. doi: 10.1016/j.jallcom.2016.05.086. [DOI] [Google Scholar]
- 70.Yuan F., Iida K., Langer M., Hänisch J., Ichinose A., Tsukada I., Sala A., Putti M., Hühne R., Schultz L., et al. Influence of substrate type on transport properties of superconducting FeSe0.5Te0.5 thin films. Supercond. Sci. Technol. 2015;28:065005. doi: 10.1088/0953-2048/28/6/065005. [DOI] [Google Scholar]
- 71.Leo A., Sylva G., Braccini V., Bellingeri E., Martinelli A., Pallecchi I., Ferdeghini C., Pellegrino L., Putti M., Ghigo G., et al. Anisotropic Effect of Proton Irradiation on Pinning Properties of Fe(Se, Te) Thin Films. IEEE Trans. Appl. Supercond. 2019;29:1–5. doi: 10.1109/TASC.2019.2893592. [DOI] [Google Scholar]
- 72.Si W., Zhou J., Jie Q., Dimitrov I., Solovyov V., Johnson P.D., Jaroszynski J., Matias V., Sheehan C., Li Q. Iron-chalcogenide FeSe0.5Te0.5 coated superconducting tapes for high field applications. Appl. Phys. Lett. 2011;98:262509. doi: 10.1063/1.3606557. [DOI] [Google Scholar]
- 73.Mele P. Superconducting properties of iron chalcogenide thin films. Sci. Technol. Adv. Mater. 2012;13:054301. doi: 10.1088/1468-6996/13/5/054301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Ozaki T., Wu L., Zhang C., Si W., Jie Q., Li Q. Enhanced critical current in superconducting FeSe0.5Te0.5 films at all magnetic field orientations by scalable gold ion irradiation. Supercond. Sci. Technol. 2018;31:024002. doi: 10.1088/1361-6668/aaa3c4. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data sets that support the findings in this study are available from the corresponding author upon reasonable request.