Out-of-Equilibrium Biophysical Chemistry: The Case for Multidimensional, Integrated Single-Molecule Approaches

Abstract

Out-of-equilibrium processes are ubiquitous across living organisms and all structural hierarchies of life. At the molecular scale, out-of-equilibrium processes (for example, enzyme catalysis, gene regulation, and motor protein functions) cause biological macromolecules to sample an ensemble of conformations over a wide range of time scales. Quantifying and conceptualizing the structure–dynamics to function relationship is challenging because continuously evolving multidimensional energy landscapes are necessary to describe nonequilibrium biological processes in biological macromolecules. In this perspective, we explore the challenges associated with state-of-the-art experimental techniques to understanding biological macromolecular function. We argue that it is time to revisit how we probe and model functional out-of-equilibrium biomolecular dynamics. We suggest that developing integrated single-molecule multiparametric force–fluorescence instruments and using advanced molecular dynamics simulations to study out-of-equilibrium biomolecules will provide a path towards understanding the principles of and mechanisms behind the structure–dynamics to function paradigm in biological macromolecules.

Structure–Dynamics–Function Relationship in Biomolecules

The biological macromolecules that comprise life have long been considered to have a robust structure–function relationship.¹ Structure seems to determine function in some biomolecules, while function drives structure for others.¹ Either way, the structure–function paradigm provides a widely successful framework for understanding the molecular origins of life. However, the structure–function paradigm portrays a static picture of biomolecules in living organisms. Functional biomolecules are often dynamic; they undergo large structural transitions and small fluctuations essential to their physiological functions.² Functional biomolecules also can be unstructured. Both intrinsically disordered proteins (IDPs)³⁻⁵ and proteins with intrinsically disordered regions (IDRs)^6,7 have critical biological functions. Thus, the paradigm for understanding biomolecular mechanisms is shifting from a structure–function toward a structure–dynamics–function relationship.

Molecular biophysics research aims to detail the mechanistic principles underlying the structure–dynamics–function relationships in biomolecular systems (for definitions of terms first used in italics, see Box 1). Biophysicists characterize biomolecular systems by their free energy states and transitions between them due to both equilibrium and nonequilibrium processes. In this free energy framework, some transitions are large, slow (greater than microsecond) changes in structural conformation between the macrostates of a system,⁸⁻¹¹ like protein domain rearrangements.¹² Other transitions are small, fast (less than microsecond) changes in structural configuration among energetically similar microstates within a conformational macrostate. Transitions between microstates include small-scale displacements like amino acid side chain rotations and solvent interaction changes, as well as larger-scale displacements, like protein backbone fluctuations in secondary structures and loops.^10,13

Free energy landscapes(14−17) model a system as a continuum of thermodynamic states at equilibrium,¹⁸ often with significantly reduced dimensionality (1 or 2 dimensions down from 3N – 6, see Box 1).¹⁹ However, from whole organisms down to individual macromolecules, living systems function under out-of-equilibrium conditions²⁰⁻²² and with complex multidimensional dynamics. While conventional free energy landscapes are widely successful at explaining the folding and functional data for relatively simple biomolecular systems at thermodynamic equilibrium, they struggle to explain multidimensional processes involving nonequilibrium conditions.

In this Perspective, we discuss the role free energy landscapes play in models and our understanding of functional mechanisms in biomolecules. There are many excellent reviews of folding energy landscapes,²³⁻²⁷ so here we focus on functional, rather than folding, biomolecular processes. We illustrate some limitations of the energy landscape paradigm and highlight the benefits of extending the current theoretical framework, experimental approaches, and means to represent data to improve our understanding of complex, nonequilibrium biomolecular function.

Definitions of Key Terms As We Use Them in This Perspective

Box 1.

Key Definitions:

• Biomolecular system (abbreviated herein as system): a closed thermodynamic system consisting of a biomolecule or biomolecular assembly that is distinct from and does not exchange matter with the environment.

• Environment (or surroundings): the matter in the proximity of a system but not included in the designation of the system. The environment consists of coordinating biomolecules, small molecules, ions, and solvent molecules.

• Gibbs free energy (abbreviated herein as free energy): the internal energy of a system, or the potential of that system available to perform work. Changes in free energy of a system, ΔG, are ΔG = ΔH – TΔS where ΔH is the change in the enthalpy, T is the absolute temperature, and ΔS is the change in the entropy of the system.

• Equilibrium process: a transition in thermodynamic state that occurs without the net transfer of energy into or out of the system

• Nonequilibrium process (also out-of-equilibrium or far-from-equilibrium): a transition in thermodynamic state that occurs due to or results in the net transfer of energy into or out of the system

• Macrostate: a long-lived (microsecond or longer) state corresponding to a local free energy minimum of a system. A macrostate is often associated with a biomolecule’s function or as an element of a more complex, multistep functional process.

• Microstate: a short-lived (microsecond or shorter) state corresponding to the specific free energy of a system, often very close in energy to a macrostate and associated with thermal fluctuations. The collection of microstates near to a local energy minimum constitute a macrostate.

• Structural conformation: the set of structures, often represented by a mean structure or lowest energy structure, associated with a macrostate

• Structural configuration: the specific structure associated with a microstate

• Free energy landscape (abbreviated herein as energy landscape or landscape): the mapping of all thermodynamically accessible Gibbs free energy states of a system in multidimensional configuration space where the 3N – 6 dimensions correspond to the positions (x, y, z) of all N atoms within the system.

• Reaction coordinate: the curvilinear path through the energy landscape that is consistent with the system’s Hamiltonian²⁸ and defines the path of least action. It represents the most probable sequence of structural transitions taken by a system between macrostates. The reaction coordinate is found analytically or computationally by analyzing a complete energy landscape.^29,30

• Observable coordinate: the coordinate on which experimental observations of free energy are made in biomolecular systems. The observable coordinate is easily conflated with the reaction coordinate in the interpretation of experimental results, but it is frequently independent of the reaction coordinate.

• Detailed balance: a thermodynamic principle of kinetic systems that states that each elementary process a complex or cyclic system can perform (i.e., a transition from macrostate A to macrostate B) must be equilibrated with its reverse process (i.e., a transition from macrostate B to back to macrostate A) as a direct consequence of microscopic reversibility at thermodynamic equilibrium

• Flux: the flow of biomolecule through an energy landscape. For example, an ensemble of biomolecules exhibits flux if they progress from state A through state B to state C on average in the violation of detailed balance. Therefore, flux is only a property of nonequilibrium systems. The identification of a system that exhibits flux through any phase space is sufficient to identify the process as a nonequilibrium process.³¹

• Functional free energy landscape: the region of a free energy landscape of that is thermodynamically accessible to a biomolecule as it performs its function.

• Folding free energy landscape: the region of an energy landscape of that is thermodynamically accessible to a biomolecule during protein folding, for example.

Equilibrium Energy Landscapes

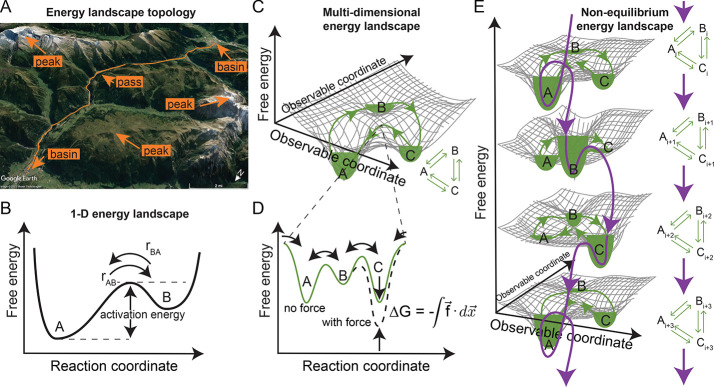
A biomolecular system’s equilibrium population and functional dynamics can be modeled using the energy landscape formalism. Take a topological landscape as an analog to a biomolecule’s free energy landscape. The equilibrium population of states arises from the depths of the landscape’s energy basins (local minima, Figure 1A), with molecular ensembles populating lower energy valleys more heavily than higher energy ones; they rarely sample states near peaks (local maxima, Figure 1A). Functional dynamics arise from individual molecules transitioning within that equilibrium population of states, which can be conceptualized as a particle moving through an energy landscape with overdamped Brownian motion.³² Transitions between local energy basins occur through passes between the peaks in the free energy landscape (saddle points, Figure 1A). The higher these passes, the less likely a system will undergo a transition between the neighboring basins.

Figure 1.

Schematic representations of free energy landscapes under equilibrium and nonequilibrium conditions. (A) A 2-dimensional topological landscape is an analog to a biomolecule’s multidimensional functional energy landscape. The path of least action (orange line) traverses a mountainous landscape between populated local minima in basins (towns in valleys) through the saddle point (pass) and avoiding the local maxima (peaks) altogether. Topological image from GoogleEarth.¹⁸⁴ (B) Schematic representation of the1-D projection of a free energy landscape along a reaction coordinate for a system with two macrostates, A and B, similar to the path of least action in panel A. At thermodynamic equilibrium, the height of the energy barrier (activation energy) determines the forward and backward rate constants, and a detailed balance, r_AB = r_BA, is maintained between the states. (C) Schematic of a multidimensional energy landscape and its corresponding chemical reaction equation (inset), representing a biomolecule that undergoes cyclical functionality. At equilibrium, microscopic reversibility, and thus a detailed balance, exists between the macrostates, and the system exhibits no net flux. The path of least action (green line) traverses the landscape between populated local minima in basins (A, B, and C, filled with green to represent the equilibrium population of the macrostate) in the landscape through the saddle points (passes) and avoiding the local maxima (peaks) altogether. (D) Schematic representation of the1-D projection of the free energy landscape in panel C along the reaction coordinate opened at the saddle point between states A and C. As the system is cyclic, the reaction coordinate is cyclic as well, and the free energy landscape is continuous (cyclic boundary conditions) at both ends of the plot. Force drives the system from the “no force” equilibrium state (solid green line) to a new “with force” equilibrium condition by tilting the energy landscape along the observable coordinate corresponding to the direction of force. This projects back to the reaction coordinate in a way that affects macrostate C and the transition states between B and C (dashed black line). (E) Energy flow into the system from panel C drives it into out-of-equilibrium conditions wherein transitions between the macrostates of the system are not balanced by reverse processes, and there is a net circulation through the states. The reaction coordinate (purple arrows) can be conceptualized as a spiral (tilted in a 1-D projection) that cycles through the local basins in the energy landscape but constantly goes downhill. Such systems are often studied in quasi-equilibrium states (green lines and fill) stabilized by force or an inactive analog of a substrate. Note that the spiral 1-D energy landscape is cyclical, that is, if i + 1 > n, then the system cycles back to i = 1 rather than to n + 1, where n is the number of macrostates experienced by the system during its functional cycle (in this case, n = 3).

In his seminal work, Kramers³³ described the way systems are most likely to move through energy landscapes: along a unique reaction coordinate. Projecting a biomolecule’s functional dynamics along a one-dimensional (1-D) reaction coordinate is conceptually appealing. It reduces dimensionality from 3N – 6 (Box 1) to one easily represented dimension (Figure 1B) and helps to conceptualize properties of complex systems at thermodynamic equilibrium. For example, a detailed balance of states exists within a population at thermodynamic equilibrium as a direct consequence of microscopic reversibility. Consider a system with two states, A and B (Figure 1B). The transition rate from A to B, r_AB = k₊ρ_A, where k₊ is the forward rate constant and ρ_A is the population of state A, must be balanced by reverse transitions at rate r_BA = k_–ρ_B, such that r_AB = r_BA. The detailed balance at thermodynamic equilibrium precludes a net flux of the population through a series of macrostates.^31,34,35 Even if the system is cyclical (i.e., its reaction coordinate loops back on itself, Figure 1C, green line, and the 1-D projection of its energy landscape along the reaction coordinate has cyclic boundary conditions, Figure 1D, green line),³⁶ transitions from one state to the next must be individually and simultaneously balanced.

Despite the proven utility of 1-D energy landscapes, several simplifications inherent to this conceptualization make functionally important biomolecular dynamics less clear and may lead to the misinterpretation of experimental results, among other potential problems. For example, experiments typically yield data on experimentally tractable observable coordinates, such as end-to-end distance, radius of gyration, bond distances, bond angles, or affinities between the interacting molecules, rather than actual reaction coordinates.^37,38 Only in the most simple systems, a slip-bond type receptor–ligand interaction, for example, do the reaction coordinate and the observable coordinate coincide.³⁹ Therefore, one must carefully consider how data collected along an observable coordinate projects onto the reaction coordinate to make a genuinely quantitative analysis using the 1-D energy landscape paradigm, as discussed for folding energy landscapes.^23,40−43

Out-of-Equilibrium Energy Landscapes

Out-of-equilibrium biomolecular systems are nonisolated, which implies that they exchange energy or matter with the environment. Cytoskeletal motor proteins⁴⁴ and DNA helicases⁴⁵ walk along filaments and perform useful work with energy supplied from ATP; ribosomes polymerize proteins,^46,47 and tubulin undergoes dynamic instability⁴⁸ with energy supplied from GTP; photosystems I and II transfer electrons to acceptor molecules with energy supplied from photons;⁴⁹ ATP-synthase phosphorylates ADP with energy supplied from a chemical potential due to ion concentration differences across the mitochondrial membrane;⁵⁰ and riboswitches regulate gene expression⁵¹ and allosteric effector molecules regulate enzyme activity^52,53 with energy supplied from ligand binding. Nonequilibrium biochemical and biophysical processes in biological macromolecules ranging from enzyme catalysis and allosteric regulation to force production and electron transport, for example, underlie nearly every fundamental biological function.

One-dimensional representations of energy landscapes along single reaction coordinates (e.g., Figure 1B,D) do not represent nonequilibrium, functional biomolecular systems particularly well. There are two critical differences between nonequilibrium and equilibrium systems that affect their conceptualization using energy landscapes. First, the nature of the energy landscape itself, that is, the topological contours of a multidimensional landscape, can evolve as material or energy exchanges with the environment (Figure 1E). Examples include post-translational modifications that lower barriers between basins⁵⁴ and allosteric ligand binding that modifies the topography of entire regions of multidimensional energy landscapes.⁵² Second, the exchange of energy or material can change a system’s dynamics within the energy landscape. For example, the fluctuation–dissipation theorem⁵⁵ and Kramer’s theory can require additional terms corresponding to the exchange of energy,⁵⁶ or the principle of detailed balance can be violated, that is, the forward and backward paths through an energy landscape can be different, one-way, or irreversible or exhibit hysteresis.⁵⁷

Current approaches to representing out-of-equilibrium phenomena within the framework of energy landscapes tend to model nonequilibrium systems as a series of static 1-D energy landscapes corresponding to each altered condition, that is, before and after ligand binding or as a function of force (Figure 1E, green). This approach assumes that the system undergoes kinetic processes to populate the lowered states in the same way that would occur through a dynamically changing landscape. However, the kinetics at the new equilibrium do not necessarily reflect the kinetics and structural dynamics associated with the nonequilibrium process that evolves the energy landscape in the first place (Figure 1E, purple). For example, the process of an external force directed along the reaction coordinate performing mechanical work and deforming the biomolecule may significantly alter the system’s energy landscape, causing a continual evolution of the landscape’s contours. Experimentally quantifying the energy landscape of biomolecular systems undergoing nonequilibrium processes is more challenging than for those of equilibrium processes,⁵⁸ and it also highlights the importance of properly identifying a reaction coordinate that follows the evolving functional free energy landscape of a nonequilibrium process. In the example of Figure 1E, the reaction coordinate follows the purple path. Nonetheless, doing so profoundly impacts our understanding of a biomolecular system’s mechanism, and thus it is worth the effort.

The framework presented in Figure 1 also calls for three possible cases.

Case 1: The exchange rate of conformational transitions (k_c) is faster than the exchange rate between functional states (k_f). E. coli dihydrofolate reductase, which catalyzes an essential reaction for glycine and purine syntheses, exemplifies this case. The conformational states of the enzyme exchange at faster rates than its substrate and cofactor binding and catalysis processes.⁵⁹ The enzyme populates various intermediate conformations, including the ground and excited states, that depend on the steady state turnover rate and hydride transfer.⁵⁹ The conformational exchange takes place within the microsecond to millisecond time scale, while the exchange rate between functional states occurs between millisecond and second scales (Figure 2A).⁵⁹

Figure 2.

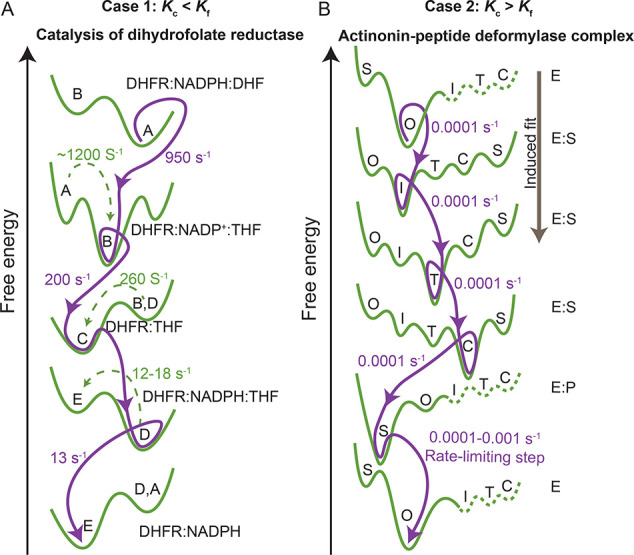
Free energy landscape for the conformational states observed during enzyme catalysis. (A) Free energy changes observed during the catalytic activity of dihydrofolate reductase (DHFR) interaction with its substrate dihydrofolate (DHF) in the presence of NADPH cofactor. Various conformational states A, B, C, D, and E are shown. Adapted from Boehr et al.⁵⁹ (B) Schematic representation of free energy changes observed during the enzyme–substrate interaction of actinonin-peptide deformylase (AtPDF) complex via an induced-fit mechanism. The open (O), superclosed (S), intermediate (I), transition (T), and enzyme–substrate complex (C) conformational states are shown. Adapted from Fieulaine et al.⁶⁰

Case 2: The exchange rate of conformational transitions is slower than the exchange rate between functional states. Peptide deformylase, which is an enzyme that catalyzes formate, exemplifies this case. The actinonin-peptide deformylase complex formation is an induced fit process that populates several intermediate conformations at it transverses its functional free energy landscape from an initial open state to the final closed state.⁶⁰ However, the steps in ligand binding, catalysis, and product release are limited by the conformational exchange that occurs at shorter time scales.⁶⁰ For the enzyme to function, it must overcome these limiting rates by moving along the reaction coordinate through an induced fit mechanism that reduces the energy barrier for catalysis (Figure 2B).⁶⁰

Case 3:

The exchange rate of conformational transitions is similar to the exchange rate between functional states. This scenario is the most challenging to experimental approaches since functional state transitions and conformational changes that occur simultaneously cannot be unambiguously separated.

To probe exchange rates that belong to these cases, and to probe nonequilibrium conditions ensemble perturbation, methods such as laser-based temperature jump (T-jump),^61,62 pH jump,⁶³ and rapid mixing,^64,63 are useful. With the T-jump technique, one can drive the system into higher energy, low populated states using laser-induced T-jumps and follow the nonequilibrium dynamics as it relaxes with high temporal resolution (nanosecond to millisecond). Rapid-mixing and pH-jump assays provide temporal resolution of microseconds to seconds and nanoseconds to seconds, respectively. Recent advances in 2D-IR spectroscopy⁶⁵ also enable one to probe the nonequilibrium dynamics of the system. Crucial is that these methods can reach high temporal resolution probing short-lived functional states.

Multidimensional Energy Landscapes

A one-dimensional projection of the energy landscape along the reaction coordinate is conceptually elegant and quantitatively convenient. However, it is common practice to use a one-dimensional experimental observable that might not reflect the true reaction coordinate. For example, at thermodynamic equilibrium, systems can experience dynamics that are not experimentally captured entirely along the reaction coordinate. Thermal fluctuations displace complex systems in directions with components orthogonal to the reaction coordinate as they sample microstates near to, but not along, the reaction coordinate. The dynamics of a system in these other dimensions can be essential for the molecule’s function.^34,66,67 These considerations are particularly important when the observable reaction coordinates either do not align with the reaction coordinate or fail to capture the system’s critical dynamics. Multidimensional changes such as these can be difficult or impossible to capture on a 1-D reaction coordinate projection of the energy landscape.

Nonequilibrium systems exacerbate the need to improve representations of multidimensional energy landscapes. Nonequilibrium processes, including the application of external force,⁶⁸ allosteric cofactors,⁶⁹ protein–protein interactions,⁷⁰ post-translational modifications,⁵⁴ and temperature⁷¹ and pH changes,⁷² as well as other energy transfer mechanisms⁷³ and environmental perturbations,⁷⁴ can impact biomolecular systems in ways that nonuniformly distort the multidimensional free energy landscape. Consider a biomolecular system subject to external loading that displaces its atoms along dimensions other than the direction of the force due to its anisotropic nature. Such oblique translations along orthogonal dimensions could have significant direct functional effects.¹⁹ Additionally, they could destabilize intramolecular interactions in remote areas of the molecule leading to other changes to the energy landscape, causing unfolding of other structural domains, or changing interactions with solvent (environment) molecules.¹⁰ Any combination of these effects likely alters the energy landscape’s contours and changes the reaction coordinate’s path through the multidimensional energy landscape space.⁷⁵⁻⁷⁷ Therefore, reducing a multidimensional energy landscape into 1-D does not adequately represent the system’s dynamics and can mask physiologically relevant accessible conformations, configurations, and transition paths.^78,79

To understand, model, and make predictions about multidimensional, nonequilibrium molecular biological processes, we suggest that the field needs to move beyond 1-D representations of observable coordinates in the equilibrium free energy landscapes. To do so, we need computational and experimental tools to visualize and probe these systems. However, this suggested approach remains challenging. To illustrate the problem’s magnitude, take the relatively simple system of the thiamine pyrophosphate (TPP) riboswitch’s ligand sensing domain as an example. The aptamer domain of the TPP riboswitch has about 110 RNA bases; that is nearly 3N – 6 ≈ 5000 dimensions! Measuring, analyzing, conceptualizing, and representing a 5000-dimensional system is an overwhelmingly complex problem unlikely to impart understanding in any meaningful way. However, as we will discuss when we revisit this example further below, a single-dimensional or even two-dimensional representation may be too simple to capture essential mechanisms of the system.

Mapping the Multidimensional Functional Energy Landscape in Equilibrium and Nonequilibrium Systems

For decades, structural biology’s goal has been to find and present representative structures corresponding to local minima (i.e., macrostates) in the functional energy landscape,^37,80 and X-ray crystallography and cryo-electron microscopy (cryo-EM) have been widely successful at doing so. We have learned much about biological macromolecular mechanisms by determining structures in various conditions (e.g., ligand-bound and unbound states) and inferring dynamics between these structures. Further progress can be made using methods that capture dynamics directly, including nuclear magnetic resonance (NMR) spectroscopy, electron paramagnetic resonance (EPR) spectroscopy, and ultrafast pump–probe spectroscopy, particularly when integrated with X-ray crystallography and cryo-EM.⁸¹

Other techniques have significant roles in improving the mapping of functional energy landscapes for biomolecular systems. Single-molecule techniques, including fluorescence spectroscopy,⁸² super-resolution microscopy,⁸³ optical tweezers,⁸⁴ magnetic tweezers,⁸⁵ and atomic force microscopy,⁸⁶ have the advantage of disentangling heterogeneous populations within the ensemble and monitor transitions in real-time across many decades of spatiotemporal-force resolution. Dynamic simulation methods have developed into a robust tool for precisely understanding the properties (structure, recognition, and function) of biomolecular systems on a time scale that is otherwise inaccessible and are routinely applied to study dynamic events, thermodynamic properties, and time-dependent (kinetic) phenomena of many biophysical processes.⁸⁷ Computational methods such as Langevin (stochastic) dynamics,^88,89 Brownian dynamics,^90,91 Monte Carlo simulations,⁹² and molecular dynamics (MD) simulations using all-atom or coarse-grained⁹³ representations of molecules coupled with enhanced sampling approaches such as temperature replica exchange^94,95 can be used to complement experimental techniques such as NMR,⁹⁶ FRET,^27,70 force spectroscopy,⁹⁷ and other biophysical tools to explain the dynamics nature of interconverting ensembles.⁹⁸ MD describe the time evolution of conformations of biological molecules and generate thermodynamically consistent trajectories through equilibrium energy landscapes with high temporal and spatial resolution⁹⁹ as well as nonequilibrium landscapes through techniques like steered MD.¹⁰⁰ Moreover, MD simulations and other computational solvers (e.g., Poisson–Boltzmann equation solvers¹⁰¹) can map out multidimensional energy landscapes constrained by observations and predict the ensemble of microstates that make up any given macrostate.¹⁰²

Force Spectroscopy

Single-molecule force spectroscopy has successfully been used to determine folding free-energy landscapes of biomolecules with externally applied force in both quasi-static and nonequilibrium experiments on molecules as they both unfold and refold.^{16,80,103−106} The approach effectively “tilts” the free energy landscape in the direction of pulling and changes the relative depths of the basins and the heights of the hills between them (Figure 1D, dashed black line). Tilting an energy landscape favors partially and fully unfolded macrostates, enabling one to acquire quantitative data about these otherwise low populated states and rarely occurring transitions in more detail.⁴¹ Even for systems that are generally not subject to external loading, if done precisely, for example, based on an X-ray crystallography structure, or on a simple enough system, for example, a DNA hairpin or short peptide, externally applied forces can be directed along the reaction coordinate and the shifted, nonphysiological equilibrium states can be used to understand the physiologically relevant biomolecular system.^16,23,24,36

Moreover, the external forces applied by force spectroscopy techniques can help map multidimensional functional energy landscapes in equilibrium and nonequilibrium systems. External forces can mimic and probe the energy landscape tilting effects of energy fluxes associated with nonequilibrium processes in motor proteins,^107−111 riboswitches,⁸⁴ chaperones,¹¹² kinases,¹¹³ CRISPR/Cas9,¹¹⁴ and many others.^109,115,116 When taken in the context of other structural data, force spectroscopy can aid in characterizing multidimensional energy landscapes for both equilibrium and nonequilibrium conditions as well as identifying the reaction coordinates along which systems traverse these landscapes.

Fluorescence Spectroscopy

Single-molecule multiparameter fluorescence spectroscopy (smMFS) is a time-resolved technique using all the dimensions of intrinsic fluorescence information that one can obtain from a chromophore, that is, its absorption and fluorescence spectra and its fluorescence quantum yield, lifetime, and anisotropy, to quantify the dynamic properties of biological macromolecules.¹¹⁷ State-of-the-art smMFS data analyses enable resolution of a target molecules’ structural and dynamic characteristics¹¹⁸ at time scales from picoseconds to hours and length scales that reach angstrom precision when used in combination with FRET.^118,119 When extended to multicolor FRET, smMFS allows one to monitor each of the dimensions of intrinsic fluorescence information along multiple observable coordinates simultaneously.^117,120 Also, the single-molecule nature of smMFS data can allow researchers to distinguish regions of energy landscapes under nonequilibrium conditions hidden in ensemble measurements.¹²¹ Particularly when taken in the context of other structural data, smMFS can also help identify reaction coordinates and characterize the multidimensional energy landscape.

Molecular Dynamics

MD simulations use Newton’s laws and parametrized force fields to model the position of atoms in a system as a function of time.^122,123 The all-atom approach of MD allows one to probe the multidimensional aspect of free energy landscapes in great detail. Specifically, MD simulations allow one to calculate multiple possible conformational and configurational trajectories through highly multidimensional (all 3N – 6 dimensions) energy landscapes. MD simulations can be used to predict and validate experimental observables made with complementary techniques, such as NMR,⁹⁶ FRET,^27,70 force spectroscopy,⁹⁷ and other biophysical tools. MD simulation packages, including CHARMM,¹²⁴ AMBER,¹²⁵ NAMD,¹²⁶ and GROMACS,¹²⁷ can include external forces with the conventional force fields and other external perturbations in targeted and steered MD simulations. These approaches enable one to identify plausible reaction coordinates, design force and fluorescence spectroscopy experiments, and determine conformational dynamics of biological molecules under nonequilibrium conditions.^128−130

Usually, conventional all-atom MD simulations with parallel computing can reach time scales up to microseconds that capture many physiologically important dynamics but still fall short of covering the wide range of functionally relevant time scales up to milliseconds and seconds.^8,131 Also, conventional MD simulations can rarely unveil the features of the high energy transition states that lie in regions of the free energy landscape, as the simulated systems often get trapped in local-minimum conformations.¹³² To overcome this limitation, enhanced sampling methods such as replica exchange MD¹³³ and metadynamics¹³⁴ have been developed to handle the inherent quasi-nonergodicity¹³² and analyze complex dynamics, determine structural information, and efficiently sample the rugged folding landscape of biophysical systems.^135,136 Discrete molecular dynamics (DMD), an event-driven MD approach featuring higher sampling efficiency over conventional MD,^137−139 has been developed to efficiently study the dynamics of biomolecules.¹⁴⁰ The increased computational efficiency results from the usage of discretized potential functions and recalculation of atomic ballistic equations only for atoms that are involved in a collision event.^141,142 The DMD force field incorporates the CHARMM van der Waals interaction parameters, the Lazaridis and Karplus implicit solvent model¹⁴³ (the effective energy function, EEF1), screened electrostatic interactions between charged residues, and explicit modeling of hydrogen bonds. Replica exchange DMD coupled with the implicit solvent model accelerates sampling of the complex multiple-basin energy landscape and has high predictive power in describing conformational transitions of biological molecules under nonequilibrium conditions,^128−130 identifying plausible reaction coordinates, and resolving the supertertiary structure of multidomain proteins.^144,145 Moreover, the structural and thermodynamic data generated by coarse-grained MD and DMD¹⁴⁶ simulations can be used to study the mechanisms of larger-scale, slower processes.¹⁴⁷

Integrated Approaches

In recent years, efforts to integrate these approaches led to more detailed reconstructions of functional biomolecular energy landscapes. smFRET used in combination with MD simulations bridged multiple length and time scale limitations associated with each technique independently. The combination has been used to validate the leucine–isoleucine–valine binding protein (LIV-BP) as a biosensor,¹⁴⁸ investigate rapid dynamics along the reaction coordinate,¹⁴⁹ capture dynamic binding and allosteric processes, quantify supertertiary and transient conformations, and probe the equilibrium dynamics for biomolecular states.^119,11,150 Additionally, optical tweezers used in combination with multiscale molecular dynamics simulations have characterized the effects of octanoyl-CoA on the folding stability of acyl-CoA binding protein¹⁵¹ and revealed how disease-causing mutations in kinesin-3 motors affect force generation in one dimension through allosteric effects on the ATP hydrolysis site in another dimension of its multidimensional energy landscape.¹⁵² Single-molecule fluorescence spectroscopy combined with force spectroscopy approaches provided mechanistic details for force-induced changes and local conformational dynamics in DNA nanostructures¹⁵³ and out-of-equilibrium conformational dynamics in the protein–DNA interactions of the E. coli DNA repair helicase (UvrD) system.¹⁵⁴ The discoveries of complex biological mechanisms rooted in the details of the structure–function–dynamics relationship and made by integrating multiple approaches would have been impossible to find if the data were collected in isolation.

Despite these significant insights into various biological mechanisms, the overarching principles governing out-of-equilibrium dynamics within biological macromolecule multidimensional energy landscapes are yet to be clearly understood. We suggest a path forward that builds on the remarkable progress made in recent years by integrating techniques. Studies that simultaneously analyze data collected from multiple independent techniques, often through collaborations among multiple research groups, is a fantastic first step, and they have already yielded remarkable results, some of which we highlighted above. However, we suggest novel, integrated instruments that probe single-molecule biomolecular systems in and out of equilibrium, along multiple dimensions, and over many orders of length, time, and force scales simultaneously would significantly accelerate discovery. Such instruments will synergistically combine multiple techniques into a single instrument to make real-time, simultaneous, multiparameter single-molecule measurements of biomolecular dynamics.

The TPP Riboswitch: A Case for Integrative Single-Molecule Multidimensional Approaches

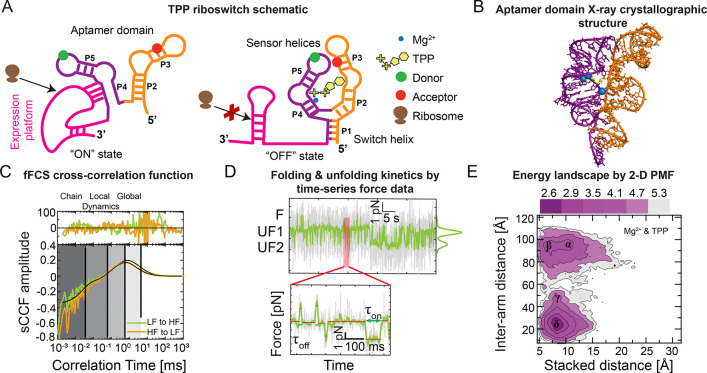
Riboswitches are noncoding gene regulatory segments of mRNA.^155,156 Riboswitches, as their name indicates, switch whether a gene gets expressed in response to small metabolites and metal ions. Such is the case for the Arabidopsis thaliana thiamine pyrophosphate (TPP) riboswitch.^155,157 The TPP riboswitch has two distinct functional domains: the TPP ligand sensing aptamer domain and the splice-regulating expression platform (Figure 3A,B). Mechanistically, the sensor helices of the aptamer domains coordinate with TPP, which, in turn, causes the P1 switch helix to base-pair, leading to subsequent structural changes in the expression platform domain that ultimately regulate gene expression.^41,158,159

Figure 3.

Multidimensional smFRET and optical tweezers data show the folding and unfolding kinetics for the riboswitch. (A) Schematic representation of TPP riboswitch in the ON (left) and OFF (right) state conformations, which activate and inactivate the expression platform (magenta) by enabling and disrupting ribosomes (brown). TPP (yellow) and Mg²⁺ (blue circle) ligands coordinate with the pyrimidine sensor helix (P2 and P3 helices, orange) and the pyrophosphate sensor helix (P4 and P5 helices, purple), which comprise the aptamer domain along with the P1 switch helix. Donor (green circle) and acceptor (red circle) fluorophores in the sensor helices enable probing aptamer domain dynamics with smFRET and MFS. (B) Ball and stick representation of the TPP riboswitch’s aptamer domain X-ray crystallographic structure (pyrimidine sensor helix, orange, and pyrophosphate sensor helix, purple) when complexed with TPP (yellow) and coordinating Mg²⁺ ions (blue) (PDB ID: 2GDI(163)). This structure represents a P1/P2 co-stacked, P1 switch helix base-paired state. (C) Filtered FCS species cross-correlation function (sCCF) vs correlation time for TPP riboswitch in apo conditions. There are four state transition rates with different time scales (vertical black lines). Darker to lighter shaded regions represent from intrachain to local and global conformational dynamics, respectively. Raw and functional fit correlation data are shown in colored and black lines, respectively. Note that LF indicates low FRET, and HF indicates high FRET. (D) Transitions between the switch helix base-paired (F) and multiple unfolded states (UF1 and UF2) in the time-series force spectroscopy data are identified by sudden increases and decreases of force within the optical tweezers. States of order 100 ms (τ) are identified with a step-finding algorithm (inset). (E) Two-dimensional potential of mean force (PMF) calculated with discrete molecular dynamics (DMD) represents the aptamer domain’s energy landscape quantified along intersensor helix arm and P1/P2 helix co-stacking distance observable coordinates. The PMF shows multiple conformational states (basins) corresponding to sensor helix open states with no co-stacking (α) and with co-stacking (β), a partially closed sensor helix state with co-stacking (γ), and closed sensor helix state with co-stacking (δ). Adapted from Ma et al.¹⁶¹

Recently, optical tweezer data were used to quantify the TPP riboswitch’s aptamer domain folding energy landscape.^41,160 However, the functional energy landscape is less clear. In ligand-free conditions, the P1 switch helix is not base-paired (Figure 3A),¹⁶¹ and the sensor helices undergo rapid structural conformation transitions through a relatively flat free energy landscape.¹⁵⁸ The dynamics of the sensor helices slow in the presence of the TPP ligand, which correlates with the base-pairing of the P1 switch helix.¹⁶² However, there is not a transition to a static, stable X-ray crystallography-like structure.¹⁶² The energy landscape model of this switching mechanism suggests that TPP and Mg²⁺ tilt the functional energy landscape through a nonequilibrium process that allosterically lowers the P1 helix base-paired basin.

To resolve the functional mechanism of the TPP riboswitch, we recently carried out smMFS and optical tweezers measurements with DMD simulations independently to study the TPP binding process and subsequent transition to the translation-inhibiting state in a set of experiments that bridge multiple time scales.¹⁶¹ These combined results show that an excess of TPP and coordinating Mg²⁺ ion concentrations is necessary to drive the sensor helices toward a structural configuration (Figure 3C) consistent with X-ray crystallography data (Figure 3B).¹⁶³ We performed filtered fluorescence correlation spectroscopy (fFCS) and time-correlated single-photon counting (TCSPC) measurements to probe the site-specific exchange process by using characteristic fluorescence and time-resolved decays.^165,166 A global fit of species-specific auto- and cross-correlation data gave four relaxation times (Figure 3C), indicating interconversion among at least five different states. We found that the relaxation times among these states span time scales from 100 ns to milliseconds. Under different buffer conditions, our results showed that the relative population and the transition rates between the states are sensitive to the ligand concentrations. To probe the long-lived states (greater than millisecond time scale) dynamics, we measured the aptamer domain’s P1 switch helix unfolding transitions using a passive optical trap. Analysis of the optical tweezer time traces revealed that the dynamics between the folded (F) and unfolded states (UF) are on the order of 100s of milliseconds under load (Figure 3D) and 10s of seconds in the absence of a load.¹⁶¹ Further, we employed replica exchange DMD simulations to sample the conformational space of the riboswitch under multiple conditions, including the ligand-free apo state, partially bound states with either Mg²⁺ or TPP, and the holo state with both ligands. Under each condition, we mapped these dynamics onto two-dimensional energy landscapes using replica exchange DMD simulations and weighted histogram analysis method¹⁶⁷ (e.g., PMF of the holo RNA in Figure 3E), where the “interarm distance” dimension corresponds to the sensor helix open-to-closed axis, that is, transitions between structures represented by the “ON” and “OFF” states (Figure 3A), and the “stacked distance” dimension corresponds to P1/P2 helix stacking (Figure 3B). The simulation results suggested that co-stacking between P1 and P2 helix coupled to the opening and closing dynamics of the arms. In the presence of Mg²⁺ and TPP, the computed PMF of the interarm distance vs co-stacking distance shows two distinct peaks; interarm distance at 24.8 Å represents a closed state ensemble and the population with peaks at 85.2 and 95.1 Å resembles an open state ensemble (Figure 3E). In agreement with FRET measurements, the two-dimensional PMF histogram suggests the appearance of a prominent population peak for the closed state and simultaneous reduction in the open state in the Mg²⁺ and TPP buffer, a low-population closed state in the Mg²⁺ buffer, and a tailing toward a closed state and appearance of an intermediate state in the TPP buffer.¹⁶¹ Including the “ON” state with P1 unfolded after losing the P1/P2 co-stacking that was not sampled in silico, we identified at least five conformational ensembles with low energy barriers between them whose depths, and therefore populations, are strong functions of whether the TPP and Mg²⁺ ligands are bound. Integrating the results from multiple independent techniques enabled us to propose a model in which the TPP riboswitch aptamer domain can follow each of two pathways through its functional multidimensional energy landscape and that this mechanism underlies a kinetic rheostat-like function of the Arabidopsis thaliana TPP riboswitch.

Using an integrated instrument that simultaneously maintained the TPP riboswitch’s aptamer domain in an optical trap and collected intensity-based smFRET trajectories, Duesterberg et al.⁸⁴ identified concurrent transitions in the force and FRET data. The experiments’ simultaneous measurement enabled them to distinguish differences in the sensor helix orientation in various TPP-binding states (Figure 4) that the same data collected separately would not have found. However, these data could not resolve the complex configurational and conformational heterogeneity associated with rapid fluctuations (Figure 3C) due to the temporal resolution limitations of intensity-based smFRET trajectories.¹⁶¹ Even with state-of-the-art combined technique instrumentation, it remains challenging to build a map of the quantitative, multidimensional, nonequilibrium functional energy landscape for the TPP riboswitch’s aptamer domain that captures how the rapid conformational dynamics of the sensor helices lead to slower switch helix actuation and P1/P2 co-stacking. We need more advanced tools that combine single-molecule force and time-resolved multiparameter FRET techniques to elucidate how conformational dynamics underly the functional mechanisms of TPP riboswitch.

Figure 4.

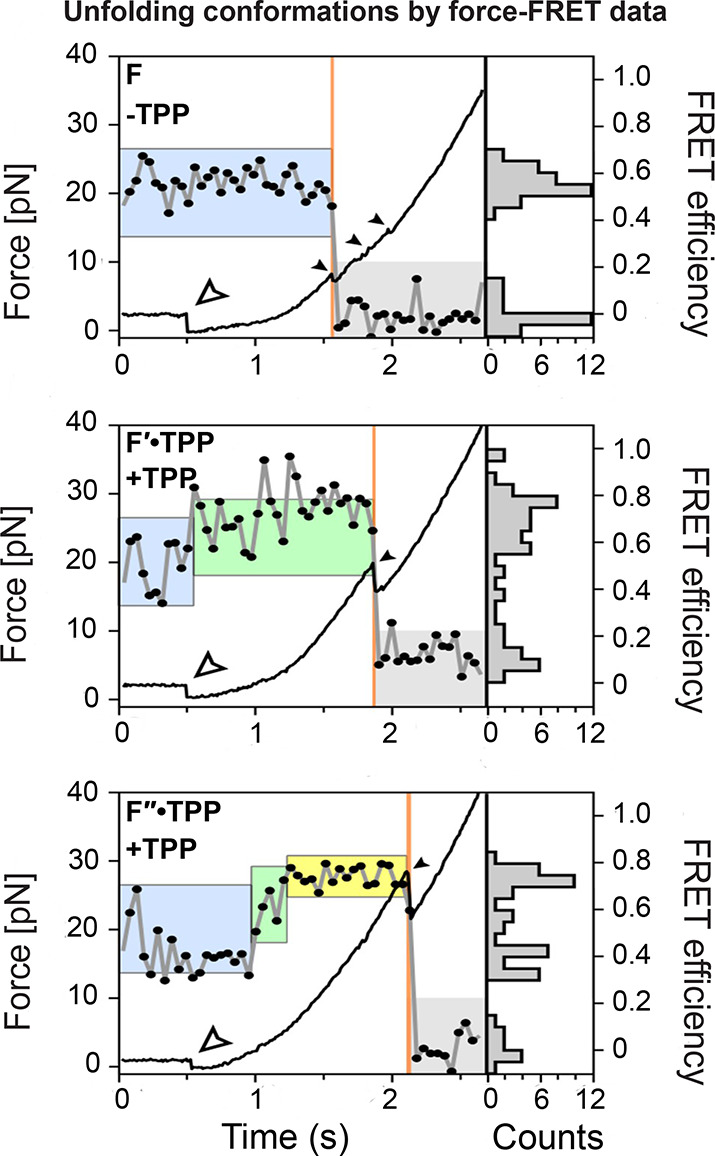
Simultaneously acquired force-FRET data reveal that TPP binding correlates with structural changes within the TPP riboswitch. Force (optical tweezer data, black line) and FRET trajectories (smFRET data, gray line with black circles) reveal the unfolding conformations of the TPP riboswitch’s aptamer domain. F (no TPP, top), F′·TPP (with TPP, middle) and F″·TPP (with TPP, bottom) represent the no TPP bound, weak TPP binding, and strong TPP binding states of the riboswitch, respectively. The apo (blue box), weak TPP-bound (green box), and strong TPP-bound (yellow box) states, as identified based on FRET, correspond to increasing switch helix unfolding forces, as quantified by optical tweezers. Small filled arrows indicate opening transitions and refolding period end points. Open arrows mark the force ramp starting points. Adapted from Duesterberg et al.⁸⁴

Perspective

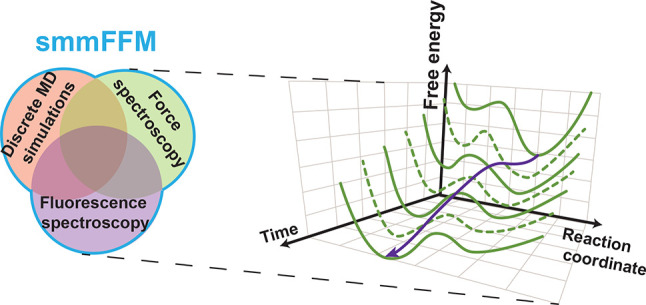
We must develop and build new instruments to probe structural dynamics across many decades of spatiotemporal resolution and along multiple simultaneous dimensions in equilibrium and nonequilibrium conditions to characterize the multidimensional complexities of biomolecules relevant for living organisms. Such rapid, simultaneous, multidimensional data acquisition would enable researchers to quantify distinct reaction coordinate pathways as a system’s functional energy landscape evolves in out-of-equilibrium conditions, for example, as ligands bind to the TPP riboswitch’s aptamer domain. It is crucial to investigate biomolecular processes with high spatiotemporal resolution because these critical functional dynamics occur over a broad range of time and length scales (Figure 5 and Table 1). The further development and proliferation of integrated single-molecule force and multiparametric fluorescence spectroscopic instruments, for example, a single-molecule multidimensional fluorescence and force microscope (smmFFM) that combines ultrafast optical tweezers with smMFS, will enable probing multidimensional energy landscapes of more biomolecular systems under out-of-equilibrium conditions.

Figure 5.

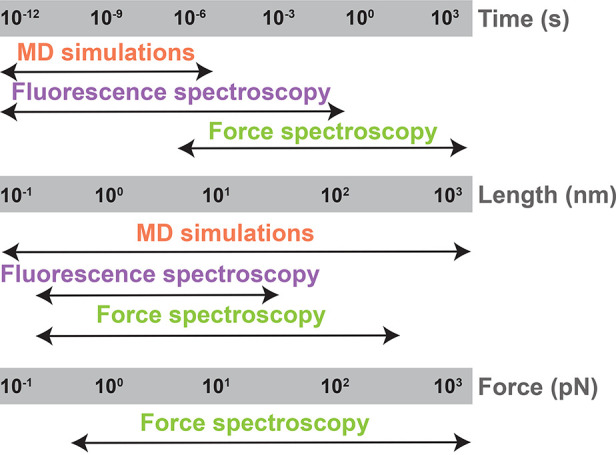
Schematic model shows the ability to probe biomolecular structure–dynamics–function with length, time, and force scales in studies that combine MD simulations with integrated fluorescence and force spectroscopy instruments.

Table 1. Various Biological Functions with Various Time Scale, Length Scale and Force Range Measured Using Different Methods.

event	methods	scale/range	refs
Time Scale (s)
side chain motions	NMR relaxation dispersion	10–12 to 10–9	(168)
protein folding	Optical tweezers	10–6 to 1	(24)
gene splicing	FCS and FRAP	10 to 103	(169,170)
gene regulation	FRAP	10–3 to 100	(171)
ion channel gating	smFRET	10–6 to 10–3	(172)
translation	E. coli and mammalian cell lines	1 to 60	(173)
domain motion	smFRET	10–8 to 10–3	(144,174)
ligand binding	MD simulations	10 to 100	(60)
signal transduction	smFRET	10–9 to 10–3	(175)
enzyme catalysis	NMR relaxation dispersion	10–6 to 10–3	(10)
Length Scale (nm)
E. coli	DIC microscopy	>103	(176)
organelles	nucleus	103 to 10
membrane thickness	cryo-electron tomography	5 to 10	(177)
extracellular vesicles	extracellular vesicle imaging	102 to 103	(178)
ribosomes	cryo-EM	5 to 10	(179)
proteins	gel filtration and electron microscopy	5 to 50	(180)
Force Range (pN)
ion channel gating	atomic force microscopy	1 to 10	(181)
chromosome segregation	electron microscopy	0.1 to 1	(182)
motor proteins	force-feedback optical trap	7 to 10	(183)
molecular extension	optical tweezers	1 to 10	(161)

Beyond instrument development, we further suggest it is critical to apply, extend and, most importantly, integrate computational methods, analytical tools, and conceptual frameworks to understand these data. A strategy adapting and extending the methodologies that successfully quantify folding energy landscapes^23−26,84 to analyze functional energy landscapes likely would be fruitful. Additionally, it will be essential to develop elegant and broadly understandable but rigorous representations of these data’s complexities. Extensions to the static representations of one- and two-dimensional landscapes widely used today would better capture the underlying dynamics of multidimensional, nonequilibrium systems.

Taking the riboswitch case as an example, simultaneously applied integrated approaches like the smFFM can address both specific and broadly fundamental questions such as the following: (1) How do sensor helix conformational dynamics and switch helix base paring coordinate? (2) How do TPP and Mg²⁺ ligand binding to the sensor helices drive the conformational and configurational transitions in the aptamer domain structure? (3) Which functional pathways identified with equilibrium experiments are significant in the more biologically relevant, out-of-equilibrium conditions that occur as the ligands bind? (4) Can a single reaction coordinate adequately model the TPP riboswitch function, or are multiple reaction coordinates necessary to understand its function? Beyond riboswitches, the combined integrated approaches will be important in the study of nearly all biomolecular systems, including allosteric mechanisms of enzymes, cytoskeletal and nucleic acid motor proteins, functional roles of intrinsically disordered proteins and domains, biomolecular aggregates and phase-separated condensates, gene regulatory and differential gene expression mechanisms, membrane fusion processes, ion channel gating, and signal transduction, just to name a few; other examples are listed in Table 1.

In summary, the energy landscapes of biomolecular systems are highly complex. The construction of multidimensional landscapes is cumbersome even in the simplest cases and essentially impossible for larger ones using independently applied experimental, computational, and theoretical techniques. One must carefully choose the observable coordinates to probe biomolecular function along the reaction coordinates to map multiple possible trajectories through a multidimensional space. Energy must be added to or taken from a system while simultaneously making biophysical and biochemical measurements to get details about a biomolecule’s intrinsic mechanistic pathways under out-of-equilibrium conditions. In this context, advanced integrative approaches, such as the combination of advanced optical tweezers and fluorescence methods, can be the way of the future. Specifically, we suggest that single-molecule multiparametric fluorescence spectroscopy integrated with ultrafast optical tweezers, that is, the smFFM, and combined advanced MD simulations can enable researchers to access the spatiotemporal regimes important for function. Widespread use of such integrated approaches will boost our understanding of a broad swath of biomolecular mechanisms and help the scientific community to engineer biology and develop future therapeutic agents.

Biographies

Narendar Kolimi is currently a postdoctoral fellow working with Dr. Hugo Sanabria in the single molecule biophysics group, Clemson University, USA. He completed B.Sc. in Biotechnology and M.Sc. in Biochemistry from Osmania University, Hyderabad, India. Following, he received his Ph.D. under the supervision of Dr. Thenmalarchelvi Rathinavelan in the Department of Biotechnology, Indian Institute of Technology Hyderabad, India, in 2018. During his Ph.D., he did research on secondary structural characteristics of unusual nucleic acid conformations in relevance to mechanisms and pathogeneses of trinucleotide repeat expansion disorders. The major focus of his research was towards structural analyses of biomolecules and their roles in various human neurological disorders. Later, he joined Dr. Sanabria’s group where his research interests include structure and dynamics of complex structure of nucleic acids and their interaction with neuronal proteins using fluorescence techniques such as single molecule FRET combined with molecular dynamics simulations.

Ashok Pabbathi is currently an Assistant Professor at the Department of Industrial Chemistry, Mizoram University, Aizawl, Mizoram, India. He graduated from Osmania University, Hyderabad, India, with a B.Sc. in Chemistry. He received his M.Sc. and Ph.D. in Chemistry from School of Chemistry, University of Hyderabad, Hyderabad, India. During his Ph.D. work, he pursued research on protein and DNA dynamics in aqueous-ionic liquid solutions using fluorescence correlation spectroscopy (FCS). Prior to joining Dr. Alper’s group at Clemson University, USA as a postdoctoral fellow, he went on to study the membrane fusion process employing fluorescence methods and optical tweezers at Technion-Israel Institute of Technology, Israel, and protein–DNA interactions using AFM and TIRF microscopy at University of Nebraska Medical Center, USA. His current research interests focus on understanding biophysical mechanisms underlying motor proteins, active materials, and protein–DNA interactions using single-molecule biophysical tools.

Nabanita Saikia is an Assistant Professor of Chemistry at Navajo Technical University. She has a Ph.D. in Computational and Theoretical Chemistry from the Department of Chemical Sciences at Tezpur University, India. Her doctoral research investigated the structure, energetics, and electronic properties of functionalized single-wall carbon nanotubes, graphene-based nanomaterials, and graphene oxide as carrier modules for therapeutic applications in tuberculosis and cancer therapy. The research made original contributions to understanding nanotechnology-based drug delivery systems to optimize therapeutics in biomedicine. Her current research implements computational techniques such as first-principles density functional theory, molecular docking, and MD methods to study the interactions of biological molecules with nanomaterials for applications in molecular recognition, biosensing, and self-assembly. She worked as a postdoctoral research fellow in the research group of Dr. Feng Ding at Clemson University. She developed in silico protocols to benchmark the conformational dynamics and structural ensembles of intrinsically disordered proteins and signaling scaffold proteins, investigated the putative role of interdomain linkers in regulating the conformational dynamics of the PDZ1–PDZ2 tandem of PSD-95, and resolved the structural heterogeneity in the domain organization of the PSG core supramodule of PSD-95 in the microsecond time scale by integrating replica-exchange DMD simulations with smFRET, MFD, and disulfide mapping gel assays to identify the limiting conformational states within signaling scaffold protein, PSD-95.

Feng Ding is an Associate Professor of Physics at Clemson University, USA. He obtained his Ph.D. from Boston University (2004) and worked as a postdoctoral fellow (2004–2006), research associate (2006–2008), and Research Assistant Professor (2008–2012) at the University of North Carolina at Chapel Hill before being hired as an Assistant Professor at Clemson University (2012–2017). His research focuses on understanding the structure, dynamics, and function interrelationship of biomolecules and molecular complexes. He was recipient of a Postdoctoral Award for Research Excellence (UNC, 2005), CAREER Award (US National Science Foundation, 2016), and Clemson Outstanding Young Researcher and Board of Trustee Awards (Clemson, 2017).

Hugo Sanabria is an Associate Professor in the Department of Physics and Astronomy at Clemson University. He graduated from Tec of Monterrey, Mexico, with a B.S. in Physics Engineering. He pursued an M.S. and Ph.D. in Physics at the University of Houston under Dr. John H. Miller’s supervision. His thesis was on applications of dielectric spectroscopy to study biopolymers. Dr. Sanabria received a Keck Fellowship from the Gulf Coast Consortia for his postdoctoral research with Dr. M. Neal Waxham at the University of Texas Health Science Center in Houston. There he studied Ca²⁺ signaling proteins involved in learning and memory processes. Later, he was awarded an Alexander von Humboldt fellowship at Heinrich Heine University, in Germany, under Dr. Claus A. M. Seidel’s supervision, where he developed and enhanced single-molecule methodologies to study the structure and dynamics of proteins. In 2014, he joined Clemson University, and in 2016, he was named CU School of Health Research Faculty Scholar. He is a recipient of the prestigious NSF CAREER award, the 2019 Board of Trustees Excellence award, and the 2019 HORIBA Young Fluorescence Investigator Award. NSF and NIH fund his research program.

Joshua Alper is an Assistant Professor in the Department of Physics and Astronomy and the Department of Biological Sciences at Clemson University. He has a B.S., M.Eng., and Ph.D., all in mechanical engineering, from the University of Rochester, Tufts University, and the Massachusetts Institute of Technology, respectively. His thesis was on applications of ultrafast pulsed laser irradiation in engineered nano-biosystems. Dr. Alper received a Marie Curie International Incoming Fellowship and worked with Dr. Jonathon Howard on the biophysics of axonemal dynein and ciliary motility at the Max Planck Institute of Molecular Cell Biology and Genetics in Dresden, Germany, and later at Yale University. In 2015, he joined Clemson University faculty. He is an Assistant Professor in the Department of Physics and Astronomy and the Department of Biological Sciences, and his research interests are in the molecular and cellular biophysics of the cytoskeleton, pathogenic parasites, and eukaryotic cilia, among other systems. NSF and NIH fund his research program.

Author Present Address

^§ Department of Industrial Chemistry, Mizoram University, Aizawl, Mizoram 796004, India

Author Present Address

^⊥ School of Applied Technology, Navajo Technical University, Chinle, Arizona 86503, United States.

Author Contributions

^∥ N.K. and A.P. contributed equally to this work. J.A. and H.S. supervised the writing of the manuscript. All authors contributed to the writing of the manuscript.

The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

The authors declare no competing financial interest.