A classification approach to estimating human circadian phase under circadian alignment from actigraphy and photometry data

Abstract

The time of dim light melatonin onset (DLMO) is the gold standard for circadian phase assessment in humans, but collection of samples for DLMO is time and resource intensive. Numerous studies have attempted to estimate circadian phase from actigraphy data, but most of these studies have involved individuals on controlled and stable sleep-wake schedules, with mean errors reported between 0.5 and 1 hours. We found that such algorithms are less successful in estimating DLMO in a population of college students with more irregular schedules: mean errors in estimating the time of DLMO are approximately 1.5–1.6 hours. We reframed the problem as a classification problem and estimated whether an individual’s current phase was before or after DLMO. Using a neural network, we found high classification accuracy of about 90%, which decreased the mean error in DLMO estimation - identifying the time at which the switch in classification occurs - to approximately 1.3 hours. To test whether this classification approach was valid when activity and circadian rhythms are decoupled, we applied the same neural network to data from inpatient forced desynchrony studies in which participants are scheduled to sleep and wake at all circadian phases (rather than their habitual schedules). In participants on forced desynchrony protocols, overall classification accuracy dropped to 55–65% with a range of 20–80% for a given day; this accuracy was highly dependent upon the phase angle (i.e., time) between DLMO and sleep onset, with highest accuracy at phase angles associated with nighttime sleep. Circadian patterns in activity, therefore, should be included when developing and testing actigraphy-based approaches to circadian phase estimation. Our novel algorithm may be a promising approach for estimating the onset of melatonin in some conditions and could be generalized to other hormones.

Introduction

Circadian rhythms are oscillations in behavior and physiology with a period of approximately 24 h. At the cellular level, these rhythms are driven by transcriptional-translational feedback loops¹, resulting in oscillations both in transcription of approximately 50% of genes in at least one organ² and in expression of many drug targets. This motivates the growing interest in chronotherapeutic approaches, in which drug intake is timed to maximize efficacy and minimize side effects³.

Misalignment between internal circadian rhythms and the environment, which occurs with jetlag, shiftwork, and circadian disorders, has been linked to adverse health outcomes, including cardiovascular disease, metabolic disease, and cancer⁴. Methods are needed, therefore, to shift the phase of the circadian clock to align with the environment. Both the magnitude and direction of the phase shift caused by both photic and non-photic (including pharmaceutical) interventions depends on the phase (i.e., time) at which the intervention is delivered^5–8. Thus, we must be able to precisely assess an individual’s current circadian phase⁹ before applying interventions.

The gold standard for circadian phase assessment in humans is dim light melatonin onset (DLMO). This phase assessment technique requires the collection of multiple hours of blood or saliva samples under low light conditions, usually in an inpatient setting, for later melatonin assay. This method is time-consuming and resource-intensive. Furthermore, it does not allow for circadian phase to be assessed continuously or in real-time, limiting its usefulness for timing interventions. These limitations motivate the need for an alternative method of circadian phase estimation. Recent research has focused on two main approaches, using a genetic assay or less invasive actigraphy data¹⁰.

Several methods have been proposed to estimate circadian phase using panels of circadian-cycling genes and proteins (reviewed in Crnko et al.¹¹). Machine learning algorithms¹² have reduced the number of genes used for these panels from over 100¹³ to about a dozen genes in monocytes extracted from whole blood¹⁴. Most of these approaches have mean errors between 1 and 2 hours (Table S1). These methods still have the limitations that the collection of samples is invasive and results are not available in real-time.

Actigraphy data can be collected non-invasively in real-time. These data can include activity counts, light levels, skin temperature, and/or heart rate. There are three main model categories for estimating circadian phase using actigraphy data: limit cycle oscillator models, regression models, and neural network models¹⁵; their errors are between 0.4 and 1.1 h (Table S2). Limit cycle models use actigraphy data as input to differential equations-based models, most commonly the Kronauer model¹⁶ or its amended version which includes a non-photic component¹⁷, to predict how the series of light inputs shifts oscillator phase¹⁸. Some regression models have used derived markers of actigraphy rhythms, such as the time of peak activity or the time when wrist temperature begins to increase, to estimate DLMO¹⁹. Another approach has used an adaptive notch filter (ANF) to derive harmonic estimates to estimate phase shifts²⁰. The limit cycle, linear regression, and ANF models all require several days of data for (i) the limit cycle result to be insensitive to initial conditions or (ii) to define average activity markers, limiting their utility for a phase assessment that can be performed quickly (with the goal of real-time assessment). Other regression models have used light and skin temperature recordings from multiple skin electrodes over a 24 h period to estimate circadian phase with a mean error of 0.7 h²¹. Recent neural networks have had success in prediction when the model’s exact functional form is unknown²². Using the same input data but increasing the flexibility of the model by training a neural network, this mean error was decreased to 0.4 h²³. A similar approach in a different population, but with seven days of actigraphy recordings, found a mean error of 0.6 h in a population with habitual day active schedules²⁴, with similar accuracies when using just a single wrist temperature sensor. These studies are limited due to small sample sizes (n<25) and the fact that participants follow regular, controlled schedules. Moreover, the same neural network model produced mean errors of over 2 h for participants on night shift schedules²⁵, suggesting that the model does not generalize well to populations with less regular schedules or when the individual is awake at circadian phases usually associated with sleep. More recent work has again explored using differential equations-based models with some success in shift workers, although absolute mean errors remained higher^26–28 than those reported in these models for participants with aligned schedules.

We therefore tested the generalizability of neural network-based models to a population of college students who had a high range in regularity in their sleep schedules²⁹. We also developed a novel classification-based approach, which we tested in the college student population and in participants on inpatient forced desynchrony protocols in which sleep and wake occurred at all circadian phases to determine the effect of circadian misalignment on DLMO estimation.

Materials and Methods

The studies were approved by the Partners Human Research Committee and were performed according to the principles outlined by the Helsinki Declaration. Appropriate informed consent was obtained. Details of each study are in the original publications^30–35.

Actigraphy Data from a College Student Population

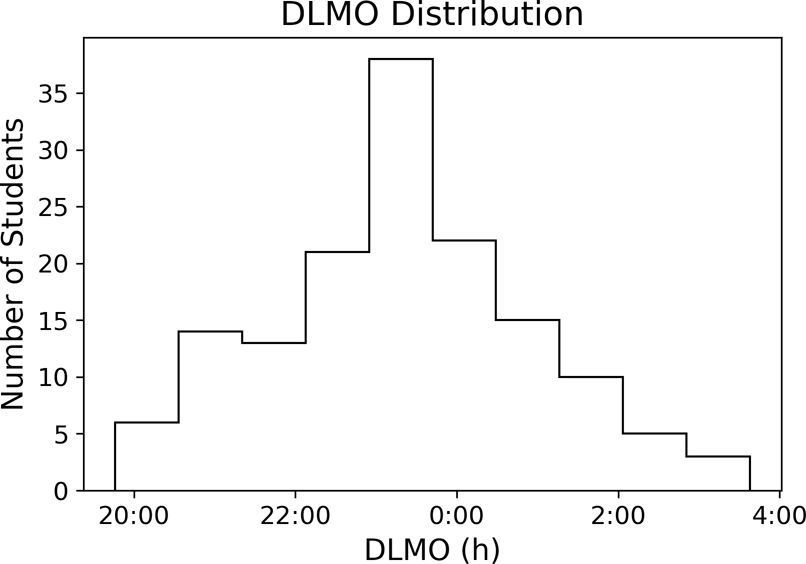
Data are from 174 participants from cohorts of ~30 undergraduate students each across six different semesters for ~30 days while students lived at school^30,36. Participants completed demographic, psychological, and sleep habit questionnaires at the beginning of the study (“static data”). For all days, participants wore an actiwatch (Motionlogger, AMI, Ardsley, NY) that collected minute-by-minute light levels and activity counts (zero crossing mode) in addition to a Q-sensor (Affectiva, Boston, MA) that collected skin temperature readings at 8 Hz. At one time during these ~30 days, participants were admitted to an inpatient facility for DLMO assessment. This data set was chosen because there was a wide distribution of DLMO values (Figure 1) with mean DLMO value of 23.3±1.58 h and range of ~8 h, broader than the ~5 h range which is typical of the adult population³⁷.

Figure 1. DLMO in the Study of College Students.

Histogram showing the distribution of the timing of DLMO in this population.

Actigraphy Data from Forced Desynchrony Protocols

Data are from four inpatient forced desynchrony (FD) protocols. During an FD, participants are placed on a non-24-h schedule that is outside of the range of entrainment of the circadian clock, allowing for the decoupling of rest-activity patterns and circadian rhythms. The four FD protocols are summarized in Table S3. Minute-by-minute light and activity data and hourly blood melatonin data from the FD portion of the study were used. For each day, we defined the phase angle of entrainment as the difference between DLMO and scheduled sleep start.

DLMO Determination

DLMO was calculated by linearly interpolating the time at which melatonin levels crossed the 5 pg/mL threshold in saliva or 10 pg/mL threshold in blood ²⁹.

Data Cleaning and Standardization

We wanted our method to be capable of estimating DLMO using only a limited timeframe of data, so we restricted our input data to the 24 hours immediately before the day of DLMO assessment. For training and testing our model, we considered only participants who had complete light and activity recordings for this day. For skin temperature data, we computed the average value for each minute and linearly interpolated missing values. Data were removed from further analysis if more than a minute of skin temperature recordings were missing from the end of the 24 h period or if total activity, light, or temperature recordings for the 24 h period were less than 3 standard deviations below the population mean, suggesting device malfunction. Data from 27 participants were removed.

To reduce the number of model inputs, we computed the average value of light, activity, and skin temperature within a 30-minute bin. We then standardized these binned inputs by participant for each data type (see Supplementary Information). We also compared performance using the median instead of the average.

The data were randomly split into a training (n=118) and independent test set (n=29), where we performed 10-fold cross-validation within the training set (which was randomly split into 10 test sets for cross-validation) to fit the hyperparameters of the model.

Continuous Neural Networks

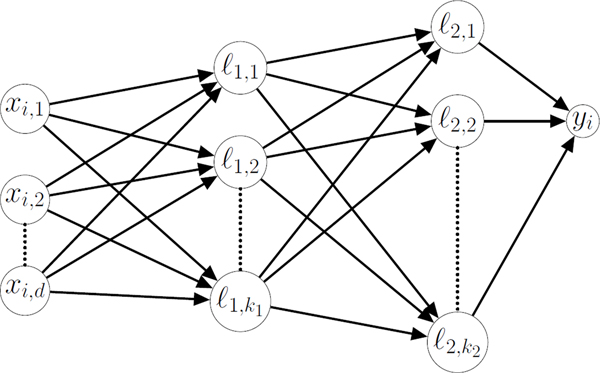
We first trained (using the college student data) a neural network to continuously estimate time of DLMO. We implemented a basic feedforward hidden layer neural network architecture with one and two hidden layers with hyperbolic tangent activation functions in the keras package in Python (Figure 2). To increase robustness, we also introduced dropout into these models, where models are randomly thinned during training to reduce overfitting to particular data features³⁸. We varied the hyperparameters of the number of nodes in each layer (between 10 and 100 in multiples of 10 for the single hidden layer model, and all combinations of between 10 and 50 in multiples of 10 for the two hidden layer model) and dropout rate (between 0.1 and 0.5 in multiples of 0.1). For each of these models we trained the weights of the model using Adam optimization (learning rate = 0.005 for 500 iterations) to minimize the sum of the squared error between our estimated DLMO and the experimentally measured DLMO value on each of the cross-validation splits. We then chose the hyperparameter with the lowest mean cost function for our final model architecture, retrained this model on the full training set, and used the weights from training to evaluate the model on the test set.

Figure 2. Example Neural Network.

A schematic of a neural network, where x is a vector of input data for d input features where x_{i, v} is the vth feature for the ith participant and y_i is the network output for the ith participant. In the case of the continuous neural network, y_i is a continuous variable representing the network’s prediction of the time of DLMO for the ith participant. In the case of the classification neural network, y_i falls between 0 and 1 and if y_i< 0.5, the timepoint is classified as falling before DLMO. Nodes l_m,n represent hidden nodes in the network, where m is the layer of the node, and n is the index of the node within each layer. The value of each node is determined by $l_{m,n}=\tanh \left(\sum _{n=1}^{k_{m-1}}{w}_{m,n}{l}_{m-1,n}+b_n\right)$ for b_n a fit constant. The number of nodes in each layer, k_m for b_n a fit constant. The number of nodes in each layer, k_m, is a hyperparameter which was selected through cross validation.

We also tested the performance of long short-term memory (LSTM) architectures fitting a single layer of LSTM units (where we fit this hyperparameter between 10 and 50 in multiples of 10), which include recurrent loops with memory lags. LSTMs have had success when analyzing time series data³⁹ such as our 24 h actigraphy recordings, and recurrent neural networks, such as LSTMs, have been previously applied to the college student dataset⁴⁰

Classification Approach to DLMO Estimation

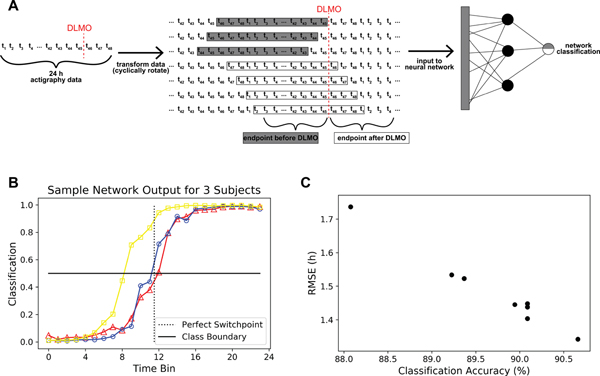
We also developed a novel approach to estimate the timing of DLMO, based on classification. Using this approach, we could effectively increase our sample size using the existing data. While our population was larger than those used to fit previous phase estimation models, it was still small for machine learning applications; the number of samples in our model was smaller than the number of parameters in the model because of the parameters for the nodes in the hidden layers. Rather than estimating the time of DLMO directly, we predicted whether the last timepoint in a 24 h series of data falls before or after DLMO; we shifted a 24 h interval of data (Figure 4A), where for each participant we have 6 h (12 datapoints in 30-minute bins) of samples where the last timepoint occurs before DLMO and 6 h of samples where the last timepoint occurs after DLMO. This approach created a balanced dataset and allowed us to increase the number of samples in our dataset 24-fold.

Figure 4. Outputs of the Classification Algorithm and Relationship to DLMO Estimation Accuracy A.

A schematic for the process of using actigraphy data in our classification algorithm. We use 24 h of actigraphy data, where data are binned into 30-minute time-bins for a total of 48 datapoints for each datatype, so t_i represents the ith 30-minute bin of activity, light, and skin temperature data. We create a classification problem, where we predict whether the endpoint of an interval of 24 h of data falls before or after DLMO using a neural network. B. Classification neural network outputs for three test participants. For each participant, each line shows the 24 predictions of whether the time series falls before or after DLMO by rotating our 24 h series of data. Outputs less than 0.5 are classified as occurring before DLMO and outputs greater than 0.5 are classified as occurring after DLMO. A perfectly accurate classifier would have the switch in classification between time-bins 11 and 12. C. Comparison of classification accuracy versus the resulting root mean squared error in DLMO estimation based on where the switch in classification occurs for the different models in Table 3.

We compared the same neural network structures, but with rectified linear unit (ReLU, outputs the greater of the input and 0) activation between layers. To make the networks predict a classification we introduced a sigmoidal nonlinearity in the output, and instead of using the squared error loss as our cost function, we used cross entropy loss to train the model with stochastic gradient descent (learning rate=0.001 for 100 iterations).

Our trained model outputs class labels for each 24 h time series (rather than a continuous-time estimation). From these class labels, we could then estimate a value for DLMO by taking the midpoint of the times that the class labels switch from before to after DLMO.

Circadian Rhythmicity of Activity Levels

The circadian phase of each actigraphy data point was calculated using circadian period (i.e., slope) and starting phase (i.e., intercept) from the linear regression of DLMO collected during the FD portion of each experiment. Data were then assigned to 3-h circadian time bins (one-eighth of the participant’s circadian period) and 3-h wake duration time bins. Within each time bin, we used Zero Inflated Poisson (ZIP)-based statistics on activity levels for each participant. We then averaged bins across participants within each of the FD protocols. We tested for differences by circadian phase and time awake within each of the 4 FD protocols using repeated-measures ANOVA using SAS 9.4.

Results

Previous Methods Do Not Generalize to the College Student Population

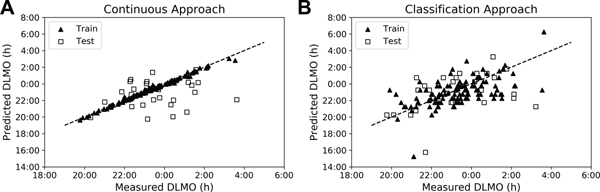
We first tested whether machine learning, actigraphy-based models like those used in more tightly-controlled, small-sample-size populations^23,24 would extend to college students living at their school on self-selected, sleep-wake schedules. We found root mean squared errors (RMSE) of approximately 1.6 h for most models, with the best performing models (LSTMs) having errors of about 1.5 h for the average features (Table 1). When using the median (instead of average) features, (i) there was not much improvement except in the case of the full data set with all the demographic and actigraphy features, where errors decreased to about 1.4 h, but (ii) there were more consistent results across the models because the model predicted the mean DLMO of the dataset (Table S6, Figure S2). The Pearson’s R for the relationship between experimentally measured DLMO and the continuous model estimated phase in the training set was 0.99 (p<<<0.01), it was 0.17 (p=0.38) for the test set (Figure 3A). These errors are higher than those reported in the populations with more regular schedules and perform only minimally better than simply predicting the population mean, suggesting that these models do not generalize well to populations with irregular schedules.

Table 1. Performance of Continuous Neural Network Models for DLMO Estimation in College Students.

The root-mean-squared-error (RMSE) in cross-validation (mean ± standard deviation) and on the independent test set between the DLMO estimated by our models and the experimentally measured DLMO on different subsets of the data. Static data were collected only once per study; they include demographic data and baseline questionnaires.

Cross-Validation Results
Model	Full Dataset	Actigraphy Data	Activity & Skin Temperature	Activity & Light	Light & Skin Temperature	Static Data
Single Layer	1.68±0.44 (30 nodes)	2.00±0.88 (30 nodes)	2.62±1.69 (10 nodes)	1.68±0.37 (10 nodes)	2.32±1.22 (10 nodes)	2.66±1.67 (10 nodes)
Single Layer with Dropout	1.54±0.42 (p=0.3)	1.77±0.74 (p=0.4)	2.52±1.99 (p=0.1)	1.57±0.35 (p=0.1)	1.82±0.69 (p=0.1)	1.80±0.38 (p=0.3)
Double Layer	1.58±0.31 (30x10 nodes)	1.62±0.38 (10x10 nodes)	2.24±0.42 (10x30 nodes)	1.58±0.31 (50x10 nodes)	1.73±0.67 (30x10 nodes)	2.34±1.50 (10x10 nodes)
Double Layer with Dropout	1.59±0.30 (p=0.1)	1.62±0.34 (p=0.1)	1.82±0.46 (p=0.5)	1.59±0.30 (p=0.1)	1.81±0.69 (p=0.2)	1.64±0.38 (p=0.1)
LSTM	1.94±1.07 (10 units)	1.57±0.30 (50 units)	1.57±0.31 (20 units)	1.57±0.31 (20 units)	1.57±0.30 (40 units)	-
LSTM with Dropout	1.41±0.30 (p=0.5)	1.51±0.31 (p=0.4)	1.55±0.33 (p=0.5)	1.57±0.30 (p=0.1)	1.57±0.31 (p=0.1)	-
Test Results
Model	Full Dataset	Actigraphy Data	Activity & Skin Temperature	Activity & Light	Light & Skin Temperature	Static Data
Single Layer	2.15	2.17	8.29	1.59	2.58	1.88
Single Layer with Dropout	1.65	1.74	8.13	1.66	2.16	1.89
Double Layer	1.58	1.58	9.20	1.58	1.58	1.62
Double Layer with Dropout	1.64	1.65	5.56	1.65	1.73	1.62
LSTM	1.58	1.57	1.58	1.57	1.58	-
LSTM with Dropout	1.47	1.51	1.56	1.58	1.58	-

Figure 3. Neural Network Based Estimations of DLMO.

Scatter plot showing experimentally measured DLMO vs. model estimated phase for the training and test sets with the single layer model for continuous neural networks (A) and classification neural networks (B). The dashed line represents perfect estimation.

A Classification Approach Improves Phase Estimation Accuracy in the College Student Population

The classification approach could predict whether a timepoint was before or after DLMO based on 24 h of data with high accuracy (~90%) for both the training and test set (Table 2, Table S4) for both average and median features. Predictions were more consistent when using the median features (Tables S7–S8).

Table 2. Performance of Classifiers for DLMO Estimation in College Students.

The classification accuracy of whether a timepoint falls before or after experimentally observed DLMO in cross-validation (mean ± standard deviation) and on the independent test set on different subsets of the data.

Cross-Validation Results
Model	Full Dataset	Actigraphy Data	Activity & Skin Temperature	Activity & Light	Light & Skin Temperature
Single Layer	89.1±3.7 (100 nodes)	89.4±3.6 (90 nodes)	88.8±3.4 (50 nodes)	89.8±3.4 (90 nodes)	87.0±3.0 (30 nodes)
Single Layer with Dropout	89.3±3.4 (p=0.4)	89.3±3.2 (p=0.3)	89.1±2.9 (p=0.5)	89.5±3.8 (p=0.5)	87.1±3.4 (p=0.2)
Double Layer	88.9±3.6 (50x50 nodes)	89.3±3.6 (30x50 nodes)	89.2±3.5 (30x40 nodes)	90.0±3.9 (40x40 nodes)	86.8±3.7 (30x40 nodes)
Double Layer with Dropout	89.3±3.3 (p=0.4)	89.5±3.4 (p=0.3)	88.7±3.2 (p=0.1)	89.6±3.8 (p=0.4)	87.1±2.9 (p=0.2)
Test Results
Model	Full Dataset	Actigraphy Data	Activity & Skin Temperature	Activity & Light	Light & Skin Temperature
Single Layer	90.7	90.2	89.1	89.9	86.1
Single Layer with Dropout	89.9	90.2	89.8	89.8	85.8
Double Layer	90.1	90.9	89.4	90.5	86.4
Double Layer with Dropout	89.2	89.8	88.8	90.1	85.1

A sample output of the classification neural network is shown in Figure 4B; we have presented the data so that the switch in classification should occur between the eleventh and twelfth time-bin for perfect accuracy. We found that the changes in class prediction usually only crossed the decision boundary once; in cases where this was not true, we defined the switch as the first time that the decision boundary was crossed for simplicity. The RMSE for these estimations decreased in all models when using the average features (Table 3) with the best performing models producing an RMSE of 1.3–1.4 hours (R=0.59 (p<<<0.01) in the training set and R=0.40 (p=0.03) in the test set (Figure 3B)). Even seemingly small improvements in classification accuracy can lead to large improvements in RMSE (Figure 4C), which suggests that the errors in the classification occur near the decision boundary. In 16% of participants, the change in classification occurs within 15 minutes of measured DLMO, and in 35% of participants, the switch occurs within 30 minutes. However, the classification approach did not improve over the continuous approach when using the median features, suggesting that the increased variance provided by the average is important to the success of the classification approach (Table S9).

Table 3. Classification Performance vs. RMSE in Estimated DLMO.

A comparison of classification accuracy (predicting if a timepoint falls before or after DLMO) to the resulting RMSE between estimated DLMO, calculated based on the switch in classification, and the experimentally measured DLMO for different classification models.

Model	Full Dataset		Actigraphy Dataset
	Test Accuracy	Test RMSE	Test Accuracy	Test RMSE
Single Layer	90.7	1.34	90.2	1.36
Single Layer with Dropout	89.9	1.45	90.2	1.42
Double Layer	90.1	1.40	90.9	1.30
Double Layer with Dropout	89.2	1.53	89.8	1.82
Logistic Regression	88.1	1.74	90.4	1.33
SVM (linear kernel)	89.4	1.52	90.7	1.37
SVM (polynomial kernel)	90.1	1.44	89.9	1.45
SVM (RBF kernel)	90.1	1.45	90.5	1.39

Accuracy of the Classification Approach Depends on the Phase Angle Between DLMO and Sleep Onset

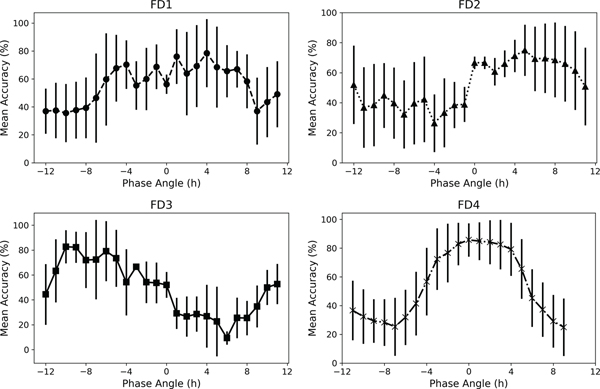
We fit the model to the training set of light and activity patterns in the college sleep students and tested the performance in the FD datasets. In the FD data, overall classification accuracy dropped to approximately 50–60% (Table 4), preventing a meaningful determination of DLMO based on switches between class labels. Within individual participants, we found that classification accuracy could vary between 20% and 80% depending upon the day in the protocol, probably due to the phase angles between sleep onset and DLMO; a FD schedule includes all possible phase angles, while the phase angle is typically 2.2 ± 1.0 h in aligned populations⁴¹. Mean classification accuracy was higher for days where the phase angles were those of alignment (approximately −4 to 4 h) (Figure 5).

Table 4. Performance of Classification Models for DLMO Estimation in Forced Desynchrony (FD) Protocols.

Classification accuracy performance on four different FD protocols to test for generalization of these models originally fit to activity and light level data from the college student population.

Model	FD1	FD2	FD3	FD4
Single Layer	54.1	52.3	51.8	57.2
Single Layer with Dropout	54.9	53.1	51.0	56.7
Double Layer	53.4	54.3	52.1	57.4
Double Layer with Dropout	54.8	53.6	51.6	57.0

Figure 5. Classification Accuracy in Forced Desynchrony (FD) Protocols is Dependent on Phase Angle Between Sleep Onset and DLMO.

The mean (standard deviation) accuracy of the neural networks classification for days relative to the phase angle (between sleep onset and DLMO) for each of the 4 different FD protocols.

To further explore these findings, we analyzed the activity data relative to circadian and wake duration bins. There were significant differences in activity levels by circadian phase (p<0.007) and wake duration (p<0.001) for all four FD studies (Figure S3). The circadian rhythm of activity was highest at circadian times 13.5–19.5 h and lowest at −1.5–0.5 h relative to DLMO.

Discussion

Our classification-based method showed improvement over the continuous approaches in college students on self-selected schedules, suggesting that our model may be more generalizable since the range of observed phases (Figure 1) is also broader in college students compared to healthy participants studied under inpatient conditions. The range of errors in estimating circadian phase in both our continuous models (which were based on previous approaches^23,24) and classification models, however, are greater than previous studies^19,21,23,24. While our and other methods were successful in estimating DLMO in populations on “normal” schedules, they were less successful when circadian phase and rest-activity rhythms were misaligned (as is common with rotating shiftwork and circadian disorders); in such conditions, phase shifting interventions may be the most valuable. Therefore, there is still a need for further improvement in circadian phase estimation in misaligned conditions.

Desired Accuracy for Clinical Utility

Repeated measures of DLMO in this college population⁴² and studies on the variance of DLMO assessment show typical fluctuations of less than an hour⁴³. Therefore, a single phase estimate may be useful for clinical and other applications. The accuracy required for phase estimation methods to be clinically useful, however, may depend on the application⁹. Errors of approximately one hour may be acceptable to predict cognitive performance, but efficacy of phase shifting decreases from about 80% to 60% if errors in the timing of a light pulse increase from 1 to 2 hours¹⁵, resulting in possible errors in the shifted phase⁴⁴.

Further Improvements to the Classification Approach

Although our population is larger than in previous studies, training the model on still larger populations could be beneficial for refining the model, as machine learning approaches have greatest success on large datasets because of the large number of parameters that are needed in these models. One possible reason the classification approach was more successful in estimating DLMO than the continuous models was because that approach increased our dataset size. Using this same expanded dataset but predicting time to DLMO from a specific time based on 24 h of data in a continuous framework, did not improve errors in DLMO estimation; this suggests the classification approach confers additional benefits beyond just more effectively using data.

Our classification accuracy may have performed poorly on the FD protocols because our training set of college students was not representative of these misaligned schedules, so using broader training data may lead to improvements. Some initial experiments in training on the FD datasets suggest some limited generalizability to the population of college students with approximately 70% accuracy. This is still lower than attained in our models trained in the college student population (as reported above), suggesting that other differences (i.e., controlled light and temperature environments) between the inpatient and outpatient populations may be important to the higher accuracy for models trained in the college population. To what extent classification accuracy depends on the training and testing demographic populations (e.g., circadian phase tends to be earlier in older populations⁴⁵) should be explored.

Larger populations may also allow for other types of machine learning models to be implemented. Convolutional neural networks are highly effective in classifying images⁴⁶, and may also be effective here if classification is dependent on the location of a specific feature of the actigraphy data waveform. Recent research has explored physics-informed neural networks, which, by introducing physical laws as constraints, can solve differential equations⁴⁷. Based on the success of the differential equation-based approaches in estimating circadian phase¹⁸, adding known dynamics about the impact of light in creating phase shifts in combination with neural networks may be a promising direction to pursue.

As these networks are further developed, other features of the input data could be considered. In our analysis, we did not find improvements when using smaller time-bins for the data (Tables S5 and S10), but the length of the time-bin does put a lower bound on accuracy. For data to correspond to a circadian cycle, we chose to use a 24 h interval of data. Requiring 24 h of data limits the ability to immediately assess circadian phase so shorter time intervals are preferrable, but we found that accuracy decreased with decreasing time intervals of data (Figure S1). Incorporating data from when actigraphy and a single DLMO measurement were available in addition to current actigraphy data may also be valuable for future predictions, given the relative consistency of DLMO⁴².

Significance of Activity Rhythms and Challenges Under Circadian Misalignment

Our results demonstrate that activity levels may be important both for circadian phase estimation and other applications using activity as an input because of its circadian variation. Lowest accuracy in our classification approach was seen across models using average features when activity was not included as a model input, unlike previous studies that suggested skin temperature data was more important for prediction accuracy^21,23.

Circadian variation may explain why the actigraphy-based approaches are highly limited in their predictive ability under circadian misalignment; FD protocols result in activity levels at circadian phases different than “normal”: higher levels during scheduled wake during the circadian “night” and lower levels during scheduled sleep during the circadian “day”. Circadian misalignment is common in individuals working night shifts and those with circadian rhythm sleep disorders: two populations that may need accurate phase assessments for interventions. Thus, a different data source or methodology may be required for phase assessment in these populations because of these changes in timing of behaviors and/or different light sensitivities in people with circadian disorders^48,49.

We have presented a novel, machine learning approach in using actigraphy to estimate DLMO that is effective in outpatient, circadian-aligned populations. The classification-based approach introduced here is not limited to the prediction of the rise in melatonin but could also be used to estimate the timing of other hormones.

Data Availability Statement

We will make the datasets available to other investigators upon request. Outside investigators should submit their request in writing to Dr. Klerman. The request must be in accordance with MGB Policies, Harvard Medical School (HMS), and Harvard University guidelines. Such datasets will not contain identifying information per the regulations outlined in HIPAA. Per standard MGB policies, we will require a data-sharing agreement from any investigator or entity requesting the data.