Differential impacts of contact tracing and lockdowns on outbreak size in COVID-19 model applied to China

Abstract

The COVID-19 pandemic has led to widespread attention given to the notions of “flattening the curve” during lockdowns, and successful contact tracing programs suppressing outbreaks. However a more nuanced picture of these interventions’ effects on epidemic trajectories is necessary. By mathematical modeling each as reactive quarantine measures, dependent on current infection rates, with different mechanisms of action, we analytically derive distinct nonlinear effects of these interventions on final and peak outbreak size. We simultaneously fit the model to provincial reported case and aggregated quarantined contact data from China. Lockdowns compressed the outbreak in China inversely proportional to population quarantine rates, revealing their critical dependence on timing. Contact tracing had significantly less impact on final outbreak size, but did lead to peak size reduction. Our analysis suggests that altering the cumulative cases in a rapidly spreading outbreak requires sustained interventions that decrease the reproduction number close to one, otherwise some type of swift lockdown measure may be needed.

1. Introduction

The COVID-19 pandemic began in Wuhan, China, where infections grew rapidly and spread throughout the country in late December 2019 and January 2020. In order to contain the virus, drastic measures, such as travel restrictions alongside extensive lockdowns and contact tracing efforts, were implemented. The overall success of these control strategies in suppressing the outbreak in China has been recognized in several studies (WHO, 2020, Kraemer et al., 2020). An important question is which intervention had the largest impact, or in more detail, quantifying the effect of each intervention on case reduction. The problem is relevant not only for retrospective analysis, as all countries including China face the task of controlling ongoing or possible second wave outbreaks of COVID-19, along with future emerging epidemics.

Important strategies for the fight against COVID-19 are often classified as non-pharamaceutical interventions (NPIs) because consensus vaccines or treatments may not be widely available or enough effective. The effectiveness and aims of NPIs may vary by country and type of intervention. While the goal of large-scale lockdowns and social distancing is often characterized as “flattening the curve”, whereas successful contact tracing may suppress outbreaks, a more nuanced picture of their potential impact on epidemic trajectories is necessary. A few studies have quantified impact of travel restrictions (Lai et al., 2020, Tian et al., 2020) and lockdowns inducing large-scale changes in contact patterns or depletion of susceptible individuals (Zhang et al., 2020, Maier and Brockmann, 2020), showing the efficacy of these interventions in China. Yet, the precise qualitative and quantitative effect of brute force interventions such as lockdowns (or widespread social distancing), versus the more targeted strategy of contact tracing, on the outbreak shape is less explored.

Traditionally the influence of control strategies on outbreaks has been theoretically investigated in compartmental ordinary differential equation models of the susceptible-infected-recovered (SIR) type. Analysis yields the herd immunity (or critical vaccination) threshold for suppressing an outbreak by proportionally reducing the effective reproduction number, ${\mathcal{R}}_e$, below one, along with a nonlinear relationship between ${\mathcal{R}}_e$ and final outbreak size when ${\mathcal{R}}_e$ is above one. Furthermore, inference of parameters by fitting the model to data can help to determine the effect of interventions. However both the analytical and parameter estimation approaches are challenged by the dynamic nature of control strategies as public health authorities and individuals react to an evolving outbreak.

While the early phase of COVID-19 can be characterized by exponential growth, case saturation occurred much earlier than would be predicted by the basic SIR model due to the comprehensive control measures that have been deployed. In particular, stringent lockdown with broad (self- and contact tracing) quarantine interventions reduced the pool of susceptible individuals, effective contact rate and secondary transmissions. Several models have utilized time-dependent transmission or isolation rates to capture the dynamics (Lai et al., 2020, Tang et al., 2020), and recent work has also considered removal of susceptible individuals at a constant rate (Maier and Brockmann, 2020). Here we develop a generalized SIR-type model incorporating a total (government mandated and individual) self-quarantine rate, along with contact tracing, both depending on force of infection, to fit an observed reactionary public health system and derive novel formulae for outbreak size.

To quantify the impacts of contact tracing and comprehensive social distancing (self-quarantine or lockdowns), we simultaneously utilize case and quarantined contact data from China to estimate parameters in our model. Furthermore, through computational and theoretical analysis of the model, we can explore the sensitivity of distinct epidemic measures (e.g. outbreak size, peak number of infected, timing and extent of self-quarantine) to interpretable control parameters. These investigations allow us to dissect how combinations of NPIs, such as contact tracing and lockdowns, may influence sequential outbreaks through loosening and tightening of control measures. The emergent picture is of distinct qualitative impacts of contact tracing and lockdowns on the outbreak, variable in scope and timing, and dependent on underlying disease parameters. A better understanding of these differential effects can help shape or suppress the epidemic curve of COVID-19 in a sustainable and socially acceptable manner.

2. Model with self-quarantine and contact tracing

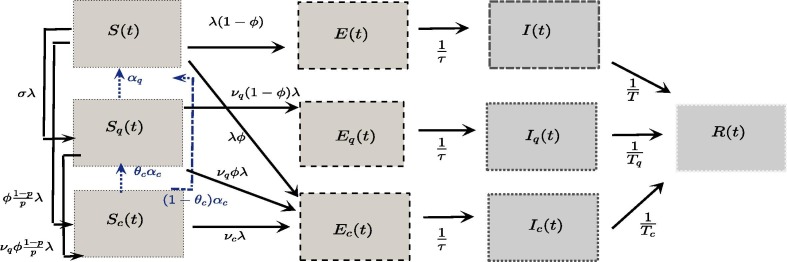
We develop a disease outbreak model (Fig. 1 ) with contact tracing and lockdown (self-quarantine) measures. For a population with fixed size N, we first divide the non-quarantined individuals (not contact-traced or self-quarantined) into susceptible (S), exposed (E) and infectious (I) classes. We define the mean incubation period $\tau$, baseline transmission rate $\beta$ and mean infection period T associated with the infected compartments. A widely used intervention for COVID-19 (and other infectious diseases) is contact tracing; where contacts of infected cases are tracked and monitored, informed of their risk status, quarantined or tested, in order to effectively isolate infected individuals, reduce secondary infections, and identify transmission chains (Bradshaw et al., 2021). In prior work on contact tracing during Ebola outbreaks (Browne et al., 2015), we derive an SEIR model by approximating integral equations, which led to all transmission events being stratified according to whether they will be contact traced and, if so, the contact’s infection status (incubating or infectious for some average period) at the time of tracing. Motivated by this approach, and for fitting our model to data on total quarantined contacts in China (Section 4), we consider contact traced susceptible ($S_c$), exposed ($E_c$), and infectious individuals ($I_c$) in our model.

Fig. 1.

Full model of COVID-19 with reactive contact tracing and self-quarantine. We extend the basic SEIR model describing Susceptible (S), pre-infectious Exposed (E), Infectious (I), and Reported case (R) compartments to also include contact-traced ($S_c,E_c,I_c$) and (lockdown or social distancing following) self-quarantined ($S_q,E_q,I_q$) individuals. See Table 1 and SI Appendix for model descriptions, and (2) for simplified “perfect quarantine” system.

Susceptible individuals whom contact infectious individuals (resulting in the contact tracing), are transitioned to $S_c$ and $E_c$ compartments at the rates $\frac{1-p}{p}\varphi \lambda (t)$ and $\varphi \lambda (t)$, respectively, where $\lambda (t)$ is the force of infection, $\varphi$ is the proportion of contacts with an infected case that are traced, and p is the probability of transmission upon contact. To justify these transition rates, consider the simplest case where only non-quarantined (not traced) infectious individuals can transmit the virus, where $\lambda (t)=\beta I(t)/N$ with $\beta$ the product of transmission probability p and the contact rate c. Then $\left(\frac{1-p}{p}\varphi +\varphi \right)\mathit{pc}(I(t)/N)S(t)=\varphi c(I(t)/N)S(t)$ yields the total amount of contact events at time t which will be contact traced. While there are inherently delays between contact event and tracing, our model separates contact traced individuals at the moment of contact into the $S_c$ and $E_c$ compartment (we do adjust for this delay when fitting contact tracing data). For the proportion of contacts whom are infected and traced ($E_c,I_c$), we assume an associated transmission rate ${\beta }_c$ and infectious period $T_c$, reflecting the effective reduced secondary transmissions induced by the action of contact tracing which is generally imperfect (for example, due to tracing individual after they become infectious). We also consider the reduction in susceptibility due to contact tracing, ${\nu }_c$, and the mean duration of quarantine (or monitoring), $1/{\alpha }_c$, for contact traced susceptible individuals ($S_c$). While our formulation simplifies some aspects of Browne et al. (2015), by explicitly linking tracing to contact events and its mode of action, we capture the essential mechanisms of contact tracing in a tractable way.

In order to describe the lockdowns and self-quarantine actions taken by both governments and individuals reacting to COVID-19 incidence, define the self-quarantined classes of susceptible ($S_q$), exposed ($E_q$), and infectious ($I_q$) individuals. We model the primary mechanism of lockdown/self-quarantine - sheltering large portions of susceptible population – by having susceptible individuals transition to $S_q$ at rate $\sigma \lambda (t)$, where $\sigma$ is a proportionality constant with respect to force of infection $\lambda (t)$, denoted as the self-quarantine (rate) factor. The product of $\sigma$ with force of infection is a phenomenological relation between lockdown/self-quarantine rates and current infection levels. Indeed, several studies from various countries (Fang et al., 2020, Chudik et al., 2020, Sheridan et al., 2020, C. Xiong et al., 2020, Gupta et al., 2020, Goolsbee and Syverson, 2021) have shown that population activity measures (e.g. within-city mobility, economic transactions, percentage of people staying/working at home) were primarily driven by individual reaction to media and perceived risk tied to COVID-19 case incidence, and secondarily influenced by government mandates, also inherently related to case counts, but enacted in a temporally discrete manner with other factors affecting their proclamation. Although reporting accuracy and delays in response complicate the relationship between human behavioral changes and raw infection incidence, for simplicity, here we consider self-quarantine ($\sigma$) proportional to force of infection ($\lambda (t)$). In C.2, we adjust for the response delay by rescaling $\sigma$ so that susceptible quarantine rate depends on instantaneous change in reported case numbers, and also check robustness of results with a delay model for self-quarantine proportional to daily reported cases.

We define susceptibility, transmissibility and infectious period for self-quarantined compartments, determined by parameters ${\nu }_q,{\beta }_q$, and $T_q$, respectively, measuring the looseness of lockdown or social distancing measures. The exit rate or rate of return from self-quarantine is given by constant (per-capita) rate ${\alpha }_q$. For analytical tractability and superior parameter identifiability, we neglect transiting of non-quarantined infected individuals ($E,I$) to $E_q,I_q$ status. Thus the overall infectious and exposed period (serial interval) remain constant, which can be interpreted as averaging an evolving serial interval (e.g. due to improving non-pharmaceutical interventions (Ali et al., 2020)) over the outbreak timeframe. However, in Appendix C.3 we do consider fitting an alternative version of our simplified model below with non-constant serial interval, where infected individuals become self-quarantined (locked-down) as formulated above.

The full system of equations, including susceptible (S), exposed (E) and infectious (I) individuals; self-quarantined susceptible ($S_q$), exposed ($E_q$) and infectious ($I_q$) individuals; contact-traced susceptible ($S_c$), exposed ($E_c$), and infectious ($I_c$) individuals; and the decoupled compartments of (safely) isolated reported cases (R) with a subset of currently quarantined contact-traced cases ($R_c$), is given below.

Full Model:

$$\begin{array}{cc}\hfill S^{\prime }& =-S\left(1+\psi \right)\lambda +(1-{\theta }_c){\alpha }_c{S}_c+{\alpha }_q{S}_q\hfill \\ \hfill {(S_c)}^{\prime }& =S\frac{(1-p)}{p}\varphi \lambda +\frac{(1-p)}{p}{\nu }_q{\varphi }_q{S}_q\lambda -{\alpha }_c{S}_c-{\nu }_c{S}_c\lambda \hfill \\ \hfill {(S_q)}^{\prime }& =\sigma S\lambda -{\alpha }_q{S}_q+{\theta }_c{\alpha }_c{S}_c-{\nu }_q\left(1+\frac{(1-p)}{p}{\varphi }_q\right)S_q\lambda \hfill \\ \hfill E^{\prime }& =\left(1-\varphi -\xi \right)S\lambda +\left(1-{\varphi }_c-{\xi }_c\right){\nu }_c{S}_c\lambda \hfill \\ \hfill & +\left(1-{\varphi }_q-{\xi }_q\right){\nu }_q{S}_q\lambda -\frac{1}{\tau }E\hfill \\ \hfill {(E_c)}^{\prime }& =\varphi S\lambda +{\varphi }_c{\nu }_c{S}_c\lambda +{\varphi }_q{\nu }_q{S}_q\lambda -\frac{1}{\tau }{E}_c\hfill \\ \hfill {(E_q)}^{\prime }& =\xi S\lambda +{\xi }_c{\nu }_c{S}_c\lambda +{\xi }_q{\nu }_q{S}_q\lambda -\frac{1}{\tau }{E}_q\hfill \\ \hfill I^{\prime }& =\frac{1}{\tau }E-\frac{1}{T}I,{(I_c)}^{\prime }=\frac{1}{\tau }{E}_c-\frac{1}{T_c}{I}_c\hfill \\ \hfill {(I_q)}^{\prime }& =\frac{1}{\tau }{E}_q-\frac{1}{T_q}{I}_q{R}^{\prime }=\frac{1}{T}I+\frac{1}{T_q}{I}_q\hfill \\ \hfill {(R_c)}^{\prime }& =\frac{1}{T_c}{I}_c-{\alpha }_c{R}_c\hfill \end{array}$$ (1)

Here $\lambda =\left(\beta I+{\beta }_q{I}_q+{\beta }_c{I}_c\right)/N$ is “force of infection”, $\psi =\frac{1-p}{p}\varphi +\sigma$ is total (contact-traced and self-) quarantine factor and $C_q=S_c+E_c+I_c+R_c$ is the number of quarantined contacts at time t. In addition to the proportion $\varphi$ of non-quarantined contacts (from $S(t)$) whom are traced, we let ${\varphi }_q$ and ${\varphi }_c$ represent the proportion of self-quarantined and traced contacts (from $S_q$ and $S_c$, respectively) whom will become traced (or remain traced for $S_c$) after a contact at time t. We also introduce the proportion of transitions to self-quarantine states after infection, $\xi ,{\xi }_q$, and ${\xi }_c$ from $S,S_q$, and $S_c$ compartments, respectively. The parameter ${\theta }_c$ defines the fraction of susceptible individuals who return to “social-distanced” (self-quarantined) after completing contact-traced protocol. The additional transition probabilities allow flexibility in the model for deriving final size relations and reducing to special cases of the model. When fitting the full model, we take $\varphi ={\varphi }_q,{\varphi }_c=1,\xi ={\xi }_c=0,{\xi }_q=1-{\varphi }_q$ (see Fig. 1), which specifies that the proportion of non-quarantined and quarantined susceptible individuals contact-traced upon infection is uniform, while all contact-traced susceptible individuals continue to be traced, along with assuming that the only transmission events resulting in immediate transition to a self-quarantined infected state ($E_q$) are among self-quarantined susceptibles whom become infected (and are not contact traced).

A simplified version of the model assumes no secondary transmissions derive from self-quarantined or contact traced states, ${\nu }_c={\nu }_q={\beta }_c={\beta }_q=0$, an indefinite self-quarantine period, ${\alpha }_q=0$, 100 % of susceptibles returning from contact traced quarantine become self-quarantined, ${\theta }_c=1$, along with the assumption (explained in paragraph above) that $\xi ={\xi }_c=0$. This “perfect quarantine” model, reduces to the following system:

$$\begin{array}{cc}\hfill S^{\prime }& =-\left(1+\frac{(1-p)}{p}\varphi +\sigma \right)\beta \mathit{SI}/N,\hfill \\ \hfill E^{\prime }& =\left(1-\varphi \right)\beta \mathit{SI}/N-\frac{1}{\tau }E,\hfill \\ \hfill I^{\prime }& =\frac{1}{\tau }E-\frac{1}{T}I,R^{\prime }=\frac{1}{T}I+\frac{1}{T_c}{I}_c,\hfill \\ \hfill {(S_c)}^{\prime }& =\frac{(1-p)}{p}\varphi \beta \mathit{SI}/N-{\alpha }_c{S}_c,{(E_c)}^{\prime }=\varphi \beta \mathit{SI}/N-\frac{1}{\tau }{E}_c,\hfill \\ \hfill {(I_c)}^{\prime }& =\frac{1}{\tau }{E}_c-\frac{1}{T_c}{I}_c,{(R_c)}^{\prime }=\frac{1}{T_c}{I}_c-{\alpha }_c{R}_c,\hfill \\ \hfill {(S_q)}^{\prime }& =\sigma \beta \mathit{SI}/N+{\alpha }_c{S}_c\hfill \end{array}$$ (2)

where we included decoupled compartments of contact-traced (fit to data) and self-quarantined susceptible individuals, for clarity. We use the simplified system (2) as our main model for fitting data on daily provincial cases and quarantined contacts in Section 4. The vastly reduced number of parameters increases model identifiability in the data fits, which we also show to be robust in generating our main conclusions. Because of data uncertainties discussed further in Section 4, we also consider versions of the models which include unreported cases. In particular, we introduce an additional parameter $\rho$, the probability a non-traced infected individual becomes a reported case (see (C.1) in C.3). Finally, we note the utility in the perfect quarantine model (2) for obtaining simple formulas for final and peak outbreak size, which we derive in the next section.

3. Reproduction number and outbreak size

The (time-dependent) effective reproduction number, ${\mathcal{R}}_e={\mathcal{R}}_0(t)$ can measure pathogen transmission potential throughout the outbreak, even as the susceptible pool is reduced through self-quarantine and infection. Define the current susceptibility and infection transition probabilities of the population by $\mathcal{S}=\left(1-\varphi -\xi \right)S(t)+\left(1-{\varphi }_c-{\xi }_c\right){\nu }_c{S}_c(t)+\left(1-{\varphi }_q-{\xi }_q\right){\nu }_q{S}_q(t),{\mathcal{S}}^c=\varphi S+{\varphi }_c{\nu }_c{S}_c+{\varphi }_q{\nu }_q{S}_q$ and ${\mathcal{S}}^q=\xi S+{\xi }_c{\nu }_c{S}_c+{\xi }_q{\nu }_q{S}_q$, and by the next-generation approach (Van den Driessche and Watmough, 2002), we calculate ${\mathcal{R}}_e$:

$${\mathcal{R}}_e=(\beta T\mathcal{S}+{\beta }_c{T}_c{\mathcal{S}}^c+{\beta }_q{T}_q{\mathcal{S}}^q)/N$$ (3)

At the outset of the outbreak or initial time of consideration, $t=t_0$, we denote the baseline reproduction number (without contact tracing, $\varphi =0$), ${\mathcal{R}}_{0,b}$, and basic reproduction number ${\mathcal{R}}_0$. We summarize definitions of key parameters and quantities in Table 1 In the “perfect quarantine” model (2), the reproduction numbers reduce to the simple formulas:

$${\mathcal{R}}_{0,b}=\beta T\mathrm{and}{\mathcal{R}}_0={\mathcal{R}}_{0,b}(1-\varphi )\text{.}$$ (4)

Table 1.

Key model parameters and quantities.

$\lambda =\frac{\beta I+{\beta }_q{I}_q+{\beta }_c{I}_c}{N}$	force of infection of non-quarantined, self-quarantined & contact-traced infected.
$\varphi$	Proportion of contacts traced & quarantined
$\sigma$	susceptible self-quarantine factor
$p$	probability of transmission upon contact
$\psi =\sigma +\frac{1-p}{p}\varphi$	total susceptible quarantine factor (proportionality constant relative to force of infection)
${\nu }_q$	Relative susceptibility of self-quarantined
${\alpha }_q,{\alpha }_c$	Exit rate from self-, contact-traced quarantine
$\tau$	time to infectious (incubation period)
$T,T_q,T_c$	infectious period (time to isolation) of non-quarantined, self-quarantined, contact-traced
${\mathcal{R}}_{0,b},{\mathcal{R}}_0,{\mathcal{R}}_e$	reproduction numbers (baseline, with contact tracing, effective).

Note that in model (C.1) with unreported cases, ${\mathcal{R}}_0={\mathcal{R}}_{0,b}(1-\varphi \rho )$, where the impact of contact tracing is reduced by the proportion of reported cases, $\rho$.

Next we present novel analytical relations between ${\mathcal{R}}_0$, self-quarantine factor $\psi$, and the final and peak size of an outbreak in our model. To do so, we assume an indefinite quarantine period (${\alpha }_q=0$), as in system (2). In this way, the outbreak size can represent magnitude of first, second or subsequent waves dependent on contact tracing and self-quarantine parameters. First, denote the total self-quarantined or traced (quarantined) susceptible population with variable $S_m=S_c+S_q$, and define the final (cumulative) epidemic size ${\mathcal{C}}_{\infty }≔N-S(\infty )-S_m(\infty )$, along with the final proportion of (not quarantined) susceptible $S_m=S_c+S_q$ individuals $U_{\infty }≔\frac{S(\infty )}{S(t_0)}$ (starting from $t=t_0$). We derive the following theorem about asymptotic behavior and final size starting from the outset of an outbreak (proof and general formula for arbitrary initial conditions in A).

Theorem 1

Consider model(1)with non-negative initial conditions satisfying$\beta (E(t_0)+I(t_0))+{\beta }_q(E_q(t_0)+I_q(t_0))+{\beta }_c((E_c(t_0)+I_c(t_0))>0$. Then all variables remain non-negative and${\lim }_{t\to \infty }(E(t)+I(t)+E_q(t)+I_q(t)+(E_c(t)+I_c(t))=0$. Next suppose that$\varphi ={\varphi }_c={\varphi }_q,\xi ={\xi }_c={\xi }_q,{\alpha }_q=0,(1-{\theta }_c){\alpha }_c=0$. In addition let${\nu }_c={\nu }_q=:\nu$, and suppose that$t_0=0$with$I(0)+I_q(0)+I_c(0)\approx 0$. Then the following final size formula holds:

$$\begin{array}{cc}\hfill \ln \left(U_{\infty }\right)& =(1+\psi ){\mathcal{R}}_0\left(U_{\infty }-1+\frac{\psi }{1+\psi -\nu }\left({\left(U_{\infty }\right)}^{\nu /(1+\psi )}-U_{\infty }\right)\right)\hfill \\ \hfill {\mathcal{C}}_{\infty }& =N\left(1-\frac{\psi }{1+\psi -\nu }\left(\frac{1-\nu }{\psi }{U}_{\infty }+U_{\infty }^{\nu /(1+\psi )}\right)\right)\text{.}\hfill \end{array}$$ (5)

In the special case of the “perfect quarantine” (2), the formula reduces to:

$$\ln \left(U_{\infty }\right)={\mathcal{R}}_0\left(U_{\infty }-1\right),{\mathcal{C}}_{\infty }=\frac{1}{1+\psi }N(1-U_{\infty }),$$ (6)

where ${\mathcal{R}}_0=(1-\varphi ){\mathcal{R}}_{0,b}$, as defined in (4). Furthermore, in this case, we find the peak non-quarantined infected (and exposed) individuals, ${\mathcal{I}}_{\mathit{peak}}≔{\max }_{t>0}(E(t)+I(t))$, to satisfy the following relation (derivation in Appendix):

$${\mathcal{I}}_{\mathit{peak}}=\frac{1}{1+\psi }\frac{N}{{\mathcal{R}}_{0,b}}\left({\mathcal{R}}_0-\ln {\mathcal{R}}_0-1\right)\text{.}$$ (7)

In (6), (A.6), note the classical relation between final or peak outbreak size and ${\mathcal{R}}_0$ when $\psi =0$. Self-quarantine ($\sigma$) is expected to have almost all weight in the total susceptible quarantine factor ($\psi =\sigma +\varphi (1-p)/p$) because the goal of lockdowns, as opposed to contact tracing $(\varphi )$, is to shield large segments of susceptible population. Even if p becomes small, the amount of contacts traced will be limited by resources, whereas very large segments of population can self-quarantine through lockdowns or behavioral change. Thus, both final and peak outbreak size, ${\mathcal{I}}_{\mathit{peak}}$ and ${\mathcal{C}}_{\infty }$, have an approximate simple inverse proportionality relationship with $\sigma$. In contrast, contact tracing, primarily acting through the proportional reduction in baseline reproduction number (${\mathcal{R}}_0=(1-\varphi ){\mathcal{R}}_{0,b}$), has distinct influences on peak and final size. We calculate relative sensitivities of 6-(A.6) to $\psi$ and $\varphi$,

$${\mathcal{C}}_{\infty }^{\psi }≔\frac{\partial {\mathcal{C}}_{\infty }}{\partial \psi }\frac{1}{{\mathcal{C}}_{\infty }}=-\frac{1}{1+\psi }$$ (8)

$$\begin{array}{cc}\hfill {\mathcal{C}}_{\infty }^{\varphi }& ≔\frac{\partial {\mathcal{C}}_{\infty }}{\partial \varphi }\frac{1}{{\mathcal{C}}_{\infty }}=\frac{{\mathcal{U}}_{\infty }}{1-{\mathcal{U}}_{\infty }\left(1-\varphi \right){\mathcal{R}}_{0,b}},\hfill \\ \hfill {\mathcal{I}}_{\mathit{peak}}^{\psi }& ≔\frac{\partial {\mathcal{I}}_{\mathit{peak}}}{\partial \psi }\frac{1}{{\mathcal{I}}_{\mathit{peak}}}=-\frac{1}{1+\psi }\hfill \\ \hfill {\mathcal{I}}_{\mathit{peak}}^{\varphi }& ≔\frac{\partial {\mathcal{I}}_{\mathit{peak}}}{\partial \varphi }\frac{1}{{\mathcal{I}}_{\mathit{peak}}}=\frac{1}{1-\varphi }\ln \frac{1}{\left(1-\varphi \right){\mathcal{R}}_{0,b}}\text{.}\hfill \end{array}$$ (9)

Observe that as ${\mathcal{R}}_0\nearrow \infty ,{\mathcal{I}}_{\mathit{peak}}^{\varphi }\searrow -\infty$, whereas, although difficult to show analytically, we numerically observe that ${\mathcal{C}}_{\infty }^{\varphi }$ goes to zero as ${\mathcal{R}}_0$ becomes large. Thus, contact tracing has more influence on peak size, but less impact on final size.

Although there are inherent issues with measuring rate of new incidence due to the delay between transmission and case reporting, the inverse proportions dependent on susceptible quarantine factor ($\psi$) can be used as a simple retrospective or implementation guide for lockdown efficacy. For instance, given that $\psi$ is relative to force of infection, to reduce the outbreak size by $90\%$ (compared to no lockdown case $\psi \approx 0$), the authorities would need to have implemented strict quarantine at approximately 9 times the force of infection. Note that ${\mathcal{R}}_{0,b}$ is the ratio of force of infection ($\frac{\beta I}{N}$) and reported prevalence rate ($\frac{I}{\mathit{NT}}$). Thus, as a rule of thumb, the quarantine rate (or magnitude in a defined time period) must be $9\times {\mathcal{R}}_{0,b}$ times the rate (or amount) of incoming reported cases to reduce the outbreak size by $90\%$. If case underreporting is also considered, then the quarantine rate factor must be increased even more to control an outbreak, with $\sigma$ then rescaled by ${\mathcal{R}}_{0,b}/\rho$, where $\rho$ is proportion of cases reported. In practice, officials may look at aggregated cell phone or mobility data to assess population quarantine behavior and compare with case reports. Quarantine rate may need to far exceed the pace of new infections, as shown below, very large values of $\psi$ were instrumental for China rapidly curbing their epidemic.

4. Data fitting & distinct quarantine efficacies in China

In order to quantify relative efficacies of contact tracing and self-quarantine (lockdown) interventions during the COVID-19 outbreak in China, we performed model fitting using reported case and mortality data for each province of China, along with (daily number of) quarantined contacts in all of China obtained from daily reports by NHC (NHC, 2020). The outbreak was not localized to a single population during the timeframe of our study, Jan. 21–Mar. 19 2020, although the province of Hubei had a large share of the total cases. Because the large number of parameters in the full model (2) and the likelihood that fitting a total of 30 provincial case and quarantine data sets may result in overfitting, we first utilize the simplified model (2) to obtain parameter estimates for each province. A change in case counting procedures around Feb. 12 in Hubei province prevented us from reliably fitting daily case counts in this province from Feb. 11–Feb. 13, and certainly there were a large number of unreported cases over the timeframe. Later in this section, we adjust our provincial daily case fitting by inferring the ratio of unreported cases ($1/\rho$ in model (C.1)) in all of China using daily reported case and death data, along with the quarantined contacts. Furthermore, we verified robustness of our parameter estimations and results by fitting the full model (1) and Fig. 1) simultaneously to cumulative reported cases and daily quarantined contacts in all China, along with exploring alternative formulations of self-quarantine rate (e.g using mobility data) and different quarantine/infection residence time distributions, and decreasing infectious periods due to lockdowns (see C). Details of fitting procedures and results not contained in this section can be found in B.

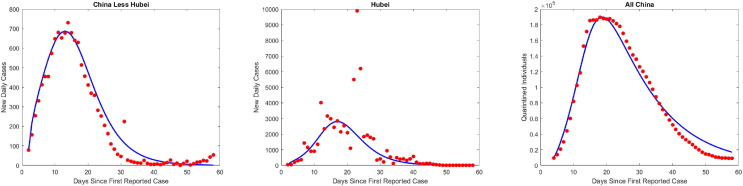
First, for each province in China we simultaneously fit model (2) to daily case incidence and an inferred number of quarantined contacts, weighting the available aggregated quarantine contact data for all of China by province reported case load distributed by an assumed exponential quarantine duration of mean $14\mathit{days}$ with delay of 3 days between contact and tracing (see B.1). We implemented a nonlinear weighted least squares algorithm, using daily reported cases ($R_i(t)-R_i(t-1)$ in (2)) and the inferred quarantined contacts (multiplied by a positive weight). To increase model identifiability, we reduced the number of parameters in (2) to 4 parameters ($I_0,{\mathcal{R}}_{0,b},\sigma$ and $\varphi$) by fixing the incubation period (time to infectiousness, $\tau =3$ days (He et al., 2020)), infectious period (time to isolation, $T=4.64$ days (Bi et al., 2020)), and probability of transmission given contact, $p=.06$, in line with other studies (Bi et al., 2020, Sun et al., 2020). Plots for these fits can be found in Figs. S1 and S2, and parameter values are presented in Table D.5. We find that $\sigma$ and $\varphi$ being significantly higher in these other provinces than in Hubei (or the all China fit). Indeed, comparison of the values in Table D.5, Table D.6 suggests that segregating between China Less Hubei and Hubei alone is sufficient to capture this difference. The higher values for $\sigma$ in China Less Hubei are likely explained by the other provinces having the advantage of responding to the outbreak in Hubei, along with their local cases, so that their lockdowns could be enacted faster (with larger magnitude relative to local force of infection). The larger values of contact tracing coverage $\varphi$ in China Less Hubei may be attributed to a smaller caseload enabling this relatively resource-intensive control strategy.

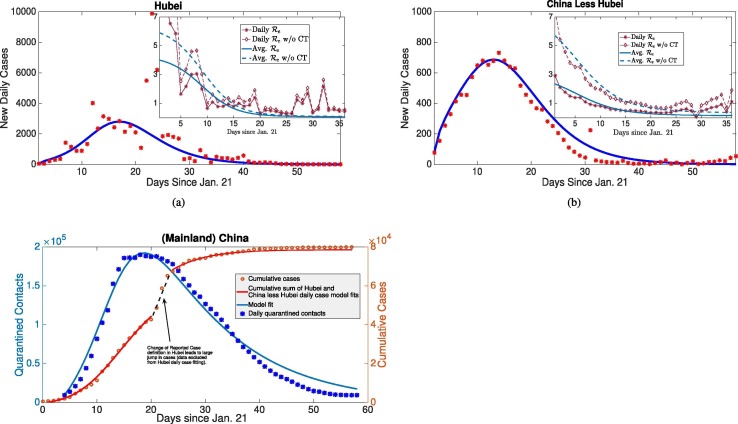
We refined our analysis by fitting the two corresponding daily reported case datasets from Hubei and China less Hubei, along with the sum of their respective quarantine contact compartments to the aggregated China daily quarantine contacts (Fig. 2 ). The estimated basic reproduction numbers (with contact tracing) are ${\mathcal{R}}_0=4.07(\mathit{CI}3.54-4.12)$ and ${\mathcal{R}}_0=2.47(\mathit{CI}2.16-2.77)$ for Hubei and China less Hubei, respectively. Complete parameter values and uncertainty analysis (method described in B.5) are presented in D. We also calculate time-dependent ${\mathcal{R}}_e$ by directly utilizing the daily case data and estimates of the serial interval (generation time) distribution (Browne et al., 2015, Bi et al., 2020, Ferretti et al., 2020), alongside ${\mathcal{R}}_e$ obtained from our estimated parameters from model fitting. Although China less Hubei had larger contact tracing level than Hubei ($\varphi =0.59$ versus $\varphi =0.32$), it also had significantly higher estimates of self-quarantine rate ($\sigma =1.14\times {10}^5$ versus $\sigma =1.26\times {10}^3$). The results indicate strict population-wide lockdowns were the main quarantine measure (as opposed to contact tracing) which rapidly contained the outbreak in China by rapidly decreasing ${\mathcal{R}}_e$ (see Fig. 2, Fig. 2(b)).

Fig. 2.

Model recapitulates case and contact tracing data, estimates large rate of self-quarantine (via lockdown) rapidly contains outbreak. (a), (b) Daily reported cases (incidence) of Hubei and China less Hubei fit to model (2). Also, average and daily impact of contact tracing on ${\mathcal{R}}_e$ (inserted figures) from estimated parameters and statistical generation time distribution approach. (c) Daily number of quarantined contacts in mainland China simultaneously fit with daily incidences of Hubei and China less Hubei (in (a), (b)) shown alongside inferred cumulative cases from sum of incidence fits and data. By quantifying relative magnitudes of contacts traced and incidence, we can determine efficacy of contact tracing versus broader lockdowns in our distinct quarantine model. The reduction in ${\mathcal{R}}_e$ with or without contact tracing due to self-quarantine/lockdowns was the major factor to rapidly contain the outbreak in China.

Next, we observe an inverse proportionality relationship between province outbreak size and corresponding estimated self-quarantine factor ($\sigma$), supporting theoretical predictions of our final size formula (6) (Fig. 3 ). Indeed, the 30 provincial cumulative case counts over the study period are inversely proportional to fitted $\sigma$ values, whereas contact tracing ($\varphi$) did not have a significant correlation with province outbreak size. This inverse relationship was also true of province peak size versus self-quarantine factor, but contact tracing had a larger impact here than for the case of cumulative cases, as illustrated by distinctly flatter peak size sensitivity curves (with respect to varying $\sigma$) for provinces with larger proportion of contacts traced, $\varphi$. The small effect of contact tracing on final size, but larger influence on peak size, concurs with our derived sensitivity analysis when ${\mathcal{R}}_0$ is relatively large. To further corroborate the heterogeneous impacts of contact tracing, we calculate outbreak sizes if $\varphi =0$, finding peak infection reductions of $28\%$ in Hubei versus $45\%$ in China less Hubei. However, the decrease in final outbreak size due to contact tracing was only $1.6\%$ (Hubei) and $5.6\%$ (China less Hubei), respectively.

Fig. 3.

Model fitting shows that COVID-19 outbreaks in Chinese provinces mimic derived inverse proportionality relationship with self-quarantine rate and limited differential impacts of contact tracing. (a) Data points represent cumulative reported cases during Jan. 21-Mar. 19 of 30 provinces in China plotted at estimated self-quarantine factor ($\sigma$) obtained from provincial daily incidence data and inferred daily number of quarantined contacts (weighted from aggregated China data) simultaneously fit to model (2). The solid lines represent calculated cumulative cases from final size formula (6) while varying $\sigma$ from $1\%$ to $100\%(\mathit{fitted}\mathit{value})$ of the estimated $\sigma$ (${\sigma }_f$) and fixing other parameter estimates for each province. All province output is colored according to a colormap from minimum to maximum estimated contact tracing parameter $\varphi$. (b) The same output as (a) displayed on log–log scale. (c) Analogous graph as (b) with respect to peak size for each province instead of cumulative cases (again displayed on log–log scale to aid viewing distinct province curves). Note the distinctively flatter peak size curves (with respect to varying $\sigma$) of provinces with high estimated contact tracing ($\varphi$) demonstrating the larger influence of contact tracing in keeping peak size small even as the lockdown scale ($\sigma$) decreases.

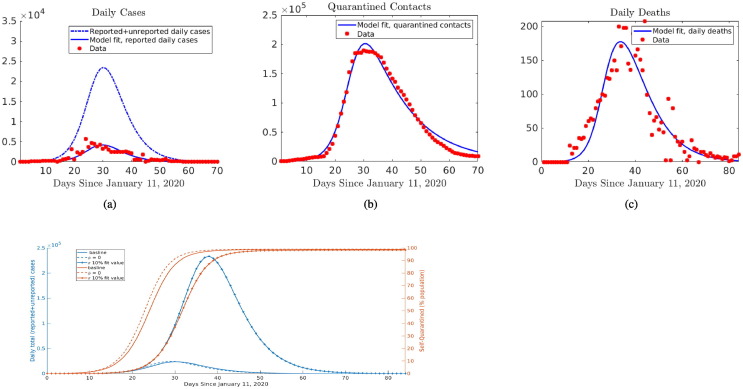
To quantify how large numbers of unreported cases associated with COVID-19 impacts our results on overall contact tracing and self-quarantine effectiveness in China, we simultaneously fit system (C.1) to daily reported cases, deaths, and quarantined contacts (Fig. 4 (a)–(c)). By using the additional mortality data, in conjunction with estimates of the case fatality ratio within feasible bounds, true infection numbers can be inferred. Because of dates where both reported case and mortality data in Hubei province are skewed by large number of cases being added, we re-distribute the excess cases according to proportion of the cumulative count occurring in a day, so that the daily incidence curve shape and total (cumulative) reported infections and deaths are retained over the timeframe. We assume that the delay between infection and death follows a gamma distribution, with mean time until death estimated at $\mu =14.64\mathit{days}$, in line with retrospective studies from China (Zhou et al., 2020). The infection fatality ratio (IFR) was found to be $\xi =.0109$, which is in the lower range of Wu et al. (2020). The rather large estimate of unreported cases, in which “true” total (reported and unreported cases are $1/\rho =7.78\times$ reported case count ($\rho$ is estimated proportion of reported cases), likely leads to decreased IFR. In addition, we find an increased estimate of ${\mathcal{R}}_0=4.5475$ when starting from the earlier date of Jan. 11 and incorporating the unreported cases, the parameter fits for $\sigma$ and $\varphi \rho$ (3365 and 0.0542, respectively) suggest even a larger difference in the relative efficacies of self-quarantine and (reported case) contact tracing in controlling the outbreak in China. When accounting for the estimated low reporting rate, contact tracing only results in 0.3% reduction in total (reported and unreported) cases and $3\%$ reduction in peak total cases. In contrast, reducing self-quarantine rate factor to 10% of fitted value, equivalent to an approximate 10 day delay in 50% of population being self-quarantined, leads to $10\times$ more cases (Fig. 4(d)). However, the unreported cases may include asymptomatic infections, exhibit reduced transmission, share clustered contacts with reported cases, and have different onsets than redistributed excess cases. Thus we conduct further sensitivity analysis below on fitting all cumulative reported cases and quarantined contacts without smoothing datasets.

Fig. 4.

Results for fitting model (C.1) in all of China simultaneously to daily reported case, quarantined contact, and death data. The model allows inference of ratio of “true” total cases to reported cases ($1/\rho$ in model (C.1)), so that we obtain: (a) the trajectory of “true” total cases (dash-dot curve), accounting for both reported and unreported cases, in addition to the fit of daily reported cases, (b) the daily quarantined contacts, and (c) daily deaths, displayed alongside data. (d) Contact tracing has minimal effect on total cases or self-quarantined in model fit with unreported cases, in contrast reducing $\sigma$ to 10% of its estimated value (delaying self-quarantine of majority of population by 10 days) has large impact on outbreak.

We extend the simplified model (spatially segregated) daily incidence fits to estimate additional parameters in full model by simplifying the fitting procedure using cumulative cases for all of China. Sensitivity analysis on the main control parameters for the all China fit (Fig. 5 ) reveals minimal contact tracing level impact on final outbreak size, yet larger effect on reducing peak infection levels (Fig. 5(d)), concurring with our analytical calculations ((6), (A.6), (8), (9) and results when fitting province daily incidence. In general, we observe that the time to peak increases with $\varphi$, reflecting the curve flattening, however this time period eventually decreases for sufficiently large values of $\varphi$ as contact tracing effectively suppresses the outbreak (Fig. S8 in Supplementary Materials). In addition, with sufficiently large contact tracing coverage, outbreak size can be significantly reduced when there is less stringent lockdown (less total quarantined and more time to enact quarantine). Yet even in this case, some level of broader social distancing measures is almost certainly needed in combination with contact tracing.

Fig. 5.

Sensitivity analysis of contact tracing and self-quarantine. All together the figures illustrate how contact tracing ($\varphi$) has less impact on outbreak size (${\mathcal{C}}_{\infty }$) than self-quarantine ($\sigma$) due to underlying concavity of their nonlinear relationships derived in final size formula (6). Fitted parameter values for total cumulative cases in China show that rapidly implemented lockdowns contained the outbreak, where a delay of 2 weeks in $95\%$ of susceptible population being self-quarantined would result in a 10-fold increase in cumulative cases. Although contact tracing had little effect ($2\%$) on final outbreak size, it “flattened the curve”, reducing peak infected by $34\%$. (a) Contact tracing (CT) proportion $\varphi$ versus outbreak size ${\mathcal{C}}_{\infty }$ (nonlinear relationship) and reproduction number ${\mathcal{R}}_0$ (linear relationship) for 3 levels of self-quarantine (SQ) factor $\sigma$ differing by order of magnitude of 10. (b) ${\mathcal{C}}_{\infty }$ as a (nonlinear) function of $\sigma$ for 3 levels of SQ susceptibility reduction ${\nu }_q$. (c) Total (final) self-quarantined individuals, along with time until $50\%,75\%,95\%$ of population is self-quarantined as SQ factor $\sigma$ varies. (d) Epidemic curve trajectories for 3 levels of CT proportion $\varphi$ marked in (a). (e, f) Contour maps of outbreak size and peak infected (with time to peak inserted) depending on CT proportion $\varphi$ and SQ rate $\sigma$.

As predicted by our derived inverse proportionality relationship (6), there are escalating costs as $\sigma$ decreases, i.e. as self-quarantine action lessens relative to ongoing infection rate (Fig. 5(b)). For example, if the estimated time for $50\%$ of initial susceptible population of China to be self-quarantined ($\sim 2$ weeks from Jan. 21) had been delayed by just one week, then the total number of cases would be approximately 10 times larger (Fig. 5(c)). Notice that population self-quarantine dynamics are similar whether the model is fit from Jan. 11 (Fig. 4) or Jan. 21, showing the advantage of the infection-rate dependent “lockdown factor” being independent of start time in our model. In the full model, the additional parameters ${\nu }_q,{\beta }_q$ (measuring looseness of the lockdown) also impacts the outbreak size (Fig. 5(b)). Going from ${\nu }_q,{\beta }_q/\beta \approx 0$ (as predicted for China) to ${\nu }_q={\beta }_q/\beta =0.05$ to ${\nu }_q={\beta }_q/\beta =0.15$, the outbreak size would increase by a factor of 1.14 and 1.45, respectively. In addition, the estimated exit rate from self-quarantine (${\alpha }_q$) for China was estimated to be very small, emphasizing the strictness of the lockdown.

5. Quarantine Interventions for COVID-19 2nd Wave

A major question has been how lockdown measures should be loosened after some level of controlling COVID-19, while optimally responding to any subsequent outbreaks induced by the relaxations. Here we analyze how the scale and rate of different reactive contact-based interventions affect 2nd wave outbreaks under two different scenarios of loosening, namely Instantaneous Return of Several Sectors (IRSS) or via Gradual Return of Self-Quarantined (GRSQ). The goal is to attain qualitative insights on strategies for shrinking, flattening or delaying (not necessarily independent phenomena (Feng et al., 2020)) subsequent outbreaks. By varying self-quarantine factor $\sigma$, contact tracing probability $\varphi$ and looseness of social distancing $\nu$ under the distinct relaxation policies in our model parameterized to data from China, we observe potential consequences of different measures.

Simulating the instantaneous return of $80\%$ of self-quarantined individuals (IRSS strategy), with no change in parameters (and crucially the same “reactive lockdown” factor $\sigma$) we observe that the cumulative number of infected cases for the 2nd wave (outbreak size) and peak infected was $75\%$ and $58\%$, respectively, of the 1st wave. Furthermore, a similar number of individuals as during the first wave lockdown re-enter self-quarantine about 6 weeks after relaxation (see Fig. 6 (a)). When the contact tracing efforts are enhanced after lockdown (to $\varphi =.65$), outbreak size and peak infected are $54\%$ and $16\%$, respectively, of the 1st wave, and the curve is flattened, i.e. the peak outbreak size shrunk and the time to peak outbreak size increased. When contact tracing is doubled to $\varphi =0.75$, or if other sustained non-quarantine measures (e.g. face mask usage) reduce ${\mathcal{R}}_0$ to same level together with more intermediate contact tracing of $\varphi =0.5$, the 2nd wave outbreak size and peak infected are $25\%$ and $3\%$, respectively, of the 1st wave. In addition, the number of individuals re-entering self-quarantine was reduced, revealing that contact tracing, or sustained interventions aimed at reducing ${\mathcal{R}}_0$, can be an effective tool for managing the epidemic without a large-scale lockdown or with less stringent public quarantine measures.

Fig. 6.

Combined impact of contact tracing and responsive social distancing (self-quarantine) measures under distinct re-opening strategies. Model simulations predict 2nd wave outbreak shape after instantaneous re-normalization of several sectors (IRSS) by releasing $80\%$ of self-quarantined (a–c) versus gradual return of self-quarantined (GRSQ) to normalcy (d–f). Increased contact tracing levels ($\varphi$) can flatten or suppress (when highly effective) subsequent outbreak in (a, d). Social distancing measures responsive to new incidence shrink the outbreak size dependent on rate ($\sigma$) and looseness (${\nu }_q$) of self-quarantine in (b, e) and (c, f), respectively. In addition to the differential effects on daily infected counts of contact tracing and responsive self-quarantine (flattening versus crushing), observe the much longer delay in 2nd wave under the GRSQ re-opening policy, which can buy time for effective treatments or vaccines.

In the case of GRSQ strategy, after containing initial outbreak with lockdown, we increase the return to “normalcy” rate to $\alpha =0.01$, where half the social-distanced return to normalcy in the approximate half-life time given by $t_{1/2}=\ln 2/\alpha =72\mathit{days}$. Assuming other parameters remain constant (including the reactive SQ factor $\sigma$) the second peak, emerging with a 100 day delay, reduced to $42\%$ of the first wave, however the number of infected individuals settle into a rather large quasi-equilibrium resulting in more cumulative cases (see Fig. 6(d)). Here there is a balance of force of infection induced self-quarantine ($\sigma \lambda$) and reversion of individuals to their normal contact behavior ($\alpha$), leading to an insufficient amount of population social distancing for reducing cases below a certain level. On the other hand, after loosening the lockdown, when the contact tracing efforts are enhanced or doubled, the peak size significantly diminished ($27\%$ or $0.3\%$ of 1st wave), along with the number of self-quarantined. Importantly, for about 6 months (or the whole year in the case of doubling $\varphi$), the number of infected cases stayed significantly low. Gradual release of self-quarantined individuals with increasing contact tracing efforts can be used as a strategy to gain time until vaccination or keeping the virus at bay, while reinstating societal interactions in a carefully measured stepwise fashion, as was the case in China with no second wave appearing after the initial fast spreading outbreak was put under control.

Responsive re-implementation of lockdown (or social distancing) measures can be crucial for reducing any second wave outbreak, in particular in scenarios where contact tracing and/or face-mask usage did not become as efficient as was the case in China. Reduction in SQ factor $\sigma$ by $1/2$ (or $1/4$), as predicted simply by the inverse proportionality in the derived final size formula (6), results in twice (or four times) more cumulative cases for the 2nd wave, and the simulations show the same relations between peak size (see Fig. 6(b)). Although the number of self-quarantined individuals eventually become the same with the different SQ rates, the delay in implementing large-scale self-quarantine (in response to incidence) makes significant differences in the final (and peak) outbreak size. For the simulations presented in Fig. 6(b), a delay of just 9 days from the baseline parameter case results in twice as many infections, and a delay of 18 days induces four times the infected individuals. Compared to instantaneous release, the increased quarantine exit rate ($\alpha$) under gradual return resulted in larger (but delayed) peak and total outbreak size inversely proportional to declines in SQ factor $\sigma$ (see Fig. 6(e)). Finally, varying the looseness of the quarantine (measured by uniform susceptibility and infectivity values ${\nu }_q={\beta }_q/\beta$) from perfect quarantine to $25\%$ (or to $50\%$) looseness, leads to approximately $1.3$ times (or to 2 times) more total and peak infections during the outbreak. Different from the rate of SQ, the proportionality relations are nonlinear, thus a slight looseness in social distancing can still offer an effective intervention, but the cases will increase at a growing rate as the measures become less strict (see Fig. 6, Fig. 6(f)).

6. Discussion

In this study, we compare how two distinct types of contact-based interventions, namely contact tracing and large-scale lockdowns/self-quarantine measures, impact single or sequential COVID-19 outbreaks. We find that contact tracing generally is less effective in decreasing outbreak size for rapidly spreading pathogens (high baseline reproduction number ${\mathcal{R}}_{0,b}$), unless the tracing is very efficient and large scale, or combined with other measures to force ${\mathcal{R}}_0\approx 1$. On the other hand, widespread lockdowns/social distancing interventions can lower outbreak size inversely proportional to an increase in the rate of self-quarantine. Our analysis indicates that China benefited from the heavy influence of lockdowns by rapidly containing the quickly growing COVID-19 cases, and, despite massive efforts, contact tracing was less influential in bringing down the epidemic.

Despite the difference in the targeted nature of contact tracing versus the more indiscriminate lockdown measures, we contend there is a similar reactive quality to both control strategies. Contact tracing reacts to reported cases by tracking and (to varying degrees) quarantining individuals whom have been contacted. Mass self-quarantine reflects a natural response by both governments and individuals that intensifies as cases build, a phenomenon that has been labeled as “exponential whiplash” (In Europe, 2020). These features motivate us to construct a COVID-19 model with both contact tracing (mechanistically) and self-quarantine (phenomenologically) dependent on force of infection. In contrast to another model that assumes a linear rate of self-quarantine (Maier and Brockmann, 2020), the nonlinear social distancing rate captures a contagion-like behavioral response to infected cases, and allows us to derive novel formulae for final outbreak size.

An important distinction between contact tracing and lockdowns is their mode of action, namely preventing onward secondary infections by early tracking of likely infected cases in the former and large-scale depletion (or shielding) of susceptible individuals for the latter. This contrast determines how they affect the major epidemiological quantities of reproduction number and outbreak size in our “transmission-reactive” formulation. In particular, contact tracing proportionally reduces ${\mathcal{R}}_0$, akin to vaccination, leading to a nonlinear relationship with final outbreak size, which decreases substantially only as ${\mathcal{R}}_0$ approaches one. The responsive self-quarantine factor does not affect ${\mathcal{R}}_0$, and we derive a simple inverse proportionality with outbreak size. This can be translated to a time of action for quarantine measures, analytically demonstrating the escalating impacts of delaying implementation of responsive lockdowns beyond a critical time period, which has been observed in other studies via simulation (Dehning et al., 2020, Pei et al., 2020). Even though similar levels of self-quarantine would eventually be reached in our model as incidence grows, the cost of delays can result in a large excess of cases.

We recapitulate the relative efficacies of contact tracing and self-quarantine control measures in COVID-19 outbreak in China using a systematic and robust data fitting procedure. Several versions of our model provide good simultaneous fits to both daily reported case and quarantined contact data from China (by province, region, or aggregated), along with an extension using daily death data which estimates unreported cases, case fatality ratio and the delay distribution between infection and death. Our formulation of contact tracing and self-quarantine dependent on force of infection enables us to identify the relative magnitudes of the two control terms, and thereby to quantify the efficacy both of past interventions and likely future ones. In particular, we find qualitatively distinct effects of contact-tracing and lock-down on containing, and more broadly shaping, an outbreak of a disease such as COVID-19. All our analyses (including using mobility data and other alternative model fitting scenarios in C) are consistent with our theoretical results that large-scale population quarantines are needed for effectively reducing final/peak size of pathogens with high baseline reproduction number ${\mathcal{R}}_{0,b}$, whereas contact tracing can flatten curve, but is relatively ineffective in affecting outbreak size unless it decreases ${\mathcal{R}}_0$ close to one. When accounting for the estimated low reporting rate, parameter fits suggest even a larger difference in the relative efficacies of self-quarantine and (reported case) contact tracing in controlling the outbreak in China. We assert that contact-tracing, dependent as it is on contact events, can only “flatten the curve” while having minimal impact on the final size of the epidemic with high ${\mathcal{R}}_{0,b}$. Lock-down and related measures that lead to self-quarantine, by contrast, prevent contacts from occurring in the first place and therefore have the potential to reduce the epidemic final size.

Our main result on differential impacts of lockdowns and contact tracing also implicates distinct metrics for officials to monitor when enacting each intervention. For reactive lockdowns, the key measurement is rate of population-wide quarantine compared to incidence or incoming reported cases. For contact tracing, ${\mathcal{R}}_e$ may be the important quantity because the final outbreak size is only substantially altered as ${\mathcal{R}}_e$ becomes closer to 1. Although we find that the extensive lockdowns were a much larger factor in controlling COVID-19 outbreak size in China, our sensitivity analysis shows that contact tracing did dampen and delay peak number of infected despite its more limited impact on the cumulative count. In this way, contact tracing flattened the incidence curve, easing the strain on limited hospital resources. A combination of expeditiously enacted contact-based interventions may be the best strategy, where effective contact tracing, along with sustained interventions aimed at reducing ${\mathcal{R}}_0$ (public face mask wearing, social distancing, etc.), can synergistically suppress an outbreak, and reduce the scale of lockdown measures necessary for altering rapidly rising case numbers. However COVID-19 has proved to be a particular challenge and large-scale lockdowns have been a needed antidote for controlling outbreaks in several countries. In this case, drastic self-quarantine orders can hopefully reduce case numbers to manageable levels that allow for effective contact tracing after easing restrictions.

The capacity to respond to the continuing threat of COVID-19 will be vital for minimization of sequential epidemic waves. We investigated control measures under an instantaneous normalization of contact for a large portion (or several sectors) of the population versus a more gradual release of self-quarantined individuals back into social interactions. Our results show that increased contact tracing efforts can alter the second outbreak shape, either reducing and spreading out the number of infected or completely suppressing cases for highly efficient tracing. Social distancing or lockdown measures responsive to incidence can effectively compress the second peaks, with the timing being critical again and the scale dependent on the underlying ${\mathcal{R}}_0$. Either measure will depend upon sufficient case detection and reporting, highlighting the importance of testing. Furthermore, indefinite or reoccurring strict lockdowns are likely to impart too high of an economic cost, and our model shows that looser restrictions and contact tracing can still control a second wave. Additionally, the strategy of gradual release of quarantined sectors can substantially delay the second wave, possibly buying time for effective treatments or vaccines to be widely available.

A major part of this work was to incorporate data on the quarantined contacts compiled for all of China. Obtaining provincial quarantine records or more detailed contact tracing data quantifying the proportion of reported cases whom were traced can allow for superior accuracy in estimating efficacy of contact tracing. A recent study of detailed contact tracing records in Hunan province of China (Sun et al., 2020) did come to a similar conclusion as our work that lockdowns had larger impact, and contact tracing alone is not likely to be sufficient for controlling COVID-19. The results here explain the differential effects that contact tracing and reactive population-wide self-quarantine have on reducing cumulative cases in a rapid spreading outbreak. This knowledge and further investigation may offer insights for the public health response to COVID-19.

CRediT authorship contribution statement

Cameron J. Browne: Conceptualization, Methodology, Software, Formal analysis, Investigation, Supervision. Hayriye Gulbudak: Conceptualization, Methodology, Formal analysis, Investigation, Supervision. Joshua C. Macdonald: Software, Formal analysis, Data curation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Reproduction number, final and peak size

The time-dependent effective reproduction number ${\mathcal{R}}_t$ can be defined utilizing the next-generation approach (Van den Driessche and Watmough, 2002). First define the feasible region for the system (1) as

$$\mathrm{\Gamma }=\left\{z={(S,S_c,S_q,E,E_c,E_q,I,I_c,I_q)}^T|N≔{\displaystyle \sum _{i=1}^9}{z}_i⩽N_0\right\},$$

where $N_0$ is the initial total population size (of all compartments). We note that the system (1) is quasi-positive, and thus its solutions remain non-negative when their initial values are nonnegative. Summing the right-hand sides of (1), we find that $N^{\prime }(t)=0$. Thus the solutions the system (1) remain in $\mathrm{\Gamma }$ when their initial values are in $\mathrm{\Gamma }$. Notice that any susceptible population distributed among the defined classes, $S,S_c,S_q,{\mathcal{E}}_0≔{(S,S_c,S_q,0,0,0,0,0)}^T$ is a disease-free equilibrium of system (1).

We define a next-generation matrix by considering the linearized system at the disease-free equilibrium, ${\mathcal{E}}_0$. Write the linearized “infection” sub-system as $x^{\prime }=(F-V)x$, where F contains entries corresponding to new infections, $-V$ contains all other transition terms in the Jacobian matrix evaluated at ${\mathcal{E}}_0$, and $x={(E,E_c,E_q,I,I_c,I_q)}^T$. Define the current susceptibility and infection transition probabilities of the population by $\mathcal{S}=\left(1-\varphi -\xi \right)S+\left(1-{\varphi }_c-{\xi }_c\right){\nu }_c{S}_c+\left(1-{\varphi }_q-{\xi }_q\right){\nu }_q{S}_q,{\mathcal{S}}^c=\varphi S+{\varphi }_c{\nu }_c{S}_c+{\varphi }_q{\nu }_q{S}_q$ and ${\mathcal{S}}^q=\xi S+{\xi }_c{\nu }_c{S}_c+{\xi }_q{\nu }_q{S}_q$. Thus, we consider the following matrices:

$$\begin{array}{cc}\hfill F& =\left(\begin{array}{cccccc}0\hfill & 0\hfill & 0\hfill & \mathcal{S}\beta /N\hfill & \mathcal{S}{\beta }_c/N\hfill & \mathcal{S}{\beta }_q/N\hfill \\ 0\hfill & 0\hfill & 0\hfill & {\mathcal{S}}^c\beta /N\hfill & {\mathcal{S}}^c{\beta }_c/N\hfill & {\mathcal{S}}^c{\beta }_q/N\hfill \\ 0\hfill & 0\hfill & 0\hfill & {\mathcal{S}}^q\beta /N\hfill & {\mathcal{S}}^q{\beta }_c/N\hfill & {\mathcal{S}}^q{\beta }_q/N\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right),\hfill \\ \hfill V& =\left(\begin{array}{cccccc}\frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 0\hfill \\ -\frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 1/T\hfill & 0\hfill & 0\hfill \\ 0\hfill & -\frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 1/T_c\hfill & 0\hfill \\ 0\hfill & 0\hfill & -\frac{1}{\tau }\hfill & 0\hfill & 0\hfill & 1/T_q\hfill \end{array}\right)\text{.}\hfill \end{array}$$

The next-generation matrix describing expected number of new infections (by the different types of infectious cases) is then defined as ${\mathit{FV}}^{-1}$. The effective reproduction number, ${\mathcal{R}}_e$, is the spectral radius $\varrho ({\mathit{FV}}^{-1})$:

$${\mathcal{R}}_e=\varrho ({\mathit{FV}}^{-1})=\beta T\mathcal{S}+{\beta }_c{T}_c{\mathcal{S}}^c+{\beta }_q{T}_q{\mathcal{S}}^q$$ (A.1)

Proof Proof of Theorem 1: —

Non-negativity and boundedness of solutions has already been demonstrated. Now, inspired by final size derivation in Arino et al. (2007), we write the model as follows:

$$x^{\prime }=\pi \mathit{Dy}\beta \mathit{bx}-\mathit{Vx}$$ (A.2)

$$\begin{array}{cc}\hfill y^{\prime }& =-\mathit{Dy}\beta \mathit{bx}+g(y)\beta \mathit{bx}+\mathit{Ay},\mathrm{where}\hfill \\ \hfill \pi & =\left(\begin{array}{ccc}1-\varphi -\xi \hfill & 1-{\varphi }_c-{\xi }_c\hfill & 1-{\varphi }_q-{\xi }_q\hfill \\ \varphi \hfill & {\varphi }_c\hfill & {\varphi }_q\hfill \\ \xi \hfill & {\xi }_c\hfill & {\xi }_q\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \end{array}\right),b^T=\left(\begin{array}{c}0\hfill \\ 0\hfill \\ 0\hfill \\ 1/N\hfill \\ \frac{{\beta }_c}{N\beta }\hfill \\ \frac{{\beta }_q}{N\beta }\hfill \end{array}\right),\hfill \\ \hfill D& =\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\nu }_c\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\nu }_q\hfill \end{array}\right),A=\left(\begin{array}{ccc}0\hfill & (1-{\theta }_c){\alpha }_c\hfill & {\alpha }_q\hfill \\ 0\hfill & -{\alpha }_c\hfill & 0\hfill \\ 0\hfill & {\theta }_c{\alpha }_c\hfill & -{\alpha }_q\hfill \end{array}\right),\hfill \\ \hfill g(y)& =S\left(\begin{array}{c}-\left(\frac{1-p}{p}\varphi +\sigma \right)\hfill \\ \frac{1-p}{p}\varphi \hfill \\ \sigma \hfill \end{array}\right)+{\nu }_q{S}_q\left(\begin{array}{c}0\hfill \\ \frac{1-p}{p}{\varphi }_q\hfill \\ -\frac{1-p}{p}{\varphi }_q\hfill \end{array}\right),y=\left(\begin{array}{c}S\hfill \\ S_c\hfill \\ S_q\hfill \end{array}\right),\hfill \end{array}$$

and $x={(E,E_c,E_q,I,I_c,I_q)}^T$, as before. First, we show that the number of infected individuals eventually go to zero, i.e.

$${\displaystyle \underset{t\to \infty }{\lim }}(E(t)+I(t)+E_q(t)+I_q(t)+E_c(t)+I_c(t))=0\text{.}$$

In order to prove this first statement, notice

$$\begin{array}{cc}\hfill & {(x+\pi y)}^{\prime }=-\mathit{Vx}+\pi g(y(t))\beta \mathit{bx}(t)+\pi \mathit{Ay}\hfill \\ \hfill & \Rightarrow x(t_0)-x(\infty )+\pi (y(t_0)-y(\infty ))\hfill \\ \hfill & =V{\int }_{t_0}^{\infty }x(t)\mathit{dt}-{\int }_{t_0}^{\infty }\pi g(y(t))\beta \mathit{bx}(t)\mathit{dt}-{\int }_{t_0}^{\infty }\pi \mathit{Ay}(t)\mathit{dt}\hfill \\ \hfill & \Rightarrow V{\int }_{t_0}^{\infty }x(t)\mathit{dt}=x(t_0)-x(\infty )+\pi (y(t_0)-y(\infty ))\hfill \\ \hfill & +{\int }_{t_0}^{\infty }\pi \left(\mathit{Ay}(t)+g(y(t))\beta \mathit{bx}(t)\right)\mathit{dt}\text{.}\hfill \end{array}$$ (A.3)

Notice that the column sums of the integrand on the right-hand side of Eq. (A.3), ${\mathbf{1}}^T\pi \left(\mathit{Ay}(t)\mathit{dt}+g(y(t))\beta \mathit{bx}(t)\right)$, is zero. Thus, summing columns on both sides of Eq. (A.3), we find:

$$\begin{array}{cc}\hfill & {\int }_{t_0}^{\infty }\left(\frac{1}{T}I(t)+\frac{1}{T_c}{I}_c(t)+\frac{1}{T_q}{I}_q(t)\right)\mathit{dt}=\hfill \\ \hfill & {\left[(E+E_c+E_q+I+I_c+I_q+S+S_c+S_q)(t)\right]}_{t=t_0}^{\infty }\hfill \end{array}$$

Since solutions are bounded and non-negative for all $t⩾t_0$, the above equation implies that ${\int }_{t_0}^{\infty }\left(I(t)+I_c(t)+I_q(t)\right)\mathit{dt}$ is finite. Additionally, it is clear from system (1) that

$$\begin{array}{cc}\hfill & {\int }_{t_0}^{\infty }\frac{1}{\tau }\left(E(t)+E_c(t)+E_q(t)\right)\mathit{dt}=\hfill \\ \hfill & {\int }_{t_0}^{\infty }\left(\frac{1}{T}I(t)+\frac{1}{T_c}{I}_c(t)+\frac{1}{T_q}{I}_q(t)\right)\mathit{dt}+{\left[(I+I_c+I_q)(t)\right]}_{t=t_0}^{\infty },\hfill \end{array}$$

which implies that ${\int }_{t_0}^{\infty }\left(E(t)+E_c(t)+E_q(t)\right)\mathit{dt}$ is also finite. Therefore, we conclude that ${\lim }_{t\to \infty }(E(t)+I(t)+E_q(t)+I_q(t)+E_c(t)+I_c(t))=0$, proving the first statement.

Next, by the assumption ${\alpha }_q=0,(1-{\theta }_c){\alpha }_c=0$, we obtain:

$$\begin{array}{cc}\hfill S^{\prime }& =-S(1+\psi )\beta \mathit{bx}\hfill \\ \hfill \Rightarrow \ln \left(\frac{S(t_0)}{S(\infty )}\right)& =(1+\psi )\beta b{\int }_{t_0}^{\infty }x(t)\mathit{dt}\hfill \\ \hfill \Rightarrow \ln \left(\frac{S(t_0)}{S(\infty )}\right)& =(1+\psi )\beta {\mathit{bV}}^{-1}\left(x(t_0)+\pi (y(t_0)-y(\infty ))\right),\hfill \end{array}$$ (A.4)

after multiplying Eq. (A.3) by $V^{-1}$ to find ${\int }_{t_0}^{\infty }x(t)\mathit{dt}$, since assuming $\varphi ={\varphi }_c={\varphi }_q,\xi ={\xi }_c={\xi }_q$ implies that $\pi \left(\mathit{Ay}(t)+g(y(t))\right)=\mathbf{0}$.

Using assumption $\nu ={\nu }_c={\nu }_q$, we can derive the following relationship between S and $S_m≔S_c+S_q$:

$$\begin{array}{cc}\hfill S_c^{\prime }+S_q^{\prime }& =-\frac{(1-p)\varphi }{p(1+\psi )}{S}^{\prime }-\frac{\sigma }{1+\psi }{S}^{\prime }-S_c{\nu }_c\lambda (t)-S_q{\nu }_q\lambda (t)\hfill \\ \hfill S_m^{\prime }& =-c_1{S}^{\prime }+c_2\frac{S^{\prime }}{S}{S}_m,\mathrm{where}{c}_1=\frac{\psi }{1+\psi },c_2=\frac{\nu }{1+\psi }\hfill \\ \hfill \Rightarrow & {\left(S_m(t)S^{-c_2}(t)\right)}^{\prime }=-c_1{S}^{\prime }(t)S^{-c_2}(t)\hfill \\ \hfill \Rightarrow & S_m(\infty )S^{-c_2}(\infty )-S_m(t_0)S^{-c_2}(t_0)\hfill \\ \hfill & =\frac{c_1}{-c_2+1}\left(S^{-c_2+1}(t_0)-S^{-c_2+1}(\infty )\right)\hfill \end{array}$$ (A.5)

Define the final (cumulative) epidemic size ${\mathcal{C}}_{\infty }$, and the final proportion of susceptible (not monitored) individuals $U_{\infty }≔\frac{S(\infty )}{S(t_0)}$. When plugging in (A.5) into (A.4), we derive the following relationship:

$$\begin{array}{cc}\hfill \ln \left(U_{\infty }\right)& =(1+\psi ){\mathcal{R}}_e\left(U_{\infty }-1-\frac{S_m(t_0)}{S(t_0)}\left(U_{\infty }^{\nu /(1+\psi )}+1\right)\right)\hfill \\ \hfill & +\left(\frac{\psi }{1+\psi -\nu }\left(U_{\infty }^{\nu /(1+\psi )}-U_{\infty }\right)\right)-(1+\psi )\beta {\mathit{bV}}^{-1}x(t_0)\hfill \\ \hfill {\mathcal{C}}_{\infty }& =N-S(\infty )-S_m(\infty ),\hfill \\ \hfill {\mathcal{C}}_{\infty }& =S(t_0)\left[\frac{N}{S(t_0)}-\frac{\psi }{1+\psi -\nu }\left(\frac{1-\nu }{\psi }{U}_{\infty }+U_{\infty }^{\nu /(1+\psi )}\right)\right]\hfill \\ \hfill & -S_m(t_0)U_{\infty }^{\nu /(1+\psi )},\hfill \end{array}$$

where N is total population size and $\beta {\mathit{bV}}^{-1}x(t_0)=\beta T(E(t_0)+I(t_0))/N+{\beta }_q{T}_q(E_q(t_0)+I_q(t_0))/N+{\beta }_c{T}_c(E_c(t_0)+I_c(t_0))/N$.

If we start from the beginning of an outbreak, letting $t_0=0$, then

$$\begin{array}{cc}\hfill \ln \left(U_{\infty }\right)& =(1+\psi ){\mathcal{R}}_0\left(U_{\infty }-1+\frac{\psi }{1+\psi -\nu }\left({\left(U_{\infty }\right)}^{\nu /(1+\psi )}-U_{\infty }\right)\right)\hfill \\ \hfill {\mathcal{C}}_{\infty }& =N\left(1-\frac{\psi }{1+\psi -\nu }\left(\frac{1-\nu }{\psi }{U}_{\infty }+U_{\infty }^{\nu /(1+\psi )}\right)\right)\text{.}\hfill \end{array}$$

In the case that $\nu =0$, the formula reduces to:

$$\ln \left(U_{\infty }\right)={\mathcal{R}}_0\left(U_{\infty }-1\right),{\mathcal{C}}_{\infty }=N\frac{1}{1+\psi }(1-U_{\infty }),$$

where ${\mathcal{R}}_0=\beta (1-\varphi )T$ and $I(0)\approx 0$ in this case at the outset of the outbreak.

Furthermore in the above special case, along with the restriction that $\nu =0$, a formula measuring peak infected levels can be derived along the lines of the method outlined in Feng (2007). For simplicity, we consider the instance of perfect quarantine (${\beta }_q={\beta }_c=0$) in model (2). Define ${\mathcal{I}}_{\mathit{peak}}(t)≔E(t)+I(t)$. Then it is not hard to see that ${\mathcal{I}}_{\mathit{peak}}^{\prime }(t)=0$ when ${\mathcal{R}}_e(t)=1$, where ${\mathcal{R}}_e(t)={\mathcal{R}}_0\frac{S(t)}{N}$. Let $t_p$ the time of peak (non-quaratined) infected, where ${\mathcal{I}}_{\mathit{peak}}(t_p)={\mathcal{I}}_{\mathit{peak}}≔{\max }_{t>0}\mathcal{Y}(t)$. Then we obtain the following: If we obtain the formula if ${\mathcal{I}}_{\mathit{peak}}(0)=E(0)+I(0)\approx 0$:

$$\begin{array}{cc}\hfill \frac{d{\mathcal{I}}_{\mathit{peak}}}{\mathit{dS}}& =\frac{1}{1+\psi }\left(1-\frac{1}{{\mathcal{R}}_e(t)}\right)\hfill \\ \hfill \Rightarrow {\int }_0^{t_p}d({\mathcal{I}}_{\mathit{peak}}(t))& ={\int }_0^{t_p}\frac{1}{1+\psi }\left(1-\frac{N}{{\mathcal{R}}_{0}S(t)}\right)d(S(t))\hfill \\ \hfill \Rightarrow {\mathcal{I}}_{\mathit{peak}}& =\frac{N}{\left(1+\psi \right){\mathcal{R}}_{0,b}}\left(\ln \frac{1}{{\mathcal{R}}_0}+{\mathcal{R}}_0-1\right)\text{.}\hfill \end{array}$$ (A.6)

Appendix B. Data fitting to models

We utilize data on total reported cases and quarantined contacts in mainland China published in publicly available daily reports by NHC (National Health Commission of the People’s Republic of China) (NHC, 2020). There are possible issues with the case data as detailed by other researchers (Tsang et al., 2020); most notably a change in case counting procedures on Feb. 12 in Hubei province causing an abrupt decrease then sharp increase in reported cases. Although utilizing all cumulative cases reported in China was desirable for model fitting, the data discrepancies, along with potential statistical issues, motivate us to comprehensively test different assumptions in our fitting process. First, because fitting of the model to cumulative incidence data leads to inconsistent assumptions on independence of errors and may cause possible bias (King et al., 2015), we fit the model to the actual daily incidence (inferred from cumulative case data) and to the quarantined contact data as before. Second, the outbreak was not localized to a single population during the timeframe considered, therefore we test the effects of spatial aggregation on parameter estimates.

Due the case counting issues in Hubei around Feb. 12, we excluded the daily incidence numbers for this province (also when fitting incidence for all China) on Feb. 11–13 from our data fitting. We conducted various other explorations of different modeling assumptions including (i) investigation of susceptible self-quarantine rates dependent on mobility data or proportional to rate of reported cases (instead of force of infection), (ii) allowing more general residence time distributions for quarantine periods, and incubation and infectious periods, (iii) including unreported cases in the model (see (C.1)) and fitting the additional dataset of daily deaths. Furthermore, in order to include all cumulative reported cases (and deaths for (C.1)) despite data irregularities, we consider a re-distribution of excess cases according to daily proportion of cumulative totals (Section C.3), and fitting full and simplified model ((2), (1)) to raw cumulative reported cases (Section B.3). All of these additional modeling exercises are summarized below in the following subsections.

B.1. Provincial daily reported case & quarantined contact (DRCQC) fits

For each province we simultaneously fit simplified model (2) to daily case incidence and an inferred number of quarantined individuals for that province. Note that we do not include the provinces of Tibet, which had only one confirmed case, and Hong Kong, where the peak daily case total occurred well after the time frame considered. Furthermore because quarantined contact data was only available aggregated for all of China (from NHC (NHC, 2020)), we estimated the number of quarantined individuals for each province, labeled $i=1,\dots :,30$, as follows:

$$\left\{\begin{array}{c}{Q}^{(i)}(0)=\left(\frac{R^{(i)}(1)-R^{(i)}(0)}{R(1)-R(0)}\right)Q(0)\hfill \\ Q^{(i)}(t)=\left(\frac{{\int }_3^{t+3}{e}^{-s/14}(R^{(i)}(s+1)-R^{(i)}(s))\mathit{ds}}{{\int }_3^{t+3}{e}^{-s/14}(R(s+1)-R(s))\mathit{ds}}\right)Q(t),\hfill & t>0,\hfill \end{array}\right)$$

where $Q^{(i)}(t),(R^{(i)}(t+1)-R^{(i)}(t))$ are the inferred provincial daily quarantine and reported cases, respectively and $Q(t),R(t)$ are the national quarantine and daily case totals on day t post Jan. 21. Here $R^{(i)}(t)=R^{(i)}(t)+R_c^{(i)}(t)$ is provincial reported cases in the model (2) for each province $i=1,\dots ,30$, and $R(t)={\sum }_{i=1}^{30}{R}^{(i)}(t),Q(t)={\sum }_{i=1}^{30}\left(S_c^{(i)}(t)+E_c^{(i)}(t)+I_c^{(i)}(t)+R_c^{(i)}(t)\right)$ represent national counts with respective variables in model (2). Here, the assumption is that quarantined contacts are proportional to reported case load, and as specified in our model, quarantine duration is exponentially distributed with mean $14\mathit{days}$ and we assume a fixed delay of 3 days from contact to tracing. We utilized a nonlinear weighted least squares algorithm, minimizing the objective function $J^{(i)}(t)=R^{(i)}(t+1)-R^{(i)}(t)+{\mathit{wQ}}^{(i)}(t)$ for each province $i=1,\dots ,30$, where $w=0.05$ is a chosen positive weight. The fitting optimization algorithm is implemented in MatLab via the lsqcurvefit function, which utilizes the interior-reflective Newton method. Plots for these fits can be found in Figs. S1 and S2 as Supplementary Materials. Fit parameter values are presented in Table D.5.

B.2. Hubei, China less Hubei, all China DRCQC fits

Because of the outbreak originating in Hubei, we consider fitting the model separately for Hubei and China less Hubei. We utilize the same fitting method as B.1 with the advantage of not having to infer provincial quarantine data. In particular, we minimize the objective function $J(t)={\sum }_{k=1}^{30}{R}^{(k)}(t+1)-R^{(k)}(t)+\mathit{wQ}(t)$, where $k=1,2$ represent Hubei and China Less than Hubei, respectively. For all of these fits the data used were daily case totals, inferred from cumulative case totals $R^{(k)}(t)$, and nationally aggregated quarantined counts $Q(t)$, with both $R^{(k)}(t)$ directly available in the raw data. To obtain the fit for China less Hubei and Hubei in this circumstance we simultaneously fit their respective case data and the sum of their respective quarantine model compartments with initial conditions chosen where appropriate based upon initial relative reported cases and under the assumption that the probability of transmission given contact, $p=.06$, in line with other studies (Bi et al., 2020, Sun et al., 2020). The results of these fittings are summarized in Table D.6 and Fig. B.1 .

Fig. B.1.

Spatially segregated fits corresponding to values in Table D.6.

B.3. All China total daily case & death, reported cumulative case (and DQC) fits

We also utilize raw and re-distributed case and death data in order to use all daily reports including February 11–13 and April 17, 2020, where there were large jumps in case and death counts for Hubei province, respectively. With the raw data, fitting reported cumulative case (CC) data for all China allows us to avoid error that would come with fitting daily case counts for Feb. 11–13, along with avoiding concentrating the excess cases in Hubei province. On the other hand, redistributing the excess reported cases and deaths during these dates when large numbers were added to Hubei totals, allows us to confidently fit both daily cases and deaths for all China, along with quarantined contacts, in Section C.3. We implement an analogous weighted least squares algorithm as in Section B.1, B.2. First, we use objective function $J(t)=R(t)+\mathit{wQ}(t)$ for fitting both simplified model (2) and full model (1) to raw CC data, $R(t)$, and daily quarantined contacts, $Q(t)$. Estimated parameters are in Table D.3, Table D.1, along with corresponding Figs. S6 and S7. Next, we use objective function $J(t)=(R(t+1)-R(t))+w_1(D(t+1)-D(t))+w_{2}Q(t)$ to fit model (C.1) to re-scaled daily case and death data, along with daily quarantined contacts. See Section C.3 for the model (C.1) with unreported cases and further details on the fitting process, along with Table D.4 and corresponding Fig. 4, Fig. 4, Fig. 4, Fig. 4(d).

B.4. Weekly ${\mathcal{R}}_e$

In addition to computing ${\mathcal{R}}_0$ by parameter estimation of differential equation models, we utilize an alternative purely statistical approach incorporating both the case and quarantined contact data to infer ${\mathcal{R}}_e$ and efficacy of contact tracing developed in a prior study of the 2014–2015 Ebola outbreak (Browne et al., 2015). The method, based on Wallinga and Teunis (2004), measures ${\mathcal{R}}_e$ directly from reported case data and estimates of the serial interval (generation time) distribution. We utilize serial interval distributions from a large study of cases and their contacts in Shenzhen, China (Bi et al., 2020). The serial interval for (untraced) reported cases is taken to be $\mathit{Gamma}(2.29,0.36)$ resulting in mean $6.29\mathit{days}$. The serial interval for infections caused by contact-traced cases is taken to be $\mathit{Gamma}(1.8,0.5)$ resulting in mean $3.6\mathit{days}$. Let ${\mathcal{R}}_e^{(j)}$ be the daily reproduction number, ${\mathcal{R}}_{e,n}^{(j)}$ be the daily reproduction number if there was no contact tracing, $U_j$ be the untraced reported cases on day $j,T_j$ be the traced reported cases on day $j,{\pi }_j,{\omega }_j$ be the c.d.f. of serial interval distributions, and $\kappa ={\beta }_c/\beta$ be the proportion of transmissions caused by traced cases (relative to untraced). Then see Table D.2.

$$\begin{array}{cc}\hfill \mathbb{E}({\mathcal{R}}_e^{(j)})& =\frac{1}{U_j+\kappa T_j}{\displaystyle \sum _n}\left({\pi }_n{U}_{j+n}+\kappa {\omega }_n{T}_{j+n}\right)\hfill \\ \hfill \mathbb{E}({\mathcal{R}}_{e,n}^{(j)})& =\frac{1}{U_j+\kappa T_j}{\displaystyle \sum _n}\left({\pi }_n{U}_{j+n}+{\omega }_n{T}_{j+n}\right)\hfill \end{array}$$

Note that $\kappa =0$ for the simplified (perfect tracing) model. Since the amount of infected quarantined contacts is not available in the data, we utilize the predicted relative transmission and incidence of contact-traced individuals from our model fit to assess ${\mathcal{R}}_e$ with and without contact tracing. The results (Fig. 2, Fig. 2(b) in main text) estimate the proportion of reported cases which are traced contacts and reduction of ${\mathcal{R}}_e$ due to contact tracing.

B.5. Uncertainty quantification

We used the following method to generate $95\%$ confidence intervals for the selected quantities appearing in Table D.1, Table D.6.

• 1.Simultaneously fit the simplest model to daily case totals for China less Hubei Province, Hubei Province, and national quarantined data as described in the proceeding section.
• 2.
  Based on the two fit daily case total curves, and under the assumption that the reporting error is normally distributed and relative in magnitude to the reported total at each data point:

  $$y_i=g(x(t_i),\widehat{\xi })+{∊}_i{∊}_i\sim n(0,y_i·s^2),$$

  where g is the true number of daily cases and $\widehat{\xi }$ the set of true parameter values. We generated 10,000 datasets and refit the model to each of them and the original quarantine data simultaneously. For the results in Table D.1, Table D.6 a value of $s=.5$ was used because this value causes the synthetic data-sets to cover the original data except for the outliers around February 12, when there was a change in the method of reporting cases in Hubei province (see Fig. S3 in Supplementary Materials).
• 3.If fitting aggregate case totals sum the results from step 4 to obtain cumulative case numbers
• 4.Produce scatter plots and correlation values for each of the fit parameters based on these generated data for the cumulative data fitting (see Figs. S4 and S5 in Supplementary Materials, respectively).
• 5.Arrange the generated values in increasing order and remove the top and bottom $2.5\%$ in order to obtain the desired approximate $95\%$ Confidence Intervals.

Appendix C. Model variations

C.1. Model with unreported cases

In addition, we consider a version of the model which includes unreported cases. Let $\rho$ be the probability a non-(contact-) traced infected individual becomes a reported case (we assume that all contact-traced cases are reported). Then in the simplified model (2), the equations become:

$$\begin{array}{cc}\hfill S^{\prime }& =-\left(1+\psi \right)\beta \mathit{SI}/N,E^{\prime }=\left(1-\varphi \rho \right)\beta \mathit{SI}/N-\frac{1}{\tau }E,\hfill \\ \hfill I^{\prime }& =\frac{1}{\tau }E-\frac{1}{T}I,R^{\prime }=\frac{\rho }{T}I+\frac{1}{T_c}{I}_c,\hfill \end{array}$$ (C.1)

$$\begin{array}{cc}\hfill {(S_c)}^{\prime }& =\frac{(1-p)}{p}\varphi \rho \beta \mathit{SI}/N-{\alpha }_c{S}_c,{(E_c)}^{\prime }=\varphi \rho \beta \mathit{SI}/N-\frac{1}{\tau }{E}_c,\hfill \\ \hfill {(I_c)}^{\prime }& =\frac{1}{\tau }{E}_c-\frac{1}{T_c}{I}_c,{(R_c)}^{\prime }=\frac{1}{T_c}{I}_c-{\alpha }_c{R}_c,\hfill \\ \hfill D(t)& =\xi {\int }_0^t\frac{a^{\eta -1}\exp (-\eta a/\mu )}{\mathrm{\Gamma }(\eta ){(\mu /\eta )}^{\eta }}\beta S(t-a)I(t-a)/\mathit{Nda},\hfill \end{array}$$ (C.2)

where $\xi$ is case fatality ratio and decoupled death compartment $D(t)$ is fit to daily death data in order to estimate true number of infections and proportion of reported cases, $\rho$. For this fitting, we re-scaled the death and case data in the following manners, so that the ultimate cumulative total would be reached while retaining the same shape to the data:

$$\widehat{d}=\frac{d}{d(t)}·d(T)$$

where d is the cumulative death data and $d(t),d(T)$ are the cumulative deaths at the end of the time interval considered for fitting and the cumulative deaths as of mid-April, 2020 when there was a large jump in Cumulative deaths. Because of the delay between infection and death, along with deaths showing up in data starting Jan. 18, the model fit is initiated at Jan. 11 instead of Jan. 21. Early in the data there is a gap in reported death data, these missing values were estimated via simple linear interpolation prior to applying the above scaling. A similar approach was taken for dealing with the irregularities in reported cases.

C.2. Exploration of different self-quarantine rates

The models considered so far incorporate mass self-quarantine proportional to force of infection, e.g. $\sigma \lambda (t)$ in (2), as a simple proxy for reactionary lockdowns, individual behavior change, etc., occurring population-wide during the outbreak. In reality, this proportionality relationship has several limitations. In particular, there is a delay between new incidence and case reporting which may delay the action of self-quarantine with respect to force of infection. Additionally, while public health proclamations are generally reactionary, other factors may come into play. In order to test the robustness of our simplification we explore different (susceptible) self-quarantine rates here. First, if we simply take self-quarantine rate dependent on the (instantaneous) rate of change in (cumulative) reported case prevalence, $R^{\prime }(t)/N$, then we obtain the modified factor $\tilde{\sigma }$:

$$\tilde{\sigma }\frac{R^{\prime }(t)}{N}S(t)=\tilde{\sigma }\left(\frac{1}{T}\right)I(t)S(t)=\sigma \lambda (t)\Rightarrow \tilde{\sigma }=\sigma {\mathcal{R}}_{0,b}\text{.}$$ (C.3)

Thus, the form of self-quarantine rate is preserved (proportional to $I(t)S(t)$), but the proportionality constant is modified in such a way that the factor must be ${\mathcal{R}}_{0,b}\times$larger when relative to rate of reporting to reach compared to the equivalent quarantine levels when proportional to force of infection. If we consider underreporting as in system (C.1), then the factor is ${\mathcal{R}}_{0,b}/\rho$.

Next, we consider the following delay equation with self-quarantine dependent on daily reported cases, which modifies the susceptible compartment in (2) as

$$S^{\prime }(t)=-\frac{\beta }{N}\left(1+\frac{(1-p)}{p}\varphi \right)I(t)S(t)-\tilde{\sigma }\frac{\left(R(t)-R(t-1)\right)}{N}S(t)\text{.}$$ (C.4)

Here, the factor proportional to (prevalence of) new reported cases within the past 24 h, $\tilde{\sigma }(R(t)-R(t-1))/N$, replaces the force of infection relationship ($\sigma \lambda (t)$). In Fig. B.2 , we show simulations of the delay system plotted with the original model output (corresponding to all China daily incidence fit) for different values of $\tilde{\sigma }$ (relative to $\sigma$) in (C.4). Notice that the incidence trajectory of original model fit is bounded between outbreak simulations of the delay model corresponding to $\tilde{\sigma }={\mathcal{R}}_{0,b}\sigma$ (lower bound) and $\tilde{\sigma }=({\mathcal{R}}_{0,b}/2)\sigma$. This is consistent with the predicted magnification of $\sigma$ derived above in (C.3), and possibly not exactly matching due to the fact that $\left(R(t)-R(t-1)\right)>R^{\prime }(t)$ at the beginning of the outbreak.

Fig. B.2.

Fitted daily case incidence trajectory in original ODE model (dashed black) alongside simulations with modified self-quarantine proportionality constant $\tilde{\sigma }$ relative to daily reported case variable ($R(t)-R(t-1)$) in DDE model (C.4).

Finally, we utilize Baidu mobility data for within-cities, namely City Movement Intensity (WCMI) (C.D. Lab, 2020), as a proxy for the rate of self-quarantine in China during the timeframe. We consider the following modification to the susceptible compartment in (2)

$$S^{\prime }(t)=-\frac{\beta }{N}\left(1+\frac{(1-p)}{p}\varphi \right)I(t)S(t)-\tilde{\sigma }(t)S(t)\text{.}$$ (C.5)

We consider the form

$$\tilde{\sigma }(t)=\left\{\begin{array}{cc}{\sigma }_m\hfill & 0<t⩽t_q\hfill \\ 0\hfill & t_q<t,\hfill \end{array}\right)$$

where ${\sigma }_m$ is the rate and $t_q$ is the duration in exponential decay of mobility fit to the WCMI data separately for Hubei and China less Hubei via non-linear least squares method applied to function $\mathit{WCMI}(t)=(\mathit{WCMI}(0)-b)e^{-{\sigma }_{m}t}+b$ (with b as a lower bound for movement intensity). Utilizing this fitted self-quarantine rate ${\sigma }_m$ in (C.5), we fit the remaining model parameters to the model, this time fitting p, instead of fixing $p=.06$, with the susceptible compartment as described above. The results are consistent with our original model where $\sigma$ is fitted proportionality constant relative to force of infection (see Table D.6 along with Fig. C.3, Fig. C.4 ).

Fig. C.3.

Total self-quarantined trajectory in model fit, alongside Baidu (WCMI) mobility data, see also Table D.6, (C.5).

Fig. C.4.

Model fit using mobility data to approximate ${\sigma }_m$, see also Table D.6, (C.5).

C.3. Time variable serial interval

The final alternative modeling assumption we consider is the possibility of time variable serial interval, as suggested by Ali et al. (2020). We do so by modifying (2) to add additional loss terms due to the lockdown (self-quarantine rate proportional to force of infection) in the Infected and Exposed compartments:

$$\begin{array}{cc}{I}^{\prime }\hfill & =\frac{1}{\tau }E-\frac{1}{\tau }I-\sigma \beta I^2/N\hfill \\ E^{\prime }\hfill & =(1-\varphi )\beta \mathit{SI}/N-\frac{1}{\tau }E-\sigma \beta \mathit{EI}/N\hfill \end{array}$$ (C.6)

We assume the same (initial) infectious period value $T=4.64$. Under this alternative assumption we fit (C.6) for China less Hubei Province and Hubei Province (see Fig. C.5 ). The residual for this fitting was similar to the fitting of the base simplified model. Comparing the fit parameter values to the base assumption (see Table D.6) this results in decreases in both $\sigma$ and $\varphi$. It is expected with the decreasing serial interval of infected cases that less (self)-quarantine will be needed to control the disease, but simulations show that the trajectory of total (self)-quarantined is very close to the original (constant exposed and infectious period) model fit (see Fig. C.5). Furthermore, the main result of minimal impact from contact tracing compared to self-quarantine is preserved, along with the observation that $\sigma$ and $\varphi$ are relatively larger for China less Hubei than they are for Hubei.

Fig. C.5.

Model fit with time variable serial interval and comparison of total self-quarantined trajectory with original fitted model with constant serial interval, see also Table D.6.

C.4. Residence times of quarantine, exposed and infectious periods

We considered two possible alternatives for the distribution of quarantine residence times besides the base assumption of an exponential distribution with mean time of 14 days: a gamma distribution with shape parameter $\alpha$ and scale parameter $\beta$ constrained by $\beta =14{\alpha }^{-1}$ so that a mean residency time of 14 days was retained; and a Weibull distribution with shape parameter $\lambda$ and scale parameter $\kappa$ similarly constrained by $\lambda =14{\left[\mathrm{\Gamma }(1+{\kappa }^{-1})\right]}^{-1}$, with the unconstrained parameters being determined by nonlinear least squares fit to the data together with $I_0,\beta$ (and so ${\mathcal{R}}_{0,b}$), $p,\sigma$, and $\varphi$. As can be seen in Fig. S9 both of these resulted in distributions with similar shape, and resulted in a slight reduction in residual, with the fit Weibull distribution having the lowest residual value. These fit distributions indicate that more individuals spend close to no time in quarantine, presumably as testing results are returned (Luo et al., 2020), and fewer individuals spend significantly more than 14 days in quarantine as would be indicated by the baseline assumption that quarantine residency time is exponentially distributed. However the fit parameter values themselves are comparable (see Table D.6).

We additionally considered the possibility of the infectious and exposed residency times following an Erlang distribution via the linear chain trick using the following system of ODEs:

$$\begin{array}{cc}\hfill S^{\prime }& =-\left(1+\psi \right)\beta \mathit{SI}/N,E_1^{\prime }=\left(1-\varphi \right)\beta \mathit{SI}/N-\frac{n_e}{\tau }{E}_1,\hfill \\ \hfill E_j^{\prime }& =\frac{n_e}{\tau }\left(E_{j-1}-E_j\right)2⩽j⩽n_e\hfill \\ \hfill I_1^{\prime }& =\frac{n_e}{\tau }{E}_{n_e}-\frac{n_i}{T}{I}_1,I_k^{\prime }=\frac{n_i}{T}\left(I_{k-1}-I_k\right)2⩽k⩽n_i\hfill \\ \hfill R^{\prime }& =\frac{n_i}{T}{I}_{n_i}+\frac{n_i}{T_e}{(I_c)}_{n_i},{(S_c)}^{\prime }=\frac{(1-p)}{p}\varphi \beta \mathit{SI}/N-{\alpha }_c{S}_c,\hfill \\ \hfill {(E_c)}_1^{\prime }& =\varphi \beta \mathit{SI}/N-\frac{n_i}{\tau }{(E_c)}_1,{(E_c)}_j^{\prime }=\frac{\mathit{ni}}{\tau }({(E_c)}_{j-1}-{(E_c)}_j),\hfill \\ \hfill {(I_c)}_1^{\prime }& =\frac{n_e}{\tau }{(E_c)}_{n_e}-\frac{n_i}{T_e}{I}_c,{(I_c)}_k^{\prime }=\frac{n_i}{T_e}({(I_c)}_{k-1}-{(I_c)}_k)2⩽k⩽n_i,\hfill \\ \hfill {(R_c)}^{\prime }& =\frac{n_i}{T_e}{I}_c-{\alpha }_c{R}_c,I={\displaystyle \sum _{s=1}^{n_i}}{I}_{s}2⩽j⩽n_e\hfill \end{array}$$ (C.7)

In order to obtain an upper bound for the number of stages in Eq. (C.7) we took the variance and standard deviation for the distributions of T and $T_e$ given in Bi et al. (2020) (where they are assumed to be log normal), fixed the mean to be the values given in table S1, and set the variances equal, solved for $n_i$ and rounded up. This process resulted in an upper bound of at most two stages.

With this in mind we considered three cases, $n_i=2$ and $n_e=1,n_i=1$ and $n_e=2$, and finally $n_i=2$ and $n_e=2$. The fit parameter values corresponding to these fittings are given in Table D.6, and associated fitting plots are Fig. S10. We additionally plotted the log normal distributions given in Bi et al. (2020) together with exponential distributions and Erlang distributions with the same mean (Fig. S9 in Supplementary Materials). In Fig. S9 the considered Erlang and Exponential distributions for $\tau$ are shown. The primary difference in these distributions is that under the exponential assumption a greater proportion of individuals become rapidly infectious and have a shorter infectious period respectively. The primary effects of the Erlang assumption for infectious dwell time are to increase $I_0$, as well as overall case totals, and decrease $\sigma$, as indicated by the fit values in Table S5 and the plots in Fig. S10. In turn an Erlang assumption for time until infectiousness lowers the fit value for $I_0$ and increases $\sigma$ and $\varphi$. Simultaneously assuming both dwell times follow an Erlang distribution results in more moderate increases in $I_0$ and $\varphi$, as well as a slight decrease in $\sigma$ (See Table D.6). The assumption that infectious period (T) is exponential results in better fits than the case of Erlang distribution, whereas either distribution for time until infectiousness ($\tau$) provides good fits to the data.

Furthermore, we tested how varying the means for the quarantine, exposed and infectious periods affects the fitting results (see Fig. S9 in Supplementary Materials). For the quarantine duration, we vary the (exponential distribution) parameter from $1/20$ to $1/4$, with $1/14$ as our baseline assumption (mean duration of 14  days). The parameter fits and results do not change significantly with the varied mean quarantine duration. For exposed ($\tau$) and infectious periods (T and $T_c$) under the assumption of exponential durations, we vary $\tau$ from 2 to 4, along with varying T and $T_c$ in the reported 95% confidence intervals of (4.13,5.1) and (2.08,3.31), respectively, given in Bi et al. (2020). The parameter fits and results are robust to varying means $\tau ,T$ and $T_c$.

Appendix D. Tables

See Table D.1, Table D.2, Table D.3, Table D.4, Table D.5, Table D.6 .

Table D.1.

Bootstrapped Confidence Intervals for Selected Quantities using the simplified model and aggregate case totals.

	95% CI	MLE	Mean	Std. Dev.	ARE
$I_0$	(748.2, 927.4)	778.1	818.6	48.97	5.99
$\beta$	(1.22, 1.36)	1.29	1.28	3.36	2.14
$\sigma$	(1137, 1362)	1240	1244	56.5	3.56
$\varphi$	(0.345, 0.456)	0.377	0.385	0.028	5.24
$p$	(0.075, 0.096)	0.082	0.083	0.0048	4.16
${\mathcal{R}}_0$	(3.37, 3.80)	3.74	3.65	0.119	2.71
${\mathcal{R}}_{0,b}$	(5.67, 6.29)	6.0	5.95	0.156	2.14

Table D.2.

Model variables and parameters.

Variable/Parameter	Description	Estimation
Variables
$S(t),E(t),I(t)$	(Non-quarantined) susceptible, exposed and infectious individuals
$S_q,E_q(t),I_q(t)$	Self-quarantined (social-distanced) susceptible, exposed and infectious individuals
$S_c(t),E_c(t),I_c(t)$	Contact-traced susceptible, exposed and infectious individuals
$R(t)$	Isolated reported cases
$R_c(t)$	Currently quarantined contact-traced cases
Parameters
$\beta ,{\beta }_q,{\beta }_c$	Transmission rate (for unmonitored infectious)	1,2,
$\varphi ,{\varphi }_q{\varphi }_c$	Proportion of (non-quarantined,self-quarantined, already initially traced) contacts traced (or remaining traced)	3, ${\varphi }_q=\varphi ,{\varphi }_c=1$
$\sigma$	self-quarantine (social distancing or lockdown) factor	3
$p$	probability of transmission upon contact	3
${\nu }_q,{\nu }_c$	Reduction in susceptibility for self-quarantined, contact-traced susceptible individuals	2, 0
${\alpha }_q,{\alpha }_c$	Rate of exit from self-, contact-traced quarantine	2, 14 (days)
${\theta }_c$	Fraction of susceptible individuals who return to “social-distanced” (self-quarantined) after completing contact-traced protocol	1
$\tau$	Average time to infectiousness (includes pre-symptomatic)	$3$ (He et al., 2020)
$T,T_q,T_c$	Average infectious period (time to isolation) of non-quarantined, self-quarantined, contact-traced	$4.64$, $2.71$, $2.71$ (Bi et al., 2020)
$S(0)=N$	Total initial susceptible population 4

1. $\beta$ fitted under various assumptions (see Table D.1, Table D.5 & D.6).

2. Fixed at 0 in simplified model, fit in full model (see Table D.3).

3. Fit in full & simplified model (see Table D.1, Table D.3).

4. Population or aggregated populations of provinces in China (N.B. of Statistics of China, 2019).

Table D.3.

Fit Quantities for full Model using aggregate case totals (${\mathcal{R}}_{0,b}=6$ considering results in Table D.1 and improved identifiability)

Quantity	Point Estimate
$I_0$	793.584
$\varphi$	0.4345
${\beta }_q/\beta$	2.33172e-14
$\sigma$	1235.8
$\nu$	1.13e-12
${\beta }_c/\beta$	0.1654
$p$	0.0946
$\alpha$	4.135e-14
${\mathcal{R}}_0$	3.6447

Table D.4.

Fit quantities for model incorporating death data, see C.3 and equation (C.1).

Quantity	Point Estimate	Notes
$I_0$	77.0	on Jan. 11,2020
${\mathcal{R}}_{0,b}$	4.808
${\mathcal{R}}_0$	2.782
$\sigma$	3364.8
$\varphi$	.42147
$\rho$	.12853	probability of case being detected
$\xi$	.010875	Infection Fatality Ratio (IFR)
$a_g$	2.0254	Gamma Shape parameter
$b_g$	7.2301	Gamma Location parameter
$\mu$	14.6439	mean time until death, $\mu =a_g·b_g$

Table D.5.

Fit Parameter Values for Provinces of China using Daily Case totals and approximate Quarantined Individuals for each Province except Hong Kong, due to its peak daily case total occurring significantly after the end of available quarantine data; and Tibet, which had one confirmed case during the outbreak.

province	$I_0$	${\mathcal{R}}_{0,b}$	$\sigma$	$\varphi$	${\mathcal{R}}_0$
Anhui	24.2010	6.0000	64210.0	0.41338	3.519720
Beijing	22.2280	4.9219	59285.0	0.60144	1.961672
Chongqing	33.1070	5.3588	61349.0	0.62185	2.026430
Fujian	22.5090	5.2140	147520.0	0.67986	1.669210
Gansu	6.1867	5.2320	318820.0	0.58251	2.184308
Guangdong	55.2860	6.0000	90103.0	0.51555	2.906700
Guangxi	18.5600	4.2585	203190.0	0.64409	1.515643
Guizhou	2.0885	6.0000	231250.0	0.31685	4.098900
Hainan	4.2958	6.0000	60484.0	0.49998	3.000120
Hebei	3.0933	6.0000	219520.0	0.32616	4.043040
Heilongjiang	5.4071	6.0000	65261.0	0.26693	4.398420
Henan	12.3730	6.0000	55652.0	0.30274	4.183560
Hubei	324.8000	6.0000	1178.3	0.32015	4.079100
Hunan	32.8380	6.0000	61102.0	0.45320	3.280800
Inner Mongolia	1.8439	6.0000	379400.0	0.45947	3.243180
Jiangsu	15.1090	6.0000	123090.0	0.41810	3.491400
Jiangxi	22.8750	6.0000	44021.0	0.40488	3.570720
Jilin	1.7670	6.0000	258030.0	0.36291	3.822540
Liaoning	3.9735	6.0000	302290.0	0.40183	3.589020
Macau	1.0651	6.0000	54198.0	0.67337	1.959780
Ningxia	1.7890	6.0000	94699.0	0.41355	3.518700
Qinghai	1.4552	6.0000	275660.0	0.64266	2.144040
Shaanxi	8.6792	6.0000	148260.0	0.48639	3.081660
Shandong	16.4910	6.0000	173500.0	0.47499	3.150060
Shanghai	12.5000	6.0000	66041.0	0.47770	3.133800
Shanxi	4.3513	6.0000	244730.0	0.44902	3.305880
Sichuan	16.7490	6.0000	163170.0	0.48628	3.082320
Tianjin	3.0767	6.0000	123960.0	0.44167	3.349980
Xinjiang	1.4438	5.5720	343980.0	0.37189	3.499829
Yunnan	9.0932	6.0000	252570.0	0.54209	2.747460
Zhejiang	51.7310	6.0000	40251.0	0.48586	3.084840

Table D.6.

Bootstraped Confidence Intervals for Selected Quantities using Daily Case Totals. ${\sigma }_m$ is the exponential rate of mobility decay.

	Param	95% CI	Pt. Est.	Mean	Std. Dev.	ARE
China	$I_0$	(304.06, 568.13)	393.08	396.12	63.401	11.407
Less	${\mathcal{R}}_{0,b}$	(4.3009, 6.0)	6.0	5.7742	0.47993	3.763
Hubei1	$\sigma$	(100100.0, 127610.0)	114070.0	113240.0	7011.4	4.9488
	$\varphi$	(0.35645, 0.63956)	0.58842	0.53327	0.073158	11.423
	${\mathcal{R}}_0$	(2.1537, 3.3206)	2.4695	2.6702	0.30214	11.396
${\sigma }_m$ from	$I_0$	–	457.61	–	–	–
mobility	${\mathcal{R}}_{0,b}$	–	5.8033	–	–	–
data	$\varphi$	–	0.59027	–	–	–
	$p$	–	0.050985	–	–	–
	${\sigma }_m$	–	0.1051	–	–	–
	${\mathcal{R}}_0$	–	2.3778	–	–
time	$I_0$	–	443	–	–	–
variable	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
serial	$\sigma$	–	77068	–	–	–
interval 1	$\varphi$	–	0.37	–	–	–
	${\mathcal{R}}_0$	–	3.78	–	–	–
	$I_0$	(410.92, 648.33)	487.2	516.21	60.431	10.547
Hubei1	${\mathcal{R}}_{0,b}$	(5.7131, 6.0)	6.0	5.9804	0.082126	0.32743
	$\sigma$	(1112.9, 1406.2)	1260.1	1249.0	74.413	4.7559
	$\varphi$	(0.27846, 0.40932)	0.32135	0.33809	0.034025	9.2804
	${\mathcal{R}}_0$	(3.4661, 4.3292)	4.0719	3.9591	0.22086	4.6969
${\sigma }_m$ from	$I_0$	–	487.2	–	–	–
mobility	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
data	$\varphi$	–	0.32135	–	–	–
	$p$	–	.06	–	–	–
	${\sigma }_m$	–	0.1859	–	–	–
	${\mathcal{R}}_0$	–	3.7622	–	–	–
time	$I_0$	–	644.44	–	–	–
variable	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
serial	$\sigma$	–	699.03	–	–	–
interval 1	$\varphi$	–	0.21	–	–	–
	${\mathcal{R}}_0$	–	4.74	–	–	–
	$I_0$	(745.83, 809.05)	787.55	773.52	17.143	2.2695
China1	${\mathcal{R}}_{0,b}$	(5.9288, 6.0)	6.0	5.9955	0.023302	0.075615
	$\sigma$	(20906.0, 25382.0)	23495.0	23186.0	1147.4	3.9386
	$\varphi$	(0.32521, 0.4018)	0.36897	0.3637	0.019656	4.3037
	${\mathcal{R}}_0$	(3.588, 4.0367)	3.786	3.8168	0.11491	2.4572
Gamma	$I_0$	–	810.733	–	–	–
Quarantine	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
Assumption 1	$\sigma$	–	23463.0	–	–	–
	$\varphi$	–	0.37296	–	–	–
	${\mathcal{R}}_0$	–	3.7622	–	–	–
Weibull	$I_0$	–	812.079	–	–	–
Quarantine	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
Assumption 1	$\sigma$	–	23486.1	–	–	–
	$\varphi$	–	0.37309	–	–	–
	${\mathcal{R}}_0$	–	3.7615	–	–	–
Infectious	$I_0$	–	1259.6	–	–	–
Erlang	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
Assumption	$\sigma$	–	18118.0	–	–	–
only 1	$\varphi$	–	0.33983	–	–	–
	${\mathcal{R}}_0$	–	3.9610	–	–	–
Exposed	$I_0$	–	732.18	–	–	–
Erlang	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
Assumption	$\sigma$	–	30887.0	–	–	–
only 1	$\varphi$	–	0.50246	–	–	–
	${\mathcal{R}}_0$	–	2.9852	–	–	–
Simultaneous	$I_0$	–	1053.1	–	–	–
Erlang	${\mathcal{R}}_{0,b}$	–	6.0	–	–	–
Assumption 1	$\sigma$	–	20864.0	–	–	–
	$\varphi$	–	0.42596	–	–	–
	${\mathcal{R}}_0$	–	3.4442	–	–	–

1. $p$ fixed at 0.06.

Appendix E. Materials

Source code data have been deposited in GitHub ( https://github.com/jcmacdonald-codesData?tab=projects).

Supplementary data

The following are the Supplementary data to this article: