Plasma cell sensor using photonic crystal cavity

Abstract

The performance of one-dimensional photonic crystal for plasma cell application is studied theoretically. The geometry of the structure can detect the change in the refractive index of the plasma cells in a sample that infiltrated through the defect layer. We have obtained a variation on the resonant peak positions using the analyte defect layer with different refractive indices. The defect peak of the optimized structure is red-shifted from 2195 to 2322 nm when the refractive index of the defect layer changes from 1.3246 to 1.3634. This indicates a high sensitivity of the device (S = 3300 nm/RIU) as well as a high Q-factor (Q = 10³). The proposed sensor has a great potential for biosensing applications and the detection of convalescent plasma.

Introduction

Blood plasma is one of the human blood components that plays an important role in the osmotic effect inside the vessels (Kenner 1989). The concentration of blood plasma is an indication for some diagnoses such as disorder of cardiovascular, leukemia, and autoimmune (Cakmak et al. 2013). Also, exchanging convalescent plasma has attracted more attention as a potential therapy for COVID-19 that created a sense of panic globally (Chen et al. 2020; Shen et al. 2020; Keith et al. 2020; Ahn, et al. 2020). Researchers are attempting to get immunity from recovered COVID-19 patients with "convalescent" plasma (Kupferschmidt and Cohen 2020). Therefore, studying and detecting an abnormal concentration of blood plasma is vitally important for COVID-19 therapy. One of the efficient approaches to estimate the concentration of blood plasma is by measuring its refractive index (RI) as RI of the blood plasma is a function of its concentration (${\mathrm{c}}_{\mathrm{p}})$ according to this equation (El-Khozondar et al. 2019):

$${\mathrm{n}}_{\mathrm{p}}=1.32459+0.001942{\mathrm{c}}_{\mathrm{p}}$$ 1

In the last few decades, 1D, 2D, and 3D photonic crystals (PCs) and phononic crystals have been received extensive attention in sensing applications as a biochemical sensor, salinity sensor, and filters (El-Khozondar et al. 2019; Arafa et al. 2017; Beheiry et al. 2010; Natesan et al. 2018; Arunkumar et al. 2019; Amiri et al. 2019; Elsayed and Mehaney 2018; Zaky et al. 2020; Abd El-Ghany et al. 2020; Zaky and Aly 2020; Khateib et al. 2020). The PCs are periodic structures of alternating dielectrics (Abd El-Ghany et al. 2020; Aly and Elsayed 2012; Aly et al. 2020a; Aghajamali et al. 2015; Nayak et al 2017, 2018, 2019; Guo et al. 2020a; Srivastava and A. J. J. O. S. Aghajamali, and N. Magnetism 2017; Shiri et al. 2019; Zhou et al. 2021), nanocomposites (Aly et al. 2018a), superconductors (Aly et al. 2019, 2018b), or metal with different refractive indices in one, two or three directions (Yablonovitch 1987; Shaban et al. 2017; Winn et al. 1998). There is a forbidden region for a specific range of wavelengths in a propagated electromagnetic wave. this forbidden region is called the photonic bandgap (PBG) (Aly 2008; Aly and Hanafey 2011). Owing to the multiple Bragg scattering mechanism, This PBG is created (Hassan et al. 2015; Zaky and Aly 2021a, 2021b; Zaky et al. 2021).

Photons are localized through the PBG as a resonant peak by introducing a defect layer inside the PCs (Aly and Elsayed 2012). Any change in the concentration of the defect layer samples increases the refractive index (Aly et al. 2020b). This increase in the refractive index causes strong electric field confinement and shifts the defect peak to the longer wavelengths (red-shift) according to Bragg law (Aly et al. 2020b). Therefore, the defective PCs are used as an optical refractive index sensor (Fan et al. 2015).

In this work, we employed a one-dimensional photonic crystal 1D-PC as a blood plasma sensor. The blood plasma layer is introduced as a defect layer within the 1D-PC and the change in the RI is investigated. Inside the PBG, a resonant defect peak is created (Aly et al. 2020b; Peng et al. 2018). By changing the concentration of the blood plasma sample layer, the RI changes, as well as the resonant defect peak position will be red-shifted because of the strong light confinement through it. Recently, many researchers developed experimentally, highly stable, low cost, and highly efficient 1D-PC for different applications (Peng et al. 2018; Faneca et al. 2018).

In 2019, Khozondar et al. (El-Khozondar et al. 2019) proposed a plasma blood sensor by using a ternary photonic crystal. They achieved a sensitivity of 51.49 nm/RIU. Ahmed et al. (Ahmed et al. 2019) used D-shaped photonic crystal fiber (PCF) to sense the blood plasma. They estimated a sensitivity value equal to 5.8 nm/gL-1. In 2020, Ying, et al. proposed a PCF filled with liquid crystal as a RI sensor with a sensitivity of 2275 nm/RIU (Guo et al. 2020b). Yongbo, et al. designed PCF based on surface plasmon resonance that has a high sensitivity of 21 200 nm/RIU (Fu et al. 2020). Abadla, et al. investigated a binary PC comprising a defect layer for hemoglobin detection with sensitivity 167 nm/RIU (Abadla and Elsayed 2020). As shown in Table 3, The proposed sensor was designed with high sensitivity, low detection limit, and high quality-factor comparing with many published reports (Abadla and Elsayed 2020; Mohamed et al. 2016; Banerjee 2009).

Table 3.

Comparison of sensitivity, Q-factor, DL, and sensing analyte of the proposed structure with other one-dimensional PC sensors in literature

Reference	S (nm/RIU)	Q-factor	DL(RIU)	Sensing analyte
El-Khozondar et al. (2019)	51	***	***	Blood plasma
Abadla and Elsayed (2020)	167	***	***	Hemoglobin concentration
Aly et al. (2020b, 2019)	1100	106	10–8	Glucose concentration
Banerjee (2009)	24	***	***	Blood glucose
Mohamed et al. (2016)	1118	***	10–3	Blood glucose
This work	3300	103	10–5	Blood plasma

*** means not be calculated

Design and theoretical model

Figure 1 shows the schematic diagram of the proposed sensor which consists of $Air/(Ge/Ca{F}_2{)}^N/P/(Ge/Ca{F}_2{)}^N/Si{O}_2$. The first layer A is $\mathit{Ge}$, the second layer B is $Ca{F}_2.$ P is a defect layer filled with a sample of blood analytes with different concentrations. The thickness of the layers are $d_1,$ $d_2$, and d_p, while the RI are $n_1,n_2$, and n_p, respectively. N is the number of periods. The analyte of plasma cells is sandwiched as a defect layer between two identical binary periodic structures. This structure was deposited on ${\mathrm{SiO}}_2$ (layer S) as a substrate with a thickness of 2 mm. The $(Ge/Ca{F}_2)$ PC was theoretically designed (Sharma et al. 2012). We select $\mathit{Ge}$ and $Ca{F}_2$ as dielectric materials because they have high contrast in refractive indices and will make a wide photonic band gap in the selected region (infra-red) with low loss (near to zero Extinction coefficient) in this regions, as will mentioned in the next section (Nunley, et al. 2016; Kruschwitz and Pawlewicz 1997).

Fig. 1.

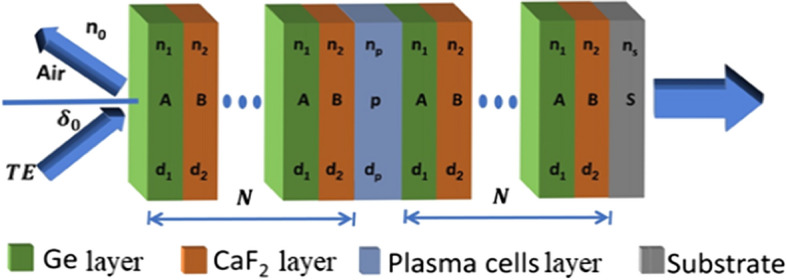
Schematic diagram of the 1D-PC in which the plasma layer is incorporated

Homogeneous films of $Ge\mathrm{and}Ca{F}_2$ can be prepared by spray pyrolysis deposition, spin-coating, radio frequency (RF) magnetron sputtering, plasma-enhanced chemical vapor deposition (PECVD), and some others as we listed in our last paper (Aly et al. 2020b). During the fabrication of the design, a layer of a certain material can be deposited as a defect film, and this film can be etched with a strong chemical solution (Etching prosses). Then, the blood sample is injected into this etched layer.

Transfer matrix method (TMM) is used to study the interaction between the incident optical wave (IR-region) and the current PC structure as the following equation (Li and Lin 2003):

$$\begin{array}{c}\mathrm{Y}=\left(\begin{array}{cc}{\mathrm{Y}}_{11}\hfill & {\mathrm{Y}}_{12}\hfill \\ {\mathrm{Y}}_{21}\hfill & {\mathrm{Y}}_{22}\hfill \end{array}\right)\hfill \end{array}=({\mathrm{y}}_1{\mathrm{y}}_2{)}^{\mathrm{N}}({\mathrm{y}}_{\mathrm{p}})({\mathrm{y}}_1{\mathrm{y}}_2{)}^{\mathrm{N}},$$ 2

where $Y_{11}$, $Y_{12}$, $Y_{21}$ and $Y_{22}$ are the transfer matrix elements, $y_1,y_2,y_{\mathrm{p}}$ are the characteristic matrix for $\mathit{Ge}$, $Ca{F}_2$ and the defect layer which are given by:

$$\begin{array}{cc}& y_i=\left(\begin{array}{cc}\cos {\mathrm{\Phi }}_i\hfill & -i\sin {\mathrm{\Phi }}_i/q_i\hfill \\ -i{q}_{i}sin{\mathrm{\Phi }}_i\hfill & \cos {\mathrm{\Phi }}_i\hfill \end{array}\right),i=\mathrm{A},\mathrm{B},\mathrm{P}\hfill \end{array}$$ 3

where Φ_i is the phase difference at each layer given by:

$${\mathrm{\Phi }}_i=\frac{2\pi n_i{d}_i\cos {\delta }_i}{\lambda },$$

q for s-polarization of light is q_i = n_i cosδ_i. Also, δ₁, δ_2, and δ_p are the incident angle on the Ge, CaF_2, and P layers according to Snell’s law:

$$\begin{array}{c}{n}_0\sin {\delta }_0=n_1\sin {\delta }_1=n_2\sin {\delta }_2=n_p\sin {\delta }_p\hfill \end{array}.$$ 4

For N periods of the structure, we used the Chebyshev polynomials of the second kind to get the matrix ($y_1{y}_2$)(${}^N$Wu et al. 2005). Now, the transmittance coefficient can be given by:

$$\begin{array}{cc}t\hfill & =\frac{2q_0}{(Y_{11}+Y_{12}{q}_s)p_0+(Y_{21}+Y_{22}{q}_s)}\hfill \end{array},$$ 5

where the values of q for the s-polarization of air (q_s) and substrate (q_s) can be calculated as: $q_0=n_0\cos {\delta }_0$, and $q_s=n_s\cos {\delta }_s$. Finally, the transmittance can be written in terms of transmission coefficient as:

$$\begin{array}{cc}T\hfill & =100\ast \frac{q_s}{q_0}\left|t^2\right|\hfill \end{array}.$$ 6

Results and discussions

The proposed structure consists of two layers and the lattice parameter is $\mathrm{D}={\mathrm{d}}_1+{\mathrm{d}}_2$, where ${\mathrm{n}}_1=4.23$,${\mathrm{d}}_1=180\mathrm{nm}$, ${\mathrm{n}}_2=1.42,$ ${\mathrm{d}}_2=100\mathrm{n}$ m, and ${\mathrm{d}}_{\mathrm{p}}=1100\mathrm{nm}$. Additionally, Fig. 2 shows various RI values of the plasma samples which depend on the concentration of the plasma sample in the blood (c_p) that measured in the unit of (g/L) according to Eq. 1.

Fig. 2.

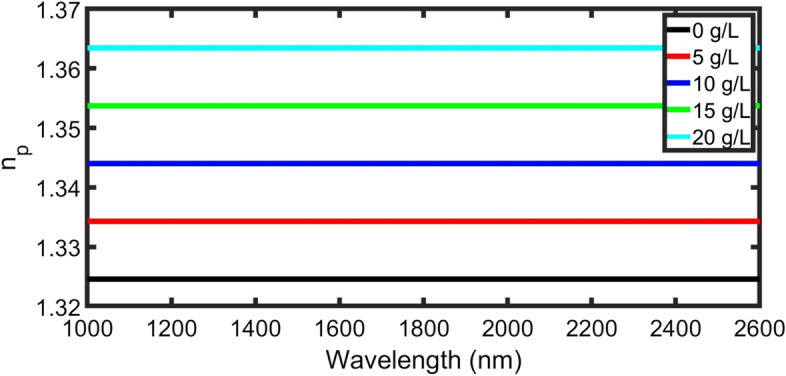
RI of blood plasma as a function on the incident wavelength at different concentrations from 0 to 20 (g/L)

The Matlab simulation tool is used to study the transmission spectra of the proposed defective PC (Aly and Elsayed 2012; Shaban et al. 2020). To enhance the sensing performance of our sensor, three types of transmission calculations were performed. Firstly, we study the effect of the number of layers (N) at the normal incident light and d_p = 1100 nm on sensor performance. Secondly, we repeat the above calculations for different thicknesses of the blood plasma sample by keeping the number of periods at the selected optimized value. Thirdly, we do the same calculations for different incident angles by keeping both the number of periods and thickness at the selected optimized values.

Figure 3 shows the transmittance of the structure as a function of different incident wavelengths at 0, 5, 10, 15, and 20 g/L plasma concentration with $d_p=1100\mathrm{n}$ m and incident angle δ₀ = 0˚. The PBG extended within the infrared regions from 1695 nm(left) to 2380 nm (right) in the absence of the defect layer(black line). The width of the bandgap is equal to 685 nm with cutoff transmittance amplitude through it. Multiple Bragg scattering between the incident, scattered and reflected light prevents the incident light to travel through the structure (Mulder et al. 2012). This large width of the PBG due to the high contrast between the two materials of the unit cell refractive indices.

Fig. 3.

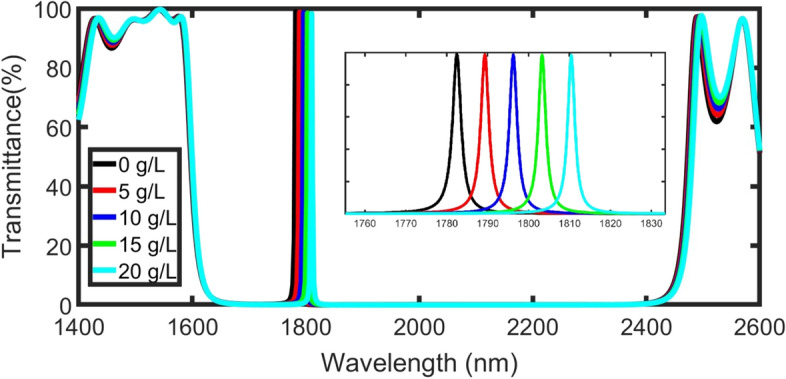
transmittance for TE (transverse electric wave)polarization of the structure as a function of incident wavelength for 0, 5, 10, 15, 20 g/L blood plasma concentration at d_p = 1100 nm, N = 5, and incident angle δ₀ = 0˚

To evaluate the sensor performance, some parameters such as sensitivity, quality factor, detection limit, and figure of merit should be examined quantitatively. The equation of sensitivity is given by Ayyanar et al. (2018):

$$\begin{array}{cc}& S=\mathrm{\Delta }{\lambda }_p/\mathrm{\Delta }{n}_p\hfill \end{array},$$ 7

where $\mathrm{\Delta }{\lambda }_p$ is the shift in the position of the defect peak ($\mathrm{\Delta }{\lambda }_p={\lambda }_{\mathit{bloodplasmasample}}-{\lambda }_{\mathit{water}}$), and $\mathrm{\Delta }{n}_p=n_{\mathit{bloodplasmasample}}-n_{\mathit{water}}$ is the RI difference between different blood plasma samples.

When the defect layer is immersed with water( $n_p=1.3246)$, a defect peak appears at λ_p = 1782 nm with transmittance amplitude (T_p = 98.8%). The resonant peak is due to the light confinement through the blood plasma layer.

The ability of any sensor for measuring a very small change in the resonant wavelength also depends on the figure of merit (FOM). FOM is a very important parameter because it is directly proportional to the sensitivity (S) of the proposed sensor and inversely proportional to the full width at half maximum of the transmission of the resonant peak ($\mathrm{FWHM}$)according to the following equation:

$$\begin{array}{c}\mathrm{FOM}=\mathrm{S}/\mathrm{FWHM}\hfill \end{array}$$ 8

The decrease in FWHM leads to increasing the quality factor (Q-factor) of the sensor as the relation (Beheiry et al. 2010; White and Fan 2008):

$$\begin{array}{c}\mathrm{Q}={\mathrm{\lambda }}_{\mathrm{p}}/\mathrm{FWHM}\hfill \end{array}$$ 9

Another parameter related to S and Q is called the detection limit, which indicates the smallest change in RI can be detected, as following equation (Beheiry et al. 2010; White and Fan 2008);

$$\begin{array}{c}\mathrm{DL}=\frac{{\mathrm{\lambda }}_{\mathrm{p}}}{20\mathrm{S}\mathrm{Q}}\hfill \end{array}$$ 10

A very low DL indicates a good sensor for resolving small RI changes. the value of signal-to-noise (SNR) is calculated by Abadla and Elsayed (2020):

$$\mathrm{SNR}=\frac{\mathrm{\Delta }{\mathrm{\lambda }}_{\mathrm{p}}}{\mathrm{FWHM}}.$$ 11

Finally, the resolution(RS) of the proposed sensor that represents the smallest resonant shift that can be detected accurately is given by Abadla and Elsayed (2020):

$$\mathrm{RS}=\frac{2(FWHM)}{{3(\mathrm{SNR})}^{1/4}}.$$ 12

Effect of the number of layers (N)

By increasing the number of layers (N) from 2 to 5 layers, the resonance of defect peaks is slightly blue-shifted (decrease in wavelength), ${\mathrm{\lambda }}_{\mathrm{FWHM}}$ decreases and the PBG shrink, as shown in Fig. 4. Besides, the sensitivity and $\mathrm{\Delta }{\mathrm{\lambda }}_{\mathrm{p}}$ slightly increase but Q-factor significantly increases due to the decrease of ${\lambda }_{\mathit{FWHM}}$, as well as the detection limit decreases. But at values of N higher than N = 6, FOM seems to be constant.

Fig. 4.

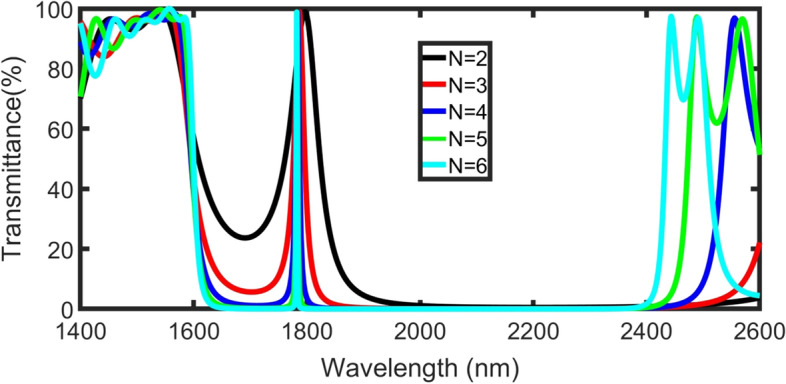
transmittance power for TE polarization of the structure as a function of incident wavelength for 0 g/L plasma concentration at $d_p=1100\mathrm{n}$ m, incident angle ${\phi }_0=0$˚ and different values of N

We have considered the number of layers (N = 6) is the optimum condition to maintain a high- FOM (high S and Q but low FWHM and DL), as cleared in Fig. 5. Blue-line is 4th-order polynomial fitted data between N and FWHM (R² = 99%) that can be considered as:

$$\begin{array}{cc}& \mathrm{FWHM}=0.33N^4-7.5N^3+63N^2-2.4e^{2}N+3.4e^2\hfill \end{array}.$$ 13

Fig. 5.

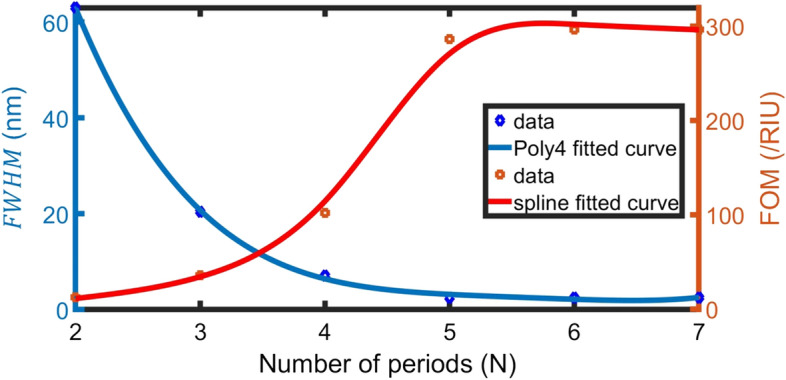
Effect of N on FWHM and FOM at normal incidence, $d_p=1100\mathrm{nm}$, and 0 g/L blood plasma concentration

Effect of the plasma layer concentration:

According to Eq. 1, the blood plasma RI changes from 1.3246 to 1.3634. When the concentration of blood plasma changed from 0 to 20 (g/L), the resonant peak is shifted to the right region (redshift) to maintain the optical path difference constant as the formula of standing wave states:

$$\begin{array}{cc}& \mathrm{\gamma }=m\lambda =n_{\mathit{eff}}a,\hfill \end{array}$$ 14

where $\mathrm{\gamma },m,\lambda ,n_{\mathit{eff}},a$ are the optical path difference, an integer, the wavelength of the incident light, the effective RI of the design, and geometric path difference, respectively (Zeng et al. 2014). The transmission spectrum in Fig. 3 illustrates the defect peak shift from 1782 $n$ m to 1810 $n$ m with $\mathrm{\Delta }{\lambda }_p$=28 $n$ m when the blood plasma concentration varied from 0 to 20 (g/L). The sensitivity at these conditions equals 721 $n$ m/RIU.

Effect of plasma layer thickness

When the thickness of the blood plasma layer thickness increases, the incident IR waves passes through a long geometric path inside the plasma layer, a strong interaction occurs between the plasma layer and the incident light, and the difference of the resonant defect peak position sift (Δλ_p) increases (Aly and Zaky 2019), as shown in Figs. 6a, b. The resonant defect peak position is red-shited as well due to the standing wave formula (Eq. 14).

Fig. 6.

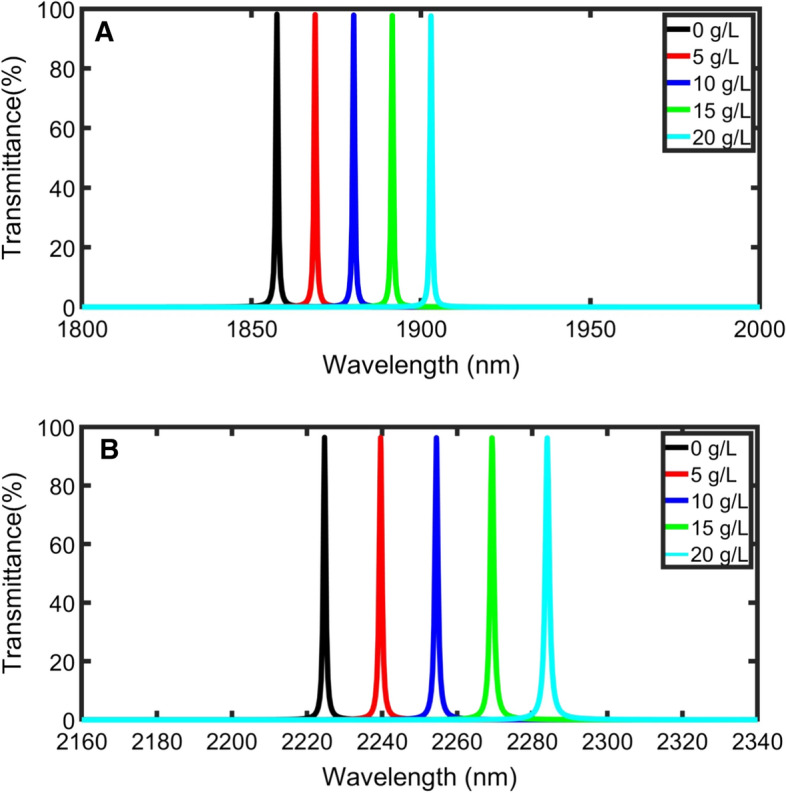
transmittance power for TE polarization of the structure as a function of normal incident wavelength for 0, 5, 10, 15, and 20 g/L plasma concentration; (A) at $d_p=4000\mathrm{n}$ m, (B) at $d_p=10000\mathrm{n}$ m

Figure 7 shows the change of sensitivity with the increase of the blood plasma sample layer thickness from 1100 to 10,000 m$\mathrm{n}$. At defect layer thicknesses higher than 5000 nm, the value of sensitivity seems to be constant, and new resonant defect peaks enter the PBG. By increasing the defect layer thickness than 10,000 nm, sensitivity slightly increases, and much sample volume will be needed. For these reasons, this thickness is considered the optimum defect layer thickness. The highest sensitivity for normal incidence (1528 nm/RIU) corresponding to defect mode thickness of 10,000 nm.

Fig. 7.

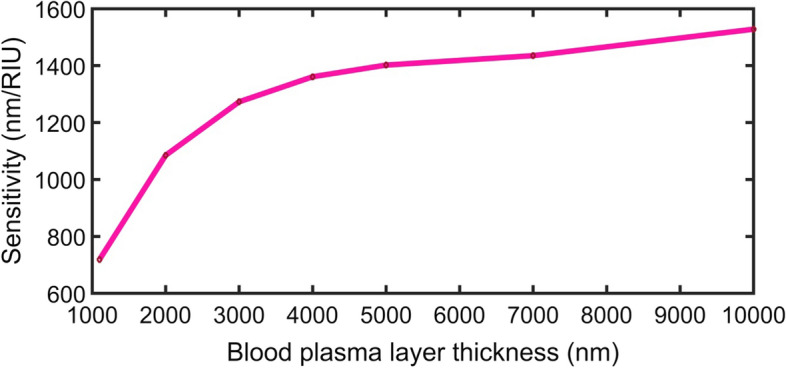
Variation of sensitivity with the defect layer thickness for normal incident light

Effect of the incident angle on sensitivity

Finally, to take a closer look at the dependence of resonant peak on the incident angle, the transmittance powers as a function of the angle of incidence are studied in the Table. 1 at the defect layer thickness of 10,000 nm. The effect of changing the incident angle on the resonant defect peak as well as on the position of the bandgap can be explained by using Bragg–Snell law (Schroden et al. 2002; Aly et al. 2012):

$$\begin{array}{cc}q\lambda \hfill & =2L\sqrt{n_{\mathit{eff}}^2-{\sin }^2{\delta }_0}\hfill \end{array}$$ 15

where q is the order of diffraction, λ is the wavelength, L is the interplanar spacing, n_eff is the effective index of refraction, and δ₀ is the incident angle. According to Eq. 15, by increasing the incident angle (δ₀), λ decreases (blue shifted).

Table 1.

The sensitivity as a function of the angle at d_p = 10,000 nm

δ0 (degree)	Δλp (nm)	S(nm/RIU)	Transmission power (%)
0	59.3	1528	98.8
30	68.5	1765	94.6
60	98.1	2528	82.6
85	126.6	3263	27

It can be observed that by increasing the angle from 0° to 85°, the sensitivity of the sensor significantly increases from 1528 nm/RIU to 3263 nm/RIU with a decrease in the transmission power (from 96 to 27%). In contrast, a further increase in the angle makes the sensitivity constant and leads to a significant decrease in transmission power until it reaches zero at 90°. Other papers reported this behavior (Armstrong and O'Dwyer 2015; Sharma et al. 2015).

From the above studies, N = 6, thickness d_p = 10,000 nm, and incident angle δ₀ = 85° are considered as optimum conditions (Fig. 8). In Table 2, Eq. 7 is used to calculate the sensitivity of different blood plasma concentrations. The Q-factor of the proposed sensor is very significant from 1.8 × 10³ to 5.1 × 10³, which makes it accurate. This is due to the resonant narrow peak (low FWHM). Also, This device recorded a high FOM from 1.9 × 10³ to 8.1 × 10³_, a very low DL ( about $10^{-5}$ RIU). This means that this plasma sensor has a high potential for RI sensing applications.

Fig. 8.

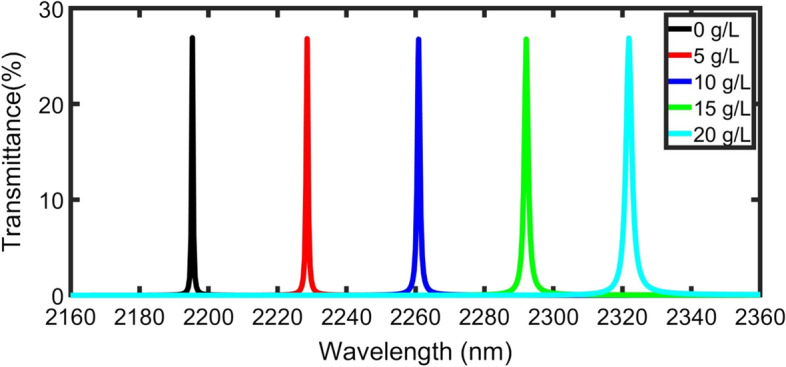
Transmission power for TE polarization of the 1DTPC as a function of normal incident wavelength for 0, 5, 10, 15, and 20 g/L plasma concentration at optimum conditions (d_p = 10,000 and δ₀ = 85˚)

Table 2.

Sensor parameters for different plasma concentrations at d_p = 10,000 nm and angle of incidence of 85°

Cp (g/L)	N (RIU)	λp (nm)	S (nm/RIU)	FWHM (nm)	FOM (/RIU)	Q-Factor	SNR	SR
0	1.3246	2195	–	0.432	–	5.1 × 103	–	–
5	1.3343	2229	3505	0.604	8.1 × 103	3.7 × 103	56.3	0.147
10	1.3440	2261	3299	0.868	3.8 × 103	2.6 × 103	36.9	0.235
15	1.3537	2292	3196	1.292	2.5 × 103	1.8 × 103	24.0	0.389
20	1.3634	2322	3093	1.676	1.9 × 103	3.4 × 103	17.9	0.543

We perform linear fitting to the RI of the plasma blood sample (Fig. 9) and the defect peak position values from (Table 2). It is cleared that the position of the defect peak is red-shifted by increasing the RI. The slope of the fit represents the sensitivity of the sensor (3300 nm/RIU) and we get the following equation;

$$\begin{array}{cc}{\lambda }_p\hfill & =3300n_p-2100,(R^2=0.99)\hfill \end{array},$$ 16

where ${\lambda }_p$ is the defect peak position, $n_p$ is the plasma blood sample RI.

Fig. 9.

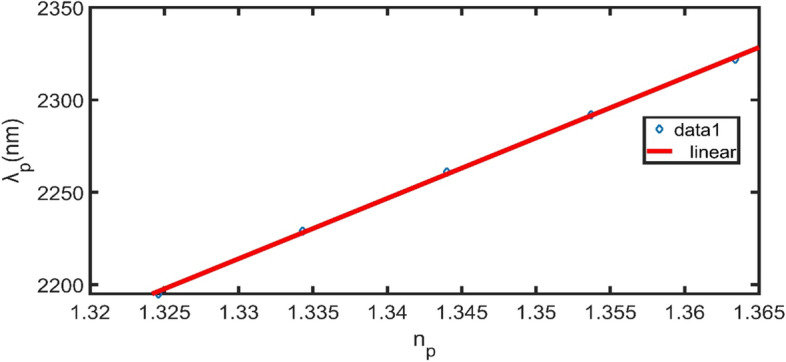
The position of defect peak vs RI of the plasma blood sample

Since the major innovation of this manuscript is to reduce the cost of the proposed sensor, we use the microcavity structure. the 1D-PC is very simple in fabrication than others (2D and 3D) because of its simplest structure and very low cost compared to 2D and 3D structures (Pandey et al. 2017; Li 2014). As cleared in Table 3, most of the previous works that used the 1D-PC and some of the others that used 2D-PC recorded a very low sensitivity and Q-factor, but in this proposed structure, we recorded a super sensitivity (S = 3300 nm/RIU) at the optimum conditions (Abadla and Elsayed 2020; Mohamed et al. 2016; Banerjee 2009).

Conclusion

In the present study, we have investigated a plasma blood sample sensor by using a binary one-dimensional photonic crystal sensor and study the effect of the plasma cell concentration. The layer thickness, number of periods, and incidence angle are significant parameters on the sensitivity of the proposed sensor. The defect peak of the optimized structure is red-shifted from 2195 to 2322 nm with the RI of the defect layer changes from 1.3246 to 1.3634. These results mean that the high sensitivity of the device (S = 3300 nm/RIU) and a high Q-factor is possible (Q = 10³). These advantages make this design is very important for biosensing applications, especially in case of a very limited change in blood plasma concentration that may help in COVID-19 therapy.