Rooting the Animal Tree of Life

Abstract

Identifying our most distant animal relatives has emerged as one of the most challenging problems in phylogenetics. This debate has major implications for our understanding of the origin of multicellular animals and of the earliest events in animal evolution, including the origin of the nervous system. Some analyses identify sponges as our most distant animal relatives (Porifera-sister hypothesis), and others identify comb jellies (Ctenophora-sister hypothesis). These analyses vary in many respects, making it difficult to interpret previous tests of these hypotheses. To gain insight into why different studies yield different results, an important next step in the ongoing debate, we systematically test these hypotheses by synthesizing 15 previous phylogenomic studies and performing new standardized analyses under consistent conditions with additional models. We find that Ctenophora-sister is recovered across the full range of examined conditions, and Porifera-sister is recovered in some analyses under narrow conditions when most outgroups are excluded and site-heterogeneous CAT models are used. We additionally find that the number of categories in site-heterogeneous models is sufficient to explain the Porifera-sister results. Furthermore, our cross-validation analyses show CAT models that recover Porifera-sister have hundreds of additional categories and fail to fit significantly better than site-heterogenuous models with far fewer categories. Systematic and standardized testing of diverse phylogenetic models suggests that we should be skeptical of Porifera-sister results both because they are recovered under such narrow conditions and because the models in these conditions fit the data no better than other models that recover Ctenophora-sister.

Introduction

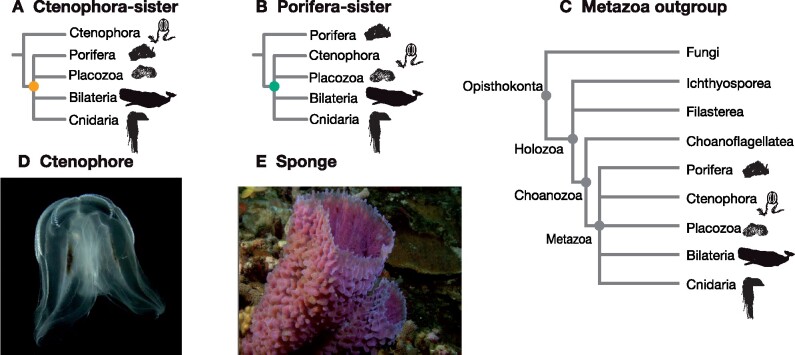
Historically, there was little debate about the root of the animal tree of life. Porifera-sister (fig. 1E), the hypothesis that the animal root marks the divergence of Porifera (sponges) from all other animals (fig. 1B), was widely accepted though rarely tested. By contrast, there has long been uncertainty about the placement of Ctenophora (comb jellies) (fig. 1D) in the animal tree of life (Wallberg et al. 2004). The first phylogenomic study to include ctenophores (Dunn et al. 2008) suggested a new hypothesis, now referred to as Ctenophora-sister, that ctenophores rather than sponges are our most distant living animal relative (fig. 1A). Since then, many more phylogenomic studies have been published (fig. 2), with some analyses finding support for Ctenophora-sister, some for Porifera-sister, and some neither (King and Rokas 2017) (table 1, supplementary text S1, Supplementary Material online). The extensive technical variation across these studies has been important to advancing our understanding of the sensitivity of these analyses to a variety of factors, demonstrating for example that outgroup and model selection can have a large impact on these results (fig. 3A). But the extensive technical variation has also made it difficult to synthesize these results to understand the underlying causes of this sensitivity. Several factors make the resolution of the root of the animal tree a particularly challenging problem. For one, the nodes in question are the deepest in the animal tree of life. Another factor that has been invoked is branch lengths (e.g., supplementary figs. S1 and S2, Supplementary Material online), which are impacted by both divergence times and shifts in the rate of evolution. Some sponges have a longer root to tip length, indicating an accelerated rate of evolution in those lineages. The stem branch of Ctenophora is longer than the Porifera stem branch, which, together with a more typical root-to-tip distance, is consistent with a more recent radiation of extant ctenophores (Podar et al. 2001) than extant poriferans. The longer ctenophore stem branch has led some to suggest that Ctenophora-sister could be an artifact of long-branch attraction to outgroups (Pisani et al. 2015; Kapli and Telford 2020).

Fig. 1.

Two alternative phylogenetic hypotheses for the root of the animal tree. (A) The Ctenophora-sister hypothesis posits that there is a clade (designated by the orange node) that includes all animals except Ctenophora, and that Ctenophora is sister to this clade. (B) The Porifera-sister hypothesis posits that there is a clade (designated by the green node) that includes all animals except Porifera, and that Porifera is sister to this clade. Testing these hypotheses requires evaluating the support for each of these alternative nodes. (C) The animals and their outgroup choice, showing the three progressively more inclusive clades Choanozoa, Holozoa, and Opisthokonta. (D) A ctenophore, commonly known as a comb jelly. (E) A poriferan, commonly known as a sponge.

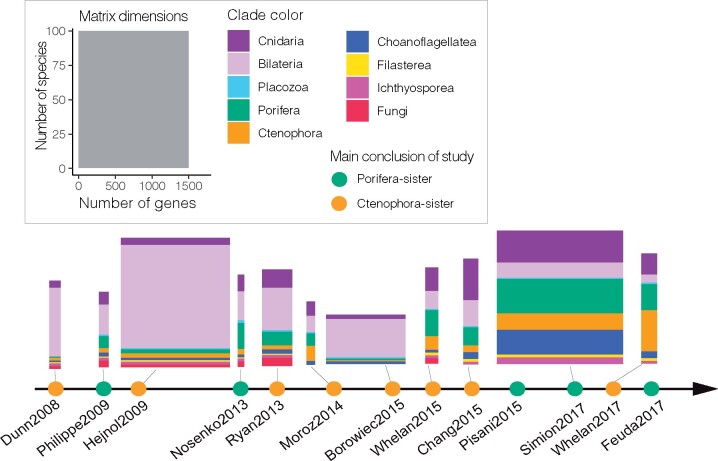
Fig. 2.

An overview of previous phylogenomic studies on animals. The horizontal axis is a time-series showing the main conclusions of previous phylogenomic studies that indicated their analyses supported Ctenophora-sister (orange nodes) or Porifera-sister (green nodes) based on their main conclusion from each study. Each of the primary matrices considered here is shown above the axis, color coded by taxon sampling. Horizontal size is proportional to the number of genes sampled, vertical size to the number of species sampled. Only 11 matrices were shown here since three studies (Pisani et al. 2015; Whelan and Halanych 2016; Feuda et al. 2017) are based entirely on previously published data and gene-partition data is not available from one study (Pick et al. 2010).

Table 1.

Overview of Data Matrices Used in this Study

Study	Matrix	Clade	No. Genes	No. Sites	No. Taxa	Inferred Sister Lineage	Journal	No. Citations
Dunn et al. (2008)	Dunn2008	Opisthokonta	150	21,152	64	Ctenophora-sister	Nature	1794
Philippe et al. (2009)	Philippe2009	Opisthokonta	129	30,257	55	Porifera-sister	Current Biology	649
Hejnol et al. (2009)	Hejnol2009	Opisthokonta	1487	270,580	94	Ctenophora-sister	Proceedings of Biological Sciences	707
	Hejnol2009_subsampled	Opisthokonta	844	55,594	94	Ctenophora-sister
Pick et al. (2010)						Porifera-sister	Molecular Biology and Evolution	326
Nosenko et al. (2013)	Nosenko2013_nonribo_9187	Opisthokonta	35	9,187	63	Ctenophora-sister	Molecular Phylogenetics and Evolution	221
	Nosenko2013_ribo_14615	Opisthokonta	87	14,615	71	Porifera-sister
Ryan et al. (2013)	Ryan2013_est	Opisthokonta	406	88,384	61	Ctenophora-sister	Science	534
Moroz et al. (2014)	Moroz2014_3d	Opisthokonta	114	22,772	46	Ctenophora-sister	Nature	491
Whelan et al. (2015)	Whelan2015_D1	Opisthokonta	251	59,733	76	Ctenophora-sister	Proceedings of the National Academy of Sciences of the United States of America	220
	Whelan2015_D10	Opisthokonta	210	59,733	70	Ctenophora-sister
	Whelan2015_D20	Opisthokonta	178	81,008	65	Ctenophora-sister
Borowiec et al. (2015)	Borowiec2015_Best108	Choanozoa	108	41,808	36	Ctenophora-sister	BMC Genomics	104
	Borowiec2015_Total1080	Choanozoa	1080	384,981	36	Ctenophora-sister
Pisani et al. (2015)	Ryan2013_est	Opisthokonta	406	88,384	60	Porifera-sister	Proceedings of the National Academy of Sciences of the United States of America	206
	Whelan_D6	Opisthokonta	115	33,403	70	Porifera-sister
Chang et al. (2015)	Chang2015	Opisthokonta	170	51,940	77	Ctenophora-sister	PNAS	119
Whelan and Halanych (2016)	Philippe2009	Opisthokonta	129	30,257	55	Ctenophora-sister	Systematic Biology	37
	Nosenko2013_nonribo_9187	Opisthokonta	35	9,187	63
	Nosenko2013_ribo_14615	Opisthokonta	87	14,615	71
Simion et al. (2017)	Simion2017	Opisthokonta	1719	401,632	97	Porifera-sister	Current Biology	220
	Simion2017_subsampled	Opisthokonta	1719	110,602	97	Porifera-sister
Feuda et al. (2017)	Chang2015	Opisthokonta	170	51,940	77	Ctenophora-sister	Current Biology	119
	WhelanD20	Opisthokonta	178	81,008	65	Porifera-sister
Whelan et al. (2017)	Whelan2017b_full	Holozoa	212	68,062	80	Ctenophora-sister	Nature Ecology and Evolution	79
	Whelan2017b_strict	Choanozoa	117	49,388	76	Ctenophora-sister

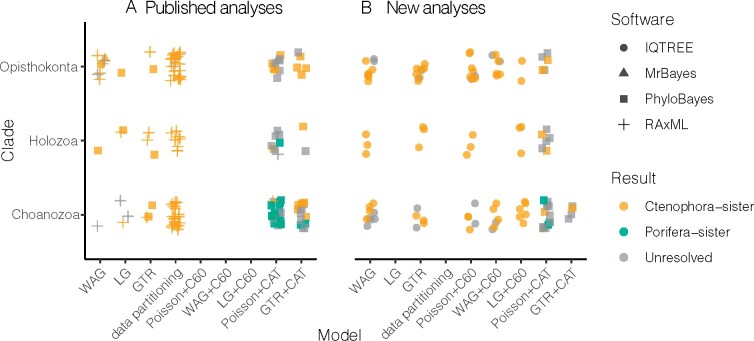
Fig. 3.

Summary of phylogenomic results from previous studies and reanalysis conducted in this study. Each point represents a phylogenetic analysis with a support of bootstrap values less than 90% or a posterior probability less than 95% are considered as unresolved. The clades are organized with increased outgroup sampling higher on the vertical axis, and the models are organized in general by increasing complexity in terms of numbers of parameters to the right on the horizontal axis. (A) Analyses transcribed from the literature (related to supplementary table S1, Supplementary Material online). (B) New phylogenomic analyses conducted in this study (related to supplementary table S2, Supplementary Material online). Over 1,011,765 CPU hours (~115 CPU years) were used for this study.

To advance this debate, it is critical to understand why different studies yield different results, which can only be achieved by examining variation in methods and results of different studies in a standardized and systematic framework. Here, we synthesize data and results from 15 previous phylogenomic studies that tested the Ctenophora-sister and Porifera-sister hypotheses (fig. 2, table 1). This set includes all phylogenomic studies of amino acid sequence data published before 2018 for which we could obtain data matrices with gene partition annotations ( Laumer2018 data matrix is thus not included here; Laumer et al. 2018). Among these 15 studies, 3 studies (Pisani et al. 2015; Whelan and Halanych 2016; Feuda et al. 2017) are based entirely on previously published data, and gene-partition data are not available from one study (Pick et al. 2010).

Variation in Models and Sampling across Published Analyses

The models of sequence evolution in the studies considered here differ according to two primary components: the exchangeability matrix $R$ and amino acid equilibrium frequencies $\Pi$. The exchangeability matrix $R$ describes the relative rates at which one amino acid changes to another. The studies considered here use exchangeabilities that are the same between all amino acids (Poisson, also referred to as F81), or different. If different, the exchangeabilities can either be fixed based on previously empirically estimated rates (WAG or LG), or independently estimated from the data (GTR). The analyses considered here have site-homogeneous exchangeability models (site-homogeneous model), which means that the same matrix is used for all sites. The equilibrium frequencies describe the expected frequency of each amino acid, which captures the fact that some amino acids are much more common than others.

The published analyses differ in whether they take a homogeneous approach and jointly estimate the same frequency across all sites in a partition or add parameters that allow heterogeneous equilibrium frequencies that differ across sites. Heterogeneous approaches include CAT (Lartillot and Philippe 2004), which is implemented in the software PhyloBayes (Lartillot et al. 2013) and has been widely applied to phylogenomic studies of deep animal relationships. The models that are applied in practice are heavily influenced by computational costs, model availability in software, and convention. While studies often discuss CAT and WAG models as if they are mutually exclusive, we note that these particular terms apply to nonexclusive model components—CAT refers to heterogeneous equilibrium frequencies across sites and WAG to a particular exchangeability matrix. In this literature, CAT is generally shorthand for Poisson+CAT and WAG is shorthand for WAG+homogeneous equilibrium frequency estimation. To avoid confusion on this point, here we always specify the exchangeability matrix first (e.g., GTR), followed by modifiers that describe the accommodation of heterogeneity in equilibrium frequencies (e.g., CAT). If site-homogeneous equilibrium frequencies are used, we refer to the exchangeability matrix alone. Gamma-rate heterogeneity, a scalar that accommodates the total rate of change across sites, is used in almost every analysis conducted here and we generally omit its designation. Some analyses partition the data by genes and use different models for each gene (supplementary text S2, Supplementary Material online).

High-throughput sequencing allows investigators to readily assemble matrices with hundreds or thousands of protein-coding genes from a broad diversity of animal species (table 1). Studies of animal phylogeny have used a wide variety of different approaches to identifying and selecting genes and taxa for their matrices. As a result, the genes selected for analysis in each study vary widely (fig. 2, supplementary fig. S3, Supplementary Material online). Gene sampling varies in several ways, including in the fractions of single-copy orthologs (e.g., BUSCO genes) and ribosomal protein genes in the matrix (supplementary fig. S4, Supplementary Material online).

Ingroup taxon sampling also varies widely between studies (fig. 2, supplementary fig. S3, Supplementary Material online). Sampling of ingroup taxa (animals) in early studies was biased toward Bilateria. Sampling of nonbilaterian animals, including sponges and ctenophores, has improved over time (supplementary fig. S3, Supplementary Material online). Within each clade, there is often considerable variation in taxon sampling and therefore often little species overlap across studies (supplementary fig. S3, Supplementary Material online). This variation is in part because newer sequencing technologies in more recent studies are usually not applied to the exact same species that were included in earlier studies.

Sampling of outgroup taxa (nonanimals, in this case) is critical to phylogenetic rooting questions since the node where the outgroup subtree attaches to the ingroup subtree is the root of the ingroup. There has therefore been extensive focus on improving outgroup sampling when testing phylogenetic hypotheses about rooting (Graham et al. 2002). Most studies addressing the animal root have removed more distantly related outgroup taxa in some analyses to explore the effect of outgroup selection to ingroup topology (Ryan et al. 2013; Pisani et al. 2015). Three progressively more inclusive clades have often been investigated: Choanozoa (animals plus most closely related Choanoflagellatea), Holozoa (Choanozoa plus more distantly related Holozoa), and Opisthokonta (Holozoa + Fungi).

Results and Discussion

Variation in Results across Published Analyses

We parsed 136 previous phylogenetic analyses from 15 studies (fig. 3A and supplementary table S1, Supplementary Material online). The conclusions of five studies strongly favor Porifera-sister and ten favor Ctenophora-sister (table 1). Three studies are based entirely on previously published data, and the remainder add data for one or more species.

Our summary of previous phylogenetic analyses (fig. 3A) shows that Ctenophora-sister is supported in analyses that span the full range of outgroup sampling and models used to date, including some analyses with restricted outgroup sampling and models that accommodate site-heterogeneous equilibrium frequencies with CAT. This is consistent with previous assessments of the problem (Whelan and Halanych 2016) but is drawn from a much more extensive and systematic examination. The only analyses that support Porifera-sister have reduced outgroup sampling (Choanozoa, Holozoa) and site-heterogeneous models with CAT. Model adequacy assessments generally favor GTR+CAT over Poisson+CAT or site-homogeneous models (Pisani et al. 2015; Feuda et al. 2017), but because GTR+CAT is so parameter rich, many analyses that use a model with GTR+CAT do not converge. The fact that Porifera-sister is recovered only for particular models with particular outgroup sampling indicates that model and outgroup interact, and that this interaction is fundamental to understanding the range of results obtained across analyses.

New Standardized Analyses of Published Matrices

One of the challenges of interpreting support for the placement of the animal root across published studies is that different programs, software versions, and settings have been used across analyses. This extensive variation, which has been shown to influence the reproducibility of phylogenetic inference (Darriba et al. 2018; Shen et al. 2020), makes it difficult to identify the primary factors that lead to different results. Here, we first reanalyze the primary matrices from each study under the same conditions with IQ-TREE (Nguyen et al. 2015) with multiple evolutionary models. We selected this tool because it has greater model flexibility than most other phylogenetic tools (Zhou et al. 2018) (fig. 3B; supplementary table S2, Supplementary Material online). Importantly, it has the site-heterogeneous C models (C1–C60 equilibrium frequencies) (Si Quang et al. 2008) that, like CAT, allow for the accommodation of heterogeneity in equilibrium amino acid frequencies across sites.

For each of the published studies, we selected the matrix that was the primary focus of the manuscript or has been reanalyzed extensively in other studies, for further analysis. For each of these matrices, we progressively trimmed taxon sampling to create Opisthokonta, Holozoa, and Choanozoa versions, where permitted by original outgroup sampling. This produced 36 data matrices from 11 studies that presented new sequence data and for which partition data were available.

For all but the three largest matrices, we tested the relative fit of a variety of models, both with and without C10–C60 accommodation of site heterogeneity in equilibrium frequencies, using ModelFinder (Kalyaanamoorthy et al. 2017) in IQ-TREE. In all cases, models with C60 fit these matrices better than the site-homogeneous models. This is consistent with the importance of accommodating site heterogeneity noted by previous investigators (Lartillot and Philippe 2004; Philippe et al. 2009; Nosenko et al. 2013; Pisani et al. 2015; Feuda et al. 2017; Simion et al. 2017). We then inferred support under the best-fit model (supplementary table S3, Supplementary Material online), except for the three largest matrices where we used LG+C60. We then analyzed each matrix under a panel of standard site-heterogeneous and site-homogeneous models, including WAG, GTR, and Poisson+C60 (supplementary table S2, Supplementary Material online).

All IQ-TREE analyses, apart from unresolved analyses (for Moroz2014_3d and all Nosenko 2013 matrices), supported Ctenophora-sister (fig. 3B). No IQ-TREE analyses supported Porifera-sister, including those that restrict outgroup sampling to Choanoflagellatea and use models with site-heterogeneous equilibrium frequencies (fig. 3B lower right; supplementary table S2, Supplementary Material online), the conditions under which published PhyloBayes CAT analyses recover strong support for Porifera-sister (fig. 3A). Moreover, we found similar results when only Fungi or Holozoa are used as outgroups (supplementary table S4, Supplementary Material online). To further verify this difference in a controlled manner, we reran PhyloBayes analyses with CAT, using both Poisson and GTR substitution matrices, for some matrices that had led to support for Porifera-sister in published analyses. Consistent with published results, some of these supported Porifera-sister.

Our new analyses show that, with restricted outgroup sampling, analyses of the same matrices with two different means of accommodating site heterogeneity in equilibrium frequencies (C60 in IQ-TREE and CAT in PhyloBayes) yield different results. This indicates that the traditional framing of the problem, which posits that accommodating site heterogeneity leads to support for Porifera-sister, is incorrect. Rather, our results suggest that there is something about the PhyloBayes CAT analyses specifically that leads to support for Porifera-sister.

Category Number Explains Differences between Site-Heterogeneous Analyses

There are several factors, including variations in models (C60 vs CAT), software (PhyloBayes vs IQ-TREE), and implementation details (e.g., number of categories used to accommodate site heterogeneity) that could explain the new variation in results noted here among site-heterogeneous models. In published analyses of the animal root, these factors were confounded since all previous heterogeneous analyses used the CAT model in PhyloBayes. Here, we seek to deconfound these factors to gain a finer-grained perspective on why results differ between analyses of the same matrices.

A primary difference between the C (e.g., C60) and the CAT site-heterogeneous models is the number of equilibrium frequency categories. The standard CAT model employs a Dirichlet process prior to inferring the number of equilibrium frequency categories, so the number of categories is variable (Lartillot and Philippe 2004). IQ-TREE implements C models (Si Quang et al. 2008) with a fixed number of categories that can range from 10 (C10) to 60 (C60). Differences in analysis results could therefore be due to differences in the number of categories. The number of categories inferred by CAT in PhyloBayes can be very high (supplementary table S5, Supplementary Material online), with a mean here of 623.5 categories for Poisson+CAT analyses in all matrices and 1,026 categories for GTR+CAT analyses in several representative matrices. This requires a very large number of additional estimated parameters.

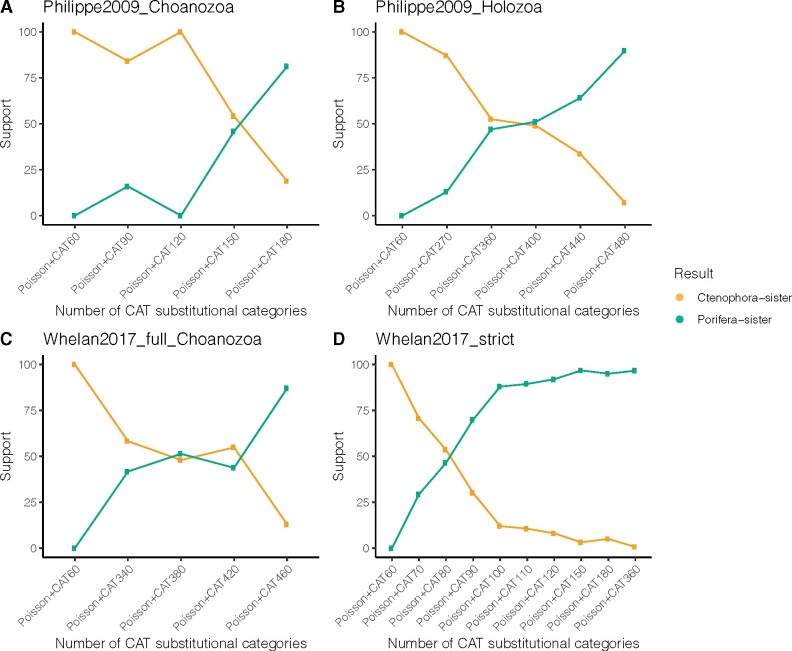
We examined the specific impact of this large difference in category number on the position of the animal root. It is currently not possible to use more than 60 categories for C models in IQ-TREE, but the number of categories can be set a priori in PhyloBayes using nCAT. We therefore varied the number of categories in PhyloBayes analyses (fig. 4; supplementary table S6, Supplementary Material online). We found that Poisson+nCAT60 analyses in PhyloBayes, like Poisson+C60 and WAG+C60 in IQ-TREE analyses, provide strong support of Ctenophora-sister (fig. 4). This indicates that the difference in results between unconstrained CAT analyses in PhyloBayes and C60 analyses in IQ-TREE is not due to differences in the software or other implementation factors, but due to the large difference, in excess of 10-fold, in the number of site categories. When we increased the number of categories in PhyloBayes nCAT analyses, we observe the transition from support for Ctenophora-sister to an unresolved root to Porifera-sister (fig. 4). For example, for the Whelan2017_strict matrix this transition occurs between 60 and 120 categories when using Poisson+nCAT model. Due to computational limitations of GTR models, we only ran GTR+CAT and GTR+nCAT60 models on representative matrices with Choanozoa sampling. We found that for Whelan2017 matrices, support shifted from Porifera-sister with Poisson+CAT model to Ctenophora-sister using GTR+CAT model. Moreover, we also found all results strongly supported Ctenophora-sister with GTR+nCAT60 models.

Fig. 4.

Sensitivity analyses with representative data matrices were analyzed by different number of equilibrium frequency categories (nCAT) in PhyloBayes. Statistical support values (posterior probabilities) were obtained from three data matrices using the site-heterogeneous Poisson+CAT model with different categories. (A) Phlippe2009_Choanozoa; (B) Philippe2009_Holozoa; (C) Whelan2017_full_Choanozoa; (D) Whelan2017_strict. Statistical support for Ctenophora-sister and Porifera-sister is indicated in orange and green, respectively. Support values from the sensitivity analyses are shown in supplementary table S6, Supplementary Material online.

These results further clarify when analyses support Porifera-sister (e.g., Whelan2017: supplementary fig. S1, Supplementary Material online; Philippe 2009: supplementary fig. S2, Supplementary Material online): when outgroup sampling is restricted (Choanozoa), when a Poisson (rather than a GTR) exchange matrix is used, and when a very large number of site categories is used (unconstrained CAT, giving hundreds of equilibrium frequency categories). Analyses under other conditions either support Ctenophora-sister or are unresolved. This is consistent across published analyses and our new panels of analyses. The question, then, is not why similar analyses give different results, but how we should interpret variation in results when we run analyses that differ in these specific respects. If we fix the first two features to conditions that are necessary for Porifera-sister support (Choanozoa taxon sampling and a Poisson exchange matrix), there are several insights that we can glean from examining how the number of equilibrium frequency categories impacts results that sheds light on the interpretation of those results.

The first insights regard model fit. ModelFinder selects site-heterogeneous C60 models according to BIC (supplementary table S3, Supplementary Material online), but IQ-TREE often gives a warning under C60 that the model may overfit, with too many categories, because some mixture weights are close to 0 (supplementary table S7, Supplementary Material online). In PhyloBayes, cross-validation is a reliable and suggested approach to evaluate the fit of models, and is also often used to test whether there is a significant improvement in the fit of different substitution models to the datasets (Lartillot et al. 2009). We evaluated Poisson+CAT and Poisson+nCAT60 models with cross-validation in PhyloBayes for the Whelan2017_strict and Philippe2009_Choanozoa matrices. For both matrices, we found nearly identical distributions of cross-validation scores for Poisson+nCAT60 and Poisson+CAT models (supplementary fig. S5, Supplementary Material online). A paired t-test analysis shows that there is no significant difference between them for either matrix (Whelan2017_strict: corrected P value = 0.192; Philippe2009_Choanozoa: corrected P value = 0.516). Cross-validation therefore does not support the hypothesis that the unconstrained CAT models are a better fit than the models with 60 categories. Interestingly, our results are consistent with those of a recent simulation study showing that the CAT model often overestimates the true number of categories in the data (Whelan and Halanych 2016). Moreover, it has been also suggested that the number of categories inferred from CAT strongly correlated with the number of characters from the alignment (Whelan and Halanych 2016). In summary, these results suggest that the narrow analysis conditions (Choanozoa taxon sampling, Poisson exchange matrix, and unconstrained CAT models that use hundreds of categories) under which Porifera-sister are obtained lack statistical support.

The second insights related to the allocation of sites to equilibrium frequency categories. Each new category adds the same number of parameters, but that site can be allocated to any number of categories. If, as we add categories, those categories are allocated to a small fraction of sites, then the cost of estimating parameters of those additional categories is high relative to the fraction of the data they help explain. By examining category allocations in the last chain samples of analyses of the Philippe2009_Choanimalia, and Whelan2017_strict matrices (supplementary fig. S6C and D, Supplementary Material online), which have 510 and 471 categories, respectively, we find that the fraction of sites allocated to the 50% of the least frequent categories is 2.97% in the analysis of the Philippe2009_Choanozoa matrix and 3.46% in the analysis of the Whelan2017_strict matrix. This long tail of categories that apply to a very small fraction of sites is in stark contrast to nCAT60 analyses, constrained to 60 categories, which have no such long tail of rare categories (supplementary fig. S6A and B, Supplementary Material online). Although these results are only beginning to address the issue (because we only looked site allocation from one generation after the convergence of PhyloBayes runs and the site allocations vary extensively between generations), our finding that a very large number of categories applies to such a small fraction of data may help explain why increasing the number of categories more than 10-fold has so little impact on the predictive power of these far more complex models.

Phylogenetic Signal

To further explore the phylogenetic signal of different models we discussed above, we quantified the phylogenetic signal for Porifera-sister and Ctenophora-sister topologies across three representative data matrices when varying outgroup sampling and model (supplementary fig. S7, Supplementary Material online). By calculating differences in log-likelihood scores for these topologies for every gene ($\Delta$|lnL|) in each matrix when using site-homogeneous models in IQ-TREE, we found that the Ctenophora-sister had the higher proportions of supporting genes in every analysis. Moreover, outgroup choice has little impact on the distribution of the support for phylogenetic signals in analyses with site-homogeneous models. This finding is largely consistent with the previously observed distribution of support for Ctenophora-sister in other data matrices (Shen et al. 2017).

Although a higher proportion of genes support Ctenophora-sister with site-heterogeneous C60 models, the phylogenetic signal decreases in many genes using C60 models compared to site-homogeneous models. In an extreme case, in matrices from Ryan2013_est nearly 30% of genes changed from strong $\Delta$|lnL|>2) to weak Ctenophora-sister signal ($\Delta$|lnL|<2) (supplementary fig. S7, Supplementary Material online; supplementary table S8, Supplementary Material online). In contrast to the C60 models, there is a major increase in phylogenetic signal in Poisson+CAT models in PhyloBayes towards Porifera-sister, and outgroup choice has a major effect of the distribution of phylogenetic signal (supplementary fig. S7, Supplementary Material online). For example, in Whelan2017_full matrix, we found that the number of genes that support Ctenophora-sister in analyses with CAT decreases from 57.5% in matrices with distant outgroups (Holozoa) to 35.4% when outgroups are restricted (Choanozoa, supplementary table S8, Supplementary Material online).

Amino Acid Recoding Does Not Accommodate Site Heterogeneity

Another approach that has been used to address base compositional heterogeneity across taxa is recoding (Feuda et al. 2017; Laumer et al. 2019). For example, Feuda et al. recoded the full set of twenty amino acids into six groups of amino acids. These groups tend to have more frequent evolutionary changes within them than between them (Susko and Roger 2007). Recoding could, like CAT and C models, address variation across sites, but it could also accommodate variation across lineages, and it was suggested that this approach favors Porifera-sister (supplementary fig. S8, Supplementary Material online; Feuda et al. 2017).

Feuda et al. hypothesized that recoding would reduce potential artifacts due to differences across species in amino acid frequencies. They interpreted the finding that their analyses are sensitive to recoding as evidence that such an artifact exists and that they successfully addressed it by recoding. However, an alternative hypothesis is that recoding impacts phylogenetic analyses because it discards a lot of information.

These two hypotheses can be tested by applying new recoding schemes that also reduce twenty states down to six but are based on random grouping rather than empirical frequencies of amino acid exchange. Empirical and random recodings both discard the same amount of information, but only empirical recoding reduces the impact of amino-acid frequency as intended. Different results between empirical and random recoding would be consistent with the hypothesis that the empirical approach works as intended to accommodate compositional heterogeneity. Similar results would suggest that the impact of recoding is due to discarding information. Here we focus on a single analysis with a posterior predictive score that supports Porifera-sister, the GTR+CAT analysis of the SR-6 recoded Whelan data. We created four new random recoding schemes by shuffling the amino acids in the SR-6 scheme (see Materials and Methods). When we applied each of these randomized codes to the Whelan matrix and analyzed them under the GTR+CAT model with PhyloBayes-MPI, we observed similar results as for the empirical SR-6 recoding. Specifically, like SR-6 recoding, random recoding increases support for Porifera-sister and improves the apparent adequacy of models to explain the heterogeneity of states across taxa (PP taxon hetero mean and max, supplementary fig. S9, Supplementary Material online).

These analyses suggest that the major impact of recoding on phylogenetic analyses is data reduction, not accommodation of compositional heterogeneity across species (supplementary text S3, Supplementary Material online; supplementary figs. S8 and S9, Supplementary Material online). Consistent with a recent simulation study on data recoding (Hernandez and Ryan 2021), these findings indicate that recoding can be a problematic method for addressing heterogeneity.

Conclusions

Resolving the placement of the root in the animal tree of life has proven very challenging (King and Rokas 2017; Laumer et al. 2019). By synthesizing past phylogenomic studies and performing new analyses, we find that support of Porifera-sister is only recovered by site-heterogeneous CAT models with restricted outgroup sampling, and then only in some such analyses. Through controlled analyses we are able to identify the specific aspect of the models that is involved in this variation—the number of categories used to accommodate site heterogeneity in equilibrium frequency (fig. 4). Notably, the 10-fold difference in category number seen in the more complex CAT models that support Porifera-sister does not improve model fit according to cross-validation. This suggests that we should not privilege these narrow analysis conditions that recover Porifera-sister over the much broader range of conditions that recover Ctenophora-sister.

Pin-pointing category number as an issue with a large effect on analyses of the animal root will help guide future analyses that address this question. We hope that the work we have conducted here to consolidate many data sets and analyses in standard formats will make it easier for other investigators to engage in this particularly interesting and difficult phylogenetic problem, and that this problem can be a testbed to develop methods and tools that will help with other difficult phylogenetic problems as well. Advances on the question of the animal root will come from progress on other fronts as well. For example, there are many organisms that are highly relevant to this problem, in the particular outgroup, ctenophore, and sponge taxa, for which no genome or transcriptome data are available (King and Rokas 2017). More broadly, there are very few chromosome-level genome assemblies for animals outside of Bilateria. Future analyses focused on complete genomes rather than transcriptomes and partial genomes will have multiple advantages. Data matrices derived from these more complete sources will have a lower fraction of missing sequences. Complete gene sampling within each species will also greatly improve analyses of gene duplication and loss, a critical step in building phylogenomic matrices such as those presented here. Analyses of this new generation of matrices derived from complete genomes will be well served by understanding the sources of analysis variation in the generation of matrices that came before them.

Materials and Methods

Data and Code Availability

The main data and results associated with the main text and supplementary materials are available in the GitHub data repository at https://github.com/dunnlab/animal_tree_root (last accessed June 16, 2021). All tree files, intermediate results, and scripts/commands associated with this study are available in the Figshare data repository at https://doi.org/10.6084/m9.figshare.13122881 (last accessed June 16, 2021).

Data Selection and Wrangling

We retrieved matrices from each publication (table 1), storing the raw data in this manuscript’s version control repository. We manually made some formatting changes to make the batch processing of the matrices work well, for example, standardizing the format of Nexus CHARSET blocks. All changes made are tracked with git.

Matrix Comparison and Annotation

Taxon Name Reconciliation

We programmatically queried the NCBI Taxonomy database to standardize the names of samples in each matrix. We also used a table where manual entries were needed (manual_taxonomy_map.tsv), for example, authors of the original matrix indicate species names in the original manuscript. For a table summarizing all samples and their new or lengthened names, see taxon_table.tsv.

Sequence Comparisons

Using the original partition files for each matrix, we separated each sequence for each taxon from each partition. Because many of the matrices had been processed by the original authors to remove columns that are poorly sampled or highly variable, these matrix-derived sequences can have deletions relative to the actual gene sequences.

We used DIAMOND v0.9.26 (Buchfink et al. 2015) to compare each sequence to all others using default diamond Blastp parameters. We further filtered DIAMOND results such that we retained hits for 90% of partitions (pident > 50.0, eValue < 1e−5, no self vs self). We ran BUSCO with default parameters for all sequences against the provided Metazoa gene set. We also ran a BLAST+ v2.8.1 (Camacho et al. 2009) blastp search against the SwissProt (Boeckmann et al. 2003) database, filtering results such that we retain at least one hit for ~97% of partitions (pident > 50.0, eValue < 1e−15).

Partition Network

We used the sequence similarity comparisons described above to compare partitions.

We constructed a network with Python and NetworkX v2.2 (Hagberg et al. 2008) where each node is a partition, and each edge represents a DIAMOND sequence-to-sequence match between sequences in the partitions. We extracted each connected component from this network. We further split these components if the most connected node (i.e., most edges) had two times more the standard deviation from the mean number of edges in the component it is a member of and if removing that node splits the component into two or more components. We then decorated every node in the partition network with the most often found SwissProt BLAST+ result and BUSCO results to see which components contain which classes and families of genes. See partition_network_summary in Rdata for a summary tally of each part of the comparison.

Phylogenetic Analyses

Phylogenetic Analyses in IQ-TREE

To investigate the phylogenetic hypotheses and distribution of the phylogenetic signal in studies aiming to find the root position of animal phylogeny, we considered 16 data matrices from all phylogenomic studies that were constructed from EST, transcriptomic, or genomic data (table 1). Because different choices of substitution models could largely influence phylogenetic inference of the placement of the root position of animal phylogeny (e.g., site-heterogeneous vs site-homogeneous models), we first investigated model-fit from each matrix using ModelFinder in IQ-TREE v1.6.7, including site-heterogeneous C10–C60 profile mixture models (C60 models) as variants of the CAT models in ML framework (C10–C60 model were included for model comparison via -madd option). We included models that are commonly used in previous analyses, including site-homogeneous Poisson, WAG, LG, GTR models plus C10–C60 models in the model testing. For computational efficiency, the GTR+C60 models were not included in model testing since it requires to estimate over 10,000 parameters. For large matrices like those from Hejnol2009, Borrowiec2015, and Simion2017, model testing is also not computational feasible so only LG+C60 models were used since LG/WAG+C60 models were suggested as the best-fit model in all other matrices.

We then reanalyzed each matrix under a panel of evolutionary models, including WAG, GTR, Poisson+C60, and the associated best-fit model identified above. Nodal support was assessed with 1000 ultrafast bootstrap replicates for each analysis. Because of the large size of Hejnol2009 and Simion2017, it was not computationally feasible to analyze the whole matrix using the C60 model or CAT site-heterogeneous models. To circumvent his limitation, we reduced the data size from their full matrices to facilitate computational efficiency for site-heterogeneous models. For Hejnol2009 matrix, we instead used the 330-gene matrix constructed by Hejnol et al. (2009), since the main conclusion for their study is based on this subsampled matrix; For Simion2017 matrix, we only included the most complete 25% of genes (genes that were present in less than 79 taxa were removed; 428 genes were kept). It should be noted that the main conclusion of Simion et al. was also based on selection of 25% of genes for their jackknife approach.

Outgroup Taxa Sampling with C60 and CAT Models

Because different choices of outgroups could also affect phylogenetic inference as suggested in previous analyses, we parsed the full data matrices into three different types of outgroups: Choanozoa, Holozoa, and Opisthokonta. These data sets include the same set of genes but differ in the composition of outgroup species. Choanozoa only includes Choanoflagellatea outgroup; Holozoa also includes more distantly related Holozoans; Opisthokonta also includes Fungi. For each Choanozoa data matrix, both C60 models in IQ-TREE and Poisson+CAT models in PhyloBayes were conducted. The maximum likelihood analysis was performed using the best-fit substitution model identified as above and nodal support was assessed with 1,000 ultrafast bootstrap replicates using IQ-TREE. Moreover, Bayesian inference with the site-heterogeneous Poisson+CAT model was done with PhyloBayes-MPI v1.8. To minimize computational burden, GTR+CAT models were only performed in the representative Choanozoa matrices from Philippe2009, Ryan2013_est, and Whelan2017_full.

For several Choanozoa matrices indicated strong support for the hypothesis that sponges are the sister group to the remaining Metazoa using the Poisson+CAT model, Bayesian inference with Poisson+CAT model was also conducted to Holozoa and Opisthokonta data matrices with the same settings as above. For all the analyses with Poisson+CAT models in PhyloBayes, two independent chains were sampled every generation. Tracer plots of MCMC runs were visually inspected in Tracer v1.6 to assess stationarity and appropriate burn-in. Chains were considered to have reached convergence when the maxdiff statistic among chains was below 0.3 (as measured by bpcomp) and effective sample size > 50 for each parameter (as measured by tracecomp). A 50% majority-rule consensus tree was computed with bpcomp, and nodal support was estimated by posterior probability. Most PhyloBayes runs converged, although several large matrices have not reached convergence after at least a month’s computational time. For those matrices that were not converged, PhyloBayes analyses were run for at least two weeks. We also summarized the average number of substitutional categories inferred for each PhyloBayes analysis using Tracer.

To examine the effects of distantly related outgroups on the phylogenetic inference, we also conducted analyses based on using only Fungi, only Holozoa as outgroups in Philippe2009 and Whelan2015_D20 data matrices using site-homogeneous, C60, and Poisson+CAT models.

Phylogenetic Distribution of Support

To investigate the distribution of phylogenetic signal of the animal-root position in data matrices, we considered three major data matrices from three studies that had different topology between ML and BI using the CAT model in our reanalysis, including Philippe2008, Ryan2013_est, and Whelan2017_full data matrices. We examined two hypotheses: Ctenophora-sister (T1) and Porifera-sister (T2) to the rest of metazoans, under a panel of evolutionary models with different outgroup schemes (Choanozoa and the full matrix). For IQ-TREE analysis in each data matrix, site-wise likelihood scores were inferred for both hypotheses using IQ-TREE (option -g) with the LG+G4 model. The two different phylogenetic trees passed to IQ-TREE 1.6.12 (via -z) were the tree where Ctenophora-sister and a tree modified to have Porifera placed as the sister to the rest of the animals. The numbers of genes and sites supporting each hypothesis were calculated from IQ-TREE output and Perl scripts from a previous study (Shen et al. 2017). By calculating gene-wise log-likelihood scores between T1 and T2 for every gene, we considered a gene with an absolute value of log-likelihood difference of two as a gene with strong (|ΔlnL| > 2) or weak (|ΔlnL| < 2) phylogenetic signal as done in a previous study (Smith et al. 2020).

For Poisson+CAT and LG in PhyloBayes, we only considered the Philippe2009 and Whelan2017 matrices due to computational efficiency. Since the default option in PhyloBayes does not provide the feature to calculate site-wise log likelihood for every generation, we replaced the line “int sitelogl = 0” with “int sitelogl = 1” in the file named “ReadSample.cpp” and installed PhyloBayes 4.1c so that site-wise log-likelihood value can be stored to a file that ends with “.sitelogl” (via readpb –sitelogl). For each condition, we first calculated site-wise log likelihoods for each of two hypotheses (T1 and T2) using pb (via –T) and then stored site-wise log likelihood (a total number of samples for each site is 20) every ten until 300th generations, after discarding the first 100 generations using readpb (via -sitelogl -x 100 10 300). Next, we normalized site-wise log-likelihood value across 20 samples for each of two hypotheses (T1 and T2) and combined normalized site-wise log-likelihood values of T1 and T2 into a single file that was used to calculate gene-wise log-likelihood scores between T1 and T2 with Perl scripts from a previous study (Shen et al. 2017).

Sensitivity Analyses with Different Number of Substitutional Categories

To explore how the number of substitutional categories may affect the phylogenetic inference related to the animal phylogeny, we conducted PhyloBayes analyses with a panel of different substitutional categories in the Whelan2017_strict (ncat = 60, 70, 80, 90, 110, 120, 150, 180, 360), Whelan2017_full_Choanozoa (nCAT = 60, 340, 380, 420, 460), Philippe2009 (nCAT = 60, 90, 120, 150, 180) Philippe2009_Holozoa (nCAT = 360, 400, 440, 480) and Ryan2013_est (ncat = 60). To compare the results between Poisson+CAT and GTR+CAT and minimize computational burden, GTR+CAT and GTR+CAT60 models were only performed in the representative Choanozoa matrices from Philippe2009, Ryan2013_est and Whelan2017_full. All PhyloBayes analyses were carried out using the same settings as above (see Outgroup taxa sampling with C60 and CAT models section), except when a different number of categories was used.

To compare the allocation of frequency categories across sites in the Philippe2009_Choanozoa and Whelan2017_strict matrices for the constrained Poisson+CAT60 model and unconstrained Poisson+CAT model, we parsed the information of PhyloBayes chain files by sampling one in every 1000 generations after burnin determined above. The scripts and subsampled chain files are in the “./trees_new/frequency” subdirectory of the git repository.

Cross-validation Analyses

Bayesian cross-validation implemented in PhyloBayes-MPI was used to compare the fit of Poisson+nCAT60 and Poisson+CAT models coupled with a gamma distribution of site-rate heterogeneity in Whelan2017_strict and Philippe2009_Choanozoa data matrices. Ten replicates were run, each replicate consisting of a random subsample of 10,000 sites for training the model and 2,000 sites for computing the cross-validation likelihood score. For each run, 5,000 generations were run and the first 2,000 generations were discarded as burn-in. To compare if there is significant difference of cross-validation scores between nCAT60 and CAT models, we conducted a paired T-test with P value adjusted by Bonferroni methods using R package rstatix (Team 2019).

Performance of Data Recoding

All code used for the analyses presented here is available in a git repository at https://github.com/caseywdunn/feuda_2017 (last accessed June 16, 2021). The randomized recoding analyses are in the recoding/alternative subdirectory of the git repository.

The original SR-6 recoding scheme is “APST CW DEGN FHY ILMV KQR” (Susko and Roger 2007), where spaces separate amino acids that are placed into the same group. This recoding is one member of a family of recodings, each with a different number of groups, based on clustering of the JTT matrix. The other recoding used by Feuda et al. (2017), KGB-6 and D-6, are based on different matrices and methods.

The alt_recode.py script was used to generate the randomized recoding schemes and apply the recodings to the data. To create the randomized recoding schemes, the amino acids in the SR-6 recoding were randomly reshuffled. This creates new recodings that have the same sized groups as SR-6. The new recodings were, from random-00 to random-03:

MPKE AY IDGQ TRC WNLF SVH

EIFT WL QVPG NKM SCHA RYD

LCQS GK WPTI VRD YEFN MAH

IWQV TY KDLM ESH APCF GRN

To apply these to the data, each amino acid was replaced with the first amino acid in the group. When applying random-00, for example, each instance of R and C would be replaced by a T.

The 20 state matrices are the same across all analyses since they are not recoded. Since all 20 state matrices are the same, variation between 20-state results (as in the left side of each pane of supplementary fig. S9, Supplementary Material online) gives insight into the technical variance of the inference process.

Each new matrix was analyzed with PhyloBayes-MPI. Analyses were run for 1,000 generations, and a 200 generation burnin applied. The resulting tree files and posterior predictive scores were parsed for display with the code in manuscript.rmd.

The statistics presented in supplementary figure S8A, Supplementary Material online were parsed from the Feuda et al. manuscript into the file tidy_table_3.tsv and rendered for display with the code in manuscript.rmd.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.