Applying Mixed-Effects Modeling to Behavioral Economic Demand: An Introduction

Abstract

Behavioral economic demand methodology is increasingly being used in various fields such as substance use and consumer behavior analysis. Traditional analytical techniques to fitting demand data have proven useful yet some of these approaches require preprocessing of data, ignore dependence in the data, and present statistical limitations. We term these approaches “fit to group” and “two stage” with the former interested in group or population level estimates and the latter interested in individual subject estimates. As an extension to these regression techniques, mixed-effect (or multilevel) modeling can serve as an improvement over these traditional methods. Notable benefits include providing simultaneous group (i.e., population) level estimates (with more accurate standard errors) and individual level predictions while accommodating the inclusion of “nonsystematic” response sets and covariates. These models can also accommodate complex experimental designs including repeated measures. The goal of this article is to introduce and provide a high-level overview of mixed-effects modeling techniques applied to behavioral economic demand data. We compare and contrast results from traditional techniques to that of the mixed-effects models across two datasets differing in species and experimental design. We discuss the relative benefits and drawbacks of these approaches and provide access to statistical code and data to support the analytical replicability of the comparisons.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40614-021-00299-7.

Introduction

The concept of behavioral economic demand (hereafter “demand”) has proven useful in a variety of settings including drug addiction (Acuff et al., 2020; Aston & Cassidy, 2019; González-Roz et al., 2019; Kaplan et al., 2018; Strickland, Campbell, et al., 2020a; Strickland & Lacy, 2020), public policy (Hursh & Roma, 2013), health behaviors (Bickel et al., 2016), and others (Gilroy, Kaplan, & Leader, 2018a; Hayashi et al., 2019; Henley et al., 2016; Kaplan et al., 2017; Reed et al., 2016; Strickland, Marks, & Bolin, 2020b; Yates et al., 2019). Demand has been evaluated in both humans and nonhuman animals (Bentzley et al., 2012; Fragale et al., 2017; Strickland & Lacy, 2020). Methods for elucidating trends in consumption and demand have included experiential self-administration (Johnson & Bickel, 2006) and hypothetical responding (Strickland, Campbell, et al., 2020a).

The economic concept of demand characterizes the relationship between the consumption or purchasing of a substance or commodity and some constraint, such as price (Reed et al., 2013). In nonhuman animal self-administration work, demand is captured by (1) increasing the ratio requirement necessary to obtain the reinforcer, and/or (2) decreasing the dose of the reinforcer while keeping the response requirement constant. This ratio of cost (e.g., responses) to benefit (e.g., drug obtained) is referred to as “unit price.”1 In human work, participants may self-administer or endorse their hypothetical consumption of the reinforcers (e.g., alcoholic drinks, cigarettes) across a range of prices. This latter approach is commonly referred to as a hypothetical purchase task (Roma et al., 2015). In behavioral economics rooted in the operant framework, the relation between reinforcer price and consumption typically follows a nonlinear relationship, where increments in low prices are met with relatively little change in consumption and relatively more rapid declines in consumption are observed as prices increase (see Figure 1). A core aspect resulting from fitting a function to the demand curve is the rate of change in elasticity, where elasticity is the proportional change in consumption relative to a proportional change in price (Gilroy et al., 2020).

Fig. 1.

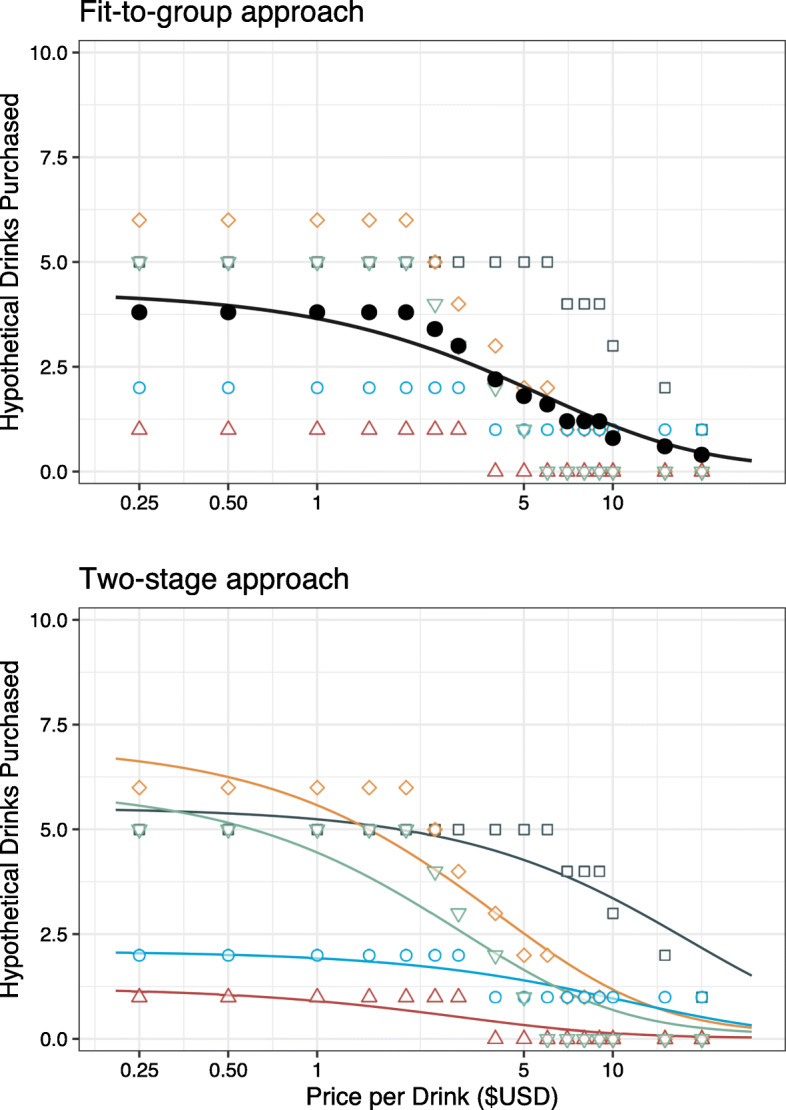
Two Common Nonlinear Regression Methods. Subset of Alcohol Purchase Task data from Kaplan and Reed (2018). Note: Top panel: Individual points in different colors and open shapes and mean values in filled black circles. The black line shows the best fit line using the fit-to-group approach. Notice that only one curve is generated for the entire sample, even though there are many individual points that fall above and below the mean points. Bottom panel: The same individual points as the top panel, now illustrating the first stage of the two-stage approach where one regression line is fit for each participant

An in-depth discussion of the various metrics the demand curve provides and their associations with clinical measures is beyond the scope of this article. For further discussion, we encourage readers to consult other texts (e.g., González-Roz et al., 2019; Kaplan et al., 2019; Martínez-Loredo et al., 2021; Reed et al., 2013). In this article, we will note that change in elasticity is one of several different metrics that a demand curve provides, along with intensity, P_max, O_max, and breakpoint. Whereas change in elasticity is necessarily derived based on the results of regression, intensity, which represents the level of consumption at free or near free costs, can be derived either by regression or by observing the data directly (e.g., how many drinks would someone take if they were free). Breakpoint, or the first price at which nothing is consumed (either by self-report or by not earning the reinforcer) is most often observed directly from the data but can be derived using some equations (e.g., Zhao et al., 2016). Finally, O_max (i.e., maximum expenditure across all the prices) and P_max (i.e., either the price associated with O_max or the price at which the demand curve shifts from an inelastic to elastic portion) can be observed from the data directly (e.g., finding the maximum expenditure among the prices tested) or derived (e.g., via exact solution; Gilroy et al., 2019). Because breakpoint, O_max, and P_max are easily obtained from the data and by existing tools (e.g., Gilroy et al., 2019; Kaplan et al., 2019; http://www.behavioraleconlab.com/resources%2D%2D-tools.html) and do not fundamentally differ due to differences in statistical fitting techniques, the analyses presented here will focus on the two primary indices generated from the demand curve: intensity and change in elasticity.

Just as there is variability in how demand is collected, there is variability in how demand is analyzed (Kaplan et al., 2018; Reed et al., 2020) and demand is typically analyzed in one of two ways. The first approach is to fit a demand model to the overall group-level consumption. We call this the “fit-to-group” approach (see Table 1). The second “two-stage” approach is to fit a demand model separately to each individual dataset (stage 1) and use the resulting individual-subject demand parameter estimates in subsequent analyses (stage 2). The “fit-to-group” approach is shown in the top panel of Fig. 1 and the “two-stage” approach is shown in the bottom panel of Figure 1. Although these approaches are relatively easy to execute, both methods have limitations that behavioral economists conducting this research should be aware of and we will describe the relative benefits and limitations later in this article. To overcome some of these limitations, recent efforts in behavior analysis (Bottini et al., 2020; DeHart & Kaplan, 2019; Gilroy & Kaplan, 2020) and behavioral economics (Acuff et al., 2021; Collins et al., 2014; Hofford et al., 2016; Kaplan et al., 2020; Liao et al., 2013; Powell et al., 2020; Strickland et al., 2016a; Young, 2017; Zhao et al., 2016) have been made to encourage the use of mixed-effects models (i.e., mixed-models, multilevel models), which is a modeling approach that integrates the relative advantages of these two approaches into a single stage analysis. However, we are not aware of any accessible materials specifically tailored for behavioral economists for implementing the mixed-effects modeling approach for behavioral economic demand.

Table 1.

Terms and Definitions

Term	Classic Frequentist Definition	Additional information
Parameter	Values that we do not know but wish to estimate with data. For demand, these are Q0, α, and error variance. Frequentist statistical approaches assume these true population values are unknown constants.
Effect	Effects are parameters that predict the response. In demand, these are Q0 and α.
Fit-to-group approach	Fitting to means: At each cost, compute the average consumption across individuals. Fit a demand model to this single series of averages or mean values. By replacing the full data with sample means, overall variability is ignored. This method is not appropriate for statistical inference and suitable for descriptive, graphical, and theoretical equation testing purposes only. Pooling data: Data from all individuals is included and a single, group-level curve is fit. This variation assumes all data points are independent leading to incorrect standard errors for estimators. This is a fixed effects analysis and in both cases parameters invariant across the whole sample are estimated. Typical demand models exhibit relatively low error variance in this analysis compared to models based on individual subjects (i.e., two-stage-approach).	The fit-to-group approach is one of several terms used to describe this method. In areas outside of behavioral economics, the fit-to-group approach is also referred to as (complete) pooling or pooled regression (see definition to the left and definition associated with fixed effects) and does not preprocess data into means.
Two-stage approach	Fit a demand model to each individual’s data series separately, ignoring any information about the sample as a whole. This first stage produces a collection of fixed effect estimates of α and Q0 for each individual. These estimates subjected to an additional second stage of statistical analysis to make group comparisons (e.g., t-tests, analysis of variance).	The two-stage approach is one of several terms used to describe this method. Other terms include: no pooling (data from each subject is fit separately and no data are “combined” together). One way to think of this approach is to consider it an “amnesia” model where nothing about one subject’s parameters influences another subject’s parameters (McElreath, 2018).
Mixed-effects modeling	Mixed-effect modeling for demand data is the main subject of this article. Mixed-effect models are models that can incorporate both fixed and random effects. In demand, a mixed-effects modeling framework allows the researcher to simultaneously model underlying trends in effects, individual-specific departures from these trends (i.e., random effects), and quantify error variance in the context of a single model.	Mixed-effects modeling is one of several different terms to describe incorporating fixed and random effects. Other terms used include multilevel modeling, hierarchical modeling, and partial-pooled modeling. One benefit of these models is the ability to incorporate additional fixed (and random) effects directly in the model.
Fixed effects	Fixed effects are assumed constant in the broader population from which the observed data are drawn. The sample data are used to produce estimates of these parameters, and the resulting estimates have with some degree of imprecision (i.e., standard error).
Random effects	Random effects induce variability in parameters attributable to differences in how individuals respond. For example, demand analysis might treat α and Q0 as random effects and thus estimate a unique α and Q0 for each participant within a single model. Random effects follow a probability distribution that imparts the ability for these effects to vary among individuals.
Error variance	Error variance describes what is left unaccounted for in the model. Error is quantified by averaging the squared residual (i.e., the vertical difference between observed and expected consumption) across each data point in the analysis. Error variance is an unavoidable aspect of any typical statistical analysis. The only way to eliminate error variance would be to choose a function that exactly replicates the observed data. Because the broad purpose of statistical reasoning is to probabilistically generalize trends to a population larger than the observed data, functions which replicate the exact data are typically overfit for the purpose of generalization and thus statistically they would essentially be useless. This is why any typical analysis incorporates error variance.
Ordinary least squares	The ordinary least squares approach estimates parameters as those values which minimize the error variance. This technique of estimation is used in the fit-to-group and the two-stage approach.
Maximum likelihood estimates	Maximum likelihood estimates are those parameter values that make the observed data “most likely.” In particular, the likelihood function is the joint distribution of the data taken as a function of the parameters. Maximum likelihood searches the entire space of parameter values to determine those values which maximize the likelihood function, and these optimizing values are the maximum likelihood estimates. Maximum likelihood and its variants are essential tools for mixed modeling implementation.

As a result, the goal of the current article is to provide an easily accessible introduction and overview to mixed-effects models in studies of operant demand. A more in-depth discussion regarding the relative merits of the mixed-model approach in demand, including quantitative comparisons can be found in Yu et al. (2014) and others (Collins et al., 2014; Zhao et al., 2016). In the current article, we will first discuss the nonlinear approach to fitting demand curve data and introduce important terminology and concepts (see Table 1). Then, we will orient readers to a previously published human hypothetical Alcohol Purchase Task dataset (Kaplan & Reed, 2018) consisting of a single sample of participants under one experimental condition. Using this dataset, we will illustrate the two common approaches to fitting demand curve data and discuss their relative benefits and limitations. Then, we will provide an overview of nonlinear mixed-effects modeling and apply this approach to the dataset, comparing and contrasting with the earlier approaches. We will then extend these analyses to a nonhuman dataset (Koffarnus et al., 2012) with one sample of monkeys who each self-administered a series of drugs and other reinforcers. Throughout we will conduct the analyses in the open-source R statistical software (R Core Team, 2020). To facilitate open-source documentation (Gilroy & Kaplan, 2019), data and code to perform these analyses can be found at the corresponding author’s GitHub repository.2 That is, all data and code necessary to reproduce the contents of this document, as well as additional figures and tables, are available as an R Markdown document (i.e., a document containing both text and code that can be rendered into other document types) in the GitHub repository. Whereas this article will remain static, the R Markdown document will be updated occasionally based on advances and improvements in the R statistical software. We encourage interested readers to consult and interact with this R Markdown document.

In sum, we hope this article will provide readers a high-level understanding of traditional approaches to analyzing demand curve data and limitations associated with those techniques, while also helping readers understand how mixed-effects modeling can enhance and help move towards best practices in demand analysis. Although we do not expect all readers will spontaneously start conducting all their demand analyses within a mixed-model methodology, we hope this article might also help readers be able to better evaluate demand analyses. In addition, for those researchers who rely on or work closely with statisticians in their work, this article and the associated R Markdown document may serve as an excellent resource for their collaborators. This article, however, is not a strict tutorial on how to implement mixed-effects models nor on how to get started with the R statistical software.3 Those who have some familiarity with R will benefit greatly from executing the code line-by-line in the associated R Markdown document.

Nonlinear Fitting of Demand Curve Data

Demand data are often fitted with a nonlinear exponential decay model using ordinary least squares regression (see Gilroy, Kaplan, Reed, et al., 2018b; Table 1), which estimates parameter values (values that we do not know but wish to estimate with the collected data) by minimizing the squared difference between observed consumption values and the predicted consumption values.4 The differences between the observed and predicted data are referred to as the residuals. Due to the increasing use of hypothetical purchase tasks where zero values are often observed, the following nonlinear model (Koffarnus et al., 2015) has proven useful in characterizing these data:

$$Q_j=Q_0·{10}^{k\left(e^{-\alpha Q_0{C}_j}-1\right)}+{\epsilon }_j,j=1,\dots ,k$$

where Q_j represents quantity of the commodity purchased/consumed at the j-th price point and C_j is the j-th price, and these are known from the data. This model estimates Q₀, representing unconstrained purchasing when C_j = $0.00 (i.e., the intercept), and α, representing the rate of change in elasticity across the demand curve (i.e., most analogous to a slope parameter; see Gilroy et al. (2020) for more on the interpretation of elasticity in operant demand). The term k represents the range of data (e.g., quantities purchased) in logarithmic units and can be solved as a fitted parameter or can be set as a constant by determining a priori an appropriate range. The model is structured as an exponential decay function so the k parameter restricts the range of consumption to a specific lower non-zero asymptote. Finally, the error (ε) term5 is assumed to be normally distributed with mean of 0 and variance of σ². We use this model for illustrative purposes only in this introduction, although mixed-effects models can be implemented on the demand model of the user’s choice (e.g., Gilroy et al., 2021; Liao et al., 2013; Yu et al., 2014), including the nonlinear model from which the above model was formulated (Hursh & Silberberg, 2008). To be clear, the purpose of this introduction is not to compare different quantitative or conceptual models. The purpose of this article is to provide a high-level overview of different statistical fitting techniques regardless of the model chosen. Readers are directed towards Strickland et al. (2016b), Fragale et al. (2017), and Gilroy et al. (2021) for additional information regarding how different models perform.

Example Application: Human Hypothetical Purchase Task

Dataset

The dataset is from Kaplan and Reed (2018) in which participants completed a hypothetical alcohol purchase task (APT; Kaplan et al., 2018). A total of 1,100 participants initially completed the task in full (4 participants were excluded for missing data). An additional 108 participants were not included because they had fewer than three positive consumption values. The APT consisted of 17 prices, expressed as price per drink ($0.00, $0.25, $0.50, $1.00, $1.50, $2.00, $2.50, $3.00, $4.00, $5.00, $6.00, $7.00, $8.00, $9.00, $10.00, $15.00, and $20.00). Participants reported how many alcoholic drinks they would purchase and consume at each of the 17 prices.

Systematicity

Stein et al. (2015) proposed three criteria by which to suggest demand data are systematic. These criteria include (1) trend, (2) bounce, and (3) reversals from zero. We applied these criteria to the data for identifying unsystematic response patterns. Overall, data were highly systematic with a total of 148 unique participants failing at least one of the criteria. Although in typical approaches to analyzing demand these unsystematic responses may be excluded, we will include these cases to demonstrate the robustness of the mixed-model estimates of Q₀ and α. Although we recommend researchers screen for systematicity and report these numbers, the researcher must determine whether to retain these participant datasets in a mixed-effects model analysis. One approach we recommend is to analyze the data including all participants and compare these results to the subset of data that pass the criteria to determine whether the removal of nonsystematic data alters the interpretation of results (Young, 2017).

Common Approaches to Analyzing Demand Curve Data

In our experience with the literature, for the most part there are two common ways to analyze demand curve data. These approaches are differentiated by whether the study is interested in inferring what is common across individuals (fit-to-group approach) or is interested in inferring the degrees and causes of variation among the individuals (two-stage approach). Said another way, the former approach is primarily concerned with generalizing about the broader “population” (as defined in each experiment) whereas the latter approach is primarily concerned with individual trends.

Fit-to-Group Approach

We have observed two ways in which researchers fit a single curve to the overall group when they are interested in making population-level inferences. In the interest of full clarity and the recommendation that researchers specify their method of analysis in future research, we name and distinguish these two ways. However, both of these approaches treat variability in the data incorrectly and thus produce inaccurate measures of precision (i.e., standard errors) for estimators, which leads to misleading and/or incorrect statistical inference.

Fitting to means

The first method relies on averaging individual participant responses within a group at each price, then fitting a single curve through the series of price-specific group means (e.g., Hursh & Silberberg, 2008). This method, therefore, fits a curve to n data points, where n equals the number of prices. By replacing the full data with a series of sample means, overall variability in the data is overlooked. This replacement leads to unrealistic standard errors that are typically much smaller than appropriate. This method can result in astonishingly high R² values (≥ .97), but the “excellent fits” are an outcome of the substantially reduced variability (e.g., see Hursh & Silberberg, 2008; Kaplan et al., 2018). Thus, this method is not appropriate for statistical inference and is suitable for descriptive, graphical, and theoretical equation testing (e.g., Hursh & Silberberg, 2008) purposes only.

Pooling data

The second method relies on “pooling” all participant data together and fitting a single curve through n * k data points, where n equals the number of prices and k equals the number of participants. This method implicitly assumes all data points (even those gathered on the same individual) are independent, which is not realistic. This implicit assumption of independence among all data is not reasonable and leads to incorrect standard errors for estimators.

These two methods of the fit-to-group approach typically result in nearly identical point estimates (e.g., Q₀, α) but differ in the size of the estimates’ standard errors and the model’s residual standard error (i.e., the amount of information “left over” and not accounted for by the model). It is important to recognize that neither of these approaches furnish correct, realistic statistical inference, but fortunately the next two approaches work better. For the purposes of this article, when we refer to the “fit-to-group” approach we are referring to the “pooling” method (i.e., we fit the model to n * k data points), which retains all individual subject data. At the time of this writing, this pooled method is the default in GraphPad Prism (GraphPad Software, San Diego, California USA, www.graphpad.com), a common curve-fitting program used by behavioral economists. In the R package beezdemand (Kaplan et al., 2019), the user must specify the method in which they want the data aggregated (e.g., “mean” or “pooled”).

Illustration of the fit-to-group approach

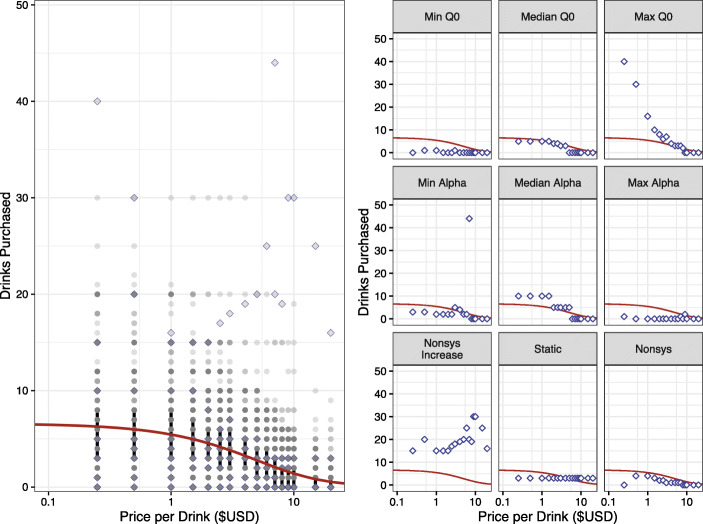
The current APT dataset comprises only one group; therefore this approach will yield one Q₀ and one α for the entire sample (i.e., population-level fixed effect; see Table 1). No individual-specific parameters can be estimated using this approach. We can see the results of this method in Figure 2. The left panel shows the overall fit from this model in red along with the observed individual responses and the vertical lines at each price represent the interquartile range (the middle 50% of the data). The right panel displays a subset of individual participants and their responses. Note how the red lines (the prediction from the model) are identical across individual participant plots because this method only returns population-level estimates of Q₀ and α.

Fig. 2.

Results from the Fit-to-Group Approach. Note: Left panel: Individual points in gray and subset of participants from right panel in open purple diamonds. Black vertical bars indicate the interquartile range between 25% and 75%. The red line shows the best fit line from the fit-to-group approach. Right panel: A subset of participants and their responses. The red line in each pane is identical to the fit-to-group approach demonstrating each participant has the identical predicted values. Visual inspection reveals that the best fit line is inadequate to characterize the data for a number of participant datasets

Benefits and limitations of the fit-to-group approach

A benefit to preprocessing data into means prior to curve fitting is that no data need to be necessarily excluded. Participants who report zero consumption (incompatible with the log scale of analysis in some equations) can still be included as curves are fit to the averaged data, so long as some participants in the sample have greater than zero consumption. As a rule, convergence (i.e., the state when the fitting algorithm obtains a set of parameter estimates based on some predefined threshold) is more easily achieved when the model is fit to averaged consumption data or using the pooled method, effectively smoothing abrupt transitions from one price to the next, which is a response pattern sometimes observed at the individual level (e.g., see “Median α” plot in Figure 2). Notwithstanding these benefits, this approach is limited (beyond the statistical issues we outlined above) in that all participants share the same Q₀ and α values and as such, participant-level comparisons cannot be conducted. This approach does not allow for investigations into how participant-specific demand parameters may relate to other factors (e.g., response to treatment, demographic variables). In addition, any inferences made at the group level should not be assumed to hold true at the individual level, as this is known as the “ecological fallacy” (Robinson, 1950).

Two-Stage Approach

The second commonly used approach is to fit a regression model to each participant. Unlike the fit-to-group approach, the two-stage approach does not try and fit the average response pattern over all participants. Rather, subject-specific Q₀ and α values are estimated in the first stage. The second stage is to make inferences about variation in the fitted $\widehat{\alpha }$ and $\widehat{Q_0}$ values using other statistical tests such as t-tests, analysis of variance, or even mixed-effects models.

Illustration of the two-stage approach

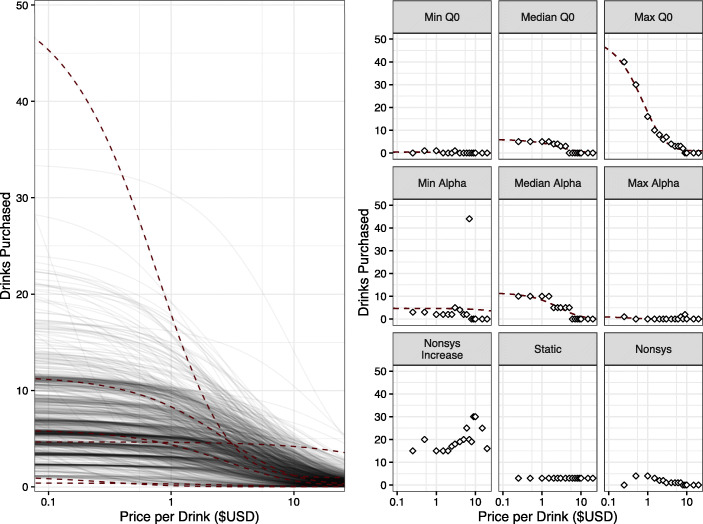
For this dataset (992 participants), a total of 935 demand curves were able to be fit, each resulting in a $\widehat{Q_0}$ and an $\widehat{\alpha }$ value. Unique to the two-stage approach is that on occasion (depending on the task and participant sample) certain participant’s data are especially difficult or unable to be fit using operant demand models. The failure to converge may be due to relatively few positive consumption values, that these data do not follow the “typical” downward sloping function, or that starting values are not appropriately identified. As a result, a total of 57 participants’ data were excluded from this analysis. The left panel of Figure 3 depicts the individual fits to a subset of participants’ data. Contrast Figure 3 with Figure 2. Although this two-stage approach will typically result in predicted lines fitting closest to the data (compared to other approaches), such predictions may not be “generalizable” to either other participants (or individuals in a population) or other experimental conditions. That is, relatively more parameter fits are being conducted than is necessary. This lack of generalizability is partly due to the model being optimized to a small amount of data relative to what else is “known” in the experiment (e.g., Do other participants respond in similar ways to an experimental manipulation? Do participants tend to respond in a manner more like their other responses regardless of other experimental manipulations?).

Fig. 3.

Results from the First Stage Model Fitting from the Two-Stage Approach. Note: Left panel: Individual best fit lines in gray and subset of participants' best fit lines from right panel in maroon dashed line. Note here because of this approach, no overall group-level best fit curve is generated. Right panel: A subset of participants and their responses. The maroon dashed lines show best fit lines for each participant. As illustrated in the bottom three panes, one of the limitations of the two-stage approach is that irregular datasets often times do not yield usable demand metrics. In these cases, no model predictions are obtained and demand parameters from these models cannot be used in subsequent analyses

Benefits and limitations of the two-stage approach

A benefit of the two-stage approach is that demand parameters at the individual participant level can be obtained and used for downstream (i.e., stage 2) comparisons. Several limitations are associated with this approach. One limitation is that demand parameters may be either difficult to estimate or not estimable for some participants with sparse data (e.g., only one or two positive consumption values) or with extreme “step” response patterns with abrupt decreases in consumption from one price to the next. These exclusions limit the scope of inference to those individuals at least somewhat described by the model. That is, if derived parameter values (Q₀ and α) from response patterns that do not follow the “typical” downward sloping function are not able to be estimated using traditional fitting algorithms, then downstream comparisons will be limited to a subset of the overall sample (this limit of scope is similar to when data that only meet systematic inclusion criteria [Stein et al., 2015] are included in an analysis). Another limitation is that individual Q₀ and α are treated as perfectly accurate estimates with no error when these parameters are used in subsequent statistical tests. Of course, the first stage model fits are imperfect, yet none of this uncertainty carries forward to the second stage of analysis. Any second stage analysis will assume the participant-specific demand parameters provided are known with complete certainty and this will provide inaccurate estimates of associated standard errors. This approach also disregards intrasubject correlations across experimental conditions, which can also affect the estimates in subsequent analyses unless special care is taken to model these correlations. Intrasubject correlation refers to the association shared between data points collected within the same subject and is a commonly observed phenomenon in repeated measures studies. This “two-stage” approach—where demand parameters are obtained in the first step and compared in a separate, second step—may result in biased conclusions and generalizability may be compromised. This approach also lacks philosophical appeal because there is no overarching model that relates individual subject parameter estimates to the population average that are of interest to researchers.

Each of these two approaches discussed have their relative benefits and drawbacks. An ideal method of incorporating the benefits of each approach would be conducted in a single stage, use all available data, incorporate covariates and experimental factors (which are usually only addressed at the second stage), and result in “population” level estimates (see Table 1) while also providing individual level predictions and accounting for intrasubject correlation. The mixed-effects modeling approach we describe next has precisely these characteristics.

Mixed-Effects Models

Several key concepts related to the mixed-effects modeling approach need to be discussed. Recall that in the fit-to-group approach we referred to the resulting group-level estimates “fixed effects” because they are considered common to all individuals within a group and thus invariant within the observational unit (i.e., participant). At the highest degrees of generality, fixed effects may describe the underlying population structure and do not vary from one individual to the next.

A “random effect” is a model term that varies from one individual or subgroup to the next. To model this variation, random effects are governed by probability distributions. These random effects can be thought of as deviations around population level fixed effects. By specifying random effects on model parameters (Q₀, α), we allow a given participant to deviate relatively higher or lower around the population average fixed effects. On average, these random-effect deviations will equal 0, which is just a different way of saying that on average, the individual estimates will equal the population level estimates.

The mixed-model approach introduces the ideas of shrinkage and partial pooling, which come into play when the dataset contains values unusually far from the average. For example, suppose a participant in our dataset shows much higher consumption compared to many other participants in the group. In the two-stage approach, the estimated parameters for this participant will be far from the average. Although this may certainly be a valid dataset and response pattern, unusually high (or low) values inflate estimates of individual error variance. The inflated error introduces greater uncertainty the individual’s parameter estimates, which in turn inflates uncertainty in downstream analyses of individual variation in those parameters. In this way, error propagates through each step of the analysis, resulting in confidence intervals of second stage estimates that do not accurately reflect error variance from the first stage. It is important to note that if no additional steps are taken to integrate error over each step, then estimates of the confidence intervals and other inferential statistics are likely to be incorrect. Rather, in a mixed-model approach, information from the entire group is leveraged to shrink the more imprecise estimates back towards the group average. Because this benefit relies on anomalous estimates having a certain degree of imprecision, the estimates may not differ drastically from the two-stage approach in sufficiently large samples. In the mixed-model approach, the fixed effects will more closely reflect the underlying response patterns of the individuals (e.g., these fixed-effect estimates will be influenced less by unusually high or low values) as will the random effects (estimates associated with each participant) be more reflective of the pattern of responding of the group as a whole (see Chapter 13 of McElreath, 2018 for additional examples).

The most extreme case of parameter imprecision occurs when, due to anomalies in the data, one or more parameters do not have a solution (i.e., the likelihood function is flat and the parameter sampling error is infinity). In our example, the center-bottom pane of Figure 3 shows an individual that altogether lacks the variation in responses needed to estimate both k and α. In that case, the model will not converge to a solution, and the resulting parameter estimates may take extreme values that will exert relatively greater influence on parameter estimates and the associated standard errors in the second step of the analysis. The principle of shrinkage applies to these scenarios most of all by forcing nonestimable parameters to take the values of their group means and thus have no influence on subsequent inferences. This effect could be regarded as an automatic mechanism of imputation (i.e., assigning or determining a value based on inference from other data with common characteristics) given insufficiently informative data on some individuals.

On the other hand, standard errors resulting from the fit-to-group approach may be artificially small due to inclusion of all participant data while also treating all data as independent. However, repeated measures on the same subject are typically correlated, thus containing some of the same information. In the presence of a positive correlation, standard errors should be larger than if the data are independent because there is less unique information in the data for a given sample size. This is one reason why standard errors from the fit-to-group approach are unlikely to accurately reflect the true precision in the estimate. In general, small standard errors suggest a high degree of precision in the estimates (even if the estimates are not completely accurate) and this size will affect inferences from statistical tests (e.g., considering if a difference is statistically significant or not). Although the size of the standard errors associated with the fit-to-group approach are unlikely to be accurate, simulation studies have shown standard errors resulting from mixed-effects modeling tend to be more accurate (e.g., Ho et al., 2016; Yu et al., 2014) by including all data and recognizing the correlation present within subjects.

Illustration of Mixed-Effects Models

Adapting the behavioral economic demand model (Eq. 1) for use in the mixed-effects model framework yields:

$$Q_{\mathit{ij}}=Q_{0_i}·{10}^{k\left(e^{-{\alpha }_i{Q}_{0_i}{C}_{\mathit{ij}}}-1\right)}+{\epsilon }_{\mathit{ij}},i=1,\dots ,n,j=1,\dots ,c$$

where here Q_ij represents quantity of the commodity purchased/consumed by the i-th participant at the j-th price point and C_ij is the j-th price associated with the i-th participant (again these are known from the data). $Q_{0_i}$ and α_i represent intensity and rate of change in elasticity associated with the i-th participant. Finally, the error (ε_ij) term is error associated with each individual. This and any other mixed-effects model can be expanded into matrix notation, which can be found in the Appendix.

In the statistical program R, there are several functions and packages for fitting nonlinear mixed-effects models. For the purposes of this article, we use nlme from the nlme package (Pinheiro et al., 2020; see also, e.g., nlmer from the lme4 package). As mentioned above, the code necessary to reproduce all figures and analyses is available in the corresponding author’s GitHub.6

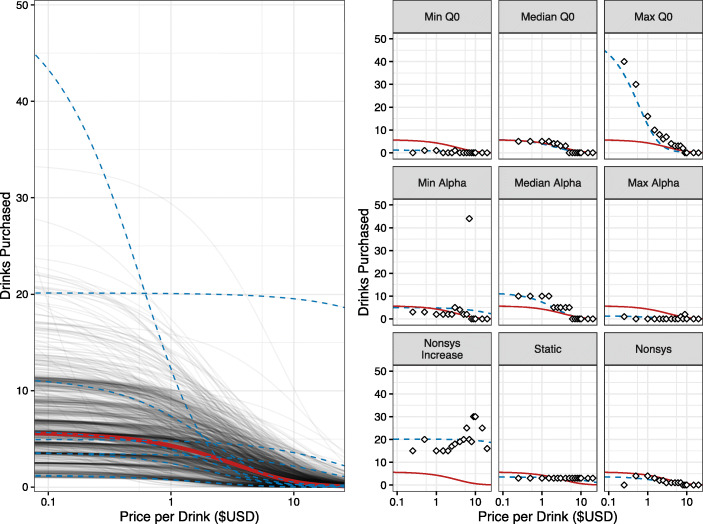
We can see the results of the mixed-effects models in Fig. 4. Several things are important to note. First, notice this model provides group-level fixed-effects predictions (left panel; red prediction line) and participant-level predictions (blue and gray lines) obtained from adding the fixed and random effects together because, again, the random effects are deviations around the group-level fixed effects associated with individual subject data. In the left panel of Figure 4 we see the group-level fixed-effect predictions approximate the average of all the lines and look similar to the left panel of Fig. 2. In the right panel of Fig. 4 we see the participant level predictions match closely to the individual points and look similar to the right panel of Fig. 3. Figure S1 in the supplemental materials shows how these two approaches differ by overlying these lines on the raw consumption data.

Fig. 4.

Results from the Mixed-Effects Model Regression. Note: Left panel: Individual predicted lines in gray, subset of participants' predicted lines from right panel in blue dashed lines, and the overall group's best fit line in solid red. Note here the mixed-effects model provides a population best fit line (i.e., fixed effects) and individual predictions (i.e., random effects), both which leverage data from all participants. Right panel: A subset of participants and their reported responses. The blue dashed lines show predicted values from participants' random effects, which deviate from the overall group’s best fit line (solid red line)

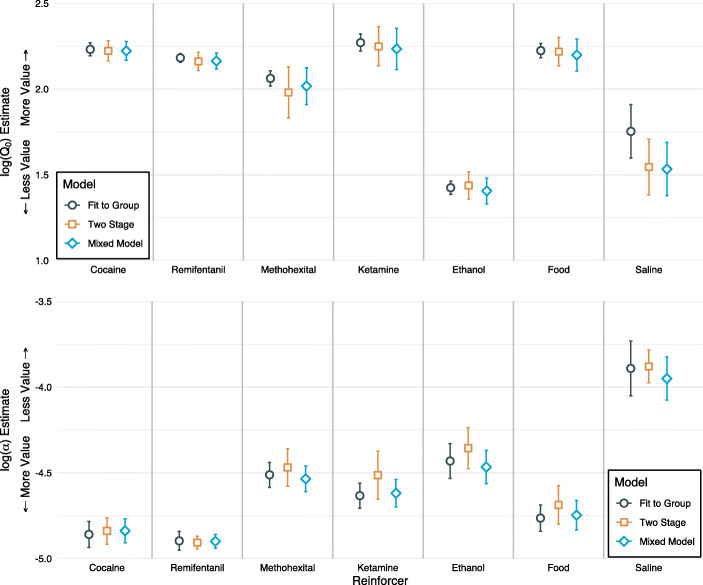
Figure 5 displays the estimates and the standard errors associated with the three approaches for log(Q₀) and log(α). This figure nicely illustrates the relative advantage of the mixed-effects modeling approach with respect to the size and accuracy of the standard errors, as discussed above. On the left side of the graph, the fit-to-group approach (circles) shows substantially smaller standard errors, whereas the middle points (two-stage approach; squares) show larger standard errors. Notice the size of the standard errors associated with the mixed-effects modeling approach (diamonds) is more similar to the two-stage approach, suggesting the fit-to-group approach overestimated the precision of the estimates. The size and accuracy of standard errors are important when conducting statistical tests to determine the extent to which certain values of Q₀ and α may be statistically different across two or more experimental groups or conditions. Too narrow of standard errors are likely to inflate Type I error (erroneously rejecting the null hypothesis and concluding an effect or difference exists when it does not), whereas too wide of standard errors are likely to inflate Type II error (failing to reject the null hypothesis and concluding the difference or effect does not exist when it does). Accuracy and proper size of standard errors is critically important for comparisons such as whether a certain drug maintains a higher abuse liability than another; an example we will illustrate using a nonhuman dataset below.

Fig. 5.

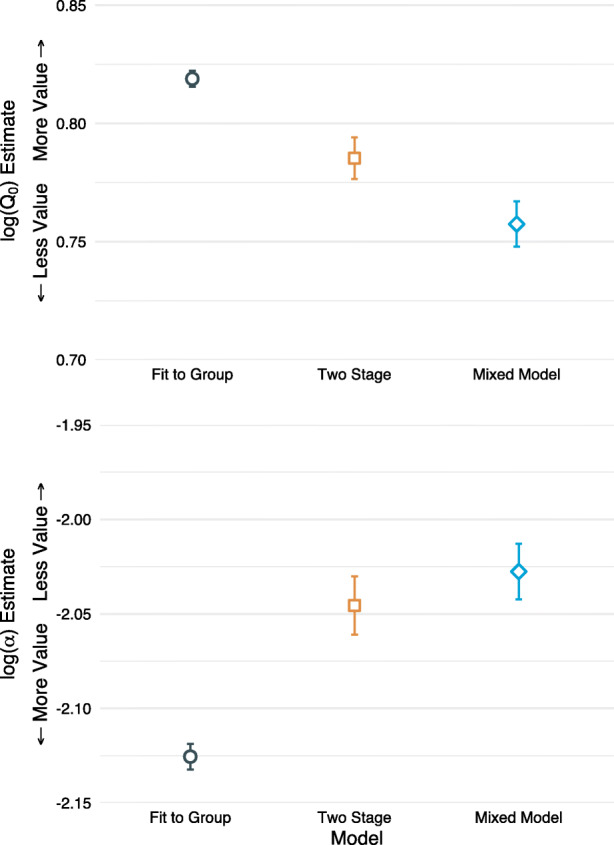
Point Estimates and Standard Errors for log(Q₀) (Top Panel) and log(α) (Bottom Panel) from Each of the Three Fitting Methods. Note: Notice how for this dataset, the fit-to-group approach (circles) tend to underestimate standard errors whereas the two-stage approach (squares) standard errors are larger. The mixed-effects modeling approach is shown in diamonds

Up to this point, we have demonstrated how the mixed-effects model can be applied to a single group and how estimates differ from the fit-to-group and two-stage approaches. We now discuss how these mixed-effects models can be extended to different types of experimental designs, including between subject and within-subject designs.

Extending the Mixed-Effects Model

Between-Subject Designs

Extending the mixed-effects models described here to between-subject designs comparing two or more groups at a single timepoint is straightforward and relatively simple. For these designs, an additional fixed effect representing the between-subject experimental manipulation is added.7 The random effects structure remains the same. Additional covariates or variables of interest can be added in much the same way that a fixed-effect term representing a between-subject experimental manipulation can be added.

Crossed and Nested Designs

Special care must be taken to understand the experimental design and data structure to properly specify how the random effects should be estimated in designs incorporating repeated measurements. Two types of these designs are crossed and nested design. For example, a nested design might measure demand over several days among two groups of participants with one group receiving active medication and the other group receiving placebo. These demand measurements are nested within participant and participant is nested within drug group (active vs. placebo). However, drug group is a between-groups factor because a participant can be in only one group or the other. These types of models are most easily implemented in various mixed-effects modeling packages in the R Statistical Software.

Crossed designs are those in which there are no inherent levels or nesting. For example, a crossed design might be measuring demand over consecutive days among participants who experience two different doses of a drug. Whereas demand measurements are nested within participant (similar to above), all participants experience both doses of the drug. Therefore, there are sources of variation at both the participant level and at the experimental manipulation level but without exclusive nesting. It is important to note that “. . . nested effects are an attribute of the data, not the model” (Errickson, n.d.). There may be experiments where no specific manipulation is implemented. In these cases, a mixed-effects model can still be fit and this model formulation will be relatively simple compared to more complex experimental designs. Here we will illustrate an example of a nonhuman self-administration dataset with no inherent levels of nesting between monkeys and drugs. We will demonstrate how the mixed-effects model can estimate multiple fixed effects of interest (i.e., different reinforcers) and how we can use these models to directly compare differences in demand parameters using null-hypothesis testing.

Example Application: Nonhuman Self-Administration

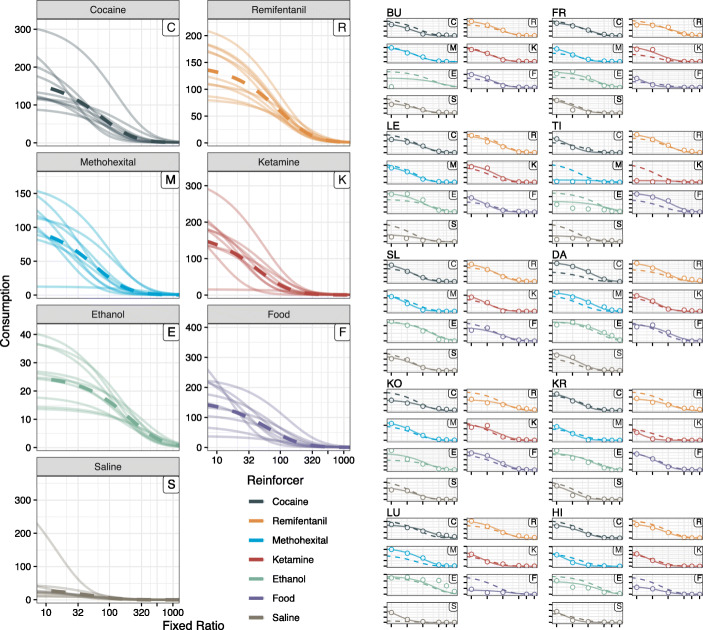
The following example illustrates application of the mixed-effects model to nonhuman animal data published in Koffarnus et al. (2012). The monkeys responded on increasing fixed-ratio schedules (i.e., “prices”) to earn infusions of the various reinforcers. The drugs used included cocaine, ethanol, ketamine, methohexital, and remifentanil. Two additional conditions were tested including food (sucrose pellets) and saline infusions.

As we showed earlier in the article, we will first demonstrate modeling by fitting a single curve to all the data within each reinforcer (fit-to-group approach), as well as fitting to each monkey for each reinforcer (two-stage approach). Finally, we show how the mixed-effects model provides us with both predictions at the reinforcer level, as well as individual monkey level for each reinforcer, and how we can use estimated marginal means (i.e., least-square means) to compare reinforcing efficacy (α) of the reinforcers.

Fit-to-Group and Two-Stage Approaches

Our first approach fits a single demand curve to each of the seven reinforcers. This was the analysis method used in the original article (Koffarnus et al., 2012). The left panel of Figure S2 (Supplemental Materials) displays the fitted curve to each of the reinforcers, the 25% and 75% interquartile range (vertical black lines), and the individual data. The right panel shows these group-level fits within each monkey. Notice here how for some monkeys, the predicted lines are far from the points (e.g., Saline for LE, TI). This discrepancy between the population-level predictions and some proportion of the individual data is similar to what was observed with the APT dataset. Figure 6 displays the estimates and standard errors from the model (circles) and results from the analyses show Saline resulted in the highest log(α) and Cocaine and Remifentanil with the lowest. Other reinforcers were intermediary.

Fig. 6.

Point Estimates and Standard Errors for log(Q₀) (Top Panel) and log(α) (Bottom Panel) from Each of the Three Fitting Methods for Each Reinforcer. Note: Results of the mixed-effects modeling approach (diamonds) are consistent with and provide more accurate standard errors compared to the fit-to-group (circles) and two-stage (squares) approaches

As in the human example, we show the first stage of fitting the model using the two-stage approach. We encounter the same limitations as in the human example; namely, we are unable to derive population-level (i.e., reinforcer-level) estimates of Q₀ or α and we are unable to obtain individual-level fits for BU Ethanol. The left panel of Figure S3 shows the individual monkey fits within each reinforcer and the right panel displays these fits within each monkey and for each reinforcer. As is expected, these lines fit the individual data well. Figure 6 displays the averaged estimates and standard errors from this two-stage approach (squares). The results of this approach are consistent with those of the fit-to-group approach—Saline and Cocaine/Remifentanil showing the highest and lowest log(α), respectively.

Mixed-Effects Model

Figure 7 displays the results of the mixed-effects modeling approach. Both panels show prediction lines from the fixed-effect estimates for each of the drugs (thick lines) and the subject-level predictions from the random effects (light lines). As shown and demonstrated in the human example, the mixed-effects model provides information (i.e., predictions) at the population level (in this case the reinforcer level) as well as at the individual level. In this mixed-effects model, we fit each reinforcer as a nominal (categorical) fixed effect. In models where categorical fixed effects are used, we can use estimated marginal means to compare the values of log(α) for each nominal category. Estimated marginal means provide the mean response values for a model’s factors adjusting for any covariates (Lenth, 2019). In the current models, the estimated marginal means are equivalent to the model effects given there are no covariates for which to account. The values are shown in Figure 6 (diamonds). The results of the mixed-effects model are consistent with the findings from the traditional approaches, suggesting Saline and Cocaine/Remifentanil maintained the highest (lowest reinforcing value) and lowest (highest reinforcing value) log(α), respectively.

Fig. 7.

Results from the Monkey Mixed-Effects Model Regression. Note: Left panel: Dashed colored lines indicate the fixed effect predictions from the mixed model, whereas the solid, transparent colored lines show individual predicted lines as extracted from the random effects. Note here the mixed-effects model provides best fit lines for each reinforcer as well as individual predictions, both which leverage data from all participants and all conditions. Right panel: Individual monkeys and their consumption. The solid, transparent colored lines show predicted values from participants' random effects, which deviate from the overall group means (dashed colored lines)

Comparing Coefficient Values

One additional benefit of fitting these nonlinear mixed-effects demand models is the relative ease in which statistical comparisons can be made. Using the fit-to-group approach, traditional methods of statistical tests are largely limited to those such as the extra sum-of-squares F-test and comparisons in Akaike Information Criteria (AIC, AICc). Using the two-stage approach, comparisons techniques are more numerous and range in complexity (e.g., t-tests, analysis of variance, mixed-effects models). The relative benefits and drawbacks of these comparison methods will not be contrasted here; rather, we note that post-hoc pairwise comparisons can be determined directly from the model and with no need to extract parameter values and use in subsequent tests, as is required in the two-stage approach. For example, we used a powerful and flexible R package (emmeans; Lenth, 2019) to conduct pairwise comparisons (t-tests) of log(α) from the mixed-effects model and adjusted p-values using false discovery rate (see Table S1). The results suggest largely conform to those displayed in the bottom panel of Figure 6. Saline’s log(α) was statistically significantly higher (lower valuation) than all other reinforcers tested. Cocaine and Remifentanil’s log(α)’s were significantly lower (higher valuation) compared to all other reinforcers except Food and each other.

Other Considerations

Beyond the introduction and basic concepts laid out here in the re-analysis of a human APT dataset and nonhuman self-administration dataset, there are additional considerations for fitting mixed-effects models to behavioral economic operant demand data. One consideration is the determination of convergence criteria. Convergence criteria can be relatively lenient (i.e., finding “good enough” estimates and looking no further after the criteria is met) or they can be relatively strict. With data that follow the typical exponential decay function of demand (i.e., systematic), convergence can more easily be obtained under strict criteria. With data that are relatively more “unsystematic,” strict criteria may not result in convergence and these criteria may need to be relaxed (e.g., increasing tolerance). Another reason convergence may not be achieved is because starting values may be too far away from the optimal solution. This problem is also present in traditional approaches to fitting demand curve data (e.g., fit-to-group, two-stage) and nonlinear modeling in general. If convergence issues are encountered, we suggest relaxing the convergence criteria until a solution is determined. Then the estimates from this model may be used as starting values for another model where convergence criteria are tightened once more. Given the complexity of demand curve data and some quantitative models to describe these data, some amount of relaxation of convergence criteria may be acceptable (in our anecdotal experience, we have found tolerance < 0.01 may be an acceptable limit). However, when encountering datasets or models that do show difficulty converging, the researcher should ensure they are specifying the model correctly and may consider reporting difficulty fitting the model.

Finally, mixed-effects models may be solved using Bayesian methods and Markov Chain Monte Carlo (MCMC) as opposed to maximum likelihood estimation. Methods such as these have been successfully applied to behavioral economic demand data (Ho et al., 2016). MCMC has the added benefits of producing empirical posterior (or under frequentist assumptions, sampling) distributions for all parameters in the model and does not suffer from certain convergence problems with maximum likelihood estimation in small samples. Several packages in the R statistical software can solve mixed-effects models using Bayesian methods (e.g., brms, rstanarm). We recommend one package in particular—brms—because this package provides even greater flexibility than nlme or lme4 and the syntax (e.g., writing the model) is highly similar to that of lme4.

Conclusion

Mixed-effects models are becoming a more popular means by which to analyze complex behavioral economic demand data. Although this modeling technique is more complicated than traditional approaches to analysis (i.e., fit-to-group, two-stage), our goal here is to make the motivation, interpretation, and execution of the mixed-effects modeling technique more accessible for the analysis of demand data. In this article we have used two datasets (i.e., a hypothetical purchase task, nonhuman animal self-administration) to (1) illustrate the traditional approaches to demand modeling, (2) discuss the relative benefits and limitations of these approaches, (3) provide an overview of the mixed-effects framework, (4) illustrate the results of this framework, and (5) describe how results from the mixed-effects modeling technique correspond with the traditional methods. In order to facilitate execution of these techniques, we have made a fully reproducible document available at the corresponding author’s GitHub page as a repository. There, this code can be inspected, executed, and adapted for researchers’ own endeavors.

Appendix

A Word about Maximum-Likelihood Estimation

Mixed-effects models are typically solved via maximum-likelihood estimation (see Table 1; note these models can also be solved via other techniques such as Markov Chain Monte Carlo but this is beyond the scope of the current article). A brief overview of this approach follows. First, a likelihood function (which relates to the observed data to the parameters the experimenter is interested in) is evaluated for an initial candidate set of parameters during a single iteration of the model evaluation. The algorithm assesses the shape of the likelihood surface at these parameter values, then picks a new set of parameter values to achieve a higher likelihood in the next iteration. The model continues to iteratively select both individual subject (i.e., random effect) and group (i.e., fixed effect) parameter values and evaluate the likelihood in this manner until the algorithm reaches the maximum of the likelihood function. This final set of random- and fixed-effect values is the set that make the observed data “most likely” to have occurred, and thus serve as the parameter estimates based on the observed data. Restricted maximum likelihood is frequently used for mixed-effects models because it typically produces variance estimates with less bias than traditional maximum likelihood (Liao & Lipsitz, 2002; Meza et al., 2007). However, regular maximum likelihood estimation is used for comparing fixed effects across different mixed-effects models. For more in-depth discussion, see Bates et al. (2015). The primary difference, therefore, between maximum likelihood estimation and nonlinear least squares regression is that the former determines the coefficients that maximize the probability of the observed data, whereas the latter minimizes the error (deviations between the predicted and observed values).

Expanding into Matrix Notation

We expand this in matrix notation to describe how the individual estimates $Q_{0_i}$ and α_i are the sum of the fixed effects β₁ and β₂ and random effects b_1i and b_2i. The random effects b_i are distributed based on a multivariate normal (MN) distribution with mean 0 and variance equal to ψ. Because the b_i random effects index the individual, we assume the sampling distribution of these two effects may be correlated to some extent with each other, which is shown in the expansion of ψ.

$$\left(\genfrac{}{}{0pt}{}{Q_{0_i}}{{\alpha }_i}\right)=\left(\genfrac{}{}{0pt}{}{{\beta }_1}{{\beta }_2}\right)+\left(\genfrac{}{}{0pt}{}{b_{1_i}}{{b_2}_i}\right)=\mathit{\beta }+{\mathit{b}}_{\mathit{i}}\mathit{,}{\mathit{b}}_{\mathit{i}}~\mathit{MN}\left(0,\psi \right),{ϵ}_{\mathit{ij}}~N\left(0,{\sigma }^{2}f\left(p_j\right)\right)$$

and

$$\psi =\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_{12}\\ {\sigma }_{12}& {\sigma }_2^2\end{array}\right)$$

In essence, the fixed effects β₁ and β₂ are analogous to the parameters we obtain from the fit-to-group approach and the random effects b_1i and b_2i are analogous to those we obtain from the two-stage approach. Here the difference is we leverage all the available data; in other words, how does the sample as a whole respond (i.e., fixed effects) and how do individuals respond relative to the sample (i.e., random effects).

Funding

Brent A. Kaplan and Mikhail N. Koffarnus's roles were funded by the National Institute on Alcohol Abuse and Alcoholism of the National Institutes of Health under award number R01 AA026605 to MNK. Kevin McKee’s role was funded by the National Center for Advancing Translational Sciences of the National Institutes of Health, Award Number KL2TR003016. The content of this manuscript is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The funding source did not have a role in writing this manuscript or in the decision to submit it for publication. All authors had full access to the data in this study and the corresponding author had final responsibility for the decision to submit these data for publication.

Data availability

Data is available at: https://github.com/brentkaplan/mixed-effects-demand

Declarations

Conflicts of interest

None of the authors have conflicts of interest to report.

Code availability

Code is available at: https://github.com/brentkaplan/mixed-effects-demand