OptM: estimating the optimal number of migration edges on population trees using Treemix

Abstract

The software Treemix has become extensively used to estimate the number of migration events, or edges (m), on population trees from genome-wide allele frequency data. However, the appropriate number of edges to include remains unclear. Here, I show that an optimal value of m can be inferred from the second-order rate of change in likelihood (Δm) across incremental values of m. Repurposed from its original use to estimate the number of population clusters in the software Structure (ΔK), I show using simulated populations that Δm performs equally as well as current recommendations for Treemix. A demonstration of an empirical dataset from domestic dogs indicates that this method may be preferable in large, complex population histories and can prioritize migration events for subsequent investigation. The method has been implemented in a freely available R package called “OptM” and as a web application (https://rfitak.shinyapps.io/OptM/) to interface directly with the output files of Treemix.

Introduction

One of the fundamental aspects of modern population genetics is using allele-frequency measurements to recreate the various demographic events that define an extant species. However, species and their constituent populations often contain complex demographic histories that may include various instances and fluctuations in migration, population size, and fragmentation. These complex demographic scenarios often require large amounts of genetic data to be sufficiently resolved. Recent advances in sequencing and genotyping technologies [notably for single-nucleotide polymorphisms (SNPs)] have made the generation of genome-wide allele frequency data for multiple populations increasingly tractable [1], thus limiting studies of demographic history primarily to the statistical models and computational capabilities available.

A graph-based model for describing the relationships between populations was recently described by Pickrell and Pritchard [2]. This approach is able to estimate population splits and migration by first building a tree model of the populations then subsequently adding migration events (or edges) between populations that poorly fit the tree model. Pickrell and Pritchard implemented their model in a software package called Treemix, which has been used to infer gene flow between populations of many species including fungi (e.g., [3]), plants (e.g., [4]), reptiles (e.g., [5]), mammals (e.g., [6–9]), and numerous others. Treemix allows the user to model any number of migration edges, and the authors suggested that, based upon simulations, a model that explains 99.8% of variation in the relatedness between populations is sufficiently robust to infer the number of migration edges. Nevertheless, real-world demographic histories are often more complex and this approach may underestimate or overestimate the number of migrations edges. For example, when the ratio of the number of admixed to unadmixed populations is quite large, Treemix may simply account for this by shortening the branch to the unadmixed populations in the tree rather than adding multiple migration edges [2].

In this study, I propose the application of an ad hoc statistic similar to the method described by Evanno et al. [10] for the software Structure [11] to determine the optimal number of migration events to include when using Treemix. I demonstrate on simulated populations that this approach performs equally as well as the 99.8% variation threshold suggested by Pickrell and Pritchard [2]. However, using an empirical example of domestic dogs and wolves, I show the utility of this approach under large, complex demographic histories when the recommended threshold becomes difficult to obtain.

Materials and methods

Approach

Inferring the most probable number of migration events in a model, or m, is akin to inferring the most likely number of populations, K, when using the software Structure [11]. Structure is perhaps the most widely used program for inferring population structure and admixture [12], and over the past two decades has become a standardized tool for population genetic studies [13]. When using Structure, it was recommended to infer the most likely value for K by (i) performing multiple runs with various values for K, (ii) plotting the log posterior probability of the data given K (“$\ln P\left(D\right)$,” or simply “L(K)”) for each run, and (iii) observing the value of K where L(K) reaches a plateau and/or the variance begins to increase [14]. However, Evanno et al. [10] demonstrated that this approach may not be accurate and proposed a new method that improves the ability to predict the true value of K. The method proposed by Evanno et al. calculated an ad hoc statistic, ΔK, based upon the second-order rate of change in L(K).

I propose here that the same procedure proposed by Evanno et al. can be used to estimate the most likely value for m when using Treemix. The only difference is m can have values ≥0 whereas K must be ≥1. The software Treemix calculates composite log-likelihoods for each run using models both without migration edges (m = 0) and with m edges. I define these likelihoods as L(m) and they are analogous to the L(K) values produced by Structure. By performing multiple runs with different values for m, the same methodology to calculate ΔK can be used to calculate its migration equivalent, Δm. I refer users to Evanno et al. [10] and Supplementary File S1 for a complete description of the model and its calculations. I have implemented the method in a software package called OptM v0.1.5 available for the R programming language through CRAN [15] (https://cran.r-project.org); designed specifically for use with the output files produced by Treemix v1.13 (https://bitbucket.org/nygcresearch/treemix; RRID: SCR_021636). OptM was built originally using R v3.2.2, but has been tested extensively to function properly on various platforms (i.e., Windows and Unix) through the current version R v4.1.1. Its dependencies include the packages SiZer (≥v0.1-4), stats, splines, grDevices, and boot (≥v1.3-20). With regard to the input files, OptM analyzes all the Treemix output files in a given folder with the suffixes “.llik,” “.cov.gz,” and “.modelcov.gz” generated by default using Treemix. OptM generates an output table with the calculations and an estimated optimal value of m and includes a plotting function “plot_optM” to visualize the results and produce publication-ready figures. Alternatively, OptM incorporates added functionality to estimate m using change points estimated from threshold models often employed in ecology (see Ref. [16] and Supplementary File S1). OptM can fit parametric models such as piecewise linear, bent cable, simple exponential, and non-linear least squares to the L(m) values across runs and compare them with the Akaike information criterion [17]. The non-parametric “significant zero crossings” method (SiZer) [16] is also available for comparison purposes.

Testing using simulations

I generated four simulated datasets each comprising 20 populations that evolved according to a serial bottleneck scenario using the whole-genome coalescent simulator Argon v0.1 (https://palamaralab.github.io/software/argon/; RRID: SCR_021635) [18]. The population graph without any migration events was identical to that in Pickrell and Pritchard [2] (Supplementary Fig. S1). The simulations each assumed an effective population size of 10⁴ and all populations are descended from a common ancestor 2000 generations in the past. However, within each simulated dataset, 1, 3, 5, or 8 migration events were included 100 generations in the past. The source and recipient population for each migration event were selected at random without replacement, and the recipient population received 30% of its genetic ancestry from the source population. Each simulation produced 60 chromosomes (30 diploid individuals) of 250 megabases for each of the 20 populations. The simulations included a mutation rate of 10⁻⁸ substitutions $·$ site⁻¹$·$ generation⁻¹ and recombination rate of 10⁻⁸ recombination $·$ site⁻¹$·$ generation⁻¹. The simulation parameters were identical to that of Pickrell and Pritchard [2]—resulting in patterns of diversity and linkage disequilibrium consistent with that of SNP genotype data for many modern human datasets [19] (see Supplementary File S1). To further recapitulate patterns in observed datasets, all loci with a minimum allele frequency <0.05 were removed using Vcftools v0.1.13 (https://vcftools.github.io/index.html; RRID: SCR_001235) [20]. The resulting datasets were run using Treemix v1.13 with a global set of rearrangements (-global), and a randomly selected window size (-k) of between 100 and 1000 SNPs (50 SNP increments). The number of migration events (-m) varied between 1 and 10 [Treemix natively calculates the L(m = 0) for each run] and 10 replicates were performed for each value of m. Although the parameter “-k” can be fixed across runs, the simulated datasets generally created strong signals that resulted in convergence upon the same composite likelihood across all runs for each value of m. This produced a standard deviation across runs of zero, and thus Δm becomes undefined. In this scenario OptM will generate a warning to the user, but the practice of permuting across “-k” or across the set of input SNPs will improve the reliability of estimates of Δm. The resulting likelihood files produced by Treemix were analyzed and visualized using the functions in OptM. See Supplementary File S1 for a complete description of the methods including computer code used.

Empirical example

I applied this method to an empirical dataset composed of 532 domestic dogs from 48 breeds and 15 wolves genotyped for ∼174,000 SNPs on the CanineHD BeadChip [21, 22]. In order to accurately estimate allele frequencies, we removed breeds with less than eight individuals genotyped. The SNPs were filtered to include only autosomal loci with a minimum allele frequency ≥0.05 and a genotyping rate ≥0.9 using Plink v1.07 (https://zzz.bwh.harvard.edu/plink/; RRID: SCR_001757) [23]. Individuals with a genotyping rate ≤0.9 were omitted from the analysis. The resulting dataset was run using Treemix v1.13 with the same parameters as above with the exceptions of a window size (-k) of 500 SNPs and number of migration events (-m) between 1 and 40. Again, 10 replicates were performed for each value of m and the resulting files were analyzed using OptM (see Supplementary File S1).

Results and discussion

Simulated examples

Four simulated datasets containing either 1 (M1), 3 (M3), 5 (M5), or 8 (M8) migration events from a serial bottleneck model of 20 populations were generated (Supplementary Fig. S1). Each migration edge was simulated with 30% admixture (referred to as “migration weight,” or $\widehat{w}$, by Pickrell and Pritchard [2]), which Treemix was able to accurately infer (range of $\widehat{w}$ 27% - 33%; Table 1) in all datasets. However, in M5, Treemix incorrectly reported a migration edge from populations 11 → 4 rather than populations 6 → 3 in all iterations, and in M8 a single iteration incorrectly assigned a migration edge between populations 15 → 10 rather than populations 6 → 3 (Table 1). In M8, Treemix reported in 9/10 iterations migration from the common ancestor of populations 19 and 20 into population 10, rather than populations 19 → 10 (Table 1). The latter error is understandable as populations 19 and 20 only separated ten generations previously. Nevertheless, Treemix was able to accurately and consistently infer the correct migration edges across the simulated datasets and is a testament to the utility of this algorithm in inferring population histories.

Table 1:

Admixture proportions inferred by Treemix for 1 (M1), 3 (M3), 5 (M5), or 8 (M8) simulated migration edges (rows)

Migration edge	M1	M3	M5	M8
13 → 5	0.30 (0.0011)	0.30 (0.00062)	0.32 (0.0016)	0.29 (0.0036)
4 → 12		0.29 (0.00015)	0.27 (0.0014)	0.28 (0.00024)
7 → 16		0.30 (0.00037)	0.31 (0.023)	0.31 (0.00024)
6 → 3			0.33 (0.0011)a	0.31 (0.00098)b
9 → 17			0.28 (0.0086)	0.29 (0.00027)
15 → 1				0.29 (0.076)
14 → 8				0.29 (0.00029)
19 → 10				0.30 (0.012)c

The direction of the simulated migration is reported in the first column (source → sink). The standard deviation from 10 iterations is shown within parentheses.

^aTreemix incorrectly inferred the migration edge 11 → 4 rather than 6 → 3 for all 10 iterations.

^bTreemix correctly inferred the 6 → 3 migration edge in 9/10 iterations, but one iteration incorrectly reported a 15 → 10 edge.

^cIn 9/10 iterations, Treemix reported the source of this migration edge to be the common ancestor of 19 and 20, or 19/20 → 10.

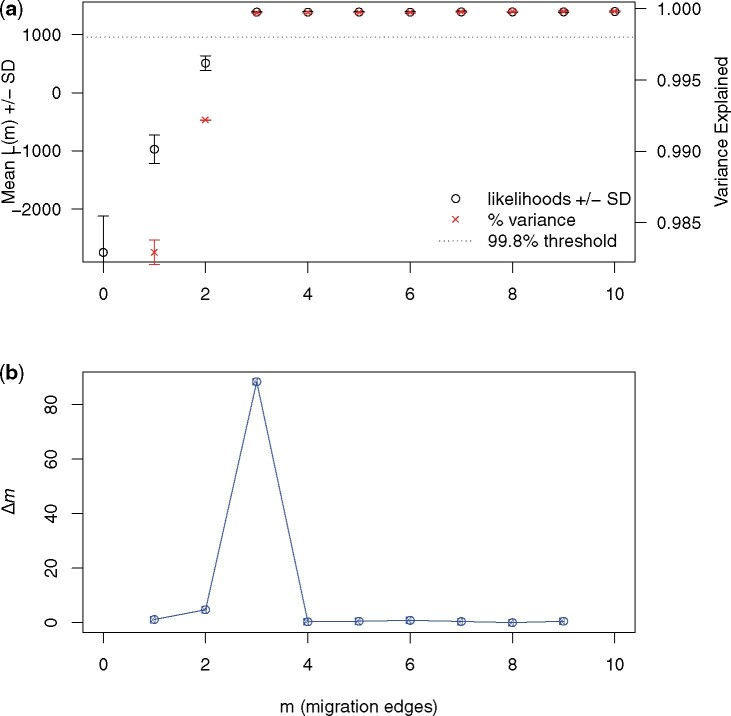
When using the method in OptM to infer the optimal value for m from 0 to 10 simulated migration edges, the highest value for the second-order rate of change in likelihood, or Δm, identified the correct number of simulated migration edges in all four datasets (Fig. 1, Supplementary Fig. S2). The inferences based on Δm for datasets M3, M5, and M8 were equivalent to those suggested by the authors of Treemix based upon the 99.8% variation cutoff [2]. However, for dataset M1, which had only one migration edge, the 99.8% threshold was exceeded even when no migration edges were inferred, but OptM was able to correctly identify this situation. As a result, OptM may outperform the previous method when the true number of migration edges is very small. OptM was also used to fit piecewise linear, bent cable, simple exponential, and non-linear least squares threshold models to L(m) (Supplementary Table S1 and Fig. S3), albeit the Δm method outperformed these models.

Figure 1:

The output produced by OptM for the simulated dataset with m = 3 migration edges. (a) The mean and standard deviation (SD) across 10 iterations for the composite likelihood L(m) (left axis, black circles) and proportion of variance explained (right axis, red “x”s). The 99.8% threshold (horizontal dotted line) is that recommended by Pickrell and Pritchard [2]. (b) The second-order rate of change (Δm) across values of m.

Empirical example

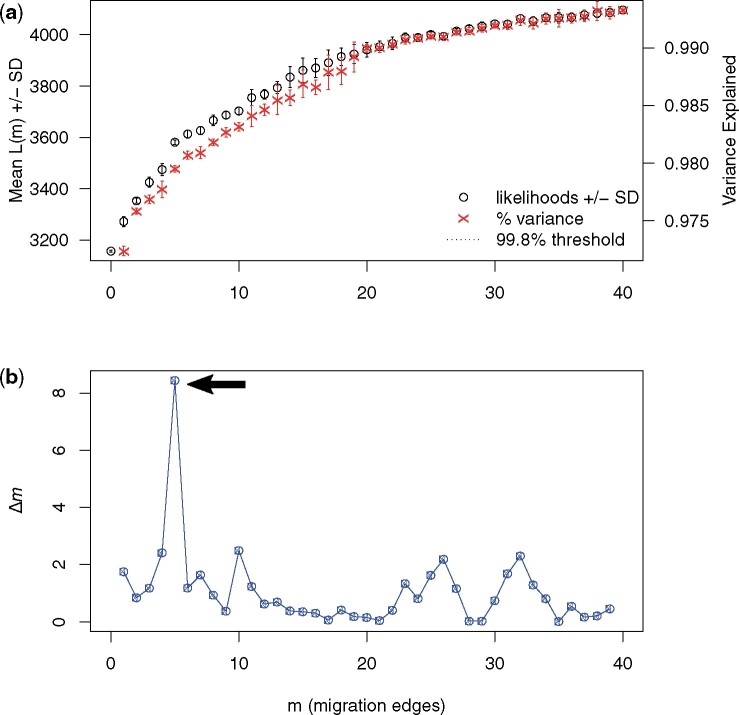
I ran Treemix on an empirical dataset that, after filtering, contained 496 domestic dogs from 34 breeds, 12 wolves, and >138 000 SNPs. I ran 400 instances of Treemix, 10 iterations for m = 1–40 migration edges. Even after including 40 migration edges, the 99.8% recommended threshold for stopping the addition of migration edges was not met (Fig. 2a). Rather, OptM suggested that five migration edges should be optimally included (Figs 2b and 3).

Figure 2:

The output produced by OptM for an empirical dataset of domestic dogs. A total of 10 iterations were run for each possible number of migration edges, m = 1–40. (a) The mean and standard deviation (SD) for the composite likelihood L(m) (left axis, black circles) and proportion of variance explained (right axis, red “x”s). The 99.8% threshold is that recommended by Pickrell and Pritchard [2], but not visible here because the threshold is still not met at m = 40 edges. OptM produces a warning to notify the user that this threshold is not visible. (b) The second-order rate of change (Δm) across values of m. The arrow indicates the peak in Δm at m = 5 edges.

Figure 3:

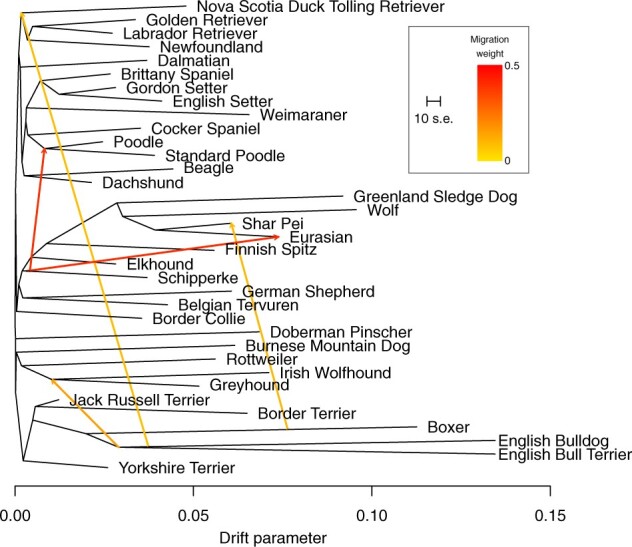
The tree structure of the graph inferred by Treemix for the 34 dog breeds and gray wolf populations. Five migration edges were allowed as inferred by OptM. The migration edges are colored according to their weight ($\widehat{w}$). The scale bar indicates ten times the average standard error of the values in the covariance matrix.

Although each of the 10 iterations at m = 5 inferred a slightly different set of migration edges, five migrations edges were substantially more common than the others (Table 2). These included $\widehat{w}$ = 9.3% (SD 0.68%) from the boxer into the Shar-Pei, similar to the $\widehat{w}$ = 8% reported by Pickrell and Pritchard [2] for the same edge using a different set of SNPs. This edge is likely the result of the Shar-Pei being considered an ancient breed [24, 25] and the fact that most canine SNPs on commercial genotyping chips were ascertained from the boxer’s genome [2, 22]. Extensive gene flow from the Schipperke into the Eurasian ($\widehat{w}$ = 41% SD 0.36%) is consistent with the known European × East Asian spitz-type hybrid origin of the Eurasian and has been observed elsewhere [25]. Gene flow from the Schipperke into the Poodle ($\widehat{w}$ = 41% SD 0.48%) is less clear, as this migration edge has yet to be described, but could be a result of the fact that 65.1% of SNPs on the CanineHD beadchip were ascertained from a Boxer-Poodle comparison [22]. The remaining two notable migration edges were from the English Bulldog into the ancestor of the Nova Scotia Duck Tolling Retriever, Labrador Retriever, Golden Retriever, and Newfoundland ($\widehat{w}$ = 8.5% SD 0.23%) and both the English Bulldog + English Bull Terrier into the Irish Wolfhound and Greyhound ($\widehat{w}$ = 21% SD 0.63%). All of the breeds included in these two migration edges originate from the British Isles, and probably illustrate the many cross-breeding events that took place to create hybrid varieties that would excel in dog fighting contests prior to the strict studbook keeping in the middle to late nineteenth century [8, 26, 27]. All migration edges inferred by Treemix appeared early on the various branches (Fig. 3), and thus most likely represent ancient gene flow that predates modern breed development and the complex nature of domestic dog evolutionary history.

Table 2:

Summary of all the migrations edges inferred across 10 iterations at m = 5 (the optimal number inferred by OptM)

Source lineage	Recipient lineage	$\widehat{\mathit{w}}$ (SD)	Number of iterations
Box	ShP	0.093 (0.0068)	9/10
Sci	Eur	0.41 (0.0036)	9/10
Sci	StP+PdL	0.41 (0.0048)	9/10
EBD	NSD+((LRe+GRe)+NFd)	0.085 (0.0023)	8/10
EBD+EBT	IrW+Gry	0.21 (0.0063)	7/10
EBT	IrW+Gry	0.16 (0.00094)	2/10
EBD+EBT	NSD+((GRe +LRe)+NFd)	0.11 (NA)	1/10
EBD+EBT	(Rtw+BMD)+(NSD+((GRe+LRe)+NFd))	0.086 (NA)	1/10
EBD	ShP	0.046 (NA)	1/10
EBD	IrW+Gry	0.15 (NA)	1/10
ShP	Box	0.10 (NA)	1/10
StP	(((GSl+(Wlf+(ShP+Eur)))+FSp)+Elk)+Sci	0.15 (NA)	1/10
StP	((((Wlf+(ShP+Eur))+GSl)+FSp)+Elk)+Sci	0.17 (NA)	1/10

$\widehat{w}$, migration weight, Breed abbreviations are as follows: Box, Boxer; BMD, Burnese Mountain Dog; Elk, Elkhound; EBD, English Bulldog; EBT, English Bull Terrier; Eur, Eurasian; FSp, Finnish Spitz; GRe, Golden Retriever; GSl, Greenland Sledge Dog; Gry, Greyhound; IrW, Irish Wolfhound; LRe, Labrador Retriever; NFd, Newfoundland; NSD, Nova Scotia Duck Tolling Retriever; PdL, Poodle; Rtw, Rottweiler; Sci, Schipperke; ShP, Shar-Pei; StP, Standard Poodle; Wlf, wolf.

Conclusions

I have demonstrated here that the method of Evanno et al. [10] developed for inferring the number of population clusters from Structure and implemented in OptM can be repurposed to infer the optimal number of migration edges using Treemix. Using simulated population genomic data, OptM performs equally as well as the currently recommended threshold of 99.8% variation explained. However, when tested on empirical data of numerous populations and complex evolutionary history (where the true m is quite large), OptM can suggest a quantitative and producible measure of the optimal number of migration edges that best explain the tree graph. It must be noted that OptM is not attempting to infer the actual number of migration edges, although in less complex scenarios this is possible, but rather a reduced number that can be prioritized for their ability to best improve the fit to the tree model.

Although OptM is very fast, it requires multiple runs of the Treemix algorithm which can be computationally intensive, especially for large values of m. However, multiple iterations of Treemix, especially while varying the SNP-block length (-k) and/or bootstrapped across the input SNPs, can reduce the effects of spurious or weak migration edges. Furthermore, the relative height of various peaks in Δm can indicate other values for m worth exploring, although at less explanatory power than the maximum Δm [10]. The method of OptM does not resolve occasional shortcomings already described for ΔK (i.e., the K = 2 conundrum) [28] or Treemix, notably when migration is between closely related populations without outgroups, such as incorrect directionality, admixture in populations related to a truly admixed population, and underestimated migration weights when admixture proportions are high [2]. Nevertheless, with the ever-increasing availability of population genomic data for a variety of species, OptM serves a valuable purpose in providing a robust and reproducible tool for inferring the optimal number of migration events that can best explain extant levels of genetic variation from complex population histories.

Supplementary data

Supplementary data is available at Biology Methods and Protocols online.

Data availability

OptM v0.1.5 is currently available through CRAN (https://cran.r-project.org/web/packages/OptM) or web application (https://rfitak.shinyapps.io/OptM/; Supplementary Fig. S4). Additional computer code for generating the simulated datasets and running OptM is available in Supplementary File S1, and an example configuration file for the simulations can be found in Supplementary File S2. The domestic dog dataset from Vaysse et al. [22] is publicly available at http://dogs.genouest.org/SWEEP.dir/Supplemental.html.