Dirac equation and thermodynamic properties with the Modified Kratzer potential

Abstract

In this work, we present the analytical solutions of Dirac equation for modified Kratzer potential in the pseudospin and spin symmetry limits using the formula method. The energies of the pseudospin and spin symmetry limit are obtained analytically and numerically. The numerical values are compared with those obtained in literature. Furthermore, we study the thermodynamic properties of some diatomic molecules within the nonrelativistic spin symmetry limits.

Dirac equation; Modified Kratzer potential; Formular method; Thermodynamic properties.

1. Introduction

The significance of spin and pseudospin symmetries in Dirac equation and their contributions in nuclear and Hadron physics is worthy of note [1, 2, 3, 4]. As a result, some authors have discussed Dirac equation under various interactions [5, 6, 7, 8, 9, 10].

Over the years, thermodynamic properties of various systems have been reported. For instance, Supermi et al. [11], studied thermodynamic properties of some molecules with q-deformed modified Poschl-Teller plus Manning Rosen potential. Ikot et al. [12] discussed thermodynamic properties of screened Kratzer potential. Thermodynamic properties have been investigated under the improved Rosen-Morse model [13]. In a recent study, Njoku et al. [14], investigated the thermodynamics of the Hua potential. Other reports of thermodynamic properties can be found in Refs. [15, 16, 17, 18, 19, 20, 21].

Motivated by previous reports on Dirac equation and the study of thermodynamic properties, we present here, the solutions of Dirac equation with modified Kratzer potential (MKP) using the formula method [22]. We further discuss results on thermodynamic properties of the $X^1{\sum }_g^{+}$ state of chlorine (Cl₂) molecule and $X^1{\sum }_g^{+}$ state of Nitrogen (N₂) molecule. The MKP [23] is derived from a standard Kratzer potential [24]. This potential serves as a model for vibrations in diatomic molecules [25, 26, 27], and therefore deserves studying. The MKP studied here is of the form

$$V\left(r\right)=D_e{\left(\frac{r-r_e}{r}\right)}^2\text{,}$$ (1)

where $D_e,r_e$ and $r$ are the dissociation energy, the equilibrium internuclear separation and the internuclear separation.

2. Spin and pseudospin symmetries of Dirac equation

The Dirac equation with scalar, S(r) and vector potential, V(r) is given as $(c=\hslash =1)$ [28].

$$\begin{array}{l}{\hat{H}}_D\Psi \left(r\right)=E_{n\kappa }\Psi \left(r\right)\\ {\hat{H}}_D=\alpha .\overrightarrow{p}+\beta (\mu +S\left(r\right))+V\left(r\right)\end{array}\}\text{,}$$ (2)

where $\mu ,E_{n\kappa },\overrightarrow{p}=-i\hslash \overrightarrow{\nabla }$are the reduced mass, relativistic energy of the system, and momentum operator respectively. $\alpha ,\beta$ are the 4 × 4 Dirac matrices given by

$$\alpha =\left(\begin{array}{ll}0\hfill & {\sigma }_i\hfill \\ {\sigma }_i\hfill & 0\hfill \end{array}\right),\beta =\left(\begin{array}{ll}I\hfill & 0\hfill \\ 0\hfill & -I\hfill \end{array}\right)$$

where I is the 2 × 2 identity matrix and ${\sigma }_i$ the Pauli matrices defined by

$${\sigma }_1=\left(\begin{array}{ll}0\hfill & 1\hfill \\ 1\hfill & 0\hfill \end{array}\right),{\sigma }_2=\left(\begin{array}{ll}0\hfill & -i\hfill \\ i\hfill & 0\hfill \end{array}\right),{\sigma }_3=\left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & -1\hfill \end{array}\right)$$

The spinor, $\Psi \left(r\right)$ can be written as

$$\Psi \left(r\right)=\frac{1}{r}\left(\begin{array}{ll}{F}_{n\kappa }\left(r\right)\hfill & Y_{jm}^l(\theta ,\phi )\hfill \\ i{G}_{n\kappa }\left(r\right)\hfill & Y_{jm}^{\tilde{l}}(\theta ,\phi )\hfill \end{array}\right)\text{,}$$ (3)

where $F_{n\kappa }\left(r\right)$ and $G_{n\kappa }\left(r\right)$ radial wave functions represent the upper and lower components of the Dirac spinors. $Y_{jm}^l(\theta ,\phi )$ is the spherical harmonic of the spin component and $Y_{jm}^{\tilde{l}}(\theta ,\phi )$ is the spherical harmonic of the pseudo spin component. $l$ and $\tilde{l}$are the orbital and pseudo-orbital quantum numbers, while $\kappa$ and m are the spin-orbit coupling operator and the projection on z-axis. If the spinor in Eq. (3) is used, the following coupled radial differential equations from the Dirac equation is obtained.

$$\begin{array}{l}\left(\frac{d}{dr}-\frac{\kappa }{r}\right)G_{n\kappa }\left(r\right)=(\mu -E_{n\kappa }+\Sigma \left(r\right))F_{n\kappa }\left(r\right)\\ \left(\frac{d}{dr}+\frac{\kappa }{r}\right)F_{n\kappa }\left(r\right)=(\mu +E_{n\kappa }-\Delta \left(r\right))G_{n\kappa }\left(r\right)\end{array}\}\text{.}$$ (4)

Solving the coupled differential equations in Eq. (4), we obtain two uncoupled equations

$$\frac{d^2{F}_{n\kappa }\left(r\right)}{d{r}^2}-\frac{\kappa (\kappa +1)}{r^2}{F}_{n\kappa }\left(r\right)-(\mu -E_{n\kappa }+\Sigma \left(r\right))(\mu +E_{n\kappa }-\Delta \left(r\right))F_{n\kappa }\left(r\right)+\frac{\frac{d\Delta \left(r\right)}{dr}\left(\frac{d}{dr}+\frac{\kappa }{r}\right)F_{n\kappa }\left(r\right)}{(\mu +E_{n\kappa }-\Delta \left(r\right))}=0$$ (5)

$$\frac{d^2{G}_{n\kappa }\left(r\right))}{d{r}^2}-\frac{\kappa (\kappa -1)}{r^2}{G}_{n\kappa }\left(r\right)-(\mu -E_{n\kappa }+\Sigma (r\left)\right)(\mu +E_{n\kappa }-\Delta (r\left)\right)G_{n\kappa }\left(r\right)-\frac{\frac{d\Sigma \left(r\right)}{dr}\left(\frac{d}{dr}-\frac{\kappa }{r}\right)G_{n\kappa }\left(r\right))}{(\mu -E_{n\kappa }+\Sigma (r\left)\right)}=0,$$ (6)

where, $\kappa (\kappa +1)=l(l+1),\kappa (\kappa -1)=\tilde{l}(\tilde{l}+1),\Delta \left(r\right)=V\left(r\right)-S\left(r\right),\Sigma \left(r\right)=V\left(r\right)+S\left(r\right)$.

Eqs. (5) and (6) correspond respectively to the spin and the pseudospin and spin symmetry case.

2.1. Pseudospin symmetry limit

The pseudospin symmetry limit coincides with the case where $\frac{d\sum \left(r\right)}{dr}=0,\sum \left(r\right)=C_{ps}$ = constant. With this condition, Eq. (6) reduces to

$$\frac{d^2{G}_{n\kappa }\left(r\right))}{d{r}^2}-\frac{\kappa (\kappa -1)}{r^2}{G}_{n\kappa }\left(r\right)-(\mu -E_{n\kappa }+C_{ps})(\mu +E_{n\kappa }-\Delta (r\left)\right)G_{n\kappa }\left(r\right)=0\text{,}$$ (7)

where $\kappa =-\tilde{l}$ and $\kappa =\tilde{l}+1$ for $\kappa <0$ and $\kappa >0$, respectively. $\Delta \left(r\right)$ is set as the modified Kratzer potential, changing Eq. (7) to

$$\frac{d^2{G}_{n\kappa }\left(r\right))}{d{r}^2}-\frac{\kappa (\kappa -1)}{r^2}{G}_{n\kappa }\left(r\right)-\left(\mu -E_{n\kappa }+C_{ps}\right)\left(\mu +E_{n\kappa }-D_e{\left(\frac{r-r_e}{r}\right)}^2\right)G_{n\kappa }\left(r\right)=0\text{.}$$ (8)

2.2. Spin symmetry limit

In the spin symmetry limit, $\frac{d\Delta \left(r\right)}{dr}=0;\Delta \left(r\right)=C_s=$constant. Thus, Eq. (5) reduces to

$$\frac{d^2{F}_{n\kappa }\left(r\right)}{d{r}^2}-\frac{\kappa (\kappa +1)}{r^2}{F}_{n\kappa }\left(r\right)-(\mu -E_{n\kappa }+\Sigma \left(r\right))(\mu +E_{n\kappa }-C_s)F_{n\kappa }\left(r\right)=0\text{,}$$ (9)

where $\kappa =l$ and $\kappa =-l-1$ for $\kappa <0$ and $\kappa >0$, respectively. $\sum \left(r\right)$is set as the modified Kratzer potential, changing Eq. (9) to

$$\frac{d^2{F}_{n\kappa }\left(r\right)}{d{r}^2}-\frac{\kappa (\kappa +1)}{r^2}{F}_{n\kappa }\left(r\right)-\left(\mu -E_{n\kappa }+D_e{\left(\frac{r_e-r}{r}\right)}^2\right)\left(\mu +E_{n\kappa }-C_s\right)F_{n\kappa }\left(r\right)=0\text{.}$$ (10)

To solve Eqs. (8) and (10), we employ the formula method, which is discussed in the next section.

3. Formula method for bound state solutions

The formula method [22] is used to obtain solutions of second order differential equations. To use this method, we consider a second-order differential equation of the form [29].

$$\frac{d^2\psi \left(s\right)}{d{s}^2}+\frac{c_1-c_{2}s}{s\left(1-c_{3}s\right)}\frac{d\psi \left(s\right)}{ds}+\frac{{\xi }_1{s}^2+{\xi }_{2}s+{\xi }_3}{s^2{\left(1-c_{2}s\right)}^2}\psi \left(s\right)=0$$ (11)

where $c_1\mathrm{...}{c}_n$,${\xi }_1,{\xi }_2,{\xi }_3$ are parametric constants and $\psi \left(s\right)$ is the wavefunction.

According to the formula method, the energy is determined from the equation

$${\left[\frac{c_4^2-c_5^2-{\left[\frac{1-2n}{2}-\frac{1}{2c_3^2}\left(c_2-\sqrt{{\left(c_3-c_2\right)}^2-4{\xi }_1}\right)\right]}^2}{2\left[\frac{1-2n}{2}-\frac{1}{2c_3^2}\left(c_2-\sqrt{{\left(c_3-c_2\right)}^2-4{\xi }_1}\right)\right]}\right]}^2-c_5^2=0,c_3\ne 0\text{,}$$ (12)

where,

$$\begin{array}{l}{c}_4^2=\frac{\left(1-c_1\right)+\sqrt{{\left(1-c_1\right)}^2-4{\xi }_3}}{2}\\ c_5^2=\frac{1}{2}+\frac{c_1}{2}-\frac{c_2}{2c_3}+\sqrt{{\left(\frac{1}{2}+\frac{c_1}{2}-\frac{c_2}{2c_3}\right)}^2-\left(\frac{{\xi }_1}{c_3^2}+\frac{{\xi }_2}{c_3}+{\xi }_3\right)}\end{array}\}\text{.}$$ (13)

The wave function is obtained by

$$\psi \left(s\right)=N_n{s}^{c_4^2}{{\left(1-c_{3}s\right)}^{c_5^2}}_2{F}_1\left(-n,n+2\left(c_4^2+c_5^2\right)+\frac{c_2}{c_3}-1;2c_4^2+c_1;c_{3}s\right)\text{.}$$ (14)

where ₂$F_1\left(a,b;c;d\right)$is a hypergeometric function.

For the case where $c_3\to 0$, Eq. (11) gives

$$\frac{d^2\psi \left(s\right)}{d{s}^2}+\frac{c_1-c_{2}s}{s}\frac{d\psi \left(s\right)}{ds}+\frac{{\xi }_1{s}^2+{\xi }_{2}s+{\xi }_3}{s^2}\psi \left(s\right)=0.$$ (15)

The energy Eq. (12) and the wave function are, thus, transformed respectively to

$${\left[\frac{B-c_3{c}_2-n{c}_2}{2c_4+c_1+2n}\right]}^2-c_5^2=0$$ (16)

and

$$\psi \left(s\right)=N_n{s}^{c_4}\exp {\left(-c_{5}s\right)}_1{F}_1\left(-n,2c_4+c_1,2(c_5+c_2)s\right),$$ (17)

with

$$\begin{array}{l}\underset{c_3\to 0}{\lim }{c}_4=\frac{\left(1-c_1\right)+\sqrt{{\left(1-c_1\right)}^2-4{\xi }_3}}{2}\\ \underset{c_3\to 0}{\lim }{c}_5=-\frac{c_2}{2}+\sqrt{{\left(\frac{c_2}{2}\right)}^2-{\xi }_3}\end{array}\}.$$ (18)

4. Solutions of Dirac equation with modified Kratzer potential

4.1. Pseudospin symmetry case

To solve Eq. (8), we make transformations $G_{n\kappa }\left(r\right)=r^{\frac{1}{2}}{g}_{n\kappa }\left(r\right)$, which gives

$$\frac{d^2{g}_{n\kappa }\left(r\right)}{d{r}^2}-\frac{1}{r}\frac{d{g}_{n\kappa }\left(r\right)}{dr}+\frac{A{r}^2+Br+C}{r^2}{g}_{n\kappa }\left(r\right)=0,$$ (19)

where,

$$\begin{array}{l}A={\epsilon }_2(D_e-{\epsilon }_1)\\ B=-2{\epsilon }_2{D}_e{r}_e\\ C={\epsilon }_2{D}_e{r}_e^2-\kappa (\kappa -1)-\frac{1}{4}\\ {\epsilon }_1=\mu +E_{n\kappa }\\ {\epsilon }_2=\mu -E_{n\kappa }+C_{ps}\end{array}\}.$$ (20)

Comparing Eqs. (19) and (15), it is established that

$$c_1=c_2=c_3=0,c_4=\sqrt{-C},c_5=\sqrt{-A}.$$ (21)

The energy equation of the pseudospin symmetry limit is thus obtained from

$$(\mu +E_{n\kappa }-D_e){\left(1+2n+\sqrt{{(2\kappa -1)}^2+4D_e{r}_e^2(E_{n\kappa }-\mu -C_{ps})}\right)}^2+(E_{n\kappa }-\mu -C_{ps}){\left(2D_e{r}_e\right)}^2=0.$$ (22)

And the corresponding wave function is

$$G_{n\kappa }\left(r\right)=N_n{r}^{\frac{1}{2}+\sqrt{-C}}{e^{-\sqrt{-Ar}}}_1{F}_1\left(-n,2\sqrt{-C}+1,2\sqrt{-A}s\right).$$ (23)

The upper component of the Dirac spinor is obtained for the pseudospin symmetry case from

$$F_{n\kappa }\left(r\right)=\frac{1}{\mu -E_{n\kappa }+C_{ps}}\left(\frac{d}{dr}-\frac{\kappa }{r}\right)G_{n\kappa }\left(r\right)$$ (24)

$F_{n\kappa }\left(r\right)$ is only defined for $E_{n\kappa }\ne \mu +C_{ps}$ and valid for negative energy values [30].

4.2. Spin symmetry case

To solve Eq. (10), we make the transformation $F_{n\kappa }\left(r\right)=r^{\frac{1}{2}}{f}_{n\kappa }\left(r\right)$, and we have

$$\frac{d^2{f}_{n\kappa }\left(r\right)}{d{r}^2}-\frac{1}{r}\frac{d{f}_{n\kappa }\left(r\right)}{dr}+\frac{\alpha r^2+\beta r+\gamma }{r^2}{f}_{n\kappa }\left(r\right)=0$$ (25)

where

$$\begin{array}{l}\alpha ={\epsilon }_3(-D_e-{\epsilon }_4)\\ \beta =2{\epsilon }_3{D}_e{r}_e\\ \gamma =-{\epsilon }_3{D}_e{r}_e^2-\kappa (\kappa -1)-\frac{1}{4}\\ {\epsilon }_1=\mu +E_{n\kappa }-C_s\\ {\epsilon }_2=\mu -E_{n\kappa }+\sum \left(r\right)\end{array}\}.$$ (26)

Following same procedures as used in previous section, the energy equation of the spin symmetry limit is thus obtained from

$$(\mu -E_{n\kappa }+D_e){\left(1+2n+\sqrt{{(2\kappa +1)}^2+4D_e{r_e}^2(\mu +E_{n\kappa }-C_s)}\right)}^2-(\mu +E_{n\kappa }-C_s){\left(2D_e{r}_e\right)}^2=0$$ (27)

And the corresponding wave function as

$$F_{n\kappa }\left(r\right)=N_n{r}^{\frac{1}{2}+\sqrt{-\gamma }}{e^{-\sqrt{-\alpha r}}}_1{F}_1\left(-n,2\sqrt{-\gamma }+1,2\sqrt{-\alpha }s\right).$$ (28)

The lower component of Dirac spinor is obtained for the spin symmetry case from

$$G_{n\kappa }\left(r\right)=\frac{1}{\mu +E_{n\kappa }-C_s}\left(\frac{d}{dr}+\frac{\kappa }{r}\right)F_{n\kappa }\left(r\right).$$ (29)

$G_{n\kappa }\left(r\right)$ is defined for $E_{n\kappa }\ne -\mu +C_s$ and valid for positive energy solutions [30].

4.3. Non-relativistic limit of the spin symmetry case and thermodynamic properties

The non-relativistic limit is obtained in the exact symmetry condition (C_s = 0) by making the following transformations $\mu +E_{n\kappa }\to \frac{2\mu }{{\hslash }^2},E_{n\kappa }-\mu \to E_{nl},F_{n\kappa }\left(r\right)\to R_{nl}\left(r\right),\kappa \to l$ on Eq. (27) to obtain the non-relativistic rotational-vibrational energy spectra

$$E_{nl}=D_e-\frac{{\hslash }^2}{2\mu }{\left(\frac{\frac{4\mu D_e{r}_e}{{\hslash }^2}}{1+2n+\sqrt{{(2l+1)}^2+\frac{8\mu D_e{r}_e^2}{{\hslash }^2}}}\right)}^2.$$ (30)

Eq. (30) is consistent with the energy equation in Refs. [23, 31, 32].

The vibrational energy levels of the modified Kratzer potential is derived by setting l = 0 as

$$E_n=D_e-\frac{{\hslash }^2}{2\mu }{\left(\frac{\Pi }{2(n+\sigma )}\right)}^2,$$ (31)

where

$$\begin{array}{l}\sigma =\frac{1}{2}+\frac{1}{2}\sqrt{1+\frac{8\mu D_e{r}_e^2}{{\hslash }^2}}\\ \Pi =\frac{4\mu D_e{r}_e}{{\hslash }^2}\end{array}\}.$$ (32)

The closest value to the maximum energy can be obtained by setting $\frac{d{E}_n}{dn}{|}_{n=\lambda }=0$,

$$\lambda =\left[\frac{1}{2}+\frac{1}{2}\sqrt{1+\frac{8\mu D_e{r}_e^2}{{\hslash }^2}}\right],$$ (33)

where the bracket in Eq. (33) indicates an integer inferior to n.

Partition functions is the first point in the study of thermodynamic properties. The partition function can be obtained using

$$Z\left(\beta \right)=\sum _{n=0}^{\lambda }{e}^{-\beta E_n},\beta =\frac{1}{k_{B}T},$$ (34)

where $k_B$ is the Boltzmann constant and T is the temperature. In the present study, the upper bound of partition is denoted as $\lambda$. However, in the framework of superstatistics, the upper bound partition is set at infinity.

By use of Eqs. (31) and (34), the partition function is derived as

$$Z(\beta ,\lambda )=\sum _{n=0}^{\lambda }\exp \left(-\beta \left(D_e-\frac{{\hslash }^2}{2\mu }{\left(\frac{\frac{4\mu D_e{r}_e}{{\hslash }^2}}{1+2n+\sqrt{1+\frac{8\mu D_e{r}_e^2}{{\hslash }^2}}}\right)}^2\right)\right).$$ (35)

With $\rho =n+\sigma$, the partition function in classical limit gives

$$Z=\underset{\sigma }{\overset{\sigma +\lambda }{\int }}{e}^{-D_e\beta +\frac{P}{{\rho }^2}\beta }d\rho ,$$ (36)

where,

$$P=\frac{{\hslash }^2{\Pi }^2}{8\mu }.$$

We evaluate Eq. (36) with the use of Maple to obtain the partition function as

$$Z=\frac{-P\beta \sqrt{\pi }erf\left(\frac{\sqrt{-P\beta }}{{(\sigma +\lambda )}^2}\right)+P\beta \sqrt{\pi }erf\left(\frac{\sqrt{-P\beta }}{{\sigma }^2}\right)-\sqrt{-P\beta }((-\sigma -\lambda )e^{\frac{P\beta }{{(\sigma +\lambda )}^2}}+\sigma e^{\frac{P\beta }{{\sigma }^2}})}{\sqrt{-P\beta }{e}^{\beta D_e}},$$ (37)

where,

$$erf\left(z\right)=\frac{2}{\pi }\underset{0}{\overset{z}{\int }}{e}^{-t^2}dt.$$ (38)

Using partition function, the thermodynamic properties can be evaluated as:

• i.Vibrational Internal energy

$$U(\beta ,\lambda )=-\frac{\partial \ln Z(\beta ,\lambda )}{\partial \beta }.$$ (39)

• ii.Vibrational Free Energy

$$F(\beta ,\lambda )=-\frac{1}{\beta }\ln Z(\beta ,\lambda ).$$ (40)

• iii.Vibrational Entropy

$$S(\beta ,\lambda )=k\ln Z(\beta ,\lambda )-k\beta \frac{\partial \ln Z(\beta ,\lambda )}{\partial \beta }.$$ (41)

• iv.Vibrational Specific Heat Capacity

$$C(\beta ,\lambda )=k{\beta }^2\frac{{\partial }^2\ln Z(\beta ,\lambda )}{\partial {\beta }^2}.$$ (42)

5. Results and discussions

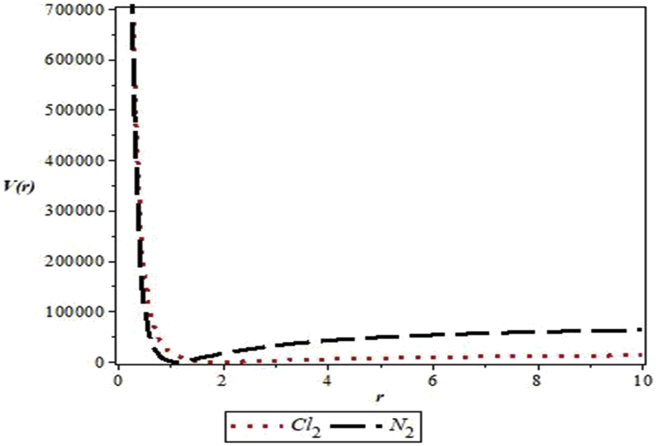
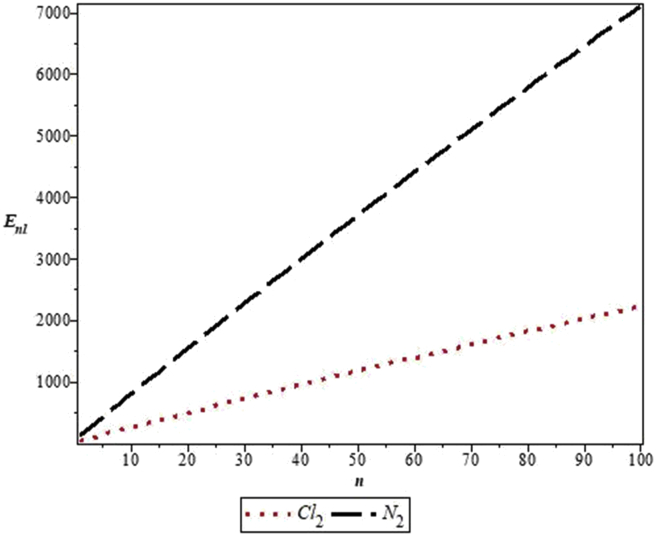
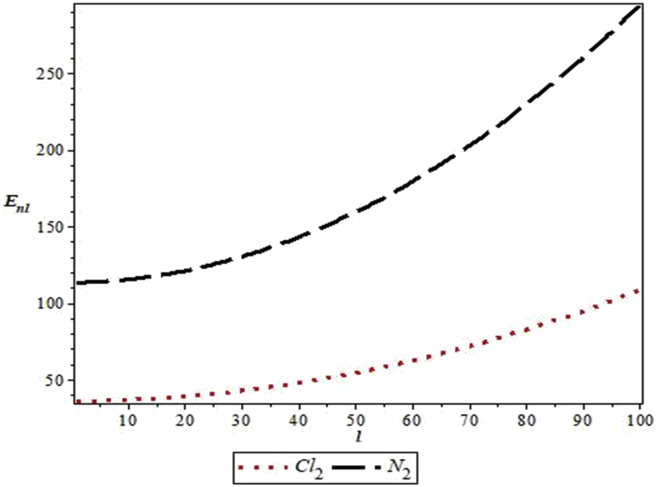
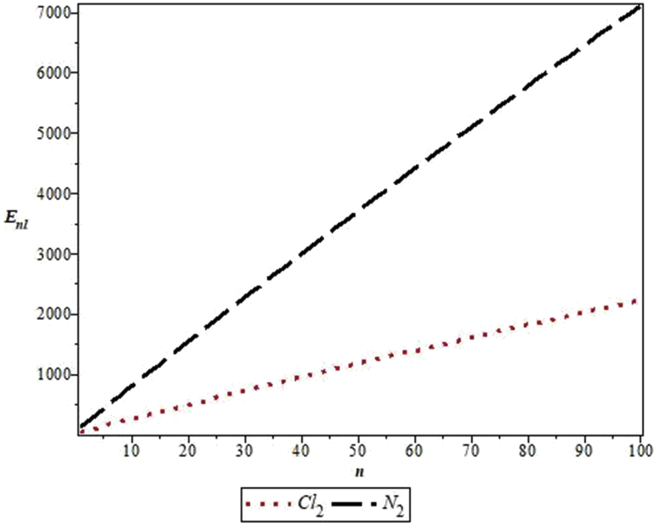
The parameters used in the work are as follows: D_e = 20276 cm⁻¹, r_e = 1.987 Å and μ = 2.924 × 10⁻²³g for Cl₂ [33] and D_e = 79885 cm⁻¹, r_e =1.097 Å and μ =1.171 × 10⁻²³g for N₂ [34]. Figure 1 shows the shape of MKP for the diatomic molecules. Figure 2 represents the energy variation of MKP with n in the non-relativistic limit for the diatomic molecules. It is noticed that the energy increases monotonically as quantum number, n, increases. A similar trend is observed for energy variation with quantum number, l. This is consistent with the results in Table 3 (see Figure 3).

Figure 1.

Variation of the modified Kratzer potential with internuclear distance for the selected diatomic molecules.

Figure 2.

Variation of the non-relativistic energy of the modified Kratzer potential with vibrational quantum number, n, for the selected diatomic molecules.

Table 3.

Non-relativistic Ro-Vibrational energies (-eV) for N₂ and Cl₂ molecules.

N	l	N2	Cl2
0	0	9.886490948	2.505270210
	1	9.899589673	2.511372818
	2	9.902281223	2.512753610
	3	9.903237634	2.513252127
	4	9.903682573	2.513485309
1	0	9.899749647	2.511528332
	1	9.902291694	2.512764785
	2	9.903239555	2.513254208
	3	9.903683122	2.513485907
	4	9.903925036	2.513612811
2	0	9.902339916	2.512812450
	1	9.903243988	2.513258958
	2	9.903684107	2.513486975
	3	9.903925354	2.513613157
	4	9.904071310	2.513689774
3	0	9.903264508	2.513279413
	1	9.903686382	2.513489418
	2	9.903925924	2.513613777
	3	9.904071510	2.513689993
	4	9.904166284	2.513739766
4	0	9.903696943	2.513500000
	1	9.903927243	2.513615195
	2	9.904071870	2.513690383
	3	9.904166418	2.513739912
	4	9.904231416	2.513774061

Figure 3.

Variation of the non-relativistic energy of the modified Kratzer potential with rotational quantum number, l, for the selected diatomic molecules.

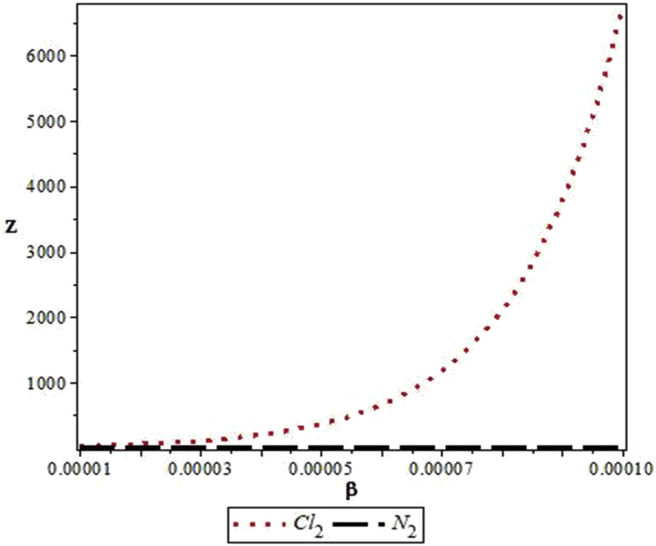
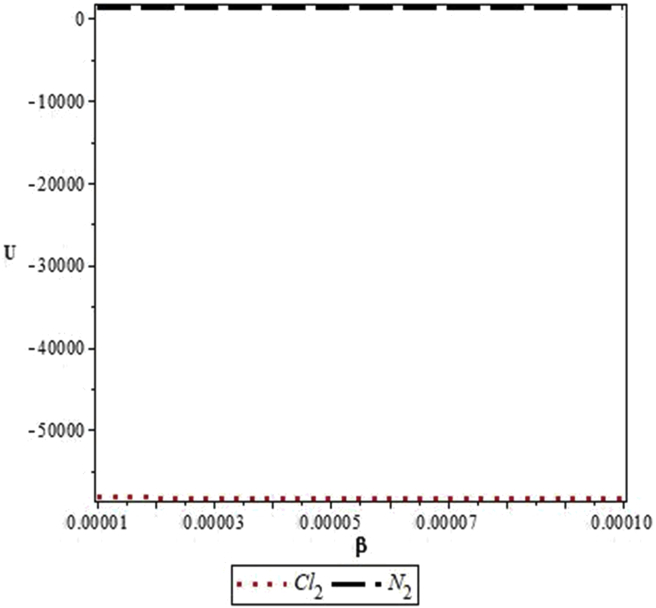
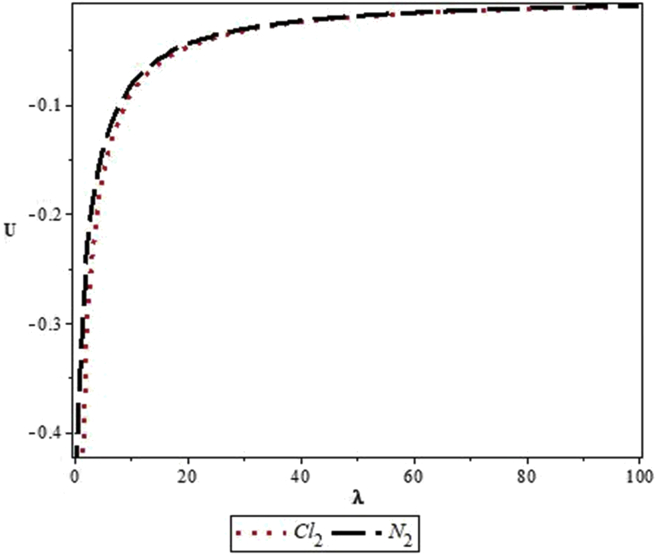
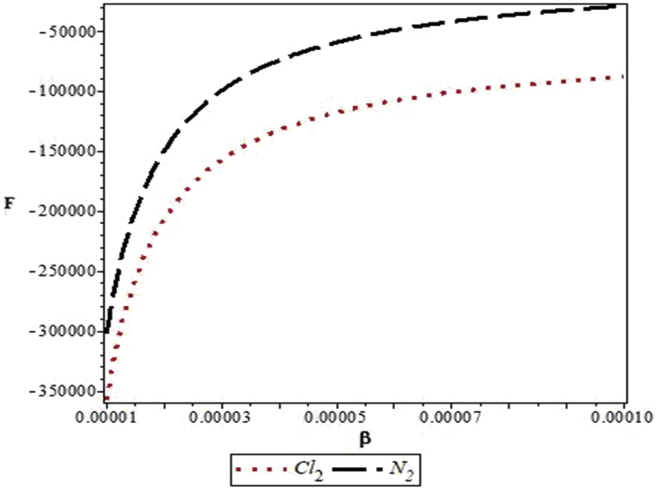
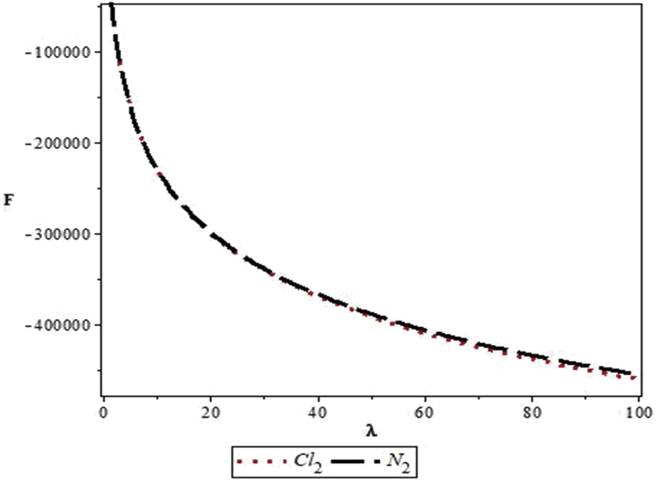
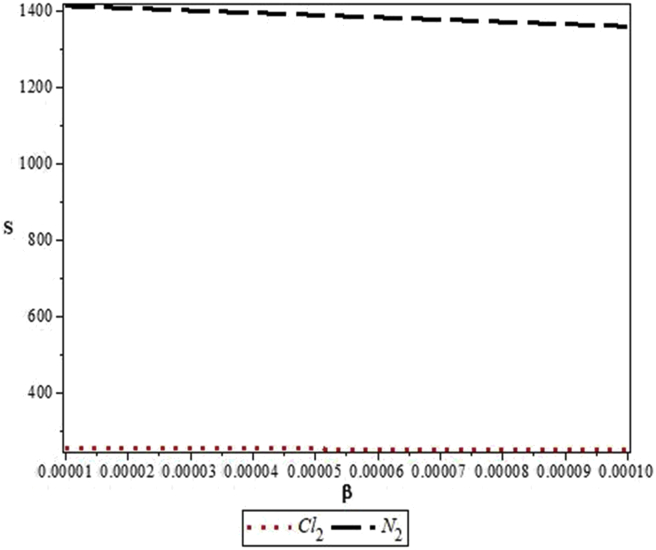
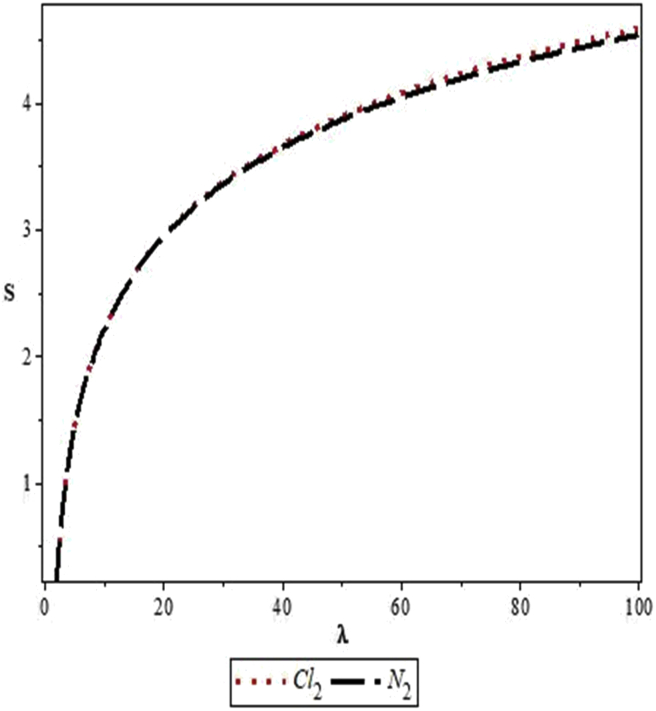
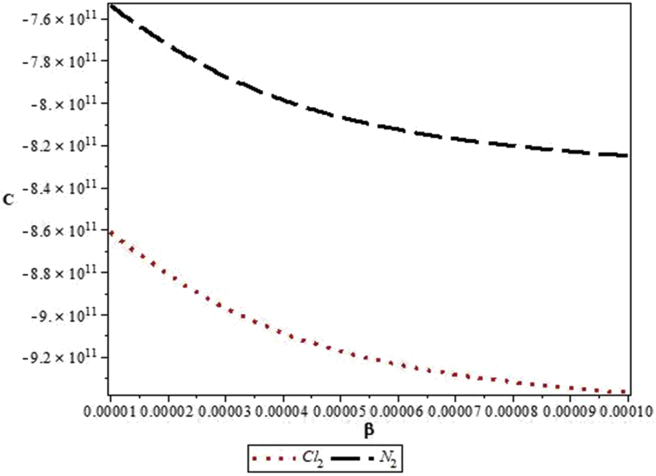
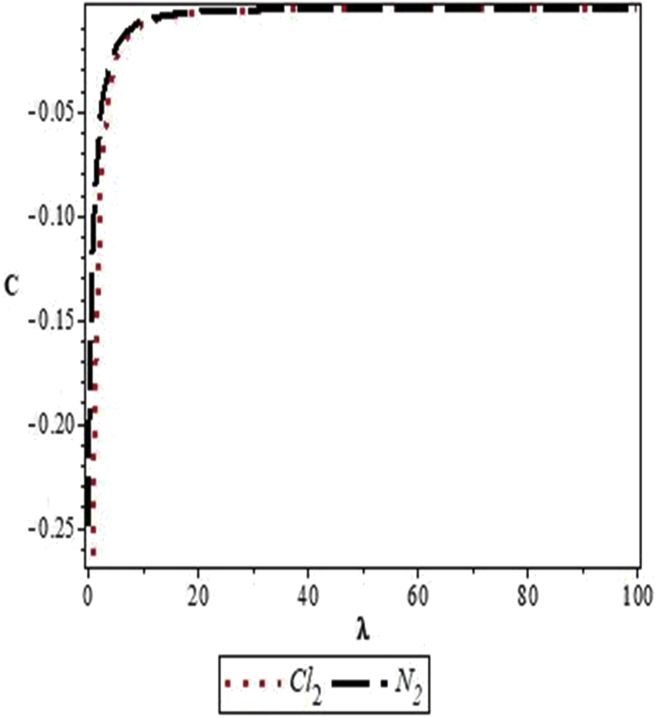
Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 are plots showing variations of various thermodynamic properties of the diatomic molecules with the temperature parameter, β, and the upper bound vibrational quantum number, λ. In Figure 4, the partition function, Z, increases as β increases for the Cl₂ molecule, but decreases for the N₂ molecule. This implies that the probability of finding a particle in a state with quantum number, n, decreases as temperature decreases for the Cl₂ molecule, but increases with decrease in temperature for the N₂ molecule. In Figure 5, the partition function for both molecules is observed to increase sharply as λ increases. A careful look at Figure 6 shows that the vibrational internal energy, U, decreases as β increases for both molecules. In Figure 7, U is observed to increase with increasing λ for both molecules. In Figure 8, the vibrational free energy, F, is observed to increase as β increases for both molecules. In Figure 9, the reverse trend is observed for the variation of F with β. A close observation of Figure 10 shows that the vibrational entropy, S, decreases as β increases for both molecules. On the other hand, S, is observed to increase as λ increases for both molecules as observed in Figure 11. The vibrational specific heat capacity, C, decreases as β increases as observed in Figure 12. For both molecules, in Figure 13, C increases sharply, then, tends to a constant value beyond λ = 20.

Figure 4.

Variation of the vibrational partition function of the modified Kratzer potential with temperature parameter, β, for the selected diatomic molecules.

Figure 5.

Variation of the vibrational partition function of the modified Kratzer potential with upper bound vibrational quantum number, λ, for the selected diatomic molecules.

Figure 6.

Variation of the vibrational internal energy, U, of the modified Kratzer potential with temperature parameter, β, for the selected diatomic molecules.

Figure 7.

Variation of the vibrational internal energy, U, of the modified Kratzer potential with upper bound vibrational quantum number, λ, for the selected diatomic molecules.

Figure 8.

Variation of the vibrational free energy, F, of the modified Kratzer potential with temperature parameter, β, for the selected diatomic molecules.

Figure 9.

Variation of the vibrational free energy, F, of the modified Kratzer potential with upper bound vibrational quantum number, λ, for the selected diatomic molecules.

Figure 10.

Variation of the vibrational entropy, S, of the modified Kratzer potential with temperature parameter, β, for the selected diatomic molecules.

Figure 11.

Variation of the vibrational entropy, S, of the modified Kratzer potential with upper bound vibrational quantum number, λ, for the selected diatomic molecules.

Figure 12.

Variation of the vibrational specific heat capacity, C, of the modified Kratzer potential with temperature parameter, β, for the selected diatomic molecules.

Figure 13.

Variation of the vibrational specific heat capacity, C, of the modified Kratzer potential with upper bound vibrational quantum number, λ, for the selected diatomic molecules.

Tables 1 and 2 present numerical values of the spin and pseudospin symmetry limits of the modified Kratzer potential computed from Eqs. (24) and (29) with the parameters μ = 5, D_e =1.25fm⁻¹, r_e = 0.35fm and C_s=C_ps = 0, for various values of n and κ. In Table 1, the energy levels in the same line such as (1s_1/2, 0d_3/2), (1p_3/2, 0f_5/2) etc, are seen to be degenerate, thus, constituting pseudospin doublets. Also, all the energy levels have negative values. In Table 2, it is observed that states on the same line such as (0p_3/2, 0p_1/2), (0d_5/2, 0d_3/2) etc, show degeneracy. These states constitute the spin doublet. Table 3 presents numerical values of the non-relativistic energies of MKP for the $X^1{\sum }_g^{+}$state of the Cl₂ molecule and the $X^1{\sum }_g^{+}$state of the N₂ molecule.

Table 1.

Bound state energy eigenvalues in fm⁻¹ of the pseudospin symmetry limit of the modified Kratzer potential for various values of κ and n, with C_ps = 0.

$\tilde{l}$	$n,\kappa <0$	$\left(l,j\right)$	$E_{n,\kappa <0}$ Present Method	$E_{n,\kappa <0}$ NU Method [35]	$E_{n,\kappa <0}$ AIM Method [30]	$\begin{array}{l}n-1,\\ \kappa >0\end{array}$	$\left(\begin{array}{l}l+2,\\ j+1\end{array}\right)$		$E_{n-1,\kappa >0}$ Present Method	$E_{n-1,\kappa >0}$ NU Method [35]	$E_{n-1,\kappa >0}$ AIM Method [28]
1	0, -2	1s1/2	-3.484888194	-3.48488819	-3.484888	0, 2	0d3/2	-3.484888194		-3.48488819	-3.484888
2	0, -3	1p3/2	-3.630625750	-3.63062575	-3.630626	0, 3	0f5/2	-3.630625750		-3.63062575	-3.630626
3	0, -4	1d5/2	-3.678048142	-3.67804814	-3.678048	0, 4	0g7/2	-3.678048142		-3.67804814	-3.678048
4	0, -5	1f7/2	-3.701324189	-3.70132419	-3.701324	0, 5	0h9/2	-3.701324189		-3.70132419	-3.701324
1	1, -2	2s1/2	-3.612692508	-3.61269251	-3.612693	1, 2	1d3/2	-3.612692508		-3.61269251	-3.612693
2	1, -3	2p3/2	-3.675416052	-3.67541605	-3.675416	1, 3	1f5/2	-3.675416052		-3.67541605	-3.675416
3	1, -4	2d5/2	-3.700566747	-3.70056675	-3.700567	1, 4	1g7/2	-3.700566747		-3.70056675	-3.700567
4	1, -5	2f7/2	-3.714443810	-3.71444381	-3.714444	1, 5	1h9/2	-3.714443810		-3.71444381	-3.714444

Table 2.

Bound state energy eigenvalues in fm⁻¹ of the spin symmetry limit of the modified Kratzer potential for various values of κ and n, with C_s = 0.

$l$	$n,\kappa <0$	$\left(\begin{array}{l}l,\\ j=l+\frac{1}{2}\end{array}\right)$	$E_{n,\kappa <0}$ Present Method	$E_{n,\kappa <0}$ NU Method [35]	$E_{n,\kappa <0}$ AIM Method [30]	$n,\kappa >0$	$\left(\begin{array}{l}l,\\ j=l-\frac{1}{2}\end{array}\right)$	$E_{n,\kappa >0}$ Present Method	$E_{n,\kappa >0}$ NU Method [35]	$E_{n,\kappa >0}$ AIM Method [28]
1	0, -2	0p3/2	5.910474168	5.91047417	5.910474	0, 1	0p1/2	5.910474168	5.91047417	5.910474
2	0, -3	0d5/2	6.057790795	6.05779079	6.057791	0, 2	0d3/2	6.0577907956	6.05779079	6.057791
3	0, -4	0f7/2	6.131238354	6.13123835	6.131238	0, 3	0f5/2	131238354	6.13123835	6.131238
4	0, -5	0g9/2	6.170506754	6.17050675	6.170507	0, 4	0g7/2	6.170506754	6.17050675	6.170507
1	1, -2	1p3/2	6.075595221	6.07559522	6.075595	1, 1	1p1/2	6.075595221	6.07559522	6.075595
2	1, -3	1d5/2	6.135814276	6.13581428	6.135814	1, 2	1d3/2	6.135814276	6.13581428	6.135814
3	1, -4	1f7/2	6.172013170	6.17201317	6.172013	1, 3	1f5/2	6.172013170	6.17201317	6.172013
4	1, -5	1g9/2	6.194019070	6.19401907	6.194019	1, 4	1g7/2	6.194019070	6.19401907	6.194019

6. Conclusions

We present solutions of Dirac equation in the spin and pseudospin symmetry limits with the MKP using formula method. Our result shows the accuracy of the formula method in relation to other methods as our numerical values are in agreement with those obtained in literature. Furthermore, thermodynamic functions are reported for the Cl₂ and N₂ molecules. Various plots for the various thermodynamic properties against β and λ are presented. Thus, it is concluded that the MKP is a good model for studying the thermodynamic properties of molecules.

Declarations

Author contribution statement

C.P. Onyenegecha, I.J. Njoku: Conceived and designed the analysis; Analyzed and interpreted the data; Wrote the paper.

A. Omame, C.J. Okereke, E. Onyeocha: Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.