Automated radiomic analysis of CT images to predict likelihood of spontaneous passage of symptomatic renal stones

Abstract

Purpose

To evaluate the ability of a semi-automated radiomic analysis software in predicting the likelihood of spontaneous passage of urinary stones compared with manual measurements.

Methods

Symptomatic patients visiting the emergency department with suspected stones in either kidney or ureters who underwent a CT scan were included. Patients were followed for up to 6 months for the outcome of a trial of passage. Maximum stone diameters in axial and coronal images were measured manually. Stone length, width, height, max diameter, volume, the mean and standard deviation of the Hounsfield units, and morphologic features were also measured using automated radiomic analysis software. Multivariate models were developed using these data to predict subsequent spontaneous stone passage, with results expressed as the area under a receiver operating curve (AUC).

Results

One hundred eighty-four patients (69 females) with a median age of 56 years were included. Spontaneous stone passage occurred in 114 patients (62%). Univariate analysis demonstrated an AUC of 0.83 and 0.82 for the maximum stone diameter determined manually in the axial and coronal planes, respectively. Multivariate models demonstrated an AUC of 0.82 for a model including manual measurement of maximum stone diameter in axial and coronal planes. The same AUC was found for a model including automatic measurement of maximum height and diameter of the stone. Further addition of morphological parameters measured automatically did not increase AUC beyond 0.83.

Conclusion

The semi-automated radiomic analysis of urinary stones shows similar accuracy compared with manual measurements for predicting urinary stone passage. Further studies are needed to predict clinical impacts of reporting the likelihood of urinary stone passage and improving inter-observer variation using automatic radiomic analysis software.

Introduction

Acute renal colic is a common presentation in the emergency department (ED), with a lifetime risk of 12% in men and 6% in women [1]. Since the late 1990s, non-contrast-enhanced X-ray computed tomography (CT) has been established as an essential element of the management protocol, replacing intravenous pyelography (IVP) as the imaging modality of choice in evaluating suspected urinary stones [2-5]. Ultrasonography is an alternative to CT, especially in pediatric patients, given its lack of ionizing radiation and increased accuracy in this group [6]. However, CT remains the modality of choice in many cases due to its higher sensitivity and specificity [7]. An important consideration for patients diagnosed with the urinary stone disease during an ED visit is assessing the likelihood of spontaneous stone passage after discharge. Several consensus recommendations describe the likelihood of spontaneous passage based on stone size, typically defined as the maximum diameter in the axial reconstruction, and its location. Multiple studies have reported that stones with a diameter of up to 6 mm have a 50% chance to pass spontaneously; bigger stones have a much lower likelihood and will likely require eventual surgical intervention [8, 9].

Manual measurement of stone size by a radiologist in order to estimate spontaneous passage is an essential step in the evaluation of acute renal colic. Compared with other physicians, radiologists measure the stone diameter objectively in higher percentages [10]. Moreover, they can help to uncover serious complications of nephrolithiasis such as abscess formation and sepsis. Yet, the manual measurement of stone size has several limitations. First, manual measurements of stone diameter are influenced by technical acquisition and reconstruction parameters, including reconstruction kernel and display settings. Moreover, since urinary stones come in different shapes, the measured axial diameter does not always coincide with the actual maximum stone diameter, and therefore, axial measurements incorrectly predict the likelihood of spontaneous stone passage by 17% [11]. A new approach was proposed by Demehri et al. to predict spontaneous stone passage that incorporates the maximum stone axial area. This approach resulted in an increased area under a receiver operating curve (AUC) to predict spontaneous passage compared to stone axial diameter (from 0.80 to 0.84). The largest increase in model performance was reported for stones 5 to 10 mm in size [12].

A semi-automated radiomic analysis software previously developed by our team can automatically segment urinary stones and compute stone linear size variables, volume, and surface morphology measures. The main aim of the current study was to determine if radiomic measures extracted with this software could achieve an equal accuracy for predicting spontaneous stone passage compared with manual measurement of stone size.

Materials and methods

Patient population

This retrospective study was performed after obtaining Mayo Clinic institutional review board approval. Patient consent was waived. All symptomatic patients 18 years of age or older that underwent a CT scan using our routine lower dose urinary stone CT protocol based on the clinical indication during a visit to our Emergency Department between 1st April 2016 and 30th of December of 2017 that had previously consented to retrospective use of their medical records for research purposes were included. Only obstructive stones, which were causing either complete or partial obstruction, were included in the measurements. Patients with multiple stones on the same side without clearcut dominant obstructive stone, and those with the stone already in the bladder, were excluded. Moreover, 63 patients who could not be followed-up were excluded. After exclusions, a total number of 184 patients were enrolled in the study.

Data acquisition

The clinically indicated unenhanced CT scan of the abdomen and pelvis was performed on a 128-slice CT scanner (Somatom Definition Flash or Edge, Siemens Healthineers, Forchheim, Germany) in single energy mode using a low-dose protocol (120 Quality reference mAs, 120 reference kV, slider bar of 8) ranging from the diaphragm to the pelvic floor. Diagnostic images were reconstructed using iterative reconstruction method and a soft body kernel (I30) with a slice thickness of 5 mm and an increment of 2.5 mm for axial images and a slice thickness of 3 mm and an increment of 2.5 mm for coronal images. For the automatic computation, 1.0-mm thick slices with an increment of 0.8 mm were either reconstructed on the scanner or an offline reconstruction computer system using the same kernel settings as mentioned previously.

Stone measurement

The maximum axial stone diameter and location were determined by two radiology research fellows (RM and PM) who were blinded to clinical CT reports. Manual measurements were obtained using the 5-mm axial and 3-mm coronal images. Stone location was categorized into the renal calyces, renal pelvis, upper ureter, middle ureter, distal ureter, ureterovesical junction, and ureteropelvic junction. Stones already in the bladder were excluded.

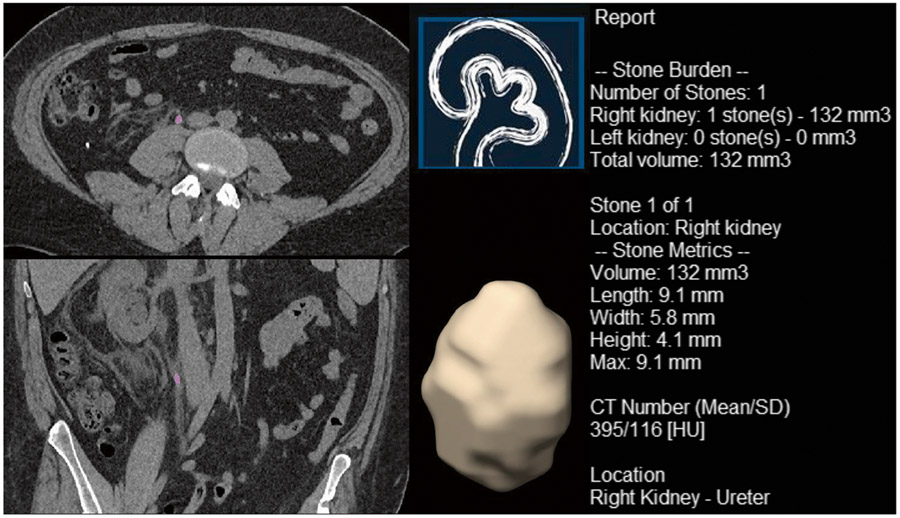
Reconstructed thin slices data sets were processed offline using in-house developed semi-automated stone analysis software (qSAS 1.2, Mayo Clinic, Rochester) based on a commercial software package (MATLAB, The MathWorks Inc., Natick, MA, 2018). In order for the software to perform the measurements, a radiology technologist manually identified the obstructed stone in each case. Subsequently, the software automatically performed the analysis of size, density, and morphology of the stone. This included maximum stone diameter in any direction (MDA), maximum cross-sectional area in the axial surface (CA), the maximum dimension in three primary planes of X, Y, and Z (MDX, MDY, and MDZ) to determine length, width, and height, and stone volume (SV) as defined by an adaptive threshold algorithm (as the shape may be irregular). It should be noted that length, width, and height were determined based on the longest, middle, and shortest stone diameter among the 3 planes, respectively, and not based on which of the imaging axis they belonged to. The algorithm also performed an analysis of the mean and standard deviation of the Hounsfield units (HU) measurement as indicators of stone density as well as shape index, peak curvature, and mean curvature as indicators of surface morphology (SM) [13]. Fig. 1 shows an example of the output provided by the automated radiomic analysis software. Table 1 lists the manual and automated measurements obtained from the lower dose renal CT scan available for this study.

Fig. 1.

An example of the output provided by in-house developed software used to predict the spontaneous passage of urinary stone in a 36-year-old male

Table 1.

Study variables measured manually or via automated radiomic analysis software.

Manual measurements

•Diameter of stone in axial plane (mm) • Diameter of stone in coronal plane (mm)

Automatic size measurements

• Length (mm) • Width (mm) • Height (mm) • Max diameter (mm) • Volume (mm3)

Other automated measurements

• Mean HU • SD HU • Shape index • Peak curvature • Mean curvature

Variables registration and outcome assessment

Clinical outcome was determined by reviewing the electronic patient medical records and follow-up CT exams when available. Therapy at the time of the emergency department visit was based on the decision of the supervising urologist at the time of the CT scan. The spontaneous stone passage was defined only if observed during the follow-up period without the need for an invasive procedure. Information regarding administered medication, complications during the follow-up period, and clinical indications for interventional procedures were recorded for further analysis. The primary outcome assessment was spontaneous stone passage versus the need for any type of interventional stone removal.

Statistical analysis

All data were analyzed using R: A language and environment for statistical computing version 3.6.2 (R Core Team, R Foundation for Statistical Computing, Vienna, Austria). Descriptive statistics of continuous variables are provided as mean ± standard deviation for normally distributed variables and median (range) for non-parametric variables. Continuous variables were compared using the paired Student’s t test for normally distributed data and the Mann-Whitney U test for non-normally distributed data. The correlation between continuous variables was measured using Pearson correlation coefficient for normally distributed data and Spearman’s rank correlation coefficient for non-normally distributed data. Lin’s concordance correlation coefficient was used to investigate the inter-observer variability between the manual and automatic measurements. Events during follow-up, such as interventions and re-hospitalization, are described as absolute frequencies (percentage). Chi-square test and Fisher’s exact test were used to compare frequencies as applicable.

The association between different manual and automated measurements and subsequent urinary stone passage was assessed using univariate logistic regression. For the multivariable models, LASSO regression was used for variable selection to decrease multicollinearity issues and increase predictive accuracy. Predictive accuracy of all models was measured using the area under the curve (AUC). Odds ratios (OR) were used to describe the chance of stone passage. An OR of 1 indicates that the variable has no predictive value for determining the spontaneous passage of the stone. Cut-off values for different parameters were determined by finding where the sensitivity and specificity were optimum. Lower OR means that there is less chance of spontaneous stone passage for higher values of the parameter. Factors with lower OR could be considered as better predictors for the need for invasive intervention. A two-sided p value of 0.5 was considered as statistically significant.

Results

Patient characteristics

The study population included 184 patients, 115 (62.5%) male and 69 (37.5%) female, with a median age of 56.5 years and a range of 23 to 96 years.

The obstructive stone was on the right side in 87 patients (47.3%). The most common stone location was distal ureter in 60 patients (32.6%), followed by upper ureter and ureterovesical junction (UVJ) each in 43 (23.4%), middle ureter in 24 (13.0%), ureteropelvic junction (UPJ) in 9 (4.9%), renal pelvis in 4 (2.2%), and upper renal calyces in 1 (0.5%).

Spontaneous passage of the stone was observed in 114 patients (62.0%), while 70 patients (38.0%) required interventions. The number of stones in each of the 7 designated locations was significantly different between the two groups (with spontaneous passage of the stone vs. with need for stone extraction intervention, P value < 0.001). Stones in the upper ureter are less likely to pass spontaneously, whereas stones in the ureterovesical junction are more likely to pass spontaneously (44.2% vs. 86.0%, Table 2). However, there was no statistically significant difference between the number of stones on the right and left side (P value = 0.24). Table 2 summarizes the location of the stone for stones with and without spontaneous passage. Please see the supplementary table for a comparison of various measurements (size, density, and morphology) between stones passed spontaneously and stone requiring extraction.

Table 2.

The location of renal stones in patients who experienced spontaneous passage of the stone and those who required stone extraction interventions

	No spontaneous passage	Spontaneous passage	Total
Right side	37 (42.5%)	50 (57.5%)	87
Left side	33 (34.0%)	64 (66.0%)	97
Upper renal calyces	0 (0.0%)	1 (100.0%)	1
Renal pelvis	3 (75.0%)	1 (25.0%)	4
Upper ureter	24 (55.8%)	19 (44.2%)	43
Middle ureter	9 (37.5%)	15 (62.5%)	24
Distal ureter	22 (36.7%)	38 (63.3%)	60
Ureterovesical junction	6 (14.0%)	37 (86.0%)	43
Ureteropelvic junction	6 (66.7%)	3 (33.3%)	9

Data are presented as frequency (percentage)

The percentages of spontaneous stone passage for stones with a maximum axial stone diameter of ≥ 4 mm, ≥ 6 mm, ≥ 8 mm, and ≥ 10 mm on manual measurements were 40.9%, 12.8%, 12.5%, and 0%, respectively.

The percentages of spontaneous stone passage for stones with a maximum coronal stone diameter of ≥ 4 mm, ≥ 6 mm, ≥ 8 mm, and ≥ 10 mm on manual measurements were 45.0%, 24.5%, 4.3%, and 0%, respectively.

The percentages of spontaneous stone passage for stones with a maximum stone diameter of ≥ 4 mm, ≥ 6 mm, ≥ 8 mm, and ≥ 10 mm on automated measurements were 51.5%, 35.7%, 23.8%, and 4.0%, respectively.

There was statistically significant and strong correlations between manual measurements of maximum stone diameter in axial and coronal planes, and automatic measurements of maximum stone diameter (P value < 0.001 for both, r = 0.873 and r = 0.923, respectively). The supplementary figure shows the relationship between these variables. Lin’s concordance correlation coefficients between manual measurements of maximum stone diameter in axial and coronal planes and automatic measurements of maximum stone diameter were CCC = 0.69 (95% CI = 0.63–0.75), and CCC = 0.79 (95% CI = 0.74–0.83), respectively.

Univariate analysis

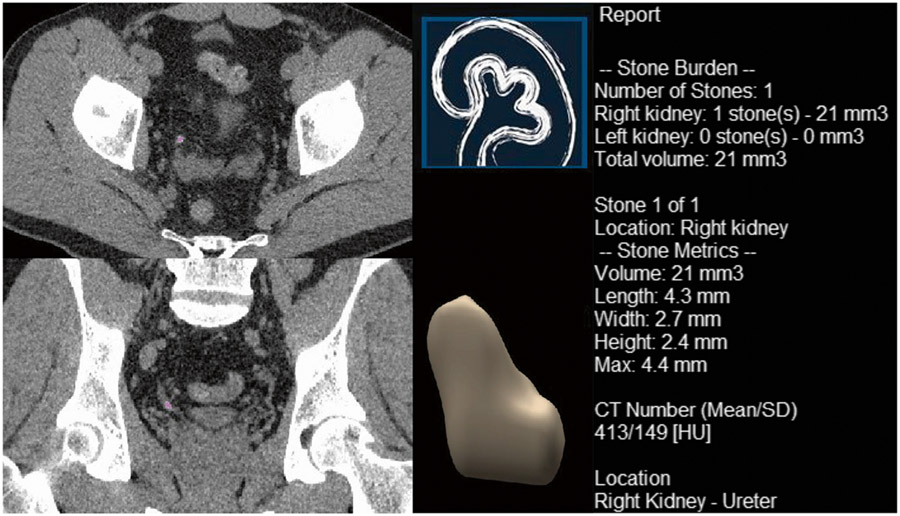
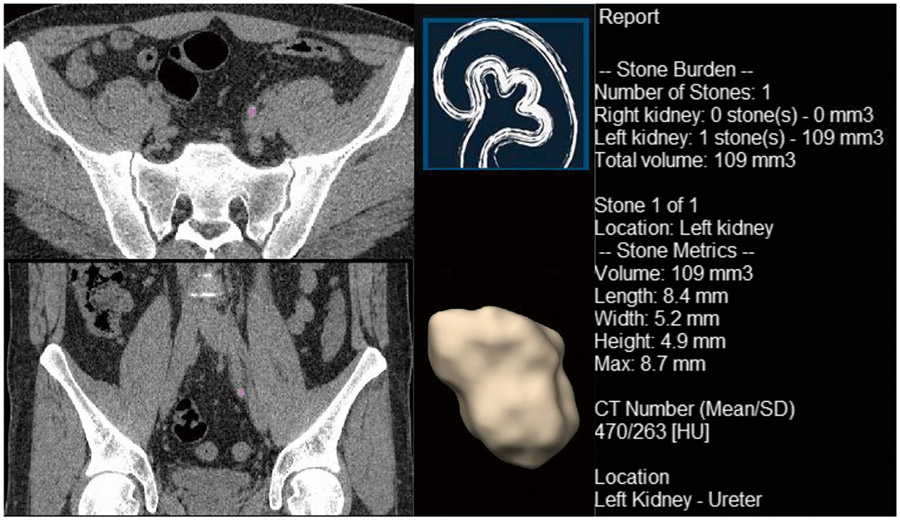
Univariate analysis identifies multiple measurements, which were significantly associated with spontaneous stone passage (Table 3). For manual measurements, the diameter of the stone in either axial or coronal plane were significant predictors of the subsequent spontaneous stone passage (OR = 0.49 [95% CI: 0.39 to 0.62, P value < 0.001] and 0.52 [95% CI: 0.42 to 0.64, P value < 0.001], AUC = 0.83 and 0.82, respectively). The three automated measurements that best predicted subsequent spontaneous stone passage were height of the stone (OR = 0.40 [95% CI: 0.29 to 0.55, P value < 0.001], AUC = 0.81), mean curvature (OR = 0.80 [95% CI: 0.74 to 0.86, P value < 0.001], AUC = 0.82), and volume (OR = 0.83 [95% CI: 0.77 to 0.89, P value < 0.001], AUC = 0.81); however, each radiomic parameters assessed was associated with spontaneous stone passage when the optimal threshold was selected: diameter of stone in axial plane (< 4.6 mm vs ≥ 4.6 mm), and diameter of stone in coronal plane (< 4.9 mm vs ≥ 4.9 mm) on manual measurements, length (< 6.05 mm vs ≥ 6.05 mm), width (< 4.15 mm vs ≥ 4.15 mm), height (< 2.65 mm vs ≥ 2.65 mm), max diameter (< 6.05 vs ≥ 6.05 mm), volume (< 51.55 mm³ vs ≥ 51.55 mm³), mean HU (< 389.9 vs ≥ 389.9), SD HU (< 203.1 vs ≥ 203.1), shape index (< 0.03415 vs ≥ 0.03415), peak curvature (> 0.01015 vs ≤ 0.01015), and mean curvature (< − 0.1424 vs ≥ − 0.1424) on automatic measurements. This includes morphological parameters comprising of shape index, peak curvature, and mean curvature (Table 3). Figures 2 shows an example of the automated radiomic analysis software applied to a urinary stone (volume = 21 mm³) that spontaneously passed. Figure 3 shows a urinary stone (volume = 109 mm³) that required intervention. The univariate model based on volume (OR passage = 0.83 per 10 mm³) predicts that the stone in Fig. 3 was about 5 times more likely to require intervention compared to the stone in Fig. 2.

Table 3.

The results of univariate analysis showing predicting factors for the need for stone extraction interventions measured manually or automatically via the automated radiomic analysis software

Variable	Odds Ratio (95% CI)	P value	AUC
Manual measurements
Diameter of stone in axial plane (per mm)	0.49 (0.39, 0.62)	< 0.001	0.83
Diameter of stone in coronal plane (per mm)	0.52 (0.42, 0.64)	< 0.001	0.82
Automatic (software)
Length (per mm)	0.66 (0.57, 0.77)	< 0.001	0.79
Width (per mm)	0.51 (0.40, 0.64)	< 0.001	0.79
Height (per mm)	0.40 (0.29, 0.55)	< 0.001	0.81
Max diameter (per mm)	0.66 (0.57, 0.76)	< 0.001	0.80
Volume (per 10 mm3)	0.83 (0.77, 0.89)	< 0.001	0.81
Mean HU (per 50 units)	0.77 (0.70, 0.86)	< 0.001	0.73
SD HU (per 50 units)	0.74 (0.63, 0.85)	< 0.001	0.68
Shape index (per 0.01)	0.78 (0.71, 0.86)	< 0.001	0.76
Peak curvature (per 0.001)	1.16 (1.06, 1.28)	< 0.001	0.72
Mean curvature (per 0.01)	0.80 (0.74, 0.86)	< 0.001	0.82

95% CI 95% confidence interval, AUC area under the curve

Fig. 2.

An example of automated radiomic analysis software displaying a urinary stone that spontaneously passed in a 49-year-old male

Fig. 3.

An example of automated radiomic analysis software displaying a urinary stone that required intervention in a 37-year-old male

Multivariate analysis

Multivariable models are subsequently created to determine independent variables and describe their ability to predict stone passage (Table 4). The first group of models included variables manually measured. The first multivariate model which included the diameter of the stone both in axial and coronal planes measured manually had an AUC of 0.82, substantially equivalent to the two individual variables alone. When the patients’ age, gender, and interaction between variables were added to this model, AUC only marginally increased (0.83).

Table 4.

Different multivariate models predicting the need for renal stone extraction interventions

Variable	Odds ratio (95% CI)	P value
Manual measurements (AUC = 0.82)
Diameter of stone in axial plane (per mm)	0.79 (0.55, 1.16)	0.23
Diameter of stone in coronal plane (per mm)	0.62 (0.44, 0.87)	0.006
Manual measurements plus age, gender, and interaction between variables using LASSO (AUC = 0.83)
Female	0.90 (0.10, 7.86)	0.93
Diameter of stone in axial plane (per mm)	0.81 (0.54, 1.22)	0.31
Diameter of stone in coronal plane (per mm)	0.62 (0.44, 0.87)	0.006
Female* diameter of stone in axial plane (per mm)	0.93 (0.58, 1.50)	0.76
Automatic size measurements (AUC = 0.82)
Length (per mm)	3.67 (0.72, 18.7)	0.12
Width (per mm)	1.14 (0.54, 2.39)	0.73
Height (per mm)	0.84 (0.39, 1.79)	0.65
Max diameter (per mm)	0.25 (0.05, 1.20)	0.083
Volume (per 10 mm3)	0.87 (0.68, 1.10)	0.25
Automatic size measurements reduced model using LASSO (AUC = 0.82)
Height (per mm)	0.60 (0.37, 0.96)	0.033
Max diameter (per mm)	0.79 (0.64, 0.99)	0.037
Automatic size and morphologic measurements reduced using LASSO (AUC = 0.82)
Height (per mm)	0.91 (0.51, 1.64)	0.76
Max diameter (per mm)	0.89 (0.70, 1.15)	0.37
Mean HU (per 50 units)	0.90 (0.78, 1.03)	0.13
Shape index (per 0.01)	0.93 (0.82, 1.07)	0.32
Mean curvature (per 0.01)	0.93 (0.80, 1.07)	0.30
Automatic size and morphologic measurements plus interaction using LASSO (AUC = 0.83)
Height (per mm)	1.07 (0.90, 1.28)	0.45
Max diameter (per mm)	0.99 (0.96, 1.03)	0.70
Shape index (per unit)	0.16 (0.02, 1.34)	0.094
Mean curvature (per unit)	0.19 (0.03, 1.48)	0.12
Mean HU (per unit)	1.00 (1.00, 1.00)	0.70
Height*mean HU	1.00 (1.00, 1.00)	0.22
Automatic size and morphologic measurements plus age, gender, and interaction between variables using LASSO (AUC = 0.83)
Female	0.98 (0.83, 1.15)	0.77
Height (per mm)	1.05 (0.88, 1.26)	0.58
Max diameter (per mm)	0.99 (0.95, 1.03)	0.58
Shape index (per unit)	0.38 (0.03, 5.48)	0.48
Mean curvature (per unit)	0.23 (0.03, 1.82)	0.16
Mean HU (per unit)	1.00 (1.00, 1.00)	0.79
Height*mean HU	1.00 (1.00, 1.00)	0.29
Female*shape index	0.32 (0.03, 4.13)	0.39

95% CI 95% confidence interval. Odds ratios were used to describe the chance of spontaneous stone passage. A lower odds ratio indicates a lower chance of spontaneous passage for higher values of the parameter. In a multivariate model, the overall odds ratio for stone passage will be determined by multiplying odds ratios for all included variables

The second group of models included variables automatically measured using the radiomics software. A model which included only size measurements (length, width, height, max diameter, and volume of the stone) also resulted in an AUC of 0.82. A reduced version of this model which only included the height and max diameter of the stone with the use of LASSO to get rid of multicollinearity had the same AUC of 0.82. Another model which included size and the stone morphologic parameters height, max diameter, mean HU, shape index, and mean curvature and employed LASSO to account for multicollinearity had an AUC of 0.82. When interactions between these variables were added to this model, AUC only marginally increased (0.83). Finally, when patients’ age, gender and interaction between variables were added to the model, the AUC remained unchanged at 0.83.

Discussion

The current study demonstrates that several urinary stone variables derived from manual and automatic size measurements were good predictors for spontaneous stone passage (AUC 0.81–0.83). Notably, multivariate models combining either manual or automatic measurements (including indicators of stone density and morphological parameters such as sphericity) did not yield significant improvements compared to univariate models. It should be noted that the decision to include these variables were based on the currently available evidence indicating their effects on the formation and retention of renal stones [14, 15].

Stone size linear measurements have been shown to be accurate predictors of spontaneous urinary stone passage [16-18]. Likewise, in the current study, both manual measurements of stone size acted as accurate predictors of stone passage, while automatic measurements performed equally but not better. Surprisingly, the addition of several additional factors including morphologic features did not improve the accuracy of predictive models for stone passage compared with models which only included size variables. A likely explanation for these findings is the strong correlation between morphological features and stone size. For example, the mean curvature of the stone surface showed a strong correlation with the max diameter of the stone itself (r = 0.762).

The accuracy of CT scan measurements for predicting spontaneous stone passage observed in the current study are in line with previous reports. In one study, Demehri et al. showed that the maximum diameter of the stone has an AUC of 0.80 in predicting the need for stone extraction interventions [12], equivalent to the AUC observed in our study when using the maximum stone diameter automatically measured by the radiomic analysis software.

In a previous study, Jendeberg et al. evaluated the accuracy of an automated segmentation algorithm in comparison with manual measurements in 391 patients referred with suspected urinary stones [19]. The authors found that the automated segmentation algorithm performed similarly to the manual measurements. In line with their study, we found that the accuracy of the automated radiomic analysis software in predicting spontaneous passage of urinary stones was at least as good as the manual measurement. Unlike in the Jendeberg study, our algorithm was not developed or tuned on the population of stones used in this study, thus removing a potential accuracy bias. As a result, one can conclude that automated algorithms could be an acceptable replacement for the manual measurement of stone size in predicting the chance of spontaneous passage.

The use of the semi-automated radiomic analysis software used in the current study could provide several potential advantages. There is no need for a radiologist to operate the software, it is easy to use, can be performed quickly by a radiologic technologist, and it can potentially include the probability of passage of the stone in the image report automatically. Moreover, it has the potential to be fully automated in the future so the interpreting radiologist can receive the measurements without the need for technicians’ manual selection of the stone. Furthermore, it could potentially eliminate inter-observer variability. It has been reported that there could be up to 20% of inter-observer variability for the linear measurement of stone size [20].

There are several limitations to the current study. First, this study was retrospective in nature. Thus, further prospective studies are warranted to test the validity of its findings. Second, the sample size was relatively small for the number of variables included, although we used the minimum sample size required for the inclusion of each variable in the multivariate analysis. We did not have enough cases for some of the stone locations to include stone location in our models for the likelihood of spontaneous stone passage. Third, the slice thickness was different for the manual and automatic measurements. However, there was a significant and strong correlation for linear size measurements between the two methods. Finally, it would be ideal to have several readers perform manual measurements of the stone diameters in order to calculate inter-observer variability.

In conclusion, semi-automated radiomic analysis can predict urinary stone passage at least as accurately as manual radiologist measurements. The semi-automated analysis could potentially be performed more quickly than manual reads and be more reproducible. Further prospective clinical validation of the developed models is warranted.

Data Availability

Available upon request from the corresponding author.