Design and analysis of a 2-year parallel follow-up of repeated ivermectin mass drug administrations for control of malaria: Small sample considerations for cluster-randomized trials with count data

Abstract

Background

Cluster-randomized trials allow for the evaluation of a community-level or group-/cluster-level intervention. For studies that require a cluster-randomized trial design to evaluate cluster-level interventions aimed at controlling vector-borne diseases, it may be difficult to assess a large number of clusters while performing the additional work needed to monitor participants, vectors, and environmental factors associated with the disease. One such example of a cluster-randomized trial with few clusters was the “efficacy and risk of harms of repeated ivermectin mass drug administrations for control of malaria” trial. Although previous work has provided recommendations for analyzing trials like repeated ivermectin mass drug administrations for control of malaria, additional evaluation of the multiple approaches for analysis is needed for study designs with count outcomes.

Methods

Using a simulation study, we applied three analysis frameworks to three cluster-randomized trial designs (single-year, 2-year parallel, and 2-year crossover) in the context of a 2-year parallel follow-up of repeated ivermectin mass drug administrations for control of malaria. Mixed-effects models, generalized estimating equations, and cluster-level analyses were evaluated. Additional 2-year parallel designs with different numbers of clusters and different cluster correlations were also explored.

Results

Mixed-effects models with a small sample correction and unweighted cluster-level summaries yielded both high power and control of the Type I error rate. Generalized estimating equation approaches that utilized small sample corrections controlled the Type I error rate but did not confer greater power when compared to a mixed model approach with small sample correction. The crossover design generally yielded higher power relative to the parallel equivalent. Differences in power between analysis methods became less pronounced as the number of clusters increased. The strength of within-cluster correlation impacted the relative differences in power.

Conclusion

Regardless of study design, cluster-level analyses as well as individual-level analyses like mixed-effects models or generalized estimating equations with small sample size corrections can both provide reliable results in small cluster settings. For 2-year parallel follow-up of repeated ivermectin mass drug administrations for control of malaria, we recommend a mixed-effects model with a pseudo-likelihood approximation method and Kenward–Roger correction. Similarly designed studies with small sample sizes and count outcomes should consider adjustments for small sample sizes when using a mixed-effects model or generalized estimating equation for analysis. Although 2-year parallel follow-up of repeated ivermectin mass drug administrations for control of malaria is already underway as a 2-year parallel trial, applying the simulation parameters to a crossover design yielded improved power, suggesting that crossover designs may be valuable in settings where the number of available clusters is limited. Finally, the sensitivity of the analysis approach to the strength of within-cluster correlation should be carefully considered when selecting the primary analysis for a cluster-randomized trial.

Introduction

Cluster-randomized trials (CRTs) allow for the evaluation of an intervention applied beyond the individual at the community or group level. For vector-borne diseases like malaria, interventions aimed at controlling mosquitoes are often only applied at the village level, making CRTs an appropriate study design.^1–3 A recent example of a CRT that evaluated a vector control intervention was the “efficacy and risk of harms of repeated ivermectin mass drug administrations for control of malaria (RIMDAMAL)” trial.⁴ Conducted in 2015, RIMDAMAL was a two-arm CRT that evaluated the role of ivermectin (a drug that kills mosquitoes) on the incidence of malaria episodes for untreated children in eight rural villages in Burkina Faso over one rainy season (NCT02509481). The outcome of interest was the number of malaria episodes in children under the age of 5 who did not receive the intervention; thus, the primary hypothesis was that ivermectin treatment of adults and older children (at least 90 cm tall) would affect the mosquito population structure thereby reducing parasite transmission and the risk of malaria episodes in younger children. A CRT design was used because the hypothesis requires treatment of the majority of the community in order to benefit the community’s younger children. The study reported a risk difference of −0.49 malaria episodes in favor of the intervention group (95% confidence interval (CI): −0·79 to −0·21).

For studies like RIMDAMAL that require a CRT design to evaluate cluster-level interventions aimed at controlling vector-borne diseases, it may be difficult to assess a large number of clusters while performing the additional work needed to follow large numbers of participants for safety and efficacy outcomes, and to evaluate the vectors, pathogens, and environmental factors associated with the disease. The primary purpose of this article is to evaluate analysis approaches for CRTs with count outcomes and few clusters in the context of RIMDAMAL II (a larger 2-year parallel follow-up study of repeated ivermectin mass drug administrations for control of malaria. Furthermore, RIMDAMAL II simulation parameters were applied to different study designs (single-year, 2-year crossover) and different numbers of clusters (including stronger cluster correlations) to provide guidance for other studies with similar outcomes and limited access to large numbers of clusters.

Overview of RIMDAMAL II

The results from RIMDAMAL suggested a reduction in malaria incidence within the treatment villages and RIMDAMAL II aims to confirm the role of ivermectin as a malaria control mechanism. Currently underway, RIMDAMAL II (NCT03967054) is a double-blind placebo-controlled cluster-randomized design that evaluates 14 villages over two rainy seasons in Burkina Faso. Expanding the age range from RIMDAMAL, RIMDAMAL II aims to observe the effect of ivermectin on the cumulative malaria incidence (the primary outcome) for children under 10 years of age via weekly visits over the course of each rainy season. Furthermore, RIMDAMAL II employs a monthly ivermectin dosing regimen that leverages public health infrastructure already in place for ongoing malaria control interventions. RIMDAMAL II is designed to provide 80% power for a rate ratio of 0.560 under the assumption that the rate of malaria episodes per child per year is 0.619 with ivermectin and 1.088 without. Full power calculation details can be found in the supplementary material.

Overview of CRT designs and analysis approaches

CRT designs have been described in detail elsewhere.^5–7 Briefly, CRTs may use a parallel design in which one group of clusters receives an intervention and one group serves as a control. Alternatively, crossover designs where all groups receive the intervention and control in different periods may provide more power over parallel studies, particularly in small sample settings.^8–10 While other study designs exist, such as stepped-wedge CRTs, parallel and crossover designs are emphasized here.

The analysis of any CRT must account for correlation between participants within the same cluster. Cluster-level and individual-level analyses are the two general frameworks used to account for the correlation within clusters.^5–7 Cluster-level approaches generate a summary statistic for each cluster and then analyze those summaries, and individual-level approaches model the participant-level data as the outcome. Analyses using cluster-level summary statistics have been found to perform robustly for CRTs with a small number of clusters and have therefore been recommended in such cases (fewer than 30 clusters) although they can also result in a loss of power.⁷ In spite of this, a recent review showed that individual-level analyses are more common and often do not apply small sample corrections, potentially leading to an increased Type I error rate.¹¹ The two main approaches to individual-level analyses are mixed-effects models and generalized estimating equations (GEEs).¹² The major distinction between the two methods is that GEEs use a population-averaged interpretation while mixed-effects models yield cluster-specific interpretations because they require a fully specified likelihood.^7,12 The analysis of the RIMDAMAL trial used an individual-level model in the form of a GEE without a small sample adjustment and did not originally account for within-village correlation. Given the relatively small number of clusters, a cluster-level analysis was proposed as an alternative.¹³ Upon re-analysis, which explored both cluster-level and individual-level analyses, the conclusions of RIMDAMAL were not altered.¹⁴

Previous work in the context of continuous (i.e. non-count) outcomes^15,16 has simultaneously evaluated individual-level analyses with small sample corrections relative to cluster-level or fixed-effects models. We aim to extend this work to count outcomes by simultaneously evaluating individual-level models and cluster-level summaries within three different CRT design frameworks in order to inform the analysis methods for the RIMDAMAL II trial and provide guidance for other small sample CRTs with few clusters.

Methods

Analysis strategies

Cluster-level and individual-level analysis methods were applied to simulated data from three distinct study designs: a single-period (one-year) CRT, a 2-year cluster-randomized parallel trial, and a 2-year cluster-randomized crossover trial. While different study designs require different parameters to appropriately evaluate the treatment effect, similar approaches were applied to all three designs. All models use the same number of clusters and the same number of individuals per cluster; thus, neither the number of clusters nor the sample size in each cluster were treated as random (supplementary material—simulation details. p. 1). Each model has been labeled (e.g. CL1 to refer to Cluster-Level Analysis 1, IL1 to refer to Individual-Level Analysis 1) to direct the reader to the corresponding code and model equations in the supplementary material.

Cluster level.

For the single-period analysis, four methods were evaluated. Two methods summarized the mean rate within each village, one summarized the total number of episodes within each village, and one used an adjusted residual model. The two mean rate analyses included an unadjusted t-test (CL1) as well as a variance and size weighted t-test with the weighting calculated using estimates from a one-way analysis of variance (ANOVA) as previously described (CL2).¹⁶ The cluster summaries that modeled the total number of episodes utilized a Gaussian error family (referred to as size weighted Gaussian) and included an offset for the number of people within each village (CL3). The adjusted residual method (CL4) allowed for the addition of covariates by fitting a Poisson generalized linear model without the treatment effect, generating cluster-level means based on the residuals, and then applying an unweighted t-test to the residuals based on treatment group.^7,17

For the 2-year parallel analyses, we used two previously recommended approaches for modeling rate data with small sample sizes¹⁷ plus two additional models that accounted for a time variable. For the recommended models, an unadjusted t-test evaluated the mean rate over person-time (CL5), whereas the adjusted residual method accounted for time and sex when generating the Poisson residuals (CL6). The two other models summarized mean rate within each cluster-period and then modeled a treatment and time covariate in a Gaussian regression framework (CL7—unweighted, CL8—weighted). Cluster-period is defined as the year of the trial nested within the cluster (14 villages × 2 years = 28 cluster-periods). For the crossover analyses, we extended a previously described approach for binary data¹⁸ to our mean cluster-period rates because the more traditional calculation of differences¹⁹ did not easily allow for direct comparisons to other methods (CL9). Cluster-level analyses were performed using R.²⁰

Individual level.

Individual-level approaches accounted for correlation at the following levels: cluster, cluster-period, or both. A sex covariate was added to all models in order to evaluate how the addition of a relevant covariate to each model impacted the results. Mixed-effects models and GEEs were fit in SAS using PROC GLIMMIX, because small sample corrections are readily available in the procedure.²¹ An important caveat is that the utilization of PROC GLIMMIX means that a traditional GEE with a quasi-likelihood is not fit. Here, models fit using PROC GLIMMIX are referred to as “GEE” models, although technically they are often called “GEE-type” models.²¹ For mixed-effects models, both maximum likelihood and pseudo-likelihood approximation methods were evaluated; a Kenward–Roger correction²² was also evaluated in the pseudo-likelihood approach. For maximum likelihood, both the Laplace and Adaptive Gaussian Quadrature methods were used with 10 quadrature points used for the latter method, based on previous recommendations.²³ For the GEEs, empirical standard errors as well as two small sample corrections were evaluated. The first small sample correction, proposed by Morel, Bokossa, and Neerchal (MBN),²⁴ has been shown to produce unbiased results in both continuous and binary outcomes;²⁵ the second correction, proposed by Fay and Graubard,²⁶ has been shown to perform well with highly unbalanced data in a binary CRT setting.²⁷

For the single-year study, treatment and sex were treated as fixed effects and village was a random effect (IL1–IL8). For the parallel study, two approaches were used; the first utilized a fixed effect for treatment, sex, and time with a random effect for cluster (IL9–IL16), while the other approach incorporated cluster-period as a second random effect and removed the fixed effect for time (IL17, IL18). In the crossover analyses, cluster was either treated as a fixed effect (IL19–IL26) or a random effect (IL27, IL28), and cluster-period was analyzed as a random effect regardless of how cluster was treated in the model, as previously described.¹⁹

Simulation study

As the primary purpose of this article was to determine the most appropriate study design and analysis procedure for RIMDAMAL II, simulation parameters were selected that were consistent with the assumptions that were made prior to the start of the study. Minimal enrollment information (range of cluster sizes, average cluster size) was used to construct the simulation study. The final simulations had a total of 1317 subjects distributed across 14 clusters with a fixed number of subjects in each cluster and in each rainy season (supplementary material—simulation details, p. 1). A Poisson mixed-effects model was used to simulate individual counts of malaria episodes over two rainy seasons separately while maintaining the same within-cluster correlation across seasons. Such approach not only allowed for each season to be evaluated separately to explore differences in expected treatment effects between years but also allowed for the evaluation of parallel and crossover 2-year designs by combining both seasons into one dataset. The simulation parameters, scenarios, and analysis methods that were compared are summarized in Table 1, and the details are provided in the supplementary material along with example code. The analysis methods were run on 1000 simulated data sets for each scenario, and methods were compared based on the bias of the estimated effect, the power and Type I error rate, and the precision of the 95% CI as measured by the proportion of 95% CIs that include the true mean effect (the “coverage” probability).

Table 1.

Summary of simulation study.

Analysis methods were evaluated using the results from 1000 simulated data sets, each of which was analyzed using the analysis methods applied to the simulated number of episodes^a for each of the villages in the two treatment conditions. Simulation details and model code are given in the supplementary material. Any abbreviations that have been used for ease of readability in all following tables and figures have been defined here.

Scenarios simulated
Treatment effect		Rate ratio: eβ1 = 1.0, 0.9, 0.8, 0.7, 0.6, $\frac{0.619}{1.088}$
Number of clusters		6, 10, 14, 18
Effect of year		α: Year 1 = e0.0843–0.1054 year 2 = e 0.0843 – 0.1054
One rainy season		Separate analyses of the first- and second-year results
Two rainy seasons (parallel)		Analysis of combined Year 1 and Year 2 data
Two rainy seasons (crossover)		Analysis of data from a crossover design
Metrics evaluated
Bias		Difference between the estimated and true value for β1
Coverage		Proportion of 95% confidence interval that includes β1
Power		Probability of rejecting the null hypothesis: eβ1 = 1.0
Summary of models compared
Category	Name	Method of model fitting
MM	Mixed models	PL: Pseudo-likelihood
		PLKR: Pseudo-likelihood, Kenward-Roger correction
		ML: Laplace: Laplace approximation to the likelihood
		ML: AGQ-10: Adaptive Gaussian quadrature
GEEs	Generalized estimating equations
		Using model-based standard error
		Using empirical standard error
		Using MBN correction, proposed by Morel, Bokossa, and Neerchal
		Using FG correction, proposed by Fay and Graubard
	Cluster-level analyses
		Unweighted t-test
		Size weighted
		Variance weighted
		Adjusted residual

^aThe number of episodes was simulated to follow a Poisson distribution with mean rate λ_ijk denoting the rate with treatment i = (0,1) in village j = 1 ,…, 7 and subject k = 1 ,…, N_ij; X₁ = 0 satisfying log(λ_ijk) = α + β₁X_i + β₂X_ijk + u_ij, where X_i = 0 (control) or X_i = 1 (Ivermectin), and X_ijk = 0 (female) or X_ijk = 1 (male) and α = intercept; β₁ = log of the rate ratio treatment versus control; β₂ = log of the rate ratio male versus females; and u_ij = random village effect: u_ij ∼ N(0, 0.05 or 0.10).

Results

Generally, cluster-level and individual-level analyses with a small sample correction performed well in all settings. Results are shown in Figures 1–3 and are tabulated in Tables 2 and 3, as well as in Supplemental Table 1. For the maximum likelihood models, differences between the Laplace and Adaptive Gaussian Quadrature approaches were miniscule. Differences in bias are discussed, but all methods provided unbiased estimates, and observed differences can be attributed, in part, to simulation variability.

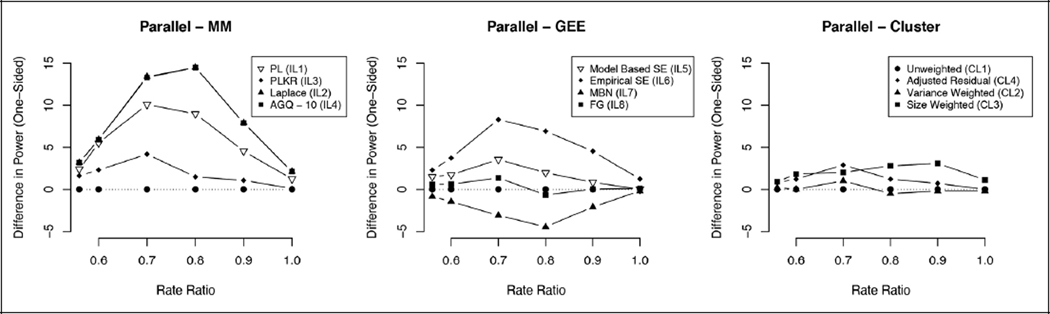
Figure 1. Difference in power relative to unweighted t-test (one rainy season).

Single-year graphs indicating the difference in one-sided power (in favor of protective ivermectin effect) for the three analysis frameworks, mixed-effects models (MM), generalized estimating equations (GEE), and cluster-level summaries relative to the unweighted t-test for a range of rate ratios. A rate ratio of 1 reflects the null model. The first rate ratio of approximately 0.56 reflects the expected rate ratio for RIMDAMAL II.

Table 2.

Two rainy seasons: comparison of the crossover and parallel designs.

	Bias	Coverage	Power	Type 1 error
Two-year parallel design
MM 1: PL (IL9)	−0.0018	93.10	99.10	7.92
MM 1: PLKR (IL11)	−0.0018	93.10	98.60	4.91
MM 1: Laplace (IL10)	−0.0025	91.10	99.40	10.10
MM 1: AGQ-10 (IL12)	−0.0025	91.10	99.40	10.10
MM 2: PL (IL17)	−0.0017	92.88	99.08	7.76
MM 2: PLKR (IL18)	−0.0017	92.88	98.58	4.59
GEE: Model-based SE (IL13)	−0.0027	92.96	98.39	5.25
GEE: Empirical SE (IL14)	−0.0027	90.95	98.59	7.77
GEE: MBN correction (IL15)	−0.0027	95.68	94.87	2.52
GEE: FG correction (IL16)	−0.0025	93.16	97.28	4.74
Cluster level: Treatment + Time (CL7)	−0.0030	89.80	99.70	16.40
Cluster level: Weighted treatment + Time (CL8)	−0.0040	86.60	99.50	17.10
Cluster level: Unweighted t-test (CL5)	−0.0030	94.70	97.50	4.70
Cluster level: Adjusted residual (CL6)	0.0050	94.00	98.20	5.20
Two-year crossover design
MM 3: PL (IL19)	0.0049	97.27	100.00	2.46
MM 3: PLKR (IL21)	0.0049	97.47	93.02	0.92
MM 3: Laplace (IL20)	0.0071	95.00	100.00	5.20
MM 3: AGQ-10 (IL22)	0.0071	95.00	100.00	5.20
MM 4: PL (IL27)	0.0061	97.37	100.00	2.37
MM 4: PLKR (IL28)	0.0061	97.47	100.00	1.86
GEE: Model-based SE (IL23)	0.0051	96.36	100.00	1.82
GEE: Empirical SE (IL24)	0.0051	88.54	100.00	9.09
GEE: MBN correction (IL25)	0.0051	96.57	100.00	2.03
GEE: FG correction (IL26)	0.0052	90.16	100.00	7.39
Cluster level: Treatment + Time + Fixed cluster (CL9)	−0.0030	90.90	100.00	5.80

PL: pseudo-likelihood; PLKR: pseudo-likelihood Kenward–Roger correction; AGQ-10:: Adaptive Gaussian Quadrature with 10 quadrature points; GEE: generalized estimating equation; SE: standard error; MBN: Morel, Bokossa, and Neerchal; FG: Fay and Graubard.

Bias, coverage, power, and Type I error rate for 2-year, 14-cluster, crossover, and parallel designs. These models were simulated from an assumed village random effect variance of 0.05. Mixed-effects model 1 (MM1): Time modeled as fixed, random effect for cluster; Mixed-effects model 2 (MM2): Random effects for cluster and cluster-period; Mixed-effects model 3 (MM3): Cluster modeled as fixed effect, random effect for cluster-period; Mixed-effects model 4 (MM4): Random effects for cluster and cluster-period. Labels in the parentheses (e.g. (IL9)) are meant to direct the reader to model descriptions in the text and code in the supplementary material.

Table 3.

Power and Type I error for different 2-year parallel design.

	6 clusters		10 clusters		14 clusters		18 clusters
	Power	Type 1 error	Power	Type 1 error	Power	Type 1 error	Power	Type 1 error
Models—Random effect of 0.05
MM 1: PL (IL9)	80.8	12.2	94.7	7.7	99.1	7.9	99.7	6.5
MM 1: PLKR(ILII)	58.0	4.5	89.3	4.4	98.6	4.9	99.4	5.2
MM 1: Laplace (ILI0)	88.0	18.4	96.6	11.2	99.4	10.1	99.9	8.3
MM 1: AGQ-10 (ILI2)	88.0	18.4	96.6	II.1	99.4	10.1	99.9	8.3
GEE: Model-based SE (ILI3)	59.2	5.1	89.0	4.6	98.4	5.3	99.3	5.2
GEE: Empirical SE (ILI4)	73.3	8.2	92.4	7.0	98.6	7.8	99.6	6.5
GEE: MBN correction (ILI5)	48.5	2.9	80.7	2.5	94.9	2.5	98.8	3.8
GEE: FG correction (ILI6)	56.1	3.6	87.8	3.6	97.3	4.7	99.3	4.8
Cluster level: Treatment + Time (CL7)	85.8	16.8	97.3	13.9	99.7	16.4	100.0	16.0
Cluster level: Weighted treatment + Time (CL8)	88.2	17.8	97.6	16.5	99.5	17.1	100.0	17.4
Cluster level: Unweighted t-test (CL5)	57.7	4.8	88.5	4.6	97.5	4.7	99.3	5.4
Cluster level: Adjusted residual (CL6)	57.8	4.8	88.2	4.6	98.2	5.2	99.3	5.2
Models—Random effect of 0.10
MM 1: PL (IL9)	60.0	10.1	77.4	8.7	90.6	6.8	93.8	6.8
MM 1: PLKR(ILII)	35.6	3.8	66.2	5.3	86.4	4.4	90.9	5.0
MM 1: Laplace (ILI0)	71.2	15.5	83.1	12.8	92.8	8.1	95.9	8.6
MM 1: AGQ-10 (ILI2)	71.2	15.5	83.1	12.8	92.8	8.1	95.9	8.6
GEE: Model-based SE (ILI3)	34.7	4.1	67.1	5.3	86.8	5.1	91.4	5.8
GEE: Empirical SE (ILI4)	51.0	7.9	74.0	8.6	89.2	6.6	92.1	6.9
GEE: MBN correction (ILI5)	28.8	2.8	54.6	2.4	75.6	2.3	86.6	3.5
GEE: FG correction (ILI6)	35.4	3.2	64.6	3.9	83.6	4.4	89.7	4.5
Cluster level: Treatment + Time (CL7)	65.8	14.2	86.8	16.9	96.1	15.7	98.1	15.4
Cluster level: Weighted treatment + Time (CL8)	71.7	16.9	88.4	18.9	96.5	17.0	97.9	19.4
Cluster level: Unweighted t-test (CL5)	32.9	4.0	61.9	5.2	83.1	4.2	90.2	4.6
Cluster level: Adjusted residual (CL6)	33.0	4.2	62.3	5.0	83.0	4.3	90.1	4.7

PL: pseudo-likelihood; PLKR: pseudo-likelihood Kenward-Roger correction; AGQ-IO: Adaptive Gaussian Quadrature with 10 quadrature points; GEE: generalized estimating equation; SE: standard error; MBN: Morel, Bokossa, and Neerchal; FG: Fay and Graubard; RIMDAMAL II: 2-year parallel follow-up of repeated ivermectin mass drug administrations for control of malaria.

Power and Type I error rates for 2-year parallel designs with a range of total cluster numbers (6, 10, 14, and 18) and two different village random effect variances for (0.05 and 0.10). The simulated intervention effect is the expected effect for RIMDAMAL II, as in Table 2. Labels in the parentheses (e.g. (IL9)) are meant to direct the reader to model descriptions in the text and code in the supplementary material.

One rainy season

With separate single-year analyses conducted in Year 1 and Year 2, all cluster-level analysis methods maintained a Type I error rate at or below 5%. Properties for the single-year analyses including Type I error rate are summarized in Supplemental Table 1. The size weighted Gaussian model had improved power over the other cluster-level models, along with a reduction in the coverage probability at 92.8%. The variance and size weighted t-test showed a slight improvement in power over the unweighted method but had a higher Type I error rate. For the individual-level models, the pseudo-likelihood models were the least biased relative to the maximum likelihood and GEE models with the GEE models having the most bias. The 95% CIs from the GEE with MBN correction had the highest coverage probability in both years, slightly better than the pseudo-likelihood models. The maximum likelihood models had the best power but the worst Type I error rate at 9.7%. The small sample corrections provided good control of the Type I error but somewhat lower power; the MBN GEE model had the lowest power (Figure 1).

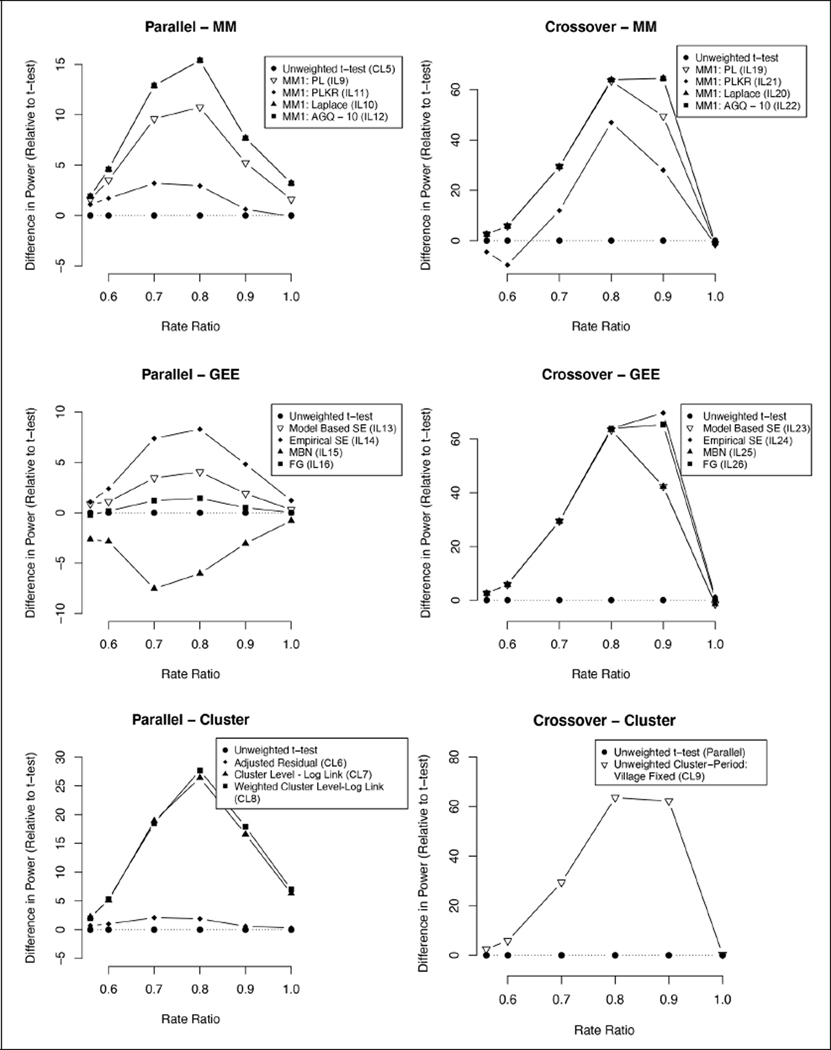
Two rainy seasons—parallel study design

In contrast to the single-season results, all cluster-level analyses were more biased than the individual-level models (Table 2). The inclusion of time as a covariate for the cluster-level models yielded lower coverage probability relative to the previously recommended cluster-level methods, which had the highest coverage probability. Although the time covariate cluster models had high power, they had unacceptably high Type I error rates. The adjusted residual method had improved power over the unadjusted t-test approach but had slightly greater Type I error. Consistent with the single-period analysis, the pseudo-likelihood models were the least biased and GEEs were the most biased. The GEE with MBN correction was the only model above 95% coverage (at 95.68%), outperforming the cluster-level analyses. For the pseudo-likelihood models, the coverage was slightly better when time was treated as a fixed effect instead of using a random effect for cluster-period. The mixed-effects models generally had greater power (Figure 2), but all models had power above 97% with the exception of the GEE with MBN correction. The GEEs and pseudo-likelihood models with two random effects were prone to convergence issues. Only the small sample corrections yielded Type I error rates below 5% (Table 2).

Figure 2. Difference in power relative to unweighted t-test (parallel versus crossover—two rainy seasons).

Graphs indicating the difference in one-sided power for the three analysis frameworks (MM, GEE, and cluster-level summaries) and two multi-season study designs (parallel versus crossover) relative to the parallel unweighted t-test for a range of rate ratios. A rate ratio of 1 reflects the null model. The first rate ratio of approximately 0.56 reflects the expected rate ratio for RIMDAMAL II. Models with two random effects were excluded because they were generally similar and difficult to discriminate in the figure.

Two rainy seasons—crossover study design

The cluster-level approach was the least biased of all crossover models but had low coverage probability at 90.90% and slightly elevated Type I error (Table 2). The pseudo-likelihood models again had the least biased estimates for the treatment effect, slightly better than the GEE. Regardless of random effect designation for time, the pseudo-likelihood models had exceptional coverage. All models with the exception of the pseudo-likelihood Kenward–Roger model had power at 100% (see Table 2 and Figure 2). The small sample size corrections had extremely conservative Type I errors, with the pseudo-likelihood Kenward–Roger model yielding a Type I error rate below 1%. The GEE models were highly prone to convergence issues relative to the other methods—around 7% did not converge.

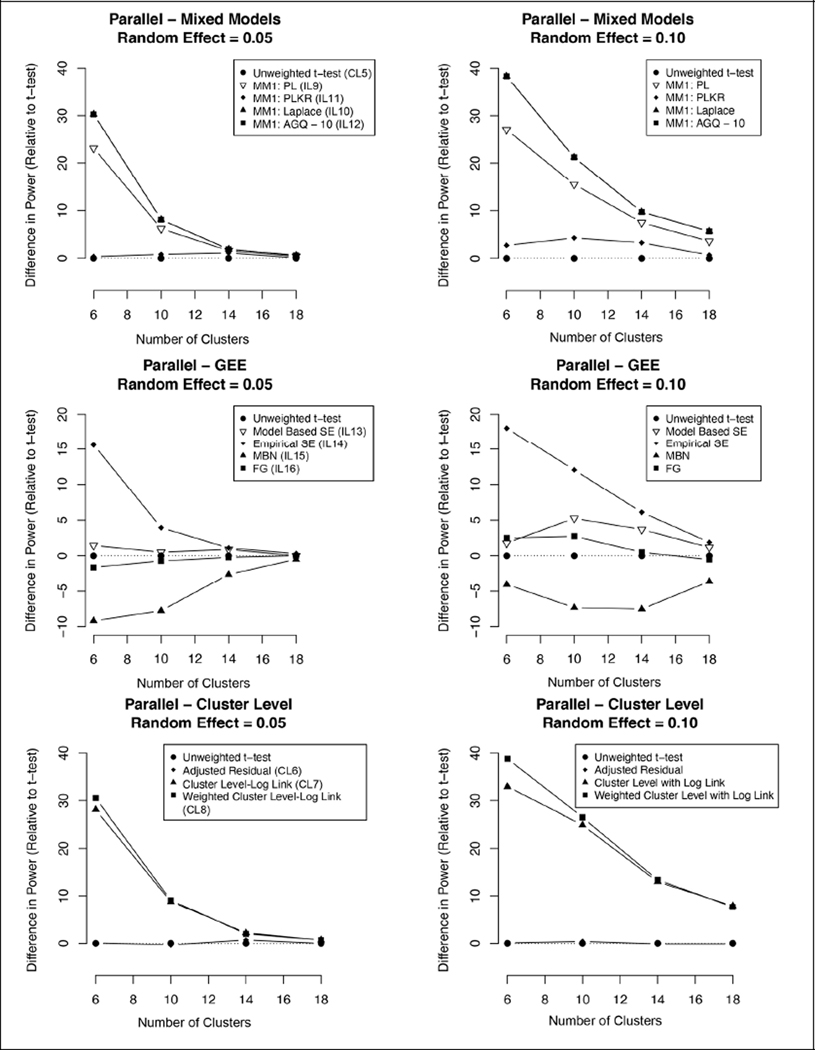
Two rainy seasons—additional simulations.

Applying the 2-year parallel design to a range of different numbers of clusters and increasing the expected cluster random effect variance from 0.05 to 0.10 yielded similar results. A similar trend was observed where Type I errors were excessive for individual-level models without a small sample correction (Table 3). Both the Kenward–Roger adjusted mixed-effects model and the unweighted t-test maintained acceptable Type I error rates and had similar power across different numbers of clusters and stronger within-cluster correlations, with the individual-level model slightly outperforming in power. The differences in power between methods were minimized as the number of clusters increased; this convergence toward similar power was slower for the simulations with greater within-cluster correlations (Figure 3). As the number of clusters increased, the individual-level models without small sample size adjustments had lower Type I error rates.

Figure 3. Difference in power relative to unweighted t-test (2-year parallel design—cluster sizes and random effect variance).

Graphs indicating the difference in one-sided power for the three analysis frameworks relative to the unweighted t-test for a range of cluster sizes and two different random effect variances. Only 2-year parallel designs are shown; crossover and single-year study designs with differing cluster and random effect sizes were not simulated.

Discussion

A study must be sufficiently powered, and the analysis methods must produce accurate and precise estimates of the intervention effects. In particular, analytic methods for CRTs with a small number of clusters must be chosen based on careful comparison of power, Type I error rate, bias, and the precision of the estimate (coverage probability).¹⁶ Our simulation study shows that previously recommended cluster-level analyses for rates and individual-level analyses that include a small sample correction both yield reliable power and control the Type I error rate without jeopardizing estimate precision.

Because RIMDAMAL II is conducted over 2 years, we have emphasized results relevant to the analysis of 2-year trials but briefly summarize the results for single-period designs. For cluster-level approaches, we recommend the unweighted t-test or the adjusted residual model if covariates are included. The variance and size weighted Gaussian models for cluster-level analysis did not confer any clear advantage over other approaches. Although the variance weighted approaches have been shown to perform better for cluster-level analysis with more unbalanced data,¹⁶ we concur that caution must be exercised when estimating variances in small sample settings.⁷ The pseudo-likelihood Kenward–Roger model is recommended for individual-level analyses, consistent with previous work.²³ In the RIMDAMAL II setting, the pseudo-likelihood Kenward–Roger model was less biased and had better power but worse coverage and Type I error compared to the unweighted t-test, suggesting that the strengths and weaknesses of either approach must be carefully considered when selecting an analysis method (as discussed below).

For the parallel two-period analysis, we again recommend the unweighted t-test or adjusted residual method in a cluster-level setting and the pseudo-likelihood Kenward–Roger approach with time as a fixed variable for an individual-level model. When examining the crossover study design, we found improved power and coverage over the parallel study design. This observation reflects the reduced variability of a within-cluster estimate of the treatment effect from a crossover design, which can in turn improve power.¹⁰ Since the cluster-level crossover approach performed worse than the individual-level models, we recommend an individual-level approach using the pseudo-likelihood Kenward–Roger method given the increased flexibility and improved coverage in this setting.

Although RIMDAMAL II is currently ongoing and designed as a parallel group trial, our results show that a crossover study can provide greater power given similar parameters. Such results suggest that crossover designs could potentially be considered for CRTs with count outcomes and a small number of clusters as a means to improve power—a finding that has been previously discussed with respect to continuous, binary, and count outcomes.^8–10,28 Although higher power is an important consideration, we acknowledge concern over the potential for unforeseen period and carryover effects that might introduce bias in a crossover design. In Burkina Faso, a washout period over an entire dry season could minimize carryover effects from a previous season of ivermectin distribution, but unforeseen carryover effects would be an important consideration. While the crossover design would allow for all clusters to receive the ivermectin intervention, the parallel design offers the ability to evaluate both the long-term effect of ivermectin and the robustness of the treatment in the same villages across years with potentially different levels of transmission. More complex simulation studies that further compare the merits of crossover studies relative to parallel studies in small sample settings may help define scenarios where one design is superior to the other.

Based on the additional simulations, it is clear that individual-level models should use small sample corrections when the number of clusters is small. Furthermore, the strength of within-cluster correlation should be considered when choosing an analysis method because it is clear that differences in correlation will impact the power and Type I error rate. Regarding the selection of methods that yield population-averaged (GEEs) versus cluster-specific interpretations (mixed-effects models), the estimand for both methods is the incidence rate ratio between treatment arms even though the methods differ in their approach to estimating that ratio. Ultimately, the selection of the analysis method may depend on a variety of factors (e.g. random effect complexity, strength of correlation, number of clusters, interpretation), and we did not conduct an in-depth evaluation of the direct relationships between these two models. Previous work discusses these kinds of models, and their relationship, in the context of count outcomes in greater detail.²⁹

For the analysis of RIMDAMAL II, we recommend an individual-level analysis using the pseudo-likelihood Kenward–Roger approach. While the individual-level and cluster-level analysis approaches had their strengths in the simulation study, the question of interest must also guide the analysis decision. As there are other relevant mechanisms of interest (effect of age, sex, direct effect of ivermectin for children old enough to receive it) on the outcome, an individual-level model is appealing because it allows for the simultaneous evaluation of these variables along with the treatment effect. We must note, however, that RIMDAMAL II is not powered to conduct inference on such secondary and tertiary questions of interest and similarly designed studies should be mindful of such issues. Notwithstanding these considerations related to power, the ability to simultaneously generate estimates on other variables is a valuable, hypothesis generating tool that only individual-level models can provide. While we recommend the individual-level analysis, we caution against the use of overly complex models in the context of small sample size CRTs.²³ Namely, additional nested random effects to account for households within clusters and repeated measurements on individuals may be too complex in small sample settings and sensitivity studies may be required to explore how more complex designs may impact the results. Furthermore, we note as others have that CRTs with small sample sizes may only be justified with very strong treatment effects.¹⁶

In the vector-borne disease community, when interventions must be randomized at the village level, it is vital to find a balance between the often-limited number of clusters and the often-conservative recommended statistical approaches. For our simulation study, we found that an individual-level model confers improved power and increased flexibility over the more conservative unweighted t-test approach and therefore recommend the more flexible approach. However, as with any simulation study, these results inform the properties of the analysis methods in the scenarios that were studied. Additional simulation studies are required to extend these results into other settings.

Limitations

This article focused on providing a recommendation for one particular study. We did not explore differences in cluster sizes and note that further exploration into the matter may help elucidate when weighting strategies are well justified. The simulation study uses data simulated from the assumed Poisson model, so results may not extend to misspecified models or to non-Poisson count data. We did not study additional sources of correlation such as household nested within a village. The simulation studies of this article would have to be extended to evaluate the merits, and possible disadvantages, of including additional levels of nesting within the village. In our discussions of coverage probability, we only utilized Wald CIs and did not investigate other score-based options that might provide better coverage probability. We note that carryover effects and cluster-period random effects were not explored in the simulation study, and studies of these effects are needed to fully evaluate analysis methods for crossover designs. Finally, we did not consider Bayesian approaches despite previous work suggesting strong performance in small sample settings.¹⁵ Although the RIMDAMAL results might suggest an informative prior for RIMDAMAL II, the differences in study design make it difficult to adequately recommend priors, an aspect of the Bayesian framework that is non-trivial because in studies with few clusters, informative priors may give biased estimates relative to frequentist methods.³⁰