Abstract
Many outcomes in arthroplasty research are analyzed as time-to-event outcomes using survival analysis methods. When comparison groups are defined after a time-delayed exposure or intervention, a period of immortal time arises and can lead to biased results. In orthopaedics research, immortal time bias often arises when a minimum amount of follow-up is required for study inclusion or when comparing outcomes in staged bilateral versus unilateral arthroplasty patients. We present an explanation of immortal time and the associated bias, describe how to correctly account for it using proper data preparation and statistical techniques, and provide an illustrative example using real-world arthroplasty data. We offer practical guidelines for identifying and properly handling immortal time to avoid bias.
Keywords: survival analysis, total joint arthroplasty, immortal time bias
Introduction
Immortal time bias is becoming more widespread in medical research[1]. It is pervasive in the literature and is often unrecognized by experts, including statisticians, peer reviewers and editors. Immortal time bias has previously been noted in the calculation of readmissions in the American College of Surgeons National Surgical Quality Improvement Program (NSQIP) database[2, 3]. It has also been noted as a common issue for analysis of staged bilateral arthroplasty[4, 5]. Some journals may have inadvertently contributed to the problem by requiring at least two years of follow-up for each patient, which in turn may be misinterpreted by researchers as suggesting patients with less than two years of follow-up should be entirely excluded from the analysis. This statement leads many researchers to consider excluding patients with less than 2 years of follow-up from their analyses, which introduces immortal time bias. Immortal time bias distorts the true event rates and leads to inaccurate estimates, comparisons, and conclusions. As this bias is created in the study design and analysis of the data, it is often correctable. Therefore, it is crucial to understand this phenomenon in order to recognize it as a reader or reviewer, and to avoid it as a researcher through careful study design and appropriate statistical analysis. This paper presents an explanation of immortal time bias, demonstrates the impact of this bias using real-world arthroplasty data, and provides guidelines for recognizing and preventing it when analyzing time-to-event outcomes.
Immortal time bias explained
The term immortal time applies to a period of time between the beginning of study observation and the last follow-up in which neither death nor the study outcome can occur[1, 6]. This arises when the subjects are divided into comparison groups based on a potential risk factor that is unknown at study entry but is identified at a later point during follow-up (e.g., staged bilateral THA vs. unilateral THA, or manipulation under anesthesia (MUA) following TKA vs. no MUA after TKA). This identification of a risk factor during follow-up will be hereafter referred to as an exposure, and individuals will be described as either “exposed” or “unexposed” depending on whether they had the risk factor identified during follow-up. In this setting, the time between study entry and determination of the risk group is termed “immortal time” because subjects had to both 1) survive long enough and be followed long enough to experience the exposure (i.e., determine which group they are in), and 2) not experience the study outcome or other precluding event prior to the exposure. In other words, a subject with a risk factor that is identified after the initiation of study follow-up has immortal time, and is guaranteed to not have had the study outcome prior to exposure.
Immortal time bias creates methodological challenges in many disease areas[7-9] including orthopaedics, and can lead to overestimation of the event rates in the unexposed group, underestimation of the event rates in the exposed group, or both. For example, consider a study examining the impact of manipulation under anesthesia (MUA) after primary total knee arthroplasty (TKA) on implant revision rates. In this hypothetical study design, MUA is the exposure and implant revision is the outcome of interest. Patients who underwent MUA (prior to revision TKA or last follow-up) are in the exposed group, whereas patients who underwent revision TKA, had final follow-up, or died prior to or without undergoing MUA are in the unexposed group. Thus, by definition, no patient in the exposed group (MUA) could have been revised, died, or had final follow-up prior to undergoing MUA, because if they had, they would be in the unexposed group. Hence the time between primary TKA and MUA is immortal time. If immortal time is not properly accounted for either in the study design or in the analysis, immortal time bias will arise[1]. This bias typically imparts an artificial advantage to the group with the immortal time (MUA group in the above example), but the direction of the bias can be in either direction. As a result, estimates of the true event rate and between-group comparisons are biased and inaccurate.
Examples of immortal time in orthopaedics research include:
Comparison of patients who underwent staged bilateral versus unilateral TJA[4]. The time between the first surgery and second contralateral surgery is immortal because the patient must remain alive and not be lost to follow-up after the first surgery in order to subsequently receive the second contralateral surgery.
Comparison of mortality in patients who underwent multiple revision surgeries[10]. The time between the first and second revision surgery is immortal because the patient must remain alive and under active follow-up after the initial revision surgery in order to subsequently receive the second revision surgery.
Evaluation of effectiveness of certain drugs in prevention of revision in patients who underwent TJA[11, 12]. The patient must remain alive, be free of implant revision surgery, and not be lost to follow-up after the initial surgery to be in the drug prescription group.
Comparison of early versus delayed surgery in patients with anterior cruciate ligament tears where patients must remain alive, be free of other knee surgeries, and not be lost to follow-up to be in the delayed reconstruction group[13].
Comparison of early versus delayed surgery in hip fracture patients[14].
Comparison of patients who underwent manipulation under anesthesia (MUA) following primary total knee arthroplasty (TKA) to patients who underwent primary TKA with no subsequent manipulation under anesthesia where patients must remain alive, be free of revision TKA surgery, and not be lost to follow-up prior to undergoing MUA.
The concept of immortal time bias is demonstrated graphically in Figure 1. Panel A depicts the follow-up timeline of two fictional cohorts from study entry to study outcome or last follow-up. The study population is divided into the two cohorts based on whether subjects experienced a particular exposure after study entry. The top line represents the unexposed group and shows that individuals in this cohort are at risk for the study outcome from study entry to last follow-up. The bottom line represents the exposed group. The period of time between study entry and the exposure is termed “immortal time”, because in order to be in the exposed group, subjects had to be followed long enough without experiencing the study outcome to have had the exposure. That is, if an individual experienced the study outcome or had his or her most recent follow-up prior to experiencing the exposure, he or she would by definition be included in the unexposed group; only those who experienced the exposure prior to the study outcome or last follow-up are in the exposed group. If this immortal time is incorrectly assigned to subjects in the exposed group, they will have an artificially lower outcome rate due to the inclusion of the event-free period of the immortal time. Sometimes, in an attempt to correct this bias, the immortal time period is simply excluded and the study follow-up for the exposed group is started at the time of the exposure (Figure 1, panel B). But rather than being a correction, this merely trades one problem for another. By excluding and ignoring the immortal time, subjects in the exposed and unexposed groups start their follow-up at different time points and have a different follow-up pattern. In this situation the resulting bias may favor either the exposed or unexposed cohort. For example, in a simulation study to illustrate immortal time bias in the setting of staged bilateral TJA, ignoring the immortal time between the first and second TJA surgery resulted in overestimation of the risk of revision and underestimation of the risk of death because these patients remain immortal between the first and second TJA surgery[4].
Figure 1,
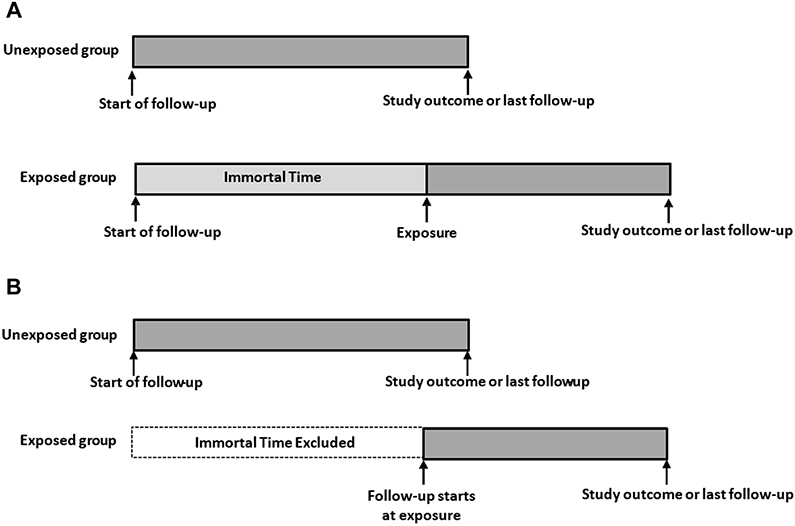
Panel A: Inappropriate assignment of immortal time; Panel B: Inappropriate exclusion of immortal time
Avoiding immortal time bias
When a period of immortal time is created due to a time-delayed exposure, proper accounting of this time requires that it is included with the unexposed group. In other words, all follow-up time from study entry to the point of exposure is assigned to the unexposed group, and only follow-up time from the point of exposure to the study outcome or last follow-up is assigned to the exposed group. This approach correctly assigns follow-up duration to the exposed and unexposed groups and eliminates the bias due to immortal time. However, since the follow-up of the exposed subjects is split between the unexposed and exposed groups, care must be taken to properly account for the exposure and follow-up in estimating rates and performing comparisons. We provide detail on how this should be done in the following paragraphs, first presenting methods for estimation of absolute risk, then discuss the technique for calculating relative risk.
For time-to-event outcomes, absolute risk is typically estimated using survival analysis, such as the Kaplan-Meier method, the cumulative incidence function, or person-years analysis. In these techniques, the required data for each study subject includes an event indicator denoting whether the individual experienced the outcome of interest or was censored at the last known follow-up, and a variable representing the duration of time from the beginning of follow-up to the study outcome or last follow-up. If calculations are to be made for 2 or more groups, the timing of the group definition (or exposure) must be carefully considered. If the exposure is known at baseline (e.g. the index surgery), the follow-up time for both groups begins at baseline and ends at the study outcome or last follow-up. However, if one or more groups are defined based on a time-delay exposure resulting in immortal time, such as an additional intervention some weeks, months, or even years after baseline or study entry, the follow-up time must be split between the unexposed and exposed groups. For those subjects, all follow-up time from study entry to the point of exposure should be assigned to the unexposed group, and only follow-up time from the point of exposure to the study outcome or last follow-up should be assigned to the exposed group (Figure 2). This can be executed in the following manner. Subjects in the exposed group will have two observations in the analysis dataset. The first observation will have a duration of time based on the date of study entry (baseline) to the date of the exposure, the group assignment will be to the unexposed group, and the outcome variable will indicate no event. The second observation will have a duration of time based on the date of exposure to the date of the study outcome or last follow-up, the group assignment will be to the exposed group, and the outcome variable will indicate either the study outcome or subject censoring, as appropriate.
Figure 2:
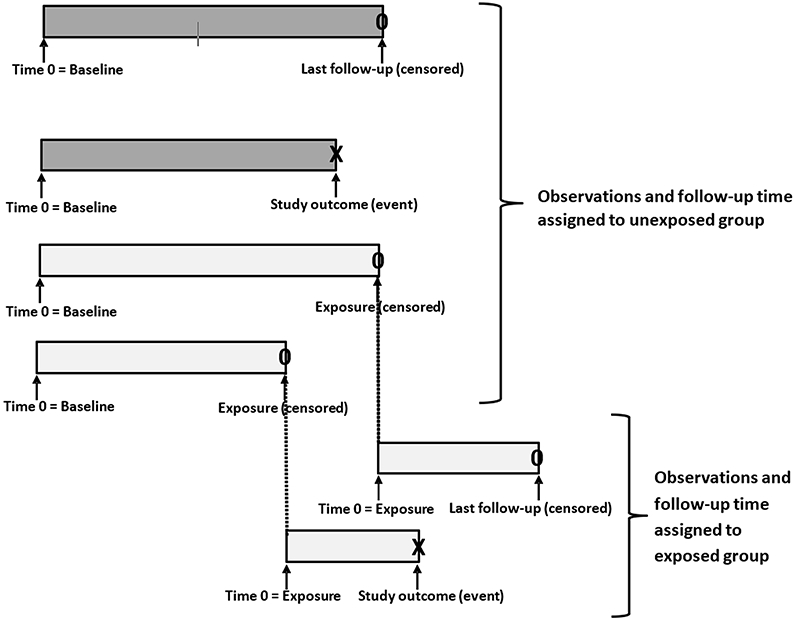
Proper assignment of follow-up time for exposed and unexposed subjects when immortal time is present
Alternatively, the absolute risk in the setting of immortal time can be estimated and displayed using a landmark analysis. As the name implies, this approach entails identifying a point in time after the beginning of follow-up at which subjects are divided into the exposed and unexposed groups and compared. This is accomplished as follows. First, any subject who experienced the study outcome, died, or were lost to follow-up prior to the landmark timepoint are excluded. Then, the remaining subjects are divided into 2 groups based on whether they experienced the exposure prior to the landmark timepoint or not. Finally, standard survivorship analysis such as Kaplan-Meier estimation is conducted starting at the landmark time point, with separate estimates being generated for the exposed and unexposed groups. Perhaps the biggest drawback to this approach is the selection of the landmark time point. It must be carefully chosen to yield meaningful results. If it is too close to the baseline, there will be very few subjects in the exposed group; if it is too far removed from the baseline, many subjects may have already experienced the study outcome or be lost to follow-up. Also, careful interpretation is required because the exposure group includes only those who experienced the exposure prior to the landmark. The timepoint used in the landmark analysis must be clearly stated as an assumption of the analyses. Often multiple landmark timepoints are used to provide a better understanding of how the choice of the landmark may have influenced the results.
As an example, consider the earlier hypothetical study evaluating the effect of MUA after primary TKA on implant revision rates. MUA is a time-based exposure since it occurs from a few weeks to several months or a year after TKA. A landmark is selected at 3 months post-TKA. Patients who underwent implant revision, died, or were lost to follow-up prior to the 3-month time point are excluded. The remaining patients are then divided into two groups according to whether they underwent MUA prior to the 3-month landmark. Standard Kaplan-Meier estimates are generated for each group with follow-up starting at the 3-month landmark.
Estimation of relative risk for time-to-event outcomes is commonly performed using Cox regression modeling and is reported using hazard ratios. When a comparison group is defined by a time-delay exposure, it needs to be included in the Cox regression model as a time-dependent covariate. While the execution of this analysis may differ between statistical software packages, the general principle is similar to that described above for calculating absolute risk using the Kaplan-Meier method. That is, follow-up time between the study baseline and the date of exposure must be included with the follow-up time of the unexposed group, and only the follow-up time from the date of exposure to the study outcome or last follow-up is counted for the exposed group. Thus, all subjects are considered to be in the unexposed group until the date of the exposure, at which point exposed subjects move into the exposed group. While software implementations vary, this is typically accomplished by organizing the required data using a counting process style.
Guidelines for the Researcher
It is recommended that researchers work with an experienced statistician when possible. The following guidelines provide basic instruction on recognizing and analyzing data in the presence of immortal time.
1. Recognizing immortal time
Carefully consider the study inclusion/exclusion criteria and the exposure or intervention that will be used to separate the cohort into groups for comparison. Are the inclusion criteria or the presence or absence of the exposure known for all patients at baseline (e.g., the date of the index surgery)? If the inclusion criteria require future knowledge or the exposure or group assignment is not known until sometime after baseline, then a period of immortal time exists, and the data will need to be collected, organized, and analyzed using appropriate methods.
2. Collecting the necessary data for proper analysis
For time-to-event outcomes, collect the data necessary for analysis using survivorship methodology. In addition to other study data, this includes the following key information:
The date of study entry or beginning of follow-up (e.g. the date of primary TJA)
The date of exposure or potential risk factor classification
The date of the study outcome (if it occurred)
The date of last clinical follow-up (if the study outcome did not occur)
Create variables to indicate risk group assignment and study outcome occurrence
3. Identifying the appropriate statistical method
To estimate event rates, use the Kaplan-Meier method. If a landmark approach will be used, determine the timing of the landmark – this effectively becomes the new baseline date for the analysis. To estimate the relative risk of the outcome in the exposed group versus the unexposed group, use Cox proportional hazards regression.
4. Correctly assigning follow-up time and performing the analysis
a. Kaplan-Meier estimation
The unexposed group consists of 1) the unexposed patients, with follow-up time defined as the time from the study baseline date (e.g. date of TJA) to either the date of the study outcome or last relevant follow-up, and 2) the exposed patients, with follow-up time defined as the time from the study baseline date to the date of the exposure (with the event indicator set to “no”). The exposed group consists of the exposed patients, with follow-up time defined as the time from the date of exposure to either the date of the study outcome or last relevant follow-up. After properly assigning the follow-up time to the 2 groups as outlined above, generate separate event rate estimates for the exposed group and unexposed group using the standard Kaplan-Meier approach.
b. Kaplan-Meier using a landmark
First, exclude any subjects that experienced the study outcome, died, or were last contacted prior to the landmark date. Divide the remaining patients into groups based on whether or not they experienced the exposure prior to the landmark date. Ignore any exposures that occurred after the landmark date. Define the study follow-up as the time from the landmark date to either the date of study outcome or last follow-up. Alternatively, the beginning of the study follow-up can start at the baseline date. After organizing the data and follow-up time, generate separate event rate estimates for the exposed group and unexposed group using the standard Kaplan-Meier approach. Kaplan-Meier curves may be drawn from the baseline study date or the landmark date.
c. Cox regression
In Cox regression, time-dependent covariates are used to avoid immortal time bias. Software implementation of this technique varies, but most commonly involves organizing the data using a counting process style. Once the data is properly organized, the Cox model with a time-dependent covariate is not difficult to perform[15].
Guidelines for the Reviewers and Readers
Examine the study inclusion/exclusion criteria. If the study excluded patients based on a minimum length of follow-up and then used survivorship methods for analysis, there is likely an immortal time bias issue.
Determine how the risk group is defined. Is the exposure known at study baseline, or did it occur at some point during follow-up? If the latter, then immortal time likely exists.
Did the authors recognize the presence of the immortal time and describe how it was accounted for in the methods section?
Were proper analysis techniques utilized?
Were the results reported and interpreted correctly and clearly?
Conclusion
In analysis of time-to-event outcomes, defining comparison groups based on an exposure that occurs after the beginning of the study follow-up results in a period of immortal time. This time between initial observation and exposure is termed immortal because, by definition, study outcomes cannot occur during this period. If this is not properly accounted for, event rates and comparisons will be biased and inaccurate. It is important to recognize and avoid this bias through proper study design, careful data organization using the guidelines presented above, and appropriate analytical techniques.
Supplementary Material
Figure 3,
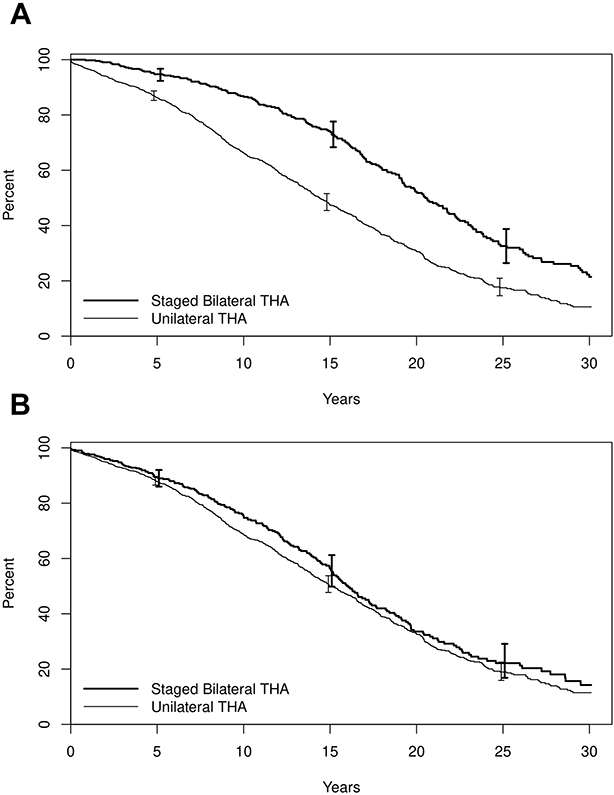
Panel A: Survival after initial THA for patients with bilateral THA (solid line) and unilateral THA (dashed line), demonstrating immortal time bias; Panel B: Survival after THA after correctly assigning follow-up time to the bilateral and unilateral THA groups.
Illustrative example of immortal time bias in total hip arthroplasty.
We will demonstrate the impact of immortal time bias using actual data comprised of a population-based cohort of patients that underwent either unilateral or bilateral total hip arthroplasty (THA). The aim of the analysis was to compare patient survival after THA among patients with unilateral vs staged bilateral THA. We show that starting follow-up at the time of the initial THA for the staged bilateral patients introduces immortal time bias. This cohort is comprised of 1933 patients who underwent THA on one hip only (n=1511) or on both hips (n=422). Among patients that underwent unilateral THA, 59% were female, and the mean age at the time of THA was 67.2 years. Within the subset of patients who underwent staged bilateral THA, 57% were female, and the mean age was 63.1 years. The outcome is patient survival after THA, with patients being followed from the date of THA to death, last follow-up, or end of study. The data were analyzed using Kaplan-Meier estimation. Figure 3, Panel A shows the Kaplan-Meier survival curves for the unilateral and staged bilateral groups, with the follow-up starting on the date of THA for the unilateral group and the date of the initial THA for the bilateral group. Within the staged bilateral group, the time between the initial THA and the THA on the contralateral side is ‘immortal time’, because, by definition these patients had to survive and be followed at least to the date of their contralateral THA. In this inappropriate inclusion of immortal time, the bias favors the patients in the bilateral THA group. The 15-year survival rate is 47% among patients who underwent unilateral THA compared to 74% among patients who underwent bilateral THA. When this data is analyzed correctly by starting follow-up at the date of the second THA for those with staged bilateral procedures and assigning the time between the initial THA and contralateral THA to the unilateral THA group, the resulting survival rates are much closer. The 15-year survival rate has increased to 50% among the unilateral THA patients and has decreased to 56% among patients with bilateral THA (Figure 3, Panel B). This much smaller unadjusted residual difference between groups may be explained in part by the differences in mean age and gender between the two groups.
Funding:
This work was funded by a grant from the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS) grant P30AR76312 and the American Joint Replacement Research- Collaborative (AJRR-C). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Suissa S. Immortal time bias in pharmacoepidemiology. American Journal of Epidemiology 167(4): 492, 2008 [DOI] [PubMed] [Google Scholar]
- [2].Lucas DJ, Haut ER, Hechenbleikner EM, Wick EC, Pawlik TM. Avoiding Immortal Time Bias in the American College of Surgeons National Surgical Quality Improvement Program Readmission Measure. JAMA Surgery 149(8): 875, 2014 [DOI] [PubMed] [Google Scholar]
- [3].Hugar LA, Borza T, Oerline MK, Hollenbeck BK, Skolarus TA, Jacobs BL. Resurrecting immortal-time bias in the study of readmissions. Health Services Research 55(2): 273, 2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].van der Pas SL, Nelissen RGHH, Fiocco M. Patients with Staged Bilateral Total Joint Arthroplasty in Registries Immortal Time Bias and Methodological Options. Journal of Bone and Joint Surgery-American Volume 99(15), 2017 [DOI] [PubMed] [Google Scholar]
- [5].Ravi B, Croxford R, Hawker G. Exclusion of patients with sequential primary total joint arthroplasties from arthroplasty outcome studies biases outcome estimates: a retrospective cohort study. Osteoarthritis and Cartilage 21(12): 1841, 2013 [DOI] [PubMed] [Google Scholar]
- [6].Levesque LE, Hanley JA, Kezouh A, Suissa S. Problem of immortal time bias in cohort studies: example using statins for preventing progression of diabetes. British Medical Journal 340, 2010 [DOI] [PubMed] [Google Scholar]
- [7].Yadav K, Lewis RJ. Immortal Time Bias in Observational Studies. Jama 325(7): 686, 2021 [DOI] [PubMed] [Google Scholar]
- [8].Dekkers OM, Groenwold RHH. When observational studies can give wrong answers: the potential of immortal time bias. Eur J Endocrinol 184(1): E1, 2021 [DOI] [PubMed] [Google Scholar]
- [9].Agarwal P, Moshier E, Ru M, Ohri N, Ennis R, Rosenzweig K, et al. Immortal Time Bias in Observational Studies of Time-to-Event Outcomes: Assessing Effects of Postmastectomy Radiation Therapy Using the National Cancer Database. Cancer Control 25(1): 1073274818789355, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Yao JJ, Hevesi M, O'Byrne MM, Berry DJ, Lewallen DG, Kremers HM. Long-Term Mortality Trends After Revision Total Knee Arthroplasty. Journal of Arthroplasty 34(3): 542, 2019 [DOI] [PubMed] [Google Scholar]
- [11].Prieto-Alhambra D, Lalmohamed A, Abrahamsen B, Arden NK, de Boer A, Vestergaard P, et al. Oral Bisphosphonate Use and Total Knee/Hip Implant Survival Validation of Results in an External Population-Based Cohort. Arthritis & Rheumatology 66(11): 3233, 2014 [DOI] [PubMed] [Google Scholar]
- [12].Lalmohamed A, van Staa TP, Vestergaard P, Leufkens HGM, de Boer A, Emans P, et al. Statins and Risk of Lower Limb Revision Surgery: The Influence of Differences in Study Design Using Electronic Health Records From the United Kingdom and Denmark. American Journal of Epidemiology 184(1): 58, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Sanders TL, Kremers HM, Bryan AJ, Fruth KM, Larson DR, Pareek A, et al. Is Anterior Cruciate Ligament Reconstruction Effective in Preventing Secondary Meniscal Tears and Osteoarthritis? American Journal of Sports Medicine 44(7): 1699, 2016 [DOI] [PubMed] [Google Scholar]
- [14].Leer-Salvesen S, Engesaeter LB, Dybvik E, Furnes O, Kristensen TB, Gjertsen JE. Does time from fracture to surgery affect mortality and intraoperative medical complications for hip fracture patients? An observational study of 73 557 patients reported to the Norwegian Hip Fracture Register. Bone Joint J 101-B(9): 1129, 2019 [DOI] [PubMed] [Google Scholar]
- [15].Fisher LD, Lin DY. Time-dependent covariates in the Cox proportional-hazards regression model. Annu Rev Public Health 20: 145, 1999 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


