Lin_F9: a Linear Empirical Scoring Function for Protein-Ligand Docking

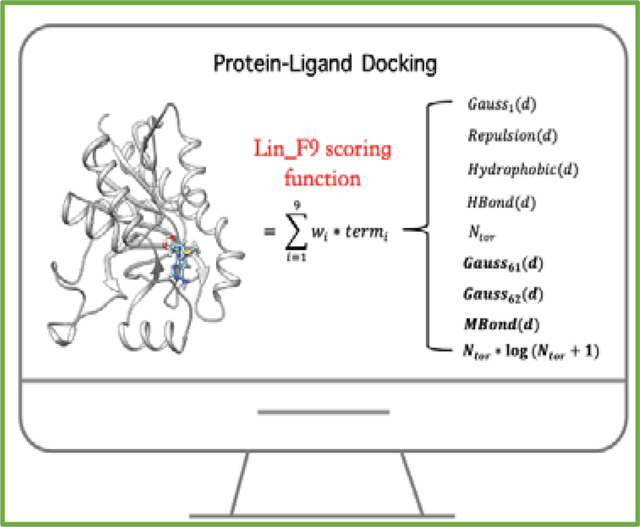
Abstract

Molecular docking is one of most widely used computational tools in structure-based drug design and is critically dependent on accuracy and robustness of the scoring function. In this work, we introduce a new scoring function Lin_F9, which is a linear combination of 9 empirical terms, including a unified metal bond term to specifically describe metal-ligand interactions. Parameters in Lin_F9 are obtained with a multi-stage fitting protocol using explicit water-included structures. For the CASF-2016 benchmark test set, Lin_F9 achieves the top scoring power among all 34 classical scoring functions for both original crystal poses and locally optimized poses with Pearson’s correlation coefficient (R) of 0.680 and 0.687 respectively. Meanwhile, in comparison with Vina, Lin_F9 achieves consistently better scoring power and ranking power with various types of protein-ligand complex structures that mimic real docking applications, including end-to-end flexible docking for the CASF-2016 benchmark test set using a single or an ensemble of protein receptor structures, as well as for D3R Grand Challenge (GC4) test sets. Lin_F9 has been implemented in a fork of Smina as an optional built-in scoring function which can be used for docking applications as well as for further improvement of scoring function and docking protocol. Lin_F9 is accessible through: https://yzhang.hpc.nyu.edu/Lin_F9/.

Graphical Abstract

Introduction

Molecular docking approach that ‘dock’ small molecules into the binding site of macromolecular target and ‘score’ their potential interactions are widely used in hit identification and lead optimization.^1–8 A most critical component of molecular docking is its scoring function. To date, a whole spectrum of scoring functions has been developed based on different assumptions and can be classified into one of the following four main categories⁹: (i) physics-based methods, (ii) empirical scoring functions, (iii) knowledge-based statistical potentials, (iv) machine-learning scoring functions. The first three types (i, ii and iii) can be grouped as classical scoring functions and they usually adopt a linear form, which is a linear combination of several force-field or empirical descriptors.^10–13 Because of the superior learning capacity on large train sets, machine-learning scoring functions developed in recent years outperform classical scoring functions for scoring accuracy on crystal structures.^14–24 However, it remains challenging for machine learning scoring functions to give accurate predictions on novel systems that are largely different from the structures in the training set. Several comparative studies^25–28 demonstrate that the scoring performance of machine learning scoring functions dropped with the decrease of the similarities between the training and test sets, while classical scoring functions are less sensitive to these differences. In addition, most machine-learning scoring functions are primarily used for re-scoring docked poses instead of being implemented as a sole scoring function for end-to-end docking. Thus, it is of significant interest to develop classical scoring functions.

Autodock Vina²⁹ is a lightweight, widely used open-source program for protein-ligand docking. Extensive comparative studies^30–35 indicate that the Vina scoring function performs quite well in docking tasks, but its scoring and ranking performances is less satisfactory. Inspired from the simple form of Vina’s empirical scoring function, a major motivation for the current work is to develop a linear empirical scoring function to improve its scoring performance by introducing new empirical terms to overcome some of its limitations to some extent, such as the description of metal-ligand interactions and mid-range interactions. In the Vina scoring function, as shown in Figure 1, #torsion (N_tor) term, which represents the penalty of ligand flexibility, is put in the denominator. Here we aim to treat N_tor term as one part of the linear form in our scoring function. Meanwhile, previous studies have indicated that more than 85% protein-ligand crystal structures have at least on water molecule involved in ligand binding site and proper treatment of water is beneficial for binding pose identification and affinity prediction.^36–47 However, for Vina and other common scoring functions, explicit water molecules were removed in their training sets. In this work, explicit water molecules are selected and treated as part of protein structure in our training set.

Figure 1.

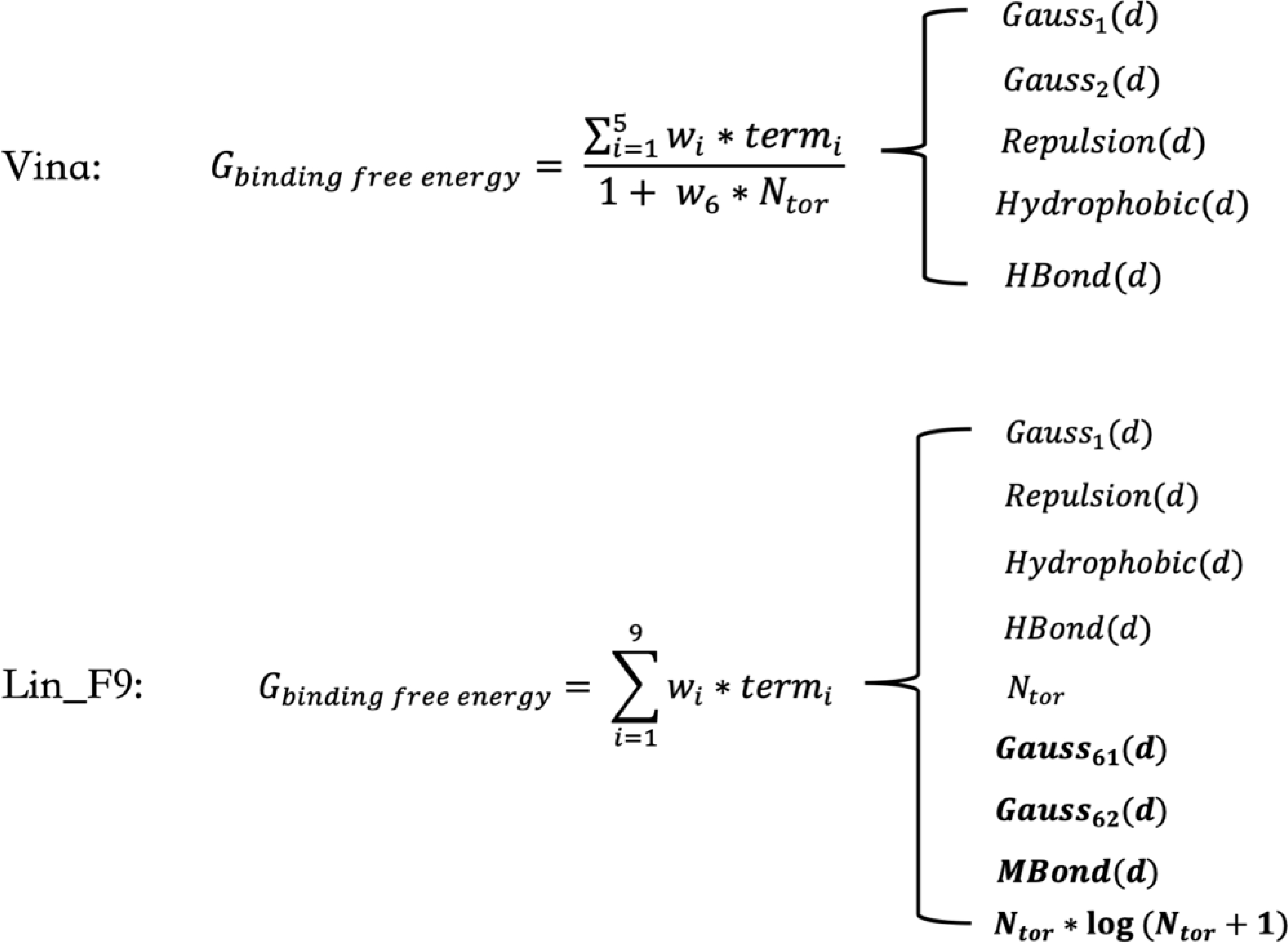
Illustration of scoring function forms of Autodock Vina and Lin_F9. The introduced new empirical terms in Lin_F9 are highlighted in bold font. w_i represents weight for the corresponding empirical term. d is atom pair center distance – sum of atomic radii for protein-ligand atom pair. N_tor is number of active torsions for ligand. Hbond represents hydrogen bond term. Mbond represents metal bond term. A detailed definitions of function forms of Gauss, Repulsion, Hydrophobic, Hbond and Mbond are illustrated in Figure 3.

Our scoring function development is based on Smina,⁴⁸ a fork of Vina, and starts with the construction of training data of protein-ligand complexes, which includes three subsets: subset A includes 204 crystal complex structures, in which no metal atom is in the binding site and the ligand has no more than 6 rotational bonds; subset B has 96 non-metal crystal complex structures containing flexible ligands (N_tor > 6); subset C is a metalloprotein subset. Based on the training subset A, machine-learning techniques are applied to explore new descriptors to improve the scoring performance on the training subset A. Two new gauss terms (Gauss₆₁ and Gauss₆₂) are used to replace Gauss₂, to make approximations for mid-range interactions. Then by mainly using subset B as a validation set, we added another torsion penalty term $N_{tor}·\mathrm{l}\mathrm{o}\mathrm{g}(N_{tor}+1)$ with a very small weight to correct the affinity of ligands with large #torsion. Finally, by differentiating metal atom from hydrogen bond donor atoms (in Vina, metal atom is treated as hydrogen bond donor), we introduce a unified metal bond term to specifically describe metal-ligand interactions based on the training subset C.

In the following, we describe the computational details for the development and extensive tests of our new scoring function Lin_F9. Lin_F9 achieves the top scoring power in comparison with other classical scoring functions on CASF-2016 benchmark³³, and it also performs relatively well for ranking power and docking power tests. Meanwhile, in comparison with Vina, Lin_F9 yields consistently better scoring power and ranking power with various types of complex structures such as locally optimized poses, flexible docking poses and ensemble docking poses, which mimic the real docking application. In addition, comparing with Vina, Lin_F9 performs consistently better on metalloprotein test set.

Methods

Training Data Preparation

The training set of protein-ligand complexes consists of three subsets:

• Subset A is a non-metal protein subset, which includes 204 crystal complex structures without any metal in ligand binding site and the ligand has no more than 6 rotational bonds. This subset is curated from PDBbind v2018 general dataset,^{33, 49, 50} and it encompasses 45 different types of prevailing protein targets, in which each target has abundant structures in PDBbind v2018 general dataset and hundreds of bioactive molecules in ChemBL 25 database⁵¹. For this non-metal subset, the negative logarithms of dissociation constants (pK_d) range from 1.31 to 9.82, covering around 8.5 orders of magnitude range of K_d.

• Subset B is another non-metal protein subset, which has 96 non-metal crystal complex structures containing flexible ligands with more than 6 rotatable bonds (N_tor > 6). Its dataset curation protocol is the same as subset A, as illustrated in Supporting Information and Figure S1.

• Subset C is a metalloprotein subset, which includes 137 zinc complexes, 22 iron (III) complexes, 28 calcium complexes and 8 manganese complexes. For this subset, metal ions are closely located to the ligands (< 4 Å). Zinc and manganese complexes are curated from PDBbind v2018 general dataset^{33, 49, 50} by the same protocol for the non-metal subset (see Figure S1). Iron and Calcium complexes are obtained from the PDBbind v2019 general dataset. Metal ions are treated as part of protein structure in subset C.

Each protein-ligand complexes in the training set has a crystal structure with overall resolution < 2 Å (except for iron (III) complexes with overall resolution < 2.5 Å), and has experimentally measured dissociation constant (K_d) binding data. To incorporate effects of explicit water molecules, each water molecule in the crystal structure which has a negative Vina score is kept as part of protein structure. The K_d value is converted to the molar Gibbs free energy ($\Delta \mathrm{G}$) with units of kcal/mol for training. It should be noted that all experimental binding data used in this work are directly obtained from PDBbind database. In the PDBbind dataset, only single binding data is provided for each complex, thus we have not considered the variation of experimental binding data in our scoring function development.

Scoring Function Development

To develop and parameterize the new scoring function Lin_F9, we have employed a multi-stage exploration and fitting protocol, as illustrated in Figure 2 and summarized below. More details can be found in Supporting Information.

Figure 2.

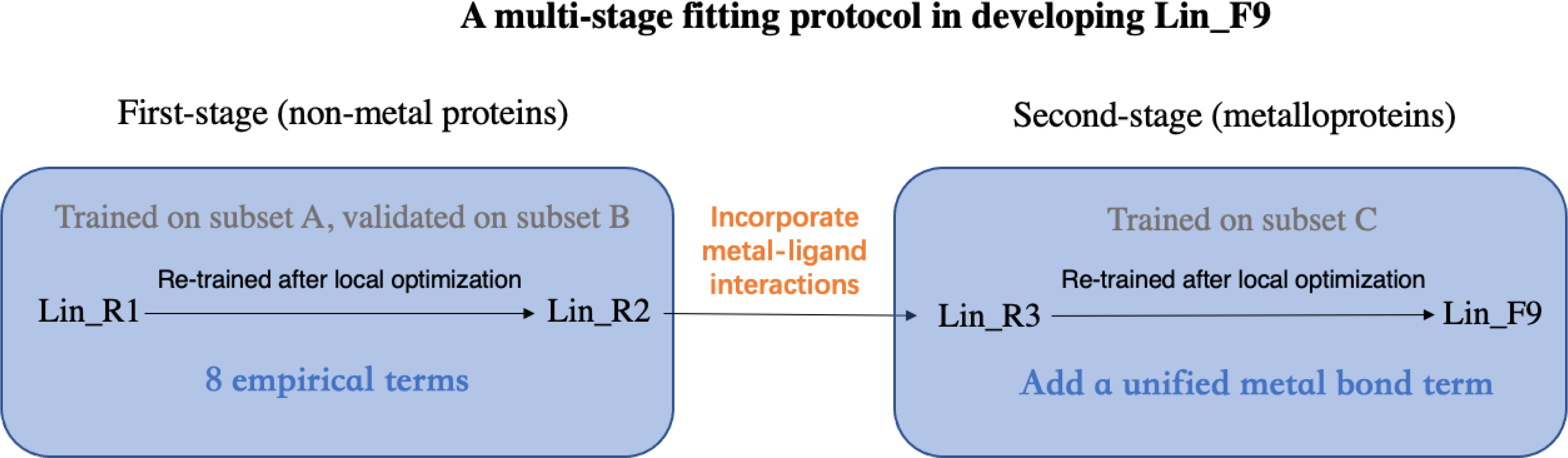
Illustration of the Lin_F9 scoring function development protocol.

First-Stage Scoring Function Development for Non-Metal Complex

Based on the crystal structure of non-metal training subset A, knowledge-based statistical potential terms (defined as a set of protein-ligand atom pair counts in different distance ranges and a ligand torsion count term, shown in Figure S2) are first explored via Random Forest approach⁵² to parameterize corrections to the Vina score, and several mid-range interaction terms (distance in [8, 12 Å] and [4, 8 Å] ranges) are found to be ranked at the top in correcting the Vina score by Permutation feature importance method⁵³. In further exploration, 21 terms, which consists of top 20 features and Vina score, are used to develop a linear scoring function by simple linear regression on subset A. In comparison with Vina, the developed linear model achieves better scoring performance (shown in Table S1) when tested on non-metal subset B and metalloprotein subset C. Despite this linear model cannot be directly implemented in docking program, its mid-range interaction terms give us insights into new feature exploration. Thus we are motivated to introduce new gauss terms to approximate such interactions to be combined with other Vina terms for further scoring function development. Based on our explorations, we replaced the Gauss₂ term in Vina with two new gauss terms, Gauss₆₁ (o=2.5, w=0.5) and Gauss₆₂ (o=5, w=0.5). Together with other five Vina empirical terms (Gauss₁, Repulsion, Hydrophobic, HBond, N_tor) as illustrated in Figure 1, the weights for the resulting seven empirical terms are fitted to the Vina locally optimized poses of non-metal training subset A using Ridge linear regression. Vina locally optimized poses are obtained by Vina local energy minimization, which is used to minimize steric clashes between the protein molecule and the ligand molecule in crystal complex structures. In order to avoid the overfitting, Ridge linear regression with cross-validation is employed for training, RidgeCV implemented in Scikit-learn package⁵⁴ is used with the default parameters, except for fit_intercept-False and CV=10 used in our fitting. Compared with Lasso regression, Ridge regression does not enforce some small weights to be zero.

Next, by evaluating the model’s performance on non-metal subset B, we find that putting #torsion (N_tor) term into the linear form over-estimates the affinity of ligands with large #torsion. To tackle this issue, another torsion penalty term N_tor∙log(N_tor+1) with a small weight of 0.02 is added as the eighth empirical term to the scoring function, which decreases Root-Mean-Square-Error (RMSE) for the subset B (N_tor > 6) while maintains the scoring performance of training subset A (N_tor <= 6), is added into the scoring function, leading to Lin_R1. Then we use Lin_R1 to re-optimize poses in the non-metal training subset A, and weights for the first seven terms in Lin_R1 are re-trained with re-optimize poses. This version is called Lin_R2, a linear scoring function that form the main components of our Lin_F9 scoring function.

Second-Stage Scoring Function Development for Metalloprotein Complex

Subset C (metalloprotein training data) is used for the second-stage scoring function development. Here, a unified metal bond term is added as the 9^th empirical term to specifically describe metal-ligand interactions for metalloprotein complex. In Vina scoring function, metal atoms are treated as general hydrogen bond donor. Here we differentiate metal atoms from hydrogen bond donor, and use a unified metal bond term to specifically describe the metal-ligand interactions. The metal bond term, as similar in hydrogen bond term, uses a step function for atom pair between metal atom and polar atom (N, O atom type) of ligand. The weight and parameters of the metal bond term are fitted with the subset C. It should be noted that, different from local optimized poses used in first-stage scoring function development, no optimization is performed to adjust crystal ligand pose in this stage. The reason is that metal atom radii are also tuned in this stage. The details of second-stage scoring function development are as follows: Firstly, 137 zinc complexes of subset C are trained to determine the weight of the metal bond term. Parameters, such as left and right inflexion points (g and b in Figure 3A) of step function, as well as Zn²⁺ radius, are tuned under systematically sampling to decrease the RMSE on the zinc training data set. After training, weight and parameters of step function are determined for this metal bond term. Then, Fe³⁺, Ca²⁺ and Mn²⁺ radii are respectively determined using 22 iron complexes, 28 calcium complexes and 8 manganese complexes in subset C. This version is called Lin_R3, comprising of Lin_R2 and a unified metal bond term. Finally, the weight of metal bond term is retrained using Lin_R3 local optimized poses. This leads to our developed scoring function, Lin_F9, which is used for performance evaluations on a variety of test sets.

Figure 3.

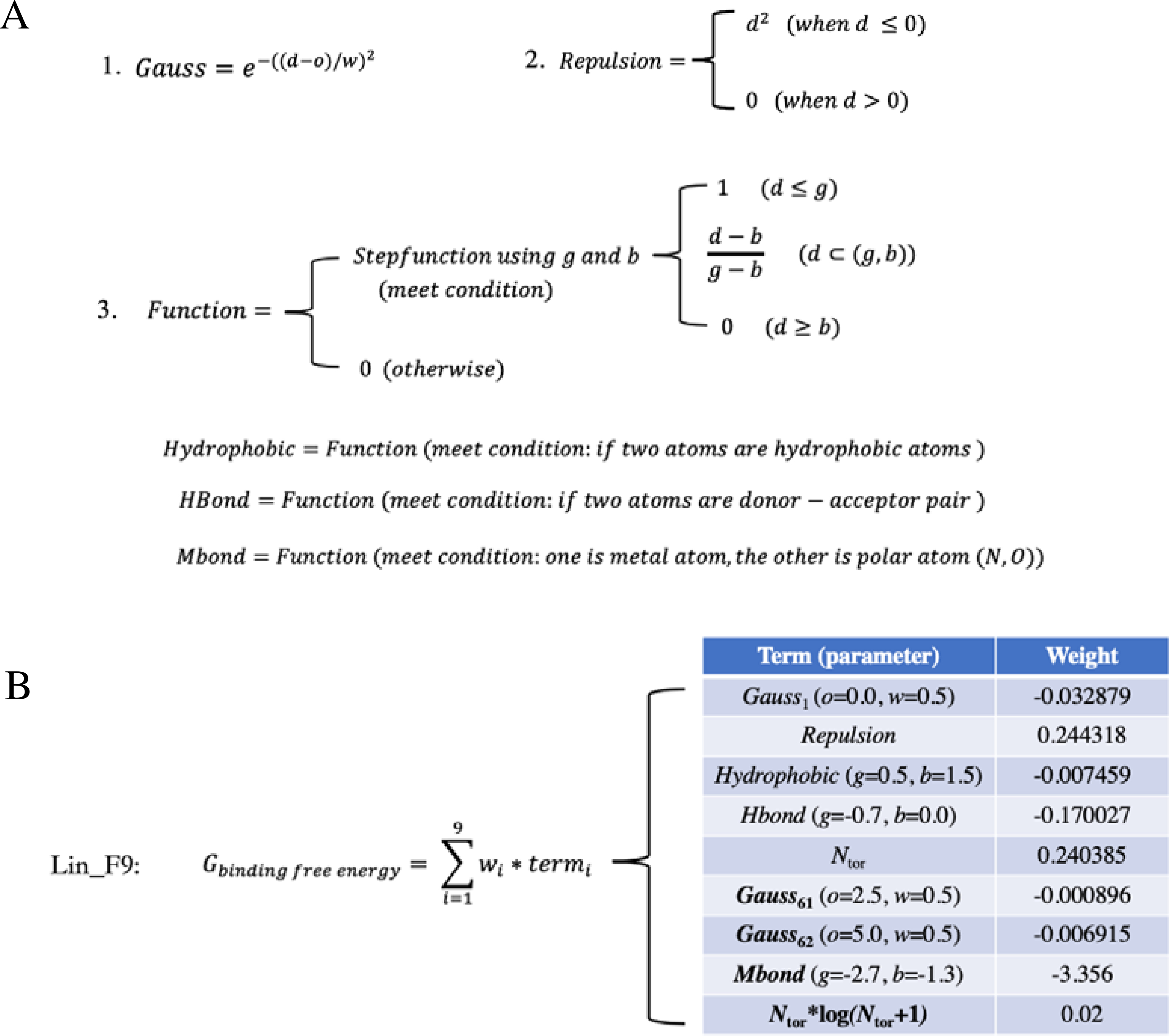
Definition of function form and parameter and weight of empirical terms in Lin_F9 scoring functions. (A) Function forms of (1) Gauss, (2) Repulsion and (3) a shared Function form for Hydrophobic, Hbond and Mbond terms. d is atom pair center distance – sum of atomic radii. o and w are parameters for gauss form. g and b are parameters for step-function form. (B) Parameter and weight of empirical terms in Lin_F9 scoring functions.

Evaluation Methods

Lin_F9 has been implemented as an optional built-in scoring function within a fork of Smina⁴⁸ docking suite. Several test sets are used to evaluate our Lin_F9 scoring function in different aspects. For our training set described in Training Data Preparation, it has no overlap with the following test sets. In addition, similarity analysis between training and test datasets is measured by two different metrics (protein sequence similarity and ligand shape similarity)²⁶ and presented in Supporting Information and shown in Figure S4. Lin_F9 scoring function predicts the changes in Gibbs free energy ($\Delta \mathrm{G}$) upon binding in units of kcal/mol, we converted its prediction to a pK_d value as follows:

$$\Delta G=-RTln{K}_d$$

$$p{K}_d=-{log}_{10}\left(\mathrm{e}\mathrm{x}\mathrm{p}\right(\Delta G/RT\left)\right)$$

where R = 0.001987 kcal K⁻¹ mol⁻¹ is the gas constant and T is the temperature in Kelvin, we assume a standard temperature of 298K.

In evaluation of metrics for test set, the bootstrapping method was chosen to analyze the confidence interval in evaluation results. We estimated the two-sided 90% confidence interval by taking 10,000 bootstrap samples of the test set, computing the corresponding metric for each sample. And taking the 5^th and 95^th percentiles of the range of bootstrapped metric as the 90% confidence interval. The confidence interval results are available in Supporting Information (Table S9 to S15).

CASF-2016 Benchmark Standard Tests

The comparative assessment of scoring functions (CASF) benchmark^30–33 provides key metrics for evaluation of scoring function for different tasks. CASF-2016³³ is the latest version of CASF benchmark. More than 30 classical scoring functions have been tested on this benchmark. The comparisons of scoring power, ranking power and docking power with other major scoring functions are carried out for evaluation in this study. Scoring power is used to evaluate the linear correlation between predicted binding affinity and experimental measured binding affinity by the Pearson’s correlation coefficient (R). Ranking power refers to the ability of a scoring function to correctly rank the known ligands of a certain target protein by their predicted binding affinities. The CASF-2016 core set includes 57 targets and 5 known ligands for each target. The average Spearman’s rank correlation coefficient (ρ) over all 57 targets is used as the quantitative indicator of ranking power. Docking power refers to the ability of a scoring function to identify the native pose among computer-generated decoys. It calculates the success rate of top scored poses similar with the crystal pose (RMSD < 2 Å). For standard tests of CASF-2016 benchmark, scoring and ranking powers are evaluated on the original crystal ligand poses as well as on the locally optimized poses, which are obtained by local optimization of crystal poses.

Extended Docking-Scoring Tests of CASF-2016 Benchmark

Besides standard assessment of Lin_F9 scoring function on CASF-2016 benchmark, we also evaluate the scoring and ranking performances with various types of protein-ligand complex structures that are generated by flexible re-docking as summarized in Table 1. The flexible re-docking poses in dry and water environment are obtained using flexible re-docking of CASF-2016 core set. In docking preparation for flexible re-docking, both the ligand conformer and protein conformation come from the corresponding crystal protein-ligand complex. Considering that real docking applications often employ computer-generated ligand conformers as inputs for docking, the end-to-end (E2E) docking protocol combines ligand conformer generation and flexible docking. For ligand conformer generation, it starts with ligand 2D SDF file, and OpenBabel 2.4.1 version⁵⁵ is used to generate maximum 10 conformers per ligand using genetic algorithm with the default options. Then all these conformers are docked to the target protein by flexible ligand docking. The best-scored pose is used for scoring and ranking powers evaluation. For docking power evaluation, the Root-Mean-Square Deviation (RMSD) between best-scored pose and crystal pose is calculated using DockRMSD.⁵⁶

Table 1.

Different docking-scoring tests of CASF-2016 benchmark.

Name	Ligand conformation for each ligand	Protein conformation for each ligand	Docking method
flexible re-docking	native ligand pose	native protein structure	flexible ligand docking
E2E docking	Computer-generated maximum 10 conformersa	native protein structure	flexible ligand docking
ensemble (E5) docking	Computer-generated maximum 10 conformers	5 protein structures (include native protein structure)	flexible ligand docking
ensemble (E4) docking	Computer-generated maximum 10 conformers	4 non-native protein structures	flexible ligand docking

^aComputer-generated maximum 10 conformers per ligand using OpenBabel.

In further evaluation, ensemble docking tests on CASF-2016 core set are carried out with the above E2E protocol. For each ligand in CASF-2016 core set, it was sequentially docked into all 5 protein structures (one native protein structure and 4 non-native protein structures) of the corresponding target in E2E manner. The best-scored pose is used for scoring and ranking performance evaluation. Meanwhile, the performance is also evaluated by excluding native protein structure in ensemble receptor structures. Altogether, docking protocols of (I) flexible re-docking, (II) E2E docking, (III) ensemble docking using all 5 protein structures and (IV) ensemble docking using 4 non-native protein structures are summarized in Table 1.

Metalloprotein Test Set

Metalloprotein test set is curated to evaluate the scoring performance of Lin_F9 on metalloprotein-ligand complexes. Both the metalloprotein train set and test set are curated simultaneously using the same data curation protocol discussed in Training Data Preparation and Supporting Information, except that complex structures with K_d binding data and K_i binding data are, respectively, prepared as training subset C and metalloprotein test set. This test set consists of 222 zinc complexes, 14 iron (III) complexes, 12 calcium complexes and 13 manganese complexes. In addition, an additional zinc metalloprotein test set are obtained from CASF-2016 core set³³. It consists of 20 protein-ligand complexes from 4 zinc metalloprotein families (Alpha-mannosidase 2, Thermolysin, Carbonic anhydrase 2, and Macrophage metalloelastase).

D3R GC4 Datasets

Drug Design Data Resource (D3R)^57–60 is a platform, which aims to promote computer aided drug discovery (CADD) by providing large and high-quality protein-ligand binding data sets as well as organizing competition to test CADD workflows in an open and blinded manner. In D3R Grand Challenge 4 (GC4),⁶⁰ two challenge inhibitor datasets regarding to two different protein targets, beta secretase 1 (BACE1) and Cathepsin S (CatS), are provided for pose prediction and affinity ranking competition. Our group has participated in GC4 BACE1 Sub-challenge for pose prediction of 20 macrocyclic BACE inhibitors and affinity ranking of 154 macrocyclic BACE inhibitors. The pose prediction of our submitted model (submitted id: ojsv7) achieved an average RMSD of 1.01 Å, but the affinity ranking of whole BACE1 dataset was less satisfactory (Spearman’s $\rho =$ 0.25, Kendall’s $\tau =$ 0.18). In further exploration after competition, the average RMSD decreased to 0.74 Å using a similarity-based constraint docking method.⁶¹ Based on our predicted complexes of whole BACE1 dataset, we test the affinity ranking performances of the Lin_F9 scoring function and Vina (as comparison). In addition, we also use two other participant’s (Max Totrov group⁶² and Guowei Wei group⁶³) predicted complexes (submitted id: 5rdda and tjny7) for affinity ranking evaluations. In addition, the affinity ranking performances on the CatS dataset (459 inhibitors) are evaluated as well, based on predicted poses obtained from Top submitter’s model (Max Totrov group,⁶² submitted id: x4svd) in D3R website. It should be noted that all the poses are locally optimized by each scoring function for corresponding scoring.

Results and Discussion

Lin_F9 Empirical Scoring Function

Our developed Lin_F9 scoring function consists of 9 empirical terms, in which function form and parameter and weight of each term are illustrated in Figure 3. Compared with Vina scoring function, the Gauss₂ (o=3.0, w=2.0) term is replaced with two new gauss terms, Gauss₆₁ (o=2.5, w=0.5) and Gauss₆₂ (o=5.0, w=0.5), to make approximations for mid-range interactions. A new torsion penalty term N_tor∙log(N_tor+1) with a small weight of 0.02 is added to Lin_F9 scoring function to correct penalty for flexible ligand. In addition, a unified metal bond term is added to specifically describe metal-ligand interactions in metalloprotein complex. This metal bond term uses a step function for atom pair between metal atom and polar atom (N, O atoms) of ligand.

Feature analysis for binding affinity prediction

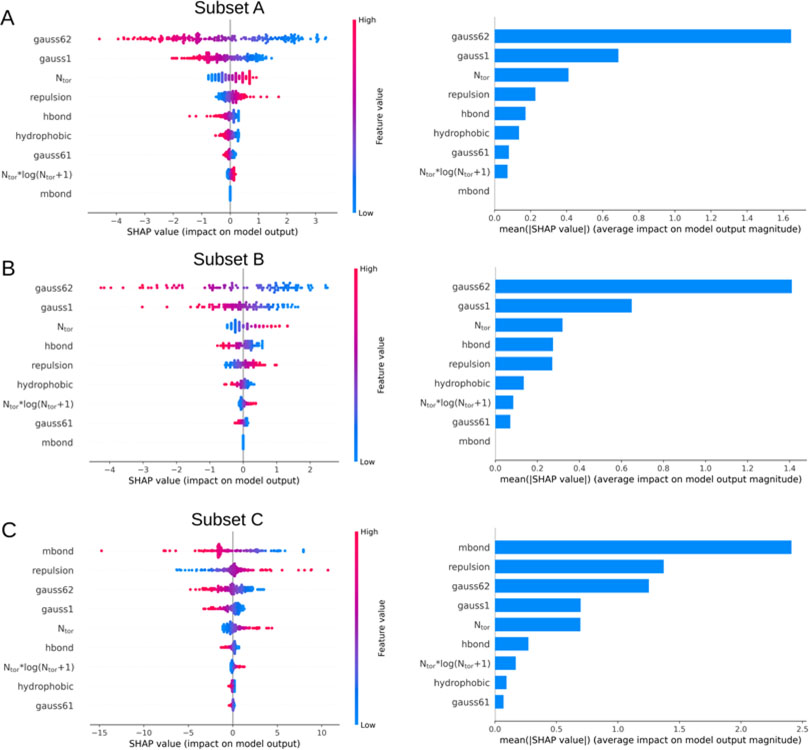
To interpret the features that contribute to predicting binding affinity, we have performed the Shapley Additive exPlanations (SHAP)⁶⁴ analysis on our training data. The SHAP method implemented in the SHAP Python library was utilized for model interpretation. To get an overview of which features are most important for our Lin_F9 model, as shown in Figure 4, we plotted the SHAP values of every feature for every sample. SHAP values reveal the distribution of the impacts each feature has in predicting binding score: for example, a high SHAP value of the Gauss₆₂ indicates that it contributes more for predicting more negative binding score (high binding affinity). For training subset A and subset B (see Figure 4A and 4B), Gauss₆₂ has the highest contribution in predicting binding score, then the second is Gauss₁. A high SHAP value of the N_tor, which represents high flexibility of ligand molecule, contributes more for predicting less negative binding score (low binding affinity). Mbond term shows zero contribution as subset A and subset B do not have any metalloprotein complexes. For training subset C (see Figure 4C), Mbond term has the highest contribution in explaining the variance of model output, then the second is repulsion term. Overall, the SHAP method was employed to explain feature contribution in predicting binding score.

Figure 4.

Feature importance analysis using SHAP method on training (A) subset A, (B) subset B and (C) subset C. For the left plots, SHAP values are shown in color (red: high; blue: low), which reveals for example that a high value of Gauss₆₂ contributes more for predicting more negative binding score (high binding affinity). For the right plots, the overall feature importance is determined by calculating the mean of absolute SHAP values for each feature.

Evaluation of Lin_F9 Scoring Function

CASF-2016 Benchmark

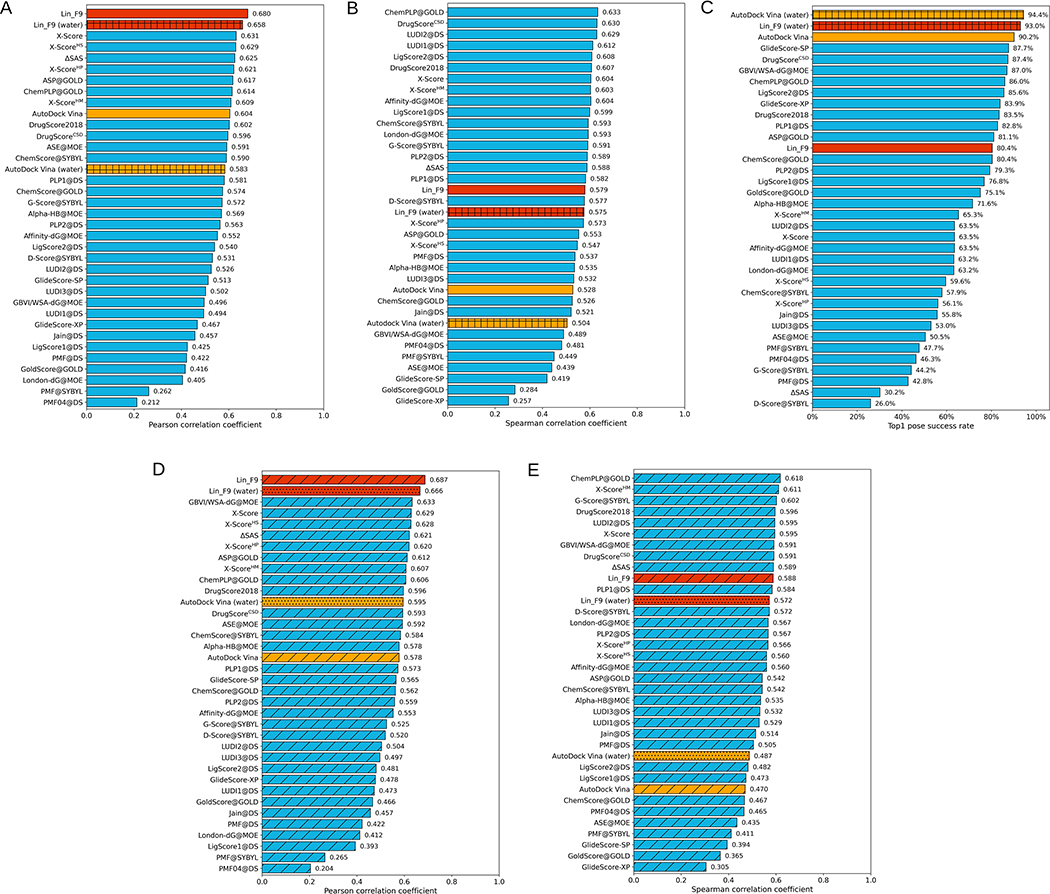
The performances of Lin_F9 are tested on standard CASF-2016 benchmark to evaluate its scoring power, ranking power and docking power, in comparison with classical scoring functions that have been evaluated by Su et al.³³ As shown in Figure 5A, Lin_F9 achieves Top 1 scoring power among all classical scoring functions reported in CASF-2016 paper. Pearson’s correlation coefficient (R) and standard deviation (SD) of Lin_F9 are 0.680 and 1.62, which are better than Vina’s scoring power (Pearson’s R = 0.604, SD = 1.73). For the ranking power, average Spearman’s rank correlation coefficient (ρ) over all 57 protein targets is used to evaluate scoring functions. As shown in Figure 5B, the ranking power of Lin_F9 is 0.579, which ranks the 17^th place among 34 classical scoring functions. Compared with Vina’s ranking power (Spearman’s ρ = 0.528), the ranking power of Lin_F9 is improved. For the docking power, Lin_F9 performs reasonably well with success rate of 80.4% for the native pose recovery at a 2.0 Å threshold for the top1 scored poses. As shown in Figure 5C, the docking power of Lin_F9 is ranked among the top one-third of the 34 classical scoring functions. It should be noted that our scoring function is trained on explicit water-included complexes. When water molecules are included in docking power test of CASF-2016 benchmark, the success rate of Lin_F9 increases from 80.4% to 93.0% at top1 pose success rate (see Figure 5C). For comparison, the success rate of best docking performer Vina increases from 90.2% to 94.4% at top1 pose success rate. The docking power of Lin_F9 improved a lot after keeping water molecules. In addition, we also performed SHAP analysis on the CASF-2016 core set to interpret average contribution of each term in Lin_F9 scoring function to the final predicted binding score (shown in Figure S5). Gauss62 consistently has the highest contribution in predicting binding score.

Figure 5.

Performances of scoring functions on CASF-2016 benchmark. (A) Scoring power and (B) ranking power evaluated for original crystal ligand poses, (C) docking power measured by success rate for top1 scored poses from random decoy poses, (D) scoring power and (E) ranking power evaluated on locally optimized ligand poses. All scoring functions are ranked in a descending order. Performances of Lin_F9 are colored red, Autodock Vina are colored orange and other scoring functions are colored cyan. Performances of scoring functions on crystal structure in water environment are filled with “+”. Performances of scoring functions on locally optimized poses in dry environment are also filled with “/”. Performances of Lin_F9 and Vina on locally optimized poses in water environment are filled with “..”. Except for performances of Lin_F9 and Vina, which are computed in the current work, performance values for all other scoring functions are from Su et al.³³

Beside evaluation using original crystal ligand poses, scoring power and ranking power tests are also carried out with locally optimized ligand poses. As shown in Figure 5D, Lin_F9 achieves consistently Top 1 scoring power among these classical scoring functions. Pearson’s R and SD of Lin_F9 are 0.687 and 1.60, respectively. For the ranking power, Spearman’s ρ of Lin_F9 is 0.588, which ranks the 10^th place among 34 classical scoring functions (see Figure 5E). The ranking power of Vina decreases from 0.528 to 0.470 after the local optimization. Therefore, scoring and ranking performances of Lin_F9 are consistently better than Vina for both crystal structures and locally optimized structures in dry environment. In addition, as shown in Figure 5D and 5E with filled “..”, we also evaluate scoring and ranking powers of Lin_F9 and Vina on locally optimized poses in water environment, in which explicit waters are kept and treated as part of protein structure. For the scoring power, compared with Vina (water) (Pearson’s R = 0.595, SD = 1.78), Pearson’s R and SD of Lin_F9 (water) are 0.666 and 1.69, respectively. For the ranking power, Lin_F9 (water) has better ranking power than Vina (water) (Lin_F9 (water): 0.572 vs Vina (water): 0.487).

Flexible Docking Tests

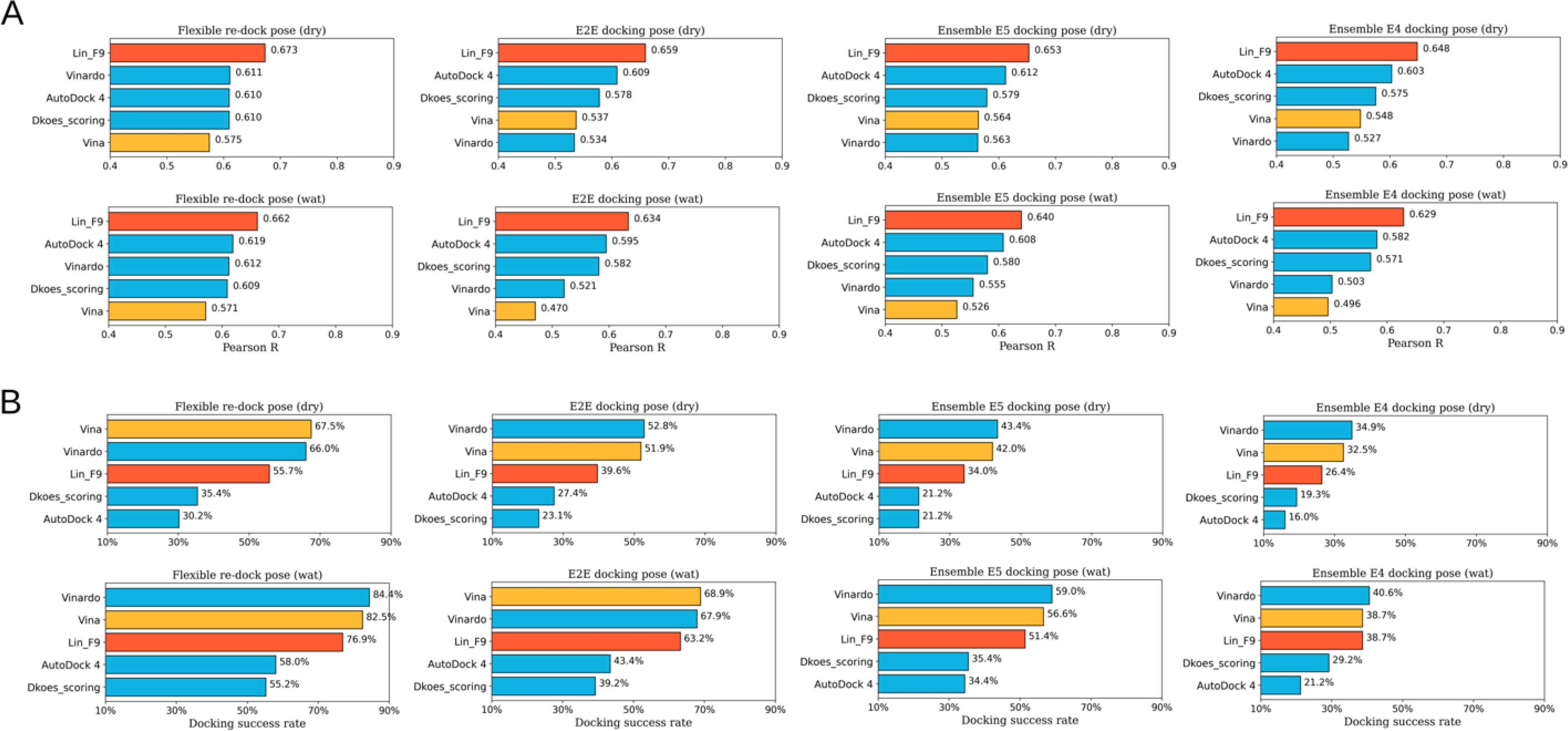
To further test the scoring power, ranking power and docking power for real docking application, several flexible docking tests of CASF-2016 core set (illustrated in Table 1) are carried out using Lin_F9, as well as 4 other classical scoring functions (Vina,²⁹ Vinardo,⁶⁵ Dkoes_scoring⁴⁸ and AutoDock 4,⁶⁶ which are optional built-in scoring functions implemented in Smina docking suite⁴⁸) for comparison.

Flexible re-docking test.

In docking preparation of flexible re-docking, both the ligand conformer and protein conformation come from the corresponding crystal protein-ligand complex. In the evaluation process, both docking poses without water (${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$) and with water molecules (${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$) are evaluated. The predicted score for each complex comes from the top1 docking pose (best-scored pose). As shown in Figure 6, scoring power of Lin_F9 outperform 4 other scoring functions in both dry and water environment. Pearson’s R of Lin_F9 on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$ and ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.686 and 0.673. For the ranking power, Spearman’s ρ of Lin_F9 on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$ and ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.622 and 0.610, which are consistently better than 4 other scoring functions. For the docking power, Vina and Vinardo are better than Lin_F9, while Dkoes_scoring and AutoDock 4 are worse than Lin_F9 for flexible re-docking test. At a 2 Å RMSD threshold for the top1 docking pose, docking success rates of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 80.0%, 83.9%, 84.9%, 56.8% and 62.8%.

Figure 6.

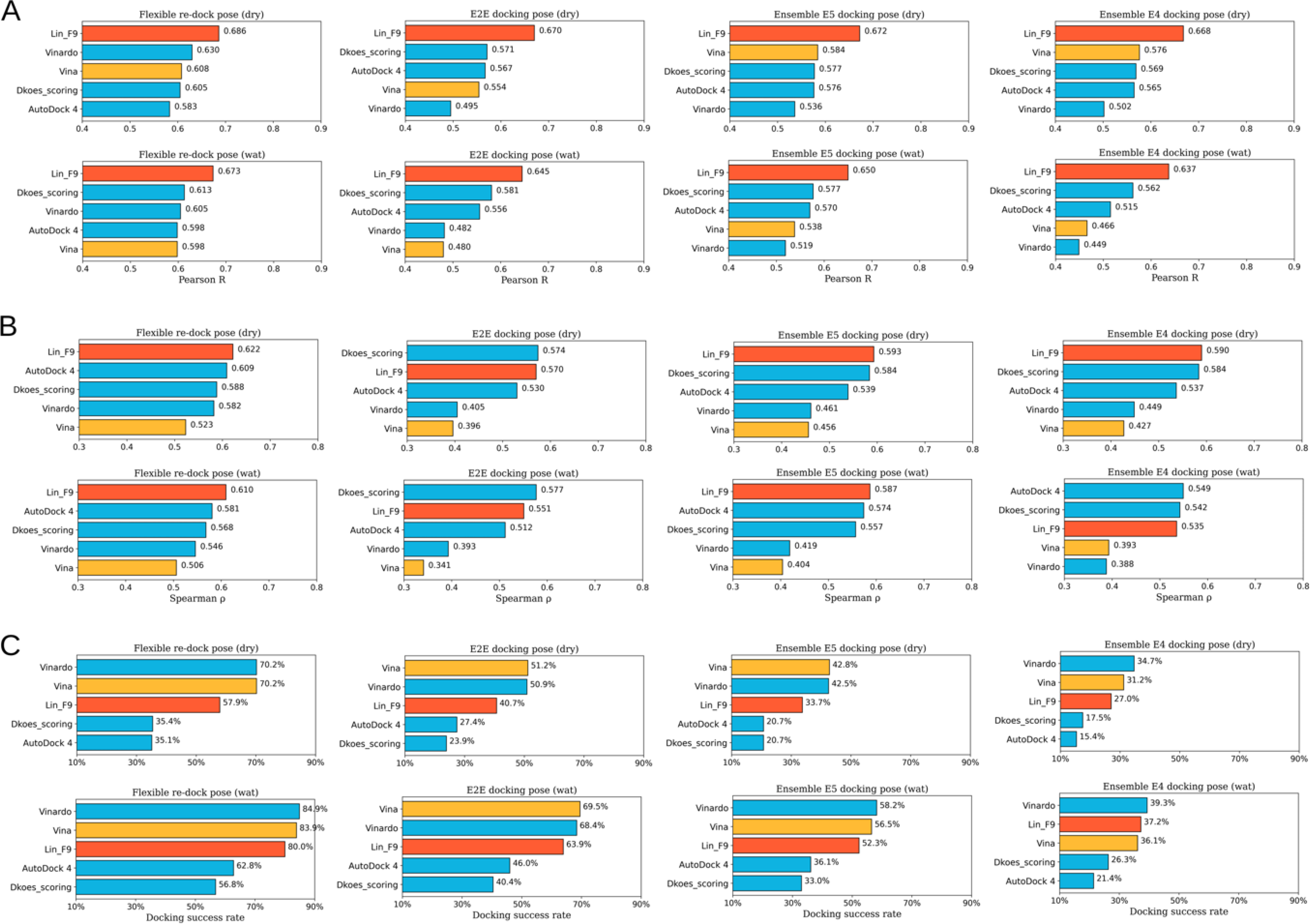
Scoring, ranking and docking powers of scoring functions on different flexible docking tests of CASF-2016 core set. (A) Pearson correlation coefficient for scoring power. (B) Spearman correlation coefficient for ranking power. (C) Docking power measured by success rate of top1 docking pose (RMSD < 2 Å). Performances of Lin_F9 and Vina are colored red and orange, other scoring functions are colored cyan. Performances on flexible re-docking poses in dry and water environments, E2E docking poses in dry and water environments, ensemble (E5) docking poses in dry and water environments, ensemble (E4) docking poses in dry and water environments are displayed from left to right.

E2E docking test.

In order to mimic the real docking process using computer-generated ligand conformers, we also evaluate the flexible docking pose of CASF-2016 core set in an end-to-end (E2E) manner, in which ligand conformer generation and flexible docking are combined. Maximum 10 conformers are generated for each small molecule, and all these conformers are docked to protein target. The conformer generation performance of this protocol is evaluated and shown in Figure S12–B. At a 2 Å RMSD threshold, 269 of 285 ligands conformation can be successfully generated. After docking, the best-scored poses are used to evaluate the scoring, ranking and scoring powers. Similar as the above, E2E docking poses without water (${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$) and with water molecules (${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$) are evaluated. As shown in Figure 6, compared with Vina, Vinardo and AutoDock 4, Lin_F9 achieves superior performance for scoring and ranking power tests. For the scoring power, Pearson’s R of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.670 and 0.645. For the ranking power, Spearman’s ρ of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.570 and 0.551. It is interesting to find that, though the scoring power of Dkoes_scoring (${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$: 0.571 and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$: 0.581) is worse than Lin_F9, the ranking power of Dkoes_scoring (${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$: 0.574 and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$: 0.577) is slightly better than Lin_F9. For the docking power, at a 2 Å RMSD threshold for the best-scored pose, docking success rates of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 63.9%, 69.5%, 68.4%, 40.4% and 46.0%.

Ensemble (E5) docking test.

Ensemble docking, in which a ligand is sequentially docked into a selected ensemble of protein structures, is a practically useful approach to incorporate protein flexibility in docking applications.⁶⁷ The CASF-2016 core set is feasible to mimic ensemble docking, as it includes 57 targets and 5 protein structures for each target. For each ligand in CASF-2016 core set, it was sequentially docked into 5 protein structures of corresponding target with the E2E protocol. After docking, the best-scored poses are used to evaluate the scoring and ranking powers. Once again, ensemble docking poses without water (${\mathrm{C}}_{\mathrm{E}5},$ in which E5 represents 5 ensemble protein structures used) and with water molecules (${\mathrm{C}}_{\mathrm{E}5}^{\mathrm{w}\mathrm{a}\mathrm{t}}$) are evaluated. As shown in Figure 6, compared with 4 other scoring functions, Lin_F9 achieves better performance for scoring and ranking power on ensemble docking poses. Scatter plots of experimental pK_d vs predicted pK_d by Lin_F9 or Vina are shown in Figure 7. For the scoring power, Pearson’s R of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}5}$ and ${\mathrm{C}}_{\mathrm{E}5}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.672 and 0.650. For the ranking power, Spearman’s ρ of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}5}$ and ${\mathrm{C}}_{\mathrm{E}5}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.593 and 0.587. Compared with previous ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}},{\mathrm{C}}_{\mathrm{E}5}$ and ${\mathrm{C}}_{\mathrm{E}5}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ show slightly better scoring and ranking powers for all 5 scoring functions. This result indicates that ensemble docking can improve the scoring and ranking performances on CASF-2016 core set. For the docking power evaluation, at a 2 Å RMSD threshold for the best-scored pose, docking success rates of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{E}5}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 52.3%, 56.5%, 58.2%, 33.0% and 36.1%.

Figure 7.

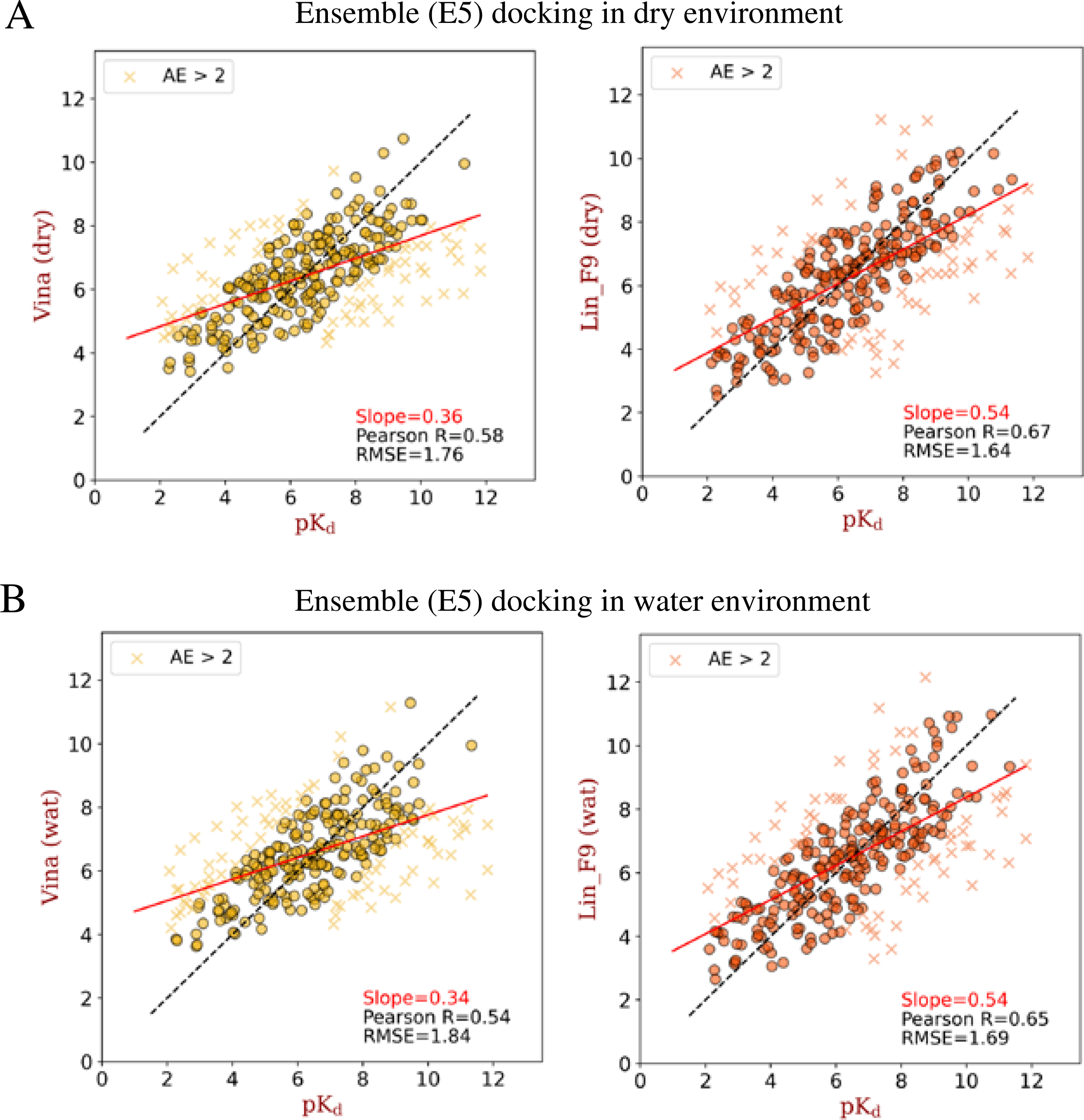
Scatter plots between experimental pK_d and ensemble (E5) docking predicted pK_d (by Vina or Lin_F9) on CASF-2016 core set. (A) Ensemble docking in dry environment and (B) ensemble docking in water environment. The absolute error in pK_d larger than 2 are plotted with marker “x”, and others are plotted with marker “o”. The solid red line for each plot corresponds to the linear fit between predicted scores and experimental pK_d, the slope value for this linear fit is shown in the plot. Also, Pearson correlation coefficient and root-mean-square error between predicted scores and experimental pK_d are shown for each plot.

Ensemble (E4) docking test.

Ensemble docking is also evaluated by excluding the native protein structure for each ligand. The ensemble docking poses without water (${\mathrm{C}}_{\mathrm{E}4},$ in which E4 represents 4 ensemble protein structures used) and with water molecules (${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$) are assessed (see Figure 6). For the scoring power, Pearson’s R of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}4}$ and ${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.668 and 0.637. For the ranking power, Spearman’s ρ of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}4}$ and ${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.590 and 0.535. But for Vina, its scoring powers (${\mathrm{C}}_{\mathrm{E}4}$: 0.576 and ${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$: 0.466) and ranking powers (${\mathrm{C}}_{\mathrm{E}4}$: 0.427 and ${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$: 0.393) are far less satisfactory. For the docking power, at a 2 Å RMSD threshold for the best-scored pose, docking success rates of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{E}4}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 37.2%, 36.1%, 39.3%, 26.3% and 21.4%.

Altogether flexible docking results indicate that the scoring and ranking performances of Lin_F9 are consistently better than 4 other scoring functions on these real docking tests, despite that the docking performance of Lin_F9 ranks at the 3^rd place. From (i) flexible-redocking test to (ii) E2E docking test to (iii) ensemble docking test including native protein structure to (iv) ensemble docking test excluding native protein structure, it can be seen that although docking performances of all 5 scoring functions varied a lot, the scoring and ranking performances of Lin_F9 is very robust, and is consistently better than 4 other scoring functions.

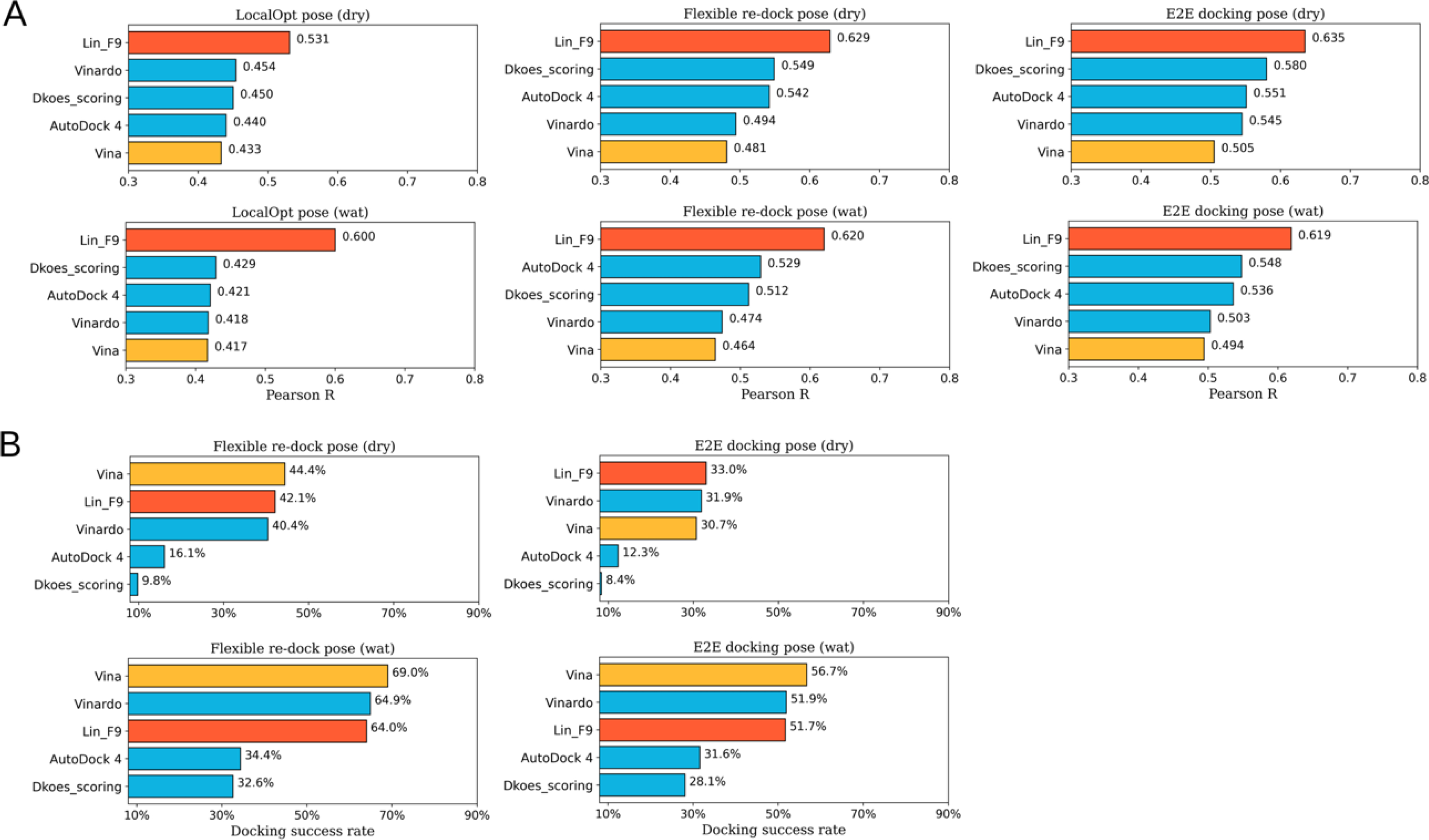
In addition, in order to validate the performance on low similarity test data, we also evaluated the scoring power achieved by Lin_F9 scoring function calibrated on the test set at overall similarity < 0.5 to our train set. The overall similarity is measured based on protein sequence similarity times ligand shape similarity, in which protein sequence similarity and ligand shape similarity are calculated using the protocol by Su et al.²⁶ As shown in Figure 8, the scoring power and docking power on above flexible docking poses are assessed. As can be seen, for the low similarity test data, the scoring power of Lin_F9 is stable and robust for different structure types. At a 0.5 overall similarity cutoff, there are 212 complexes in the test subset, the scoring powers of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$ are, respectively, 0.673, 0.575, 0.611, 0.610 and 0.610. Once again, the docking power of Lin_F9 ranks at the 3^rd place. It should be note that the low similarity test data is calibrated using the Lin_F9 training set.

Figure 8.

Scoring and docking powers of scoring functions on different flexible docking tests of low similarity complexes (overall similarity < 0.5) in CASF-2016 core set. (A) Pearson correlation coefficient for scoring power. (B) Docking power measured by success rate of top1 docking pose (RMSD < 2 Å). All annotations on this figure are the same as those in Figure 5.

Scoring Performance for Metalloprotein Complex

For metalloprotein complexes, in addition to the residue/ligand interactions, there are important coordination interactions between metal ions and ligand atoms. In vina scoring function, the metal atoms are treated as hydrogen bond donor type. Previous studies demonstrate that Vina performs not well on metalloprotein complexes, especially for zinc complexes.^{68, 69} In Lin_F9 scoring function, we use a metal bond term to specifically describe metal-ligand interactions. Here, we evaluate the scoring power on metalloprotein test set for Lin_F9, compared with 4 other classical scoring functions within Smina docking suite. For the test set, it encompasses Zn²⁺, Fe³⁺, Ca²⁺ and Mn²⁺ complexes. All the complexes have at least one metal ion within 4.0 Å from ligand atoms. As shown in Figure 9A, regarding to locally optimized poses (${\mathrm{C}}_{\mathrm{o}}$ and ${\mathrm{C}}_{\mathrm{o}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$), flexible re-docking poses (${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$ and ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$) and E2E docking poses (${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$), the scoring power of Lin_F9 on metalloprotein test set is consistently better than 4 other scoring functions. Pearson’s R of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ and ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 0.635 and 0.619. Scatter plots of experimental pK_d vs predicted pK_d of E2E docking poses are shown in Figure 10. The results indicate that, compared with Vina, Lin_F9 has better scoring accuracy as well as smaller number of cases with large errors (absolute error > 2). For the docking power (see Figure 9B), at a 2 Å RMSD threshold for the best-scored pose, docking success rates of Lin_F9, Vina, Vinardo, Dkoes_scoring and AutoDock 4 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}^{\mathrm{w}\mathrm{a}\mathrm{t}}$ are, respectively, 51.7%, 56.7%, 51.9%, 28.1% and 31.6%.

Figure 9.

Scoring and docking powers of scoring functions on locally optimized poses, flexible re-docking poses and E2E docking poses of metalloprotein test set. (A) Pearson correlation coefficient for scoring power. (B) Docking power measured by success rate of best-scored pose (RMSD < 2 Å). Performances of Lin_F9 and Vina are colored red and orange, other scoring functions are colored cyan. For each scoring function, performances on locally optimized poses in dry and water environments, flexible re-docking poses in dry and water environments, E2E docking poses in dry and water environments are displayed from left to right.

Figure 10.

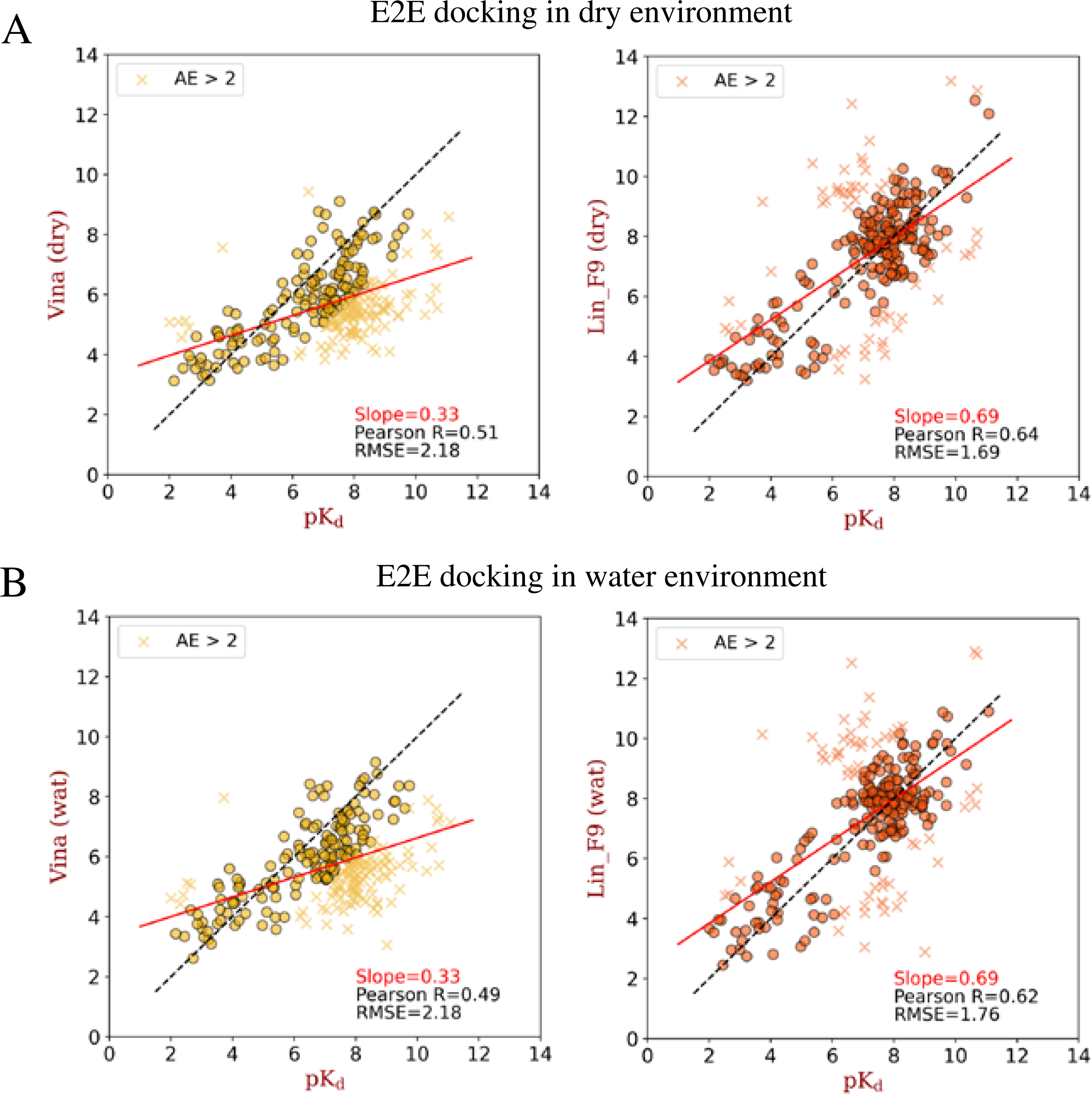
Scatter plots between experimental pK_d and E2E docking predicted pK_d (by Vina or Lin_F9) on metalloprotein test set. (A) E2E docking in dry environment and (B) E2E docking in water environment. The absolute error in pK_d larger than 2 are plotted with marker “x”, and others are plotted with marker “o”. The solid red line for each plot corresponds to the linear fit between predicted scores and experimental pK_d, the slope value for this linear fit is shown in the plot. Also, Pearson correlation coefficient and root-mean-square error between predicted scores and experimental pK_d are shown for each plot.

In addition, scoring power and docking power of Lin_F9 scoring function are also evaluated on the low similarity (overall similarity < 0.5) metalloprotein test subset to our train set. At a 0.5 overall similarity cutoff, there are only 91 complexes in the metalloprotein test subset. As shown in Figure 11, the scoring power of Lin_F9 ranks at the 2^nd or 3^rd position among all 5 scoring functions for different structure types. The docking power of Lin_F9 also ranks at the 3^rd place. We noticed that the scoring power of Lin_F9 varies the least among all 5 scoring functions when changing test subsets (see Figure S11), and is consistently better than Vina.

Figure 11.

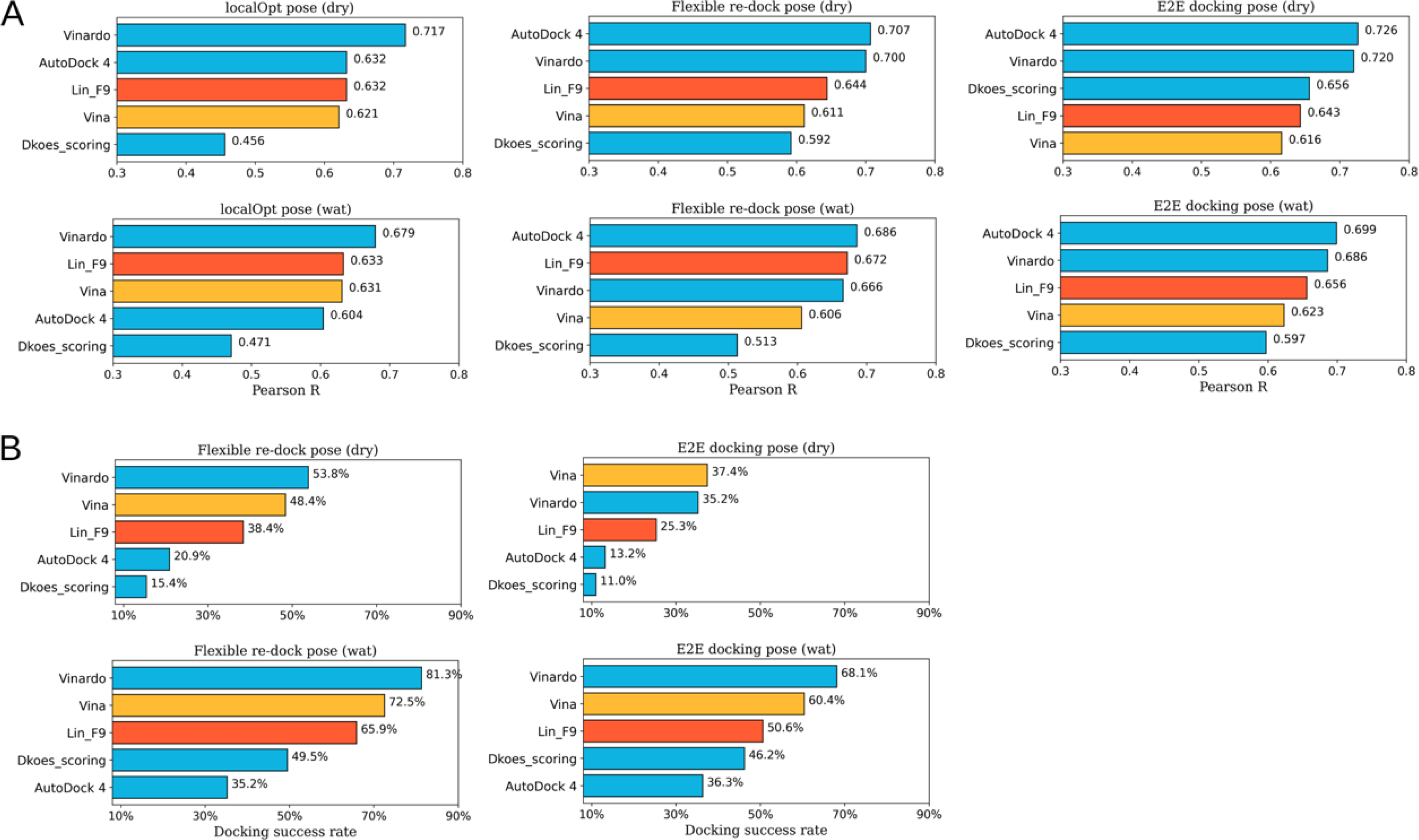
Scoring and docking powers of scoring functions on locally optimized poses, flexible re-docking poses and E2E docking poses of low similarity complexes (overall similarity < 0.5) in metalloprotein test set. (A) Pearson correlation coefficient for scoring power. (B) Docking power measured by success rate of best-scored pose (RMSD < 2 Å). All annotations on this figure are the same as those in Figure 7.

Meanwhile, an additional zinc metalloprotein test set is explored from CASF-2016 core set, in which zinc metalloprotein complexes are selected. Both scoring and ranking power of Lin_F9 and Vina are evaluated on this test set (see Table S8), and the results show that Lin_F9 perform consistently well on these zinc complexes. Pearson’s R and Spearman’s ρ of Lin_F9 on ${\mathrm{C}}_{\mathrm{E}2\mathrm{E}}$ are, respectively, 0.847 and 0.875, which are better than Vina performance (R = 0.724, ρ = 0.800). Overall, Lin_F9 also shows relatively good scoring performance for metalloprotein complexes.

Case Studies of D3R GC4

Besides the above evaluation on PDBbind test sets, we also evaluated ranking performance of Lin_F9 on two target-specific datasets provided in Drug Design Data Resource (D3R) Grand Challenge 4 (GC4).⁶⁰ These two datasets correspond to two different protein targets, beta secretase 1 (BACE1) and Cathepsin S (CatS). Both targets are of great interests for medical research and drug discovery.^70–73

BACE1 dataset.

The BACE1 dataset is composed of 154 small molecule inhibitors, in which 151 of 154 ligands have macrocycle rings. As mentioned in Method section, our group has participated in BACE1 competition for pose prediction of 20 macrocyclic ligands and affinity ranking of whole 154 ligands. The pose prediction result achieved an average RMSD of 1.01 Å for our submitted model, but our affinity ranking performance was less satisfactory (Spearman’s ρ = 0.25, Kendall’s $\tau$ = 0.18). In further exploration after competition, the average RMSD decreased to 0.74 Å using a similarity-based constraint docking method. Here, based on our predicted complexes of whole BACE1 dataset, we test the affinity ranking performances of Lin_F9 and 4 other scoring functions on locally optimized poses. As shown in Figure 12, compared with Vina, the ranking power of Lin_F9 improved a lot. Spearman’s ρ and Kendall’s $\tau$ of Lin_F9 are 0.439 and 0.311, respectively. The performance of Lin_F9 ranks the 4^th place among all the participator’s submitted predictions in D3R. It also ranks the 2^nd place among these 5 scoring functions. It is interesting to note that, the ranking power of Dkoes_scoring (Spearman’s ρ = 0.545 and Kendall’s $\tau$ = 0.388) can not only achieves the top1 among all 5 scoring functions shown in Figure 9, but also ranks the 1^st place among all submissions in D3R.

Figure 12.

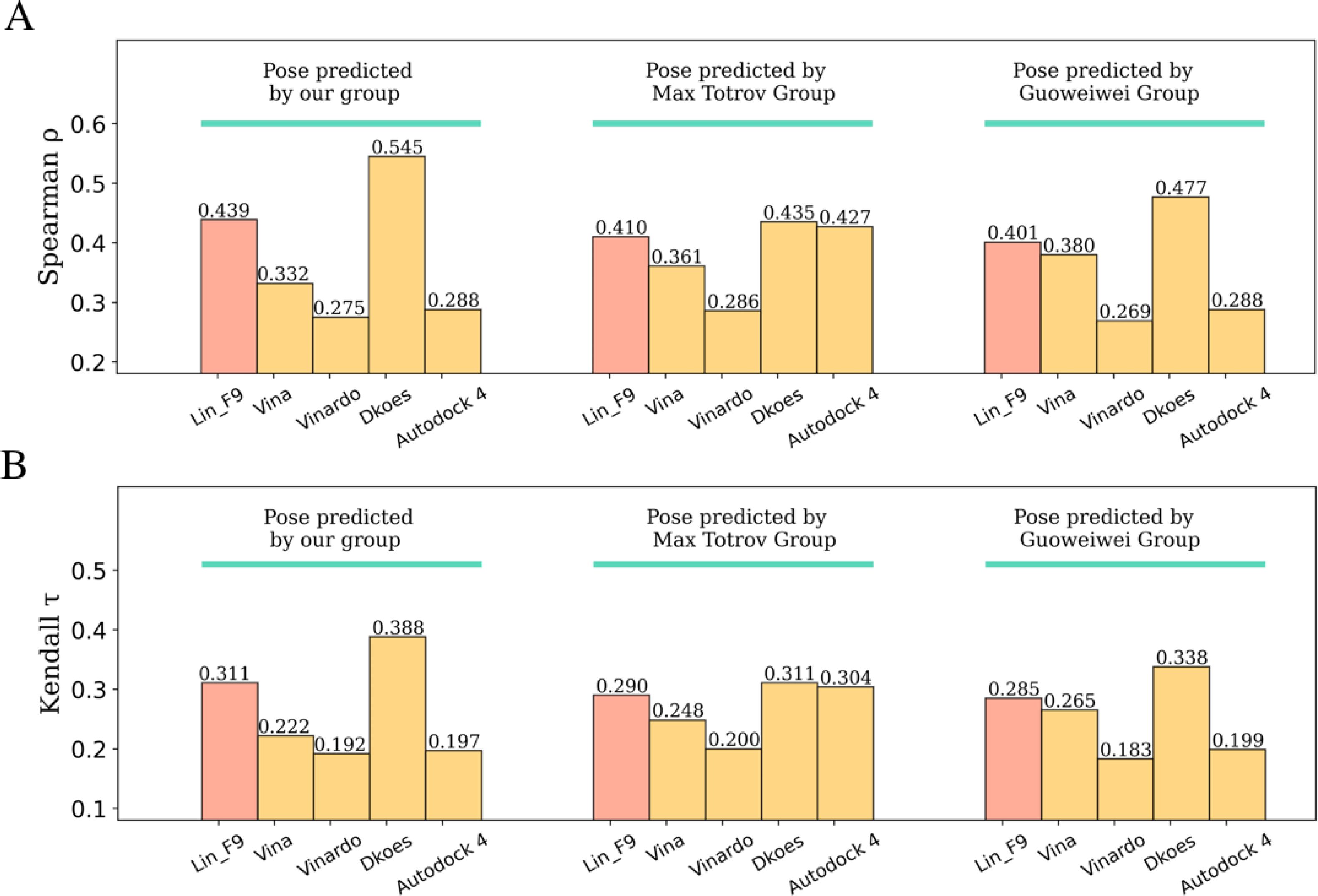
Affinity ranking performances of scoring functions on BACE1 inhibitor dataset with predicted complexes from three different groups. (A) Spearman correlation coefficient and (B) Kendall correlation coefficient for ranking power evaluation.

Beside using our predicted complexes, we also evaluate the ranking powers of Lin_F9 and 4 other scoring functions on complexes predicted by other two groups: (I) Max Totrov group,⁶² this group has achieved the 1^st place on pose prediction in Stage 1b (submitted id: 5rdda), (II) Guowei Wei group,⁶³ this group has achieved the 2^nd place on pose prediction in Stage 1b (submitted id: tjny7). Once again, compared with Vina, Lin_F9 achieves consistently better ranking power (see Figure 12). In D3R website, Spearman’s ρ of Max Totrov group prediction is 0.26, while our Lin_F9 prediction using their complexes achieves to 0.41. Spearman’s ρ of Guowei Wei group prediction is 0.43, our Lin_F9 prediction using their complexes is 0.40. It should be noted that their model either use deep learning methods (Guowei Wei group) or 3D-QSAR modeling on BACE1 training data (Max Totrov group). As a classic scoring function, Lin_F9 shows competitive ranking power on this target-specific case. It should be noted that, Dkoes_scoring achieves consistently the top 1 ranking power for complexes predicted by three different groups.

CatS dataset.

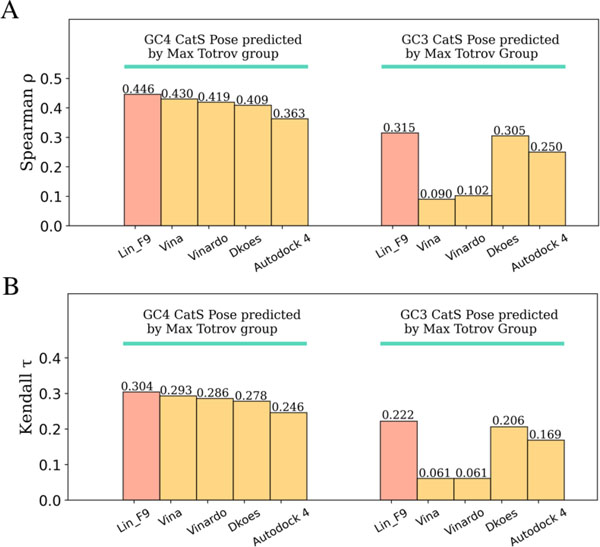
The CatS dataset encompasses 459 small molecule inhibitors, in which all the ligands share the same tetrahydro-pyridinepyrazole derivative scaffold. The challenge for ranking these CaS inhibitors may come from their large size, high flexibility and similar chemical structures. Here, complex structures come from Max Totrov group’s submitted data on D3R website.⁶² They have participated in both GC3 and GC4 CaS competition, and their submitted model achieved the 2^nd place on pose prediction in GC3 Stage 1b,⁶² despite that GC4 CatS has no pose prediction competition. Based on their predicted complexes, we evaluate the ranking power of Lin_F9 and 4 other scoring on 459 CatS inhibitors dataset in GC4 (submitted id: x4svd), as well as 136 CatS inhibitors dataset in previous GC3 (submitted id: q2k8y). As shown in Figure 13A, the ranking power of Lin_F9 is slightly better than Vina on GC4 CatS dataset (Lin_F9: 0.447 vs Vina: 0.431). On GC3 CatS dataset, the ranking power of Lin_F9 is much better than Vina (Lin_F9: 0.315 vs Vina: 0.09). Overall, as can be seen, Lin_F9 shows consistently and relatively good ranking performances on these two target-specific cases.

Figure 13.

Affinity ranking performances of scoring functions on GC4 CatS dataset and GC3 CatS dataset with predicted complexes from Max Totrov group. (A) Spearman correlation coefficient and (B) Kendall correlation coefficient for ranking power evaluation.

Conclusion

In this study, we developed a new linear empirical scoring function, Lin_F9, which is a linear combination of 9 empirical terms with weights fitting on a relatively small set of high-quality training data. In developing the Lin_F9 scoring function, explicit water molecules, mid-range interactions, metal-ligand interactions are taken into considerations. Regarding the CASF-2016 benchmark test, Lin_F9 achieves the top scoring power among all 34 classical scoring functions for both original crystal poses and locally optimized poses. Meanwhile, compared with several classical scoring functions within Smina docking suite, Lin_F9 achieves robust scoring power and ranking power for flexible docking tests, such as end-to-end flexible docking poses using a single or an ensemble of protein receptor structures, which mimic the real docking application. In addition, Lin_F9 performs relatively good scoring accuracy on metalloprotein test set and target-specific cases of D3R GC4. This work suggests that Lin_F9 is a robust scoring function and could serve as an effective tool in structure-based inhibitor design. Lin_F9 is available as an optional built-in scoring function within a fork of Smina⁴⁸ docking suite.

Data and Software Availability

Lin_F9 has been implemented in a fork of Smina⁴⁸ docking suite, and is accessible through: https://yzhang.hpc.nyu.edu/Lin_F9/. The training and test datasets are available in Supporting Information. OpenBabel 2.4.1 version⁵⁵ is used to generate ligand conformations. MGLTools⁷⁴ 1.5.4 are used for preparing PDBQT files of protein and ligand. DockRMSD⁵⁶ is used for the calculation of RMSD between docking pose and original crystal pose of the same ligand molecule.