Effect of adjustment for case misclassification and infection date uncertainty on estimates of COVID-19 effective reproduction number

Abstract

Background:

Surveillance data captured during the COVID-19 pandemic may not be optimal to inform a public health response, because it is biased by imperfect test accuracy, differential access to testing, and uncertainty in date of infection.

Methods:

We downloaded COVID-19 time series surveillance data from the Colorado Department of Public Health & Environment by report and illness onset dates for 9-Mar-2020 to 30-Sep-2020. We used existing Bayesian methods to first adjust for misclassification in testing and surveillance, followed by deconvolution of date of infection. We propagated forward uncertainty from each step corresponding to 10,000 posterior time-series of doubly adjusted epidemic curves. The effective reproduction number (R_t), a parameter of principal interest in tracking the pandemic, gauged the impact of the adjustment on inference.

Results:

Observed period prevalence was 1.3%; median of the posterior of true (adjusted) prevalence was 1.7% (95% credible interval [CrI]: 1.4%, 1.8%). Sensitivity of surveillance declined over the course of the epidemic from a median of 88.8% (95% CrI: 86.3%, 89.8%) to a median of 60.8% (95% CrI: 60.1%, 62.6%). The mean (minimum, maximum) values of R_t were higher and more variable by report date, 1.12 (0.77, 4.13), compared to those following adjustment, 1.05 (0.89, 1.73). The epidemic curve by report date tended to overestimate R_t early on and be more susceptible to fluctuations in data.

Conclusion:

Adjusting for epidemic curves based on surveillance data is necessary if estimates of missed cases and the effective reproduction number play a role in management of the COVID-19 pandemic.

Introduction

Epidemic curves are a mainstay of outbreak epidemiology and are used to describe, investigate, and track efficacy of the effort to contain disease outbreaks.¹ However, they are only as good as the information they depict: surveillance data obtained during an outbreak may be coarsened by imperfect test accuracy, bias in selection for testing, and uncertainty in date of infection.²

For COVID-19, epidemic curves are commonly depicted by “report date” of a positive SARS-CoV-2 diagnostic test, the virus that causes COVID-19, in publicly available data. Even the widely used “COVID-19 Case Surveillance Public Use Data” for the whole of the U.S., assembled by the Centers for Disease Control and Prevention (CDC) and based on surveillance collected at state and local health departments, is missing illness onset date (when symptomatic, which follows actual infection) for more than half of the cases.³ Thus, when depicting an epidemic curve by illness onset, one is tempted to make the tenuous assumption that the date of report is the date of illness,² which implies that there is no testing delay (the difference between disease onset and receiving the diagnostic test) and no reporting delay (the difference between administration of the diagnostic test and health department notification of the results). Assuming one can accurately capture the date of illness onset, then the likely window of infection is a function of the pathogen’s incubation period. Deconvolution can reconstruct epidemic curves by the date of infection, first being widely applied in public health early in the AIDS epidemic,⁴ and now beginning to be used during the COVID-19 pandemic.⁵ Infection date is of particular relevance to public health as evaluating interventions should be done proximal to infection and not reporting,⁶ for example by tracking changes in the effective reproduction number (R_t) in response to mitigation measures.

While these approaches have greatly improved our understanding of the true pandemic, there is another notable shortcoming present in surveillance data: imperfect ascertainment of COVID-19 cases in the population. Other studies have strived to improve upon the quality and accuracy of surveillance data for COVID-19, albeit by handling the lack of appropriate date issue separately from misclassification of case status.^7–9 Here we demonstrate a unified approach to doubly adjust epidemic curves by 1) accounting for misclassification in case ascertainment and 2) imputing the date of infection.

Methods

Description of data

We used publicly available COVID-19 surveillance data from the Colorado Department of Public Health & Environment downloaded on 15-Nov-2020.¹⁰ We used these data because they contain the total number of positive cases by both date of report and illness onset and corresponded to the initial wave of the pandemic. Report date serves as our principal designation of case occurrence, given that not all jurisdictions release onset date as part of their public surveillance data.³ As such, onset date in our data serves as a point of comparison. Data were left truncated before 9-Mar-2020 due to excessive zero daily counts and right truncated after 30-Sep-2020 due to the apparent commencement of a subsequent pandemic wave.

Adjustment #1: Misclassification in testing and surveillance

We adapted a previously described Bayesian approach for COVID-19 time-series misclassification.⁹ Briefly, this method worked as follows. We specified priors for sensitivity and specificity of the surveillance process (accounting for errors in testing and surveillance) as well as true prevalence of infection in the population, and the model relating the observed apparent number of reported cases to the true number of cases, accounting for time series nature of the data and accuracy of the surveillance process. Specificity was assumed to be constant in time, but sensitivity could have linear trends across the entire times. We used a uniform prior on sensitivity where the bounds varied stochastically, with a lower bound ≥0.30 and an upper bound ≤0.81. These bounds covered the posterior sensitivity observed in a similar study of another jurisdiction, where the median posterior values were observed to be approximately 60% with credible intervals between 30% and 80%.¹¹ The priors for specificity and prevalence were also bounded by uniform distributions between 0.95 and 1.00 for specificity, and between 0 and 0.05 for prevalence (independently for each day). Using the R2jags package,¹² 4 Markov chains were run for 400,000 iterations, discarding the first 1,000 for burn-in, with a thinning interval of 200. Diagnostics included kernel density visualizations of the posterior distributions and traceplots (available in the eAppendix). A parameter was considered to have converged if its Gelman–Rubin statistic was <1.2. By sampling from the posterior, we arrived at our estimate of the true distribution of cases on a given day. Further details may be found in Burstyn, Goldstein, and Gustafson⁹ and the source code (linked below). The only deviation from the previously described method is that we considered the number tested for COVID-19 to be the total population of Colorado, not numbers tested, such that misclassification referred to errors due to both testing and selection for testing. As such, and due to near-constant observed prevalence from the large denominator, only two knots were used corresponding to the start and end of the time-series, in the linear piecewise model for sensitivity.

Adjustment #2: Imputation of the latent date of infection

While adjustment #1 above yields a set of adjusted daily case counts, estimating the reproduction number, R_t, requires us to first make inference on the daily incidence of infection. To achieve this, we used the EpiNow2 package¹³, which models daily case counts as being negative binomially distributed with a mean equal to the product of a “true” underlying case count and a day-of-the-week adjustment parameter to account for differences in how data are reported.¹⁴ This “true” underlying case count was then modeled as a function of underlying daily incidence of infection counts, which were modeled as arising from a temporally smooth process, and a parameter that accounts for uncertainty in the incubation period and delay in reporting. The output from this model thus contains imputed samples of the daily incidence counts. To incorporate misclassification in the reported case time-series in our imputation step, we randomly drew 100 iterations’ worth of samples from the posterior distribution described in adjustment #1. To model the incubation period – or time from infection to illness – we assumed a log-normal distribution corresponding to a mean of 5.06 days and standard deviation of 1.52 days, informed by Lauer et al.¹⁵ Similarly, we assumed the reporting lag period had a log-normal distribution with a median of 3.5 days (interquartile range=5 days) and capped to a maximum of 30 days, based on media reporting on delays in test results in Colorado.¹⁶ The functionality of the EpiNow package was implemented using the rstan package,¹⁷ in which 4 Markov chains were run for 2,000 time-steps following a 200 step warmup period. We retained 100 random time-series from the posterior of the infection imputation for each of the 100 misclassified adjusted time-series. This corresponded to 10,000 doubly adjusted posterior time-series representing the number of COVID-19 infections for each day.

Estimation of reproductive numbers

In order to contrast the differences in inference that may result based on the observed and doubly adjusted epidemic curves, we estimated the (real time) effective reproduction number (R_t) and its accompanying 95% certainty interval using the R0 package.⁶ R_t was calculated using the real-time, time-dependent method of Cauchemez et al.,¹⁸ a Bayesian adaption of the likelihood-based approach of Wallinga and Teunis¹⁹ that makes inference on R_t by first estimating X_t, the number of cases infected by those whose disease onset occurred at time t. Because the COVID-19 pandemic is still ongoing (and more importantly, was still ongoing at the time of data collection), the approach of Cauchemez et al. partitions X_t into cases that infected before (i.e., cases that were observable) and after data collection (i.e., cases that were unobservable). Their approach then imputes these unobserved infections by conditioning on the disease’s generation time – i.e., the time between horizontally transmitted infections – which was estimated using methods described in Ganyani et al.²⁰ and is assumed a priori to be gamma distributed with a mean of 3.64 days and a standard deviation of 3.08 days. R_t was calculated for report and onset dates based on the observed surveillance data and infection date using the 10,000 doubly adjusted epidemic curves.

R version 3.6.3 (R Foundation for Statistical Computing, Vienna, Austria) was used for statistical programming; computational code and data are available to download from https://doi.org/10.5281/zenodo.5009050.

Results

Between 9-Mar-2020 and 30-Sep-2020, there were 71,737 laboratory confirmed cases of COVID-19 reported to the State of Colorado Department of Public Health and Environment. With a population of 5,758,736, this translated to a period prevalence of approximately 1.3% (95% confidence interval [CI]: 1.2%, 1.3%).

Figure 1 depicts the epidemic curves arising from both date of report and date of illness onset. There were several findings that were apparent based on these data. First, there was a left shift in the curves when accounting for delay from illness onset to testing and reporting. Second, there was a smoothing of the time series data when depicted by onset date. Because reporting may occur irregularly throughout the week in a manner unrelated to the onset of illness, the onset date should lead to a more accurate depiction of the trajectory of the epidemic.

Figure 1.

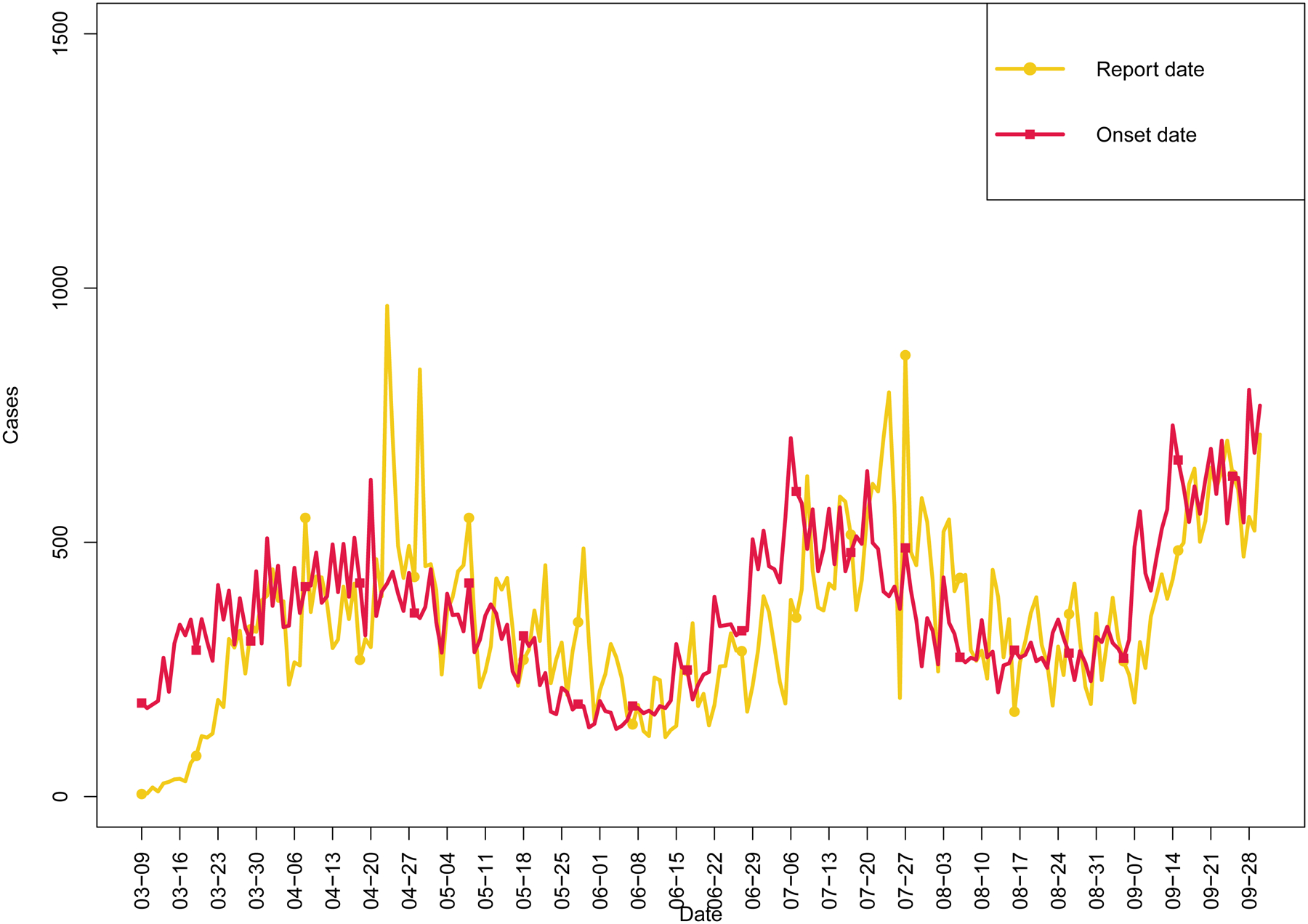
COVID-19 epidemic curves for the State of Colorado (9-Mar-2020 through 30-Sep-2020) depicting observed cases by report date and illness onset date.

After accounting for bias in the surveillance process the median of the posterior distribution of reported cases indicated that the total number of actual cases in the population for this period of time was on average 96,142 (95% credible interval [CrI]: 81,523 – 102,494). True prevalence was estimated to be higher than observed (median: 1.7%, 95% CrI: 1.4%, 1.8%), owning to near-perfect specificity of surveillance (median=100%, uncertainty arising only in the 5^th decimal place) exceeding that of sensitivity. There was evidence of sensitivity of surveillance system declining over the course of the epidemic from a median of 88.8% (95% CrI: 86.3%, 89.8%) to a median of 60.8% (95% CrI: 60.1%, 62.6%). Posterior traceplots and distributions of select parameters are available in the Supplemental Material.

Figure 2 depicts the doubly adjusted posterior distribution of the epidemic curve accounting for the incubation period of SARS-CoV-2 and any delays in testing and reporting, as well as misclassification in case ascertainment. Based on this adjustment, for cases reported on 9-Mar-2020, the first date in our time-series data, infection likely occurred on or around 28-Feb-2020. There was a trimodal distribution of the epidemic in Colorado, with an initial peak in late April, a second peak occurring towards the middle of July, and a rapid increase of cases in late September foreshadowing the forthcoming third wave in the Fall and Winter of 2020–21. As expected, the adjusted epidemic curve was left shifted and visibly smoother than the unadjusted curve.

Figure 2.

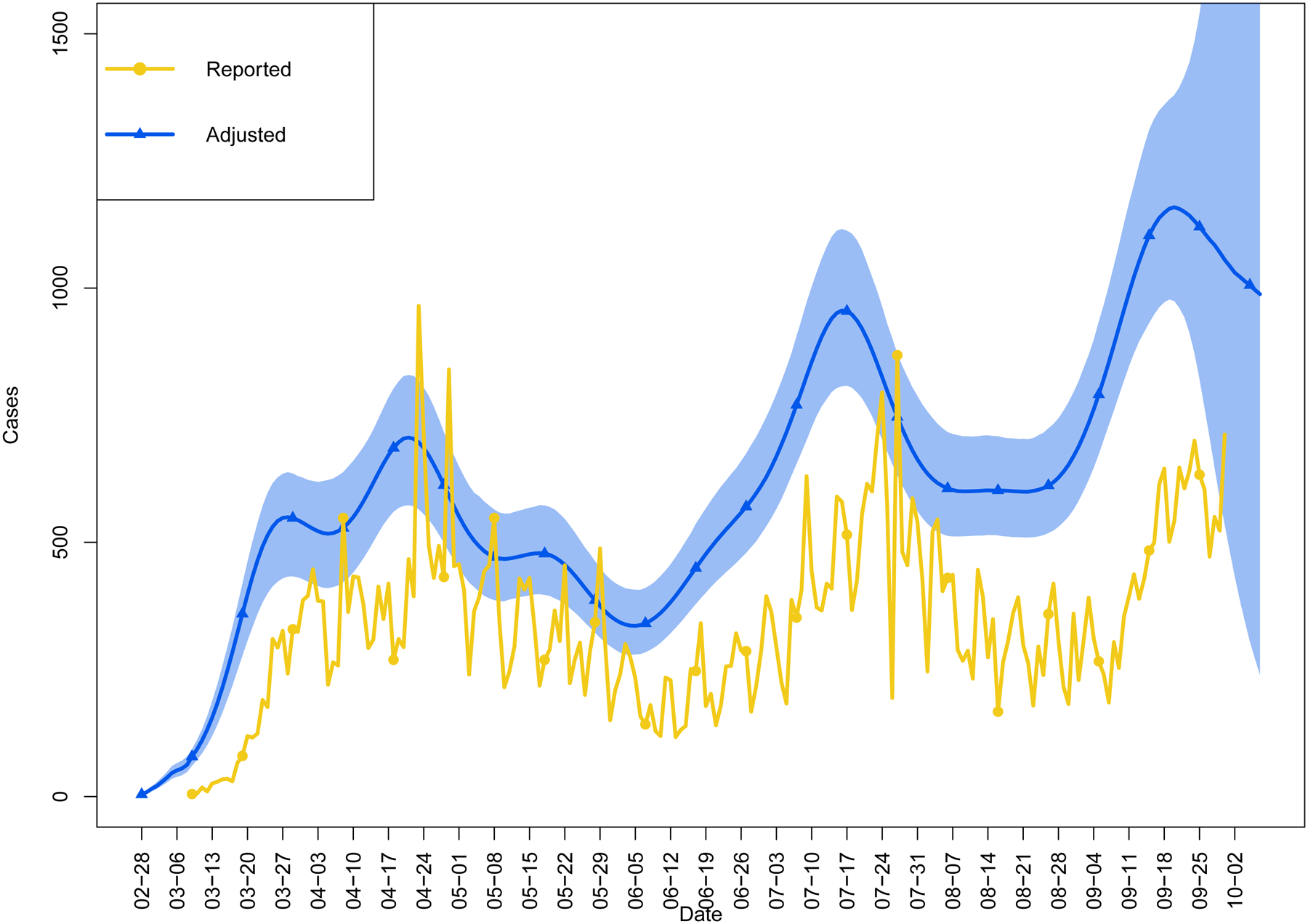
Doubly adjusted COVID-19 epidemic curve for the State of Colorado based on observed surveillance data captured between 9-Mar-2020 through 30-Sep-2020. Adjusted cases account for the incubation period and delay in testing and reporting, as well as surveillance misclassification. Shaded region indicates 95% credible interval. Observed cases by report date plotted for comparison.

Figure 3 plots R_t for the three time-series data, by observed report date, by observed illness onset date, and by the double adjustment. For each representation of the time-series data and taken across the entire date range, the mean (minimum, maximum) values were: 1.12 (0.77, 4.13) by report date, 1.05 (0.78, 2.42) by onset date, and 1.05 (0.89, 1.73) after double adjustment. At the conclusion of the time-series on 30-Sep-2020, the respective values of R_t were: 1.26 (95% CI: 1.08, 1.45) by report date, 1.18 (95% CI: 1.02, 1.33) by onset date, and 0.96 (95% CI: 0.90, 1.01) after double adjustment. Compared to the adjusted epidemic curve, the epidemic curve by report date tended to overestimate R_t during the first few weeks of the outbreak and be more susceptible to fluctuations due to spikes in reporting, which may not correspond to spikes in infection. Overall, the report date R_t was more weakly related to the doubly adjusted R_t than to onset date R_t (Spearman’s ρ=0.63 [95% CI: 0.54, 0.71] vs. 0.79 [95% CI: 0.74, 0.84], respectively).

Figure 3.

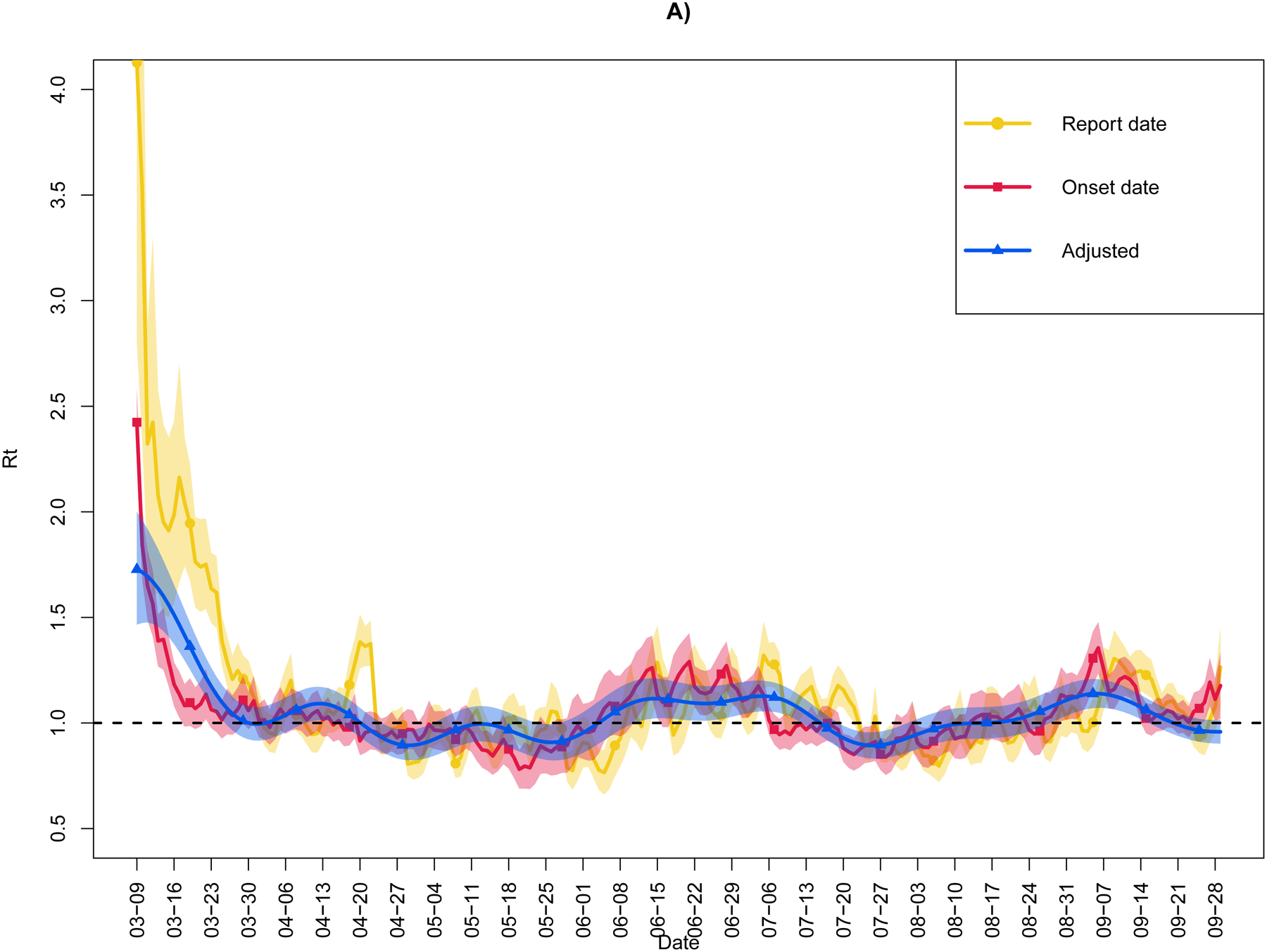
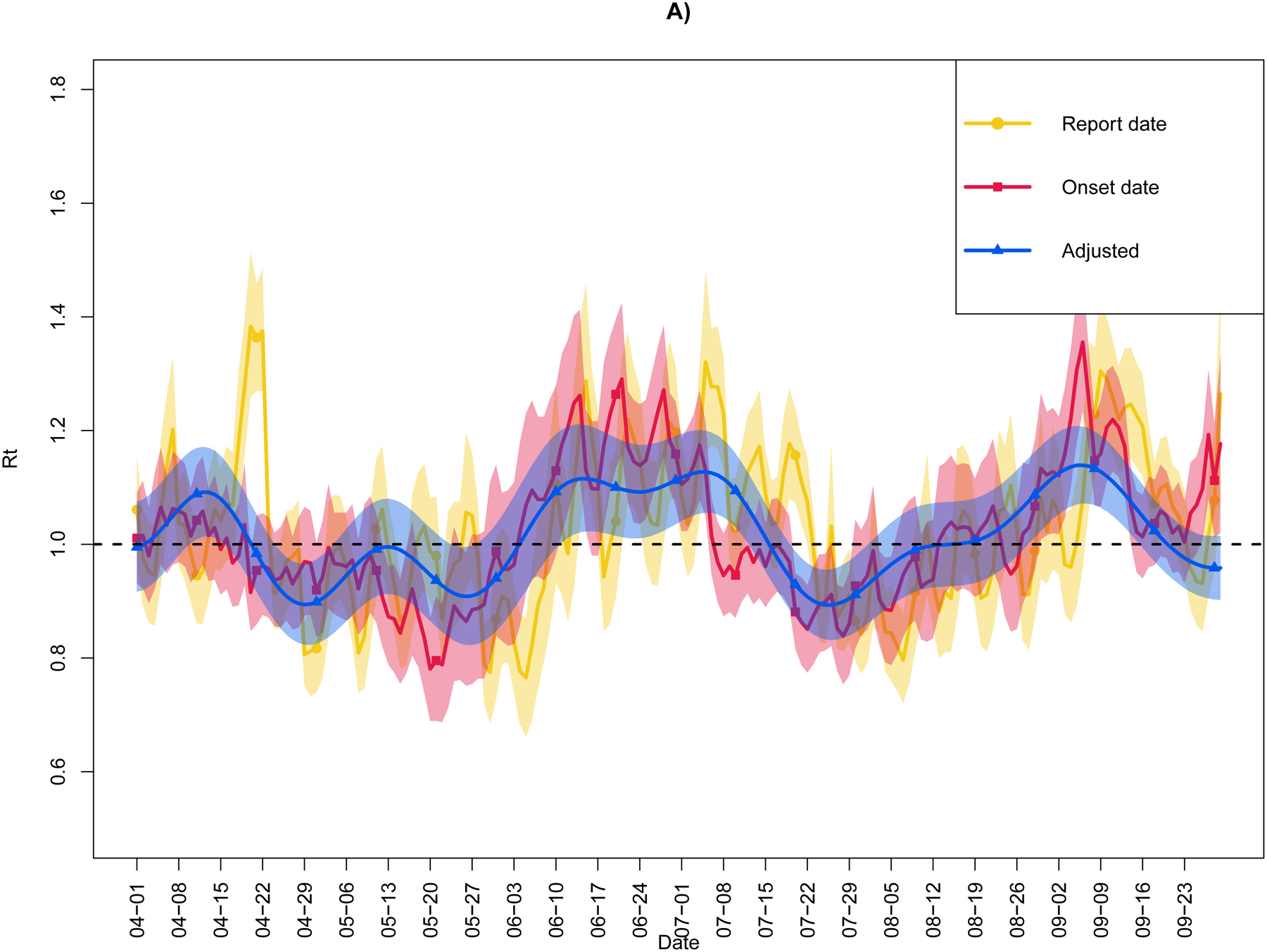
Real-time reproductive number (R_t) for the State of Colorado (9-Mar-2020 through 30-Sep-2020) as estimated from three time-series data: by observed report date, by observed illness onset date, and by the double adjustment. Adjusted cases account for the incubation period and delay in testing and reporting, as well as misclassification due to imperfect case ascertainment. Shaded regions indicate 95% confidence & credible intervals. Horizontal line denotes R_t=1. Panel A) depicts the entire time period and Panel B) focuses on post-March.

Discussion

Using COVID-19 time series surveillance data from the Colorado Department of Public Health & Environment, we applied Bayesian methods to first adjust for misclassification in testing and surveillance, followed by deconvolution of date of infection, to more accurately depict the state’s epidemic curves between 9-Mar-2020 and 30-Sep-2020. From these doubly adjusted data, we were able to obtain a more precise and valid estimate of R_t compared to use of either report or onset dates, with estimates using the report dates being especially uncertain. Comparing these two designations of case occurrence time, onset date R_t aligned closer to the double-adjusted R_t compared to report date R_t, and if investigators are presented with both options for calculating R_t, onset date is likely the better choice. This may be due to the fact that onset date is less vulnerable to fluctuations in the time-series (Figure 1), as it has already been somewhat adjusted for reporting delays. Indeed, the smoothing of the doubly adjusted epidemic curve demonstrated value for those interpreting such curves: public health has cautioned against overly interpreting sharp daily fluctuations in case counts, as these reflect artifacts of the reporting process, such as a decline in reporting over the weekend, and not necessarily a change in epidemiology.^21,22

The observed trimodal distribution in Colorado (Figure 2) may be partially explained by behavioral factors related to policy responses: the shelter in place order enacted March 26, 2020 notably lowered R_t below 1 during the “first wave,” and led to a decline in cases throughout May of 2020.^23,24 The lifting of this order on 26 April 2020 combined with the warmer weather and relaxation of laws surrounding business re-openings may have fueled the “second wave;” however, capacity for testing also increased during this time.²⁵ R_t was consistently above 1 and the case counts increased peaking in July. According to the governor, subsequent business restrictions for restaurants and bars, as well as a statewide indoor masking mandate may have then somewhat attenuated R_t and the corresponding case counts seen in August.²⁶ Yet it should also be noted that, on the whole, R_t had been rather consistent since April 2020, implying that that mitigation efforts taken since that time have been less influential than the observed fluctuation of cases may suggest. This was especially critical at the time of writing in November 2020 due to the third wave of COVID-19 in the state, which has been attributed to an increase in indoor gatherings, decreased diligence in following public health recommendations, and viral fitness in cooler and dryer climates.²⁷

Dates reported via surveillance are often ambiguous and states continually wrestle with missing data. Dates may also take on different meaning for each reported case, yet a health department may only release a single date variable. For example, the State of Washington Department of Health defines a hierarchy of five possible dates in their epidemic curve data: “1) symptom onset date, 2) diagnosis date, 3) positive defining lab date, 4) local health notification date, 5) record creation date”.²⁸ We suspect this is not a unique occurrence. Ultimately, date of infection provides the greatest insight into the source of transmission, and any surrogate date requiring deconvolution to arrive at infection date would need to be fine-tuned on a case-by-case basis. For example, reporting lag period likely differs among jurisdictions and further motivated our modeling separately from the incubation period.

The U.S. Centers for Disease Control and Prevention has used a variety of parameters in modeling efforts intended to inform COVID-19 preparedness and response plans, of which the effective reproductive number is but one indicator.²⁹ As far as we know, these models unrealistically assume perfect data. We demonstrate a method to account for known and suspected imperfections in such data via quantitative bias analysis. Such bias analyses can leverage existing health department data, with requiring de novo data collection when resources are limited, to produce the adjusted time-series and an even greater effort to perfectly capture all infected cases.

Although comparison of our work against others is impeded by lack of consistent and complete data, we note that there have been other efforts at deconvolution and a related approach known as “nowcasting” specific to COVID-19. Leung and Wu examined whether an election held in April 2020 in Wisconsin resulted in a surge in COVID-19 cases by deconvoluting infection date from report date (no association was observed).⁵ Nowcasting has been proposed as a technique to monitor real-time outbreaks when relying only on lagged reported data.^30,31 Researchers have noted the importance of accounting for reporting delays and incomplete case ascertainment when calculating R_t while cautioning against simplistic subtraction-based approaches.^32–34 Wu et al. proposed but, to our knowledge, had not implemented adjustment for misclassification in testing, when sensitivity and specificity are known, together with deconvolution of infection time using a model nearly identical to Burstyn et al.^9,35 Allowing for uncertainty in misclassification parameters is an important feature of our model, however it is not fully enmeshed with deconvolution. As such, one key weakness of our work lies in the assumption that errors in surveillance systems are independent of delays in reporting. This allowed us to develop a two-step procedure that leveraged existing statistical methods. However, we are aware that dependence of two sources of error can make our procedure both inefficient and may lead to bias. For example, one may posit that an overwhelmed public health system may have suboptimal surveillance with greater delays in reporting, and this may change over the course of the pandemic. This is an area of method-development that is worth exploring while there seems to be an equally compelling motivation to promote our approach, which cannot be worse than ignoring errors in the data. A second weakness is the lack of validation data to compare the double adjusted R_t against the true R_t: we did not have access to such data, nor are we aware if they in fact exist. Without validation data, one may consider employing a simulation study where the truth is known. In fact, we have previously vetted our misclassification approach in this fashion.¹¹ As a next step, one could consider conditioning these data on R_t to arrive at a validation time series, although this was outside the scope of our work.

We conclude by observing that adjusting for bias in epidemic curves is now accessible to epidemiologists and can lead to better use of painstakingly collected data. As was demonstrated using the State of Colorado surveillance data, the doubly adjusted curve provided a more realistic picture of the progression of R_t over time, without being susceptible to artifacts in the surveillance process. This potentially allows for improved management of the COVID-19 pandemic, if indeed estimates of missed cases and effective reproduction number play a role.

Supplementary Material

eAppendix

eAppendix. Posterior trace-plots and distributions of select parameters from the Bayesian misclassification adjustment for COVID-19 time series surveillance data obtained from the State of Colorado between 9-Mar-2020 through 30-Sep-2020.