Abstract
Background
As blood testing is radiation-free, low-cost and simple to operate, some researchers use machine learning to detect COVID-19 from blood test data. However, few studies take into consideration the imbalanced data distribution, which can impair the performance of a classifier.
Method
A novel combined dynamic ensemble selection (DES) method is proposed for imbalanced data to detect COVID-19 from complete blood count. This method combines data preprocessing and improved DES. Firstly, we use the hybrid synthetic minority over-sampling technique and edited nearest neighbor (SMOTE-ENN) to balance data and remove noise. Secondly, in order to improve the performance of DES, a novel hybrid multiple clustering and bagging classifier generation (HMCBCG) method is proposed to reinforce the diversity and local regional competence of candidate classifiers.
Results
The experimental results based on three popular DES methods show that the performance of HMCBCG is better than only use bagging. HMCBCG+KNE obtains the best performance for COVID-19 screening with 99.81% accuracy, 99.86% F1, 99.78% G-mean and 99.81% AUC.
Conclusion
Compared to other advanced methods, our combined DES model can improve accuracy, G-mean, F1 and AUC of COVID-19 screening.
Keywords: COVID-19 screening, Imbalanced data, Dynamic ensemble selection, Hybrid multiple clustering and bagging, Candidate classifier generation
1. Introduction
COVID-19, an epidemic caused by severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2), has ravaged over 200 countries around the world. As of October 4, 2020, more than 34.5 million cases and more than 1 million deaths have been reported worldwide [1]. Countries around the world have adopted strict quarantine and isolation measures to curb the spread of COVID-19. To prevent continued transmission, it is necessary to carry out effective screening for suspected cases in order to detect and isolate infected persons in time [2]. Currently, COVID-19 screening still relies heavily on reverse transcription polymerase chain reaction (RT-PCR) [3]. However, the missed detection rate of RT-PCR is about 15%-20% [4]. Moreover, it often takes hours or even days from collecting patient samples to obtaining test results [5]. Therefore, a more rapid and accurate COVID-19 detection method is needed.
Machine learning (ML) methods have been applied to detect COVID-19 due to their fast processing power and high reliability [6], [7], [8], [9], such as deep convolutional network [10], ensemble learning [11] and enhanced k-nearest neighbor (KNN) [12]. Most of these methods are based on computerized tomography (CT) and X-ray image data. However, the relatively high cost and radiation doses hinder the large-scale application of CT. Although X-ray has lower cost and radiation compared to CT, its performance in COVID-19 screening is inferior to CT. In view of the low-cost, radiation-free and easy operation of blood testing, some researchers try to detect COVID-19 from blood test data through ML methods. Brinati, Campagner [4] studied the feasibility of several different ML models to predict COVID-19 infection from routine blood test data. However, the author did not deal with the imbalanced distribution of the dataset. Banerjee, Ray [5] used ML methods to predict COVID-19 infection through full blood count data. For community patients, the synthetic minority oversampling technique (SMOTE) is used to balance the positive (COVID-19 infection) and negative (absence of COVID-19 infection) classes. Then, the artificial neural network (ANN) is used to predict COVID-19 infection and achieved 87% accuracy. However, using SMOTE alone to deal with imbalanced data may generate outlier samples and reduce the classification accuracy [13]. Therefore, it is necessary to propose a better imbalanced data processing method to improve the accuracy of COVID-19 screening from blood test data.
From the current research, the methods of dealing with imbalanced data can be roughly divided into two types: data-based methods and algorithm-based methods [14]. Data-based methods mainly include over-sampling [13], under-sampling [15] and hybrid sampling [16]. For algorithm-based methods, it can be divided into cost-sensitive learning [14] and ensemble learning [17]. The purpose of cost-sensitive learning is to minimize the cost of misclassification on the premise that the cost of misclassification is known [18]. However, for real-life problems, the prior knowledge of the cost of misclassification is often unknown, which makes the application of cost-sensitive learning difficult. Ensemble learning can improve the generalization ability to existing algorithms and has been proven to be an effective method for imbalanced data processing. Among the many ensemble learning approaches, dynamic ensemble selection (DES) as a very promising method has been proved by a large number of studies to be superior to static ensemble learning [19], [20], [21]. For a DES technique, the neighbors of each test sample, called the competence region, are used to measure the competence of each candidate classifier. Then DES selects appropriate classifiers for each test sample based on the competence measurement to form an ensemble, rather than using a unified ensemble for all test samples.
Recently, more and more DES methods have been applied to deal with imbalanced data problem and have achieved outstanding performance [20, 22, 23]. Roy, Cruz [24] compared the performance of DES combined with a preprocessing technique and static ensemble for processing imbalanced data. The experimental results show that DES have higher F-measure and G-mean relative to static ensemble methods. Hou, Wang [20] combined SMOTE and DES to assess credit risk, and tested the performance of the hybrid method on other 15 imbalanced datasets. However, these DES methods mainly use bagging [25] to train candidate classifiers, and the training sets randomly generated by bagging may not be sufficient to represent the competence regions. Moreover, these studies set fixed parameters for the base classifiers, which may reduce the fitting performance of base classifiers to different training sets.
To solve the above-mentioned problems and challenges, a novel combined DES method is proposed for imbalanced data to detect COVID-19 from complete blood count. At the data level, hybrid SMOTE and edited nearest neighbor (SMOTE-ENN) [26] is used to balance data and clean up noise. At the algorithm level, in order to improve the competence in local regions and diversity of candidate classifiers, a novel hybrid multiple clustering and bagging classifier generation (HMCBCG) method is developed to improve DES. HMCBCG adds multiple clustering to generate classifiers on the basis of bagging. Specifically, we use k-means [27] with different k values to cluster the training set repeatedly with replacement. In this way, multiple clusters with different decision boundaries can be generated, which increases the diversity of candidate classifiers. Besides, the training sets generated based on clustering are more likely to represent the local regions around the test samples than bagging. Then, all the clusters obtained by multiple clustering are used to train support vector machines (SVM) [28]. At the same time, for each cluster, we use genetic algorithm (GA) [29] to optimize the parameters of SVM to strengthen its regional competence and diversity. Finally, the base classifiers generated by bagging and SVMs based on clustering training are mixed together to form a candidate classifier pool. The contributions of this research can be summarized as:
-
I.
A combined DES method is proposed for imbalanced data to detect COVID-19 from complete blood count.
-
II.
A novel HMCBCG candidate classifier generation method is developed to improve the performance of DES.
-
III.
The proposed combined DES method can significantly improve the accuracy, G-mean, F1 and area under the curve (AUC) of COVID-19 screening than other compared advanced algorithms.
-
IV.
HMCBCG+k-nearests oracles eliminate (KNE) obtains the best performance for COVID-19 screening with 99.81% accuracy, 99.86% F1, 99.78% G-mean and 99.81% AUC.
The rest of this paper is organized as follows: Section 2 introduces previous related work. Section 3 describes the dataset and methods used in this study. In Section 4, we present the experimental setting, performance metrics, and experimental results. Section 5 provides a discussion about the experimental results. Finally, a brief summary is described in last section.
2. Related work
2.1. Intelligent computing methods in COVID-19 screening
Currently, intelligent computing methods of COVID-19 screening are mainly based on CT, X-ray and clinical blood test data. In terms of CT and X-ray, the convolutional neural network (CNN) is the most used method. Ezzat, Hassanien [30] proposed a gravity search optimized CNN to detect COVID-19 from a dataset containing CT and X-ray images, which accuracy is 98.38%. Apostolopoulos and Mpesiana [8] combined transfer learning technology with several advanced CNNs to diagnose COVID-19. The MobileNet performed best in experimental results with 96.78% accuracy. In addition, there are also some studies using other ML techniques to detect COVID-19 from medical imaging data. Chandra, Verma [11] proposed an ensemble learning method based on majority voting to detect COVID-19 from X-ray and its accuracy is 98.062%. Shaban, Rabie [12] produced a new COVID-19 detection strategy that combining feature selection and improved KNN. The recognition accuracy of this method for COVID-19 CT images is 96%. Compared with CT and X-ray, blood testing has the advantages of low-cost, radiation-free and easy operation. Therefore, some studies try to using ML to detect COVID-19 from blood test data. For example, Brinati, Campagner [4] studied several ML methods to detect COVID-19 from blood routine examination data. The results show that random forest achieved the highest accuracy. However, this study did not notice the negative impact of imbalanced data distribution on classification performance. Especially for a dataset where the number of healthy people is much larger than the number of COVID-19 infections, classifier will tend to identify healthy people and ignore infected people. Unfortunately, the cost of misdiagnosing an infected person as a healthy person is far greater than the cost of misdiagnosing a healthy person as an infected person. Although Banerjee, Ray [5] applied SMOTE to balance the different classes in the dataset for detecting COVID-19 from full blood count data, there is still room for improvement.
2.2. DES to handle imbalanced data
DES, one of the dynamic selection (DS) techniques, has been shown to outperform single-based classifiers for some classification problems [31]. DES techniques are recommended for handling imbalanced data problems since they perform local classification [32]. In recent years, more and more studies have proved that DES are superior to static ML algorithms for imbalanced data processing. We roughly classify the existing DES methods for dealing with imbalanced data into two categories. One is to directly improve DES without combining resampling methods. For example, Oliveira, Cavalcanti [33] proposed FIRE-DES algorithm to preselect those classifiers that have the ability to process decision boundary samples when the test sample is in an overlapping area. Experiments prove that FIRE-DES can improve the performance of existing DES frameworks for small imbalanced data processing. Junior, Nardini [22] developed an improved KNN to balance the sample distribution in the local region of the test sample. The intuition of this algorithm is to reduce the distance between the minority samples and the predicted sample so that more minority samples are included in the neighbors of the predicted sample. Zhao, Wang [34] introduced patch learning in DES to improve the diversity of base classifiers. Experimental results show that this patched-ensemble model performs well for multi-class imbalanced classification. Zyblewski, Woźniak [35] designed two DES methods, which are based on Euclidean distance and imbalance rate to select base classifiers. The effectiveness of these two DES methods was tested on 41 high imbalance ratio datasets.
Another kind of method is to combine preprocessing with DES to deal with imbalanced data. Zyblewski, Sabourin [36] proposed a framework that integrates data preprocessing and DES for imbalanced data stream classification. This approach uses stratified bagging to train the base classifiers. Cruz, Oliveira [37] proposed FIRE-DES++ algorithm, which improves FIRE-DES by removing noise and using the same number of instances of each class to define the competence region. Gao, Ren [23] presented a method of combining hybrid sampling based on data partition with dynamic model selection for imbalanced data. In addition, García, Zhang [38] proposed a method that hybrid preprocessing and DES to handle multi-class imbalanced data. The preprocessing part of the method obtains a balanced training set through resampling. In the candidate classifier selection part, the classifiers with a strong ability to recognize minority samples are preferentially selected through the mechanism of weighting the competence region.
However, from our knowledge, most of these DES methods are based on bagging to generate candidate classifiers. The training sets generated by random sampling of bagging may not be sufficiently representative of the competence regions. In addition, using fixed parameters to generate candidate classifiers is a common practice in existing DES methods, which may lead to insufficient fitting to the training set.
3. Materials and Methods
3.1. Data collection
The dataset for this study is obtained from the data science platform Kaggle1 . This dataset has been used for COVID-19 diagnosis through intelligent computing methods in previous research [5][55-57]. The original dataset contains 5644 cases with 111 attributes. It was provided by Hospital Israelita Albert Einstein in Sao Paulo, Brazil. Patients in the dataset were tested for COVID-19 by RT-PCR during their visit to the hospital, and other laboratory tests were also performed. All patients have been anonymized. There are a lot of missing values in the original dataset. We preprocessed the dataset as follows: First, we remove the features that are mostly missing values, and 17 features including SARS-CoV-2 test and standard complete blood count are remained. Then, samples with mostly null are also removed, and 603 cases are obtained. The distribution of negative samples and positive samples is imbalanced, being 520 and 83, respectively. Finally, multivariate imputation by chained equation (MICE) [39] is used to fill in missing values in the selected samples.
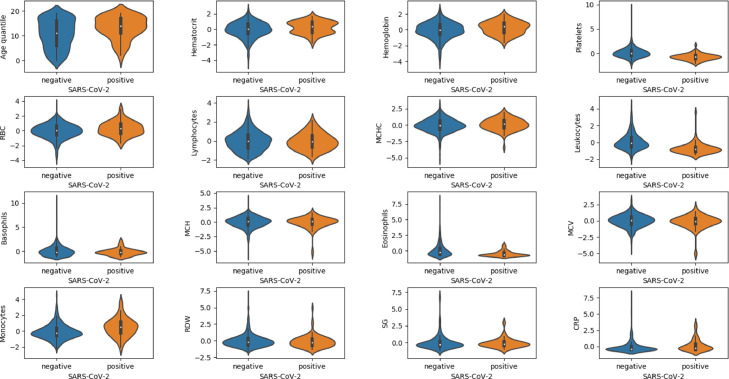
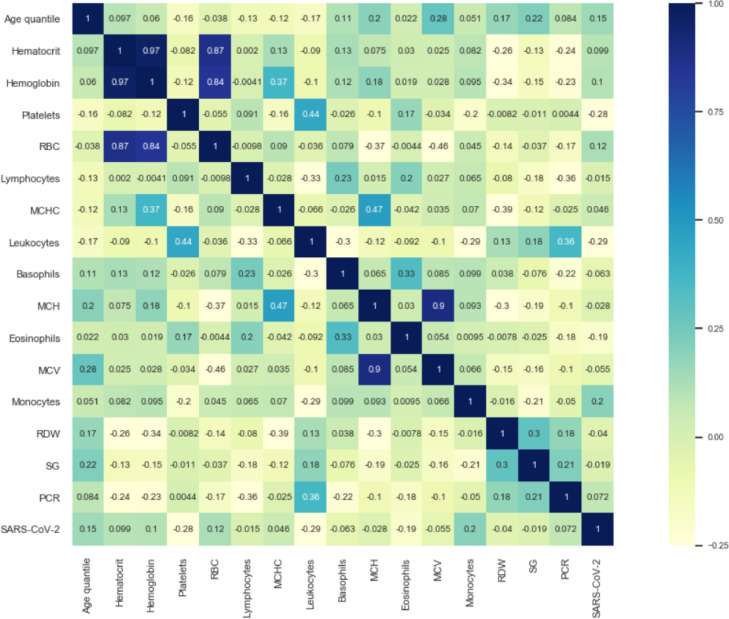
Table 1 shows the filtered features and data types. As shown in Table 1, the “SARS-CoV-2 exam result” is a binary label, negative means no COVID-19 infection, and positive means COVID-19 infection. All features except “SARS-CoV-2 exam result” are numerical features. Fig. 1 shows the sample distribution of the selected features. Fig. 2 reports the Pearson correlation coefficient of the selected features. The darker the color, the stronger the positive correlation between the two features. The lighter the color, the stronger the negative correlation.
Table 1.
The filtered features and data types.
| Features | Data Type |
|---|---|
| Age quantile | Numerical |
| Hematocrit | Numerical |
| Hemoglobin | Numerical |
| Platelets | Numerical |
| Red blood cells (RBC) | Numerical |
| Lymphocytes | Numerical |
| Mean corpuscular hemoglobin concentration (MCHC) | Numerical |
| Leukocytes | Numerical |
| Basophils | Numerical |
| Mean corpuscular hemoglobin (MCH) | Numerical |
| Eosinophils | Numerical |
| Mean corpuscular volume (MCV) | Numerical |
| Monocytes | Numerical |
| Red blood cell distribution width (RDW) | Numerical |
| Serum glucose (SG) | Numerical |
| C-reactive protein (CRP) | Numerical |
| SARS-CoV-2 exam result | Categorical |
Fig. 1.
Violin plots of selected features. Negative and positive are classified labels, negative means no COVID-19 infection, and positive means COVID-19 infection.
Fig. 2.
Pairwise Pearson correlation of selected features. The correlation value range is [-1,1]. 1 means completely positive correlation, -1 means completely negative correlation, and 0 means irrelevant.
3.2. SMOTE-ENN for preprocessing
In this paper, SMOTE-ENN is used to preprocess the COVID-19 dataset. SMOTE-ENN is a hybrid sampling method proposed by Batista, Prati [26]. SMOTE-ENN combines the advantages of both SMOTE [40] and edited nearest neighbor [41] [42], which can effectively deal with imbalanced data and remove noise. In SMOTE, a new sample is synthesized according to Eq. (1):
| (1) |
wherexsis a new synthesized sample; xrepresents a minority sample (positive sample); x′ is a randomly selected sample from the k nearest neighbors of x; random(0,1) represents a random number between 0 and 1. As a simple and effective oversampling method, SMOTE is widely used to deal with imbalanced data. ENN can identify and remove noise to make the decision boundary smoother [37]. ENN uses KNN to predict each sample in the new dataset. If the predicted result is inconsistent with the real label, the sample is removed.
3.3. HMCBCG model to improve DES
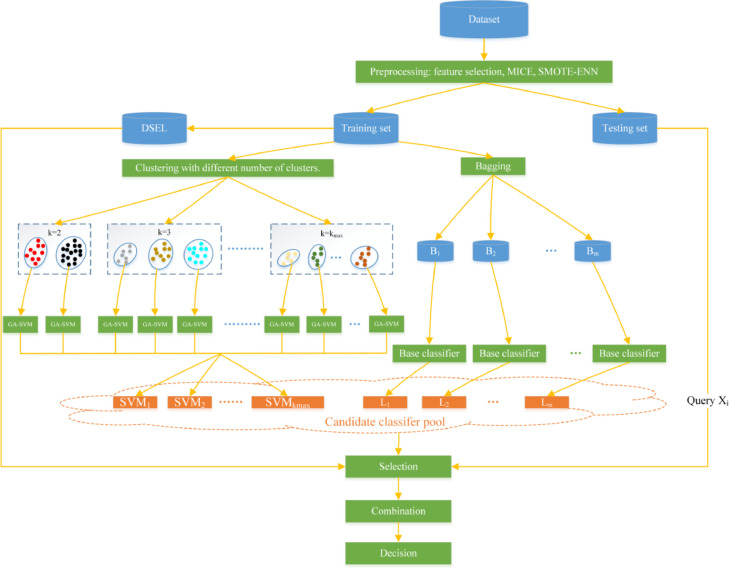
In order to strengthen the diversity of DES candidate classifiers and their regional competence, we propose a novel HMCBCG algorithm to generate candidate classifiers. As shown in Algorithm 1 and Fig. 3 , candidate classifiers generated by HMCBCG consists of two parts: one part is generated by multiple times k-means clustering with different k values, and the other part is established by bagging. In this way, subsets generated by clustering tend to have better local regional representation than the randomly generated subsets by bagging. Moreover, subsets generated by multiple times clustering based on different cluster numbers can increase the diversity of the training set. Therefore, candidate classifiers generated by combing multiple times clustering based on different cluster numbers with bagging have better diversity and local capabilities than bagging alone.
Algorithm 1.
HMCBCG model
| Input: Train data Dtr, maximum cluster numbers kmax, m base learners L1, L2,…,Lm. Set the number of samples in each subset obtained by bagging to n. |
| Output: Candidate classifier pool Ψ |
| 1: Ψ←∅ |
| 2: for 2 to kmaxdo: |
| 3: Use k-means to divide Dtr into k clusters. |
| 4: for each cluster do: |
| 5: Apply GA to optimize SVM to get the SVM with optimal parameters. |
| 6: Add the trained SVM to Ψ. |
| 7: end for 8: Shuffle all the clusters to restore Dtr. |
| 9: end for |
| 10: for 1 to m do: |
| 11: for 1 to n do: |
| 12: Randomly draw a sample from Dtr. |
| 13: end for |
| 14: Use the n samples to train a base learner. |
| 15: Add the trained base learner to Ψ. 16: Put the n samples back to restore Dtr. |
| 17: end for |
| 18: return Ψ |
Fig. 3.
Specific steps of our proposed combined DES method for COVID-19 screening. k represents the number of clusters set for each time. kmax is the maximum number of clusters. Bi is the n samples randomly selected from the training set for the i-th time. Li is the base classifier obtained by training with Bi, and m is the number of base classifiers.
Firstly, in part of generating candidate classifiers based on clustering, we cluster the training set multiple times by k-means with different k values. After each k-means clustering, we put the samples back in order to cluster the original training set again. The number of clusters for each time is taken from 2 to the preset maximum number of clusters kmax. For example, assuming that kmax=5, then the training set will be clustered 4 times, and the value of the number of clusters k will be set to 2, 3, 4, and 5 for each time.
Then, each cluster is used to train SVM. SVM is one of the most accurate and robust algorithms in the field of pattern recognition. Over the years, SVM has been widely used in classification and regression problems. The purpose of SVM is to find an optimal hyperplane to maximize the classification interval from training samples. For a dataset S={(x1, y1),(x2, y2)…(xn, yn)}, the optimal hyperplane can be shown as
| (2) |
where wTrepresents the weight vector, xmeans input vector and b is the bias. Eq. (2) can be transformed into an optimization problem as
| (3) |
By introducing Lagrangian multipliers with λi > 0(i=1,2,…,n), the optimization problem can be transformed into a dual problem as follows:
| (4) |
where C is the penalty coefficient. If C is too large, the risk of SVM falling into over-fitting will increase; otherwise, under-fitting will easily occur. For nonlinear problems, SVM needs to map the original data to a high-dimensional space through a kernel function to make it linearly separable. The classification function can be expressed as
| (5) |
where indicates the optimal Langrangian coefficient, b*denotes the optimal bias. Sgn() is a symbolic function. K < xi • xj > represents the kernel function. In this study, we chose the most commonly used radial basis function (RBF) as the kernel function of SVM. The RBF kernel function is expressed as:
| (6) |
The performance of SVM is greatly affected by the penalty coefficient C and the kernel function parameterη. In previous studies, SVM as the base classifier of DES often uses fixed parameters. In order to improve the regional competence and diversity of SVM, this paper uses GA to optimize the penalty coefficient C and the kernel function parameter η of SVM. GA is a method that searching for the optimal solution by imitating the selection, crossover and mutation in the natural evolution process. Due to the outstanding global optimization ability of GA, it has been well applied to optimization problems in many fields. In view of the above advantages, GA is used to optimize the penalty factor and the kernel function parameter of SVM. The classification accuracy of SVM is used as the fitness of GA. In this way, for each cluster, SVM with the optimal parameters is obtained.
Another part of candidate classifiers is generated by bagging. Bagging is a typical ensemble learning method, which improves prediction accuracy and robustness by combining multiple base classifiers, and can reduce variance and avoid overfitting. The specific steps of bagging are: (1) Randomly select n samples from the original dataset. (2) Use the obtained n training samples to train a base classifier. (3) Repeat steps (1) and (2) m times. The prediction result is decided by the m base classifiers collectively (usually by voting).
Finally, the candidate classifiers generated by bagging and SVMs based on clustering training are mixed to construct a DES candidate classifier pool.
3.4. Specific steps of proposed combined DES model for COVID-19 screening
Based on SMOTE-ENN preprocessing and HMCBCG optimized DES, we propose a combined DES model for imbalanced data to detect COVID-19 from complete blood count. Fig. 3 shows the flow chart of our proposed combined DES model. The specific implementation steps are as follows:
-
(1)
Perform data cleaning on the original dataset D, including feature selection and filling in missing values. Then apply SMOTE-ENN to balance the different classes in the dataset and remove noise samples. Finally, receive the cleaned dataset Dc.
-
(2)
Divide Dc into training set Dtrain and testing set Dtest. A part of samples is randomly selected from Dtrain as the validation set, which is also called dynamic selection dataset (DSEL) [37]. The remaining samples are denoted as Dtr.
-
(3)
The candidate classifier pool Ψ is generated based on the Dtr and HMCBCG method.
-
(4)
For a query sample X i in the testing set, select its k neighbors from DSEL.
-
(5)
Each classifier in Ψ is used to classify the k nearest neighbors selected from DSEL.
-
(6)
Select suitable classifiers from Ψ according to the selection criteria (usually by accuracy).
-
(7)
Combine the selected classifiers according to majority voting.
-
(8)
Determine and output the class of the query sample X i.
4. Experiments and results
4.1. Experiment setting
In this research, we chose three DES methods, including KNE [43], KNU [43] and DESKNN [44] to test the proposed HMCBCG model. We considered several configurations kmax =2,3,4,5 and the classifier generation that only uses bagging, which is recorded as NON in the experimental results. The experiment considered three data division methods of 70-30, 60-40 training-test divisions and 5-fold cross-validation. Naive bayesian [45], decision tree (DT) [46], KNN [47] and RF [48] are selected as base classifiers to train with bagging. We set the number of each type of base classifier to 10, that is, a total of 40 base classifiers are trained by bagging. In addition, the GA operators use tournament selection, uniform crossover and flipbit mutation. Set the crossover probability to 0.8 and the mutation probability to 0.1. The population size is 50 and the number of iterations is 30.
We also compared our combined DES method with several advanced algorithms, including GBDT [49], SVM, RF, LR [50] and XGBoost [51]. In this study, all the computations are performed on a Python 3.6 platform on a Windows 10 system with Intel Core i5 (1.6 GHz, 8 CPUs) with 8 GB of RAM. The results of this study are the average performance after repeating the experiment 10 times.
4.2. Performance metrics
In this research, we choose accuracy, G-mean, F1 and AUC as the evaluation indicators, which are widely used in the performance evaluation of algorithms on imbalanced data. They can be defined according to the confusion matrix in Table 2 . Accuracy, G-mean and F1 are shown as follows:
| (7) |
| (8) |
| (9) |
Table 2.
Confusion matrix.
| Actual Positive | Actual Negative | |
|---|---|---|
| Predicted Positive | TP | FP |
| Predicted Negative | FN | TN |
where ,.
AUC is the area under the receiver operating characteristic curve (ROC). The closer the AUC is to 1, the better the performance of the classifier. AUC is very suitable for evaluating imbalanced data classifiers because it is insensitive to the proportion of positive and negative examples in the dataset [52].
4.3. The performance of HMCBCG for different DES algorithms
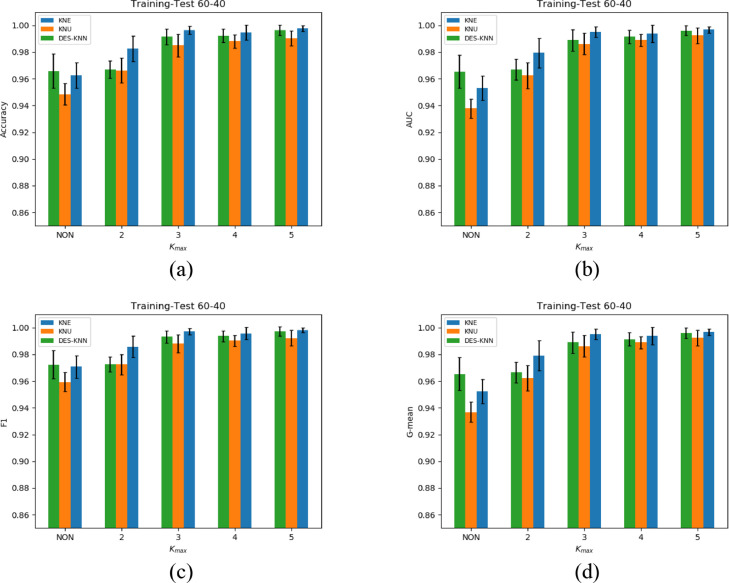
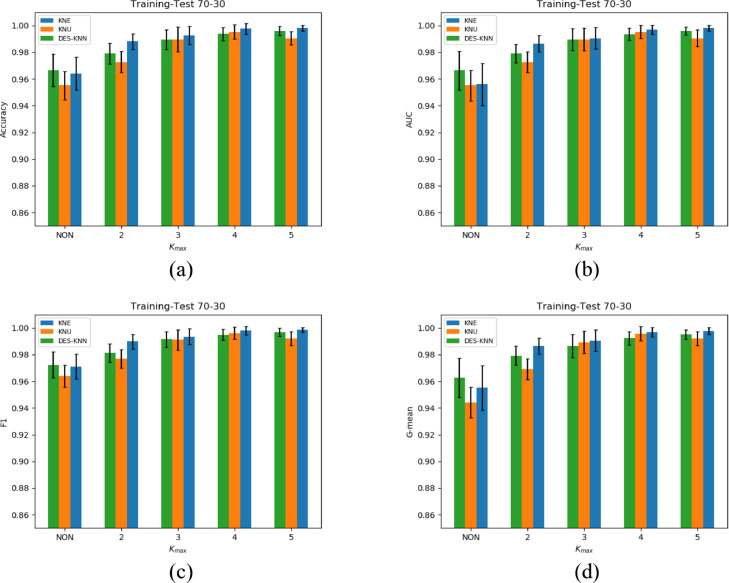
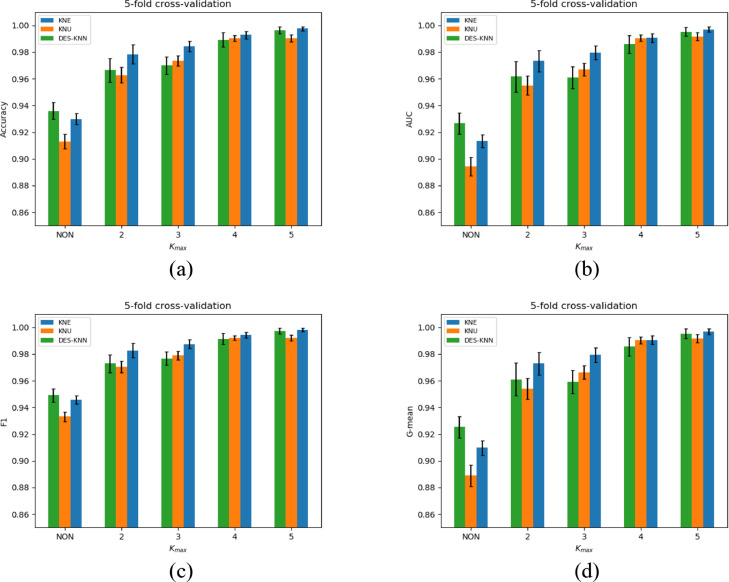
The experimental results of KNE, KNU and DES-KNN under 70-30, 60-40 divisions and 5-fold cross-validation are shown in Table 3 - 5, respectively. For the four indicators of accuracy, F1, G-mean and AUC, we have marked the best results of KNE, KNU and DES-KNN in bold. As shown in Fig. 4 - 6 , in order to better compare the performance of KNE, KNU and DESKNN for different kmax values, we have drawn bar charts of different indicators for the three division methods of 70-30, 60-40 training-test and 5-fold cross-validation.
Fig. 5.
Average performance and standard deviations comparison of KNE, KNU and DESKNN under different indicators with 60-40 division. (a) Accuracy, (b) AUC, (c) F1, (d) G-mean.
Table 3.
Mean performance and standard deviations of KNE, KNU and DESKNN under different kmax values with 70-30 division.
| Metrics | Methods | NON | kmax=2 | kmax=3 | kmax =4 | kmax =5 |
|---|---|---|---|---|---|---|
| Accuracy | KNE | 0.9640±0.0123 | 0.9880±0.0060 | 0.9926±0.0067 | 0.9976±0.0042 | 0.9981±0.0023 |
| KNU | 0.9551±0.0105 | 0.9728±0.0079 | 0.9896±0.0093 | 0.9952±0.0050 | 0.9904±0.0050 | |
| DESKNN | 0.9664±0.0122 | 0.9791±0.0076 | 0.9896±0.0073 | 0.9936±0.0051 | 0.9960±0.0033 | |
| F1 | KNE | 0.9710±0.0093 | 0.9897±0.0055 | 0.9934±0.0059 | 0.9981±0.0033 | 0.9986±0.0018 |
| KNU | 0.9639±0.0082 | 0.9769±0.0070 | 0.9911±0.0075 | 0.9961±0.0045 | 0.9920±0.0051 | |
| DESKNN | 0.9723±0.0098 | 0.9814±0.0070 | 0.9915±0.0059 | 0.9948±0.0041 | 0.9968±0.0031 | |
| G-mean | KNE | 0.9551±0.0165 | 0.9864±0.0061 | 0.9905±0.0080 | 0.9968±0.0035 | 0.9978±0.0027 |
| KNU | 0.9442±0.0116 | 0.9693±0.0078 | 0.9892±0.0085 | 0.9957±0.0054 | 0.9921±0.0050 | |
| DESKNN | 0.9625±0.0147 | 0.9793±0.0071 | 0.9865±0.0087 | 0.9924±0.0050 | 0.9951±0.0035 | |
| AUC | KNE | 0.9560±0.0159 | 0.9865±0.0061 | 0.9905±0.0080 | 0.9968±0.0035 | 0.9981±0.0022 |
| KNU | 0.9551±0.0114 | 0.9728±0.0078 | 0.9896±0.0085 | 0.9952±0.0049 | 0.9904±0.0063 | |
| DESKNN | 0.9664±0.0145 | 0.9791±0.0070 | 0.9896±0.0081 | 0.9936±0.0046 | 0.9960±0.0032 | |
Table 5.
Mean performance and standard deviations of KNE, KNU and DESKNN under different kmax values with 5-fold cross-validation.
| Metrics | Methods | NON | kmax =2 | kmax =3 | kmax =4 | kmax =5 |
|---|---|---|---|---|---|---|
| Accuracy | KNE | 0.9299±0.0040 | 0.9784±0.0070 | 0.9843±0.0040 | 0.9928±0.0028 | 0.9976±0.0016 |
| KNU | 0.9130±0.0054 | 0.9628±0.0058 | 0.9735±0.0040 | 0.9904±0.0022 | 0.9906±0.0027 | |
| DES-KNN | 0.9360±0.0064 | 0.9664±0.0088 | 0.9699±0.0065 | 0.9892±0.0054 | 0.9964±0.0028 | |
| F1 | KNE | 0.9457±0.0030 | 0.9827±0.0055 | 0.9875±0.0032 | 0.9942±0.0022 | 0.9980±0.0013 |
| KNU | 0.9330±0.0037 | 0.9703±0.0043 | 0.9789±0.0032 | 0.9921±0.0018 | 0.9922±0.0023 | |
| DES-KNN | 0.9491±0.0050 | 0.9729±0.0066 | 0.9766±0.0049 | 0.9913±0.0042 | 0.9971±0.0022 | |
| G-mean | KNE | 0.9097±0.0053 | 0.9729±0.0084 | 0.9794±0.0053 | 0.9905±0.0033 | 0.9969±0.0021 |
| KNU | 0.8889±0.0080 | 0.9539±0.0078 | 0.9662±0.0049 | 0.9903±0.0025 | 0.9915±0.0030 | |
| DES-KNN | 0.9252±0.0082 | 0.9611±0.0125 | 0.9592±0.0088 | 0.9857±0.0069 | 0.9953±0.0035 | |
| AUC | KNE | 0.9134±0.0048 | 0.9733±0.0081 | 0.9797±0.0052 | 0.9906±0.0033 | 0.9969±0.0020 |
| KNU | 0.8943±0.0069 | 0.9549±0.0071 | 0.9669±0.0048 | 0.9904±0.0024 | 0.9916±0.0029 | |
| DES-KNN | 0.9266±0.0079 | 0.9617±0.0115 | 0.9610±0.0082 | 0.9859±0.0067 | 0.9953±0.0034 | |
Fig. 4.
Average performance and standard deviations comparison of KNE, KNU and DESKNN under different indicators with 70-30 division. (a) Accuracy, (b) AUC, (c) F1, (d) G-mean.
Fig. 6.
Average performance and standard deviations comparison of KNE, KNU and DESKNN under different indicators with 5-fold cross-validation. (a) Accuracy, (b) AUC, (c) F1, (d) G-mean.
It can be seen from Fig. 4 - 6 that for different training-test divisions and kmax values, the performance of HMCBCG is improved on accuracy, F1, G-mean and AUC for KNE, KNU and DES-KNN compared with bagging directly. This shows that for different kmax values, HMCBCG can not only effectively improve the overall accuracy of COVID-19 detection, but also improve the sensitivity and specificity. From Fig. 4 - 6, we can see that HMCBCG+KNE obtains the best performance with 99.81% accuracy, 99.86% F1, 99.78% G-mean and 99.81% AUC when kmax = 5 with 70-30 division.
As can be seen from Table 3 – 5 and Fig. 4 - 6, on the whole, with the increase of kmax, the values of accuracy, F1, G-mean and AUC of KNE, KNU and DESKNN also increase. This is because as the value of kmax increases, the more different clusters are generated, the more diverse SVMs after training. In addition, GA enhances the adaptability of SVMs to different clusters. In this way, the larger the value of kmax, the more likely the optimized SVMs are to fit different competence regions of different query samples, and the higher the accuracy of DES.
For Table 3, when kmax =5, we observe that the values of 99.04% accuracy, 99.20% F1, 99.21% G-mean and 99.04% AUC of KNU have a slight decrease relative to kmax =4 which are 99.52% accuracy, 99.61% F1, 99.57% G-mean and 99.52% AUC. Similar situations can also be observed when the kmax=3, 4 of KNE and kmax=2, 3 of DES-KNN from Table 4 and Table 5 . This shows that for different data partitioning methods, the performance of KNE, KNU and DESKNN may fluctuate slightly with the increase of kmax, but overall it will improve with the increase of kmax. Another interesting observation is that whether it is 70-30, 60-40 divisions or 5-fold cross-validation, for different kmax values, HMCBCG+KNE outperforms HMCBCG+KNU and HMCBCG+DESKNN in terms of accuracy, F1, G-mean and AUC.
Table 4.
Mean performance and standard deviations of KNE, KNU and DESKNN under different kmax values with 60-40 division.
| Metrics | Methods | NON | kmax =2 | kmax =3 | kmax =4 | kmax =5 |
|---|---|---|---|---|---|---|
| Accuracy | KNE | 0.9628±0.0096 | 0.9825±0.0097 | 0.9964±0.0030 | 0.9946±0.0056 | 0.9976±0.0021 |
| KNU | 0.9484±0.0080 | 0.9663±0.0093 | 0.9850±0.0085 | 0.9880±0.0049 | 0.9904±0.0057 | |
| DES-KNN | 0.9658±0.0127 | 0.9669±0.0065 | 0.9916±0.0058 | 0.9922±0.0050 | 0.9964±0.0037 | |
| F1 | KNE | 0.9707±0.0084 | 0.9858±0.0079 | 0.9971±0.0025 | 0.9956±0.0045 | 0.9981±0.0019 |
| KNU | 0.9593±0.0072 | 0.9724±0.0077 | 0.9880±0.0068 | 0.9902±0.0040 | 0.9923±0.0059 | |
| DES-KNN | 0.9723±0.0105 | 0.9726±0.0055 | 0.9933±0.0046 | 0.9937±0.0041 | 0.9971±0.0034 | |
| G-mean | KNE | 0.9522±0.0092 | 0.9792±0.0112 | 0.9951±0.0038 | 0.9938±0.0063 | 0.9966±0.0025 |
| KNU | 0.9369±0.0074 | 0.9622±0.0097 | 0.9861±0.0080 | 0.9890±0.0045 | 0.9923±0.0058 | |
| DES-KNN | 0.9653±0.0123 | 0.9667±0.0078 | 0.9889±0.0080 | 0.9914±0.0051 | 0.9961±0.0038 | |
| AUC | KNE | 0.9531±0.0090 | 0.9794±0.0111 | 0.9951±0.0038 | 0.9938±0.0063 | 0.9966±0.0025 |
| KNU | 0.9379±0.0071 | 0.9625±0.0096 | 0.9861±0.0080 | 0.9890±0.0045 | 0.9924±0.0057 | |
| DES-KNN | 0.9654±0.0123 | 0.9668±0.0077 | 0.9889±0.0079 | 0.9914±0.0051 | 0.9961±0.0037 | |
In terms of standard deviation, we can see from Table 3 and Fig. 4 that for different values of kmax, the standard deviations of KNE, KNU and DES-KNN for all four evaluation metrics are less than bagging under the data division of 70-30. As seen in Tables 4 and Table 5, the standard deviations of KNE, KNU and DES-KNN for accuracy, F1, G-mean and AUC are comparable to bagging for both kmax =2 and kmax =3 for the 60-40 and 5-fold cross-validation data partitioning methods, while the standard deviations of these three DES methods are better than bagging when kmax =4 and kmax =5. Therefore, in most cases, the standard deviations of the improved DES based on HMCBCG are lower than that of the DES with only bagging to generate candidate classifiers, which indicates that our method has better stability and consistency.
To further verify the superiority of HMCBCG over bagging, the experimental results of KNE, KNU and DESKNN under different kmax values are subjected to paired t-tests with bagging, respectively. The paired t-test is recommended for the comparison of two classifiers on one dataset [53, 54]. A p-value less than 0.05 is considered statistically significant in this study. Tables 6 – 8 show the results of paired t-tests under 70-30,60-40 divisions and 5-fold cross-validation, respectively. As can be seen in Tables 6 – 8, except for DESKNN at kmax =2 under 60-40 partitioning, for different data divisions and DES methods, the accuracy, F1, G-mean and AUC of HMCBCG under different kmax values are significantly better than bagging.
Table 7.
Paired t-test results of KNE, KNU and DESKNN under different kmax values with bagging (60-40 division).
| Metrics | Methods |
t-value (significance) |
|||
|---|---|---|---|---|---|
| kmax =2 | kmax =3 | kmax =4 | kmax =5 | ||
| Accuracy | KNE | 4.605(0.001) | 10.759(0.000) | 8.547(0.000) | 11.967(0.000) |
| KNU | 4.577(0.001) | 8.750(0.000) | 14.642(0.000) | 11.023(0.000) | |
| DESKNN | 0.243(0.814) | 8.360(0.000) | 6.644(0.000) | 7.741(0.000) | |
| F1 | KNE | 4.352(0.002) | 9.730(0.000) | 8.127(0.000) | 10.685(0.000) |
| KNU | 3.866(0.004) | 8.075(0.000) | 13.154(0.000) | 9.511(0.000) | |
| DESKNN | 0.096(0.926) | 8.252(0.000) | 6.625(0.000) | 7.407(0.000) | |
| G-mean | KNE | 5.053(0.001) | 13.742(0.000) | 10.096(0.000) | 15.583(0.000) |
| KNU | 6.027(0.000) | 11.946(0.000) | 19.326(0.000) | 15.077(0.000) | |
| DESKNN | 0.309(0.765) | 8.461(0.000) | 6.712(0.000) | 8.336(0.000) | |
| AUC | KNE | 5.042(0.001) | 13.759(0.000) | 10.071(0.000) | 15.662(0.000) |
| KNU | 6.034(0.000) | 12.035(0.000) | 19.465(0.000) | 15.097(0.000) | |
| DESKNN | 0.293(0.777) | 8.373(0.000) | 6.680(0.000) | 8.304(0.000) | |
Table 6.
Paired t-test results of KNE, KNU and DESKNN under different kmax values with bagging (70-30 division).
| Metrics | Methods |
t-value (significance) |
|||
|---|---|---|---|---|---|
| kmax =2 | kmax =3 | kmax =4 | kmax =5 | ||
| Accuracy | KNE | 5.807(0.001) | 10.398(0.000) | 8.728(0.000) | 9.660(0.000) |
| KNU | 5.189(0.001) | 9.245(0.000) | 11.309(0.000) | 9.803(0.000) | |
| DESKNN | 3.390(0.008) | 5.955(0.000) | 7.052(0.000) | 6.696(0.000) | |
| F1 | KNE | 4.924(0.001) | 10.898(0.000) | 9.341(0.000) | 10.400(0.000) |
| KNU | 4.780(0.001) | 8.577(0.000) | 12.005(0.000) | 9.664(0.000) | |
| DESKNN | 3.158(0.012) | 6.008(0.000) | 7.505(0.000) | 6.635(0.000) | |
| G-mean | KNE | 5.260(0.001) | 8.432(0.000) | 8.048(0.000) | 8.829(0.000) |
| KNU | 5.749(0.000) | 10.784(0.000) | 12.098(0.000) | 11.999(0.000) | |
| DESKNN | 3.396(0.008) | 5.198(0.001) | 6.162(0.000) | 6.287(0.000) | |
| AUC | KNE | 5.262(0.001) | 8.607(0.000) | 8.152(0.000) | 8.980(0.000) |
| KNU | 4.172(0.001) | 8.512(0.000) | 10.055(0.000) | 8.491(0.000) | |
| DESKNN | 2.613(0.028) | 5.201(0.001) | 5.775(0.000) | 5.831(0.000) | |
Table 8.
Paired t-test results of KNE, KNU and DESKNN under different kmax values with bagging (5-fold cross-validation).
| Metrics | Methods |
t-value (significance) |
|||
|---|---|---|---|---|---|
| kmax =2 | kmax =3 | kmax =4 | kmax =5 | ||
| Accuracy | KNE | 26.103(0.000) | 30.045(0.000) | 35.859(0.000) | 47.587(0.000) |
| KNU | 36.432(0.000) | 30.539(0.000) | 38.037(0.000) | 39.005(0.000) | |
| DESKNN | 8.942(0.000) | 12.172(0.000) | 19.771(0.000) | 32.469(0.000) | |
| F1 | KNE | 25.217(0.000) | 30.800(0.000) | 35.880(0.000) | 47.868(0.000) |
| KNU | 38.880(0.000) | 31.404(0.000) | 40.176(0.000) | 41.316(0.000) | |
| DESKNN | 9.012(0.000) | 12.814(0.000) | 19.779(0.000) | 33.203(0.000) | |
| G-mean | KNE | 27.029(0.000) | 26.660(0.000) | 36.196(0.000) | 50.905(0.000) |
| KNU | 29.446(0.000) | 28.058(0.000) | 35.476(0.000) | 36.921(0.000) | |
| DESKNN | 8.359(0.000) | 9.563(0.000) | 18.263(0.000) | 28.624(0.000) | |
| AUC | KNE | 26.979(0.000) | 27.547(0.000) | 36.719(0.000) | 50.266(0.000) |
| KNU | 30.379(0.000) | 29.133(0.000) | 37.931(0.000) | 39.266(0.000) | |
| DESKNN | 8.645(0.000) | 10.061(0.000) | 18.317(0.000) | 29.270(0.000) | |
4.4. Comparison of other advanced classifiers
Table 9 shows the performance and standard deviations comparison of HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN with other advanced classifiers in term of 5-fold cross-validation when kmax=5. It can be seen from Table 9 that accuracy, F1, G-mean and AUC of HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN are higher than other advanced algorithms. HMCBCG+KNE obtains the best performance with 99.76% accuracy, 99.80% F1, 99.69% G-mean, 99.69% AUC. Furthermore, as can be seen in Table 9, HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN all produced smaller standard deviations than the other compared classifiers in terms of accuracy, F1, G-mean and AUC. This indicates that our proposed DES methods have better stability than the other five competitors.
Table 9.
Average performance and standard deviations comparison of the proposed combined DES methods with other advanced algorithms with 5-fold cross-validation (kmax=5).
| Algorithm | Accuracy | F1 | G-mean | AUC |
|---|---|---|---|---|
| HMCBCG+KNE | 0.9976±0.0016 | 0.9980±0.0013 | 0.9969±0.0021 | 0.9969±0.0020 |
| HMCBCG+KNU | 0.9904±0.0027 | 0.9920±0.0023 | 0.9915±0.0030 | 0.9916±0.0029 |
| HMCBCG+DESKNN | 0.9964±0.0028 | 0.9971±0.0022 | 0.9953±0.0035 | 0.9953±0.0034 |
| GBDT | 0.8992±0.0133 | 0.9225±0.0093 | 0.8711±0.0160 | 0.8779±0.0182 |
| SVM | 0.8943±0.0074 | 0.9192±0.0050 | 0.8617±0.0121 | 0.8698±0.0097 |
| RF | 0.9232±0.0105 | 0.9400±0.0070 | 0.9040±0.0178 | 0.9077±0.0136 |
| LR | 0.9111±0.0077 | 0.9297±0.0057 | 0.8952±0.0098 | 0.8978±0.0089 |
| XGBoost | 0.9076±0.0096 | 0.9282±0.0062 | 0.8836±0.0177 | 0.8882±0.0120 |
In addition, as shown in Table 11, paired t-tests are performed to compare the proposed combined DES approach with other classification algorithms. As can be seen in Table 11, with 5-fold cross-validation, HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN outperformed the other five advanced classifiers in terms of accuracy, F1, G-mean and AUC at the 5% significance level (kmax=5).
Table 11.
Paired t-test results of different DES methods with other advanced classifiers under 5-fold cross-validation (kmax=5).
| Metrics | Methods |
t-value (significance) |
||
|---|---|---|---|---|
| KNE | KNU | DESKNN | ||
| Accuracy | GBDT | 22.586(0.000) | 20.404(0.000) | 23.629(0.000) |
| SVM | 51.234(0.000) | 48.616(0.000) | 49.649(0.000) | |
| RF | 23.782(0.000) | 21.216(0.000) | 20.880(0.000) | |
| LR | 33.226(0.000) | 27.036(0.000) | 30.564(0.000) | |
| XGBoost | 31.493(0.000) | 29.715(0.000) | 30.851(0.000) | |
| F1 | GBDT | 24.652(0.000) | 21.902(0.000) | 26.383(0.000) |
| SVM | 60.845(0.000) | 53.136(0.000) | 56.309(0.000) | |
| RF | 26.930(0.000) | 24.392(0.000) | 24.129(0.000) | |
| LR | 34.884(0.000) | 28.173(0.000) | 32.615(0.000) | |
| XGBoost | 38.216(0.000) | 37.150(0.000) | 36.589(0.000) | |
| G-mean | GBDT | 21.292(0.000) | 19.913(0.000) | 21.923(0.000) |
| SVM | 38.987(0.000) | 40.319(0.000) | 39.413(0.000) | |
| RF | 16.859(0.000) | 16.249(0.000) | 15.745(0.000) | |
| LR | 30.414(0.000) | 27.152(0.000) | 27.980(0.000) | |
| XGBoost | 20.690(0.000) | 19.987(0.000) | 20.921(0.000) | |
| AUC | GBDT | 19.915(0.000) | 18.782(0.000) | 20.749(0.000) |
| SVM | 47.505(0.000) | 48.962(0.000) | 46.921(0.000) | |
| RF | 21.547(0.000) | 20.422(0.000) | 19.363(0.000) | |
| LR | 32.692(0.000) | 28.353(0.000) | 29.382(0.000) | |
| XGBoost | 30.037(0.000) | 29.317(0.000) | 29.804(0.000) | |
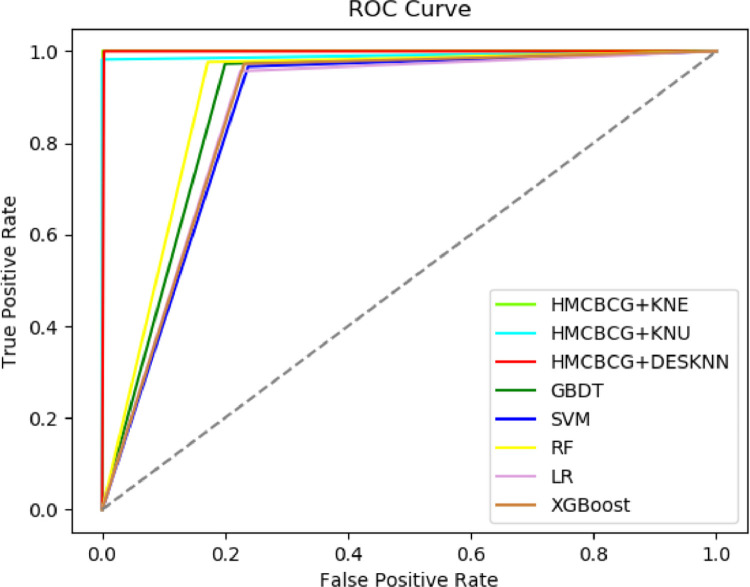
Fig. 7 further compares the ROC curves of HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN with other advanced algorithms. It can be seen from Fig. 7 that AUC values of HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN are significantly greater than other comparative algorithms. This shows that our combined DES method can simultaneously improve the detection accuracy of COVID-19 negative and positive. For a COVID-19 dataset, if the number of healthy cases is much larger than the number of virus carriers, this will cause the classifier to pay too much attention to the majority samples and a decline in the classification accuracy of the minority samples. Obviously, the cost of misclassifying a COVID-19 carrier as healthy is much greater than misdiagnosing a healthy person as COVID-19 infected. Therefore, our proposed combined DES method is more suitable for COVID-19 screening from imbalanced complete blood count data than other advanced algorithms.
Fig. 7.
Comparison of the ROC curves of HMCBCG+KNE, HMCBCG+KNU and HMCBCG+DESKNN with other advanced algorithms.
5. Discussion
In this study, a hybrid DES imbalanced data processing method is proposed to detect COVID-19 from complete cell count data. We use SMOTE-ENN to balance data distribution and clean up noise. Moreover, the HMCBCG model is proposed to improve the diversity and local capabilities of DES candidate classifiers.
We use three popular DES algorithms including KNE, KNU and DESKNN to test the performance of the proposed HMCBCG method. Then we compared the performance of the proposed combined DES model with other advanced classifiers for COVID-19 screening. As shown in Table 10 , we also compared the proposed method with previous studies. It can be seen from Table 10 that HMCBCG+KNE has better accuracy than other methods in the literature.
Table 10.
Comparison with previous works.
The key findings of the experimental results are summarized as follows: (1) For the three DES algorithms KNE, KNU and DESKNN, the performance of our HMCBCG is better than generating classifiers only by bagging. (2) HMCBCG+KNE obtains the best performance for COVID-19 screening with 99.81% accuracy, 99.86% F1, 99.78% G-mean and 99.81% AUC when kmax = 5 with 70-30 division. (3) Our proposed combined DES model is significantly better than several other advanced algorithms for COVID-19 screening, including GBDT, SVM, RF, LR and XGBoost in terms of accuracy, F1, G-mean and AUC.
These findings indicate that whether for traditional DES methods or others advanced single classifiers and static ensemble algorithms, our combined DES model has certain advantages for predicting COVID-19 infection from imbalanced complete blood count data. This method can be explored as a decision support tool for clinical practice to isolate and provide medical services for patients with COVID-19 as soon as possible, thereby optimizing the allocation of medical resources. The main limitation of this article is the sample size of the dataset. The performance of the proposed method can be enhanced by larger datasets containing patients from different regions and different hospitals.
6. Conclusion
In this paper, we propose a novel combined DES method for imbalanced data to detect COVID-19 from complete blood count data. This model combines data preprocessing and improved DES. Firstly, SMOTE-ENN is used for data preprocessing to balance the number of samples of different classes and clean up noise. Secondly, the HMCBCG method is proposed to generate candidate classifiers to improve the performance of DES. Experimental results show that our combined DES algorithm is superior to other comparative state-of-the-art methods in detecting COVID-19 from complete blood count data. In the future, we plan to use the proposed approach to detect COVID-19 from a larger complete blood count dataset. Moreover, we consider applying our model to other diseases based on imbalanced data to further test the effectiveness of the proposed method.
7. Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgments
Sincerely thank the National Natural Science Foundation of China (71571105, 71971123) for its substantial support.
Footnotes
References
- 1.Organization, W.H.Coronavirus disease (Covid-19) weekly epidemiological update and weekly operational update. 2020; Available from: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20201005-weekly-epi-update-8.pdf.
- 2.Lim J.T., et al. The costs of an expanded screening criteria for COVID-19: A modelling study. International Journal of Infectious Diseases. 2020;100:490–496. doi: 10.1016/j.ijid.2020.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Barza R., et al. Use of a simplified sample processing step without RNA extraction for direct SARS-CoV-2 RT-PCR detection. Journal of Clinical Virology. 2020;132 doi: 10.1016/j.jcv.2020.104587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brinati D., et al. Detection of COVID-19 Infection from Routine Blood Exams with Machine Learning: A Feasibility Study. Journal of Medical Systems. 2020;44(8):135. doi: 10.1007/s10916-020-01597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Banerjee A., et al. Use of Machine Learning and Artificial Intelligence to predict SARS-CoV-2 infection from Full Blood Counts in a population. International Immunopharmacology. 2020;86 doi: 10.1016/j.intimp.2020.106705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lalmuanawma S., Hussain J., Chhakchhuak L. Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: A review. Chaos, Solitons & Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ahamad M.M., et al. A machine learning model to identify early stage symptoms of SARS-Cov-2 infected patients. Expert Systems with Applications. 2020;160 doi: 10.1016/j.eswa.2020.113661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Physical and Engineering Sciences in Medicine. 2020:1. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Butt C., et al. Deep learning system to screen coronavirus disease 2019 pneumonia. Applied Intelligence. 2020:1. doi: 10.1007/s10489-020-01714-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ardakani A.A., et al. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: Results of 10 convolutional neural networks. Computers in Biology and Medicine. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chandra T.B., et al. Coronavirus disease (COVID-19) detection in Chest X-Ray images using majority voting based classifier ensemble. Expert Systems with Applications. 2021;165 doi: 10.1016/j.eswa.2020.113909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shaban W.M., et al. A new COVID-19 Patients Detection Strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier. Knowledge-Based Systems. 2020;205 doi: 10.1016/j.knosys.2020.106270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liang X.W., et al. LR-SMOTE — An improved unbalanced data set oversampling based on K-means and SVM. Knowledge-Based Systems. 2020;196 [Google Scholar]
- 14.Tao X., et al. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification. Information Sciences. 2019;487:31–56. [Google Scholar]
- 15.Lin W.-C., et al. Clustering-based undersampling in class-imbalanced data. Information Sciences. 2017;409-410:17–26. [Google Scholar]
- 16.Zhu Y., et al. EHSO: Evolutionary Hybrid Sampling in overlapping scenarios for imbalanced learning. Neurocomputing. 2020;417:333–346. [Google Scholar]
- 17.Alves Ribeiro V.H., Reynoso-Meza G. Ensemble learning by means of a multi-objective optimization design approach for dealing with imbalanced data sets. Expert Systems with Applications. 2020;147 [Google Scholar]
- 18.Li F., et al. Cost-sensitive and hybrid-attribute measure multi-decision tree over imbalanced data sets. Information Sciences. 2018;422:242–256. [Google Scholar]
- 19.Zhang Z.L., et al. A distance-based weighting framework for boosting the performance of dynamic ensemble selection. Information Processing & Management. 2019;56(4):1300–1316. [Google Scholar]
- 20.Hou W.-h., et al. A novel dynamic ensemble selection classifier for an imbalanced data set: An application for credit risk assessment. Knowledge-Based Systems. 2020 [Google Scholar]
- 21.Feng X., et al. Dynamic ensemble classification for credit scoring using soft probability. Applied Soft Computing. 2018;65:139–151. [Google Scholar]
- 22.Junior L.M., et al. A novel approach to define the local region of dynamic selection techniques in imbalanced credit scoring problems. Expert Systems with Applications. 2020 [Google Scholar]
- 23.Gao X., et al. An ensemble imbalanced classification method based on model dynamic selection driven by data partition hybrid sampling. Expert Systems with Applications. 2020;160 [Google Scholar]
- 24.Roy A., et al. A study on combining dynamic selection and data preprocessing for imbalance learning. Neurocomputing. 2018;286:179–192. [Google Scholar]
- 25.Breiman L. Bagging predictors. Mach. Learn. 1996;24(2):123–140. [Google Scholar]
- 26.Batista G.E.A.P.A., Prati R.C., Monard M.C. A study of the behavior of several methods for balancing machine learning training data. Acm Sigkdd Explorations Newsletter. 2004;6(1):20–29. [Google Scholar]
- 27.MacQueen J. Some methods for classification and analysis of multivariate observations. Proceedings of the fifth Berkeley symposium on mathematical statistics and probability; Oakland, CA, USA; 1967. [Google Scholar]
- 28.Cortes C., Vapnik V.N. Support-Vector Networks. Machine Learning. 1995;20(3):273–297. [Google Scholar]
- 29.Holland J.H. Genetic algorithms. Scientific american. 1992;267(1):66–73. [Google Scholar]
- 30.Ezzat D., Hassanien A.E., Ella H.A. An optimized deep learning architecture for the diagnosis of COVID-19 disease based on gravitational search optimization. Applied Soft Computing. 2020 doi: 10.1016/j.asoc.2020.106742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Britto A.S., Jr, Sabourin R., Oliveira L.E. Dynamic selection of classifiers—a comprehensive review. Pattern recognition. 2014;47(11):3665–3680. [Google Scholar]
- 32.Cruz R.M., Sabourin R., Cavalcanti G.D. Dynamic classifier selection: Recent advances and perspectives. Information Fusion. 2018;41:195–216. [Google Scholar]
- 33.Oliveira D.V.R., Cavalcanti G.D.C., Sabourin R. Online pruning of base classifiers for Dynamic Ensemble Selection. Pattern Recognition. 2017;72:44–58. [Google Scholar]
- 34.Zhao D., et al. Experimental Study and Comparison of Imbalance Ensemble Classifiers with Dynamic Selection Strategy. Entropy. 2021;23(7):822. doi: 10.3390/e23070822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zyblewski P., Woźniak M. International Conference on Computational Science. Springer; 2020. Dynamic Classifier Selection for Data with Skewed Class Distribution Using Imbalance Ratio and Euclidean Distance. [Google Scholar]
- 36.Zyblewski P., Sabourin R., Woźniak M. Preprocessed dynamic classifier ensemble selection for highly imbalanced drifted data streams. Information Fusion. 2021;66:138–154. [Google Scholar]
- 37.Cruz R.M.O., et al. FIRE-DES++: Enhanced online pruning of base classifiers for dynamic ensemble selection. Pattern Recognition. 2019;85:149–160. [Google Scholar]
- 38.García S., et al. Dynamic ensemble selection for multi-class imbalanced datasets. Information Sciences. 2018;445-446:22–37. [Google Scholar]
- 39.Buuren S.v., Groothuis-Oudshoorn K. mice: Multivariate imputation by chained equations in R. Journal of statistical software. 2010:1–68. [Google Scholar]
- 40.Chawla N.V., et al. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research. 2002;16:321–357. [Google Scholar]
- 41.Haixiang G., et al. Learning from class-imbalanced data: Review of methods and applications. Expert Systems with Applications. 2017;73:220–239. [Google Scholar]
- 42.Laurikkala J. Proceedings of the 8th Conference on AI in Medicine in Europe: Artificial Intelligence Medicine. Springer-Verlag; 2001. Improving Identification of Difficult Small Classes by Balancing Class Distribution; pp. 63–66. [Google Scholar]
- 43.Ko A.H.R., Sabourin R., Britto J.A.S. From dynamic classifier selection to dynamic ensemble selection. Pattern Recognition. 2008;41(5):1718–1731. [Google Scholar]
- 44.Santana A., et al. A Dynamic Classifier Selection Method to Build Ensembles using Accuracy and Diversity. SBRN 2006, The Ninth Brazilian Symposium on Neural Networks; Ribeiro Preto, SP, Brazil; 2006. October 23-27, 2006. [Google Scholar]
- 45.Lewis D.D. European conference on machine learning. Springer; 1998. Naive (Bayes) at forty: The independence assumption in information retrieval. [Google Scholar]
- 46.Karim M., Rahman R.M. Decision Tree and Naïve Bayes Algorithm for Classification and Generation of Actionable Knowledge for Direct Marketing. Journal of Software Engineering & Applications. 2013;06(4):196–206. [Google Scholar]
- 47.Altman N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. American Statistician. 1992;46(3):175–185. [Google Scholar]
- 48.Ho T.K. Proceedings of 3rd international conference on document analysis and recognition. IEEE; 1995. Random decision forests. [Google Scholar]
- 49.Friedman J.H. Greedy function approximation: a gradient boosting machine. Annals of statistics. 2001:1189–1232. [Google Scholar]
- 50.Hosmer D.W., Jr, Lemeshow S., Sturdivant R.X. Vol. 398. John Wiley & Sons; 2013. (Applied logistic regression). [Google Scholar]
- 51.Chen T., Guestrin C. Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. 2016. Xgboost: A scalable tree boosting system. [Google Scholar]
- 52.Veganzones D., Séverin E. An investigation of bankruptcy prediction in imbalanced datasets. Decision Support Systems. 2018;112:111–124. [Google Scholar]
- 53.Wang M., Chen H. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Applied Soft Computing. 2020;88 [Google Scholar]
- 54.Stapor K., et al. How to design the fair experimental classifier evaluation. Applied Soft Computing. 2021;104 [Google Scholar]
- 55.de Fátima Cobre A., et al. Diagnosis and prediction of COVID-19 severity: can biochemical tests and machine learning be used as prognostic indicators? Computers in biology and medicine. 2021 doi: 10.1016/j.compbiomed.2021.104531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Alakus T.B., Turkoglu I. Comparison of deep learning approaches to predict COVID-19 infection. Chaos, Solitons & Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Podder P., et al. Elsevier; 2021. Application of Machine Learning for the Diagnosis of COVID-19, in Data Science for COVID-19; pp. 175–194. [Google Scholar]