Abstract
Motivation
Molecular property prediction is a hot topic in recent years. Existing graph-based models ignore the hierarchical structures of molecules. According to the knowledge of chemistry and pharmacy, the functional groups of molecules are closely related to its physio-chemical properties and binding affinities. So, it should be helpful to represent molecular graphs by fragments that contain functional groups for molecular property prediction.
Results
In this article, to boost the performance of molecule property prediction, we first propose a definition of molecule graph fragments that may be or contain functional groups, which are relevant to molecular properties, then develop a fragment-oriented multi-scale graph attention network for molecular property prediction, which is called FraGAT. Experiments on several widely used benchmarks are conducted to evaluate FraGAT. Experimental results show that FraGAT achieves state-of-the-art predictive performance in most cases. Furthermore, our case studies show that when the fragments used to represent the molecule graphs contain functional groups, the model can make better predictions. This conforms to our expectation and demonstrates the interpretability of the proposed model.
Availability and implementation
The code and data underlying this work are available in GitHub, at https://github.com/ZiqiaoZhang/FraGAT.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The goal of drug discovery is to find new molecules with desired properties, including pharmacological, toxicological, pharmacokinetic properties, etc. (Schneider et al., 2020; Zhong et al., 2018). Using prediction models to evaluate these properties of a designed molecule is an essential step in the whole drug discovery process.
Conventional methods build prediction models by using the underlying physical mechanisms of molecules (Esposito et al., 2004). In the past decade, the rapid development and wide application of artificial intelligence (AI) techniques have shown its great success in many areas, especially in computer vision and natural language processing (NLP). With the increasing amassment of accessible drug data, AI techniques are being introduced into drug discovery, and a number of AI-based models for molecular property prediction have been developed (Jiménez et al., 2018; Liew et al., 2009; Melville et al., 2009; Peng et al., 2020). Particularly, with the development of graph neural networks (GNNs) in recent years (Kipf and Welling, 2017; Veličković et al., 2018), graph-based molecular property prediction is becoming a hot research topic (Coley et al., 2017; Duvenaud et al., 2015; Gilmer et al., 2017; Kearnes et al., 2016; Xiong et al., 2020; Zhou and Li, 2017).
The graph-based molecular property prediction models view molecules as graphs with attributes and use graph neural networks to extract features from these graphs (Liu et al., 2019). Usually, graph embedding is first exploited to encode the information of input molecules into feature vectors, then a network (e.g. a fully connected network, or FCN in short) is used to do prediction based on the feature vectors.
However, most of the existing models treat molecules as flat structures. These models first calculate the node embedding of each atom in a molecule, and then the graph embedding of the molecule is obtained by using a readout function. Obviously, the hierarchical structures of molecules are ignored.
According to the knowledge of chemistry and pharmacy, it is known that several atoms can form small atomic groups, which can further form larger atomic groups, and then these larger groups constitute molecules (Muller, 1994). A molecule may consist of many atomic groups, while some specific atomic groups will determine its certain molecular property. For instance, the binding between a molecule and any of its targets is in essence the interaction between some specific atomic groups of the molecule and the target protein (Guvench, 2016). These atomic groups are called functional groups. So functional groups are important features for molecule property prediction. However, extracting functional groups from molecules is computationally expensive.
In the literature, several methods split molecular graphs into small subgraphs to predict molecular properties. Armitage et al. (2019) proposed the FraGVAE model for molecular property prediction on some small datasets. This model uses a variational autoencoder to encode molecules. Each molecule is split into circular groups of radius 1, and all of these small groups constitute a fragment bag. Then, the fragment bag and the original molecular graph are encoded respectively. Liu et al. (2019) introduced N-Gram Graphs for molecule property prediction, inspired by n-grams typically used in the NLP field. The N-Gram Graph model breaks a molecular graph into a set of n-gram walks, i.e. a walk of length n in the molecular graph, which are viewed as fragments. A word embedding model is then used to embed each vertex into node embedding. And finally, a simple GNN with no learnable parameters is adopted to generate graph embedding based on the node embeddings. Although the above-mentioned methods split molecules into fragments, which are not guaranteed to be real (or valid) atomic groups in the sense of chemistry and pharmacy. Particularly, these fragments may break an aromatic ring into invalid groups (see Supplementary Fig. S1). Therefore, functional groups relevant to the molecular properties may not be represented by these fragments.
In this article, to boost the performance of molecule property prediction, we first define fragments of molecule graphs in a chemical-interpretable way, and then propose a fragment-based molecular property prediction model with a multi-scale graph attention network. In this model, molecules are broken into fragments that may be or contain functional groups of the molecules, and graph attention networks are used to encode multi-scale structural information of molecules at three levels. To the best of our knowledge, this is the first GNN-based model that tries to use fragments to represent functional groups of molecules for molecular prediction. The model is evaluated on 14 benchmark datasets, and experimental results show that our model achieves state-of-the-art performance in most cases. Furthermore, we also perform case studies, and the results show that when a molecule graph is split into two fragments, and at least one of them is functional group relevant to molecule properties, the FraGAT model achieves better prediction, which conforms to our expectation and demonstrates the interpretability of the proposed model to certain extent.
The rest of this article is organized as follows: Section 2 presents the proposed method in detail. Section 3 is performance evaluation. And Section 4 concludes this article.
2 Materials and methods
2.1 Molecular fragments
Here, we first give a chemical-interpretable definition of fragments, and introduce a simple yet effective method to extract fragments from a molecule.
2.1.1 Fragment definition
Considering the latent relationship between functional groups and molecular properties, the motivation of this work is to build a model to leverage this relationship to make predictions. However, it is non-trivial to extract the functional groups relevant to molecule properties from all possible atomic groups that constitute a molecule. So, the basic idea is to split molecule graphs into fragments that represent the atomic groups among which there might be functional groups. Then, by using these fragments to characterize a molecule, a neural network model may be able to learn the latent relationship. Here, the difficulty is twofold: how to define the fragments and how to extract such fragments from molecules.
For the convenience of discussion, in this work atomic groups are classified into two types: (i) Small atomic groups that contain no acyclic single bonds (hydrogen-depleted), which are called basic atomic groups, e.g. –OH, –NH2, –X, etc. (ii) Large atomic groups that are formed by the combinations of basic atomic groups through acyclic single bonds, such as carboxyl, tolyl, etc. We call them combined atomic groups.
Both these two types of atomic groups may be relevant to the properties of molecules. For example, a –X can affect the metabolism property and toxicity of a drug. And the influence of an xylyl that consists of two methyls and a benzene ring on the toxicity of a molecule is much stronger than that of a tolyl, which consists of one methyl and a benzene. However, the structure difference between one and two methyls is not large enough to explain the toxicity disparity. This indicates that both basic atomic groups and combined ones should be covered by the fragments used to represent molecules.
Considering that most atomic groups in a molecule connect with the other parts by acyclic single bonds (Ertl et al., 2020), the acyclic single bonds can be seen as boundaries of atomic groups. So we give a formal definition of fragments as follows:
Definition 1.
Given a hydrogen-depleted molecular graph, fragments include small subgraphs that are generated by breaking all of the acyclic single bonds, and large subgraphs formed by the combinations of small subgraphs that are connected in the original molecular graph. We call the small subgraphs basic fragments, and the large subgraphs combined fragments of the molecule graph.
Figure 1 is an example to illustrate the fragments of an aspirin molecule. Based on the definition above, both basic functional groups and combined functional groups of a molecule can be represented by single fragments.
Fig. 1.
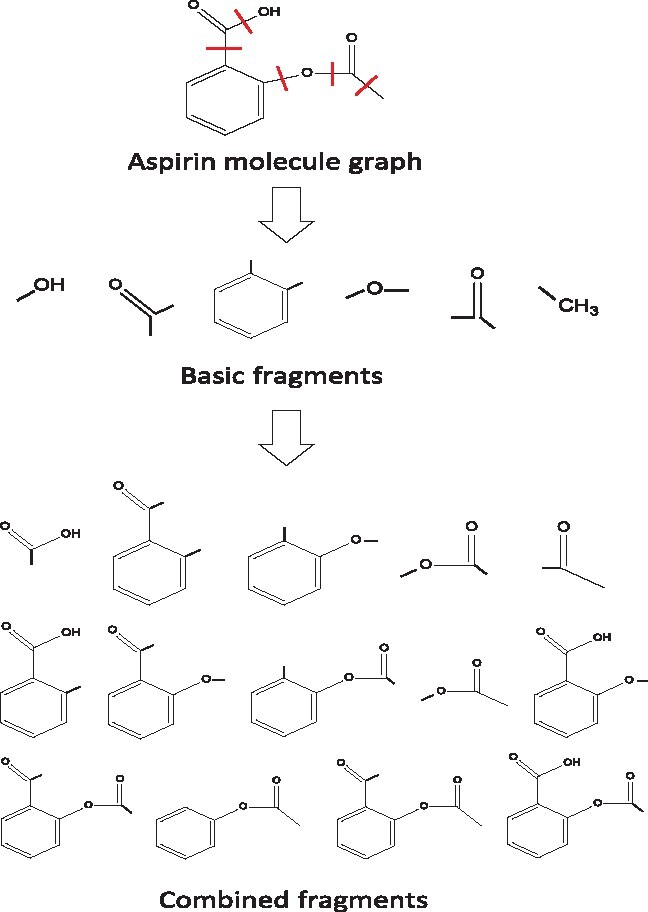
The fragments of an aspirin molecule according to Definition 1. The acyclic single bonds in aspirin are highlighted by red lines. The molecule is first split into basic fragments by breaking all of the acyclic single bonds, then these basic fragments are combined iteratively to form combined fragments
2.1.2 Fragment extraction
According to Definition 1, we can enumerate all of the fragments in a molecule. However, considering that the structures of organic chemicals are complex, which usually consist of long backbones and many branches, the number of acyclic single bonds in a molecule may be very large, as shown in Supplementary Table S1. And the number of possible fragments grows exponentially with the number of acyclic single bonds. So, it is computationally expensive to enumerate all fragments of a molecule. Here, an alternative is proposed to efficiently solve this problem as follows:
Given a molecule, all acyclic single bonds are denoted as breakable bonds. During the training phase, each time when the molecule is fed into the model, a breakable bond is randomly chosen to be broken. Thus, two subgraphs are generated. Obviously, these two subgraphs conform to the definition of fragments. So, we get two fragments, or a fragment-pair, of the molecule each time. In such a way, computational cost and memory consumption for model training can be substantially reduced.
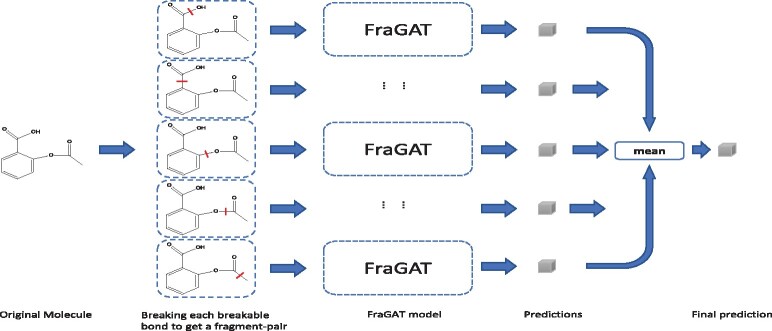
While in the evaluation phase, if we still use the randomly breaking strategy for each test molecule, the prediction will be too random. So we employ a data-augmentation method for testing. As shown in Figure 2, each molecule is augmented to a batch of ‘samples’ by breaking different breakable bonds. The batch size is Nb—the number of breakable bonds. All these samples are fed into the model, which results in a batch of predictions. The mean of these predictive results is taken as the final prediction of this molecule.
Fig. 2.
Data-augmentation in the evaluation phase. Each molecule is augmented to a batch of samples. The model makes prediction for each sample, and the mean of these predictions will be taken as the final prediction of the molecule
With this strategy, though each time the model is fed only two fragments of a molecule during the training phase, with the increase of training epochs, the model is trained with more and more fragment pairs (at most Nb unique fragment pairs). As a whole, the model is trained with enough information of each molecule, though not all information in the molecule. Actually, this strategy is a trade-off between predictive performance and computational efficiency.
2.2 Network structure
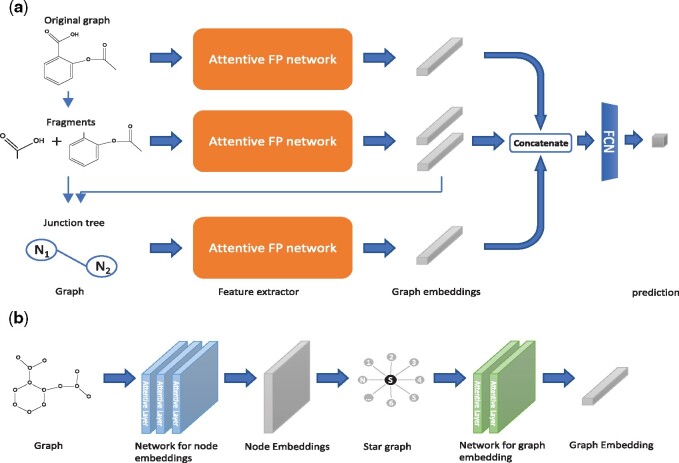
The network structure of our proposed model FraGAT is shown in Figure 3a. FraGAT uses three branches to extract and encode multi-scale structural features of a given molecule. In the first branch (the upper one in Fig. 3a), the original molecular graph is fed into the feature extractor, which encodes the original molecular graph into an embedding vector that carries the entire structural information of this molecule. In the second branch (the middle one in Fig. 3a), the original molecular graph breaks into a fragment-pair, which are fed into the extractor to obtain the embedding vectors of these two fragments. In the third branch (the bottom one in Fig. 3a), each fragment-pair is abstracted to two super nodes (each of which corresponds to a fragment) connected by the broken bond. Thus, a junction tree (a tree-structured scaffold over the fragments) (Jin et al., 2018) is generated. The embedding vectors of the two fragments extracted in the second branch are used as the initial features of the two super nodes. The junction tree is encoded by the feature extractor to obtain the connectivity information of fragments. The embedding vectors obtained through the tree branches are then concatenated as the representation vector of the processed molecule.
Fig. 3.
(a) The structure of the FraGAT network. Three branches are used to extract multi-scale structural features of a given molecule. (b) The structure of Attentive FP network (Xiong et al., 2020), which consists of two major components: the network for node embeddings and the network for graph embedding. Here, a star graph is generated to readout the node embeddings
A FCN is used to predict the properties of molecules based on the extracted representations. The prediction task can be either classification or regression. Cross-entropy and mean-squared error are used as the loss function for classification and regression, respectively. And for datasets used for multiple tasks, we have , where is the loss function of the ith task.
2.3 Attentive FP and attentive layers
In Xiong et al. (2020), the authors proposed a graph neural network structure called Attentive FP to encode structural information of molecules based on graph attentive networks (GATs). It has been shown that Attentive FP outperforms previous works, including GCN (Graph Convolutional Network) and MPNN (Message Passing Neural Network) (Xiong et al., 2020; Wu et al., 2018). So in this article, Attentive FP is adopted as feature extractor networks to get graph embeddings.
The schematic diagram of Attentive FP network is shown in Figure 3b. The molecular graph of a given molecule can be modeled as an annotated graph , where represents the set of atoms in the molecule, and represents the set of bonds between atoms. denotes the feature matrix of chemical properties of atoms, and denotes the feature matrix of chemical properties of bonds, where Fn and Fe represent the dimension of chemical property vector of atoms and bonds, respectively. The properties of atoms and bonds used in this work are presented in Table 1. All of these chemical properties can be calculated by RDKit toolkits.
Table 1.
Properties of atoms and bonds
| Indices of atomic features | Description |
|---|---|
| 0–15 | Atomic symbol encoded as a one-hot vector of [B, C, N, O, F, Si, P S, Cl, As, Se, Br, Te, I, At, metal] |
| 16–21 | Number of bonds encoded as a one-hot vector of [0,1,2,3,4,5] |
| 22 | Electrical charge |
| 23 | Number of radical electrons |
| 24–29 | Hybridization encoded as a one-hot vector of [sp, sp2, sp3, sp3d, sp3d2, other] |
| 30 | Aromaticity |
| 31–35 | Number of connected hydrogens encoded as a one-hot vector of [0,1,2,3,4] |
| 36 | Whether the atom is chiral center |
| 37–38 | Chirality type, encoded as a one-hot vector of [R, S] |
| Indices of bond features | Description |
| 0–3 | Bond type, encoded as a one-hot vector of [single, double, triple, aromatic] |
| 4 | Whether the bond is conjugated |
| 5 | Whether the bond is in a ring |
| 6–9 | Stereo, encoded as a one-hot vector of [StereoNone, StereoAny, StereoZ, StereoE] |
Note: The choice of chemical properties is the same as Xiong et al. (2020).
As shown in Figure 3b, the Attentive FP network consists of two major components. In the first component, the original annotated graph G is fed into the network, which uses k attentive layers to extract information and produce the node embeddings: , where F is the dimension of the embedding vectors. In the second component, to calculate the graph embedding of the molecule, the original molecular graph G is shrunk to a super node s. A star graph is constructed, denoted as , where and . In this component, only the feature matrix of nodes, , is needed. The features of nodes in the hypergraph are initialized as follows:
| (1) |
and
| (2) |
Then, T attentive layers are used to extract the node embedding of super node s, denoted as , which is considered as the graph embedding of this molecule.
The attentive layers constitute the backbone of the Attentive FP network for evaluating the embeddings of nodes. Figure 4 shows the structure of an attentive layer. It is a node-wise mechanism that sequentially processes one target node t and its 1-hop neighborhood N(t). The embedding of node t after the lth attentive layer is denoted as . Multiple attentive layers stack together to extract the final node embeddings.
Fig. 4.
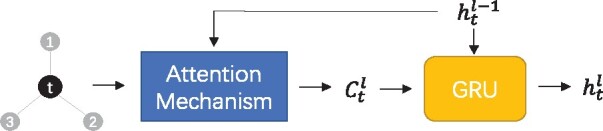
The attentive layer structure. Attention mechanism is used to aggregate information from neighbors of target node t, and GRU is used to update the embedding of t
Each attentive layer consists of two steps: aggregation and update. In the aggregation step, the target node t aggregates the information propagated from its 1-hop neighbors. An attention mechanism is used to assign weights to the messages such that the model focuses on the important message. The aggregation step with attention mechanism in the lth attentive layer can be formalized as follows:
| (3) |
| (4) |
| (5) |
The node embeddings of target node t and its 1-hop neighbors i, i.e. and , are initialized as follows:
| (6) |
| (7) |
Then, in the update step, a Gated Recurrent Unit (GRU) is used (Cho et al., 2014). It absorbs (the information aggregated from the neighbors) and (the embedding vector of target node t at the previous layer) to generate an updated embedding . The GRU learns to determine how much information aggregated from its neighbors to be exploited and how much information of the current embedding to be reserved. This mechanism can be formally described as follows:
| (8) |
It is worth noting that, as mentioned before, in the second component of the Attentive FP network, T attentive layers are used to extract . These attentive layers are responsible for calculating and updating the embedding of the super node s. The information of nodes propagates from N(s) to s, and the embeddings of nodes in N(s) remain constant.
3 Experiments and results
To evaluate the performance of our proposed FraGAT model, 14 benchmark datasets are used in our experiments. We compare our method with a number of existing methods, including the latest and state-of-the-art methods. Ablation study is also conducted to evaluate the effectiveness of the three branches in the FraGAT model. Furthermore, interpretation study is carried out to show the ability of our model to identify fragments that essentially impact molecular properties. To this end, we collected molecules that can bind with the SHP2 target to build a SHP2 dataset from published patents (see Supplementary Table S3 for details).
3.1 Experimental results on benchmarks
Datasets used in our experiments are from Wu et al. (2018), including classification and regression tasks. Statistical information of these datasets is presented in Supplementary Tables S1 and S2 of Supplementary File. For the regression tasks, root mean squared error (RMSE) is used as the metric, which is the smaller the better. And for the classification, area under ROC curve (AUC-ROC) is used, which is the larger the better. Here, we compare our model with existing methods, which are split into three groups: (i) recent (or state-of-the-art) GNN based methods, including Attentive FP (Xiong et al., 2020), N-Gram Graph (Liu et al., 2019) and CMPNN (Song et al., 2020); (ii) Early GNN based methods, including GCN, Weave, DAG (Directed Acyclic Graph), DTNN (Deep Tensor Neural Network), ANI-1 and MPNN; and (iii) traditional machine learning (ML) based methods, including Log-reg, SVM, KRR, RF, XGBoost, Multitask, Bypass and IRV. As the second and third groups contain a relatively large number of methods, we present only the best result of each group on each dataset to reduce space. Performance results of existing methods are from the published papers (Liu et al., 2019; Song et al., 2020; Xiong et al., 2020). Our experiments follow the configurations of Attentive FP in Xiong et al. (2020), including the 8:1:1 splitting ratio of train:valid:test, and the choices of splitting strategy for different datasets.
Experimental results on 13 benchmarks are presented in Table 2. As the QM9 dataset involves different tasks, we present the experimental results in Supplementary Table S4 of Supplementary File to reduce space. As shown in Table 2, we can see that our model achieves best performance on 8 of the 13 benchmark datasets, and performs the 2nd best on the remaining 5 datasets. This demonstrates the effectiveness of our fragment-based multi-scale network structure. CMPNN wins the others on two datasets. And it is surprised to see that random forest (RF) does best on the SIDER dataset. Though our model uses the Attentive FP network as feature extractors, it outperforms Attentive FP on 11 of the 13 datasets. Especially, on the BACE dataset, our method gets up to 7.7% performance improvement. From Supplementary Table S4, we also can see that our model achieves the best performance in most tasks. In summary, empirical evaluation on 14 benchmark datasets show that our method achieves the state-of-the-art performance.
Table 2.
Performance comparison on 13 benchmarks
| Dataset | Performance metric | Splitting strategy | Best result of traditional ML based methods | Best result of early GNN based methods | Attentive FP | N-Gram XGB | CMPNN | FraGAT |
|---|---|---|---|---|---|---|---|---|
| ESOL | RMSE | Random | XGBoost:0.99 | MPNN:0.58 | 0.503 | 0.731 | 0.233 | 0.478 |
| FreeSolv | RMSE | Random | XGBoost:1.74 | MPNN:1.15 | 0.736 | – | 0.819 | 0.538 |
| HIV | AUC-ROC | Scaffold | KernelSVM:0.792 | GC:0.763 | 0.832 | 0.830 | – | 0.851 |
| BACE | AUC-ROC | Scaffold | RF:0.867 | Weave:0.806 | 0.850 | – | – | 0.927 |
| BBBP | AUC-ROC | Scaffold | KernelSVM:0.729 | GC:0.690 | 0.920 | – | 0.963 | 0.933 |
| Tox21 | AUC-ROC | Random | KernelSVM:0.822 | GC:0.829 | 0.858 | 0.847 | 0.856 | 0.863 |
| SIDER | AUC-ROC | Random | RF:0.684 | GC:0.638 | 0.637 | – | 0.666 | 0.673 |
| ClinTox | AUC-ROC | Random | Bypass:0.827 | Weave:0.832 | 0.940 | 0.874 | 0.933 | 0.969 |
| Lipop | RMSE | Random | XGBoost:0.799 | GC:0.655 | 0.578 | – | – | 0.569 |
| Malaria | RMSE | Random | Linear layer:1.13 | Weave:1.07 | 0.99 | – | – | 0.987 |
| Photovoltaic | RMSE | Random | Neural Net:2.00 | MPNN:1.03 | 0.82 | – | – | 0.942 |
| MUV | AUC-ROC | Random | – | GC:0.775 | 0.843 | – | – | 0.851 |
| Toxcast | AUC-ROC | Random | Multitask:0.702 | Weave:0.742 | 0.805 | – | – | 0.803 |
Note: The best result on each dataset is bolded. ‘–’ means no data, i.e. the method has not been tested on the dataset.
3.2 Ablation study
To evaluate the effectiveness of the three branches in our FraGAT model, an ablation study is conducted. We consider three additional models for comparison as follows:
M1: using only the information of original molecular graphs, i.e. using only the upper branch. It is actually the Attentive FP network.
M2: using only the information of fragment-pairs, i.e. using only the middle branch.
M12: using the information of both the original molecular graph and the fragment-pairs, i.e. using both the upper and the middle branches.
The results of ablation study are given in Table 3. Comparing M1, M12 and the FraGAT model, we can see that with more information being considered in the model, the predictive ability is improved, which shows the effectiveness of the proposed multi-scale feature extraction network. Furthermore, the results of M2 show that even using only fragment-pairs to represent molecules, the model can still achieve relatively good predictive performance on most datasets, which demonstrates the existence of relevance between fragments and properties of molecules.
Table 3.
Results of ablation study on eight datasets
| Benchmark | Metric | M1 (attentive FP) | M2 | M12 | FraGAT |
|---|---|---|---|---|---|
| ESOL | RMSE | 0.503 | 0.528 | 0.496 | 0.478 |
| FreeSolv | RMSE | 0.736 | 0.580 | 0.544 | 0.538 |
| HIV | AUC-ROC | 0.832 | 0.767 | 0.850 | 0.851 |
| BACE | AUC-ROC | 0.850 | 0.916 | 0.925 | 0.927 |
| BBBP | AUC-ROC | 0.920 | 0.921 | 0.929 | 0.933 |
| Tox21 | AUC-ROC | 0.858 | 0.829 | 0.862 | 0.863 |
| SIDER | AUC-ROC | 0.637 | 0.658 | 0.660 | 0.673 |
| ClinTox | AUC-ROC | 0.940 | 0.962 | 0.967 | 0.969 |
Note: The best results are bolded.
3.3 Case studies
In the evaluation phase, each molecule is augmentated into a batch of samples by breaking different breakable bonds. The model may get different predictions for different samples. Thus, it is worthy of studying on which samples the model can get better predictions. Here, we conduct case studies to answer this question. To this end, when predicting the properties of a given molecule, we compare the predictions of all augmented samples, and check the two fragments of the sample with the best result.
The experiment is conducted on the SHP2 dataset to predict molecule binding affinity. Here, the binding affinity is represented by IC50, and the smaller the IC50 value is, the stronger the binding affinity is. In building the SHP2 dataset, only the molecules with the IC50 smaller than 10 μM against the SHP2 protein are included. We randomly split the SHP2 dataset into train, valid and test sets by 8:1:1. After the FraGAT model is trained, three molecules (denoted by a, b and c) are selected from the test set for case study. The structures and the breakable bonds of the three chosen molecules are shown in Figure 5. For each selected molecule, it is augmented to a set of samples by breaking different breakable bonds, and the FraGAT model does prediction for each sample, which is denoted as yi (), Nb is the number of breakable bonds. The absolute error between yi and the ground truth g, i.e. , is evaluated. The samples of each molecule are ranked by Ei. The results of all samples are shown in Supplementary Table S8, and the information of the sample with the best prediction (the minimum absolute error) of each molecule is shown in Table 4. Here, is the final prediction obtained by the model. denotes the absolute error of the final prediction, m is the label number of the breakable bond of the sample with the minimum Ei, ym is the prediction for this sample, and .
Fig. 5.
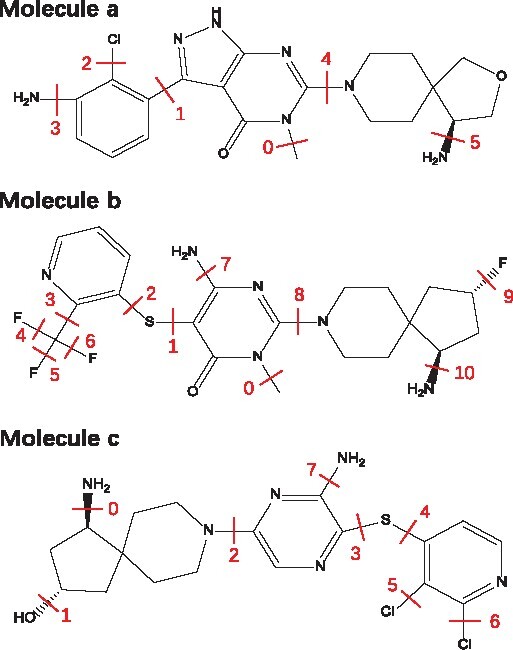
Structures of the three molecules selected from the test set of SHP2 dataset. Each red segment labeled with number indicates a breakable bond
Table 4.
Results of case studies
| Molecule a | Molecule b | Molecule c | |
|---|---|---|---|
| 0.110 | 0.021 | 0.035 | |
| G | 0.064 | 0.024 | 0.003 |
| E | 0.046 | 0.003 | 0.032 |
| M | 5 | 1 | 1 |
| ym | 0.058 | 0.039 | 0.006 |
| Em | 0.006 | 0.015 | 0.003 |
Now we check the results of molecules a, b and c in detail. For molecule a, the binding affinity is 0.064 μM. The amino-group on the spirocycle of molecule a, similar to that of the molecule SHP099 (Fortanet et al. 2016) (see Supplementary Section S9 for detail), can form ionic bond with the SHP2 protein and contributes major binding affinity to the molecule. From Figure 5, we can see that when bond #5 is broken, this amino-group is a fragment, and the resulting sample gets the best prediction, as shown in Table 4.
For molecule b, its binding affinity is 0.024 μM, better than that of molecule a. Obviously, it should not be the amino-group on the spirocycle that contributes to the stronger binding affinity. As discussed in LaMarche et al. (2020), compared with molecule a, the sulpur atom in molecule b or called thioether, makes the molecule more flexible and can form a conformation that binds more tightly with the target. As the thioether is located in the middle of the chain structure of the molecule, it cannot be extracted as a fragment by the proposed fragment extraction method. Considering samples #1 and #2, if bond #1 is broken (corresponding to sample #1), a generated fragment is the combination of the thioether and an aryl ring; When bond #2 is broken (corresponding to sample #2), the thioether combines with a more complex remaining part to form a fragment. The fragment of sample #1 is more concise than the fragment of sample #2, so it may contain less irrelevant information than the other one, which may make the model predict better. And in Supplementary Table S8, we do find that E2 of sample #2 is much larger than E1 of sample #1.
And for molecule c, its binding affinity is 0.003 μM, which is much stronger than that of the other two molecules. By molecular docking analysis (as shown in Supplementary Fig. S5), we find that the hydroxy obtained by breaking bond #1 can form an extra hydrogen bond with GLU-249 of the SHP2 target to enhance the binding affinity significantly. Obviously, E1 is the lowest value.
In addition to the sample with the lowest Ei, the fragments of other top-ranked samples are also of pharmaceutical significance. For example, the ortho-chlorine atoms on bond #5 and #6 of molecule c may fill the hydrophobic pocket in the same way as that of SHP099, which is beneficial to binding. Similar situation may also happen to the trifluoromethyl on bond #3 of molecule b (LaMarche et al., 2020). The fluorine atom on bond #9 of molecule b may combine with the SHP2 protein by water bridge effect (Gillis et al., 2015), which also benefits binding affinity. From Supplementary Table S8, we can see that the samples with these functional groups as fragments generally have smaller Ei than the other samples.
From the results of case studies above, we can see that (i) if at least one of the fragments of a sample is a functional group relevant to molecule properties, our model predicts more accurately, and (ii) our method can extract functional groups from molecule graphs, which partially explains the excellent performance of our model. In summary, our finding shows that our model can learn the relationship between functional groups and the binding affinity, which verifies the rationale of our model.
4 Conclusion
In this article, we present FraGAT, a fragment-oriented multi-scale graph attention model for molecular property prediction. In this model, a chemical-interpretable definition of fragments is proposed, and an intuitive yet effective method is proposed to split a molecule into fragments, which are or contain functional groups relevant to molecule properties. By extracting features at three hierarchical levels of molecule structures, FraGAT exploits multi-scale structural information to predict molecular properties. Experiments on 14 benchmark datasets are conducted to evaluate FraGAT, which is compared with major existing methods. Experimental results show that FraGAT can achieve the state of the art predictive performance in most cases. Ablation study is also done, which demonstrates the effectiveness of using three-level hierarchical structural information of molecules in our model. Furthermore, case studies show that when a molecule graph is split into two fragments, and at least one of them is functional group relevant to molecule properties, better prediction can be achieved. This shows the interpretability of the proposed model.
For future work, the inclusion of 3D geometric structural information is a promising direction. It is believed that the 3D structures of molecules contain important information for property prediction. So we will try to combine our fragment-based model and 3D molecule information to build more powerful models and further boost prediction performance.
Funding
This work was supported by the National Key Research and Development Program of China [2016YFC0901704], and partially by the National Natural Science Foundation of China (NSFC) [61972100 and 61772367].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Ziqiao Zhang, Shanghai Key Lab of Intelligent Information Processing, and School of Computer Science, Fudan University, Shanghai 200433, China.
Jihong Guan, Department of Computer Science and Technology, Tongji University, Shanghai 201804, China.
Shuigeng Zhou, Shanghai Key Lab of Intelligent Information Processing, and School of Computer Science, Fudan University, Shanghai 200433, China.
References
- Armitage J. et al. (2019) Fragment graphical variational autoencoding for screening molecules with small data. arXiv:1910.13325.
- Cho K. et al. (2014) On the properties of neural machine translation: encoder-decoder approaches. In Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation. Doha, Qatar, pp. 103–111. doi:10.3115/v1/W14-4012.
- Coley C.W. et al. (2017) Convolutional embedding of attributed molecular graphs for physical property prediction. J. Chem. Inf. Model., 57, 1757–1772. [DOI] [PubMed] [Google Scholar]
- Duvenaud D. et al. (2015) Convolutional networks on graphs for learning molecular fingerprints. In Proceedings of Advances in Neural Information Processing Systems 28. Montreal, Canada, pp. 2215–2223.
- Ertl P. et al. (2020) The most common functional groups in bioactive molecules and how their popularity has evolved over time. J. Med. Chem., 63, 8408–8418. [DOI] [PubMed] [Google Scholar]
- Esposito E.X. et al. (2004) Methods for applying the quantitative structure-activity relationship paradigm. In: Bajorath J. (eds.) Chemoinformatics. Methods in Molecular Biology, Vol. 275. Humana Press Inc., New Jersey, USA. pp. 131–214. [DOI] [PubMed] [Google Scholar]
- Fortanet J.G. et al. (2016) Allosteric inhibition of SHP2: identification of a potent, selective, and orally efficacious phosphatase inhibitor. J. Med. Chem., 59, 7773–7782. [DOI] [PubMed] [Google Scholar]
- Gillis E.P. et al. (2015) Applications of fluorine in medicinal chemistry. J. Med. Chem., 58, 8315–8359. [DOI] [PubMed] [Google Scholar]
- Gilmer J. et al. (2017) Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning. Vol. 70, Sydney, Australia, pp. 1263–1272.
- Guvench O. (2016) Computational functional group mapping for drug discovery. Drug Discov. Today, 21, 1928–1931. doi:10.1016/j.drudis.2016.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiménez J. et al. (2018) KDEEP: protein–ligand absolute binding affinity prediction via 3D-convolutional neural networks. J. Chem. Inf. Model., 58, 287–296. [DOI] [PubMed] [Google Scholar]
- Jin W. et al. (2018) Junction tree variational autoencoder for molecular graph generation. In Proceedings of the 35th International Conference on Machine Learning. Vol. 80, Stockholm, Sweden, pp. 2323–2332.
- Kearnes S. et al. (2016) Molecular graph convolutions: moving beyond fingerprints. J. Comput. Aided Mol. Des., 30, 595–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kipf T.N., Welling M. (2017) Semi-supervised classification with graph convolutional networks. In Proceedings of 5th International Conference on Learning Representations. Toulon, France.
- LaMarche M.J. et al. (2020) Identification of TNO155, an allosteric SHP2 inhibitor for the treatment of cancer. J. Med. Chem., 63, 13578–13594. [DOI] [PubMed] [Google Scholar]
- Liew C.Y. et al. (2009) SVM model for virtual screening of Lck inhibitors. J. Chem. Inf. Model., 49, 877–885. doi:10.1021/ci800387z. [DOI] [PubMed] [Google Scholar]
- Liu S. et al. (2019) N-gram graph: simple unsupervised representation for graphs, with applications to molecules. In Proceedings of Advances in Neural Information Processing Systems 32. Vancouver, Canada, pp. 8464–8476. [Google Scholar]
- Melville J.L. et al. (2009) Machine learning in virtual screening. Comb. Chem. High Trans. Screen., 12, 332–343. [DOI] [PubMed] [Google Scholar]
- Muller P. (1994) Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994). Pure. Appl. Chem., 66, 1077–1184. doi:10.1351/pac199466051077. [Google Scholar]
- Peng Y. et al. (2020) TOP: a deep mixture representation learning method for boosting molecular toxicity prediction. Methods, 179, 55–64. [DOI] [PubMed] [Google Scholar]
- Schneider P. et al. (2020) Rethinking drug design in the artificial intelligence era. Nat. Rev. Drug Discov., 19, 353–364. [DOI] [PubMed] [Google Scholar]
- Song Y. et al. (2020) Communicative representation learning on attributed molecular graphs. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama, Japan, pp. 2813–2838.
- Veličković P. et al. (2018) Graph attention networks. In Proceedings of 6th International Conference on Learning Representations. Vancouver, Canada.
- Wu Z. et al. (2018) MoleculeNet: a benchmark for molecular machine learning. Chem. Sci., 9, 513–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong Z. et al. (2020) Pushing the boundaries of molecular representation for drug discovery with the graph attention mechanism. J. Med. Chem., 63, 8749–8760. doi:10.1021/acs.jmedchem.9b00959. [DOI] [PubMed] [Google Scholar]
- Zhong F. et al. (2018) Artificial intelligence in drug design. Sci. China Life Sci., 61, 1191–1204. [DOI] [PubMed] [Google Scholar]
- Zhou Z., Li X. (2017) Graph convolution: a high-order adaptive approach. arXiv:1706.09916.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.