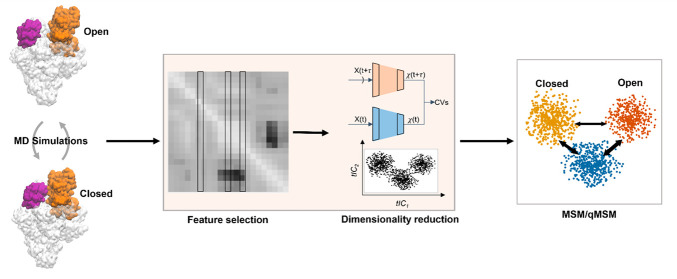
Abstract
Markov state models (MSMs) based on molecular dynamics (MD) simulations are routinely employed to study protein folding, however, their application to functional conformational changes of biomolecules is still limited. In the past few years, the field of computational chemistry has experienced a surge of advancements stemming from machine learning algorithms, and MSMs have not been left out. Unlike global processes, such as protein folding, the application of MSMs to functional conformational changes is challenging because they mostly consist of localized structural transitions. Therefore, it is critical to properly select a subset of structural features that can describe the slowest dynamics of these functional conformational changes. To address this challenge, we recommend several automatic feature selection methods such as Spectral-OASIS. To identify states in MSMs, the chosen features can be subject to dimensionality reduction methods such as TICA or deep learning based VAMPNets to project MD conformations onto a few collective variables for subsequent clustering. Another challenge for the application of MSMs to the study of functional conformational changes is the ability to comprehend their biophysical mechanisms, as MSMs built for these processes often require a large number of states. We recommend the recently developed quasi-MSMs (qMSMs) to address this issue. Compared to MSMs, qMSMs encode the non-Markovian dynamics via the generalized master equation and can significantly reduce the number of states. As a result, qMSMs can be built with a handful of states to facilitate the interpretation of functional conformational changes. In the wake of machine learning, we believe that the rapid advancement in the MSM methodology will lead to their wider application in studying functional conformational changes of biomolecules.
Keywords: Markov state models, biomolecular function, conformational change, molecular dynamics simulations, machine learning, non-Markovian dynamics
1. Introduction
Biological macromolecules often exert their functions through conformational changes:1−3 i.e., dynamic transitions between metastable conformational states. For example, the SARS-CoV-2 spike protein complex undergoes dramatic opening during recognition of the human ACE-2 receptor,4 RNA polymerases continuously translocate on the DNA template during gene transcription,5 and Src kinases’ activation-loop needs to open to make their active site accessible.6 In this Perspective, we distinguish between these functional conformational changes and global conformational changes. As functional conformational changes mostly involve slow, often hierarchical, collective transitions of protein loops and specific domains,7 it is often sufficient to describe the functionally relevant motions using only a subset of structural features (e.g., certain residue–residue distances, torsion angles, etc.). This is in sharp contrast to conformational changes, such as complete protein folding, in which the whole structure undergoes drastic changes involving a complete set of structural features.8−10 Delineating mechanisms of functional change is crucial to our understanding of numerous fundamental biological processes and facilitating rational drug design.
Functional conformational changes can be studied in fine detail by all-atom molecular dynamics (MD) simulations. However, the time scales accessible to MD simulations of complex biomolecules (at microseconds or shorter) remain orders of magnitude shorter than those of functional conformational changes (millisecond or longer). In recent years, Markov state models (MSMs) have become a popular approach to bridge this time scale gap by predicting long-time scale dynamics based on numerous short MD simulations.11−32 MSMs have been widely applied to study global conformational changes, such as the folding of small proteins (e.g., NTL933 and FiP35 WW domain34) and the dynamics of intrinsically disordered peptides (e.g., hIAPP35). In these studies, the entire structure is used to describe these global conformational changes11,22 (e.g., pairwise distances between all Cα atoms). This is not the case for complex and localized functional conformational changes of large biomolecular complexes, where it is often difficult to precisely pinpoint parts of the system relevant to function, and even more difficult to choose an appropriate set of structural features to describe them.36,37 In early MSM studies, researchers mainly chose structural features based on their a priori physical understanding of the system (e.g., distances between ligand and binding pockets for protein–ligand recognition24 or DNA/RNA and their surrounding protein motifs for RNA polymerase translocation5). This renders the construction of MSMs to study functional conformational changes time-consuming and challenging. In the past several years, novel machine learning algorithms, especially deep neural networks, have been introduced to the MSM community,38−42 promising to aid MSM construction for such complex problems.
In this Perspective, we first briefly review the MSM theory and highlight two major challenges specific to MSMs of functional mechanisms of large biomolecular complexes (section 2). We then introduce a state-of-the-art protocol for the MSM construction to study functional conformational changes together with a few examples of its recent application (section 3). Next, we discuss in detail several recently developed machine learning algorithms in our recommended protocol to address these two challenges (section 4): Algorithms for the identification of proper structural features and collective variables (CVs) to describe localized functional conformational changes of interest (e.g., Spectral-oASIS,39 feature importance selection,40 variational approach to Markov process neural network (VAMPNets),41 and state-free reversible VAMPNets (SRVs)42); and methods to produce models containing a handful of states to facilitate the interpretation of biological mechanisms (e.g., quasi-MSM (qMSM) based on the Generalized Master Equation (GME) framework43) (section 5). We hope that this Perspective will encourage researchers to apply MSMs to study challenging problems related to biomolecular functional conformational changes and other dynamic systems.
2. Overview of MSMs and Challenges for Their Application to Functional Conformational Changes
MSMs are a powerful tool that can combine disparate short MD simulations at local equilibrium to model long-time scale dynamics of complex conformational changes. Specifically, MSMs partition the conformational space into metastable states, such that intrastate transitions are fast but interstate transitions are slow. This separation of time scales ensures an MSM is Markovian (i.e., that the probability of transitioning from state i to state j depends only on the identity of i and not any previously visited state) and allows MSMs to be built from many short simulations. These probabilities can then be propagated to give long-time scale dynamics:
| 1 |
where Δt corresponds to the lag time, P(nΔt) is a vector of state populations at time nΔt, and T is the transition probability matrix.
One of the key challenges in MSM construction is correctly identifying kinetically metastable states, which requires selecting a protein’s structural features that can properly describe the slowest dynamics of conformational changes. With these chosen structural features, dimensionality reduction methods can be applied to obtain CVs, and then clustering algorithms can be used to group MD conformations into metastable states. However, it is not trivial to identify proper structural features that can describe the localized, but often complex, conformational changes underlining the function. For example, RNA polymerase II (Pol II) will translocate backward (backtrack) on the DNA template to allow the cleavage of the misincorporated nucleotide, which is a critical step to maintain accurate gene transcription. Exhaustive featurization of this system is infeasible due to its large size (e.g., the Pol II complex contains ∼3600 residues, and the consideration of distances between all the Cα atoms will lead to nearly 13 million features). Furthermore, noise due to thermal fluctuations, especially from parts of the system that do not participate in backtracking, could compromise the quality of the MSM. In early studies, features were often selected manually based on researchers’ prior knowledge of the system. For example, in the MSM studies of Pol II backtracking,44 distances between atom pairs (695 interatomic distances) that are sensitive to the backtracking of Pol II were chosen based on physical intuition, which contain backtracked RNA and DNA nucleotides, critical bridge helix residues, and two Tyr residues which are known to stabilize the nucleotide bases during backtracking. With recently developed machine learning methods, automatic selection of features becomes feasible, and we recommend a few such methods in section 4.
Another challenge for MSMs lies in the comprehension of biophysical mechanisms of functional conformational changes, as MSMs built for these processes often contain hundreds or even more states.5,23,45−49 In an MSM, the lag time must be long enough to allow transitions among states to become Markovian (or memoryless), and the memory of these transitions is mainly determined by dynamic relaxation within each state. In practice, this is challenging as the lag time is bound by the length of MD simulations available to estimate transition probabilities (T). To render the models Markovian, successful application of MSMs for functional conformational changes often contain at least hundreds of states, so that each state is sufficiently small and has relatively fast relaxation dynamics to allow affordable lag times. To address this challenge, we recommend the recently developed qMSM,43 which can accurately predict dynamics from models containing a small number of states by explicitly considering the memory of protein dynamics (see section 5).
3. Our Recommended Protocol to Build MSMs to Study Functional Conformational Changes
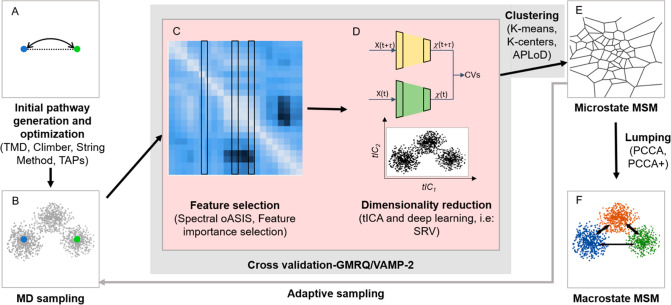
Figure 1 summarizes our recommended protocol for constructing MSMs to study how biomolecules dynamically transition between metastable states to perform their functions. In this protocol, the initial paths connecting known states (e.g., structures obtained from X-ray crystallography or cryo-EM) are first generated via approaches such as targeted MD,50 Onsager–Machlup action-based conformational state annealing (Action-CSA),51 Climber,52 or coarse-grained MD simulations53,54 and are further optimized using the String method55 or traveling-salesman-based automatic path searching (TAPS)56 (Figure 1A). Extensive MD simulations are then initiated from conformations along these optimized initial pathways (Figure 1B). Next, structural features (e.g., interatomic distances, torsion angles, etc.) that can describe functional conformational changes are selected (Figure 1C). Here, we recommend Spectral-oASIS,39 feature importance selection,40 or automatic mutual information noise omission (AMINO)57 to automatically select a proper set of features. As shown in Figure 1D, dimensionality reduction algorithms (e.g., time-lagged independent component analysis (TICA),58 VAMPNets,41 or SRVs42) can then be applied to find a few CVs. MD conformations projected onto these CVs are then grouped into microstates using various clustering algorithms.59−61 The microstate-MSM is then built and validated using the Chapman–Kolmogorov test13,16 (Figure 1E). The Chapman–Kolmogorov test can be performed by directly examining if eq 1 is satisfied:16,62 i.e., if time evolutions of state populations (P(nΔt)) obtained from MD simulations agree with the prediction of an MSM via the replication of the transition probability matrix ([T(Δt)]nP(0)). Another implementation of the Chapman–Kolmogorov test is to compare the probabilities for the system to stay in a given state between the predictions of MSMs and those obtained from MD simulations.13
Figure 1.
Key steps in MSM construction for studying functional conformational changes in proteins. (A) Pathways between two or more end points of the functional conformational changes are generated and optimized to obtain minimum free energy pathways. (B) Extensive MD simulations are performed starting from these pathways. (C) Several relevant features or physical coordinates are selected. (D) Dimensionality reduction is performed using the selected features as input. (E) Reduced dimension data is discretized to obtain microstates and the MSM is estimated. (F) Kinetic lumping is performed to group microstates to macrostates.
The cross-validation tools are recommended to avoid overfitting and to select optimal parameters from the previous steps (e.g., feature sets, number of CVs, and number of microstates). With cross-validation, the model is constructed on part of the original data and then tested on the remaining data. Models built with various parameters can be scored with objective metrics such as the generalized matrix Rayleigh quotient (GMRQ)63 or the VAMP-229 score, allowing the selection of optimal parameters. Grounded on the variational principle for conformational dynamics, both GMRQ and VAMP-2 scores favor the models that yield slower dynamics. In particular, GMRQ63 can be computed from the eigenvalues of the transition probability matrix, while VAMP-2 scores can be obtained from the time-lagged covariance matrix of input features.29
If the conformational sampling is not sufficient to build a Markovian microstate-MSM, we suggest performing adaptive sampling64−66 and repeating the previous steps (Figure 1B–E) until the model is valid. In an adaptive sampling strategy developed by Bowman and co-workers,67 additional sampling is initiated from conformations selected based on a function (e.g., the solvent accessible surface area of the solute) that balances exploration and exploitation of the previously sampled states.
Finally, the microstates can be lumped into a few metastable macrostates by grouping those microstates that can interconvert quickly. This step can be achieved via kinetic lumping algorithms,70−76 and the resulting macrostate MSM can greatly aid the interpretation of biological mechanisms (Figure 1F). It is challenging to build a Markovian macrostate-MSM since the lag time cannot exceed the length of the MD trajectories. Therefore, we recommend using qMSMs43 that encode non-Markovian dynamics via the GME formalism to build these macrostate models.
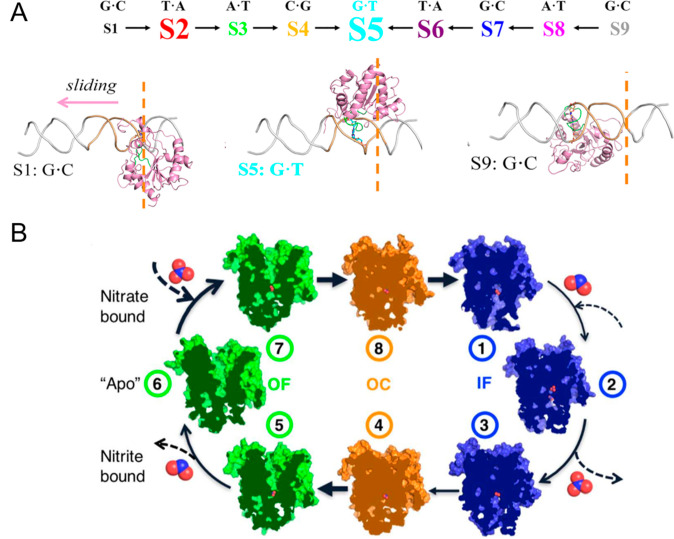
In recent years, MSMs have been successfully applied to study various protein functional conformational changes.5,45−49,77−80 For example, Da and co-workers constructed MSMs that revealed that thymine DNA glycosylases translocate along double-stranded DNA via a rotation-coupled sliding model in order to detect DNA lesions.68 To build their MSMs, they followed the protocol in Figure 1 but chose the structural features based on physical intuition. Their MSM identified two parallel pathways over nine macrostates, where state 5 (S5) is the specific interrogating complex with a mismatched base pair (Figure 2A). In another study, Shukla and co-workers applied MSMs to reveal a rocker switch mechanism in a substrate exchange cycle of a membrane transport protein, the bacterial NO3–/NO2– antiporter NarK.69 From the MSM-weighted free energy landscape, a series of important conformations during the substrate exchange cycle were identified (Figure 2B). Based on the MSM, they discovered that the exchange of NO3– and NO2– is ensured by the closure of space between two arginine residues in the binding site of the antiporter. More recently, Bowman and co-workers4 have constructed an MSM from over 1 ms of MD simulations to describe the opening of the SARS-CoV-2 spike protein complex, and reveal cryptic pockets during this process as potential drug targets.
Figure 2.
Examples of functional conformational changes elucidated by MSMs. (A) MSMs describe the mechanism of thymine DNA glycosylase sliding along double-stranded DNA to detect the mismatched pair (target site, S5). (B) Conformational change of the NarK transporter during substrate exchange is shown. Panel (A) is reproduced with permission from ref (68). Oxford University Press, 2021. Panel (B) is adapted with permission from ref (69). Elsevier, 2021.
4. Automatic Feature Selection and Dimensionality Reduction to Help Identify Metastable States Underlying Functional Conformational Changes
As discussed in section 2, it is challenging to efficiently select a subset of protein’s structural features that describe localized functional conformational changes. For this purpose, internal coordinates such as distances, contacts, and dihedral angles are generally superior to Cartesian coordinates (being independent of the overall translation and rotation of the system).81 Properly selected structural features serve as the input for dimensionality-reduction methods, and MD conformations can then be clustered into metastable states at reduced dimensions (Figure 1C–E). In this section, we introduce a few recently developed methods that could help achieve automatic feature selection and dimensionality reduction for the construction of MSMs to study functional conformational changes.
Automatic Methods for Feature Selection
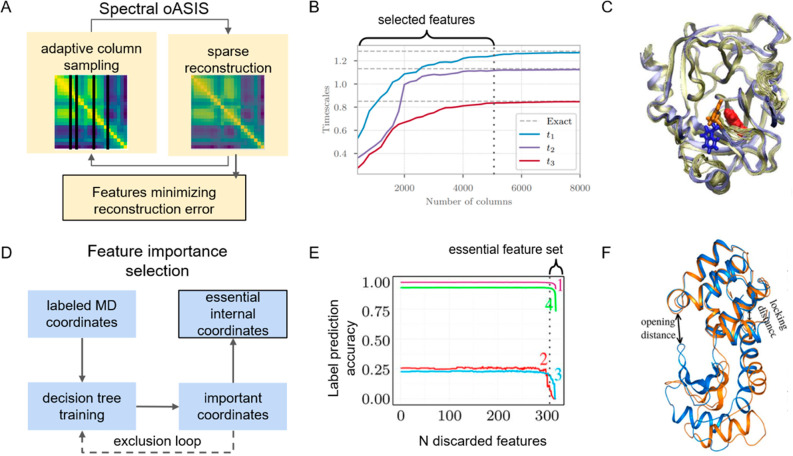
Spectral-oASIS is particularly useful for automatically selecting features for MSM construction.39 This method is based on the Nyström matrix operation theory, which can approximately reconstruct the time-lagged covariance matrix of all input features while using only a subset of features as input. Given an initial input feature set, Spectral-oASIS samples a subset of these features that best reconstructs the leading eigenfunctions of the time-lagged covariance matrix obtained from MD simulations, yielding a sparse solution to the generalized eigenvalue problem (Figure 3A). An optimal subset of features can then be selected based on the variational principle, i.e., the ability of the reconstructed matrix to reproduce the slowest time scales of the original matrix (Figure 3B). Using a benzamidine-trypsin binding process as an example, Clementi and co-workers39 demonstrated that an initial feature set of approximately 25 000 features can be reduced 5-fold while still accurately describing the slowest dynamic mode, which corresponds to the flipping of Trp215 to open the active site (Figure 3C). Notably, Sparse-TICA82 is similar to Spectral-oASIS in the sense that they both aim to find a subset of input features that can best approximate leading eigenfunctions of the time-lagged covariance matrix; however, Sparse-TICA uses a regularization approach rather than the Nyström reconstruction adopted in Spectral-oASIS.39 Sparse-TICA has also been successfully applied to study a functional conformational change of an opioid receptor, where 10 out of 4,400 features were chosen to build the MSMs.84
Figure 3.
Feature selection for functional conformational change. (A) Overview of the Spectral-oASIS algorithm. (B) Time scales of the first three TICs of the trypsin-benzamidine system are calculated using a subset of features selected by Spectral-oASIS. The optimal number of features is selected when the time scales plot levels off, which is at around 5000 out of 24 533 features. (C) Active site opening in trypsin-benzamidine can be described by the first TIC, which is calculated by using the selected features from Spectral-oASIS. The motion of the critical Trp215 is shown with sticks. (D) Overview of the feature importance selection algorithm. (E) The accuracy of T4 lysozyme is plotted as a function of the number of discarded features. Individual curves correspond to a different number of metastable states in the partitioning of the dynamics. The selected essential features are the ones after the accuracy plot begins to drop. (F) The functional change of T4 lysozyme is shown by the essential feature set. Panels (B) and (C) are reproduced from ref (39). Copyright 2018 American Chemical Society. Panels (E) and (F) are reproduced from ref (40). Copyright 2018 American Chemical Society.
Stock and co-workers40 developed an alternative method (we refer to it as “feature importance selection”) to automatically select essential features by ranking their importance in the ability to explain the labeling of the dynamics (e.g., index of metastable states). This method is based on training decision trees and only requires an input feature and the labeling of MD conformations (Figure 3D). The set of essential features can then be constructed by iteratively extracting the most important feature in the tree (Figure 3E). They demonstrated that their chosen essential features can well explain the functional dynamics of T4 lysozyme (Figure 3F). This approach has also been applied to select features prior to MSM construction in a study of ancestral mutations that activate the extracellular signal-regulated kinase (ERK2),85 in which they successfully identify the most informative features (inter-residue contacts) that can distinguish the mutant from the WT protein. AMINO is another method that holds the potential to select nonredundant features for functional conformational changes,57 even though it has yet to be applied in the MSM construction. By clustering the features using a mutual information-based metric, Tiwary and co-workers demonstrated that AMINO can achieve a significant reduction in features to describe a protein–ligand binding process: i.e., a set of 428 features containing all possible distance between protein Cα atoms and the ligand was reduced to just 8, allowing accurate computation of ligand binding free energy.57
TICA for Dimensionality Reduction
TICA is one of the most popular methods to perform dimensionality reduction in the MSM construction, which performs the eigen decomposition of the time-lagged covariance matrix.58,86 The leading eigenvectors (so-called time-lagged independent components, TICs) are linear approximations to the slowest dynamic modes of the system. When applying TICA to study functional conformational changes, we recommend using the subset of structural features chosen by Spectral-oASIS and other methods described in the previous section.87 Furthermore, we suggest using cross-validation tools, such as GMRQ63 or VAMP-2 score,28 to choose the optimal hyperparameters for the TICA analysis (e.g., number of TICs and TICA lag time).68,69,88
Emerging deep Learning Algorithms for Feature Selection and Dimensionality Reduction
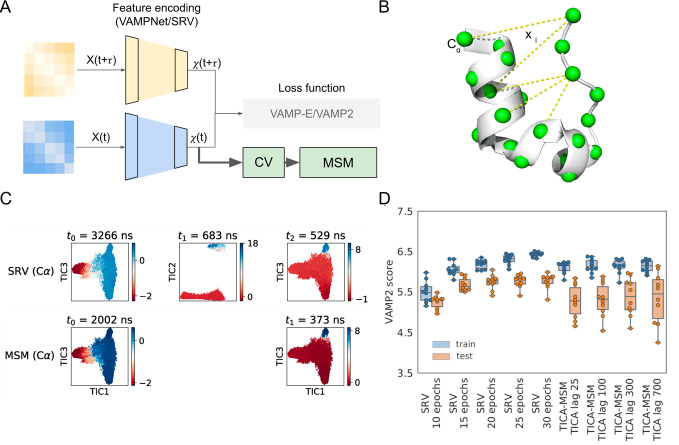
VAMPNets developed by Noé and co-workers are among the first deep learning architectures for MSM construction.41 VAMPNets adopt two encoder networks in parallel together with a specific loss function (i.e., the VAMP-229 score) based on the variational principle of the conformational dynamics. As shown in Figure 4A, the VAMP-2 score (R2) is computed based on the output of the encoder lobes: R2 = ∥C00–1/2C01C11∥F2, where C00 and C11 are the covariance matrices of the functions output by each of the two encoder lobes and C01 is the cross-covariance between lobes (i.e., time-lagged covariance). The general implementation of VAMPNets is not restricted to equilibrium data and thus does not enforce the detailed balance. To facilitate its application to equilibrium sampling, Ferguson and co-workers42 designed a variation of VAMPNets, so-called state-free reversible VAMPNets or SRV, enforcing the detailed balance by transforming the time-lagged covariance matrices into symmetric matrices. More recently, the Wu and Noé groups developed a version of VAMPNets by imposing the reversibility by introducing additional constraint variables.89 These VAMPNets-based deep learning algorithms can be used for dimensionality reduction to output a few CVs for subsequent MSM construction. Indeed, SRV has been successfully applied to construct MSMs to study the folding of the Trp-cage protein, where they chose all Cα–Cα distances (Figure 4B) as input, and output seven CVs to perform clustering to group MD conformations into 100 states.83 Compared to TICA with the same input features, SRV is able to identify an additional slow dynamic mode. Specifically, MSMs built from top CVs obtained from SRV successfully identified a dynamic mode that corresponds to the transition from a molten globule to an α-helix-like state with proline residues facing outward (denoted as a trapped intermediate state that precludes folding83), while MSMs built from top TICs failed to capture this dynamic mode (see the middle panel of Figure 4C). Furthermore, SRV was shown to be more robust than TICA for dimensionality reduction in the cross-validation test (Figure 4D).
Figure 4.
VAMPNets based CVs offer superior performance compared to TICA. (A) Schematic of the VAMPNets architecture. (B) Structure of the Trp-cage protein. The green spheres highlight Cα atoms. Representative pairwise distance features between some of the Cα atoms are shown as yellow dashed lines. (C) MD simulation structures of Trp-cage proteins are projected onto TICA coordinates and colored according to the eigenvectors discovered by SRV (Top) and TICA-MSM (Bottom). (D) Model performance is scored based on cross-validation with VAMP-2. Panels (C) and (D) are reproduced with permission from ref (83). Copyright 2019 American Chemical Society.
In theory, when applied to study functional conformational changes, these VAMPNets-based methods could achieve the goal of simultaneously selecting input features (interatomic distances, dihedral angles, etc.) and identifying their proper combinations to form CVs through the optimization of numerous parameters and their nonlinear combinations in the deep neural networks. However, considering the large number of input features and the localized nature of functional conformational changes, we anticipate that it will not be a trivial task for VAMPNets-based methods to achieve the above-mentioned goal. Therefore, we still suggest preselecting features when applying VAMPNets to study functional conformational changes.
5. Going beyond the Markovian Model: Considering Memory of Biomolecular Dynamics
As discussed in section 2, MSMs of protein dynamics with a small number of states often suffer from non-Markovianity due to the limited length of lag time, which is bound by relatively short MD simulations. To address this challenge, we have developed the qMSM method based on the GME formalism,43 in which memory kernels of protein dynamics are explicitly calculated and the dynamics are propagated with a discretized GME (eq 2)
| 2 |
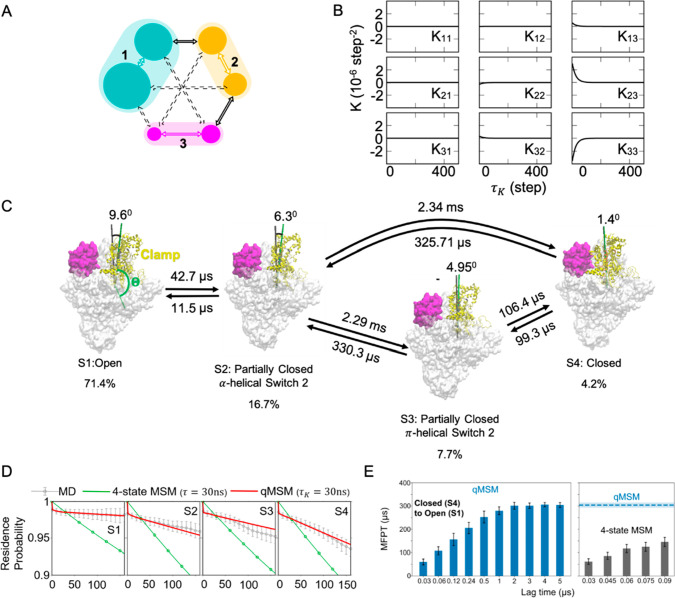
where memory kernels (K(mΔt)) can be obtained iteratively from the transition probability matrix T(t) and their derivatives Ṫ(t) at time points t = 0, Δt,... nΔt (Δt is the saving interval of MD trajectories) as well as all K(t) at previous time points. τK = nKΔt corresponds to the time until the memory kernels are relaxed to zero. qMSMs and MSMs adopt the same state decomposition. However, rather than using the transition probability matrix as in an MSM, qMSM models the dynamics using the transition tensors: K(t) (i.e., each transition element is associated with a memory kernel curve; see Figure 5A and B for memory kernels of a simple three-state model as an example).
Figure 5.
qMSMs afford precise models with a handful of states. (A) Schematic of a simple three-state model. (B) Memory kernel tensor (K) of the three-state model. (C) The mechanism of the bacterial RNA polymerase clamp domain opening is shown, where four macrostates and the MFPTs between them are identified and estimated by the qMSM. (D) Chapman–Kolmogorov tests of the qMSM and four-state MSM are compared to MD simulations. (E) MFPTs from S4 to S1 estimated using the qMSM (left) and four-state MSM (right) are shown as a function of lag time. Panels (A) and (B) are reproduced with permission from ref (43). AIP Publishing, 2020. Panels (C)–(E) are adapted with permission from ref (90). National Academy of Sciences, 2021.
For the folding of a small protein (the Fip35 WW domain), we show that qMSMs (consisting of four states) can be built from MD simulations that are an order of magnitude shorter than those required by an MSM.43 We expect that this advantage will be more prominent for the studies of functional conformational changes of more complex biomolecular systems. Recently, qMSMs have been successfully applied to elucidate the dynamics of a large functional conformational change of the bacterial RNA Polymerase (RNAP) transcription complex: i.e., the opening of the RNAP clamp.90 Bacterial RNAP has a shape that resembles a crab claw with two pincers: clamp and β-lobe (see yellow and magenta regions, respectively in Figure 5C). The opening and closing of the clamp are crucial for the initiation of bacterial gene transcription, and inhibition of the RNAP clamp opening provides a promising target for the development of antibiotics (e.g., Myxopyronin). Using qMSMs, we identified two intermediate states during the clamp opening, and our four-state qMSM predicts that the clamp opening process occurs at millisecond time scales (Figure 5C). For this system, qMSM greatly outperforms MSMs. For example, qMSMs with τk = 30 ns can already reproduce the dynamics of the original MD simulations, while MSMs predict significantly faster dynamics than MD simulations (Figure 5D). Consistently, MSM (τ = 30 ns) predicts around 6-fold shorter mean first passage times (MFPTs) than qMSM (τk = 30 ns, Figure 5E). Therefore, qMSMs have substantial advantages over MSMs in interpreting biological mechanisms by yielding models with a handful of states.
Notably, Tiwary and co-workers recently developed another algorithm based on the long short-term memory (LSTM) model to consider the memory functions of protein conformational dynamics.91 This approach is based on a recurrent network architecture that can retain the memory of the past states in a temporal sequence via gating nodes that capture lags between long-time scale events. In this deep learning approach, Tiwary and co-workers ingeniously connect the loss function with the path entropy and show that the LSTM method can accurately predict equilibrium distributions and kinetics for an alanine dipeptide and experimental single-molecular FRET data. As the recurrent neural network approach was originally developed for one-dimensional natural language processing, we expect that this LSTM approach alone may perform optimally on one-dimensional data. Nevertheless, the LSTM architecture can be incorporated into a larger framework to perform complex multidimensional tasks. For example, LSTM lies at the core of AlphaStar,94 which processes complex inputs combined with other network architectures (e.g., transformer,93 ResNet,92 etc.). We believe that the work of Tiwary and co-workers91 has great potential to be extended to handle the multidimensional MD trajectories of functional conformational changes in the future.
6. Conclusion and Future Perspective
In this Perspective, we focused on the application of MSMs to study functional conformational changes of complex biomolecules. We introduced a state-of-the-art protocol that is tailor-made for localized functional conformational changes (see Figure 1 for the summary of the protocol). In this protocol, we highlight two challenges and recommend a series of recently developed machine learning algorithms to address them. For the first challenge, which consists of properly identifying a subset of structural features that describe the slow dynamics of the functional conformational changes, we recommend several automatic feature selection methods including Spectral-OASIS,39 feature importance selection,40 and AMINO.57 The chosen features can then be subject to dimensionality reduction methods such as TICA58 or deep learning based VAMPNets41 or SRVs42 to obtain CVs for subsequent microstate clustering. For the second challenge, which consists of improving the interpretation of the biophysical mechanisms, we recommend qMSMs that can produce models containing a handful of states.43 In addition to the above two challenges, which are more specific to functional conformational changes, we note that other difficulties exist for building MSMs to study conformational dynamics. For example, the choice of clustering algorithms and distance metrics are important for the quality of MSM construction, and those issues have been extensively reviewed elsewhere.95−97
Most of the algorithms that we recommended in this Perspective for feature selection and dimensionality reduction are based on the variational principle of the conformational dynamics,29 in which the best models should theoretically yield the slowest time scales due to the variational bound. However, in practice, the slowest dynamic modes identified by these algorithms could correspond to irrelevant processes. For example, Husic and Noé98 demonstrated that the slowest dynamic mode for the folding of the Villin headpiece obtained based on the VAMP-2 score corresponds to a transition to a rare helical misfolded state, which was further examined manually by the authors and asserted to be an artifact.98 Therefore, we believe that it remains important to evaluate and confirm the relevance of the slowest dynamic modes obtained from these automatic algorithms. In addition, VAMPNets and other deep learning algorithms could theoretically be applied to perform feature selection and dimensionality reduction at the same time. However, we expect that it will be difficult for these algorithms to achieve these two aims simultaneously when studying the localized, but often complex, functional conformational changes. We thus recommend performing feature selection first (e.g., using Spectral-oASIS39) and inputting only the selected features to these deep learning algorithms.
We demonstrated that the GME-based methods, such as qMSMs, hold great promise for studying functional conformational changes, as they can be built from affordable lengths of MD simulations while only containing a few states to facilitate the understanding of biological mechanisms. In addition to qMSMs, we expect that two previously developed methods, hidden Markov models99,100 and core-set MSMs,101,102 could serve as alternative approaches to efficiently generate MSMs with a small number of states. Nevertheless, the hidden Markov model adopts a soft partitioning scheme that allows overlaps between metastable states, and this could lead to ambiguity when interpreting the biological mechanisms. In addition, the core-set MSM only focuses on the core regions of each metastable state instead of a full partitioning of the conformational space. Even though it is not trivial to correctly identify these core regions, several recent algorithms have been developed to circumvent this issue.102 Despite all these methodological advancements to automatically construct MSMs, we are also wary of the pitfalls of blind applications of these machine learning algorithms and believe that physical intuition remains invaluable. Nevertheless, we are optimistic that MSMs will be widely applied to elucidate functional conformational changes in the future.
Acknowledgments
X.H. was supported by the Hong Kong Research Grant Council (16303919, 16307718, N_HKUST635/20, and AoE/P-705/16). K.A.K. was supported by the Hong Kong PhD Fellowship Scheme (PF16-06144),
Glossary
Abbreviations
- MSM
Markov state model
- MD
molecular dynamics
- VAMP
variational approach to Markov processes
- qMSM
quasi-Markov state model
- GME
generalized master equation
- LSTM
long short-term memory
- RNAP
RNA polymerase
- TICA
time-lagged independent component analysis
- CV
collective variable
- Pol II
RNA polymerase II
- AMINO
automatic mutual information noise omission
- GMRQ
generalized matrix Rayleigh quotient
- SRV
state-free reversible VAMPNet
Author Contributions
The manuscript was written through contributions of all authors.
The authors declare no competing financial interest.
References
- Henzler-Wildman K.; Kern D. Dynamic personalities of proteins. Nature 2007, 450 (7172), 964–972. 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- Bahar I.; Lezon T. R.; Yang L. W.; Eyal E. Global Dynamics of Proteins: Bridging Between Structure and Function. Annu. Rev. Biophys. 2010, 39, 23–42. 10.1146/annurev.biophys.093008.131258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei G. H.; Xi W. H.; Nussinov R.; Ma B. Y. Protein Ensembles: How Does Nature Harness Thermodynamic Fluctuations for Life? The Diverse Functional Roles of Conformational Ensembles in the Cell. Chem. Rev. 2016, 116 (11), 6516–6551. 10.1021/acs.chemrev.5b00562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman M. I.; Porter J. R.; Ward M. D.; Singh S.; Vithani N.; Meller A.; Mallimadugula U. L.; Kuhn C. E.; Borowsky J. H.; Wiewiora R. P.; Hurley M. F. D.; Harbison A. M.; Fogarty C. A.; Coffland J. E.; Fadda E.; Voelz V. A.; Chodera J. D.; Bowman G. R. SARS-CoV-2 simulations go exascale to predict dramatic spike opening and cryptic pockets across the proteome. Nat. Chem. 2021, 13, 651–659. 10.1038/s41557-021-00707-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva D. A.; Weiss D. R.; Avila F. P.; Da L. T.; Levitt M.; Wang D.; Huang X. H. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (21), 7665–7670. 10.1073/pnas.1315751111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S.; Roux B. Src kinase conformational activation: Thermodynamics, pathways, and mechanisms. PLoS Comput. Biol. 2008, 4 (3), e1000047 10.1371/journal.pcbi.1000047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchenberg S.; Schaudinnus N.; Stock G. Hierarchical Biomolecular Dynamics: Picosecond Hydrogen Bonding Regulates Microsecond Conformational Transitions. J. Chem. Theory Comput. 2015, 11 (3), 1330–1336. 10.1021/ct501156t. [DOI] [PubMed] [Google Scholar]
- Chong S. H.; Chatterjee P.; Ham S. Computer Simulations of Intrinsically Disordered Proteins. Annu. Rev. Phys. Chem. 2017, 68, 117–134. 10.1146/annurev-physchem-052516-050843. [DOI] [PubMed] [Google Scholar]
- Schuler B.; Hofmann H. Single-molecule spectroscopy of protein folding dynamics-expanding scope and timescales. Curr. Opin. Struct. Biol. 2013, 23 (1), 36–47. 10.1016/j.sbi.2012.10.008. [DOI] [PubMed] [Google Scholar]
- Englander S. W.; Mayne L. The nature of protein folding pathways. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (45), 15873–15880. 10.1073/pnas.1411798111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chodera J. D.; Noe F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husic B. E.; Pande V. S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140 (7), 2386–2396. 10.1021/jacs.7b12191. [DOI] [PubMed] [Google Scholar]
- Prinz J. H.; Wu H.; Sarich M.; Keller B.; Senne M.; Held M.; Chodera J. D.; Schutte C.; Noe F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134 (17), 174105. 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- Malmstrom R. D.; Lee C. T.; Van Wart A. T.; Amaro R. E. Application of Molecular-Dynamics Based Markov State Models to Functional Proteins. J. Chem. Theory Comput. 2014, 10 (7), 2648–2657. 10.1021/ct5002363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman G. R.; Noeé F.; Pande V. S.. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation. In Advances in Experimental Medicine and Biology, [Online] 1st ed.; Springer Netherlands: Dordrecht, 2014. [Google Scholar]
- Chodera J. D.; Singhal N.; Pande V. S.; Dill K. A.; Swope W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007, 126 (15), 155101. 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- Pan A. C.; Roux B. Building Markov state models along pathways to determine free energies and rates of transitions. J. Chem. Phys. 2008, 129 (6), 064107. 10.1063/1.2959573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morcos F.; Chatterjee S.; McClendon C. L.; Brenner P. R.; Lopez-Rendon R.; Zintsmaster J.; Ercsey-Ravasz M.; Sweet C. R.; Jacobson M. P.; Peng J. W.; Izaguirre J. A. Modeling Conformational Ensembles of Slow Functional Motions in Pin1-WW. PLoS Comput. Biol. 2010, 6 (12), e1001015 10.1371/journal.pcbi.1001015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X. H.; Bowman G. R.; Bacallado S.; Pande V. S. Rapid equilibrium sampling initiated from nonequilibrium data. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (47), 19765–19769. 10.1073/pnas.0909088106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchete N. V.; Hummer G. Coarse master equations for peptide folding dynamics. J. Phys. Chem. B 2008, 112 (19), 6057–6069. 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- Noe F.; Schutte C.; Vanden-Eijnden E.; Reich L.; Weikl T. R. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (45), 19011–19016. 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman G. R.; Voelz V. A.; Pande V. S. Taming the complexity of protein folding. Curr. Opin. Struct. Biol. 2011, 21 (1), 4–11. 10.1016/j.sbi.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buch I.; Giorgino T.; De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A. 2011, 108 (25), 10184–10189. 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva D. A.; Bowman G. R.; Sosa-Peinado A.; Huang X. H. A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol. 2011, 7 (5), e1002054 10.1371/journal.pcbi.1002054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noe F.; Horenko I.; Schutte C.; Smith J. C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126 (15), 155102. 10.1063/1.2714539. [DOI] [PubMed] [Google Scholar]
- Bowman G. R.; Ensign D. L.; Pande V. S. Enhanced Modeling via Network Theory: Adaptive Sampling of Markov State Models. J. Chem. Theory Comput. 2010, 6 (3), 787–794. 10.1021/ct900620b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarich M.; Noe F.; Schutte C. On the Approximation Quality of Markov State Models. Multiscale Model. Simul. 2010, 8 (4), 1154–1177. 10.1137/090764049. [DOI] [Google Scholar]
- Noe F.; Nuske F. A Variational Approach to Modeling Slow Processes in Stochastic Dynamical Systems. Multiscale Model. Simul. 2013, 11 (2), 635–655. 10.1137/110858616. [DOI] [Google Scholar]
- Wu H.; Noe F. Variational Approach for Learning Markov Processes from Time Series Data. J. Nonlinear Sci. 2020, 30 (1), 23–66. 10.1007/s00332-019-09567-y. [DOI] [Google Scholar]
- Weng J. W.; Yang M. H.; Wang W. N.; Xu X.; Tian Z. Q. Revealing Thermodynamics and Kinetics of Lipid Self-Assembly by Markov State Model Analysis. J. Am. Chem. Soc. 2020, 142 (51), 21344–21352. 10.1021/jacs.0c09343. [DOI] [PubMed] [Google Scholar]
- Zeng X. Z.; Zhu L. Z.; Zheng X. Y.; Cecchini M.; Huang X. H. Harnessing complexity in molecular self-assembly using computer simulations. Phys. Chem. Chem. Phys. 2018, 20 (10), 6767–6776. 10.1039/C7CP06181A. [DOI] [PubMed] [Google Scholar]
- Zhang B. W.; Dai W.; Gallicchio E.; He P.; Xia J. C.; Tan Z. Q.; Levy R. M. Simulating Replica Exchange: Markov State Models, Proposal Schemes, and the Infinite Swapping Limit. J. Phys. Chem. B 2016, 120 (33), 8289–8301. 10.1021/acs.jpcb.6b02015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voelz V. A.; Bowman G. R.; Beauchamp K.; Pande V. S. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1–39). J. Am. Chem. Soc. 2010, 132 (5), 1526–1528. 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane T. J.; Bowman G. R.; Beauchamp K.; Voelz V. A.; Pande V. S. Markov State Model Reveals Folding and Functional Dynamics in Ultra-Long MD Trajectories. J. Am. Chem. Soc. 2011, 133 (45), 18413–18419. 10.1021/ja207470h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao Q.; Bowman G. R.; Huang X. H. Dynamics of an Intrinsically Disordered Protein Reveal Metastable Conformations That Potentially Seed Aggregation. J. Am. Chem. Soc. 2013, 135 (43), 16092–16101. 10.1021/ja403147m. [DOI] [PubMed] [Google Scholar]
- Wang W.; Cao S. Q.; Zhu L. Z.; Huang X. H. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8 (1), e1343 10.1002/wcms.1343. [DOI] [Google Scholar]
- Wang X. W.; Unarta I. C.; Cheung P. P. H.; Huang X. H. Elucidating molecular mechanisms of functional conformational changes of proteins via Markov state models. Curr. Opin. Struct. Biol. 2021, 67, 69–77. 10.1016/j.sbi.2020.10.005. [DOI] [PubMed] [Google Scholar]
- Noe F.; Tkatchenko A.; Muller K. R.; Clementi C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. 10.1146/annurev-physchem-042018-052331. [DOI] [PubMed] [Google Scholar]
- Litzinger F.; Boninsegna L.; Wu H.; Nuske F.; Patel R.; Baraniuk R.; Noe F.; Clementi C. Rapid Calculation of Molecular Kinetics Using Compressed Sensing. J. Chem. Theory Comput. 2018, 14 (5), 2771–2783. 10.1021/acs.jctc.8b00089. [DOI] [PubMed] [Google Scholar]
- Brandt S.; Sittel F.; Ernst M.; Stock G. Machine Learning of Biomolecular Reaction Coordinates. J. Phys. Chem. Lett. 2018, 9 (9), 2144–2150. 10.1021/acs.jpclett.8b00759. [DOI] [PubMed] [Google Scholar]
- Mardt A.; Pasquali L.; Wu H.; Noe F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 5. 10.1038/s41467-017-02388-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.; Sidky H.; Ferguson A. L. Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. J. Chem. Phys. 2019, 150 (21), 214114. 10.1063/1.5092521. [DOI] [PubMed] [Google Scholar]
- Cao S. Q.; Montoya-Castillo A.; Wang W.; Markland T. E.; Huang X. H. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. J. Chem. Phys. 2020, 153 (1), 014105. 10.1063/5.0010787. [DOI] [PubMed] [Google Scholar]
- Da L. T.; Pardo-Avila F.; Xu L.; Silva D. A.; Zhang L.; Gao X.; Wang D.; Huang X. H. Bridge helix bending promotes RNA polymerase II backtracking through a critical and conserved threonine residue. Nat. Commun. 2016, 7, 11244. 10.1038/ncomms11244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malmstrom R. D.; Kornev A. P.; Taylor S. S.; Amaro R. E. Allostery through the computational microscope: cAMP activation of a canonical signalling domain. Nat. Commun. 2015, 6, 7588. 10.1038/ncomms8588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanatta D. K.; Shukla D.; Lawrenz M.; Pande V. S. A network of molecular switches controls the activation of the two-component response regulator NtrC. Nat. Commun. 2015, 6, 7283. 10.1038/ncomms8283. [DOI] [PubMed] [Google Scholar]
- Shukla D.; Meng Y. L.; Roux B.; Pande V. S. Activation pathway of Src kinase reveals intermediate states as targets for drug design. Nat. Commun. 2014, 5, 3397. 10.1038/ncomms4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang H. L.; Sheong F. K.; Zhu L. Z.; Gao X.; Bernauer J.; Huang X. H. Markov State Models Reveal a Two-Step Mechanism of miRNA Loading into the Human Argonaute Protein: Selective Binding followed by Structural Re-arrangement. PLoS Comput. Biol. 2015, 11 (7), e1004404 10.1371/journal.pcbi.1004404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da L. T.; Wang D.; Huang X. H. Dynamics of Pyrophosphate Ion Release and Its Coupled Trigger Loop Motion from Closed to Open State in RNA Polymerase II. J. Am. Chem. Soc. 2012, 134 (4), 2399–2406. 10.1021/ja210656k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlitter J.; Engels M.; Kruger P. Targeted Molecular-Dynamics - a New Approach for Searching Pathways of Conformational Transitions. J. Mol. Graphics 1994, 12 (2), 84–89. 10.1016/0263-7855(94)80072-3. [DOI] [PubMed] [Google Scholar]
- Lee J.; Lee I. H.; Joung I.; Lee J.; Brooks B. R. Finding multiple reaction pathways via global optimization of action. Nat. Commun. 2017, 8, 15443. 10.1038/ncomms15443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss D. R.; Levitt M. Can. Morphing Methods Predict Intermediate Structures?. J. Mol. Biol. 2009, 385 (2), 665–674. 10.1016/j.jmb.2008.10.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okazaki K.; Koga N.; Takada S.; Onuchic J. N.; Wolynes P. G. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (32), 11844–11849. 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takada S.; Kanada R.; Tan C.; Terakawa T.; Li W. F.; Kenzaki H. Modeling Structural Dynamics of Biomolecular Complexes by Coarse-Grained Molecular Simulations. Acc. Chem. Res. 2015, 48 (12), 3026–3035. 10.1021/acs.accounts.5b00338. [DOI] [PubMed] [Google Scholar]
- Pan A. C.; Sezer D.; Roux B. Finding transition pathways using the string method with swarms of trajectories. J. Phys. Chem. B 2008, 112 (11), 3432–3440. 10.1021/jp0777059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L. Z.; Sheong F. K.; Cao S. Q.; Liu S.; Unarta I. C.; Huang X. H. TAPS: A traveling-salesman based automated path searching method for functional conformational changes of biological macromolecules. J. Chem. Phys. 2019, 150 (12), 124105. 10.1063/1.5082633. [DOI] [PubMed] [Google Scholar]
- Ravindra P.; Smith Z.; Tiwary P. Automatic mutual information noise omission (AMINO): generating order parameters for molecular systems. Mol. Syst. Des Eng. 2020, 5 (1), 339–348. 10.1039/C9ME00115H. [DOI] [Google Scholar]
- Perez-Hernandez G.; Paul F.; Giorgino T.; De Fabritiis G.; Noe F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139 (1), 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Lloyd S. P. Least-Squares Quantization in Pcm. IEEE Trans. Inf. Theory 1982, 28 (2), 129–137. 10.1109/TIT.1982.1056489. [DOI] [Google Scholar]
- Gonzalez T. F. Clustering to Minimize the Maximum Intercluster Distance. Theor Comput. Sci. 1985, 38 (2–3), 293–306. 10.1016/0304-3975(85)90224-5. [DOI] [Google Scholar]
- Liu S.; Zhu L. Z.; Sheong F. K.; Wang W.; Huang X. H. Adaptive Partitioning by Local Density-Peaks: An Efficient Density-Based Clustering Algorithm for Analyzing Molecular Dynamics Trajectories. J. Comput. Chem. 2017, 38 (3), 152–160. 10.1002/jcc.24664. [DOI] [PubMed] [Google Scholar]
- Huang X.; Yao Y.; Bowman G. R.; Sun J.; Guibas L. J.; Carlsson G.; Pande V. S. Constructing multi-resolution Markov State Models (MSMs) to elucidate RNA hairpin folding mechanisms. Pacific Symposium on Biocomputing. Pacific Symposium on Biocomputing 2009, 228–39. 10.1142/9789814295291_0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGibbon R. T.; Pande V. S. Variational cross-validation of slow dynamical modes in molecular kinetics. J. Chem. Phys. 2015, 142 (12), 124105. 10.1063/1.4916292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman M. I.; Porter J. R.; Sun X. Q.; Silva R. R.; Bowman G. R. Choice of Adaptive Sampling Strategy Impacts State Discovery, Transition Probabilities, and the Apparent Mechanism of Conformational Changes. J. Chem. Theory Comput. 2018, 14 (11), 5459–5475. 10.1021/acs.jctc.8b00500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doerr S.; Harvey M. J.; Noe F.; De Fabritiis G. HTMD: High-Throughput Molecular Dynamics for Molecular Discovery. J. Chem. Theory Comput. 2016, 12 (4), 1845–1852. 10.1021/acs.jctc.6b00049. [DOI] [PubMed] [Google Scholar]
- Voelz V. A.; Elman B.; Razavi A. M.; Zhou G. F. Surprisal Metrics for Quantifying Perturbed Conformational Dynamics in Markov State Models. J. Chem. Theory Comput. 2014, 10 (12), 5716–5728. 10.1021/ct500827g. [DOI] [PubMed] [Google Scholar]
- Zimmerman M. I.; Bowman G. R. FAST Conformational Searches by Balancing Exploration/Exploitation Trade-Offs. J. Chem. Theory Comput. 2015, 11 (12), 5747–5757. 10.1021/acs.jctc.5b00737. [DOI] [PubMed] [Google Scholar]
- Tian J. Q.; Wang L. Y.; Da L. T. Atomic resolution of short-range sliding dynamics of thymine DNA glycosylase along DNA minor-groove for lesion recognition. Nucleic Acids Res. 2021, 49 (3), 1278–1293. 10.1093/nar/gkaa1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng J.; Selvam B.; Shukla D. How do antiporters exchange substrates across the cell membrane? An atomic-level description of the complete exchange cycle in NarK. Structure 2021, 10.1016/j.str.2021.03.014. [DOI] [PubMed] [Google Scholar]
- Deuflhard P.; Huisinga W.; Fischer A.; Schutte C. Identification of almost invariant aggregates in reversible nearly uncoupled Markov chains. Linear Algebra Appl. 2000, 315 (1–3), 39–59. 10.1016/S0024-3795(00)00095-1. [DOI] [Google Scholar]
- Roblitz S.; Weber M. Fuzzy spectral clustering by PCCA plus: application to Markov state models and data classification. Adv. Data Anal Classi 2013, 7 (2), 147–179. 10.1007/s11634-013-0134-6. [DOI] [Google Scholar]
- Bowman G. R.; Meng L. M.; Huang X. H. Quantitative comparison of alternative methods for coarse-graining biological networks. J. Chem. Phys. 2013, 139 (12), 121905. 10.1063/1.4812768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W.; Liang T.; Sheong F. K.; Fan X. D.; Huang X. H. An efficient Bayesian kinetic lumping algorithm to identify metastable conformational states via Gibbs sampling. J. Chem. Phys. 2018, 149 (7), 072337. 10.1063/1.5027001. [DOI] [PubMed] [Google Scholar]
- Jain A.; Stock G. Identifying Metastable States of Folding Proteins. J. Chem. Theory Comput. 2012, 8 (10), 3810–3819. 10.1021/ct300077q. [DOI] [PubMed] [Google Scholar]
- Yao Y.; Cui R. Z.; Bowman G. R.; Silva D. A.; Sun J.; Huang X. H. Hierarchical Nystrom methods for constructing Markov state models for conformational dynamics. J. Chem. Phys. 2013, 138 (17), 174106. 10.1063/1.4802007. [DOI] [PubMed] [Google Scholar]
- Martini L.; Kells A.; Covino R.; Hummer G.; Buchete N. V.; Rosta E. Variational Identification of Markovian Transition States. Phys. Rev. X 2017, 7 (3), 031060. 10.1103/PhysRevX.7.031060. [DOI] [Google Scholar]
- Plattner N.; Doerr S.; De Fabritiis G.; Noe F. Complete protein-protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017, 9 (10), 1005–1011. 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Pardo-Avila F.; Unarta I. C.; Cheung P. P. H.; Wang G.; Wang D.; Huang X. H. Elucidation of the Dynamics of Transcription Elongation by RNA Polymerase II using Kinetic Network Models. Acc. Chem. Res. 2016, 49 (4), 687–694. 10.1021/acs.accounts.5b00536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Son C. Y.; Yethiraj A.; Cui Q. Cavity hydration dynamics in cytochrome c oxidase and functional implications. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (42), E8830–E8836. 10.1073/pnas.1707922114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da L. T.; Yu J. Base-flipping dynamics from an intrahelical to an extrahelical state exerted by thymine DNA glycosylase during DNA repair process. Nucleic Acids Res. 2018, 46 (11), 5410–5425. 10.1093/nar/gky386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sittel F.; Jain A.; Stock G. Principal component analysis of molecular dynamics: On the use of Cartesian vs. internal coordinates. J. Chem. Phys. 2014, 141 (1), 014111. 10.1063/1.4885338. [DOI] [PubMed] [Google Scholar]
- McGibbon R. T.; Husic B. E.; Pande V. S. Identification of simple reaction coordinates from complex dynamics. J. Chem. Phys. 2017, 146 (4), 044109. 10.1063/1.4974306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky H.; Chen W.; Ferguson A. L. High-Resolution Markov State Models for the Dynamics of Trp-Cage Miniprotein Constructed Over Slow Folding Modes Identified by State-Free Reversible VAMPnets. J. Phys. Chem. B 2019, 123 (38), 7999–8009. 10.1021/acs.jpcb.9b05578. [DOI] [PubMed] [Google Scholar]
- Feinberg E. N.; Pande V. S.; Farimani A. B.; Hernandez C. X. Kinetic Machine Learning Unravels Ligand-Directed Conformational Change of mu Opioid Receptor. Biophys. J. 2018, 114 (3), 56a–56a. 10.1016/j.bpj.2017.11.359. [DOI] [Google Scholar]
- Sang D. J.; Pinglay S.; Wiewiora R. P.; Selvan M. E.; Lou H. J.; Chodera J. D.; Turk B. E.; Gumus Z. H.; Holt L. J. Ancestral reconstruction reveals mechanisms of ERK regulatory evolution. eLife 2019, 8, e38805 10.7554/eLife.38805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwantes C. R.; Pande V. S. Improvements in Markov State Model Construction Reveal Many Non-Native Interactions in the Folding of NTL9. J. Chem. Theory Comput. 2013, 9 (4), 2000–2009. 10.1021/ct300878a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barros E. P.; Demir O.; Soto J.; Cocco M. J.; Amaro R. E. Markov state models and NMR uncover an overlooked allosteric loop in p53. Chem. Sci. 2021, 12 (5), 1891–1900. 10.1039/D0SC05053A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng S. J.; Wang X. W.; Zhang L.; He S. S.; Zhao X. S.; Huang X. H.; Chen C. L. Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models. Proc. Natl. Acad. Sci. U. S. A. 2020, 117 (36), 21889–21895. 10.1073/pnas.2002971117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardt A.; Pasquali L.; Noé F.; Wu H.. Deep learning Markov and Koopman models with physical constraints. In Proceedings of The First Mathematical and Scientific Machine Learning Conference; Jianfeng L., Rachel W., Eds.; PMLR: Proceedings of Machine Learning Research, 2020; Vol. 107, pp 451–475.
- Unarta I. C.; Cao S.; Kubo S.; Wang W.; Cheung P. P.-H.; Gao X.; Takada S.; Huang X. Role of bacterial RNA polymerase gate opening dynamics in DNA loading and antibiotics inhibition elucidated by quasi-Markov State Model. Proc. Natl. Acad. Sci. U. S. A. 2021, 118 (17), e2024324118 10.1073/pnas.2024324118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai S. T.; Kuo E. J.; Tiwary P. Learning molecular dynamics with simple language model built upon long short-term memory neural network. Nat. Commun. 2020, 11 (1), 5115. 10.1038/s41467-020-18959-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinyals O.; Babuschkin I.; Czarnecki W. M.; Mathieu M.; Dudzik A.; Chung J.; Choi D. H.; Powell R.; Ewalds T.; Georgiev P.; Oh J.; Horgan D.; Kroiss M.; Danihelka I.; Huang A.; Sifre L.; Cai T.; Agapiou J. P.; Jaderberg M.; Vezhnevets A. S.; Leblond R.; Pohlen T.; Dalibard V.; Budden D.; Sulsky Y.; Molloy J.; Paine T. L.; Gulcehre C.; Wang Z. Y.; Pfaff T.; Wu Y. H.; Ring R.; Yogatama D.; Wunsch D.; McKinney K.; Smith O.; Schaul T.; Lillicrap T.; Kavukcuoglu K.; Hassabis D.; Apps C.; Silver D. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575 (7782), 350. 10.1038/s41586-019-1724-z. [DOI] [PubMed] [Google Scholar]
- Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser L.; Polosukhin I. Attention Is All You Need. Adv. Neur. In 2017, 30, 6000–6010. [Google Scholar]
- He K. M.; Zhang X. Y.; Ren S. Q.; Sun J. Deep Residual Learning for Image Recognition. Proc. Cvpr Ieee 2016, 770–778. 10.1109/CVPR.2016.90. [DOI] [Google Scholar]
- Sittel F.; Stock G. Perspective: Identification of collective variables and metastable states of protein dynamics. J. Chem. Phys. 2018, 149 (15), 150901. 10.1063/1.5049637. [DOI] [PubMed] [Google Scholar]
- Glielmo A.; Husic B. E.; Rodriguez A.; Clementi C.; Noé F.; Laio A. Unsupervised Learning Methods for Molecular Simulation Data. Chem. Rev. 2021, 10.1021/acs.chemrev.0c01195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J.-h.; Wang W.; Yu Y.-q.; Gu H.-l.; Huang X. Clustering algorithms to analyze molecular dynamics simulation trajectories for complex chemical and biological systems. Chin. J. Chem. Phys. 2018, 31 (4), 404–420. 10.1063/1674-0068/31/cjcp1806147. [DOI] [Google Scholar]
- Husic B. E.; Noé F. Deflation reveals dynamical structure in nondominant reaction coordinates. J. Chem. Phys. 2019, 151 (5), 054103. 10.1063/1.5099194. [DOI] [Google Scholar]
- Noe F.; Wu H.; Prinz J. H.; Plattner N. Projected and hidden Markov models for calculating kinetics and metastable states of complex molecules. J. Chem. Phys. 2013, 139 (18), 184114. 10.1063/1.4828816. [DOI] [PubMed] [Google Scholar]
- Scherer M. K.; Trendelkamp-Schroer B.; Paul F.; Perez-Hernandez G.; Hoffmann M.; Plattner N.; Wehmeyer C.; Prinz J. H.; Noe F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11 (11), 5525–5542. 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- Schutte C.; Noe F.; Lu J. F.; Sarich M.; Vanden-Eijnden E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134 (20), 204105. 10.1063/1.3590108. [DOI] [PubMed] [Google Scholar]
- Lemke O.; Keller B. G. Density-based cluster algorithms for the identification of core sets. J. Chem. Phys. 2016, 145 (16), 164104. 10.1063/1.4965440. [DOI] [PubMed] [Google Scholar]