Phenotypic Plasticity Contributes to Maize Adaptation and Heterosis

Abstract

Plant phenotypic plasticity describes altered phenotypic performance of an individual when grown in different environments. Exploring genetic architecture underlying plant plasticity variation may help mitigate the detrimental effects of a rapidly changing climate on agriculture, but little research has been done in this area to date. In the present study, we established a population of 976 maize F₁ hybrids by crossing 488 diverse inbred lines with two elite testers. Genome-wide association study identified hundreds of quantitative trait loci associated with phenotypic plasticity variation across diverse F₁ hybrids, the majority of which contributed very little variance, in accordance with the polygenic nature of these traits. We identified several quantitative trait locus regions that may have been selected during the tropical-temperate adaptation process. We also observed heterosis in terms of phenotypic plasticity, in addition to the traditional genetic value differences measured between hybrid and inbred lines, and the pattern of which was affected by genetic background. Our results demonstrate a landscape of phenotypic plasticity in maize, which will aid in the understanding of its genetic architecture, its contribution to adaptation and heterosis, and how it may be exploited for future maize breeding in a rapidly changing environment.

Introduction

Plants are sessile, and thus in order to survive and reproduce under varying levels of moisture, temperature, light, and pathogens, they often modify metabolic, morphological, defensive, and phenological traits (Sultan 2000; Des Marais et al. 2013; Donohue 2013). The differential performance responses of a genotype across environmental gradients is depicted as phenotypic plasticity, as a joint result of overall environmental effect and the sensitivity of gene effects across environments (Bradshaw 1965; Des Marais et al. 2013). The variation of phenotypic plasticity across different genotypes is attributable to the effect of the genotype–environment interaction (G × E) (Pigliucci 2005; Kusmec et al. 2018; Arnold et al. 2019). Phenotypic plasticity has been shown to play a crucial role in the expression of phenotypic variation of numerous traits measured in different environments for both an individual plant and an entire population (Pigliucci 2005; Kusmec et al. 2018). Plant breeders may work to reduce plasticity in order to stabilize the performance of cultivars across environments, particularly in an attempt to sustain high grain yield of elite cultivars. However, an increase in plasticity may enable cultivars to adapt to fluctuating environments, optimizing crop performance under favorable conditions while alleviating performance decreases due to adverse climate changes (Nicotra et al. 2010; Kusmec et al. 2018). To feed more than 9 billion people by 2050, increasing crop yield in the face of extreme climate change must be the primary breeding goal (Ehrlich and Harte 2015). Exploring the pattern of crop phenotypic plasticity and dissecting its genetic basis may be one as-yet untried method to boost crop production, nutritional quality, and climate adaptation.

Studies exploring plant phenotypic plasticity using quantitative and population genetic approaches are available (Wu 1998; Kikuchi et al. 2017; Kusmec et al. 2017; Laitinen and Nikoloski 2019) and appear to suggest that the improvement of modern temperate maize has reduced G × E (Gage et al. 2017). This may indicate that phenotypic plasticity is heritable and has been under selection during the breeding processes. However, which traits were selected via phenotypic plasticity and whether this selection co-occurred with that for genetic values is unclear. Three hypotheses (overdominance, pleiotropy, and epistasis) have been proposed to interpret the genetic architecture of phenotypic plasticity. The overdominance model suggests that a genotype with higher heterozygosity has less phenotypic plasticity, and heterozygous individuals perform more stably when exposed to different environments (Scheiner 1993; Pigliucci 2005). The pleiotropic model states that specific genes having differentially sensitive environmental effects on phenotypic changes lead to phenotypic plasticity (Wu 1998). The epistatic model argues that genes controlling phenotypic plasticity are distinct from, but interact with, genes responsible for the genetic values across environments (Kusmec et al. 2017). Several studies have shown that pleiotropic and epistatic quantitative trait loci (QTLs) may play crucial roles on phenotypic plasticity in maize inbred populations (Kusmec et al. 2017; Li et al. 2019). What genetic mechanism regulates plasticity variation in hybrid populations had not yet been tested.

Maize (Zea mays L.) is one of the most important and productive staple crops, and is employed as food, livestock feed, and biofuels worldwide. Maize contains abundant phenotypic and genotypic diversity (Schnable et al. 2009; Yan et al. 2011) and is thus able to adapt to new environments, including the major migration from tropical to temperate regions. This migration greatly restructured metabolic, morphological, defensive, and phenological traits (Camus-Kulandaivelu et al. 2006; Liu et al. 2015; Huang et al. 2018; Xu et al. 2019; Deng et al. 2020). In past decades, maize grain production has increased more than 8-fold, largely due to maize hybrid breeding since the 1930s, as hybrids usually display greater fitness and robustness relative to inbred parent lines (Duvick 2001; Schnable and Springer 2013). We know little about how hybrid performance interacts with environmental changes, and we must consider this in order to improve the broad-spectrum adaptation of future maize hybrids.

In the present study, we developed a diverse maize F₁ population of ∼1,000 hybrids by crossing two elite testers (Zheng58 and Mo17), with 488 inbred lines, a subset of an association mapping population (Yang et al. 2011). With sequencing providing a high-density scan of genomic variants and data from 12 agronomic traits measured in 6–11 environments, we expect to address the following questions: 1) How does phenotypic plasticity contribute to trait variation under each specific environment? 2) What are the genetic bases underlying phenotypic plasticity? 3) How does plasticity participate in maize postdomestication adaptation? 4) What is the relationship of phenotypic plasticity with maize heterosis?

Results

Phenotypic Plasticity Response Patterns over Environments

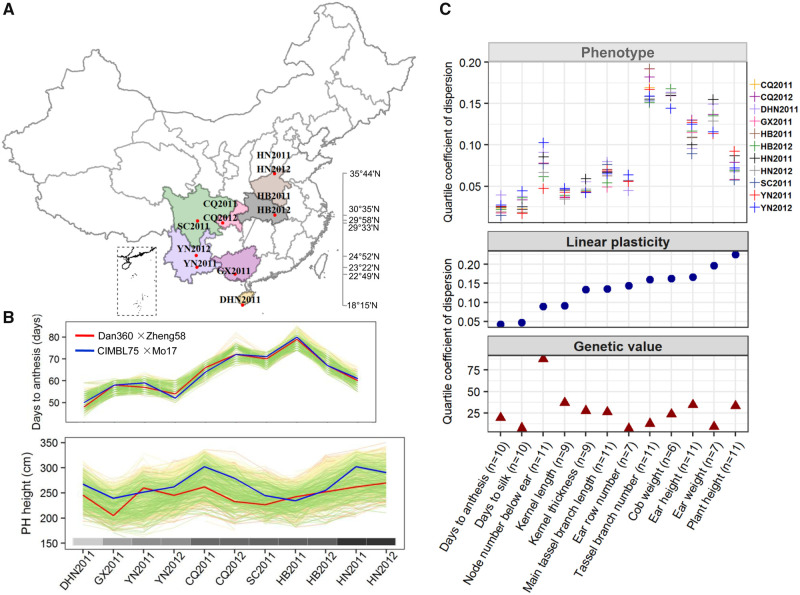
We investigated 12 morphological and agronomic traits in 976 hybrids in five to eight geographic locations including Sanya (18°15′N), Nanning (22°49′N), Honghe (23°22′N), Kunming (24°52′N), Yaan (29°58′N), Chongqing (29°33′N), Wuhan (30°35′N), and Hebi (35°44′N) in China over 2 years (2011 and 2012), totaling 6–11 environments per trait (fig. 1A and supplementary table 1, Supplementary Material online). The hybrid population and the parent individuals exhibited high phenotypic variability for each trait, and population variation of each trait varied between environments (supplementary table 2 and figs. 1–5, Supplementary Material online), indicating diverse plasticity between different genotypes. The pattern of phenotypic plasticity differed for each trait (fig. 1B and supplementary fig. 6, Supplementary Material online). We present two traits as examples (days to anthesis and plant height) to illustrate the distinct patterns of phenotypic plasticity. For days to anthesis, all individuals have a similar trend with little crossover interaction with environments of increasing latitude. In contrast, plant height exhibited complicated phenotypic plasticity over environments with frequent crossover interactions among different genotypes (fig. 1B).

Fig. 1.

Phenotypic plasticity of 12 agronomic traits in hybrid maize. (A) The 11 planting environments spanning eight latitude-based locations across China. (B) Phenotypic variability of each hybrid for days to anthesis and plant height responding to environmental gradients. Two hybrids as examples, Dan360 × Zheng58 and CIMBL75 × Mo17, flowered synchronously especially in the most northeastern environments, and the colored bar indicates the latitude change of all location sites. (C) The quartile coefficient of dispersion of 12 traits. The upper panel indicates the population variation (measured by quartile coefficient of dispersion) of the measured phenotype in different environments. The number of environments for each trait is indicated by the value within the parentheses. By the FWR model, the phenotype across environments is resolved into linear plasticity and genetic value for each hybrid. The middle panel shows the population variation of linear plasticity, whereas the bottom panel shows the population variation of genetic values across 976 F₁ hybrids.

To further quantify the variability in plasticity, all phenotypic values measured in multiple environments on the 976 F₁ hybrids were used as inputs for the Bayesian Finlay-Wilkinson regression model (FWR) on each trait (see Materials and Methods). The FWR partitions an individual’s phenotype into a genotypic main effect (hereafter called genetic value), a regression slope, and a residual value. The slope measures the linear response of a genotype to an environment, relative to the rest of the genotypes in the population, hereafter called linear plasticity. At the environment-wise population level, on an average, only 30.8% (ranging from 1.8% to 74.9%) of the overall phenotypic variation was explained by genetic effects. With the exception of ear row number (74.9%) and kernel thickness (68.7%), the majority of trait variation was due to the variance of linear plasticity (supplementary table 3, Supplementary Material online), which may be described by the environmental and G × E effects.

Taken one trait at a time, tassel branch number consistently exhibited the highest variation within the population in all environments (fig. 1C, top panel and supplementary table 2, Supplementary Material online), which may be due to the high variation of linear plasticity rather than genetic value (fig. 1C, middle and bottom panel). In contrast, node number below ear exhibited a relatively low linear plasticity variation (raking tenth overall) but displayed a high phenotypic variation (ranking fifth), which could be attributable to the highest genetic variation (where it ranked first; fig. 1C). Two flowering traits, days to anthesis and days to silk, displayed the lowest phenotypic variation, as both genetic and linear plasticity variances contributed very little to these traits (fig. 1C). On the other hand, the dramatic phenotypic differences in plant height and ear weight for hybrids grown in different environments would be due to the largest linear plasticity variation (fig. 1C), hinting at the complexity of manipulating response in grain production to changing growing environments.

The Genetic Architecture of Genetic Value and Linear Plasticity of 12 Agronomic Traits

In the maize hybrid population, genome-wide association study (GWAS) was performed for both the genetic value and the linear plasticity of 12 agronomic traits using the mixed linear model (see Materials and Methods). A total of 388 QTLs were detected influencing genetic variation, whereas 66 QTLs were found to control the linear plasticity variation (table 1 and supplementary table 4 and figs. 7 and 8, Supplementary Material online). We compared these QTLs with previously published QTLs for genetic and linear plasticity variation of 12 agronomic traits (supplementary table 4, Supplementary Material online). About 39% of the present QTLs overlapped (within 2 Mb up- and downstream) with those from eight previous genetic variation publications (Chen et al. 2014; Peiffer et al. 2014; Li et al. 2016; Pan et al. 2016; Xiao et al. 2016; Liu, Huang, et al. 2017; Xu et al. 2017; Zhang et al. 2017). A further 8.8% overlapped with two articles related to linear plasticity variation (Kusmec et al. 2017; Li et al. 2019). The low consistency of the QTLs for linear plasticity variation may result from the limited number of published studies, and the unstable nature of linear plasticity. In the present study, for each trait, 7–57 QTLs for genetic variation were detected compared with 1–18 QTLs for linear plasticity variation. On an average, 32 QTLs were detected for the genetic variation per trait, approximately six times more than was detected for the linear plasticity variation (5.5 QTLs per trait). We merged detected QTLs for genetic variation and linear plasticity variation per trait to identify consensus genomic regions (or cQTL) that affect trait variation globally, obtaining 16–59 cQTLs per trait (supplementary table 4, Supplementary Material online).

Table 1.

Summary of Genetic Architecture of the Genetic Value and Linear Plasticity for 12 Agronomic Traits.

Trait	Linear Plasticity					Genetic Value
	N a	A b	PVEa (%)c	D d	PVEd (%)e	N a	A b	PVEa (%)c	D d	PVEd (%)e
Days to anthesis	2	−0.00024 ± 0.011	1.2 ± 0.90	0.00030 ± 0.0060	0.37 ± 0.34	44	−0.027 ± 0.32	3.1 ± 3.1	0.025 ± 0.21	0.77 ± 0.67
Days to silk	2	−0.0041 ± 0.014	2.2 ± 1.2	0.00093 ± 0.0078	0.70 ± 0.76	20	0.20 ± 0.59	9.9 ± 6.0	−0.048 ± 0.32	3.0 ± 4.0
Node number below ear	9	0.0043 ± 0.051	9.4 ± 4.2	0.023 ± 0.050	7.0 ± 5.2	41	−0.010 ± 0.065	1.1 ± 0.79	0.020 ± 0.050	0.12 ± 0.12
Kernel length	3	0.0085 ± 0.040	3.5 ± 2.2	0.0040 ± 0.019	0.85 ± 1.0	16	0.019 ± 0.10	7.0 ± 4.8	0.0050 ± 0.050	2.1 ± 2.7
Kernel thickness	1	0.0084 ± 0.020	0.36 ± 0.32	−0.0060 ± 0.022	0.27 ± 0.57	50	0.030 ± 0.090	15 ± 7.1	−0.0070 ± 0.049	6.6 ± 5.8
Main tassel branch length	1	−0.0020 ± 0.059	3.7 ± 1.8	0.014 ± 0.040	2.1 ± 1.6	36	0.022 ± 1.1	14 ± 7.4	0.13 ± 0.69	6.7 ± 5.1
Ear row number	2	0.0050 ± 0.040	0.72 ± 0.67	0.0047 ± 0.033	0.25 ± 0.28	57	0.020 ± 0.32	10 ± 5.6	0.086 ± 0.19	4.7 ± 4.1
Tassel branch number	18	−0.028 ± 0.050	1.7 ± 1.5	0.019 ± 0.026	0.18 ± 0.22	31	−0.19 ± 0.24	1.8 ± 1.9	0.11 ± 0.16	0.23 ± 0.22
Cob weight	2	−0.022 ± 0.057	1.9 ± 1.4	0.015 ± 0.040	0.52 ± 0.57	41	−0.27 ± 0.84	6.1 ± 3.9	0.11 ± 0.56	1.9 ± 1.8
Ear height	14	0.0010 ± 0.11	11 ± 5.2	0.06 ± 0.10	7.6 ± 6.2	23	0.078 ± 2.7	11 ± 5.0	1.3 ± 2.1	6.5 ± 5.2
Ear weight	3	−0.010 ± 0.040	0.25 ± 0.50	0.018 ± 0.043	0.22 ± 0.38	22	−1.8 ± 4.2	5.4 ± 3.4	0.80 ± 2.7	1.8 ± 1.7
Plant height	9	0.040 ± 0.19	24 ± 6.2	0.14 ± 0.15	19 ± 13	7	0.22 ± 3.5	11.2 ± 3.1	3.7 ± 4.2	11 ± 7.6

^aQTL number for genetic value and linear plasticity variation before combining them.

^bThe average of additive effect of all cQTLs for each trait (mean ± SD).

^cThe average of phenotypic variation explained of all cQTLs for each trait using additive model (mean ± SD).

^dThe average of dominance effect of all cQTLs for each trait (mean ± SD).

^eThe average of phenotypic variation explained of all cQTLs for each trait using dominance model (mean ± SD).

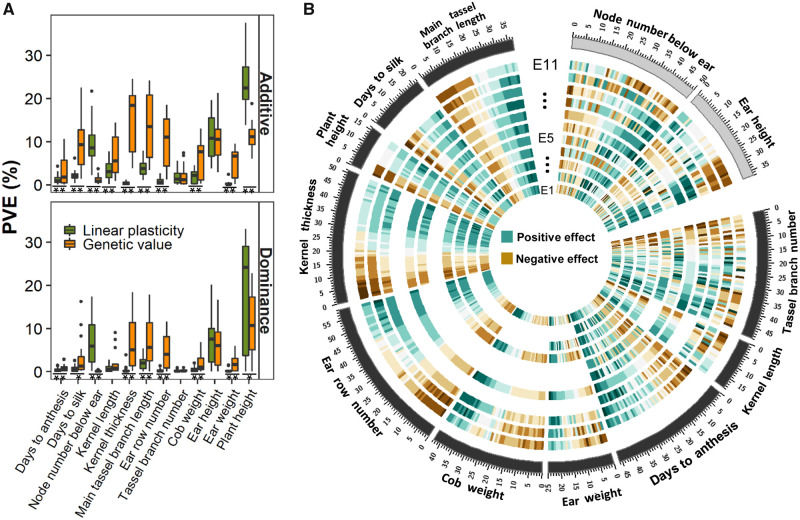
For each trait, we computed the phenotypic variation explained (PVE) per cQTL for genetic value and linear plasticity under additive and dominance models (see Materials and Methods). The average PVE of genetic value was significantly higher than that of linear plasticity under both additive (7.6% vs. 4.0%; P = 4.5E-18) and dominance (3.4% vs. 2.5%; P = 0.004) models. In the additive model, a total of 135 major QTLs contributing more than 10% of the variance per QTL were found to affect the genetic values of main tassel branch length, ear height, ear row number, kernel thickness, and plant height. Only 59 major QTLs appeared to influence linear plasticity of node number below ear, ear height, and plant height (fig. 2A). The dominance model discovered 55 and 35 major QTLs that influenced the genetic value and linear plasticity of several traits, respectively (fig. 2A). Comparing additive and dominance models, we found linear plasticity of five traits (node number below ear, kernel thickness, ear weight, ear height, and plant height) had similar QTL variance, but plant height was the only trait that exhibited similar QTL variance on the genetic value. This suggests that the genes controlling linear plasticity variation were more likely to function interactively in both additive and dominant fashion, but not genes controlling genetic value (fig. 2A).

Fig. 2.

The genetic mechanisms of linear plasticity and genetic value of 12 traits. (A) The phenotypic variation explained by the cQTLs detected for the 12 traits. For each trait, all cQTLs for linear plasticity and genetic value under additive and dominance coding were merged. ** and * indicate significant difference between groups under Student’s t-test (P < 0.01 and P < 0.05, respectively). (B) The dynamic effects of cQTLs for the 12 traits in response to environments. Under each environment, the effect of a QTL was calculated as half the difference of the trait value between major and minor homozygotes. The outer circle denotes a trait with low proportion of QTL effect sign changes (black), and a trait with high proportion of QTL effect sign changes (gray). The internal circles displayed the heatmap of QTL effects across environments, with a layer per environment, according to latitude gradients from inner to outer (E1–E11) including DHN2011 (18°15′N), GX2011 (22°49′N), YN2011 (23°22′N), YN2012 (24°52′N), SC2011 (29°58′N), CQ2011 (29°33′N), CQ2012 (29°33′N), HB2011 (30°35′N), HB2012 (30°35′N), HN2011 (35°44′N), and HN2012 (35°44′N) as shown in figure 1A.

To determine if linear plasticity is due to antagonistic pleiotropy or differential sensitivity, we estimated the effect spectrum of detected QTLs across environments (see Materials and Methods). On an average, the QTL effects changed eight times across environments, ranging from 1.3 times for kernel thickness to 29.4 times for kernel length (fig. 2B). For ten traits (main tassel branch length, days to silk, days to anthesis, plant height, kernel thickness, ear row number, ear weight, cob weight, kernel length, and tassel branch number) more than 70% of the QTLs appeared to have effects that changed in magnitude rather than in sign over ∼75% of the total environments. An average of 55% of the QTLs had positive effects in that the minor allele increased the phenotype, which ranged from 35.7% for cob weight to 71.6% for tassel branch number (supplementary table 5, Supplementary Material online). These results indicate that linear plasticity of these ten traits reacting to different environments was mainly due to differential sensitivity of QTL effects, whereas for two traits (node number below ear and ear height), the pattern of QTL effects was in sign change, and thus may be attributed to antagonistic pleiotropy (fig. 2B).

The GWAS results illustrated that the genetic architecture underlying linear plasticity of most traits is complex and highly polygenic (supplementary table 6, Supplementary Material online). More than half of the QTLs controlling linear plasticity of ear and plant height had major effects, but the other ten traits had a large proportion of polygenic QTLs (supplementary table 6, Supplementary Material online). The fact that the majority of QTL effects responsible for ten of the 12 traits varied in magnitude and not in sign across environments may indicate that many loci of small effects were favored, since they can rapidly react to changing environments. These results are consistent with previous reports that polygenic traits would reach new adaptation optima by modifying allele frequency at multiple loci to fine-tune the phenotype to fit environmental changes (Zan et al. 2017). For plasticity variation of node number below ear, ear height, ear weight, kernel thickness, and plant height, the additive and dominance effects were comparable, suggesting that heterosis for linear plasticity variation exists in hybrids.

Modeling Linear Plasticity QTL Effect to Reconstruct Individual Phenotype

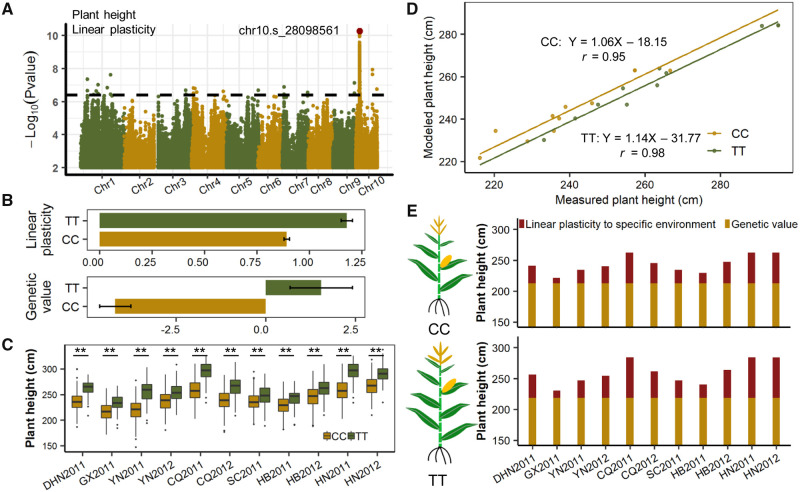
The present study provides an opportunity for us to dissect and predict how the phenotype of a genotype is shaped in specific environments by manipulating relative contributions of genetic component and linear plasticity. We used plant height (a heavily plastic trait) as an example. GWAS detected a major QTL on chromosome 10 that significantly influences the linear plasticity of plant height (P = 5.3E-11; fig. 3A). At this QTL (peak SNP chr10.s_28098561), the TT genotype conferred significantly higher plant height genetic values, and more environmental plasticity, than did the CC genotype (fig. 3B). The peak SNP was stable and identified across all 11 environments, but was associated with phenotypic variances ranging from 5.5% to 33.9% per environment (fig. 3C), which is reasonable for a highly plastic QTL (fig. 2B). Focusing on this QTL, the FWR model resolved plant height across environments into genetic value and linear plasticity by substituting a QTL genotype for the overall genotypes (see Materials and Methods). For each QTL genotype (TT or CC), the mean plant height of the hybrids in each of the 11 environments was predicted by the FWR model. The predicted plant height for the TT genotype exhibited strong correlation (r = 0.98) and low mean standard error (MSE = 13.04) to the measured plant height; this strong linear trend was also observed for the CC genotype (r = 0.95, fig. 3D). These results suggest that adequately modeling phenotypic plasticity can elevate the goodness of fit and the predictability of trait performance from genotype.

Fig. 3.

Phenotypic reconstruction by modeling genotype and environment. (A) GWAS of linear plasticity of plant height. The red dot indicates the peak SNP chr10.s_28098561 for the QTL being modeled. (B) The effects of the QTL on genetic value and linear plasticity variation of plant height. (C) The series of QTL effects on plant height across 11 environments. ** and * indicate significant difference between contrasting genotypes under Student’s t-test (P < 0.01 and P < 0.05, respectively). (D) The relationship between the measured and modeled plant height by the QTL-based FWR model. (E) The reconstruction of plant height of hybrids under different environments. For the hybrids with contrasting genotypes (CC and TT for chr10.s_28098561), in each environment, the height of stacked bars indicates the genetic value and the performance of linear plasticity for a specific environment. Linear plasticity to specific environment was the product of linear plasticity and environmental effect. The 11 environments were shown in figure 1A.

Based on the genetic value and linear plasticity estimated by the FWR model for this QTL, we can interpret varying plant height in different environments. The difference in genetic values between TT and CC was 5.8 cm regardless of environmental changes. Nevertheless, linear plasticity changed dramatically in different environments for QTL genotypes, from the negative impact that decreased height by 6.0 cm for the CC genotype in CQ2011 (29°33′N) to the positive influence that increased height by 10.0 cm for the TT genotype in CQ2011 (29°33′N) (fig. 3E). This suggests that linear plasticity may offer flexible opportunities for plants to adapt to diverse environments.

Phenotypic Plasticity Was Subjected to Selection during the Maize Tropical-Temperate Adaptation

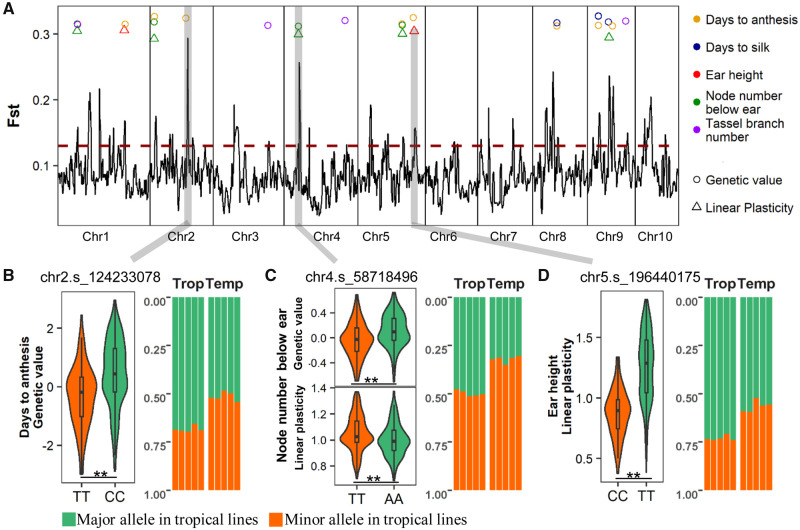
Maize underwent extensive phenotypic changes during adaptation to the diverse environments encountered when migrating from tropical to temperate regions. We can now address the question of whether phenotypic plasticity may have participated in the adaptation process. Based on genome-wide F_ST analysis, we identified 37 candidate genomic regions that were potentially under selection, by comparing allelic frequency between tropical and temperate maize (with a permutation-based threshold of F_ST = 0.13; fig. 4A). Of these selected regions, 79% were also detected in three previously published selection studies (Hufford et al. 2012; Jiao et al. 2012; Liu et al. 2015) (supplementary table 7, Supplementary Material online). According to Q_ST–F_ST analysis, the genetic value of four traits (node number below ear, tassel branch number, days to anthesis, and days to silk), and the linear plasticity of two traits (node number below ear and ear height), were found to be involved in maize adaptation to temperate regions. These traits all exhibited significant differences between temperate and tropical maize in either genetic value or linear plasticity (supplementary fig. 9A, Supplementary Material online), and divergent phenotypic patterns across environmental gradients (supplementary fig. 9B, Supplementary Material online). For genetic values and plasticity related to adaptation, there were 27 associated QTLs located in 13 of the 37 candidate selected regions (fig. 4A and supplementary table 7, Supplementary Material online).

Fig. 4.

Genomic regions responsible for adaptation-related traits as determined by selection analysis. (A) Genomic F_ST distribution between tropical and temperate maize. In the selection regions (F_ST > 0.13), the circles indicate the existence of detected QTLs of the genetic value, whereas the triangles indicate the existence of QTLs for linear plasticity. The different colors of each circle or triangle represent different traits that related to adaptation. (B–D) Three cases of selected regions that affect the genetic value and linear plasticity. The left panel indicates the effect of QTL, and the right panel indicates the allelic frequency ratio of SNPs within QTL regions, between tropical and temperate maize. The differences between pairs of genotypes were tested based on Student’s t-test (**P < 0.01).

We found a QTL affecting genetic value of days to anthesis that mapped to a region in the middle of chromosome 2 (123–132 Mb), which may be under selection (F_ST = 0.21 on an average). At this QTL (whose peak is at chr2.s_124233078), hybrids with the TT genotype flowered significantly earlier than those with the CC genotype (−0.33 vs. 0.45, P = 7.0E-10). In addition, the individuals originating from temperate environments were largely enriched with the early flowering allele (TT), relative to the tropical individuals (frequency of 0.49 for temperate and 0.31 for tropical) (fig. 4B). Our data and previous research suggest that early flowering associated mutations have accumulated in temperate maize as it evolved a reduced sensitivity to photoperiod under long-day growing regions. Examples of early flowering mutations can be found in ZmCCT9, ZmCCT10, and ZCN8 (Yang et al. 2013; Guo et al. 2018; Huang et al. 2018).

Another selected region (chr4: 48–61 Mb; F_ST = 0.19) was found to map to a QTL (peak at chr4.s_58718496) influencing the genetic value (−0.036 vs. 0.11, P = 1.3E-6) and linear plasticity (1.05 vs. 1, P = 6.4E-4) of node number below ear. At this QTL, the TT genotype, which is enriched in temperate hybrids, improved the genetic value of lodging resistance by lowering ear placement on the plant. At the same time, these hybrids have a more sensitive phenotypic response to changes in environment (fig. 4C). Interestingly, there was a selected region (188–197 Mb) on chromosome 5 that significantly influenced the linear plasticity of ear height (P = 9.4E-23), but not the genetic value (fig. 4D). The CC genotype, which conferred lower linear plasticity of ear height, has been significantly enriched in temperate maize compared with tropical (frequency of 0.43 for temperate vs. 0.27 for tropical). This also optimizes plant architecture for increased lodging resistance and machine harvesting, a strong seletion target in modern maize improvement. The selection for the CC genotype for linear plasticity at this ear height QTL can aid stabilization of the beneficial phenotype across multiple temperate growing regions.

The Genetic Architecture of Linear Plasticity Underlying Heterosis in Maize

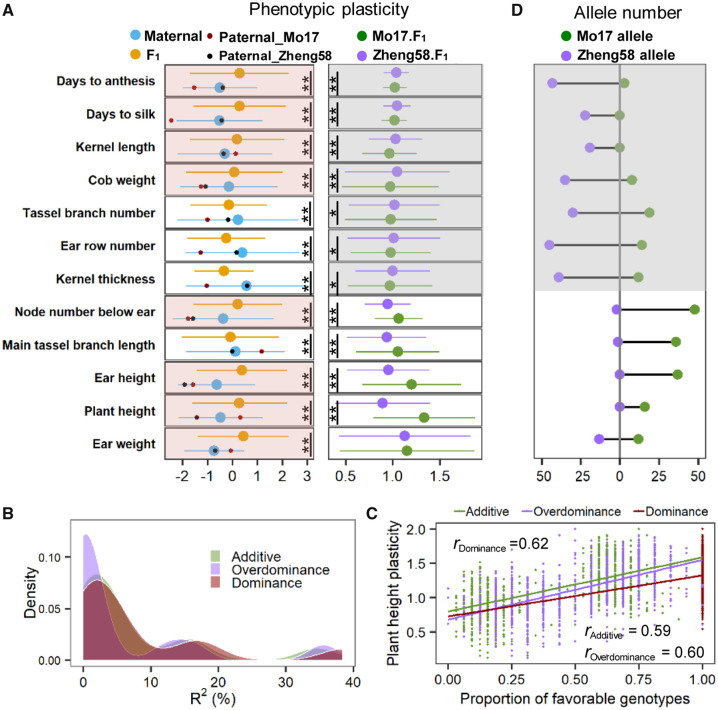
Plant hybrid vigor, or heterosis, is the phenomenon that a hybrid plant outperforms its parental inbred lines in biomass, yield, or other traits (Schnable and Springer 2013). Past heterosis studies report on how hybridization improves the genetic (or breeding) values of inbred lines in a nonadditive manner (Riedelsheimer et al. 2012; Chen 2013), which is illustrated in the present data set as well (supplementary fig. 10, Supplementary Material online). However, whether and how heterosis is coordinated by phenotypic plasticity in addition to genetic values is an interesting question. In the present study, the ∼1,000 F₁ hybrids exhibited significantly different phenotypic plasticity to environments, compared with the 488 maternal inbred lines and two paternal tester lines for all traits (fig. 5A). This suggests that hybridization reshaped phenotypic plasticity in this diverse maize population, which we will call plasticity heterosis.

Fig. 5.

The genetic architecture of plasticity heterosis in maize. (A) Heterosis of phenotypic plasticity and its relevance to genetic backgrounds. The left panel shows phenotypic plasticity between the parental inbred lines and F₁ hybrids for the 12 traits, which was measured as variance among environments per individual. The red shadow indicates the traits that exhibited higher plasticity (more phenotypically sensitive to environments) in hybrids compared with plasticity of the maternal inbred lines. The dots represent the variance among environments for the paternal inbred lines (black for Zheng58 and red for Mo17). The right panel compares the phenotypic plasticity between the two sets of F₁ populations crossed with Zheng58 and Mo17, which was measured as the linear plasticity per hybrid estimated by the FWR model. The dark shadow indicates the traits that have higher linear plasticity in the Zheng58 background. **P < 0.01, *P < 0.05. (B) The distribution of R² calculated by regressing accumulated favorable genotypes per hybrid with the linear plasticity for the 12 traits. The colors of density area indicate three heterosis models: additive, dominance, and overdominance model. (C) The relationship between proportion of favorable genotypes and linear plasticity of plant height under the additive, dominance, and overdominance model. (D) The number of favorable alleles for plasticity of the 12 traits obtained via pyramiding of favorable alleles of testers. For a given QTL, the allele that resulted in higher linear plasticity was defined as the favorable allele. Under the dominance model, the favorable homozygote and heterozygote are both counted as favorable genotypes; for the additive model, the heterozygote is defined as half a favorable genotype, and for the overdominance model, the heterozygote is the only favorable genotype. The gray shadow indicates the traits for which Zheng58 harbored more favorable alleles than Mo17.

The plasticity heterosis presented different patterns for different traits. For example, for ear weight, the F₁ hybrids appeared to be more sensitive to environmental alteration than their parental inbred lines; in contrast, ear row number had the most stable performance across environments in F₁ hybrids but not parental inbred lines (fig. 5A). We compared F₁ hybrids grouped by paternal tester (Zheng58 and Mo17) for the FWR-based linear phenotypic plasticity to environments, and found that seven traits measured in hybrids formed by crossing with Zheng58 (the Reid background tester) were more environmentally sensitive than they were measured in hybrids formed by crossing with Mo17 (the Lancaster background tester). The rest of the traits, however, were more environmentally stable (fig. 5A). These results suggest that the genetic background is critical to the expression of plasticity heterosis.

To test the use of detected QTLs to predict linear plasticity, three heterosis models were assessed (see Materials and Methods). Under the additive model, the variation in linear plasticity can be explained by an average of 7.2% (with a range of 0.05–34.6%) of the detected QTLs per trait, and the overdominance model only explained 5.8% (range 0.002–35.6%) of the plasticity variance. In comparison, the dominance model, assuming favorable alleles can completely compensate for unfavorable effects in the heterozygote, performed slightly better than the additive model and accounted for 7.8% (range 0.07–38.4%) of the plasticity variance (fig. 5B). For instance, the number of favorable alleles per hybrid was significantly correlated with linear plasticity of plant height in the dominance model (r = 0.62, P = 2.79E-104), slightly better than the overdominance model (r = 0.60, P = 5.77E-95) and additive model (r = 0.59, P = 9.87E-92) (fig. 5C).

To develop the dominance model further, we counted the number of favorable alleles carried by the two testers. Interestingly, for seven traits that manifested higher linear plasticity in Zheng58-crossed F₁ hybrids, Zheng58 harbored 33 favorable alleles and Mo17 only 8; for the traits that manifested higher linear plasticity in Mo17-crossed F₁ hybrids, all favorable alleles were found in Mo17 and none in Zheng58. Ear weight was the only trait in which F₁ hybrids crossed between the Zheng58 and Mo17 exhibited similar levels of linear plasticity, reflecting the equivalent number of favorable alleles between them (13 for Zheng58 and 12 for Mo17; fig. 5D). Thus, although the classical dominance, additive, and overdominance hypotheses all accounted for part of the genetic basis of plasticity heterosis in maize, the dominance model performed better, and provides the potential to manipulate hybrid plasticity by a linear pyramiding of favorable alleles.

Discussion

We present findings from our large population of 976 F₁ hybrids created by crossing 488 inbred lines with two elite testers (Zheng58 and Mo17). The 488 inbred lines had high levels of genetic diversity and originated from sites distributed globally, spanning tropical and temperate ecological regions (Yang et al. 2011). The two testers were carefully chosen to represent distinct heterotic groups, including a Reid-like pedigree from China and Lancaster from the United States. The large-scale phenotypic data set of the diverse hybrid populations measured across a gradient of multiple environments provides a unique opportunity to unravel the genetic basis of phenotypic plasticity, and explore whether and how the plasticity variance contributes to the tropical-temperate adaptation and heterosis in maize.

The Genetic Architecture Underlying Phenotypic Plasticity

Comparative GWAS of genetic value and linear plasticity enables us to understand the genetics of 12 agronomic traits measured in multiple environments. We detected significantly more QTLs for the genetic value (32 on an average over traits) than for linear plasticity (5.5 on an average); a similar pattern was reported previously in rye (Wang et al. 2015). Comparing the magnitude of QTL effects on the genetic and linear plasticity variation, we also found individual and cumulative effects of QTL that explain more genetic variation than plasticity variation, regardless of model used (additive or dominance) (fig. 2A). Thus, the genetic base of linear plasticity is typically polygenic, with modest effects per QTL, compared with the genetic value that we traditionally focus on. Only 8–44.8% of linear plasticity variance could be accounted for by all detected QTLs for the 12 traits in the present study, leaving considerable potential for the creation of advanced statistical tools to systematically explore the phenotypic plasticity and integrate epistasis and other omics data.

We were able to explore the influence of the detected QTL on phenotypes across the environmental continuum. Our results revealed that most of the QTLs detected for ten of the traits adjusted the magnitude of additive effect in response to changing the environment, confirming the assumption of different sensitivity. Only two traits had QTLs that changed the sign (positive to negative or vice versa) of additive effect response to environmental alteration, following antagonistic pleiotropy assumptions (Des Marais et al. 2013; Ågren et al. 2017). Antagonistic pleiotropy and differential sensitivity represent distinct mechanisms for how genetic factors adaptively respond to dynamic environmental exposure. Which mechanism was successful depended on the optimal balance between the benefit of increased fitness for each QTL in a specific environment and the potential cost of the QTL in all environments (Lowry et al. 2019). The adaption and spread of maize to multiple different growing environments must have involved the precise modulation of genes controlling key traits. For example, the precise transition time from vegetative to reproductive growth is critical for plants to avoid disastrous weather and abiotic and biotic threats. Instead of strong major genes, genes of modest effects on underlying trait plasticity may allow more flexibility to fine-tune phenotypic performance in specific environments. Analogous research found that transcriptional variants (including differential expression) are more elastic for adapting phenotypes than changes in protein-coding sequence in maize adaptation (Liu et al. 2015).

Phenotypic Plasticity Contributes to the Tropical-Temperate Adaptation in Maize

Maize (Zea mays ssp. mays) was domesticated from its wild progenitor, teosinte (Zea mays ssp. parviglumis), in southwestern Mexico between 6,000 and 9,000 years ago. Archaeological and genetic data suggest that it was introduced to the southwestern United States by 4,000 years ago, after which the temperate US maize landraces differentiated from the tropical maize (Swarts et al. 2017). Adaptation to temperate growing conditions led to many genomic and transcriptomic changes, which may underlie important agronomic and metabolic traits selected by ancient farmers (Camus-Kulandaivelu et al. 2006; Liu et al. 2015; Swarts et al. 2017; Xu et al. 2019). Previously published results show that highly selected regions for temperate adaptation contributed less G × E variance for grain yield than unselected genomic regions; this indicates improvement of temperate cultivars has reduced G × E variation in breeding populations, presumably via stabilizing highly productive cultivars over multiple environments (Gage et al. 2017). However, direct evidence whether and how phenotypic plasticity participated in maize adaptation is lacking.

The present data set represents ∼1,000 tropical and temperate hybrid genotypes chosen to create a diverse data set for important target traits, collected from all hybrid and parental lines grown in the temperate Chinese Corn Belt over a latitudinal gradient. This data set thus allows comprehensive characterization of phenotypic plasticity over a range of environments. Selected genomic regions responsible for trait plasticity contributing to temperate environment adaptation were identified. Thirteen genomic regions for several traits were found to have been selected by ancient corn farmers, assuming that the favorable allele was selected due to its high (or even visible) effect on genetic values for agronomic traits. These traits contribute to crop improvement and can modulate phenotype regardless of the effect of genotype by environment interaction.

The research presented here illustrates that genetic effect of a key trait can be selected to better fit human needs, as in the case of the vital domestication genes tb1 and tga1 (Wang et al. 2005; Studer et al. 2011), but in addition, phenotypic plasticity can be selected simultaneously or independently in the maize adaption and improvement process. Robust and large effects of domesticated alleles across environments may be favored, because the stable phenotypes promote the spread of domesticated crops from native habitats to other climates (Doust et al. 2014). However, here, we infer that polygenes with plasticity effects were involved in local adaptation of modern maize to fit specific temperate environments over a gradient, by fine tuning phenotypes. These results cannot answer how important plasticity selection is on the expression of all traits, due to the limited collection of phenotypic data; this must be addressed in future studies including data from advanced analytical platforms and comprehensive weather, soil, microbiome, and phenomics data.

New Perspectives of Heterosis in Plasticity

The study of heterosis has achieved useful understanding of hybrid superiority based on all intragenomic, intergenomic, and omics- layer interactions, which together create the genetic component of heterosis (Riedelsheimer et al. 2012; Chen 2013; Schnable and Springer 2013). We know considerably less about the effect of genome by environment interaction on heterosis, or the plasticity component of heterosis. With the present experimental design, we can explore plasticity heterosis as defined how hybrids perform compared with their parental lines with regards to phenotypic plasticity. Congruent with previous knowledge in maize, data presented here showed that genetic heterosis increased phenotypic values for plant vegetative and biomass traits, whereas it lowered phenotypic values for flowering traits (supplementary fig. 10, Supplementary Material online). Plasticity heterosis exerted an entirely distinct pattern, in that most traits showed significantly higher plasticity in the F₁ population across environments than the maternal inbred population. This indicates that the intergenomic interactions resulting from hybridization has reshaped the phenotypic response to environment alterations.

Previous studies assumed the overdominance model explained most of the variation for plasticity; in this model, a genotype with higher heterozygosity is expected to have less phenotypic plasticity (Scheiner 1993). In contrast, our experimental results suggest that the dominance hypothesis of QTL effects outperforms the additive and overdominance hypotheses to best fit the plasticity variation in the F₁ population. Furthermore, the dominance hypothesis unambiguously explains the differential plasticity between two background F₁ pools, where F₁ plasticity values are primarily attributable to the number of dominance alleles inherited from the paternal testers. Hybrid maize breeding has enhanced grain production nearly 10-fold since the 1930s (Duvick 2001), but the challenge now is to find elite hybrid commercial cultivars that can adapt well to increasingly varied maize temperate growing conditions, especially considering continuous global environmental degradation and a changing climate. Our results caution that this will be difficult and require the use of state-of-the-art technologies and scientific input to explore the phenotypic plasticity of key traits; however, through comprehensive collection of environmental, -omics, phenotypic, and microbiome data integrated via big-data-driven platforms, we can begin to exploit new plasticity reserves to improve stability of maize production.

Materials and Methods

Germplasm and Phenotypes

A total of 976 hybrids (supplementary table 8, Supplementary Material online) were developed by crossing 488 maternal inbred lines with two elite paternal testers (Zheng58 and Mo17). The maternal and paternal inbred lines are a subset of one association mapping population consisting of 513 diverse inbred lines widely used over the past 10 years (Yang et al. 2011; Xiao et al. 2017). The two testers were selected as representative members of important heterotic groups used in China and the United States. The 488 maternal inbred lines, two paternal lines, and 976 F₁ hybrids were planted in eight locations in 2 years (2011 and 2012). Due to missing data from some trials, data for 12 agronomic traits were measured in 11 environments, (location × year) were used in this study for the F₁ hybrid population and seven environments for the parental inbred population (supplementary table 1, Supplementary Material online). The trials were located in latitudes spanning 18°15′–35°44′, and longitudes from 102°42′ to 114°30′. The field experiments were planted in randomized complete block designs with 0.25-m plant spacing with normal field management (locations shown in fig. 1A and supplementary table 1, Supplementary Material online).

For each hybrid or inbred genotype, five healthy and uniform plants were chosen to phenotype 12 agrnomic traits, including cob weight, days to anthesis, days to silk, ear height, ear row number, ear weight, kernel length, kernel thickness, node number below ear, plant height, main tassel branch length, and tassel branch number. The definition and measurment standards of these traits are in supplementary table 9, Supplementary Material online. For each genotype, extreme values outside the mean plus or minus 1.7 SDs were treated as outliers and excluded for estimating the mean of multiple entries. At the population level, outliers were removed following the procedure of Kusmec et al. (2017) in which phenotypes for each line measured in fewer than three environments or outside 1.5 times the interquartile ranges (IQRs) were filtered out. Thus, about 8.5% of collected phenotypes were eliminated, leaving 4,094–7,825 available phenotypic data points for each trait (supplementary table 10, Supplementary Material online).

Phenotypic Partition for Genetic Value and Linear Plasticity, and Phenotypic Reconstruction

The phenotypic plasticity of each hybrid across environments was estimated using the Bayesian Finlay–Wilkinson regression (FWR) model based on the FWR package (Lian and de los Campos 2016). In the FWR model, the observed phenotype of an individual in one environment can be expressed as:

$$y_{ij}=\mu +g_i+(1+b_i)\times h_j+{\epsilon }_{ij},$$

where y_ij is the phenotype of the ith hybrid collected in the jth environment, μ is regression intercept as population mean, g_i is the main effect of the ith hybrid, h_j is the environmental effect of the jth environment, 1 + b_i represents the change in performance of the ith hybrid per unit change in the environmental effect (h_j), and ɛ_ij is the residual error. We treated all parameters, g, b, h, as random effects, with a mean of zero and variance–covariance matrices of $I{\sigma }_g^2$, $I{\sigma }_b^2$, $I{\sigma }_h^2$, following the previously published settings (Kusmec et al. 2017). Thus, g_i estimates the genotypic value as mean phenotype across environments. The value of 1 + b_i measures the linear plasticity of a hybrid i over environments, whereas (1 + b_i) × h_j indicates the phenotypic change of a hybrid i in a given environment j. For the 12 agronomic traits, the genetic value and linear plasticity were estimated for each hybrid. After filtering out the outliers exceeding 1.5 times IQR in the population, 924–970 data points remained for genetic value and 932–973 for linear plasticity calculations. The distributions of the genetic value and linear plasticity are illustrated in supplementary figure 11, Supplementary Material online.

We explored how a plastic QTL can predict the phenotypic performance in specific environments by selecting one major QTL associated with the linear plasticity of plant height. In the FWR model, the global genotype based on hybrid identity was replaced by the specific genotype based on QTL. Thus, the estimates of g indicate the mean phenotype for the same QTL genotype across environments. After the FWR estimation, by adding the genetic value and the product of linear plasticity and environment effect, the model-fitted plant height is predicted for each genotype per environment.

Sequencing and Genotype Imputation

The maize association mapping panel that included 488 maternal inbred lines and two paternal testers used in the present study had been previously resequenced with deep coverage (∼20×, Liu et al. 2017; Yang et al. 2019). Using these sequencing efforts allowed us to obtain an ultrahigh-density variation map with 12,749,556 SNPs (B73 reference AGPv4.32). Filtering heterozygous SNPs and any genotype missing in either of the two testers resulted in 11,580,040 SNPs from all maternal and both paternal lines. The genotypes of the 976 F₁ hybrids were deduced based on parental genotype. The missing genotypes in the hybrids were imputed using the Beagle software (Browning and Browning 2007). To evaluate the accuracy of imputation, we randomly masked 40,000,000 known genotypes (∼4.6% of the total loci × individual genotype combinations on chromosome 10), and then imputed them using Beagle. When compared with the real genotypes, the accuracy of ten imputation replications was 99.56% on an average, which was high enough for subsequent analyses. After imputation, the SNPs with less than three genotypes (two homozygote and one heterozygote) or minor allele frequency lower than 0.03 were filtered out, leaving 2,668,862 high-quality SNPs for further analyses (supplementary table 11, Supplementary Material online).

GWAS for Genetic Value and Linear Plasticity

Using the high-density SNP data set across the genome, GWAS was performed using the linear mixed model through the EMMAX algorithm (Kang et al. 2010) for the genetic value and linear plasticity of the 12 traits. Three GWAS schemes were deployed by encoding SNP genotypes as additive, dominant, and recessive, as described by Huang et al. (2015). The kinship matrix was calculated with a centered identity-by-state matrix, by replacing negative values with zero (Yu et al. 2006). The genome-wide significant P value thresholds were set following the adjusted Bonferroni method for correcting for multiple tests (P  < 1/N, where N is the number of markers used for GWAS; Johnson et al. 2010). The following procedure was used to declare a QTL as significant: all significant SNPs within 500 kb were merged into one locus, followed by merging flanking loci (<5 Mb). In the case of loci containing fewer than five significant SNPs, a suggestive P value cutoff (ten times significant P value) was used. Loci that still contained at least one significant SNP and at least five suggestive SNPs were retained as significant QTLs. The physical regions covered by suggestive SNPs for each QTL were treated as the confidence intervals of QTL, and the most significant SNP for each QTL was regarded as the peak SNP.

Variance of Genetic Value and Linear Plasticity Explained by Detected QTLs

In the F₁ hybrid population, the variance explained by each QTL (PVE) was estimated using a linear regression model. The coding of QTL genotypes followed additive and dominance models. In the additive model, the minor homozygote was coded as “2,” the major homozygote as “0,” and the heterozygote as “1.” In the dominance model, both homozygotes were coded as “0” and the heterozygote as “1.” The QTL variance was calculated by comparing the full model to the reduced model, and the formula was expressed as:

$$\mathrm{PVE}=1-\frac{{\mathrm{RSS}}_1}{{\mathrm{RSS}}_0},$$

where PVE is phenotypic variance explained by a QTL or multiple QTLs, ${\mathrm{RSS}}_0$ is the squared sum of residuals in the reduced model only fitting the intercept, ${\mathrm{RSS}}_1$ is the squared sum of residuals in the full model fitting the intercept and a QTL variable or multiple QTL variables (additive or dominance coding). Peak SNPs that failed to reach significance in either additive- or dominance-based regression models were excluded from further analysis. All analyses were implemented in the R function “lm” (R Core Team 2012).

Identification of the Patterns of Phenotypic Plasticity Response to Environments

The genetic basis of the interaction between genotype and environment may be explained as antagonistic pleiotropy or differential sensitivity, according to variable patterns of QTL effects across environments (Des Marais et al. 2013). In order to understand the pattern of phenotypic plasticity observed in the present study, we re-estimated the additive effect of consensus QTLs on phenotype of the 12 traits in all environments. For each QTL, the effect pattern was regarded as antagonistic pleiotropy if effect signs differed in at least a quarter of the environments; otherwise it was regarded as differential sensitivity. For each trait, the effect pattern was regarded as following antagonistic pleiotropy if more than 70% of the significantly associated QTLs displayed antagonistic pleiotropy; otherwise the entire trait was regarded as displaying differential sensitivity.

Q_ST–F_ST Comparisons

To assess whether the 12 agronomic traits were selected during the tropical-temperate adaptation, either by means of the genetic value or linear plasticity, we performed the Q_ST–F_ST method described previously (Beleggia et al. 2016; Xu et al. 2019). The population of 488 maternal inbred lines included 204 tropical lines and 156 temperate lines; the rest included 128 mixed or undetermined lines (Yang et al. 2011). Thus, in the population of 976 hybrids, there were 408 and 312 hybrids of tropical and temperate origins, respectively. Although hybridization with the testers had introduced heterozygosity into the hybrid population, it did not change the population structure, so the parameters of population genetics (F_ST and F_IS) could still be logically computed with the 204 tropical and 156 temperate maternal lines.

F_ST was calculated from the 2,668,862 genome-wide SNPs using the software VCFtools via a 5-Mb sliding window with 1-Mb steps (Danecek et al. 2011). F_ST significance threshold was determined by permuting the lines between tropical and temperate groups 1,000 times. For each permutation, we recorded the 30th F_ST (∼0.001%) from high to low, and the 15th maximum value was chosen as the threshold across 1,000 permutations.

Q_ST was calculated based on the formula (McKay and Latta 2002) expressed as:

$$Q_{\text{ST}}=(1+F_{\text{IS}}){\delta }_{\mathrm{B}}{}^2/[(1+F_{\text{IS}}){\delta }_{\mathrm{B}}{}^2+2{\delta }_{\mathrm{w}}{}^2],$$

where δ_B² is the between-subpopulation variance component and δ_w² is the within-subpopulation variance component, estimated between 408 and 312 hybrids with tropical and temperate origins, respectively, and based on ANOVA of genetic value and linear plasticity of the 12 traits. The inbreeding coefficient (F_IS) was estimated using the whole-genome SNPs in maternal lines with the software GCTA (Yang et al. 2011). The 95% confidence intervals of Q_ST were obtained through bootstrapping individuals with replacement 1,000 times. For each phenotype, the 95% confidence interval for Q_ST was compared with the F_ST threshold. The phenotypes with a lower boundary Q_ST interval higher than the F_ST significance threshold were considered to have been selected during the adaptation process.

Comparing F₁ Hybrids and Parental Lines for the Genetic Value and Plasticity

With the goal of illustrating the heterotic effect in phenotypic plasticity, we compared the hybrids with the parent inbred lines by estimating the trait variance among environments. For one trait, individuals with higher variance were considered more sensitive to changing environment, and thus, this variance is another measurement of phenotypic plasticity. We referred to the difference in plasticity between the hybrids and parent inbred lines as plasticity heterosis. In contrast, the best linear unbiased prediction value of an individual across environments was used to assess the genetic values between the hybrids and the parent inbred lines, which we referred to as the genetic heterosis. However, when comparing the plasticity heterosis obtained by crossing all maternal lines with Zheng58 and Mo17, the linear plasticity derived from the FWR model was used.

Heterosis Models and QTL-Based Predictability

To determine the optimal genetic model that best explains the linear plasticity in the hybrid set, we tested three classical heterosis models by encoding detected QTLs differently. By assuming the allele of a QTL that results in the higher linear plasticity to be the favorable allele, the three heterosis model are: 1) additive model, in which for each plasticity QTL of a trait, the SNP site with the favorable homozygous alleles was coded as “1,” the heterozygote as “0.5” and unfavorable homozygote as “0”; 2) dominance model, in which the SNP sites with favorable homozygous and heterozygous alleles were both coded as “1,” and the unfavorable homozygote as “0”; 3) overdomiance model, in which the heterozygous SNP sites were coded as “1,” and both two homozygotes as “0.” Under distinct heterosis assumptions, for each trait, the proportion of favorable genotypes across all detected QTLs harbored by each individual (the maternal, paternal parents, and hybrids) was estimated. A linear model was built by regressing the estimated proportion of favorable genotypes to the measured linear plasticity in the F₁ hybrid population, and the model fit value (R²) indicated the prediction ability of the detected QTLs for linear plasticity under different heterosis assumptions.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.