Abstract
Working with electronic health records (EHRs) is known to be challenging due to several reasons. These reasons include not having: 1) similar lengths (per visit), 2) the same number of observations (per patient), and 3) complete entries in the available records. These issues hinder the performance of the predictive models created using EHRs. In this paper, we approach these issues by presenting a model for the combined task of imputing and predicting values for the irregularly observed and varying length EHR data with missing entries. Our proposed model (dubbed as Bi-GAN) uses a bidirectional recurrent network in a generative adversarial setting. In this architecture, the generator is a bidirectional recurrent network that receives the EHR data and imputes the existing missing values. The discriminator attempts to discriminate between the actual and the imputed values generated by the generator. Using the input data in its entirety, Bi-GAN learns how to impute missing elements in-between (imputation) or outside of the input time steps (prediction). Our method has three advantages to the state-of-the-art methods in the field: (a) one single model performs both the imputation and prediction tasks; (b) the model can perform predictions using time-series of varying length with missing data; (c) it does not require to know the observation and prediction time window during training and can be used for the predictions with different observation and prediction window lengths, for short- and long-term predictions. We evaluate our model on two large EHR datasets to impute and predict body mass index (BMI) values and show its superior performance in both settings.
Keywords: Recurrent Neural Network, Adversarial Training, Electronic Health Record
1. INTRODUCTION
As more health systems around the world adopt standardized methods of collecting individuals’ health data in electronic health record (EHR) formats, unprecedented opportunities for using modern data mining and machine learning techniques on these large-scale datasets have been arising. The application of such data-driven techniques offers great hopes to shift healthcare systems in almost every aspect and make achieving precision medicine goals more promising. However, the wide adoption of EHR data does not mean that the data is complete and without any flaws. Several issues make working with real-world EHR data challenging, including unequal lengths of time-series, irregular intervals between the recorded elements, and missing entries [31]. The time intervals might be different within a sample (patient) or in between the samples. Additionally, using a single source of EHR data, different lengths of observation and prediction windows might be necessary, among different patients or for studying different health outcomes of interest. These issues can hinder the performance of any classification or regression tasks using EHR data.
There is a large body of literature dedicated to addressing irregular patterns and missingness in EHRs (more discussed in Section 4). While existing studies have often looked at the problems of imputation [9, 35] and prediction [7, 14, 24, 32] separately, our approach combines these two tasks, leading to a superior prediction performance and more flexibility in using the trained models. Our proposed model, named Bi-GAN, uses a bidirectional recurrent neural network (RNN) in a generative adversarial network (GAN) setting to learn the distribution of the input data. Bi-directional RNN learns from the longitudinal data in both forward and backward directions to estimate the missing values. By learning to generate synthetic data similar to the distribution of the input data, the GAN architecture can effectively guide the bidirectional RNN to learn the overall distribution of the EHR data and impute missing values. Our model learns from all the observed entries to impute any in-between missing entries, and also to predict future entries by similarly treating those as missing entries. This configuration makes it unnecessary to define the exact observation and prediction windows at the time of training and therefore solves another issue in the EHR predictive models, where the observation and prediction windows need to be known at the training time. In this way, our proposed model can be used as an effective “any-time prediction tool.” We show that our proposed model obtains superior performance for both the imputation and prediction tasks. In particular, our study makes the following contributions:
We present a bidirectional RNN model in a generative adversarial setting that combines the imputation and prediction tasks using EHRs.
We evaluate our model in an obesity case study using two large EHR datasets related to the records from around 70,000 pediatric and 34,000 adult patients over 10 years. We show that our model outperforms the state-of-the-art models for both imputation and prediction tasks.
2. PROBLEM SETUP
For simplicity, we formulate the problem of imputing and predicting a single measurement variable in multivariate EHR time-series, which we will refer to as the target variable using only the diagnosed conditions component of the EHRs. The same method should be extendable to the case where the target is also multivariate. As an example of uni- versus multi-variable target prediction, consider the problem of estimating an individual’s BMI using all the recorded conditions of that individual in the past 10 years, versus estimating her BMI, height, and blood pressure using the same input.
Let be a multivariate time-series in EHR dataset that represents the conditions diagnosed and the values for the target variable in T timestamps, where T = (t1, t2,….tn) and xti ∈ (0, 1)d is the d-dimensional ti-th observation vector of X observed at the time ti and be the j-th feature value at a time ti. Let the target variable be where j = 1. For simplicity, we will drop j and represent the target variable as xti. We call X as the data vector representing all the conditions and target variable values recorded at all timestamps for a patient. The values in X could be missing at any time and we will impute and predict values only for the target variable. We call x as the target vector which contains the target variable values (or xti.) for all T timestamps. We also define the mask vector m such that it indicates which components of x are missing in the following way:
By following this formulation, we will have m = [mt1, mt2,…,mtn], where mti ∈ {0, 1}. Following the standard schema used in bidirectional models, we consider both forward and backward directions. The forward direction refers to the natural direction from the earlier to later timesteps in the time-series data, and the backward direction refers to the opposite. To record the time gap between the values in x in the forward direction, we define as the time gap vector such that:
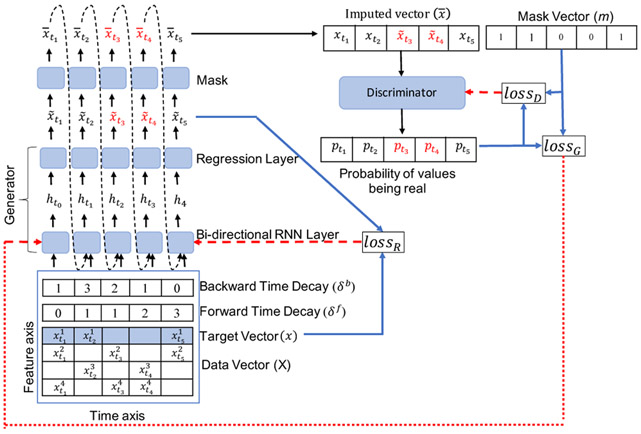
This way, will show the difference in the time of the last observed value and the current time step in the forward direction. We calculate , which is the time gap between the last observed value and the current time step in the backward direction, in a similar manner. For calculating , we reverse the timestamps to T′ = (tn,….t2, t1). Figure 1 shows the calculation of the time gaps δf and δb for the target vector x, where the time-series are recorded at (t1, t2, t3, t4, t5). Each column in X represents the observations for each timestamp. The top row in X is the target vector. Empty cells show the missing entries.
Figure 1:
Bi-GAN architecture overview. The blue arrows show the loss calculations and red dashed arrows show the loss back-propagation. Data vector X along with target vector x (shown in blue shaded row) and its forward and backward decay vectors are given as input to the the the bidirectional RNN. It generates values in both forward and backward direction (we do not show forward and backward values separately for image clarity). The regression layer generates the final generated values . Mask is used to obtain the imputed vector , which contains the generated values for the missing values (shown in red) and the observed values x (shown in black), when the values are not missing. Dashed arrows show that values are given as input to the next timestamp. The discriminator takes imputed vector to predict the probability of whether the values are fake () or real (x). It uses the mask vector as the ground truth to calculate its loss.
2.1. Method
Our proposed model, Bi-GAN, is a GAN-based architecture that works internally using bidirectional recurrent dynamics. This model consists of a generator (G) and a discriminator (D). We use bidirectional long short-term memory (LSTM) cell layers for the recurrent components in G and D. G uses a bidirectional recurrent dynamical system, where each value is generated twice; once by its predecessor values in the forward direction and another time by its successor values in the backward direction.
Our goal is to fill in the missing values for a single target variable x in X. The output of G would be a univariate time-series of values of that target variable. As shown in Figure 1, G receives the multivariate time-series data X as the input and outputs the imputed values for the target variable shown by (marked by the blue color in the data vector X). The generated values in are used to replace the missing values in the input x to obtain the output :
| (1) |
where x and are the univariate time-series of the target variable in the input X, and the generated output respectively; m is the mask vector for the target variable, and ⊙ shows the element-wise product operation. We calculate for every timestamp and give as the input to the bi-directional RNN at timestamp ti, as shown in Equation 3. This adds the recurrent dynamics [6] to our model, so that at every timestamp ti, the bi-directional RNN uses the previously imputed value if the value is missing and observed value if the value is not missing to estimate the value at the next timestamp.
G consists of a recurrent component for time-series representation, and a regression component to generate the final output from the output of the recurrent layers. For G, we use one layer of bidirectional recurrent cells. Consider a standard recurrent cell represented by,
| (2) |
where σ is the sigmoid function, Wh, Uh, and bh are the model parameters, and hti–1 is the hidden state from the previous timestamp. We extend the standard recurrent component shown in Equation 2, by,
| (3) |
| (4) |
where is the imputed values as shown in Equation 1 at time ti, and and are the model parameters. is the temporal decay factor calculated using added to the hidden state calculations. Additional calculations, similar to the forward case (Equation 3 and 4 above) are also used for the backward direction in the bidirectional recurrent layers (for calculating and ). Here , are calculated in such a way that , and the higher the values of and , smaller the values of and . By using the decay factors, we can calculate the confidence in the forward and backward imputed values. For instance, in Figure 1, is missing and the observed successor value, , is closer than the observed predecessor value, . In this case, the value generated for in the backward imputed vector should be more reliable.
The regression component of the generator is a fully-connected layer that generates the values for the target variable using the output of the recurrent layer. The regression component (for the forward direction) is represented as:
| (5) |
where is the generated value in the forward direction and and are the model parameters. will be calculated in the backward direction in the same way as shown in Equation 5.
As shown in Figure 1, the forward and backward imputed vectors are combined to calculate the final generated values:
| (6) |
where and , are two combination factors. These combination factors are trained as the model parameters based on the time gap values in the forward and backward directions (, and ). They help to control the influence of the forward and backward imputed values based on how far the last observed value in any of the two directions was. The combination factor in the forward direction is calculated as:
| (7) |
Where and are trained jointly with other parameters of the model. is calculated for the backward direction similar to in Equation 7. As we consider , in(0, 1], the higher the and , the smaller the values of and .
2.2. Loss Definitions
The model is trained using four different losses. To ensure that the outputs generated by the generator G are close to the actual (observed) values, we use the mean absolute error between the actual values and the corresponding generated values. This loss is defined as the masked reconstruction loss (lossR). To calculate this loss, we mask the input (x) and the output () of the generator:
| (8) |
We also use a consistency loss (lossc), which is the difference between the forward and backward generated values:
| (9) |
The discriminator D consists of one bidirectional recurrent layer of LSTM cells. Using a binary cross-entropy loss, we train D to maximize the probability of correctly classifying the actual (as real) and the generated values (as fake):
| (10) |
where lossD is the classification loss for the discriminator. is the probability of an actual value being classified as real, and is the probability of a generated value being classified as fake. In a way, D is trained to correctly reproduce the mask vector.
We simultaneously train G to minimize the probability that D correctly identifies the fake instances:
| (11) |
where lossG is the classification loss for G. Lowering lossG equals to decreasing the probability that D classifies the fake instances as fake. We merge all the losses for G and D as follows:
| (12) |
| (13) |
Figure 1 shows lossR, lossG, and lossD by blue lines, while the red lines show the backpropagation of the calculated loss values.
2.3. Imputation and Prediction Implementation
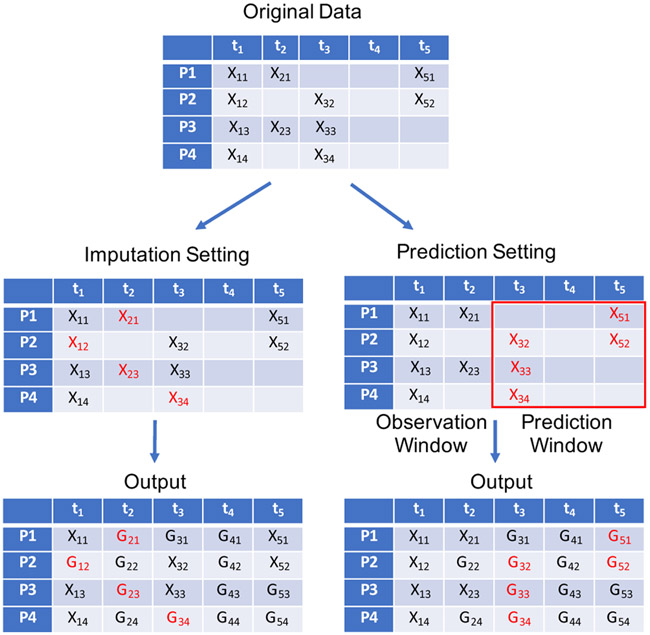
After presenting the structure of Bi-GAN, we can now explain how it can be used for imputation and prediction tasks. We segment the medical history of each patient into fixed-length disjoint periods and then align all the consecutive timestamps for all the patients. Any missing timestamps are padded with zeros. These padded values are treated as missing values. We use the mask vector to preserve the missingness of the data. Patients with shorter medical histories will have most of the missing values after the end of the last observed timestamp and patients with longer medical histories could have missing values in between their observed timestamps. For example, in Figure 2 and in the Original Data matrix, patient P1 and P2 have in-between missing timestamps, and patient P3 and P4 also have missing timestamps at the end of the last observed timestamp t3. During the training phase, the model learns to fill in all the missing values for all the patients with different lengths of the medical histories. Our model is trained once to fill in all the missing values, regardless of they are in-between the observed timestamps or at the end of the last observed timestamp. Filling in-between the observed timestamps are used for the imputation task and filling the values at the end of the last observed timestamp is used for the prediction task.
Figure 2:
Imputation and Prediction settings for Bi-GAN.
During the test phase, we can use any of the two different settings; i.e., the imputation or prediction to evaluate the model’s performance. Figure 2 shows the imputation and prediction settings for Bi-GAN, where the input data only consists of the values of the univariate target variable that is being imputed for the patients P1 to P4 on the timestamps t1 to t5. Missing values are represented by empty cells. In the imputation setting (the left side in Figure 2), a few values are randomly deleted from the original matrix, shown in red. The model fills in all the missing and deleted values. The masked reconstruction loss (lossR), reported as the imputation performance of the model is then calculated for the values represented in red.
In the prediction setting (the right side in Figure 2), we divide the time-series data into observation and a prediction window with the desired length. In Figure 2, we set the observation window to include t1 and t2 and the prediction window to include t3 to t5. We delete all the observed values in the prediction window shown in red. The model fills in all the missing and deleted values as shown in the corresponding output matrix. The masked reconstruction loss (lossR), reported as the prediction performance of the model is calculated for the values represented in red. Since we only define the observation and prediction window sizes in the testing phase and not during the training phase, we can use this model to predict with different observation and prediction windows at the time of deployment.
3. EXPERIMENT ANALYSIS
We conduct a series of experiments using two different EHR datasets that we introduce further later: Nemours Pediatric and All of Us. We use these datasets in a obesity case study, where we impute and predict BMI values using conditions as the input. Obesity is a major public health concern, often considered as an important risk factors to many other chronic and infectious diseases [4, 5, 28]. Despite their limitations, BMI values are the standard measures for determining obesity status [1, 27]. While used for studying similar tasks, the two datasets that we use have distinct characteristics (including the age groups and geographical coverage) enabling us to evaluate the proposed method in a more comprehensive manner. To maintain consistency in our experiments, for both datasets, we have included patients with 10-years of data in the cohort extracted from each dataset.
Using the two cohorts, first, we evaluate the imputation and prediction performance of Bi-GAN in comparison to five other baselines. Second, we evaluate the imputation performance of Bi-GAN with various missing rates, and its prediction performance with different observation and prediction window lengths. Finally, we evaluate the effects of Bi-GAN’s components on its performance through a series of ablation analyses.
We conduct our experiments using 5-fold cross-validations (80% train data and 20% test data). We randomly take 5% of the samples from the training set as the validation set, fix the best model on the validation set, and report the performance on the test data. We run the experiments for a maximum of 200 epochs until the validation loss stops decreasing for 20 epochs continuously. We provide more details of the implementation of our model in the Appendix B. We report MAE (mean absolute error) as the performance metric with 95% CI (confidence interval). Following the imputation and prediction settings described in Section 2.3, the imputation is performed by randomly removing 10% of the data points, and prediction is performed using the first two years as the observation window and the last eight years as the prediction window.
3.1. Datasets
3.1.1. Nemours Pediatric.
The EHR data in our first dataset is extracted from Nemours Children’s Health System, which is a large pediatric health system in the US serving four states. A more detailed description of this dataset and our preprocessing steps for preparing the EHR data is presented in an earlier work [13]. All the data access and processing steps were approved by a local institutional review board. For the childhood obesity case study, we used the 10 initial years of data for the patients, starting from their birth. We used the MedDRA [18] hierarchy to group the conditions from a total of 20,298 to 607 conditions. The final cohort used in this study consisted of 66,878 patients and 607 conditions.
3.1.2. All of Us.
The All of Us dataset is a publicly available data repository with two tiers of data access containing semi-nationally representative data from the US [19]. The dataset contains various types of data elements donated by the participants, which also includes the participants’ EHR data. The maximum and mean length of medical history for the patients were around 38 years and 5 years (at the time of defining our cohort). For our experiments, we extracted data for patients with 10 years of medical history. Our final cohort had 34,226 patients with 810 unique conditions. A more detailed description of the steps for the cohort extraction for this dataset is provided in the Appendix A.
3.1.3. Data Processing.
After selecting the cohorts, we represented all the conditions as binary variables (1 if present, and 0 if not recorded for the visit). We segmented the time-series data into disjoint 3-month windows and combined all observations within each window. We took the maximum BMI values for the segmented windows to account for the highest BMI risk in each segmented window. Since the patients in both cohorts had 10 years of data, we obtained 40 timestamps for each patient by segmenting data into 3-month periods. If a patient did not have any visit over a certain 3-month period, that period’s timestamp entries were padded by zeros and the BMI values were marked as missing. BMI values were also missing for the timestamps where a patient has a recorded visit, but the BMI was not recorded for the patient during that period. We use these two datasets to impute and predict patients’ BMI values. The missing ratio for the BMI values was 72% and 92% in the Nemours Pediatric and All of Us dataset, respectively.
3.2. Results
3.2.1. Baseline comparison.
We compare the performance of our proposed model (Bi-GAN) with other baseline methods for both imputation and prediction. In Table 1 and Table 2, we report the MAE scores for Bi-GAN and five other imputation methods listed below:
Table 1:
Imputation performance in MAE (95% CI)
| Algorithm | Nemours Pediatric | All of Us |
|---|---|---|
| Bi-GAN | 1.39 (0.10) | 4.22 (0.18) |
| BRITS-I | 2.78 (0.08) | 4.98 (0.21) |
| MRNN | 2.99 (0.02) | 5.64 (0.23) |
| MICE | 2.167 (0.01) | 7.36 (0.01) |
| KNN | 2.24 (0.02) | 5.71 (0.03) |
| MEAN | 1.78 (0.02) | 5.29 (0.03) |
Table 2:
Prediction performance in MAE (95% CI)
| Algorithm | Nemours Pediatric | All of Us |
|---|---|---|
| Bi-GAN | 1.93 (0.07) | 5.64 (0.08) |
| BRITS-I | 7.46 (0.27) | 6.06 (0.11) |
| MRNN | 3.93 (0.02) | 6.83 (0.08) |
| MICE | 17.38 (0.01) | 29.31 (0.09) |
| KNN | 17.38 (0.01) | 30.04(0.03) |
| MEAN | 17.38 (0.01) | 30.04(0.03) |
BRITS-I (Bidirectional Recurrent Imputation for Time Series) [6] is a bidirectional RNN model that imputes the values in the time-series data. The EHR time-series in our experiments do not have a classification label that gives overall disease diagnosis to a patient’s EHR data such as a mortality label given to a patient’s ICU EHR data. Therefore, we did not use the classification layer of the BRITS-I model as it will not add to the performance of the EHR datasets in our experiments.
MRNN (Multi-directional Recurrent Neural Networks) [36] is a bi-directional RNN that imputes the missing values using concatenated hidden states from both the forward and backward directions. It does not use the imputed values at the previous timestamp to estimate the next value and treats imputed values as constants.
MICE (Multiple Imputation by Chained Equations) [2] is a popular imputation method that estimates the missing values over a number of iterations. We initialize the missing values with the mean of the observed values and run the MICE imputation over 5 iterations.
KNN (k-nearest neighbors) uses the k nearest neighbor observed values of a patient to impute its missing values. We use k=10 for training KNN. We used the fancyimpute [29] implementation of KNN.
Mean is used to impute the missing values for a patient by calculating the arithmetic mean of its observed values.
We choose a series of imputation methods for the baseline comparison, since our proposed model is trained as an imputation model to impute the missing values for in-between and future timestamps. It is during the testing phase that we evaluate its performance for imputation and prediction tasks separately, as explained in Section 2.3. Similar to our proposed model, we train the baseline imputation methods to impute in-between and future timestamps values and test all methods in both imputation and prediction settings. Table 1 shows that Bi-GAN performs better than other baseline methods in imputation settings.
When using the model for prediction, we delete all the values in the prediction window. Table 2 shows that Bi-GAN achieves the best prediction performance compared to the other baseline methods in both EHR datasets. By deleting the values of the prediction window, all the values on the right side of the time-series are deleted. So, when the bi-direction network runs in the backward direction (right to left), it will not have a reference of the observed values to estimate values at the next timestamps. Therefore, the values generated by the bi-direction recurrent dynamics in the backward direction are less accurate than in the forward direction. This is the reason that BRITS-I does not perform well in the prediction settings, as it uses the mean of the forward and backward imputed values. Whereas, our proposed model (Bi-GAN), takes the weighted sum of the forward and backward imputed values using the combination factors (λf and λb), which are trained as the model parameters. This way, our model learns the best way for combining the forward and backward imputed values in both the imputation and prediction settings. In our model, we also observe that in the imputation setting, λf and λb, vaiy such that λf is higher, if the last observed value is closer from the left than the right side of time-series (and vice-versa). In the prediction setting, λb is closer to zero and λf is closer to 1, as in the prediction setting, values are only present on the left side (observation window) and absent on the right side (prediction window). Mean, KNN, and MICE baselines also do not work well in the prediction settings, as they rely on the observed values, while in the prediction setting, only the values in the observation window are observed and all the values in the prediction window are empty.
3.2.2. Varying missing rates.
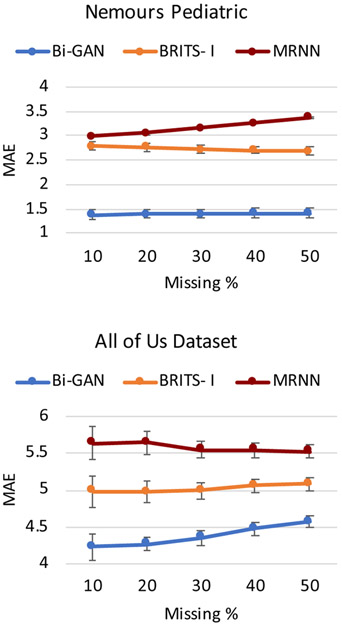
We also evaluate the performance of Bi-GAN on the EHR datasets with various missing rates in the imputation setting. Figure 3 shows the performance of Bi-GAN along with the two other more competitive baselines: BRITS-I and MRNN imputation methods. We use different missing rates of 10%, 20%, 30%, 40%, and 50% by removing BMI values from the test data. As the figure shows, Bi-GAN performs better than BRITS-I and MRNN for different missing rates.
Figure 3:
Imputation performance comparison between Bi-GAN, BRITS-I and MRNN with different missing rates - 10%, 20%, 30%, 40% and 50%. The graph shows the MAE with 95% CI (shown by error bars).
3.2.3. Varying prediction window lengths.
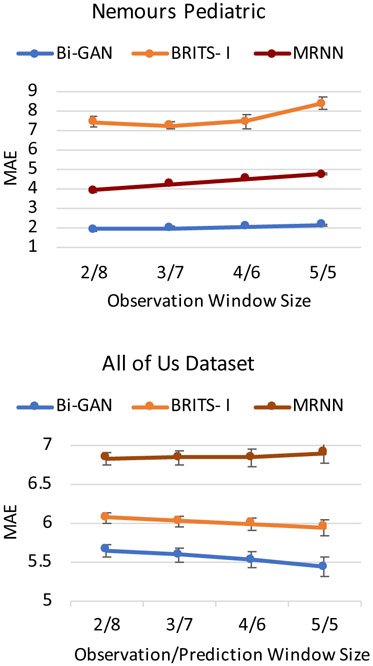
In the prediction setting, we also evaluate the performance of the methods by varying the observation and prediction window sizes. For the time-series of length 10 years (40 timestamps), we use the observation window sizes of 2 years (8 timestamps), 3 years (12 timestamps), 4 years (16 timestamps), and 5 years (20 timestamps); and corresponding prediction window sizes of 8 years (32 timestamps), 7 years (20 timestamps), 6 years (20 timestamps), and 5 years (20 timestamps). Figure 4 shows that as the size of the observation window increases (or as the prediction window becomes shorter and moving from the long- to short-term predictions) the performance of all models increases. However, Bi-GAN outperforms BRITS-I and MRNN methods in all the observation and prediction window sizes.
Figure 4:
Prediction performance comparison between Bi-GAN, BRITS-I and MRNN with different observation windows (2, 3, 4, 5 years) and prediction windows (8, 7, 6, 5 years), respectively. The graph shows the MAEs with 95% CI (shown by error bars).
3.2.4. Ablation analysis.
Our model without the discriminator and the combination factors (λf and λb) is comparable to BRITS-I [6] model without the time-series classification layer. The components that potentially improved the performance of Bi-GAN compared to the state-of-the-art methods include the use of a GAN-like architecture by adding a discriminator and adding lossG and lossD. Also, we included λf and λb as the model parameters to be used as the combination factors to combine the values obtained from the forward and backward directions. For the setting "w/o λf and λb", we use the mean of forward and backward estimated values. Table 3 shows that the performance is best in both imputation and prediction settings, when all the components are included. This shows that GAN learns from the distribution of the observed data that guides the RNN network to estimate values closer to the underlying distribution of training data. Also as discussed previously, we observe that taking a weighted sum of the forward and backward estimated values using the model parameters (λf and λb) achieves a better performance than taking the mean of the forward and backward estimated values.
Table 3:
The model performance with and without various components, MAE (95% CI).
| Nemours Pediatric | All of Us | |||
|---|---|---|---|---|
| Model | Imputation | Prediction | Imputation | Prediction |
| Bi-GAN | 1.39 (0.10) | 1.93 (0.07) | 4.22 (0.18) | 5.64 (0.08) |
| w/o λf & λb | 2.72 (0.02) | 5.24 (0.01) | 5.20 (0.20) | 5.79 (0.06) |
| w/o lossG & lossD | 1.48 (0.02) | 2.25 (0.01) | 4.51 (0.19) | 5.91 (0.07) |
| w/o lossG, lossD, λf & λb |
2.78 (0.08) | 7.46 (0.27) | 4.98 (0.21) | 6.06 (0.11) |
3.3. Data Sharing and Reproducibility
Our implementation code is publicly available at https://github.com/healthylaife/BiGAN. Processed and one-hot encoded data files for the Nemours Pediatric dataset can be made available upon signing a data use agreement. The details of extracting the publicly available All of Us data are presented in the Appendix A. Our entire All of Us workbench is available on the All of Us Research Program and can be accessed by the registered users on the system.
4. RELATED WORK
Traditional imputation methods – There has been a substantial amount of research dedicated to the methods that can handle missing values in EHRs. Case deletion methods, where instances with missing elements are deleted, are among the simplest methods that may ignore some important information in EHRs [21, 30]. Also, interpolation methods [12, 22, 30] that use local interpolations to impute missing values are other options, which may discard important temporal patterns across time. Multivariate Imputation by Chained Equations (MICE), [2] that was one of our baseline methods, is perhaps the most popular method in this category It uses a chained equation over various iterations to estimate the missing values after an arbitrary initialization. Autoregressive methods, like ARIMA and SARIMA, fit a parameterized stationary model [15]. Machine learning models like KNN [3], expectation-maximization [25], and matrix factorization [16] are also among the common methods. A major concern about almost all these methods is that they do not consider some or all of the temporal dependencies between the variables.
RNN-based imputation – Because of RNNs’ inherent capabilities in recognizing sequential patterns in time-series, many RNN-based methods have been presented for imputing time-series in EHR data. To name one illustrative example, Codella et al. [9] used ensemble methods including two RNN-based algorithms to impute laboratory test scores in EHR data. RNN-based autoencoder networks have also been used to impute missing values in EHR data. Autoencoder networks learn the distribution of observed data to estimate missing values. Yin et. al. [34] used a time-aware autoencoder to learn from the data distribution of training data and also for considering the irregularities in the time intervals between the EHR time-series data. We use the temporal decay factor to consider the effect of irregular time intervals between the EHR time-series data. Jun et al. [20] use variational autoencoders to incorporate the variance in the latent distribution of the data. This model was later enhanced by Mulyadi et al. [26] by adding recurrent layers to consider the temporal dynamics and the correlations between the input features during the training. We use the generative adversarial network as a generative model to learn the latent distribution of the data to estimate the missing values. As discussed earlier, a close study to our work is the BRITS model [6], which uses bi-directional recurrent dynamics to enhance the imputation performance by estimating values in both forward and backward directions. The imputed values are the simple mean of the forward and backward imputation from the bi-directional recurrent model. Our method uses the weight parameters to take the weighted sum of the forward and backward imputed values. These weighted parameters are learned as the model parameters. By using the weighted parameters, the bidirectional recurrent model is able to perform both imputation and prediction tasks simultaneously. Also, the addition of the GAN architecture further guides the RNN to effectively impute the missing values, leading to improve the performance of both the imputation and prediction tasks.
GAN-based Imputation – GANs have proven to be strong choices for generating synthetic datasets [8, 11]. In this way, GANs’ ability to generate synthetic samples similar to the actual data distribution can be utilized to impute missing values in the data, such that the imputed values are close to the distribution of the actually observed values [33]. GAN-based imputation models generally introduce a generator to impute the missing values, that are similar to the underlying distribution of the observed data to fool the discriminator that distinguishes whether the data is observed or generated [35]. To implement the GAN components for imputing time-series data, some studies have used RNN architectures [10]. A good example of such studies is the work by Luo et al. [23], where they use modified gated recurrent units (GRUs) in a GAN structure to impute the missing data in multivariate time-series data. In some of the existing imputation studies, the imputation and prediction tasks are performed asynchronously, by performing the prediction task separately using the imputed data. An example of these explicit separations is the two-stage framework proposed by Hwang et al [17] that includes a missing data imputation and disease prediction. Building on this recent line of research, in this paper, we used a bi-directional RNN architecture in a GAN setting to perform both imputation and prediction in EHR data simultaneously.
5. CONCLUSION
In this study, we have presented a generative adversarial network with bi-directional recurrent units for performing both imputation and prediction on EHR data. By approaching the task of prediction as to the imputation of future values, we were able to train a single model to perform the imputation and prediction tasks concurrently. Our model can be used with different observation and prediction window sizes for short-term and long-term predictions. We have shown that our proposed model outperforms several state-of-the-art imputation methods, which are used for both imputation and prediction tasks. In particular, in estimating future BMI values, our proposed model achieved imputation and prediction MAE of 1.39 and 4.22 on a large pediatric EHR dataset, and 1.93, 5.64 on another adult EHR dataset. These can be compared to the MAEs of 2.78, 4.98, and 3.93, 6.06 obtained by the closest performance by a state-of-the-art imputation model.
Our study has several limitations, including being evaluated in only specific settings (such as estimating the BMI values). In the future, our model can be extended to multi-task imputation and prediction, where we impute and predict a range of measurements such as blood pressure, cholesterol, glucose level, besides the BMI for the patient’s visits. We also plan to include other modalities of EHR data such as medications and procedures as input to impute and predict different measurement values.
CCS CONCEPTS.
• Computing methodologies → Neural networks; • Applied computing → Health informatics.
ACKNOWLEDGMENTS
The authors would like to thank the PEDSnet team (PEDSnet.org), as well as Daniel Eckrich and Christopher Pennington for their help in extracting the Nemours EHR datasets from PEDSnet. The All of Us Research Program is supported by the National Institutes of Health. In addition, the All of Us Research Program would not be possible without the partnership of its participants. Please check the program’s website for the full list of contributions.
Our study was supported by the NIH awards: 3P20GM103446-20S1 and 5P20GM113125-05, as well as Robert Wood Johnson Foundation’s award 76778.
A. COHORT SELECTION
The All of Us data is organized into tables according to the OMOP CDM. We extracted separate cohorts for males and females from the All of Us database. We extracted all males (sex at birth) and females (sex at birth) data from the condition_occurence table. The total number of males and females in the data are 39,885 and 71,121, respectively. To get the visit timestamp information for the conditions recorded in the condition_occurence table, we map the data with the data from the visit_occurrence table. We used visit timestamps and date of birth information to calculate an age for all patients. After deleting any rows where age could not be calculated due to missing information, we got 28,494 and 54,781 males and females, respectively. The total number of unique condition codes for both male and female cohorts are 14,791 and 18,347, respectively. We take two steps to reduce the number of unique condition codes. We first calculated the mean number of patients per condition code. The mean number of males and females per condition code is 54, 96 respectively and the number of condition codes with a patient count above the mean values is 2,082, 2,342 respectively. We removed the condition codes with a patient count less than the mean values of 54 males and 96 females. After removing such rare condition codes, we grouped the condition codes using the “Is A” relationship from the concept_relationship table. After grouping condition codes, we got 28,169 males and 54,430 females with 610 and 662 condition codes, respectively. We combined both male and female data files to obtain combined 810 condition codes. We finally selected the cohort with a minimum of 2 years of medical length and a maximum of 10 years of medical length to get 11,152 males and 23,074 females. We further added the BMI values from the measurement table to the selected cohort. Our final cohort had 34,226 patients (11,152 males and 23,074 females) with 810 unique conditions.
B. IMPLEMENTATION DETAILS
We run the experiments for a maximum of 100 epochs until the validation loss stops decreasing for 20 epochs continuously. For training models, we use Adam optimizer with a mini-batch of 200 patients. We have different dimensions in the bi-directional RNN network for training with the Nemours Pediatric and All of Us dataset owing to different dimensions of inputs in both datasets. The hidden layer in the bi-directional RNN network is of dimensions 200 and 400 for the Nemours and All of Us dataset respectively. The final output layer after the bi-directional RNN network is a fully connected layer with an output dimension of 1 to generate BMI value for each timestamp. Discriminator has a hidden layer of dimension 10, then two fully connected layers of 5 and 1 neurons with LeakyRelu activation applied after the first fully connected layer. The final layer of the discriminator is a sigmoid layer to classify fake and real labels. All methods are implemented in PyTorch 1.2.1.
Contributor Information
Mehak Gupta, University of Delaware Newark, Delaware, USA.
H. Timothy Bunnell, Nemours Children’s Health System Willmington, Delaware, USA.
Thao-Ly T. Phan, Nemours Children’s Health System Willmington, Delaware, USA
Rahmatollah Beheshti, University of Delaware Newark, Delaware, USA.
REFERENCES
- [1].Adab Peymane, Pallan Miranda, and Whincup Peter H. 2018. Is BMI the best measure of obesity? [DOI] [PubMed] [Google Scholar]
- [2].Azur Melissa J, Stuart Elizabeth A, Frangakis Constantine, and Leaf Philip J. 2011. Multiple imputation by chained equations: what is it and how does it work? International journal of methods in psychiatric research 20, 1 (2011), 40–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Batista Gustavo E. A. P. A. and Monard Maria Carolina. 2003. An analysis of four missing data treatment methods for supervised learning. Applied Artificial Intelligence 17, 5-6 (2003), 519–533. 10.1080/713827181 arXiv: 10.1080/713827181 [DOI] [Google Scholar]
- [4].Beheshti Rahmatollah, Jalalpour Mehdi, and Glass Thomas A.. 2017. Comparing methods of targeting obesity interventions in populations: An agent-based simulation. SSM - Population Health 3 (2017), 211–218. 10.1016/j.ssmph.2017.01.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Bray George A. 2004. Medical consequences of obesity. The Journal of Clinical Endocrinology & Metabolism 89, 6 (2004), 2583–2589. [DOI] [PubMed] [Google Scholar]
- [6].Cao Wei, Wang Dong, Li Jian, Zhou Hao, Li Lei, andLi Yitan. 2018. BRITS: Bidirectional Recurrent Imputation for Time Series. In Advances in Neural Information Processing Systems, Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, andGarnett R (Eds.), Vol. 31. Curran Associates, Inc. https://proceedings.neurips.cc/paper/2018/file/734e6bfcd358e25ac1db0a4241b95651-Paper.pdf [Google Scholar]
- [7].Choi Edward, Bahadori Mohammad Taha, Schuetz Andy, Stewart Walter F, and Sun Jimeng. 2016. Doctor ai: Predicting clinical events via recurrent neural networks. In Machine learning for healthcare conference. PMLR, 301–318. [PMC free article] [PubMed] [Google Scholar]
- [8].Choi Edward, Biswal Siddharth, Malin Bradley, Duke Jon, Stewart Walter F., and Sun Jimeng. 2017. Generating Multi-label Discrete Patient Records using Generative Adversarial Networks. In Proceedings of the 2nd Machine Learning for Healthcare Conference (Proceedings of Machine Learning Research, Vol. 68), Doshi-Velez Finale, Fackler Jim, Kale David, Ranganath Rajesh, Wallace Byron, and Wiens Jenna (Eds.). PMLR, Boston, Massachusetts, 286–305. http://proceedings.mlr.press/v68/choi17a.html [Google Scholar]
- [9].Codella J, Sarker H, Chakraborty P, Ghalwash M, Yao Z, and Sow D. 2019. eXITs: An Ensemble Approach for Imputing Missing EHR Data. In 2019 IEEE International Conference on Healthcare Informatics (ICHI). 1–3. 10.1109/ICHI.2019.8904779 [DOI] [Google Scholar]
- [10].Esteban Cristóbal, Hyland Stephanie L, and Rätsch Gunnar. 2017. Real-valued (medical) time series generation with recurrent conditional gans. arXiv preprint arXiv:1706.02633 (2017). [Google Scholar]
- [11].Frid-Adar Maayan, Diamant Idit, Klang Eyal, Amitai Michal, Goldberger Jacob, and Greenspan Hayit. 2018. GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing 321 (2018), 321–331. 10.1016/j.neucom.2018.09.013 [DOI] [Google Scholar]
- [12].Fung David S. 2006. Methods for the estimation of missing values in time series. (2006). [Google Scholar]
- [13].Gupta Mehak, Phan Thao-Ly T, Bunnell Timothy, and Beheshti Rahmatollah. 2019. Obesity Prediction with EHR Data: A deep learning approach with interpretable elements. arXiv preprint arXiv:1912.02655 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hardt Michaela, Rajkomar Alvin, Flores Gerardo, Dai Andrew, Howell Michael, Corrado Greg, Cui Claire, and Hardt Moritz. 2020. Explaining an increase in predicted risk for clinical alerts. In Proceedings of the ACM Conference on Health, Inference, and Learning. 80–89. [Google Scholar]
- [15].Harvey Andrew C. 1990. Forecasting, structural time series models and the Kalman filter. (1990). [Google Scholar]
- [16].Hastie Trevor, Mazumder Rahul, Lee Jason D., and Zadeh Reza. 2015. Matrix Completion and Low-Rank SVD via Fast Alternating Least Squares. Journal of Machine Learning Research 16, 104 (2015), 3367–3402. http://jmlr.org/papers/v16/hastie15a.html [PMC free article] [PubMed] [Google Scholar]
- [17].Hwang Uiwon, Choi Sungwoon, Lee Han-Byoel, and Yoon Sungroh. 2017. Adversarial training for disease prediction from electronic health records with missing data. arXiv preprint arXiv:1711.04126 (2017). [Google Scholar]
- [18].ICH. 2020. Medical Dictionary for Regulatory Activities. https://www.meddra.org/how-to-use/basics/hierarchy [Google Scholar]
- [19].All of Us Research Program Investigators. 2019. The “All of Us” research program. New England Journal of Medicine 381, 7 (2019), 668–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Jun E, Mulyadi AW, and Suk H. 2019. Stochastic Imputation and Uncertainty-Aware Attention to EHR for Mortality Prediction. In 2019 International Joint Conference on Neural Networks (IJCNN). 1–7. 10.1109/IJCNN.2019.8852132 [DOI] [Google Scholar]
- [21].Kaiser Jiri. 2014. Dealing with Missing Values in Data. Journal of Systems Integration 5 (01 2014), 42–51. 10.20470/jsi.v5i1.178 [DOI] [Google Scholar]
- [22].Kreindler David M and Lumsden Charles J. 2012. The effects of the irregular sample and missing data in time series analysis. Nonlinear Dynamical Systems Analysis for the Behavioral Sciences Using Real Data 135, 2 (2012). [PubMed] [Google Scholar]
- [23].Luo Yonghong, Cai Xiangrui, Ying ZHANG Jun Xu, and xiaojie Yuan. 2018. Multivariate Time Series Imputation with Generative Adversarial Networks. In Advances in Neural Information Processing Systems, Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, and Garnett R (Eds.), Vol. 31. Curran Associates, Inc. https://proceedings.neurips.cc/paper/2018/file/96b9bff013acedfb1d140579e2fbeb63-Paper.pdf [Google Scholar]
- [24].Maragatham G and Devi Shobana. 2019. LSTM model for prediction of heart failure in big data. Journal of medical systems 43, 5 (2019), 1–13. [DOI] [PubMed] [Google Scholar]
- [25].Mazumder Rahul, Hastie Trevor, and Tibshirani Robert. 2010. Spectral Regularization Algorithms for Learning Large Incomplete Matrices. Journal of Machine Learning Research 11, 80 (2010), 2287–2322. http://jmlr.org/papers/v11/mazumder10a.html [PMC free article] [PubMed] [Google Scholar]
- [26].Mulyadi Ahmad Wisnu, Jun Eunji, and Suk Heung-Il. 2020. Uncertainty-Aware Variational-Recurrent Imputation Network for Clinical Time Series. arXiv preprint arXiv:2003.00662 (2020). [DOI] [PubMed] [Google Scholar]
- [27].Nevill Alan M, Stewart Arthur D, Olds Tim, and Holder Roger. 2006. Relationship between adiposity and body size reveals limitations of BMI. American Journal of Physical Anthropology: The https://www.overleaf.com/project/60688d7143264083ae2e9b33Official Publication of the American Association of Physical Anthropologists 129, 1 (2006), 151–156. [DOI] [PubMed] [Google Scholar]
- [28].Ramazi Ramin, Perndorfer Christine, Soriano Emily, Laurenceau Jean-Philippe, and Beheshti Rahmatollah. 2019. Multi-Modal Predictive Models of Diabetes Progression. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics (Niagara Falls, NY, USA) (BCB ’19). Association for Computing Machinery, New York, NY, USA, 253–258. 10.1145/3307339.3342177 [DOI] [Google Scholar]
- [29].Rubinsteyn Alex and Feldman Sergey. 2020. fancyimpute. https://pypi.org/project/fancyimpute [Google Scholar]
- [30].Silva Luciana O. and Zárate Luis E.. 2014. A Brief Review of the Main Approaches for Treatment of Missing Data. Intell. Data Anal. 18, 6 (Nov. 2014), 1177–1198. [Google Scholar]
- [31].Xiao Cao, Choi Edward, and Sun Jimeng. 2018. Opportunities and challenges in developing deep learning models using electronic health records data: a systematic review. Journal of the American Medical Informatics Association 25, 10 (06 2018), 1419–1428. 10.1093/jamia/ocy068 arXiv:https://academic.oup.com/jamia/article-pdf/25/10/1419/34150605/ocy068.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Xu Enliang, Zhao Shiwan, Mei Jing, Xia Eryu, Yu Yiqin, and Huang Songfang. 2019. Multiple MACE Risk Prediction using Multi-Task Recurrent Neural Network with Attention. In 2019 IEEE International Conference on Healthcare Informatics (ICHI). IEEE, 1–2. [Google Scholar]
- [33].Yahi Alexandre, Vanguri Rami, Elhadad Noémie, and Tatonetti Nicholas P. 2017. Generative adversarial networks for electronic health records: A framework for exploring and evaluating methods for predicting drug-induced laboratory test trajectories. arXiv preprint arXiv:1712.00164 (2017). [Google Scholar]
- [34].Yin Changchang, Liu Ruoqi, Zhang Dongdong, and Zhang Ping. 2020. Identifying Sepsis Subphenotypes via Time-Aware Multi-Modal Auto-Encoder. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery amp; Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 862–872. 10.1145/3394486.3403129 [DOI] [Google Scholar]
- [35].Yoon Jinsung, Jordon James, and van der Schaar Mihaela. 2018. GAIN: Missing Data Imputation using Generative Adversarial Nets. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80), Dy Jennifer and Krause Andreas (Eds.). PMLR, 5689–5698. http://proceedings.mlr.press/v80/yoon18a.html [Google Scholar]
- [36].Yoon Jinsung, Zame William R, and van der Schaar Mihaela. 2017. Multidirectional recurrent neural networks: A novel method for estimating missing data. In Time Series Workshop in International Conference on Machine Learning. [Google Scholar]