Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Sep 2;15(9):14786–14793. doi: 10.1021/acsnano.1c04766

Mitrofanovite Pt3Te4: A Topological Metal with Termination-Dependent Surface Band Structure and Strong Spin Polarization

Jun Fujii †, Barun Ghosh ‡, Ivana Vobornik †,*, Anan Bari Sarkar ‡, Debashis Mondal †, Chia-Nung Kuo §,⊗, François C Bocquet ∥,⊥, Lixue Zhang #, Danil W Boukhvalov 7,8, Chin Shan Lue §,⊗, Amit Agarwal ‡,*, Antonio Politano 9,10,*
PMCID: PMC8482756  PMID: 34472336

Abstract

graphic file with name nn1c04766_0005.jpg

Due to their peculiar quasiparticle excitations, topological metals have high potential for applications in the fields of spintronics, catalysis, and superconductivity. Here, by combining spin- and angle-resolved photoemission spectroscopy, scanning tunneling microscopy/spectroscopy, and density functional theory, we discover surface-termination-dependent topological electronic states in the recently discovered mitrofanovite Pt3Te4. Mitrofanovite crystal is formed by alternating, van der Waals bound layers of Pt2Te2 and PtTe2. Our results demonstrate that mitrofanovite is a topological metal with termination-dependent (i) electronic band structure and (ii) spin texture. Despite their distinct electronic character, both surface terminations are characterized by electronic states exhibiting strong spin polarization with a node at the Γ point and sign reversal across the Γ point, indicating their topological nature and the possibility of realizing two distinct electronic configurations (both of them with topological features) on the surface of the same material.

Keywords: topological metals, surface states, STM/STS, spintronics, ARPES

Introduction

Topological metals are materials with nontrivial band crossings or band inversions near the Fermi energy, giving rise to peculiar quasiparticle excitations.1−8 They can be classified based on the dimensionality and degeneracy of their band crossings.9 Prominent examples include Dirac,10 Weyl,11 nodal-line,12 and nodal-surface metals.9 In topological metals, bulk superconductivity can also coexist with topologically nontrivial states, as demonstrated for PbTaSe213 enabling the intriguing perspective of Majorana Fermions in solid-state physics. Furthermore, the heterostructures of topological metals are being pursued as suitable candidates for potential applications in quantum computing.14 The fascinating technological capabilities of topological metals are also confirmed by recent reports indicating their superior efficiency in catalytic reactions and hydrogen production, as demonstrated for the case of the Pt-based alloys PtAl and PtGa.15

Among the various families of materials showing gapless Dirac Fermions, the transition-metal dichalcogenide TMX2 (TM = Pd, Pt; X = Se, Te), crystallizing in the same structure as the naturally occurring mineral “moncheite”,16 was demonstrated to host type-II Dirac fermions,17 with application capabilities in plasmonics,10 catalysis,18 nanoelectronics,19 and wearable electronics.20 These properties can be tuned by varying (i) the position of the Fermi level with respect to the degenerate Dirac (or Weyl/nodal line) point and (ii) the strength of the spin–orbit coupling.

Mitrofanovite Pt3Te4, belonging to the “moncheite” family of materials with trigonal space group R3̅m (No. 166), has recently been discovered as a natural mineral in the Kola Peninsula, Russia,21 and in different zones in the Canadian Shield.22 Its atomic structure is constituted by alternating layers of hexagonal PtTe2 and Pt2Te2 (or PtTe) which are stacked along the vertical direction and held together by weak van der Waals interactions. Very recently, mitrofanovite has been demonstrated to be an efficient and stable catalyst for hydrogen evolution reaction (HER) with an overpotential of 39.6 mV and a Tafel slope of 32.7 mV/dec together with a high current density exceeding 7000 mA/cm2.23

Here, we explore the electronic properties of Pt3Te4 by means of scanning tunneling microscopy (STM)/spectroscopy (STS) and spin- and angle-resolved photoemission spectroscopy (spin-ARPES) in conjugation with density functional theory (DFT). We demonstrate that mitrofanovite is a topological metal hosting spin-polarized surface states. Interestingly, we find that Pt3Te4 has two distinct surface terminations with radically different electronic properties. These distinct terminations are observed at different terraces on the same face of the cleaved crystal. Despite differences in the corresponding electronic band structure, both surface terminations host spin-polarized states, exhibiting typical polarization reversal across the zone center, characteristic of spin-momentum locking. Thus, mitrofanovite offers termination-dependent electronic and surface properties enabling tunable device functionalities for nanoelectronics, spintronics, optoelectronics, and plasmonic applications.

Results and Discussion

Identification of Two Distinct Surface Terminations

The unit cell of Pt3Te4 is composed of alternating blocks of PtTe2 and Pt2Te2 units stacked vertically, as depicted in Figure 1a for the side view and in the red and green boxes in the inset of Figure 1d for top views. Specifically, in the PtTe2 subunit, one atomic Pt layer is sandwiched between the two Te layers. Contrariwise, in the Pt2Te2 subunit, two layers of Pt atoms are sandwiched between two Te layers. For such a crystal structure, two cleavage planes are feasible, resulting either in (i) a PtTe2 termination (marked by a red line in Figure 1a) or (ii) a Pt2Te2 termination (green line in Figure 1a). For the sake of completeness, also a PtTe termination is in principle feasible. However, as the energy per surface unit for the PtTe-terminated slab is more than 1 eV larger than for the PtTe2- and Pt2Te2-terminated slab, this type of termination can be excluded from further discussion.

Figure 1.

Figure 1

Open in a new tab

(a) Side view of the Pt3Te4 crystal structure with the two different cleavage planes—Pt2Te2 (green) and PtTe2 (red) terminations are identified. (b) Pt-4f XPS spectra for the Pt2Te2 (top) and PtTe2 (bottom) terminations, respectively. (c) Hexagonal LEED pattern obtained on both terminations. (d) 3D STM topographic image (100 nm × 100 nm) showing the adjacent terraces of different terminations separated by a step; the four insets framed green (red) are the top view of the crystal structure and the atomically resolved STM image (7 nm × 7 nm) for the Pt2Te2 (PtTe2) terminations. (e and g) STS spectra measured on the Pt2Te2 and the PtTe2 terraces. We observe a zero-bias peak only on the PtTe2 termination. (f) Height profile along the black line in panel d.

Thus, the existence of two distinct interfaces at the surface of the mitrofanovite crystal enables tunable electronic, spintronic, and plasmonic properties of the electrode contact for exploitation in micro- and nanoelectronics.

By means of high-resolution X-ray spectroscopy (XPS) on an as-cleaved sample, we identified two distinct spectral components in the region of Pt-4f core levels. In our experimental configuration (low-energy photons of 120 eV in normal emission geometry), the probing depth is 4.2 ± 0.1 Å, based on the effective attenuation length according to the Tanuma–Powel–Penn (TPP-2M) formula.24 This is comparable with the size of the single Pt2Te2 subunits (4.02 Å). Therefore, we expect that the two surfaces with different terminations will be reflected by different Pt binding energies (BE).

Consistent with our expectations, we observe a splitting in the Pt-4f core levels, with J = 7/2 components having a BE of 71.5 and 72.4 eV. To assign the two spectral components, we computed core-level shifts based on the charge distribution in the Pt2Te2 subunit. We found that, in the Pt–Te bonds, the charge on the Pt sites is reduced by 0.363 electrons compared to the Pt–Pt bonds. The intensity ratio between the two spectral components is 1.0 ± 0.1 in the Pt2Te2-termination. Concerning the PtTe2-terminated surface, we observe a suppression of the Pt-4f component related to Pt–Pt bonds up to 75%. The total quenching was not obtained, due to the combined effect of the limited spatial resolution (beam size 150 × 50 μm2) and the insufficient probing depth to selectively choose the contributions from the PtTe2 subunit only, whose size is 2.71 Å.

The two different surface terminations were further identified by means of scanning tunneling microscopy (STM) experiments. The three-dimensional STM topographic image (100 × 100 nm2) in Figure 1d highlights the adjacent large terraces separated by a step on a cleaved surface of mitrofanovite. The height profile shown in Figure 1f of the step in Figure 1d reveals a stacking of 0.73 nm, with respect to the Pt2Te2 termination. This stacking distance is consistent with the distance between the Pt2Te2 (depicted in the left green-framed inset of Figure 1d) and PtTe2 (depicted in the left red-framed inset of Figure 1d) subunits shown schematically in Figure 1a. The corresponding atomic resolution STM image of the Pt2Te2 (PtTe2) terrace is shown in the right inset of Figure 1d, within the green (red) box.

To compare the local electronic density of states (LDOS) on the two distinct surface terminations, we measured the differential conductance (or dI/dV) plots with STS on both the Pt2Te2 (Figure 1e, green curve) and the PtTe2 (Figure 1g, red curve) terminations, respectively. We find that the two different terminations show very different dI/dV characteristics over a wide range of the chemical potential (from −2.0 to 2.0 eV), highlighting distinct surface electronic properties and density of states (DOS) of the two terminations. Specifically, we observe a zero-bias peak in the local DOS for the PtTe2 (Figure 1g) surface termination, while such a feature is absent on the Pt2Te2-terminated surface (Figure 1e).

Below we will show explicitly that the zero-bias peak arises from an electron pocket in the surface states of the Pt2Te2-terminated surface.

Bulk Band Structure and Topology

In order to further assess the dissimilarities in the surface electronic properties of the two terminations, we explored the electronic structure and spin texture of Pt3Te4. The bulk electronic band structure, without and with including the spin–orbit coupling (SOC) is shown in Figure 2a, b. The band structure clearly indicates the metallic character of the system. We find that the bands near the Fermi level predominantly arise from the Te p states. The interplay between the different chalcogen p-derived states gives rise to a type-I bulk Dirac Fermion along the Γ-Z direction of the Brillouin zone. This Dirac cone is also protected by the rotation symmetry, as confirmed by our symmetry analysis. The bands marked by Δ5,6 and Δ4 (see Figure 2b) have opposite rotation (C3) characters (−1 and +1, respectively) which prevents their hybridization and stabilizes the Dirac crossing. Other than this Dirac crossing, four different bands (marked explicitly in Figure 2b) cross the Fermi level, resulting in several hole and electron pockets. The Fermi surfaces corresponding to these four bands are shown in Figure 2d.

Figure 2.

Figure 2

Open in a new tab

Calculated bulk band structure of Pt3Te4 along with the orbital character (a) excluding and (b) including the spin–orbit coupling. The irreducible representations of the bands at the Γ point are shown. The Dirac point along the Γ-Z direction is highlighted in the red circle. There are four bands crossing the Fermi level—marked as bands 1, 2, 3, and 4. Bands 1, 2, and 3 primarily result in hole pockets, while band 4 mainly leads to an electron pocket. (c) The bulk and the (111) surface projected Brillouin zone of the primitive cell with the high-symmetry points marked explicitly. (d) Fermi surfaces for four bands crossing the Fermi surface, clearly showing the presence of several hole and electron pockets arising from bands 1–4.

The bulk band structure of mitrofanovite displays multiple crossings between the valence and the conduction bands. This indicates the possibility of formation of topologically protected states. Furthermore, the Γ4+ (band 3) and the Γ4– (band 4) bands are locally separated by a gap at every k-point. Therefore, to pin down the exact topology of this system, we computed the 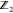Inline graphic topological invariants. As Pt3Te4 preserves the inversion symmetry, the topological invariant is calculated using the parity-based method developed by Fu-Kane.25 The details of the number of occupied bands with a specific parity is presented in Table S1 of the Supporting Information. Based on the calculated parity of the occupied bands, the strong topological invariant (ν0) is found to be zero and all the three weak topological invariants are nonzero. The four component 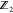Inline graphic invariant is found to be (0; 111). As Pt3Te4 hosts Dirac cones, it has a Fermi surface like a metal, and it is characterized by a nontrivial topological index, which results in spin-polarized topological surface states, we classify it as a topological metal.

Spin-ARPES Results

The nontrivial topological invariant indicates the presence of topological surface states, displaying spin-momentum locking. To experimentally explore the topological surface states and their spin texture, we used spin- and angle-resolved photoemission spectroscopy (spin-ARPES).

Given the surface sensitivity of the technique (probing depth of the order of 10 Å in our experimental conditions), we find that the measured electronic band structure is strongly termination dependent. This is evident in the two distinct data sets reported in Figures 3 and 4 obtained on the same sample just by changing the position between the two different terraces. The measured electronic dispersion along the surface Γ-K direction, for the PtTe2 and the Pt2Te2 terminations, is shown in Figures 3a and 4a, respectively, with the corresponding Fermi surfaces reported in Figures 3d and 4d. We ascribed those data to the two terminations by comparing the experimental results with the theoretically calculated surface band structure for a semi-infinite geometry terminating in either the PtTe2 or the Pt2Te2.

Figure 3.

Figure 3

Open in a new tab

Experimental results and theoretical calculations for the PtTe2 termination. (a) Band dispersion along Γ-K measured with hν = 22 eV. Red dotted lines indicate the positions in the momentum space where the spin spectra in part b and the resulting spin polarization in part c were measured. All spin data are related to the component perpendicular to the momentum (i.e., perpendicular to Γ–K), and there is a clear spin inversion between positive and negative momenta (i.e., between (i) and (iii)). (d) Measured Fermi surface.; (e) Calculated spectral function and (f) the corresponding spin texture. (g) Calculated Fermi surface.

Figure 4.

Figure 4

Open in a new tab

Pt2Te2 termination. Experimental results and theoretical calculations for the Pt2Te2 termination: (a) Band dispersion along the surface Γ-K direction measured with hν = 22 eV; red dotted lines indicate the positions in the momentum space where the spin spectra in part b and the resulting spin polarization in part c were measured; all spin data are related to the component perpendicular to the momentum (i.e., perpendicular to Γ–K), and there is a clear spin inversion between positive and negative momenta. (d) Measured Fermi surface. (e) Calculated spectral function. (f) Corresponding spin texture. (g) Calculated Fermi surface.

For the PtTe2 termination, we find that the surface spectral function has several bands, including the surface termination-induced electron pocket at the center of the Brillouin zone (see Figure 3a and 3e). In addition, we also identify four hole-like bands crossing the Fermi energy. Since these spectral features show almost no dependence on the photon energy (i.e., no kz dispersion is observed, see Supporting Information Figure S2), all of them can be ascribed to the two-dimensional surface states. The measured Fermi surface for the PtTe2 termination in Figure 3d clearly shows that the electron pocket at Γ is surrounded by a hole pocket with 6-fold rotation symmetry. The spin-polarization of these states is measured along three representative k points (Γ and two symmetric points at positive and negative k) marked by dashed lines in Figure 3a. We acquired data for the spin in-plane direction perpendicular to the crystal momentum, typically indicative of spin-momentum locking.

The resulting spin resolved spectra and spin polarization are shown in Figure 3b and 3c, respectively. While at Γ (Figure 3b) the spin up (red) and spin down (blue) spectra are the same, resulting in zero spin polarization (Figure 3c), the situation is different for the two spectra taken at the two symmetric k points around Γ. In fact, in panels (i) and (iii) the blue and red spectra are inverted, while the spin polarization is basically the same, but of opposite sign, in agreement with the spin-momentum locking. Note that not only the states at the Fermi energy exhibit spin polarization. It extends over the whole energy range probed in our experiment. All these features are well captured by our theoretical calculations for the semi-infinite geometry (see Figure 3e–g).

In contrast to the numerous bands crossing the Fermi energy for PtTe2, for Pt2Te2 termination only two evident Fermi crossings along the ΓK direction (Figure 4a) exist. In general, for the Pt2Te2 termination, the number of electronic states below the Fermi energy is relatively lower as compared to the PtTe2-terminated surface. Additionally, the surface electron pocket at the Γ point in the vicinity of the Fermi energy, observed for the PtTe2 termination, is absent for the Pt2Te2 termination (see Figure 4a). These differences are also reflected in the zero-bias peak observed on the PtTe2 but not on Pt2Te2 terrace, where the number of states at the Fermi energy is relatively low. The theoretical Fermi surface plots for the two terminations indicate that both of them display a 6-fold rotation symmetry (see Figures 3d and Figure 4d). Similar to PtTe2 termination, also on Pt2Te2 we detect spin-polarized states (Figure 4b and c) with the polarization inversion across Γ reflecting spin-momentum locking, evidenced as well in the calculated spin-resolved dispersion in Figure 4f.

Independent of the band structure differences, for both the terminations the calculated spin-resolved electronic spectral function (see Figures 3f and 4f) indicates that mitrofanovite is a strongly spin–orbit interacting system, with the surface states displaying spin-momentum locking. From the data in Figure 3b–c and in Figure 4b–c, for the PtTe2 and Pt2Te2 terminations, respectively, we find that for both the terminations the spin polarization is zero at the Γ point (Figure 3c, panel (ii), and Figure 4c, panel (iii). However, the spin polarization is finite and reaches up to 50% on the two sides of the Γ point, with clear polarization inversion of the corresponding states (between panels (i)–(iii) for PtTe2 and between panels (i)–(v) and (ii)–(iv) for the Pt2Te2 termination). Additionally, we observed spin-polarized states exhibiting spin-momentum locking over the full energy range that we probed. This observation is consistent with calculations for the spin-texture of the surface states in a finite-slab geometry (Figures 3f and 4f). The large value of the measured spin polarization and the spin-momentum locking are also consistent with the topological origin of the observed surface states and the topological nature of Pt3Te4.

Interestingly, Pt-class type-II Dirac semimetal PtTe2 also hosts multiple topological surface states in a wide energy range, which arise from various band inversions within the Te p-orbital manifold.26,27 Similarly to PtTe2, Pt3Te4 exhibits topological surface states deep in the valence bands. However, there are significant differences in the surface states. For example, the Dirac-like surface state at the Γ point observed for the PtTe2 termination in Pt3Te4 is absent in bulk PtTe2. Moreover, PtTe2 hosts an electron-pocket-like surface state near the Fermi level, which arises from the band inversions in the upper conduction bands, which are absent in Pt3Te4.

The observed surface states with robust spin polarization in Pt3Te4 can be exploited for making electrical devices for spin-injection and spin-detection.28 Furthermore, the spin-momentum locked states in Pt3Te4 indicate that it can have a large spin–orbit torque. Thus, it can be used as a candidate in spin-torque devices for applications in computation, logic, and memories.28

Finally, as validated by atomic force microscopy (AFM) experiments in Supporting Information Figure S4, mitrofanovite-based surfaces also provide outstanding ambient stability even for prolonged storage in air. The chemical reactivity of both terminations is practically the same, as indicated by calculations reported in Table S1 of the Supporting Information.

Conclusions

In summary, we have demonstrated that the recently discovered ambient-stable mitrofanovite Pt3Te4 is a topological metal with termination-dependent surface states and spin polarization using a combination of ARPES and STS experiments and ab initio calculations. More interestingly, we find that the two distinct terminations (PtTe2 and Pt2Te2) can arise as different terraces on the same face of the cleaved crystal. The two terminations have dissimilar electronic surface states, even though both terminations host spin-polarized surface states. The spin-polarized surface states display polarization reversal across the zone center, which is a characteristic feature of the spin-momentum locking. Our demonstration of termination-dependent electronic surface properties and spin polarization in Pt3Te4, combined with its excellent ambient stability, makes it an interesting candidate for exploring potential nanoelectronics, spintronics, optoelectronics, and plasmonic applications in mitrofanovite-based heterostructures and interfaces.

Methods

Single-Crystal Growth

Single crystals of Pt3Te4 were grown by the self-flux method. Unlike the case of PtTe2,29 the growth window of Pt3Te4 is narrow. The mixtures of high-purity Pt foil and Te ingots with the molar ratio of 51:49 were inserted in an alumina crucible and sealed into an evacuated quartz ampule. The quartz ampule was heated to 1080 °C for 24 h and then slowly cooled to 975 °C at a rate of 1 °C/h. The excess flux was separated by centrifugation above 970 °C and mechanical polishing. Shiny platelike Pt3Te4 single crystals were harvested with a dimension of 4 × 3 × 0.4 mm3. The flat surface of the crystal corresponds to the (001) plane, as identified by XRD analyses reported in Figure S1 of the Supporting Information.

STM-ARPES

STM/STS were obtained with in situ STM/S (introduced in ref (30)) on the same surfaces for which the ARPES data in Figures 3 and 4 were collected. The topographic images (Figure 1e and the right-side insets) were measured with constant current mode. The dI/dV curves (Figures 1f and 1h) were numerically obtained from the measured I–V curves. All STM/STS experiments were carried out at room temperature.

Spin-ARPES experiments were carried out on the APE-LE beamline at Elettra synchrotron, described in ref (31). We note here that with the available beam-spot size on the sample of 150 × 50 μm2, we could clearly distinguish between two different situations regarding the electronic band structures (as summarized in Figures 3 and 4) simply by moving the sample in front of the beam. This is feasible, considering that the size of terraces on as-cleaved Pt3Te4 surfaces exceeds 150 μm2.

Computational Framework

First-principles calculations for the electronic properties were carried out using DFT, as implemented in the Vienna ab initio Simulation Package (VASP).32,33 The exchange-correlation effects were incorporated using the Perdew–Burke–Ernzerhof (PBE) implementation of the generalized gradient approximation (GGA).34 A plane wave basis set with a cutoff energy of 500 eV was used. The ionic relaxation was performed until the force on each atom was lower than 10–3 eV/Å. The self-consistency convergence criteria for the total energies were set to 10–7 eV, and a Γ-centered 8 × 8 × 8 Monkhorst–Pack k-point grid35 was used to perform the Brillouin zone integration. We constructed the tight binding model with the atom centered “Wannier-like” orbitals using the VASP2WANNIER9036 interface. A surface energy spectrum was obtained within the iterative Green’s function method following the implementation in the WannierTools package.37

Acknowledgments

This work has been partly performed in the framework of the nanoscience foundry and fine analysis (NFFA-MUR Italy Progetti Internazionali) facility. L.Z. acknowledges funding by the National Natural Science Foundation of China (No. 21775078). F.C.B. acknowledges funding by the DFG through the SFB 1083 Structure and Dynamics of Internal Interfaces (Project A 12). D.W.B. acknowledges support by Ministry of Science and Higher Education of the Russian Federation (through the basic part of the government mandate, Project No. FEUZ-2020-0060) and Jiangsu Innovative and Entrepreneurial Talents Project. B.G. and A.A. acknowledge funding from Science and Engineering Research Board (SERB) and Department of Science and Technology (DST), government of India. A.A. thanks the HPC facility at IIT Kanpur for computational resources. C.S.L. and C.N.K. acknowledge funding by the Ministry of Science and Technology of Taiwan (MOST-110-2124-M-006-010).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c04766.

  • Additional information about (i) experimental characterization, (ii) the topological invariants, (iii) ARPES measurements, and (iv) ambient stability of Pt3Te4 (PDF)

Author Contributions

∇ J.F., B.G., and I.V. contributed equally. The project was conceived and coordinated by A.P. STM/STS experiments were carried out by J.F. The theoretical model was elaborated by B.G., A.B.S., and A.A. LEED experiments were carried out by F.C.B. and A.P. Spin-ARPES and XPS experiments were performed by D.M., J.F., and I.V. Ambient stability was addressed by D.W.B., L.Z., and A.P. Samples were grown by C.N.K., C.S.L., and A.P. The paper was written by J.F., I.V., B.G., A.A., and A.P.

The authors declare no competing financial interest.

Supplementary Material

nn1c04766_si_001.pdf (991.9KB, pdf)

References

  1. Breitkreiz M.; Brouwer P. W. Large Contribution of Fermi Arcs to the Conductivity of Topological Metals. Phys. Rev. Lett. 2019, 123 (6), 066804. 10.1103/PhysRevLett.123.066804. [DOI] [PubMed] [Google Scholar]
  2. Hosen M. M.; Dimitri K.; Nandy A. K.; Aperis A.; Sankar R.; Dhakal G.; Maldonado P.; Kabir F.; Sims C.; Chou F.; Kaczorowski D.; Durakiewicz T.; Oppeneer P. M.; Neupane M. Distinct Multiple Fermionic States in a Single Topological Metal. Nat. Commun. 2018, 9 (1), 3002. 10.1038/s41467-018-05233-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kumar N.; Sun Y.; Nicklas M.; Watzman S. J.; Young O.; Leermakers I.; Hornung J.; Klotz J.; Gooth J.; Manna K.; Süß V.; Guin S. N.; Förster T.; Schmidt M.; Muechler L.; Yan B.; Werner P.; Schnelle W.; Zeitler U.; Wosnitza J.; Parkin S. S. P.; Felser C.; Shekhar C. Extremely High Conductivity Observed in the Triple Point Topological Metal MoP. Nat. Commun. 2019, 10 (1), 2475. 10.1038/s41467-019-10126-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Li Y.; Haldane F. D. M. Topological Nodal Cooper Pairing in Doped Weyl Metals. Phys. Rev. Lett. 2018, 120 (6), 067003. 10.1103/PhysRevLett.120.067003. [DOI] [PubMed] [Google Scholar]
  5. Nayak J.; Wu S. C.; Kumar N.; Shekhar C.; Singh S.; Fink J.; Rienks E. E. D.; Fecher G. H.; Parkin S. S. P.; Yan B.; Felser C. Multiple Dirac Cones at the Surface of the Topological Metal LaBi. Nat. Commun. 2017, 8, 13942. 10.1038/ncomms13942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Shao D. F.; Gurung G.; Zhang S. H.; Tsymbal E. Y. Dirac Nodal Line Metal for Topological Antiferromagnetic Spintronics. Phys. Rev. Lett. 2019, 122 (7), 077203. 10.1103/PhysRevLett.122.077203. [DOI] [PubMed] [Google Scholar]
  7. Wang Z.; Gresch D.; Soluyanov A. A.; Xie W.; Kushwaha S.; Dai X.; Troyer M.; Cava R. J.; Bernevig B. A. MoTe2: A Type-II Weyl Topological Metal. Phys. Rev. Lett. 2016, 117 (5), 056805. 10.1103/PhysRevLett.117.056805. [DOI] [PubMed] [Google Scholar]
  8. Ortiz B. R.; Teicher S. M.; Hu Y.; Zuo J. L.; Sarte P. M.; Schueller E. C.; Abeykoon A. M.; Krogstad M. J.; Rosenkranz S.; Osborn R. CsV3Sb5: A Z2 Topological Kagome Metal with a Superconducting Ground State. Phys. Rev. Lett. 2020, 125 (24), 247002. 10.1103/PhysRevLett.125.247002. [DOI] [PubMed] [Google Scholar]
  9. Li S.; Yu Z.-M.; Yao Y.; Yang S. A. Type-II Topological Metals. Frontiers of Physics 2020, 15 (4), 43201. 10.1007/s11467-020-0963-7. [DOI] [Google Scholar]
  10. Politano A.; Chiarello G.; Ghosh B.; Sadhukhan K.; Kuo C.-N.; Lue C. S.; Pellegrini V.; Agarwal A. 3D Dirac Plasmons in the Type-II Dirac Semimetal PtTe2. Phys. Rev. Lett. 2018, 121 (8), 086804. 10.1103/PhysRevLett.121.086804. [DOI] [PubMed] [Google Scholar]
  11. Armitage N.; Mele E.; Vishwanath A. Weyl and Dirac Semimetals in Three-Dimensional Solids. Rev. Mod. Phys. 2018, 90 (1), 015001. 10.1103/RevModPhys.90.015001. [DOI] [Google Scholar]
  12. Bansil A.; Lin H.; Das T. Colloquium: Topological Band Theory. Rev. Mod. Phys. 2016, 88 (2), 021004. 10.1103/RevModPhys.88.021004. [DOI] [Google Scholar]
  13. Guan S.-Y.; Chen P.-J.; Chu M.-W.; Sankar R.; Chou F.; Jeng H.-T.; Chang C.-S.; Chuang T.-M. Superconducting Topological Surface States in the Noncentrosymmetric Bulk Superconductor PbTaSe2. Sci. Adv. 2016, 2 (11), e1600894. 10.1126/sciadv.1600894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Sato M.; Ando Y. Topological Superconductors: a Review. Rep. Prog. Phys. 2017, 80 (7), 076501. 10.1088/1361-6633/aa6ac7. [DOI] [PubMed] [Google Scholar]
  15. Yang Q.; Li G.; Manna K.; Fan F.; Felser C.; Sun Y. Topological Engineering of Pt-Group-Metal-Based Chiral Crystals toward High-Efficiency Hydrogen Evolution Catalysts. Adv. Mater. 2020, 32 (14), 1908518. 10.1002/adma.201908518. [DOI] [PubMed] [Google Scholar]
  16. Xiao Z.; Laplante A. Characterizing and Recovering the Platinum Group Minerals––A Review. Miner. Eng. 2004, 17 (9–10), 961–979. 10.1016/j.mineng.2004.04.001. [DOI] [Google Scholar]
  17. Bahramy M. S.; Clark O. J.; Yang B. J.; Feng J.; Bawden L.; Riley J. M.; Marković I.; Mazzola F.; Sunko V.; Biswas D.; Cooil S. P.; Jorge M.; Wells J. W.; Leandersson M.; Balasubramanian T.; Fujii J.; Vobornik I.; Rault J. E.; Kim T. K.; Hoesch M.; Okawa K.; Asakawa M.; Sasagawa T.; Eknapakul T.; Meevasana W.; King P. D. C. Ubiquitous Formation of Bulk Dirac Cones and Topological Surface States from a Single Orbital Manifold in Transition-Metal Dichalcogenides. Nat. Mater. 2018, 17 (1), 21–28. 10.1038/nmat5031. [DOI] [PubMed] [Google Scholar]
  18. D’Olimpio G.; Guo C.; Kuo C.-N.; Edla R.; Lue C. S.; Ottaviano L.; Torelli P.; Wang L.; Boukhvalov D. W.; Politano A. PdTe2 Transition-Metal Dichalcogenide: Chemical Reactivity, Thermal Stability and Device Implementation. Adv. Funct. Mater. 2020, 30 (5), 1906556. 10.1002/adfm.201906556. [DOI] [Google Scholar]
  19. Xu H.; Guo C.; Zhang J.; Guo W.; Kuo C. N.; Lue C. S.; Hu W.; Wang L.; Chen G.; Politano A.; Chen X.; Lu W. PtTe2-Based Type-II Dirac Semimetal and Its van der Waals Heterostructure for Sensitive Room Temperature Terahertz Photodetection. Small 2019, 15 (52), 1903362. 10.1002/smll.201903362. [DOI] [PubMed] [Google Scholar]
  20. Kireev D.; Okogbue E.; Jayanth R. T.; Ko T.-J.; Jung Y.; Akinwande D. Multipurpose and Reusable Ultrathin Electronic Tattoos Based on PtSe2 and PtTe2. ACS Nano 2021, 15 (2), 2800–2811. 10.1021/acsnano.0c08689. [DOI] [PubMed] [Google Scholar]
  21. Subbotin V. V.; Vymazalová A.; Laufek F.; Savchenko Y. E.; Stanley C. J.; Gabov D. A.; Plášil J. Mitrofanovite, Pt3Te4, a New Mineral from the East Chuarvy Deposit, Fedorovo-Pana Intrusion, Kola Peninsula, Russia. Mineral. Mag. 2019, 83 (4), 523–530. 10.1180/mgm.2018.150. [DOI] [Google Scholar]
  22. Makvandi S.; Pagé P.; Tremblay J.; Girard R. Exploration for Platinum-Group Minerals in Till: A New Approach to the Recovery, Counting, Mineral Identification and Chemical Characterization. Minerals 2021, 11 (3), 264. 10.3390/min11030264. [DOI] [Google Scholar]
  23. Bae D.; Park K.; Kwon H.; Won D.; Ling N.; Baik H.; Yang J.; Park H. J.; Cho J.; Yang H. Mitrofanovite, Layered Platinum Telluride, for Active Hydrogen Evolution. ACS Appl. Mater. Interfaces 2021, 13 (2), 2437–2446. 10.1021/acsami.0c16098. [DOI] [PubMed] [Google Scholar]
  24. Tanuma S.; Powell C. J.; Penn D. R. Calculations of Electron Inelastic Mean Free Paths (IMFPS). IV. Evaluation of Calculated IMFPs and of the Predictive IMFP Formula TPP-2 for Electron Energies Between 50 and 2000 eV. Surf. Interface Anal. 1993, 20 (1), 77–89. 10.1002/sia.740200112. [DOI] [Google Scholar]
  25. Kane C. L.; Mele E. J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95 (22), 226801. 10.1103/PhysRevLett.95.226801. [DOI] [PubMed] [Google Scholar]
  26. Yan M.; Huang H.; Zhang K.; Wang E.; Yao W.; Deng K.; Wan G.; Zhang H.; Arita M.; Yang H. Lorentz-Violating Type-II Dirac Fermions in Transition Metal Dichalcogenide PtTe2. Nat. Commun. 2017, 8 (1), 257. 10.1038/s41467-017-00280-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ghosh B.; Mondal D.; Kuo C.-N.; Lue C. S.; Nayak J.; Fujii J.; Vobornik I.; Politano A.; Agarwal A. Observation of Bulk States and Spin-Polarized Topological Surface States in Transition Metal Dichalcogenide Dirac Semimetal Candidate NiTe2. Phys. Rev. B 2019, 100 (19), 195134. 10.1103/PhysRevB.100.195134. [DOI] [Google Scholar]
  28. Tang J.; Chang L.-T.; Kou X.; Murata K.; Choi E. S.; Lang M.; Fan Y.; Jiang Y.; Montazeri M.; Jiang W.; Wang Y.; He L.; Wang K. L. Electrical Detection of Spin-Polarized Surface States Conduction in (Bi0.53Sb0.47)2Te3 Topological Insulator. Nano Lett. 2014, 14 (9), 5423–5429. 10.1021/nl5026198. [DOI] [PubMed] [Google Scholar]
  29. Dey S.; Jain V. K. Platinum Group Metal Chalcogenides. Platinum Metals Review 2004, 48 (1), 16–28. [Google Scholar]
  30. Panaccione G.; Vobornik I.; Fujii J.; Krizmancic D.; Annese E.; Giovanelli L.; MacCherozzi F.; Salvador F.; De Luisa A.; Benedetti D.; Gruden A.; Bertoch P.; Polack F.; Cocco D.; Sostero G.; Diviacco B.; Hochstrasser M.; Maier U.; Pescia D.; Back C. H.; Greber T.; Osterwalder J.; Galaktionov M.; Sancrotti M.; Rossi G. Advanced Photoelectric Effect Experiment Beamline at Elettra: A Surface Science Laboratory Coupled with Synchrotron Radiation. Rev. Sci. Instrum. 2009, 80 (4), 043105. 10.1063/1.3119364. [DOI] [PubMed] [Google Scholar]
  31. Bigi C.; Das P. K.; Benedetti D.; Salvador F.; Krizmancic D.; Sergo R.; Martin A.; Panaccione G.; Rossi G.; Fujii J. Very Efficient Spin Polarization Analysis (VESPA): New Exchange Scattering-Based Setup for Spin-Resolved ARPES at APE-NFFA Beamline at Elettra. J. Synchrotron Radiat. 2017, 24 (4), 750–756. 10.1107/S1600577517006907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kresse G.; Furthmüller J. Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  33. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59 (3), 1758. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  34. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  35. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13 (12), 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  36. Marzari N.; Vanderbilt D. Maximally Localized Generalized Wannier Functions for Composite Energy Bands. Phys. Rev. B 1997, 56 (20), 12847. 10.1103/PhysRevB.56.12847. [DOI] [Google Scholar]
  37. Wu Q.; Zhang S.; Song H.-F.; Troyer M.; Soluyanov A. A. WannierTools: An Open-Source Software Package for Novel Topological Materials. Comput. Phys. Commun. 2018, 224, 405–416. 10.1016/j.cpc.2017.09.033. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn1c04766_si_001.pdf (991.9KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES