A hybrid mathematical modelling approach for energy generation from hazardous waste during the COVID-19 pandemic

Abstract

The COVID-19 virus in a short time has caused a terrible crisis that has been spread around the world. This crisis has affected human life in several dimensions, one of which is a sharp increase in urban waste. This increase in waste volume during the pandemic, in addition to the intense increase in costs associated with the risks of virus contagion through infectious waste. In this study, a hybrid mathematical modelling approach including a Bi-level programming model for infectious waste management has been proposed. At the higher level of the model, government decisions regarding the total costs related to infectious waste must be minimized. At this level, the collected infectious waste is converted into energy, the revenue of which is returned to the system. The lower level relates to the risks of virus contagion through infectious waste, which can be catastrophic if ignored. This study has considered the low, medium, high and very high prevalence scenarios as key parameters for the production of waste. In addition, the uncertainty in citizens’ demand for waste collection was also included in the proposed model. The results showed that by energy production from waste during the COVID-19 pandemic, 34% of the total cost of collecting and transporting waste can be compensated. Finally, this paper obtained useful managerial insights using the data of Kermanshah city as a real case.

Graphical abstract

The indexes

i

A citizen's index

j

A hospitals index

w

A total waste index

w'

A MW index

w''

An IW index

e

An energy generated index

f

A collection centre index

r

A recycling centre index

h

A waste incinerator centre index

v

A special shipper index

k

A capacity level for the collection centres

l

A capacity level for the recycling centres

The parameters

$n_i^w$

The number of persons that exposed to risk of virus contagion by waste $w$ in locations $i$

$n{\prime }_{fh}^{w^{″}}$

The number of persons that exposed to risk of virus contagion by IW $w^{″}$ during transportation from the collection centre $f$ to the waste incinerator centers $h$

$n^{\prime }{\prime }_{jh}^{w^{″}}$

The number of persons that exposed to risk of virus contagion by IW $w^{″}$ during transportation from the hospital $j$ to the waste incinerator centers $h$

$n^{″}{\prime }_h^{w^{″}}$

The number of persons that exposed to risk of COVID-19 via IW unit $w^{″}$ at location of waste incinerator centres $h$

$c{s}_{if}^w$

The cost of collecting each $w$ from the location $i$ by the collection centre $f$

$c{r}_{fr}^{w^{\prime }}$

The cost of transporting a MW unit $w^{\prime }$ from the collection center $f$ to the recycling centers $r$

$c{w}_{fh}^{w^{″}}$

The cost of transporting an IW unit $w^{″}$ from the collection center $f$ to the waste incinerator centres $h$

$c{h}_{jh}^{w^{″}}$

The cost of transporting an IW unit $w^{″}$ from the hospital $j$ to the waste incinerator centers $h$

$p{k}_k^{w^{″}}$

Sale price per unit of energy generated $k$ by each unit waste $w^{″}$

$p{r}_g^{w^{″}}$

Sale price per unit of material recycled $g$ from each unit waste $w^{\prime }$

$c{f}_f^k$

The cost of setting up a collection centre $f$ with capacity level $k$

$c{l}_r^l$

The cost of setting up a recycling centre $r$ with a capacity level $l$

$r{a}^w$

Relative risk of virus contagion by each unit waste $w$

$r{b}^{w^{″}}$

Relative risk of virus contagion by each unit waste $w^{″}$

$e{g}^{w^{″}}$

Relative energy generated by each unit waste $w^{″}$

$m{r}^{w^{\prime }}$

Relative material recycled by each unit waste $w^{\prime }$

$vo{l}^w$

The unit volume of waste $w$

$d_i^w$

The demand for collection waste unit $w$ by citizen $i$

$fs{c}_f^k$

The capacity level $k$ of the collection centers $f$

$rw{c}_r^l$

The capacity level $l$ recycling centers $r$

The decision variables

${\mu }_{if}^w$

The amount of separated waste $w$ by the citizen $i$ which is collected by the collection center $f$

${\phi }_{fr}^{l{w}^{\prime }}$

The amount of a MW unit$w^{\prime }$ moved from the collection center $f$ with the capacity level $l$ to the recycling centers $r$

${\xi }_{fhv}^{k{w}^{″}}$

The amount of IW unit $w^{″}$ moved from the collection center $f$ with the capacity level $k$ to the waste incinerator centers $h$ by special shipper $v$

${\Omega }_{jhv}^{w^{″}}$

The amount of IW unit $w^{″}$ moved from the hospital $j$to the waste incinerator centers $h$ by special shipper $v$

${\alpha }_f^k$

1 if setting up a collection centre $f$ with capacity level $k$ otherwise 0

${\beta }_r^l$

1 if setting up a recycling centre $r$ with a capacity of $l$ otherwise 0

Abbreviations Discribtions

PPE

Personal Protective Equipment

IW

Infectious Waste

MSW

Municipal Solid Waste

MW

Municipal Waste

WTE

Waste-To-Energy

OR

Operations Reaserch

KKT

Karush - Kuhn - Tucker

HMM

Hybrid Mathematical Modelling

1. Introduction

In recent years, SARS-Cov-1 and MERS viruses, which belong to the coronavirus family, have caused widespread epidemics. In December 2019, a new type of this family called (COVID-19) was reported in Wuhan, China, which quickly caused a global health emergency (World Health Organization, 2020). The crisis caused by COVID-19 has significantly increased the volume of Infectious Waste (IW), which poses a high risk of driving the disease (Valizadeh and Mozafari, 2021). Recently, with the widespread prevalence of COVID-19, serious environmental problems have arisen in the field of waste management (Nzediegwu and Chang, 2020). Due to the dramatic increase in demand for disposable products, Personal Protective Equipment (PPE), laboratory kits, and plastic devices such as syringes used in prevention and treatment, a new environmental crisis is occurring (Klemeš et al., 2020). PPE, aprons, and disposable gloves are commonly used to protect people from pathogens and contaminants (Singh et al., 2020). While previously the use of these supplies was common only in hospitals and industrial centres, the prevalence of COVID-19 necessitated their use in home quarantine and personal protection, which led to the rapid accumulation of IW. In this regard, a new environmental challenge has emerged to deal with the myriad amounts of COVID-19 waste. For example, in China, approximately 468.9 tonnes of IR are generated in association with COVID-19 in hospitals per day (Peng et al., 2020). This in turn will cause environmental and health problems if collected, transported and managed inappropriately (Nzediegwu and Chang, 2020). The threat of unsafe disposal of this waste is palpable and immediate (Singh et al., 2020). In the wake of this crisis, some organizations have issued guidelines to raise awareness and encourage solid waste management measures to protect public health and the environment (SWANA, 2020).

Recent research has shown that the COVID-19 virus can remain on surfaces for up to 9 days (Kampf et al., 2020), although the lifespan of the virus depends on the type of material. The COVID-19 can survive up to 3 days on plastic surfaces and up to 4 days on solid surfaces (Nghiem et al., 2020). Thus, improper handling of PPE and other healthcare waste can increase the prevalence of viral diseases in the environment (Nzediegwu and Chang, 2020). Improper management of infectious waste during epidemics can lead to further disease outbreaks (Valizadeh et al., 2021). However, landfills are a potential threat to the area due to environmental pollution (Escamilla-García et al., 2020). These places are often open which leads to air pollution. This issue is more worrying in third world countries because waste disposal in most developing countries such as the Philippines, Thailand, Malaysia, Indonesia, India, Bangladesh, Cambodia, Vietnam, and Palestine are performed in open locations (Mol and Caldas, 2020; Ferronato et al., 2020).

Waste management solutions should not only be healthy and environmentally sound but also economically viable. Among the thermal methods, incineration has been identified as the main Waste-To-Energy (WTE) method (Reddy, 2019). Since COVID-19 waste is not recyclable and should be discarded immediately, other methods such as energy recovery may be beneficial. Energy generation from waste is one of the most important economic programs, in line with the EU's commitments under the 2030 Sustainable Development Programme (Malinauskaite et al., 2017). The main objective of this study is to provide a mathematical model for the collection of large volumes of IW caused by the COVID-19 crisis. To illustrate the research question, we present a case study from Kermanshah. We shows generation of IW during COVID-19 pandemic by country in Table 1 .

Table 1.

Generation of IW during COVID-19 pandemic by country (Agamuthu and Barasarathi, 2020).

Country	Amount of waste generated during COVID-19 (kg/bed/day)	Percentage of increase in CW generation during COVID-19 pandemic	References
Taiwan	0.9–2.7	No data	Chiang et al. (2006)
Jordan	3.95	1000%	Abu-Qdais et al. (2020)
Wuhan, People's Republic of China	0.6–2.5	213%	Yu et al. (2020)
Bandung, Indonesia	2.2	17%	Damanhuri (2020)
Penang, Malaysia	0.4–1.0	27%	This case study; Astro Awani (2020)
Thailand	2.9	No data	Institute for Global Environmental Strategies (2020)
Mexico	2.0–2.2	No data	Institute for Global Environmental Strategies (2020)

Due to the virus being carried by surfaces, separating IW from other Municipal Waste (MW) at the source seems to be a good solution. This research specifically answers the following questions: (1) How can an efficient model be developed to make decisions about energy generation from COVID-19 infectious waste? (2) How can we consider the concern of driving the COVID-19 virus by IW in waste collection and transportation models? (3) Given the widespread COVID-19 crisis and the large volume generated in MW and IW, how can manage the cost of waste collection?

Section 2 briefly provides the literature review. We provide the research methodology in Section 3 and formulate the mathematical model in Section 4. The results of solving the model and the case study survey are provided in Section 5. Finally, conclusions and future suggestions are presented in Section 6.

2. Literature review

Today, waste engineering and management have become a considerable issue as one of the world's advanced sciences and an inseparable part of urban management. There are some recent studies on municipal waste management. Abdelli et al. (2016) proposed an optimization of municipal solid waste collection in terms of collection cost and polluting emissions (carbon oxides, carbon dioxides, nitrogen oxides and particulate matter). Soltani et al. (2017) provided a decision support framework is required to assess various waste treatment options and predict the optimal decision, considering multiple criteria and conflicting preferences of multiple stakeholders. Similarly, Rahimi et al. (2020) proposed a decision support system for site location of landfill considering sustainable aspects including environmental, economic, and social criteria. Asefi et al. (2019) proposed a two-stage stochastic optimization approach to effectively support the cost-effective WM transportation system by determining the optimal fleet size and decomposition, vehicles routes and capacity-allocation to the system components. Bui et al. (2020) studied effective municipal solid waste management capability under uncertainty in Vietnam.

In this section, literature related to the research problem is classified into three subsections. In the first one, the studies related to energy generation are reviewed in subsections 2.1. The studies related to Bi-level programming problems in waste management are reviewed in subsections 2.2. Finally, the research gap and contributions of this study are given in Subsection 2.3.

2.1. Energy generation from waste

Population growth, changes in lifestyle and increased consumption have led to more waste generation (Abila, 2014). This waste generation has been multiplied COVID-19's pandemic. Thus, the energy crisis on one hand and the increase in municipal waste due to the COVID-19 epidemic on the other hand have become challenges for governments. In 2011, Norway recycled almost 40% of its waste. They buried only about 2% of the remaining waste (Valizadeh, 2020). In this regard, many researchers have examined energy production from waste from different perspectives. Stein (2012) studied new energy generation from waste technologies. Abila (2014) explored the options for municipal waste management and advanced the discussion towards energy derivation and improved material recovery in Nigeria. Safar Korai et al. (2017) examined the feasibility of energy generation from municipal solid waste and available management practices in Pakistan. Khan and Kabir (2019) examined waste-to-energy generation technologies and developing economies. Agaton et al. (2020) proposed an investment model to analyze the economic feasibility of waste-to-energy projects in developing countries using the Philippines as a case study. Melikoglu (2020) provided a study that predicts food waste and used it as the energy potential of Turkish hospitals. Zhao and You (2021) provided the optimization of large-energy-water-waste nexus systems for New York State under the COVID-19 pandemic to alleviate environmental and health concerns. Some studies in this area are presented in Table 2 .

Table 2.

Research on the hazardous waste collection under uncertainty.

Authors	Energy type		Objective			Method			Uncertain
	Electrical	Bio Gas	Economic	Environmental	Social	laboratory	Statistical	OR	Fuzzy optimization	Robust optimization
Schneider and Bogdan (2011)			✓					✓	✓
Lou et al. (2013)			✓	✓			✓		✓
Nayal et al. (2016)		✓	✓	✓			✓
Zhang et al. (2017)	✓		✓					✓
de Mello et al. (2018)		✓	✓				✓
Ribeiro et al. (2018)		✓		✓		✓			✓
Hazra et al. (2018)		✓		✓			✓
Gopal et al. (2019)		✓	✓					✓
Fetanat et al. (2019)	✓		✓				✓
Haraguchi et al. (2019)			✓				✓
Katinas et al. (2019)		✓	✓					✓	✓
Zhang et al. (2019)	✓	✓		✓				✓
Hu et al. (2020)	✓		✓					✓		✓
Zhao and You (2021)	✓		✓	✓				✓
Current research	✓		✓	✓	✓			✓		✓

2.2. Survey of the Bi-level programming problems in waste management

The Bi-level scheduling problem is a type of multi-level scheduling approach that deals with the interaction of leader and follower decision-makers (Safaei et al., 2018). There is a line of research in the field of waste management that considers Bi-level programming problems for model formulation. Chen et al. (2015) created a quantitative forecasting model by combining forecasting and scenario analysis to forecast municipal solid waste in Beijing. They introduced a Bi-level programming problem in which greenhouse gas reduction and system cost decrease was considered at the upper and lower levels, respectively. Xu and Wei (2012) studied the problem of location and allocation in construction and demolition waste management by presenting a Bi-level model.

Among recent research in this field, Pouriani et al. (2019) provided a solid municipal waste management network to minimize various costs and presented a Bi-level linear programming model. Muneeb et al. (2018) presented a Bi-level decision model for solid municipal waste management in which minimizing the net shipment costs and maximizing the revenue of medical facilities were considered at the first and second levels, respectively. Sadeghian Sharif et al. (2018) investigated solid municipal waste management network as well as production policies from the organization perspective. The results showed that the proposed method can reduce the complexity of the problem and save significantly computational time. Yazdanbakhsh (2018) provided a Bi-level life cycle assessment framework to model alternative waste management approaches in which the effects are measured and compared at two scales of strategy and decision making. Saeidi-Mobarakeh et al. (2020) proposed a Bi-level mathematical model to model hazardous waste management. To deal with uncertainty, they considered possible, optimistic and pessimistic scenarios for the key parameters. Table 3 illustrates the detailed specification of the Bi-level programming approaches adopted in waste management problems.

Table 3.

Researchers conducted in the field of Bi-level programming applications in the WM issues.

Authors	Waste		Function type			Waste type		The country of the case study
	Hazardous	Non- Hazardous	Cost	Risk		Municipal	Hospital
Das et al., 2012		✓	✓			✓		–
Zhang and Huang (2014)		✓	✓			✓		–
Chen et al. (2015)		✓	✓			✓		China
Inghels et al. (2016)		✓	✓			✓		–
Nguyen-Trong et al. (2017)		✓	✓			✓		Vietnam
De Bruecker et al. (2018)		✓	✓			✓		Belgium
Yazdanbakhsh et al. (2018)		✓	✓			✓		Iran
Sadeghian Sharif et al. (2018)		✓	✓			✓		Iran
Calabrò and Komilis, 2019		✓	✓			✓		Italy
Muneeb et al. (2020)		✓	✓				✓	–
Saeidi-Mobarakeh et al. (2020)	✓		✓	✓			✓	Iran
Yu et al. (2020)		✓	✓			✓		–
Blazquez & Paredes-Belmar (2020)		✓	✓			✓		Chile
Hannan et al., 2020		✓	✓			✓		–
Lu et al. (2020)		✓	✓			✓		China
Vu et al. (2021)	✓			✓			✓	Canada
Wang et al. (2021)	✓		✓	✓		✓		Canada
Panzone et al. (2021)		✓	✓			✓		England
Valizadeh et al. (2021)	✓		✓	✓	✓	✓	✓	Iran
Yazdani et al. (2021)		✓	✓			✓		Australia
Current research	✓		✓	✓	✓	✓	✓	Iran

2.3. Research gap and contributions

As can be seen from Table 1, Table 2, no research to date has considered the energy generation from COVID-19 infectious waste. This process is useful in three ways. First, the hazardous waste is destroyed, and the virus is prevented from spreading. Second, after incineration, the volume of waste is greatly reduced, and less space is required for disposal. This brings environmental benefits. Third, the energy produced by this method has economic value and can partially offset government costs. There is also little research on the risk of virus contagion through waste. Other research has focused on scheduling waste transportation and collection at regular intervals. However, in this study, we propose a hybrid mathematical model that addresses two important concerns related to waste management during pandemic COVID-19. Due to the multiplication of infectious waste generation, the first concern of governments is the proper management of costs in this situation (which due to the existing economic crisis by the spread of the virus is very important). The second concern is the risk of virus contagion through infectious waste, which has been widely used due to the use of hygiene items and face masks (PPT). Meanwhile, concerns about sustainable energy production remain a challenging issue for many governments. To take these concerns into account, we developed a Bi-level model to minimize the risk of virus contagion through infectious waste, in addition to considering the total cost. We also considered practical assumptions such as waste separation at source and installation of collection centres and special transportation for infectious waste collection in the context of the global crisis. In this research, the revenue of the generated energy returns to the system. The contributions of this study are categorized as below:

• i.As the first innovation in this study, we consider the energy generation from COVID-19 infectious waste. One advantage of this action is government revenue from non-recyclable waste, which can offset some of the costs associated with waste management. On the other hand, leaving infectious waste from COVID-19 at the disposal site can cause serious health and environmental problems. By burning this waste in incinerators, in addition to repelling potential viruses, the energy can be produced.
• ii.Researchers have ignored waste collection programs as Bi-level in the literature, mainly focusing only on reducing the length of transportation paths and reducing costs. Therefore, this paper proposes a Bi-level programming problem for waste collection and transportation planning in which the concern of the governments for economy and environment is considered as a leader and the contractor's concern as a social concern is considered as a follower. This paper uses hybrid mathematical modelling with a Bi-level model approach (leader-follower) to address two important issues. To the best of our knowledge, few studies have used hybrid mathematical modelling with a Bi-level model approach (leader-follower) to improve waste management during a pandemic.
• iii.Finally, we present the proposed model as a robust model combining the Karush - Kuhn - Tucker (KKT) conditions and the Benders decomposition method. We consider the potential uncertainty of the COVID-19 outbreak by considering different scenarios. According to our research, no research has considered the virus outbreak scenarios in waste planning problems, and this research is unique. Moreover, the proposed model finally evaluates the robustness of the model and the robustness of the solution with real data.

3. Research methodology

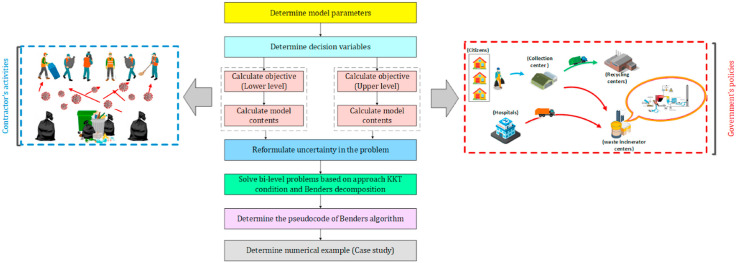
To fill the research gap described in the previous section, this study seeks a solution to minimize the total cost of waste management and the risk of COVID-19 virus contagion through waste. To achieve these objectives, a hybrid mathematical modelling (HMM) based on a Bi-level model (leader-follower approach) was proposed. To this end, as shown in Fig. 1 , the research method was divided into three steps:

• ⁃Phase 1: First, the indicators are presented. Then, by defining the parameters and decision variables, the objective function is formulated for each level (upper and lower). Finally, the problem constraints are defined to achieve the defined objectives.
• ⁃Phase 2: In the hybrid mathematical model in this research, consider the uncertainty of the proposed model, the parameter ${\rho }^s$ related to the probability of occurrence of each scenario is determined. Once the Bi-level problem has been formulated, it is necessary to transform the problem into a unit-level problem. The reason for this is that solving the model in the current situation is complicated and might be infeasible. Therefore, the Karush–Kuhn–Tucker (KKT) conditions have been used to level the proposed model. This method considers the constraints of the relationship between two levels of the proposed model. The details of which are given below.
• ⁃Phase 3: Due to the dimensions of the problem and the complexity of the proposed model, the Benders decomposition algorithm is used.

Fig. 1.

The proposed HMM for the problem.

The structure of the proposed HMM is shown in Fig. 1.

4. Model formulation

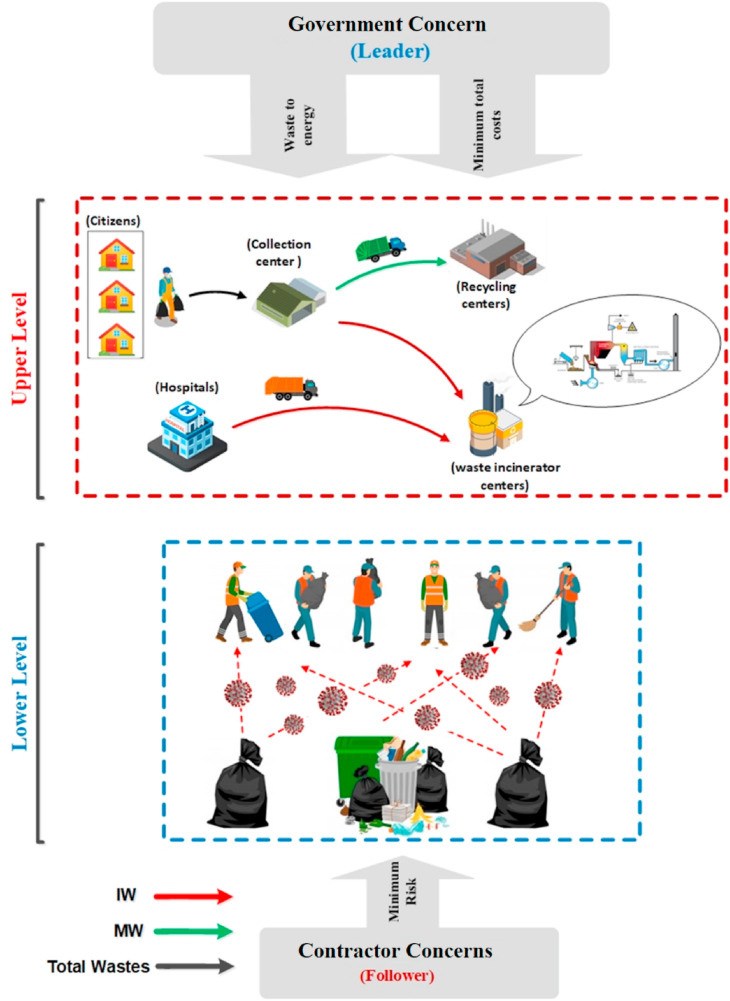
To manage waste during the COVID-19 pandemic better, all wastes are categorized into two categories: IW and MW. This can be done by citizens at home. Separated waste is collected from the citizens and transferred to the collection centres. The MW is then transported to recycling centres, and IW is shipped to waste incinerator centres by special carriers. The IW produced by hospitals is transported directly to the waste incinerator centres. IW is converted into electrical energy using incinerators and MW waste is returned to the production cycle after recycling. Therefore, by formulating the problem model, two main outcomes are pursued: (i) energy generation from infectious waste of COVID-19 and wastes collection during to COVID-19 pandemic with minimum cost. (ii) collecting and transporting all waste with minimum risk of virus contagion. In this study, the unit of all wastes includes hazardous and non-hazardous and capacities based on Kg. All costs and prices are in dollars. All volumes are based on m³ and finally, the unit of risk is determined on the basis of percentage. To explain the concept, Fig. 2 exhibits the schematic formation of the proposed leader-follower programming model.

Fig. 2.

The proposed leader-follower model.

With the outbreak of COVID- 19, the government especially urban management are not well prepared to collect the high volume of generated MW. By designing an HMM, this study considers various aspects of the problem. To achieve this, the following three assumptions are made:

Assumption 1

We assume that separating the waste at the source prevents all the waste from becoming viral and helps reduce the spread of the virus through the waste. After separation, the waste is divided into two categories: hazardous infectious waste (not recyclable and converted into energy) and non-hazardous municipal waste (recyclable).

Assumption 2

In this article, we assume that the risk of virus contagion for each type of waste (domestic infectious waste and medical infectious waste) are fairly equal.

Assumption 3

The number of vehicles, persons of the waste collectors, and capacity of municipal incinerators is considered constant in this study. In other words, we cannot bring a new vehicle or person into the waste management network.

$\mathcal{A}=\sum _{f\in F}\sum _{k\in K}c{f}_f^k{\alpha }_f^k+\sum _{r\in R}\sum _{l\in L}c{l}_r^l{\beta }_r^l$	The fixed cost related to setting up facilities
$\mathcal{G}=\sum _{i\in I}\sum _{f\in F}\sum _{w\in W}c{s}_{if}^w{d}_i^w{\mu }_{if}^w$	The cost of collection wastes
$\mathcal{Q}=\sum _{f\in F}\sum _{r\in R}\sum _{l\in L}\sum _{w^{\prime }\in W}c{r}_{fr}^{w^{\prime }}{\varphi }_{fr}^{l{w}^{\prime }}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{h\in H}c{h}_{jh}^{w^{″}}{\Omega }_{jhv}^{w^{″}}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}c{w}_{fh}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}$	The cost of transportation wastes
$\mathcal{P}=\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}e{g}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{h\in H}k{w}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The revenue caused to energy generated from wastes
$\mathcal{V}=\sum _{w^{\prime }\in W}\sum _{l\in L}\sum _{f\in F}\sum _{r\in R}m{r}^{w^{\prime }}{\varphi }_{fr}^{l{w}^{\prime }}$	The revenue caused to wastes recycled
$\mathcal{X}=\sum _{w\in W}\sum _{i\in I}\sum _{f\in F}{n}_i^{w}r{a}^w{\mu }_{if}^w$	The risk of virus contagion during wastes collection
$\mathcal{Y}=\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}n{\prime }_{fh}^{w^{″}}r{b}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}+\sum _{w^{″}\in W}\sum _{j\in J}\sum _{h\in H}\sum _{v\in V}{n}^{\prime }{\prime }_{jh}^{w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The risk of virus contagion during wastes transportation
$\mathcal{Z}=\sum _{w^{″}\in W}\sum _{j\in J}\sum _{h\in H}\sum _{v\in V}{n}^{″}{\prime }_h^{w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The risk of virus contagion during wastes incineration

The upper-level of model for the function of cost (leader) is designed as follows:

$$Min{Z}_1=\left(\mathcal{A}+\mathcal{G}+\mathcal{Q}\right)-\left(\mathcal{P}+\mathcal{V}\right)$$ (1)

s.t.

$$\sum _{i\in I}\sum _{w\in W}{d}_i^{w}vo{l}^w{\mu }_{if}^w\le \sum _{k\in K}fs{c}_f^k{\alpha }_f^k\forall f\in F$$ (2)

$$\sum _{k\in K}{\alpha }_f^k\ge 1\forall f\in F$$ (3)

$$\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }}=1\forall l\in L,w^{\prime }\in Wandr\in R$$ (4)

$$\sum _{f\in F}\sum _{w^{\prime }\in W}{\varphi }_{fr}^{l{w}^{\prime }}\le rw{c}_r^l{\beta }_r^l\forall r\in R,l\in L$$ (5)

$$\sum _{l\in L}{\beta }_r^l\ge 1\forall r\in R$$ (6)

$${\varphi }_{fr}^{l{w}^{\prime }}\ge 0\forall l\in L,w^{\prime }\in W,f\in Fandr\in R$$ (7)

$${\alpha }_f^k,{\beta }_r^l\in \left\{\mathrm{0,1}\right\}\forall f\in F,k\in K,r\in R,l\in L,$$ (8)

In this model, Eq. (1) shows the upper-level problem (leader). This objective is related to minimize the total cost of the government. The first term indicates the fixed cost related to setting up facilities. The second term determines of the cost of collection wastes. The third term indicates the cost of transportation wastes. The fourth, fifth terms indicate of revenue caused to energy generated and wastes recycled. Constraint (2) indicates the limits of collection centre capacity. Constraint (3) indicates that there is at least one collection centre active for waste collection. Constraint (4) ensures that there is at least one unit of MW transported from the collection centre to the recycling centres. Constraint (5) ensures that the volume of MW transported from the collection centre to the recycling centres does not exceed the capacity of the recycling centres. Constraint (6) ensures that there is at least one active recycling centre for recycling waste. Constraint (7) are the non-negativity constraints of the continuous variables. Constraint (8) indicates the (0–1) variable.

The lower-level of model for the risk function (follower) is also designed as follows:

$$Min{Z}_2=\mathcal{X}+\mathcal{Y}+\mathcal{Z}$$ (9)

s.t.

$$\sum _{f\in F}{\mu }_{if}^w=1\forall i\in I,w\in W$$ (10)

$$\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}}\le \sum _{f\in F}{\mu }_{if}^w\forall i\in I,w^{″}\in W,w\in W$$ (11)

$$\sum _{v\in V}{\xi }_{fhv}^{k{w}^{″}}=1\forall i\in I,w^{″}\in W$$ (12)

$$\sum _{j\in J}{\Omega }_{jhv}^{w^{″}}=1\forall w^{″}\in W,h\in H,v\in V$$ (13)

$$\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}}+\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }}+\sum _{j\in J}{\Omega }_{jhv}^{w^{″}}\le \sum _{f\in F}{\mu }_{if}^w\forall i\in I,l\in L,r\in R,w^{\prime }\in W,w^{″}\in W,w\in W$$ (14)

$$\sum _{i\in I}\sum _{f\in F}{\mu }_{if}^w\le vo{l}^w\forall i\in I,w\in W$$ (15)

$${\mu }_{if}^w\ge 0,{\xi }_{fhv}^{k{w}^{″}}\ge 0,{\Omega }_{jhv}^{w^{″}}\ge 0\forall i\in I,f\in F,w\in W,w^{″}\in W,k\in K,h\in Handv\in V$$ (16)

Equation (9) represents the lower level objective function related to the risk of the contagion of COVID-19 virus from infectious waste which must minimize. The first statement is related to the risk of contagion of virus to the persons collecting the waste, the second statement indicates the risk of contagion of virus to the persons who are transporting the waste from the collection centre to the waste incinerator centres, and the third statement indicates the risk of contagion of virus from the persons who are transporting the waste from hospitals to the waste incinerator centres. Constraint (10) ensures that there is at least one unit of the MW for collection. Constraint (11) ensures that the amount of IW transported per special consignment from the collection centre to the waste incinerator centres is not more than MW (all waste). Constraint (12) indicates that at least one IW consignment is transported per special consignment from the collection centre to the waste incinerator centres. Constraint (13) ensures that at least one IW consignment is transported by special consignment from hospitals to waste incinerator centres. Constraint (14) indicates the balance between various volume of wastes. Constraint (15) relates to the volume of waste. Finally, constraint (16) is the non-negativity constraint of continuous variables.

4.1. Robust formulation

Robust optimization is a scenario-based method used to deal with uncertainty in programming problems (Valizadeh et al., 2020). This method was first proposed in 1995 by Mulvey et al. (Valizadeh et al., 2021). Robust optimization includes two types of robustness: “solution robustness” and “model robustness” (Edalatpour et al., 2018). In a two-stage stochastic programming model with a resource function, decisions related to the cost of the variables in the first stage and the average costs of the variables in the second stage are considered (Louveaux and Birge, 2001). To model the problem using two-stage stochastic programming, the decision variables should be separated into two categories: the cost function and the risk function. In this study, the decision variable related to installation of interim stations facilities $\left({\alpha }_f^k\right)$and the other variable of installation of recycling centres $\left({\beta }_r^l\right)$ is the decision of executive contractors. Under uncertain outbreak conditions COVID-19, the possible scenarios are denoted $s=\{1,\dots .,S\}$ and the following notations in relation to the scenarios can be redefined:

• $d_i^{ws}$The demand for waste collection $w$ from citizen $i$ under scenario $s;$

• ${\rho }^s$The probability of occurrence of scenario $s$;

• ${\mu }_{if}^{ws}$The number of wastes $w$ collected by the collection centre $f$ from the citizen location $i$ under scenario $s$;

• ${\varphi }_{fr}^{l{w}^{\prime }s}$The number of wastes $w$ transported from the collection centre $f$ with the capacity level $l$ to the recycling centres $r$ under scenario $s$;

• ${\xi }_{fhv}^{k{w}^{″}s}$The amount of IW unit $w^{″}$ moved from the collection centre $f$with the capacity level $k$ to the waste incinerator centres $h$ by special shipper $v$ under scenario $s$;

• ${\Omega }_{jhv}^{w^{″}s}$The amount of IW unit $w^{″}$ moved from the hospital $j$to the waste incinerator centres $h$ by special shipper $v$ under scenario $s$;

$\mathcal{A}=\sum _{f\in F}\sum _{k\in K}c{f}_f^k{\alpha }_f^k+\sum _{r\in R}\sum _{l\in L}c{l}_r^l{\beta }_r^l$	The fixed cost related to setting up facilities
${\mathcal{G}}_s=\sum _{i\in I}\sum _{f\in F}\sum _{w\in W}\sum _{s\in S}{\rho }^{s}c{s}_{if}^w{d}_i^w{\mu }_{if}^w$	The cost of collection wastes under scenario $s$;
${\mathcal{Q}}_s=\sum _{f\in F}\sum _{r\in R}\sum _{l\in L}\sum _{w^{\prime }\in W}\sum _{s\in S}{\rho }^{s}c{r}_{fr}^{w^{\prime }}{\varphi }_{fr}^{l{w}^{\prime }}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{h\in H}\sum _{s\in S}{\rho }^{s}c{h}_{jh}^{w^{″}}{\Omega }_{jhv}^{w^{″}}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}{\rho }^{s}c{w}_{fh}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}$	The cost of transportation wastes under scenario $s$;
${\mathcal{P}}_s=\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}{\rho }^{s}e{g}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}+\sum _{w^{″}\in W}\sum _{k\in K}\sum _{h\in H}\sum _{s\in S}{\rho }^{s}k{w}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The revenue caused to energy generated from wastes under scenario $s$;
${\mathcal{V}}_s=\sum _{w^{\prime }\in W}\sum _{l\in L}\sum _{f\in F}\sum _{r\in R}\sum _{s\in S}{\rho }^{s}m{r}^{w^{\prime }}{\varphi }_{fr}^{l{w}^{\prime }}$	The revenue caused to wastes recycled under scenario $s$;
${\mathcal{X}}_s=\sum _{w\in W}\sum _{i\in I}\sum _{f\in F}\sum _{s\in S}{\rho }^s{n}_i^{w}r{a}^w{\mu }_{if}^w$	The risk of virus contagion during wastes collection under scenario $s$;
${\mathcal{Y}}_s=\sum _{w^{″}\in W}\sum _{k\in K}\sum _{f\in F}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}{\rho }^{s}n{\prime }_{fh}^{w^{″}}r{b}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}+\sum _{w^{″}\in W}\sum _{j\in J}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}{\rho }^s{n}^{\prime }{\prime }_{jh}^{w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The risk of virus contagion during wastes transportation under scenario $s$;
${\mathcal{Z}}_s=\sum _{w^{″}\in W}\sum _{j\in J}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}{\rho }^s{n}^{″}{\prime }_h^{w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}}$	The risk of virus contagion during wastes incineration under scenario $s$;

Considering these new notations for the uncertain conditions of the COVID- 19 outbreak, the mathematical model developed in the previous section will be transformed as follows:

$$Min{Z}_1=\mathcal{A}+\sum _{s\in S}{\rho }^s\left(\left[{\mathcal{G}}_s+{\mathcal{Q}}_s\right]-\left[{\mathcal{P}}_s+{\mathcal{V}}_s\right]\right)+\lambda \sum _{s\in S}{\rho }^s\left(\left(\left[{\mathcal{G}}_s+{\mathcal{Q}}_s\right]-\left[{\mathcal{P}}_s+{\mathcal{V}}_s\right]\right)-\sum _{s^{\prime }\in S}{\rho }^{s^{\prime }}\left[{\mathcal{G}}_{s^{\prime }}+{\mathcal{Q}}_{s^{\prime }}\right]-\left[{\mathcal{P}}_{s^{\prime }}+{\mathcal{V}}_{s^{\prime }}\right]+2{\theta }_s\right)-\omega \sum _{s\in S}\sum _{i\in s}{\rho }^s{\delta }_{is}$$ (17)

s.t.

$$\left(\left(\left[{\mathcal{G}}_s+{\mathcal{Q}}_s\right]-\left[{\mathcal{P}}_s+{\mathcal{V}}_s\right]\right)-\sum _{s^{\prime }\in S}{\rho }^{s^{\prime }}\left[{\mathcal{G}}_{s^{\prime }}+{\mathcal{Q}}_{s^{\prime }}\right]-\left[{\mathcal{P}}_{s^{\prime }}+{\mathcal{V}}_{s^{\prime }}\right]+{\theta }_s\right)\ge 0\forall s\in S$$ (18)

$$\sum _{i\in I}\sum _{w\in W}{d}_i^{ws}vo{l}^w{\mu }_{if}^{ws}\le \sum _{k\in K}fs{c}_f^k{\alpha }_f^k\forall f\in F,s\in S$$ (19)

$$\sum _{k\in K}{\alpha }_f^k\le 1\forall f\in F$$ (20)

$$\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }s}=1\forall l\in L,w^{\prime }\in W,s\in Sandr\in R$$ (21)

$$\sum _{f\in F}\sum _{w^{\prime }\in W}{\varphi }_{fr}^{l{w}^{\prime }s}\le rw{c}_r^l{\beta }_r^l\forall r\in R,l\in L,s\in S$$ (22)

$$\sum _{l\in L}{\beta }_r^l\le 1\forall r\in R$$ (23)

$${\varphi }_{fr}^{l{w}^{\prime }s},{\theta }_s\ge 0\forall l\in L,w^{\prime }\in W,f\in F,r\in Rands\in S$$ (24)

$${\alpha }_f^k,{\beta }_r^l\in \left\{\mathrm{0,1}\right\}\forall f\in F,k\in K,r\in R,l\in L,r\in R,l\in L$$ (25)

$$Min{Z}_2=\sum _{s\in S}{\rho }^s\left({\mathcal{X}}_s+{\mathcal{Y}}_s+{\mathcal{Z}}_s\right)+\lambda \sum _{s\in S}{\rho }^s\left(\left({\mathcal{X}}_s+{\mathcal{Y}}_s+{\mathcal{Z}}_s\right)-\sum _{s^{\prime }\in S}{\rho }^{s^{\prime }}\left({\mathcal{X}}_{s^{\prime }}+{\mathcal{Y}}_{s^{\prime }}+{\mathcal{Z}}_{s^{\prime }}\right)+2{\theta }_s\right)-\omega \sum _{s\in S}\sum _{i\in s}{\rho }^s{\delta }_{is}$$ (26)

s.t.

$$\left(\left({\mathcal{X}}_s+{\mathcal{Y}}_s+{\mathcal{Z}}_s\right)-\sum _{s^{\prime }\in S}{\rho }^{s^{\prime }}\left({\mathcal{X}}_s+{\mathcal{Y}}_s+{\mathcal{Z}}_s\right)+{\theta }_s\right)\ge 0\forall s\in S$$ (27)

$$\sum _{f\in F}{\mu }_{if}^{ws}=1\forall i\in I,w\in W,s\in S$$ (28)

$$\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}s}\le \sum _{f\in F}{\mu }_{if}^{ws}\forall i\in N,w^{″}\in W,w\in W,s\in S$$ (29)

$$\sum _{v\in V}{\xi }_{fhv}^{k{w}^{″}s}=1\forall i\in I,w^{″}\in W,s\in S$$ (30)

$$\sum _{j\in J}{\Omega }_{jhv}^{w^{″}s}=1\forall w^{″}\in W,h\in H,v\in V,s\in S$$ (31)

$$\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}s}+\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }s}+\sum _{j\in J}{\Omega }_{jhv}^{w^{″}s}\le \sum _{f\in F}{\mu }_{if}^{ws}\forall i\in I,l\in L,l\in L,r\in R,w^{\prime }\in W,w^{″}\in W,w\in W,s\in S$$ (32)

$$\sum _{i\in I}\sum _{f\in F}{\mu }_{if}^{ws}\le vo{l}^w\forall i\in I,w\in W,s\in S$$ (33)

$${\mu }_{if}^{ws}\ge 0,{\xi }_{fhv}^{k{w}^{″}s},{\theta }_s\ge 0,{\Omega }_{jhv}^{w^{″}s}\ge 0\forall i\in I,f\in F,w\in W,w^{″}\in W,k\in K,h\in H,v\in Vand,s\in S$$ (34)

The proposed stochastic programming model considers citizens' demand for MW collection during the outbreak of COVID- 19. The upper level of this Bi-level programming problem (17) - (25) is related to the cost function (leader), and the lower level sub-problem (26) - (33) related to the risk function (follower). Each level seeks to optimize its objectives with its own constraints. In this model, probabilities depend on the scenarios that describe future situations.

4.2. Karush - Kuhn - Tucker (KKT) condition

The KKT conditions, which are the required optimization, are as follows.

$$\nabla f\left(x\right)=\sum _{i-1}^m{\lambda }_i\nabla g_i\left(x\right)$$ (35)

s.t:

$${\lambda }_i{g}_i\left(x\right)=0i=1,\dots ,m$$ (36)

$$g_i\left(x\right)\le 0i=1,\dots ,m$$ (37)

$${\lambda }_i\ge 0i=1,\dots ,m$$ (38)

The Bi-level model of this research can be transformed into a single-level model using relations defined (35) to (38). In the first step, we need to define dual variables for all constraints of the lower level problem, and then we should replace the KKT condition of the lower-level with the upper-level problem. Next, we implement the KKT condition as well as the Benders decomposition method on the problem.

4.3. Benders decomposition method

Using the solution obtained by the main problem, fixing the integer variables as input to the dual problem, a higher level can be set for the problem (Benders, 1962). The sub-problem consists of continuous variables and related constraints, but the main problem consists of the correct variables and a continuous variable that connects the two problems. An optimal solution to the main problem provides a lower level for the objective function. Using the solution obtained by the main problem, by fixing the integer variables as the input of the dual problem, a higher level can be defined for the problem. This solution is also used to make a Benders cut that includes continuous variables added to the main objective of the problem. In the next iteration, a new lower limit is obtained for the main problem, which is guaranteed to be better than the previous lower limit. Thus, the main problem and sub-problem are sequentially solved until a termination condition is reached, which is a reduction in the distance between the upper and lower limits to a small number. In this sense, the Benders decomposition method can lead to an optimal solution within finite iterations. Before developing the main issues and sub-problems within the framework of the method, we first present a general formulation of our problem below:

$$Min\left(Z\right)=\mathcal{A}+BSW(x,y|\alpha ,\beta )$$ (39)

s.t:

$$\sum _{k\in K}{\alpha }_f^k\ge 1\forall f\in F$$ (40)

$$\sum _{l\in L}{\beta }_r^l\ge 1\forall r\in R$$ (41)

The above problem can be expressed as follows:

$$Min\left(Z\right)=\mathcal{A}+BSW(x,y|\hat{\alpha },\hat{\beta });$$ (42)

s.t:

$$\sum _{k\in K}{\alpha }_f^k\ge 1\forall f\in F$$ (43)

$$\sum _{l\in L}{\beta }_r^l\ge 1\forall r\in R$$ (44)

Where $BSW(x,y|\hat{\alpha },\hat{\beta })$ is the Benders sub-problem, which is discussed in the next section. Benders' sub problem $BSW(x,y|\hat{\alpha },\hat{\beta })$ is a minimization problem that provides the optimal value of continuous variables (x, y) for constant variables $(\hat{\alpha },\hat{\beta })$. For our problem, $BSW(x,y|\hat{\alpha },\hat{\beta })$ can be formulated as follows:

$$min\left[{\mathcal{G}}_s+{\mathcal{Q}}_s\right]-\left[{\mathcal{P}}_s+{\mathcal{V}}_s\right]+{\mathcal{X}}_s+{\mathcal{Y}}_s+{\mathcal{Z}}_s$$ (45)

s.t.

$$\sum _{i\in I}\sum _{w\in W}{d}_i^{ws}vo{l}^w{\mu }_{if}^{ws}\le \sum _{k\in K}fs{c}_f^k{\hat{\alpha }}_f^k\forall f\in F,s\in S$$ (46)

$$\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }s}\le 1\forall l\in L,w^{\prime }\in W,r\in Rands\in S$$ (47)

$$\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }s}\ge 1\forall l\in L,w^{\prime }\in W,r\in Rands\in S$$ (48)

$$\sum _{f\in F}\sum _{w^{\prime }\in W}{\varphi }_{fr}^{l{w}^{\prime }s}\le rw{c}_r^l{\hat{\beta }}_r^l\forall r\in R,l\in L,s\in S$$ (49)

$$\sum _{f\in F}{\mu }_{if}^{ws}\le 1\forall i\in I,w\in W,s\in S$$ (50)

$$\sum _{f\in F}{\mu }_{if}^{ws}\ge 1\forall i\in I,w\in W,s\in S$$ (51)

$$\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}s}\le \sum _{f\in F}{\mu }_{if}^{ws}\forall i\in I,w^{″}\in W,w\in W,s\in S$$ (52)

$$\sum _{v\in V}{\xi }_{fhv}^{k{w}^{″}s}\le 1\forall i\in I,w^{″}\in W,s\in S$$ (53)

$$\sum _{v\in V}{\xi }_{fhv}^{k{w}^{″}s}\ge 1\forall i\in I,w^{″}\in W,s\in S$$ (54)

$$\sum _{j\in J}{\Omega }_{jhv}^{w^{″}s}\le 1\forall w^{″}\in W,h\in H,v\in V,s\in S$$ (55)

$$\sum _{j\in J}{\Omega }_{jhv}^{w^{″}s}\ge 1\forall w^{″}\in W,h\in H,v\in V,s\in S$$ (56)

$$\begin{array}{l}\sum _{v\epsilon V}{\xi }_{fhv}^{k{w}^{″}s}+\sum _{f\in F}{\varphi }_{fr}^{l{w}^{\prime }s}+\sum _{j\in J}{\Omega }_{jhv}^{w^{″}s}\le \sum _{f\in F}{\mu }_{if}^{ws}\forall i\in I,l\in L,r\in R,w^{\prime }\in W\\ ,w^{″}\in W,w\in W,s\in S\end{array}$$ (57)

$$\sum _{i\in I}\sum _{f\in F}{\mu }_{if}^{ws}\le vo{l}^w\forall w\in W,s\in S$$ (58)

$${\mu }_{if}^{ws}\ge 0,{\varphi }_{fr}^{l{w}^{\prime }s}\ge 0,{\xi }_{fhv}^{k{w}^{″}s}\ge 0,{\Omega }_{jhv}^{w^{″}s}\ge 0\forall i\in I,j\in J,r\in R,f\in F,h\in H,v\in V,k\in K,w\in W,w^{\prime }\in W,{w^{\prime }}^{\prime }\in W,l\in L,s\in S$$ (59)

Note that the constraints (21), (28), (30) and (31) in the proposed stochastic model were converted according to Eqs. (47), (48), (50), (51), (53), (54), (55), (56) respectively, without changing the response space and the optimal solution.

The dual sub-problem $BSW\left(x,y|\hat{\alpha },\hat{\beta }\right)$ is used to generate Benders cuts for the main problem. To obtain the dual problem, the dual variables: ${\pi }_{fs}^1,{\pi }_{l{w}^{\prime }rs}^2,{\pi }_{l{w}^{\prime }rs}^3,{\pi }_{rls}^4,{\pi }_{iws}^5,{\pi }_{iws}^6,{\pi }_{i{w}^{″}ws}^7,{\pi }_{i{w}^{″}s}^8,{\pi }_{i{w}^{″}s}^9,{\pi }_{w^{″}hvs}^{10},{\pi }_{w^{″}hvs}^{11},{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12},{\pi }_{ws}^{13}$

For Constraints (46) to (59) are introduced, respectively. Considering these variables, the dual problem$DBSW({\pi }^1,{\pi }^2,{\pi }^3,{\pi }^4,{\pi }^5,{\pi }^6,{\pi }^7,{\pi }^8,{\pi }^9,$ ${\pi }^{10},{\pi }^{11},{\pi }^{12},{\pi }^{13}|\hat{\alpha },\hat{\beta })$ will be as follows:

$$max\sum _{f\in F}\sum _{s\in S}\left({\pi }_{fs}^1\sum _{k\in K}fs{c}_f^k{\hat{\alpha }}_f^k\right)-\sum _{l\in L}\sum _{w^{\prime }\in W}\sum _{r\in R}\sum _{s\in S}\left(-{\pi }_{l{w}^{\prime }rs}^2+{\pi }_{l{w}^{\prime }rs}^3\right)-\sum _{r\in R}\sum _{l\in L}\sum _{s\in S}\left({\pi }_{rls}^4\sum _{l\in L}rw{c}_r^l{\hat{\beta }}_r^l\right)-\sum _{i\in I}\sum _{w\in W}\sum _{s\in S}\left(-{\pi }_{iws}^5+{\pi }_{iws}^6\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\pi }_{i{w}^{″}ws}^7\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{s\in S}(-{\pi }_{i{w}^{″}s}^8+{\pi }_{i{w}^{″}s}^9)-\sum _{w^{″}\in W}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}(-{\pi }_{w^{″}hvs}^{10}+{\pi }_{w^{″}hvs}^{11})-\sum _{i\in I}\sum _{k\in K}\sum _{r\in R}\sum _{w^{\prime }\in W}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\right)-\sum _{w\in W}\sum _{s\in S}\left({\pi }_{ws}^{13}\sum _{w\in W}vo{l}^w\right)$$ (60)

s.t:

$$d_i^{ws}vo{l}^w{\pi }_{fs}^1-{\pi }_{iws}^5+{\pi }_{iws}^6-{\pi }_{ws}^{13}vo{l}^w\le {\rho }^{s}c{s}_{if}^w{d}_i^{ws}{\mu }_{if}^{ws}\forall i,f,w,s$$ (61)

$$-{\pi }_{l{w}^{\prime }rs}^2+{\pi }_{l{w}^{\prime }rs}^3-{\pi }_{rls}^{4}rw{c}_r^l{\hat{\beta }}_r^l-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}c{r}_{fr}^{w^{\prime }}fs{c}_f^k{\varphi }_{fr}^{l{w}^{\prime }s}\forall i,l,r,w,w^{\prime },w^{″},f,r,s$$ (62)

$$-{\pi }_{l{w}^{\prime }rs}^2+{\pi }_{l{w}^{\prime }rs}^3-{\pi }_{rls}^{4}rw{c}_r^l{\hat{\beta }}_r^l-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}m{r}^{w^{\prime }}{\varphi }_{fr}^{l{w}^{\prime }}\forall i,l,r,w,w^{\prime },w^{″},f,r,s$$ (63)

$$-{\pi }_{w^{″}hvs}^{10}+{\pi }_{w^{″}hvs}^{11}-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}c{h}_{jh}^{w^{″}}{\Omega }_{jhv}^{w^{″}s}\forall i,j,r,w,w^{\prime },w^{″},h,v,k,s$$ (64)

$$-{\pi }_{w^{″}hvs}^{10}+{\pi }_{w^{″}hvs}^{11}-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^s{n}_{jh}^{"w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}s}\forall i,j,r,w,w^{\prime },w^{″},h,v,k,s$$ (65)

$$-{\pi }_{w^{″}hvs}^{10}+{\pi }_{w^{″}hvs}^{11}-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}k{w}^{w^{″}}{\Omega }_{jhv}^{w^{″}}\forall i,j,r,w,w^{\prime },w^{″},h,v,k,s$$ (66)

$$-{\pi }_{w^{″}hvs}^{10}+{\pi }_{w^{″}hvs}^{11}-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^s{n}^{″}{\prime }_h^{w^{″}}r{b}^{w^{″}}{\Omega }_{jhv}^{w^{″}}\forall i,j,r,w,w^{\prime },w^{″},h,v,k,s$$ (67)

$$-{\pi }_{i{w}^{″}s}^8+{\pi }_{i{w}^{″}s}^9-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}c{w}_{fr}^{w^{″}s}{\xi }_{fhv}^{k{w}^{″}s}\forall i,r,f,w,w^{\prime },w^{″},h,v,k,s$$ (68)

$$-{\pi }_{i{w}^{″}s}^8+{\pi }_{i{w}^{″}s}^9-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}e{g}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}}\forall i,r,f,w,w^{\prime },w^{″},h,v,k,s$$ (69)

$$-{\pi }_{i{w}^{″}s}^8+{\pi }_{i{w}^{″}s}^9-{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12}\le {\rho }^{s}n{\prime }_{fh}^{w^{″}}r{b}^{w^{″}}{\xi }_{fhv}^{k{w}^{″}s}\forall i,r,f,w,w^{\prime },w^{″},h,v,k,s$$ (70)

$${\pi }_{fs}^1,{\pi }_{l{w}^{\prime }rs}^2,{\pi }_{l{w}^{\prime }rs}^3,{\pi }_{rls}^4,{\pi }_{iws}^5,{\pi }_{iws}^6,{\pi }_{i{w}^{″}ws}^7,{\pi }_{i{w}^{″}s}^8,{\pi }_{i{w}^{″}s}^9,{\pi }_{w^{″}hvs}^{10},{\pi }_{w^{″}hvs}^{11},{\pi }_{ikr{w}^{\prime }{w}^{″}ws}^{12},{\pi }_{ws}^{13}\ge 0\forall i,w,w^{\prime },w^{″},f,h,v,k,l,s$$ (71)

Now, the main Benders problem will be modelled as follows:

$$\underset{\alpha ,\beta ,\gamma }{Min}z$$ (72)

s.t:

$$z\ge \mathcal{A}-\sum _{f\in F}\sum _{s\in S}\left({\hat{\pi }}_{fs}^{1a^{\prime }}\sum _{k\in K}fs{c}_f^k{\hat{\alpha }}_f^k\right)-\sum _{l\in L}\sum _{w^{\prime }\in W}\sum _{r\in R}\sum _{s\in S}\left(-{\hat{\pi }}_{l{w}^{\prime }rs}^{2a^{\prime }}+{\hat{\pi }}_{l{w}^{\prime }rs}^{3a^{\prime }}\right)-\sum _{r\in R}\sum _{l\in L}\sum _{s\in S}\left({\hat{\pi }}_{rls}^{4a^{\prime }}\sum _{l\in L}rw{c}_r^l{\hat{\beta }}_r^l\right)-\sum _{i\in I}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{iws}^{5a^{\prime }}+{\hat{\pi }}_{iws}^{6a^{\prime }}\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{i{w}^{″}ws}^{7a^{\prime }}\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{i{w}^{″}s}^{8a^{\prime }}+{\hat{\pi }}_{i{w}^{″}s}^{9a^{\prime }}\right)-\sum _{w^{″}\in W}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}\left(-{\hat{\pi }}_{w^{″}hvs}^{10a^{\prime }}+{\hat{\pi }}_{w^{″}hvs}^{11a^{\prime }}\right)-\sum _{i\in I}\sum _{k\in K}\sum _{r\in R}\sum _{w^{\prime }\in W}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{ikr{w}^{\prime }{w}^{″}ws}^{12a^{\prime }}\right)-\sum _{w\in W}\sum _{s\in S}\left({\hat{\pi }}_{ws}^{13a^{\prime }}\sum _{w\in W}vo{l}^w\right)\forall a^{\prime }=1,\dots ,A^{\prime }$$ (73)

$$\sum _{f\in F}\sum _{s\in S}\left({\hat{\pi }}_{fs}^{1b^{\prime }}\sum _{k\in K}fs{c}_f^k{\hat{\alpha }}_f^k\right)-\sum _{l\in L}\sum _{w^{\prime }\in W}\sum _{r\in R}\sum _{s\in S}\left(-{\hat{\pi }}_{l{w}^{\prime }rs}^{2b^{\prime }}+{\hat{\pi }}_{l{w}^{\prime }rs}^{3b^{\prime }}\right)-\sum _{r\in R}\sum _{l\in L}\sum _{s\in S}\left({\hat{\pi }}_{rls}^{4b^{\prime }}\sum _{l\in L}rw{c}_r^l{\hat{\beta }}_r^l\right)-\sum _{i\in I}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{iws}^{5b^{\prime }}+{\hat{\pi }}_{iws}^{6b^{\prime }}\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{i{w}^{″}ws}^{7b^{\prime }}\right)-\sum _{i\in I}\sum _{w^{″}\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{i{w}^{″}s}^{8b^{\prime }}+{\hat{\pi }}_{i{w}^{″}s}^{9b^{\prime }}\right)-\sum _{w^{″}\in W}\sum _{h\in H}\sum _{v\in V}\sum _{s\in S}\left(-{\hat{\pi }}_{w^{″}hvs}^{10b^{\prime }}+{\hat{\pi }}_{w^{″}hvs}^{11b^{\prime }}\right)-\sum _{i\in I}\sum _{k\in K}\sum _{r\in R}\sum _{w^{\prime }\in W}\sum _{w^{″}\in W}\sum _{w\in W}\sum _{s\in S}\left(-{\hat{\pi }}_{ikr{w}^{\prime }{w}^{″}ws}^{12b^{\prime }}\right)-\sum _{w\in W}\sum _{s\in S}\left({\hat{\pi }}_{ws}^{13b^{\prime }}\sum _{w\in W}vo{l}^w\right)\le 0\forall b^{\prime }=1,\dots ,B^{\prime }$$ (74)

In this model, Eq. (72) indicates the objective function of the main problem. The set of constraints (73) indicates the optimal cuts that are added to the main problem after reaching the optimal solution in the sub-problem. The parameters ${\hat{\pi }}_{fs}^{1a^{\prime }},$ ${\hat{\pi }}_{l{w}^{\prime }rs}^{2a^{\prime }}$ $,{\hat{\pi }}_{l{w}^{\prime }rs}^{3a^{\prime }},{\hat{\pi }}_{rls}^{4a^{\prime }},$ ${\hat{\pi }}_{iws}^{5a^{\prime }},{\hat{\pi }}_{iws}^{6a^{\prime }},{\hat{\pi }}_{i{w}^{″}ws}^{7a^{\prime }},{\hat{\pi }}_{i{w}^{″}s}^{8a^{\prime }},{\hat{\pi }}_{i{w}^{″}s}^{9a^{\prime }}$ $,{\pi }_{w^{″}hvs}^{10a^{\prime }},{\pi }_{w^{″}hvs}^{11a^{\prime }}$ $,$ ${\hat{\pi }}_{ikr{w}^{\prime }{w}^{″}ws}^{12a^{\prime }}$ and ${\hat{\pi }}_{ws}^{13a^{\prime }}$ are the values of the dual variables obtained from the solution of the sub-problem. We note that these values are considered as constant values in the cut constraints. Equation (74) are feasible cuts that can be added to the main problem if the sub-problem is infeasible. The parameters, ${\hat{\pi }}_{fs}^{1b^{\prime }},$ ${\hat{\pi }}_{l{w}^{\prime }rs}^{2b^{\prime }}$ , ${\hat{\pi }}_{l{w}^{\prime }rs}^{3b^{\prime }},{\hat{\pi }}_{rls}^{4b^{\prime }},$ ${\hat{\pi }}_{iws}^{5b^{\prime }},$ ${\hat{\pi }}_{iws}^{6b^{\prime }},{\hat{\pi }}_{i{w}^{″}ws}^{7b^{\prime }},{\hat{\pi }}_{i{w}^{″}s}^{8b^{\prime }},{\hat{\pi }}_{i{w}^{″}s}^{9b^{\prime }},{\pi }_{w^{″}hvs}^{10b^{\prime }},{\pi }_{w^{″}hvs}^{11b^{\prime }}$ $,$ ${\hat{\pi }}_{ikr{w}^{\prime }{w}^{″}ws}^{12b^{\prime }}$ and ${\hat{\pi }}_{ws}^{13b^{\prime }}$ are the values of the dual variables obtained from the solution of the sub-problem and are also considered as constant values in the cutting constraints.

The solution process of Benders decomposition for the problem (72) - (74) are as follows. We must first find a solution to the main problem by solving the main problem without any cuts. The pseudocode of the general process of the Benders algorithm is shown in Algorithm 1.

5. Case study

The city of Kermanshah has a population of about one million people who, like other cities in Iran, are highly infected with the COVID-19 virus. Under normal circumstances, the amount of waste production per person is 700 g per day, which has increased to about 900 g per day due to the outbreak of COVID-19 in Kermanshah. Like other parts of Iran, the city's municipality holds a public tender to select contractors to collect the waste. In Kermanshah, three waste recycling centres with a capacity of 700 tons per day are separating and recycling the waste produced, which are marked with green stars in Fig. 3 . In addition, the location of other sites such as collection centres, hospitals and waste disposal centres in Kermanshah is shown in Fig. 3.

Fig. 3.

Locations of collection, recycling and waste disposal centres, and hospitals in Kermanshah.

The values for each of the parameters defined in Tables A-1 and A-2 are provided. These data were collected with the support of various departments, namely the municipality, environment and websites.

Table A-3 shows the amount of waste collected at 18 hospitals. In addition, the costs of transporting waste to the next location (waste incinerator centres) are specified. Besides table A-4 shows the amount of waste collected by 10 temporary stations and, the costs of transporting waste to the next location (which can be recycling centres or waste disposal locations) are specified. Note that due to the use of special shipper to transport infectious waste, some costs may be higher than for normal waste.

5.1. Model solving and data analysis

We considered possible scenarios for the severity of the outbreak. In fact, the severity of the outbreak was estimated using the indicators of the Iran Crisis Team, which is based on the number of cases and the number of victims per day. Based on these scenarios, four conditions are considered: blue (low prevalence), yellow (medium prevalence), orange (high prevalence) and red (very high prevalence). Note that according to these scenarios, the government imposes restrictions on travel. In addition, all citizens must wear face masks which, as mentioned in the introduction, these restrictions dramatically increase the production of infectious waste. Table 4 shows the amount of waste generated by 10 collection centres.

Table 4.

The amount of waste generated in different scenarios.

Possibility	The volume of wastes (Per tones)										Scenarios
	1	2	3	4	5	6	7	8	9	10
0.15	1044	1198	1155	1025	1303	1246	12,55	1003	1014	1166	Very high prevalence
0.35	1078	923	1010	1015	1016	1040	1002	958	936	993	High prevalence
0.25	839	889	869	882	853	838	866	877	941	855	Medium prevalence
0.25	745	799	792	712	727	793	796	739	723	712	Low prevalence

Table 5 compares the first-stage decisions produced by the deterministic and stochastic models. At first, it can seem that the configuration of the waste management network is very different from the change in focus on the severity of virus prevalence. Second, in different scenarios (with the possibility of 0.15, 0.35, 0.25, 0.25), a deterministic model can also provide a good first-step decision. The interesting point is the numbers obtained for the upper-level of the problem. As can be seen, total costs have increased from low to medium prevalence scenarios. However, in the medium prevalence scenario, the total cost is −204,841. In the high prevalence scenario, the total cost has reached −1,764,197. These negative values indicate the government's profit in these two scenarios. In other words, despite the significant increase in the amount of wastes, the produced benefit surpasses the associated cost. The produced benefit is caused by energy generated and waste recycled.

Table 5.

The first stage decisions in different scenarios.

Scenario	Goal	Bi-level		Possibility
		Deterministic	Stochastic
Very high prevalence	Cost	−1,764,197	−6,987,983	0.15
	Risk	8,581,102	6,979,584
High prevalence	Cost	−204,841	−862,087	0.35
	Risk	7,219,411	5,723,245
Medium prevalence	Cost	724,809,464	663,607,449	0.25
	Risk	6,476,452	5,037,512
Low prevalence	Cost	640,758,079	578,929,568	0.25

Fig. 4 and Table 6 show the optimal results obtained for the leader, follower and the Bi-level problem. Note that the optimal point of the Bi-level model does not necessarily represent the Pareto boundary in the multi-objective problem (Safaei et al. 2017). In other words, the answers for a bi-objective problem are not equal to the answers obtained for a Bi-level problem. This may be due to the existence of common constraints in the Bi-level model, which is not the case in the bi-objective model, and in the bi-objective of a model, there is not necessarily a common constraint between the two objectives. Thus, some researchers deny the relationship between the results of the Bi-level model and the Pareto frontier (Clark and Westerberg, 1988; Candler, 1988; Wen and Hsu, 1989; However, some researchers believe that the optimal solution of a Bi-level problem relates to the Pareto frontier created between the objectives of the problem (Ünlü, 1987) Finally, there is no consensus among the researchers in the field.

Fig. 4.

The equilibrium created by Bi-level model.

Table 6.

Numerical results obtained from the leader, follower, and Bi-level models.

Models	Upper-level objective	Lower-level objective
Leader's model	−2,384,540	758,210
Follower's model	420,160	469,275
Bi-level model	−1,602,766	683,438

Table 7 shows government revenue from energy generation from IW incineration and government revenue from MW recycling. As can be seen from Table 7, the revenue to cost ratio is 104%. In other words, 4% of government revenue is earned. Government revenue was expected to be higher, but due to significant costs during the COVID-19 pandemic, including an increase in the number of transporters and an increase in the capacity of collection and recycling centres, government revenue was earned 2,384,540, according to Table 6. Interestingly, 34% of the total waste collection and transportation costs were borne by COVID-19-related IW incineration alone.

Table 7.

Analyze of the government revenue to total cost.

Row	Revenue	Percent	$\mathbf{R}\mathbf{e}\mathbf{v}\mathbf{e}\mathbf{n}\mathbf{u}\mathbf{e}/\mathbf{C}\mathbf{o}\mathbf{s}\mathbf{t}$
Total	67,251,311	100%	104%
Energy generation	22,358,705	39%	34%
Waste recycling	44,892,606	51%	69%

5.2. Sensitivity analysis

According to the explanations provided in Section 3.1, to achieve optimal flexibility, the robustness of the model and the robustness of the solution should be evaluated. For this purpose, a sensitivity analysis is shown in Fig. 5 . As can be seen in Fig. 6 , the robustness of the model varies based on the value of $\mathrm{\omega }$. Fig. 5 shows that as the value of $\mathrm{\omega }$ increases, the robustness of the solution increases. But as the value of ω increases, we see a downward trend in the robustness of the model. This is due to the nature of minimization of the model. That is, for more values, although the model robustness is feasible, there is a need to increase the cost in each scenario. Due to the Bi-level nature of the proposed model, increasing the value of $\mathrm{\omega }$ in each scenario (which indicates higher prevalence of the virus) also increases the risk of virus contagion. Furthermore, according to the analysis obtained, the best value for the robustness of the model is in the range 800. This while the best value for the robustness of the solution is in the range 950.

Fig. 5.

Sensitivity analysis for the model robustness and the solution robustness.

Fig. 6.

The result of solving the model.

Here is the result of solving the model in Fig. 6. As shown in Fig. 6 (a), the cost of waste collection and waste transportation increased over 10 repetitions. This figure shows that the cost of waste transportation was higher than the cost of waste collection, which was significantly reduced over 10 repetitions. On the other hand, as shown in Fig. 6 (b), the risk of virus contagion from the de waste of $w^{\text{″}}$ is higher than the risk of virus contagion from waste, which is due to the fact that de waste also includes waste hospitals. Although hospital waste has become safe at its source, it is still hazardous. In addition, some volumes of $w^{\text{″}}$ waste include infectious waste generated by ordinary citizens. In any case, the risk of virus contagion from waste was reduced at an almost uniform rate, which indicates the efficiency of the proposed model. In addition, the values obtained in the 10 repetitions of the problem-solution related to government revenue from energy production and waste recycling are shown in Fig. 6 (c). As can be seen in Fig. 6 (C), revenue grows in different repetitions. In other words, as the amount of waste increases, the amount of government revenue also increases. It is also observed that the revenue value from recycling value during different repetitions was more than the revenue from energy generation.

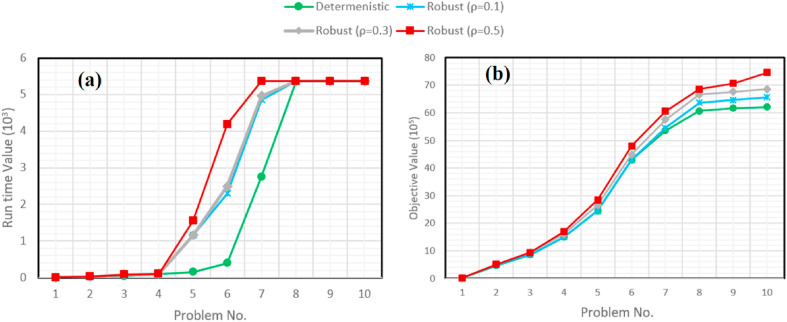
To examine the model more closely and examine the feasibility of the model based on the fluctuations of the uncertain parameters, in Fig. 7 , the sensitivity analysis of the model is performed based on the change in parameter ρ. According to Fig. 7 (a), it can be observed that the results obtained for the model in robust mode show much better responses. Moreover, in Fig. 7 (b) you can see the performance of the proposed model based on the solution time.

Fig. 7.

Sensitivity analysis of the model based on the parameter ρ

As the data analysis showed, this study was able to provide a hybrid mathematical model that converts infectious waste into energy, as well as offset the total costs associated with waste generated during the COVID-19 pandemic. The proposed model also minimizes the risk of virus contagion during the collection and transportation of infectious waste. The solution results of this model lead to useful managerial insights: (i) To prevent the spread of the COVID-19 virus through infectious waste, managers can generate energy from infectious waste and offset a part of the costs imposed during the COVID-19 epidemic. (ii) On the other hand, the results showed that the proposed model is able to consider the risk of virus contagion through infectious waste. Managers can follow the proposed model to control the risk of virus contagion through infectious waste despite the higher prevalence of the virus in different scenarios. (iii) Defining mathematical models and data as certain in applied problems reduces the flexibility of the model in uncertain conditions (in real-world), and was affected in the quality of the model. The result showed that the proposed model was feasible in uncertainty. Therefore, in the proposed model, considering the severity of the outbreak by various scenarios and uncertain demand for waste collection indefinitely can greatly help in solving this problem. (iv) The use of a Bi-level model assists the managers in managing the huge amount of waste generated during the outbreak of COVID-19 by taking into consideration the concern of the government (total costs) and the concern of the contractor (risk of virus contagion). Finally, based on the results obtained, it can be stated that in the case of energy production from waste during the COVID-19 pandemic, 34% of the total cost of waste collection and transportation can be compensated.

6. Conclusion and further research

In this study, a hybrid mathematical model for energy generation from infectious waste during the COVID-19 pandemic was proposed. Due to the great importance of costs in the waste management process as the government concern, the reduction of total costs is considered the upper level of the model. On the other hand, considering the potential risk of collection and transportation of the contaminated waste as a contractor concern, at the lower level of the proposed model the risk of virus contagion through infectious waste was considered. The results showed that in the case of incineration of IW during the COVID-19 pandemic, in addition to health and environmental benefits, a significant part of the total costs can be covered. Besides, considering the multiplier growth of municipal waste during the pandemic, the results showed that not only can the imposed costs be controlled, but a significant amount of revenue can be caused. The scenarios are four prevalence levels, which include a very high prevalence, a high prevalence, medium prevalence and low prevalence. Due to the complexity of the robust Bi-level programming problem, KKT conditions were used to convert to the one-level model. Besides, the Benders decomposition approach was also used as a solution. The results of the problem and sensitivity analysis using the case study data explain the efficiency of the model and the solution method of the proposed method. In addition, with the uncertain rate of demand for waste generation, several computational analyses have been performed and important results of managerial insight have been obtained.

Every scientific research is affected by some limitations and this study is no exception. The most important limitation of this study was the collection of real records and data to provide an efficient and realistic model that we spent much time on. According to the results of this study, it seems that since the waste collection model is a complex phenomenon by considering stochastic parameters, future research must consider the fluctuations related to waste production due to various factors, especially pandemics. To use the model and method presented in this research, we must be able to obtain a proper estimate of the parameters presented in the research model. In addition, the collected data was related to the Executive Contractors Supervision in Kermanshah Municipality, future research should be conducted regarding the situation of the corresponding areas. Therefore, to benefit from the results of this research, the results should be combined with other results to provide a better practical solution for discovering insightful knowledge in the field of waste management. Furthermore, we just concentrated on the COVID-19 pandemic; however, other future diseases may have other specifications and infection patterns which should carefully be considered.

For future research, in this research, only infectious waste is considered, in future research, other types of waste can also be considered, including industrial waste. In addition, in this study, outbreak scenarios were considered, which could be applied to the vaccine distribution scenario in the new models. Also, in this study, we assumed that the risk of contracting the virus was relatively equal for each type of waste (household infectious waste and medical infectious waste). In future research, this assumption can be ignored and the risk of infection by infectious waste can be examined more closely. Researchers can also study the prevalence of the virus through contaminated waste in another study. Finally, we examined the production of energy from the infectious waste while future researchers could suggest other solutions for waste management during the pandemic.

CRediT authorship contribution statement

Jaber Valizadeh: Conceptualization, Writing – original draft. Mehri Aghdamigargari: Writing – review & editing, Revision. Ali Jamali: Software, Data curation. Uwe Aickelin: Project administration, Visualization, Supervision. Setare Mohammadi: Investigation, Resources. Hadi Akbarzadeh Khorshidi: Validation, Methodology. Ashkan Hafezalkotob: Formal analysis, Revision.

Declaration of competing interest

The author declares that I have no known competing for financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling editor: Bin Chen

Appendix A. Supplementary data

The following is the Supplementary data to this article: