Abstract
Currently, the most common replacement heart valve design is the ‘bioprosthetic’ heart valve (BHV), which has important advantages in that it does not require permanent anti-coagulation therapy, operates noiselessly, and has blood flow characteristics similar to the native valve. BHVs are typically fabricated from glutaraldehyde-crosslinked pericardial xenograft tissue biomaterials (XTBs) attached to a rigid, semi-flexible, or fully collapsible stent in the case of the increasingly popular transcutaneous aortic valve replacement (TAVR). While current TAVR assessments are positive, clinical results to date are generally limited to <2 years. Since TAVR leaflets are constructed using thinner XTBs, their mechanical demands are substantially greater than surgical BHV due to the increased stresses during in vivo operation, potentially resulting in decreased durability. Given the functional complexity of heart valve operation, in-silico predictive simulations clearly have potential to greatly improve the TAVR development process. As such simulations must start with accurate material models, we have developed a novel time-evolving constitutive model for pericardial xenograft tissue biomaterials (XTB) utilized in BHV (doi: 10.1016/j.jmbbm.2017.07.013). This model was able to simulate the observed tissue plasticity effects that occur in approximately in the first two years of in vivo function (50 million cycles). In the present work, we implemented this model into a complete simulation pipeline to predict the BHV time evolving geometry to 50 million cycles. The pipeline was implemented within an isogeometric finite element formulation that directly integrated our established BHV NURBS-based geometry (doi: 10.1007/s00466-015-1166-x). Simulations of successive loading cycles indicated continual changes in leaflet shape, as indicated by spatially varying increases in leaflet curvature. While the simulation model assumed an initial uniform fiber orientation distribution, anisotropic regional changes in leaflet tissue plastic strain induced a complex changes in regional fiber orientation. We have previously noted in our time-evolving constitutive model that the increases in collagen fiber recruitment with cyclic loading placed an upper bound on plastic strain levels. This effect was manifested by restricting further changes in leaflet geometry past 50 million cycles. Such phenomena was accurately captured in the valve-level simulations due to the use of a tissue-level structural-based modeling approach. Changes in basic leaflet dimensions agreed well with extant experimental studies. As a whole, the results of the present study indicate the complexity of BHV responses to cyclic loading, including changes in leaflet shape and internal fibrous structure. It should be noted that the later effect also influences changes in local mechanical behavior (i.e. changes in leaflet anisotropic tissue stress-strain relationship) due to internal fibrous structure resulting from plastic strains. Such mechanism-based simulations can help pave the way towards the application of sophisticated simulation technologies in the development of replacement heart valve technology.
Keywords: soft tissue mechanics, bioprosthetic heart valve, simulation, time evolving properties
1. INTRODUCTION
1.1. Background
The most popular replacement heart valves continue to be the ‘bioprosthetic’ heart valves (BHV), and are typically fabricated from glutaraldehyde-crosslinked pericardial xenograft tissue biomaterials (XTBs) sutured to a rigid or semi-flexible stent [1, 2]. While these devices continue to benefit many patients in the short term, failure due to fatigue induced structural deterioration along with tissue mineralization continue to be the central issues limiting their durability [3, 4]. Currently, the BHV durability is assessed through costly and time-consuming in-vitro accelerated wear testing (AWT) and pre-clinical animal model-based evaluations. AWT, while required by regulatory agencies, is an empirically developed methodology that provides only limited information on durability using accelerated frequencies (10–15 Hz), and utilizes aphysiologic loading patterns that do not realistically load the valve. Thus, the relation between AWT evaluations and long-term durability remains unclear at best. In contrast, large animal models are primarily focused on limited-term (¡6 months) implant responses (mainly calcification) and thus cannot capture long-term mechanical fatigue effects. While biological interactions with blood elements and immunological processes are evident in BHV [1, 2], basic functional durability issues remain largely unaddressed.
Increasingly, transcutaneous aortic valve replacement (TAVR) devices are utilized for patients contraindicated for open heart surgery, with growing interest in more general use. While current TAVR assessments are positive, results to date are generally for <2 years. Since TAVRs are constructed using thinner XTB leaflets, their mechanical demands are substantially greater than standard BHV and have associated aggravated durability problems. Paradoxically, further evolution of TAVR designs require thinner leaflets, which are required to maintain lasting durability even after being tightly folded for delivery. These requirements increase the already high functional demands that exist for traditional surgically placed valves. To date, TAVR devices have focused largely on improved delivery strategies, while the leaflet biomaterials used have remained relatively unchanged and have the same limited intrinsic durability. Yet, most BHV leaflet research has focused almost exclusively on mitigation of calcification, This is puzzling as calcification affects less than half of failed BHV, while tears due to degradation are the predominant mode of failure. Thus, xenograft design optimization to enhance durability represents a unique and major step forward in the development of the next generation of BHVs.
1.2. On the mechanisms of BHV structural failure
In general, the mechanisms of structural deterioration and eventual failure of BHVs can be generally divided into two broad categories: i) biologically-driven tissue degeneration and mineralization, and ii) mechanical fatigue [5]. Mineralization is the accumulation of mineral deposits (mainly calcium phosphate) within the BHV leaflet tissues, commonly occurring in the commissure region and basal areas of the cusp [6, 7, 8]. This results in reduced flexibility and weakened tissue, which affects the normal mechanical functioning of the valve and eventually leads to leaflet tearing and valve failure. The causes of calcification and techniques to mitigate its effects have been extensively studied in literature [6, 9, 10, 11, 12]. Calcium phosphate deposits are a result of the reaction between phospholipids in the cell membrane remnants and the calcium in the extracellular matrix (ECM). Thus, common mitigation strategies involve hindering this reaction, by a) reducing phosphate availability using reagents such as surfactants and ethanol which extract the phospholipids, or pretreating the tissue with trivalent metal ions (e.g. FeCl3 and AlCl3) which react with phosphate thereby making it unavailable for calcification [6, 13, 14] and b) preventing calcium influx using chemical agents that covalently bind to the bioprosthetic tissue, such as amino-oleic acid (AOA) [6, 15, 16]. Pre-treatment of the BHV tissue with glutaraldehyde is also known to increase calcification, because of the presence of residual aldehydes which act as sites for Ca accumulation, and many mitigation strategies attempt to block these aldehydes [17, 18, 19, 20].
In contrast, while mineralization-reducing methods have been investigated for some time [6, 9, 10, 11], the mechanisms that underlie XTB mechanical fatigue remain poorly understood. Mechanical fatigue occurs due to cyclic loading of the valve over time and includes damage to the collagen fibers as well as breakdown of the non-fibrous part of the extracellular matrix (ECM). Fourier transform infrared spectroscopy results have shown structural damage to collagen fibers at the molecular level in as little as 50 million cycles [21], which was not detectable at the tissue level at this stage. Importantly, it has been noted that both calcific and structural damage processes can occur in parallel or independently [3, 4]. Structural damage has been found to occur in areas of the valve that were not affected by calcification and are subject to high mechanical forces, suggesting that mechanical fatigue can independently contribute to structural deterioration of the valve [3, 4, 22, 23, 24, 25]. Other studies have strongly suggested that cyclic stresses may disrupt the collagen architecture and may induce further calcification [26, 27, 28, 29, 30]. Thus, understanding how mechanical fatigue contributes to BHV structural deterioration may guide the design development of BHVs so that the degradation due to cyclic stresses can be minimized.
1.3. BHV leaflet plastic behaviors
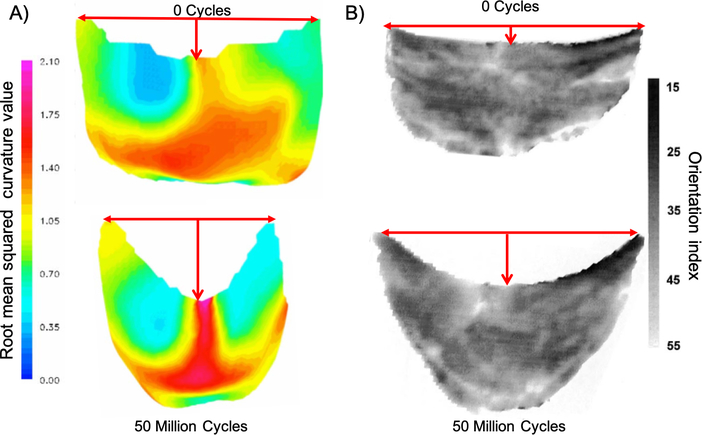
To clarify the responses of BHV to in vivo loading, we have previously demonstrated that BHV leaflets can undergo significant changes in geometry and collagen fiber architecture within 50 million cycles (equivalent to 2 years in vivo operation) (Fig. 1) [31, 32]. These studies indicated that cyclic loading can lead to permanent deformation in the BHV geometry, especially in the central belly region which are also the locations where tissue failure has been observed. These and other studies [33, 34, 35] have demonstrated that BHV XTB can undergo plastic deformations not associated with damage.
Figure 1:
A) The 3D unloaded geometry of a BHV leaflet before and after cyclic loading, with the color indicating the local root mean squared curvature. The most significant change in geometry is in the belly region. B) BHV leaflet collagen fiber architecture, showing that the collagen fiber architecture is convected by the dimensional changes. The grayscale scale bar shows the orientation index (OI), which is the proportional to the angle containing 50 % of fibers. The lack of changes in the OI suggests that minimal damage to the collagen fiber architecture has occurred.
As stated above, pericardial XTB are the dominant biomaterial used for BHV leaflets. They are typically fabricated from bovine pericardium and stabilized using an aqueous solution of glutaraldehyde, which suppresses immunogenic reactions by crosslinking proteins. The main mechanical effect of glutaraldehyde treatment is to produce exogenous crosslinks that induce four-fold increase in XTB bending stiffness [36], but paradoxically it does not increase the stiffness of the collagen fibers themselves [37]. In addition, it has been shown that exogenous cross-links increase collagen fiber-fiber mechanical interactions, which can account for up to 30% of the stress in the fully loaded state. The glutaraldehyde cross-linking process involves a Schiff-base aldehyde reaction, which is unstable at room and body temperatures. These cross-links thus constantly undergo a scission-healing process. The continuous scission-healing process allows an irreversible plastic-like deformation to occur as the BHV undergoes dynamic loading during operation. This irreversible deformation is not associated with damage, as it is only a result of change in the unloaded reference configuration. We have classified the BHV fatigue process into three stages: early (2–5 years), intermediate (2–10 years) and late (up to failure) (Fig. 2). This is consistent with the significant changes in geometry that occur within the first 50 million cycles (Fig. 1), where tissue and fiber level damage has not yet reached a level where it is detectable. The resulting changes in stress patterns begin to induce damage in the intermediate term, and eventually lead to failure in the late stage. We have noted previously [38] that plasticity is the dominant effect during the first stage of BHV cyclic loading. Although this type of plastic behavior is not associated with structural damage, it results in significant changes in BHV geometry, microstructure, and mechanical properties [31, 32]. This can lead to changes in stress patterns that can have a significant impact on subsequent structural damage.
Figure 2:
We speculate that the effects of cyclic loading on BHVs can be divided into three stages: early, intermediate and late. Figure reproduced from [38]
1.4. The need for BHV simulations of the fatigue process
Despite their importance, simulation of fatigue effects remain in their infancy, with only a handful of studies performed. Martin et al. have conducted a series of rigorously done initial studies of the BHV fatigue process, based on a phenomenological model for long-term fatigue damage with stress softening and permanent set [39, 40, 41]. However, the constitutive models utilized in these studies were based on a limited phenomenological modeling approach, with simulations taken from fatigue information scaled from only 10 million cycles. We have previously shown that plastic deformations can continue to at least 35 million cycles, and likely require at least 50 million cycles to reach the full limit [37, 38]. Moreover, there is an upper bound to the plastic deformations, limited by the deforming local collagen structure. Such mechanistic insights will help optimally utilize XTB biomaterials and aid in the development of future replacement valve designs. Serrani et al. have developed a computational model of a polymeric heart valve (PHV) leaflet while simulating the leaflet behavior under a quasi-static pressure load, with the aim of optimizing the PHV structure [42]. However, they have only considered the effect of a single loading cycle. Furthermore, this work is focused on polymeric materials which, while behaving similarly at the bulk level, greatly differ in the underlying mechanisms of their respective mechanical behaviors. To our knowledge, realistic microstructural models of the XTB fatigue process have yet to be incorporated in to current simulation methodologies.
1.5. Goals of the present study
As a first step towards addressing these goals, we developed a novel numerical simulation framework for the time evolving properties of BHVs in response to cyclic loading during using a structurally-based XTB plasticity constitutive model [37, 38]. We utilized this framework to predict the geometric and structural changes that occurs within the BHV to 50 million cycles, wherein all plastic deformations will have occurred. To facilitate the time evolving simulation, we utilized an effective model [43] to represent the response of the plasticity constitutive model [38] at each time step to considerably improve computational efficiency. The entire pipeline was implemented in an isogeometric finite element analysis framework specialized for quasi-static loading conditions, based on our previous work[44, 45]. Simulation results included time-evolving changes in leaflet shape (curvature), collagen fiber architecture (orientation and recruitment), as well as rates of change. Conclusions and future recommendations are then discussed.
2. METHODS
2.1. Overview
In simulating BHV cyclic loading, we utilized a structurally based plasticity model for time-dependent behavior. This approach was based on an elastic model of crosslinked tissues that explicitly incorporated key features of the collagen fiber architecture, namely, recruitment and rotation, as well as their mechanical interactions augmented by the presence of exogenous cross-links [37]. The plasticity model then extended this approach by accounting for time-dependent changes in the exogenously cross-linked (EXL) ‘matrix’ (i.e. all non-fibrous tissue components) during early-to-mid stages of cycling [38]. While shown to be quite accurate and predictive, this approach is computationally inefficient due to the presence of quadruple integral terms. We thus utilized an effective constitutive model in place of the structural constitutive model at each time point in the actual simulations, with the effective model parameters fit to the structural model output at each time step (Fig. 3). The material model subroutines were then custom integrated into an isogeometric finite element code [44, 46, 45], specialized for quasi-static simulations. In the following, we describing the simulation framework and specific simulations performed.
Figure 3:
The framework for using the effective constitutive model to improve the efficiency of using complex meso- or multi-scale models (micro-models) in numerical simulations. Here, A) effective constitutive models act as an intermediate step between micro-models and numerical simulations, where micro-models inform the changes to the effective constitutive model, and the effective constitutive model is then used for the FE simulation. B) An example of how this may be implemented for a time-evolving simulation is shown.
2.2. Soft tissue plasticity model
The details of the structural plasticity model have been presented in [38]. To clarify the presentation, the elastic and plastic modeling sections are presented separately in the following.
2.2.1. Elastic model
In brief, we utilize the fact that pericardial XTBs are a form of exogenously cross-linked soft collagenous tissues. We thus assumed that there are three contributors to the bulk XTB mechanical response: 1) the collagen fibers, 2) exogenously cross-linked matrix (i.e. all non-fibrous tissue components, including cellular remnants), and 3) the mechanical interactions between the collagen fibers and the cross-linked matrix. We further assumed that, at the bulk level, the XTBs can be modeled as an incompressible, pseudo-hyperelastic material [47], thus
| (1) |
| (2) |
where Ψ is the total strain energy of the tissue, p is the Lagrange multiplier for enforcing incompressibility, C = FT · F is the right Cauchy-Green deformation tensor, F is the deformation gradient tensor, S is the second Piola-Kirchhoff stress tensor, and ϕcol is the mass fraction of collagen fibers, and Ψcol, Ψm, and Ψint are the strain energy contributions of the collagen, the matrix and the interactions respectively. This formulation assumes all the incompressibility effects to be strictly in the matrix phase only.
The model formulation is based on the classic Lanir-type three-scale homogenization scheme [48, 49] for general soft tissue structures. In this approach, scale one is the individual fiber, scale two is an ensemble of fibers that all have a common orientation n, and scale three is the tissue level wherein the contribution from all fiber ensembles are summed. For scale one, the collagen fibers were described by a linear relation between the first Piola-Kirchhoff Stress P and the collagen fiber stretch ratio λf. As collagen fibers are typically undulated in the unloaded state, they require use of an effective slack stretch λs, which defines the stretch necessary to straighten the fiber but does not require detailed knowledge of the unloaded fiber geometry. λs is used in scale two where the fiber ensemble response formulation is obtained using a probability distribution function of the fiber slack length, Γs(λs). Γs(λs) has been defined in detail in [37]. In the final third scale, response from all fiber ensembles are integrated over all orientations, weighed by the collagen fiber orientation distribution function (ODF), Γθ. In this approach Ψcol is given by
| (3) |
where ηcol is the collagen fiber modulus of the fiber. For the cross-linked matrix mechanical response, we utilized the following modified Yeoh model for the matrix contribution Ψmat
| (4) |
where ηmat is the EXL matrix modulus, a and b are the exponents of the Yeoh model, r is the relative weight between the two terms and I1 is the first invariant of C. Next, we assumed that all fiber-fiber and fiber-matrix interactions can be represented at the fiber-ensemble scale level. To model the interaction term, we use the pseudo invariant I8 = n(α) ·Cn(β) to capture the mechanical interaction between two fiber ensembles oriented along n(α) and n(β) in the reference configuration (Fig. 4). We note that I8 can be further decomposed into extensional and rotational components
| (5) |
Figure 4:
The inter–ensemble interactions can be separated into rotational and extensional effects. Figure reproduced from [38].
The interaction term, Ψint, is an ensemble level term integrated over all possible pairs of ensembles, and includes only the terms (see [38] for full details), and has the following form
| (6) |
Here, the highlighted blue integrals correspond to the inner stretch terms in blue, while the red integrals correspond to the outer angular terms in red. We found that the interactions played a significant role – the interaction term accounted for about 30% of the total tissue stress in the fully loaded state [37].
2.2.2. Plasticity model
The unstable GLUT cross-linking reactions, which lead to continuous scission-healing in the EXL matrix, will induce a change in the stress-free reference configuration of the matrix over time. The embedded collagen fibers will thus convect with the matrix, undergoing rotation and extension. We refer to this as structural convection of the collagen fiber architecture. It is important to note that the plasticity was observed only in the matrix, and while the collagen fibers only convect with the matrix deformations; there is no change in the material properties of the collagen fibers themselves. As the plastic deformation increases, some of the fibers will get recruited. Since the stiffness of the collagen fibers is three orders of magnitude higher than the matrix, they can resist any further changes in geometry due to continuous scission/healing reactions in the matrix. Thus, a key takeaway of this model is that the collagen fibers will impose an upper limit on the dimensional changes of the tissue. This is a direct result of the collagen fiber recruitment resulting from the increasing plastic strains.
To model this form of plasticity, we utilized a constrained mixture model based on [50]. It is important to note here that the timescale for the plasticity events is over thousands and millions of loading cycles. Transient and inertia effects, which occurs in the time frame of a single cycle, averages out over the course of tens of thousand of cycles and does not play a significant role. It is likely that the peak stresses and folding that occurs with the dynamics of the leaflet motion plays a significant role in how damage (deterioration of collagen stiffness or tearing of the leaftlet) is accrued, but this is a whole separate effect to the plasticity modeled and simulated in this paper. As noted in our previous work [38], damage phenomena occur at an even later stage in comparison to the plasticity simulated here, and does not play a significant role in this work. In fact, it is especially important to be able to distinguish and separate the plasticity effect from structural damage so that form of the structural damage model can be accurately determined. The work done in this study as a first step to simulating BHV failure cannot be understated. Thus, for plastic effects, the dominant driver is the average or root mean squared (RMS) loaded state over thousands of cycles. In brief, after each increment in time, ‘new’ matrix material (i.e. healed in a deformed state) is created referenced to the current loaded RMS state, while the mass fraction of the ‘old’ matrix material is reduced, both occurring while conserving the total mass. The response of the matrix at the bulk level is thus
| (7) |
where b(t) is the proportion of the original amount of the EXL matrix material remaining at time t with stress contribution , and a(t, τ) is the proportion of the material newly formed at time τ with stress contribution . The rate of mass transfer between these states was described by first order kinetics [38]. Next, we account for the convection of collagen fiber architecture with plastic strain by defining the convected fiber recruitment distribution function, , and the convected fiber orientation distribution function, in terms of the original distributions and the plastic deformation .
| (8) |
| (9) |
where the subscript ‘0’ denotes the 0-cycle referential configuration, the subscript/superscript ‘t’ denotes the structurally convected (plastically deformed) unloaded configuration, and λlb and λub are the lower and upper bounds of the slack stretch. Further details about these forms are presented in [37, 38, 51].
The final model form is a function of the plasticity rate constant k, the plastic deformation Fp, the strain history A(t), and the material parameters of the constitutive model in the uncycled state. The input of the model is the applied deformation C referenced to the current unloaded state ΩP, given by the plastic deformation Fp from Ω0 (Fig. 5).
Figure 5:
Illustration of the permanent set effect under cyclic uniaxial loading showing A) the relation between the reference configurations during cyclic loading. Figure reproduced from [38], B) the transfer of mass fraction of the EXL matrix to the loaded configuration Ω(s) from the original state Ω0 and C) the resulting in changes in the unloaded geometry of the tissue.
The full model form is
| (10) |
where the collagen contribution is
| (11) |
the contribution of the interactions is
| (12) |
where,
| (13) |
| (14) |
| (15) |
| (16) |
and the contribution of the EXL matrix is
| (17) |
where is the stretch of the fiber ensemble oriented along θ, and λs,θ is the slack stretch of the fiber ensemble oriented along θ.
2.3. Effective material modeling approach
An obvious challenge in using Eqn. (10)–(17) is the substantial computational cost of evaluating the quadruple integrals. To circumvent this issue, we utilized a recently developed effective soft tissue constitutive model to perform the actual finite element computations [52]. This basic form has been shown to able to fully reproduce the response of a wide range of planar soft tissues, along with a method for robust and fast-convergent parameter estimation. The form of this effective constitutive model is given by
| (18) |
where Qmax = Q(Emax) is a scaling factor that helps reduce parameter covariance by normalizing the exponential part of the equation (see [52] for details).
The method to determine the effective model parameters are presented in Zhang et al. [52]. The first step is to generate a set of synthetic data, which should not be done arbitrarily. This is done along a set of optimal loading paths which minimize the covariance between model parameters. We have shown that optimal loading paths with the use of the scaling factors Qmax is sufficient for determining a unique set of parameters using gradient algorithms, i.e. this approach improves the ellipticity about the minimum. The maximum strain energy value, which could be determine from the plasticity constitutive model, matches closely with the parameter c0 in Eqn. 18 making it an excellent value for the initial guess, while the exponent parameters bi are generally very consistent in value over time. As such, parameter estimation for the effective model is generally very quick. The parameter constraints are likewise presented in Zhang et al. [52]. The effective model sufficiently preserves the mechanical response of glutaraldehyde pericardium used in this study such that we were able to obtain similar structural model parameters by fitting to synthetic data generate from the effective model in comparison to fitting the structural model directly, i.e. the parameter are within 10−3 in most cases. Some difference are inevitable due to the the lack of complexity in comparison to the plasticity constitutive model but the overall response is qualitatively preserved.
2.4. Simulation framework
In this next section, we introduce a time dependent simulation framework, which integrates these models into a holistic setup to simulate in-vivo cyclic loading for BHVs to 50 million cycles. We divide the simulation framework into the following major stages (Fig. 6):
Figure 6:
Flowchart explaining the execution of the different components of the time dependent simulation framework.
Model formulation and quasi-static simulations of the initial state.
Updating the material model parameters for the next time step.
Updating the current geometry for the next time step.
Steps 2 and 3 are repeated for each subsequent time step until the maximum time limit is reached. Details of each step are provided in the following sections.
2.4.1. Initial state model and quasi-static simulation
Next, we first established the following initial (referential) model primary components: 1) The BHV geometry, 2) the mechanical properties, and 3) mapped collagen fiber architecture. We utilized an established BHV geometry from [44], bovine pericardium properties from [37], and homogeneous circumferential aligned collagen fiber orientation distributions. A custom in-house isogeometric finite element software was used, based on the framework developed by Hsu and co-workers [44, 46, 45]. Briefly, the finite element code was purposed for dynamics and fluid–structure interaction simulations of heart valves [53, 54, 55], focusing mostly on the tri-leaflet semilunar valves. The tri-leaflet geometry is based on the commonly used Edwards Pericardial Heart Valve with Kirchhoff–Love shell elements for the leaflets [46] and finite element solver developed by Hsu et al. [44].
We utilized this code to simulate leaflet deformation under physiological quasi-static transvalvular pressure of 80 mmHg. A total of 484 Bézier elements were used for each leaflet, with a leaflet density of 1.0 g/cm3 and a uniform leaflet thickness of 0.386 mm [44]. Contact between leaflets was handled by a penalty-based approach and imposed at quadrature points of the shell structure [56], and a clamped boundary condition is applied to the leaflet attachment edge. For simplicity and consistency, the collagen fiber direction was assumed to be aligned to the circumferential direction of each leaflet. The bioprosthetic heart valve stent was fixed and undeformable, thus serving as a stationary reference for the leaflets. A similar validation process as the one presented by Wu et al. [45] was used to verify the implementation.
2.4.2. Evolution of leaflet material behaviors
The loading history data for the current timestep, as obtained from the FE code, is used to predict the change in material properties using the plasticity constitutive model. Next, the mechanical response from the plasticity model is sampled along optimal loading paths and then fitted to equation 18. The parameters of equation 18 are changed in the finite element model and this effective model is then used to perform the simulation. This effective model (Eqn. 18) acts as an intermediate between the constitutive model and the finite element model for quasistatic simulation of BHVs (Fig. 3A) and drastically simplifies the implementation of the numerical model by keeping the constitutive model form the same. The full implementation of the FE model and the boundary conditions are presented in [53, 54, 55]. Briefly, the stent of the valve are assumed to be rigid and prescribed with a zero displacement boundary condition and a transvalvular pressure difference, oscillating from 0 to 80 mmHg at 10 Hz, was applied across the closed valve.
2.4.3. Geometry update due to plastic strains
To obtain the plastic strain, we need to use optimization, since the plasticity constitutive model has no analytical inverse form. The plasticity model can find local change in reference geometry using equation 17 and
| (19) |
Since this is being solved for each element locally, it is not sufficient for generating a geometrically compatible mesh. To generate a mesh for the updated reference configuration in the following time step, we will need to perform another FE simulation with load free boundary condition and an internal residual stress. First, we find the local change in geometry from Eqn. 19. Next, we will compute an equivalent stress using Eqn. 10, by
| (20) |
This stress, SP, is equivalent of a residual stress corresponding to the local change in geometry, which is then added to the following weak form
| (21) |
where, y is the midsurface displacement, the derivative ∂(·)/∂t|X holds material coordinates X fixed, ρ is the density, S is the 2nd Piola–Kirchhoff stress, δE is the variation of the Green–Lagrange strain corresponding to displacement variation w, f is a prescribed body force, hnet is the total traction from the two sides of the shell, and Γ0 and Γt are the shell midsurfaces in the reference and deformed configurations respectively [45, 54]. The resulting control point displacements u(x, t + 1) are then added to the finite element mesh from the previous time step to generate the new mesh in the new reference configuration.
2.5. Complete implementation
We utilized custom Python scripts to combine the individual source codes for each component of the simulation (Fig. 6). The quasi-static simulations were done using the isogeometric finite element code from Hsu et al. [44, 46, 45], only altering the input parameters and boundary conditions. The full structural (Eqn. 2) and effective models (Eqn. 18) were implemented in C++ compiled to a python module using Cython [57]. The individual components were called in sequence to perform the plastic strain simulations as follows:
Setup a quasistatic FE simulation for the first loading cycle using the initial state information (Fig. 6, Step 1)
Perform FE simulation of the loading cycle and obtain loading history data for the control points for the current time step (Fig. 6, Step 2)
Update structural model locally, compute plastic strain and residual stress from the plastic strain constitutive model in section 2.2.2 and optimal loading path data for the mechanical response (Fig. 6, Step 3)
Compute new effective model parameters from structural parameters (Fig. 6, Step 3)
Setup FE simulation with zero pressure and residual stress from the plastic strain constitutive model (Fig. 6, Step 4)
Perform FE simulation for the next stress free geometry (Fig. 6, Step 4)
Setup FE simulation for loading cycle for the next time step using the new effective model parameters, reference geometry and fiber structure
Return to step 2 in Fig. 6 and continue this loop unless final time step is reached
2.6. Evaluating time-evolving changes in BHV leaflet geometry and fiber structure
In the present study we simultaneously predicted changes in the BHV leaflet geometry and evolution of the collagen fiber structure, for a single cycle and for long-term cyclic loading up to 50 million cycles. To aid in visualizing the effects of these changes we plotted the stretch ratio λ, in circumferential and radial directions. To express the resulting shear, we determined the shear angle α from the Green’s strain tensor E using
| (22) |
We also computed the curvature tensor at each node from the NURBS position vector and its spatial derivatives. From the curvature tensor, we determined the local principal directions and magnitudes, and subsequently, calculated the Gaussian and mean curvature for the leaflet surface.
To visualize the changes in the collagen fiber architecture with deformation, we utilized a normalized orientation index ν using
| (23) |
where, σ is the standard deviation of the collagen fiber orientation distribution and σiso is the standard deviation of a uniform distribution, i.e., the orientation distribution function when the fibers are distributed uniformly and thus representing an isotropic material. Here, ν = 1 indicates a perfectly aligned distribution, whereas ν = 0 indicates that the fiber distribution is a uniform (random) distribution.
Due to the lack of experimental data, we were unable to perform detailed validation. However, as a basic validation method, we compared the geometric changes predicted by our simulations with the results in [31, 32], by comparing the ratios and , where h0 is the initial difference in height of the highest point of commmissure region, and the triple point, namely the location where the three leaflets meet, ht is the same height in the unloaded final state, and w is the width of the BHV leaflet in the initial state (Fig. 1).
3. RESULTS
3.1. Single loading response in the initial and final states.
To compare the BHV responses in the initial (0 cycles) and final (after 50 million cycles) states, we plotted the circumferential and radial stretch due to one loading cycle in the initial state, referenced to the unloaded initial state (Fig. 8c, 8d), and the stretch due to one loading cycle in the final state, referenced to the unloaded final state (Fig. 8e, 8f). In the uncycled state, the highest circumferential stretch was 1.1344, in the central belly region. The free edge also had high circumferential stretch compared to the surrounding regions, with the maximum value being 1.1315 near this region. The highest radial stretch was 1.1244, in the lateral belly region of the leaflet. In comparison, after 50 million cycles, the maximum stretch due to one loading cycle was 1.0307 in the circumferential direction and 1.029 in the radial direction. The BHV exhibited a significantly stiffer response in the final loaded state relative to the initial state and a more uniform deformation pattern was observed in the final state.
Figure 8:

(a) Arrows representing circumferential direction in the leaflet, (b) Arrows representing radial direction in the leaflet, (c) Circumferential stretch in uncycled, fully loaded state, referenced to the uncycled, unloaded configuration, (d) Radial stretch in uncycled, fully loaded state, referenced to the uncycled, unloaded configuration, (e) Circumferential stretch in cycled, fully loaded state, referenced to cycled, unloaded state, (f) Radial stretch in cycled, fully loaded state, referenced to cycled, unloaded state. Note that by 50 million cycles, the circumferential and radial stretches have been substantially reduced due to the effects of plastic deformation.
3.2. Evolution of BHV leaflet geometry and collagen fiber architecture
To analyze the changes to the BHV leaflet geometry with time, we plotted the circumferential and radial stretch, the shear angle α and the mean curvature in the unloaded configuration at six different time points over the duration of the simulation, referenced to the unloaded uncycled state (Fig. 9 – Fig. 12). Our results indicated that these dimensional changes slowed down after about 20 million cycles and nearly completely seize after 30 million cycles. The regions that exhibited the highest plasticity were the belly region and the free edge. After 50 million cycles the maximum circumferential plastic stretch in the belly region was 1.1209 and in the free edge was 1.1453, while the maximum radial stretch was 1.1104 in the lateral belly region. By 20 million cycles, the maximum plastic stretch in circumferential and radial directions had already reached 98% of the maximum value of plastic stretch at 50 million cycles. The maximum shear angle in the unloaded state at 20 million cycles was 17.64°and at 50 million cycles, it was 17.79°, near the region connected to the stent. The maximum value of mean curvature was 2.22 at 20 million cycles, and it had increased to 2.31 at 50 million cycles near the center of the free edge. The location and the value of maximum curvature was very similar to the previous results in [31, 32] (Fig 1), where the center of the free edge had a maximum mean curvature value of 2.1 at 50 million cycles. Overall, the central region of the valve had a higher curvature as predicted by our simulations, which agrees with the previous results.
Figure 9:
Time evolution of the circumferential plastic stretch in unloaded state. Here, the plasticity effects were highest in the belly region and the free edge.
Figure 12:

Time evolution of the Mean curvature in unloaded state. Curvature was highest in the belly region and the center of the free egde.
In addition, we compared the height and width ratios in the initial and final state for the BHV geometry predicted by our simulations with the BHV geometry for a stented and non-stented design previously presented in [31, 32] (Table 1). The ratios for the stented BHV design agree with our simulation results, especially when both height and width are taken into account. While there is some difference in values for the non-stented design, this is expected due to the difference in boundary condition.
Table 1:
Comparison of height and width ratios for the BHV geometry predicted by our simulations with the experimental results for BHV geometry for a stented and non-stented design previously presented in [31, 32]
| Experimental result for non-stented BHV design | 2.05 | 0.18 |
| Experimental result for stented BHV design | 1.95 | 0.06 |
| Simulation | 1.58 | 0.08 |
To visualize the corresponding changes in the collagen fiber architecture with time, we plotted the normalized orientation index, ν, at 6 distinct points in time (Fig. 13). The belly region and the free edge displayed the greatest degree of realignment. In the initial unloaded state, ν was 37.1%, whereas in the final unloaded state, the fibers had reoriented such that the maximum value of ν was 43.4% at the free edge, and the minimum value of ν was 34.4% in the lateral belly region. This indicates that the fibers had oriented towards the circumferential region and had become more aligned in the free edge and central belly region, whereas in the lateral belly region, the fibers had oriented towards the radial direction.
Figure 13:

Time evolution of the collagen fiber Normalized Orientation Index in unloaded state. Significant plasticity-induced collagen fiber reorientation occurred near the belly region and the free edge. Note that these changes were not associated with any damage mechanisms
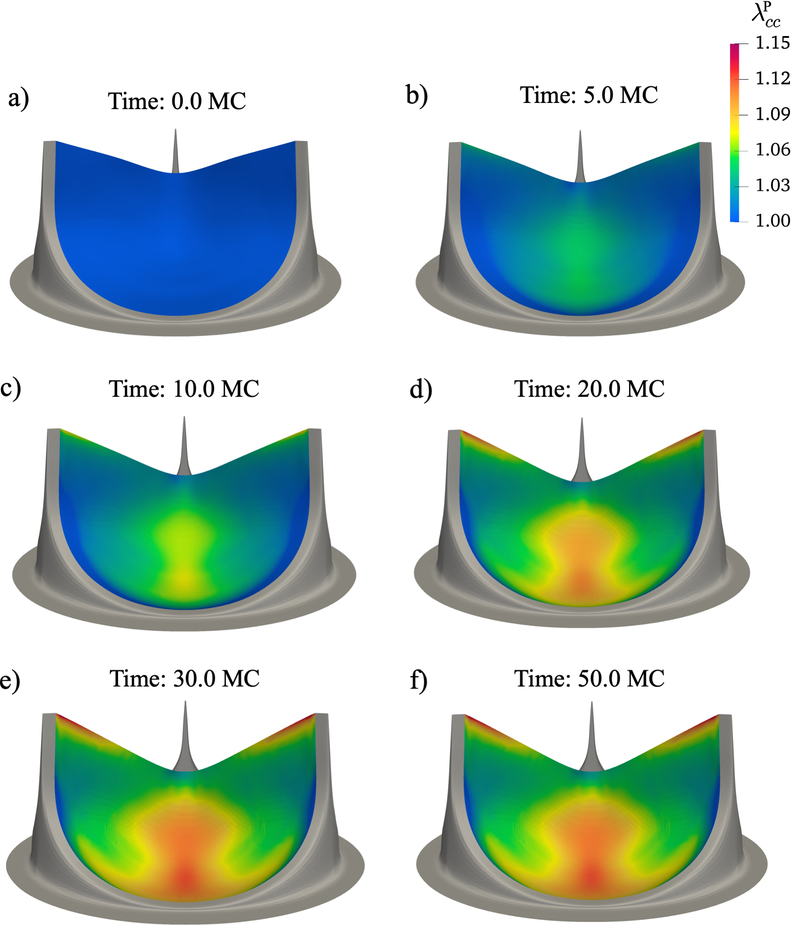
Additionally, we plotted the circumferential and radial components of S in the loaded state (Fig. 14, Fig. 15). The maximum circumferential stress was 1067 MPa near the commissure region, where we see high stress concentrations, although the range of stress in the rest of the leaflet was within 0–400 MPa. The maximum radial stress was 358 MPa in the lateral belly region.
Figure 14:
Time evolution effects on the Scc in the fully loaded state. The high circumferential stress regions were the same as the regions with highest plasticity in the circumferential direction: the belly region and the free edge. These changes are a coupled results of both the changes in leaflet geometry and tissue properties with cyclic loading.
Figure 15:
Time evolution effects on the Scc in the fully loaded state. The high circumferential stress regions were the same as the regions with highest plasticity in the radial direction: the lateral portions of the belly region. These changes are a coupled results of both the changes in leaflet geometry and tissue properties with cyclic loading.
4. DISCUSSION
4.1. Major findings
The present study represents the first micro-structural mechanism–driven simulation of XTB materials in a full BHV simulation framework. Key results indicated that the BHV responds to cyclic loading in complex ways, including permanent plastic changes to the leaflet geometry which resulted in substantial changes in leaflet shape (curvature). In addition, at the micro–structural level change to the underlying collagen fiber architecture (especially alignment) were also substantial, and also regionally variant.
These ‘plastic’ dimensional changes slowed down asymptotically, with most changes occurring in the first 20–30 million cycles (Fig. 16B, C). This is roughly equivalent to the first 6–10 months of in-vivo function. This places enormous importance on knowing this final stable unloaded geometry, as this is the geometry that the BHV will operate in for the remainder of its life, not the initial BHV design. We have shown here that we are able to predict this geometry through the plasticity model as well as the distribution of plastic deformation in the BHV leaflets, which is most significant in the belly region and the free edge. We also found that the changes in shape induced increased stresses in both the circumferential and radial directions. Moreover, we observed significant stiffening of the BHV leaflet, resulting in reduction in peak stretches due to a loading cycle (Fig. 16D). In addition, by utilizing a full structural model formulation we were also able to predict the changes to the fiber architecture with time under cyclic loading. This capability paves the path for optimizing the collagen fiber architecture in BHV along with optimizing the overall geometry, thus giving insights into the microstructural changes and their effects on the function of the BHV over time.
Figure 16:
A) BHV leaflet with a few key locations highlighted B) Triple point height in the unloaded configuration showing decay with time C) Plastic stretch in circumferential and radial directions with time at the marked locations in the BHV leaflet. Most of the dimensional changes occur in the first 20–30 million cycles. D) Peak stretch in the current loaded configuration with reference to the current unloaded configuration with time at a few key locations in the BHV leaflet. The reduction in peak stretches demonstrates significant stiffening in the BHV leaflet.
4.2. Computational considerations
The first concern with the use of any structural constitutive model in organ-level computational simulations is the computational efficiency. The accurate computation of the integral over the collagen fiber orientation distribution and the collagen fiber recruitment distribution can result in 400 to 900 times as many floating point operations as in phenomenological models, making it intractable in computational simulations with a large number of degrees of freedom. However, an approach using an effective model [43] can mitigate this problem. The computation of the structural constitutive model required a minimum 21 gauss quadrature points for Γ(θ) and 30 gauss quadrature points for D(λs). Per evaluation, the structural constitutive model time cost was 2 to 3 orders of magnitude longer to evaluate in comparison to the effective model. Because we updated the effective model per element, we shifted the cost from the structural constitutive model to the effective model by virtue of there being 16 times less elements than Gauss points. We also compared the computation time for both Ψeff (Eqn. 18) and Holzapfel-Gasser-Ogden model [58] for biaxial simulation of bioprosthetic heart valve tissues and, as expected, found no significant increase in computational cost. The total elapsed time for Ψeff is 7.58 seconds in comparison to 6.40 seconds for the Holzapfel-Gasser-Ogden model, which is evidently much faster than any micro-models can achieve.
Our rationale for why we are not running full FSI is that we are only considering modeling valve closure. This is because we were interested in simulating the fatigue process, which is driven primarily by high tensile stresses that occur in the closed state. The effects of hydrostatic forces on a closed valve can be modeled quite successfully using a uniform pressure load. We have found no significant differences between structural-only and FSI simulations of valve closure [59]. FSI clearly will take substantially more computing resources to simulate, and since it will not any simulation accuracy improvements in the present study, we did not consider it.
4.3. The effect of plasticity on bioprosthetic heart valves geometry
The mechanism underlying the observed plasticity in the XTB materials involves the scission-healing reactions in the matrix due to the Schiff-base reaction of the GLUT. GLUT treatment has the important role of suppressing the immune reaction to the BHV, but causes side effects such as stiffening the matrix, accelerating mineralization, and, as we suggested here, inducing plasticity in the BHV. These continuous scission healing reactions cause the reference configuration to evolve. As a result, the new reference configuration of the tissue is based on the proportion of the tissue whose reference configuration is in the original reference configuration and the proportion whose reference configuration is in the current configuration. The rate at which the proportion of the tissue undergoes a change in reference configuration is dependent on the proportion of the material still remaining in the original reference configuration. In theory, this process can go on indefinitely, but will be limited by the collagen fiber phase, as discussed in the next sections.
4.4. The impact of collagen fiber microstructure on BHV plasticity
The collagen fiber architecture is the major load bearing component in BHVs, and it determines the current loaded configuration geometry. To underscore its effects, we conducted the following additional simulations of BHVs with different collagen fiber architectures: A) uniformly distributed collagen fibers, B) typical bovine pericardium collagen fiber architecture, and C) native porcine aortic valve collagen fiber architecture with highly aligned collagen fibers. All simulations significantly different maximum in-plane Green-Lagrange strain (MIPE) in the fully pressure-loaded state (Fig. 17). The porcine aortic valve properties result in significant heterogeneities in the deformation of the leaflets (Fig. 17C). The pericardial valve (Fig. 17B) and the isotropic valve (Fig. 17A) on the other hand have significantly more homogeneous leaflet deformations, especially from the top-down view. Both of these undergo approximately the same deformation of 0.2 in MIPE. However, there is significant difference between the two near the commissure regions of the valve, where the isotropic case is under significantly higher strain. This zone is susceptible to failure due to tearing and delamination. It’s clear from this that the collagen fiber architecture has a significant impact on the fully loaded geometry, which determines the reference configuration that the matrix is evolving towards. This emphasizes one important reason for the need to understand the collagen fiber architecture for modeling BHVs under cyclic loading.
Figure 17:
The fully loaded state of the single cycle simulations of intact tri-leaflet valves with the collagen fiber architecture of A) a uniform collagen fiber orientation distribution, B) exogenously cross-linked bovine pericardium valve, and C) the native porcine aortic valve. A) and B) result in mostly homogeneous stress distributions with A) showing stress concentrations are the commissure regions, while C) results in a very heterogeneous stress distribution and the belly region caving in. The top row shows the side view of the valves at 80 mmHg and the bottom row shows the top-down view.
The collagen fiber architecture will also limit the amount of plasticity. It is important to reiterate here that the collagen fiber architecture remains fully intact and undamaged by this plastic deformation in this phase [38]. Plastic deformation does not continue forever, nor does the shape of the valve leaflets ever match its fully loaded state. The collagen fiber architecture evolves with the changes in the configuration of the matrix, shifting in orientation and changing in crimp. The collagen fibers are stiffer than the matrix by approximately three orders of magnitudes, and typically only extend by 3–4%. Thus, when the matrix deforms plastically, it is difficult for the matrix to exert significant deformations on the underlying collagen fiber network, it can only reorient the fibers. The stretching of collagen fibers will pull against the matrix and prevent further plasticity. This is an important mechanism, allowing the final stable geometry to be predicted from the collagen fiber architecture using our simulations. Thus, it is easy to see the importance of the collagen fiber architecture in the plasticity of BHVs, and the need for BHV designs to take into account of collagen fiber architecture to optimize durability.
For clinical applications, the measurement of this collagen fiber orientation distribution of BHV can be done non-destructively prior to being implanted into a patient. One such technique is polarized spatial frequency domain imaging [60, 61, 62], which combines polarized light imaging and spatial frequency domain imaging techniques to perform fiber orientation mapping. Polarized light imaging is a common technique taking advantage of how the orientation and alignment alters the scattering distribution of photons to measure the collagen fiber architecture. Changing the spatial frequency of the polarized light can control the imaging depth by rejecting diffuse photons. In combination with 3D projection, this offers a path to the full 3 dimensional fiber structural characterization of BHVs for simulations.
4.5. Structural damage and predicting failure
The mechanism described here for the plasticity of the BHVs is focused on the evolution of the reference configuration of the matrix and the collagen fiber architecture. A key advantage of our model is that it utilizes the structural modeling approach and can thus predict the effects of cyclic stresses at a microstructural level. This allows the computation of the recruitment of collagen fiber and thus the distribution of crimp and stretch of the collagen fibers in both the unloaded and loading configuration. This metric for the strain load on collagen fibers over time is an excellent metric for formulating structural damage at the fiber level. Experimental evidence corroborates with this theory by showing that the areas that underwent significant changes due to plasticity in our simulations also undergo significant structural damage [31]. We also found that stress concentrations were highest in the belly and the commissure region, which are known locations of calcification and tissue failure. The model predicts that the collagen fibers in areas with significant plastic changes are also under increased strain in both the loaded and unloaded configuration, and may become permanently held in a stretched state. The collagen fibers being held in a extended state more often are more likely to become damaged, where rates of failure after being extended by 7–8% increases significantly [49, 63]. Coupling this with the plasticity model presented here allows for the prediction of microstructural changes and mechanical response due to fatigue and other damage phenomena, a step towards a full fatigue damage model capable of predicting device level failure (Fig. 18).
Figure 18:
BHV fatigue as a multiscale process
4.6. Potential to improve bioprosthetic heart valve designs
In our simulations, we found that the belly region and the free edge exhibit the highest plasticity. These regions are also the most common regions of failure due to structural degeneration in BHVs. Moreover, we also found that the BHV leaflet geometry stabilizes after about 30 million cycles. The initial geometry can likely have a significant impact on loading of the BHVs. For example, higher curvatures can increase deformation in the belly region, resulting in increased plastic strains. A shorter free edge length requires larger circumferential stretch to fully close the BHV. We can use this knowledge to optimize the initial BHV geometry to reduce the peak stress and make the stress distribution more uniform in the loaded configuration after plasticity has ceased. This approach will reduce the stretch that the collagen fibers experience throughout its lifespan, which can reduce the likelihood of failure in these fibers and in turn improve the durability of the BHV leaflets. For clinical applications, a long-term clinical study similar to AWT validation studies that explore tissue strain and leaflet shape would need to be undertaken eventually, especially of explanted BHV to explore non-failure mechanisms for the changes in BHV shape and material properties, such as done by Sacks and Schoen [4]. For clinical simulations, the form of the material model is known, as well as the initial design and geometry. Inverse modeling techniques have already been established to estimate the initial behaviors [5–8]. These basic information and the approach laid out in this work should be sufficient to determine in vivo performance.
4.7. Future directions in material modeling
The plasticity model and simulation framework developed herein is a simplification of the growth and remodeling framework by removing the growth component. One potential implication is the design of devices such as tissue engineered valves, which have the possibility of growing and adaption to the surrounding environment if seeded with interstitial cells. In addition to the exogenously crosslinked tissue applications addressed herein, we have observed plasticity like phenomenon in mitral valve tissue during pregnancy [64]. In that study, our results suggested that much of the growth and remodeling in the MV leaflet does not begin immediately, but rather undergoes mostly passive leaflet enlargement until these parameters reach a critically low level, at which point growth and remodeling are triggered. This initial tissue distension process is very similar in behavior to the plasticity mechanism outlined in the present work. Thus, the current approach could be applied to the early phases of soft tissue remodeling, where non-failure mechanisms occur before the onset of growth of tissue growth and remodeling. This is a key advantage of structural approaches, which allow us to describe the mechanical response based on real, physically measurable quantities.
5. Limitations
The goal of this work is to establish a proof of concept for the simulation of the effect of plasticity on BHVs, and produce good agreement with the extant experimental data. We have shown that our plasticity model can predict the change in geometry of BHVs with cyclic loading as well as the evolution of the underlying collagen fiber architecture. This can be extended to additional simulations to explore different initial geometric and structural conditions in the future. Moreover, a fiber-level fatigue model can be developed as a starting point beyond the plasticity effects described herein (e.g. the ‘intermediate’ stage shown in Figure 2). However, this first requires sufficient experimental data to derive model parameters and to validate the model predicted outcomes. Nonetheless, we underscore that the model developed in the present study agreed well with actual accelerated wear test studies on BHVs [31, 32]. In particular, we noted similarities in the mean curvature distribution at the 50 million cycles in the discussion (Fig. 1 vs. Fig. 12).
6. Conclusions
We have developed a complete time-dependent framework for the simulation of BHVs under long-term cyclic loading. This simulation utilizes the predictive mechanism based constitutive model for the plasticity effect in exogenously crosslinked soft tissues that we previously developed. We have shown that we can use this simulation to predict the evolving geometry, microstructural changes and material property changes. These results can then be used to predict regions of increasing likelihood of structural damage and can be used to optimize the initial design of BHVs based on these factors. Most important of these effects is that the collagen fiber architecture can play a role in limiting plasticity, where the straightening of collagen fibers prevents further changes in geometry. Thus, accounting for the plasticity effect is especially important in the design of BHVs to better improve their performance and durability.
Figure 7:
Flowchart explaining how the geometry is updated
Figure 10:
Time evolution of the radial plastic stretch in unloaded state. Plasticity was highest in the belly region.
Figure 11:

Time evolution of the plasticity-induced shear angle α in unloaded state. Shear angle magnitudes were highest near the leaflet attachments.
Funding Source:
This study was supported by NIH/NHLBI grant no. R01 HL129077 and R01 HL142504.
Footnotes
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Schoen FJ, Evolving concepts of cardiac valve dynamics: the continuum of development, functional structure, pathobiology, and tissue engineering, Circulation 118 (18) (2008) 1864–80. doi: 10.1161/CIRCULATIONAHA.108.805911. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=18955677 [DOI] [PubMed] [Google Scholar]
- [2].Schoen FJ, New frontiers in the pathology and therapy of heart valve disease: 2006 Society for Cardiovascular Pathology, Distinguished Achievement Award Lecture, United States-Canadian Academy of Pathology, Atlanta, GA, February 12, 2006, Cardiovasc Pathol 15 (5) (2006) 271–9. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=16979034 [DOI] [PubMed] [Google Scholar]
- [3].Vesely I, Barber JE, Ratliff NB, Tissue damage and calcification may be independent mechanisms of bioprosthetic heart valve failure, J Heart Valve Dis 10 (4) (2001) 471–7. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=11499593 [PubMed] [Google Scholar]
- [4].Sacks MS, Schoen FJ, Collagen fiber disruption occurs independent of calcification in clinically explanted bioprosthetic heart valves, J Biomed Mater Res 62 (3) (2002) 359–71. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=12209921 [DOI] [PubMed] [Google Scholar]
- [5].Schoen F, Levy R, Tissue heart valves: Current challenges and future research perspectives, Journal of Biomedical Materials Research 47 (1999) 439–465. [DOI] [PubMed] [Google Scholar]
- [6].Schoen FJ, Levy RJ, Calcification of tissue heart valve substitutes: progress toward understanding and prevention, Ann Thorac Surg 79 (3) (2005) 1072–80. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15734452 [DOI] [PubMed] [Google Scholar]
- [7].Siddiqui R, Abraham J, Butany J, Bioprosthetic heart valves: modes of failure, Histopathology 55 (2) (2009) 135–144. [DOI] [PubMed] [Google Scholar]
- [8].Butany J, Leask R, The failure modes of biological prosthetic heart valves, Journal of long-term effects of medical implants 11 (2001) 115–35. doi: 10.1615/JLongTermEffMedImplants.v11.i34.30. [DOI] [PubMed] [Google Scholar]
- [9].Park KD, Lee WK, Yun JY, Han DK, hyun Kim S, Kim YH, Kim HM, Kim KT, Novel anti-calcification treatment of biological tissues by grafting of sulphonated poly(ethylene oxide), Biomaterials 18 (1) (1997) 47–51. doi: 10.1016/S0142-9612(96)00096-8. URL http://www.sciencedirect.com/science/article/pii/S0142961296000968 [DOI] [PubMed] [Google Scholar]
- [10].Isenburg JC, Simionescu DT, Vyavahare NR, Tannic acid treatment enhances biostability and reduces calcification of glutaraldehyde fixed aortic wall, Biomaterials 26 (11) (2005) 1237–45. doi: 10.1016/j.biomaterials.2004.04.034. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15475053 [DOI] [PubMed] [Google Scholar]
- [11].Vyavahare N, Hirsch D, Lerner E, Baskin JZ, Schoen FJ, Bianco R, Kruth HS, Zand R, Levy RJ, Prevention of bioprosthetic heart valve calcification by ethanol preincubation. Efficacy and mechanisms, Circulation 95 (2) (1997) 479–88. URL http://www.ncbi.nlm.nih.gov/htbin-post/Entrez/query?db=m&form=6&dopt=r&uid=0009008467 [DOI] [PubMed] [Google Scholar]
- [12].Flameng W, Meuris B, Yperman J, De Visscher G, Herijgers P, Verbeken E, Factors influencing calcification of cardiac bioprostheses in adolescent sheep, The Journal of thoracic and cardiovascular surgery 132 (1) (2006) 89–98. [DOI] [PubMed] [Google Scholar]
- [13].Carpentier A, Nashef A, Carpentier S, Ahmed A, Goussef N, Techniques for prevention of calcification of valvular bioprostheses, Circulation 70 (3) (1984). [PubMed] [Google Scholar]
- [14].Vyavahare NR, Hirsch D, Lerner E, Baskin JZ, Zand R, Schoen FJ, Levy RJ, Prevention of calcification of glutaraldehyde-crosslinked porcine aortic cusps by ethanol preincubation: Mechanistic studies of protein structure and water–biomaterial relationships, Journal of Biomedical Materials Research: An Official Journal of The Society for Biomaterials, The Japanese Society for Biomaterials, and the Australian Society for Biomaterials 40 (4) (1998) 577–585. [DOI] [PubMed] [Google Scholar]
- [15].Jones M, Eidbo E, Hilbert SL, Ferrans VJ, Clark RE, Anticalcification treatments of bioprosthetic heart valves: in vivo studies in sheep, J Card Surg 4 (1) (1989) 69–73. [DOI] [PubMed] [Google Scholar]
- [16].Fradet G, Bleese N, Busse E, Jamieson E, Raudkivi P, Goldstein J, Metras J, The mosaic valve clinical performance at seven years: results from a multicenter prospective clinical trial., The Journal of heart valve disease 13 (2) (2004) 239–46. [PubMed] [Google Scholar]
- [17].Grabenwöger M, Grimm M, Eybl E, Leukauf C, Müller MM, Plenck H Jr, Böck P, Decreased tissue reaction to bioprosthetic heart valve material after l-glutamic acid treatment. a morphological study, Journal of biomedical materials research 26 (9) (1992) 1231–1240. [DOI] [PubMed] [Google Scholar]
- [18].Webb CL, Benedict JJ, Schoen FJ, Linden JA, Levy RJ, Inhibition of bioprosthetic heart valve calcification with aminodiphosphonate covalently bound to residual aldehyde groups, The Annals of thoracic surgery 46 (3) (1988) 309–316. [DOI] [PubMed] [Google Scholar]
- [19].Webb CL, Schoen FJ, Levy RJ, Covalent binding of aminopropanehydroxydiphosphonate to glutaraldehyde residues in pericardial bioprosthetic tissue: stability and calcification inhibition studies, Experimental and Molecular Pathology 50 (3) (1989) 291–302. [DOI] [PubMed] [Google Scholar]
- [20].Shang H, Claessens SM, Tian B, Wright GA, Aldehyde reduction in a novel pericardial tissue reduces calcification using rabbit intramuscular model, Journal of Materials Science: Materials in Medicine 28 (1) (2017) 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Sun W, Sacks M, Fulchiero G, Lovekamp J, Vyavahare N, Scott M, Response of heterograft heart valve biomaterials to moderate cyclic loading, J Biomed Mater Res 69A (4) (2004) 658–69. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15162408 [DOI] [PubMed] [Google Scholar]
- [22].Ishihara T, Ferrans VJ, Boyce SW, Jones M, Roberts WC, Structure and Classification of Cuspal Tears and Perforations in Porcine Bioprosthetic Cardiac Valves Implanted in Patients, The American Journal of Cardiology 48 (1981) 665–678. [DOI] [PubMed] [Google Scholar]
- [23].Pomar J, Bosch X, Late tears in leaflets of porcine bioprostheses in adults, Annals of thoracic surgery 37 (1) (1984) 83–87. [DOI] [PubMed] [Google Scholar]
- [24].Stein PD, Kemp SR, Riddle JM, Lee MW, Lewis JW Jr, Magilligan DJ Jr, Relation of calcification to torn leaflets of spontaneously degenerated porcine bioprosthetic valves, The Annals of thoracic surgery 40 (2) (1985) 175–180. [DOI] [PubMed] [Google Scholar]
- [25].Vesely I, The evolution of bioprosthetic heart valve design and its impact on durability, Cardiovasc Pathol 12 (5) (2003) 277–86. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=14507578 [DOI] [PubMed] [Google Scholar]
- [26].Thubrikar MJ, Deck JD, Aouad J, Nolan SP, Role of mechanical stress in calcification of aortic bioprosthetic valves, J Thorac Cardiovasc Surg 86 (1) (1983) 115–25. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=6865456 [PubMed] [Google Scholar]
- [27].Schoen FJ, Tsao JW, Levy RJ, Calcification of bovine pericardium used in cardiac valve bioprostheses. implications for the mechanisms of bioprosthetic tissue mineralization., The American journal of pathology 123 (1) (1986) 134. [PMC free article] [PubMed] [Google Scholar]
- [28].Gabbay S, Kadam P, Factor S, Cheung TK, Do heart valve bioprostheses degenerate for metabolic or mechanical reasons?, J Thorac Cardiovasc Surg 95 (2) (1988) 208–15. URL http://www.ncbi.nlm.nih.gov/htbin-post/Entrez/query?db=m&form=6&dopt=r&uid=2963176 [PubMed] [Google Scholar]
- [29].Ferrans VJ, Boyce SW, Billingham ME, Jones M, Ishihara T, Roberts WC, Calcific deposits in porcine bioprostheses: structure and pathogenesis, The American journal of cardiology 46 (5) (1980) 721–734. [DOI] [PubMed] [Google Scholar]
- [30].Sabbah HN, Hamid MS, Stein PD, Mechanical stresses on closed cusps of porcine bioprosthetic valves: correlation with sites of calcification, The Annals of thoracic surgery 42 (1) (1986) 93–96. [DOI] [PubMed] [Google Scholar]
- [31].Smith DB, Sacks MS, Pattany PM, Schroeder R, Fatigue-induced changes in bioprosthetic heart valve three-dimensional geometry and the relation to tissue damage, J Heart Valve Dis 8 (1) (1999) 25–33. [PubMed] [Google Scholar]
- [32].Smith DB, Sacks MS, Pattany PM, Schroeder R, High-resolution magnetic resonance imaging to characterize the geometry of fatigued porcine bioprosthetic heart valves, Journal of Heart Valve Disease 6 (4) (1997) 424–432. [PubMed] [Google Scholar]
- [33].Wells SM, Sellaro T, Sacks MS, Cyclic loading response of bioprosthetic heart valves: effects of fixation stress state on the collagen fiber architecture, Biomaterials 26 (15) (2005) 2611–9. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15585264 [DOI] [PubMed] [Google Scholar]
- [34].Wells SM, Sacks MS, Effects of fixation pressure on the biaxial mechanical behavior of porcine bioprosthetic heart valves with long-term cyclic loading, Biomaterials 23 (11) (2002) 2389–99. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=12013187 [DOI] [PubMed] [Google Scholar]
- [35].Wells S, Sacks M, Effects of stress-state during fixation on the fatigue properties of bioprosthetic heart valve tissue., Transactions of the Sixth World Biomaterials Congress2 (2000) 794. [Google Scholar]
- [36].Mirnajafi A, Zubiate B, Sacks MS, Effects of cyclic flexural fatigue on porcine bioprosthetic heart valve heterograft biomaterials, J Biomed Mater Res A 94 (1) (2010) 205–13. doi: 10.1002/jbm.a.32659. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=20166221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Sacks MS, Zhang W, Wognum S, A novel fibre-ensemble level constitutive model for exogenous cross-linked collagenous tissues, Interface Focus 6 (1) (2016) 20150090. doi: 10.1098/rsfs.2015.0090. URL http://rsfs.royalsocietypublishing.org/royfocus/6/1/20150090.full.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Zhang W, Sacks MS, Modeling the response of exogenously crosslinked tissue to cyclic loading: The effects of permanent set., Journal of the mechanical behavior of biomedical materials 75 (2017) 336–350. doi: 10.1016/j.jmbbm.2017.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Martin C, Sun W, Modeling of long-term fatigue damage of soft tissue with stress softening and permanent set effects, Biomechanics and Modeling in Mechanobiology 12 (4) (2013) 645–655. doi: 10.1007/s10237-012-0431-6. URL 10.1007/s10237-012-0431-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Martin C, Sun W, Simulation of long-term fatigue damage in bioprosthetic heart valves: effects of leaflet and stent elastic properties, Biomechanics and modeling in mechanobiology 13 (4) (2014) 759–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Martin C, Sun W, Comparison of transcatheter aortic valve and surgical bioprosthetic valve durability: a fatigue simulation study, Journal of biomechanics 48 (12) (2015) 3026–3034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Serrani M, Brubert J, Stasiak J, De Gaetano F, Zaffora A, Costantino ML, Moggridge G, A computational tool for the microstructure optimization of a polymeric heart valve prosthesis, Journal of biomechanical engineering 138 (6) (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Zhang W, Zakerzadeh R, Zhang W, Sacks MS, A material modeling approach for the effective response of planar soft tissues for efficient computational simulations, Journal of the Mechanical Behavior of Biomedical Materials 89 (2019) 168–198. doi: 10.1016/j.jmbbm.2018.09.016. URL http://www.sciencedirect.com/science/article/pii/S1751616118309147 [DOI] [PubMed] [Google Scholar]
- [44].Hsu M-C, Kamensky D, Xu F, Kiendl J, Wang C, Wu MCH, Mineroff J, Reali A, Bazilevs Y, Sacks MS, Dynamic and fluid-structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models, Computational Mechanics (2015) 1–15. URL 10.1007/s00466-015-1166-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Wu MCH, Zakerzadeh R, Kamensky D, Kiendl J, Sacks MS, Hsu M-C, An anisotropic constitutive model for immersogeometric fluid-structure interaction analysis of bioprosthetic heart valves., Journal of biomechanics 74 (2018) 23–31. doi: 10.1016/j.jbiomech.2018.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Kiendl J, Hsu M-C, Wu MC, Reali A, Isogeometric Kirchhoff-Love shell formulations for general hyperelastic materials, Computer Methods in Applied Mechanics and Engineering 291 (0) (2015) 280–303. URL 10.1016/j.cma.2015.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Fung YC, Biomechanics: Mechanical Properties of Living Tissues, 2nd Edition, Springer Verlag, New York, 1993. [Google Scholar]
- [48].Lanir Y, Constitutive equations for fibrous connective tissues, J Biomech 16 (1983) 1–12. [DOI] [PubMed] [Google Scholar]
- [49].Lanir Y, A Structural Theory for the Homogeneous Biaxial Stress-Strain Relationships in Flat Collageneous Tissues, J Biomech 12 (1979) 423–436. [DOI] [PubMed] [Google Scholar]
- [50].Rajagopal KR, Wineman AS, A constitutive equation for nonlinear solids which undergo deformation induced microstructural changes, International Journal of Plasticity 8 (1992) 385–395. [Google Scholar]
- [51].Zhang W, Ayoub S, Liao J, Sacks MS, A meso-scale layer-specific structural constitutive model of the mitral heart valve leaflets, Acta Biomater 32 (2016) 238–55. doi: 10.1016/j.actbio.2015.12.001. URL http://www.ncbi.nlm.nih.gov/pubmed/26712602 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Zhang W, Zakerzadeh R, Zhang W, Sacks MS, A material modeling approach for the effective response of planar soft tissues for efficient computational simulations., Journal of the mechanical behavior of biomedical materials 89 (2019) 168–198. doi: 10.1016/j.jmbbm.2018.09.016. [DOI] [PubMed] [Google Scholar]
- [53].Xu F, Morganti S, Zakerzadeh R, Kamensky D, Auricchio F, Reali A, Hughes TJR, Sacks MS, Hsu M-C, A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid–structure interaction analysis, International Journal for Numerical Methods in Biomedical Engineering 34 (4) (2018) e2938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Wu MCH, Muchowski HM, Johnson EL, Rajanna MR, Hsu M-C, Immersogeometric fluid–structure interaction modeling and simulation of transcatheter aortic valve replacement, Computer Methods in Applied Mechanics and Engineering 357 (2019) 112556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Johnson EL, Wu MCH, Xu F, Wiese NM, Rajanna MR, Herrema AJ, Ganapathysubramanian B, Hughes TJR, Sacks MS, Hsu M-C, Thinner biological tissues induce leaflet flutter in aortic heart valve replacements, Proceedings of the National Academy of Sciences 117 (32) (2020) 19007–19016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Kamensky D, Hsu MC, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, Hughes TJ, An immersogeometric variational framework for fluid-structure interaction: application to bioprosthetic heart valves, Comput Methods Appl Mech Eng 284 (2015) 1005–1053. doi: 10.1016/j.cma.2014.10.040. URL http://www.ncbi.nlm.nih.gov/pubmed/25541566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Behnel S, Bradshaw R, Citro C, Dalcin L, Seljebotn DS, Smith K, Cython: The best of both worlds, Computing in Science & Engineering 13 (2) (2011) 31–39. [Google Scholar]
- [58].Holzapfel GA, Ogden RW, Constitutive modelling of arteries, Proceedings of the Royal Society a-Mathematical Physical and Engineering Sciences 466 (2118) (2010) 1551–1596. doi: 10.1098/rspa.2010.0058. URL ://000277038700001 [DOI] [Google Scholar]
- [59].Xu F, Johnson EL, Wang C, Jafari A, Yang C-H, Sacks MS, Krishnamurthy A, Hsu M-C, Computational investigation of left ventricular hemodynamics following bioprosthetic aortic and mitral valve replacement, Mechanics Research Communications 112 (2021) 103604, special issue honoring G.I. Taylor Medalist Prof. Arif Masud. doi: 10.1016/j.mechrescom.2020.103604. URL https://www.sciencedirect.com/science/article/pii/S0093641320301324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Goth W, Potter S, Allen ACB, Zoldan J, Sacks MS, Tunnell JW, Non-destructive reflectance mapping of collagen fiber alignment in heart valve leaflets., Annals of biomedical engineering 47 (2019) 1250–1264. doi: 10.1007/s10439-019-02233-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Goth W, Lesicko J, Sacks MS, Tunnell JW, Optical-based analysis of soft tissue structures., Annual review of biomedical engineering 18 (2016) 357–385. doi: 10.1146/annurev-bioeng-071114-040625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Yang B, Lesicko J, Sharma M, Hill M, Sacks MS, Tunnell JW, Polarized light spatial frequency domain imaging for non-destructive quantification of soft tissue fibrous structures, Biomed. Opt. Express 6 (4) (2015) 1520–1533. doi: 10.1364/BOE.6.001520. URL http://www.osapublishing.org/boe/abstract.cfm?URI=boe-6-4-1520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Buehler MJ, Atomistic and continuum modeling of mechanical properties of collagen: Elasticity, fracture, and self-assembly, Journal of Materials Research 21 (08) (2006) 1947–1961. doi: 10.1557/jmr.2006.0236. URL 10.1557/jmr.2006.0236 [DOI] [Google Scholar]
- [64].Rego BV, Wells SM, Lee C-H, Sacks MS, Mitral valve leaflet remodelling during pregnancy: insights into cell-mediated recovery of tissue homeostasis., Journal of the Royal Society, Interface 13 (125) (December. 2016). arXiv:http://rsif.royalsocietypublishing.org/content/13/125/20160709.full.pdf, doi: 10.1098/rsif.2016.0709. URL http://rsif.royalsocietypublishing.org/content/13/125/20160709 [DOI] [PMC free article] [PubMed] [Google Scholar]