ABSTRACT
Understanding the dose-response relationship between ingested pathogenic bacteria and infection probability is a key factor for appropriate risk assessment of foodborne pathogens. The objectives of this study were to develop and validate a novel mechanistic dose-response model for Campylobacter jejuni and simulate the underlying mechanism of foodborne illness during digestion. Bacterial behavior in the human gastrointestinal environment, including survival at low pH in the gastric environment after meals, transition to intestines, and invasion to intestinal tissues, was described using a Bayesian statistical model based on the reported experimental results of each process while considering physical food types (liquid versus solid) and host age (young adult versus elderly). Combining the models in each process, the relationship between pathogen intake and the infection probability of C. jejuni was estimated and compared with reported epidemiological dose-response relationships. Taking food types and host age into account, the prediction range of the infection probability of C. jejuni successfully covered the reported dose-response relationships from actual C. jejuni outbreaks. According to sensitivity analysis of predicted infection probabilities, the host age factor and the food type factor have relatively higher relevance than other factors. Thus, the developed “key events dose-response framework” can derive novel information for quantitative microbiological risk assessment in addition to dose-response relationship. The framework is potentially applicable to other pathogens to quantify the dose-response relationship from experimental data obtained from digestion.
IMPORTANCE Based on the mechanistic approach called the key events dose-response framework (KEDRF), an alternative to previous nonmechanistic approaches, the dose-response models for infection probability of C. jejuni were developed considering with age of people who ingest pathogen and food type. The developed predictive framework illustrates highly accurate prediction of dose (minimum difference 0.21 log CFU) for a certain infection probability compared with the previously reported dose-response relationship. In addition, the developed prediction procedure revealed that the dose-response relationship strongly depends on food type as well as host age. The implementation of the key events dose-response framework will mechanistically and logically reveal the dose-response relationship and provide useful information with quantitative microbiological risk assessment of C. jejuni on foods.
KEYWORDS: Bayesian predictive model, foodborne pathogen, infection mechanism, quantitative microbial risk assessment
INTRODUCTION
Dose-response models for foodborne pathogens play an important role for assessment and managing risk of food poisoning or foodborne infections. Food safety management systems are developed to systematically prevent outbreaks of foodborne illness. A quantitative approach to food safety control can be realized by development and implementation of quantitative microbial risk assessments (QMRA) for food products in existing safety management systems (1). While the exposure assessment of the QMRA helps predict the bacterial response during processing and distribution of foods, dose-response models play a key role in risk characterization, which estimates the probability of illness or infection from pathogen intake counts derived from the exposure assessment. Three main approaches for developing dose-response relationships of foodborne pathogens are available: (i) testing with human volunteers, (ii) animal tests, and (iii) epidemiological estimation from outbreak data. Although each approach has strengths and limitations, all three approaches have substantial uncertainty owing to the inherent variability in the pathogen, host, and food vehicle (2, 3). In addition, it is generally difficult to collect data at a low pathogen concentration to which a person is exposed, and it is difficult to collect relevant data during the response (3).
An alternative approach has been suggested for establishing dose-response models; the key events dose-response framework (KEDRF) (2). KEDRF is an approach based on important infection mechanisms causing foodborne illness, called key events, and available data from digestive systems to gain insight into dose-response relationships. As the method for estimating the dose-response relationship is based on infection mechanisms, KEDRF is expected to have several advantages, such as the potential of responding to low-dose infection and consideration of host health, sex, pathogen strain, and variability.
Few studies have focused on developing dose-response models based on infection mechanisms or key event models describing pathogen response in humans. Koseki et al. (4) and Koyama et al. (5) developed key event models that dynamically describe the death of some pathogens in simulated gastric fluid mimicking stomach digestion. Pujol et al. (6) described immune capacities until the occurrence of infection. Pathogens, such as Listeria, Salmonella, and Campylobacter, adhere to and invade intestinal epithelial cells and cause disease (7). Caco-2 cells are commonly used to observe the adhesion and invasion of pathogens to intestinal epithelial cells in vitro. We recently developed a model describing the invasion kinetics of pathogens in human intestinal cells (8). Although one study has previously estimated the dose-response relationship of Listeria through mathematical modeling of bacterial colonization in the human intestine after reductions in the human stomach (9), this mechanistic dose-response model does not consider cell invasion by the pathogen in terms of infection and that pathogen colonization in the intestines does not always cause infection. The final dose-response relationship model needs to describe illness and competitions with the immune system after the invasion of tissues by pathogens and the onset of illness. In these respects, KEDRF is still a developing concept. It will be desirable to develop a more sophisticated key events dose-response model to further elucidate the reality of foodborne illness.
The concept of bioaccessibility and bioactivity, which are aspects of nutrition absorption, can be applied to KEDRF to develop a more sophisticated mechanistic dose-response model. The term “bioaccessibility,” along with “bioavailability,” is a key concept to ascertain nutritional efficiency of food and food formulas developed to improve human health in terms of pharmacokinetics and nutrition (10). “Bioaccessibility” is defined as the number of chemicals or nutrients that are released from the gastrointestinal tract tissue and are made available through blood vessels via absorption. It is evaluated using in vitro digestion models, generally simulating gastric or small intestinal digestion, as revealed through a Caco-2 cell uptake test (11). While bioaccessibility and bioactivity are specific effects upon exposure to a substance, when these two concepts are considered for a pathogen, bioaccessibility represents infection and bioactivity represents the illness or symptoms. Infectious foodborne pathogens invade the tissues through the stomach and intestines, causing inflammation in the gastrointestinal tract, or travel to the affected area, such as blood or lymph, and cause symptoms. Pathogens also trigger physiological reactions through the same pathways as nutrients and chemicals (although there is also an interaction between pathogen and human bodies, we assume to simplify the pathogen’s invasion route into human bodies). As mentioned in the above paragraphs, conventional dose-response models for foodborne pathogens have not taken into account the infection mechanism in the human body. On the other hand, in nutrition and pharmacokinetics, the movement of nutrients and medications in the body has been considered for predicting effects. It would also be necessary to consider the infection mechanism in the human body for estimating more details of the dose-response relationship of foodborne pathogens. At present, it is difficult to experimentally replicate and model the competition between pathogens and immune cells, but the pathways for invading intestinal tissues have been reproduced in vitro. The definition of infection is based on bioaccessibility, including invasion into the body or retention in the intestinal tract. On the other hand, the definition of illness or virulence indicates the adverse effects in the human body corresponding to bioactivity. Although the two terms have different definitions, the infection probability should be higher than the illness probability if the infection probability is not equal to 1.0. In this manner, assessing the bioaccessibility and bioactivity of pathogens would be essential to assume a dose-response relationship based on the KEDRF concept.
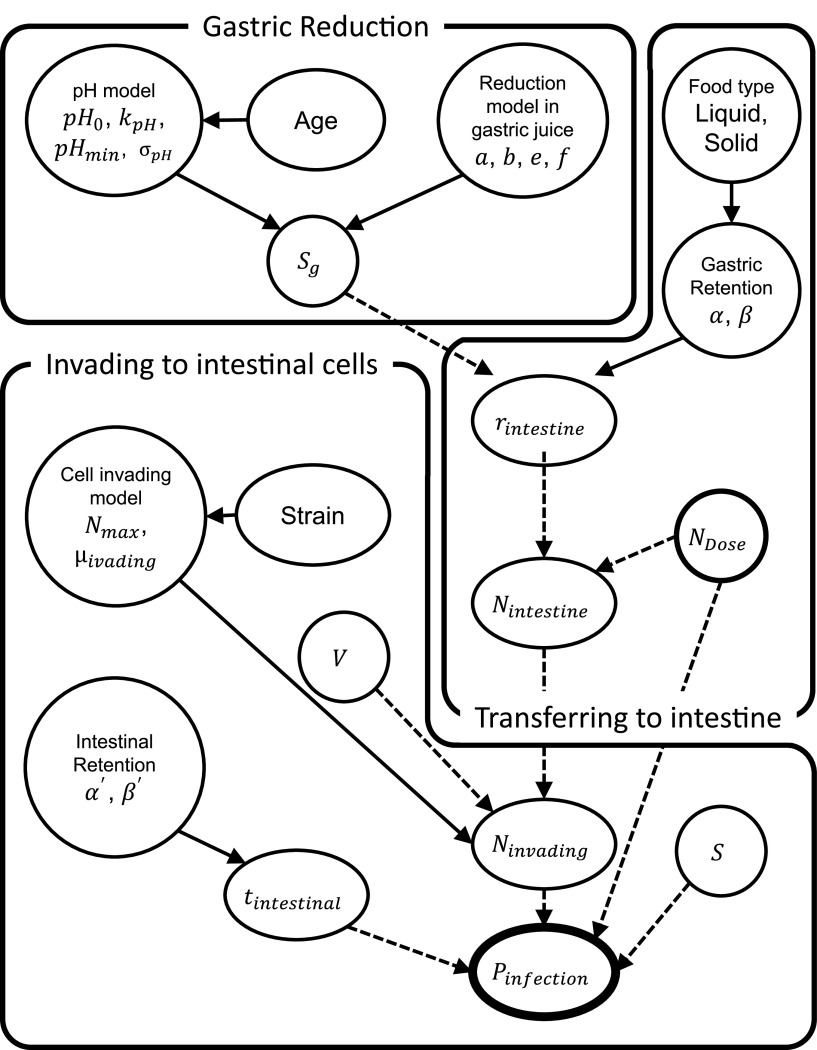
This study aimed to develop an alternative dose-response model for Campylobacter jejuni, which is known as one of the most concerning pathogenic bacteria, based on the constructed KEDRF (Fig. 1) in which food type and age of people taking in pathogens can be considered. We estimated the invasion probability, defined as the probability of infection, accounting for food type in the gastric retention time and age in the gastric pH. The estimated infection probability was compared and validated using actual epidemiological data.
FIG 1.
Directed acyclic graph of the model parameters and factors. Solid arrows indicate distributions, dashed arrows deterministic functions. The abbreviations and details of components are summarized in Table 1.
RESULTS
Gastric bacterial reduction.
The reported changes in the pH of young adult (12) and elderly (13) individuals could be successfully described using an exponential model (Fig. 2). The reference data were derived from the Heidelberg capsules, which measured the gastric pH of 34 young adult subjects (sex: 18 female, 16 male; range: 21 to 35 years old) and 79 elderly subjects (sex: 49 female, 31 male; range: 65 to 83 years old) after a simulated standard meal consisting of 6 oz of hamburger, 2 slices of bread, 2 oz of hash brown potatoes, 1 tbsp each of ketchup and mayonnaise, 1 oz each of tomato and lettuce, and 8 oz of milk (for a total of 1,000 kcal) (12, 13). All the estimated parameters of the exponential model were convergent for pH changes after liquid and solid meals among young adult and elderly individuals (Fig. S2 in the supplemental material) because the Gelman-Rubin convergence statistic (R-hut value) of parameter distributions was 1.0. The estimation of the fitted exponential model indicated that the changes in the pH in the stomachs of elderly individuals were broader than those of young adult individuals (Fig. 2).
FIG 2.
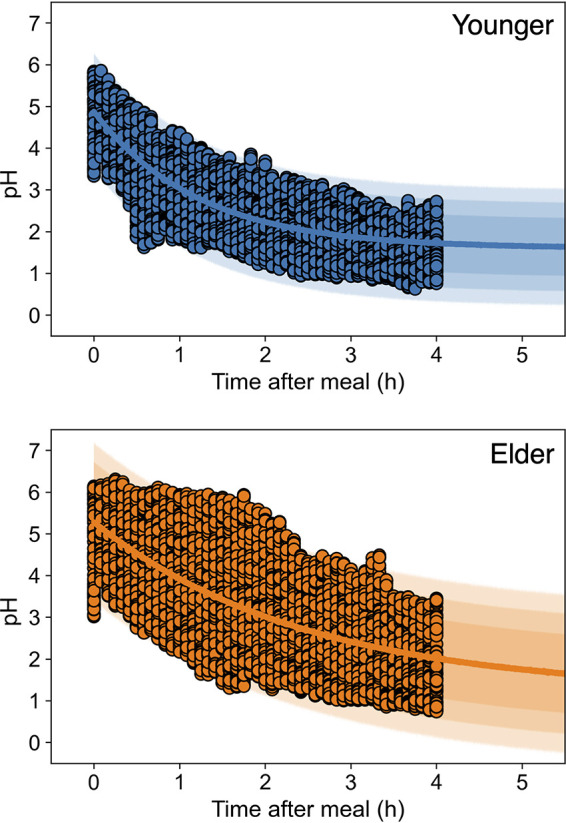
Changes in the observed pH in human stomach after-meal pH data (points) of young adult (12) (upper) and elderly (13) (lower) people, and the prediction band derived from the exponential model. The estimated parameter traceplots and distributions of Bayesian MCMC can be found in Fig. S2 of the supplemental material.
The reported predictive model for C. jejuni reduction in gastric juices (5) derived the differences in the reduction behaviors of C. jejuni in young adult and elderly people’s stomachs after a meal due to differences in pH (Fig. 3). The calculated survival ratio of elderly individuals after ingestion of liquid and solid foods was higher than that of the calculated survival transit ratio of young adult individuals.
FIG 3.
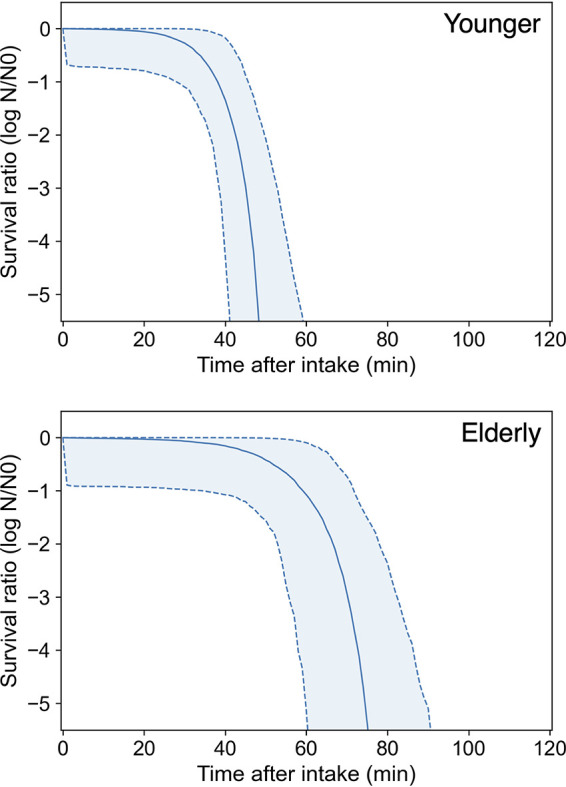
Predicted after-meal survival curves (solid curve indicates the median; dashed curve and covered range indicate the 90% prediction band) of C. jejuni in the stomach of young adult (upper) and elderly (lower) people derived from a predictive model for C. jejuni reduction in gastric juice (36).
Bacterial transfer to the small intestine.
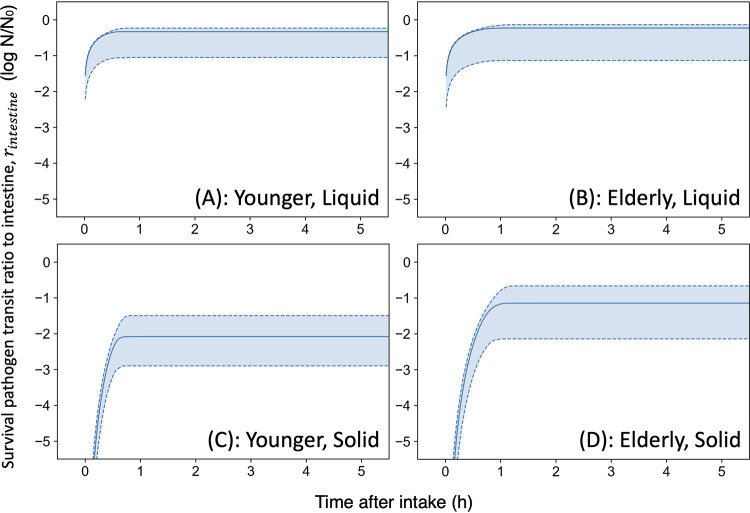
The reported changes in the retention ratio in the stomach for solids and liquids (14) could be successfully described as a cumulative gamma distribution (Fig. 4a). For the reported gastric emptying curves for a solid (99mTc-labeled omelets) and liquid (111In-labeled soft drink) meal in a healthy volunteer, liquid emptying begins instantly in an exponential fashion, while the linear emptying of solid foods begins after the lag phase (14). Estimated parameter distributions converged with Bayesian inference because all R-hut values of parameter distributions were 1.0 (Fig. S3). The mean (± standard deviation) time of estimated gastric retention of solid foods was 1.5 ± 0.52 h, and the mean of estimated gastric retention of liquid foods was 0.77 ± 0.84 h. The survival ratio of intestinal transit varied with food type and age (Fig. 5). There was a significant difference in the survival transit ratio in young adult and elderly people after eating solid food, while there was no notable difference between survival transit ratio of young adult and elderly individuals after eating liquid foods (Fig. 5a and b). In addition, considering food type differences, there was a difference in the estimated survival pathogen transit ratio regardless of age (Fig. 5). The gamma distribution is used to describe distributions of the waiting time and applied to waiting times for traffic jams and internet connections. This distribution could be appropriate to describe the time it takes for food (pathogens) entering the stomach to travel to the intestines.
FIG 4.
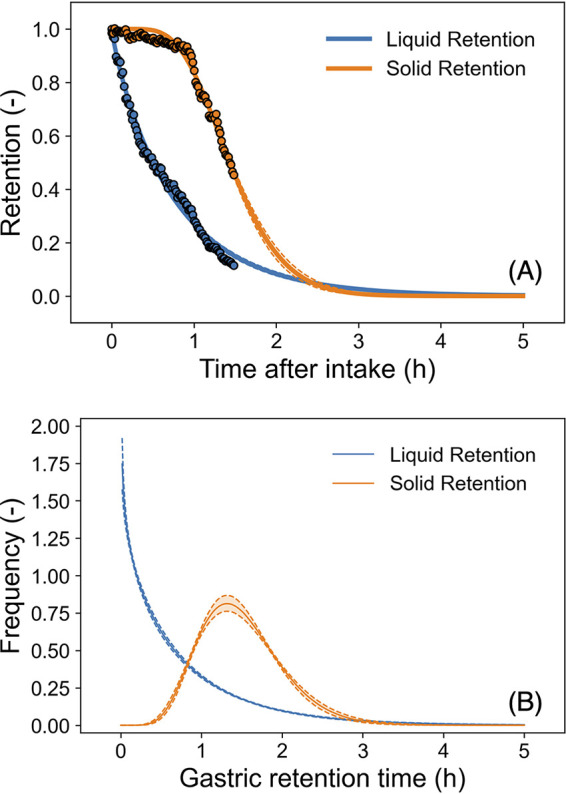
Estimated gastric retention ratio models (A and B). The reported retention ratio (14) (points in panel A) and the predicted gastric retention models based on the cumulative gamma distribution (curves in panel A); the predicted gamma densities for gastric retention time (B). The solid curve indicates the median; the dashed curve and covered range indicate the 90% prediction band. The estimated parameter traceplots and distributions of Bayesian MCMC can be found in Fig. S3 of the supplemental material.
FIG 5.
Calculated transferred survival ratio (solid curve indicates the median; dashed curve and covered range indicate the 90% prediction band) in intestine under each condition. (A to D) Young adult and liquid food (A), elderly and liquid food (B), young adult and liquid food (C), elderly and solid food (D).
Retention time in the small intestine.
The reported the colonic (large intestine) filling ratio (15) could be successfully described as a cumulative gamma distribution (Fig. 6a), and the distribution of the time for food to move to the large intestine after a meal was estimated with the gamma distribution using Bayesian inference (Fig. 6b). The reported colonic filling data was derived from 99mTc-labeled mashed potatoes (15). The estimated parameter distributions converged with Bayesian inference, since all R-hut values of parameter distributions were 1.0 (Fig. S4). The mean time of estimated intestinal retention was 5.8 ± 2.0 h.
FIG 6.
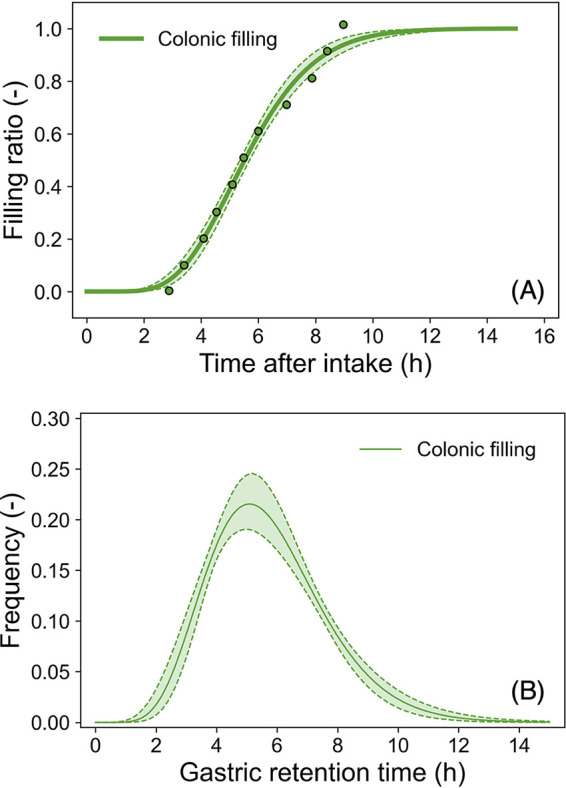
Estimated colonic (large intestine) filling ratio models (A and B). The reported colonic filling ratio (points in A) (15) and the predicted colonic filling model based on the cumulative gamma distribution (curves in panel A); the predicted gamma densities for the time for food to move from the small intestine to the large intestine after a meal (solid curve indicates the median; dashed curve and covered range indicate the 95% prediction band). The estimated parameter traceplots and distributions of Bayesian MCMC can be found in Fig. S4 of the supplemental material.
Probability of infection in human intestinal cells.
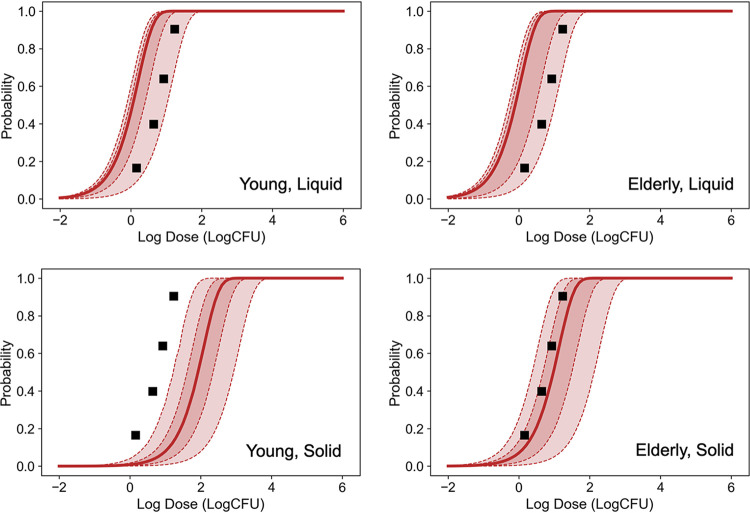
The predicted infection probabilities of C. jejuni were derived using the predicted cell-invasion model of C. jejuni (8) and they varied with food type and age (Fig. 7). Comparing the influence of the C. jejuni strain onto the predicted dose-response relationship, there were no significant differences in doses of the predicted dose-response relationships of infection probability among the three strains (within 0.5 log CFU gaps) (Fig. S7, S8, and S9) These strains were used in the referenced studies (5, 8) for predicting the reduction behavior by gastric juice and the cell-invading behavior (RIMD 0366027, RIMD 0366042, and RIMD 0366048) and had been isolated from patients of actual foodborne disease (http://rceid.biken.osaka-u.ac.jp/LIST2012(1392).htm; accessed 18 May 2021). The predicted infection probability of all three C. jejuni strains is shown in Fig. 7. Young adult and elderly individuals consuming liquid food (young adult-liquid and elderly-liquid, respectively), as well as elderly individuals consuming solid food (elderly-solid) estimated infection probabilities were similar to the reported illness probabilities derived from an actual C. jejuni outbreak for children (8 to 13 years old) with bovine milk (16), and all three strains’ 95% prediction bands covered the reported dose-response relationship despite coming from a completely different type of data source, which means that one is the real outbreak data and the other is the data of human digestive and C. jejuni reductions. The root mean square error (RMSE) of the median prediction of young adult-liquid, elderly-solid, and elderly-liquid groups were 0.69, 0.84, and 0.21 log CFU, respectively, when the logarithms of pathogen dose were assumed as objective variables. In contrast, the RMSE of the median prediction of the young adult-solid group was 1.2 log CFU and the 95% prediction band did not cover the reported dose-response relationship. The estimated infection probabilities for the young adult-liquid and elderly-liquid conditions were almost identical (0.2 log CFU gap). In contrast, the young adult-solid and elderly-solid conditions resulted in a gap of about 1.0 log CFU. The combination of conditions with the largest difference in estimates was young adult-solid and elderly-liquid, resulting in a difference of almost 2.0 log CFU.
FIG 7.
Predicted infection probability (solid curves indicate the median; dashed curve and covered ranges indicate the 60% and 95% prediction bands) of C. jejuni (total of all three strains) under each condition and the reported probability of illness (16) in an outbreak among children (8 to 13 years old) with milk (squares).
Sensitivity analysis of the framework for estimating invasion probability.
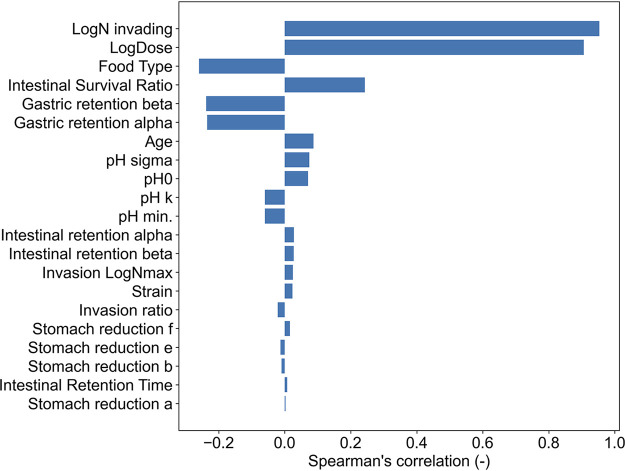
Figure 8 shows the Spearman’s rank correlation coefficients of model components (e.g., food type, model parameters, Nintestine, and tintestinal) against the infection probability. The upper factors in Fig. 8 were more relevant to the estimated infection probability. The indicators of liquid and solid food were set as 0 and 1, respectively, and the indicators of the strains were set as follows: RIMD 0366027, 1; RIMD 0366042, 2; and RIMD 0366048, 3. The indicators for age were set as the mean age of individuals subjected to the pH test (young adult: 25; elderly: 71). The most relevant factor against the infection probability was the logarithm of the invasion count, LogNinvading, to Caco-2 cells (R: 0.95; P value < 10−6). The second position of the relevant factor was the logarithm of pathogen count intake (R: 0.90; P value < 10−6). Since the infection probability was directly derived from these two factors, it is natural that these factors have the most relevance. The third position of the relevant factor was the intestinal survival ratio (R: 0.26; P value < 10−6). The relevant factors from the first to the third place were computable. The most important factors in the parametric factors were the food type (R: −0.25; P value < 10−6), the second factor was the shape parameter of the gamma distribution for gastric retention (R: −0.22; P value < 10−6), and the third factor was the rate parameter of the gamma distribution for gastric retention (R: −0.21; P value < 10−6). The factors with a P value more than 0.05 were intestinal retention α (P value = 0.06), intestinal retention β (P value = 0.11), stomach reduction a (P value = 0.11), stomach reduction b (P value = 0.38), stomach reduction e (P value = 0.058), stomach reduction f (P value = 0.15), invasion ratio (P value = 0.175), and invasion LogNmax (P value = 0.051).
FIG 8.
Spearman’s ranked correlation coefficients of parameter and computable factors against the predicted infection probability. Factors located at the upper position of this figure have a stronger relevance to infection probability. Log dose, logarithm of pathogen dose; pH 0, pH immediately after meal; pH k, Rate of decrease in pH; pH min, minimum pH value; pH sigma, SD of pH prediction; Stomach reduction a, secondary parameter of δ; Stomach reduction b, secondary parameter of δ; Stomach reduction c, secondary parameter of p; Stomach reduction d, secondary parameter of p; Gastric retention alpha, shape parameter of gamma distribution for gastric retention; Gastric retention beta, rate parameter of gamma distribution for gastric retention; Intestinal retention alpha, shape parameter of gamma distribution for intestinal retention; Intestinal retention beta, rate parameter of gamma distribution for intestinal retention; Intestinal survival ratio, survival pathogen transit ratio to intestine; Invasion rate, cell-invading rate of C. jejuni; Invasion N max, maximum invading counts to 1 cm2 of cell layer; Strain, strain indicator (RIMD 0366027: 1; RIMD 0366042: 2; RIMD 0366048: 3); Food type, food type indicator (liquid: 0; solid: 1); Age, mean age of individuals subjected to the pH test (young adult: 25; elderly: 71).
DISCUSSION
Here, this study aimed to develop an alternative dose-response model of C. jejuni, one of the most concerning pathogenic bacteria, through KEDRF, considering food type and host age. There are few human test studies with a dose-response effect (increasing trend with dose) for infection probability and data with a dose-response effect are only for illness probability (17). For these reasons, in order to assess the validity of the infection probability estimates, the illness probability was used in this study as a factor that cannot be simply compared but has a strong association. Despite the completely different approach to estimating the dose-response relationship from conventional methods, the combined predictive models developed in this study based on the KEDRF (Fig. 1) covered the reported illness probability of campylobacteriosis (16). It seems that the KEDRF has the potential to appropriately predict C. jejuni infection probability. The reported dose-response relationship (illness probability) resulted from contaminated milk consumption (16) could be properly predicted from the infection probability of the KEDRF dose-response model of this study for both young adult and elderly individuals ingesting liquid foods (Fig. 7). In addition, the predicted infection probability in this study is also similar to that reported by Teunis et al. 2018 (17), who collected and estimated multiple epidemiological data (18–21). Although the predictions by the KEDRF model in the case of liquid ingestion on the same dose level illustrated a little bit higher infection probability than those of the reported dose-response relationship, the discrepancies were within the probabilistic variation (uncertainty) as shown in Fig. 7. Furthermore, the infection probability according to the dose-response relationship estimated in this study was based on the probability of invasion into intestinal cells. Because the immune system prevents symptoms of illness after the invasion of the intestinal tissue, the illness probability being lower than the infection probability is expected.
The predicted results of this study showed a possibility that C. jejuni could invade the intestinal tissues and infect the human body even at a dose as low as 1 to 10 CFU. The previously reported epidemiological data on milk consumption also exhibited the occurrence of the disease at low doses. In contrast, the dose response of C. jejuni demonstrated herein showed a discrepancy with the previously reported model (22), which is also the most widely used dose-response relationship for C. jejuni in QMRA. The infection probability reported by Black et al. (22) was based on the presence of C. jejuni in stools, the definition of which was completely different from that examined in this study. The difference in definition might be the reason for the difference in the prediction results. It has been reported that C. jejuni growth is inhibited upon competition with the extended-spectrum β-lactamase-producing bacteria, including some strains of Escherichia coli (ESBL-E), which are widespread in nature (23). Many recent studies have reported that the healthy population is asymptomatically colonized with ESBL-E (24, 25), with colonization frequencies ranging up to 50% (26). In the colon, which is not an optimum environment for C. jejuni because of the anaerobic environment, the number of viable C. jejuni may decrease owing to competition with other intestinal bacteria. C. jejuni could be reduced before it is detected in the stool owing to competition with intestinal microbiota for nutrients or competitive effects in the gut, such as the Jameson effect (27). Considering the actual behavior of C. jejuni in the human body, it is better to discuss infection probability defined as the invasion probability, not as the existence/absence of pathogens in stool, for development of dose-response models.
While the results for the prediction were similar to those reported for illness probabilities derived from an actual C. jejuni outbreak (16), it was also possible to show the effectiveness of the implementation of the computational framework based on KEDRF. In particular, the results will be considered beneficial because the dose-response relationship depends on the food type and the age of the host. The FAO/WHO risk assessment for Listeria also emphasizes the importance of dose-response relationships in elderly and high-risk populations (28). In particular, the results of this study indicated a large difference in the infection probability (young adult: 1.9 log CFU; elderly: 1.1 log CFU) (Fig. 7) among the food types. In the sensitivity analysis, the factor related to the food type had the largest correlation among the parameters. Figure 5 shows that when consuming liquid food, the number of C. jejuni reaching the intestines was higher than that when consuming solid food, owing to the difference in the gastric retention time. The difference in the predicted infection probability between solid and liquid foods was likewise due to the difference in the gastric retention time (Fig. 8). KEDRF has the potential to estimate the probability of infection in young children since the difference between the elderly and young adult individuals was considered in this study. Compared to food type or host age variability, the strain variability used in this study had relatively weak relevance for infection probability (food type: −0.25, host age: 0.10, strain: 0.023) (Fig. 8). However, from a molecular biological point of view, the strong variability of C. jejuni virulence has been reported to depend on the host species (29, 30). The strains used in this study, which included only three, have influence on reduction behaviors in gastric juices and in the invasion behaviors into the intestinal tissue. Because the three strains compared in this study, which are all isolated from human disease, are not sufficient to determine the overall strain variability of C. jejuni, it cannot be concluded that the effect of strain variability on infection risk is weak. Nevertheless, the KEDRF concept, which can simultaneously consider various conditions such as food type and host or strain variability, would be a useful tool for estimating dose-response relationships (2, 3).
Key event models using Bayesian inference are important in KEDRF, where predictions are chained for each key event (8). This study attempted to illustrate the variability and uncertainty of pathogen behavior and the environment of the gastrointestinal tract based on Bayesian inference. Modeling using Bayesian inference has been used to describe various bacterial behaviors, such as the growth and death of various bacteria, as a method that can represent variability and uncertainty (8, 31–33). In addition, KEDRF suggests that modeling the individual variability of the digestive process in different hosts will lead to a better understanding of food poisoning incidents, such as the digestive modeling in this study (Fig. 2). The use of Bayesian inference to represent not only bacterial but also host variability will allow the estimation of appropriate dose-response relationships using mechanistic approaches.
Although this study has shown that KEDRF is a useful procedure for predicting dose-response relationships of C. jejuni, KEDRF is also effective for other types of bacteria (3). The approach used in this study consisted of a mathematical prediction model based on predictive microbiology and pharmacokinetics. The growth and death of various other pathogens, as well as the cited C. jejuni model (5, 8), have been described using predictive models (34). For many other pathogens, the present method can be applied to calculate the intestinal viable bacterial count using gastric retention time and survival kinetics in the stomach, independent of the pathogen type. In addition, the KEDRF would have potential to take into account the infection mechanisms identified by molecular biology, and it could bring us the possibility of applying fundamental information from infection mechanisms elucidated by molecular biological approaches to the macroscopic output of actual food sanitation management sites. In this manner, development of dose-response models based on KEDRF will be expected for various foodborne pathogens, combining various mechanisms for estimating infection risks.
However, the dose-response model based on KEDRF presented in this study still has certain limitations. The present study did not consider the growth of C. jejuni in the intestines because its growth rate is slower than its invasion rate (8). In contrast, a growth model is needed for fast-growing pathogenic bacteria, such as E. coli or Salmonella. Modeling the interactions between the immune system and pathogens is also required. It has been suggested that the probability of infection may be high, but the illness may not develop (17). Modeling the effect of immunity on pathogens will be necessary to predict the probability of illness. Furthermore, since the available data on the gastrointestinal tract were limited, the effect of age was reflected only in the pH change and the effect of food type was reflected only in the residence time in the stomach in this study. However, for a more realistic prediction, data corresponding to age and food types in all gastrointestinal environments, such as pH change, gastric retention time, and intestinal retention time, are needed. The use of acid blockers would also influence infection probabilities. For more realistic and appropriate predictions of the dose-response relationship based on KEDRF, it is necessary to study all the factors of infection mechanisms, including not only immune modeling and additional environmental data of the gastrointestinal tract under various conditions, but also perspectives of omics, molecular microbiology, and medical biology.
In conclusion, the behavior of C. jejuni in the gastrointestinal tract based on the KEDRF was predicted via mathematical models using Bayesian inference (Fig. 1, Fig. 6). Moreover, the respective dose-response relationships for combinations of age (young adult versus elderly) and food type (liquid versus solid) were also estimated (Fig. 7). The results of the dose-response model of KEDRF showed similar results to the reported dose-response relationship (15) (Fig. 7). Furthermore, sensitivity analysis of the prediction results showed that gastric retention time was the most relevant factor among the key events from ingestion to invasion (Fig. 8). This study demonstrated a large potential for the development of a novel dose-response model based on KEDRF. The dose-response model based on KEDRF will allow us to estimate the dose-response relationships of various pathogens with various factors, such as age, sex, chronic illness, food type, and others based on their actual infection mechanisms.
MATERIALS AND METHODS
Defining the key events of campylobacteriosis infection.
The key events of the infection mechanism for this study were designed on the basis of the KEDRF report (3). Since it is difficult to quantitatively assess pathogens in human body tissues such as blood vessels or lymphatic system, this study considered the probability of invasion into the small intestinal endothelial cells as the infection probability. The following were identified as key events: (i) pathogen reduction in the stomach; (ii) transfer to the small intestine from the stomach; and (iii) pathogen invasion into small intestinal epithelial cells. The influence of C. jejuni growth in intestines were omitted because it is reported that the invasion rate of C. jejuni is much faster than C. jejuni growth rate in broth medium (7). Figure 1 shows the diagram of the constructed model in this study, and the abbreviations are summarized in Table 1. Each key event was modeled by referring to data from the literature, and MCMC (Markov Chain Monte Carlo) simulations were performed to derive the probability of C. jejuni invading small intestinal cells based on the developed models.
TABLE 1.
Details of components in the constructed key events dose-response model
| Section | Abbreviation | Detail of components | Data source |
|---|---|---|---|
| Dose | Ndose | Pathogen count intake | Describing variables |
| pH change of gastric juice after meal | pH0 | pH immediately after meal | 12 a 13 b |
| kpH | Rate of decrease in pH | 12 a 13 b | |
| pHmin | Minimum pH value | 12 a 13 b | |
| σpH | S.D. of pH prediction | 12 a 13 b | |
| Pathogen reduction model in gastric juice | a | Secondary parameter of δ | 5 |
| b | Secondary parameter of δ | 5 | |
| e | Secondary parameter of p | 5 | |
| f | Secondary parameter of p | 5 | |
| Sg | Survival pathogen ratio in gastric juice | Computables | |
| Gastric retention of food | αgastric | Shape parameter of gamma distribution | 14 |
| βgastric | Rate parameter of gamma distribution | 14 | |
| Transit of pathogen | rintestine | Survival pathogen transit ratio to intestine | Computables |
| Nintestine | Survival pathogen transit count to intestine | Computables | |
| Cell invasion of pathogens | V | Volumes of small intestine | 35 |
| Nmax | Maximum invading counts to 1 cm2 of cell layer | 8 | |
| μ | Cell-invading rate | 8 | |
| σinvading | S.D. of invading pathogen count prediction | 8 | |
| S | Surface area of intestine | 36 | |
| Intestinal retention of food | αintestinal | Shape parameter of gamma distribution | 15 |
| βintestinal | Rate parameter of gamma distribution | 15 | |
| tintestinal | Intestinal retention time | Computables | |
| Calculation of invading probability | Pinfection | Infection (invading) probability | Objective variables |
Young adult pH.
Elder pH.
Modeling for postprandial gastric pH change among young adult and elderly individuals.
The postprandial pH changes among young adult and elderly individuals were expressed separately in a mathematical model. The exponential models (Equation 1) were fitted to the reported pH changes after a standard meal (1,000 kcal) for young adult (12) and elderly individuals (13):
| (1) |
where pH(t) denotes the pH at a time after food intake, t; pH0 denotes pH immediately after a meal; kpH denotes the decreasing rate of pH; and pHmin denotes the convergence value of pH. The parameters were estimated using Bayesian inference through pystan (ver. 2.19.). The normal distribution, which is generally used, was adopted as the prior distribution of pH, as distributions of the reported data were contrasting.
Pathogen survival in stomach with between- and within-strain variability.
The survival of C. jejuni was described using a previously reported dynamic survival model of C. jejuni (Equation 2) under artificial gastric conditions using Bayesian inference (5). The between- and within-strain variability reduction model was constructed from the data of 11 strains of C. jejuni (RIMD 0366026, RIMD 0366027, RIMD 0366028, RIMD 0366029, RIMD 0366042, RIMD 0366043, RIMD 0366044, RIMD 0366048, RIMD 0366049, RIMD 0366050, and RIMD 0366051).
| (2a) |
| (2b) |
| (2c) |
where Sg(t) denotes the bacterial survival ratio defined as the ratio of the surviving bacterial counts divided by the initial bacterial counts; p denotes the power parameter of the Weibull model; δ denotes the time of the first decimal reduction of the Weibull model; and pH̄ denotes the mean pH during the time intervals from t to t+Δt as . The parameters of the primary model, δ and p, were defined using the parameters of the secondary model (ak,bk,ek,fk), following the multivariate normal distribution of Cholesky parameterization, in which Σchol is the Cholesky factor of the covariance matrix of log(p(k,pH̄)) and log(δ(k,pH̄)) of all strains.
Bacterial transfer to the small intestine.
Changes in the gastric retention ratio were described as the cumulative gamma distribution, which is used to describe the waiting time of traffic jams and transmitting times.
Comparing the transfer time of solid foods and liquid foods, the effect on the cell invasion ability due to differences in food type was estimated. The changes in gastric retention ratio were described using the following cumulative gamma distribution fitted to the reported change in the gastric retention ratio after solid and liquid meals (14):
| (3) |
where Rg is the gastric retention ratio; α is the shape parameter; β is the rate parameter of gamma distribution; Γ(α) is the gamma function ; γ(α,βt) is the lower incomplete gamma function .
The combined equation of pH, pathogenic survival, and gastric retention model, as well as the ratio of the surviving pathogen transfer to the intestine, rintestine, was described (Equation 4; for graphical description, see Fig. S1), and discretely expressed as shown in Equation 4b:
| (4a) |
| (4b) |
where s denotes an operator; ti denotes the simulated gastric retention times from the gamma distributions; k denotes any natural number. Using Equation 4, the survival pathogen transit counts, Nintestinal, were derived as follows:
| (5) |
where Ndose denotes the intake counts of pathogens.
Bacterial invasion in intestinal cells.
Invasion of C. jejuni was described using a modified predictive model based on a previously reported C. jejuni model (8) (RIMD 0366027, RIMD 0366042, and RIMD 0366048) applying invasion count, Ninvading, to Caco-2 cells as follows:
| (6) |
where μ, Nexposure, Nmax, V, and S denote the cell invasion rate, the pathogen exposure count, the spatial maximum invading pathogen count per 1 cm2, the volume of intestinal juice (319 ml) (35), and the surface area of the small intestine (32 m2), respectively (36).
Retention time in the small intestine.
The cumulative gamma distribution was fitted to the change in the small intestinal retention ratio, Rintestinal, as the reported colonic filling ratio as follows (15):
| (7) |
Considering Equation 7, the small intestinal retention time, tintestinal , follows the gamma distribution α′ as a shape parameter and β′ as a rate parameter; Gamma(α′,β′) as follows:
| (8) |
Invasion probability in human tissues.
The probability of pathogen invasion into the cells was determined as previously described (8). One or more C. jejuni predicted infection probabilities were derived from the models as follows:
| (9) |
Spearman’s rank correlation coefficients between Pinvading and the parameters were established as a sensitivity analysis of the current dose-response model.
Computation.
All the computations were calculated under the Anaconda distribution (Python 3.7.7) (see “Data availability”). All the Bayesian inferences have been done with No-U-Turn-Sampler MCMC.
Data availability.
All the data used and the Python codes are available through GitHub (https://github.com/Hiroki-Abe/KEDRF2021).
ACKNOWLEDGMENTS
This study was supported by a grant from the Food Safety Commission, Cabinet Office, Government of Japan (Research Program for Risk Assessment Study on Food Safety, No. 1802, 2004) and a Grant-in-Aid for Japan Society for the Promotion of Science Fellows (grant number 20J11550).
We declare no competing interests.
Footnotes
Supplemental material is available online only.
Contributor Information
Shigenobu Koseki, Email: koseki@bpe.agr.hokudai.ac.jp.
Andrew J. McBain, University of Manchester
REFERENCES
- 1.Zwietering MH. 2009. Quantitative risk assessment: is more complex always better? Simple is not stupid and complex is not always more correct. Int J Food Microbiol 134:57–62. 10.1016/j.ijfoodmicro.2008.12.025. [DOI] [PubMed] [Google Scholar]
- 2.Julien E, Boobis AR, Olin SS, ILSI Research Foundation Threshold Working Group. 2009. The Key Events Dose-Response Framework: a cross-disciplinary mode-of-action based approach to examining dose-response and thresholds. Crit Rev Food Sci Nutr 49:682–689. 10.1080/10408390903110692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Buchanan RL, Havelaar AH, Smith MA, Whiting RC, Julien E. 2009. The Key Events Dose-Response Framework: its potential for application to foodborne pathogenic microorganisms. Crit Rev Food Sci Nutr 49:718–728. 10.1080/10408390903116764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Koseki S, Mizuno Y, Sotome I. 2011. Modeling of pathogen survival during simulated gastric digestion. Appl Environ Microbiol 77:1021–1032. 10.1128/AEM.02139-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Koyama K, Ranta J, Takeoka K, Abe H, Koseki S. 2021. Evaluation of strain variability in inactivation of Campylobacter jejuni in simulated gastric fluid by using hierarchical Bayesian modeling. Appl Environ Microbiol 87:e00918-21. 10.1128/AEM.00918-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pujol JM, Eisenberg JE, Haas CN, Koopman JS. 2009. The effect of ongoing exposure dynamics in dose response relationships. PLoS Comput Biol 5:e1000399. 10.1371/journal.pcbi.1000399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ribet D, Cossart P. 2015. How bacterial pathogens colonize their hosts and invade deeper tissues. Microbes Infect 17:173–183. 10.1016/j.micinf.2015.01.004. [DOI] [PubMed] [Google Scholar]
- 8.Abe H, Koyama K, Koseki S. 2021. Modeling invasion of Campylobacter jejuni into human small intestinal epithelial-like cells by Bayesian inference. Appl Environ Microbiol 87:687. 10.1128/AEM.01551-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rahman A, Munther D, Fazil A, Smith B, Wu J. 2018. Advancing risk assessment: mechanistic dose–response modelling of Listeria monocytogenes infection in human populations. R Soc Open Sci 5:180343. 10.1098/rsos.180343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fernández-García E, Carvajal-Lérida I, Pérez-Gálvez A. 2009. In vitro bioaccessibility assessment as a prediction tool of nutritional efficiency. Nutr Res 29:751–760. 10.1016/j.nutres.2009.09.016. [DOI] [PubMed] [Google Scholar]
- 11.Galanakis CM. 2016. Nutraceutical and functional food components. Academic Press, Elsevier, Cambridge, MA. [Google Scholar]
- 12.Dressman JB, Berardi RR, Dermentzoglou LC, Russell TL, Schmaltz SP, Barnett JL, Jarvenpaa KM. 1990. Upper gastrointestinal (GI) pH in young, healthy men and women. Pharm Res 7:756–761. 10.1023/a:1015827908309. [DOI] [PubMed] [Google Scholar]
- 13.Russell TL, Berardi RR, Barnett JL, Dermentzoglou LC, Jarvenpaa KM, Schmaltz SP, Dressman JB. 1993. Upper gastrointestinal pH in seventy-nine healthy, elderly, North American Men and women. Pharm Res 10:187–196. 10.1023/a:1018970323716. [DOI] [PubMed] [Google Scholar]
- 14.Hellström PM, Grybäck P, Jacobsson H. 2006. The physiology of gastric emptying. Best Pract Res Clin Anaesthesiol 20:397–407. 10.1016/j.bpa.2006.02.002. [DOI] [PubMed] [Google Scholar]
- 15.Read NW, Al-Janabi MN, Holgate AM, Barber DC, Edwards CA. 1986. Simultaneous measurement of gastric emptying, small bowel residence and colonic filling of a solid meal by the use of the gamma camera. Gut 27:300–308. 10.1136/gut.27.3.300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Teunis P, Van den Brandhof W, Nauta M, Wagenaar J, Van den Kerkhof H, Van Pelt W. 2005. A reconsideration of the Campylobacter dose-response relation. Epidemiol Infect 133:583–592. 10.1017/s0950268805003912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Teunis PFM, Bonačić Marinović A, Tribble DR, Porter CK, Swart A. 2018. Acute illness from Campylobacter jejuni may require high doses while infection occurs at low doses. Epidemics 24:1–20. 10.1016/j.epidem.2018.02.001. [DOI] [PubMed] [Google Scholar]
- 18.Evans MR, Roberts RJ, Ribeiro CD, Gardner D, Kembrey D. 1996. A milk-borne campylobacter outbreak following an educational farm visit. Epidemiol Infect 117:457–462. 10.1017/s0950268800059112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.van den Brandhof W, Wagenaar J, van den Kerkhof H. 2003. An outbreak of campylobacteriosis after drinking unpasteurized milk, 2002, the Netherlands. Int J Med Microbiol 293:548–549. [Google Scholar]
- 20.Korlath JA, Osterholrn MT, Judy LA, Forfang JC, Robinson RA. 1985. A point-source outbreak of campylobacteriosis associated with consumption of raw milk. J Infect Dis 152:592–596. 10.1093/infdis/152.3.592. [DOI] [PubMed] [Google Scholar]
- 21.Blaser MJ, Sazie E, Williams LP. 1987. The influence of immunity on raw milk— associated Campylobacter infection. JAMA 257:43–46. 10.1001/jama.1987.03390010047026. [DOI] [PubMed] [Google Scholar]
- 22.Black RE, Levine MM, Clements ML, Hughes TP, Blaser MJ. 1988. Experimental Campylobacter jejuni infection in humans. J Infect Dis 157:472–479. 10.1093/infdis/157.3.472. [DOI] [PubMed] [Google Scholar]
- 23.Hazeleger WC, Jacobs-Reitsma WF. 2016. Quantification of growth of Campylobacter and extended spectrum β-lactamase producing bacteria sheds light on black box of enrichment procedures. Front Microbiol 7:1430. 10.3389/fmicb.2016.01430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.van Duijkeren E, Wielders CCH, Dierikx CM, van Hoek AHAM, Hengeveld P, Veenman C, Florijn A, Lotterman A, Smit LAM, van Dissel JT, Maassen CBM, de Greeff SC. 2018. Long-term carriage of extended-spectrum β-lactamase-producing Escherichia coli and Klebsiella pneumoniae in the general population in The Netherlands. Clin Infect Dis 66:1368–1376. 10.1093/cid/cix1015. [DOI] [PubMed] [Google Scholar]
- 25.Islam S, Selvarangan R, Kanwar N, McHenry R, Chappell JD, Halasa N, Wikswo ME, Payne DC, Azimi PH, McDonald LC, Gomez-Duarte OG. 2018. Intestinal carriage of third-generation cephalosporin-resistant and extended-spectrum β-lactamase-producing Enterobacteriaceae in healthy US children. J Pediatric Infect Dis Soc 7:234–240. 10.1093/jpids/pix045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kiratisin P, Chattammanat S, Sa-Nguansai S, Dansubutra B, Nangpatharapornthawee P, Patthamalai P, Tirachaimongkol N, Nunthanasup T. 2008. A 2-year trend of extended-spectrum β-lactamase-producing Escherichia coli and Klebsiella pneumoniae in Thailand: an alert for infection control Trans R Soc Trop Med Hyg 102:460–464. 10.1016/j.trstmh.2008.02.005. [DOI] [PubMed] [Google Scholar]
- 27.Jameson JE. 1962. A discussion of the dynamics of Salmonella enrichment. J Hyg (Lond) 60:193–207. 10.1017/s0022172400039462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Food and Agriculture Organization, World Health Organization. 2004. Risk assessment of Listeria monocytogenes in ready-to-eat foods. http://www.fao.org/3/y5394e/y5394e.pdf.
- 29.Mourkas E, Taylor AJ, Méric G, Bayliss SC, Pascoe B, Mageiros L, Calland JK, Hitchings MD, Ridley A, Vidal A, Forbes KJ, Strachan NJC, Parker CT, Parkhill J, Jolley KA, Cody AJ, Maiden MCJ, Kelly DJ, Sheppard SK. 2020. Agricultural intensification and the evolution of host specialism in the enteric pathogen Campylobacter jejuni. Proc Natl Acad Sci USA 117:11018–11028. 10.1073/pnas.1917168117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Atterby C, Mourkas E, Méric G, Pascoe B, Wang H, Waldenström J, Sheppard SK, Olsen B, Järhult JD, Ellström P. 2018. The potential of isolation source to predict colonization in avian hosts: a case study in Campylobacter jejuni strains from three bird species. Front Microbiol 9:591. 10.3389/fmicb.2018.00591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Koyama K, Aspridou Z, Koseki S, Koutsoumanis K. 2019. Describing uncertainty in Salmonella thermal inactivation using Bayesian statistical modeling. Front Microbiol 10:2239. 10.3389/fmicb.2019.02239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang L, Li C. 2020. Growth of Clostridium perfringens in cooked chicken during cooling: one-step dynamic inverse analysis, sensitivity analysis, and Markov Chain Monte Carlo simulation. Food Microbiol 85:103285. 10.1016/j.fm.2019.103285. [DOI] [PubMed] [Google Scholar]
- 33.Garre A, Zwietering MH, Besten den HMW. 2020. Multilevel modelling as a tool to include variability and uncertainty in quantitative microbiology and risk assessment. Thermal inactivation of Listeria monocytogenes as proof of concept. Food Res Int 137:109374. 10.1016/j.foodres.2020.109374. [DOI] [PubMed] [Google Scholar]
- 34.Ross T, McMeekin TA, Baranyi J. 2014. Predictive microbiology and food safety. InEncyclopedia of food microbiology, 2nd ed. Academic Press, Elsevier, Cambridge, MA. [Google Scholar]
- 35.Schiller C, Frohlich C-P, Giessmann T, Siegmund W, Monnikes H, Hosten N, Weitschies W. 2005. Intestinal fluid volumes and transit of dosage forms as assessed by magnetic resonance imaging. Aliment Pharmacol Ther 22:971–979. 10.1111/j.1365-2036.2005.02683.x. [DOI] [PubMed] [Google Scholar]
- 36.Helander HF, Fändriks L. 2014. Surface area of the digestive tract—revisited. Scand J Gastroenterol 49:681–689. 10.3109/00365521.2014.898326. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1 to S9. Download AEM.01299-21-s0001.pdf, PDF file, 0.8 MB (811.7KB, pdf)
Data Availability Statement
All the data used and the Python codes are available through GitHub (https://github.com/Hiroki-Abe/KEDRF2021).