Strength and Deformability of Fibrin Clots: Biomechanics, Thermodynamics, and Mechanisms of Rupture

Abstract

Fibrin is the major determinant of the mechanical stability and integrity of blood clots and thrombi. To explore the rupture of blood clots, emulating thrombus breakage, we stretched fibrin gels with single-edge cracks of varying size. Ultrastructural alterations of the fibrin network correlated with three regimes of stress vs. strain profiles: the weakly non-linear regime due to alignment of fibrin fibers; linear regime owing to further alignment and stretching of fibers; and the rupture regime for large deformations reaching the critical strain and stress, at which irreversible breakage of fibers ahead of the crack tip occurs. To interpret the stress-strain curves, we developed a new Fluctuating Spring model, which maps the fibrin alignment at the characteristic strain, network stretching with the Young modulus, and simultaneous cooperative rupture of coupled fibrin fibers into a theoretical framework to obtain the closed-form expressions for the strain-dependent stress profiles. Cracks render network rupture stochastic, and the free energy change for fiber deformation and rupture decreases with the crack length, making network rupture more spontaneous. By contrast, mechanical cooperativity due to the presence of inter-fiber contacts strengthens fibrin networks. The results obtained provide a fundamental understanding of blood clot breakage that underlies thrombotic embolization.

Graphical abstract

Introduction

Fibrin, a naturally occurring biomaterial, is the main mechanical component of blood clots, and it plays a paramount role in stemming bleeding and wound healing. The gelation or coagulation of blood is an evolutionary mechanism geared to sealing the circulatory system and preventing blood loss in the event of injury. The formation of a blood clot that plugs a vessel wall injury results from enzymatic conversion of the soluble plasma glycoprotein, fibrinogen, into a polymeric insoluble fibrin clot, the reaction preserved across all vertebrate species from fish to mammals [1,2]. Fibrin formation begins with the thrombin-catalyzed cleavage of fibrinopeptides from fibrinogen, resulting in the conversion of fibrinogen into fibrin monomers. Fibrin monomers self-polymerize into half-staggered linear oligomers that elongate into protofibrils ~0.5 μm in length built of about 20 monomers. The protofibrils aggregate laterally to form ~100–200-nm-thick fibers organized into a branched network [3,4]. The fibrin network is further stabilized mechanically and chemically by covalent crosslinking that is introduced by the transglutaminase Factor XIIIa [5,6]. While fibrin is not the only component of a blood clot, it has been shown that the fibrin network provides the structural integrity of blood clots. The structure of fibrin, which is influenced by the kinetics of fibrin formation, biochemical microenvironment, as well as the presence of blood cells such as platelets and erythrocytes, largely determines the mechanical properties of whole blood clots and thrombi. Apart from its role in blood clots, fibrin is a versatile and widely used biomaterial and hydrogel with great extensibility, viscoelasticity, and strain stiffening properties in shear, tension, and compression, all of which have been shown on a network level as well as an individual fiber level [7].

Although blood clotting is a protective mechanism, sometimes pathological blood clots are formed within a vessel (thrombosis), which block blood flow and impair tissue oxygen and nutrient supply, resulting in severe thrombotic conditions such as myocardial infarction, ischemic stroke, or venous thrombosis. If a portion of the thrombus, called an embolus, breaks off, it is carried by blood flow and blocks smaller vessels downstream, which creates a life-threatening condition called thrombotic embolism. Thrombosis associated with embolism (thromboembolism) is a leading cause of morbidity and mortality worldwide. For example, while a thrombus in the lower limb (deep vein thrombosis) can remain relatively stable over an extended period of time, if a portion of this thrombus breaks off, it can become lodged in the trunk of a lung artery or its branches (pulmonary embolism), causing a 10-fold higher mortality rate compared with deep vein thrombosis alone [8].

Despite the tremendous clinical importance, thromboembolism is an understudied problem. While much is known about the viscoelastic properties and deformability of blood clots and fibrin gels, almost nothing is known about fibrin’s ability to resist rupture. Understanding the mechanisms behind the rupture of fibrin has the potential to shed light on why some thrombi break or embolize, while others remain stable, and how the rupture occurs. Here we developed the Fluctuating Spring (FS) model of the entire network of fibrin fibers to describe the mechanical response of networks with single-edge cracks, and to explore the dynamics of their tensile deformation accessible in mechanical testing performed on macroscopic fibrin gel samples. The FS model links the dynamic structural alterations in fibrin networks to the stochastic nature of their force-induced remodeling and incorporates the elements of structural damage to account for their irreversible rupture. Building on the experimental evidence provided by scanning electron microscopy and transmission electron microscopy, the FS model considers: i) the small-amplitude deformation of the fibrin network due to alignment of fibrin fibers; ii) the large-amplitude deformation of the fibrin network due to further alignment and stretching of fibrin fibers; and iii) the rupture of the fibrin network due to irreversible breakage of all structure elements (individual fibers and their conglomerates). The latter results in mechanical failure of the entire fibrin network.

The FS-model based theory was applied to interpret the stress-strain profiles collected for samples of fibrin gels with no crack and with single-edge cracks with a broad 7–35%-range of crack sizes. Excellent agreement was observed between the experimental and theoretical stress-strain profiles, which validates the FS model. The theory describes the deformations at small and large strains, and fracture of the fibrin network at very large strains exceeding the strain threshold. Here, we demonstrate how the FS theory can be used to analyze the experimental stress–strain profiles to gather valuable information about the average mechanical properties of fibrin networks (critical stress and critical strain for rupture). These quantities carry information about the limits of the mechanical strength and extensibility of fibrin networks, and the material properties of fibrin networks such as the elastic modulus of the network. We also show how the FS theory can be applied to resolve the entire probability distributions of critical stresses and critical strains, and to calculate the thermodynamic state functions, including the free energy changes associated with the network deformation and fracture. Taken together, the application of the Fluctuating Spring model to the fibrin network has led to a better understanding of the structural biomechanics underlying the mechanical (in)stability of blood clots and fibrin biomaterials.

Materials and Methods

Pooled human blood plasma and plasma clots:

Citrated human blood plasma was obtained from 25 healthy donor plasma samples (outdated plasma from the Blood Bank of the University of Pennsylvania and the State University of New York, Stony Brook), pooled together, and filtered. Pooled plasma was stored at −80°C in aliquots and thawed by heating up to 37°C immediately prior to use. The fibrinogen concentration was 2.7±0.2 g/l. Clotting of a ~15 ml sample was initiated through the addition of 25 mM CaCl₂ (final) and 1:80 dilution of thromboplastin (Plastinex, Bio/Data Corp), after which the sample was immediately transferred into a custom made dog-bone shape Teflon mold, 30mm × 30mm × 10mm as previously described [9]. Plasma was allowed to clot overnight at 4°C to ensure full factor XIIIa-catalyzed cross-linking of fibrin, which was confirmed by SDS-PAGE in reducing conditions by formation of a γ-dimer band and α-chain polymers. Clots were stored overnight in a humid chamber to prevent drying.

Measuring the force-displacement response of fibrin gels with controlled defects:

Following polymerization and cross-linking, the mold was disassembled, and the fibrin gel was slid out of the non-sticky Teflon mold without disturbing the architecture and placed into the custom designed Velcro-based clamps in an Instron 8500 tensile tester. The exposed testing volume of the gel sample of dimensions 30 mm × 30 mm × 6.5 mm was V₀ = lwh = 5,850 mm³, where l = 30 mm is the length, w = 30 mm is the width and h = 6.5 mm is the thickness of the fibrin gel sample. The sample was somewhat thinner than the 10-mm depth of the Teflon mold due to slight gel syneresis. To remove any slack in the gel, the sample was preloaded to 0.3% strain and a linear crack was inserted into a single edge of the clot perpendicular to the direction of tensile loading (see Fig. 1A). Cracks ranged in length from 1.5 mm to 10.5 mm, i.e. 5–35% of the sample width (w = 30 mm). The cracks were inserted along the long (30 mm) edge of the clot, orthogonal to the direction of loading. The experimental setup used here is a classic mode I fracture assay. Strain-driven pulling force was applied to the upper clamp at a rate of 3 mm/min until clot rupture occurred, the rate of 3 mm/min is an equilibrium rate. The stress (σ)–strain (ε) profiles (σε-curve) were collected for samples throughout the time course of the experiment. When transforming the experimental values of the average force f to the values of the average stress $\sigma =\frac{f}{A}$, we approximated the cross-sectional area of the sample with the crack A to decrease with the crack size α, i.e. A = (1 − α)wh. We ignored the stress variation with the distance from the crack tip. Numerical values of A for all sample tested are accumulated in Table S1. High-definition videos (Supporting Movie) were made of the front and side views to track sample deformation and rupture. A total of 20 fibrin samples with no crack and with various crack lengths were tested.

Figure 1.

Experimental stress-strain analysis of the dynamics of deformation and rupture of a fibrin clot with single-edge crack. Panel A : Snapshots of a fibrin gel sample (30 mm ×30 mm ×6.5 mm) with a 12-mm-crack inserted in a single edge of the sample at times that correspond to the dynamic mechanical regimes I–III. The fibrin gel sample was strained at a constant rate of 3 mm/min. Panel B : Experimental stress-strain profile (σε-curve, left y -axis) and the slope-strain profile (dσ/dε vs. ε curve; right y -axis) for a gel sample similar to the one displayed in panel A, but with a 6-mm-crack size. The σε-curve shows the following dynamic mechanical regimes: the weakly non-linear regime I of network deformation with an increasing slope dσ/dε due to alignment of fibrin fibers at the characteristic strain for alignment ε₀; the linear regime II of network deformation with a roughly constant slope (dσ/dε), which corresponds to the elastic modulus yN_max (y –elastic modulus of single multifiber thread, N_max – total number of multifiber threads), and the rupture regime III, which sets in at the strain threshold ε* when fibrin fibers begin to rupture. Regime III is characterized by the critical stress σ_cr (peak stress) attained at the critical strain σ_cr, when all multifiber threads have ruptured. For the σε-curve displayed in panel B, regime III is characterized by the stress maximum (σ_cr = 1.53 kPa ) attained at the critical strain ε_cr = 31%, which marks the complete rupture of the fibrin gel sample, and sudden stress decrease to zero for ε > 31%.

Scanning electron microscopy:

Cylindrical fibrin clots 2 mm × 50 mm without or with a crack were stretched to a certain extent to follow structural rearrangements of fibers under tension. Following manual stretching in a home-made stretching device, fibrin samples were washed in phosphate buffered saline, pH 7.4, and fixed in 2% glutaraldehyde in the stretched state to prevent relaxation upon removal from the clamps, so that the fibrin network was imaged in the stretched state. After cutting out a piece of fixed gel containing a crack or a similar uncracked counterpart, the samples were dehydrated in ascending concentrations of ethanol (30–100vol%), dried with hexamethyldisilazane, sputter-coated with gold-palladium, and imaged using an FEI Quanta250 FEG scanning electron microscope (FEI, Hillsboro, OR). Images were analyzed to quantify fibrin fiber alignment (order parameter) at the crack tip or in the middle of uncracked clots through the use of the ImageJ software. The angle θ between randomly selected individual fibrin fibers (n = 100) and the direction of applied pulling force was calculated for strains of ε = 0; 50% and 100% and the order parameter was calculated as cos(2θ). We found that fibrin fibers forming the unstrained fibrin gels were randomly oriented (isotropic), whereas the strained fibrin gels were made of fibrin fibers that were strongly aligned (anisotropic). The order parameter cos(2θ), where θ is the angle formed by fibrin fibers in the direction of applied strain ε, was used to quantitate the extent of alignment of fibrin fibers in the strained fibrin gels. A low value of cos(2θ) reflects random orientation, whereas a large value of cos(2θ) closer to 1 reflects increased alignment. Widths of fibrin fibers were determined for randomly selected individual fibers (n ≥ 25) to assess bundling and densification of the fibers. Image analysis was performed using ImageJ software.

Transmission electron microscopy:

Glutaraldehyde-fixed stretched clots without a crack prepared as described for scanning electron microscopy were washed overnight in 0.1 M sodium cacodylate buffer, pH 7.4, containing 150 mM NaCl. After post-fixation with 2% osmium tetroxide, the samples were stained en bloc with 2% uranyl acetate, dehydrated through a graded ethanol series, and embedded in PolyBed 812 (Polysciences Inc.). Thin longitudinal or transverse sections were stained with uranyl acetate and bismuth subnitrite and examined with a JEOL JEM-1010 transmission electron microscope fitted with a Hamamatsu digital camera and AMT imaging software.

Statistical analysis:

All statistics were completed using the software package Prism GraphPad 6.0. Samples were analyzed for statistical significance using two-tailed unpaired t-tests or a Kruskal-Wallis test with a 95% confidence level (p<0.05). All data are presented as mean ± SEM. Correlation analysis was performed using the Spearman correlation coefficient (r).

Results

Dynamic regimes of forced deformation and rupture of fibrin gels:

We applied strain-driven tension to the gels with cracks of varying length inserted into an edge of the fibrin gel sample (Fig. 1A). Visually, during tensile deformation, first the sample extended in the tensile direction with little to no change in the crack size. Then, the crack began to broaden and blunt under increasing strain without any detectable growth in the direction perpendicular to the direction of force application. Once the strain reached the strain threshold point ε*, the crack began to grow very rapidly in the transverse direction until the clot sample broke completely at some value of the critical strain ε_cr (see Supporting Movie). Tensile deformation and mechanical failure of the cracked gel samples was quantitatively analyzed using the stress-strain profiles (σε-curves), which were collected as described in Materials and Methods. All the experimental stress-strain profiles are accumulated in Fig. S1 in the Supporting Information (SI). A representative σε-curve for a sample of fibrin gel with 6-mm single-edge crack, which corresponds to 20% of the sample width, is displayed in Fig. 1B.

Visual inspection of the shape of stress-strain profiles (σε-curves) and the profiles of the first derivative of the stress with respect to the strain (dσ/dε vs. ε curves) displayed in Fig. 1B showed that the mechanical response of the fibrin fiber network can be partitioned into the following three distinctly different dynamic mechanical regimes: 1) the initial weakly non-linear regime I of network deformation for small values of strain (ε < 10–15%) with a rapidly increasing slope (dσ/dε) of the σε-curves; 2) the linear regime II of deformation for intermediate values of strain (10–15% < ε < 30–40%) with a roughly constant slope; and 3) the rupture regime III for the large deformations that exceed the critical strain threshold ε* (ε > ε* = 30–40%). The latter (regime III) is characterized by the stress maximum (critical stress) σ_cr attained at the critical strain ε_cr (such that σ_cr = σ(ε_cr)), which marks the rupture of the fibrin gel sample (mechanical failure), and sudden decrease of σ (and dσ/dε) to zero for ε > ε_cr (for ε > ε*). There is a difference between the strain threshold ε* and the critical strain ε_cr. While ε* is the strain at which structural elements begin to rupture, ε_cr is the strain at which all structural elements along the crack axis have ruptured. This strain interval Δε = ε_cr − ε*, which accounts roughly for half of the width of the strain peak, can be clearly seen by analyzing the profile of the slope dσ/dε as a function of ε in regime III (see Fig. 1B).

Therefore, we characterized quantitatively the dynamic mechanical regimes I and II in terms of the maximum stress σ_I,II, maximum strain ε_I,II, and the average slope dσ_I,II/dε_I,II, which were extracted from the experimental σε-profiles. In regime I, the maximum strain ε_I was set to be equal to the characteristic strain ε₀, at which the first derivative levels off, i.e. ε_I = ε₀, and the maximum stress was calculated as σ_I = (ε_I). In regime II, the maximum strain ε_II was set to be equal to the strain threshold ε*, at which the slope dσ/dε starts to sharply decrease, i.e. ε_II = ε*, and the maximum stress was calculated as σ_II = (ε_II). Regime III was quantified using the critical values of stress σ_cr and strain ε_cr, the half-width of the strain peak Δε, and the average slope dσ_III/dε_III for ε* < ε < ε_cr. The critical strain ε_cr is the strain at which the stress attains the maximum σ = σ_cr (stress peak). To capture the dependence of all these quantities on the crack size α, we divided the experimental stress-strain profiles into three groups for samples with small crack (α < 10%), medium-size crack (10% < α < 20%), and large-size crack (α > 20%). Numerical values of these quantities for 18 experimental σε-profiles for fibrin gels with crack are displayed in Fig. S1 and are compared in Table I with numerical values of the same quantities obtained from 2 experimental σε-profiles for fibrin gel samples without crack.

Table I. Quantitative analysis of stress-strain curves for fibrin gels with single-edged cracks of different sizes:

Displayed for the dynamic mechanical regimes I and II are the maximum stress σ_I,II, the maximum strain ε_I,II, and the average slope dσ_I,II/dε_I,II obtained from the experimental stress-strain profiles (see Fig. 1). For regime III, we extracted the strain threshold ε*, the critical strain (rupture strain) ε_cr, the half-width of the stress peak Δε = ε_cr − ε*, the critical stress (peak stress) σ_cr, and the average slope dσ_III/dε_III (for ε* < ε < ε_cr). Numerical values of all these quantities extracted from the experimental σε-curves for fibrin gel sample with crack (n = 18) for different ranges of crack size α: 7–9%, 11–19% and 20–35% are compared with values of same quantities from the σε-curves for fibrin gel sample with no crack (n = 2). One-way ANOVA test was used to determine the p-values to estimate the statistical significance.

crack size α, %	0 (n=2)	7–9 (n=3)	11–19 (n=6)	20–35 (n=9)	significance
Regime I
εI, %	16.0 ± 1.3	9.6 ± 0.7	10.7 ± 2.6	9.3 ± 1.9	p = 0.2889
σI, kPa	0.8 ± 0.2	0.32 ± 0.1	0.42 ± 0.3	0.33 ± 0.15	p = 0.9100
$\frac{d{\sigma }_I}{d{\epsilon }_I}$, a.u.	5.0 ± 0.6	3.5 ± 1.4	4.1 ± 1.6	3.7 ± 1	p = 0.7208
Regime II
εII, %	70.2 ± 7.5	42.4 ± 3.0	35.2 ± 4.5	29.7 ± 3.6	p = 0.0018
σII, kPa	4.0 ± 0.6	2.1 ± 0.2	1.8 ± 0.3	1.4 ± 0.3	p = 0.0039
$\frac{d{\sigma }_{II}}{d{\epsilon }_{II}}$, a.u.	6.1 ± 0.04	5.4 ± 0.2	6.0 ± 0.7	6.0 ± 0.6	p = 0.1848
Regime III
Δε, %	3.0 ± 0.1	2.3 ± 1.0	5.0 ± 3.5	4.5 ± 2.0	p = 0.1961
εcr, %	73.3 ± 7.6	44.6 ± 2.0	40.2 ± 3.3	34.2 ± 3.6	p = 0.0003
σcr, kPa	4.1 ± 0.6	2.2 ± 0.2	1.9 ± 0.2	1.5 ± 0.3	p = 0.0021
$\frac{d{\sigma }_{III}}{d{\epsilon }_{III}}$, a.u.	2.6 ± 0.2	2.7 ± 1.6	1.1 ± 1.1	0.27± 0.25	p = 0.0039

Regime I corresponds to short ~10% elongation of the network (with increasing slope dσ_II/dε_II; see Fig. 1B), which occurs without any detectable changes in the crack region (see Fig. 1A). The presence of a crack results in a decrease in the average maximum stress reached in regime I by ~3-fold, i.e. from σ_I = 0.8 kPa for samples without a crack to σ_I = 0.33 kPa (p = 0.003; Fig. S2A). The presence of a crack also decreases ε_I by ~2-fold and dσ_I/dε_I by ~1.4-fold (Fig. S2A). The size of the crack α does not significantly affect the average slope dσ_I/dε_I, the maximum strain ε_I, and, hence, the maximum stress σ_I in this regime (Table I; Fig. S2B–D). Regime II corresponds to the linear extension of the network (with roughly constant slope dσ_II/dε_II; see Fig. 1B), which was found to be only weakly sensitive to the presence and size of the crack α (Table I). For example, the presence and size of the crack did not change much the average slope dσ_II/dε_II of the σε-profiles (Fig. S3A,B). However, the presence of a crack did decrease the average value of the threshold strain ε* by 2.5-fold (p = 0.0015) and σ_II by 2.6 fold (p = 0.0015) (Fig. S3A). The maximum stress in regime II, σ_II, was also found to be inversely proportional to the size of the crack α (r = −0.609; p = 0.007; Fig. S3D). The maximum strain ε_II at which the maximum stress was attained also was observed to decrease with increasing crack size α (r = −0.588; p = 0.010; Fig. S3C). Regime III corresponds to forced rupture of the clots (see stress peak in the σε-curve in Fig. 1B), which results in a sharp decay of σ signifying the mechanical failure of the entire piece of gel (Fig. 1B). This regime begins with the onset of defect growth in the direction perpendicular to that of tensile force application and culminates in the eventual rupture of the fibrin clots (Fig. 1A). The regime III is influenced by the size of the crack α (Table I). We also analyzed the half-width of the stress peaks Δε (strain range). This quantity corresponds to macroscopic deformation ahead of the crack tip before the rapid growth of the crack across the width of the sample occurs. Interestingly, Δε seemed to correlate with the size of the crack α, but this regularity did not reach statistical significance (Table I). The instantaneous slope of the σε-curves in regime III, dσ_III/dε_III, was found to correlate directly with crack size (p < 0.0001; Fig. S4B). For example, dσ_III/dε_III, was 10-fold larger for cracks α < 10% of the sample width when compared to α > 20% (Table 1). Also, the critical values of stress (σ_cr) and strains (ε_cr) were found to decrease with increasing crack size α (Figure S4C, D; see also Table I).

Ultrastructural changes in fibrin network and at the crack tip and motivation for Fluctuating Spring model:

To understand the emergence of three distinctly different dynamic mechanical regimes, we followed the structural alterations of the fibrin network during the course of deformation and rupture processes. Here, scanning and transmission electron microscopy were utilized to examine the area ahead of the crack in partially ruptured fibrin clots. First, we compared the scanning electron microscopy images of unstrained versus strained fibrin gels (Fig. 2). In the unstrained fibrin networks, isotropic fibers had a low order parameter, cos(2θ) = 0.25 (Fig. 2A and 2D). However, when the fibrin gels were stretched, the fibers began to align, which resulted in a substantial increase in the average order parameter to 0.71 for ε = 50% strain and to 0.84 for ε = 100% strain (Fig. 2B–2D). Hence, the scanning electron microscopy images revealed that the initial forced elongation of fibrin fibers forming the network in Regime I is due to fiber alignment in the direction of applied force. The strain rates visualized here correspond to the localized strains at 100 μm ahead of the crack tip, which we have previously shown reaches a logarithmic strain of 1.04 in this region immediately prior to rupture [9].

Figure 2.

Forced alignment and densification of fibrin fibers. Scanning electron microscopy images showing the structure of fibrin fibers in the unstrained fibrin gel samples at ε = 0% strain (panel A), at ε = 50% strain (panel B), and at ε = 100% strain (panel C). Panel D shows the dependence of order parameter cos(2θ) (θ is the ensemble average angle formed by individual fibrin fibers), which quantifies the extent of alignment of fibrin fibers forming the fibrin network. For a sample of fibrin network with unaligned fibrin fibers cos(2θ) = 0, and cos(2θ) = 1 for a sample in which fibrin fibers are completely aligned (see Materials and Methods). A KruskalWallis test followed by a Dunn’s post hoc test was used to determine the statistical significance (** p < 0.01 and **** p < 0.0001; see Materials and Methods). Transmission electron microscopy images showing the structure of unstrained fibrin gel samples (panel E) and the strained fibrin gel samples, in which fibrin fibers are both aligned and approximated laterally to each other (panel F). Scale bars in E and F are 500 nm. Examples of multifiber threads are marked with arrows (panels C, F).

Next, we analyzed the transmission electron microscopy images of the unstrained fibrin gels, which showed an isotropic network of fibrin fibers with randomly oriented fibers that were cut transversely, longitudinally or at an angle in the section plane (Fig. 2E). This is in contrast to the strained fibrin gel samples, in which individual fibrin fibers were found to be aligned and approximated to each other with a propensity to aggregate laterally (Fig. 2F). Fibrin fibers in the stretched clot underwent densification and bundling, reaching 508±24 nm (n ≥ 25) in diameter compared to individual fibrin fibers in unstrained clots with an average thickness of 127±3 nm (n ≥ 25; p < 0.0001). In line with the results of transmission electron microscopy of stretched uncracked clots, in the cracked clots marked fiber alignment and fiber densification ahead of the propagating crack tip was observed using high-resolution scanning electron microscopy (Fig. 3A). The fiber alignment and fiber densification were detected to occur right before the onset of fiber rupture along the edge of the crack tip (Fig. 3B). The forced rupture of fibrin fibers was revealed by the presence of broken fiber ends (Fig. 3C).

Figure 3.

Scanning and transmission electron microscopy of fibrin gel. Panels A-C display scanning electron microscopy images of stretched and ruptured fibrin gel (Materials and Methods), including an image of the crack tip fixed at the moment of crack propagation (panel A), showing simultaneous fiber alignment and densification ahead of the crack tip (B) and fiber rupture along the edge of the crack (panel C). Panels D and E show transmission electron micrographs of transverse sections of fibrin gel in the unstretched clot (panel D) and stretched clot (panel E). These images convey tension-induced lateral fiber bundling and formation of multifiber threads (arrows) spanning the network. Mag bars in A = 500 mm, C = 30 um, and in D and E = 500 nm.

Analysis of electron microscopy images of the fibrin network and comparison of images of unstrained versus strained fibrin networks demonstrated that the fibrin fibers exist in two mechanical states: state 1, in which the unaligned fiber fibers form an isotropic network with low order parameter (cos(2θ)); and state 2, in which the densified fibers are fully aligned along the direction of an applied pulling force with high order parameter. This means that when a tensile stress is applied to a fibrin network, the initial network elongation occurs due to tension-induced alignment of fibrin fibers, which triggers the network transition from state 1 of unaligned fibrin fibers to state 2 of aligned fibers. This observation correlates well with the increasing slope in the non-linear regime I (dσ_I/dε_I), as observed in the experimental stress-strain profiles (Fig. 1B). Indeed, the larger the number of aligned fibrin fibers forming the network, the larger the network stiffness and the stronger the mechanical response. Subsequent elongation of the fibrin network in state 2 occurs due to further alignment of fibrin fibers and stretching of fully aligned fibers, which corresponds to the linear deformation regime II with a constant slope dσ_II/dε_II (Fig. 1B). That the slope dσ_II/dε_II does not increase but remains roughly constant in regime II implies that nearly all fibrin fibers have become aligned in the direction of applied force, and that there are no more fibers that can add to the stiffness of the entire network. Finally, when the strain in the fibrin network exceeds the limits of extensibility of individual fibrin fibers, they begin to rupture, which corresponds to a sharp decay of the slope dσ_III/dε_III to zero (Fig. 1B). At this point, all fibers ahead of the crack tip have become ruptured when the stress in the network reaches the critical value (maximum) σ(ε_cr) = σ_cr and the slope dσ_III/dε_III = 0, which signifies the complete mechanical failure.

To illuminate the complete physical picture underlying the dynamic structural changes in the network of stretched fibrin fibers, we also analyzed the transmission electron micrographs of the transverse sections of fibrin gels (see Materials and Methods), which are displayed in Fig. 3D and 3E. Direct comparison of transmission electron microscopy images of transverse sections of the unstretched clot (Fig. 3D) versus the stretched clot (Fig. 3E) showed that, under the influence of external mechanical factors, ~100–140-nm thick fibrin fibers combine together laterally to form even thicker bundles of fibers. We refer to these tension-induced bundles of fibrin fibers as multifiber threads ~200–500 nm in diameter spanning the clot sample (Figure 2 and 3). These multifiber threads form in dynamic regimes I and II at the intermediate values of deformation (10–15% < ε < 30–40%). Hence, analysis of transmission electron micrographs revealed tension-induced lateral fiber bundling and formation of multifiber threads under the influence of applied force. This is in addition to the alignment of fibrin fibers in the direction of applied tensile force. The experimental observations described above, which include: the fiber alignment (regimes I and II); the fiber stretching (regime II); the multifiber thread formation (regimes I and II); and the breakage of fibrin fibers (regime III) under the influence of increasing tensile stress, have provided a structural basis for the development of a minimal model of mechanical deformation of the fibrin network.

Fluctuating Spring model of tensile deformation of the fibrin network:

Mechanical excitations –

The Fluctuating Spring (FS) model describes a stretched fibrin network as a collection of N mechanically coupled multifiber threads formed by several individual fibrin fibers (Figure 2 and 3). In state 1 of the intact fiber network, the fibrin fibers (and multifiber threads) are not aligned. As the results of scanning and transmission electron microscopy measurements show, the pulling force aligns the multifiber threads in the direction of mechanical loading. For this reason, we model a strain-dependent population of the multifiber threads formed by aligned fibrin fibers N(ε) to grow with ε, i.e.

$$N(\epsilon )=N_{\mathit{\text{max}}}\left(1-e^{-\raisebox{1ex}{$\epsilon $}\!\left/ \!\raisebox{-1ex}{${\epsilon }_0$}\right.}\right)$$ (1)

where ε₀ is the characteristic strain for fiber alignment and N_max is the total number of multifiber threads in the fibrin network. The population of state 1 of unaligned fibers, p₁ = 1 − N(ε)/N_max, decreases and the population of state 2 of aligned fibers, p₂ = 1 − p₁ = N(ε)/N_max, increases with the strain ε. This results in an increase of the elastic modulus of the fibrin network yN(ε) with ε (y is the average elastic modulus of a multifiber thread) approaching the maximum, yN_max for ε > ε₀ in regime II. This is reflected in the observed increase of the slope dσ_I/dε_I of the experimental stress-strain profiles in dynamic regime I (Fig. 1B, Table 1). The mechanical response in regime I is due to alignment of fibrin fibers and is weakly non-linear, i.e. σ(ε) = yN(ε)ε. This correlates well with the leveling off of the slope dσ_I/dε_I in regime I (Fig. 1B). The elastic modulus approaching the maximum yN_max marks the transition to the linear regime II, in which σ(ε) = yN_maxε (Fig. 1B).

Rupture probability:

The strength of multifiber threads is non-uniform due to differences in their size and length and variation in the strength of inter-fiber crosslinks. The stress is larger at the crack tip (Fig. 3), and so we assumed, for simplicity, equal and local load shearing. Therefore, the failure of multifiber threads is a stochastic process, which can be described by a probability distribution. When the stress in the fibrin network exceeds the critical threshold value σ(ε*), which occurs at the strain threshold ε = ε*, the multifiber threads begin to rupture. Here, ε* marks the transition to regime III of fiber rupture, and the stress reaches the maximum (peak stress). This is correlated with a sharp decay of the slope dσ_III/dε_III to zero for ε* < ε < ε_cr in regime III (Fig. 1B). As multifiber threads break, the crack propagates across the fiber network. At any given value of ε, there are n threads that have already failed and N_max − n threads that have survived, and so the mechanical response in regime III is given by σ(ε) = y(N_max − n)ε = yN_maxε(1 − n/N_max), where s = 1 − n/N_max is the survival probability of individual multifiber threads. In the continuum limit when N_max is large (>100), the discrete probability s can be replaced by its continuous counterpart. Because the network fails only when all multifiber threads ahead of the crack tip have ruptured, the strongest thread at the crack tip determines the rupture transition, and so the statistics of the extremes determines the network failure. For this reason, we use the Weibull distribution to model the survival probability [10]:

$$S=\mathit{\text{exp}}\left[-{\left(\frac{\epsilon }{2\Delta \epsilon }\right)}^m\right]$$ (2)

with the strain-scale parameter 2Δε (roughly equal to the width of stress peak), and the shape parameter m, which accounts for the extent of cooperativity among stretched multifiber threads. Weibull statistics is widely used in probabilistic approaches to fracture mechanics to describe, e.g. the damage evolution in fiber-reinforced composite materials and degradation of fibrous materials [11–14]. Rupture occurs as the first, second, etc. multifiber thread break sequentially under the load, resulting in the remaining threads being exposed to increasing loads and, hence, rupturing more rapidly due to the positive cooperativity between the fibers (m > 1). When m = 1, the rupture transitions in individual threads are not cooperative, i.e. multifiber threads rupture independently (one by one), and the survival probability is given by a simple exponential function, exp(−ε/2Δε). In the linear regime II, s(ε) = 1.

Dynamic force response:

To describe a fibrin network with a crack using the FS model, we need to adjust the total number of structure elements (multifiber threads) N_max. For example, for a sample with α = 20%-crack, the total number of multifiber threads in Eq. (1) is N_max(1 − α), where α = l₀/w is the crack size with l₀ being the crack length and w = 30 mm is the sample width (see Materials and Methods). With the probability of structural damage and the crack size accounted for, we obtain the master equation for the mechanical response of the fibrin network with a single-edge crack σ(ε) in the entire range of mechanical deformation (i.e. in regimes I–III):

$$\sigma (\epsilon )=Y\epsilon \mathit{\text{exp}}\left[-\theta \left(\epsilon -{\epsilon }^{*}\right){\left(\frac{\left(\epsilon -{\epsilon }^{*}\right)}{2\Delta \epsilon }\right)}^m\right]$$ (3)

In Eq. (3), Y = y(ε)(1 − α) is the strain-dependent elastic modulus of the fibrin network, which approaches the maximum value Y_max = yN_max(1 − α) in regime II, and θ(ε) is the Heaviside step function. Because the multifiber threads break only when ε > ε*, in Eq. (3) the survival probability s(ε) is shifted by ε* to the right along the ε – axis. In what follows, we used the FS model to describe the experimental σε – profiles for fibrin networks without crack and with single-edge cracks of size α.

Fluctuating Spring model-based analysis of experimental stress-strain profiles:

We applied the FS model to characterize the dynamic mechanical properties of fibrin networks in regimes I–III. We performed a numerical fit of the experimental stress-strain profiles collected for different values of size of single-edge cracks using the master equation (3), to obtain the FS model parameters (Table II). As before, we divided the experimental stress-strain profiles into three groups for samples with small crack (α < 10%), medium-size crack (10% < α < 20%), and large-size crack (α > 20%), to capture the dependence of parameters of the FS model on the crack size α. Representative experimental profiles of σ vs. ε are directly superposed with the theoretical σε-curves in Fig. 4. Parameters of the FS model are summarized in Table II for samples with no crack (α = 0%) and for the following size ranges for a single-edge crack: α = 7–9%, 11–19%, and 20–35% of the sample width. These parameters are the following: the characteristic strain for fiber alignment ε₀, the network elastic modulus Y_max, the half-width of stress peak Δε, and the cooperativity parameter m. We estimated the strain threshold ε* using the profiles of the slope (dσ/dε vs. ε) of the experimental stress-strain curves (Fig. 1B) as the strain at which the slope dσ/dε starts to decrease to zero. Numerical values of all model parameters obtained for each of all 20 experimental stress-strain profiles are accumulated in Table S2. The theoretically estimated range for the elastic modulus, Y_max = 5–5.7 kPa for all 20 experimental σε-curves (Table II), agrees with the experimental range of the slope in regime II, dσ_II/dε_II = 5.4–6.1 kPa (Table I). The theoretical range of characteristic strain for fiber alignment ε₀ = 6.9–13.8% (Table II) correlates well with the experimental 9.3–16.0%-range for ε_I in regime I (Table I). The theoretical values of the half-width of the stress peak Δε =1.3–6.4% (Table II) show good agreement with the experimental range of Δε =2.3–5.0% in regime III (Table I). These several points of agreement between the experimental quantities and their theoretical estimates validate the FS model.

Table II. Parameters of Fluctuating Spring model of forced deformation of fibrin networks:

Accumulated are the numerical values of the following quantities (average values and standard deviations): characteristic strain for fiber alignment ε₀, elastic modulus for the fibrin network Y_max, the half-width of the stress peak Δε, and the cooperativity parameter m. The values of these parameters are extracted from the numerical fit of theoretical σε-curves (Eq. (3)) to the experimental σε-profiles obtained for fibrin gel with no crack (n = 2), and for fibrin gel samples with crack for different ranges of crack size α (n = 18): 7–9%, 11–19% and 20–35% (Figs. 1 and 4). Also shown are the values of strain threshold ε*, extracted from the experimental σε profiles, and the stress range Δσ obtained from the values of the half-width of the stress peak (Δε) using the formula Δσ = Y_maxΔε (see Eqs. (2) and (3)).

crack size α, %	0 (n=2)	7–9 (n=3)	11–19 (n=6)	20–35 (n=9)
ε0,%	6.9 ± 0.4	13.8 ± 11.8	10.7 ± 9.0	8.0 ± 3.2
Ymax, kPa	5.7 ± 0.2	5.3 ± 0.8	5.5 ± 0.5	5.0 ± 0.5
Δε, %	1.3 ± 0.4	2.8 ± 1.3	6.2 ±3.5	6.4 ± 3.8
m	12.5 ± 0.7	8.3 ± 0.9	4 ± 1.0	3.3 ± 0.9
ε*, %	70.0 ± 9.9	40.9 ± 0.4	34.1 ± 1.9	28.0 ± 2.5
Δσ, Pa	72 ± 22.9	154 ± 79	344±103	334±110

Figure 4.

Dynamics of mechanical deformation and rupture of fibrin networks. Shown are representative experimental stress-strain profiles (σε-curves; black data points) which quantify the mechanical response of the fibrin network without crack α = 0% and with a single-edge crack size α = 7–9% (panel A), α = 11–17% (panel B) and α = 22–33% (panel C). These are directly compared with the theoretical σεcurves (red curves) obtained using the Fluctuating Spring model (Eq. (3)). Numerical values of parameters of the FS model are accumulated in Table 2 (see also Figs. S7–S9 for more examples of fits of theoretical σε-curves to the experimental stress strain profiles).

Of all the model parameters, only the elastic modulus Y_max and the half-width of the stress peak Δε were found to be independent of the crack size α (see Table II), which also agrees with the experimental results for the slope dσ_II/dε_II in regime II (Table I). The other parameters (ε₀ and m) showed a weak dependence on α. The characteristic strain for alignment ε₀ and the cooperativity parameter m decreased with the increasing crack size α, whereas the half-width of stress peak Δε increased with increasing α (Table II; see also Table S2 and Fig. S5), but the latter trend was not statistically significant (p = 0.1961; see Table I). For example, ε₀ decreases from 13.8% for α = 0.07–0.09% to 8.0% for α = 0.20–0.35%, and m decreases from 8.3 for α = 0.07–0.09% to 3.3 for α = 0.20− 0.35% (Table II). This is because in fibrin gel samples with a larger crack, there are fewer initially intact multifiber threads (N_max, see Eq. (1) above), and so they tend to align at lower values of the characteristic strain ε₀ and weakly cooperate (lower m) to sustain the external stress. Analysis of the experimental σε-profiles revealed that ε* decreases with increasing α (Table II). Overall, fibrin gels without cracks are characterized by smaller values of the characteristic strain for fiber alignment ε₀, half-width of the stress peak Δε, and by larger values of the elastic modulus Y_max, strain threshold for rupture ε*, and cooperativity parameter m (Table II).

The results obtained demonstrate that the FS theory captures fine features of the experimental stress-strain profiles, including: the weakly non-linear regime I of elongation of the fibrin network (fiber alignment), linear regime II (further fiber alignment and stretching), and regime III of rupture of the fiber network (fibers’ breakage). Hence, the FS theory can be used as a theoretical framework to quantitate the dynamic mechanical properties of the fibrin networks. Using the results of theoretical modeling of the experimental stress-strain profiles summarized in Table II, we estimated the total number of multifiber threads (N_max) reinforcing stretched fibrin networks. In dynamic regime II, the network can be viewed as a collection of fibrin fiber springs arranged in series (i.e. connected laterally) and in parallel (connected longitudinally). The experimentally measured average stiffness of single 10-μm long fibrin fiber is equal to k_f ≈ 10 pN/nm [15]. Because the initial length of fibrin network is 30 mm, there are ~3000 fibrin fibers (fiber springs) that need to be coupled longitudinally (arranged in series) to span the 30 mm length. A collection of 3000 fiber springs has the stiffness K_st= k_f/3000. The fibrin gel has > 99% water (see Materials and Methods), and so the stiffness of fibrin network K_net (without water) accounts for ~1% of the stiffness of fibrin clot samples. By dividing Y_max ≈ 5.0 kPa for fibrin gel with α = 7–9% crack size (Table II) by 100, by multiplying the obtained value by the cross-sectional area A ≈ 200 mm² (Table S1) and by dividing the value obtained by the initial length 30 mm, we arrive at the stiffness of fibrin network K_net ≈ 330 pN/nm. Treating the network as a collection of N_st 30-mm long strands arranged in parallel, we obtain N_st = K_net/K_st = 10⁵. Finally, by dividing N_st = 10⁵ by 5, which is the average number of fibrin fibers that combine together laterally to form each multifiber thread (see Fig. 3D and 3E), we obtain the total number of multifiber threads, N_max = N_st/5 ≈ 20,000.

Crack size dependence of mechanical strength and deformability of fibrin networks:

We applied the FS theory to probe the dependence on crack size α of the limits of mechanical strength of fibrin networks (peak stress σ_cr) and extensibility of fibrin networks (critical strain ε_cr). In the rupture regime III, when ε > ε*, the master equation for σ(ε) (Eq. (3)) becomes

$$\sigma (\epsilon )=Y_{\mathit{\text{max}}}\mathit{\epsilon }\text{exp}\left[-{\left(\frac{\left(\epsilon -{\epsilon }^{*}\right)}{2\Delta \epsilon }\right)}^m\right]$$ (4)

By taking the derivative of σ(ε) with respect to ε in Eq. (4) and by setting it equal to zero, we obtain the equation for the critical strain:

$$\frac{m}{2\Delta \epsilon }{\left(\frac{\left({\epsilon }_{cr}-{\epsilon }^{*}\right)}{2\Delta \epsilon }\right)}^{m-1}{\epsilon }_{cr}=1$$ (5)

Eq. (5) cannot be solved for ε_cr in closed form for arbitrary m, and so we solved Eq. (5) numerically. The values of ε_cr were then substituted into Eq. (4) to obtain the values of σ_cr.

The results of calculation of σ_cr and ε_cr are compared in Table III with the experimental values of these quantities (from Table I). Overall, fibrin gels without cracks are characterized by larger values of the average critical strain ε_cr and the average critical stress σ_cr (Table III). Theoretical predictions for σ_cr and ε_cr agree very well with the experimental values, namely that both σ_cr and ε_cr decrease with the increasing α. For example, ε_cr and σ_cr decrease from 72% and 4.1 kPa for samples with no crack to 34.2% and 1.5 kPa for larger cracks (α = 20–35%), respectively (Table III). This is because fibrin networks with larger cracks are reinforced by a smaller number of structural elements (multifiber threads) N_max, which rupture at lower σ_cr and, hence, lower ε_cr. That ε_cr and σ_cr are directly correlated (r = 0.82, p < 0.0001) is not unexpected, because, in general, larger (smaller) values of strain correspond to higher (lower) values of stress. We also estimated the critical stress per multifiber thread σ_cr,thr by dividing the critical stress for the entire fibrin network σ_cr by the total number of multifiber threads N_max; σ_cr,thr was found to decrease with increasing α from 205 mPa for samples with no crack to 106 mPa for the larger cracks (α = 20–35%, see Table III). The results obtained point to an important role of mechanical coupling among fibrin fibers in the rupture resistance of a clot.

Table III. Limits of mechanical strength and thermodynamics of deformation and rupture of fibrin networks.

Shown are the estimated values of the average critical stress σ_cr and the average critical strain ε_cr for fibrin networks with no crack and with crack for different ranges of crack size obtained using Eq. (5), which are compared with the same quantities extracted from the stress-strain-spectra (separated by a slash; see Table I). Estimated values of the average critical stress per single multifiber thread (σ_cr.thr) are shown in parentheses. Also shown are the thermodynamic state functions: the free energy changes in regime I (ΔG_I), and regimes II and III (ΔG_II,II), and the total free energy change ΔG_tot. The theoretical values of ε_cr, σ_cr, ΔG_I, ΔG_II,II and ΔG_tot are calculated using Eqs. (4), (5), (S8), (S9) and (S10), respectively, and the values of parameters of the Fluctuating Spring model from Table II for samples without crack (n = 2) and with single-edge crack for three ranges of crack size α (n = 18): 7–9%, 11–19% and 20–35%. The values of ΔG_tot, obtained by performing the numerical integration of experimental σε-curves (Figs. 4 and S8–S10), are separated by a slash.

parameters	crack size α, %
	0 (n = 2)	7–9 (n = 3)	11–19 (n = 6)	20–35 (n = 9)
ε cr	72%/73%	44 %/45 %	39%/40%	33% /34%
σ cr	4.1 kPa /4.1 kPa (205 mPa)	3.1 kPa /2.2 kPa (119 mPa)	2.5 kPa /2.0 kPa (117 mPa)	1.6 kPa /1.5 kPa (106 mPa)
ΔGI	0.04 mJ	0.2 mJ	0.1 mJ	0.03 mJ
ΔGII,III	8.7 mJ	2.4 mJ	1.9 mJ	1.1 mJ
ΔGtot	8.74 mJ /8.6 mJ	2.6 mJ /2.5 mJ	2.0 mJ /1.8 mJ	1.13 mJ /1.1 mJ

Statistics of mechanical strength and deformability of fibrin networks with cracks:

The information about the average mechanical strength and average deformability of fibrin networks is contained in σ_cr and ε_cr. Yet, the stress-strain curves show large variability in their mechanical response (Fig. 4; see also Figs. S2 and S7–S9). One piece of evidence pointing to high stochasticity of rupture of the fibrin network is an observed large variability of rupture strains, especially for fibrin networks with larger cracks. This is reflected in the values of half-width of the stress peak Δε, which increase with increasing α (Table II). This stochasticity of rupture can also be gleaned, e.g., by analyzing the range of values of stress for rupture Δσ = Y_maxΔε. Table II shows that Δσ increases with increasing α due to the increasing in Δε and that the standard deviations of Δσ are comparable to the averages, i.e. Δσ =72±22.9 Pa for samples with no crack vs. Δσ =334±110 Pa for α =20–35% crack (Table II). Hence, the average quantities are not sufficient to describe the statistics of critical stresses and critical strains.

Therefore, we used the FS model to derive the closed-form expressions for the probability distribution of critical stresses (see SI for derivation),

$$p(\sigma )=\{\begin{array}{c}0,\sigma \le {\sigma }^{*}\\ \frac{m}{2\Delta \sigma }{\left(\frac{\sigma -{\sigma }^{*}}{2\Delta \sigma }\right)}^{m-1}\text{exp}\left[-{\left(\frac{\sigma -{\sigma }^{*}}{2\Delta \sigma }\right)}^m\right],\sigma >{\sigma }^{*}\end{array}$$ (6)

where σ* = σ(ε*) = Y_maxε* is the stress threshold, and the probability distribution of critical strains,

$$p(\epsilon )=\{\begin{array}{c}0,\epsilon \le {\epsilon }^{*}\\ \frac{m}{2\Delta \epsilon }{\left(\frac{\epsilon -{\epsilon }^{*}}{2\Delta \epsilon }\right)}^{m-1}\text{exp}\left[-{\left(\frac{\epsilon -{\epsilon }^{*}}{2\Delta \epsilon }\right)}^m\right],\epsilon >{\epsilon }^{*}\end{array}$$ (7)

Using the experimental σε-profiles, we constructed the histograms of critical stresses and critical strains. By dividing the critical stress for rupture by the total number of multifiber threads across the clot (1 − α)N_max, we obtained the histogram of critical stresses per thread, which is compared in Fig. 5 with the theoretical curve of p(σ) reconstructed with Eq. (6) and parameters of the FS model (Table II). The histogram of critical strains is compared with the theoretical curve of p(ε) obtained with Eq. (7) (see the inset in Fig. 5). The curves of p(σ) and p(ε) closely approximate the experimental histograms; both p(σ) and p(ε) are broad and have long tails, which implies strong stochasticity of the mechanical response of deformed fibrin networks (Fig. 5). The large standard deviation of 0.05 Pa for p(σ) is quite comparable with the 0.12-Pa average critical stress per multifiber thread and the ~0.10-Pa most probable critical stress (the maximum of p(σ)). We obtained similar results for the distribution p(ε). To summarize, the FS model makes it possible to gather information about the entire distributions of critical deformations and peak stresses by using the experimental stress-strain curves.

Figure 5.

Statistics of mechanical strength and deformability of fibrin networks. The experimental histogram-based estimates and theoretical curves of the probability distribution of critical stress values for rupture of the fibrin network per multifiber thread p(σ), and the probability distribution of critical strains for rupture of the fibrin network p(ε) (the inset). The histograms and theoretical curves of p(σ) and p(ε) are displayed for fibrin networks with single edge crack in the α = 7–35% range of crack size. The histograms were obtained by combining n = 18 values of critical forces from 18 experimental stress-strain profiles (see Materials and Methods). The bin size selection was performed as described previously [39]. Theoretical curves of p(σ) and p(ε) were obtained using Eqs. (7) and Eq. (6), respectively, and values of parameters of the FS model from Table 2.

Thermodynamics of mechanical deformation and rupture of fibrin networks:

The area under the stress-strain profile is equal to the total work performed to deform the fibrin network, i.e. $w(\epsilon )=V{\int }_0^{\epsilon }\sigma \left({\epsilon }^{\prime }\right)d{\epsilon }^{\prime }$ (here ε′ denotes the variable of integration), which is equal to the equilibrium free energy change, i.e. w(ε) = ΔG(ε). Here, V = V₀(1 − α) is the volume of the sample fibrin network with a single-edged crack of size α and V₀ = 5,850 mm³ is the volume of the sample without a crack (30 mm × 30 mm × 6.5 mm; see Materials and Methods). We used the experimental stress-strain profiles for fibrin gel samples with cracks α = 0–35% (Fig. 4) to estimate the free energy changes for mechanical deformation and rupture of the fibrin network. In regime I (ε < ε₀), fibrin fibers align but not stretch, which is mainly an entropic process. In regime II (ε₀ < ε < ε*), further alignment and stretching of fibrin fibers occurs. In regime III (ε > ε*), the irreversible stretching of fibrin fibers ahead of the crack tip results in their eventual rupture. Hence, the dynamic mechanical regimes I–III involve the enthalpic and entropic contributions due to alignment and stretching of fibrin fibers. This is in addition to free energy change associate with the water expulsion from the fibrin gel in regimes I–III.

We used the FS model to obtain the analytical expressions for the free energy change in regime I, ΔG_I, in regimes II and III, ΔG_II,III, and for the total free energy change in regimes I–III, ΔG_tot = ΔG_II,III + ΔG_I, which are given, respectively, by Eqs. (S8), (S9), and (S10) in the SI. We used these equations and parameters of the FS model (from Table II) to calculate the values of ΔG_I, ΔG_II,II and ΔG_tot accumulated in Table III. ΔG_I and ΔG_II,II come to 0.03–0.2 mJ and 1.1–8.7 mJ, respectively, which results in 1.1–8.74-mJ values for ΔG_tot (Table III). We see that the theoretical values of ΔG_tot agree very well with the experimental estimates obtained by numerical integration of the stress-strain profiles (Table III). Overall, fibrin gels without cracks are characterized by larger values of ΔG_I, ΔG_II,II, and ΔG_tot (Table III). All three energy functions decrease with increasing α.

Discussion

Fibrin is a unique biomaterial and a major component and mechanical determinant of hemostatic blood clots and obstructive thrombi. The fibrin clot must be able to withstand a variety of hydrodynamic forces from blood flow, contracting platelets, and extravascular muscle contractions. In addition to the well-known important roles played by fibrin in blood clots, it is also a versatile biomaterial with exceptional and tunable mechanical properties that have been intensely studied over the past decades [16–18]. While most of the studies in fibrin biomechanics were focused on viscoelasticity and deformability of intact fibrin gels, the mechanisms of fibrin mechanical disintegration or rupture remained largely unknown, despite their tremendous theoretical as well as practical importance. Although fracture of materials has long been critically important for many technologies, the fracture of hydrogels is a nascent research topic [19,20], so its application to fracture of fibrin is novel and there are only a few studies on this problem [9,21–23]. Theoretically, the forced rupture of fibrin is a part of the fracture mechanics of hydrogels, but the structural and physical properties of fibrin networks makes them unique. The biophysics of fracture of fibrin gels involves thermodynamic aspects as well as structural mechanisms of molecular unfolding and breakage of fibrin fibers followed by the release of strain energy (relaxation) or the source of energy required to fracture the biomaterial. This is in addition to dynamic structural alterations in a fibrin gel associated with water expulsion and hydrophobic interactions, which accompanies structural changes in stretched individual fibrin fibers.

While the viscoelastic properties of fibrin have been well studied [7], almost nothing is known about the fracture of blood clots. An exceptionally important clinical aspect of fibrin rupture is the disintegration of thrombi in the blood stream, which results in the common and dangerous medical condition called thrombotic embolism [24]. Intravascular blood clots experience multifarious mechanical forces that can lead to their rupture and blockage of downstream vessels with pieces called thrombotic emboli. There is growing evidence pointing to the high clinical relevance of fibrin mechanics in relation to thrombotic embolization. When fibrin polymerization was blocked in microfluidic clotting studies of whole blood perfused over a collagen surface, the growing thrombus embolized at very low shear rates, in contrast to normal clotting [25]. The platelet-driven contraction of clots in patients with pulmonary embolism was found to be significantly impaired compared to that of isolated venous thrombosis, suggesting that mechanical compaction of thrombi reduces the risk of embolization [26]. Stiffness of the fibrin scaffold of occlusive thrombi is a major determinant for the effectiveness of their mechanical damage and removal to restore the impaired blood flow [27]. These and other findings strongly indicate that the structure and mechanics of blood clots and thrombi affect the likelihood of their rupture, while the mechanisms of mechanical rupture of thrombi has not even been considered. The mechanical stability of thrombi and formation of emboli are associated strongly with local and systemic inflammation that affects the composition of thrombi, including incorporation of neutrophil extracellular traps [28,29]. Therefore, deciphering the fundamental mechanisms of fibrin rupture is necessary for understanding thrombotic embolization, which can inform development of new approaches to predict and prevent this life-threatening condition.

From the practical standpoint, the ability of fibrin gels to break determines the mechanical stability of fibrin-based engineered tissues, grafts, and hemostatic sealants widely used in surgery [30–32]. In this work, we were able 1) to obtain the mechanical characteristics, 2) to resolve the structural mechanisms, and 3) to estimate the thermodynamic state functions associated with forced deformation and rupture of fibrin gels. By directly coupling the experimental characterization of the mechanical deformation and rupture of physiologically relevant fibrin gels with a simple macroscopic model of the fibrin network, we have provided qualitative as well as quantitative characteristics of fibrin rupture. These efforts have resulted in a better understanding of the structural biomechanics underlying the mechanical (in)stability of blood clots and thrombi.

Experimental advancements:

Our experimental approach is based on the controlled forced failure of cracked fibrin gels made of human blood plasma that recapitulate natural blood clots and artificial biomaterials. The experimental model of pulling on a cracked specimen has been widely used in fracture mechanics to quantify the fracture toughness as well as to determine mechanisms underlying the rupture resistance of various biomaterials, including fibrin hydrogels [9,19,33,34]. Here, as a methodological and conceptual development, the stretching and rupture of the fibrin gels were followed simultaneously with accurate stress-strain measurements combined with high-definition 3D macroscopic visual recordings of the crack propagation and electron microscope snapshots of the fibrin ultrastructure in different parts of cracked and un-cracked clots in the longitudinal and transverse directions at various strains. In particular, our study focuses on analysis of the portion of stress-strain curves following the maximum stress for rupture, which corresponds to the maximum strain for rupture (regime III in Figure 1), which contains information about the thermodynamics and structural mechanisms of breakage of the fibrin hydrogel. Here, we described and analyzed the structure of unstrained versus strained fibrin networks using high-resolution scanning and transmission electron microscopy. These morphological techniques clearly demonstrated that fibrin fibers exist in two mechanical states corresponding to an isotropic network and the densified, aligned fibers. In addition to the alignment of fibrin fibers in the direction of applied tensile force, we were able for the first time to demonstrate the physical fiber rupture along the edge of the crack. As a totally novel and important finding, transmission electron micrographs revealed tension-induced lateral fiber bundling and formation of multifiber threads under the influence of applied force.

Theoretical development:

We developed a new theory based on the phenomenological Fluctuating Spring model, which can be used to analyze the experimental curves for the macrostress as a function of the macrostrain, in order to quantify the macroscopic material behavior of biological fiber networks without cracks and with cracks or arbitrary size in all dynamic regimes of their mechanical deformation, with a particular focus of fibrin fiber networks. The longitudinal mechanical response of the fibrin network is non-linear (Figs. 1 and 4; see also Figs. S2, S7, S8, and S9). The origin of this nonlinearity is geometric (straightening of multifiber threads; Fig. 2) and is also due to fiber mechanics and behavior of the crosslinks. Although the constitutive non-linear relation for a single-fiber component is known [15,35,36], the physical properties of the multifiber system (fibrin network) is not the sum of properties of single-fiber components, and so the dynamics of deformation and damage of the multifiber system is complex. This is in addition to the strong mechanical cooperativity owing to the presence of inter-fiber crosslinks, which reinforce the fibrin network (Fig. 2). Also, the stress and strain fields in the fibrin network with cracks are expected to vary substantially from one point to another. The strength of multifiber threads is non-uniform due to differences in their size and length, variation in the strength of inter-fiber crosslinks, and so the evolution of progressive rupture of multifiber threads is non-trivial. The mechanism of load transferring from broken to intact multifiber threads is not known, but the stress is expected to be larger at the crack tip (Fig. 3), and so we assumed, for simplicity, equal and local load shearing. Therefore, the failure of multifiber threads is a stochastic process, and so we described the evolution of progressive rupture of multifiber threads by a probability distribution. The FS model treats the fibrin network as a material in which the bending mode (fiber alignment), axial deformation mode (fiber stretching), and failure are connected in series. The inter-fiber crosslinks are treated as connectors capable of transmitting tension when tension does not exceed the critical threshold. The softer mode, i.e. alignment in regime I, stretching in regime II, and failure in regime III, defines the observed macroscopic network behavior.

We applied the FS model to provide an analytically tractable mathematical framework for the interpretation of the experimental stress-strain profiles for fibrin networks with and without single-edge cracks of varying size. That is, the FS theory uses the experimental stress-strain profiles (Fig. 4) as the input to gather information not only about the average mechanical properties of a protein network (Table II), but also about the entire distribution of these properties, and information about the energetics of network deformation and rupture (Fig. 5). We have estimated the following quantities: 1) the characteristic strain for fiber alignment ε₀; ii) the elastic modulus for the fibrin network Y_max; iii) the range of strain in which network rupture sets in (half-width of the stress peak) Δε; and iii) the mechanical coupling (cooperativity parameter) m; (Table II). Of these parameters, ε₀, Y_max, and Δε can be determined experimentally, whereas m is assumed. The FS theory also provides testable predictions for the following quantities: v) the average critical stress σ_cr and the average critical strain ε_cr for network rupture (Eqs. (4) and (5)); and vi) the distributions of critical stresses p(σ) and critical strains p(ε) for network rupture (Eqs. (6) and (7)). Furthermore, the FS theory enables one to calculate the following thermodynamic state functions: vii) the free-energy change for alignment of fibrin fibers ΔG_I (entropy-driven process; Eq. (S8)); viii) the free-energy change for stretching of fibrin fibers ΔG_II,II (enthalpy-driven process; Eq. (S9)); and ix) the total free-energy change ΔG_tot (Eq. (S10)). Importantly, the distributions p(σ) and p(ε) capture the structural and functional heterogeneity of individual fibrin fibers and their multifiber threads that form in the deformed network. The thermodynamic state functions ΔG_I, ΔG_II,III, and ΔG_tot completely characterize the energetics of mechanical deformation and rupture of fibrin networks. The experimental qualitative and quantitative characterization in combination with theoretical analysis, made possible by the application of the FS theory, have led to the biomechanical, structural, and thermodynamic insights illuminating the mechanisms of rupture of cracked fibrin gels.

Rupture of fibrin gel is a complex multiphase process:

We found that the mechanical response of fibrin gels subjected to ramping stress is characterized by three dynamic mechanical regimes, each reflecting distinctly different strain-dependent biomechanical mechanisms of deformation. In particular, regime III provides information about the rupture of the fibrin network. Based on theoretical analysis of the stress-strain curves obtained for various values of crack size, the following quantitative information about the mechanical properties has been gathered:

1. Cracks promote fibrin clot rupture proportionately to their size. We found that the limits of mechanical strength σ_cr and deformability ε_cr, and the strain threshold for fiber rupture ε* all decrease with increasing crack size α (Table III). For example, in the presence of a crack, the stress decreases by ~3-fold in regimes I and II (Figs. 1 and 2). That the presence of a crack or defect significantly weakens fibrin clots can help inform the mechanisms of thrombotic embolization and can be used in the design of fibrin biomaterials. That σ_cr and ε_cr decrease with increasing α can be understood by considering Eqs. (5) for σ_cr in the limit of zero cooperativity (m = 1). In this case, the critical stress is given by the formula σ_cr = Y_maxε_cr = yN_max(1 − α)ε_cr, which shows that while larger ε_cr means higher σ_cr, larger α corresponds to lower σ_cr. Regimes II and III are significantly influenced by crack size α (Figs. 1 and 2). This effect is driven by the fact that there are fewer structure elements in a network with larger crack N_max(1 − α), i.e. 13,000 multifiber threads for α = 35% (sample with crack) vs. 20,000 multifiber threads for α = 0 (sample with no crack), that couple together to sustain the external stress. Hence, a network with a larger crack ruptures at a lower stress and smaller strain compared to a network with a smaller crack.

2. Cracks Render Rupture of Fibrin Networks Stochastic. The stress-strain curves show different shapes and large variations in the scales of strains and stresses, especially for fibrin networks with larger cracks (Fig. 4 and Table II; see also Fig. S1). These features are also reflected in the broad and long-tailed probability distributions for critical strains p(ε) and critical stresses p(σ) (Fig. 5), which show that the statistics of strength and deformability are characterized by large standard deviations. The relative fluctuations of the critical stress given by the ratio of the average stress fluctuation Δσ_cr and the average stress σ_cr, Δσ_cr/σ_cr, are expected to decrease with the system size N_max = 13,000–20,000 when the multifiber threads are decoupled (m = 1); yet, our results show that the fluctuations and the average quantities are comparable, i.e. Δσ_cr~σ_cr (Fig. 5). Therefore, the presence of cracks and structural defects in a fibrin network broadens the range of strains and the range of stresses within which the rupture of fibrin network occurs, thus rendering the network rupture stochastic.

3. Coupled fibrin fibers reinforce cracked fibrin networks. In the FS model, the cooperativity parameter m takes into account the mechanical coupling of individual fibrin fibers, which links them through the branch points or other inter-fiber contacts. To better understand this phenomenon, we calculated the σε-curves for three representative networks formed by dynamically coupled fibrin fibers with the single-edge crack of size α = 9% (m = 8.5), 15% (m = 3.0) and 30% (m = 2.5) and for three hypothetical networks with the same size of single-edge crack formed by decoupled fibrin fibers (m = 1). The larger m the stronger the coupling among the multifiber threads. For example, the values of m = 3.0 and 1.0 would correspond to two networks of fibrin fibers connected by few branch points and no branch points, respectively. The theoretical σε-curves are compared in Fig. 6 (see the inset), which shows that the networks reinforced by coupled fibrin fibers are characterized by larger values of the critical strain and the critical stress. For a fibrin network with α =15% and m = 3, σ_cr = 1.75 kPa and ε_cr = 40.6% as compared to σ_cr = 1.55 kPa and ε_cr = 36% for a hypothetical network with m = 1. This is a critical stress difference of 0.2 kPa and the critical strain difference of 4.6%. We see that mechanical cooperativity due to the presence of branch points and direct criss-crossing or oblique inter-fiber contacts [37] plays important role in fibrin biomechanics. Therefore, mechanisms of connectivity between the fibrin fibers extends the limits of strength and deformability of fibrin networks, and thus, prolongs the lifetime of cracked fibrin networks. This might be a universal mechanism of stabilization of fibrin fibers with structural defects.

Figure 6.

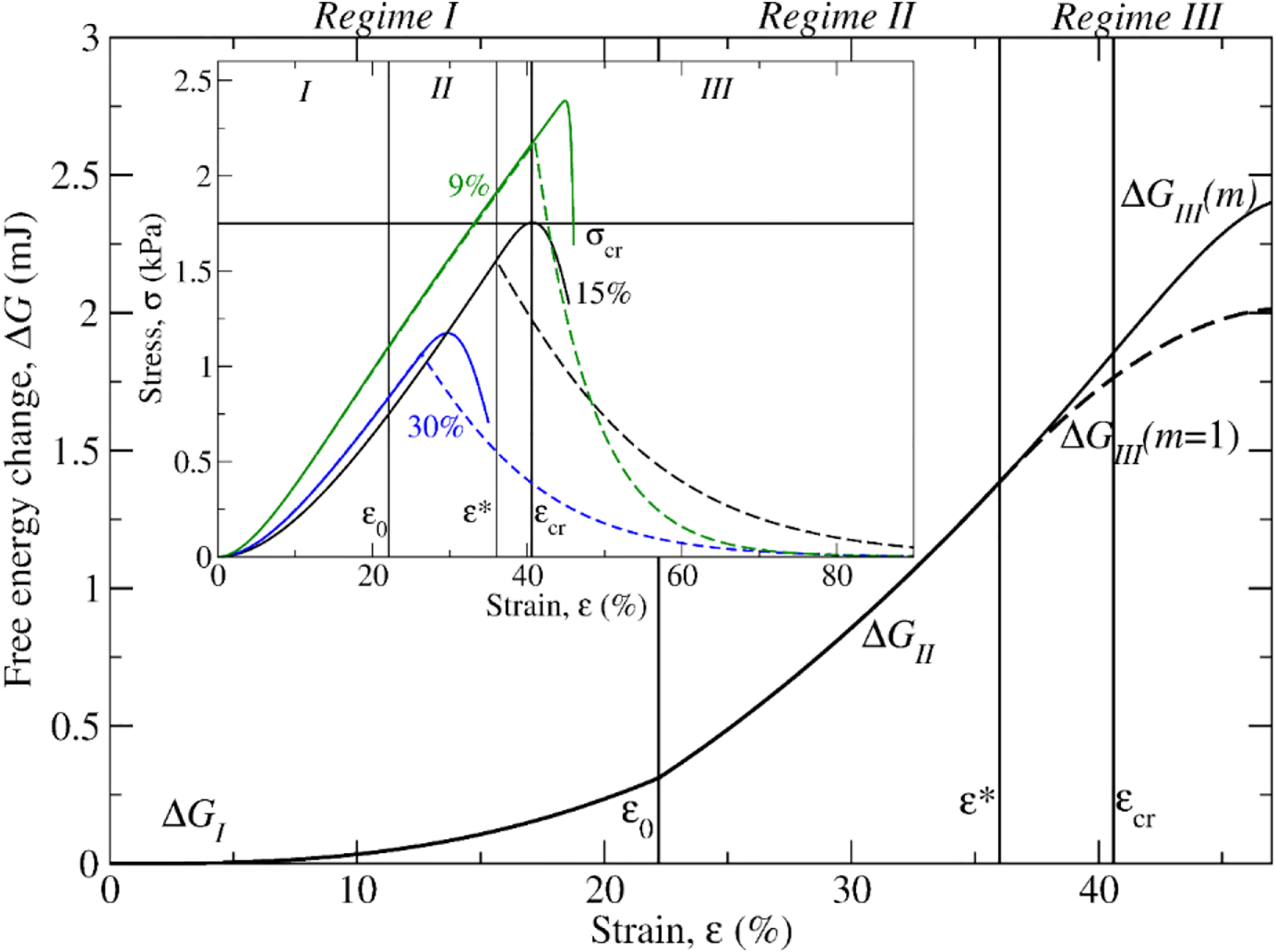
Influence of mechanical cooperativity on mechanics and thermodynamics of deformation and rupture of fibrin networks. Compared are the theoretical profiles of the free energy change ΔG as a function of strain ε for the mechanical deformation (regimes I and II) and rupture (regime III) of the fibrin network reinforced by the mechanically coupled fibrin fibers with the cooperativity parameter m = 3.0 and with a single-edge crack of size α = 15% (solid curve), and with the hypothetical network formed by uncoupled fibrin fibers (m = 1.0) but with the same α = 15% crack size (dashed curve: see Table S2). Compared in the inset are the σε-curves for three different fibrin networks reinforced by the dynamically coupled fibrin fibers with the single-edge crack of size α = 9% (m = 8.5; solid green curve), 15% (m = 3.0; solid black curve) and 30% (m = 2.5; solid blue curve) and the σε-curves for the hypothetical networks formed by uncoupled fibrin fibers but with the same size of single-edge crack α = 9% (m = 1; dashed green curve), 15% (m = 1; dashed black curve) and 30% (m = 1; dashed blue curve).

This newly revealed phenomenon of inter-fiber cooperativity that leads to formation of multifiber threads and increased rupture resistance of fibrin networks may have important physiological implications. It is known that blood clots and thrombi undergo platelet-driven contraction, resulting in volume shrinkage and reduced obstructiveness of thrombotic masses. One of the main structural consequences of contraction is compaction of a clot, redistribution of the fibrin to the surface, and densification of fibrin networks, which implies stronger inter-fiber interactions such as fiber criss-crossing. This is a possible new mechanism that imparts contracted blood clots with increased mechanical stability and higher resistance to rupture. In agreement with this proposal, there is a direct correlation of impaired contractility of blood clots and a higher incidence of thrombotic embolization in patients with deep venous thrombosis [26].

Structural mechanisms of fibrin rupture:

Our detailed analysis of the structural changes of strained fiber networks have helped us to resolve the ultrastructural underpinnings of the mechanisms of tensile deformation and rupture of fiber networks. Direct comparison of the electron micrographs of strained versus unstrained samples revealed the following structural alterations: 1) the initial weakly non-linear dependence of the stress σ on the strain ε in a fiber network at low strain (ε < 10%) is due to alignment of fibrin fibers along the direction of applied force (Fig. 2A, B, D); 2) the subsequent fibrin network extension for 10–30% strain is due to further alignment and stretching of fibrin fibers that leads to network densification and fiber unfolding and bundling (Fig. 2C, F); and 3) the force-induced rupture of the fibrin network and crack advancement across the clot is due to irreversible breakage of individual fibrin fibers (Fig. 3). The analysis of the ultrastructure of fibrin provided the foundation for the FS model, as it revealed the transition from an unaligned state to an aligned state. Our results show that the initial macroscopic elongation of the fibrin gels does occur due to microscopic alignment of the individual fibers. When the strain exceeds the limits of fibrin extensibility of multifiber threads, they begin to rupture. In effect, we observed this breakage in the proximity of the crack tip (Fig. 3). Fibrin fibers form a continuous space filling network that is under tension with no fiber ends. Thus, the presence of newly formed breaks in the fibrin network beyond the initial crack length confirm the breakage of individual fibrin fibers (Figure 3). These results are further confirmed by the presence of fiber ends in the transmission electron microscopy images of stretched fibrin networks that were formed in the absence of a crack (Figure 2).

Thermodynamics of deformation and rupture of fibrin networks:

The free energy changes for all fibrin networks were found to be large and positive (1.2–2.6 mJ), because it takes energy to deform a network, expel water from the network, and rupture fibrin fibers. The positivity of free energy changes is expected for a non-spontaneous (i.e. driven) process (Table III) based on the second law of thermodynamics. Interestingly, the free energy changes in the three dynamic mechanical regimes I and II–III, ΔG_I and ΔG_II,III, and the total free energy change ΔG_tot decrease with the crack size α, implying that the presence of cracks in a fibrin network makes the network rupture more spontaneous. The analytical expressions for ΔG_I, ΔG_II,III, and ΔG_tot presented in SI show that these thermodynamic state functions are in fact negatively correlated with the crack size α (see the pre-factor V₀(1 − α) in Eqs. (S5)–(S7)).

To quantify the influence of mechanical cooperativity on the thermodynamics of deformation and rupture of the fibrin network, we compared the free energy changes ΔG for fibrin networks formed by coupled versus decoupled fibrin fibers. As an example, we compared the profiles of ΔG for a representative network formed by coupled fibers with a single-edge crack of size α = 15% and m = 3.0 and a hypothetical network with the same crack formed by decoupled fibrin fibers with m = 1. The profiles of ΔG for these networks calculated with Eqs. (S8)–(S10) are directly superposed in Fig. 6, which shows that while ΔG in regimes I and II are identical for the networks with m = 3.0 versus m = 1, there is a substantial difference between the profiles of ΔG in regime III. Here, ΔG = 0.46 mJ for a network with m = 3 (network with branch points) versus ΔG = 0.36 mJ for a network with m = 1 (uncoupled free fibers), which makes up the large ΔG_exc = 0.1-mJ energy difference. This difference is the excess energy ΔG_exc (Eq. (S11) in SI) required to rupture the network with connected fibers compared to the network formed by free fibers. Hence, it takes more energy to disrupt the network of interconnected mechanically coupled fibrin fibers.

It has been shown in our previous study [38] that in addition to the large extensibility of fibrin clots, fibrin gels display a dramatic decrease in volume that accompanies fibrin stretching, due mainly to water expulsion followed by multiscale structural rearrangements spanning 6 orders of magnitude, from the mesoscale down to fiber bundling and to molecular unfolding in fibrin molecules. We used the FS model to estimate the free energy change associated with the expulsion of water from the fibrin gel. The free energy change per single fibrin fiber of initial ~10-μm length and ~100–200-nm diameter ΔG_fib estimated based on the experimental stress-strain curve for single fiber [15], comes to ΔG_fib ≈ 10⁻¹² J. The total number of 10-μm long fibrin fibers in a fibrin network of volume V₀ = 5850 mm³ used in this work is N_f ≈ 3 × 10⁸. By multiplying together ΔG_fib and N_f, we obtain the total free energy change associated with the alignment and stretching of the entire fibrin network without water ΔG_net = 0.3 mJ. The free energy change associated with the water expulsion ΔG_wat is the difference between the total free energy change for the fibrin gel (water plus fibrin network) ΔG_tot (from Table III) and the free energy change for the fibrin network ΔG_net, i.e. ΔG_wat = ΔG_tot − ΔG_net = (1100–2500) μJ – 300 μJ = (800–2200) μJ. Hence, the overwhelming ~75–90% of this energy comes from expulsion of water and corresponding structural changes, including potential rearrangements of the protein hydration layer in the fibrin network. By dividing ΔG_wat by the volume of an intact fibrin gel sample V₀, we obtain the range of energy per unit volume, i.e. (800–2200) μJ /5850 mm³ ≈ (0.1–0.4) μJ/mm³.

Conclusions

Using a combination of experimental and theoretical approaches, we explored the structural biomechanics and thermodynamics of the rupture of blood clots. Because fibrin is the main mechanical determinant of blood clots and intravascular thrombi, macroscopic clots made of human blood plasma were analyzed without or with linear incisions (cracks) of varying length at an edge. The samples were stretched in the direction perpendicular to the cracks followed by tracking the stress-strain curves and electron microscopy to watch the ultrastructural changes at the crack tip and other parts of a clot. The stress-strain profiles were analyzed with a new theory, which is based on the Fluctuating Spring model that describes a fibrin network as a collection of coupled fibrin fibers undergoing stress-induced alignment, stretching, and rupture.

From the experimental data and theoretical analysis, important information was gleaned regarding the dynamic mechanical behavior and thermodynamic properties of fibrin gels preceding and during their force-induced rupture. The critical stresses and critical strains decreased with the increasing crack size. The larger cracks were associated with larger variability of the critical stresses and critical strains, thus reflecting the stochastic nature of rupture events associated with the breakage of individual fibers. The free energy changes for rupture reached 1.1–8.6 mJ and were dominated by the energy contribution associated with the expulsion of water from the fibrin gel, with the energy changes for stretching of fibrin fibers playing a minor role. The rupture resistance of clots was found to be enhanced by mechanical cooperativity among individual fibrin fibers, which has important physiological implications related to natural contraction or compaction of blood clots. These important processes determine the mechanical stability and resistance of fibrin clots to thrombotic embolization.

The results obtained elucidate precise structural and thermodynamic mechanisms of the rupture of blood clots and thrombi that have fundamental importance for fracture mechanics of hydrogels and that provides a basis for understanding thrombotic embolization. The Fluctuating Spring model can be used to characterize the dynamics of mechanical deformation of other protein networks with cracks and to interpret the stress-strain profiles available from mechanical testing experiments on biological hydrogels.

Statement of significance.

Fibrin, a naturally occurring biomaterial, is the major determinant of mechanical stability and integrity of blood clots and obstructive thrombi. We tested mechanically fibrin gels with single-edge cracks and followed ultrastructural alterations of the fibrin network. Rupture of fibrin gel involves initial alignment and elastic stretching of fibers followed by their eventual rupture for deformations reaching the critical level. To interpret the stress-strain curves, we developed Fluctuating Spring model, which showed that cracks render rupture of fibrin networks more spontaneous; yet, coupled fibrin fibers reinforce cracked fibrin networks. The results obtained provide fundamental understanding of blood clot breakage that underlies thrombotic embolization. Fluctuating Spring model can be applied to other protein networks with cracks and to interpret the stress-strain profiles.